Evaluation of Energy Price Liberalization in Electricity Industry: A Data-Driven Study on Energy Economics
Abstract
:1. Introduction
1.1. Research Challenge
1.2. Literature Review
2. Proposed Methodology and Mathematical Modeling
2.1. Research Taxonomy
- Step 1: Defining the specification of the variables, for more details see Table 1;
- Step 3: Determining optimal lag length with three criteria, in which the optimal lag is set two in this work, see Table 4;
- Step 4: Estimating the pre-defined variables in the VAR model that calculates and analyze how variables affect each other, more details can be found in Table 5;
- Step 5: Introducing a new price increase (or impulse), based on the real-life policy made in Iran to remove considerable energy-related subsides, for investigating its impacts on the energy intensity and the end-user reactions. Analyzing impulsive response function (IRF) trend to obtain policy viewpoints, which resulted in Figure 1, Figure 2, Figure 3 and Figure 4;
- Step 7: Normalization of the co-integrated vector to interpret estimation results using Equation (28) and develop a long-term relationship, results in Table 8;
- Step 8: Estimating VECM to discover the variables convergence, due to the VECM coefficient set 0.15, more details can be seen in Table 9;
2.2. Vector Autoregressive (VAR) Model
- Etiological can conduct economies with times series, this method has been used in macroeconomics in developing countries.
- Examining economic shocks to evaluate shocks is another considerable advantage. Since every economy can be affected differently, due to these shocks.
- The third benefit is the variance variable during the period related to the second application of this method. It means how each variable can influence on the other variables.
- In the VAR method used, all the variables are considered intrinsic.
2.3. Determining the Optimal Lag
2.4. Impulsive Response Function (IRF)
2.5. Johansen Juselius Method
- (1)
- making VAR coefficient matrix, which is known as A matrix;
- (2)
- characteristic root matrix, known as λ, resulted from the characteristic equation defined as:
- (3)
- each characteristic vector has calculated from the characteristic root matrix, given as:
- (4)
- the R matrix has formed and the inverse matrix is calculated, then the row that associated with the non-unit root is represented as a converge vector.The mathematical form of the vector regression model is:where Y is a vector consisting of some variables within the existing model, is delay lag, A is an intercept of vector component of the equation, and E is a vector of random error elements which are normally distributed with constant mean and zero variance.
3. Data Analysis and Discussion
3.1. Statistical Specification Variables
| Variable | Unit | Minimum | Maximum | Average | Standard Deviation | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
| Energy Intensity | kJ/$ | 6.1 × 10−1 | 1.91 × 100 | 9.9 × 10−1 | 2.7 × 10−1 | 1.7 × 100 | 6.47 × 100 |
| GDP | $ | 4.78 × 104 | 3.59 × 105 | 1.56 × 105 | 9.93 × 104 | 6.7 × 10−1 | 2.05 × 100 |
| Labor | − | 6.1 × 102 | 6.69 × 103 | 1.94 × 103 | 1.21 × 103 | 1.94 × 100 | 8.42 × 100 |
| Normalized Capital | − | 3.0 × 10−1 | 5.4 × 10−1 | 3.1 × 10−1 | 1.5 × 10−1 | 5.0 × 10−2 | 1.62 × 100 |
| Price of electricity | $/kWh | 5.0 × 10−5 | 1.5 × 10−2 | 2.6 × 10−3 | 1.06 × 10−2 | − | − |
| Price of diesel | $/m3 | 7.0 × 10−5 | 9.0 × 10−2 | 5.3 × 10−3 | 6.36 × 10−2 | − | − |
| Price of oil | $/L | 3.0 × 10−5 | 5.0 × 10−2 | 3.9 × 10−3 | 3.53 × 10−2 | − | − |
| Price of gas | $/m3 | 3.0 × 10−5 | 2.0 × 10−2 | 2.5 × 10−3 | 1.41 × 10−2 | − | − |
3.2. Estimation of the VAR Model Considering Unit Root Test
| Variable | Status of the Variables Examined in the Test | ||
|---|---|---|---|
| Without the Intercept and Trend | With the Intercept and Trend | Without the Intercept and Trend | |
| ADF | ADF | ADF | |
| Intensity | −1.9984 (0.0456) | −2.7123 (0.2388) | −2.2781 (0.1851) |
| GDP | 3.5395 (0.9997) | −3.0333 (0.1403) | −0.2549 (0.9207) |
| Labor | 0.2877 (0.7628) | −2.7382 (0.2310) | −3.6616 (0.0100) |
| Capital | −1.3807 (0.1520) | −2.8423 (0.0660) | −2.9244 (0.0540) |
| Price of electricity | 3.1679 (0.9993) | −1.0181 (0.9267) | −0.7277 (0.8251) |
| Price of diesel | 3.1904 (0.9993) | −2.4617 (0.3431) | 1.1714 (0.9972) |
| Price of oil | 2.1538 (0.9909) | −2.3534 (0.3950) | 0.5463 (0.9857) |
| Price of gas | 2.8086 (0.9980) | −1.7117 (0.7218) | −0.0822 (0.9429) |
| Variable | Status of the Variables Examined in the Test | ||
|---|---|---|---|
| No Width of Origin and Process | With the Breadth of Origin and Process | With Width from Origin and without Trend | |
| ADF | ADF | ADF | |
| ∆ Energy intensity | −2.890 (0.0053) | −6.3195 (0.0001) | −6.0471 (0.0000) |
| ∆ GDP | −3.006 (0.0039) | −3.0333 (0.0003) | −4.9946 (0.0004) |
| ∆ Labor | −3.9005 (0.0004) | −18.565 (0.0000) | −17.288 (0.0001) |
| ∆ Capital | −9.0104 (0.0000) | −8.8058 (0.0000) | −8.9657 (0.0000) |
| ∆ Price of electricity | −3.1224 (0.0029) | −4.1825 (0.0130) | −4.2365 (0.0024) |
| ∆ Price of diesel | −3.3575 (0.0015) | −4.3562 (0.0008) | −4.0946 (0.0035) |
| ∆ Price of oil | −5.0149 (0.0000) | −6.0782 (0.0001) | −5.8520 (0.0000) |
| ∆ Price of gas | −3.7621 (0.0005) | −5.0735 (0.0015) | −5.1808 (0.0002) |
| Lag Number | HQC | SBC | AIC |
|---|---|---|---|
| 0 | 1.084610 | 1.338728 | 0.965075 |
| 1 | −6.933941 | −4.646879 | −8.009753 |
| 2 | −9.855918 (*) | −5.535913 (*) | −11.888010 (*) |
3.3. Autoregressive Test Results
| Price of Gas | Price of Oil | Price of Diesel | Price of Electricity | Capital | Labor | GDP | Intensity | |
|---|---|---|---|---|---|---|---|---|
| Intensity (−1) | −0.1216 | 0.3594 | 0.5922 | 0.2122 | 0.6752 | −0.1034 | −0.0268 | 0.7384 |
| Intensity (−2) | 0.5885 | 1.0093 | 0.3545 | −0.1430 | −0.6557 | −0.0972 | −0.1607 | −0.0841 |
| GDP (−1) | 4.4270 | 4.5451 | 5.0829 | 2.1345 | −1.5615 | 0.2841 | 1.1236 | −0.3034 |
| GDP (−2) | −2.7353 | −1.9393 | −3.0193 | −1.2840 | 2.5690 | 0.2472 | −0.2408 | 0.3312 |
| Labor (−1) | −0.0602 | −0.0806 | 0.0023 | 0.0616 | −0.1876 | −0.0114 | 0.0783 | 0.1445 |
| Labor (−2) | −0.0402 | −0.0963 | −0.1252 | 0.0060 | −0.0544 | 0.0262 | 0.0568 | −0.0352 |
| Capital (−1) | 0.0008 | −0.0435 | 0.0765 | −0.0937 | −0.2121 | 0.0044 | 0.0246 | 0.0261 |
| Capital (−2) | −0.1640 | −0.1640 | −0.2809 | 0.0001 | −0.1147 | 0.0109 | −0.0205 | 0.0048 |
| Price electricity (−1) | −0.3758 | −1.2849 | −1.3216 | 0.3151 | −0.4380 | 0.0040 | −0.1876 | −0.0346 |
| Price electricity (−2) | −0.7133 | −0.4715 | −0.2026 | −0.5629 | −0.7764 | 0.0723 | 0.1219 | −0.1191 |
| Price diesel (−1) | −0.6063 | −0.3449 | −0.6460 | −0.7502 | 0.6706 | 0.0129 | 0.0316 | −0.0095 |
| Price diesel (−2) | −0.8776 | −1.4823 | −1.5820 | −0.3411 | −0.2006 | 0.0302 | −0.2544 | 0.0488 |
| Price oil (−1) | 0.0695 | 0.2540 | 0.6871 | 0.2933 | −0.5183 | 0.0034 | −0.0105 | 0.1115 |
| Price oil (−2) | 0.6847 | 0.1192 | 0.4179 | −0.0448 | 0.5276 | −0.0116 | 0.1472 | −0.1075 |
| Price gas (−1) | 1.4846 | 1.8582 | 1.6168 | 0.5400 | 0.2268 | −0.0853 | −0.0829 | 0.2443 |
| Price gas (−2) | 0.9908 | 0.6053 | 0.3828 | 0.9667 | 0.5003 | 0.0341 | 0.2021 | −0.0669 |
| R2 | 0.9931 | 0.9557 | 0.9719 | 0.9971 | 0.7075 | 0.9992 | 0.9978 | 0.8553 |
| R2 justified | 0.9846 | 0.9013 | 0.9373 | 0.9936 | 0.3475 | 0.9982 | 0.9952 | 0.6772 |
| F-test | 117.3000 | 17.5500 | 28.1200 | 284.0900 | 1.9655 | 1046.4 | 383.23 | 4.8028 |
3.4. The Energy Intensity Reaction Due to Shocks in Electricity Energy Price

3.5. The Energy Intensity Reaction Due to Shocks in Diesel Energy Price


3.6. The Energy Intensity Reaction Due to Shocks in Gas Energy Price
3.7. The Energy Intensity Reaction Due to Shocks in Oil Energy Price
3.8. Estimation of a Long-Term Relationship
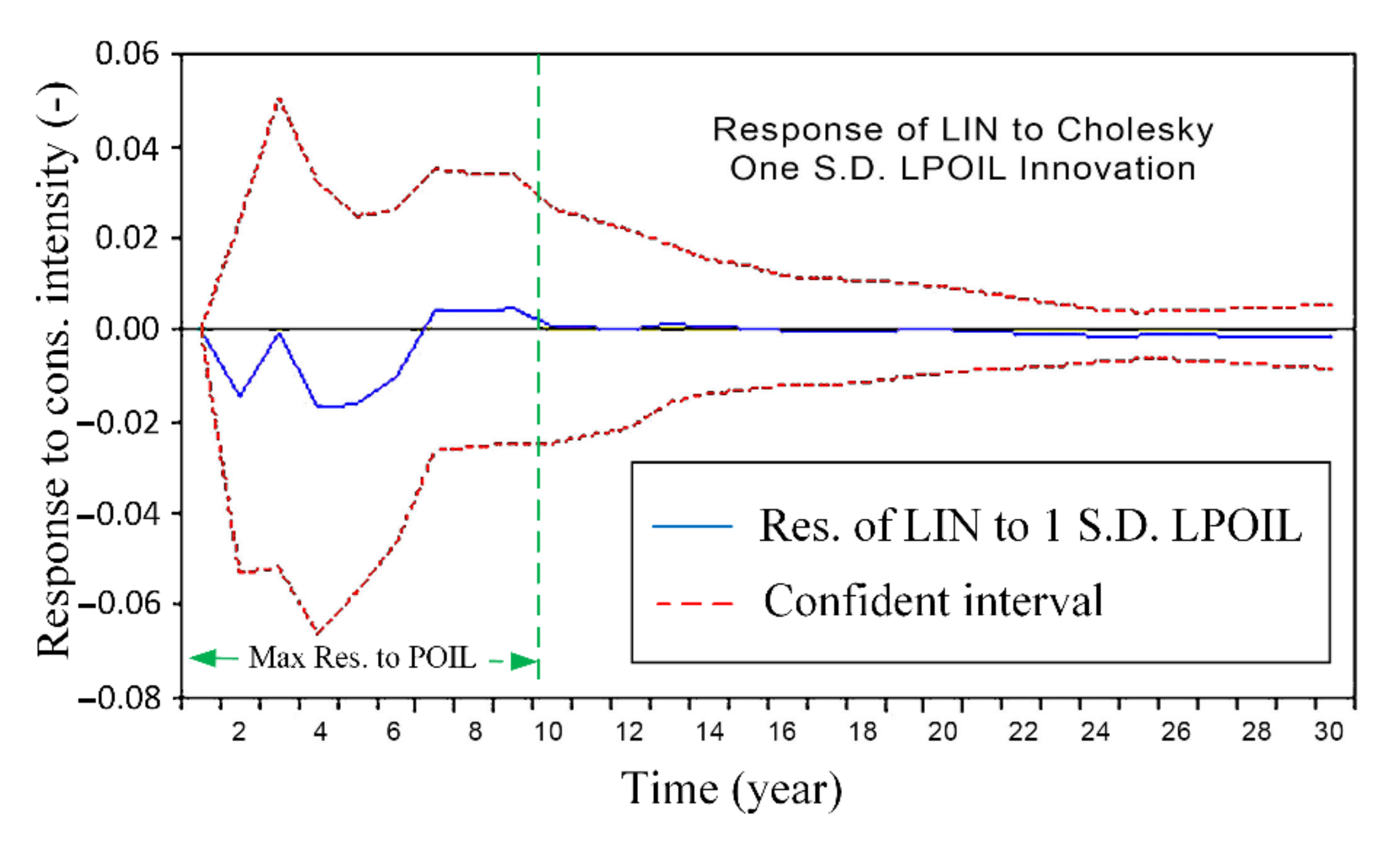
4. Normalization of the Co-Integrated Vector
| The Number of Convergence Vectors Based on the Null Hypothesis | The Number of Convergence Vectors Based on the against Null Hypothesis | Test Statistics | Critical Value |
|---|---|---|---|
| r = 0 | r = 1 | 229.4940 | 52.3626 |
| r ≤ 1 | r = 2 | 70.4923 | 46.2314 |
| r ≤ 2 | r = 3 | 50.3124 | 40.0775 |
| r ≤ 3 | r = 4 | 31.2800 | 33.8768 |
| r ≤ 4 | r = 5 | 0.1356 | 9.1645 |
| The Number of Convergence Vectors Is Based on the Null Hypothesis | The Number of Convergence Vectors Based on the against Hypothesis | Test Statistics | Critical Value |
|---|---|---|---|
| r = 0 | r = 1 | 428.447 | 159.520 |
| r ≤ 1 | r = 2 | 198.950 | 125.610 |
| r ≤ 2 | r = 3 | 128.46 | 95.750 |
| r ≤ 3 | r = 4 | 78.148 | 69.810 |
| r ≤ 4 | r = 5 | 46.868 | 47.856 |
Estimation of Vector Error Correction Model (VECM)
| Intensity | GDP | Capital | Labor | Electricity Price | Diesel Price | Gas Price | Oil Price | c |
|---|---|---|---|---|---|---|---|---|
| 1 | −0.0109 | 0.2725 | −0.6173 | 0.3803 | 0.5856 | 0.7750 | 0.7643 | 0.5888 |
| ∆ Energy Intensity | ∆ GDP | ∆ Capital | ∆ Labor | ∆ Price of Electricity | ∆ Price of Diesel | ∆ Price of Gas | ∆ Price of Oil | VECM |
|---|---|---|---|---|---|---|---|---|
| −0.101 | −0.753 | 0.005 | 0.126 | 0.101 | 0.225 | 0.152 | 0.165 | −0.153 |
| (−0.684) | (−3.597) | (0.558) | (3.352) | (1.482) | (2.572) | (−2.138) | (−2.938) | (−2.885) |
5. Conclusions
5.1. Research Contribution and Findings
5.2. Future Directions
5.3. Policy Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Nicolli, F.; Vona, F. Energy market liberalization and renewable energy policies in OECD countries. Energy Policy 2019, 128, 853–867. [Google Scholar] [CrossRef] [Green Version]
- Gajdzik, B.; Sroka, W.; Vveinhardt, J. Energy Intensity of Steel Manufactured Utilising EAF Technology as a Function of Investments Made: The Case of the Steel Industry in Poland. Energies 2021, 14, 5152. [Google Scholar] [CrossRef]
- Ginevičius, R.; Bilan, Y.; Kądzielawski, G.; Novotny, M.; Kośmider, T. Evaluation of the Sectoral Energy Development Intensity in the Euro Area Countries. Energies 2021, 14, 5298. [Google Scholar] [CrossRef]
- Energy Ministry of Iran. Energy Balance 1981–2012. Electricity and Energy Macro Planning Office. Available online: www.pep.moe.gov.ir (accessed on 10 June 2021).
- Jayaprakash, S.; Nagarajan, M.D.; de Prado, R.P.; Subramanian, S.; Divakarachari, P.B. A Systematic Review of Energy Management Strategies for Resource Allocation in the Cloud: Clustering, Optimization and Machine Learning. Energies 2021, 14, 5322. [Google Scholar] [CrossRef]
- Szymczyk, K.; Şahin, D.; Bağcı, H.; Kaygın, C.Y. The Effect of Energy Usage, Economic Growth, and Financial Development on CO2 Emission Management: An Analysis of OECD Countries with a High Environmental Performance Index. Energies 2021, 14, 4671. [Google Scholar] [CrossRef]
- Callau-Zori, M.; Samoila, L.; Orgerie, A.-C.; Pierre, G. An experiment-driven energy consumption model for virtual machine management systems. Sustain. Comput. Inform. Syst. 2018, 18, 163–174. [Google Scholar] [CrossRef] [Green Version]
- Jeong, D.; Park, C.; Ko, Y.M. Short-term electric load forecasting for buildings using logistic mixture vector autoregressive model with curve registration. Appl. Energy 2021, 282, 116249. [Google Scholar] [CrossRef]
- Li, M.; Zhang, Y. Bootstrapping multivariate portmanteau tests for vector autoregressive models with weak assumptions on errors. Comput. Stat. Data Anal. 2022, 165, 107321. [Google Scholar] [CrossRef]
- Guefano, S.; Tamba, J.G.; Azong, T.E.W.; Monkam, L. Methodology for forecasting electricity consumption by Grey and Vector autoregressive models. MethodsX 2021, 8, 101296. [Google Scholar] [CrossRef]
- Bojnec, Š.; Križaj, A. Electricity Markets during the Liberalization: The Case of a European Union Country. Energies 2021, 14, 4317. [Google Scholar] [CrossRef]
- Topcu, E.; Altinoz, B.; Aslan, A. Global evidence from the link between economic growth, natural resources, energy consumption, and gross capital formation. Resour. Policy 2020, 66, 101622. [Google Scholar] [CrossRef]
- Rehman, A.; Ma, H.; Ahmad, M.; Ozturk, I.; Işık, C. Estimating the connection of information technology, foreign direct investment, trade, renewable energy and economic progress in Pakistan: Evidence from ARDL approach and cointegrating regression analysis. Energy Econ. 2021, 92, 104937. [Google Scholar]
- Sheng, X.; Gupta, R.; Ji, Q. The impacts of structural oil shocks on macroeconomic uncertainty: Evidence from a large panel of 45 countries. Energy Econ. 2020, 91, 104940. [Google Scholar] [CrossRef]
- Zhao, X.-G.; Hu, S.-R. Does market-based electricity price affect China’s energy efficiency? Energy Econ. 2020, 91, 104909. [Google Scholar]
- Norouzi, N.; Bashashjafarabadi, Z.; Meybodi, S.M.Y. An Economic Evaluation of the Use of Wind Farms in Iran, Taking into Account the Effect of Energy Price Liberalization Policy. Univers. J. Bus. Manag. 2021, 1, 49–61. [Google Scholar]
- Salmanzadeh-Meydani, N.; Ghomi, S.M.T.F. The causal relationship among electricity consumption, economic growth and capital stock in Iran. J. Policy Modeling 2019, 41, 1230–1256. [Google Scholar] [CrossRef]
- Oryani, B.; Koo, Y.; Rezania, S. Structural Vector Autoregressive Approach to Evaluate the Impact of Electricity Generation Mix on Economic Growth and CO2 Emissions in Iran. Energies 2020, 13, 4268. [Google Scholar] [CrossRef]
- Pezzutto, S.; Grilli, G.; Zambotti, S.; Dunjic, S. Forecasting Electricity Market Price for End Users in EU28 until 2020—Main Factors of Influence. Energies 2018, 11, 1460. [Google Scholar] [CrossRef] [Green Version]
- Pan, X.; Uddin, M.K.; Saima, U.; Jiao, Z.; Han, C. How to do industrialization and trade openness influence energy intensity? Evidence from a path model in case of Bangladesh. Energy Policy 2019, 133, 110916. [Google Scholar] [CrossRef]
- Szőke, T.; Hortay, O.; Farkas, R. Price regulation and supplier margins in the Hungarian electricity markets. Energy Econ. 2021, 94, 105098. [Google Scholar] [CrossRef]
- Gujarati, D.N. Basic Econometrics, 4th ed.; McGrowHill: New York, NY, USA, 2003; pp. 1–1027. ISBN 0-07-112342-3. [Google Scholar]
- Sims, C.A.; Stock, J.H.; Watson, M.W. Inference in Linear Time Series Models with Some Unit Roots. Econometrica 1990, 56, 113–144. [Google Scholar] [CrossRef]
- Li, W.; Liao, J. A comparative study on trend forecasting approach for stock price time series. In Proceedings of the 2017 11th IEEE International Conference on Anti-Counterfeiting, Security, and Identification (ASID), Xiamen, China, 27–29 October 2017; pp. 74–78. [Google Scholar]
- Caporale, G.M.; Gil-Alaña, L.A. Fractional cointegration and tests of present value models. Rev. Financ. Econ. 2004, 13, 245–258. [Google Scholar] [CrossRef] [Green Version]
- Stock, J.H.; Watson, M.W. Vector Autoregressions. J. Econ. Perspect. 2001, 15, 101–115. [Google Scholar] [CrossRef] [Green Version]
- Watson, M.W. Vector Autoregressions and Cointegration. In Handbook of Econometrics; Engle, R., McFadden, D., Eds.; Elsevier Science Ltd.: Amsterdam, The Netherlands, 1994; Volume IV, pp. 2844–2915. [Google Scholar]
- Bakhsh, S.S.; Khansari, Z.H. Application of Eviews in Econometrics; Institute of Economic Affairs: Tehran, Iran, 2005. [Google Scholar]
- Carta, S.; Medda, A.; Pili, A.; Reforgiato Recupero, D.; Saia, R. Forecasting E-Commerce Products Prices by Combining an Autoregressive Integrated Moving Average (ARIMA) Model and Google Trends Data. Future Internet 2018, 11, 5. [Google Scholar] [CrossRef] [Green Version]
- Engle, R.F.; Yoo, B.S. Cointegrated Economic Time Series: An Overview with New Results. In Long-Run Economic Relationships: Readings in Cointegration; Engle, R.F., Granger, C.W.J., Eds.; Oxford University Press: Oxford, UK, 1991; pp. 1–301. [Google Scholar]
- Engle, R.F.; Granger, C.W.J. Cointegration and Error Correction: Representation, Estimation and Testing. Econometrica 1987, 55, 251–276. [Google Scholar] [CrossRef]
- Johansen, S. Estimation and Hypothesis Testing of Cointegration Vectors in Gaussian Vector Autoregressive Models. Econometrica 1991, 55, 1551–1580. [Google Scholar] [CrossRef]
- Abbasi, F.; Riaz, K. CO2 emissions and financial development in an emerging economy: An augmented VAR approach. Energy Policy 2016, 90, 102–114. [Google Scholar] [CrossRef]
- Cavanaugh, J.E. Unifying the Derivations for the Akaike and Corrected Akaike Information Criteria. Stat. Probab. Lett. 2000, 33, 201–208. [Google Scholar] [CrossRef]
- Snipes, M.; Taylor, D.C. Model selection and Akaike Information Criteria: An example from wine ratings and prices. Wine Econ. Policy 2014, 3, 3–9. [Google Scholar] [CrossRef] [Green Version]
- Rossi, R.; Murari, A.; Gaudio, P.; Gelfusa, M. Upgrading Model Selection Criteria with Goodness of Fit Tests for Practical Applications. Entropy 2020, 22, 447. [Google Scholar] [CrossRef] [Green Version]
- Maïnassara, Y.B.; Kokonendji, C.C. Modified Schwarz and Hannan-Quinn information criteria for weak VARMA model. Stat. Inference Stoch. Process. 2016, 19, 199–217. [Google Scholar] [CrossRef]
- Hall, R.A.; Inoue, A.; Nason, J.M.; Rossi, B. Information criteria for impulse response function matching estimation of DSGE models. Econometrics 2012, 170, 499–518. [Google Scholar] [CrossRef] [Green Version]
- Virginia, E.; Ginting, J.; Elfaki, F.A.M. Application of GARCH Model to Forecast Data and Volatility of Share Price of Energy (Study on Adaro Energy Tbk, LQ45). Int. J. Energy Econ. Policy 2018, 8, 131–140. [Google Scholar]
- Ariyo, A.A.; Adewumi, A.O.; Ayo, C.K. Stock Price Prediction Using the ARIMA Model. In Proceedings of the 2014 UKSim-AMSS 16th International Conference on Computer Modelling and Simulation, Cambridge, UK, 26–28 March 2014; pp. 106–112. [Google Scholar]
- Zhou, M.; Yan, Z.; Ni, Y.; Li, G. An ARIMA approach to forecasting electricity price with accuracy improvement by predicted errors. In Proceedings of the IEEE Power Engineering Society General Meeting, Denver, CO, USA, 6–10 June 2004; Volume 2, pp. 233–238. [Google Scholar]
- Ky, D.X.; Tuyen, L.T. A Higher Order Markov Model for Time Series Forecasting. Int. J. Appl. Math. Stat. 2018, 57, 1–18. [Google Scholar]
- Central Bank of the Islamic Republic of Iran. Available online: https://tsd.cbi.ir/Display/Content.aspx (accessed on 10 June 2021).
- Iran Statistics Center. Available online: https://www.amar.org.ir (accessed on 10 June 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tabatabaei, T.S.; Asef, P. Evaluation of Energy Price Liberalization in Electricity Industry: A Data-Driven Study on Energy Economics. Energies 2021, 14, 7511. https://doi.org/10.3390/en14227511
Tabatabaei TS, Asef P. Evaluation of Energy Price Liberalization in Electricity Industry: A Data-Driven Study on Energy Economics. Energies. 2021; 14(22):7511. https://doi.org/10.3390/en14227511
Chicago/Turabian StyleTabatabaei, Tayebeh Sadat, and Pedram Asef. 2021. "Evaluation of Energy Price Liberalization in Electricity Industry: A Data-Driven Study on Energy Economics" Energies 14, no. 22: 7511. https://doi.org/10.3390/en14227511
APA StyleTabatabaei, T. S., & Asef, P. (2021). Evaluation of Energy Price Liberalization in Electricity Industry: A Data-Driven Study on Energy Economics. Energies, 14(22), 7511. https://doi.org/10.3390/en14227511






