A Novel Model of Electromechanical Contactors for Predicting Dynamic Characteristics
Abstract
:1. Introduction
- A new topology of the contactor is proposed. On the basis of the new contactor, a parameterized model of EMFA is established based on the equivalent magnetic circuit method.
- To simulate the physical process of dual power switching, the equivalent magnetic circuit model, mechanical dynamics model, and magnetohydrodynamic model are established, and they complete the serial calculation.
- On the basis of simulation, the production of the principle prototype is completed. Related experiments are completed through oscilloscope and high-speed photography. The accuracy of the simulation and the practicability of the contactor are verified.
2. Basic Principle
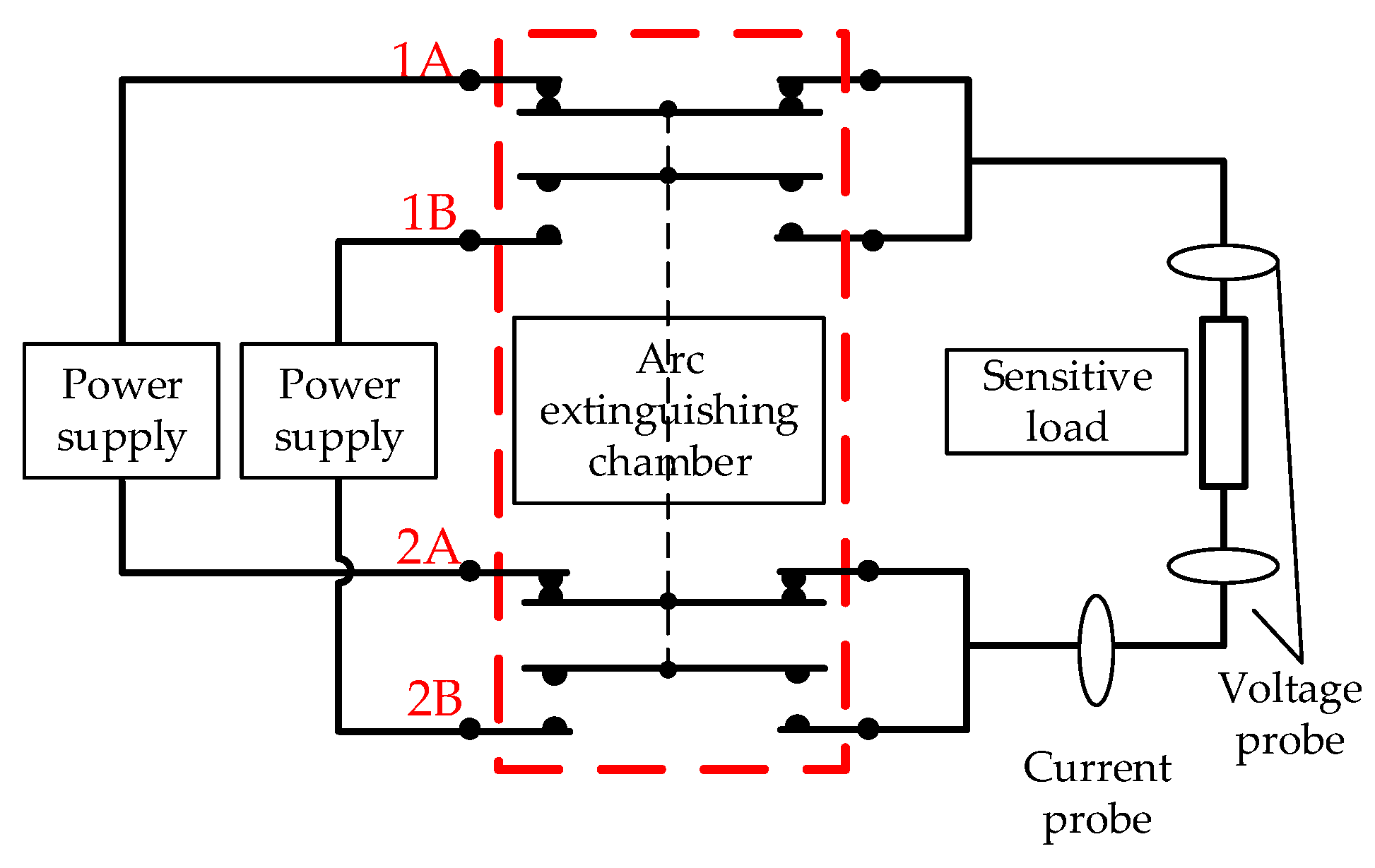
2.1. Basic Principles of Dual Power Switching
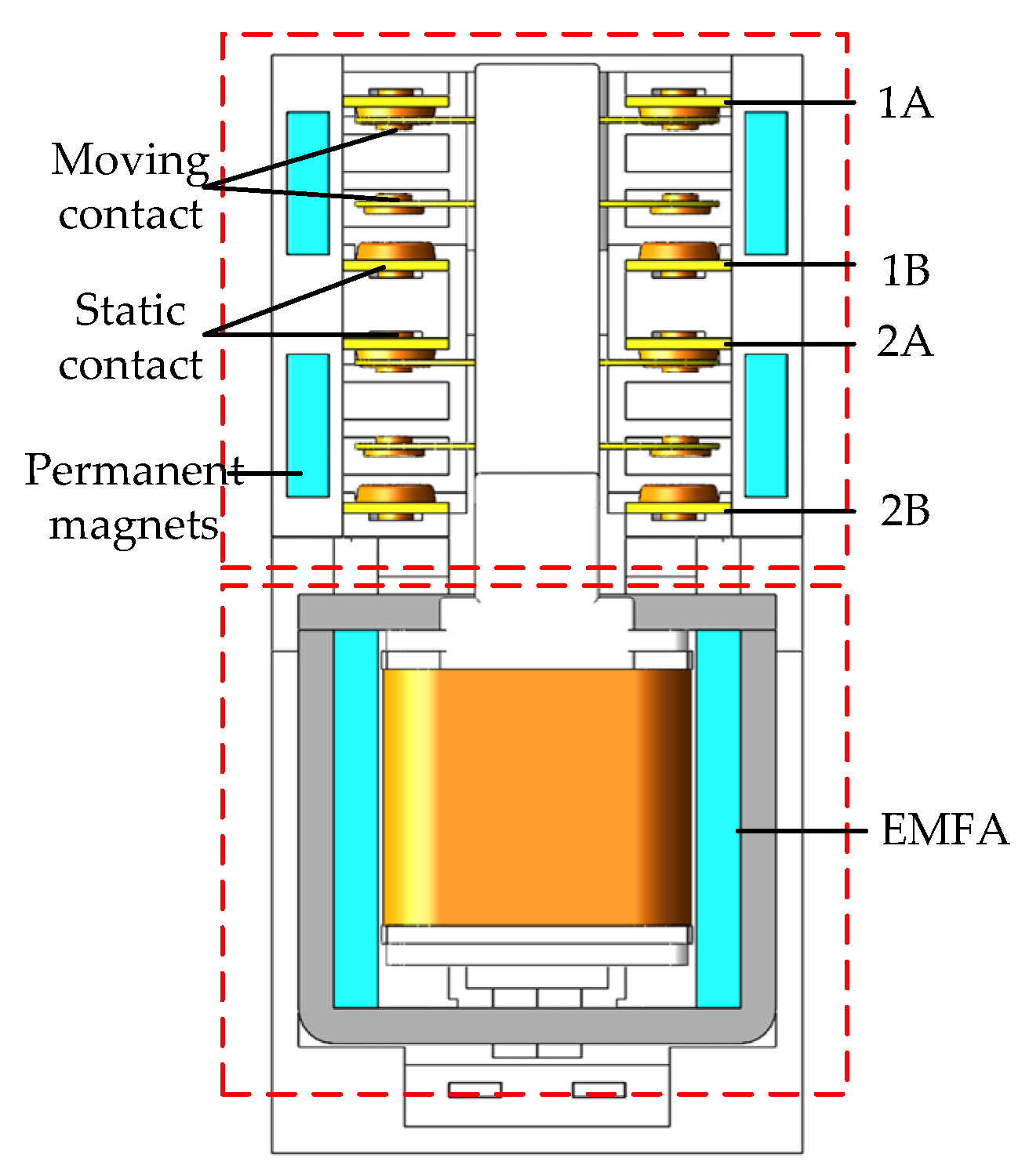
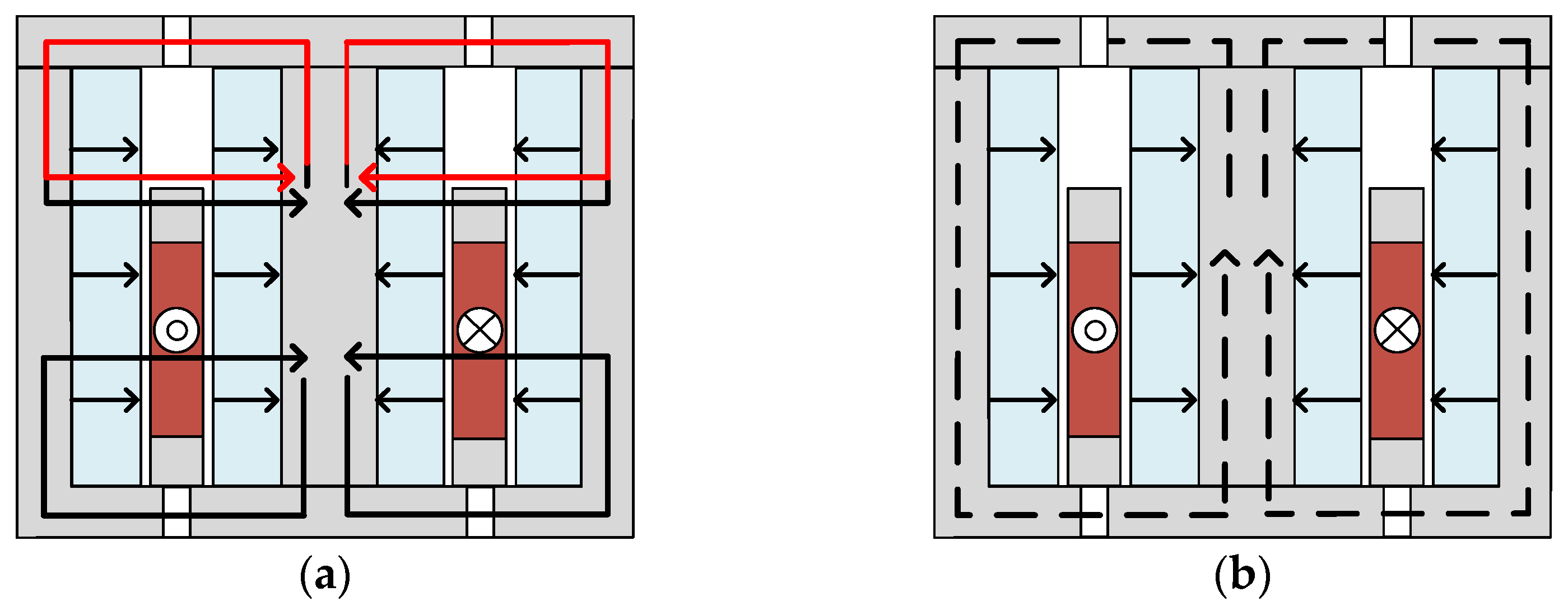
2.2. Basic Principle of High-Speed Contactor
3. Basic Mathematical Model
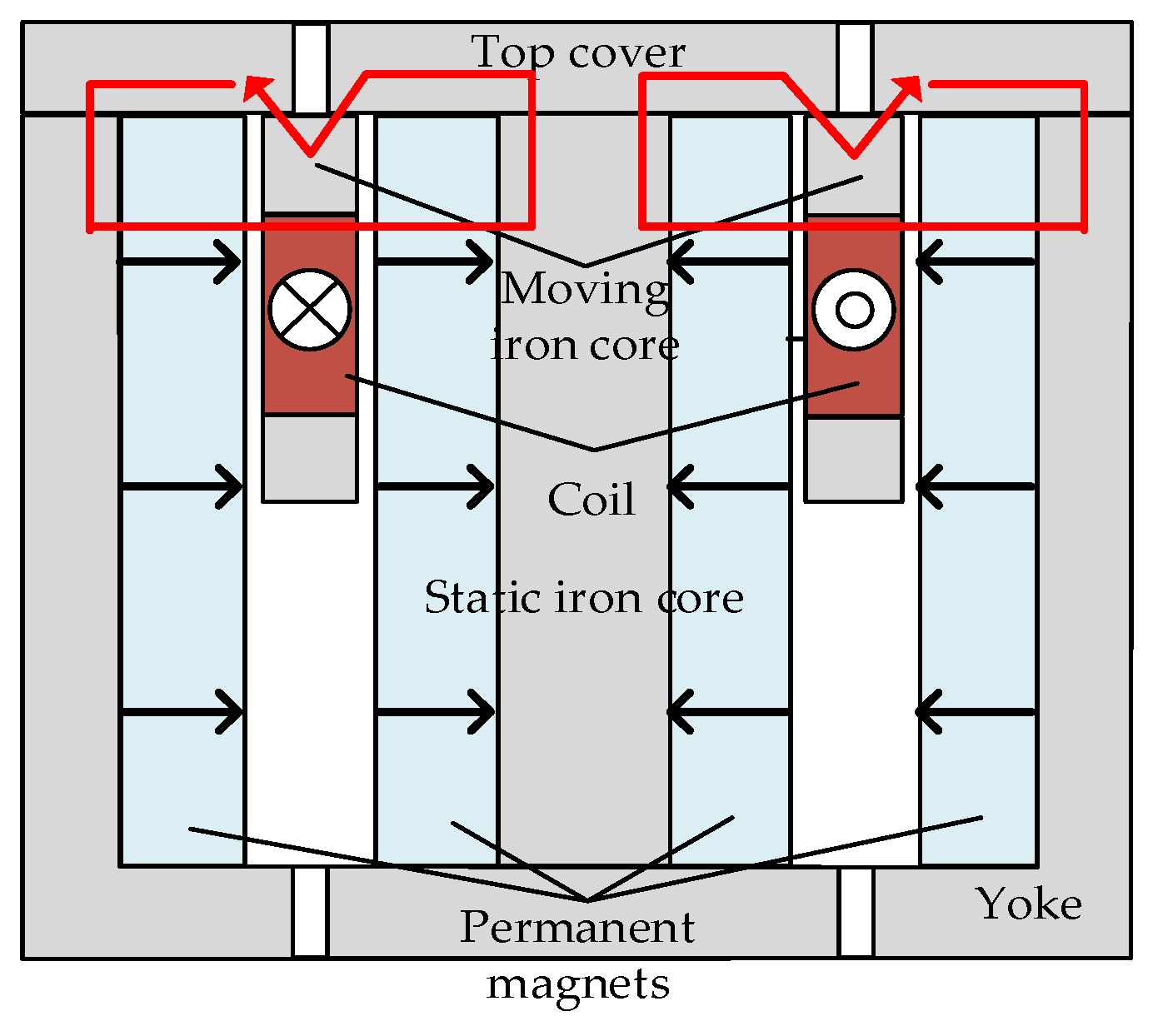
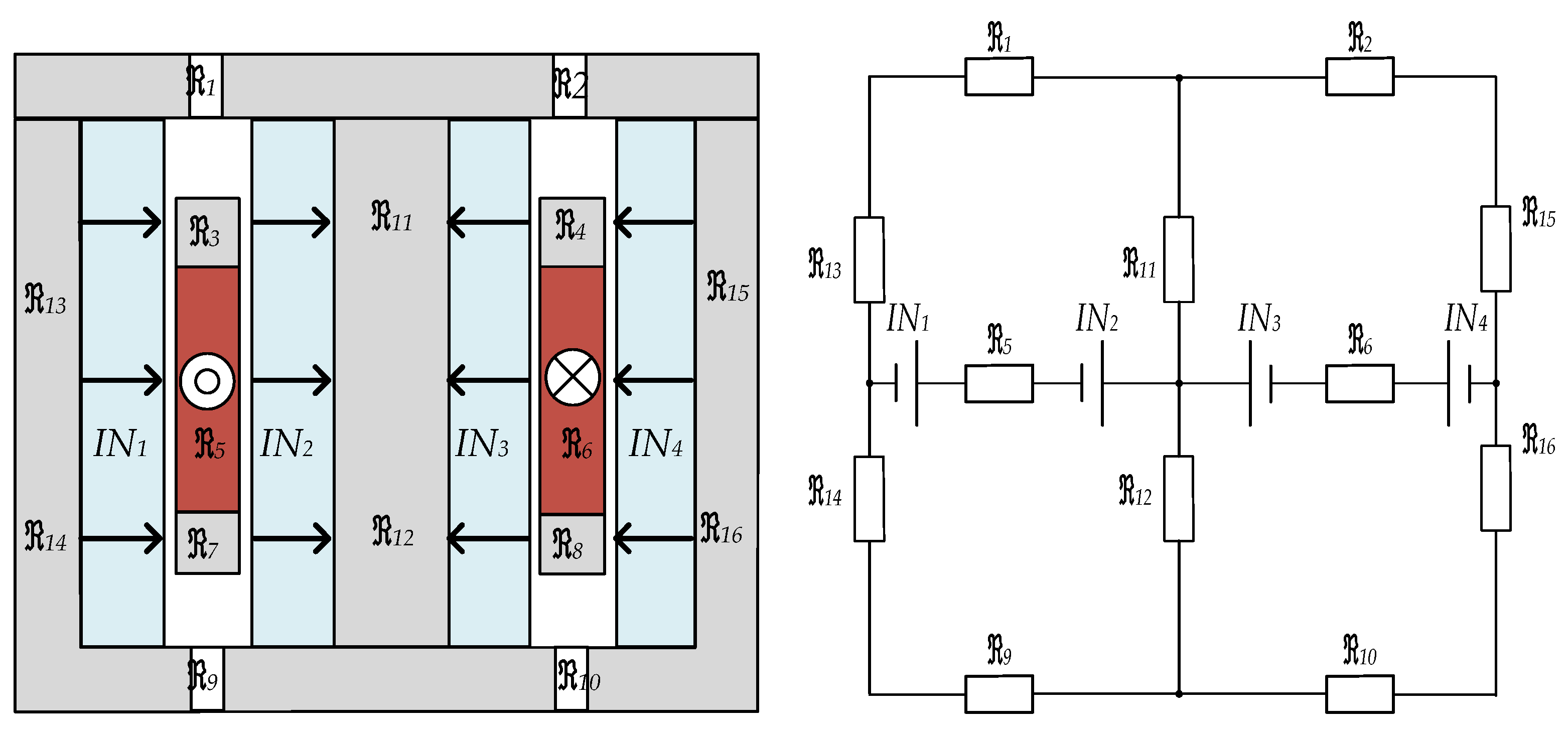
3.1. Principle of Equivalent Magnetic Circuit Simulation
3.2. Principle of Mechanical Dynamics Simulation
3.3. Principle of Magnetohydrodynamic Simulation
4. Modeling and Simulation
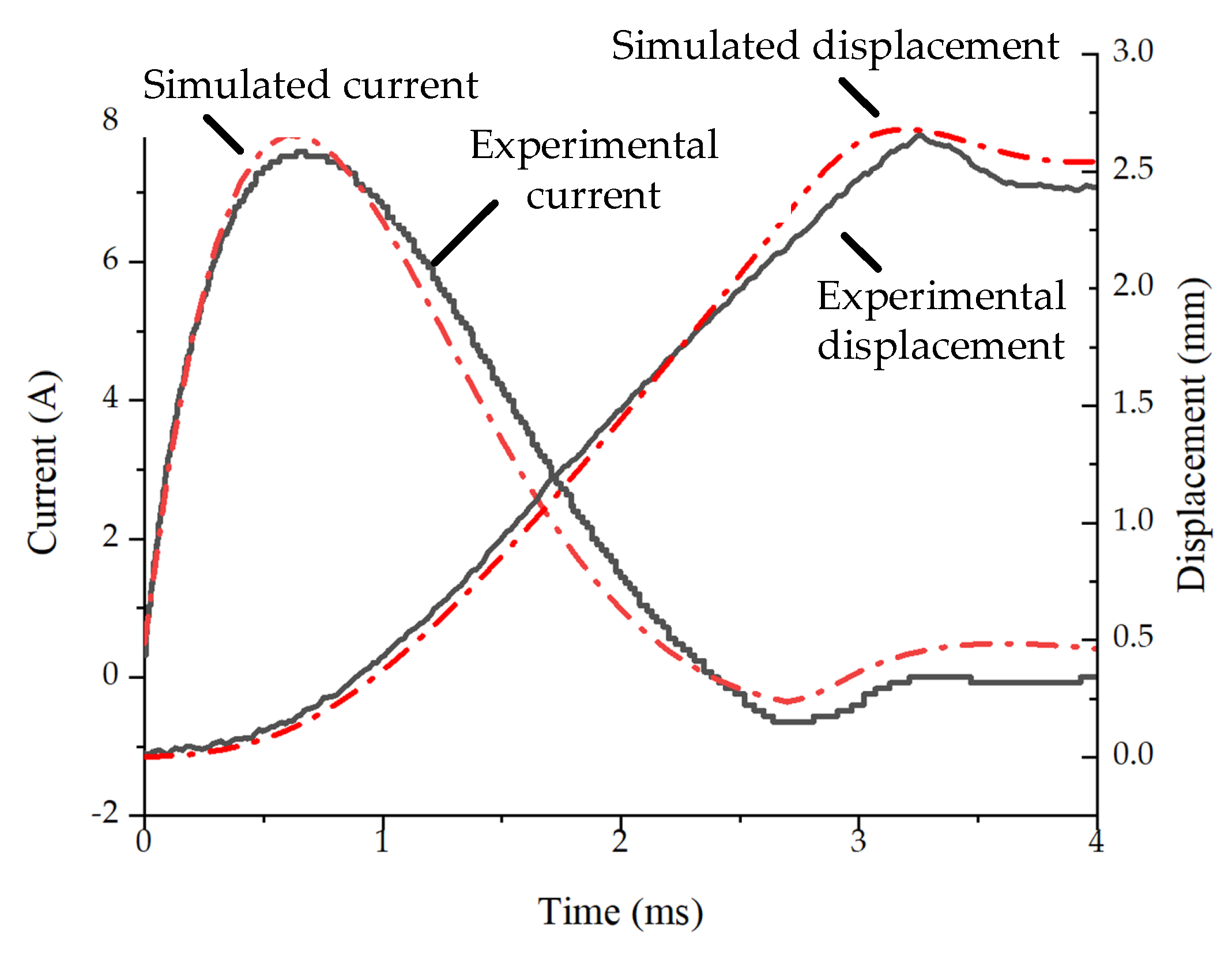
4.1. Electromechanical Co-Simulation
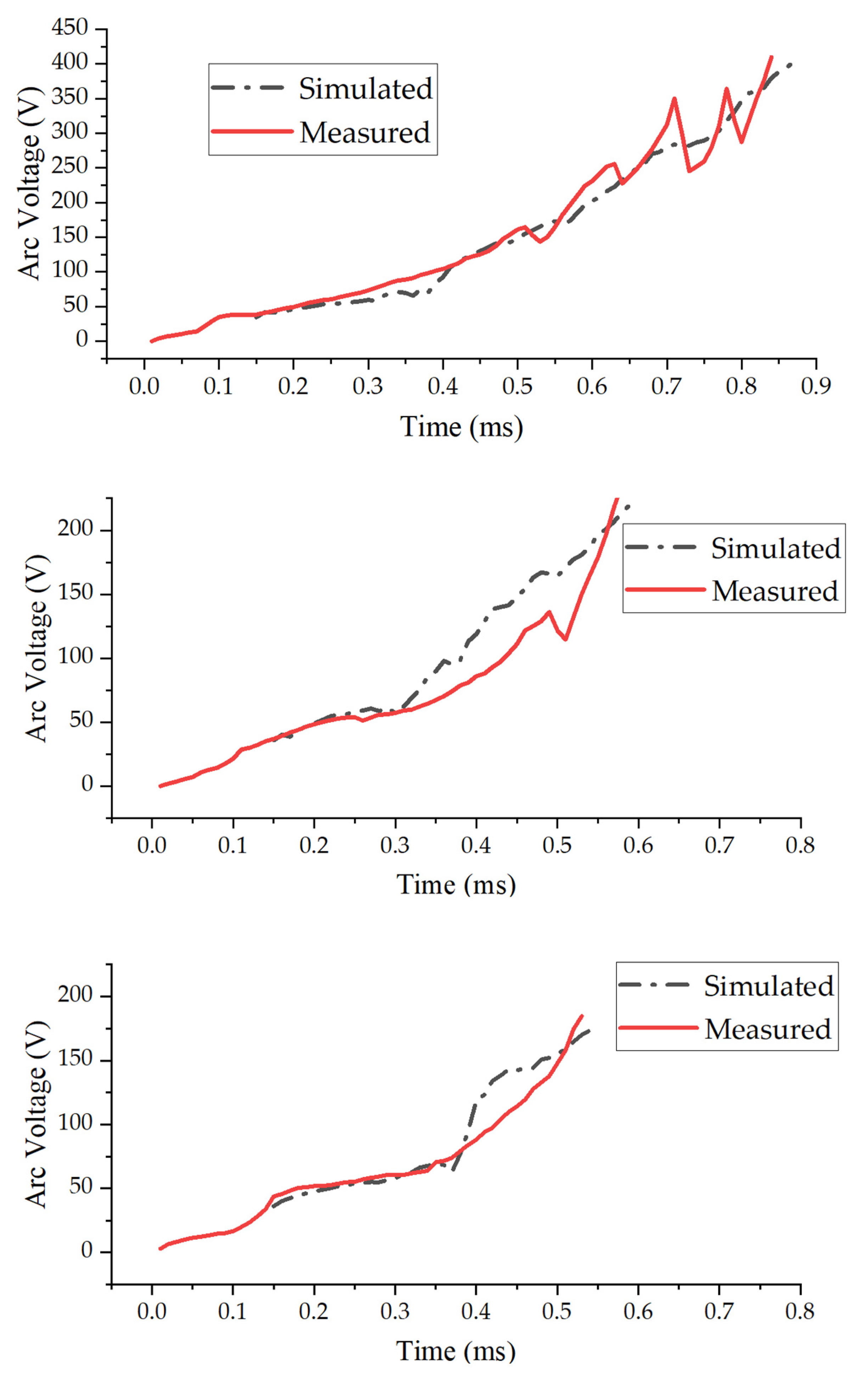
4.2. Magnetohydrodynamic Simulation
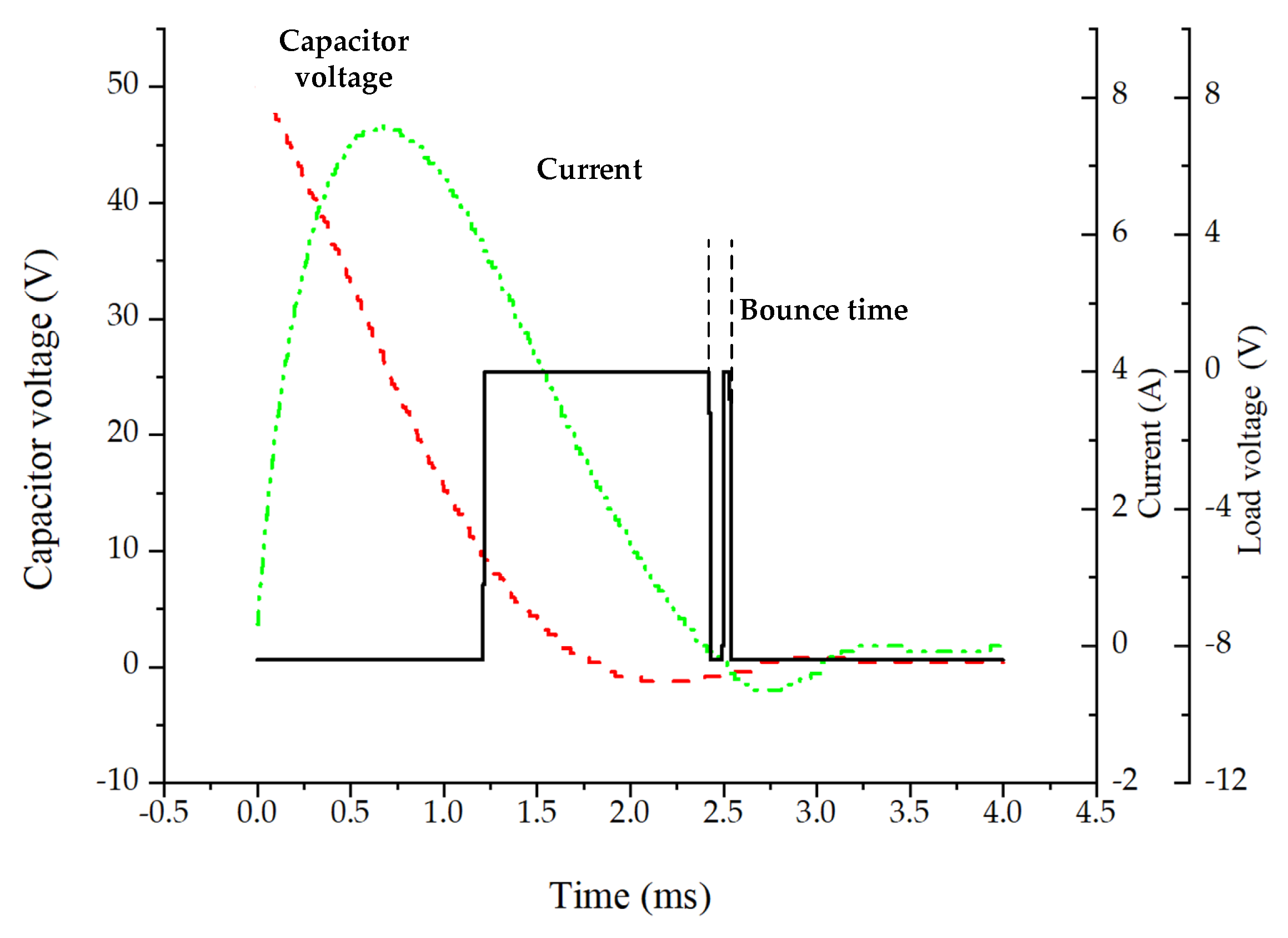
5. Experiment and Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Tian, B.; Mao, C.; Lu, J. 400 V/1000 kVA Hybrid Automatic Transfer Switch. IEEE Trans. Ind. Electron. 2013, 60, 5422–5435. [Google Scholar] [CrossRef]
- Mokhtari, H.; Dewan, S.B.; Iravani, M.R. Analysis of a static transfer switch with respect to transfer time. IEEE Trans. Power Deliv. 2002, 17, 190–199. [Google Scholar] [CrossRef]
- Geng, H.; Zhang, X.; Zhang, Y.; Hu, W.; Lei, Y.; Xu, X.; Wang, A.; Wang, S.; Shi, L. Development of Brushless Claw Pole Electrical Excitation and Combined Permanent Magnet Hybrid Excitation Generator for Vehicles. Energies 2020, 13, 4723. [Google Scholar] [CrossRef]
- Ro, J.; Bak, H.; Jung, H. Characteristic analysis and design of a novel lorentz force driving actuator for a molded case circuit breaker. IET Electr. Power Appl. 2015, 9, 1–9. [Google Scholar] [CrossRef]
- Fang, S.; Lin, H.; Ho, S.L. Magnetic Field Analysis and Dynamic Characteristic Prediction of AC Permanent-Magnet Contactor. IEEE Trans. Magn. 2009, 45, 2990–2995. [Google Scholar] [CrossRef]
- Fang, S.; Lin, H.; Ho, S.L. Transient Co-Simulation of Low Voltage Circuit Breaker with Permanent Magnet Actuator. IEEE Trans. Magn. 2009, 45, 1242–1245. [Google Scholar] [CrossRef]
- Shu, L.; Wu, L.; Wu, G.; Wu, Z. A Fully Coupled Framework of Predicting the Dynamic Characteristics of Permanent Magnet Contactor. IEEE Trans. Magn. 2016, 52, 1–7. [Google Scholar] [CrossRef]
- Tang, L.; Xu, Z.; Bala, V. Contactor Modeling Technology Based on an Artificial Neural Network. IEEE Trans. Magn. 2018, 54, 1–8. [Google Scholar]
- Tang, L.; Han, Z.; Xu, Z. Neural Network-Based Co-Simulation Technology for Intelligent Contactors. IEEE Trans. Magn. 2020, 56, 1–8. [Google Scholar]
- Wang, X.; Lin, H.; Fang, S. Dynamic performance analysis of permanent magnet contactor with a flux-weakening control strategy. J. Appl. Phys. 2011, 109, 07E707. [Google Scholar] [CrossRef] [Green Version]
- Espinosa, A.G.; Ruiz, J.R.; Morera, X.A. A Sensorless Method for Controlling the Closure of a Contactor. IEEE Trans. Magn. 2007, 43, 3896–3903. [Google Scholar] [CrossRef]
- Wang, X.; Lin, H.; Ho, S.L.; Fang, S.; Jin, P. Analysis of Dynamic Characteristics of Permanent Magnet Contactor With Sensorless Displacement Profile Control. IEEE Trans. Magn. 2010, 46, 1633–1636. [Google Scholar] [CrossRef]
- Fang, S.; Chen, Y.; Ni, H.; Lin, H.; Wang, X.; Zhu, B.; Zhang, Y. A Novel Breaking Strategy for Reduced Response Time of Electromagnetic Contactor by Reverse Voltage Application. Energies 2019, 12, 789. [Google Scholar] [CrossRef] [Green Version]
- Dong, E.; Qin, T.; Wang, Y.; Duan, X.; Zou, J. Experimental Research on Speed Control of Vacuum Breaker. IEEE Trans. Power Deliv. 2013, 28, 2594–2601. [Google Scholar] [CrossRef]
- Tang, L.; Han, Z.; Xu, Z. A Sequential Adaptive Control Strategy for the Contact Colliding Speed of Contactors Based on Fuzzy Control. IEEE Trans. Ind. Electron. 2021, 68, 6064–6074. [Google Scholar] [CrossRef]
- Lin, H.; Wang, X.; Fang, S.; Jin, P.; Ho, S.L. Design, Optimization, and Intelligent Control of Permanent-Magnet Contactor. IEEE Trans. Ind. Electron. 2013, 60, 5148–5159. [Google Scholar] [CrossRef]
- Ruiz, J.R.; Espinosa, A.G. A Novel Parametric Model for AC Contactors. IEEE Trans. Magn. 2008, 44, 2215–2218. [Google Scholar] [CrossRef]
- Li, H.; Cui, L.; Ma, Z.; Li, B. Multi-Objective Optimization of the Halbach Array Permanent Magnet Spherical Motor Based on Support Vector Machine. Energies 2020, 13, 5704. [Google Scholar] [CrossRef]
- Ma, R.; Rong, M.; Yang, F.; Wu, Y.; Sun, H.; Yuan, D.; Wang, H.; Niu, C. Investigation on Arc Behavior During Arc Motion in Air DC Circuit Breaker. IEEE Trans. Plasma Sci. 2013, 41, 2551–2560. [Google Scholar] [CrossRef]
- Yin, J.; Wang, Q.; Li, X. Simulation Analysis of Arc Evolution Process in Multiple Parallel Contact Systems. IEEE Trans. Plasma Sci. 2018, 46, 2788–2793. [Google Scholar] [CrossRef]
- Rong, M.; Ma, R.; Chen, J.; Hou, C.; Sun, Y. Numerical Investigation on Arc Behavior in Low-Voltage Arc Chamber Considering Turbulence Effect. IEEE Trans. Plasma Sci. 2014, 42, 2716–2717. [Google Scholar] [CrossRef]
- Chen, F.; Xu, Y.; Cao, Z.; Wang, Z.; Ma, X. Hybrid Kinetic-MHD Simulations of Vacuum Arc Using Field-Circuit Coupling Method. IEEE Trans. Magn. 2020, 56, 1–4. [Google Scholar] [CrossRef]





| Equations | at | Φ | ГΦ | SΦ |
|---|---|---|---|---|
| Mass conservation | 1 | 1 | 0 | 0 |
| Momentum conservation | 1 | ux | η | −әp/əx + (jyBz − jzBy) |
| 1 | uy | η | −әp/əy + (jzBx − jxBz) | |
| 1 | uz | η | −әp/əz + (jxBy − jyBx) | |
| Energy conservation | 1 | h | λ/Cp | σE2-qrad |
| Electrical field | 0 | ϕ | σ | 0 |
| Magnetic field | 0 | Ax | 1 | −u0jx |
| 0 | Ay | 1 | −u0jy | |
| 0 | Az | 1 | −u0jz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Wang, Y.; Zhang, L.; Xue, S.; Dong, E.; Zou, J. A Novel Model of Electromechanical Contactors for Predicting Dynamic Characteristics. Energies 2021, 14, 7466. https://doi.org/10.3390/en14227466
Wang G, Wang Y, Zhang L, Xue S, Dong E, Zou J. A Novel Model of Electromechanical Contactors for Predicting Dynamic Characteristics. Energies. 2021; 14(22):7466. https://doi.org/10.3390/en14227466
Chicago/Turabian StyleWang, Gongrun, Yongxing Wang, Lifan Zhang, Shutian Xue, Enyuan Dong, and Jiyan Zou. 2021. "A Novel Model of Electromechanical Contactors for Predicting Dynamic Characteristics" Energies 14, no. 22: 7466. https://doi.org/10.3390/en14227466
APA StyleWang, G., Wang, Y., Zhang, L., Xue, S., Dong, E., & Zou, J. (2021). A Novel Model of Electromechanical Contactors for Predicting Dynamic Characteristics. Energies, 14(22), 7466. https://doi.org/10.3390/en14227466





