Bragg Mirrors for Thermal Waves
Abstract
:1. Introduction
2. Thermal Waves—Cattaneo-Vernotte Equation
3. Thermal Superlattice
4. Thermal Bragg Mirrors
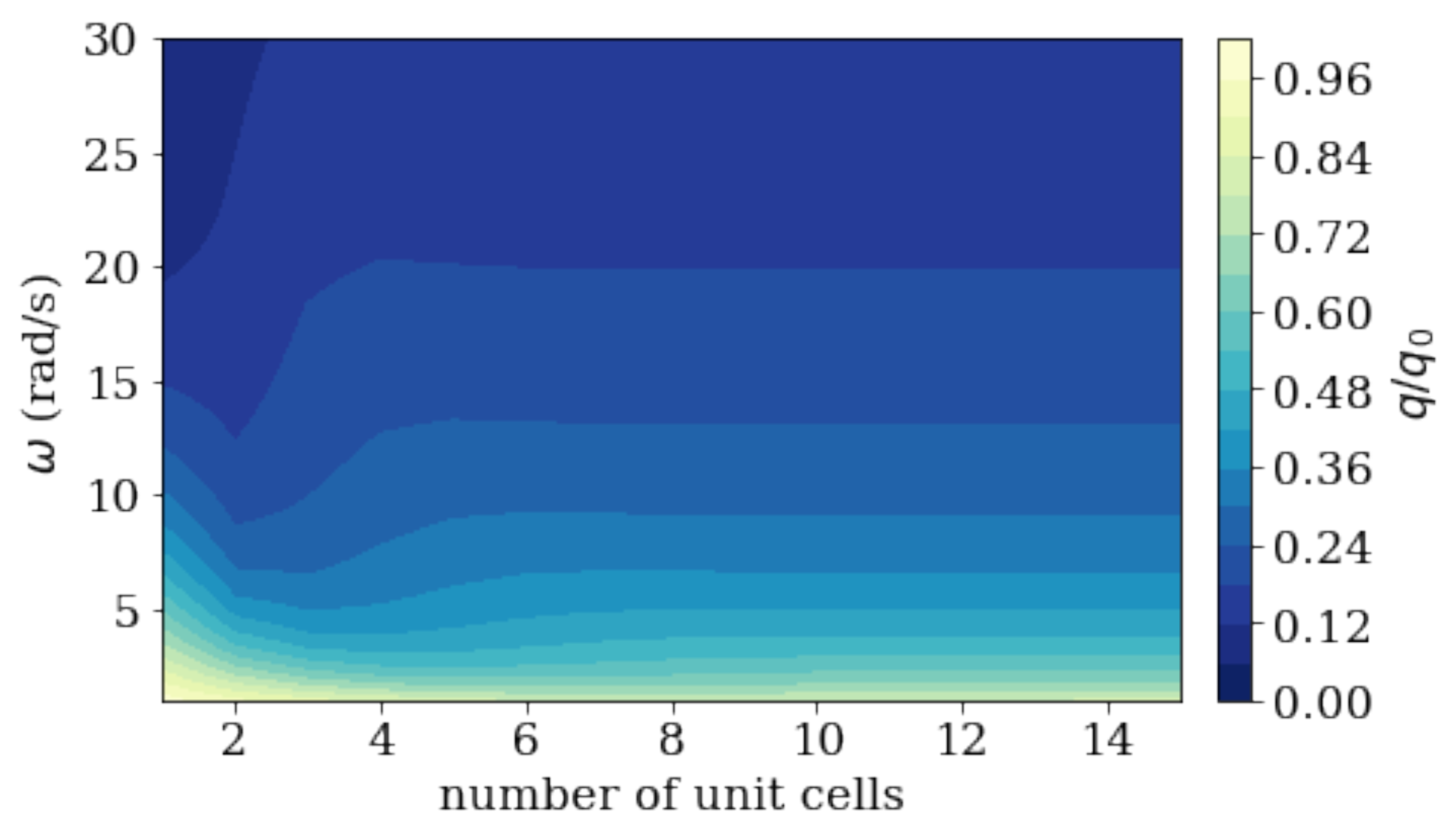
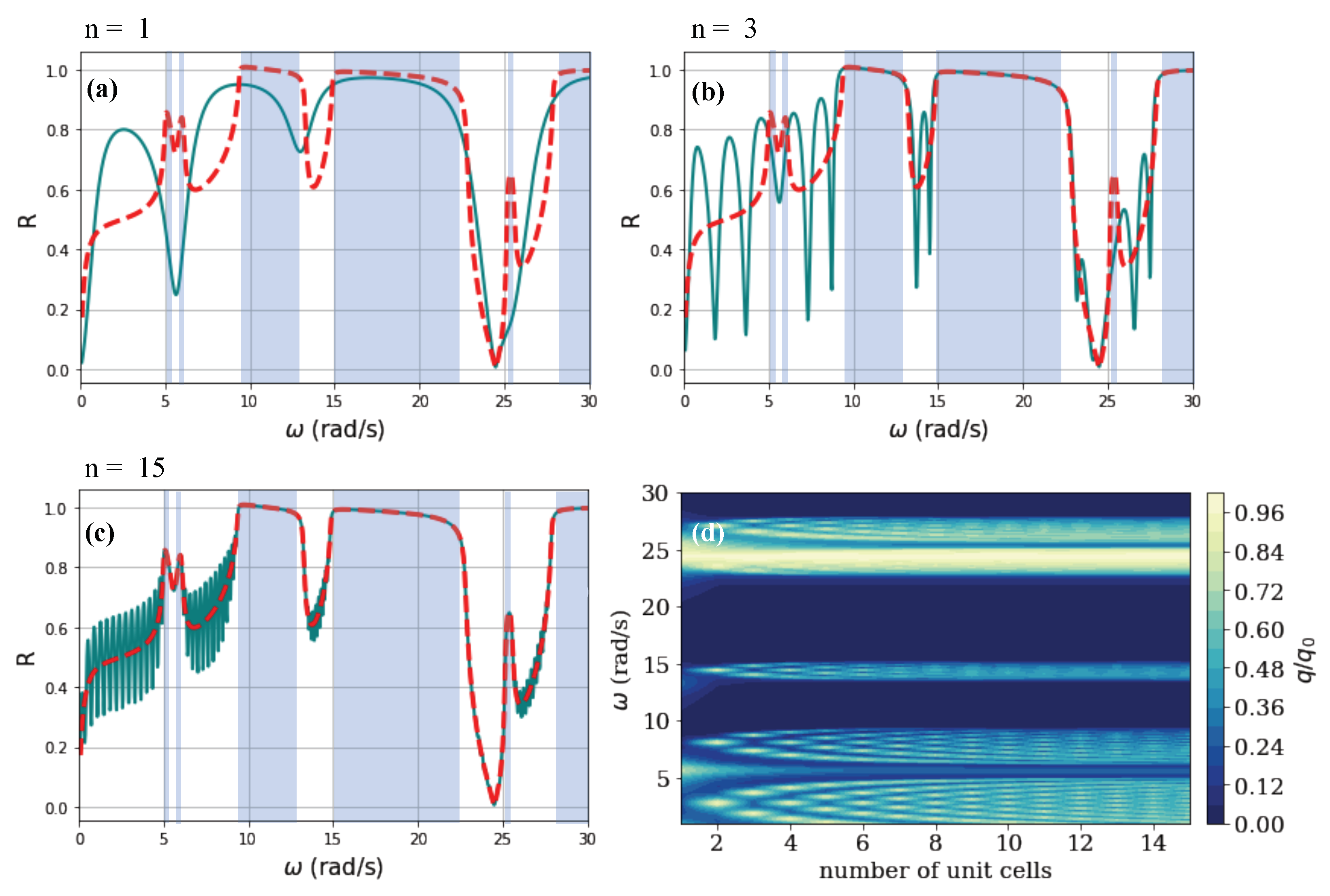
Tuning of the Thermal Reflectance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cattaneo, C. Sulla Conduzione Del Calore; Springer: Berlin/Heidelberg, Germany, 2011; p. 485. [Google Scholar]
- Vernotte, P. Les paradoxes de la théorie continue de lequation de la chaleur. CR Acad. Sci. Paris 1958, 246, 3154–3155. [Google Scholar]
- Kaminski, W. Hyperbolic Heat Conduction Equation for Materials with a Nonhomogeneous Inner Structure. J. Heat Trans. 1990, 112, 555–560. [Google Scholar] [CrossRef]
- Cassol, G.O.; Dubljevic, S. Hyperbolicity of the heat equation. IFAC-PapersOnLine 2019, 52, 63–67. [Google Scholar] [CrossRef]
- Joseph, D.D.; Preziosi, L. Heat waves. Rev. Mod. Phys. 1989, 61, 41. [Google Scholar] [CrossRef]
- Marín, E.; Vaca-Oyola, L.; Delgado-Vasallo, O. On thermal waves velocity: Some open questions in thermal waves’ physics. Rev. Mex. Fis. E 2016, 62, 1–4. [Google Scholar]
- Gandolfi, M.; Benetti, G.; Glorieux, C.; Giannetti, C.; Banfi, F. Accessing temperature waves: A dispersion relation perspective. Int. J. Heat Mass Trans. 2019, 143, 118553. [Google Scholar] [CrossRef] [Green Version]
- Roetzel, W.; Putra, N.; Das, S.K. Experiment and analysis for non-Fourier conduction in materials with non-homogeneous inner structure. Int. J. Therm. Sci. 2003, 42, 541–552. [Google Scholar] [CrossRef]
- Graßmann, A.; Peters, F. Experimental investigation of heat conduction in wet sand. Heat Mass Transf. 1999, 35, 289–294. [Google Scholar] [CrossRef]
- Jaunich, M.; Raje, S.; Kim, K.; Mitra, K.; Guo, Z. Bio-heat transfer analysis during short pulse laser irradiation of tissues. Int. J. Heat Mass Transf. 2008, 51, 5511–5521. [Google Scholar] [CrossRef]
- Mandhukar, A.; Park, Y.; Kim, W.; Sunaryanto, H.J.; Berlin, R.; Chamorro, L.P.; Bentsman, J.; Ostoja-Starzewski, M. Heat conduction in porcine muscle and blood: Experiments and time-fractional telegraph equation model. J. R. Soc. Interface 2019, 16, 20190726. [Google Scholar] [CrossRef] [PubMed]
- Mitra, K.; Kumar, S.; Vedevarz, A.; Moallemi, M.K. Experimental Evidence of Hyperbolic Heat Conduction in Processed Meat. J. Heat Transfer 1995, 117, 568–573. [Google Scholar] [CrossRef]
- Xu, F.; Seffen, K.A.; Lu, T.J. Non-Fourier analysis of skin biothermomechanics. Int. J. Heat Mass Transf. 2008, 51, 2237–2259. [Google Scholar] [CrossRef]
- Kovács, R.; Ván, P. Generalized heat conduction in heat pulse experiments. Int. J. Heat Mass Transf. 2015, 83, 613–620. [Google Scholar] [CrossRef] [Green Version]
- Ahmadikia, H.; Fazlali, R.; Moradi, A. Analytical solution of the parabolic and hyperbolic heat transfer equations with constant and transient heat flux conditions on skin tissue. Int. J. Heat Mass Transf. 2012, 39, 121–130. [Google Scholar] [CrossRef]
- Huberman, S.; Duncan, R.A.; Chen, K.; Song, B.; Chiloyan, V.; Ding, Z.; Maznev, A.A.; Chen, G.; Nelson, K.A. Observation of second sound in graphite at temperatures above 100 K. Science 2019, 364, 375–379. [Google Scholar] [CrossRef] [Green Version]
- Beardo, A.; López-Suárez, M.; Pérez, L.A.; Sendra, L.; Alonso, M.I.; Melis, C.; Bafaluy, J.; Camacho, J.; Colombo, L.; Rurali, R.; et al. Observation of second sound in a rapidly varying temperature field in Ge. Sci. Adv. 2021, 7, eabg4677. [Google Scholar] [CrossRef] [PubMed]
- Farhat, M.; Guenneau, S.; Chen, P.Y.; Alù, A.; Salama, K.N. Scattering Cancellation-Based Cloaking for the Maxwell-Cattaneo Heat Waves. Phys. Rev. Appl. 2019, 11, 044089. [Google Scholar] [CrossRef] [Green Version]
- Chen, A.L.; Li, Z.Y.; Ma, T.X.; Li, X.S.; Wang, Y.S. Heat reduction by thermal wave crystals. Int. J. Heat Mass Transf. 2018, 121, 215–222. [Google Scholar] [CrossRef] [Green Version]
- Gandolfi, M.; Giannetti, C.; Banfi, F. Temperonic crystal: A superlattice for temperature waves in graphene. Phys. Rev. Lett. 2020, 125, 265901. [Google Scholar] [CrossRef]
- Ordóñez-Miranda, J.; Alvarado-Gil, J. Effective thermal properties of layered systems under the parabolic and hyperbolic heat conduction models using pulsed heat sources. J. Heat Transf. 2011, 133. [Google Scholar] [CrossRef]
- Vázquez, F.; Ván, P.; Kovács, R. Ballistic-Diffusive Model for Heat Transport in Superlattices and the Minimum Effective Heat Conductivity. Entropy 2020, 22, 167. [Google Scholar] [CrossRef] [Green Version]
- Estrada-Wiese, D.; del Río, J.A.; de la Mora, M.B. Heat transfer in photonic mirrors. J. Mater. Sci. Mater. Electron. 2014, 25, 4348–4355. [Google Scholar] [CrossRef] [Green Version]
- Borca-Tasciuc, T.; Liu, W.; Liu, J.; Zeng, T.; Song, D.W.; Moore, C.D.; Chen, G.; Wang, K.L.; Goorsky, M.S.; Radetic, T.; et al. Thermal conductivity of symmetrically strained Si/Ge superlattices. Superlattices Microstruct. 2000, 28, 199–206. [Google Scholar] [CrossRef]
- Chen, G.; Neagu, M. Thermal conductivity and heat transfer in superlattices. Appl. Phys. Lett. 1997, 71, 2761–2763. [Google Scholar] [CrossRef]
- Esquivel-Sirvent, R.; Cocoletzi, G. Band structure for the propagation of elastic waves in superlattices. J. Acoust. Soc. Am. 1994, 95, 86–90. [Google Scholar] [CrossRef]
- El Boudouti, E.H.; Djafari-Rouhani, B. Acoustic waves in finite superlattices. Phys. Rev. B 1994, 49, 4586–4592. [Google Scholar] [CrossRef] [PubMed]
- De la Cruz, G.G. Bulk and surface plasmons in graphene finite superlattices. Superlattices Microstruct. 2019, 125, 315–321. [Google Scholar] [CrossRef]
- Jena, S.; Tokas, R.B.; Thakur, S.; Udupa, D.V. Tunable mirrors and filters in 1D photonic crystals containing polymers. Phys. E Low-Dimens. Syst. Nanostructures 2019, 114, 113627. [Google Scholar] [CrossRef]
- Al-sheqefi, F.; Belhadj, W. Photonic band gap characteristics of one-dimensional graphene-dielectric periodic structures. Superlattices Microstruct. 2015, 88, 127–138. [Google Scholar] [CrossRef]
- Kone, I.; Domingue, F.; Reinhardt, A.; Jacquinot, H.; Borel, M.; Gorisse, M.; Parat, G.; Casset, F.; Pellissier-Tanon, D.; Carpentier, J.; et al. Guided acoustic wave resonators using an acoustic Bragg mirror. Appl. Phys. Lett. 2010, 96, 223504. [Google Scholar] [CrossRef]
- Herrera, L. Causal heat conduction contravening the fading memory paradigm. Entropy 2019, 21, 950. [Google Scholar] [CrossRef] [Green Version]
- Barletta, A.; Zanchini, E. Hyperbolic heat conduction and local equilibrium: A second law analysis. Int. J. Heat Mass Transf. 1997, 40, 1007–1016. [Google Scholar] [CrossRef]
- Özısık, M.N. Heat Conduction; Wiley-Interscience Publication: Hoboken, NJ, USA, 1993. [Google Scholar]
- Bockh, P.V.; Wetzel, T. Heat Transfer, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 1993; Volume 4. [Google Scholar]
- Ostoja-Starzewski, M. A derivation of the Maxwell–Cattaneo equation from the free energy and dissipation potentials. Int. J. Eng. Sci. 2009, 47, 807–810. [Google Scholar] [CrossRef]
- Thidé, B. Electromagnetic Field Theory; Upsilon Books: Uppsala, Sweden, 2004. [Google Scholar]
- Camacho de la Rosa, A.; Becerril, D.; Gómez-Farfán, G.; Esquivel-Sirvent, R. Time-Harmonic Photothermal Heating by Nanoparticles in a Non-Fourier Medium. J. Phys. Chem. C 2021, 125, 22856–22862. [Google Scholar] [CrossRef]
- Berto, P.; Mohamed, M.S.A.; Rigneault, H.; Baffou, G. Time-harmonic optical heating of plasmonic nanoparticles. Phys. Rev. B 2014, 90, 035439. [Google Scholar] [CrossRef] [Green Version]
- Green, D.R. Thermal Surface Impedance for Plane Heat Waves in Layered Materials. J. Appl. Phys. 1966, 37, 3095–3099. [Google Scholar] [CrossRef]
- Li, B.c.; Zhang, S.y. The effect of interface resistances on thermal wave propagation in multi-layered samples. J. Phys. D Appl. Phys. 1997, 30, 1447. [Google Scholar] [CrossRef]
- Pérez-Álvarez, R.; García-Moliner, F. Transfer Matrix, Green Function and Related Techniques: Tools for the Study of Multilayer Heterostructures; Publicacions de la Universitat Jaume I: Castellón, Spain, 2004. [Google Scholar]
- Patel, H.A.; Garde, S.; Keblinski, P. Thermal resistance of nanoscopic liquid-liquid interfaces: Dependence on chemistry and molecular architecture. Nano Lett. 2005, 5, 2225–2231. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.R.; Vo, T.Q.; Kim, B. Manipulating thermal resistance at the solid–fluid interface through monolayer deposition. RSC Adv. 2019, 9, 4948–4956. [Google Scholar] [CrossRef] [Green Version]
- Knobel, R. An Introduction to the Mathematical Theory of Waves; American Mathematical Society: Providence, RI, USA, 2000; Volume 3. [Google Scholar]
- Ranut, P.; Nobile, E. On the effective thermal conductivity of metal foams. J. Phys. Conf. Ser. 2014, 547, 012021. [Google Scholar] [CrossRef]
- Kundu, B. Exact analysis for propagation of heat in a biological tissue subject to different surface conditions for therapeutic applications. Appl. Math. Comput. 2016, 285, 204–216. [Google Scholar] [CrossRef]
- Craciunescu, O.I.; Howle, L.E.; Clegg, S.T. Experimental evaluation of the thermal properties of two tissue equivalent phantom materials. Int. J. Hypertherm. 1999, 15, 509–518. [Google Scholar]
- Sánchez, A.; Porta, A.V.; Orozco, S. Photonic band-gap and defect modes of a one-dimensional photonic crystal under localized compression. J. Appl. Phys. 2017, 121, 173101. [Google Scholar] [CrossRef]
- Scalora, M.; Bloemer, M.J.; Pethel, A.S.; Dowling, J.P.; Bowden, C.M.; Manka, A.S. Transparent, metallo-dielectric, one-dimensional, photonic band-gap structures. J. Appl. Phys. 1998, 83, 2377–2383. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P. Band-gap engineering in periodic elastic composites. Appl. Phys. Lett. 1994, 64, 1085–1087. [Google Scholar] [CrossRef]
- Esquivel-Sirvent, R.; Noguez, C. Theory of the acoustic signature of topological and morphological defects in SiC/porous SiC laminated ceramics. J. Appl. Phys. 1997, 82, 3618–3620. [Google Scholar] [CrossRef]

| Material | Thermal Conductivity (Wm K) | Specific Heat Capacity (J kg K) | Mass Density (Kg m) | Response Time (s) |
|---|---|---|---|---|
| epidermis (m1) | 0.235 | 3600 | 1500 | 1 |
| dermis (m2) | 0.445 | 3300 | 1116 | 20 |
| Al | 237 | 921 | 2707 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Camacho de la Rosa, A.; Becerril, D.; Gómez-Farfán, M.G.; Esquivel-Sirvent, R. Bragg Mirrors for Thermal Waves. Energies 2021, 14, 7452. https://doi.org/10.3390/en14227452
Camacho de la Rosa A, Becerril D, Gómez-Farfán MG, Esquivel-Sirvent R. Bragg Mirrors for Thermal Waves. Energies. 2021; 14(22):7452. https://doi.org/10.3390/en14227452
Chicago/Turabian StyleCamacho de la Rosa, Angela, David Becerril, María Guadalupe Gómez-Farfán, and Raúl Esquivel-Sirvent. 2021. "Bragg Mirrors for Thermal Waves" Energies 14, no. 22: 7452. https://doi.org/10.3390/en14227452
APA StyleCamacho de la Rosa, A., Becerril, D., Gómez-Farfán, M. G., & Esquivel-Sirvent, R. (2021). Bragg Mirrors for Thermal Waves. Energies, 14(22), 7452. https://doi.org/10.3390/en14227452