3DHIP-Calculator—A New Tool to Stochastically Assess Deep Geothermal Potential Using the Heat-In-Place Method from Voxel-Based 3D Geological Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mathematical Background of the HIP Method
2.2. Mathematical Background of the Monte Carlo Method
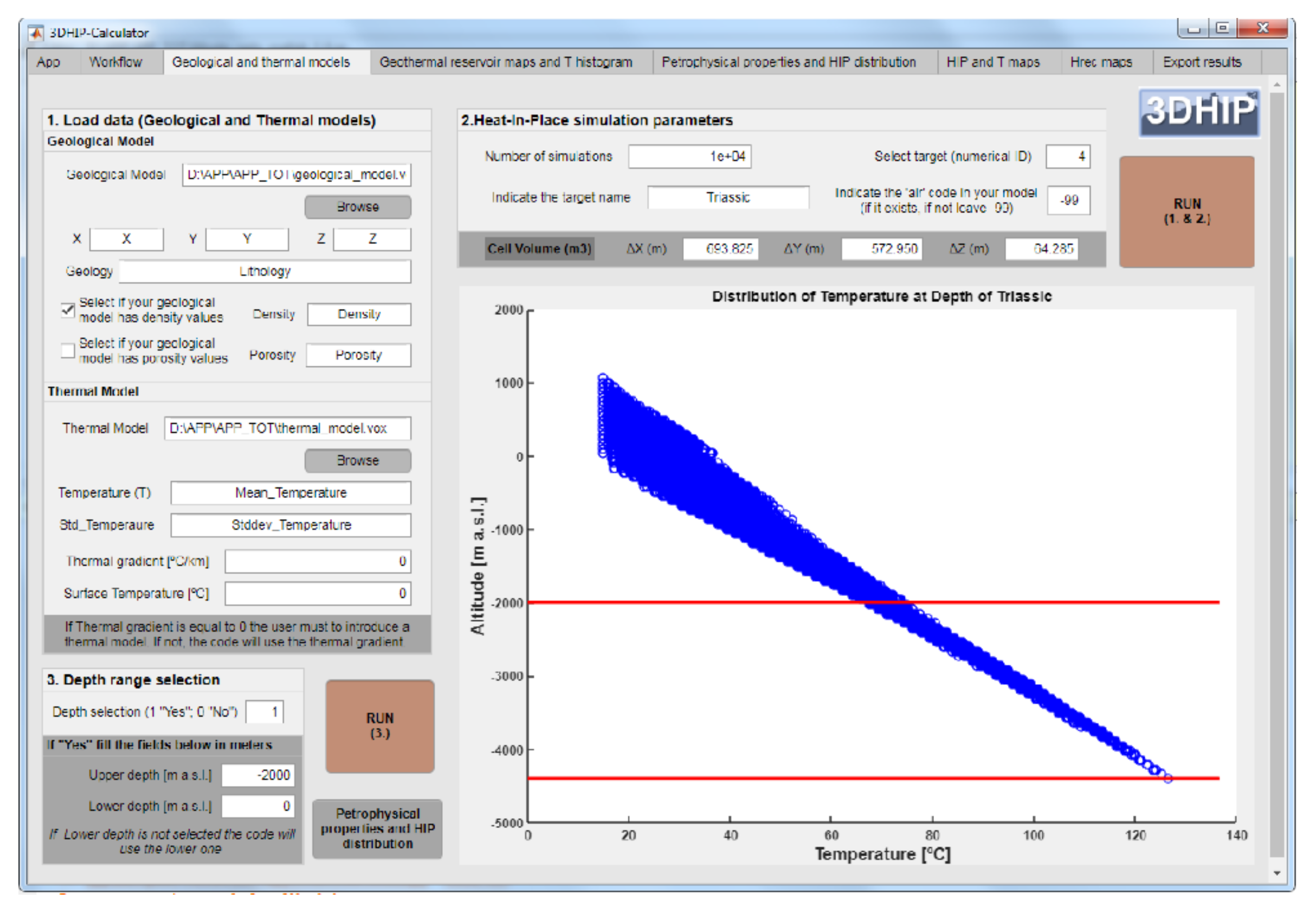
2.3. Program Description
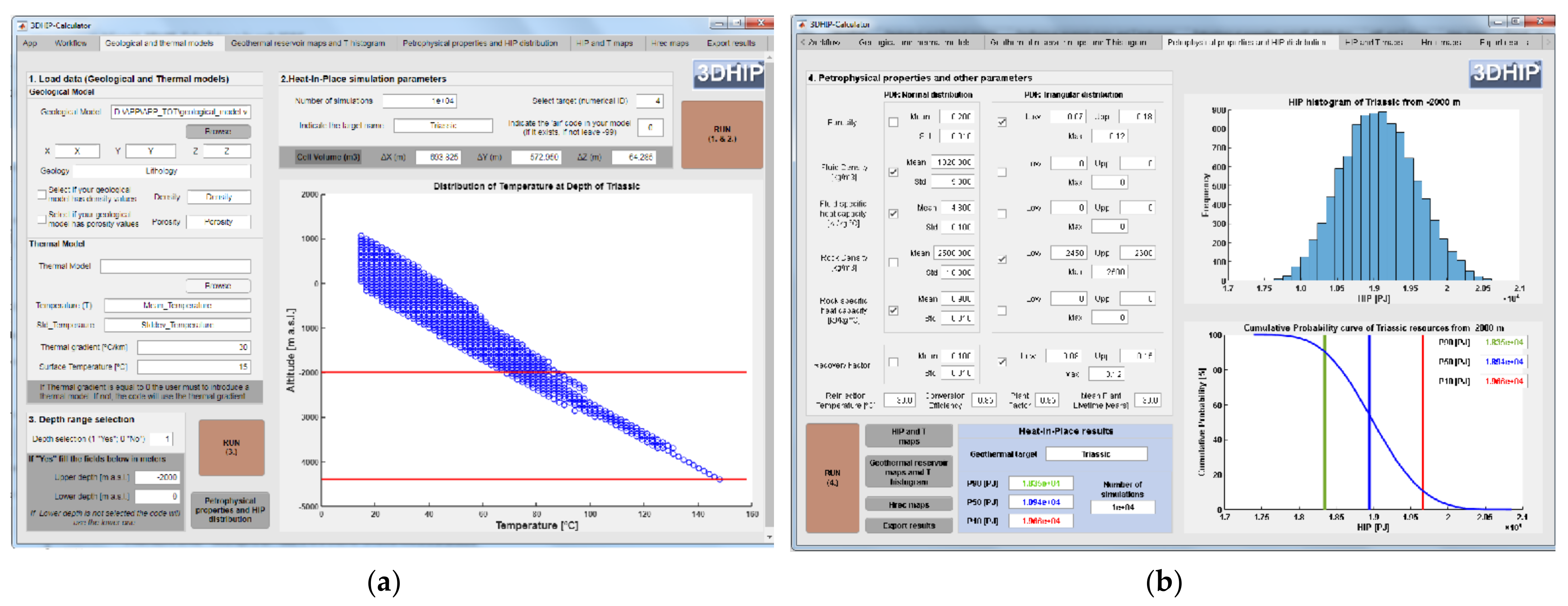
2.3.1. Pre-Processing: Input Data
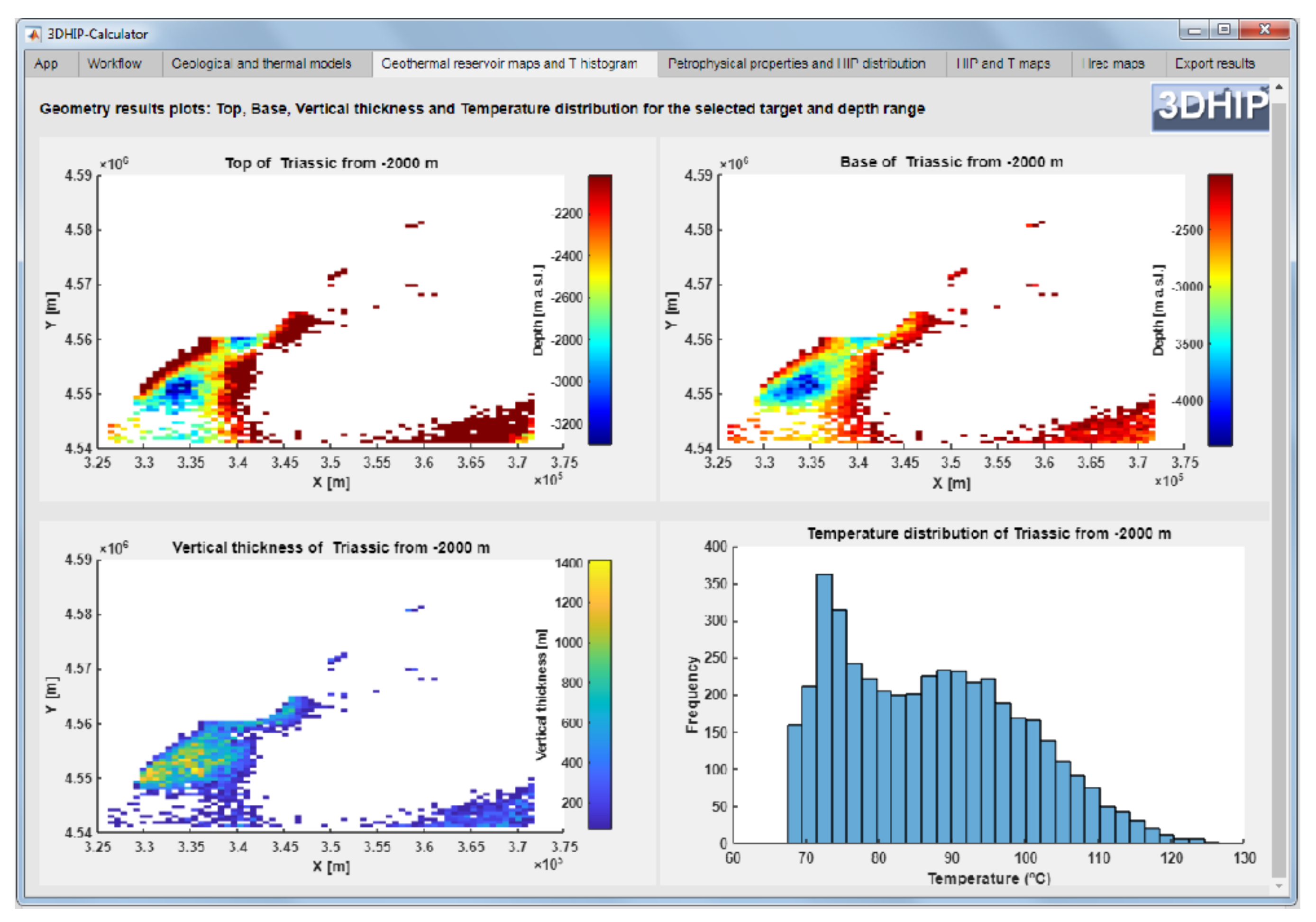
2.3.2. Post-Processing: Output Data
- Generate a CDF for each voxel, from which a probability 10% (P10) (very low confidence of the estimation and high values), P50, and P90 (high confidence of the estimation and low values) are extracted. Furthermore, the mean and standard deviation are also calculated.
- Generate a CDF for the entire investigated target (e.g., geological unit, reservoir, etc.) summing the voxel values, and the P10, P50, and P90 are calculated. This approach is only used for the HIP calculation and not for the Hrec one.
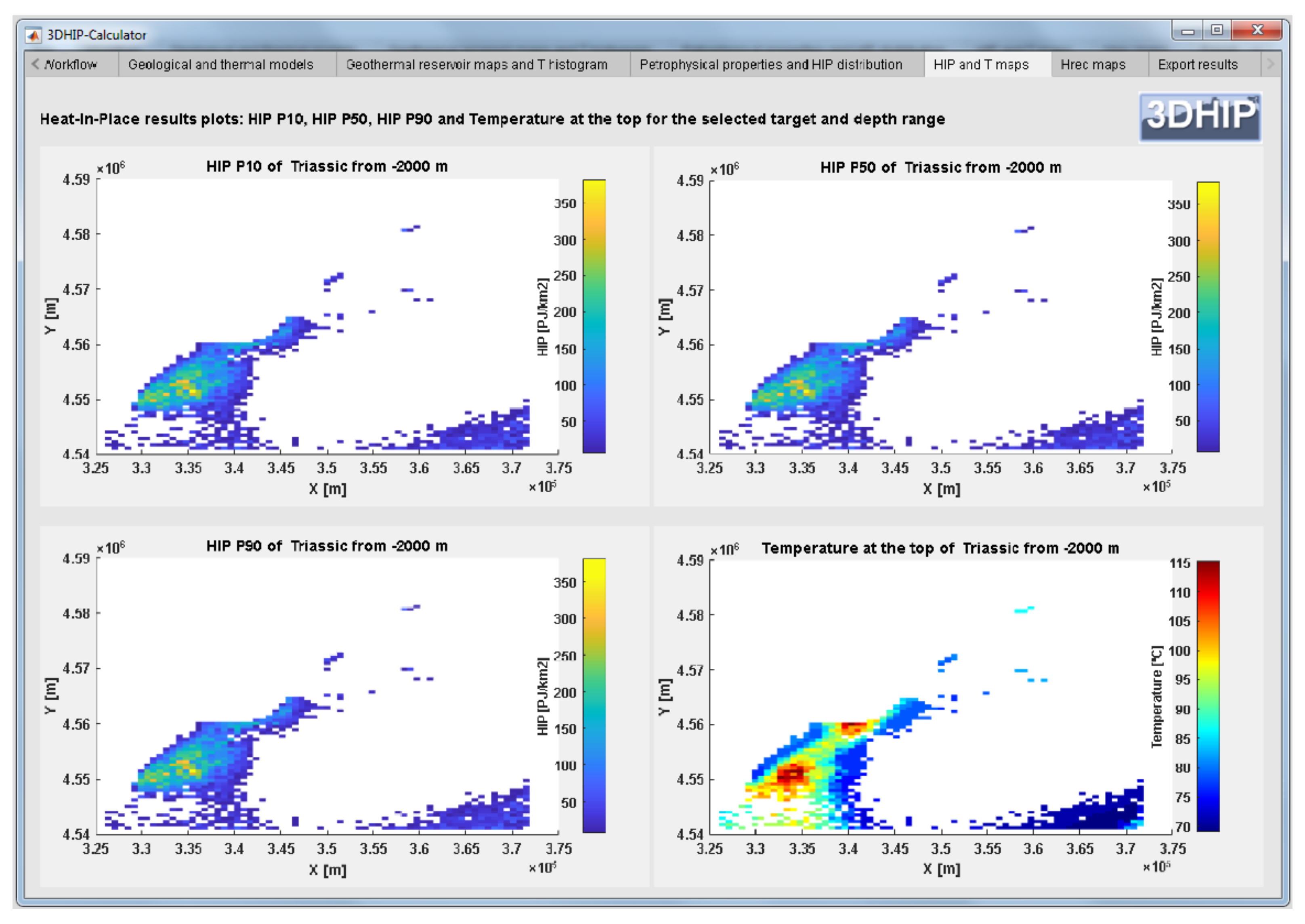
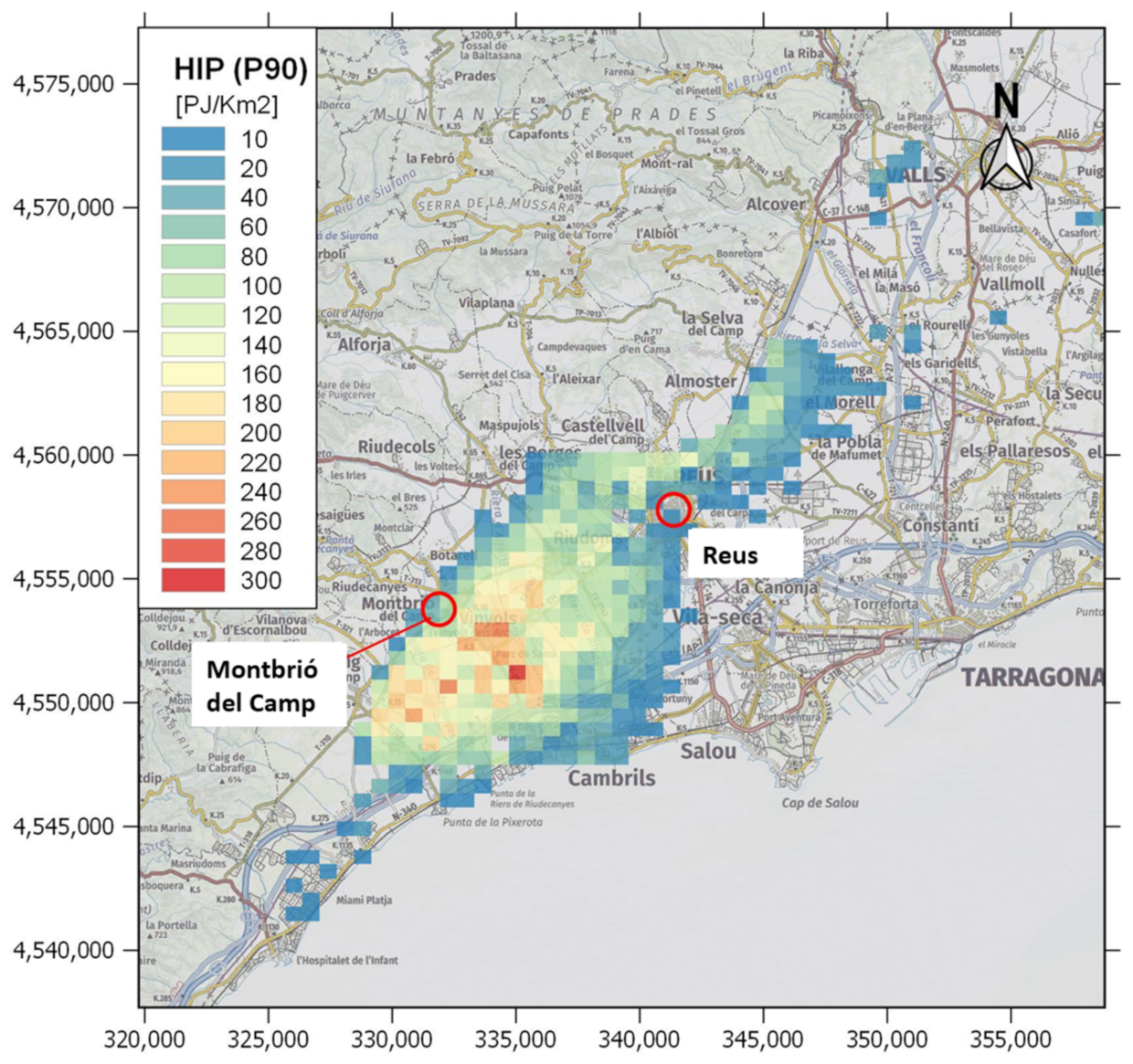
- Generate 2D maps using the relationship between the vertical sum of the values calculated in each voxel with respect to the area occupied by the voxel (in km2). The P10, P50, and P90 of HIP and Hrec are then estimated.
- The application allows exporting two ASCII files with all results for further post-processing and generates an automatic report that summarizes the input data and the main results.
2.3.3. Modeling Scenarios Depending on Data Availability
3. Example Case Study—The Reus-Valls Basin (NE, Spain)
3.1. Geological Setting

3.2. The Potential Hot Deep Sedimentary Aquifers
3.2.1. Example 1: Using a Single-Voxel 1D Geological Model
3.2.2. Example 2: Using a 3DGM but Not a 3DTM
3.2.3. Example 3: Using Both a 3DGM and a 3DTM
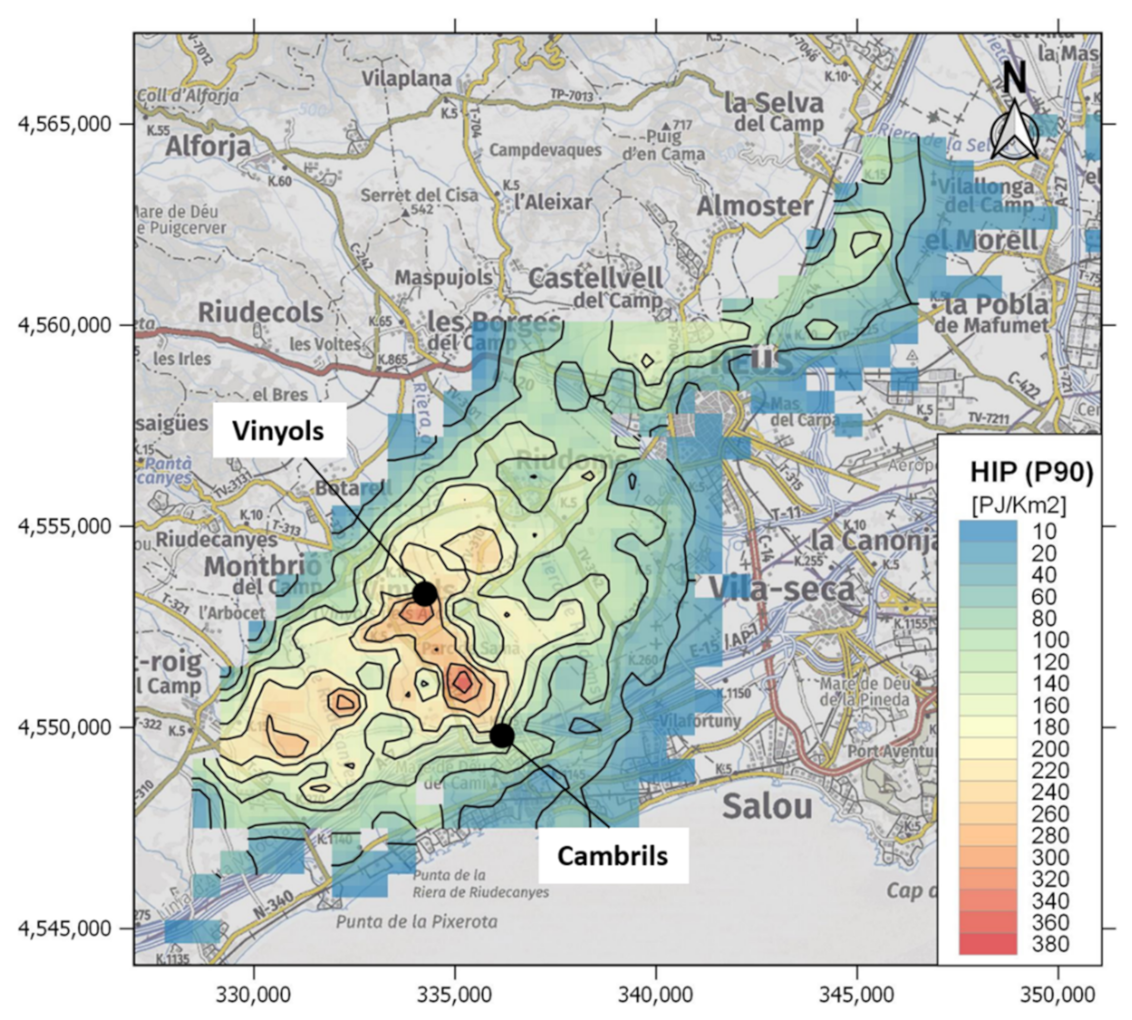
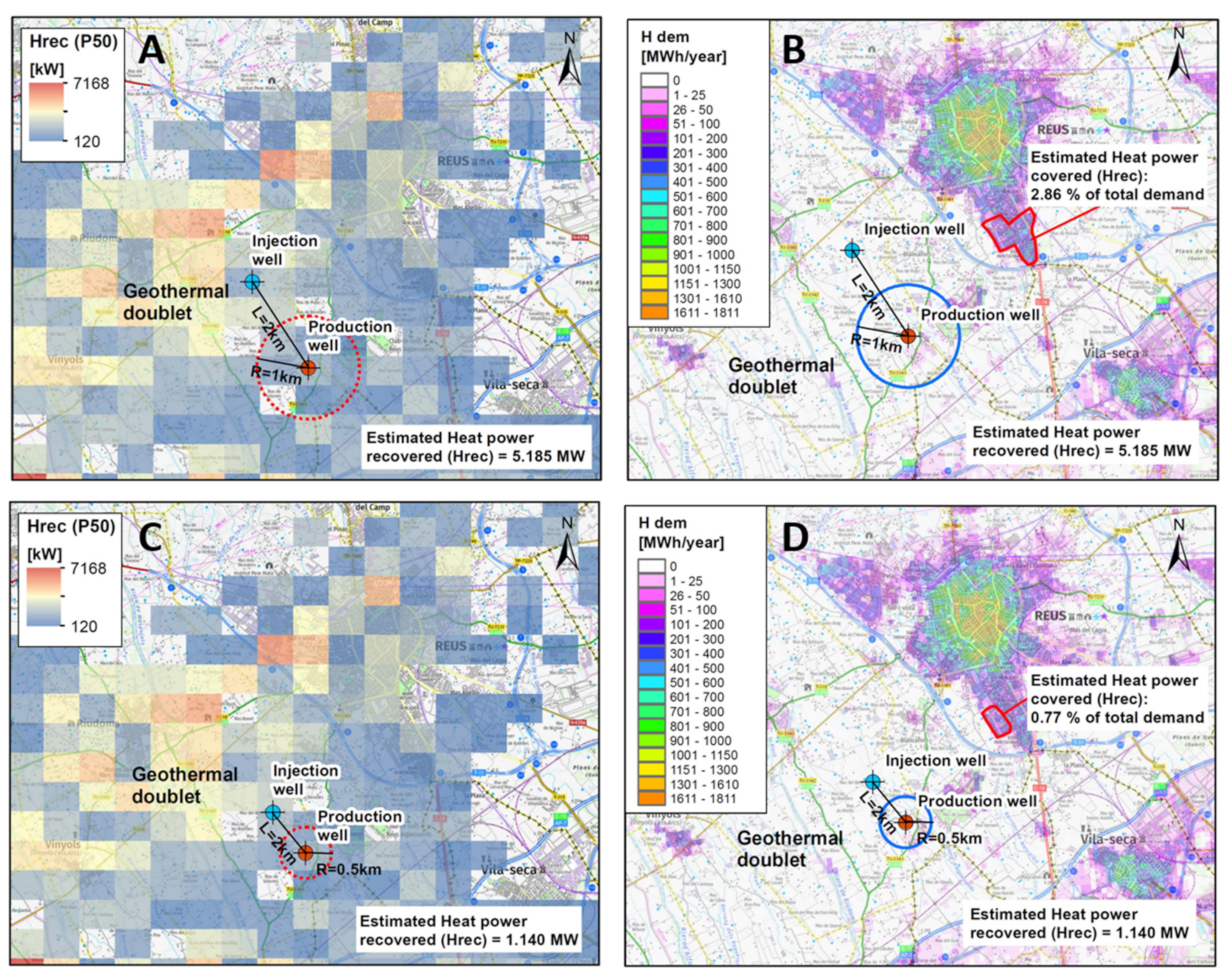
3.2.4. Example 4: The Use of the Recoverable Heat (Hrec) Values
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bertani, R. Geothermal Power Generation in the World 2010–2015 Update Report. In Proceedings of the World Geothermal Congress 2015, Melbourne, Australia, 19–25 April 2015; pp. 19–25. [Google Scholar]
- Sigfússon, B.; Uihlein, A. 2015 JRC Geothermal Energy Status Report; EUR 27623 EN; Joint Research Center: Petten, The Netherlands, 2015; p. 59. [Google Scholar] [CrossRef]
- Van Wees, J.-D.; Boxem, T.; Angelino, L.; Dumas, P. A Prospective Study on the Geothermal Potential in the EU. GEOLEC Project; EC: Utrecht, The Netherlands, 2013; p. 97. [Google Scholar]
- Agemar, T.; Weber, J.; Moeck, I. Assessment and Public Reporting of Geothermal Resources in Germany: Review and Outlook. Energies 2018, 11, 332. [Google Scholar] [CrossRef] [Green Version]
- Muffler, P.; Cataldi, R. Methods for Regional Assessment of Geothermal Resources. Geothermics 1978, 7, 53–89. [Google Scholar] [CrossRef] [Green Version]
- Williams, C.F. Updated Methods for Estimating Recovery Factors for Geothermal Resources. In Proceedings of the Thirty-Second Workshop on Proceedings, Geothermal Reservoir Engineering, Stanford University, Stanford, CA, USA, 22 January 2007; p. 7. [Google Scholar]
- Williams, C.F.; Reed, M.J.; Mariner, R.H. A Review of Methods Applied by the U.S. Geological Survey in the Assessment of Identified Geothermal Resources; U.S. Geological Survey: Reston, VA, USA, 2008; p. 30.
- Garg, S.K.; Combs, J. Appropriate Use of USGS Volumetric “Heat in Place” Method and Monte Carlo Calculations. In Proceedings of the Thirty-Fourth Workshop on Geothermal Reservoir Engineering, Stanford University, Stanford, CA, USA, 1 February 2010; p. 7. [Google Scholar]
- Garg, S.K.; Combs, J. A Reexamination of USGS Volumetric “Heat in Place” Method. In Proceedings of the Thirty-Sixth Workshop on Geothermal Reservoir Engineering, Stanford University, Stanford, CA, USA, 31 February 2011; p. 5. [Google Scholar]
- Garg, S.K.; Combs, J. A Reformulation of USGS Volumetric “Heat in Place” Resource Estimation Method. Geothermics 2015, 55, 150–158. [Google Scholar] [CrossRef]
- Limberger, J.; Boxem, T.; Pluymaekers, M.; Bruhn, D.; Manzella, A.; Calcagno, P.; Beekman, F.; Cloetingh, S.; van Wees, J.-D. Geothermal Energy in Deep Aquifers: A Global Assessment of the Resource Base for Direct Heat Utilization. Renew. Sustain. Energy Rev. 2018, 82, 961–975. [Google Scholar] [CrossRef]
- Trumpy, E.; Botteghi, S.; Caiozzi, F.; Donato, A.; Gola, G.; Montanari, D.; Pluymaekers, M.P.D.; Santilano, A.; van Wees, J.D.; Manzella, A. Geothermal Potential Assessment for a Low Carbon Strategy: A New Systematic Approach Applied in Southern Italy. Energy 2016, 103, 167–181. [Google Scholar] [CrossRef]
- Miranda, M.M.; Raymond, J.; Dezayes, C. Uncertainty and Risk Evaluation of Deep Geothermal Energy Source for Heat Production and Electricity Generation in Remote Northern Regions. Energies 2020, 13, 4221. [Google Scholar] [CrossRef]
- Arango-Galván, C.; Prol-Ledesma, R.M.; Torres-Vera, M.A. Geothermal Prospects in the Baja California Peninsula. Geothermics 2015, 55, 39–57. [Google Scholar] [CrossRef] [Green Version]
- Pol-Ledesma, R.-M.; Carrillo-de la Cruz, J.-L.; Torres-Vera, M.-A.; Membrillo-Abad, A.-S.; Espinoza-Ojeda, O.-M. Heat Flow Map and Geothermal Resources in Mexico / Mapa de Flujo de Calor y Recursos Geotérmicos de México. Terra Digit. 2018. [Google Scholar] [CrossRef]
- Hurter, S.; Schellschmidt, R. Atlas of Geothermal Resources in Europe. Geothermics 2003, 32, 779–787. [Google Scholar] [CrossRef]
- Nathenson, M. Methodology of Determining the Uncertainty in the Accessible Geothermal Resource Base of Identified Hydrothermal Convec-Tion Systems; Open-File Report; U.S. Geological Survey: Menlo Park, CA, USA, 1978; p. 51.
- Rubinstein, R.Y.; Kroese, D.P. Simulation and the Monte Carlo Method, 3rd ed.; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 2017; ISBN 978-1-118-63220-8. [Google Scholar]
- Shah, M.; Vaidya, D.; Sircar, A. Using Monte Carlo Simulation to Estimate Geothermal Resource in Dholera Geothermal Field, Gujarat, India. Multiscale Multidiscip. Model. Exp. Des. 2018, 1, 83–95. [Google Scholar] [CrossRef]
- Trota, A.; Ferreira, P.; Gomes, L.; Cabral, J.; Kallberg, P. Power Production Estimates from Geothermal Resources by Means of Small-Size Compact Climeon Heat Power Converters: Case Studies from Portugal (Sete Cidades, Azores and Longroiva Spa, Mainland). Energies 2019, 12, 2838. [Google Scholar] [CrossRef] [Green Version]
- Palisade Corporation. @Risk for Excel; Palisade Corporation: Ithaca, NY, USA, 2014. [Google Scholar]
- Oracle. Oracle Crystal Ball Spreadsheet Functions for Use in Microsoft Excel Models; Oracle: Austin, TX, USA, 2014. [Google Scholar]
- Arkan, S.; Parlaktuna, M. Resource Assessment of Balçova Geothermal Field. In Proceedings of the World Geothermal Congress 2005, Antalya, Turkey, 24–29 April 2005. [Google Scholar]
- Yang, F.; Liu, S.; Liu, J.; Pang, Z.; Zhou, D. Combined Monte Carlo Simulation and Geological Modeling for Geothermal Resource Assessment: A Case Study of the Xiongxian Geothermal Field, China. In Proceedings of the World Geothermal Congress 2015, Melbourne, Australia, 19–25 April 2015; pp. 19–25. [Google Scholar]
- Halcon, R.M.; Kaya, E.; Penarroyo, F. Resource Assessment Review of the Daklan Geothermal Prospect, Benguet, Philippines. In Proceedings of the World Geothermal Congress 2015, Melbourne, Australia, 19–25 April 2015; pp. 19–25. [Google Scholar]
- Barkaoui, A.-E.; Zarhloule, Y.; Varbanov, P.S.; Klemes, J.J. Geothermal Power Potential Assessment in North Eastern Morocco. Chem. Eng. Trans. 2017, 61, 1627–1632. [Google Scholar] [CrossRef]
- Pocasangre, C.; Fujimitsu, Y. Geothermics A Python-Based Stochastic Library for Assessing Geothermal Power Potential Using the Volumetric Method in a Liquid-Dominated Reservoir. Geothermics 2018, 76, 164–176. [Google Scholar] [CrossRef]
- Zhu, Z.; Lei, X.; Xu, N.; Shao, D.; Jiang, X.; Wu, X. Integration of 3D Geological Modeling and Geothermal Field Analysis for the Evaluation of Geothermal Reserves in the Northwest of Beijing Plain, China. Water 2020, 12, 638. [Google Scholar] [CrossRef] [Green Version]
- Calcagno, P.; Baujard, C.; Dagallier, A.; Guillou-Frottier, L.; Genter, A. Three-Dimensional Estimation of Geothermal Potential from Geological Field Data: The Limagne Geothermal Reservoir Case Study (France). In Proceedings of the Geothermal Resources Council GRC Annual Meeting, Reno, NV, USA, 4–7 October 2009; p. 326. [Google Scholar]
- Van Wees, J.-D.; Juez-Larre, J.; Bonte, D.; Mijnlieff, H.; Kronimus, A.; Gesse, S.; Obdam, A.; Verweij, H. ThermoGIS: An Integrated Web-Based Information System for Geothermal Exploration and Governmental Decision Support for Mature Oil and Gas Basins. In Proceedings of the World Geothermal Congress 2010, Bali, Indonesia, 25 April 2010; p. 7. [Google Scholar]
- Kramers, L.; van Wees, J.-D.; Pluymaekers, M.P.D.; Kronimus, A.; Boxem, T. Direct Heat Resource Assessment and Subsurface Information Systems for Geothermal Aquifers; the Dutch Perspective. Neth. J. Geosci. 2012, 91, 637–649. [Google Scholar] [CrossRef] [Green Version]
- Vrijlandt, M.A.W.; Struijk, E.L.M.; Brunner, L.G.; Veldkamp, J.G.; Witmans, N.; Maljers, D.; van Wees, J.D. ThermoGIS Update: A Renewed View on Geothermal Potential in the Netherlands. In Proceedings of the European Geothermal Congress 2019, The Hague, The Netherlands, 11 June 2019; p. 10. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Herms, I.; Piris, G.; Colomer, M.; Peigney, C.; Griera, A.; Ledo, J. 3D Numerical Modelling Combined with a Stochastic Approach in a MATLAB-Based Tool to Assess Deep Geothermal Potential in Catalonia: The Case Test Study of the Reus-Valls Basin. In Proceedings of the World Geothermal Congress 2020 + 1, Reykjavik, Iceland, 24–27 October 2021; p. 9. [Google Scholar]
- ICGC. Geothermal Atlas of Catalonia: Geoindex-Deep-Geothermal. 2020. Available online: https://www.icgc.cat/en/Public-Administration-and-Enterprises/Tools/Geoindex-viewers/Geoindex-Deep-geothermal-energy (accessed on 15 October 2021).
- Colmenar-Santos, A.; Folch-Calvo, M.; Rosales-Asensio, E.; Borge-Diez, D. The Geothermal Potential in Spain. Renew. Sustain. Energy Rev. 2016, 56, 865–886. [Google Scholar] [CrossRef]
- Arrizabalaga, I.; De Gregorio, M.; De Santiago, C.; Pérez, P. Geothermal Energy Use, Country Update for Spain. In Proceedings of the European Geothermal Congress 2019, The Hague, The Netherlands, 11 June 2019; p. 9. [Google Scholar]
- Beardsmore, G.R.; Rybach, L.; Blackwell, D.; Baron, C. A Protocol for Estimating and Mapping Global EGS Potential. Geotherm. Resour. Counc. Trans. 2010, 34, 301–312. [Google Scholar]
- Hurter, S.; Haenel, R. Atlas of Geothermal Resources in Europe; Official Publications of the European Communities, European Commission: Luxembourg, 2002. [Google Scholar]
- Lavigne, J. Les Resources Geothérmiques Françaises-Possibilités de Mise En Valeur. Ann. Mines 1977, 57–72. [Google Scholar]
- Williams, C.F. Development of Revised Techniques for Assessing Geothermal Resources. In Proceedings of the Twenty-Ninth Workshop on Geothermal Reservoir Engineering, Stanford University, Stanford, CA, USA, 26 January 2004; p. 5. [Google Scholar]
- Lund, J.W.; Boyd, T.L. Direct Utilization of Geothermal Energy 2015 Worldwide Review. Geothermics 2016, 60, 66–93. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Bai, Y.; Wang, Z.; Hu, J.; Hu, D.; Wang, Y.; Hu, S. Assessment of Geothermal Resources in the North Jiangsu Basin, East China, Using Monte Carlo Simulation. Energies 2021, 14, 259. [Google Scholar] [CrossRef]
- MathWorks. MATLAB; The MathWorks, Inc.: Natick, MA, USA, 2019. [Google Scholar]
- Moeck, I.; Beardsmore, G.R. A New ‘Geothermal Play Type’ Catalog: Streamlining Exploration Decision Making. In Proceedings of the Thirty-Ninth Workshop on Geothermal Reservoir Engineering, Stanford University, Stanford, CA, USA, 24 February 2014; p. 8. [Google Scholar]
- De la Varga, M.; Schaaf, A.; Wellmann, F. GemPy 1.0: Open-Source Stochastic Geological Modeling and Inversion. Geosci. Model Dev. 2019, 12, 1–32. [Google Scholar] [CrossRef] [Green Version]
- Massana, E. L’activitat Neotectònica a Les Cadenes Costaneres Catalanes. Ph.D. Thesis, University of Barcelona, Barcelona, Spain, 1995. [Google Scholar]
- Cabrera, L.; Calvet, F. Onshore Neogene record in NE Spain: Vallès–Penedès and El Camp half-grabens (NW Mediterranean). In Tertiary Basins of Spain; Friend, P.F., Dabrio, C.J., Eds.; Cambridge University Press: Cambridge, UK, 1996; pp. 97–105. ISBN 978-0-521-46171-9. [Google Scholar]
- Moeck, I.S. Catalog of Geothermal Play Types Based on Geologic Controls. Renew. Sustain. Energy Rev. 2014, 37, 867–882. [Google Scholar] [CrossRef] [Green Version]
- ICGC. Base Geològica 1:50.000 de Catalunya. Available online: https://www.icgc.cat/en/Public-Administration-and-Enterprises/Downloads/Geological-and-geothematic-cartography/Geological-cartography/Geological-map-1-50-000 (accessed on 1 January 2021).
- Moeck, I.S.; Dussel, M.; Weber, J.; Schintgen, T.; Wolfgramm, M. Geothermal Play Typing in Germany, Case Study Molasse Basin: A Modern Concept to Categorise Geothermal Resources Related to Crustal Permeability. Neth. J. Geosci. 2019, 98, e14. [Google Scholar] [CrossRef] [Green Version]
- Lopez, S.; Hamm, V.; Le Brun, M.; Schaper, L.; Boissier, F.; Cotiche, C.; Giuglaris, E. 40 Years of Dogger Aquifer Management in Ile-de-France, Paris Basin, France. Geothermics 2010, 39, 339–356. [Google Scholar] [CrossRef]
- Blöcher, G.; Reinsch, T.; Henninges, J.; Milsch, H.; Regenspurg, S.; Kummerow, J.; Francke, H.; Kranz, S.; Saadat, A.; Zimmermann, G.; et al. Hydraulic History and Current State of the Deep Geothermal Reservoir Groß Schönebeck. Geothermics 2016, 63, 27–43. [Google Scholar] [CrossRef]
- Haffen, S.; Géraud, Y.; Diraison, M.; Dezayes, C.; Siffert, D.; Garcia, M. Temperature Gradient Anomalies in the Buntsandstein Sandstone Reservoir, Upper Rhine Graben, Soultz, France. In Proceedings of the Tu D203 09—76th EAGE Conference & Exhibition 2014, Amsterdam, The Netherlands, 16 June 2014. [Google Scholar]
- Zapatero, M.A.; Reyes, J.L.; Martínez, R.; Suárez, I.; Arenillas, A.; Perucha, M.A. Estudio Preliminar de las Formaciones Favorables para el Almacenamiento Subterráneo de CO2 en España; Instituto Geológico y Minero de España (IGME): Madrid, Spain, 2009; p. 135. [Google Scholar]
- AURENSA. Proyecto de Almacenamientos Subterraneos de Gas. Reus; Auxiliar de Recursos y Energía, S.A.: Madrid, Spain, 1996; p. 65. [Google Scholar]
- Campos, R.; Recreo, F.; Perucha, M.A. AGP de CO2: Selección de Formaciones Favorables en la Cuenca del Ebro; Informes Técnicos Ciemat; CIEMAT: Madrid, España, 2007; p. 124. [Google Scholar]
- Marzo, M. El Bundstandstein de los Catalánides: Estratigrafía y Procesos Sedimentarios. Ph.D. Thesis, Universitat de Barcelona, Barcelona, Spain, 1980. [Google Scholar]
- Zapatero, M.A.; Suárez, I.; Arenillas, A.; Marina, M.; Catalina, R.; Martínez-Orío, R. Proyecto Europeo GeoCapacity. Assessing European Capacity for Geological Storage of Carbon Dioxide; Instituto Geológico y Minero de España (IGME): Madrid, España, 2009; p. 162. [Google Scholar]
- ICGC. Model d’Elevacions Del Terreny de Catalunya 15 × 15 Metres (MET-15) v2.0. 2018. Available online: https://www.icgc.cat/Descarregues/Elevacions/Model-d-elevacions-del-terreny-de-15x15-m (accessed on 11 January 2021).
- ICGC. Mapa Geològic Comarcal de Catalunya. Full Del Baix Camp. 2006. Available online: https://www.icgc.cat/en/Public-Administration-and-Enterprises/Downloads/Geological-and-geothematic-cartography/Geological-cartography/Geological-map-1-50-000 (accessed on 11 January 2021).
- ICGC. Model 3D Geològic de Catalunya. 2013. Available online: https://www.icgc.cat/ca/Administracio-i-empresa/Descarregues/Cartografia-geologica-i-geotematica/Cartografia-geologica/Model-geologic-3D-de-Catalunya (accessed on 15 January 2020).
- ICGC. Base de Dades de Sondejos de Catalunya (BDSoC). 2015. Available online: https://www.icgc.cat/ca/Administracio-i-empresa/Eines/Visualitzadors-Geoindex/Geoindex-Prospeccions-geotecniques (accessed on 15 January 2020).
- Scott, S.W.; Covell, C.; Júlíusson, E.; Valfells, Á.; Newson, J.; Hrafnkelsson, B.; Pálsson, H.; Gudjónsdóttir, M. A Probabilistic Geologic Model of the Krafla Geothermal System Constrained by Gravimetric Data. Geotherm. Energy 2019, 7, 29. [Google Scholar] [CrossRef] [Green Version]
- Scott, S.; Covell, C.; Juliusson, E.; Valfells, Á.; Newson, J.; Hrafnkelsson, B.; Pálsson, H.; Gudjónsdóttir, M. A Probabilistic Geologic Model of the Krafla Geothermal System Based on Bayesian Inversion of Gravimetric Data. In Proceedings of the World Geothermal Congress 2020 + 1, Reykjavik, Iceland, 24–27 October 2021; p. 13. [Google Scholar]
- ICGC. Base de Dades Geofísica de Catalunya. 2013. Available online: https://www.icgc.cat/Administracio-i-empresa/Serveis/Geofisica-aplicada/Geoindex-Tecniques-geofisiques (accessed on 15 January 2020).
- Fullea, J.; Afonso, J.C.; Connolly, J.A.D.; Fernàndez, M.; García-Castellanos, D.; Zeyen, H. LitMod3D: An Interactive 3-D Software to Model the Thermal, Compositional, Density, Seismological, and Rheological Structure of the Lithosphere and Sublithospheric Upper Mantle: LITMOD3D-3-D Interactive code to model lithosphere. Geochem. Geophys. Geosyst. 2009, 10. [Google Scholar] [CrossRef] [Green Version]
- Carballo, A.; Fernández, M.; Jiménez-Munt, I. Corte Litosférico al Este de La Península Ibérica y Sus Márgenes. Modelización de Las Propiedades Físicas Del Manto Superior. Física Tierra 2011, 23, 131–147. [Google Scholar] [CrossRef] [Green Version]
- Agemar, T.; Weber, J.; Schulz, R. Deep Geothermal Energy Production in Germany. Energies 2014, 7, 4397–4416. [Google Scholar] [CrossRef]
- Oldenburg, C.M.; Rinaldi, A.P. Buoyancy Effects on Upward Brine Displacement Caused by CO2 Injection. Transp. Porous Media 2011, 87, 525–540. [Google Scholar] [CrossRef] [Green Version]
- Lukosevicius, V. Thermal Energy Production from Low Temperature Geothermal Brine—Technological Aspects and Energy Efficiency; ONU Geothermal Training Programme; Orkustofnum—National Energy Authority: Grensasvegur, Reykjavik, Iceland, 1993; p. 42.
- Ayala, C. Basement Characterisation and Cover Deformation of the Linking Zone (NE Spain) from 2.5D and 3D Geological and Geophysical Modelling. In Proceedings of the 8th EUREGEO, Barcelona, Spain, 15–17 June 2015; p. 23. [Google Scholar]
- Willems, C.J.L.; Nick, H.M. Towards Optimisation of Geothermal Heat Recovery: An Example from the West Netherlands Basin. Appl. Energy 2019, 247, 582–593. [Google Scholar] [CrossRef]
- Veldkamp, J.G.; Pluymaekers, M.P.D.; van Wees, J.-D. DoubletCalc 2D (v1.0) Manual; TNO 2015 R10216; TNO: Utrecht, The Netherlands, 2015. [Google Scholar]
- Arrizabalaga, I.; De Gregorio, M.; De Santiago, C.; García de la Noceda, C.; Pérez, P.; Urchueguía, J.F. Country Update for the Spanish Geothermal Sector. In Proceedings of the World Geothermal Congress 2020 + 1, Reykjavik, Iceland, 24–27 October 2021. [Google Scholar]


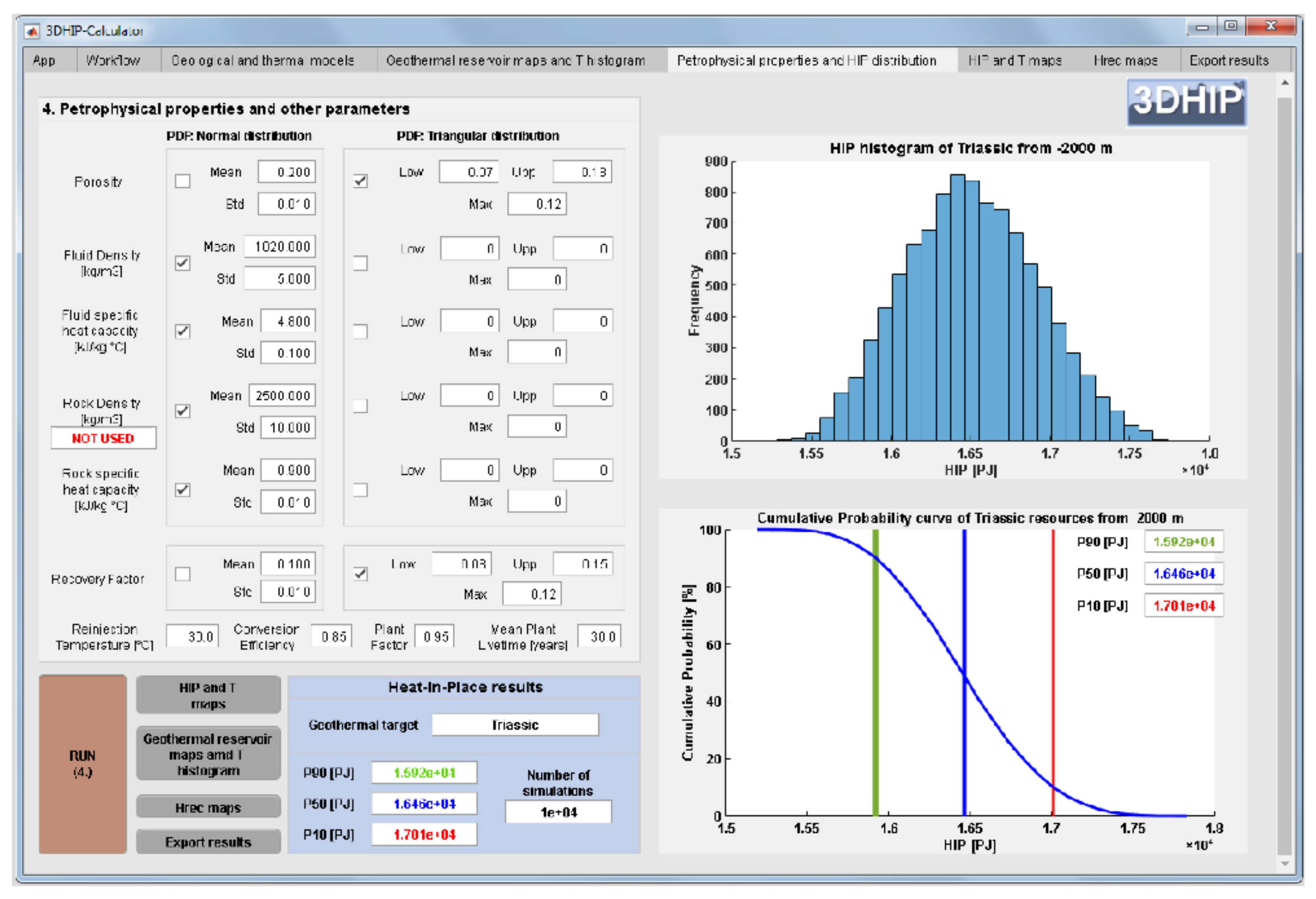
| Property | Units | PDFs | Values | |
|---|---|---|---|---|
| Petrophysical | Porosity | - | Triangular | Low: 0.07, Max: 0.12, Upp: 0.18 |
| Fluid Density | kg/m3 | Normal | Mean: 1020, SD: 5 | |
| Fluid specific heat capacity | kJ/kg·°C | Normal | Mean: 4.8, SD: 0.1 | |
| Rock density | kg/m3 | Triangular | Low: 2450, Max: 2500, Upp: 2600 | |
| Rock specific heat capacity | kJ/kg·°C | Normal | Mean: 0.9, SD: 0.01 | |
| Operational | Recovery factor | - | Triangular | Min: 0.08, Max: 0.12, Upp: 0.15 |
| Reinjection temperature | °C | - | 30 | |
| Conversion efficiency | - | - | 0.85 | |
| Plant factor | - | - | 0.95 | |
| Mean plant lifetime | years | - | 30 |
| Hrec—Recoverable Heat vs. Estimated R—Radius of Influence | Hrec P10 (kWt) | Hrec P50 (kWt) | Hrec P90 (kWt) |
|---|---|---|---|
| R = 0.5 km | 1337 | 1140 | 927 |
| R = 1 km | 6127 | 5185 | 4211 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piris, G.; Herms, I.; Griera, A.; Colomer, M.; Arnó, G.; Gomez-Rivas, E. 3DHIP-Calculator—A New Tool to Stochastically Assess Deep Geothermal Potential Using the Heat-In-Place Method from Voxel-Based 3D Geological Models. Energies 2021, 14, 7338. https://doi.org/10.3390/en14217338
Piris G, Herms I, Griera A, Colomer M, Arnó G, Gomez-Rivas E. 3DHIP-Calculator—A New Tool to Stochastically Assess Deep Geothermal Potential Using the Heat-In-Place Method from Voxel-Based 3D Geological Models. Energies. 2021; 14(21):7338. https://doi.org/10.3390/en14217338
Chicago/Turabian StylePiris, Guillem, Ignasi Herms, Albert Griera, Montse Colomer, Georgina Arnó, and Enrique Gomez-Rivas. 2021. "3DHIP-Calculator—A New Tool to Stochastically Assess Deep Geothermal Potential Using the Heat-In-Place Method from Voxel-Based 3D Geological Models" Energies 14, no. 21: 7338. https://doi.org/10.3390/en14217338
APA StylePiris, G., Herms, I., Griera, A., Colomer, M., Arnó, G., & Gomez-Rivas, E. (2021). 3DHIP-Calculator—A New Tool to Stochastically Assess Deep Geothermal Potential Using the Heat-In-Place Method from Voxel-Based 3D Geological Models. Energies, 14(21), 7338. https://doi.org/10.3390/en14217338






