An Inclination in Thermal Energy Using Nanoparticles with Casson Liquid Past an Expanding Porous Surface

Abstract

The physical aspects of inclined MHD nanofluid toward a stretching sheet embedded in a porous medium were visualized, which has numerous applications in industry. Two types of nanoparticles, namely copper and aluminum oxide, were used, with water (limiting case of Casson liquid) as the base fluid. Similarity transformations were used to convert the partial differential equations into a set of ordinary differential equations. Closed solutions were found to examine the velocity and temperature profiles. It was observed that an increment in the magnitude of the Hartmann number, solid volume fraction, and velocity slip parameter brought a reduction in the velocity profile, and the opposite behavior was shown for the permeability parameter in $Cu$–water and $A{l}_2{O}_3$–water nanofluids. The temperature field, local skin friction, and local Nusselt number were further examined. Moreover, the study of $Cu$ and $A{l}_2{O}_3$ is useful to boost the efficiency of thermal conductivity and thermal energy in particles. Reduction was captured in the velocity gradient and temperature gradient against changes in the thermal radiation number. The opposite trend was tabulated into motion with respect to the volume fraction number for both cases ($Cu$–water and $A{l}_2{O}_3$–water).

1. Introduction

Magneto-hydrodynamics (MHD) is the examination of fluid mechanics associated with electrically conducting fluids alongside an electromagnetic field, which has huge industrial applications. MHDs have various applications, which are dependent on their extensive utilization in industry and are used at the mechanical level. For example, just a few specific applications are MHD power generators, nuclear reactor cooling, small MHD pumps, bearing, and boundary impact, which are affected by the relationship to magnetic fields and electrically conducting fluids. The hydrodynamic boundary layers are fundamentally influenced by the electrically conducting fluid and magnetic fields. The hydromantic boundary layer can be viewed in a couple of specialized frameworks using fluid metallics as well as plasma streams similar to the crossover of magnetic fields. For example, through Lorentz forces, the control of a fluid flow might be achieved. Recently, a few research articles have managed the boundary layer stream issue by extending the surface of navigated fluid flow under the effect of magnetic fields [1,2,3,4,5,6,7,8]. The study of fluid flow over an extended surface is a fundamental problem in various mechanical applications, such as the extrusion and ejection of polymers onto a wind-up roller. This involves arranging a limited separation distance. Several studies have been conducted to address the boundary layer problems that occur when a surface is extended into a nearby region, as well as the magnetic field problems [9,10,11,12,13,14,15].

The incremental additions in thermal conductivity have a basic effect on improving the heat transport behaviors of fluids. A mechanical researcher can combine, control, and induce heat transport with a few assembly tools, starting with the singular strategy stream and then moving on to the next, according to the critical goal of the research. These techniques are given a source of energy deterioration and treat fluid heating or cooling. These improvements related to heating or cooling within the mechanical technique might cause protection of imperativeness, a decrease in activity time, an increase in the heating process and lengthening the working device’s lifespan. The progression of predominant thermal conductivity of fluids for the improvement of transformation heat transfer is being pursued at the moment. Thus, the presence of increased heat flow structures causes enhanced heat transfer or progress toward the improvement heat exchange. Researchers have endeavored to specifically improve the low thermal conductibility of the ordinary transform of the heat of fluids, utilizing the macroscopic effective medium theory (EMT) presented by Maxwell [16] in 1873 for the suitable properties of a blend.

Nanoparticles are created utilizing distinct materials, such as carbide ceramics ($Sic$ and $Tic$), metal nitrides ($AiN$ and $SiN$), oxide ceramics ($A{l}_2{O}_3$ and $CuO$), metals ($Cu$, $Ag$ and $Au$), carbon (for example, precious stones (diamond), carbon nanotubes, graphite, and fullerene), and functionalized nanoparticles [17,18,19,20,21,22]. A few preliminary exploratory outcomes [23] have shown, for example, an increase in the conductivity of heat by 60% in general, as might be obtained for a nanofluid containing water ($H_{2}O$) and 5% of copper oxide ($CuO$) nanoparticles. Masuda et al. [24] demonstrated that a significant application of nanofluids is the conductivity of the heat increasing. As of late, Buongiorno examined the effective seven-slip system to perceive the inertia, Brownian movement, thermophoresis, Magnus impact, bottle dissemination, fluid seepage, and attraction (gravitation) settling. He achieved a cultivated review of the convective vehicle in the nanofluids. A recent examination [25] observed that an upgrade in the transformation of heat within sight of nanoparticles can assume an imperative part in different physical calculations [26]. Shafiq et al. [27] discussed an enhancement in thermal energy and the diffusion of mass by inserting nanoparticles toward an expanding surface containing microorganisms via the zero mass flux condition. Shafiq et al. [28] studied thermal aspects using slip and convective conditions by inserting nanoparticles along with the Darcy–Forchheimer law. Rasool et al. [29] performed experiments related to entropy generation in MHD Williamson liquid, considering the effects of chemical reactions within entropy generation toward a porous surface. Abo-Dahab et al. [30] discussed the magnetohydrodynamic flow in Casson material over a porous surface. Mebarek-Oudina et al. [31] studied an increase in thermal energy using hybrid nanoparticles and nanoparticles toward a porous heated enclosure. Swain et al. [32] used an exponentially porous surface to analyze the flow and thermal characterizations considering nanoparticles via slip conditions. Some recent contributions covering numerous physical aspects and computational approaches have been reported in [33,34,35,36,37].

The impact of inclined MHD nanofluid provoked by a stretching sheet embedded in a porous medium was investigated. Two types of nanoparticles, copper and aluminum oxide, were used, with water as the base fluid. Similarity transformations were used to convert the partial differential equations into a set of ordinary differential equations. Such a developed problem has not been investigated yet. The current work is organized as follows: Section 1 is related to the introduction, and the preparation of the model is explained in Section 2. Section 3 addresses the solution to the problem. Graphical outcomes are discussed in Section 4. The last section contains the primary consequences of the problem.

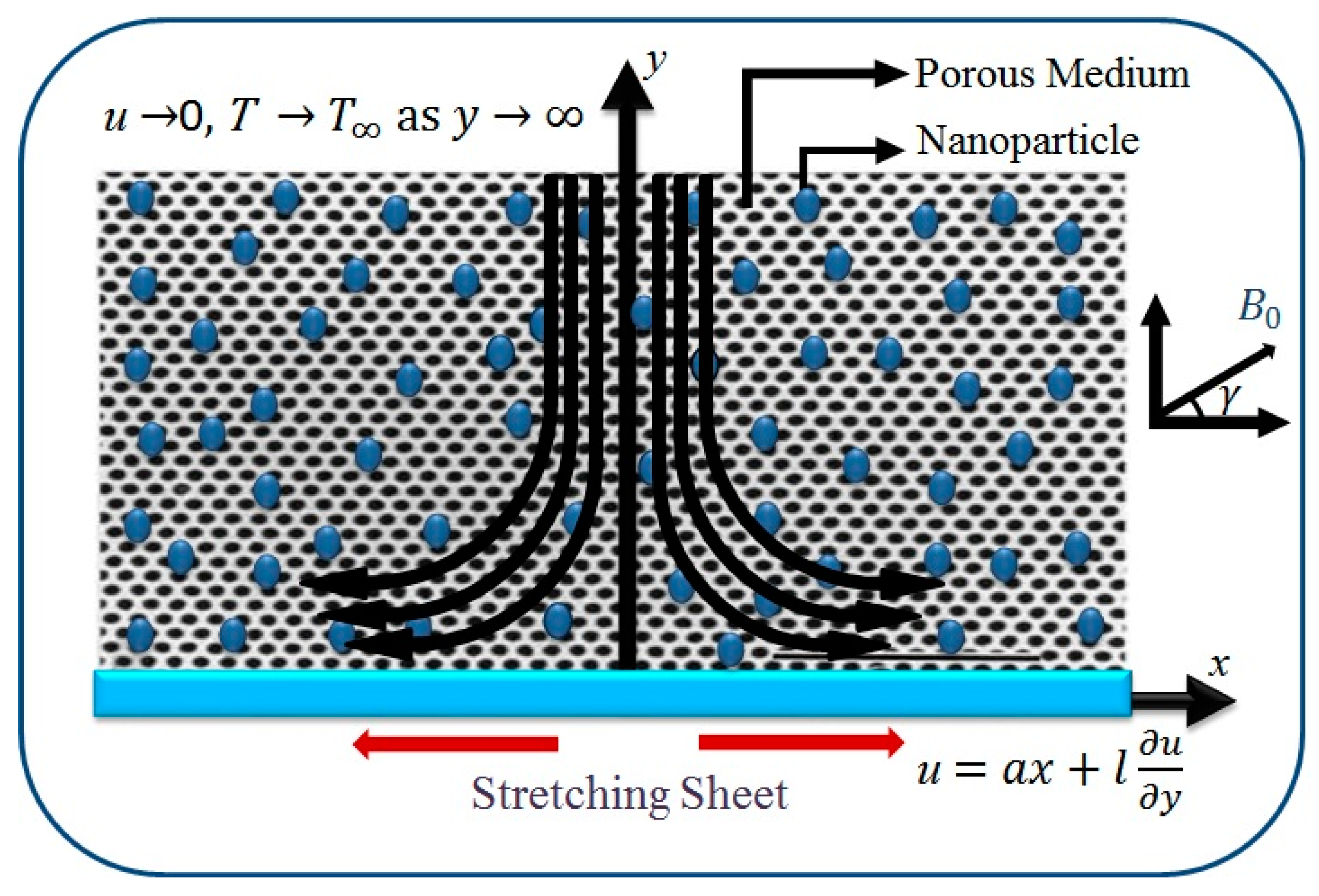
2. Mathematical Formulation

Suppose a 2D (two-dimensional), steady incompressible flow of a nanofluid over an extending sheet with slip impacts at the surface saturated in a porous medium, as shown in Figure 1. In this unique situation, water is considered the base liquid, with two specific types of metal nanoparticles: copper, with the formula ($Cu$), and aluminum oxide, with the formula ($A{l}_2{O}_3$). The inclined magnetic field is applied to the y-axis of magnetic field $B_0$ with an angle $\gamma$, which is an acute angle that is ordinary to the surface, and the $x$-axis is parallel to the sheet. Motion into the copper and aluminum oxide over a surface with the movement of the wall was noticed. The effect of the induced magnetic field was ignored. Heat energy characterizations were established in the presence of thermal radiation. Slip conditions were used to analyze flow behavior and thermal aspects. A steady flow and incompressible flow were addressed. It was assumed that the effect of a magnetic field is neglected at the threshold of attraction. However, the applied attractive field typically happens at the surface with the transverse magnetic field at $\gamma =\frac{\pi }{2}$ i.e., $Sin\left(\frac{\pi }{2}\right)=1.$ The assumptions are listed below.

➢

Two-dimensional flow for steady and incompressible flows;

➢

Slip conditions are used;

➢

Thermal radiation is addressed;

➢

A constant magnetic field is considered;

➢

An expanding surface is taken out;

➢

Two kinds of nanoparticles ($Cu$ and $Ag$) in the base fluid ($H_{2}O)$ are inserted in a Newtonian liquid.

BLA (boundary layer approximations) were used to model the required PDEs, and the PDEs are:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,$$

(1)

$$u\frac{\partial u}{\partial x}+v\frac{\partial v}{\partial y}=\left(1+\frac{1}{\delta }\right)\frac{{\mu }_{nf}}{{\rho }_{nf}}\frac{{\partial }^{2}u}{\partial y^2}-\frac{{\sigma }_{nf}{B}_0^2}{{\rho }_{nf}}uSi{n}^2\gamma -\frac{{\mu }_{nf}}{{\rho }_{nf}}\frac{u}{k_p},$$

(2)

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k_{nf}}{{\left(\rho C_P\right)}_{nf}}\frac{{\partial }^{2}T}{\partial y^2}+\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k_{*}{\left(\rho C_P\right)}_{nf}}\frac{{\partial }^{2}T}{\partial y^2}$$

(3)

These are subjected to the boundary conditions:

$$\begin{gathered} u=ax+l\frac{\partial u}{\partial y}, v=v_w, T_w=T_{\infty }+A{\left(\frac{x}{l}\right)}^2\mathrm{when}y=0, \\ u\to 0, T\to T_{\infty }\mathrm{at}y\to \infty \end{gathered}$$

(4)

The variation in variables of the current study is:

$$\begin{gathered} u=ax{f}^{\prime }\left(\eta \right), v=-{\left(a{\nu }_f\right)}^{\frac{1}{2}}f\left(\eta \right), \eta =y{\left(a{\nu }_f\right)}^{\frac{1}{2}}, \\ \theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }} \end{gathered}$$

(5)

Applying transformation (5) produces the following:

$$\begin{array}{c}\frac{1}{A_1{A}_2}\left(1+\frac{1}{\delta }\right)f^{‴}+f{f}^{″}+\left(f^{\prime }{f}^{\prime }-\frac{A_4}{A_2}MSi{n}^2\gamma f^{\prime }\right)-\frac{1}{A_1{A}_2}{K}_I{f}^{\prime }=0\\ f=0, f^{\prime }\left(0\right)=1+\frac{\beta }{A_2}{f}^{″}\left(0\right), f\prime (\infty ) \to 0\end{array}\},$$

(6)

$$\begin{array}{c}\left(1+\frac{4A_5}{3N}\right){\theta }^{″}+\frac{A_3}{A_5}Prf{\theta }^{\prime }-2\frac{A_3}{A_5}Pr{f}^{\prime }\theta =0\\ \theta \left(0\right)=1, \theta (\infty )\to \infty \end{array}\},$$

(7)

The associated correlations among nanoparticles are:

$$\begin{gathered} A_1={\left(1-\varphi \right)}^{2.5}, A_2=\left(1-\varphi +\frac{{\left(\rho C_P\right)}_s}{{\left(\rho C_P\right)}_f}\varphi \right), A_3=\left(1-\varphi +\frac{{\rho }_s}{{\rho }_f}\varphi \right), \\ {A}_4=\left(1+\frac{\left(\frac{{\sigma }_s}{{\sigma }_f}-1\right)\varphi }{\left(\frac{{\sigma }_s}{{\sigma }_f}+2\right)-\varphi \left(\frac{{\sigma }_s}{{\sigma }_f}-1\right)}\right),A_5=\frac{K_s+2K_f-2\varphi \left(K_f-K_s\right)}{K_s+2K_f-\varphi \left(K_f-K_s\right)},L=\frac{\beta }{A_1}. \end{gathered}$$

The Hartmann number, slip parameter, and Prandtl number are captured as:

$$M=\frac{{\left(B_0\right)}^2{\sigma }_f}{a{\rho }_f}, \beta =\frac{l}{{\left(\frac{a}{{\nu }_f}\right)}^{1/2}}, Pr=\frac{C_P\mu }{k}, N=\frac{k_{*}{k}_{nf}}{{\left(T_{\infty }\right)}^{3}4{\sigma }^{*}}, K_I=\frac{{\nu }_f}{k_{p}a}.$$

The skin friction coefficient and rate of heat transfer are modeled as:

$$\begin{gathered} C_f=\frac{{\tau }_w}{{\rho }_f{\left(u_w\right)}^2}, C_f=\frac{R{e}_x^{-1/2}}{A_1}{f}^{″}\left(0\right), \\ {N}_u=\frac{x{q}_w}{k_f\left(T_w-T_{\infty }\right)},N{u}_{x}R{e}_x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}=-\left(\frac{K_{nf}}{K_f}+\frac{4}{3N}\right){\theta }^{\prime }\left(0\right). \end{gathered}$$

The local Reynolds number is $Re\left(=\frac{x{u}_w}{{\nu }_f}\right).$

3. Exact Solution of Problem

The exact solution was implemented with Equations (6)–(7) using MATLAB. The required function is considered here:

$$\mathrm{f}(\mathsf{\eta })=\frac{\mathrm{X}-{\mathrm{Xe}}^{-\mathsf{\alpha }\mathsf{\eta }}}{\mathsf{\alpha }}$$

(8)

X = $\frac{1}{\beta \alpha +1}$, and α = $\frac{1}{6} \frac{1}{\beta }$ (−72MA₁β²cos(θ)² + 72MA₁β² + 108A₁β²A₂ − 8 + 12$\sqrt{3}$ (A₁ (4M³$A_1^2$β⁴cos(θ)⁶ − 12M³$A_1^2{\beta }^4$cos(θ)⁴ + 8M²A₁β⁴cos(θ)² + 12M³$A_1^2{\beta }^4$cos(θ)² − 16M²A₁β²cos(θ)² + 4cos(θ)²M − 4M³$A_1^2{\beta }^4$ + 8M²A₁β² − 4M − 36MA₁β²cos(θ)²A₂ + 36MA₁β²A₂ + 27A₁β²$A_2^2$ − 4A₂))^1/2 β)^1/3 − $\frac{2}{3}$ (3MA₁β²cos(θ)² − 3MA₁β² − 1)/(β (−72MA₁β²cos (θ)² + 72 MA₁β² + 108A₁β²A₂ − 8 + 12$\sqrt{3}$ (A₁ (4M³$A_1^2$β⁴cos(θ)⁶ − 12M³$A_1^2{\beta }^4$cos(θ)⁴ + 8M²A₁β⁴cos(θ)² + 12M³$A_1^2{\beta }^4$cos(θ)² − 16M²A₁β²cos(θ)² + 4cos(θ)²M − 4M³$A_1^2{\beta }^4$ + 8M²A₁β² − 4M − 36MA₁β²cos(θ)²A₂ + 36MA₁β²A₂ + 27A₁β²$A_2^2$ − 4A₂))^1/2 β)^1/3 − $\frac{1}{3\beta } \frac{1}{6} \frac{1}{\beta }$ (−72MA₁β² cos(θ)² + 72 MA₁β² + 108A₁β²A₂ − 8 + 12$\sqrt{3}$ (A₁ (4M³$A_1^2$β⁴cos(θ)⁶12M³$A_1^2{\beta }^4$cos(θ)⁴ + 8M²A₁β⁴cos(θ)² + 12M³$A_1^2{\beta }^4$cos(θ)² − 16M²A₁β²cos(θ)² + 4cos(θ)²M − 4M³$A_1^2{\beta }^4+$8M²A₁β² − 4M − 36MA₁β²cos(θ)²A₂ + 36MA₁β²A₂ + 27A₁β²$A_2^2$ − 4A₂))^1/2β)^1/3 − $\frac{2}{3}$(3MA₁β²cos(θ)² − 3MA₁β² − 1)/(β (−72MA₁β²cos(θ)² + 72MA₁β² + 108A₁β²A₂ − 8 + 12$\sqrt{3}$ (A₁(4M³$A_1^2$β⁴cos(θ)⁶ − 12M³$A_1^2{\beta }^4$cos(θ)⁴ + 8M²A₁β⁴cos(θ)² + 12M³ $A_1^2{\beta }^4$cos(θ)² − 16M²A₁β²cos(θ)² + 4cos(θ)²M − 4M³$A_1^2{\beta }^4+$8M²A₁β² − 4M − 36MA₁β²cos(θ)²A₂ + 36MA₁ β²A₂ + 27A₁β² $A_2^2$ − 4A₂))^1/2β)^1/3 − $\frac{1}{3\beta }\frac{1}{6}\frac{1}{K_1\beta }$ ((−72K₁β²cos(θ)²A₁M + 108K₁β²A₁A₂ + 72K₁β²A₁M + 72β²A₁A₂ + 12$\sqrt{3}$ ($\frac{1}{K_1}$ (A₁ (4$K_1^3$β⁴cos(θ)⁶$A_1^2$M³ − 12$K_1^3$β⁴cos(θ)⁴$A_1^2$M³ − 12$K_1^2$β⁴cos(θ)⁴$A_1^2$A₂M² + 12$K_1^3$β⁴cos(θ)²$A_1^2$M³ + 24$K_1^2$β⁴cos(θ)²$A_1^2$A₂M² − 4$K_1^3$β⁴$A_1^2$M³ + 8$K_1^3$β²cos(θ)⁴A₁M² + 12K₁β⁴cos(θ)² $A_1^2{A}_2^2$M − 12$K_1^2$β⁴$A_1^2$A₂M² − 36$K_1^3$β²cos(θ)²A₁A₂M − 16$K_1^3$β²cos(θ)²A₁M² − 12K₁β⁴$A_1^2{A}_2^2$M − 36$K_1^2$β²cos(θ)²A₁A₂M − 4β⁴$A_1^2{A}_2^3+$27$K_1^3{\beta }^2{A}_1 A_2^2+$36$K_1^3{\beta }^2$A₁A₂M + 8$K_1^3{\beta }^2$A₁M² + 36$K_1^2{\beta }^2{A}_1{A}_2^2+$16$K_1^2{\beta }^2$A₁A₂ M + 4$K_1^3$cos(θ)²M + 8K₁β²A₁$A_2^2$ − 4$K_1^3$A₂ − 4$K_1^3$M − 4$K_1^2$A₂)))^1/2 β − 8 K₁) $K_1^2$)^1/3 − $\frac{2}{3}$ (3K₁β² cos(θ)² A₁M − 3K₁β²A₁M − 3β²A₁A₂ − K₁)/(β (−72K₁β²cos(θ)²A₁M + 108K₁β²A₁A₂ + 72 K₁β²A₁M + 72 β²A₁A₂ + 12$\sqrt{3}$ ($\frac{1}{K_1}$ (A₁(4$K_1^3$β⁴cos(θ)⁶$A_1^2$M³ − 12$K_1^3$β⁴cos (θ)⁴$A_1^2$M³ − 12$K_1^2$β⁴cos(θ)⁴$A_1^2$A₂M² + 12$K_1^3$β⁴cos(θ)²$A_1^2$M³ + 24$K_1^2$β⁴cos(θ)²$A_1^2$A₂M² − 4$K_1^3$β⁴$A_1^2$M³ + 8$K_1^3$β²cos(θ)⁴A₁M² + 12K₁β⁴cos(θ)² $A_1^2{A}_2^2$M − 12$K_1^2$β⁴$A_1^2$A₂M² − 36$K_1^3$β²cos(θ)²A₁A₂M − 16$K_1^3$β²cos(θ)²A₁M² − 12K₁β⁴$A_1^2{A}_2^2$M − 36$K_1^2$β² cos(θ)²A₁A₂M − 4β⁴$A_1^2{A}_2^3+$27$K_1^3{\beta }^2{A}_1 A_2^2+$36$K_1^3{\beta }^2$A₁A₂M + 8$K_1^3{\beta }^2$A₁M² + 36$K_1^2{\beta }^2{A}_1{A}_2^2+$16 $K_1^2{\beta }^2$A₁A₂M + 4$K_1^3$cos(θ)²M + 8K₁β²A₁$A_2^2$ − 4$K_1^3$A₂ − 4$K_1^3$M − 4$K_1^2$A₂)))^1/2 β − 8 K₁) $K_1^2$)^1/3 − $\frac{1}{3\beta }.$

4. Outcomes and Discussion

The features of MHD provoked by a stretching sheet embedded in a porous medium were captured. In

Table 1. Thermal properties of $Cu, A{l}_2{O}_3$, and water.

Physical Properties	Water	$\mathit{C}\mathit{u}$	$\mathit{A}{\mathit{l}}_2{\mathit{O}}_3$
$\rho$	997.1	8933	3970
$C_P$	4179	385	765
$K$	0.613	400	40
$Pr$	6.135
$\sigma$	$5.5\times {10}^{-6}$	$35\times {10}^6$	$59.6\times {10}^6$

, the thermo-physical properties of water, and furthermore, each nanoparticle, are introduced in the shaping of the thickness, definite warmth, and thermal conductivity.

Table 2. Comparative study for dimensionless stress.

${\mathit{K}}_1$	[33]	Present
$0$	−1.167721	−1.167726
$0.5$	−1.366245	−1.366218
$1.0$	−1.539056	−1.539091
$1.5$	−1.694089	−1.694029
$2.0$	$-1.835965$	$-1.835947$

presents the comparative analysis. It was recorded that the obtained solution is in full agreement with the findings reported in [37]. Prior to examining the comportment of the compelling profiles, we conducted an examination with the accessible outcomes in this work. It was clearly observed that the outcomes were exact for the preventive case in the examination. Two significant types of nanoparticles—copper, with the formula $Cu$, and aluminum oxide—were analyzed inside a base liquid of water. The impact of the nanoparticles’ volume fraction with the base liquid of water was discussed through the velocity and temperature for the recommended surface heat flow (see Figure 2a,b). The velocity field was decreased by enhancing the value of the permeability parameter, and the opposite behavior was shown in the case of $A{l}_2{O}_3$–water, as examined in Figure 2a,b. It can be seen in Figure 3a that an expansion in the nanoparticle volume fraction diminished the velocity behaviors of the nanofluid ($Cu$–water). Considering $A{l}_2{O}_3$–water, it was discovered that a rise in the nanoparticle volume portion increased the velocity profiles Figure 3b. The declining role of the velocity profiles was investigated versus the impact of $\beta$, visualized by Figure 4a,b. In Figure 4a,b, the temperature profile shows the behavior of Cu–water and aluminum dioxide Al₂O₃ with contact volume ϕ expansion of nanoparticle. Temperature was inclined versus the role of the volume fraction number. The velocity and temperature profile of the nanofluid worked counter to the rising slip state estimate. This process of expanding the sheet may involve only some transmission to the liquid. Figure 5a,b separately reflect the impacts of the radiation boundaries on the temperature profiles for Cu–water and Al₂O₃−water. It may indicate that the temperature of the radiation boundary N decreases its power. Figure 6 shows that the physical action and velocity profile decrease and the temperature profile increases progressively for both copper water (Cu–water) and aluminum oxide water (Al₂O₃–water) (Figure 7a,b). Figure 8a,b separately reflect the impacts of the radiation boundaries on the temperature profiles for Cu-water and Al₂O₃−water. It may indicate that temperature increases versus $\gamma .$

In addition, Cu–water nanofluid was shown to have higher surface friction compared to Al₂O₃–water. Figure 9a,b delineate the effects on the number of surface forces of the attractive boundary versus $K_I$, but the opposite treatment was found against $M$ and $\gamma .$The nearby Nusselt number increased, and the estimates of the nanoparticle volume part ϕ increments could be seen very well. In Figure 10, Cu–water was found to refer to the rate of warmth movement faster than Al₂O₃–water. In Figure 11, the Nusselt neighborhood number was reduced for both Cu–water and Al₂O₃–water and for the velocity slip and magnetic limit. Moreover, Al₂O₃–water was shown to have a low rate of heat movement relative to Cu–water. The modified point and magnetic boundary consolidated results showed that these restrictions minimized the behavior of the neighborhood Nusselt number.

5. Conclusions

In this article, we studied the effects of an inclined magnetic field, velocity slip, porous medium, and thermal radiation on a nanofluid passed over a material for stretching. For the prescribed surface, this study evaluated temperature with two kinds of nanofluids ($Cu$–water and $A{l}_2{O}_3$–water). The inclined magnetic field obtained appeared enforceable with an aligned angle, in which the aligned angle ranged between $0$ and $\pi /2$. The following were the dominant basic results:

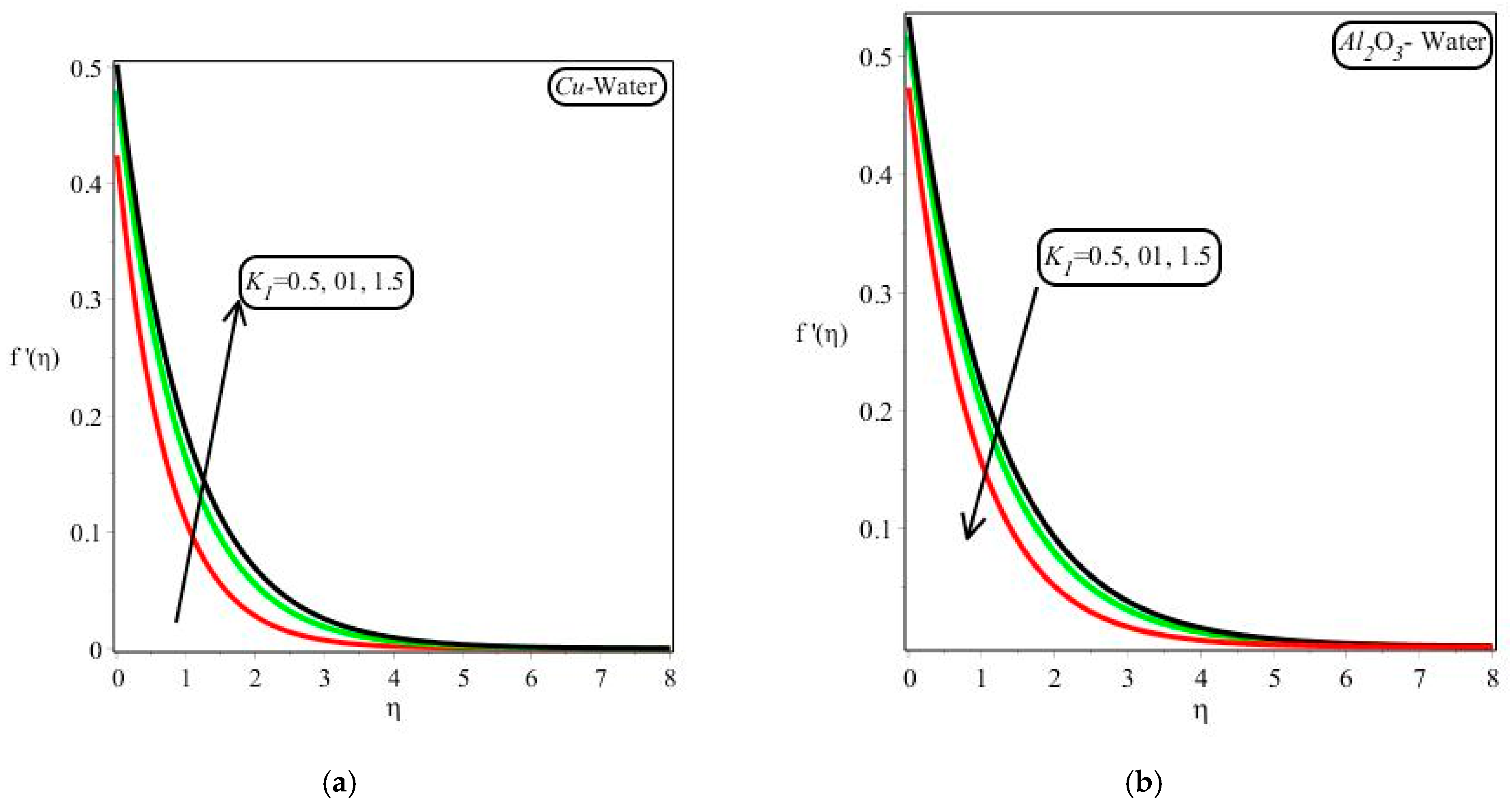
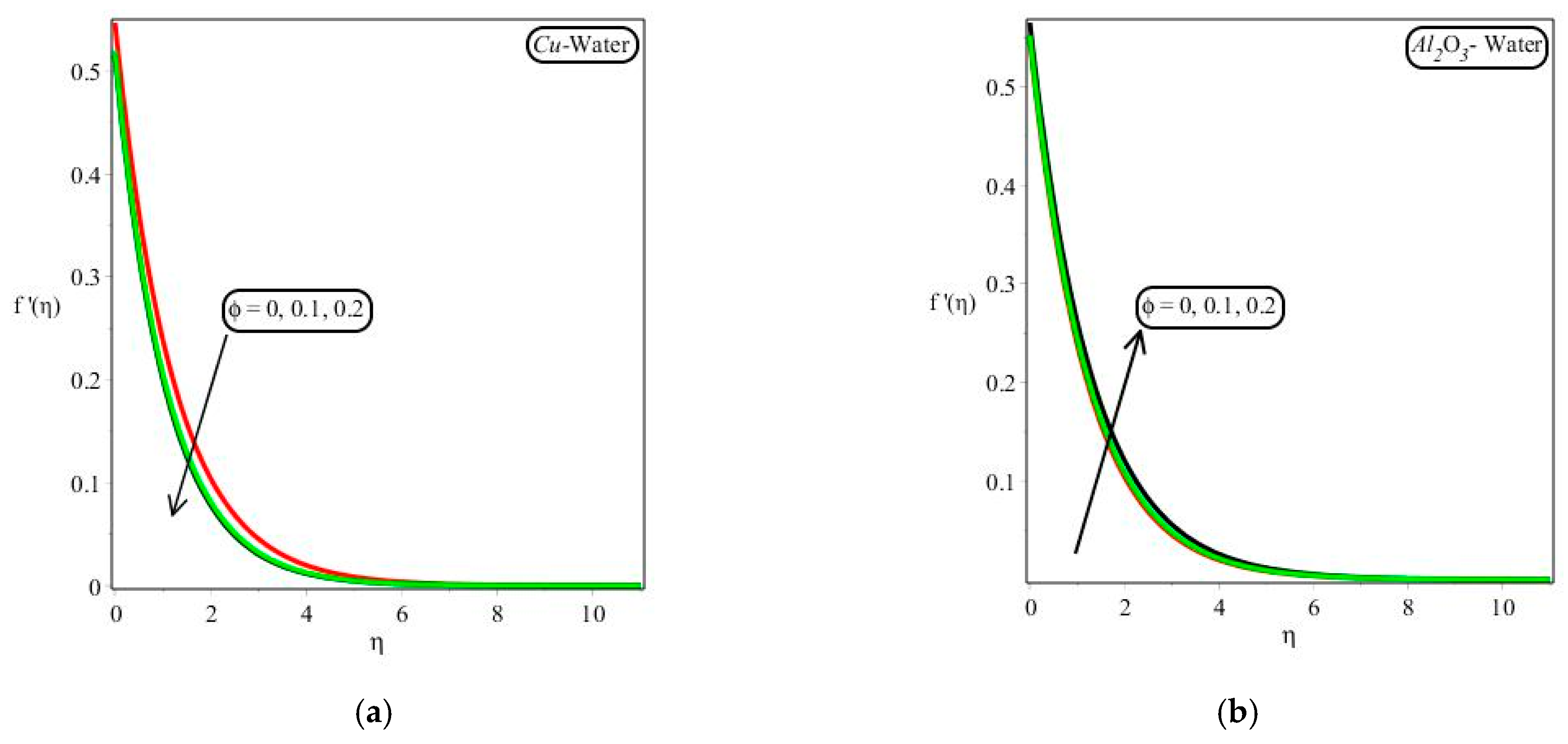
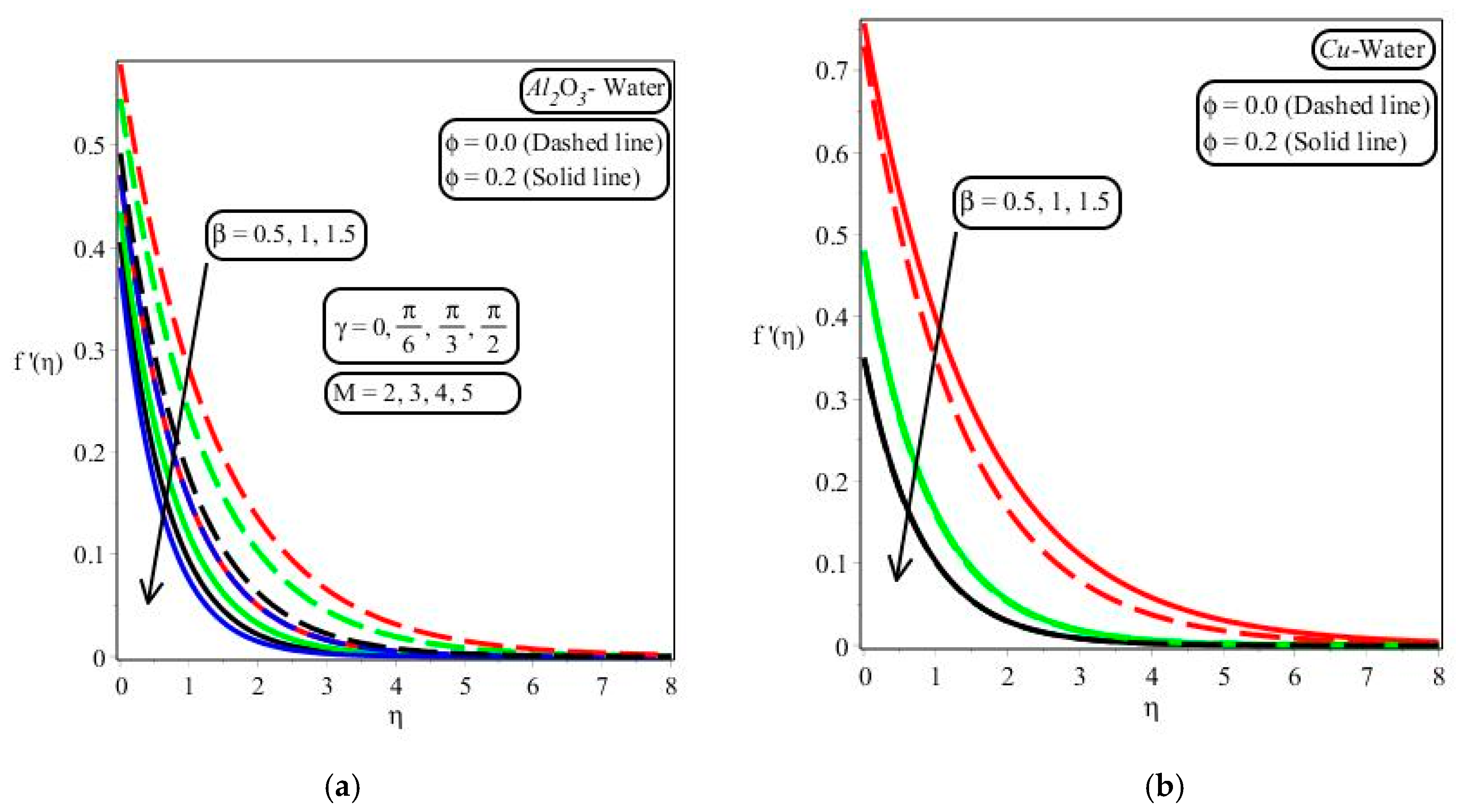
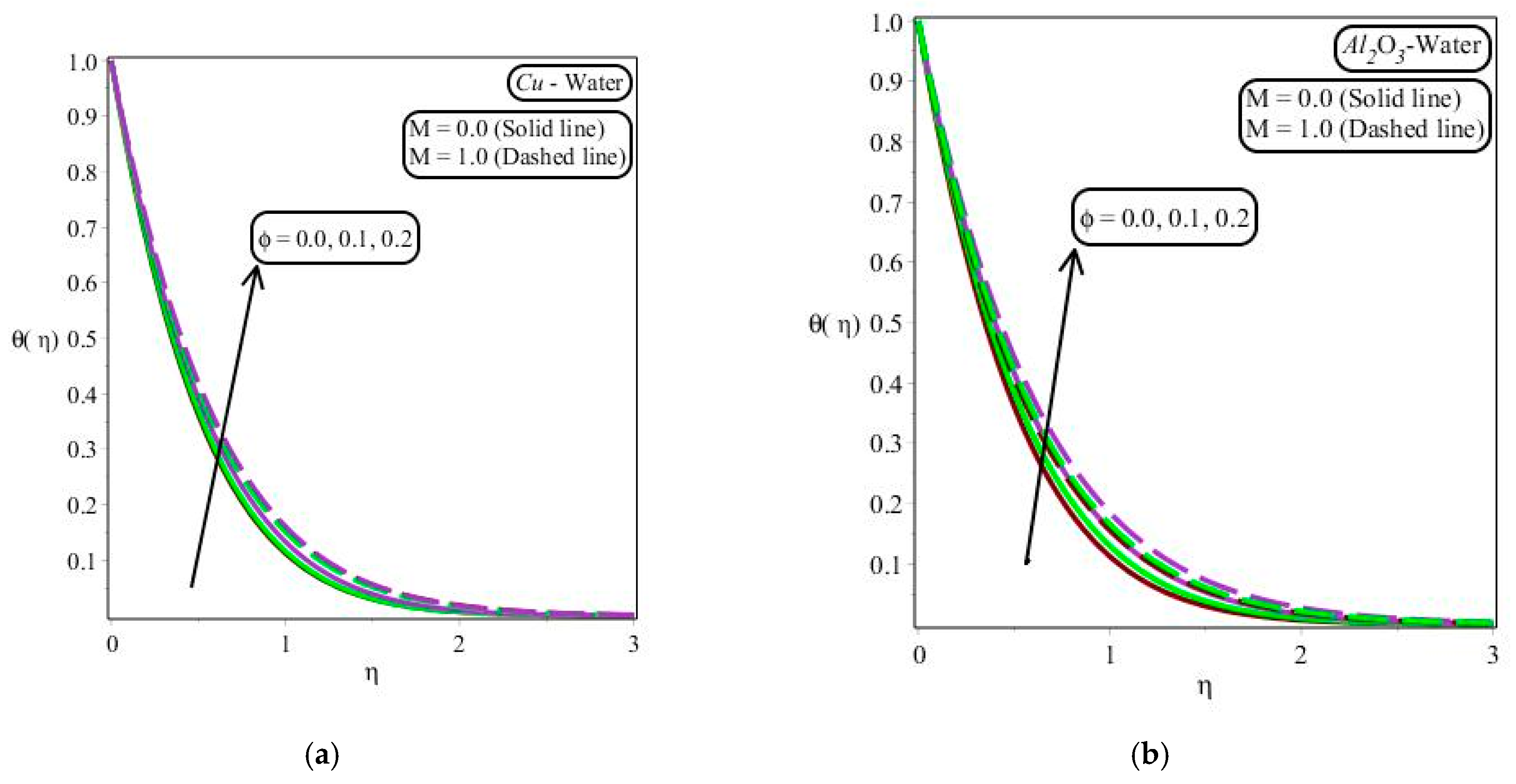
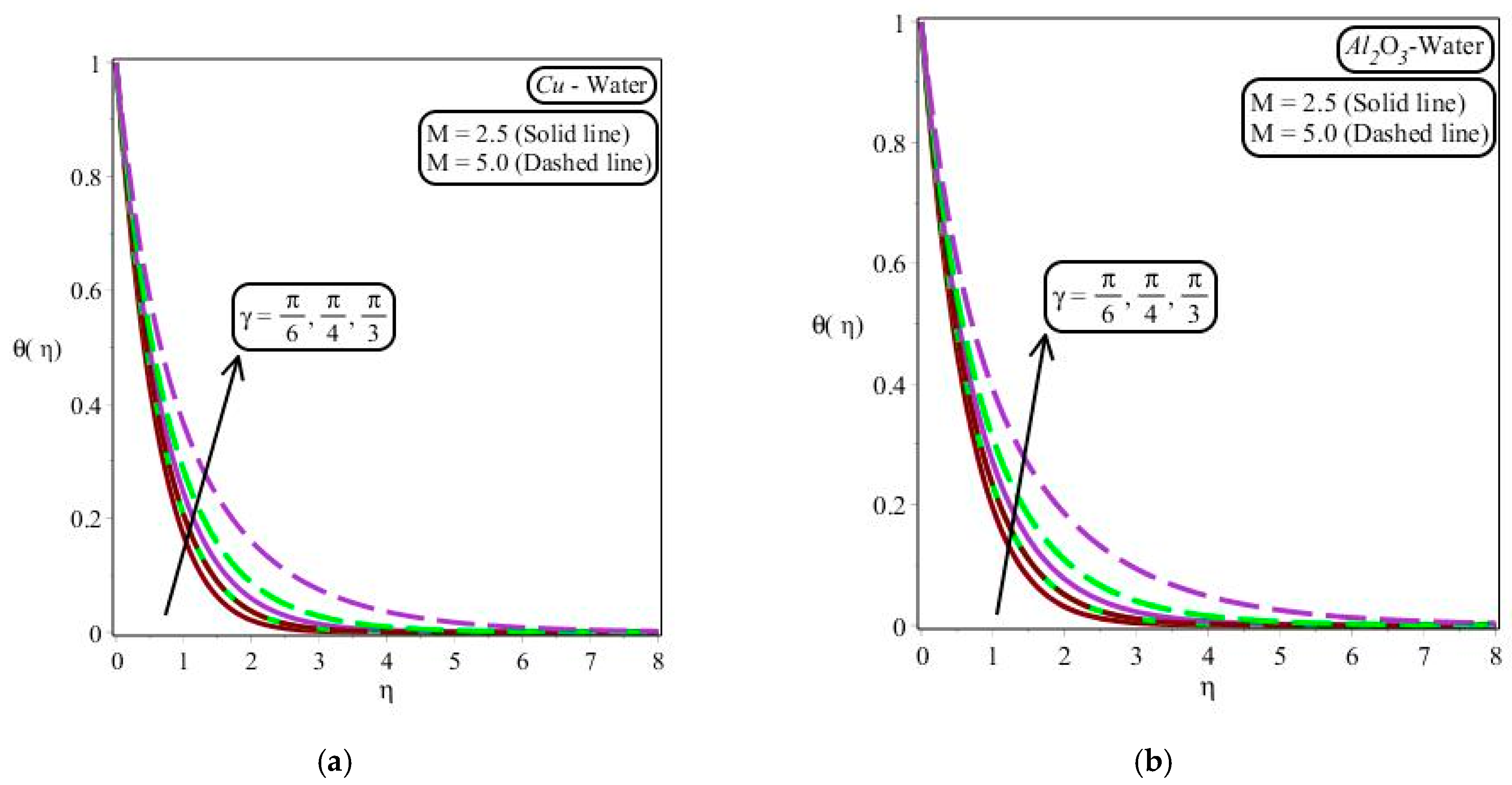
• The nanofluid velocity profile decreased with rising nanofluid values of the fraction rate of the nanoparticle, magnetic parameters, and slip parameter for $Cu$–water and $A{l}_2{O}_3$ water;
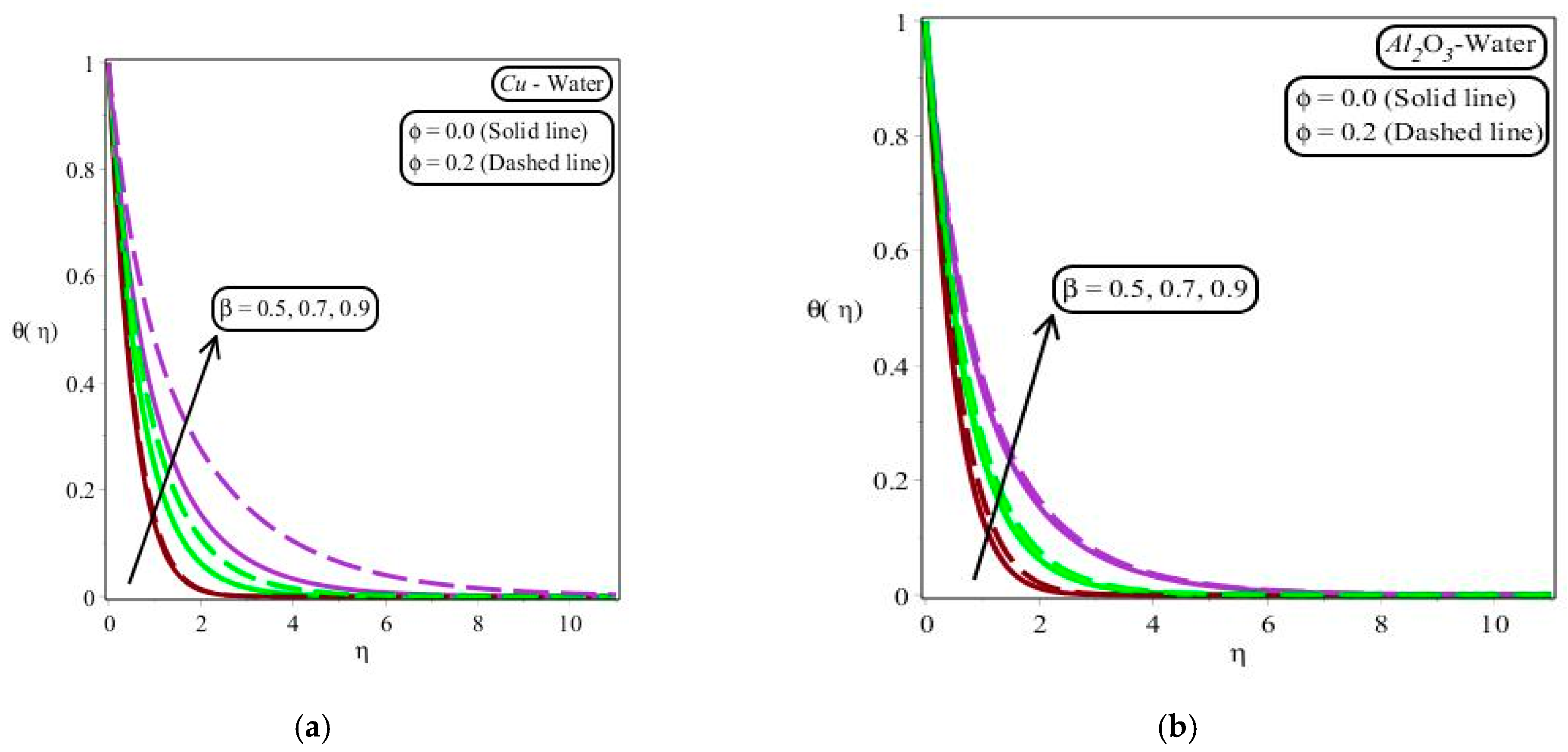
• The amount of thermal energy was enhanced against the increment in the volume fraction and slip parameter;
• The impacts of volume fraction were most significant in enhancing the thickness associated with the thermal layers;
• The study of $Cu$ and $A{l}_2{O}_3$ was useful to boost the efficiency of thermal conductivity and thermal energy into particles;
• Thermal radiation brings about a decline in the production of heat energy;
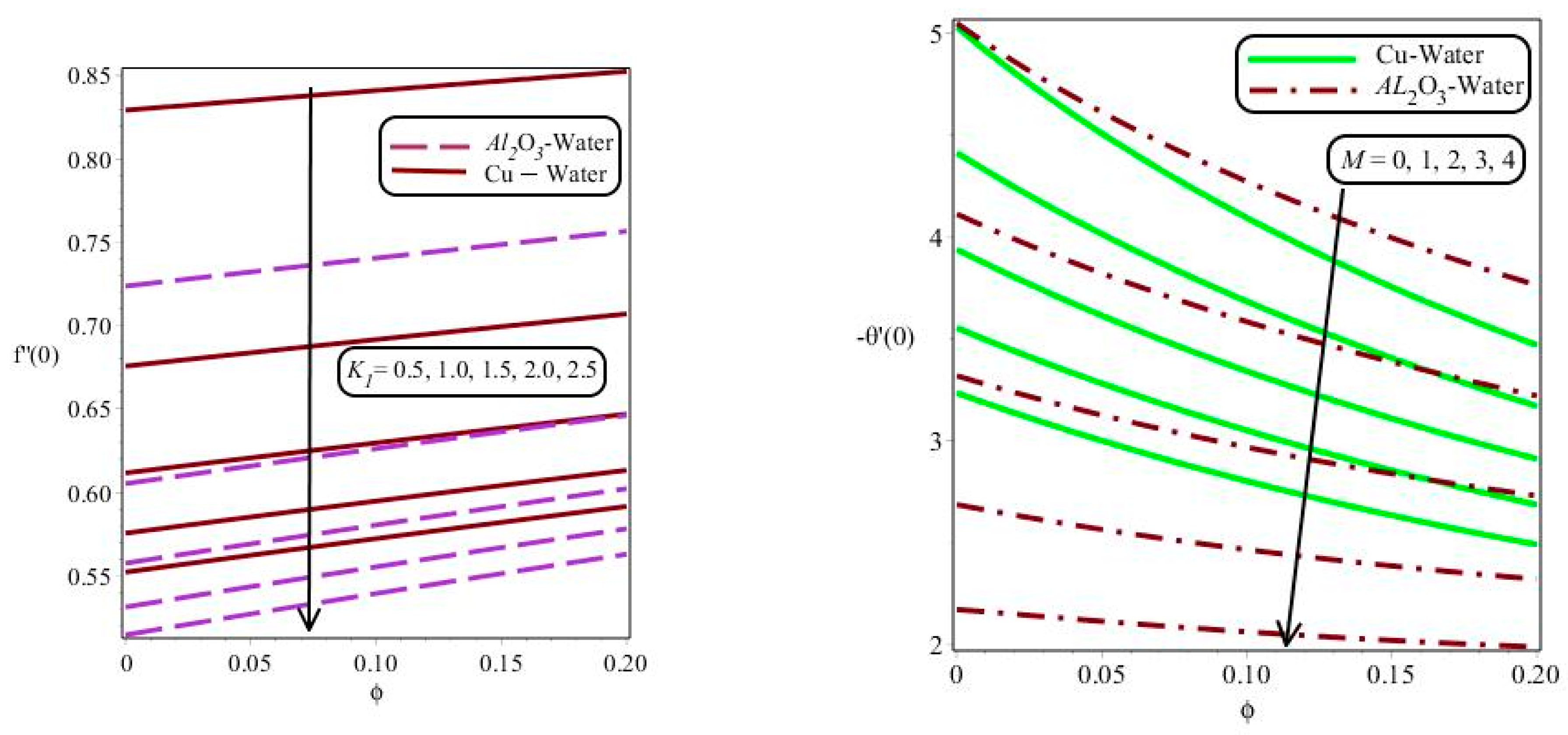
• Reduction was captured in the velocity gradient and temperature gradient against a change in the thermal radiation number;
• The opposite trend was tabulated into motion with respect to the volume fraction number for both cases ($Cu$–water and $A{l}_2{O}_3$–water);
• Variation in fluid number produces frictional force into the motion of fluid particles.