Modified Beetle Annealing Search (BAS) Optimization Strategy for Maxing Wind Farm Power through an Adaptive Wake Digraph Clustering Approach
Abstract
:1. Introduction
- A decentralized coordination control scheme is achieved by controlling the yaw angles and axial factors to maximize power conversion on the wind farm. Large-scale wind farms are divided into several decoupled subsets, and then the local controller only controls the local subset’s data. The proposed control scheme enables efficiency in the real-time application by optimizing the decentralized coordination to reduce computational burden and information exchange.
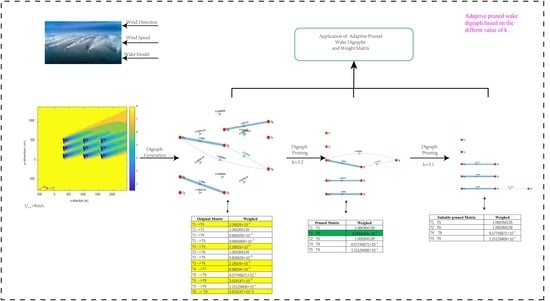
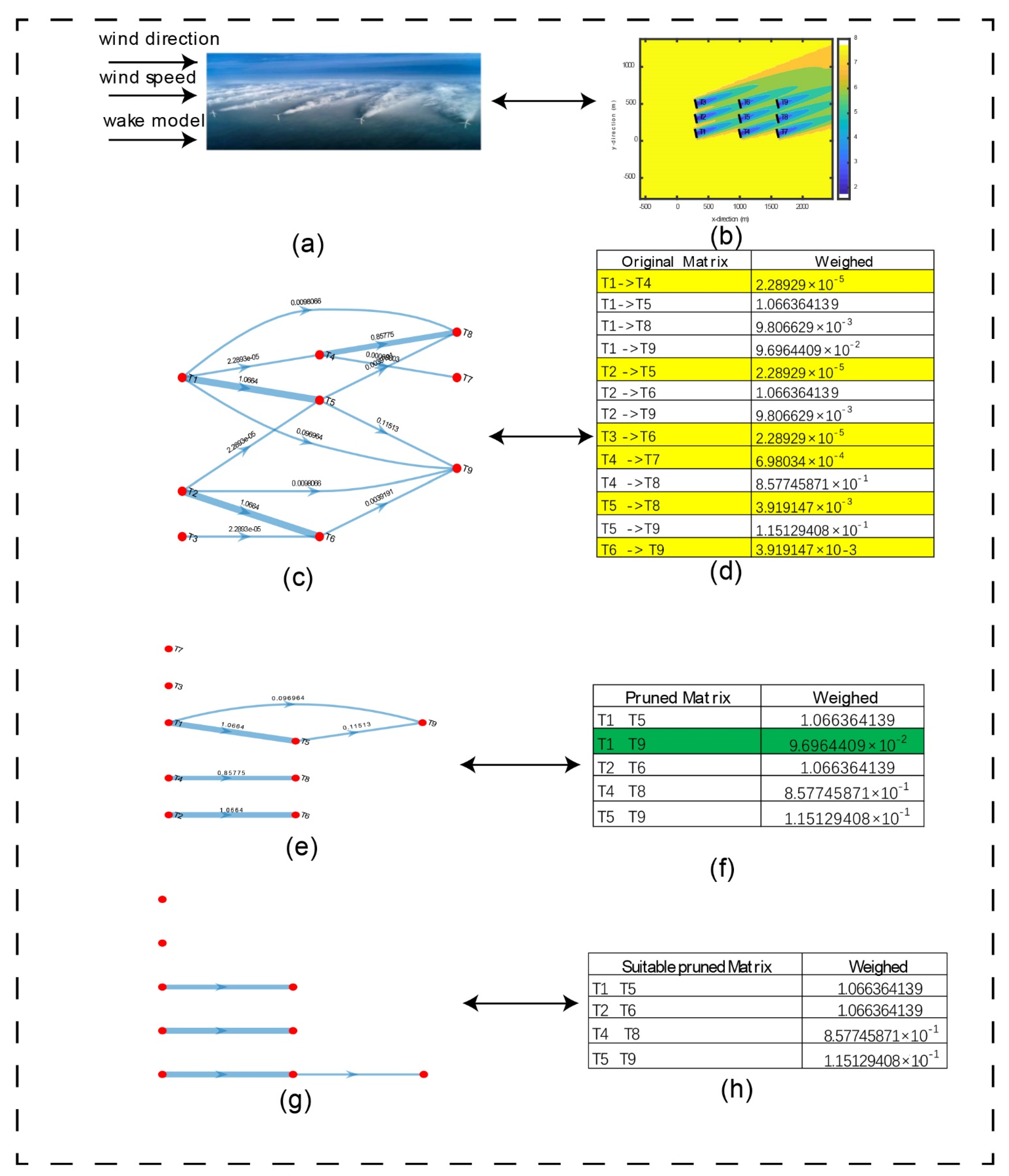
- A wake-based graph adaptive pruning approach is presented to split a large wind farm into several clustering subsets. This approach aims to find a decoupled sub-graph that can preserve essential distribution characteristics of the original wake direction graph. We adopt a graph clustering algorithm to divide turbines via wake graphs adaptive pruning constraint, and threshold which is a vital point parameter to control the number of groups of the pruned wake digraph.
- We develop a modified BSA optimization algorithm based on adaptive pruned communication architectures. The Monte Carlo (MC) law of Simulate Anneal (SA) is introduced to improve the BAS, which significantly improves the reproducibility and stability of the algorithm. Finally, the improved algorithm is applied for wake steering control and maximum power conversion on the wind farm.
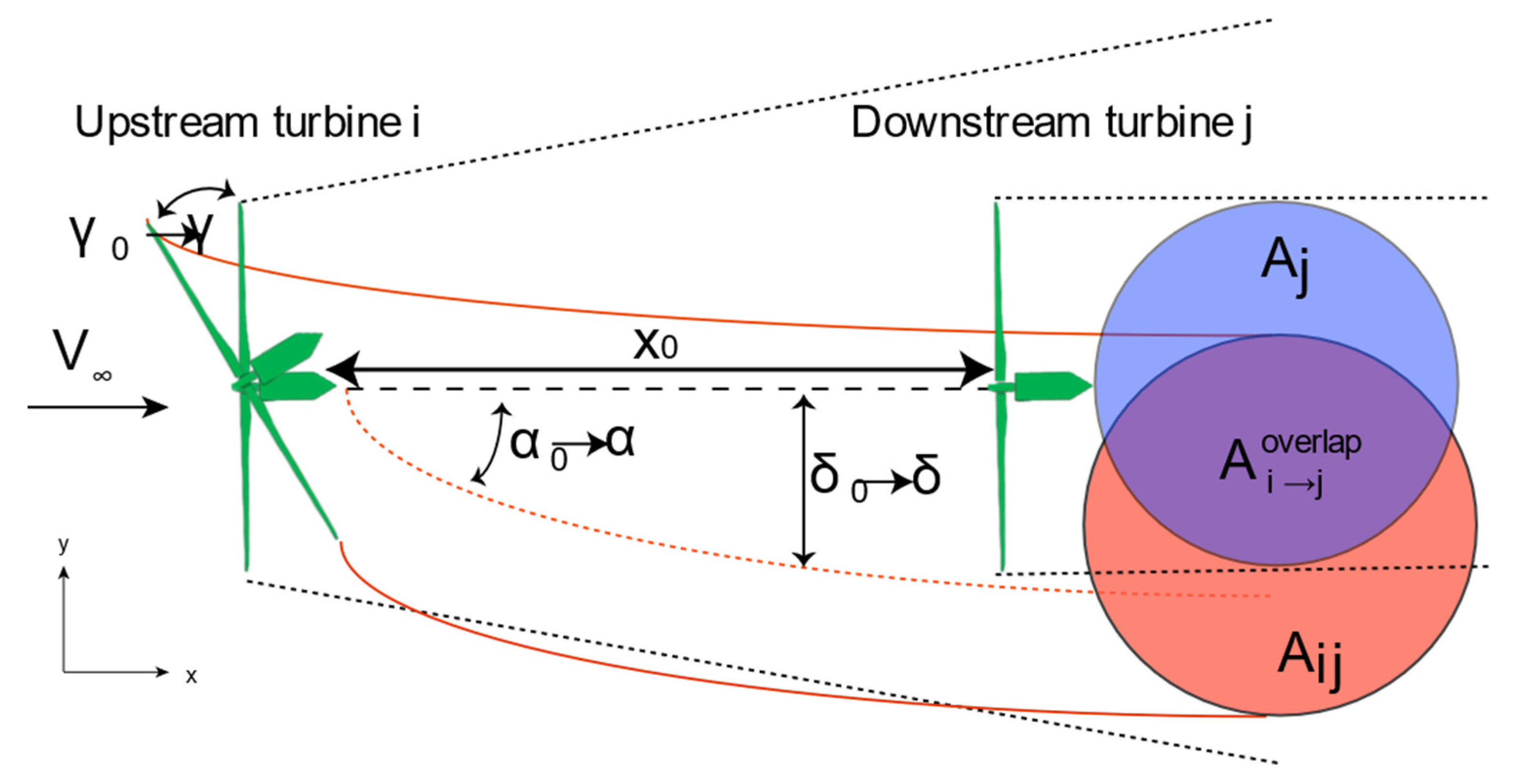
2. Gaussian-Based Wake Model Considering Yaw Angle
3. Clustering Turbine via Pruning Wake Digraph
3.1. The Original Wake Graph of Wind Farm
- The communication neighbors of vertex (turbine) are denoted by .
- The set of shared turbine in communication neighbors between the subset and subset , are denoted as where represents the shared turbine numbers in different subsets.
3.2. Decoupled Communication Scheme of Wind Farm Based on Adaptive Pruned Algorithm
- The adaptive threshold , is one hyper-parameter, and is the basic threshold.
- Basic threshold is defined as the geometric median of the whole wake weight coefficients. The central idea of the geometric median is as follows: given the set of points ,…,,…, find a value that minimizes the sum of Euclidean distance:where .
| Algorithm 1: The method of clustering turbine via pruning wake digraph (Adaptive pruned wake digraph algorithm) |
| Step 1: Based on the layout of the position of the wind farm , collect all relevant parameters, including wind direction , wind speed . Additionally, the parameters of the wind turbines, for example, the rotor diameter , the physical distance between WTs, and the overlap wake area , etc. |
| Step 2: Calculate the threshold , and set the initial hyper-parameter , step hyper-parameter . Step 3: Obtain the pruned digraph from the original wake digraph according to the global threshold according to the global threshold . Step 4: Digraph clustering. Firstly, define the leading turbines for each subset that is experiencing free-stream velocity . Secondly, each leading turbine decides the communication neighbors through the connectivity information of the digraph by a depth-first tree search (BFS) algorithm into the same subset . Step 5: If there is a set of shared turbines , we need to continue to tune the value of k by set , go back to Step 3. If not, go directly to step 6. Step 6: Calculate the output power and calculating time with the value from step 5, save the parameters. Step 7: If the coefficients of are not all 0, continue to tune the value by setting , go back to Step 2. If the coefficients of are all 0, go to step 8. |
| Step 8: Based on the adaptive pruned wake digraph , we can establish turbine clustering subsets and analyze all the parameters with different , and select the suitable value . |
4. Wind Farm Control Strategy
4.1. The Output Power Optimization Problem
4.2. Monte Carlo Law with the BAS(MC-BAS) Controller for Wind Turbines
| Algorithm 2: The grouped MC-BAS methodology for wind farm power production (MC-BAS Algorithm) |
| Result: The best yaw angles and the best axial factors and the best output power . Input: Establish output objective function , where variable and initialize the parameters ,,,,. While () do |
 |
| End |
- 1.
- Random direction vectorTo simulate the search behavior of longicorn, its direction vector is defined as [47]:where denotes a random function, and k represents position dimensions.
- 2.
- The coordinate of both right-hand and left-hand sides of the antennae of beetles are presented as [47]:where represents the number of iterations; and denote the spatial position of the right and left beetles of longicorn beetles in the iteration, respectively; represents the exploitability of antennae sensing length in the iteration.
- 3.
- Fitness value:where and denote the fitness value of the right beetle and the left beard in the current spatial position; is the fitness function as Equation (9).
- 4.
- Pre-update position:Pre-update the position of the beetles based on the iteration, and the is a symbol function; is the step size factor of the algorithm in the iteration.
- 5.
- Accepted solution using the Monte Carlo lawThe Monte Carlo law of the SA algorithm is embedding into BAS. In the iterative process, the probability is used to accept the inferior solution to improve the global optimization ability of BAS:where denotes a pre-update position, denotes the best position in the last iteration; exp (.) represents the exponential function; is the higher temperature.
- 6.
- Step size:where and denote antennae length and step size, and is the initial value, where and is the step size factor of the algorithm in the iteration, and the two parameters and are set by the user.
5. Validation and Discussion
5.1. Processing the Adaptive Pruning Wake Redirect Digraph
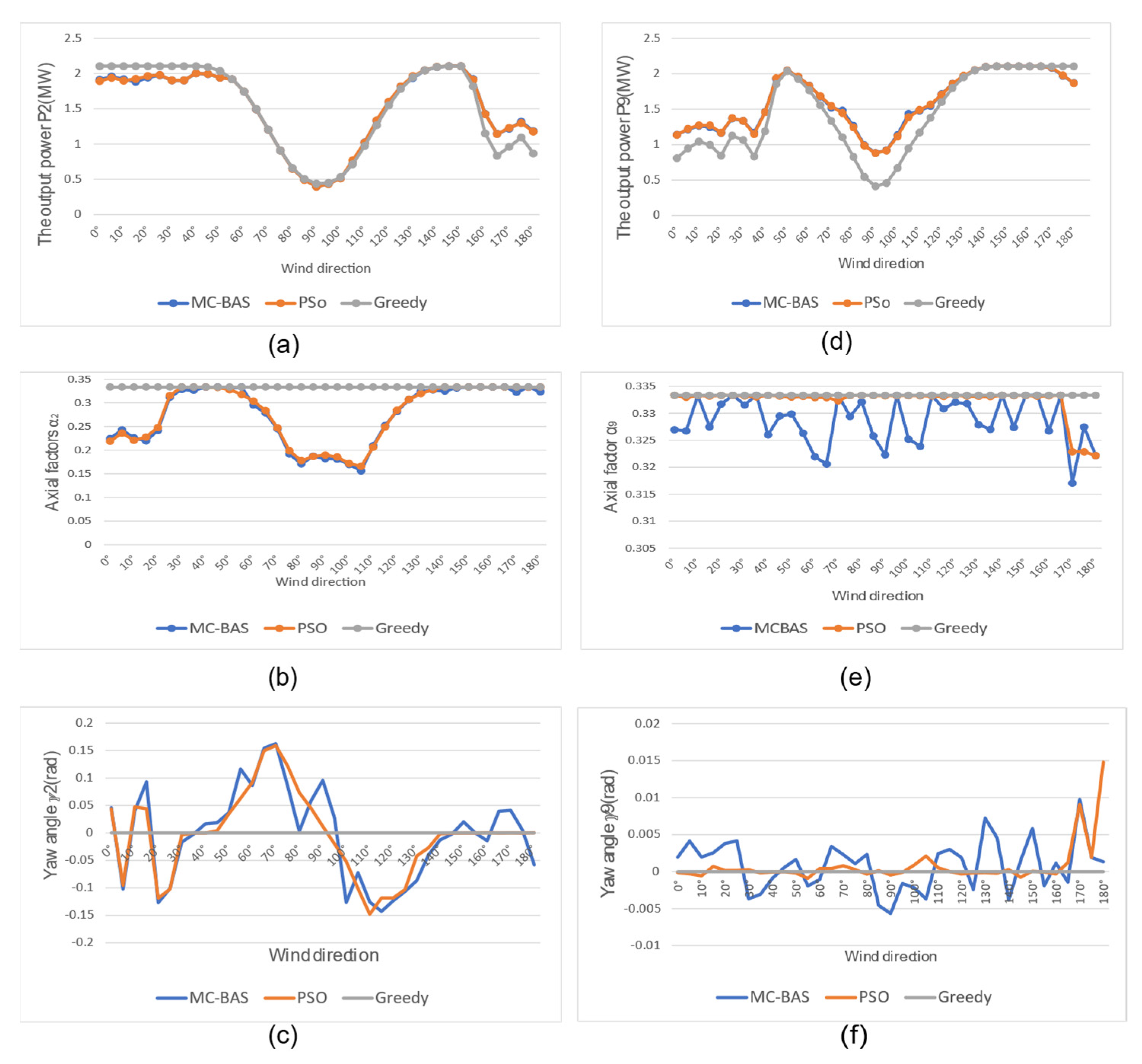
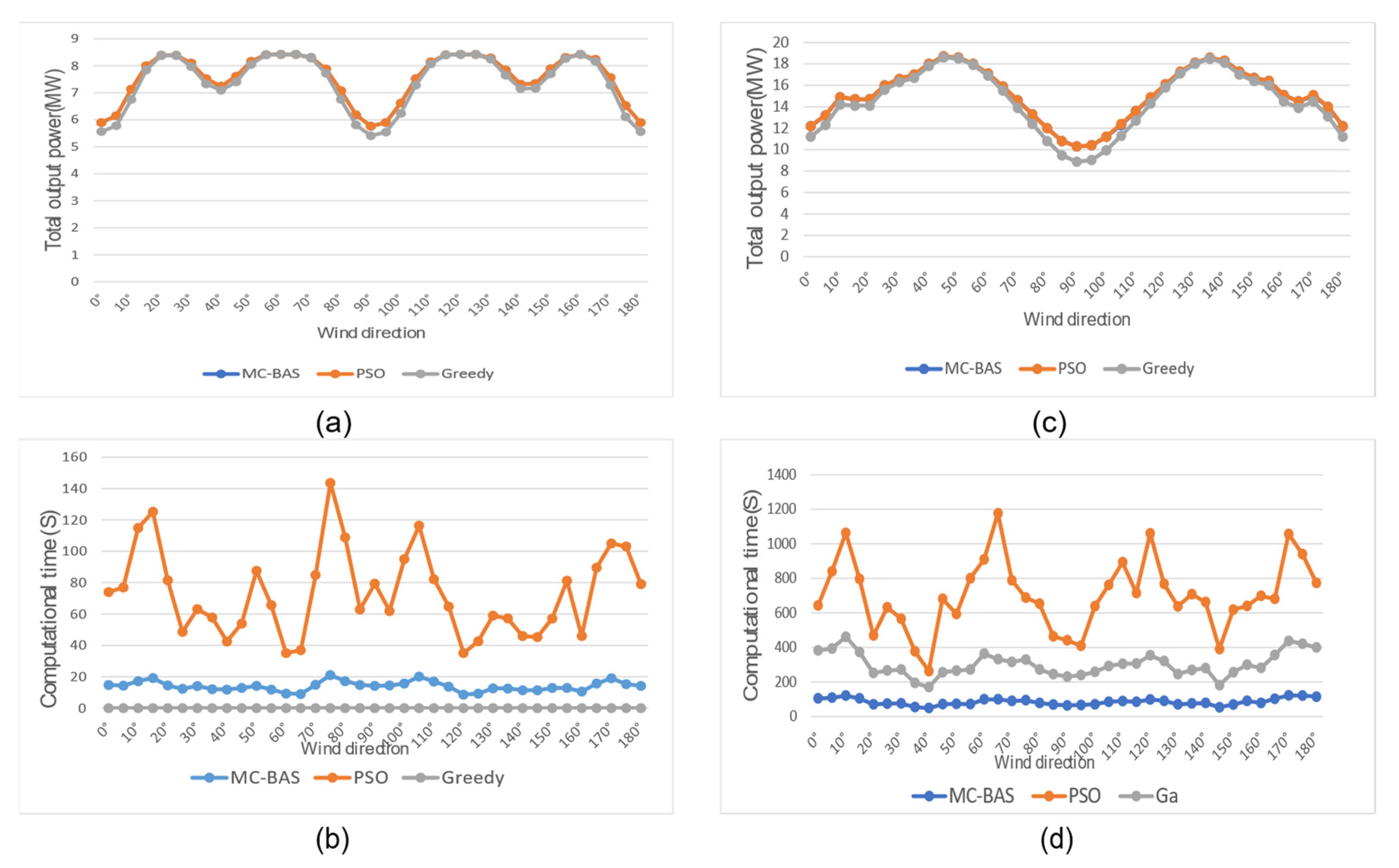
5.2. The Combined Evaluation of the Decentralized MC-BAS Algorithm
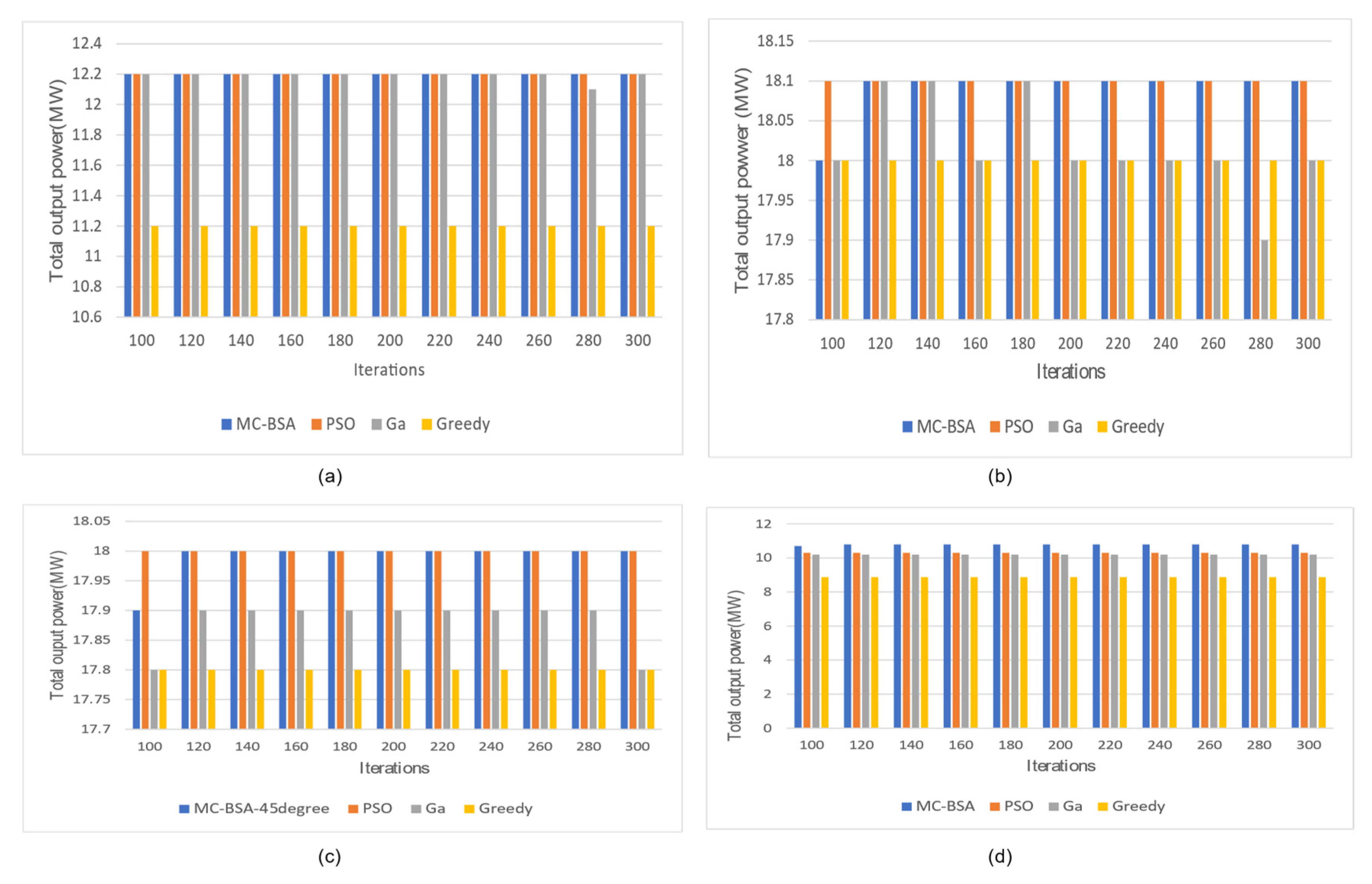
5.3. The Advantage of MC-BAS over Other Algorithms
6. Conclusions
- The proposed adaptive pruning algorithm fully considers the real-time power optimization control goals, providing a suitable method of grouping to avoid obtaining a sub-optimization result due to the unsuitable communication topology. The vital point of the adaptive pruned digraph is to uncover the accurate global threshold corresponding to the different wind by setting the suitable parameter . Moreover, the proposed method was verified to be efficient by the Simulink result, and the off-line look-up table was constructed in Appendix B.
- This work presents a modified BAS algorithm to raise BAS’s ability and efficiency for dealing with high-dimensional nonlinear problems. The BAS can use fewer iterations to rapidly search for the fitness function maximum in the parameter selection space. Meanwhile, the Monte Carlo (MC) law of Simulate Anneal (SA) was introduced to improve the reproducibility and stability of the algorithm by avoiding blind searching and escaping the local traps minima.
- For a large-scale wind farm, real-time state information may be excessive for the high communication and computational burden—centralized control approaches might fail. However, the adaptive pruned digraph decentralized operation can solve this problem by dividing the large-scale wind farm into several decoupled subsets; the local controller only deals with the local subset.
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
Appendix A
| P_rate | 5 MW |
| D | 126 m |
| 6.9 rpm | |
| 12.1 rpm | |
| 90° | |
| Gearbox ratio | 97:1 |
| Rated wind speed | 11.4 m/s |
| 0.485 | |
| Hub height | 90 m |
Appendix B
| 0° | 15° | 30° | 45° | 60° | 75° | 90° | 105° | 120° | 135° | 150° | 165° | 180° | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5.6 | 2.4 | 3.5 | 4.8 | 6.8 | 16.5 | 31.6 | 19.9 | 7.5 | 5.3 | 4.3 | 3.8 | 6.2 | ||
| 5.9 | 2.8 | 3.9 | 5.1 | 7.4 | 16.9 | 31.8 | 21.3 | 8.0 | 5.7 | 4.5 | 5.3 | 6.7 | ||
| 10 m/s | 6.2 | 3.3 | 4.2 | 5.7 | 7.6 | 17.6 | 41.8 | 27.3 | 9.6 | 6.7 | 5.8 | 6.9 | 7.6 | |
| 11 m/s | 6.8 | 3.9 | 6.4 | 8.4 | 18.9 | 43.4 | 29.8 | 10.9 | 7.9 | 6.9 | 7.3 | 7.6 | 9.4 |
References
- Song, D.; Zheng, S.; Yang, S.; Yang, J.; Dong, M.; Su, M.; Hoon Joo, Y. Annual Energy Production Estimation for Variable-Speed Wind Turbine at High-Altitude Site. J. Mod. Power Syst. Clean Energy 2021, 9, 684–687. [Google Scholar] [CrossRef]
- Song, D.; Chang, Q.; Zheng, S.; Yang, S.; Yang, J.; Hoon Joo, Y. Adaptive Model Predictive Control for Yaw System of Variable-Speed Wind Turbines. J. Mod. Power Syst. Clean Energy 2021, 9, 219–224. [Google Scholar] [CrossRef]
- Wang, L. Numerical Optimization of Wind Farm Layout and Control Strategy; Queensland University of Technology: Brisbane City, Australia, 2017. [Google Scholar]
- Serrano González, J.; Burgos Payán, M.; Santos, J.M.R.; González-Longatt, F. A Review and Recent Developments in the Optimal Wind-Turbine Micro-Siting Problem. Renew. Sustain. Energy Rev. 2014, 30, 133–144. [Google Scholar] [CrossRef]
- Chen, X.; Huang, L.; Liu, J.; Song, D.; Yang, S. Peak Shaving Benefit Assessment Considering the Joint Operation of Nuclear and Battery Energy Storage Power Stations: Hainan Case Study. Energy 2022, 239, 121897. [Google Scholar] [CrossRef]
- Kirchner-Bossi, N.; Porté-Agel, F. Wind Farm Area Shape Optimization Using Newly Developed Multi-Objective Evolutionary Algorithms. Energies 2021, 14, 4185. [Google Scholar] [CrossRef]
- Ahmad, T.; Basit, A.; Anwar, J.; Coupiac, O.; Kazemtabrizi, B.; Matthews, P. Fast Processing Intelligent Wind Farm Controller for Production Maximisation. Energies 2019, 12, 544. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Wang, L.; Song, D.; Huang, C.; Huang, L.; Wang, J. Incorporating Environmental Impacts into Zero-Point Shifting Diagnosis of Wind Turbines Yaw Angle. Energy 2022, 238, 121762. [Google Scholar] [CrossRef]
- Song, D.; Yang, J.; Su, M.; Liu, A.; Liu, Y.; Joo, Y. A Comparison Study between Two MPPT Control Methods for a Large Variable-Speed Wind Turbine under Different Wind Speed Characteristics. Energies 2017, 10, 613. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Fang, L.; Song, D.; Su, M.; Yang, X.; Huang, L.; Joo, Y.H. Review of Control Strategy of Large Horizontal-Axis Wind Turbines Yaw System. Wind Energy 2021, 24, 97–115. [Google Scholar] [CrossRef]
- Harrison, M.; Bossanyi, E.; Ruisi, R.; Skeen, N. An Initial Study into the Potential of Wind Farm Control to Reduce Fatigue Loads and Extend Asset Life. J. Phys. Conf. Ser. 2020, 1618, 022007. [Google Scholar] [CrossRef]
- Kanev, S.K.; Savenije, F.J.; Engels, W.P. Active Wake Control: An Approach to Optimize the Lifetime Operation of Wind Farms: Active Wake Control: An Approach to Optimize the Lifetime Operation of Wind Farms. Wind Energy 2018, 21, 488–501. [Google Scholar] [CrossRef]
- Xiao, X.-Y.; Yang, R.-H.; Zheng, Z.-X.; Wang, Y. Cooperative Rotor-Side SMES and Transient Control for Improving the LVRT Capability of Grid-Connected DFIG-Based Wind Farm. IEEE Trans. Appl. Supercond. 2019, 29, 1–5. [Google Scholar] [CrossRef]
- Ahmed, S.D.; Al-Ismail, F.S.M.; Shafiullah, M.; Al-Sulaiman, F.A.; El-Amin, I.M. Grid Integration Challenges of Wind Energy: A Review. IEEE Access 2020, 8, 10857–10878. [Google Scholar] [CrossRef]
- Shafiullah, G.M.; Amanuallh, M.T.O.; Shawkat Ali, A.B.M.; Wolfs, P. Potential Challenges of Integrating Large-Scale Wind Energy into the Power Grid–A Review. Renew. Sustain. Energy Rev. 2013, 20, 306–321. [Google Scholar] [CrossRef]
- Wang, L.; Li, H.-W.; Wu, C.-T. Stability Analysis of an Integrated Offshore Wind and Seashore Wave Farm Fed to a Power Grid Using a Unified Power Flow Controller. IEEE Trans. Power Syst. 2013, 28, 2211–2221. [Google Scholar] [CrossRef]
- Zha, X.; Liao, S.; Huang, M.; Yang, Z.; Sun, J. Dynamic Aggregation Modeling of Grid-Connected Inverters Using Hamilton’s-Action-Based Coherent Equivalence. IEEE Trans. Ind. Electron. 2019, 66, 6437–6448. [Google Scholar] [CrossRef]
- Chowdhury, M.A.; Shen, W.X.; Hosseinzadeh, N.; Pota, H.R. A Novel Aggregated DFIG Wind Farm Model Using Mechanical Torque Compensating Factor. Energy Convers. Manag. 2013, 67, 265–274. [Google Scholar] [CrossRef]
- Dhoot, A.; Antonini, E.G.A.; Romero, D.A.; Amon, C.H. Optimizing Wind Farms Layouts for Maximum Energy Production Using Probabilistic Inference: Benchmarking Reveals Superior Computational Efficiency and Scalability. Energy 2021, 223, 120035. [Google Scholar] [CrossRef]
- Wakasa, Y.; Yamasaki, S. Distributed Particle Swarm Optimization Based on Primal-Dual Decomposition Architectures. Stoch. Syst. Theory Appl. 2015, 2015, 97–101. [Google Scholar] [CrossRef]
- Annoni, J.; Dall’Anese, E.; Hong, M.; Bay, C.J. Efficient Distributed Optimization of Wind Farms Using Proximal Primal-Dual Algorithms. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 4173–4178. [Google Scholar]
- Katic, I.; Højstrup, J.; Jensen, N.O. A Simple Model for Cluster Efficiency. In EWEC’86. Proceedings; Palz, W., Sesto, E., Eds.; A. Raguzzi: Rome, Italy, 1987; Volume 1, pp. 407–410. [Google Scholar]
- Sizhuang, L.; Youtong, F. Analysis of the Jensen’s Model, the Frandsen’s Model and Their Gaussian Variations. In Proceedings of the 2014 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014; pp. 3213–3219. [Google Scholar]
- Kuo, J.Y.J.; Romero, D.A.; Beck, J.C.; Amon, C.H. Wind Farm Layout Optimization on Complex Terrains—Integrating a CFD Wake Model with Mixed-Integer Programming. Appl. Energy 2016, 178, 404–414. [Google Scholar] [CrossRef]
- Bastankhah, M.; Porté-Agel, F. Experimental and Theoretical Study of Wind Turbine Wakes in Yawed Conditions. J. Fluid Mech. 2016, 806, 506–541. [Google Scholar] [CrossRef]
- Gebraad, P.M.O.; van Dam, F.C.; van Wingerden, J.-W. A Model-Free Distributed Approach for Wind Plant Control. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 628–633. [Google Scholar]
- Deljouyi, N.; Nobakhti, A.; Abdolahi, A. Wind Farm Power Output Optimization Using Cooperative Control Methods. Wind Energy 2021, 24, 502–514. [Google Scholar] [CrossRef]
- Ni, Y.; Li, C.; Du, Z.; Zhang, G. Model order reduction based dynamic equivalence of a wind farm. Int. J. Electr. Power Energy Syst. 2016, 83, 96–103. [Google Scholar] [CrossRef]
- Fang, R.; Shang, R.; Wu, M.; Peng, C.; Guo, X. Application of Gray Relational Analysis to K-Means Clustering for Dynamic Equivalent Modeling of Wind Farm. Int. J. Hydrogen Energy 2017, 42, 20154–20163. [Google Scholar] [CrossRef]
- Shu, T.; Song, D.; Hoon Joo, Y. Decentralised Optimisation for Large Offshore Wind Farms Using a Sparsified Wake Directed Graph. Appl. Energy 2022, 306, 117986. [Google Scholar] [CrossRef]
- Charikar, M.; Guha, S.; Tardos, É.; Shmoys, D.B. A Constant-Factor Approximation Algorithm for the k-Median problem. J. Comput. Syst. Sci. 2002, 65, 129–149. [Google Scholar] [CrossRef] [Green Version]
- Quiroga-Novoa, P.; Cuevas-Figueroa, G.; Preciado, J.L.; Floors, R.; Peña, A.; Probst, O. Towards Better Wind Resource Modeling in Complex Terrain: A k-Nearest Neighbors Approach. Energies 2021, 14, 4364. [Google Scholar] [CrossRef]
- Ali, M.; Ilie, I.-S.; Milanovic, J.V.; Chicco, G. Wind Farm Model Aggregation Using Probabilistic Clustering. IEEE Trans. Power Syst. 2013, 28, 309–316. [Google Scholar] [CrossRef]
- Ma, S.; Geng, H.; Yang, G.; Pal, B.C. Clustering-Based Coordinated Control of Large-Scale Wind Farm for Power System Frequency Support. IEEE Trans. Sustain. Energy 2018, 9, 1555–1564. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, J. Wind Turbine Clustering Algorithm of Large Offshore Wind Farms Considering Wake Effects. Math. Probl. Eng. 2019, 2019, 6874693. [Google Scholar] [CrossRef]
- Marden, J.R.; Ruben, S.D.; Pao, L.Y. A Model-Free Approach to Wind Farm Control Using Game Theoretic Methods. IEEE Trans. Control Syst. Technol. 2013, 21, 1207–1214. [Google Scholar] [CrossRef]
- Park, J.; Law, K.H. Bayesian Ascent: A Data-Driven Optimization Scheme for Real-Time Control With Application to Wind Farm Power Maximization. IEEE Trans. Contr. Syst. Technol. 2016, 24, 1655–1668. [Google Scholar] [CrossRef]
- Thomas, J.J.; Annoni, J.; Fleming, P.A.; Ning, A. Comparison of Wind Farm Layout Optimization Results Using a Simple Wake Model and Gradient-Based Optimization to Large Eddy Simulations. In Proceedings of the AIAA Scitech 2019 Forum; American Institute of Aeronautics and Astronautics: San Diego, CA, USA, 2019. [Google Scholar]
- Gebraad, P.M.O.; van Wingerden, J.W. Maximum Power-Point Tracking Control for Wind Farms. Wind Energy 2015, 18, 429–447. [Google Scholar] [CrossRef]
- Lee, J.; Son, E.; Hwang, B.; Lee, S. Blade Pitch Angle Control for Aerodynamic Performance Optimization of a Wind Farm. Renew. Energy 2013, 54, 124–130. [Google Scholar] [CrossRef]
- Li, W.; Özcan, E.; John, R. Multi-Objective Evolutionary Algorithms and Hyper-Heuristics for Wind Farm Layout Optimisation. Renew. Energy 2017, 105, 473–482. [Google Scholar] [CrossRef] [Green Version]
- Tumari, M.Z.M.; Suid, M.H.; Ahmad, M.A. A Modified Grey Wolf Optimizer for Improving Wind Plant Energy Production. Indones. J. Electical Eng. Comput. Sci. 2020, 18, 1123. [Google Scholar] [CrossRef]
- Dongran, S.; Liu, J.; Yang, Y.; Yang, J.; Su, M.; Wang, Y.; Gui, N.; Xuebing, Y.; Huang, L.; Joo, Y.H. Maximum Wind Energy Extraction of Large-Scale Wind Turbines Using Nonlinear Model Predictive Control via Yin-Yang Grey Wolf Optimization Algorithm. Energy 2021, 221, 119866. [Google Scholar] [CrossRef]
- Tian, J.; Su, C.; Soltani, M.; Chen, Z. Active Power Dispatch Method for a Wind Farm Central Controller Considering Wake Effect. In Proceedings of the IECON 2014—40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 5450–5456. [Google Scholar]
- Song, D.; Fan, X.; Yang, J.; Liu, A.; Chen, S.; Joo, Y.H. Power Extraction Efficiency Optimization of Horizontal-Axis Wind Turbines through Optimizing Control Parameters of Yaw Control Systems Using an Intelligent Method. Appl. Energy 2018, 224, 267–279. [Google Scholar] [CrossRef]
- Rezaei, N.; Uddin, M.N.; Amin, I.K.; Othman, M.L.; Marsadek, M. Genetic Algorithm-Based Optimization of Overcurrent Relay Coordination for Improved Protection of DFIG Operated Wind Farms. IEEE Trans. Ind. Applicat. 2019, 55, 5727–5736. [Google Scholar] [CrossRef]
- Jiang, X.; Li, S. BAS: Beetle Antennae Search Algorithm for Optimization Problems. arXiv 2017, arXiv:1710.10724. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; NREL/TP-500-38060; National Renewable Energy Laboratory: Golden, CO, USA, 2009; p. 947422. [Google Scholar]
- Siniscalchi Minna, S. Advanced Wind Farm Control Strategies for Enhancing Grid Support. Ph.D. Thesis, Polytechnic University of Catalonia, Barcelona, Spain, 2019. [Google Scholar]
- King, R.; Hamlington, P.; Dykes, K.; Graf, P. Adjoint Optimization of Wind Farm Layouts for Systems Engineering Analysis. In Proceedings of the 34th Wind Energy Symposium, San Diego, CA, USA, 4 January 2016. [Google Scholar]
- King, R.N.; Dykes, K.; Graf, P.; Hamlington, P.E. Optimization of Wind Plant Layouts Using an Adjoint Approach. Wind Energy Sci. 2017, 2, 115–131. [Google Scholar] [CrossRef] [Green Version]

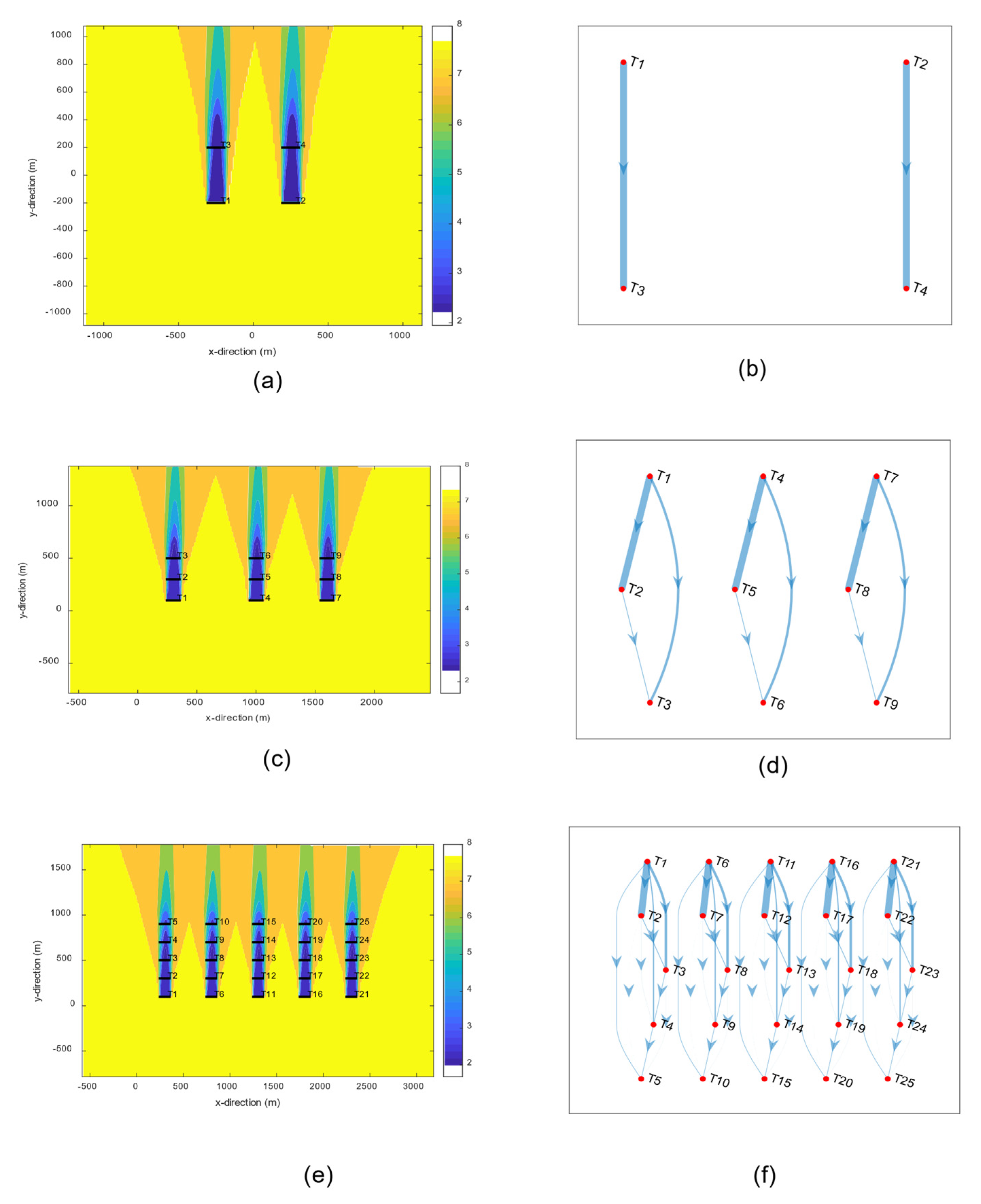
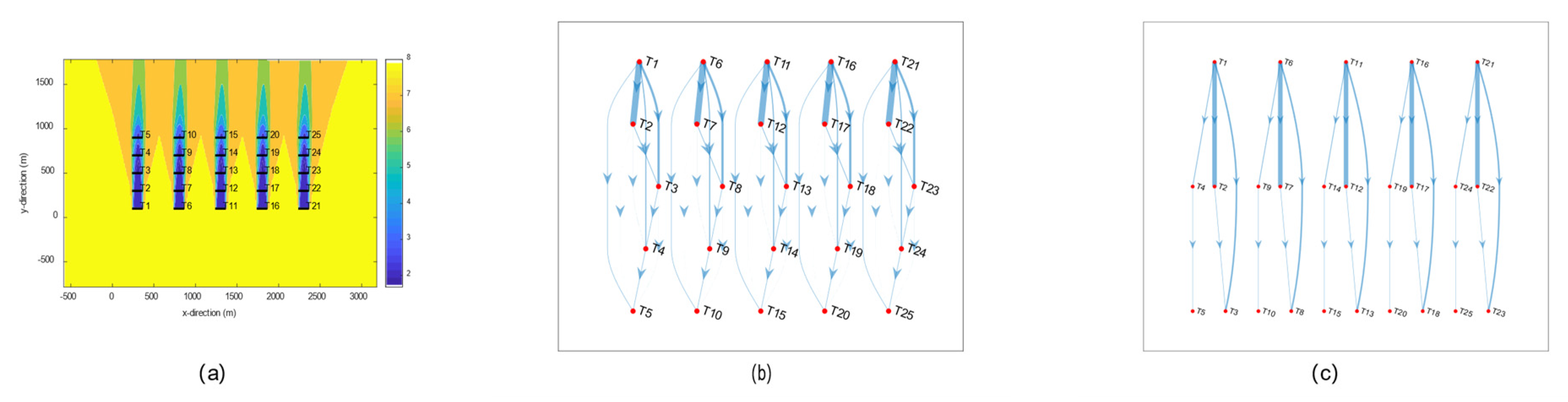
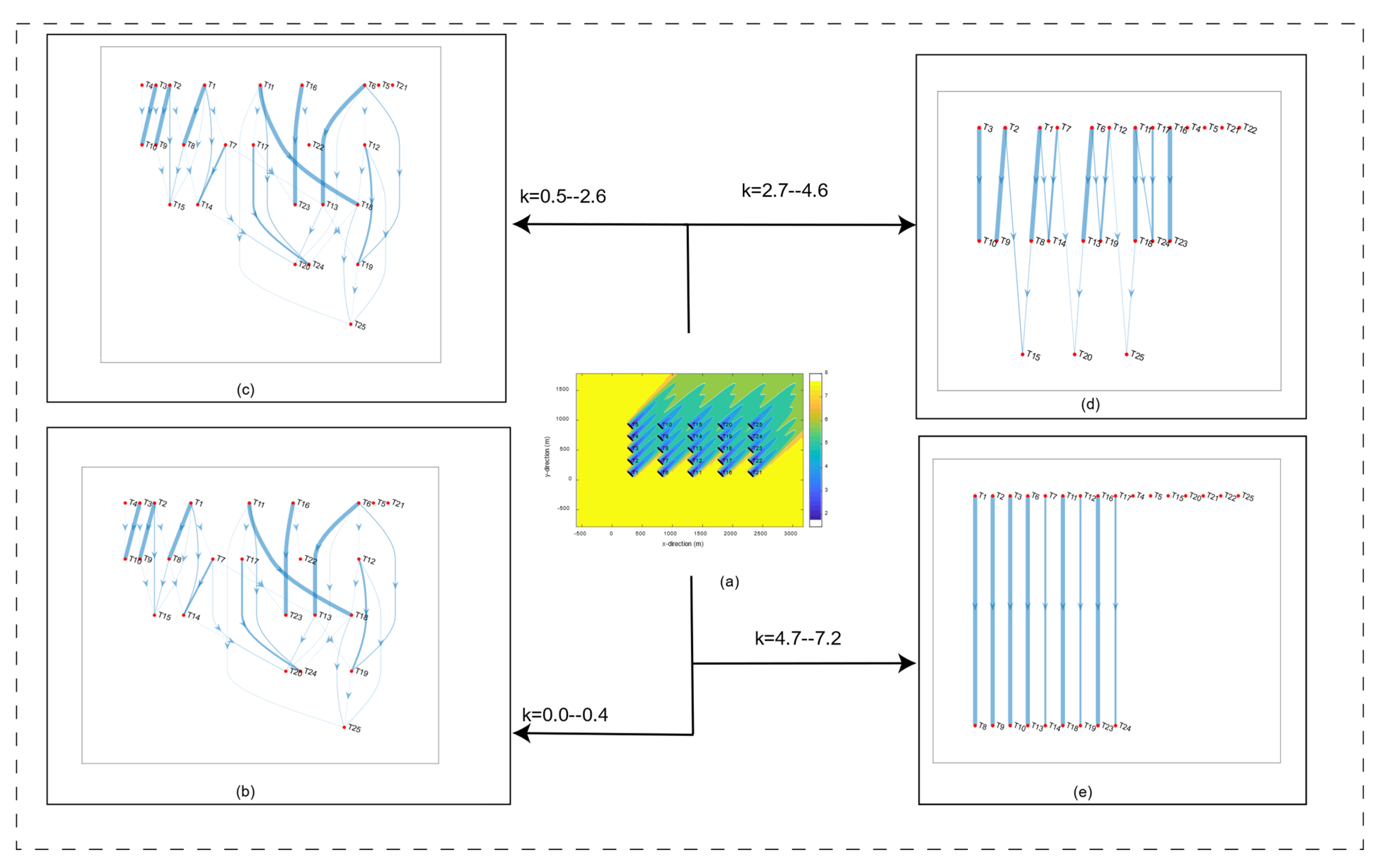


| No of Subsets | With ST or Not | |
|---|---|---|
| 0–0.4 | 9 | Yes |
| 0.5–2.6 | 13 | Yes |
| 2.7–4.6 | 13 | No |
| 4.7–7.2 | 16 | No |
| 7.3 | 21 | NO |
| Baseline Power | Total Power (W) | Groups | T(s) | ΔP | |
|---|---|---|---|---|---|
| 2.7 | 3.23E+07 | 3.62 × 107 | 13 | 2.84 × 102 | 12.19% |
| 2.8 | 3.23E+07 | 3.62 × 107 | 13 | 2.44 × 102 | 12.19% |
| 3.3 | 3.23E+07 | 3.62 × 107 | 13 | 2.42 × 102 | 12.19% |
| 3.8 | 3.23E+07 | 3.62 × 107 | 13 | 2.36 × 102 | 12.19% |
| 4.3 | 3.23E+07 | 3.58 × 107 | 13 | 2.35 × 102 | 10.95% |
| 4.8 | 3.23E+07 | 3.58 × 107 | 13 | 2.32 × 102 | 10.95% |
| 5.3 | 3.23E+07 | 3.51 × 107 | 13 | 2.30 × 102 | 8.78% |
| 5.7 | 3.23E+07 | 3.43 × 107 | 13 | 2.26 × 102 | 6.30% |
| 5.8 | 3.23E+07 | 3.03 × 107 | 16 | 3.57 × 102 | −6.10% |
| 6.3 | 3.23E+07 | 3.03 × 107 | 16 | 3.59 × 102 | −6.10% |
| 6.8 | 3.23E+07 | 3.01 × 107 | 16 | 3.66 × 102 | −6.72% |
| 7.3 | 3.23E+07 | 3.01 × 107 | 21 | 3.66 × 102 | −6.72% |
| φ | k | P(W) | ∆P | T(s) |
|---|---|---|---|---|
| Baseline | 2.4556 × 107 | 0% | 0.1896 | |
| k1 = 0.1 | 2.8528 × 107 | 16.18% | 276.245 | |
| k2 = 5.6 | 2.8526 × 107 | 16.17% | 211.5501 | |
| k3 = 11.7 | 2.0173 × 107 | −17.85% | 243.3781 | |
| Baseline | 2.4973 × 107 | 0% | 0.1659 | |
| k1 = 1.6 | 2.8554 × 107 | 14.34% | 268.4627 | |
| k2 = 2.4 | 2.8152 × 107 | 12.73% | 138.1018 | |
| k3 = 2.7 | 2.1252 × 107 | −14.90% | 189.6079s | |
| Baseline | 3.1375 × 107 | 0% | 0.1595 | |
| k1 = 1.9 | 3.3643 × 107 | 7.23% | 276.8732 | |
| k2 = 3.5 | 3.2142 × 107 | 2.45% | 239.3284 | |
| k3 = 4.1 | 2.9763 × 107 | −5.14% | 293.1692 | |
| Baseline | 3.9268 × 107 | 0% | 0.1402 | |
| k1 = 2.5 | 4.1118 × 107 | 4.57% | 284.4385 | |
| k2 = 5.7 | 4.0926 × 107 | 4.16% | 226.5321 | |
| k3 = 7.3 | 3.8126 × 107 | −2.97% | 366.5429 | |
| Baseline | 3.0271 × 107 | 0.00% | 0.1385 | |
| k1 = 0.9 | 3.2014 × 107 | 5.76% | 259.6893 | |
| k2 = 6.8 | 3.1139 × 107 | 2.87% | 271.8649 | |
| k3 = 7.9 | 2.7853 × 107 | −7.99% | 350.6543 | |
| Baseline | 2.3257 × 107 | 0% | 0.1243 | |
| k1 = 0.6 | 2.5473 × 107 | 9.53% | 174.9643 | |
| k2 = 16.5 | 2.4385 × 107 | 4.85% | 136.9856 | |
| k3 = 27.3 | 2.1072 × 107 | −9.39% | 181.6532 | |
| Baseline | 1.8731 × 107 | 0% | 0.1133 | |
| k1 = 0.0 | 2.2795 × 107 | 21.70% | 112.5742 s | |
| k2 = 31.6 | 2.1596 × 107 | 15.30% | 98.7756 s | |
| k3 = 83.7 | 1.6765 × 107 | −12.00% | 117.329 s |
| Wind Direction | Control Method | P_Total (w) | ΔP_Total | T_Total (s) |
|---|---|---|---|---|
| Centralized Greedy | 2.4556 × 107 | 0.00% | 0.1896 | |
| Centralized MC-BAS | 2.8529 × 107 | 16.18% | 636.5711 | |
| Decentralized MC-BAS (k1 = 0.1) | 2.8528 × 107 | 16.17% | 276.245 | |
| Decentralized MC-BAS (k2 = 5.6) | 2.8526 × 107 | 16.17% | 211.5501 | |
| Centralized Greedy | 3.1281 × 107 | 0.00% | 0.1279 | |
| Centralized MC-BAS | 3.4255 × 107 | 9.51% | 466.0449 | |
| Decentralized MC-BAS (k1 = 1.6) | 3.4254 × 107 | 9.50% | 218.4627 | |
| Decentralized MC-BAS (k2 = 2.4) | 3.4252 × 107 | 9.50% | 138.1018 | |
| Centralized Greedy | 3.9268 × 107 | 0.00% | 0.1102 | |
| Centralized MC-BAS | 4.2164 × 107 | 7.37% | 286.72145 | |
| Decentralized MC-BAS (k1 = 2.5) | 4.1118 × 107 | 4.57% | 284.4385 | |
| Decentralized MC-BAS (k2 = 5.7) | 4.0926 × 107 | 4.16% | 226.5321 | |
| Centralized Greedy | 1.8731 × 107 | 0.00% | 0.1133 | |
| Centralized MC-BAS | 2.3853 × 107 | 27.35% | 399.0926 | |
| Decentralized MC-BAS (k1 = 0.0) | 2.2795 × 107 | 21.70% | 112.5742 | |
| Decentralized MC-BAS (k2 = 31.6) | 2.1596 × 107 | 15.24% | 98.7756 |
| 0° | 5° | 10° | 15° | 20° | 25° | 30° | 35° | 40° | 45° | 50° | 55° | 60° | |
| ▲MCBAS | 9% | 7% | 5% | 4% | 4% | 3% | 2% | 2% | 1% | 1% | 1% | 1% | 1% |
| ▲PSO | 9% | 7% | 5% | 4% | 4% | 3% | 2% | 2% | 1% | 1% | 1% | 1% | 1% |
| 65° | 70° | 75° | 80° | 85° | 90° | 95° | 100° | 105° | 110° | 115° | 120° | 125° | |
| ▲MCBAS | 3% | 5% | 7% | 11% | 14% | 16% | 15% | 13% | 9% | 7% | 3% | 2% | 1% |
| ▲PSO | 3% | 5% | 7% | 11% | 14% | 16% | 15% | 13% | 9% | 7% | 3% | 2% | 1% |
| 130° | 135° | 140° | 145° | 150° | 155° | 160° | 165° | 170° | 175° | 180° | |||
| ▲MCBAS | 1% | 0% | 1% | 2% | 2% | 3% | 4% | 4% | 3% | 7% | 9% | ||
| ▲PSO | 1% | 0% | 1% | 2% | 2% | 3% | 4% | 4% | 3% | 7% | 9% |
| 0° | 5° | 10° | 15° | 20° | 25° | 30° | 35° | 40° | 45° | 50° | 55° | 60° | |
| ▲MCBAS | 6% | 6% | 6% | 2% | 0% | 0% | 2% | 3% | 2% | 3% | 1% | 0% | 0% |
| ▲PSO | 6% | 6% | 6% | 2% | 0% | 0% | 2% | 3% | 2% | 3% | 1% | 0% | 0% |
| 65° | 70° | 75° | 80° | 85° | 90° | 95° | 100° | 105° | 110° | 115° | 120° | 125° | |
| ▲MCBAS | 0% | 0% | 2% | 5% | 7% | 7% | 6% | 6% | 3% | 1% | 0% | 0% | 0% |
| ▲PSO | 0% | 0% | 2% | 5% | 6% | 6% | 6% | 6% | 3% | 1% | 0% | 0% | 0% |
| 130° | 135° | 140° | 145° | 150° | 155° | 160° | 165° | 170° | 175° | 180° | |||
| ▲MCBAS | 1% | 3% | 2% | 2% | 2% | 1% | 0% | 1% | 4% | 7% | 6% | ||
| ▲PSO | 1% | 3% | 2% | 2% | 2% | 1% | 0% | 1% | 4% | 7% | 6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Joo, Y.-H.; Song, D. Modified Beetle Annealing Search (BAS) Optimization Strategy for Maxing Wind Farm Power through an Adaptive Wake Digraph Clustering Approach. Energies 2021, 14, 7326. https://doi.org/10.3390/en14217326
Chen Y, Joo Y-H, Song D. Modified Beetle Annealing Search (BAS) Optimization Strategy for Maxing Wind Farm Power through an Adaptive Wake Digraph Clustering Approach. Energies. 2021; 14(21):7326. https://doi.org/10.3390/en14217326
Chicago/Turabian StyleChen, Yanfang, Young-Hoon Joo, and Dongran Song. 2021. "Modified Beetle Annealing Search (BAS) Optimization Strategy for Maxing Wind Farm Power through an Adaptive Wake Digraph Clustering Approach" Energies 14, no. 21: 7326. https://doi.org/10.3390/en14217326
APA StyleChen, Y., Joo, Y.-H., & Song, D. (2021). Modified Beetle Annealing Search (BAS) Optimization Strategy for Maxing Wind Farm Power through an Adaptive Wake Digraph Clustering Approach. Energies, 14(21), 7326. https://doi.org/10.3390/en14217326