1. Introduction
In the context of the transition to sustainability in power systems, transactive control (TC) has emerged as a form for coordinating the multiple agents in power systems (consumers; producers; distributed system operators—DSOs; transmission system operators—TSOs; aggregators, etc.) in order to optimize their operation to reduce the system’s costs, provide ancillary services, and enhance energy quality, among others [
1]. TC methods consider agents’ particularities, priorities, interests, and autonomy [
2]. The core objective is to reach an optimal allocation of resources (e.g., generation, controllable devices, and loads) in a decentralized form by only allowing actors to exchange minimal information (e.g., total consumption) among themselves [
3]. These decentralized and transparent characteristics make TC an attractive solution for load control in the residential sector in which privacy is a main concern and a large number of consumers exist [
4]. Therefore, the main motivation of the approach proposed in this paper is to deploy TC based solutions to unveil the flexibility offered by residential loads in order to cope with new challenges in power systems.
An effective method of implementing TC is by non-cooperative game theory because it allows modeling agents’ preferences, priorities, conflicting interests, and complex interactions in a decentralized manner [
5]. When applied to the load control in the residential sector, game theoretic methods capture load scheduling interactions between mid-size to small-size consumers that negotiate their load flexibility until an equilibrium is reached and all consumers are satisfied with the result [
6]. Mohsenian-Rad et al. [
7], who conducted one of the first studies in this field, proposed a non-cooperative game approach to schedule residential appliances by considering consumers’ preferences. In this pioneering study, the authors adopted simple load models with continuous decision variables, constant daily energy to be scheduled, and no operation constraints. Additionally, to divide the market results among participants, this study considered a billing mechanism that allocates the total quadratic cost according to the energy share of each individual consumer. Later on, other studies extended this discussion on billing mechanisms applied to transactive load control by analyzing the fairness of different methodologies [
8], studying potential cheating behaviors [
9], proposing alternatives to avoid untruthfulness of consumers [
10], and analyzing other costs models [
11].
At the same time, other works have focused on implementation aspects, for example, by developing a game-theoretic software framework to simulate demand response of electric vehicles and evaluate real-world use cases [
12], by proposing new coordination algorithms that require less communication among participants and consider communication losses [
13], by analyzing the stability of the Nash Equilibria when non-quadratic payoffs are designed [
14], by introducing a market mechanism able to deal with a large population of devices [
15], and by considering the role of utilities/aggregators [
16,
17,
18]. These contributions kept using relatively simple models to describe controllable loads, particularly using continuous variables to describe the scheduling problem.
Recently, new forms of load have been introduced as resources of TC in the context of non-cooperative games. For example, the authors of [
19] added electric vehicles (EV) to the continuous non-cooperative game model while addressing the uncertainty related to the number of EVs in a system. On a separate path, the authors of [
20] replicated the study of reference [
7] in a more realistic manner, including a simplified form of heating, ventilation, and air conditioning (HVAC) systems modeled as continuous loads but without explicitly representing their operation constraints. A better representation of consumers’ discomfort associated with HVAC loads was added as part of the cost function in reference [
21] together with additional energy supply constraints.
None of the studies referred above explicitly modeled thermostatically controlled loads (TCLs), particularly with respect to power/temperature comfort characteristics. The lack of attention to TCLs in the context of non-cooperative games is a significant gap. This is because these loads are a main source of flexibility in the residential sector [
22] and are widely explored in other forms of control (for example, centralized optimization, time-varying incentives, and dynamic pricing schemes [
23,
24,
25,
26,
27,
28,
29]) and are present in other TC models (for instance, auction theory and game theoretic models that apply other solving methods such as the Nikaido–Isoda function or mean-field approaches, multi-agent simulation, and fast control strategies) [
30,
31,
32,
33,
34,
35]. Controlling TCLs raise new challenges for the game models because they imply representing consumers’ comfort preferences and their operation constraints. The characteristics of thermal control have not been explored in the literature of TC with non-cooperative games discussed in the last paragraphs, which assumes simple operation models for the controllable loads. Thus, understanding the practical implications of TCLs aspects is key to allow extending transactive energy control to these loads.
Moreover, the aforementioned literature on non-cooperative games relies on the assumption that control is continuous. As demonstrated by the authors of [
36], modeling the control with continuous variables allows some important guarantees in terms of uniqueness/optimality of the Nash Equilibria (NE) when applying game theory to these type of problems. However, thermostatically controlled loads, such as many other residential appliances, often have an on/off control activated by a thermostat, which, realistically, implies an integer (binary) representation. This means that, in practical terms, the equilibrium guarantees that a continuous space might not fully apply to the TC in the residential sector, particularly in situations where the number of consumers is small and the controllable resources are highly discrete. Even though a few studies have considered this discrete nature of residential control, e.g., in the context of potential games [
37] and generalized ordinal potential games [
38], introducing more complex types of loads such as TCLs remains unexplored.
In summary, transactive control offers important decentralized characteristics that are suitable to residential demand side management. Current technological solutions developed around non-cooperative game theory have shown promising results, but they were unable to properly include TCLs, which is the largest source of flexibility among domestic loads. Moreover, two aspects of TCLs control are not fully addressed by the current theory of non-cooperative games: (1) the operation model of thermal loads, which includes temperature constraints, and (2) the on/off nature of the decisions, which produces the problematic integer and changes equilibria conditions. Therefore, it is important to understand the implications of these theory gaps in the real-world implementation of TC in the residential sector.
To address these issues, this paper advances the state of the art of day-ahead load scheduling of residential consumers by providing a game-theoretic framework in order to properly include domestic on/off TCLs in transactive control based on non-cooperative games. The specific contributions are the following:
We formulate a game with binary variables representing the on/off control of TCLs and explicitly model the consumers’ comfort constraints;
We discuss the theoretical foundations of this integer TCLs game, and we show that local or global optimal equilibria can be reached;
We generalize the paper’s results to two types of cost functions often applied to energy communities: quadratic and peak pricing.
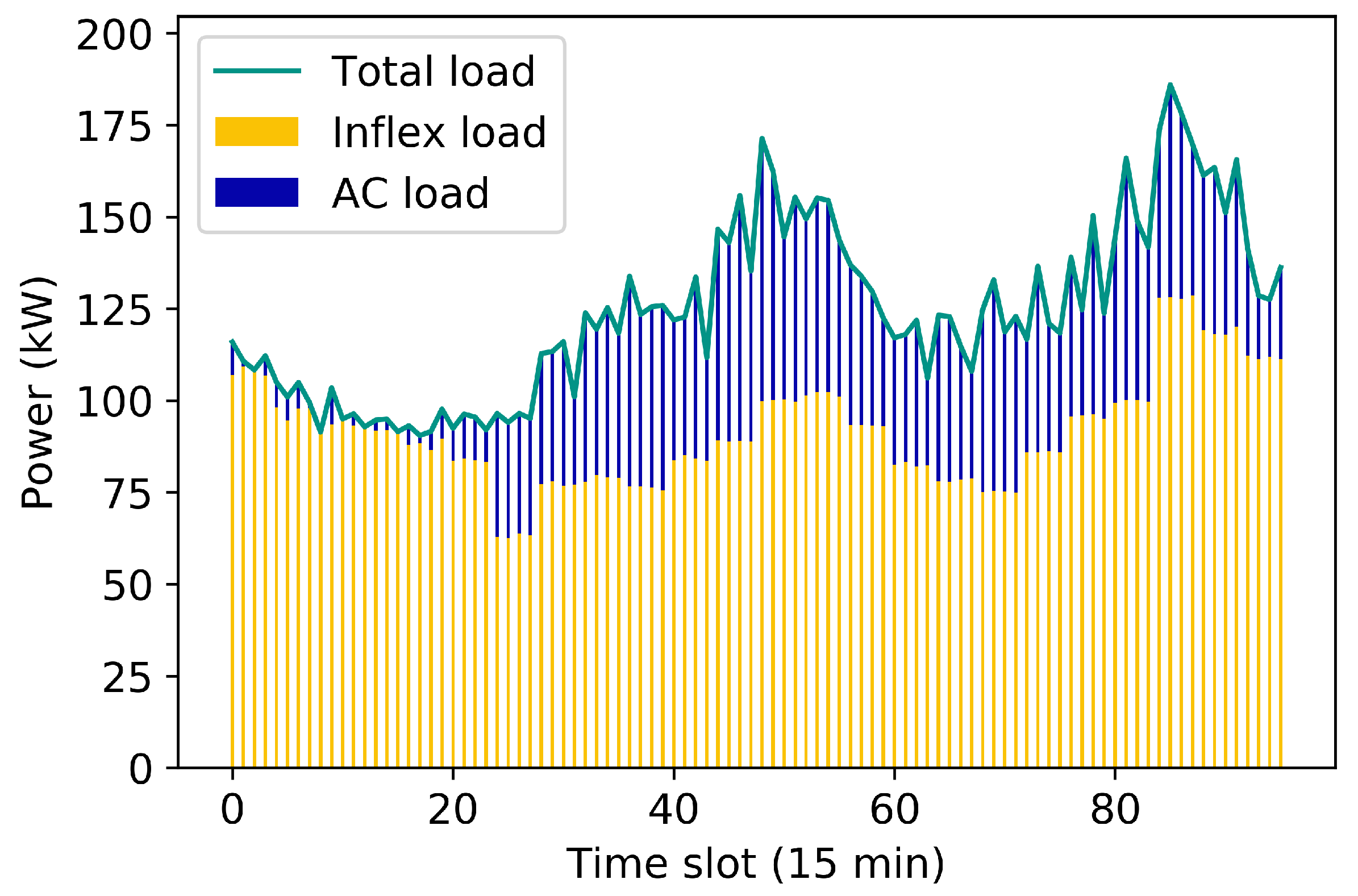
All the aforementioned contributions are analyzed theoretically and validated through simulations with real data. We create a realistic case study using information gathered from an LV network in the south of Spain with 201 consumers and evaluate the impacts of the TCLs load model and its integer characteristic in this context.
The rest of this paper is organized as follows. In
Section 2, we present the system model, including the new framework to incorporate integer thermal loads into the set of controllable appliances and the community cost functions analyzed. We then present the proposed game in
Section 3, including the discussion about the integer nature of the loads and the applicability to multiple total cost functions. Finally, we present simulation results in
Section 4, and we conclude the work in
Section 5.
3. Thermal Loads Scheduling as a Game
In this section, we present a non-cooperative game designed to coordinate the thermostatically controlled loads (TCLs) when the cost functions described above are applied to the community. The preferences and market parameters follow the definitions in the previous sections. We discuss the assumptions of this model when applied to TCLs, the existence of equilibrium points when integer loads are present, the model advantages, its general applicability, and the market and price formation. We also present the algorithm used to solve the game together with an analysis of its computational complexity and communication overhead.
The definition of the proposed non-cooperative TCLs scheduling game is given by a tuple in which the following is the case:
is the set of consumers living in the community and participating in the scheduling game (i.e., players);
denotes the action space for consumer
. This set is composed by feasible scheduling vectors,
, that respect users’ comfort constraints defined in Equation (
6);
is the utility function user
receives. It is defined as the negative of consumers’ bill, which is a share of the community’s total cost (either quadratic or peak pricing). The utility function is shown in Equation (
12), in which
can be Equation (
8) or (
10). The share
depends on the billing mechanism, and we use a version that bills each consumer according to his/her energy consumption during the scheduling horizon—see Equation (
13). This is a popular billing model in the literature of non-cooperative scheduling games [
7,
8,
9,
10,
11,
19,
36,
37], and we analyze its advantages and limitations when applied to the game with TCLs.
In this billing setting, if two participants n and m have total load after the scheduling game is solved, then consumer n will pay times consumer m’s bill. Moreover, the sum of all consumers’ payments will be equal to the community’s total cost: note that .
3.1. Model Assumptions
In this paper, we assume that TCLs have a fixed total energy to be scheduled in the billing period in line with the load models reported in the literature [
7,
8,
9,
10,
11,
13,
19,
20,
21,
36,
37,
38]. This assumption makes the factor
constant for each
and consumers seek to minimize the community’s total cost in order to increase their own utility. Therefore, consumers must coordinate their controllable load schedules to optimize the community’s consumption; otherwise, they will pay more.
Moreover, we consider that the aggregation platform contracts the community’s load in the market and chooses one of the total cost functions defined in
Section 2.3 to drive the game. This buying process is out of the scope of this paper, and we assume that the platform’s benefits/costs are included in the parameters of the chosen function. Moreover, we also consider that the risks of imbalances between the result of the day-ahead scheduling game and the real consumption of the community are taken by the aggregation platform (e.g., it measures the probability of consumers’ deviating from the equilibrium in real time and add the imbalances’ cost to the parameters of the total cost functions).
We also assume that the consumers’ uncontrollable load is forecasted by their energy management systems using past consumption data and a forecasting method. Thus, this load is considered deterministic, and its prediction method and errors (including the difference between the forecasted and real consumption) are out of the scope of this paper.
3.2. Equilibrium Points of the Integer Game
In games, the players’ goal is to choose and play optimal strategies, i.e., those resulting in larger utilities. However, the best strategy for a player depends on the choices of the other players. Therefore, one solution of a game is a Nash Equilibrium (NE): a strategy profile from which no player has incentive to deviate. In our setting, a strategy profile
is an NE if, for all consumers
, the following holds.
The billing studied in this paper guarantees the existence of the Nash Equilibrium for the game with integer thermal loads. With the fixed factor
multiplying the total community’s cost, consumers seek to minimize this function. If the total cost function has a minimum, it will be the Nash Equilibrium of the game [
50]: no consumer would be better off by unilaterally moving from this solution if the others are playing it as this would increase the total cost and consumers’ bills as a consequence. This can be seen by replacing the utility Equation (
12) in the NE Equation (
14). Due to the integer nature of the variables, the NE can be a local or global minimum [
50]. Both total cost functions studied in this paper are convex, meaning they have minimum points that can be local or global optima of the community’s scheduling problem and equilibria points as a consequence. In the results section, we show that solutions of the game are optimum or close to optimum values.
3.3. Advantages of the Game Model
The game model is designed to divide the total cost of the community according to a fixed share, which brings a coordination aspect to the game: All participants intend to minimize this total cost function, and minimum values for the entire community are equilibria. Here, it is important to note that, despite the name, non-cooperative games can be intentionally created to achieve cooperation goals [
51], as shown by the design of our utility function.
Moreover, any total cost function with a minimum point (local or global) can be used in this setting, e.g., convex functions as the quadratic and peak pricing studied here. The existence of a Nash Equilibrium is guaranteed for any community’s total cost function with a minimum value, allowing the implementation of this model in multiple market contexts.
Another interesting advantage is that cheating behavior is discouraged in this model. As consumers’ bills equal a fixed share times the total cost function, any behavior that results in a non-equilibrium solution and does not minimize the cost will also harm the cheater participant.
Finally, in this non-cooperative game, the interactions between consumers to reduce their individual energy bills can be mimicked by the iterative and decentralized learning algorithm described in
Section 3.5. The idea is to reach an equilibrium point, the Nash Equilibrium (NE) [
52], which is a stable solution. This also means that the autonomy of consumers is respected during the process because they decide their schedules individually and locally, according to their constraints and preferences.
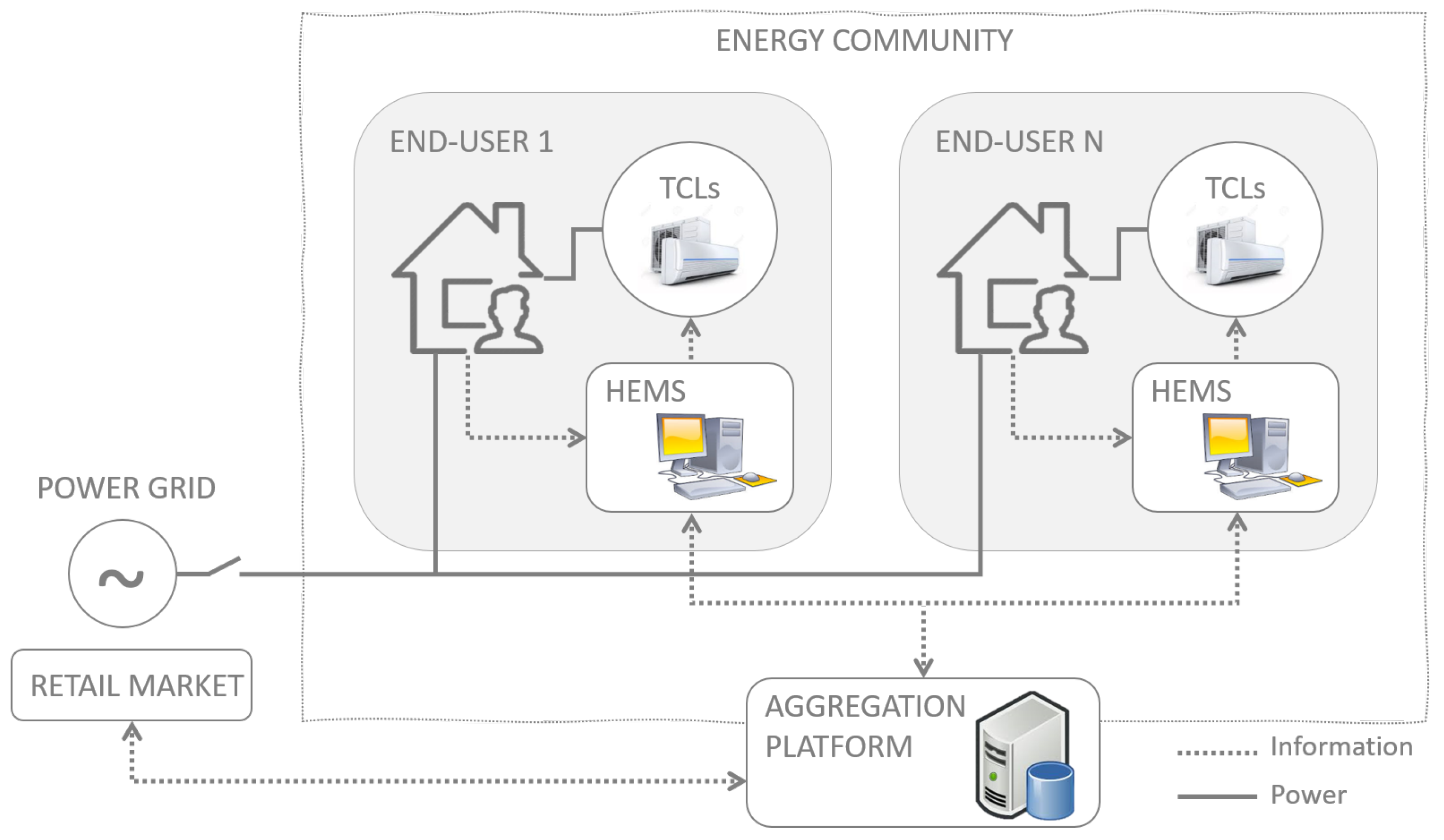
3.4. On Market and Price Formation
The smart energy communities studied in this paper are inside energy markets. In this section, we provide a discussion on how the interactions between consumers, energy community, aggregation platform, and the current energy markets might happen.
Energy communities are an important aspect to the clean energy transition. By moving citizens to the fore, public acceptance of renewable energy projects is increased, which makes private investments on clean energy more attractive. Moreover, they can provide direct benefits to citizens such as cheaper electricity bills and higher energy efficiency. Finally, this organization model can help provide flexibility to electricity markets through, for instance, storage systems and demand response.
A new regulation has been implemented to provide a legal framework for energy communities’ constitution and market participation. For instance, the European Parliament and Council passed directive 944 in 2019 authorizing citizens to organize themselves in energy communities and participate in the energy markets [
53]. In this context, the consumers considered in our scope would be able to trade in the energy markets through their energy communities and aggregation platforms.
More specifically, the definitions of the total cost function and its parameters (e.g., , , and for the quadratic, , and e for the peak pricing) are a result of the trading process between the aggregation platform and the energy markets when buying the community’s load. The community participants are, therefore, price-takers in the definition process of these parameters because they cannot influence wholesale/retail markets prices, even when joining forces as a community.
On the other hand, consumers inside the community have the power to influence the final total cost: By choosing their strategies (appliances schedules), the value to be split between them is optimized, as well as their utilities. This inside-community trading process results in consumers who know the impact of their choices in the game results. Therefore, within the boundaries of their community and given a total cost function, consumers are price makers. One should note that the focus of this paper is on the negotiation process among consumers and on this price-making characteristic. This inside-community negotiation process is better described by the algorithm used to solve the game, which is presented in the next section—see
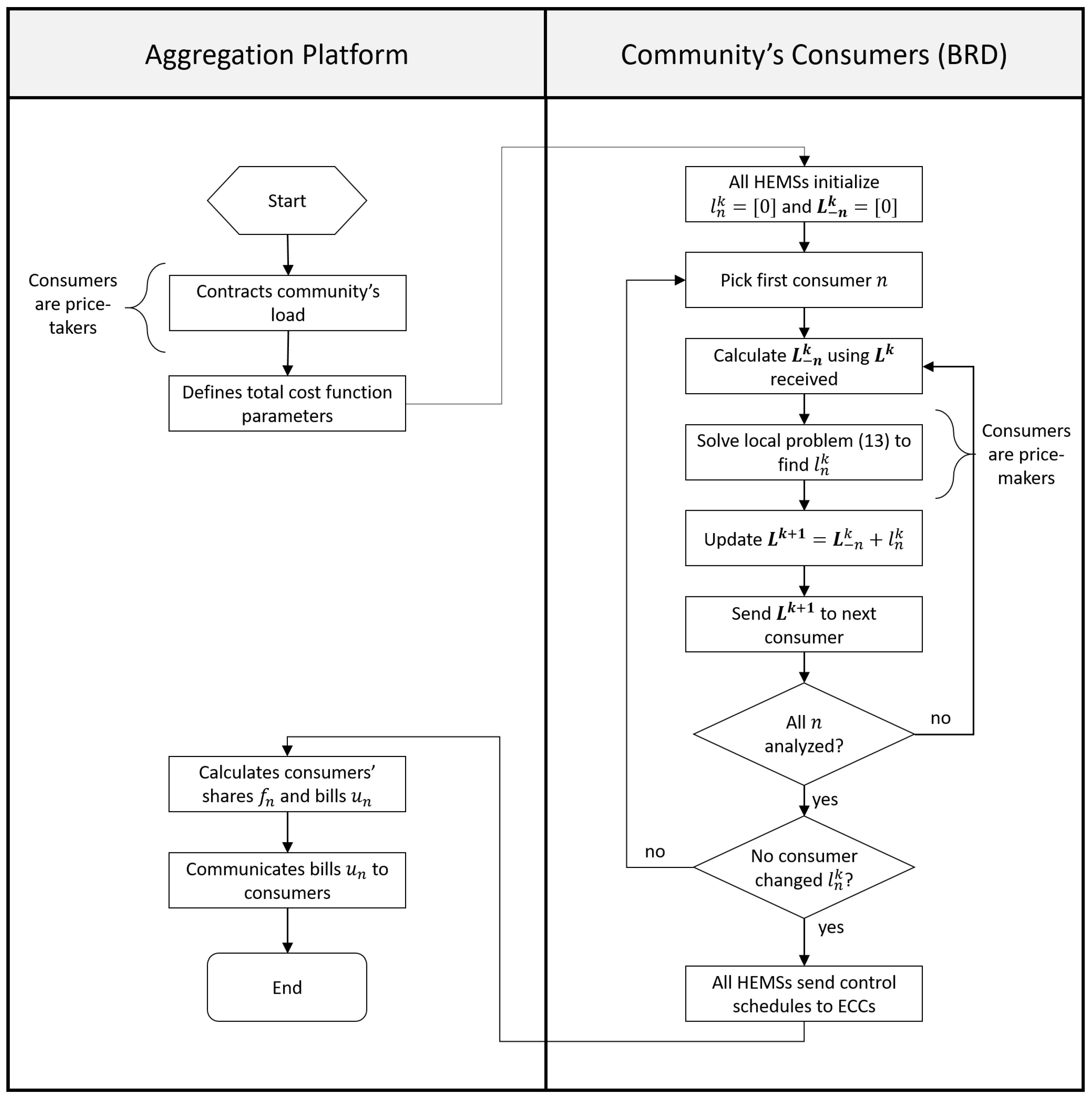
Figure 2.
3.5. Best Response Algorithm
To find a solution to the proposed game, we use the Best Response Dynamics (BRD), which is a learning method applied to solve games; in other words, it finds equilibrium points. It is a sequential decision model in which consumers take turn and best respond to opponents’ last strategies (TCLs schedules in our framework). We use a version in which consumers communicate the total group’s load instead of their individual profiles, which results in less message exchanges and reduces the privacy issue [
10].
The algorithm works as follows. Assuming that each consumer’s home energy management system keeps track of opponents’ total consumption vector () and the total load of all players is initialized with zeros , each iteration of the gameplay consists of three steps:
Consumers receive the total load vector and calculate the load of opponents using their previous best strategies;
They update their strategies
as a response to
by solving the local MIQP (
15) with
defined by (
8), if the quadratic total cost function is applied, or the local MILP (
15) with
defined by (
10), if the peak pricing total cost function is applied;
Consumers add their local strategy to the opponents’ total consumption vector and send this new aggregated consumption profile to the next player.
As BRD converges to a Nash Equilibrium for games in which all consumers have the same concave utility function (the negative of the total cost) [
50], the process continues until an equilibrium is reached and consumers can no longer reduce their bills when changing their schedules.
As shown in
Figure 2, this algorithm is decentralized and each consumer has the autonomy to schedule locally his/her TCLs. The aggregation platform is responsible for defining the cost function parameters. However, consumers’ decisions are taken locally by their HEMSs through the BRD. Moreover, because of the design of the utility function, i.e., the billing proportional to each participant’s share, the consumers aim at minimizing the global objective (the total cost). Finally, their shares and bills are calculated by the aggregation platform after receiving consumers’ loads.
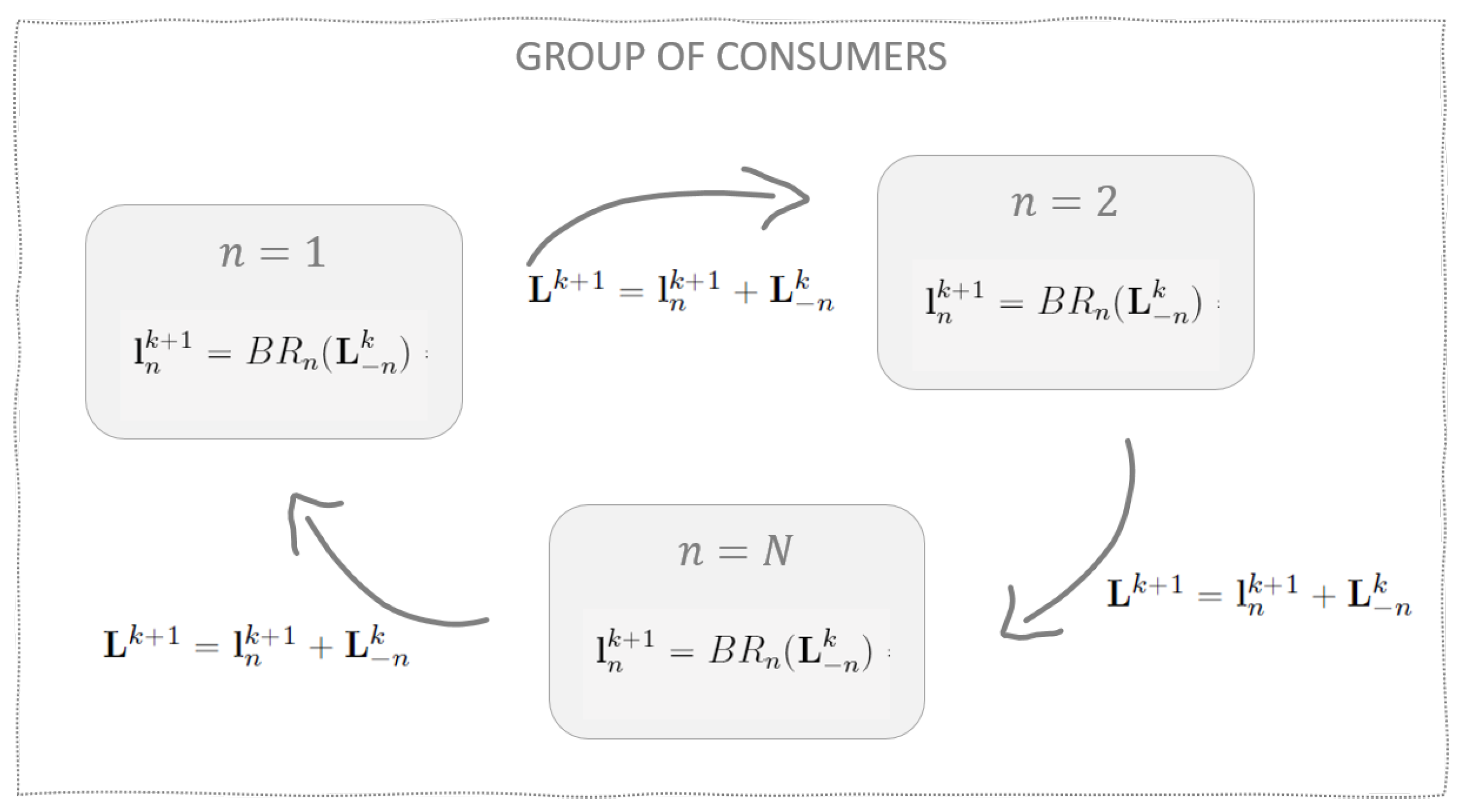
One should notice that community participants communicate the group’s total load. This design guarantees users’ privacy as they do not share individual preferences, strategies, or load profiles: their personal consumption is integrated in the total load vector and no participant knows the opponents’ individual values. This aspect is better illustrated in
Figure 3 in which
is the total load vector communicated between consumers, and
is the local consumption vector, which is known by participant
n only. Other methods to enhance data privacy and secrecy can be added to the algorithm, e.g., multi-party computation protocol (MPC) [
10] or Institute of Electrical and Electronics Engineers (IEEE) 2030.5 standard [
54].
3.6. Computational Complexity and Communication Overhead
In this section, the computational complexity and communication overhead of the Best-Response Algorithm is analyzed in comparison to the centralized model. An homogeneous scenario is considered: All consumers of the community have one air conditioner with operation described by Equation (
4) and same parameters (i.e., performance, thermal capacity, thermal resistance, and power rate), as well as same preferences
and
. Moreover, a constant outside temperature
during the day-ahead horizon is examined, which is also equal for all community participants. If
(
) is less than (greater than) or equal to the minimum (maximum) temperature the thermal load can reach, the space of solutions of the binary problem of one consumer is
. In the worst case, one iteration of the Best Response Algorithm would have to explore this entire space to find a solution. Moreover, this must be performed for each consumer
sequentially. Finally, the BRD will take
r rounds to converge, resulting in a worst-case complexity of
. For the centralized model, all consumers’ problems are solved simultaneously, and the computation complexity is, thus,
.
When realistic preferences on the minimum and maximum temperatures are considered, the complexity decreases as the space of feasible solutions also decreases according to Equation (
4). However, this worst-case analysis provides insight on what influences the BRD resolution time: the size of the time slots, the consumers’ preferences, and the number of consumers. One should notice that the number of rounds of the BRD is proportional to the number of consumers in the game, but it is also impacted by other factors such as the path to reach the minimum total cost (which is related to algorithm’s playing order) and the complexity of one iteration given the opponents’ consumption vector.
Finally, each iteration of the BRD means one exchange of messages; thus, the communication overhead is equal to
. The analytical conclusions on computational complexity and communication overhead are summarized in
Table 1.
3.7. General Applicability of the Model
The game model can be extended to other appliances. For instance, different types of thermostatically controlled loads (TCLs) have similar behavior to the ACs presented—as shown in reference [
26]—and can be modeled using Equations (
1)–(
3). Moreover, shiftable appliances, such as washing machines, also have an on/off control, resulting in the same conclusions on equilibrium points presented in
Section 3.2. Even devices that can be modeled as continuous variables (e.g., an electric vehicle) could be added to the model without changing its properties. This can be explained by the fact that consumers try to optimize the total cost function in order to minimize their own bills. Therefore, all conclusions related to the existence of Nash Equilibria, convergence of BRD, application of total cost functions with minimum values, and nonexistence of cheating behavior are applicable and do not depend on the appliances controlled and their constraints.
Moreover, uncertainties could be added to the model. For instance, uncertainty on participants’ final consumption, especially the non-controllable loads, can be a risk to the total cost consumers or the aggregation platform will pay depending on the demand-side management contracts they agree upon. In
Section 3.1, those uncertainties were assumed deterministic, and the risks are taken by the aggregation platform, but they can be modeled as stochastic variables in the scope of our proposition without changing the nature and properties of the non-cooperative game. One could add an expectation over the base load probability function in Equation (
12). It is clear that simulation results could be different if uncertainties are considered, but consumers will continue seeking to minimize the total community cost in the uncertain framework, the game will have a Nash Equilibrium for any convex function considered, and the best response algorithm will converge.
5. Conclusions
In this paper we advanced the state of the art of non-cooperative games applied to the day-ahead load scheduling of residential consumers by adding thermostatically controlled loads (TCLs) into the set of appliances considered in the transactive control (TC). We proposed a game model for the residential community to schedule their flexible TCLs—more specifically, air conditioners—with the objective of minimizing consumers and community costs. Consumers’ comfort constraints were modeled explicitly, and their TCL’s operation was described with binary variables in order to represent the on/off nature of the control.
We showed the following: (1) the integer nature of the control can lead to optimal or close to optimal solutions; (2) the billing mechanism used is able to align individual’s goal to the community’s goal; (3) consumers’ comfort is properly modeled and respected; and (4) different total cost functions can be used depending on the market context and the objective of the demand management program. Moreover, the non-cooperative game was solved in a decentralized fashion, providing consumers with the autonomy to decide their schedules according to their preferences and interests.
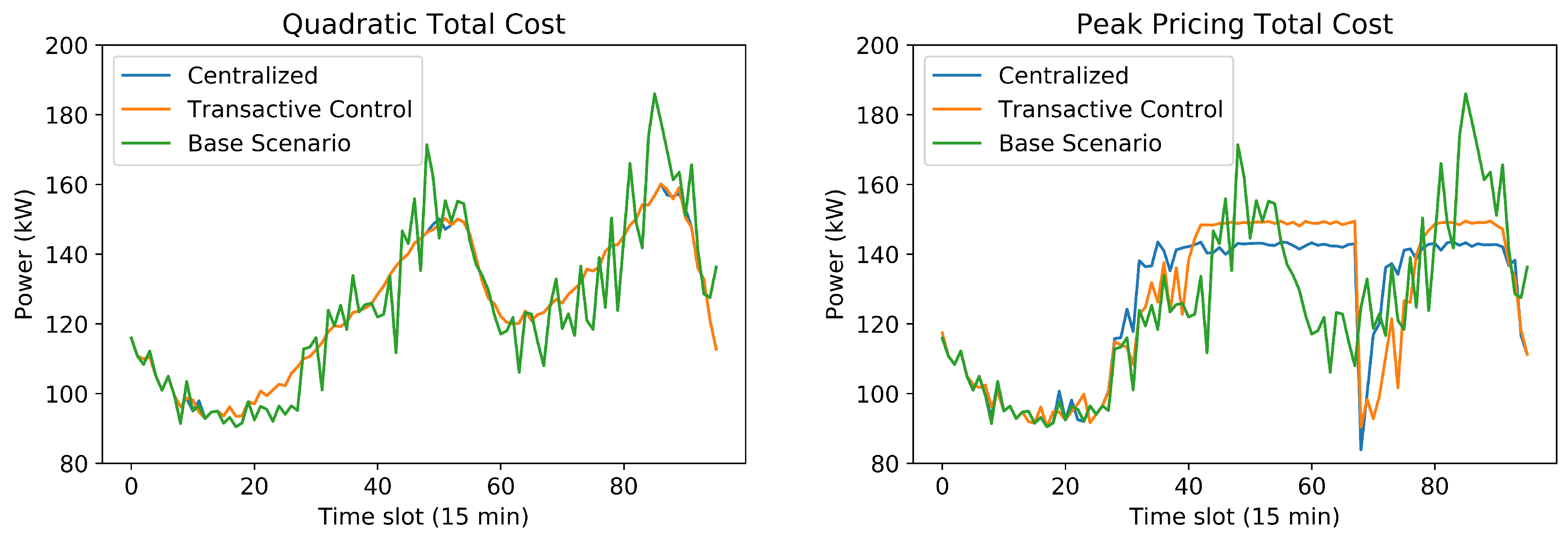
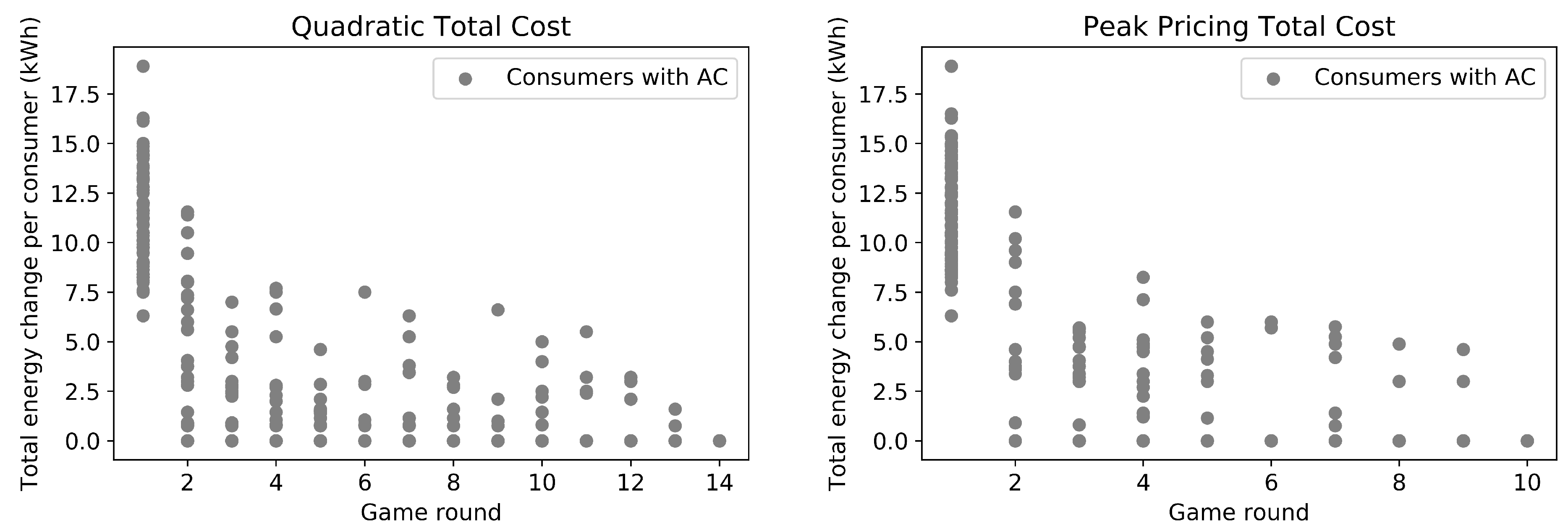
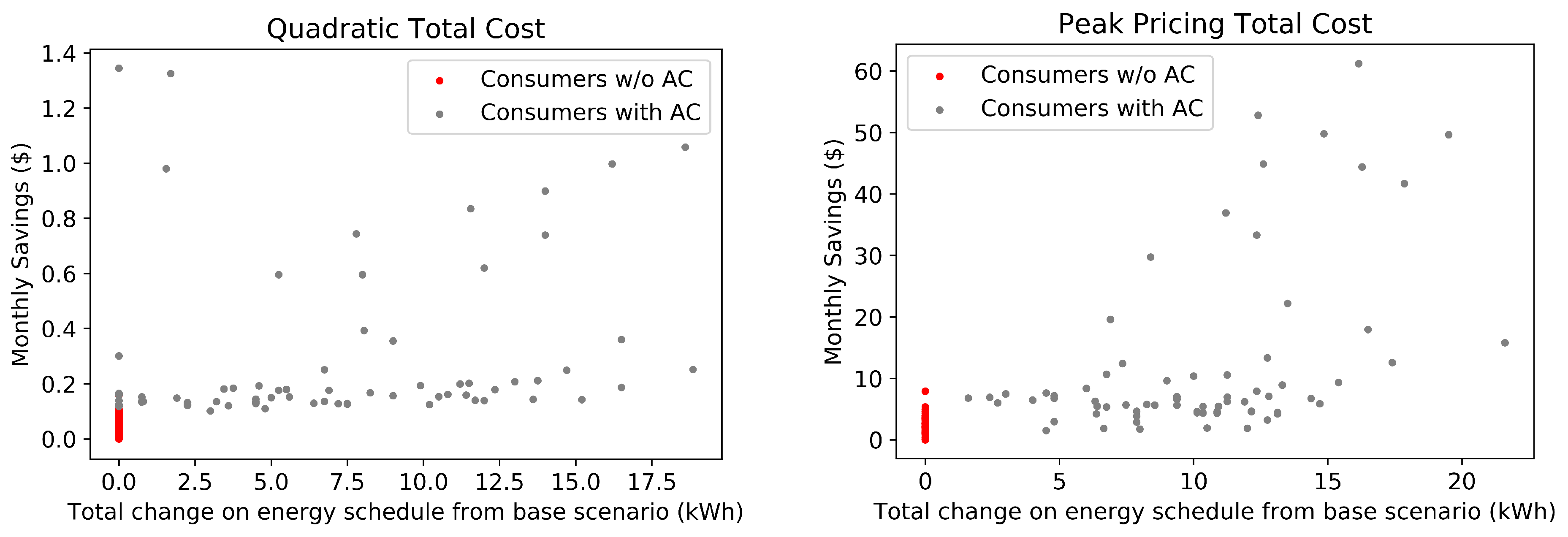
To discuss the practical application of non-cooperative games to scheduling TCLs and the aforementioned theoretical conclusions, we created a case study using real data from 201 consumers in Spain. The results showed that the TC solution is equal to the optimal one when a quadratic total cost function is used, and it is 0.80% worst than the optimal total cost when a peak pricing function is applied. Moreover, the quadratic game was able to smooth the community’s curve while the peak pricing game reduced its peak-to-average ratio. Both games converged to a Nash Equilibrium in 10 to 12 rounds. Consumers’ comfort was respected, and the internal temperature of their homes was even reduced with the TC approach. Finally, all consumers had savings compared to the scenario without energy management.