Significant Production of Thermal Energy in Partially Ionized Hyperbolic Tangent Material Based on Ternary Hybrid Nanomaterials
Abstract
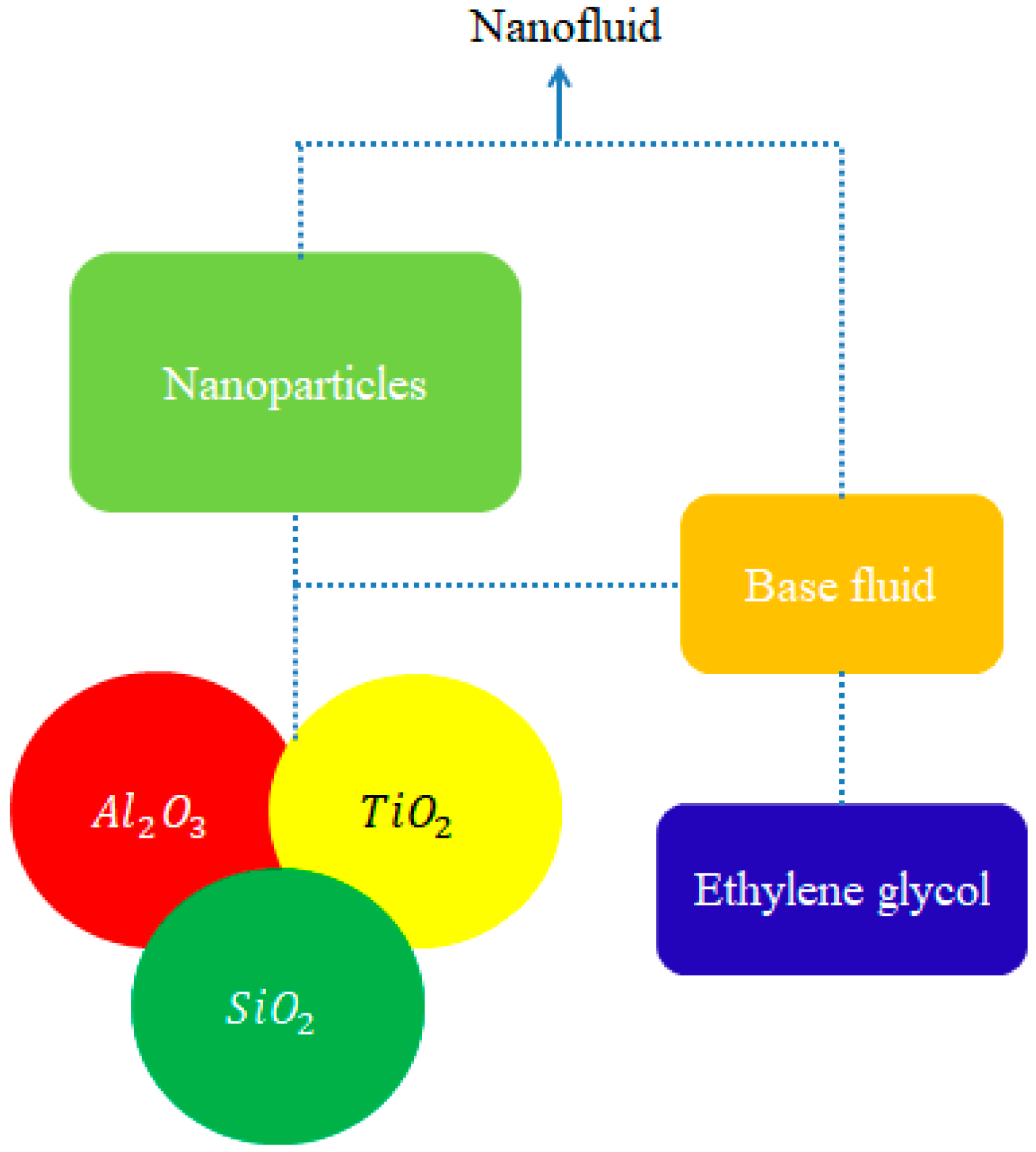
:1. Introduction
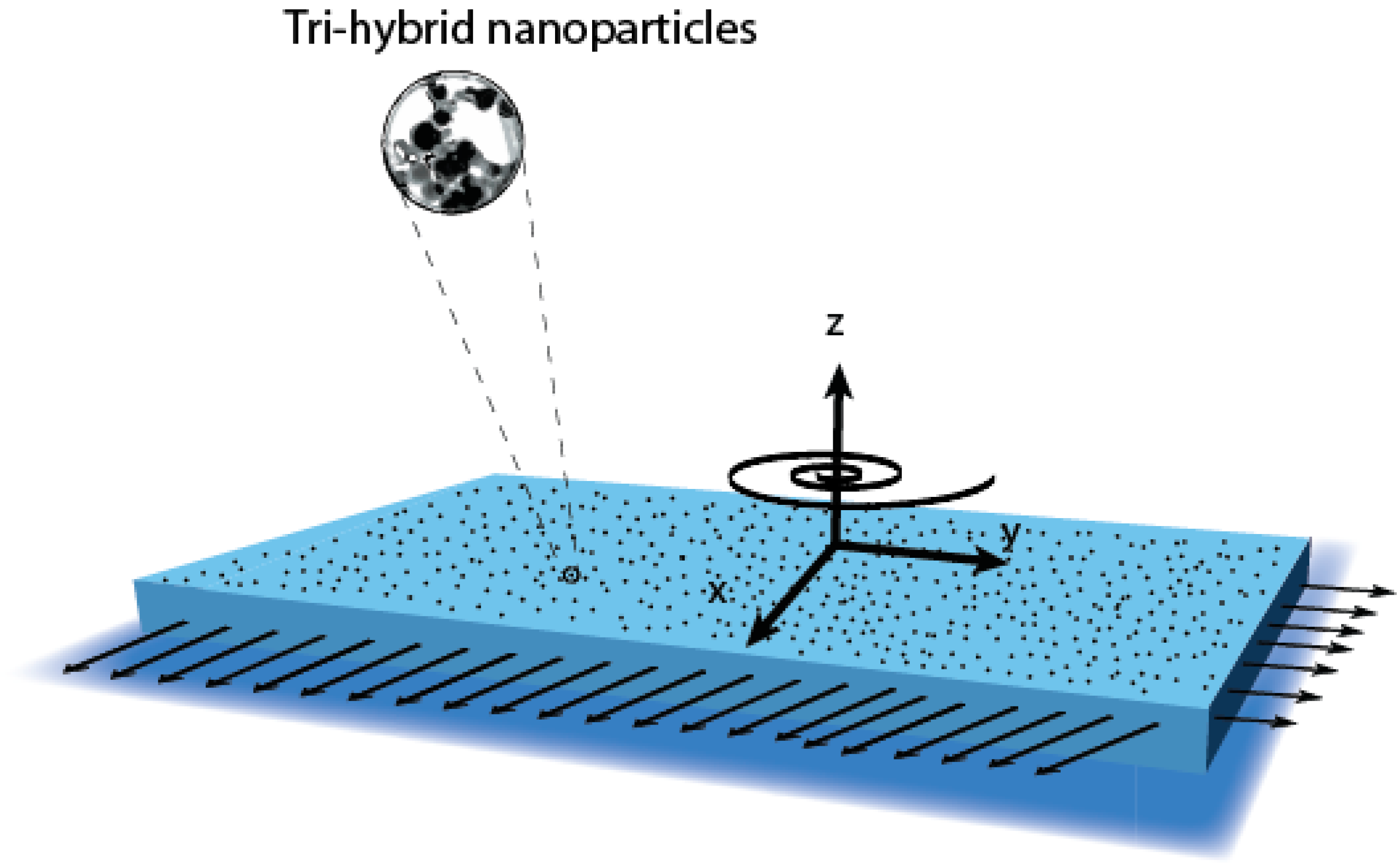
2. Statement of Developing Problem
3. Numerical Approach
4. Graphical Outcomes and Discussion
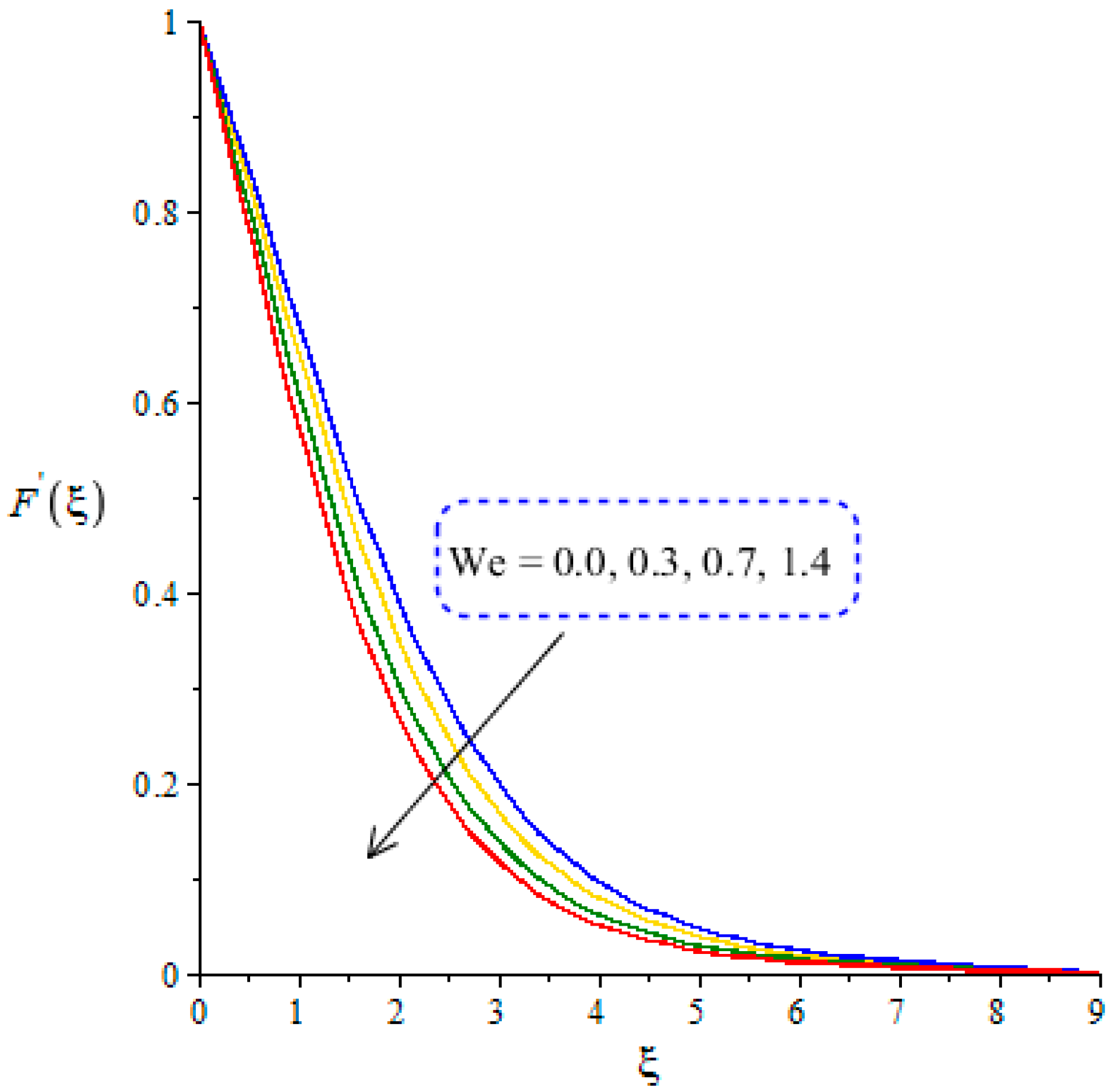
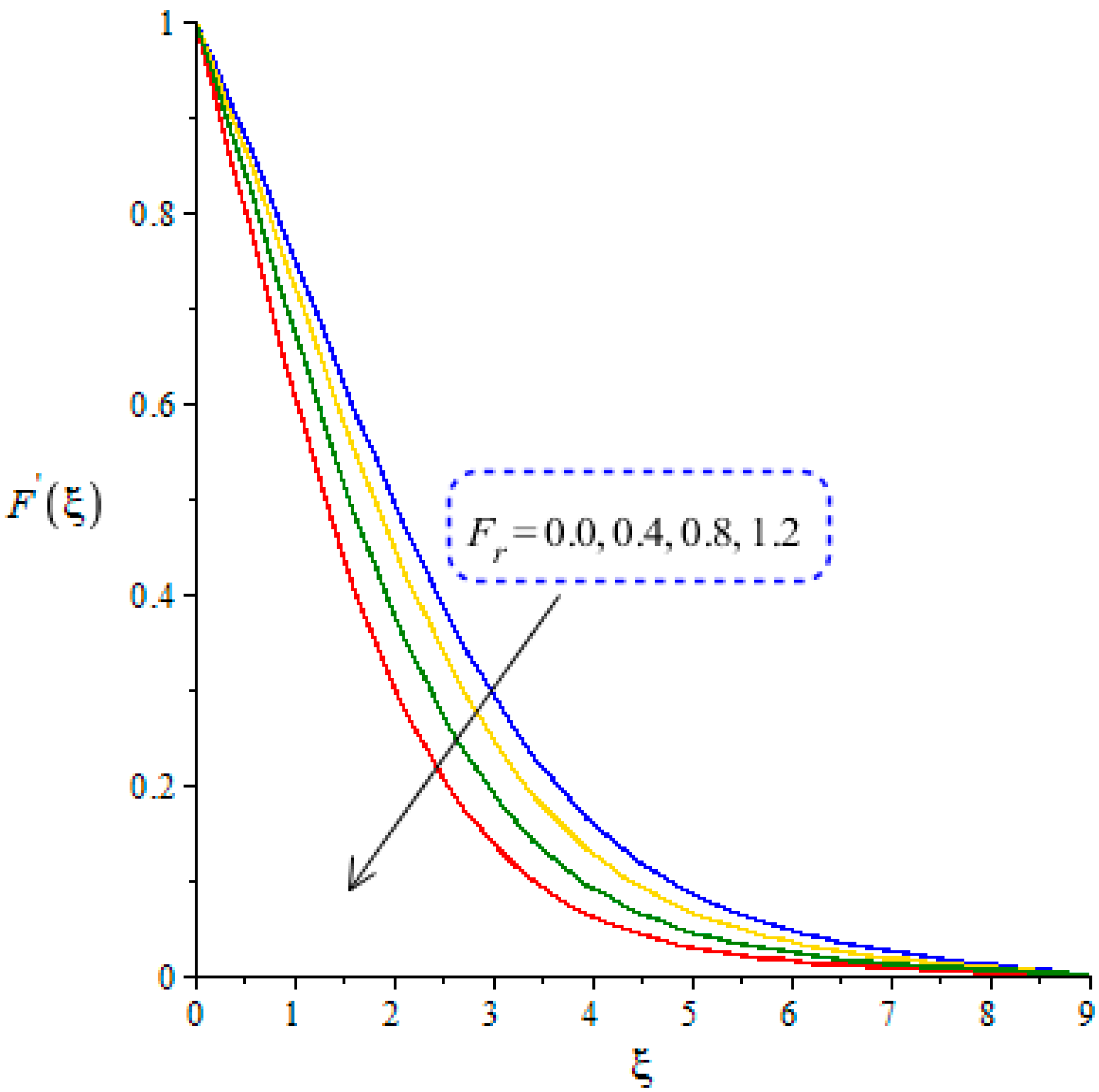
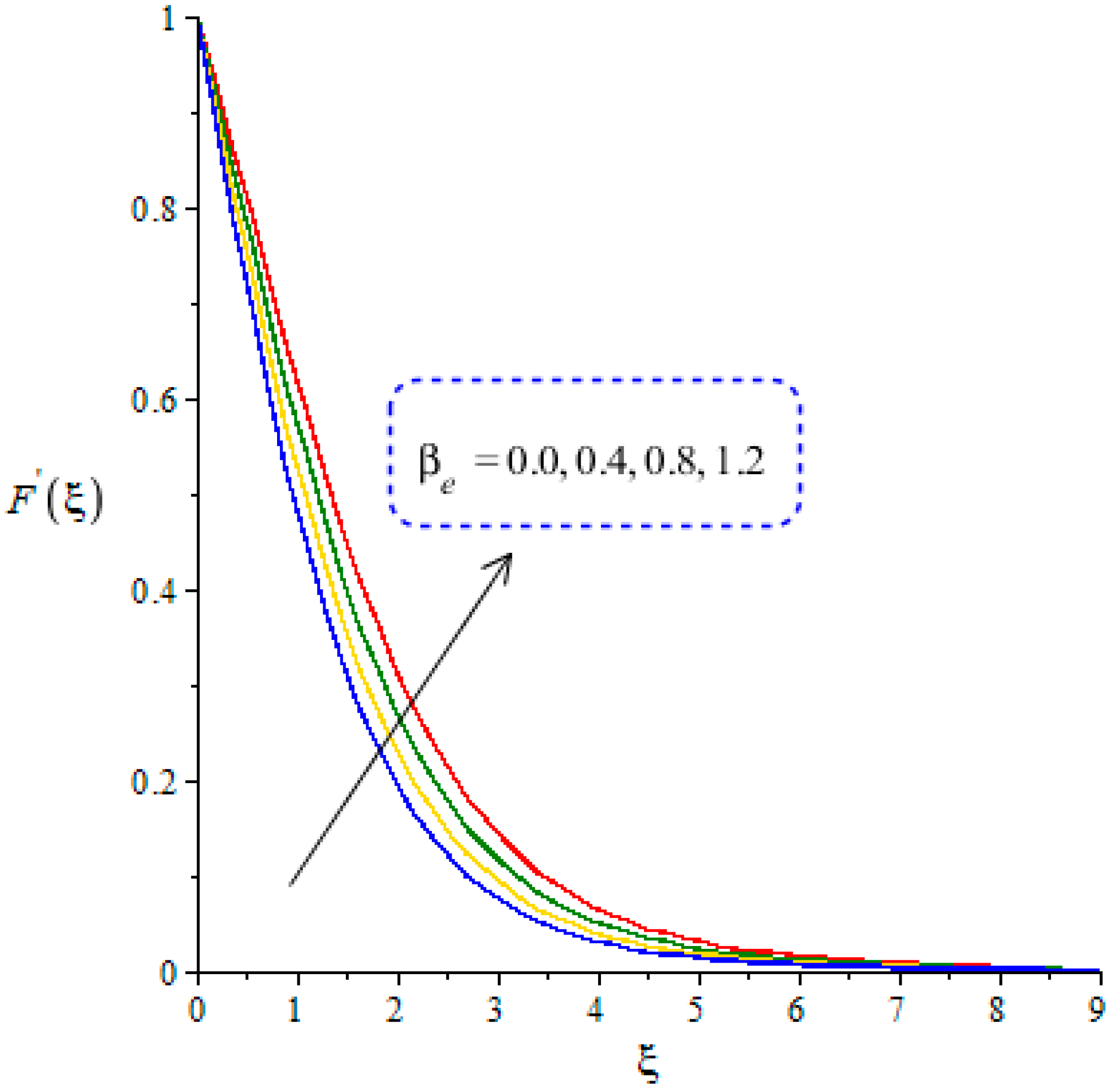
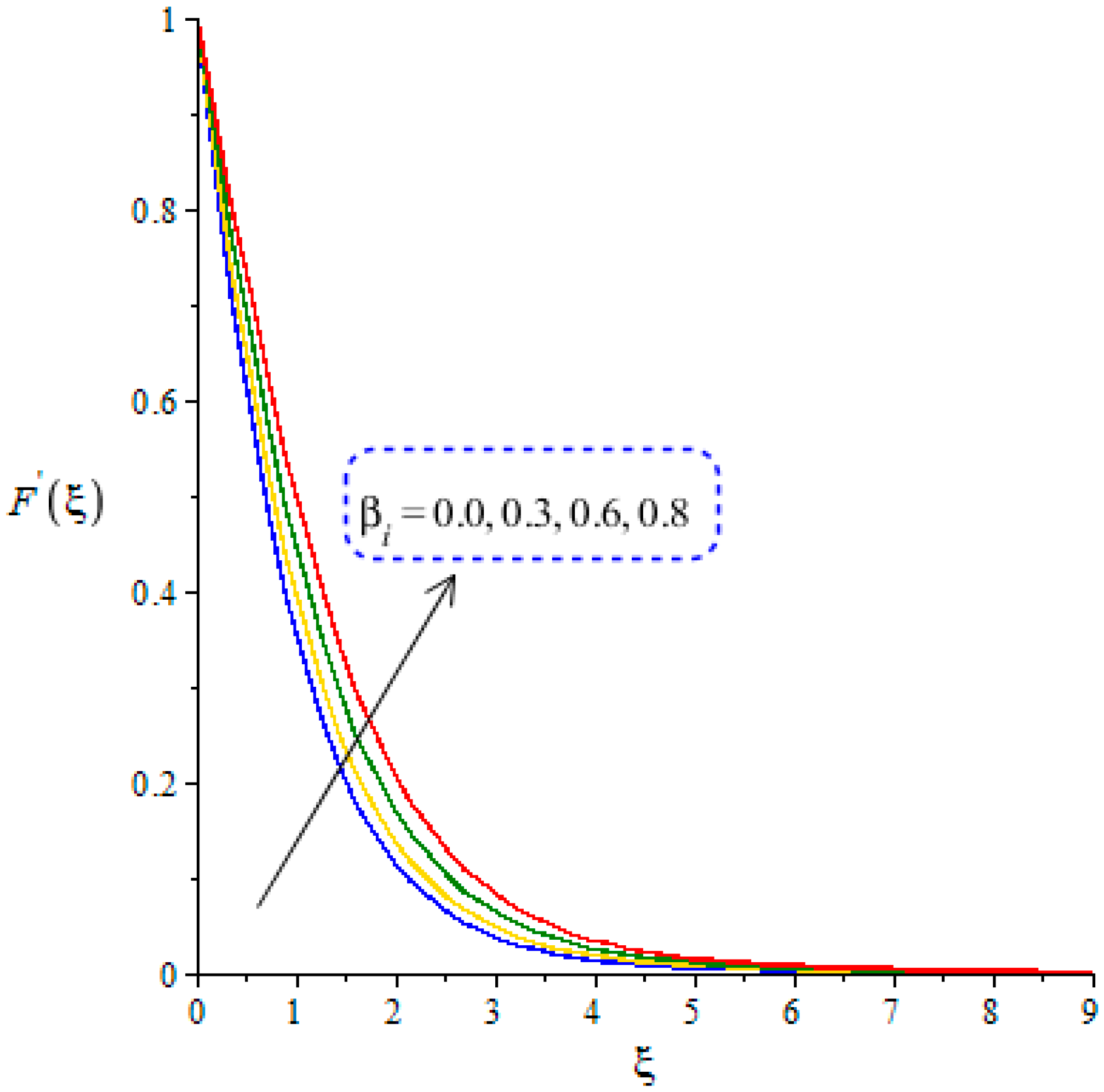
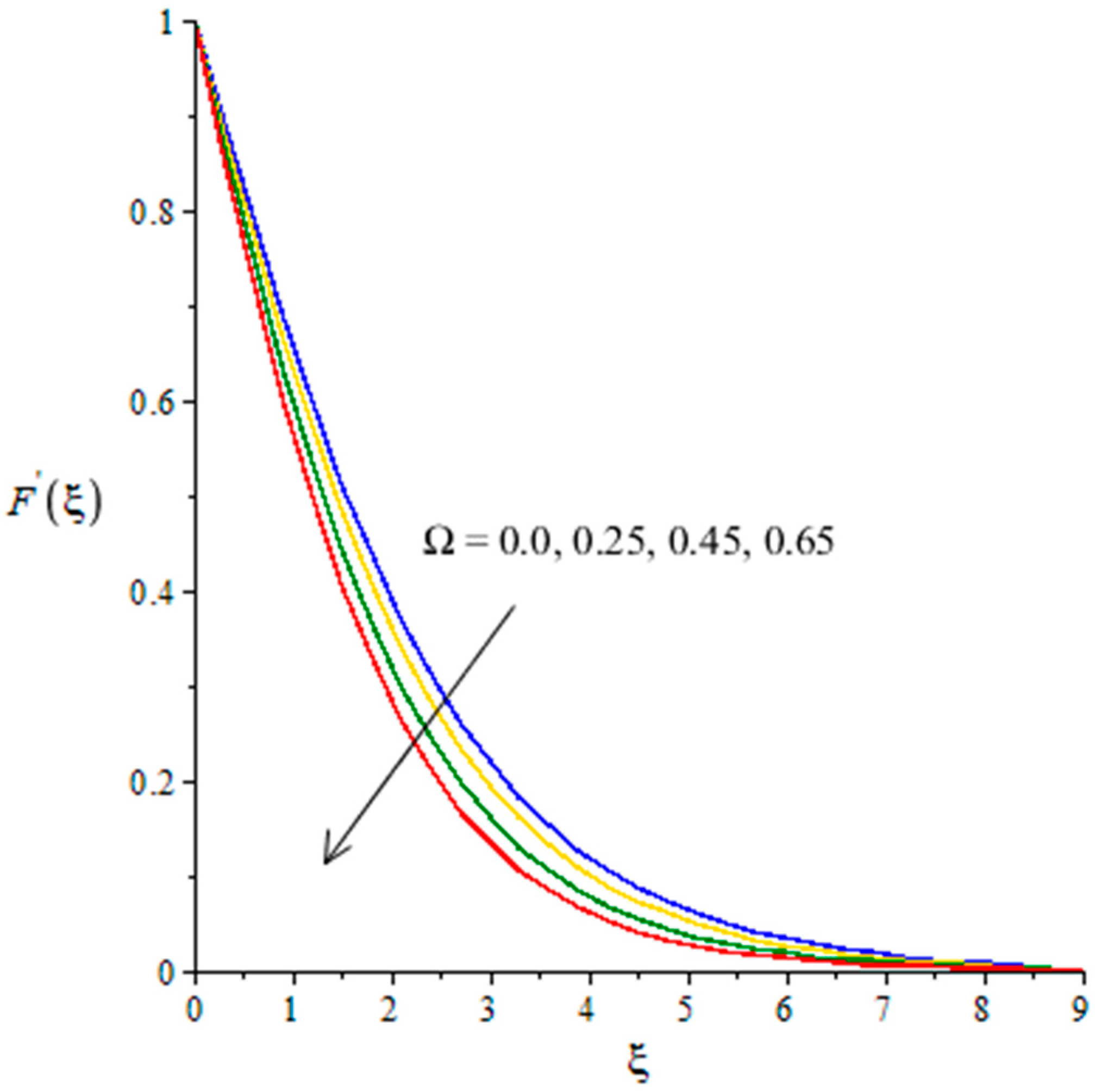
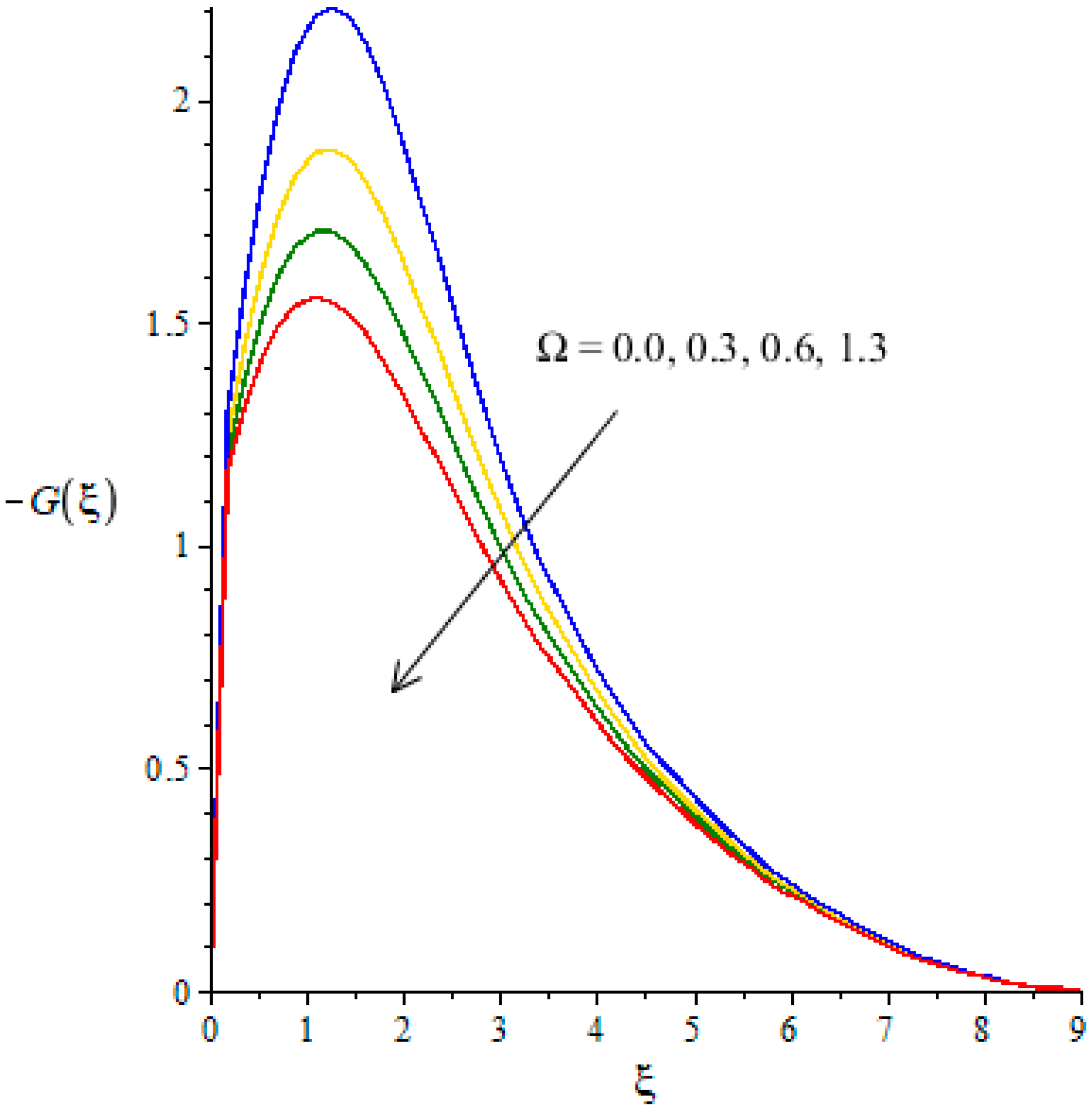
4.1. Outcomes of Velocity Profiles versus Parameters
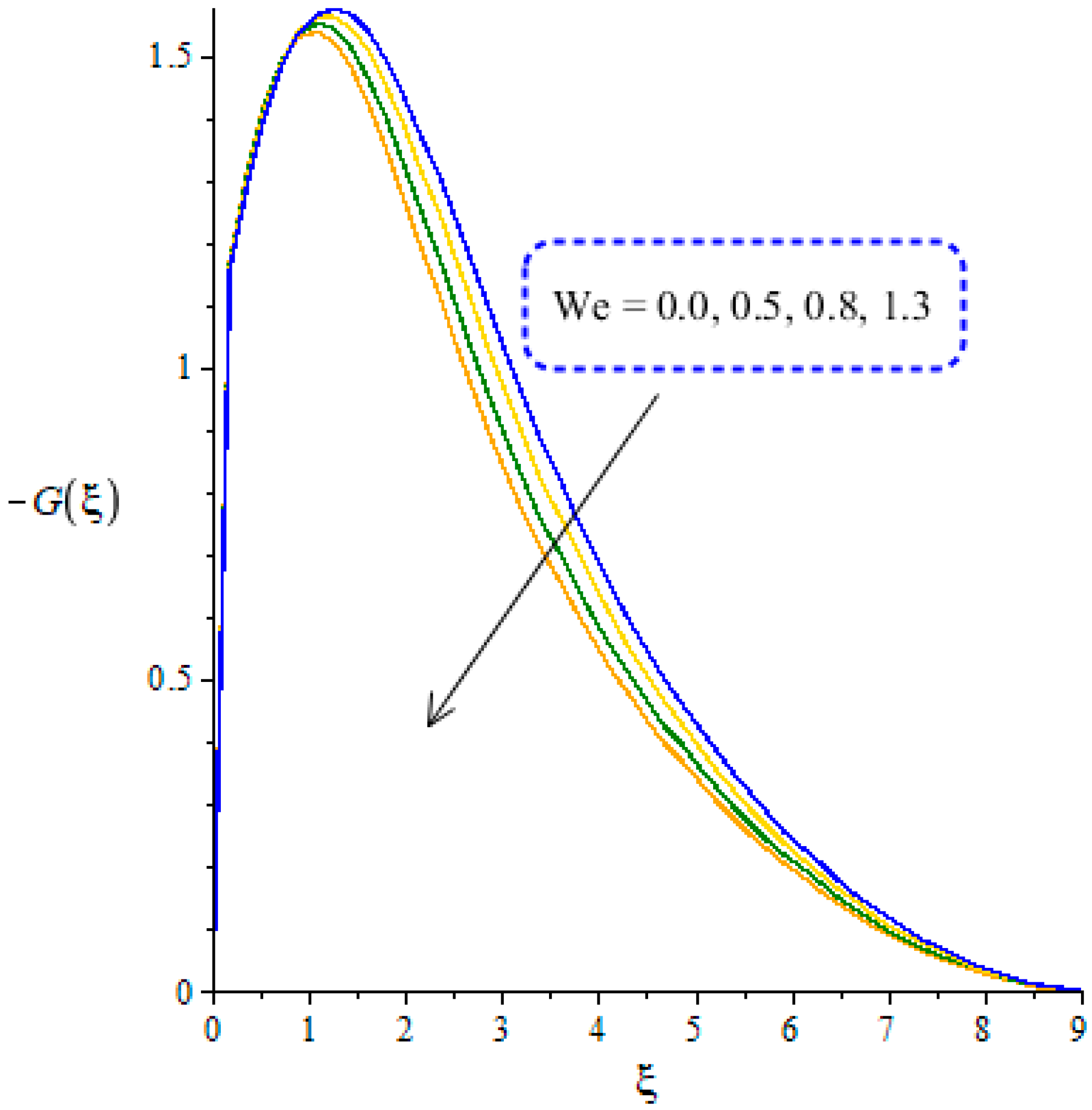
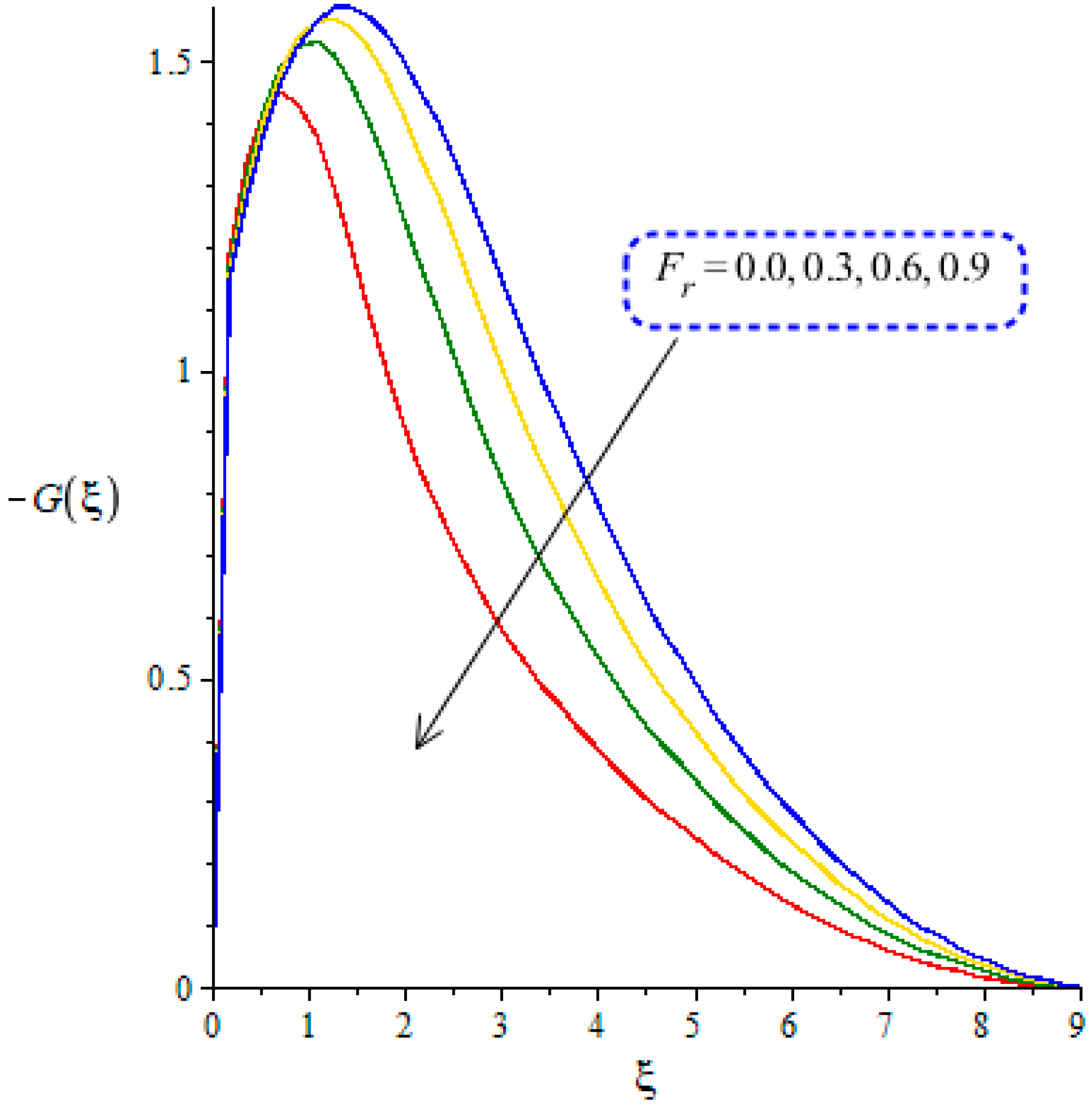
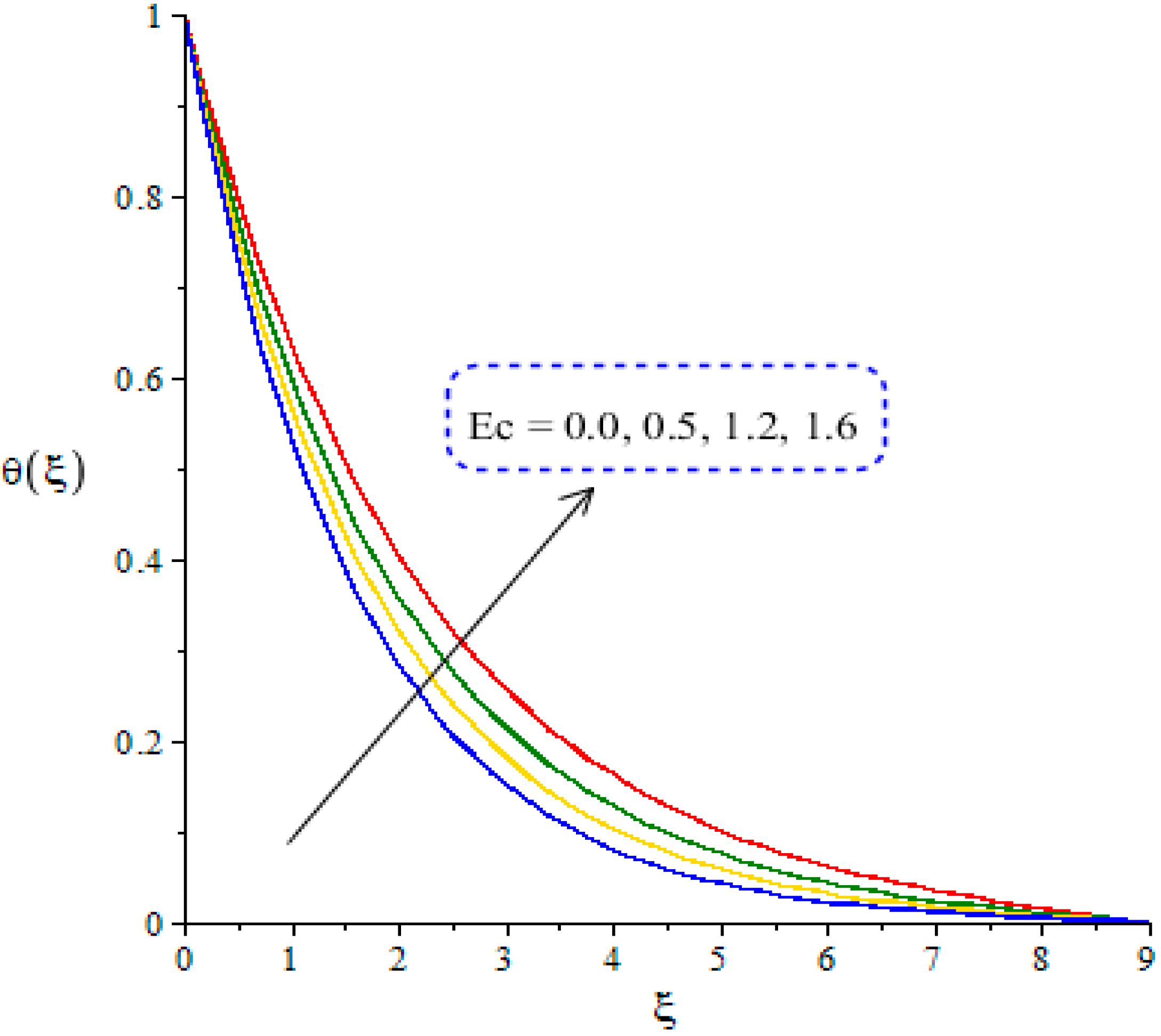
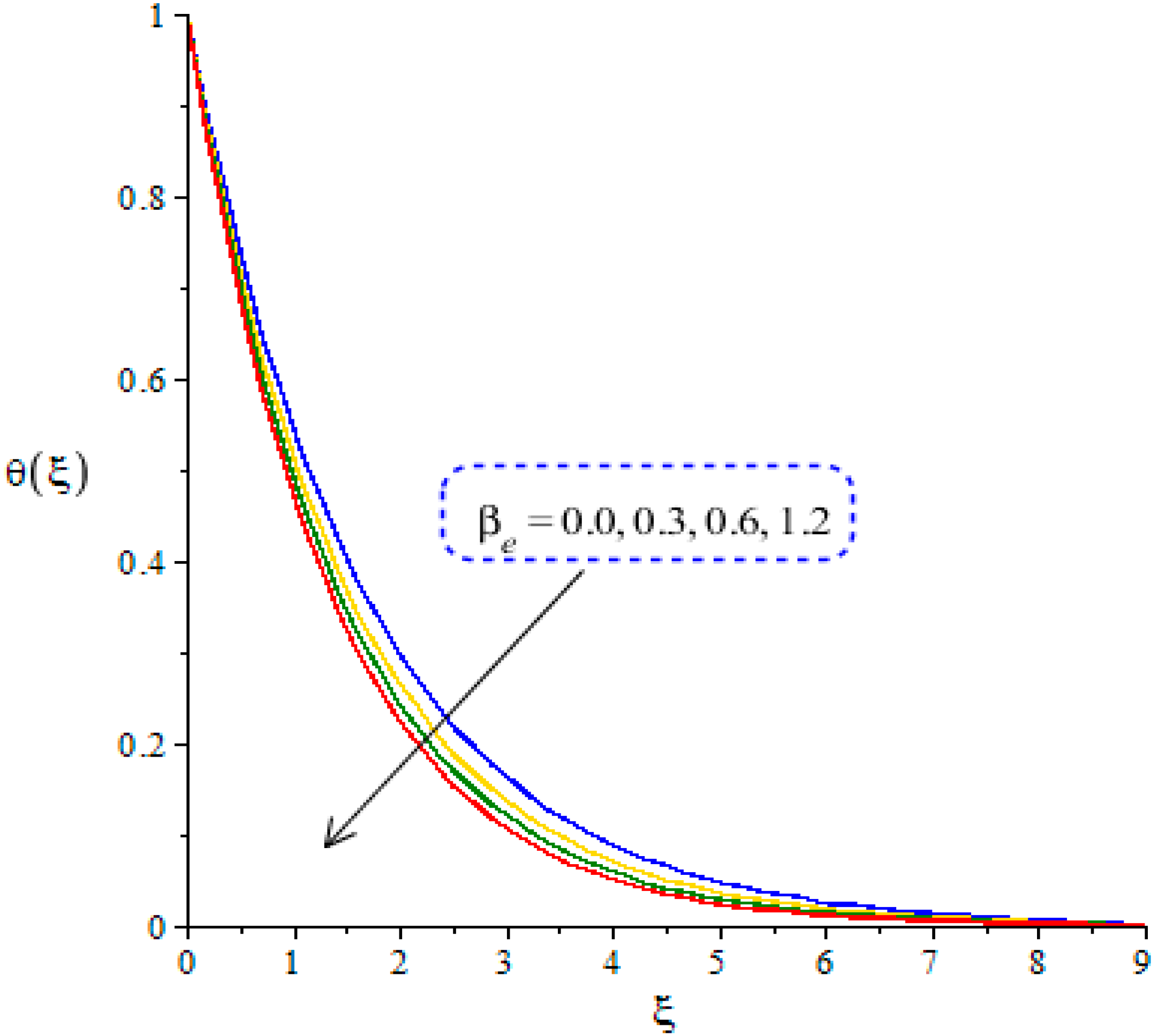
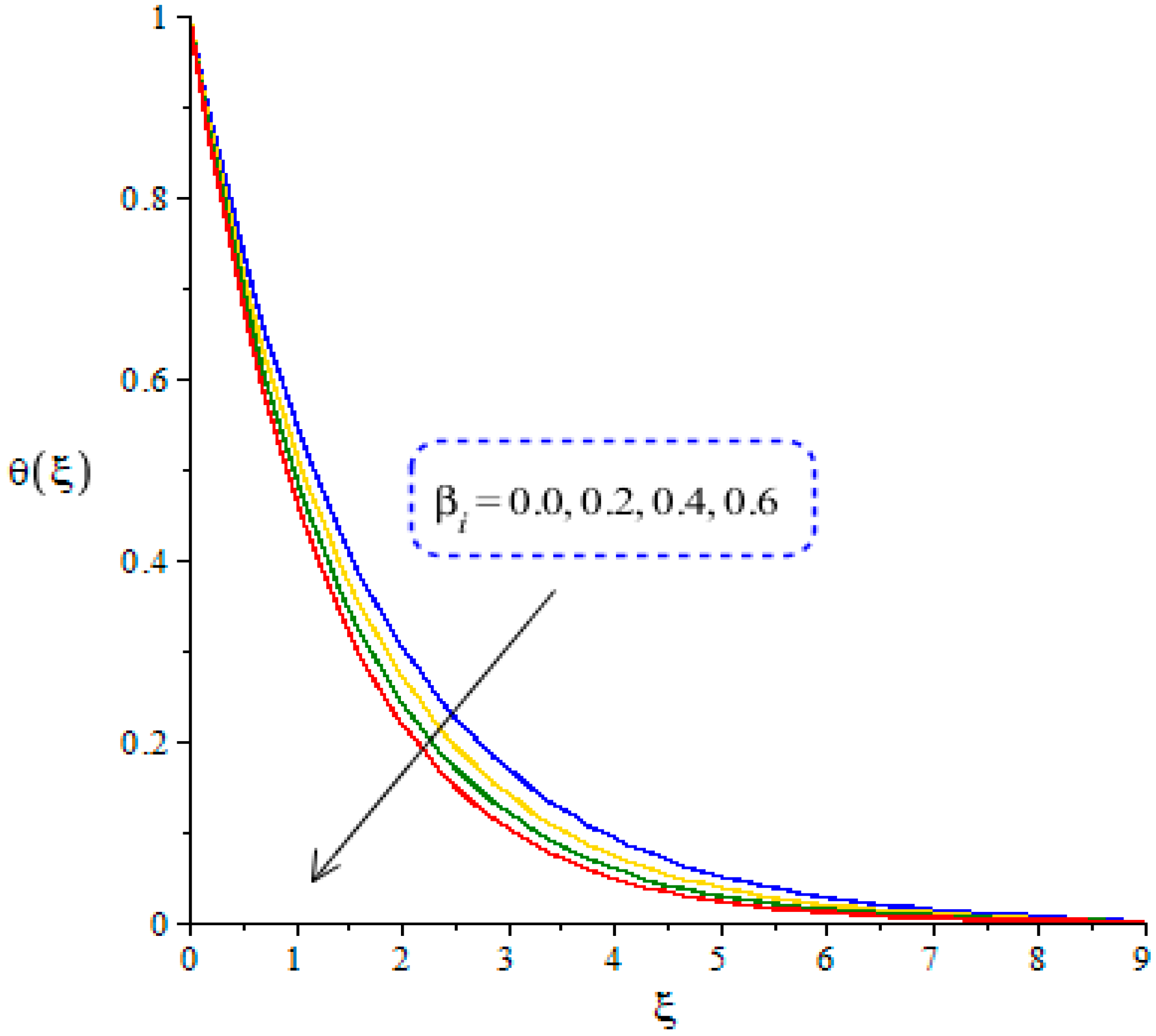
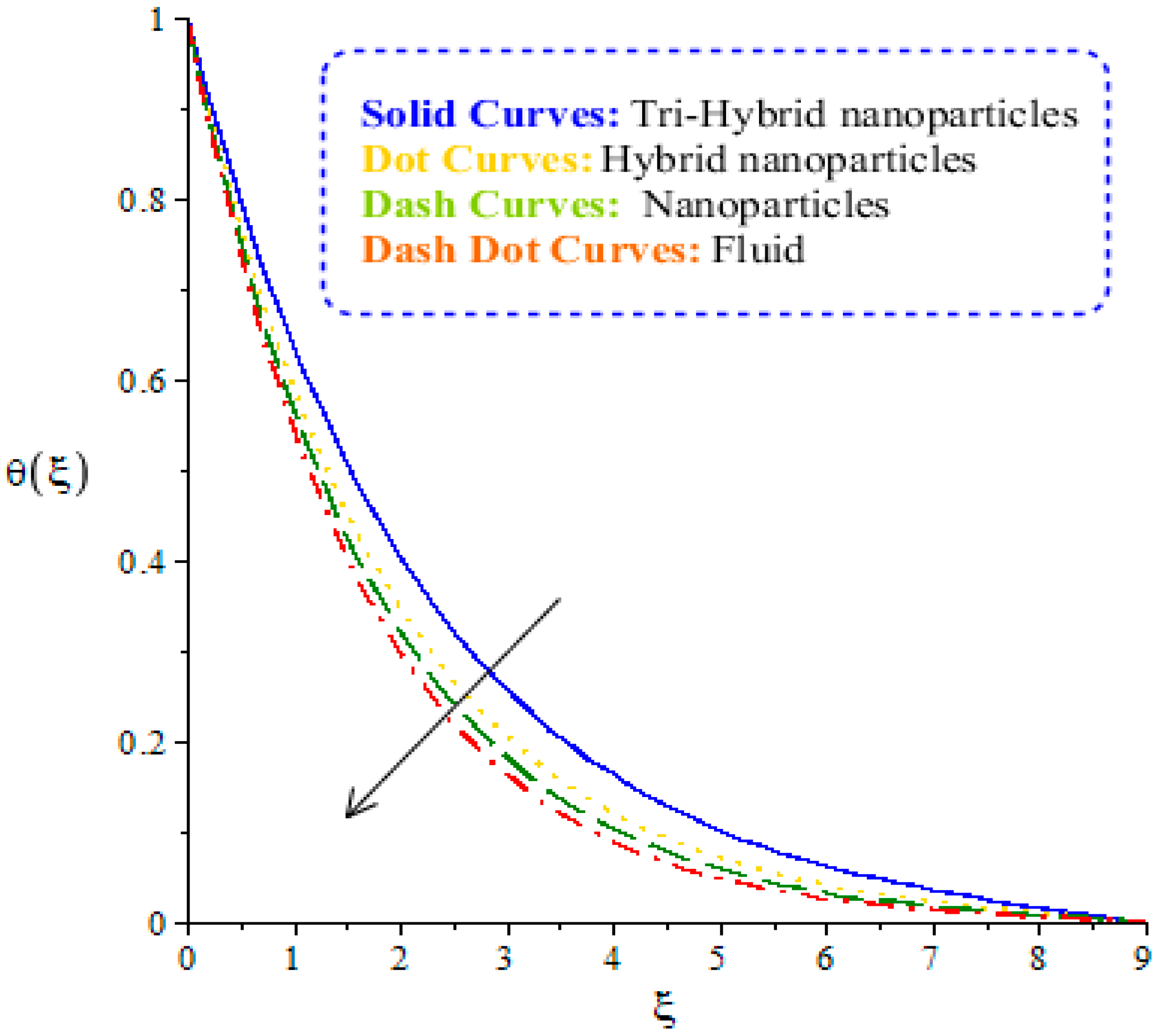
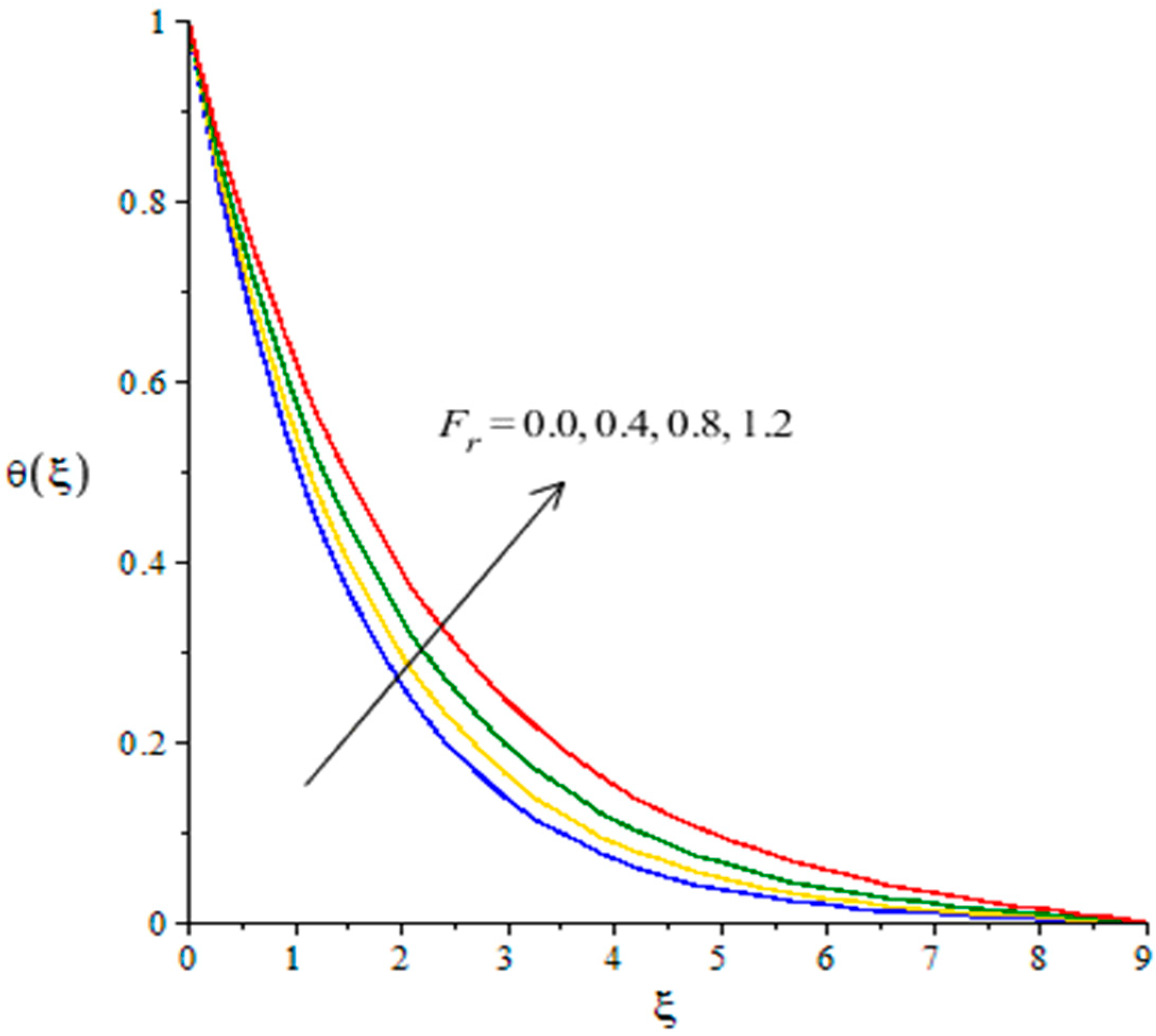
4.2. Outcomes of Temperature Profile versus Parameters
4.3. Variation of Temperature Gradient and Surface Forces versus Parameters
5. Remarks and Key Judgments
- ❖
- Ternary hybrid nanoparticles play a vital role in enhancing the performance of heat energy. Moreover, heat energy is produced by hybrid nanoparticles, nanoparticles and nanofluid;
- ❖
- Argumentation in the motion of the fluid is predicted using the higher values of ion-slip and Hall numbers, while the opposite treatment is found in the motion of fluid particles via variation in the Weissenberg and Forchheimer numbers;
- ❖
- The maximum production of thermal energy occurs when the Eckert number is increased, and declination in heat energy occurs via higher values of ion-slip and Hall numbers;
- ❖
- The maximum production of a temperature gradient can be achieved for the case of ternary hybrid nanoparticles, rather than the production of a temperature gradient for the cases of nanoparticles and hybrid nanoparticles;
- ❖
- Ternary hybrid nanoparticles boost the surface force, as compared to nanoparticles and hybrid nanoparticles;
- ❖
- Hall and ion-slip currents are significantly useful to enhance the temperature gradient, but the surface force is boosted when Hall and ion-slip numbers are enhanced.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khan, M.; Rasheed, A.; Salahuddin, T.; Ali, S. Chemically reactive flow of hyperbolic tangent fluid flow having thermal radiation and double stratification embedded in porous medium. Ain Shams Eng. J. 2021, 12, 3209–3216. [Google Scholar] [CrossRef]
- Rehman, K.U.; Alshomrani, A.S.; Malik, M.Y.; Zehra, I.; Naseer, M. Thermo-physical aspects in tangent hyperbolic fluid flow regime: A short communication. Case Stud. Therm. Eng. 2018, 12, 203–212. [Google Scholar] [CrossRef]
- Khan, M.; Rasheed, A.; Salahuddin, T. Radiation and chemical reactive impact on tangent hyperbolic fluid flow having double stratification. AIP Adv. 2020, 10, 075211. [Google Scholar] [CrossRef]
- Gharami, P.P.; Reza-E-Rabbi, S.; Arifuzzaman, S.M.; Khan, M.S.; Sarkar, T.; Ahmmed, S.F. MHD effect on unsteady flow of tangent hyperbolic nano-fluid past a moving cylinder with chemical reaction. SN Appl. Sci. 2020, 2, 1256. [Google Scholar] [CrossRef]
- Hayat, T.; Shafique, M.; Tanveer, A.; Alsaedi, A. Magnetohydrodynamic effects on peristaltic flow of hyperbolic tangent nanofluid with slip conditions and Joule heating in an inclined channel. Int. J. Heat Mass Transf. 2016, 102, 54–63. [Google Scholar] [CrossRef]
- Nawaz, M.; Madkhali, H.A.; Haneef, M.; Alharbi, S.O.; Alaoui, M.K. Numerical study on thermal enhancement in hyperbolic tangent fluid with dust and hybrid nanoparticles. Int. Commun. Heat Mass Transf. 2021, 127, 105535. [Google Scholar] [CrossRef]
- Wang, X.Q.; Mujumdar, A.S. A review on nanofluids-part I: Theoretical and numerical investigations. Braz. J. Chem. Eng. 2008, 25, 613–630. [Google Scholar] [CrossRef] [Green Version]
- Tlau, L. Fundamental flow problems considering non-Newtonian hyperbolic tangent fluid with Navier slip: Homotopy analysis method. Appl. Comput. Mech. 2020, 14. [Google Scholar] [CrossRef]
- Kebede, T.; Haile, E.; Awgichew, G.; Walelign, T. Heat and mass transfer analysis in unsteady flow of tangent hyperbolic nanofluid over a moving wedge with buoyancy and dissipation effects. Heliyon 2020, 6, e03776. [Google Scholar] [CrossRef]
- Saidulu, N.; Gangaiah, T.; Lakshmi, A.V. MHD flow of tangent hyperbolic nanofluid over an inclined sheet with effects of thermal radiation and heat source/sink. Appl. Appl. Math. Int. J. 2019, 14, 5. [Google Scholar]
- Mahdy, A.; Hoshoudy, G.A. Two-phase mixed convection nanofluid flow of a dusty tangent hyperbolic past a nonlinearly stretching sheet. J. Egypt. Math. Soc. 2019, 27, 44. [Google Scholar] [CrossRef] [Green Version]
- Shafiq, A.; Hammouch, Z.; Sindhu, T.N. Bioconvective MHD flow of tangent hyperbolic nanofluid with newtonian heating. Int. J. Mech. Sci. 2017, 133, 759–766. [Google Scholar] [CrossRef]
- Hayat, T.; Qayyum, S.; Alsaedi, A.; Shehzad, S.A. Nonlinear thermal radiation aspects in stagnation point flow of tangent hyperbolic nanofluid with double diffusive convection. J. Mol. Liq. 2016, 223, 969–978. [Google Scholar] [CrossRef]
- Shafiq, A.; Lone, S.A.; Sindhu, T.N.; Al-Mdallal, Q.M.; Rasool, G. Statistical modeling for bioconvective tangent hyperbolic nanofluid towards stretching surface with zero mass flux condition. Sci. Rep. 2021, 11, 13869. [Google Scholar] [CrossRef]
- Swain, K.; Mebarek-Oudina, F.; Abo-Dahab, S.M. Influence of MWCNT/ hybrid nanoparticles on an exponentially porous shrinking sheet with chemical reaction and slip boundary conditions. J. Therm. Anal. Calorim. 2021, 143, 915–927. [Google Scholar]
- Shafiq, A.; Mebarek-Oudina, F.; Sindhu, T.N.; Abidi, A. A study of dual stratification on stagnation point Walters’ B nanofluid flow via radiative Riga plate: A statistical approach. Eur. Phys. J. Plus 2021, 136, 407. [Google Scholar] [CrossRef]
- Mebarek-Oudina, F.; Fares, R.; Aissa, A.; Lewis, R.W.; Abu-Hamdeh, N.H. Entropy and convection effect on magnetized hybrid nano-liquid flow inside a trapezoidal cavity with zigzagged wall. Int. Commun. Heat Mass Transf. 2021, 125, 105279. [Google Scholar] [CrossRef]
- Marzougui, S.; Mebarek-Oudina, F.; Magherbi, M.; Mchirgui, A. Entropy generation and heat transport of Cu–water nanoliquid in porous lid-driven cavity through magnetic field. Int. J. Numer. Methods Heat Fluid Flow 2021. [Google Scholar] [CrossRef]
- Pushpa, B.V.; Sankar, M.; Mebarek-Oudina, F. Buoyant Convective Flow and Heat Dissipation of Cu– Nanoliquids in an Annulus Through a Thin Baffle. J. Nanofluids 2021, 10, 292–304. [Google Scholar] [CrossRef]
- Upreti, H.; Pandey, A.K.; Kumar, M.; Makinde, O.D. Ohmic heating and non-uniform heat source/sink roles on 3D Darcy–Forchheimer flow of CNTs nanofluids over a stretching surface. Arab. J. Sci. Eng. 2020, 45, 7705–7717. [Google Scholar] [CrossRef]
- Upreti, H.; Pandey, A.K.; Kumar, M. Thermophoresis and suction/injection roles on free convective MHD flow of Ag–kerosene oil nanofluid. J. Comput. Des. Eng. 2020, 7, 386–396. [Google Scholar] [CrossRef]
- Upreti, H.; Pandey, A.K.; Kumar, M. Assessment of entropy generation and heat transfer in three-dimensional hybrid nanofluids flow due to convective surface and base fluids. J. Porous Media 2021, 24, 35–50. [Google Scholar] [CrossRef]
- Abdelsalam, S.I.; Sohail, M. Numerical approach of variable thermophysical features of dissipated viscous nanofluid comprising gyrotactic micro-organisms. Pramana: J. Phys. 2020, 94, 67. [Google Scholar] [CrossRef]
- Sohail, M.; Shah, Z.; Tassaddiq, A.; Kumam, P.; Roy, P. Entropy generation in MHD Casson fluid flow with variable heat conductance and thermal conductivity over non-linear bi-directional stretching surface. Sci. Rep. 2020, 10, 12530. [Google Scholar] [CrossRef]
- Thumma, T.; Wakif, A.; Animasaun, I.L. Generalized differential quadrature analysis of unsteady three-dimensional MHD radiating dissipative Casson fluid conveying tiny particles. Heat Transf. 2020, 49, 2595–2626. [Google Scholar] [CrossRef]
- Chu, Y.M.; Nazir, U.; Sohail, M.; Selim, M.M.; Lee, J.R. Enhancement in Thermal Energy and Solute Particles Using Hybrid Nanoparticles by Engaging Activation Energy and Chemical Reaction over a Parabolic Surface via Finite Element Approach. Fractal Fract. 2021, 5, 119. [Google Scholar] [CrossRef]
- Nazir, U.; Sohail, M.; Ali, U.; Sherif, E.S.M.; Park, C.; Lee, J.R.; Selim, M.M.; Thounthong, P. Applications of Cattaneo–Christov fluxes on modelling the boundary value problem of Prandtl fluid comprising variable properties. Sci. Rep. 2021, 11, 17837. [Google Scholar] [CrossRef] [PubMed]
- Wakif, A.; Boulahia, Z.; Ali, F.; Eid, M.R.; Sehaqui, R. Numerical analysis of the unsteady natural convection MHD Couette nanofluid flow in the presence of thermal radiation using single and two-phase nanofluid models for Cu–water nanofluids. Int. J. Appl. Comput. Math. 2018, 4, 81. [Google Scholar] [CrossRef]
- Nazir, U.; Sohail, M.; Alrabaiah, H.; Selim, M.M.; Thounthong, P.; Park, C. Inclusion of hybrid nanoparticles in hyperbolic tangent material to explore thermal transportation via finite element approach engaging Cattaneo-Christov heat flux. PLoS ONE 2021, 16, e0256302. [Google Scholar] [CrossRef] [PubMed]
- Hayat, T.; Aziz, A.; Muhammad, T.; Alsaedi, A. Darcy-Forchheimer flow of nanofluid in a rotating frame. Int. J. Numer. Methods Heat Fluid Flow 2018. [Google Scholar] [CrossRef]
- Hayat, T.; Aziz, A.; Muhammad, T.; Alsaedi, A. Three-dimensional flow of Prandtl fluid with Cattaneo-Christov double diffusion. Results Phys. 2018, 9, 290–296. [Google Scholar] [CrossRef]
- Manjunatha, S.; Puneeth, V.; Gireesha, B.J.; Chamkha, A. Theoretical Study of Convective Heat Transfer in Ternary Nanofluid Flowing past a Stretching Sheet. J. Appl. Comput. Mech. 2021. [Google Scholar] [CrossRef]
- Hussain, A.; Elkotb, M.A.; Arshad, M.; Rehman, A.; Sooppy Nisar, K.; Hassan, A.; Saleel, C.A. Computational investigation of the combined impact of nonlinear radiation and magnetic field on three-dimensional rotational nanofluid flow across a stretchy surface. Processes 2021, 9, 1453. [Google Scholar] [CrossRef]



| 0.253 | 1113.5 | ||
| 32.9 | 6310 | ||
| 8.953 | 4250 | ||
| 1.4013 | 2270 |
| Elements | |||
|---|---|---|---|
| 30 | 1.111381874 | 0.1033029114 | 0.5394657370 |
| 60 | 1.099801938 | 0.09383147162 | 0.5228689118 |
| 90 | 1.095986356 | 0.09090534841 | 0.5173330148 |
| 120 | 1.094092658 | 0.08948371769 | 0.5145656516 |
| 150 | 0.092961517 | 0.5129036217 | 0.08864385101 |
| 180 | 0.092212214 | 0.08808914037 | 0.5117970027 |
| 210 | 0.091677016 | 0.5110058672 | 0.08769570089 |
| 240 | 0.091275719 | 0.5104110691 | 0.08740183266 |
| 270 | 0.090964277 | 0.08717415891 | 0.5099497350 |
| 300 | 0.090715774 | 0.08799298080 | 0.5099823696 |
| Hussain et al. [33] | Present Results | |||
|---|---|---|---|---|
| 0.0 | 1.00426 | 0.0 | 1.000431019 | 0.0 |
| 0.5 | 1.17189 | 0.5488 | 1.171210113 | 1.172901620 |
| 1.0 | 1.3582 | 0.8589 | 1.358181503 | 1.357812653 |
| 2.0 | 1.68033 | 1.3027 | 1.681031011 | 1.681061039 |
| 0.1 | 0.295179854 | 0.1142831221 | 0.30548038 | |
| 0.3 | 0.194084007 | 0.2967735778 | 0.60158358 | |
| 0.6 | 0.026758931 | 0.3730140256 | 0.89567749 | |
| 0.1 | 0.445563794 | 0.2710562039 | 0.54590968 | |
| 0.4 | 0.436878968 | 0.2363434625 | 0.56018140 | |
| 0.8 | 0.414948438 | 0.2214122528 | 0.59544356 | |
| 0.0 | 0.524948431 | 0.2714123242 | 0.49545303 | |
| 0.3 | 0.534948431 | 0.2814123838 | 0.43545891 | |
| 0.6 | 0.554948434 | 0.2914124206 | 0.41546269 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nazir, U.; Sohail, M.; Hafeez, M.B.; Krawczuk, M. Significant Production of Thermal Energy in Partially Ionized Hyperbolic Tangent Material Based on Ternary Hybrid Nanomaterials. Energies 2021, 14, 6911. https://doi.org/10.3390/en14216911
Nazir U, Sohail M, Hafeez MB, Krawczuk M. Significant Production of Thermal Energy in Partially Ionized Hyperbolic Tangent Material Based on Ternary Hybrid Nanomaterials. Energies. 2021; 14(21):6911. https://doi.org/10.3390/en14216911
Chicago/Turabian StyleNazir, Umar, Muhammad Sohail, Muhammad Bilal Hafeez, and Marek Krawczuk. 2021. "Significant Production of Thermal Energy in Partially Ionized Hyperbolic Tangent Material Based on Ternary Hybrid Nanomaterials" Energies 14, no. 21: 6911. https://doi.org/10.3390/en14216911
APA StyleNazir, U., Sohail, M., Hafeez, M. B., & Krawczuk, M. (2021). Significant Production of Thermal Energy in Partially Ionized Hyperbolic Tangent Material Based on Ternary Hybrid Nanomaterials. Energies, 14(21), 6911. https://doi.org/10.3390/en14216911








