Small-Scale Solar Photovoltaic Power Prediction for Residential Load in Saudi Arabia Using Machine Learning
Abstract
:1. Introduction
2. Literature Review
3. Experimental Settings
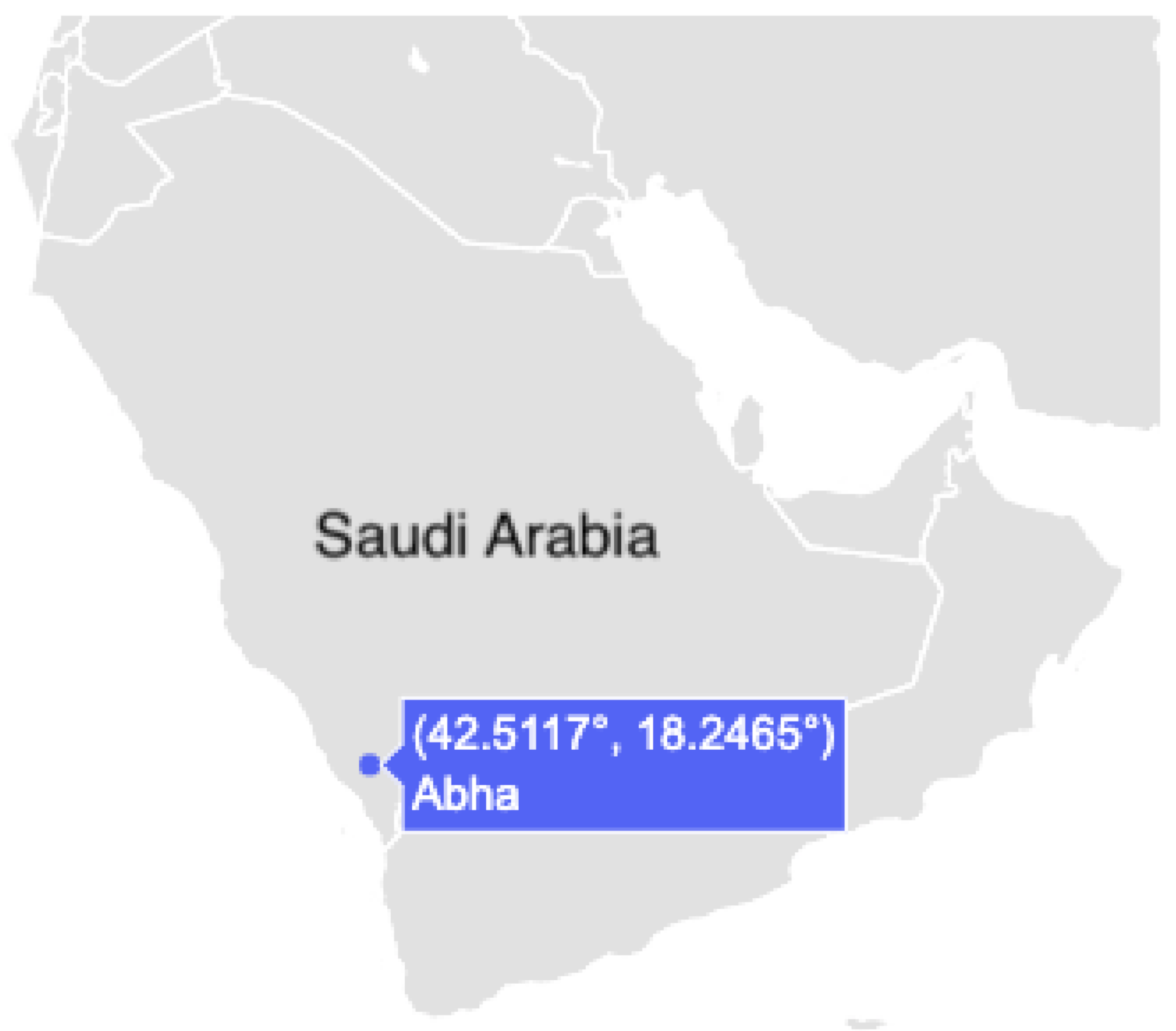
3.1. Site and Instruments
3.2. Weather Station
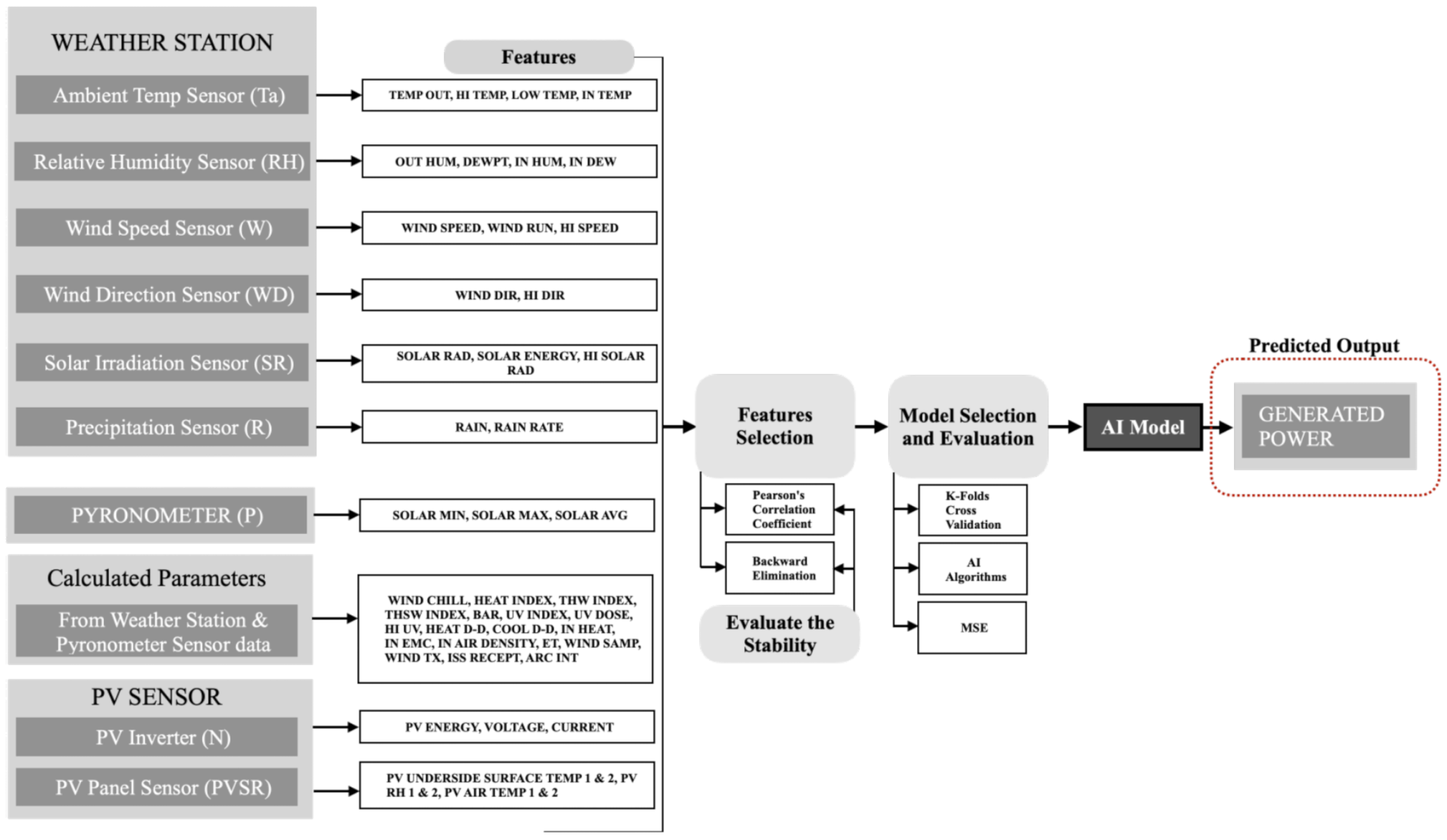
4. Methodology
4.1. Data Collection and Presentation
4.2. Data Preparation
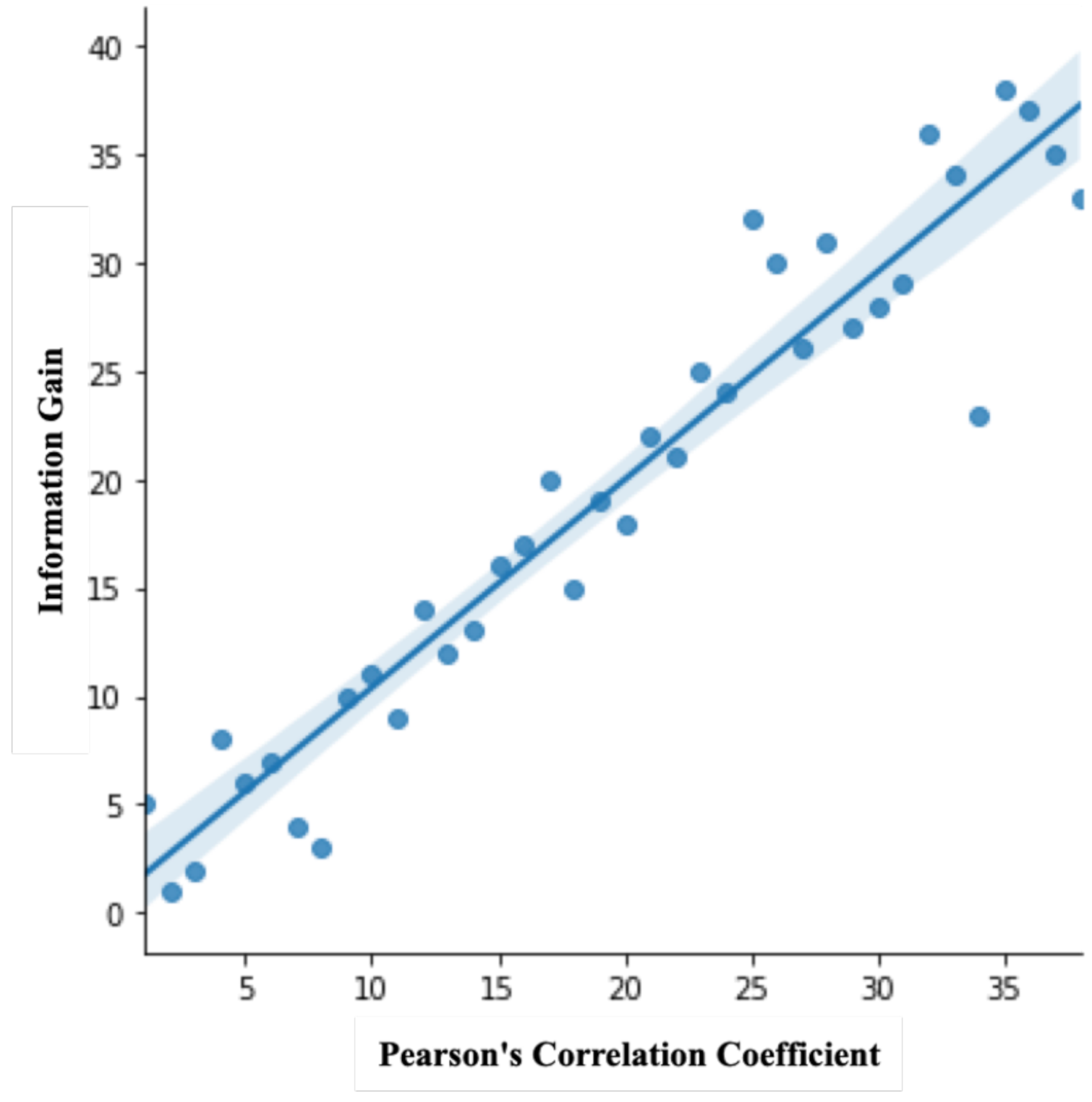
4.3. Feature Selection
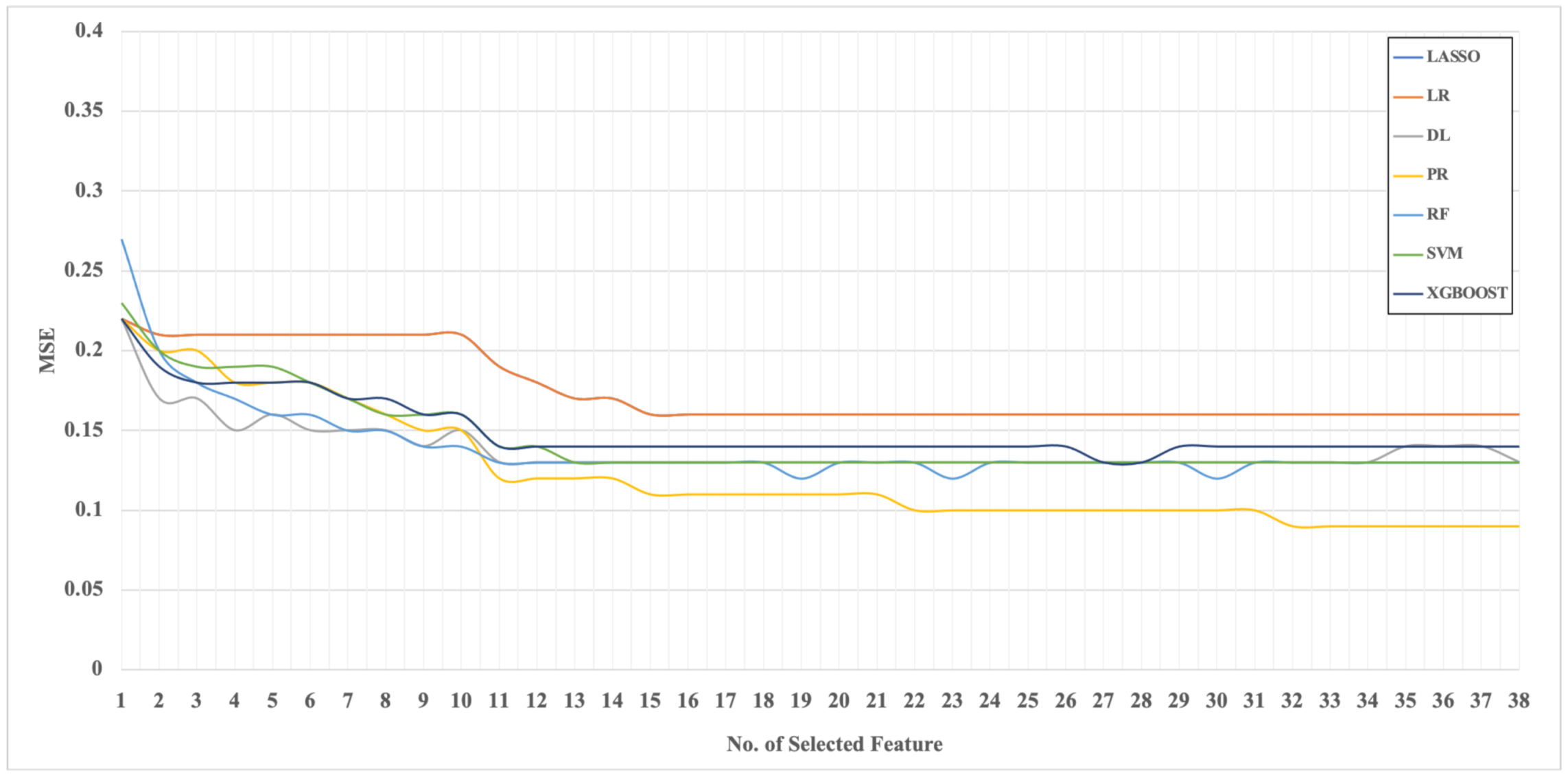
4.4. Model Selection and Evaluation
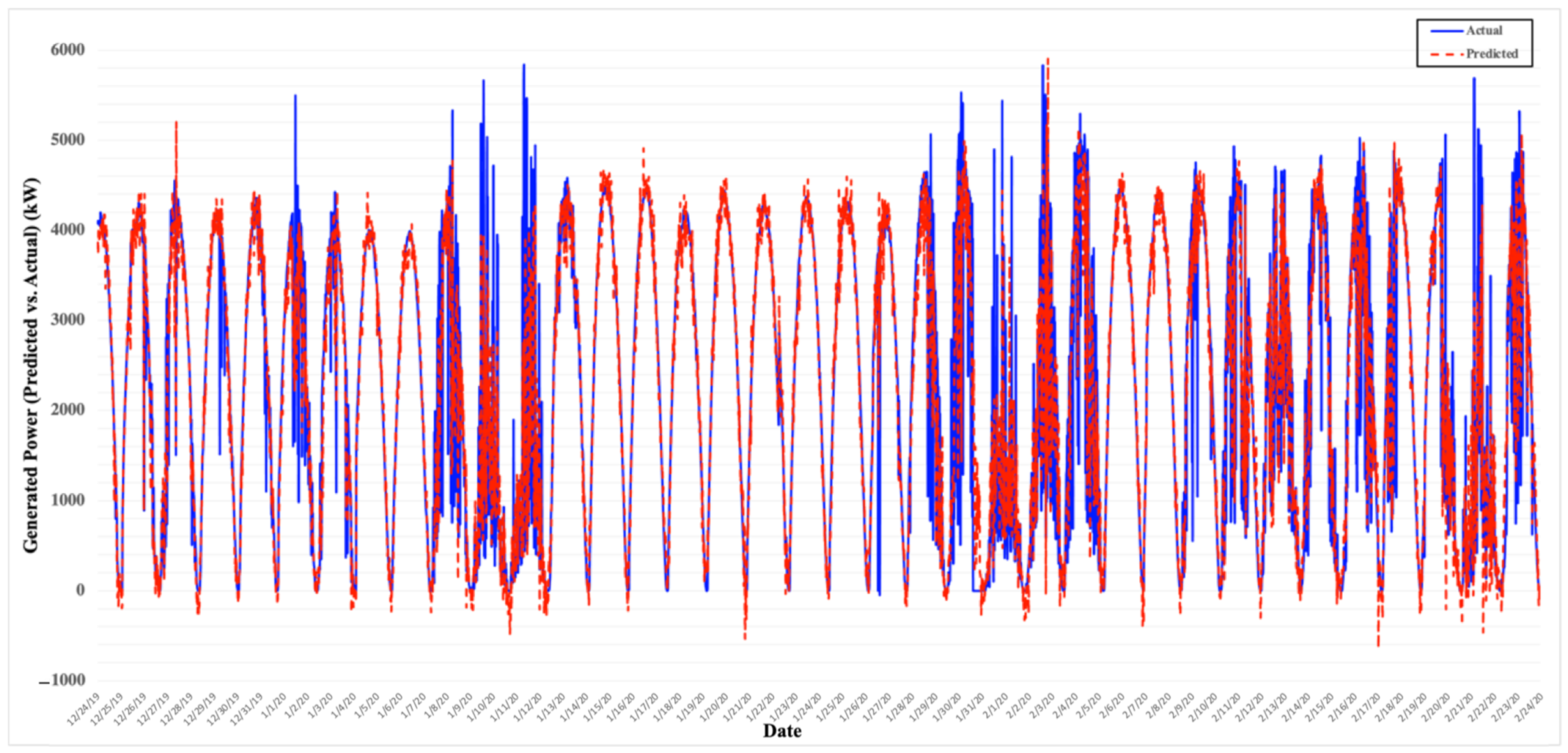
5. Results and Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Newell, R.; Raimi, D.; Aldana, G. Global Energy Outlook 2019: The Next Generation of Energy. Available online: https://www.rff.org/publications/reports/global-energy-outlook-2019/ (accessed on 11 October 2020).
- Capuano, L. International Energy Outlook 2018 (IEO2018); US Energy Information Administration (EIA): Washington, DC, USA, 2018; Volume 2018, p. 21.
- Khan, M.M.A.; Asif, M.; Stach, E. Rooftop PV potential in the residential sector of the Kingdom of Saudi Arabia. Buildings 2017, 7, 46. [Google Scholar] [CrossRef]
- EIA. FREQUENTLY ASKED QUESTIONS (FAQ). 2020. Available online: https://www.eia.gov/tools/faqs/faq.php?id=86&t=1 (accessed on 24 December 2020).
- U.S. Energy Information Administration. Total Energy Monthly Data. 2020. Available online: https://www.eia.gov/totalenergy/data/monthly/pdf/mer.pdf (accessed on 24 December 2020).
- Almaraashi, M. Short-term prediction of solar energy in Saudi Arabia using automated-design fuzzy logic systems. PLoS ONE 2017, 12, e0182429. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mazria, E.; Kershner, K. Meeting the 2030 challenge through building codes. Architecture 2008, 2030. Available online: https://sallan.org/pdf-docs/2030Challenge_Codes_WP-1.pdf (accessed on 24 December 2020).
- REN21, Global Status Report. Renewable Energy Policy Network for the 21st Century. 2020. Available online: https://www.ren21.net/wp-content/uploads/2019/05/gsr_2020_full_report_en.pdf (accessed on 24 December 2020).
- SEIA. U.S. Solar Market Insight. 2020. Available online: https://www.seia.org/us-solar-market-insight#:~:text=The%20U.S.%20installed%203.8%20gigawatts,power%2016.4%20million%20American%20homes (accessed on 24 December 2020).
- Cococcioni, M.; D’Andrea, E.; Lazzerini, B. One day-ahead forecasting of energy production in solar photovoltaic installations: An empirical study. Intell. Decis. Technol. 2012, 6, 197–210. [Google Scholar] [CrossRef]
- IRENA. Energy Profile Saudi Arabia. 2020. Available online: https://www.irena.org/IRENADocuments/Statistical_Profiles/Middle%20East/Saudi%20Arabia_Middle%20East_RE_SP.pdf (accessed on 24 December 2020).
- Amran, Y.A.; Amran, Y.M.; Alyousef, R.; Alabduljabbar, H. Renewable and sustainable energy production in Saudi Arabia according to Saudi Vision 2030; Current status and future prospects. J. Clean. Prod. 2020, 247, 119602. [Google Scholar] [CrossRef]
- Care, K. Building the Renewable Energy Sector in Saudi Arabia; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2012; Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Events/2012/Sep/5/5_Ibrahim_Babelli.pdf (accessed on 24 December 2020).
- Pazheri, F. Solar power potential in Saudi Arabia. Int. J. Eng. Res. Appl. 2014, 4, 171–174. [Google Scholar]
- Saber, E.M.; Lee, S.E.; Manthapuri, S.; Yi, W.; Deb, C. PV (photovoltaics) performance evaluation and simulation-based energy yield prediction for tropical buildings. Energy 2014, 71, 588–595. [Google Scholar] [CrossRef]
- Chowdhury, S.; Taylor, G.; Chowdhury, S.; Saha, A.; Song, Y. Modelling, simulation and performance analysis of a PV array in an embedded environment. In Proceedings of the IEEE 2007 42nd International Universities Power Engineering Conference, Brighton, UK, 4–6 September 2007; pp. 781–785. [Google Scholar]
- Chouder, A.; Silvestre, S.; Sadaoui, N.; Rahmani, L. Modeling and simulation of a grid connected PV system based on the evaluation of main PV module parameters. Simul. Model. Pract. Theory 2012, 20, 46–58. [Google Scholar] [CrossRef]
- Al-Dahidi, S.; Ayadi, O.; Adeeb, J.; Louzazni, M.; Hemidat, S.; Saidan, M.; Al-Zu’bi, S.; Nelles, M.; Hamdan, M.A.; Brawiesh, A.K.; et al. Assessment of Artificial Neural Networks Learning Algorithms and Training Datasets for Solar Photovoltaic Power Production Prediction. Front. Energy Res. 2019, 7, 130. [Google Scholar] [CrossRef] [Green Version]
- Pasion, C.; Wagner, T.; Koschnick, C.; Schuldt, S.; Williams, J.; Hallinan, K. Machine Learning Modeling of Horizontal Photovoltaics Using Weather and Location Data. Energies 2020, 13, 2570. [Google Scholar] [CrossRef]
- Brahimi, T. Using Artificial Intelligence to Predict Wind Speed for Energy Application in Saudi Arabia. Energies 2019, 12, 4669. [Google Scholar] [CrossRef] [Green Version]
- Alomari, M.H.; Adeeb, J.; Younis, O. Solar photovoltaic power forecasting in jordan using artificial neural networks. Int. J. Electr. Comput. Eng. (IJECE) 2018, 8, 497. [Google Scholar] [CrossRef]
- Mawson, V.J.; Hughes, B.R. Deep learning techniques for energy forecasting and condition monitoring in the manufacturing sector. Energy Build. 2020, 217, 109966. [Google Scholar] [CrossRef]
- Kharlova, E.; May, D.; Musilek, P. Forecasting Photovoltaic Power Production using a Deep Learning Sequence to Sequence Model with Attention. In Proceedings of the IEEE 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–7. [Google Scholar]
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; Martinez-de Pison, F.J.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Pierro, M.; Bucci, F.; De Felice, M.; Maggioni, E.; Moser, D.; Perotto, A.; Spada, F.; Cornaro, C. Multi-Model Ensemble for day ahead prediction of photovoltaic power generation. Sol. Energy 2016, 134, 132–146. [Google Scholar] [CrossRef]
- Rajabalizadeh, S.; Tafreshi, S.M.M. A Practicable Copula-Based Approach for Power Forecasting of Small-Scale Photovoltaic Systems. IEEE Syst. J. 2020, 14, 4911–4918. [Google Scholar] [CrossRef]
- Wee, Y.N.; Nor, A.F.M. Prediction of Rooftop Photovoltaic Power Generation Using Artificial Neural Network. In Proceedings of the 2020 IEEE Student Conference on Research and Development (SCOReD), Johor, Malaysia, 27–29 September 2020; pp. 346–351. [Google Scholar]
- Sabzehgar, R.; Amirhosseini, D.Z.; Rasouli, M. Solar power forecast for a residential smart microgrid based on numerical weather predictions using artificial intelligence methods. J. Build. Eng. 2020, 32, 101629. [Google Scholar] [CrossRef]
- Monteiro, C.; Fernandez-Jimenez, L.A.; Ramirez-Rosado, I.J.; Muñoz-Jimenez, A.; Lara-Santillan, P.M. Short-term forecasting models for photovoltaic plants: Analytical versus soft-computing techniques. Math. Probl. Eng. 2013, 2013, 767284. [Google Scholar] [CrossRef] [Green Version]
- Wei, C.C. Evaluation of Photovoltaic Power Generation by Using Deep Learning in Solar Panels Installed in Buildings. Energies 2019, 12, 3564. [Google Scholar] [CrossRef] [Green Version]
- Amarawardhana, K.N.; Jayasinghe, S.D.; Shahnia, F. Grid-interactive rooftop photovoltaic clusters with third-party ownership. Int. J. Smart Grid Clean Energy 2020, 9, 102–111. [Google Scholar] [CrossRef]
- Tuohy, A.; Zack, J.; Haupt, S.E.; Sharp, J.; Ahlstrom, M.; Dise, S.; Grimit, E.; Mohrlen, C.; Lange, M.; Casado, M.G.; et al. Solar forecasting: Methods, challenges, and performance. IEEE Power Energy Mag. 2015, 13, 50–59. [Google Scholar] [CrossRef]
- Pelland, S.; Remund, J.; Kleissl, J.; Oozeki, T.; De Brabandere, K. Photovoltaic and solar forecasting: State of the art. IEA PVPS Task 2013, 14, 1–36. [Google Scholar]
- Awan, A.B.; Zubair, M.; Abokhalil, A.G. Solar energy resource analysis and evaluation of photovoltaic system performance in various regions of Saudi Arabia. Sustainability 2018, 10, 1129. [Google Scholar] [CrossRef] [Green Version]
- Kandasamy, C.; Prabu, P.; Niruba, K. Solar potential assessment using PVSYST software. In Proceedings of the 2013 IEEE International Conference on Green Computing, Communication and Conservation of Energy (ICGCE), Chennai, India, 12–14 December 2013; pp. 667–672. [Google Scholar]
- Lee Rodgers, J.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Entropy, relative entropy and mutual information. Elem. Inf. Theory 1991, 2, 12–13. [Google Scholar]
- Kalousis, A.; Prados, J.; Hilario, M. Stability of feature selection algorithms: A study on high-dimensional spaces. Knowl. Inf. Syst. 2007, 12, 95–116. [Google Scholar] [CrossRef] [Green Version]
- Chung, C.J.F.; Fabbri, A.G.; Van Westen, C.J. Multivariate regression analysis for landslide hazard zonation. In Geographical Information Systems in Assessing Natural Hazards; Springer: Berlin/Heidelberg, Germany, 1995; pp. 107–133. [Google Scholar]
- Ostertagová, E. Modelling using polynomial regression. Procedia Eng. 2012, 48, 500–506. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.; Caramanis, C.; Mannor, S. Robust regression and lasso. IEEE Trans. Inf. Theory 2010, 56, 3561–3574. [Google Scholar] [CrossRef] [Green Version]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. Available online: https://dl.acm.org/doi/abs/10.1145/2939672.2939785 (accessed on 24 December 2020).
- Chang, C.C.; Lin, C.J. Training v-support vector regression: Theory and algorithms. Neural Comput. 2002, 14, 1959–1977. [Google Scholar] [CrossRef]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hopfield, J.J. Artificial neural networks. IEEE CIrcuits Devices Mag. 1988, 4, 3–10. [Google Scholar] [CrossRef]
- Sa, N.G. The Saudi Arabian Grid Code, Electronic Update as of February 2020. 2020. Available online: https://www.ecra.gov.sa/ar-sa/ECRARegulations/Codes/Documents/SAGC%20Electronic%20Update.pdf (accessed on 24 December 2020).
- Saidi, A.S. Impact of large photovoltaic power penetration on the voltage regulation and dynamic performance of the Tunisian power system. Energy Explor. Exploit. 2020, 38, 1774–1809. [Google Scholar] [CrossRef]
- Saidi, A.S. Investigation of Structural Voltage Stability in Tunisian Distribution Networks Integrating Large-Scale Solar Photovoltaic Power Plant. Int. J. Bifurc. Chaos 2020, 30, 2050259. [Google Scholar] [CrossRef]




| Tilt angle | 22° |
| Azimuth angle | −21° |
| Field type | Fixed tilted plane |
| Mechanical Characteristics | |
| Model | KS-240PC |
| Solar cells | Polycrystalline silicon 156 × 156 mm |
| No. of cells | 60 (6 × 10) |
| Dimensions | 1663 mm × 998 mm × 35 mm |
| Weight | 23.5 kg |
| Front glass | 4.0 mm tempered glass |
| Frame | Anodized aluminum alloy |
| Cell area | 2.9 m2 |
| PV module Electrical Characteristics (STC) STC: Standard test condition; 1000 W/m2, 25 °C, AM 1.5 | |
| Optimum operating voltage (Vmp) (V) | 30.12 |
| Optimum operating current (Imp) (A) | 8.21 |
| Open circuit voltage (Voc) (V) | 37.94 |
| Short circuit current (Isc) A) | 8.69 |
| Maximum power @ STC (Pmax) (W) | 240 W |
| Module efficiency | 14.8% |
| Operating module temperature | −40 °C to +85 °C |
| Maximum system voltage | 1000 V DC (IEC)/600 V DC (UL) |
| Maximum series fuse rating | 20 A |
| Power tolerance | 0/+5% |
| Temperature Characteristics NOCT: Nominal operating cell temperature, Irradiance level 800 W/m2, Spectrum AM 1.5, Wind velocity 1 m/s, Ambient temperature 20 °C | |
| Nominal operating cell temperature (NOCT) | 45 °C ± 2 °C |
| Temperature coefficient of Pmax | −0.44%/°C |
| Temperature coefficient of Voc | −0.33%/°C |
| Temperature coefficient of Isc | −0.055%/°C |
| Spectral range (20% points) | 285 to 3000 10 m |
| Calibration uncertainty | <1.2% (k = 2) |
| Rated operating temperature range | −40 to +80 °C |
| Sensitivity | 7 to 25 10 V/(W/m2) |
| Impedance | 20 to 200 |
| Maximum operational irradiance | 2000 W/m2 |
| Response time (95%) | 4.5 s |
| Temperature response | <±1% (−10 to +40 °C) and <±0.4% (−30 to +50 °C) with correction in data processing |
| SI No. | Parameter | Type of Sensor Used |
|---|---|---|
| 1 | Temperature sensor | PN junction silicon diode |
| 2 | Wind speed sensor | Solid state magnetic sensor |
| 3 | Wind direction sensor | Wind vane with potentiometer |
| 4 | Rain collector | Tipping spoon type of Tipping bucket, 0.01′′ per tip (0.2 mm with metric rain adapter) |
| 5 | Relative humidity sensor | Film capacitor element |
| 6 | Housing material | UV-resistance, ABS, Polypropylene |
| Sl No. | Parameter | Resolution | Range | Accuracy |
|---|---|---|---|---|
| 1 | Barometric pressure | 0.01′′ Hg, 0.1 mm Hg, 0.1 hPa/mb | 16.00′′ to 32.50′′ Hg, 410 to 820 mm Hg, 540 to 1100 hPa/mb | ±0.03′′ Hg (±0.8 mm Hg, ±1.0 hPa/mb) (at room temperature) |
| 2 | Clock | 1 min | 12 or 24 h format | ±8 s/month |
| 3 | Dew point | 1 °F or 1 °C. °C is converted from °F rounded to the nearest 1 °C | −105° to +130 °F (−76° to +54 °C) | ±3 °F (±1.5 °C) (typical) |
| 4 | Evapotranspiration | 0.01′′ or 0.1 mm | Daily to 32.67′′ (832.1 mm); Monthly Yearly to 199.99′′ (1999.9 mm) | Greater of 0.01′′ (0.25 mm) or ±5% |
| 5 | Forecast | Barometric Reading Trend, Wind Speed Direction, Rainfall, Temperature, Humidity, Latitude Longitude, Time of Year | —– | ——– |
| 6 | Heat Index | 1 °F or 1 °C. °C is converted from °F rounded to the nearest 1 °C | −40° to +165 °F (−40° to +74 °C) | ±3 °F (±1.5 °C) (typical) |
| 7 | Humidity | 1% | 1 to 100% RH | ±3% (0 to 90% RH), ±4% (90 to 100% RH) |
| 8 | Moon phase | 1/8 (12.5%) of a lunar cycle, 1/4 (25%) of lighted face on console | New moon, Waxing crescent, First quarter, Waxing gibbous, Full moon, Waning gibbous, Last quarter, Waning crescent | ±38 min |
| 9 | Rainfall | 0.01′′ or 0.2 mm (1 mm at totals ≥2000 mm) | 0 to 199.99′′ (0 to 6553 mm) | For rain rates up to 2/h (50 mm/h): ±4% of total or +0.01′′ (0.2 mm) (0.01′′ = one tip of the bucket), whichever is greater. For rain rates from 2/h (50 mm/h) to 4/h (100 mm/h): ±4% of total or +0.01′′ (0.25 mm) (0.01′′ = one tip of the bucket), whichever is greater |
| 10 | Rain rate | 0.01′′ or 0.1 mm | 0, 0.04/h (1 mm/h) to 96/h (0 to 2438 mm/h) | ±5% for rates less than 5′′ per hour (127 mm/h) |
| 11 | Solar radiation | 1 W/m2 | 0 to 1800 W/m2 | ±5% of full scale |
| 12 | Sunrise and sunset | 1 min | Depends | ±1 min |
| 13 | Temperature | 0.1 °F or 1 °F or 0.1 °C or 1 °C (user-selectable) °C is converted from °F rounded to the nearest 1 °C | +32° to +140°F (0° to +60 °C) | ±1 °F (±0.5 °C) |
| 14 | Temperature humidity Sun wind index | 0.1 °F or 1 °F or 0.1 °C or 1 °C (user-selectable) °C is converted from °F rounded to the nearest 1 °C | −90° to +165 °F (−68° to +74 °C) | ±4 °F (±2 °C) (typical) |
| 15 | Ultra violet (UV) radiation dose | 0.1 MEDs to 19.9 MEDs; 1 MED above 19.9 MEDS | 0 to 199 MEDs | ±5% of daily total |
| 16 | UV radiation index | 0.1 Index | 0 to 16 Index | ±5% of full scale |
| 17 | Wind direction | 16 points (22.5°) on compass rose, 1° in numeric display | 0°–360° | ±3° |
| 18 | Wind speed | 1 mph, 1 km/h, 0.4 m/s, or 1 knot (user-selectable). Measured in mph, other units are converted from mph and rounded to the nearest 1 km/h, 0.1 m/s, or 1 knot. | 1 to 200 mph, 1 to 173 knots, 0.5 to 89 m/s, 1 to 322 km/h | ±2 mph (2 kts, 3 km/h, 1 m/s) or ±5%, whichever is greater |
| Generated Power | Scaled Generated Power | |
|---|---|---|
| Count | 5402 | 5402 |
| Mean | 2336.47108 | 0 |
| Standard deviation | 1569.29464 | 1 |
| Minimum | 0 | −1.489 |
| 25% | 796.435 | −0.98145 |
| 50% | 2460.935 | 0.07932 |
| 75% | 3873.59 | 0.97959 |
| Maximum | 5828.5 | 2.22543 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohana, M.; Saidi, A.S.; Alelyani, S.; Alshayeb, M.J.; Basha, S.; Anqi, A.E. Small-Scale Solar Photovoltaic Power Prediction for Residential Load in Saudi Arabia Using Machine Learning. Energies 2021, 14, 6759. https://doi.org/10.3390/en14206759
Mohana M, Saidi AS, Alelyani S, Alshayeb MJ, Basha S, Anqi AE. Small-Scale Solar Photovoltaic Power Prediction for Residential Load in Saudi Arabia Using Machine Learning. Energies. 2021; 14(20):6759. https://doi.org/10.3390/en14206759
Chicago/Turabian StyleMohana, Mohamed, Abdelaziz Salah Saidi, Salem Alelyani, Mohammed J. Alshayeb, Suhail Basha, and Ali Eisa Anqi. 2021. "Small-Scale Solar Photovoltaic Power Prediction for Residential Load in Saudi Arabia Using Machine Learning" Energies 14, no. 20: 6759. https://doi.org/10.3390/en14206759
APA StyleMohana, M., Saidi, A. S., Alelyani, S., Alshayeb, M. J., Basha, S., & Anqi, A. E. (2021). Small-Scale Solar Photovoltaic Power Prediction for Residential Load in Saudi Arabia Using Machine Learning. Energies, 14(20), 6759. https://doi.org/10.3390/en14206759







