Calculating the Inrush Current of Superconducting Transformers
Abstract
:1. Introduction
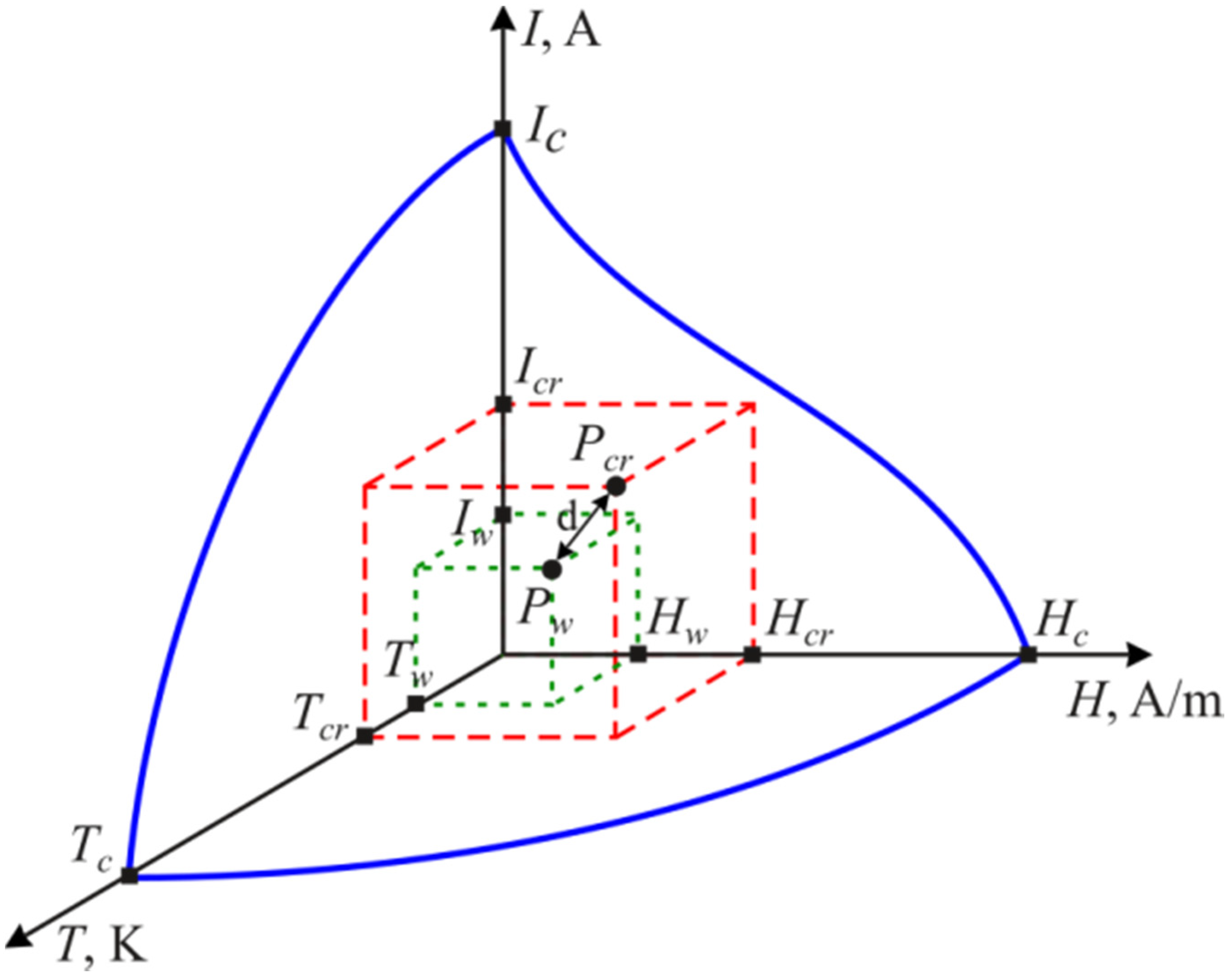
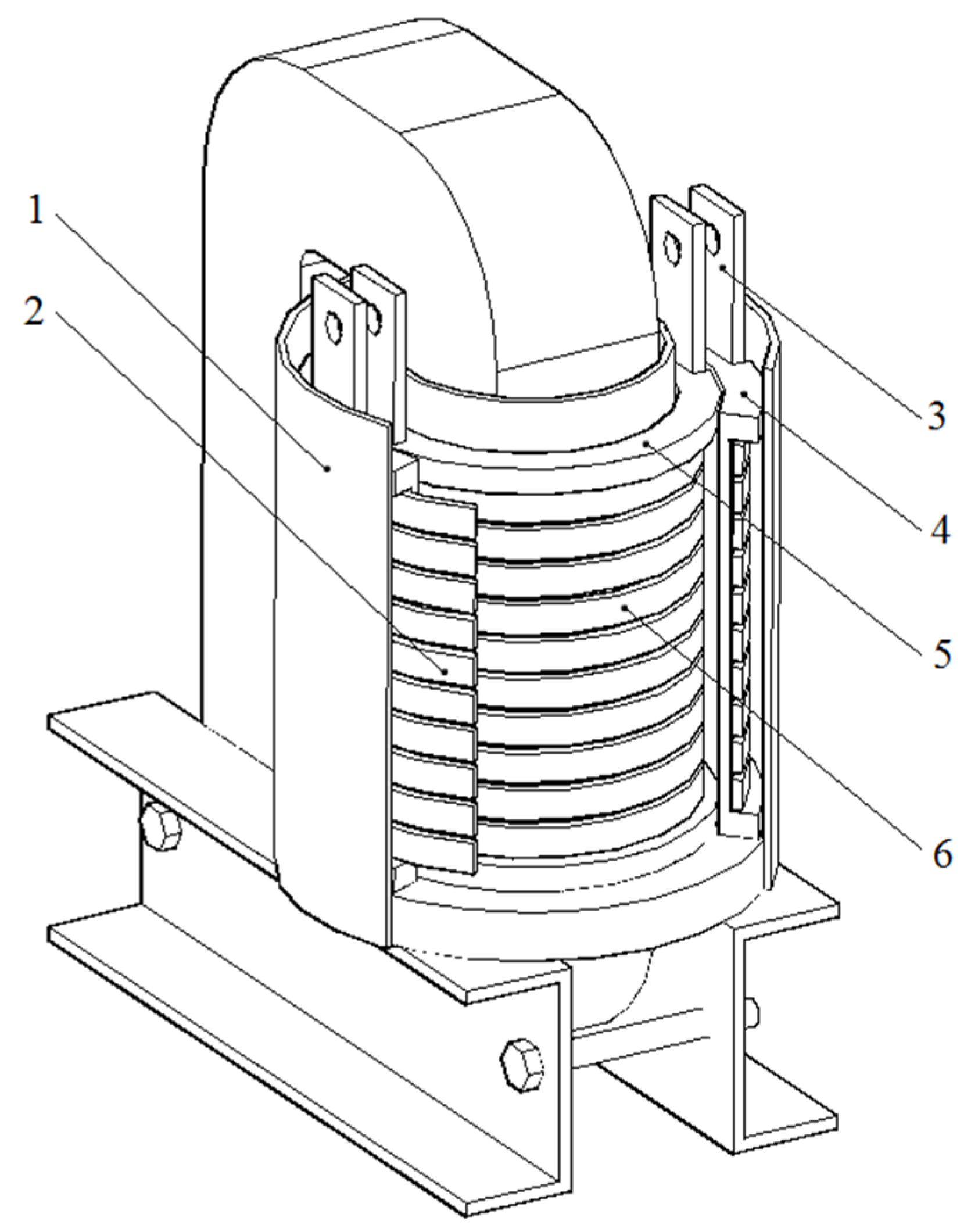
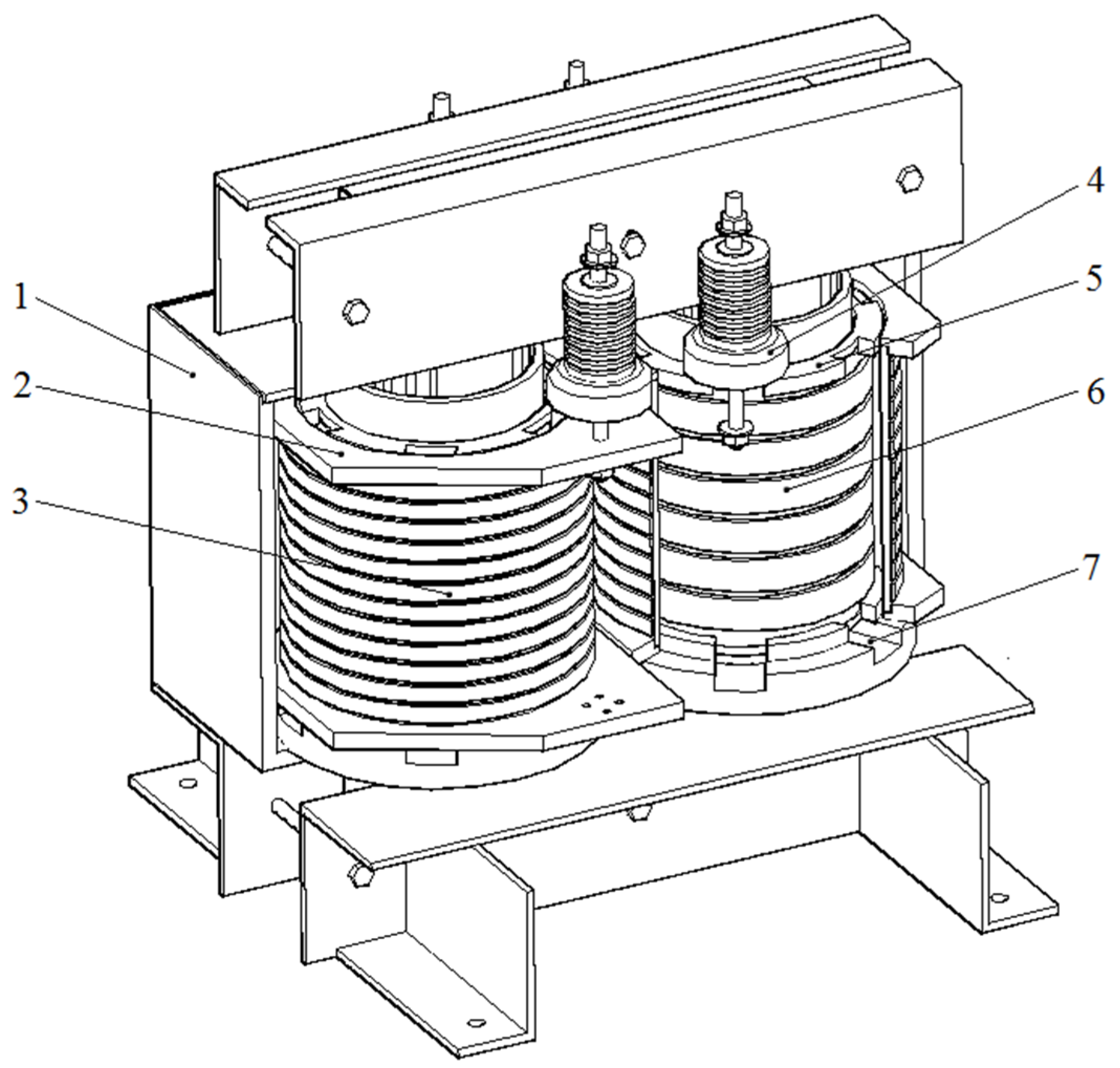
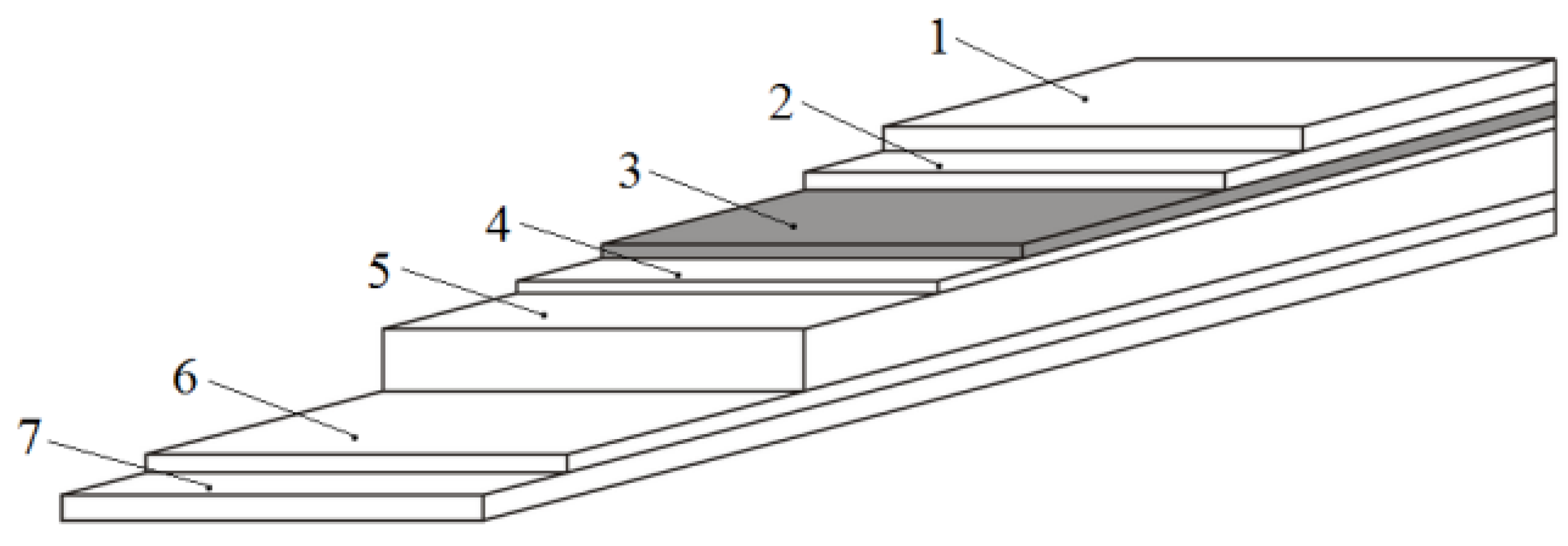
2. Superconducting Transformer
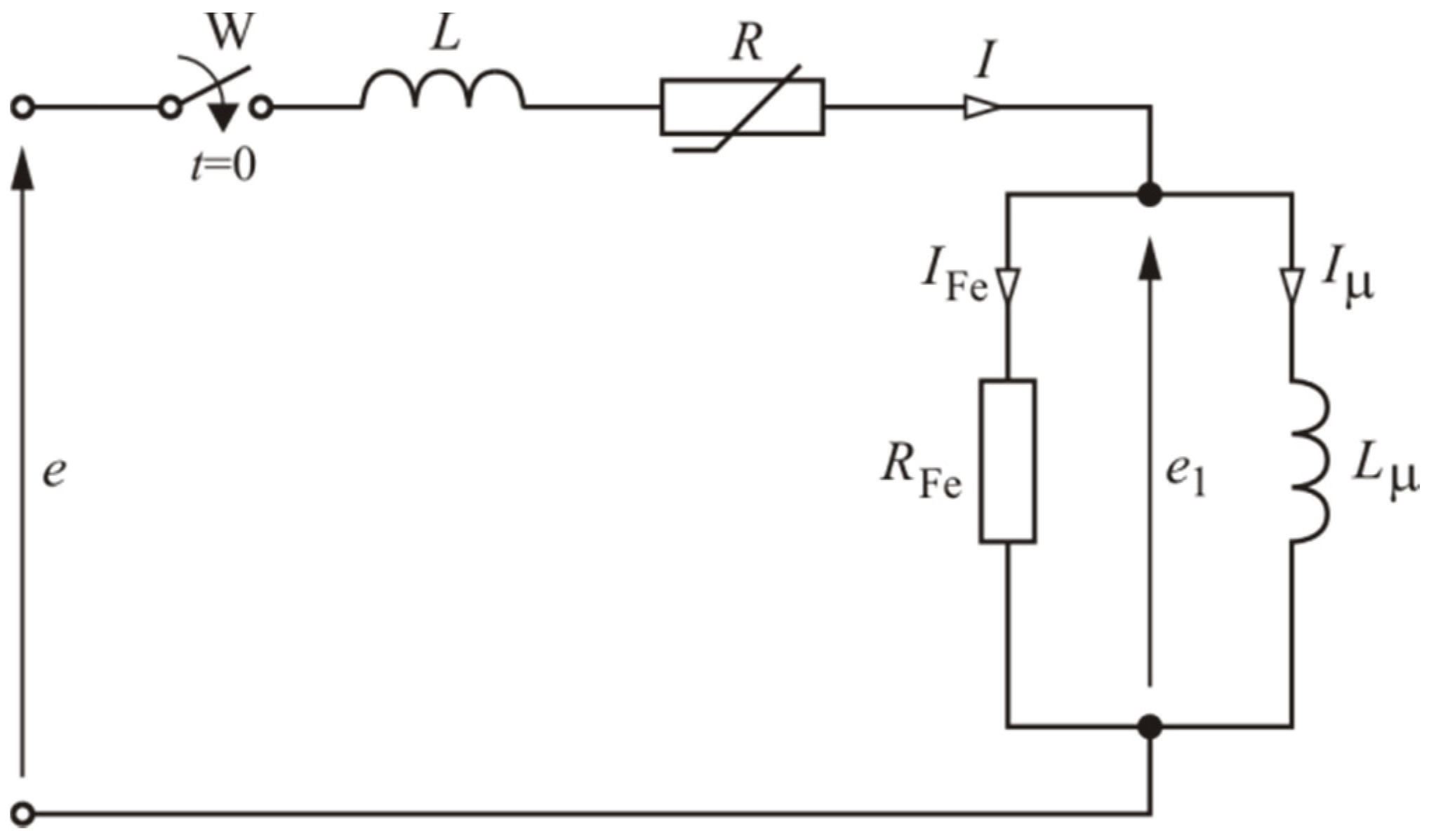
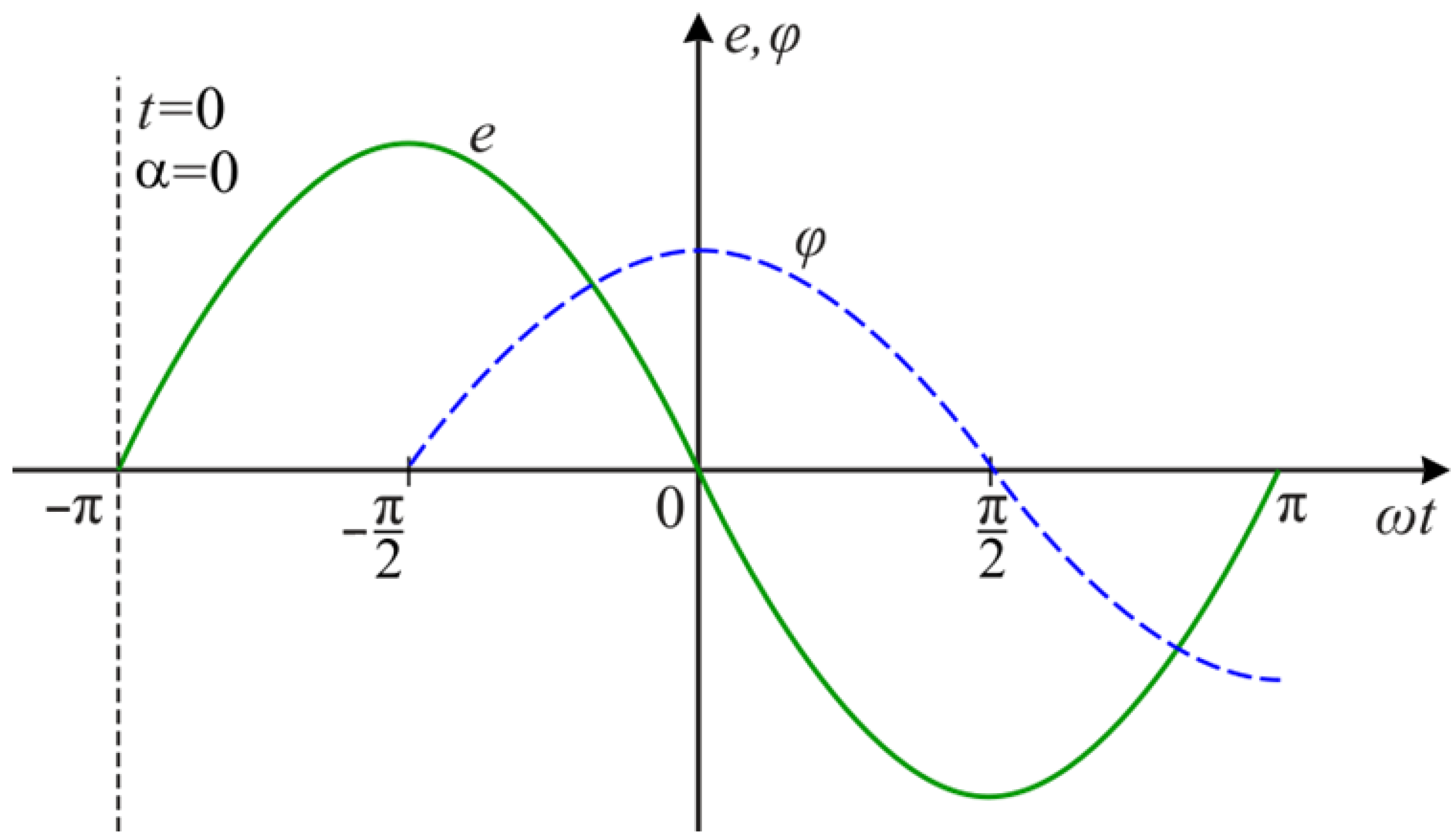
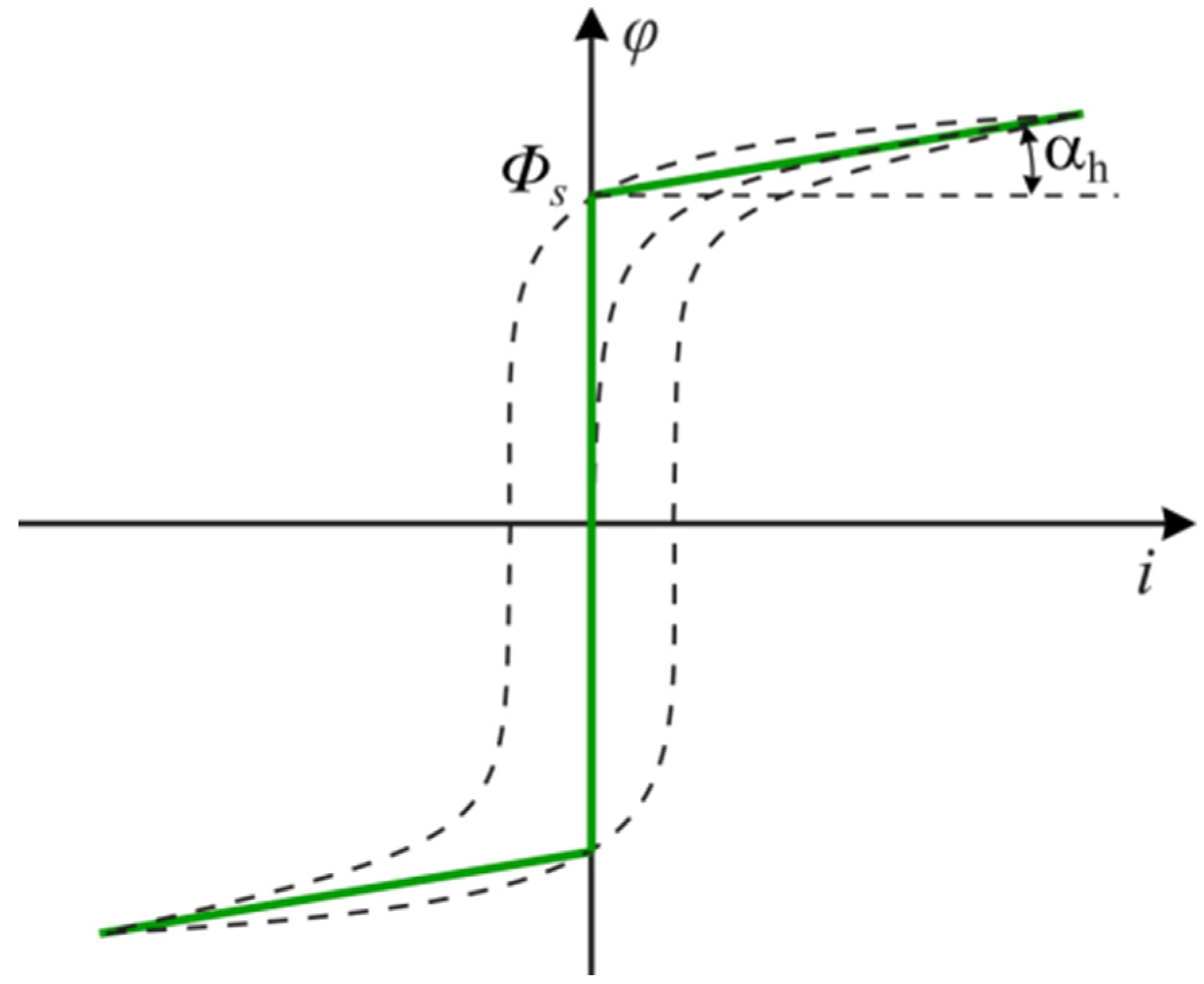
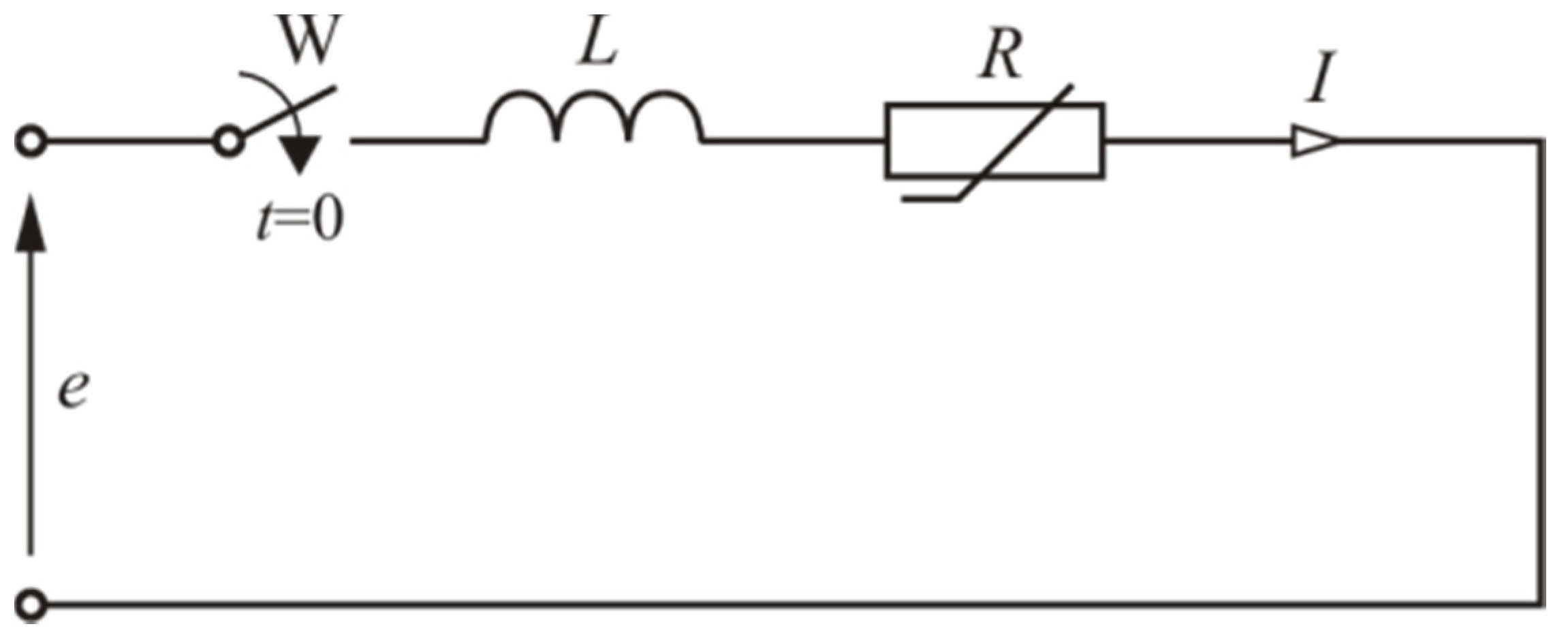
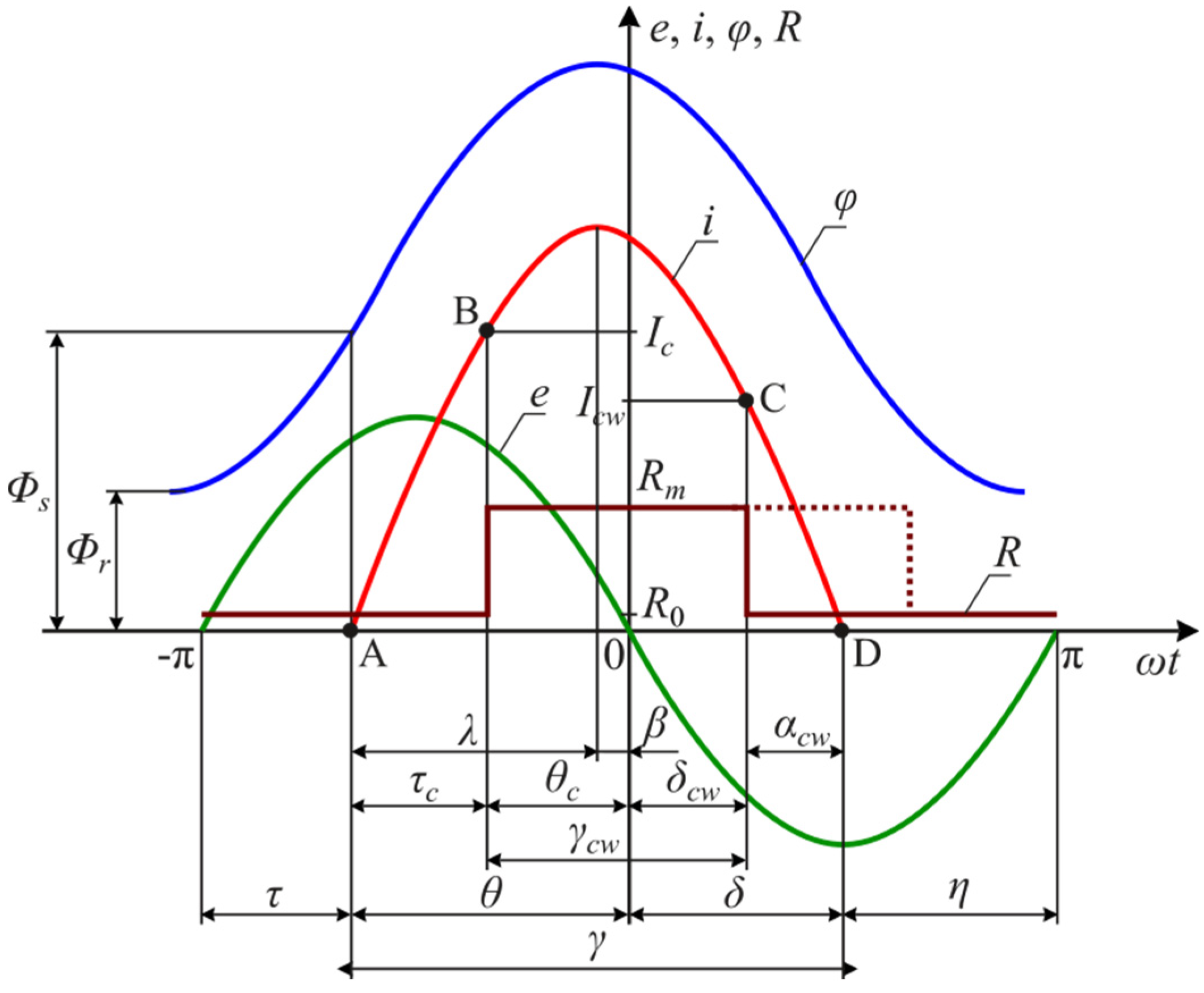
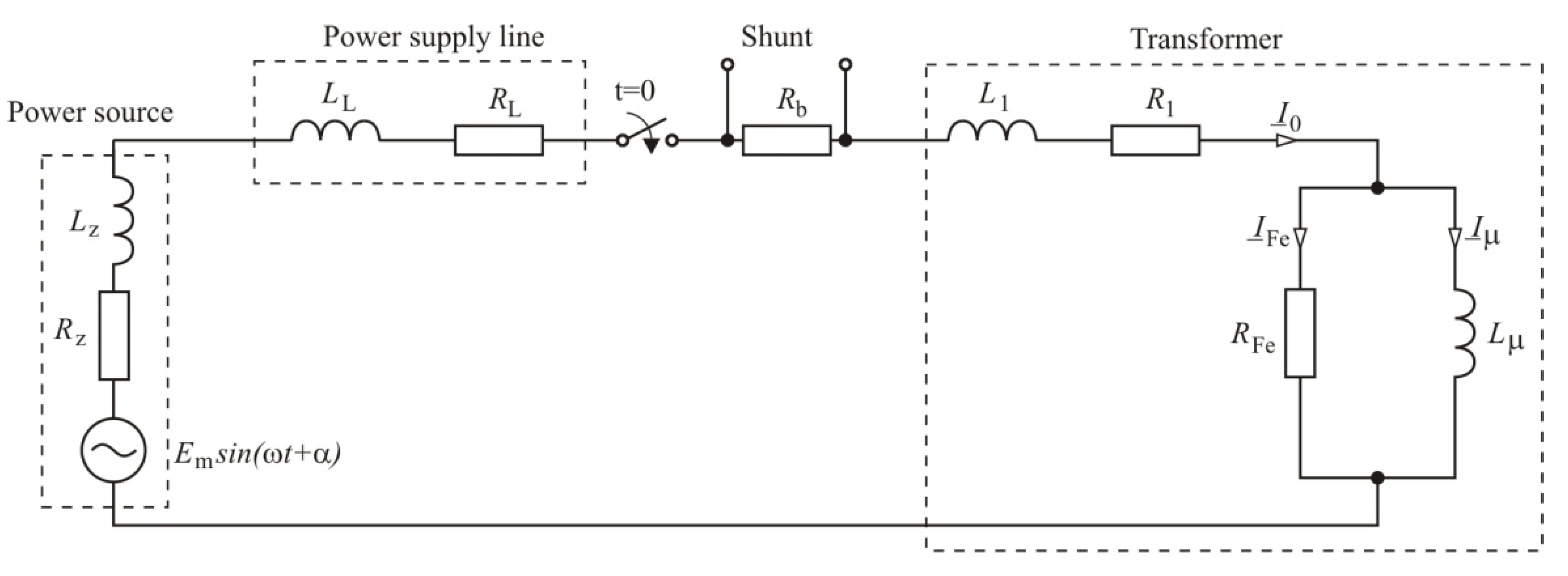
3. Stream in the Transformer Core after Switching on
4. Inrush Current of Superconducting Transformer
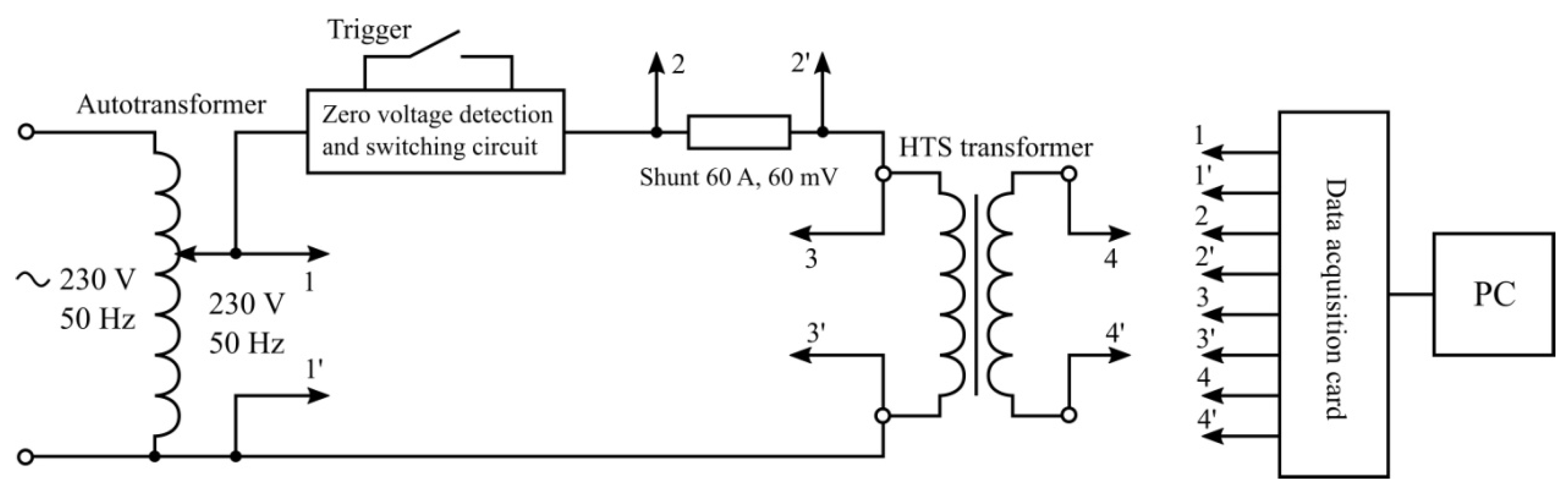
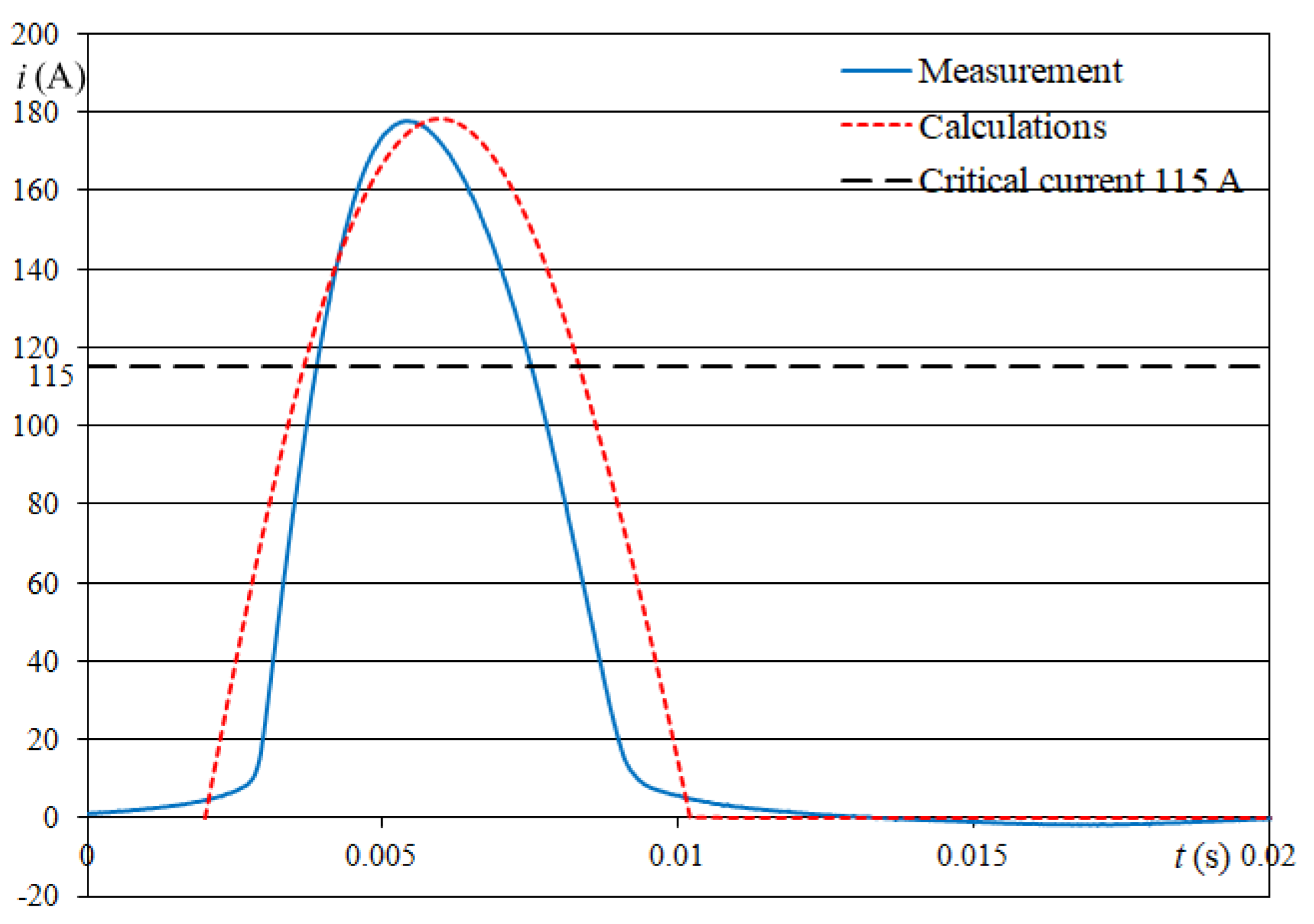
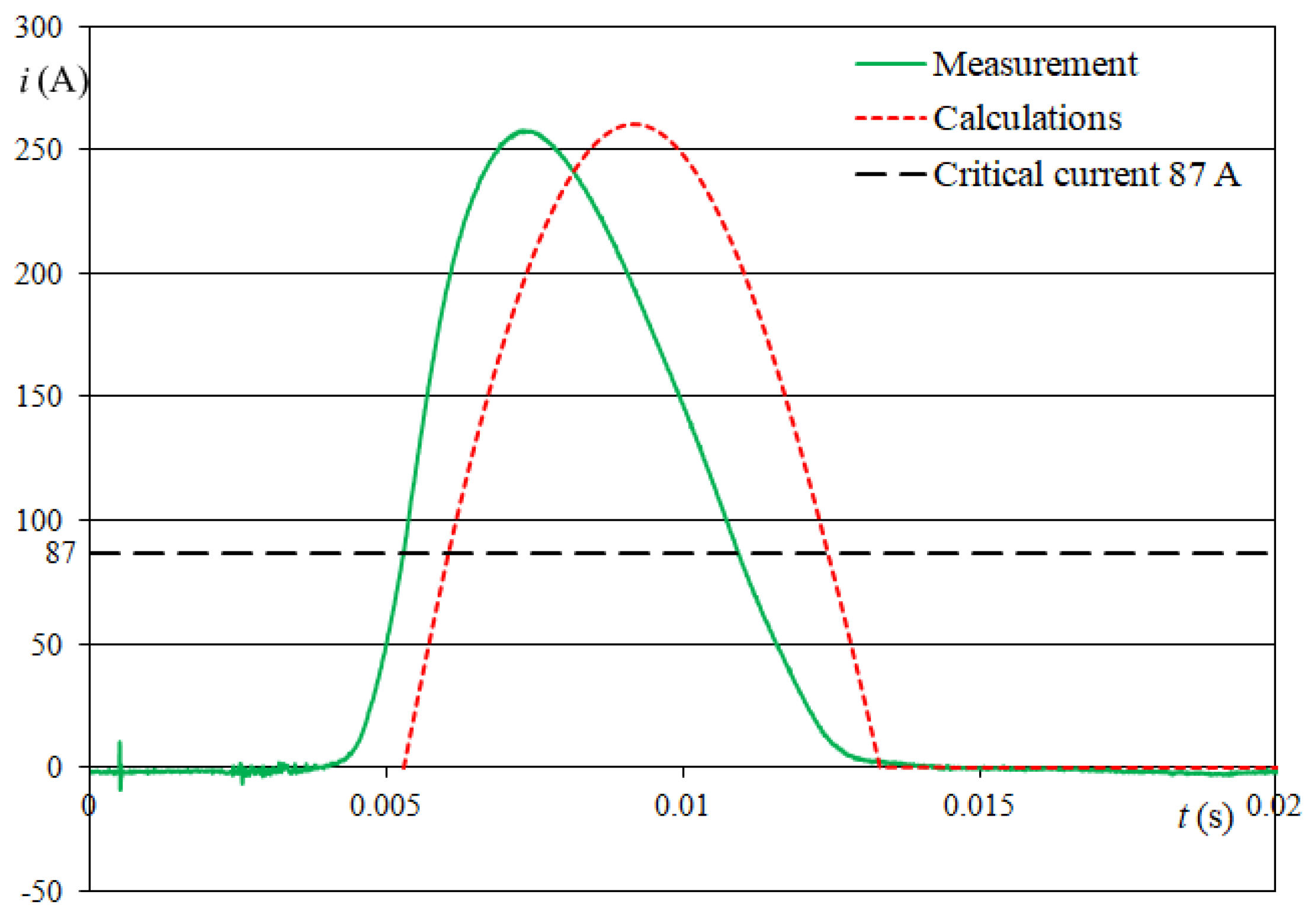
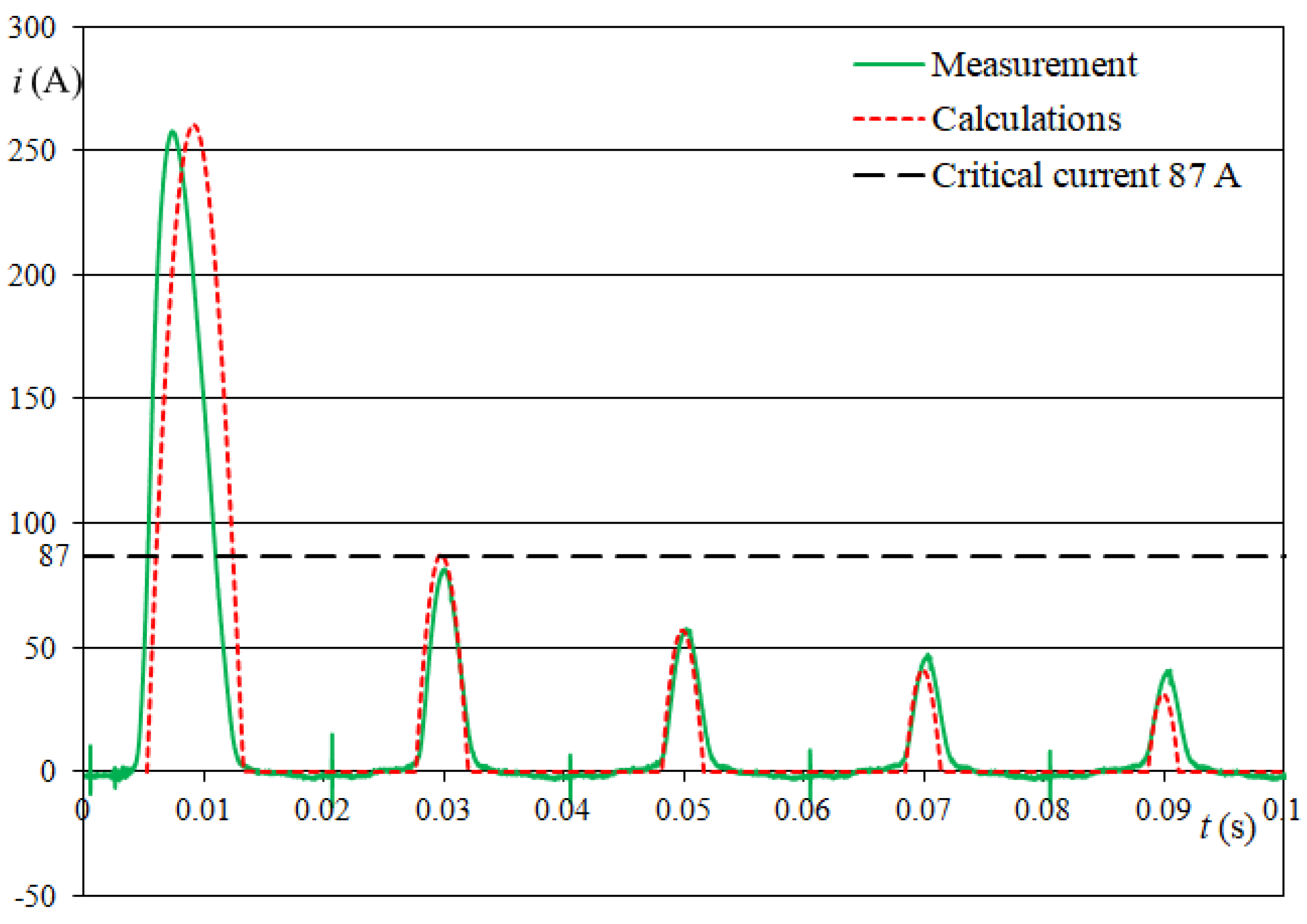
5. Experimental Verification of Calculations
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Winding cross-sectional area, |
| Ak | Iron cross sectional area of column core, |
| Bm | Maximum induction at normal transformer operation, |
| Br | Residual magnetism induction, |
| Bs | Saturation induction, |
| e | Circuit supply voltage, |
| e1 | Voltage induced in the transformer winding by the main flux, |
| E | Effective value of the circuit supply voltage, |
| HM | magnetic field strength after switching on the transformer, |
| i | Current in the circuit, |
| iμ | Reactive component of the transformer’s no load current, |
| IFe | Active component of the transformer’s idle current, |
| Ic | Critical current of the transformer’s primary winding, |
| Icw | Current at which the winding regains its superconductive state, |
| L | Inductance in the circuit when the transformer core is saturated, |
| Lμ | Inductance of the magnetisation branch of the transformer diagram, |
| R | Resistance of the circuit, |
| RFe | Resistance of the magnetisation branch of the transformer diagram, |
| t | Time, |
| X | Circuit reactance, |
| N | Number of primary windings of the transformer, |
| Z | Circuit impedance, |
| α | Voltage phase angle, |
| δ | Angle of phase shift between flow and voltage, |
| φ | Magnetic flux, |
| φf | Fixed magnetic flux component, |
| φd | Magnetic flux disturbing component, |
| Φ | Effective value of the flux, |
| Φm | Maximum flux in the core, |
| ΦM | Peak value of the flux, |
| Φr | Residual magnetism flux, |
| Φs | Saturation flux of the transformer core, |
| ω | Pulse |
References
- Steurer, M.; Frohlich, K. The Impact of Inrush Current on the mechanical stress on high voltage power transformer coils. IEEE Trans. Power Deliv. 2002, 17, 155–160. [Google Scholar] [CrossRef]
- Prikler, L.; Bánfai, G.; Bán, G.; Becker, P. Reducing the magnetizing inrush current by means of controlled energization and de-energization of large power transformers. Electr. Power Syst. Res. 2006, 76, 642–649. [Google Scholar] [CrossRef]
- Turner, R.A.; Smith, K.S. Transformer Inrush Current. IEEE Ind. Appl. Mag. 2010, 16, 14–19. [Google Scholar] [CrossRef]
- Kasztenny, B. Impact of Transformer Inrush Current on Sensitive Protection Functions. In Proceedings of the IEEE/PES Transmission and Distribution Conference and Exhibition, Dallas, TX, USA, 21–24 May 2006. [Google Scholar] [CrossRef]
- Oliveira, A.R.J.C.; Apolonio, R.; Bronzeado, H.S. A Controlled Switching Methodology for Transformer Inrush Current Elimination: Theory and Experimental Validation. In Proceedings of the 11th International Conference on Electrical Power Quality and Utilisation, Lisbon, Portugal, 17–19 October 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Chiesa, N.; Hoidalen, H.K. Novel approach for reducing transformer inrush currents: Laboratory measurements, analytical interpretation and simulation studies. IEEE Trans. Power Deliv. 2010, 25, 2609–2616. [Google Scholar] [CrossRef]
- Abdulsalam, S.G.; Xu, W. A sequential phase energization method for transformer inrush current reduction—Transient performance and practical considerations. IEEE Trans. Power Deliv. 2007, 22, 208–216. [Google Scholar] [CrossRef]
- Taylor, D.I.; Law, J.D.; Johnson, B.K.; Fischer, N. Single-phase transformer inrush current reduction using prefluxing. IEEE Trans. Power Deliv. 2012, 27, 245–253. [Google Scholar] [CrossRef]
- Persson, M.; Baig, W.; Thiringer, T. Measurements and modelling of threeand five-limb transformer behaviour during large voltage and frequency disturbances. IET Gener. Transm. Distrib. 2016, 10, 334–340. [Google Scholar] [CrossRef] [Green Version]
- Rico, J.J.; Acha, E.; Madrigal, M. The study of inrush current phenomenon using operational matrices. IEEE Trans. Power Deliv. 2001, 16, 231–237. [Google Scholar] [CrossRef]
- Adly, A. Computation of inrush current forces on transformer windings. IEEE Trans. Magn. 2001, 37, 2855–2857. [Google Scholar] [CrossRef]
- Wu, Q.; Jazebi, S.; Leon, D.F. Parameter estimation of three-phase transformer models for low-frequency transient studies from terminal measurements. IEEE Trans. Magn. 2017, 53, 710–718. [Google Scholar] [CrossRef]
- Specht, T.R. Transformer magnetizing inrush current. Trans. Am. Inst. Electr. Eng. 1951, 70, 323–328. [Google Scholar] [CrossRef]
- Holcomb, J.E. Distribution transformer magnetizing inrush current. Trans. Am. Inst. Electr. Eng. Part III Power Appar. Syst. 1961, 80, 697–702. [Google Scholar] [CrossRef]
- Specht, T.R. Transformer Inrush and Rectifier Transient Currents. IEEE Trans. Power Appar. Syst. 1969, PAS-88, 269–276. [Google Scholar] [CrossRef]
- Jamali, M.; Mirzaie, M.; Asghar Gholamian, S. Calculation and Analysis of Transformer Inrush Current Based on Parameters of Transformer and Operating Conditions. Electron. Electr. Eng. 2011, 109, 17–20. [Google Scholar] [CrossRef] [Green Version]
- Yacamini, R.; Abu-Nasser, A. Numerical calculation of inrush current in single-phase transformers. IEEE Proc. B Electr. Power Appl. 1981, 128, 327–328. [Google Scholar] [CrossRef]
- Vanti, M.G.; Bertoli, S.L.; Cabrai, S.H.L.; Gerent, A.G.; Kuo-Peng, P. Semianalytic solution for a simple model of inrush currents in transformers. IEEE Trans. Magn. 2008, 44, 1270–1273. [Google Scholar] [CrossRef]
- Chen, X.; Venkata, S.S. A three-phase three-winding core-type transformer model for low-frequency transient studies. IEEE Power Eng. Rev. 1997, 17, 85–86. [Google Scholar] [CrossRef]
- Chen, S.D.; Lin, R.L.; Cheng, C.K. Magnetizing inrush model of transformers based on structure parameters. IEEE Trans. Power Deliv. 2005, 20, 1947–1954. [Google Scholar] [CrossRef]
- Chiesa, N.; Hidalen, H.K.; Mork, B.A. Transformer model for inrush current calculations: Simulations, measurements and sensitivity analysis. IEEE Trans. Power Deliv. 2010, 25, 2599–2608. [Google Scholar] [CrossRef]
- Faiz, J.; Saffari, S. Inrush current modeling in a single-phase transformer. IEEE Trans. Magn. 2010, 46, 578–581. [Google Scholar] [CrossRef]
- Abdulsalam, S.G.; Xu, W.; Neves, W.; Liu, X. Estimation of transformer saturation characteristics from inrush current waveforms. IEEE Trans. Power Deliv. 2006, 21, 170–177. [Google Scholar] [CrossRef]
- Naghizadeh, R.A.; Vahidi, B.; Hosseinian, S.H. Modelling of inrush current in transformers using inverse Jiles–Atherton hysteresis model with a neuroshuffled frog-leaping algorithm approach. IET Electr. Power Appl. 2012, 6, 727–728. [Google Scholar] [CrossRef]
- Liu, J.; Dinavahi, V. Detailed magnetic equivalent circuit based real-time nonlinear power transformer model on FPGA for electromagnetic transient studies. IEEE Trans. Ind. Electron. 2016, 63, 1191–1202. [Google Scholar] [CrossRef]
- Wang, Y.; Abdulsalam, S.G.; Xu, W. Analytical formula to estimate the maximum inrush current. IEEE Trans. Power Deliv. 2008, 23, 1266–1268. [Google Scholar] [CrossRef]
- Jazebi, S.; de Leon, F.; Wu, N. Enhanced analytical method for the calculation of the maximum inrush currents of single-phase power transformers. IEEE Trans. Power Deliv. 2015, 30, 2590–2599. [Google Scholar] [CrossRef]
- Zirka, S.E.; Moroz, Y.I.; Arturi, C.M.; Chiesa, N.; Hoidalen, H.K. Topology-correct reversible transformer model. IEEE Trans. Power Deliv. 2012, 27, 2037–2045. [Google Scholar] [CrossRef]
- Girgis, R.S.; Tenyenuis, E.G. Characteristics of inrush current of present designs of power transformers. IEEE Power Eng. Soc. Gen. Meet. 2007, 12, 1–6. [Google Scholar] [CrossRef]
- Bertagnolli, G. Short-Circuit Duty of Power Transformers: The ABB Approach; ABB Trasformatori: Golinelli, Formigine, 1996. [Google Scholar]
- Nishimiya, S.; Ishigohka, T.; Ninomiya, A.; Arai, K. Quench Characteristic of Superconducting Transformer by Inrush Current. IEEE Trans. Appl. Supercond. 2007, 17, 1931–1934. [Google Scholar] [CrossRef]
- Meinert, M.; Binder, A. Active damping of inrush and DC-currents for high temperature Superconducting (HTS)-transformers on rail vehicles. IEEE Trans. Appl. Supercond. 2005, 15, 1851–1854. [Google Scholar] [CrossRef]
- Abdul Rahman, M.A.; Lie, T.T.; Prasad, K. The Effects of Short-Circuit and Inrush Currents on HTS Transformer Windings. IEEE Trans. Appl. Supercond. 2012, 22, 5500108. [Google Scholar] [CrossRef]
- Kalsi, S.S. Applications of High Temperature Superconductors to Electric Power Equipment; Wiley-IEEE Press: Piscataway, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Xie, Y.; Marchevsky, M.; Zhang, X.; Lenseth, K.; Chen, Y.; Xiong, X.; Qiao, Y.; Rar, A.; Gogia, B.; Schmidt, R.; et al. Second-generation HTS conductor design and engineering for electrical power applications. IEEE Trans. Appl. Supercond. 2009, 19, 3009–3013. [Google Scholar] [CrossRef]
- Rupich, M.W.; Li, X.; Sathyamurthy, S.; Thieme, C.L.H.; DeMoranville, K.; Gannon, J.; Fleshler, S. Second Generation Wire Development at AMSC. IEEE Trans. Appl. Supercond. 2013, 23, 6601205. [Google Scholar] [CrossRef]
- Nagasawa, T.; Yamaguchi, M.; Fukui, S.; Yamamoto, M. Design requirements of a high temperature superconducting transformer. Phys. C Supercond. 2002, 372–376, 1715–1718. [Google Scholar] [CrossRef]
- Berger, A.; Cherevatskiy, S.; Noe, M.; Leibfried, T. Comparison of the efficiency of superconducting and conventional transformers. J. Phys. Conf. Ser. 2010, 234, 032004. [Google Scholar] [CrossRef]
- Chang, H.; Choi, Y.S.; Sciver, S.W.; Baldwin, T.L. Cryogenic cooling temperature of HTS transformers for compactness and efficiency. IEEE Trans. Appl. Supercond. 2003, 13, 2298–2301. [Google Scholar] [CrossRef]
- Wilson, M.N. Superconducting Magnets; Oxford University Press: New York, NY, USA, 1990. [Google Scholar]
- Lei, H.; Wang, K.; Hu, R.; Ryu, H.; Abeykoon, M.; Bozin, E.S.; Petrovic, C. Iron chalcogenide superconductors at high magnetic fields. Sci. Technol. Adv. Mater. 2012, 13, 054305. [Google Scholar] [CrossRef]
- Yahiou, A.; Bayadi, A. Transformer core modeling for magnetizing inrush current investigation. Semantic Scholar. Mater. Sci. 2015, 1, 077–088. [Google Scholar]
- Yonezawa, R.; Noda, T.; Suzuki, N.; Nagashima, H.; Nomiyama, F.; Yamaguchi, N.; Honma, H.; Kitamura, S. Development of a transformer magnetizing circuit model for inrush current and residual flux calculations. IEEE Trans. Power Energy 2014, 134, 749–758. [Google Scholar] [CrossRef]
- Vahidi, B.; Bank Tavakoli, M.R.; Gharehpetian, G.B.; Hosseinian, S.H. An Algorithm for Evaluating Inrush Current in Transformers Using Jiles-Atherton Theory of Ferromagnetic Hysteresis. In Proceedings of the TENCON 2006—2006 IEEE Region 10 Conference, Hong Kong, China, 14–17 November 2006. [Google Scholar] [CrossRef]
- Sima, W.; Liu, Y.; Sun, P.; Zhou, Y.; Peng, D.; Yang, M. The Effect of Different Core Materials on Transformer Inrush Currents. In Proceedings of the IEEE International Magnetic Conference (INTERMAG), Singapore, 23–27 April 2018. [Google Scholar] [CrossRef]
- Taillefer, P.; Poutrain, L.; Sanchez, J. Limiting Voltage Dips & Inrush Currents When Energizing Power Transformers Controlled Switching of Gang Operated Switches—Theory and Case Study. In Proceedings of the 2018 IEEE/PES Transmission and Distribution Conference and Exposition (T & D), Denver, CO, USA, 16–19 April 2018. [Google Scholar] [CrossRef]
- Huang, Z.; Jia, Z.; Li, Z. Research on Transformer Saturation Characteristics of Electric Locomotive Based on Flux—Current Loop Model. In Proceedings of the 2019 9th International Conference on Power and Energy Systems (ICPES), Perth, Australia, 10–12 December 2019. [Google Scholar] [CrossRef]
- Sonnemann, W.K.; Wagner, C.L.; Rockefeller, G.D. Magnetizing Inrush Phenomena in Transformer Banks. Trans. Am. Inst. Electr. Eng. Part III Power Appar. Syst. 1958, 77, 884–892. [Google Scholar] [CrossRef]
- Wojtasiewicz, G.; Janowski, T.; Kozak, S.; Kozak, J.; Majka, M.; Kondratowicz-Kucewicz, B. Tests and Performance Analysis of 2G HTS Transformer. IEEE Trans. Appl. Supercond. 2013, 23, 5500505. [Google Scholar] [CrossRef]
- Komarzyniec, G. 14 kVA superconducting transformer with (RE)BCO windings. In Proceedings of the 2017 International Conference on Electromagnetic Devices and Processes in Environment Protection with Seminar Applications of Superconductors (ELMECO & AoS), Nałęczów, Poland, 3–6 December 2017. [Google Scholar] [CrossRef]
- Wojtasiewicz, G.; Komarzyniec, G.; Janowski, T.; Kozak, S.; Kozak, J.; Majka, M.; Kondratowicz-Kucewicz, B. Inrush Current of Superconducting Transformer. IEEE Trans. Appl. Supercond. 2013, 23, 5500304. [Google Scholar] [CrossRef]



| 8.5 kVA | 13.8 kVA | |
|---|---|---|
| Power | 8.5 kVA | 13.8 kVA |
| Frequency | 50 Hz | 50 Hz |
| Voltage Un HV/LV | 220 V/110 V | 230 V/60 V |
| Current In HV/LV | 40 A/80 A | 60 A/230 A |
| Critical current Ic HV/LV | 115 A/115 A | 87A/333 A |
| Magnetic induction | 1.6 T | 1.6 T |
| Idle current | 3.1 A | 0.7 A |
| Short circuit voltage | 0.9% | 3.2% |
| 8.5 kVA | 13.8 kVA | |
|---|---|---|
| Resistance of windings HV/LV (293 K) | 6.36 Ω/ 3.1 Ω | 2.9 Ω/ 0.57 Ω |
| Resistance of windings HV/LV (77 K) | 0.055 aΩ/ 0.027 aΩ | 0.0466 aΩ/ 0.0097 aΩ |
| Resistance of the HV/LV winding after transition to a resistive state (77 K) | 27 μΩ/ 13 μΩ | 23 μΩ/ 5 μΩ |
| Winding inductance HV/LV | 1.7 mH/ 0.4 mH | 290 μH/ 18 μH |
| Winding cross-sectional area HV | 0.0138 m2 | 0.0244 m2 |
| Length of the winding wires HV/LV | 55 m/ 27 m | 68 m/ 28 m |
| Power Source | Supply Line | Shunt | Transformer | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| LZ | RZ | EZ | fZ | LL | RL | Rb | 8.5 kVA | 13.8 kVA | ||
| RFe | Xμ | RFe | Xμ | |||||||
| 128 mH | 1.5 Ω | 230 V | 50 Hz | 0 | 11 mΩ | 1 mΩ | 960 Ω | 71 Ω | 1104 Ω | 224 Ω |
| Pulse no. | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 8.5 kVA | I (A) (Measurement) | 178 | 81.8 | 51.9 | 36.3 |
| I (A) (Calculations) | 178.2 | 79.3 | 50.2 | 36.1 | |
| δ, % (Error) | −0.1 | 3.2 | 3.4 | 0.6 | |
| 13.8 kVA | I (A) (Measurement) | 257.3 | 80.7 | 56.8 | 45.96 |
| I (A) (Calculations) | 260.7 | 87.4 | 57.0 | 41.0 | |
| δ, % (Error) | −1.3 | −7.7 | −0.4 | 12.1 |
| Pulse no. | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 8.5 kVA | γ, ° (Measurement) | 117.6 | 77 | 62,1 | 56.8 |
| γ, ° (Calculations) | 148 | 92.4 | 73.4 | 62 | |
| δ, % (Error) | −20.5 | −16.7 | −15.4 | −8.4 | |
| 13.8 kVA | γ, ° (Measurement) | 156.5 | 88.2 | 80.7 | 76.5 |
| γ, ° (Calculations) | 144.6 | 81.1 | 73.8 | 69.8 | |
| δ, % (Error) | 8.2 | 8.8 | 9.3 | 9.6 |
| Pulse no. | 1–2 | 2–3 | 3–4 | 4–5 | |
|---|---|---|---|---|---|
| 8.5 kVA | ε, ° (Measurement) | 272.9 | 291.9 | 297.2 | 313.9 |
| ε, ° (Calculations) | 247.6 | 278.2 | 292.8 | 302.4 | |
| δ, % (Error) | 10.2 | 4.9 | 1.5 | 3.8 | |
| 13.8 kVA | ε, ° (Measurement) | 255.3 | 80.2 | 56.5 | 45.2 |
| ε, ° (Calculations) | 260.7 | 78 | 58.9 | 49.2 | |
| δ, % (Error) | −2.1 | 2.8 | −4.1 | −8.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Komarzyniec, G. Calculating the Inrush Current of Superconducting Transformers. Energies 2021, 14, 6714. https://doi.org/10.3390/en14206714
Komarzyniec G. Calculating the Inrush Current of Superconducting Transformers. Energies. 2021; 14(20):6714. https://doi.org/10.3390/en14206714
Chicago/Turabian StyleKomarzyniec, Grzegorz. 2021. "Calculating the Inrush Current of Superconducting Transformers" Energies 14, no. 20: 6714. https://doi.org/10.3390/en14206714
APA StyleKomarzyniec, G. (2021). Calculating the Inrush Current of Superconducting Transformers. Energies, 14(20), 6714. https://doi.org/10.3390/en14206714





