Abstract
This paper addresses the problem of grasped object weight compensation in the one-handed manipulation of impedance controlled robots. In an exemplary identification procedure, the weight of an object and its centre of mass together with gripper kinematic configuration are identified. The procedure is based on the measurements from a 6-axis force/torque sensor mounted near the gripper. The proposed method reduces trajectory tracking errors coming from the model imprecision without compromising the main advantages of impedance control. The whole approach is applied according to the embodied agent paradigm and verified on the two-arm service robot both in simulation and on hardware. Due to the general description that follows system engineering standards, the method can be easily modified or applied to similar systems.
1. Introduction
Service robots have become more advanced, but there is still much to accomplish if one compares their abilities with those of humans. An example of a very significant service robot application is the manipulation of a grasped object, which is a typical task for everyday human life. Object manipulation is well known in robotics, even for robots equipped with many effectors [1]. In general, this assignment is preceded by grasping an object. It is worth noticing that a good deal of recent research works concerns this issue, in particular, in grasp planning [2] and learning [3]. The kinematic and dynamic properties of a manipulator’s kinematic chain change when an object is grasped. This should be taken into account during the manipulator’s controller development. Typically, for stiff position control in the manipulator’s joints, the integral part of the position controller deals with the change in plant properties caused by object grasping. The modern approaches to service robots’ control lead to changes in that paradigm.
Although it was previously introduced, position-force control is still being improved [4,5]; most promising seems to be VSA (variable stiffness actuators), e.g., [6], or impedance control, especially in the case of a robot’s end-effector contact with the environment and transition from contact-free motion to contact phase [7,8]. Such types of control are biologically inspired [9]. The compliance and damping are substantial to keep the system stable while the manipulator is in contact with the environment and transitions from contact-free motion to contact with obstacles. The main advantage of impedance control that addresses the current economic and ecological demands is its susceptibility to energy consumption optimisation [10], as, in its nature, the constraining of torques exerted in the joints prevails over the exact trajectory tracking. Impedance control algorithms are based on the computed torque method and are sensitive to the inaccuracy of a robot’s model. If a robot control law ignores the inertial properties of a grasped object, then presumably, undesirable position errors of the robot’s joints or end-effectors may be large. These errors should not be eliminated by applying integral action. Impedance control has no integrals by definition since, with an integral, a contact force would increase, and this goes against the essence of impedance control. Instead, the accuracy of the model parameters should be improved and the control should rely on the compliance [11], which is inherent in impedance control.
Our goal was to propose a model and its parameters identification procedure for a gripper and grasped object that can be effectively analysed and integrated into the control system of impedance controlled robots. To achieve this, the problem analysis and system description fulfil the system engineering standards and are based on SysML [12,13] and its application to cyber–physical systems modelling, i.e., EARL [14] version 1.2 [15]. EARL was recently used to develop systems described in, for example, [16,17]. It is based on the embodied agent theory [18] applied for different systems, especially robotics systems with varying structure [19], or with harmonised tasks [20] as well as to describe and analyse general cyber–physical structures [21] or motion control systems based on artificial intelligence methods [22]. The exemplary identification procedure takes into account the kinematic configuration of the gripper without the need for the gripper model. It addresses this model’s lack because it can be unavailable for the grippers with, for example, specific and customised structures.
The remaining part of the article is organised as follows. Section 2 starts from control system use-case analyses. Then, control system structure and behaviour descriptions are presented, emphasising impedance control laws in operational and joint space and their extension that includes object weight compensation and gripper kinematic configuration. The convenient procedure for the grasping model parameter identification is presented in Section 3. Then, Section 4 describes the experiments performed with Velma https://www.robotyka.ia.pw.edu.pl/robots/velma accessed on 10 October 2021, a custom-built two-arm service robot. Finally, Section 5 summarises the work.
2. Control System
A robot with a grasped object is modelled as an open kinematic-chain mechanism with n rigid joints. This work presents the method of adjusting the EARL based robot model so that the object’s parameters are included in the robot control law. Additionally, the experiment results connected with gravity compensation are preferred to be similar to the control without any object grasped.
The control system development and analysis starts with general use cases (Figure 1).
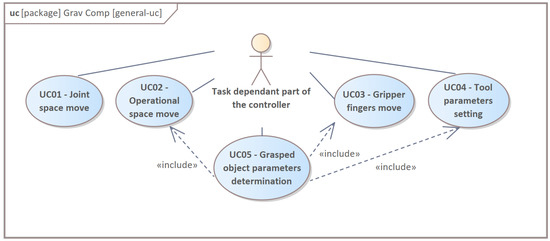
Figure 1.
System general use cases.
The variety of applications demands two modes of impedance control [23] (UC01, UC02), gripper fingers control (UC03) and tool parameters setting (UC04), and finally, the identification of the grasped object parameters (UC05), which is the main contribution of this work.
The above requirements can be satisfied with the control system of the general structure depicted in Figure 2.
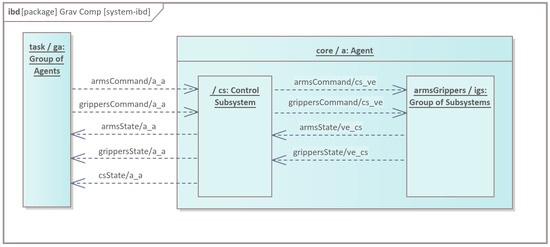
Figure 2.
System general structure.
The system consists of two main parts:
- task/ga: Group of Agents with the specific task implemented.
- core/a: Agent that realizes the core behaviours that are demanded from the point of view of the wide range of applications formulated in task/ga.
Agent core/a provides communications channels for the Group of Agents task/ga. Robot arms (UC01, 02, 04, 05) and grippers (UC03, 05) are controlled through separate channels to ease controller reconfiguration with the changes of hardware (e.g., change of gripper type). In the opposite direction, core/a informs about the arms’ state, gripper state and control subsystem core/a.cs state, which includes wrist wrench measurements. The other part of core/a is the group of subsystems armsGrippers/igs responsible for low-level control and sensor data acquisition from all effectors and receptors.
The use cases depicted in Figure 1 are allocated by primitive transition functions of Agent core/a (Figure 3).
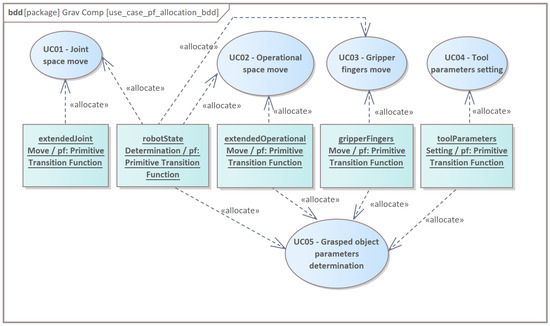
Figure 3.
Use case allocation in primitive transition functions of core/a.cs.
Those primitive transition functions should be associated with basic behaviours that will use them. It is enough to distinguish two basic behaviours as it is presented in Figure 4.
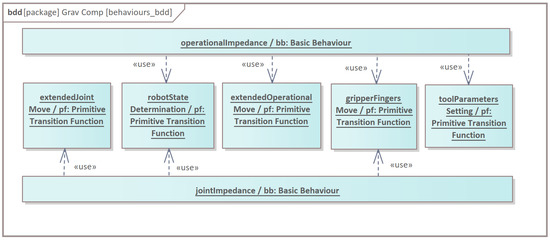
Figure 4.
Basic behaviours relation to primitive transition functions in core/a.cs.
In EARL, the basic behaviours are associated with the finite state machine, which states the general behaviour of the subsystem (Figure 5).
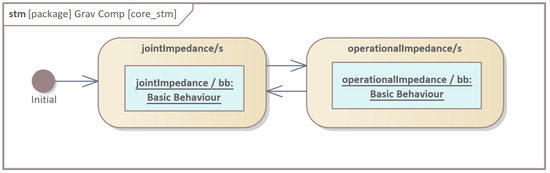
Figure 5.
Finite state machine core/a.cs.fsm.
In the following sections, the primitive transition functions core/a.cs.pf are presented, which relate to an impedance control. These functions are part of complex functions formulated to realize the joint space move Figure 6a (UC01) and operational space move Figure 6b (UC02).
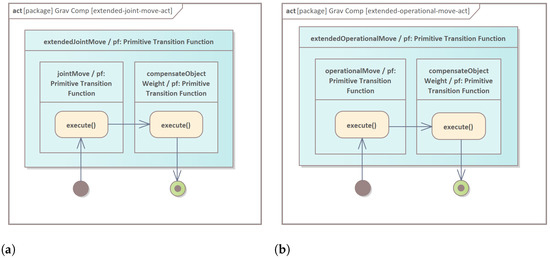
Figure 6.
Primitive transition functions core/a.cs.pf that relates an impedance control. (a) extendedJointMove/pf. (b) extendedOperationalMove/pf.
2.1. Primitive Transition Function core/a.cs.jointMove/pf
Impedance control law, both in joint and operational spaces, may be described in a hierarchical manner [24,25,26]. In joint space, it can be formulated according to [24] as Equation (1):
Herein and are the vectors of torques related to tasks and , respectively, where numbers in parentheses indicate the priority of tasks. Matrix denotes an null space projection as Equation (2):
where the matrices , are constructed, using the continuous null space projection method [25]. The Jacobian inverses used in the calculations of can be dynamically consistent [27] or not. As stated in [28], is the number of contact point pairs, as the task with higher priority determines self-collision avoidance in Equation (3):
where represents a repulsive potential field according to [29], and it is in terms of the potential energy [28]. Matrix denotes a diagonal damping, and and denote the vectors of measured joint positions and velocities, respectively.
The task with lower priority concerns joint impedance control [23] and can be expressed as Equation (4):
where is a diagonal joint stiffness matrix, is a difference vector of the desired and measured joint positions, and is a joint damping matrix calculated using the double diagonalisation method [30].
2.2. Primitive Transition Function core/a.cs.operationalMove/pf
In operational space, the impedance control law can also be formulated hierarchically [24] as Equation (5):
where , , , and are the vectors of torques related to tasks , , where i stands for the priority of the task. Matrices , , and denote the null space projection.
Let be the number of robot’s arms, each of which has one effector. The task with the lowest priority is the Cartesian impedance control [23] shown as Equation (6):
where is a Jacobi matrix, is a diagonal Cartesian stiffness matrix, is a vector of virtual spring displacement between desired and actual positions, is a Cartesian damping matrix obtained from the double diagonalisation method [30], is a vector representing normalized damping along the main directions of the task frames, and is a vector of velocity. Each of the vectors , , , and has a block structure so that the first 6 coordinates concern the first effector, the next 6, the second effector, etc. Moreover, in each block of (analogously for , , and ) the first vector denotes positions that are supplemented by a vector part of a unit quaternion. Thus, the matrices , , and must also have the appropriate block structure.
The task with higher priority than the previous one is related to vector . This task determines joint limits avoidance [31] with additional damping applied according to the double diagonalisation method [30] with constant coefficients’ values in an auxiliary diagonal damping matrix . The null space projection matrix , which relates featured tasks, and , can be set as the identity matrix. Consequently, these tasks are treated with the same priority.
The task with the second-highest priority involves self-collision avoidance. Therefore, and may be calculated analogously to and , respectively. Finally, the task with the highest priority determines the wrist collision constraint [26]. This task is similar to the former one, except that it affects only the two joints on each effector that are most distant from the robot’s base. Indeed, the main distinction between or and or , respectively, is the lower number of contact point pairs [28] in the first task.
2.3. Primitive Transition Function core/a.cs.compensateObjectWeight/pf
The grasped object and gripper configuration gravitational term can be incorporated as a sum component into the equation for the robot with the grasped object. Therefore, the robot control law can be settled as Equation (7):
where a vector of desired torques is the sum of a vector of joint torques , calculated according to the joint or Cartesian impedance control law, and a vector of object gravity compensation torques . The origin of the approach from [32] is stated in [1], where robot systems are considered in terms of kinetic and potential energy.
Let i () be the index of the chosen robot’s joint. Then, the object weight compensation torque acting in joint i can be formulated as Equation (8):
In this equation, the skew-symmetric matrix (Equation (9))
is associated with the vector that denotes the object’s centre of mass position relative to joint i. The vector represents the object’s weight, and the unit vector defines the joint’s axis of rotation. The expression is a cross product of and , and it determines the vector of torque. Hence, the torque is a scalar product of and .
Equation (8) assumes that , , and are expressed in the same coordinate system. However, it is more convenient to express quantities and in a local Cartesian coordinate system , whereas should be rather expressed in the robot’s base Cartesian coordinate system (). The frame can be bound up with the link driven by the motor in joint i. Then, Equation (8) may be rewritten as Equation (10):
where and . Herein, is the rotation matrix used to transform quantities from to . The upper left index in the bracket, e.g., j of , indicates that the quantity is expressed in the coordinate system . Let m be the object’s mass, and g be the gravitational acceleration. Then, the force can be stated as Equation (11):
The minus sign in is the result of the assumption that the axis is directed upwards and therefore against the force of gravity.
3. The Identification Procedure of the Object’s Parameters
To apply weight compensation of the object, group of agents task/ga needs to estimate the grasped object’s weight and centre of mass position and command it to agent core/a. Each robot’s manipulator (effector) is equipped with a force/torque sensor mounted between the wrist and the gripper. It is also assumed that the grasped object is rigid, and it cannot move relative to the gripper. Furthermore, the wrench measured by the force/torque sensor is established as Equation (12):
where , , and denote components of the force in operational space, and , , and are components of the torque.
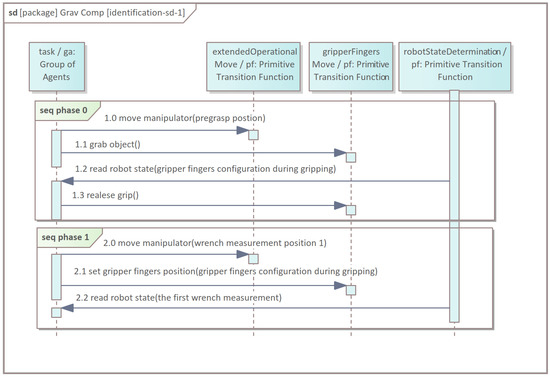
Figure 7.
Identification procedure of grasped object parameters, where primitive transition functions relate to core/a.cs.pf—phases 0 and 1.
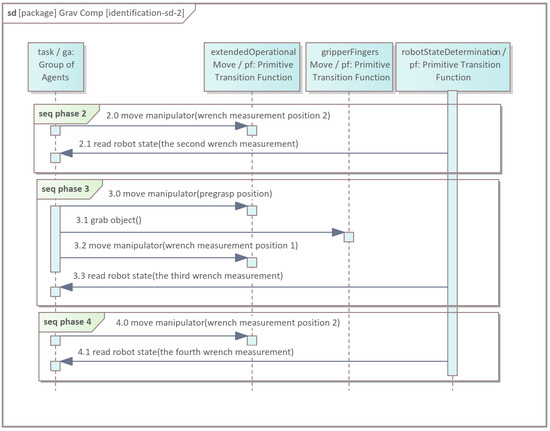
Figure 8.
Identification procedure of grasped object parameters, where primitive transition functions relate to core/a.cs.pf—phases 2, 3 and 4.
- 0.
- The selected manipulator changes the position of its gripper in order to check the grasp configuration of the gripper’s fingers (Figure 9b). When the gripper tightens on the object, the measurement of the gripper’s joint positions is taken. The grip is released.
 Figure 9. Graphical representation of the identification procedure: (a) the local coordinate frame , (b) checking the grasp configuration of the gripper’s fingers, (c–f) the wrench measurements (the numbers in upper left corners).
Figure 9. Graphical representation of the identification procedure: (a) the local coordinate frame , (b) checking the grasp configuration of the gripper’s fingers, (c–f) the wrench measurements (the numbers in upper left corners). - 1.
- The manipulator reaches the reference position for the first wrench measurement (Figure 9c). The gripper’s joint positions are set according to phase 0. The measurement is taken.
- 2.
- The gripper rotates around the axis x of the frame by , and the second reference measurement is taken (Figure 9d).
- 3.
- The manipulator grasps the object with its gripper and reaches the same position as in phase 1. The third measurement is taken (Figure 9e).
- 4.
- The arm reaches the same position as in phase 2, and the fourth measurement is taken (Figure 9f). Identification parameters can be computed and transmitted into agent core/a.
The local coordinate frame (Figure 9a) may be bound up with the manipulator’s wrist.
The object’s weight w can be obtained using the formula of Equation (13):
where the upper right index denotes the phase of the identification procedure when the measurement was made, and in the upper left indices is related to the coordinate frame . It should be noted that due to numerical conditions for the very small values of w, the procedure should stop here, and the compensation factors remain unchanged. Otherwise, the position of the object’s mass centre relative to the force/torque sensor can be computed with Equations (14)–(16):
where is the position vector that has the direction from the force/torque sensor to the object’s mass centre. For each joint i to obtain the quantity from Equation (10), the vector has to be transformed with the robot kinematic model.
4. The Verification of the Grasped Object Weight Compensation Algorithm
The approach was verified using the Velma service robot simulator [33], and then on the real robot, in both cases with a universal controller implemented within the FABRIC [34] software framework. As the use of domain-specific frameworks is a convenient approach [35], the FABRIC bases on ROS [36] and OROCOS [37]. The Velma robot has already been used in many research works described, e.g., in [2,23,26].
4.1. The Specific Realisation of Impedance Control Law for the Velma Service Robot
In the Velma robot impedance control law, only its two arms and torso are included, because other robot parts are controlled separately. Thus, the vector of desired torques from Equation (7) is represented as Equation (17):
In Equation (17), is the torso torque proportional to the current flowing through the motor Equation (18):
where is the proportionality factor. The torso controller is created using the technology presented in [38].
The vector from Equation (17) also consists of the right arm torque vector and the left arm torque vector . The arms of the Velma robot are 7-DOF redundant KUKA LWR4+ manipulators. Dynamic properties of these arms are supposed to be highly repeatable, but not identical [39]. However, the compensation algorithm described in Section 2.3 does not depend on the particular manipulator, so this issue does not affect the verification of the algorithm.
Impedance control is included in the calculation of the vector , which is specified by the KUKA Fast Research Interface (FRI) remote side. The vector denotes the manipulator’s dynamic model and is computed internally by the KUKA controller. The commanded torque vector is denoted as . For the Velma robot, the vector is specified by the robot’s research controller and is identical with or , depending on which manipulator is considered.
It should be noted that there are joints and arms (effectors) in the Velma robot control; hence, in Equation (5), the task with the highest priority is treated as two separate tasks, for the right and left arms.
4.2. Exemplary Results of Experiments
A test task concerned object manipulation. In simulation, the main aim was to move the object from one table to another with one of the Velma robot’s arms. For the purpose of the presentation, the right manipulator was chosen, but a similar outcome would be obtained with the left arm. The task was divided into three subsequent stages:
- The robot performed the identification procedure (Section 3, Figure 10a–e, starting from the convenient configuration (Figure 10a). According to phase 0 of the procedure, the robot checked the grasp configuration of the fingers of its right gripper (Figure 10b). Then, the robot took two reference wrench measurements (Figure 10c), and after that, it grasped the object (Figure 10d). Ultimately, the robot took two last wrench measurements (Figure 10e), and thanks to this, the desired parameters could be computed.
 Figure 10. The partial illustration of the test task in simulation: (a–e) stage 1, (f–g) stage 2, (h) stage 3.
Figure 10. The partial illustration of the test task in simulation: (a–e) stage 1, (f–g) stage 2, (h) stage 3. - The robot executed a sequence of the movements in Cartesian impedance control mode with linear interpolation (analogous to that described in [23]) between points (vertices) of a square (Figure 10f,g and Figure 11) lying in the plane perpendicular to the x-axis of the global coordinate system (Figure 10a).
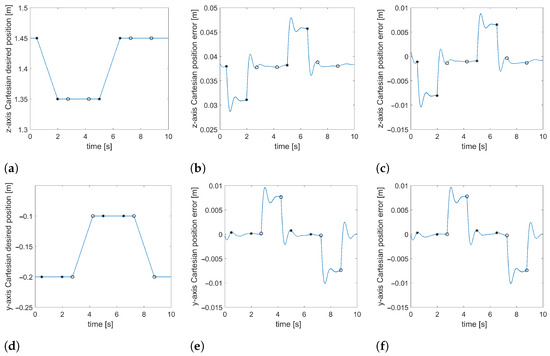 Figure 11. Experiments in simulation. The plots from control in Cartesian impedance mode with the grasped 2 kg object: (a,d) the Cartesian desired positions, (b,e) the errors with no compensation, (c,f) the errors with object weight compensation. The upper and lower rows concern the z-axis and y-axis, respectively.
Figure 11. Experiments in simulation. The plots from control in Cartesian impedance mode with the grasped 2 kg object: (a,d) the Cartesian desired positions, (b,e) the errors with no compensation, (c,f) the errors with object weight compensation. The upper and lower rows concern the z-axis and y-axis, respectively. - The robot put away the object on the other table (Figure 10h).
The test task was repeated two times for a 2 kg object. The first time, the object’s weight was not compensated, so the vector from Equation (7) was arbitrarily set to zero, and there was no necessity to perform stage 1 of the task. The second time (https://vimeo.com/567801853, accessed on 10 October 2021), the vector was computed in every control cycle, according to the compensation algorithm from Section 2.3, including the identified object’s parameters (Section 3). The computed weight Equation (13) was N, and the mass centre position vector Equations (14)–(16) was m. Hence, for , the computed object’s mass was .
Let and be the values of stiffness from the diagonal Cartesian stiffness matrix Equation (6), specified as Equation (20):
which are related to the right arm and concern components of the force and torque, respectively (analogously, and are related to the left arm). During the experiments, these values were set as and , except the identification procedure (Section 3), when they were stated to be higher, i.e., and for phases 1 and 2, and and for phases 3 and 4. Each element of the normalized damping vector Equation (6) was set to .
The selected results from stage 2 (Figure 10f,g) of the test task are presented in Figure 11. Only a part of the sequence of the movements is considered in reference to the z-axis and y-axis Cartesian desired positions (Figure 11a,d, respectively) of the right end-effector in the global coordinate frame (Figure 10a). During these movements, the x-axis Cartesian desired position was constant and equal to m.
In the first case (no compensation), the z-axis Cartesian position error (Figure 11b) between the desired and actual position was quite considerable, and it oscillated around a non-zero value. However, in the second case (with weight compensation), this error (Figure 11c) was smaller than previously, as it oscillated around zero and was comparable with the analogous one from experiments with a much lighter object (e.g., 100 times), where there was no need to utilize the mentioned compensation algorithm. In contrast to the z-axis error, the y-axis Cartesian position errors (Figure 11e,f) were almost identical in both cases because the described algorithm refers mainly to the z-axis static effects of the object’s dynamics.
After successful experiments in simulation, the experiments on the real robot (Figure 12) were performed.

Figure 12.
The partial illustration of the tests on the real robot—Velma: (a–c) stage 1, (d) stage 2.
The general test scenario was the same as in the simulation. The results were achieved for the number of test repetitions. The general nature of signals overlaps the simulation results and does not change through the subsequent test iterations (Figure 13).
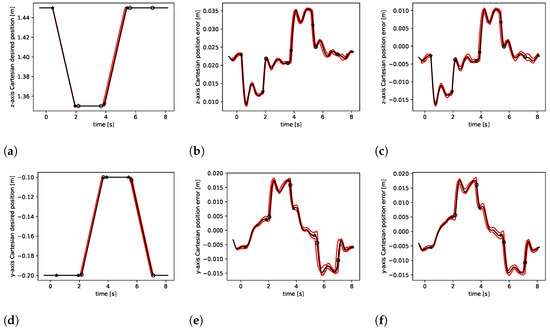
Figure 13.
Experiments on the real robot. The plots from control in Cartesian impedance mode with the grasped 2 kg object: (a,d) the Cartesian desired positions, (b,e) the errors with no compensation, (c,f) the errors with object weight compensation. The upper and lower rows concern the z-axis and y-axis, respectively. The black plot is the mean for 15 runs and red plots represent minimum and maximum values.
The differences between the results in the simulation and those of reality result primarily from force/torque measurement inaccuracies. The experimental hardware tests confirm the operation of the control system as it was intended (https://vimeo.com/618941465, accessed on 10 October 2021).
5. Conclusions
In an extensive survey [41], authors distinguish three categories of estimation methods of inertial parameters of objects: purely visual, exploratory and fixed object. As the example, authors of [42] investigate the usability of simulation data to learn manipulation tasks in an end-to-end manner with a model-free RL algorithm and train the robot controller, especially in the occurrence of an unknown object being manipulated. The works [43,44,45] consider a similar robotic platform as in our tests, but the artificial neural networks together with fuzzy logic are employed to control the robot hardware. Our exemplary approach can be assigned to fixed methods, such as that in [46,47] and evolved from [48]. It was chosen due to its accuracy, needed by impedance control and correspondence to applications, where the grasp is the indispensable part. Here, we concentrate on static error elimination, as it is one of the main problems of impedance control, where the dynamic errors in contact or free-motion are irrevocable. The verification experiments confirm that the proposed object weight compensation algorithm is correct and fulfils the expectations, as it enables to reduce the z-axis position error. Such errors can cause unexpected collisions and lead to task execution repetition or failure, even for impedance controlled manipulators. It could be especially undesirable in systems, such as autonomous robots [49], where both the energy and time to execute a task are constrained. It should be noted that the method relies on precise measurements of a wrench that, in general, is not trivial to achieve, due to the influence of end-effector inertial parameters both in static [48] and dynamic cases [50,51,52]. A survey of inertia parameter identification methods is presented in [53].
In the article, the compensation method was incorporated into the unique and versatile system with two different impedance control laws. Additionally, the exemplary mass centre parameters identification procedure addresses the problem of an unknown gripper’s model. It is convenient, due to the task-specific gripper customisations. The resultant integrated controller is the base for recent work with the Velma robot. We believe that the system description that fulfils the current system engineering standards and utilises contemporary domain-specific graphical languages will make it easier to apply the results in similar works performed by other researchers.
Author Contributions
Conceptualisation, T.W. and S.J.; methodology, T.W. and S.J.; software, S.J. and D.S.; validation, S.J.; formal analysis, T.W. and S.J.; investigation, T.W. and S.J.; resources, T.W. and D.S.; data curation, S.J.; writing—original draft preparation, T.W., S.J. and D.S.; writing—review and editing, T.W., S.J. and D.S.; visualisation, T.W. and S.J.; supervision, T.W.; project administration, T.W.; funding acquisition, T.W. and D.S. All authors have read and agreed to the published version of the manuscript.
Funding
Research was funded by the Centre for Priority Research Area Artificial Intelligence and Robotics of Warsaw University of Technology within the Excellence Initiative: Research University (IDUB) programme.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study in the collection, analyses or interpretation of data; in writing of the manuscript; or in the decision to publish the results.
References
- Khatib, O. Object Manipulation in a Multi-Effector Robot System. In Proceedings of the 4th International Symposium on Robotics, Santa Clara, CA, USA, 3–7 May 1998; MIT Press: Cambridge, MA, USA; pp. 137–144. [Google Scholar]
- Seredyński, D.; Winiarski, T.; Banachowicz, K.; Zieliński, C. Grasp planning taking into account the external wrenches acting on the grasped object. In Proceedings of the 10th International Workshop on Robot Motion and Control (RoMoCo), Poznań, Poland, 8–9 July 2015; pp. 40–45. [Google Scholar]
- Seredyński, D.; Szynkiewicz, W. Fast Grasp Learning for Novel Objects. Recent Advances in Automation, Robotics and Measuring Techniques. In Advances in Intelligent Systems and Computing (AISC); Springer: Berlin, Germany, 2016; Volume 440, pp. 681–692. [Google Scholar]
- Mazur, A.; Frontkiewicz, M.; Domski, W. Position-force control of nonholonomic mobile manipulator with simple holonomic constraint. In Proceedings of the 10th International Workshop on Robot Motion and Control (RoMoCo), Poznań, Poland, 6–8 July 2015; pp. 257–262. [Google Scholar]
- Winiarski, T.; Banachowicz, K.; Walęcki, M.; Bohren, J. Multibehavioral position–force manipulator controller. In Proceedings of the 21th IEEE International Conference on Methods and Models in Automation and Robotics, MMAR, Międzyzdroje, Poland, 29 August–1 September 2016; pp. 651–656. [Google Scholar]
- Kozakiewicz, B.; Winiarski, T. Spring based on flat permanent magnets: Design, analysis and use in variable stiffness actuator. Facta Univ. Ser. Mech. Eng. 2021. [Google Scholar] [CrossRef]
- Jezierski, E. Low cost impedance controller for robotic gripper drive with DC motor. In Proceedings of the 20th International Conference on Methods and Models in Automation and Robotics (MMAR), Międzyzdroje, Poland, 24–27 August 2015; pp. 806–811. [Google Scholar]
- Winiarski, T.; Banachowicz, K.; Seredyński, D. Multi-Sensory Feedback Control in Door Approaching and Opening; Intelligent Systems’2014; Springer International Publishing: New York, NY, USA, 2015; Volume 323, pp. 57–70. [Google Scholar]
- Pratt, G.A. Low Impedance Walking Robots. Integr. Comp. Biol. 2002, 42, 174–181. [Google Scholar] [CrossRef]
- Ghorbanpour, A.; Richter, H. An Overview of Energy-Optimal Impedance Control of Cooperative Robot Manipulators. arXiv 2021, arXiv:2106.07491. [Google Scholar]
- Ott, C.; Albu-Schäffer, A.; Kugi, A.; Hirzinger, G. On the Passivity-Based Impedance Control of Flexible Joint Robots. IEEE Trans. Robot. 2008, 24, 416–429. [Google Scholar] [CrossRef]
- Friedenthal, S.; Moore, A.; Steiner, R. A Practical Guide to SysML: The Systems Modeling Language, 3rd ed.; Morgan Kaufmann; Elsevier: Burlington, MA, USA, 2015. [Google Scholar]
- Open Management Group Systems Modeling Language-Version 1.6. 2019. Available online: https://www.omg.org/spec/SysML/1.6/PDF (accessed on 10 October 2021).
- Winiarski, T.; Węgierek, M.; Seredyński, D.; Dudek, W.; Banachowicz, K.; Zieliński, C. EARL–Embodied Agent-Based Robot Control Systems Modelling Language. Electronics 2020, 9, 379. [Google Scholar] [CrossRef]
- EARL—Embodied Agent-Based cybeR-Physical Control Systems Modelling Language-Version 1.2-Reference Manual. 2021. Available online: https://www.robotyka.ia.pw.edu.pl/papers/earl-1_2.pdf (accessed on 10 October 2021).
- Karwowski, J.; Dudek, W.; Węgierek, M.; Winiarski, T. HuBeRo-a Framework to Simulate Human Behaviour in Robot Research. J. Autom. Mob. Robot. Intell. Syst. 2021, 15, 31–38. [Google Scholar] [CrossRef]
- Winiarski, T.; Dudek, W.; Stefańczyk, M.; Łukasz, Z.; Giełdowski, D.; Seredyński, D. An intent-based approach for creating assistive robots’ control systems. arXiv 2020, arXiv:2005.12106. [Google Scholar]
- Kornuta, T.; Zieliński, C.; Winiarski, T. A universal architectural pattern and specification method for robot control system design. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 3–29. [Google Scholar] [CrossRef]
- Zieliński, C.; Stefańczyk, M.; Kornuta, T.; Figat, M.; Dudek, W.; Szynkiewicz, W.; Kasprzak, W.; Figat, J.; Szlenk, M.; Winiarski, T.; et al. Variable structure robot control systems: The RAPP approach. Robot. Auton. Syst. 2017, 94, 226–244. [Google Scholar] [CrossRef]
- Dudek, W.; Winiarski, T. Scheduling of a Robot’s Tasks With the TaskER Framework. IEEE Access 2020, 8, 161449–161471. [Google Scholar] [CrossRef]
- Kasprzak, W.; Szynkiewicz, W.; Stefańczyk, M.; Dudek, W.; Węgierek, M.; Seredyński, D.; Figat, M.; Zieliński, C. Agent-based approach to the design of a multimodal interface for cyber-security event visualisation control. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 1187–1205. [Google Scholar] [CrossRef]
- Dao, P.B. Learning Feedforward Control Using Multiagent Control Approach for Motion Control Systems. Energies 2021, 14, 420. [Google Scholar] [CrossRef]
- Winiarski, T.; Banachowicz, K.; Seredyński, D. Two mode impedance control of Velma service robot redundant arm. Progress in Automation, Robotics and Measuring Techniques. Vol. 2 Robotics. In Advances in Intelligent Systems and Computing (AISC); Springer: Berlin, Germany, 2015; Volume 351, pp. 319–328. [Google Scholar]
- Sentis, L.; Khatib, O. Synthesis of whole-body behaviors through hierarchical control of behavioral primitives. Int. J. Humanoid Robot. 2005, 2, 505–518. [Google Scholar] [CrossRef]
- Dietrich, A.; Albu-Schäffer, A.; Hirzinger, G. On continuous null space projections for torque-based, hierarchical, multi-objective manipulation. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), St. Paul, MN, USA, 14–19 May 2016; pp. 2978–2985. [Google Scholar]
- Seredyński, D.; Banachowicz, K.; Winiarski, T. Graph–based potential field for the end–effector control within the torque–based task hierarchy. In Proceedings of the 21th IEEE International Conference on Methods and Models in Automation and Robotics, MMAR, Międzyzdroje, Poland, 29 August–1 September 2016; pp. 645–650. [Google Scholar]
- Ratajczak, J.; Tchoń, K. On dynamically consistent Jacobian inverse for non-holonomic robotic systems. Arch. Control. Sci. 2017, 4, 555–573. [Google Scholar] [CrossRef][Green Version]
- Dietrich, A.; Wimböck, T.; Täubig, H.; Albu-Schäffer, A.; Hirzinger, G. Extensions to reactive self-collision avoidance for torque and position controlled humanoids. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3455–3462. [Google Scholar]
- Dietrich, A.; Wimböck, T.; Albu-Schäffer, A.; Hirzinger, G. Reactive Whole-Body Control: Dynamic Mobile Manipulation Using a Large Number of Actuated Degrees of Freedom. IEEE Robot. Autom. Mag. 2012, 19, 20–33. [Google Scholar] [CrossRef]
- Albu-Schäffer, A.; Ott, C.; Frese, U.; Hirzinger, G. Cartesian impedance control of redundant robots: Recent results with the DLR-light-weight-arms. In Proceedings of the IEEE International Conference on Robotics and Automation, Taipei, Taiwan, 14–19 September 2003; Volume 3, pp. 3704–3709. [Google Scholar]
- Winiarski, T.; Banachowicz, K. Opening a door with a redundant impedance controlled robot. In Proceedings of the 9th Workshop on Robot Motion & Control (RoMoCo), Kuślin, Poland, 3–5 July 2013; pp. 221–226. [Google Scholar]
- Mavrakis, N.; Ghalamzan, A.; Stolkin, R.; Baronti, L.; Kopicki, M.; Castellani, M. Analysis of the inertia and dynamics of grasped objects, for choosing optimal grasps to enable torque-efficient post-grasp manipulations. In Proceedings of the IEEE-RAS 16th International Conference on Humanoid Robots (Humanoids), Cancun, Mexico, 15–17 November 2016; pp. 171–178. [Google Scholar]
- Winiarski, T.; Sikora, J.; Seredyński, D.; Dudek, W. DAIMM Simulation Platform for Dual-Arm Impedance Controlled Mobile Manipulation. In Proceedings of the 7th International Conference on Automation, Robotics and Applications (ICARA), Prague, Czech Republic, 4–6 February 2021; pp. 180–184. [Google Scholar] [CrossRef]
- Seredyński, D.; Winiarski, T.; Zieliński, C. FABRIC: Framework for Agent-Based Robot Control Systems. In Proceedings of the 12th International Workshop on Robot Motion and Control (RoMoCo), Poznań, Poland, 8–10 July 2019; pp. 215–222. [Google Scholar]
- Piperidis, S.; Chrysomallis, I.; Georgakopoulos, S.; Ghionis, N.; Doitsidis, L.; Tsourveloudis, N. A ROS-Based Energy Management System for a Prototype Fuel Cell Hybrid Vehicle. Energies 2021, 14, 1964. [Google Scholar] [CrossRef]
- Quigley, M.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A.Y. ROS: An Open-Source Robot Operating System. In Proceedings of the ICRA Workshop on Open Source Software, Kobe, Japan, 12–17 May 2009; Volume 3.2. [Google Scholar]
- Bruyninckx, H. OROCOS: Design and implementation of a robot control software framework. In Proceedings of the IEEE International Conference on Robotics and Automation, Washington, DC, USA, 11–15 May 2002. [Google Scholar]
- Walęcki, M.; Banachowicz, K.; Winiarski, T. Research oriented motor controllers for robotic applications. In Robot Motion and Control 2011 (LNCiS) Lecture Notes in Control & Information Sciences; Springer Limited: London, UK, 2012; Volume 422, pp. 193–203. [Google Scholar]
- Woliński, Ł.; Wojtyra, M. Comparison of Dynamic Properties of Two KUKA Lightweight Robots. In ROMANSY 21-Robot Design, Dynamics and Control; Springer International Publishing: New York, NY, USA, 2016; pp. 413–420. [Google Scholar]
- Schreiber, G.; Stemmer, A.; Bischoff, R. The fast research interface for the kuka lightweight robot. In Proceedings of the IEEE Workshop on Innovative Robot Control Architectures for Demanding (Research) Applications How to Modify and Enhance Commercial Controllers (ICRA), Anchorage, AK, USA, 3–7 May 2010; pp. 15–21. [Google Scholar]
- Mavrakis, N.; Stolkin, R. Estimation and exploitation of objects’ inertial parameters in robotic grasping and manipulation: A survey. Robot. Auton. Syst. 2020, 124, 103374. [Google Scholar] [CrossRef]
- Shahid, A.A.; Roveda, L.; Piga, D.; Braghin, F. Learning continuous control actions for robotic grasping with reinforcement learning. In Proceedings of the 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Toronto, ON, Canada, 11–14 October 2020; pp. 4066–4072. [Google Scholar]
- Roveda, L.; Haghshenas, S.; Caimmi, M.; Pedrocchi, N.; Molinari Tosatti, L. Assisting operators in heavy industrial tasks: On the design of an optimized cooperative impedance fuzzy-controller with embedded safety rules. Front. Robot. AI 2019, 6, 75. [Google Scholar] [CrossRef]
- Roveda, L.; Haghshenas, S.; Prini, A.; Dinon, T.; Pedrocchi, N.; Braghin, F.; Tosatti, L.M. Fuzzy impedance control for enhancing capabilities of humans in onerous tasks execution. In Proceedings of the 2018 15th International Conference on Ubiquitous Robots (UR), Honolulu, HI, USA, 26–30 June 2018; pp. 406–411. [Google Scholar]
- Roveda, L.; Maskani, J.; Franceschi, P.; Abdi, A.; Braghin, F.; Tosatti, L.M.; Pedrocchi, N. Model-based reinforcement learning variable impedance control for human-robot collaboration. J. Intell. Robot. Syst. 2020, 100, 417–433. [Google Scholar] [CrossRef]
- Swevers, J.; Verdonck, W.; Naumer, B.; Pieters, S.; Biber, E. An experimental robot load identification method for industrial application. Int. J. Robot. Res. 2002, 21, 701–712. [Google Scholar] [CrossRef]
- Kubus, D.; Kroger, T.; Wahl, F.M. On-line estimation of inertial parameters using a recursive total least-squares approach. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Nice, France, 22–26 September 2008; pp. 3845–3852. [Google Scholar]
- Zieliński, C.; Winiarski, T. Motion Generation in the MRROC++ Robot Programming Framework. Int. J. Robot. Res. 2010, 29, 386–413. [Google Scholar] [CrossRef]
- Yang, K.; Li, Y.; Zhou, L.; Rong, X. Energy Efficient Foot Trajectory of Trot Motion for Hydraulic Quadruped Robot. Energies 2019, 12, 2514. [Google Scholar] [CrossRef]
- Kubus, D.; Wahl, F. Scaling and eliminating non-contact forces and torques to improve bilateral teleoperation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), St. Louis, MI, USA, 11–15 October 2009; pp. 5133–5139. [Google Scholar]
- Garcia, J.; Ortega, J.; García, A.; Martínez, S. Robotic software architecture for multisensor fusion system. IEEE Trans. Ind. Electron. 2009, 56, 766–777. [Google Scholar] [CrossRef]
- Winiarski, T.; Woźniak, A. Indirect force control development procedure. Robotica 2013, 31, 465–478. [Google Scholar] [CrossRef]
- Schedlinski, C.; Link, M. A survey of current inertia parameter identification methods. Mech. Syst. Signal Process. 2001, 15, 189–211. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).