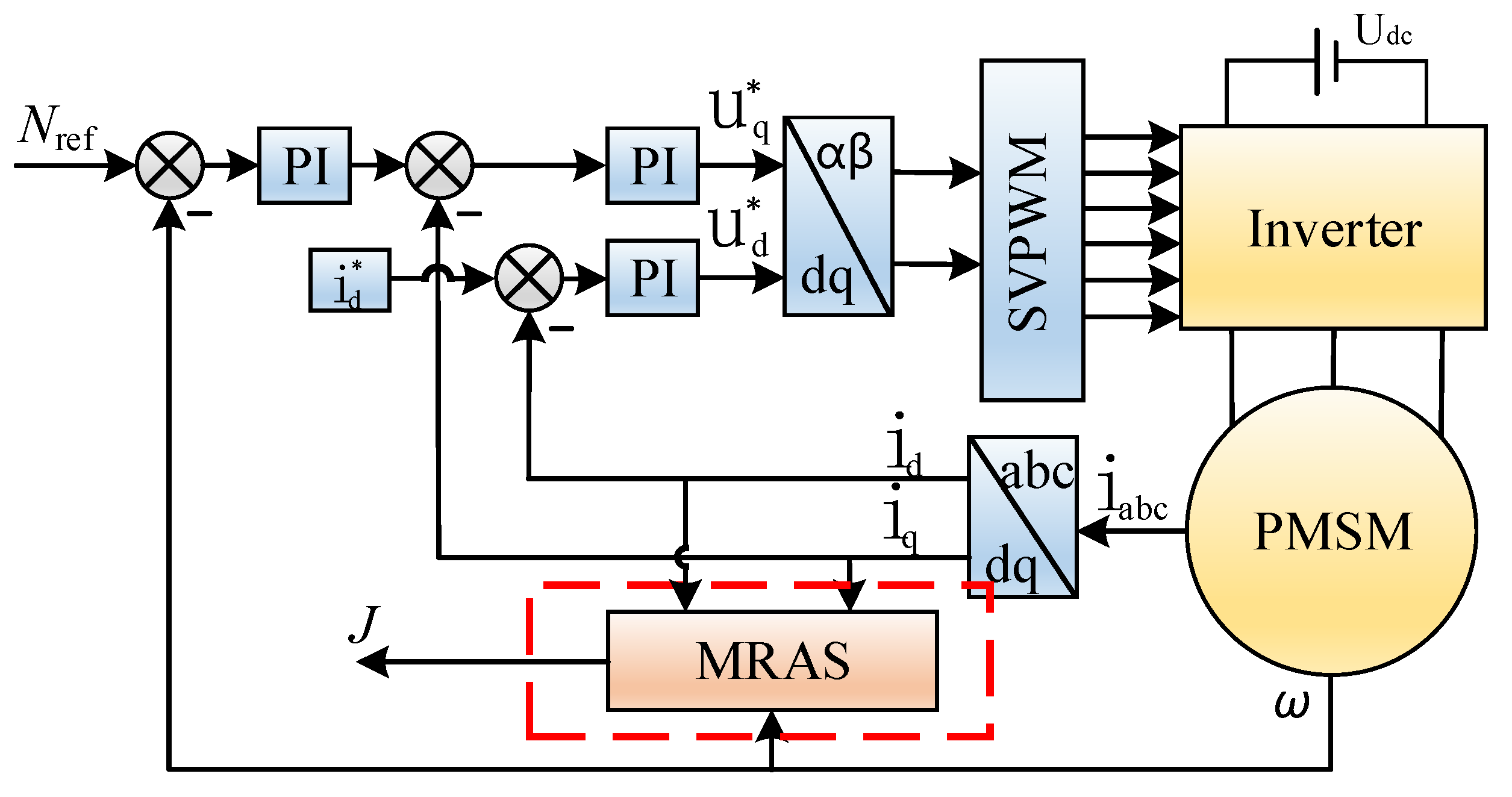
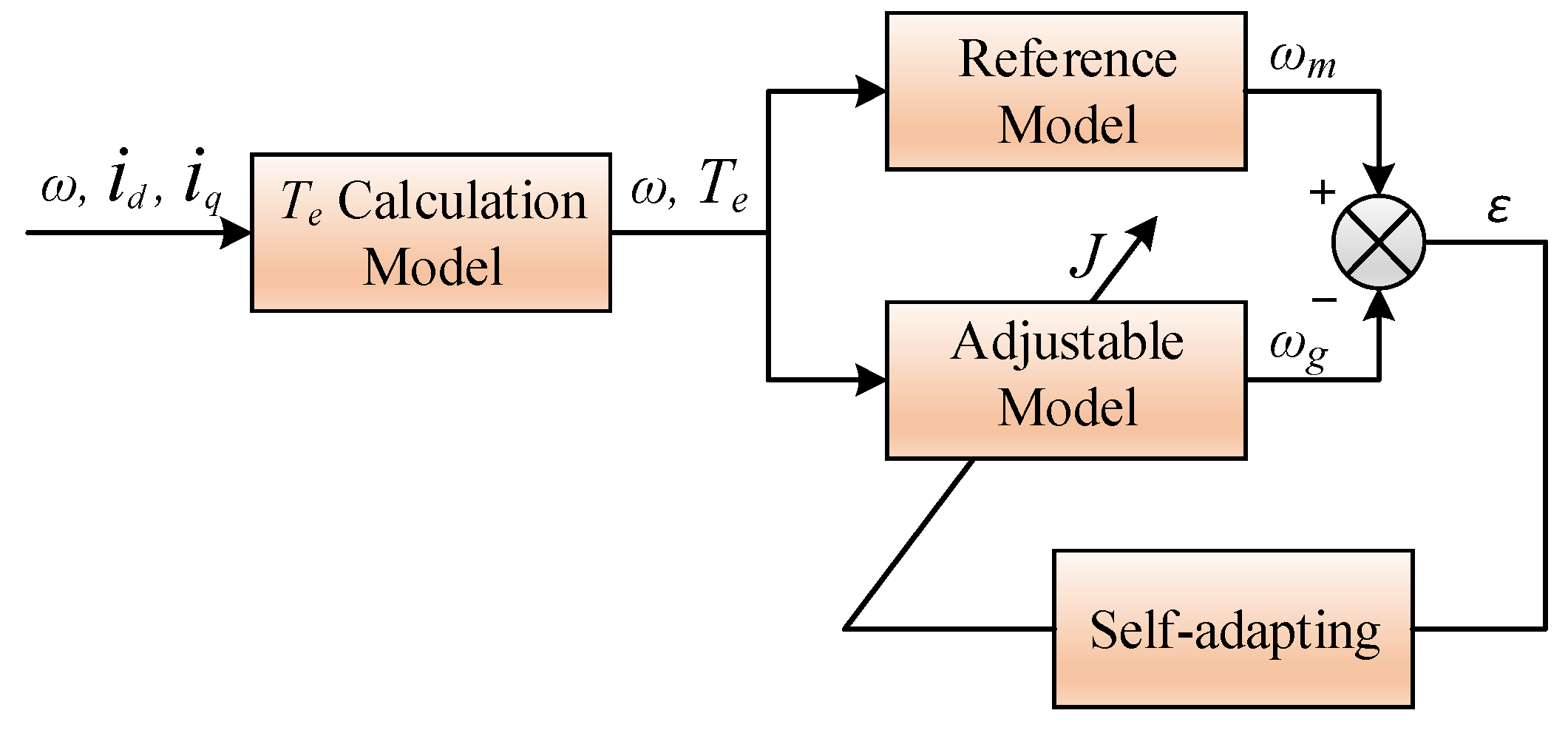
4.1. Construction of the Experimental Platform
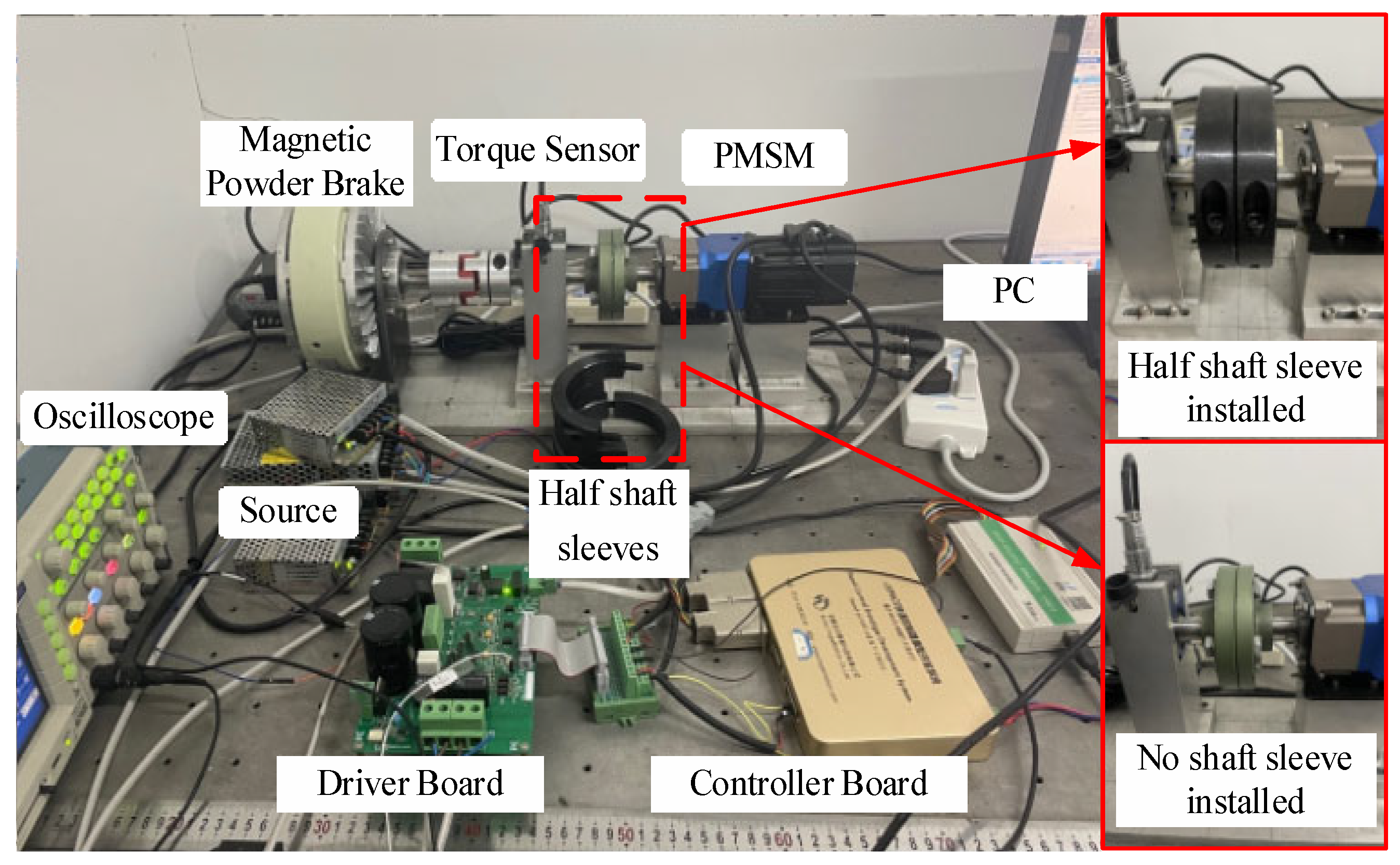
In order to verify the identification effect of the EGF-MRAS algorithm used in this paper, a PMSM control platform with an adjustable moment of inertia was built to identify the moment of inertia. The encoder is used to collect the motor speed. The adjustment of the PMSM moment of inertia is achieved by adding stainless-steel half shaft sleeves. The off-line algorithm has the characteristics of a high identification accuracy, and the off-line algorithm acceleration and deceleration method is introduced here. This method is used to measure the new moment of inertia of the motor after the stainless-steel half shaft sleeves is installed. The result can be used as the basis for judging the accuracy of the identification result.
The experiment uses one AC synchronous servo motor, several stainless-steel half shaft sleeves, 2500PPR incremental encoder, CSPACE, and the motor drive circuit board. CSPACE is a fast control prototype based on TMS320F28335DSP. It has AD, DA, IO, Encoder, PWM, and other simulation functions. After the control algorithm has been designed in MATLAB/Simulink, the DSP code can be generated and the corresponding control signals can be generated.
Figure 8 is the photo of the experimental platform.
Table 5 shows the motor parameters for the experiment.
A set of simple experiments is used to verify the feasibility of the acceleration and deceleration algorithm. Moment of inertia of the experimental motor
. The offline algorithm identification results are organized in
Table 6.
The data in
Table 7 are calculated using Equation (16):
The error between the calculated result of and the actual value is less than 0.5%. The accuracy of this offline algorithm is proven. The standard values of the moments of inertia at each level after the addition of each group of the stainless-steel half shaft sleeves are calculated as the standard for the subsequent online identification experiment results.
Magnetic powder brakes are used to generate load torque.
The 2500CPR incremental encoder is used to calculate the speed of the motor. The encoder adopts a grating structure. The grating disc rotates synchronously with the motor shaft, with a loop of 4 × 2500 pulses. So, the calculation formula of speed is as follows:
Among (17), is the actual speed of the motor in rpm. T is the sampling period. is the number of encoder pulses collected at time k. In the experiment process, the set value of the speed loop can be modified by the computer in real time.
4.3. Experimental Results and Analysis
Experiment (i): Compare the EGF-MRAS algorithm (a) with the MRAS algorithm (b) under dynamic speed.
The standard value of the experimental motor’s moment of inertia is
. In order to facilitate the calculation of the moment of inertia, the speed jitter is not completely filtered out.
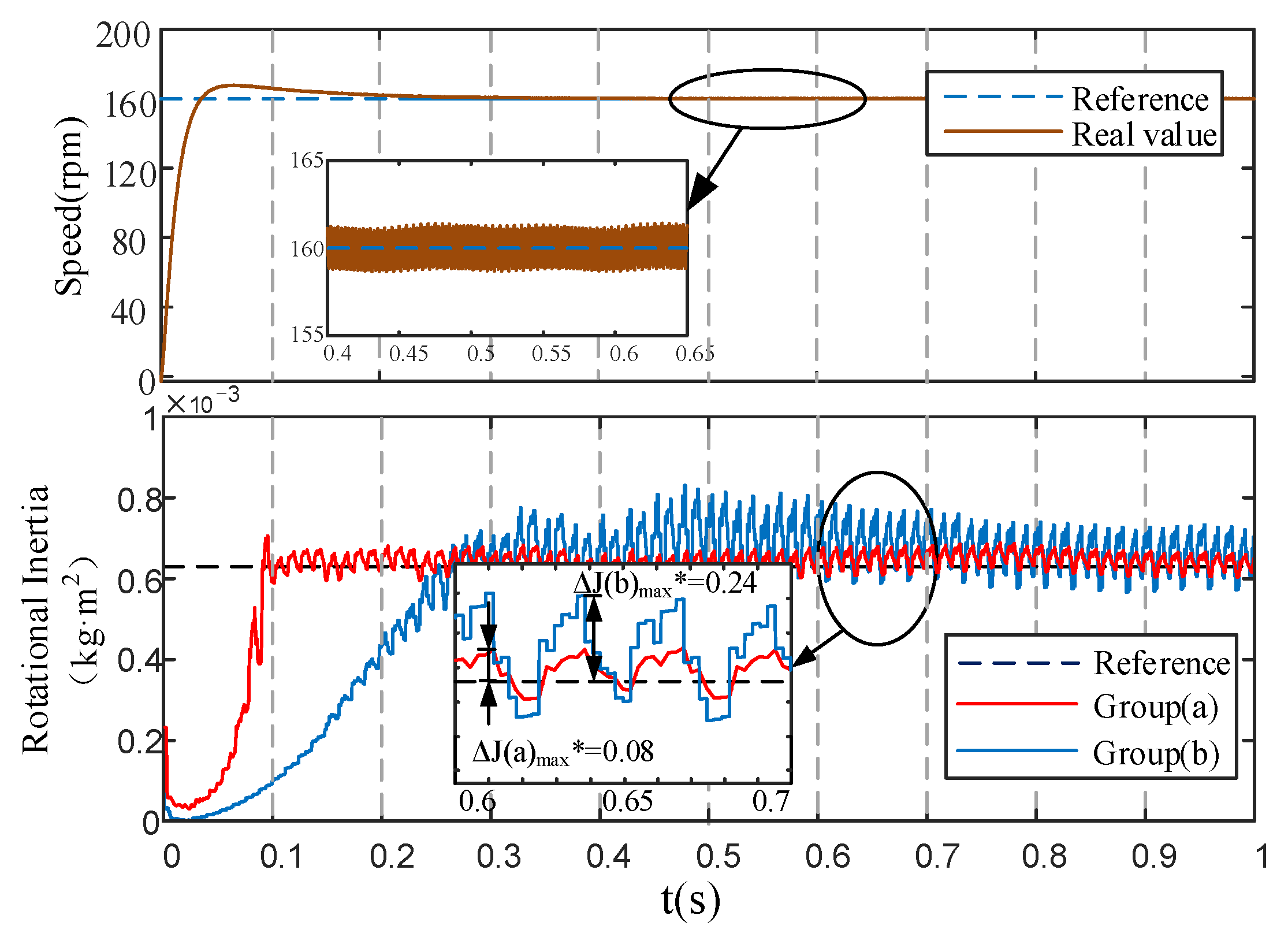
Figure 9 shows the identification results of the Algorithm (a) and Algorithm (b) experiments recorded from the start state of the motor. The calculation results of the accuracy parameters in
Figure 9 are recorded in
Table 9. In
Figure 9,
is defined.
From the experimental results in
Figure 9 and the calculation results in
Table 9, it can be seen that the overshoots of the two sets of experimental results are almost equal. However, a comparison of the calculation results of
and
shows that EGF-MRAS algorithm is 6.9% higher than MRAS algorithm in terms of stability. The EGF-MRAS algorithm is 60.8% higher than MRAS algorithm in terms of identification speed. The starting stage of the motor is about 0.1 s. At the end of the starting stage the motor runs relatively smoothly, and the EGF-MRAS algorithm can quickly and accurately calculate the moment of inertia. So, EGF-MRAS algorithm has better stability and speed.
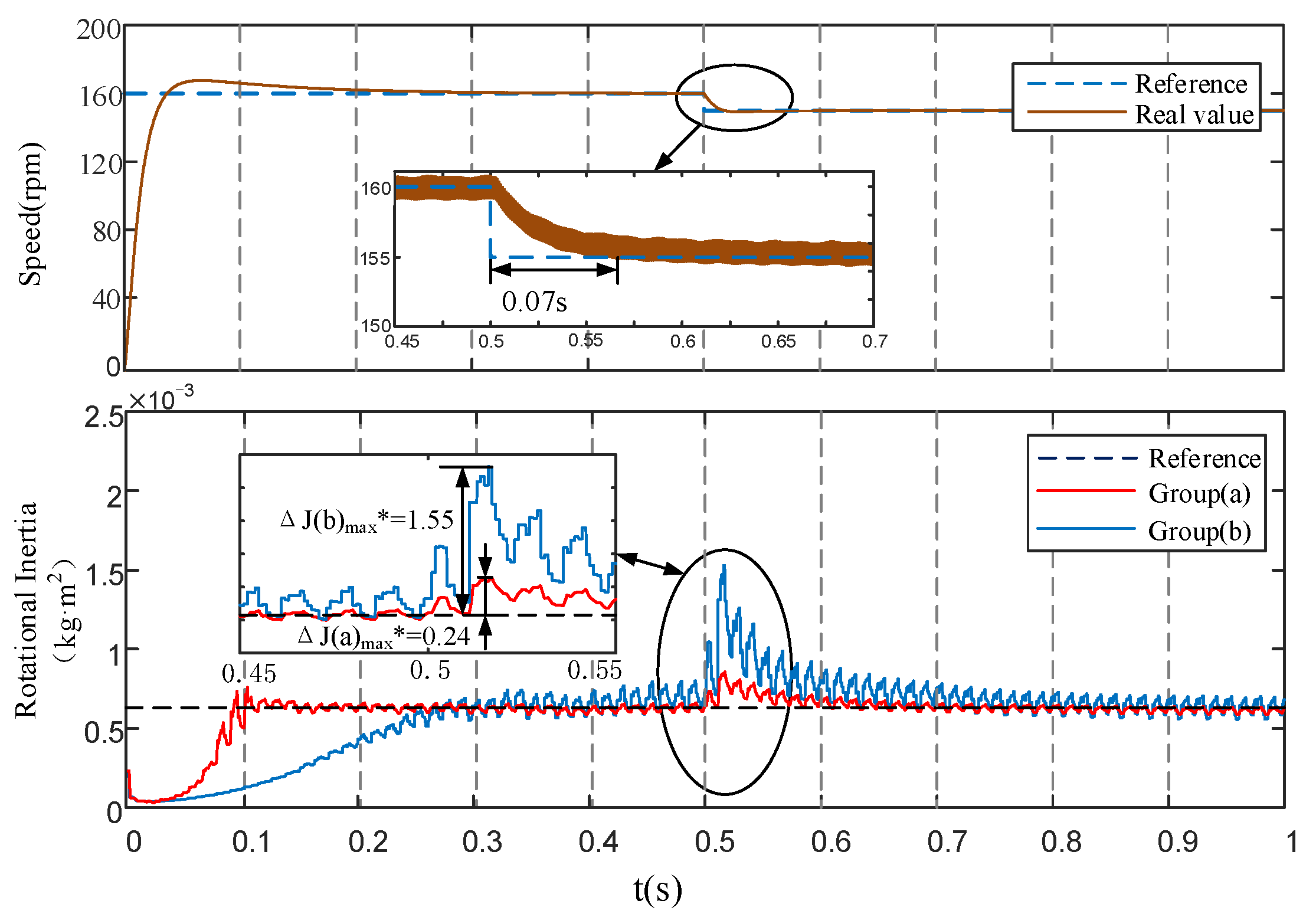
The most common fluctuation in the actual servo system is the speed disturbance. Therefore, the experiment of rotational speed disturbance was carried out. Under the condition of keeping the moment of inertia unchanged, experiments were carried out on the appearance of rotation speed disturbance, and the results are shown in
Figure 10.
From the experimental results in
Figure 10 and the calculation results in
Table 10, it can be seen that MRAS algorithm is greatly affected by speed fluctuations.The overshoot of the EGF-MRAS algorithm is significantly lower than that of the MRAS algorithm. This means that the EGF-MRAS algorithm effectively suppresses the influence of the speed interference on the overshoot of the moment of the inertia identification result.
Experiment (ii): Compare the EGF-MRAS algorithm (a) with the error integrator adaptive algorithm (c) under dynamic speed.
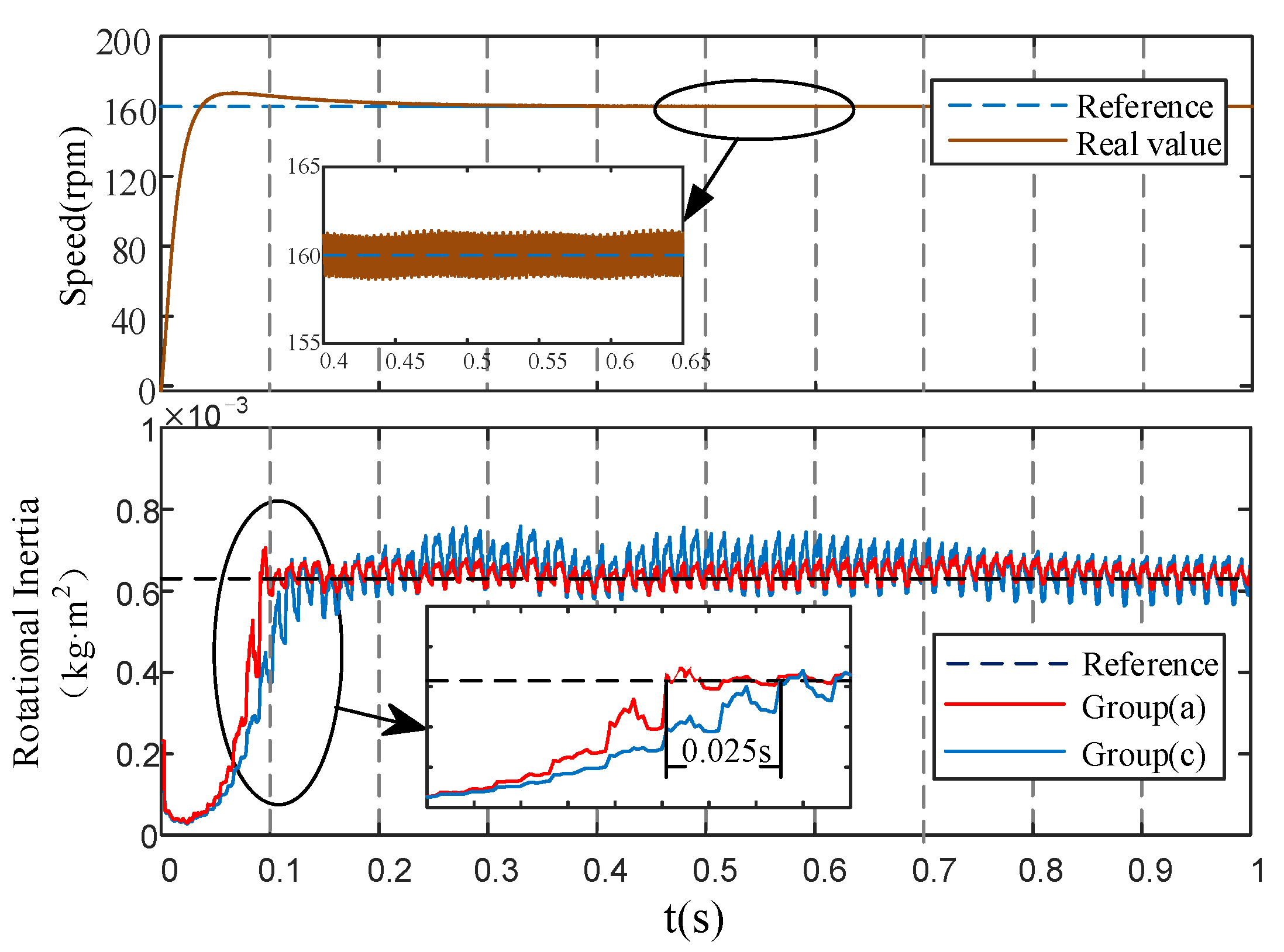
The experimental results from the start state to the steady state of the motor are recorded in
Figure 11.
From the experimental results in
Figure 11 and the calculation results in
Table 11, it can be seen that the overshoot of Algorithm (c) is slightly higher than Algorithm (a), which is about 2% higher. Algorithm (a) is 27.8% faster than that of Algorithm (c) in terms of the identification speed. Algorithm (a) is also 8.4% higher in stability than Algorithm (c). The comparison of the accuracy parameters
,
, and
shows that the dynamic performance of the EGF-MRAS algorithm is better than that of the difference integrator algorithm.
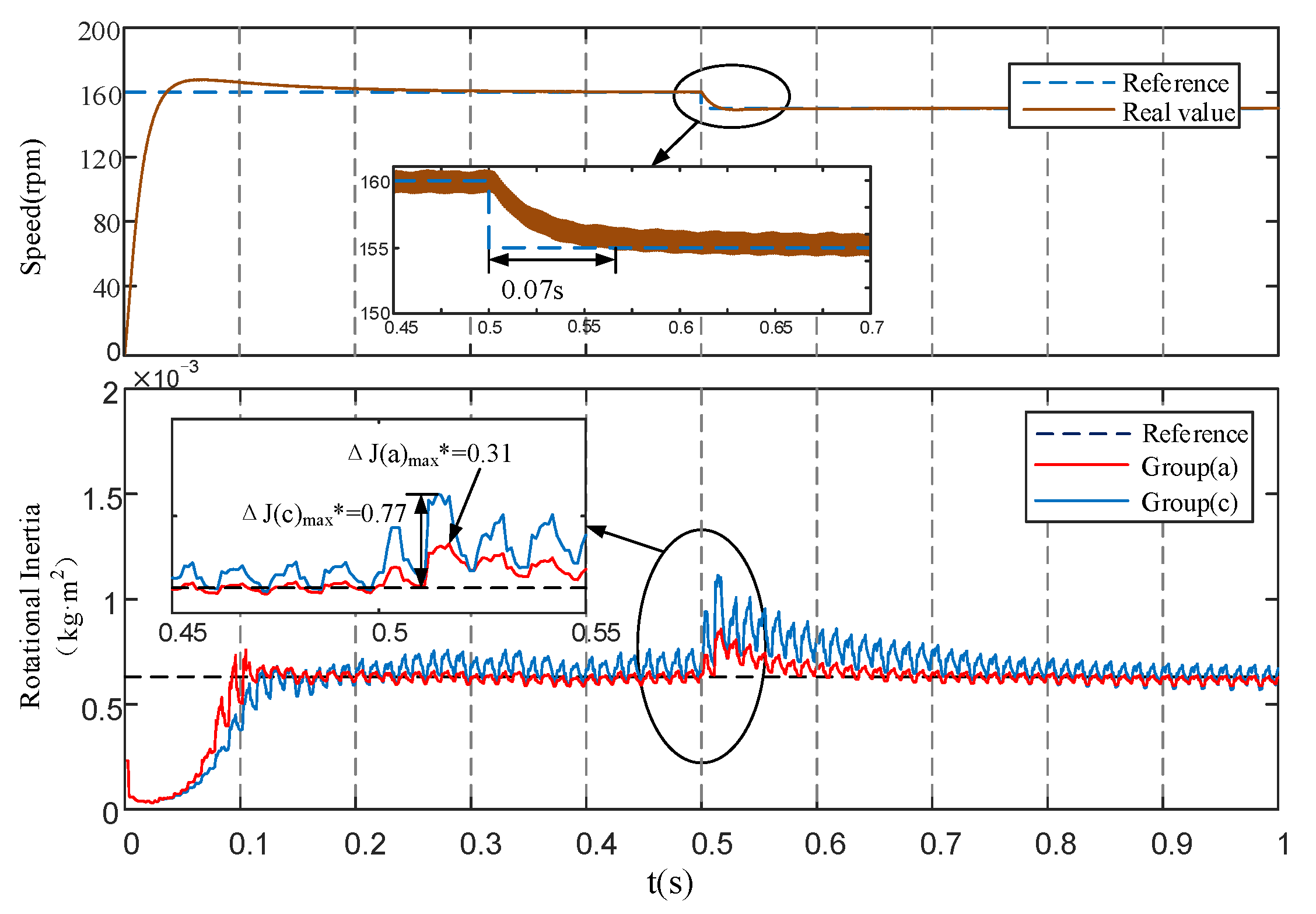
Figure 12 shows the experimental results of the appearance of the rotation speed interference while keeping the moment of inertia unchanged, and compares and analyzes the identification effect of the moment of inertia.
It can be seen from the experimental results that Algorithm (c) suppresses the interference caused by the speed disturbance to some extent, which is 33.9% higher than the algorithm (b) in Experiment (i). However, the suppression effect of Algorithm (a) is much better. Algorithm (a) is 46.3% higher than Algorithm (b) according to the accuracy parameters in
Table 10 and
Table 12. Therefore, among the three groups of algorithms, the EGF-MRAS algorithm has the strongest anti-interference performance.
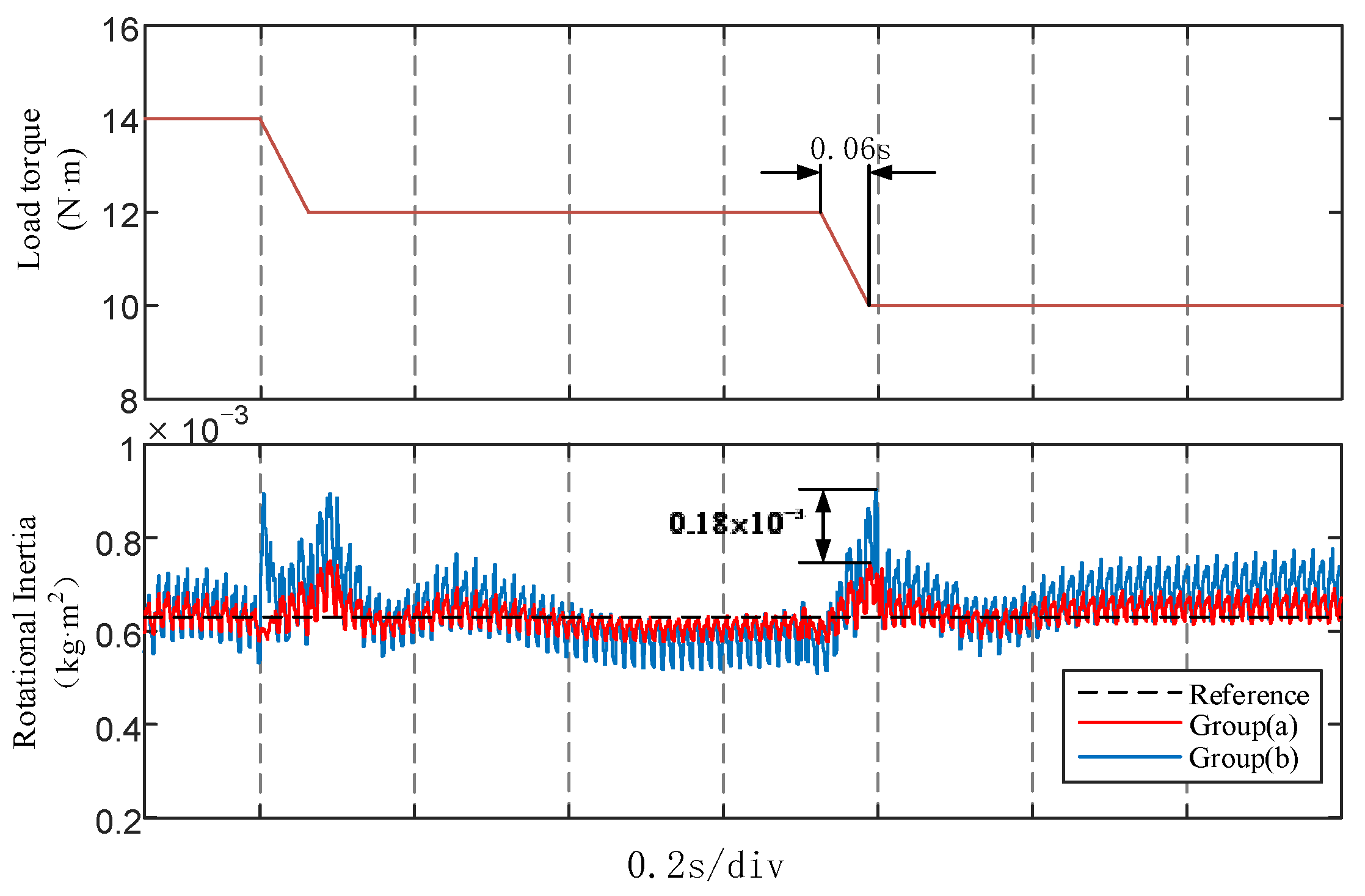
Experiment (iii): Verification experiment under dynamic load torque.
After the motor runs to steady state, the load torque is changed through the magnetic particle brake connected to the rotating shaft.
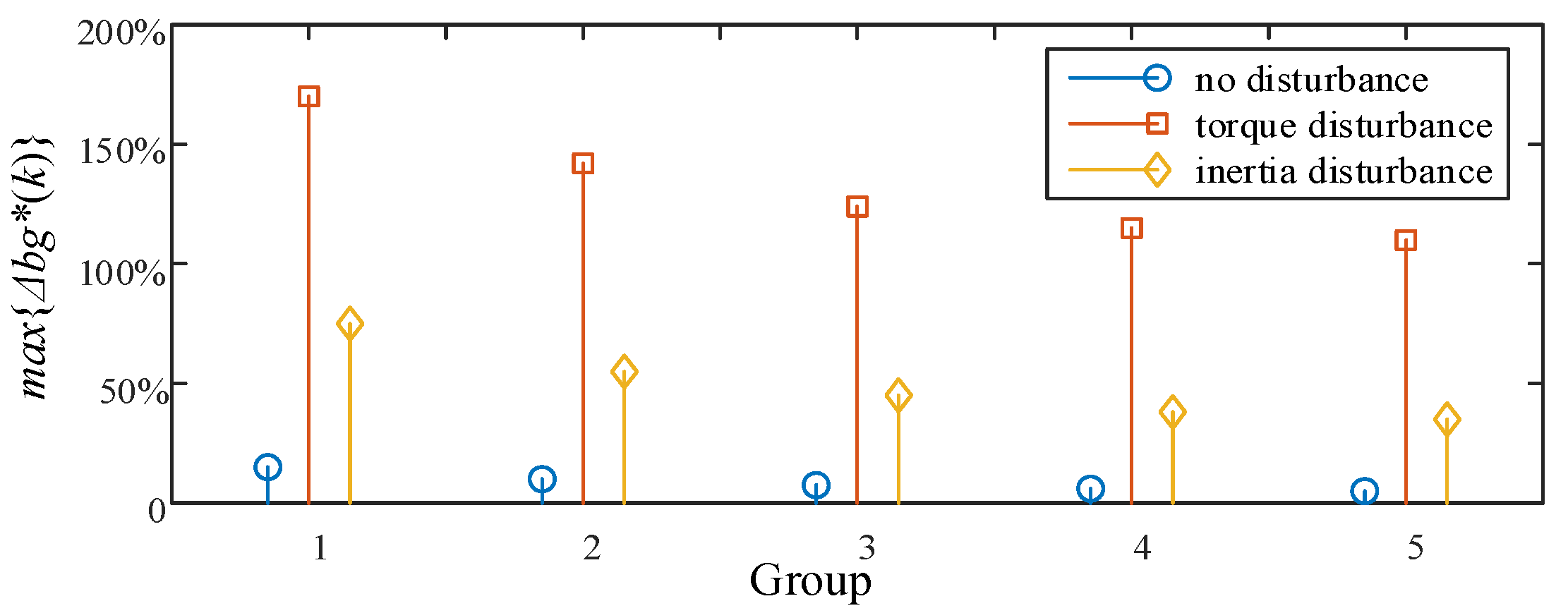
Figure 13 shows the identification results under dynamic load torque. It can be seen from the experimental results that
18.3% and
50.8%. Algorithm (a) has less errors and a faster recovery speed than Algorithm (b) under dynamic load torque. The identification accuracy of Algorithm (a) is also higher when the load torque tends to be stable. Therefore, the EGF-MRAS algorithm has better stability than the traditional MRAS algorithm.
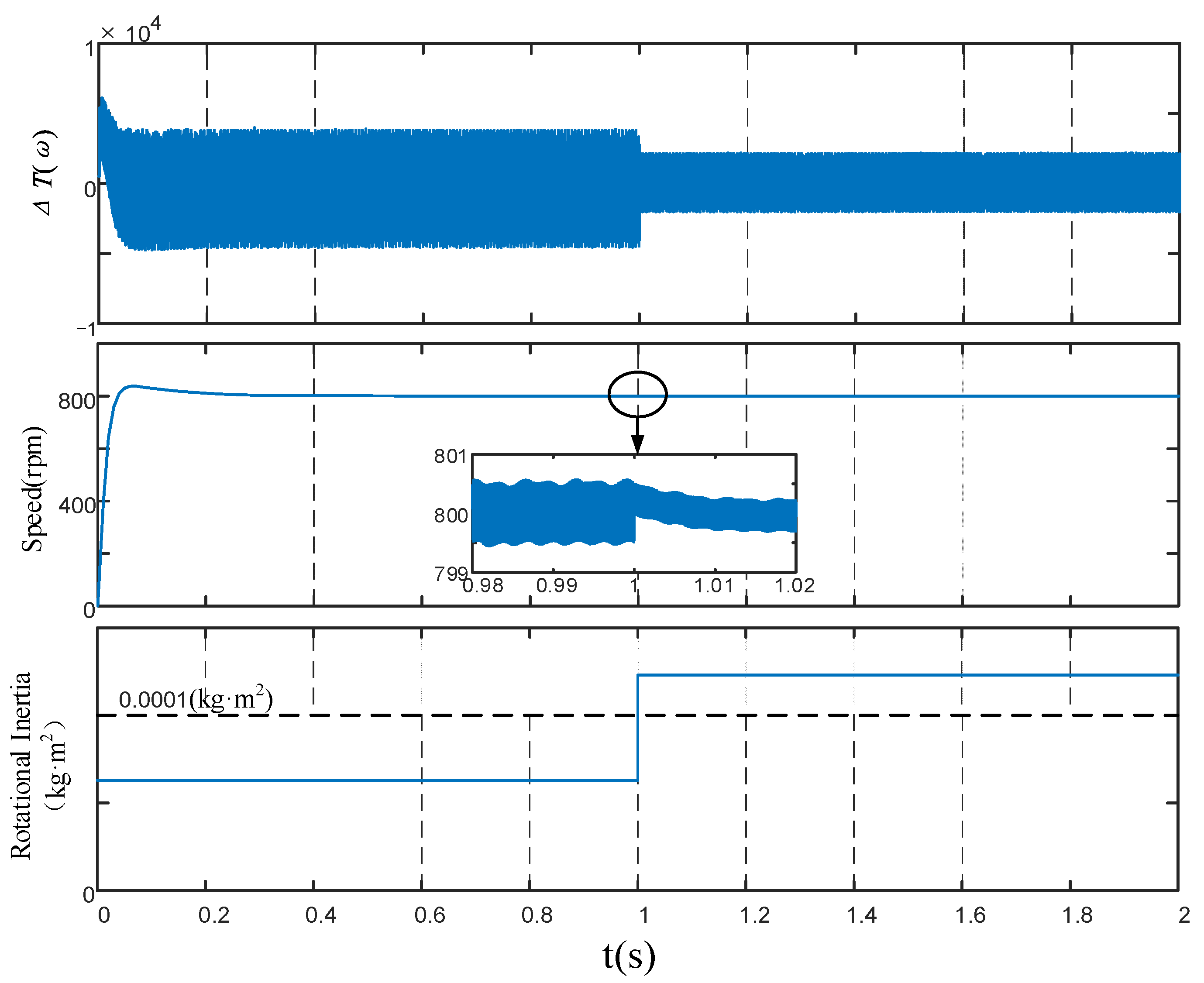
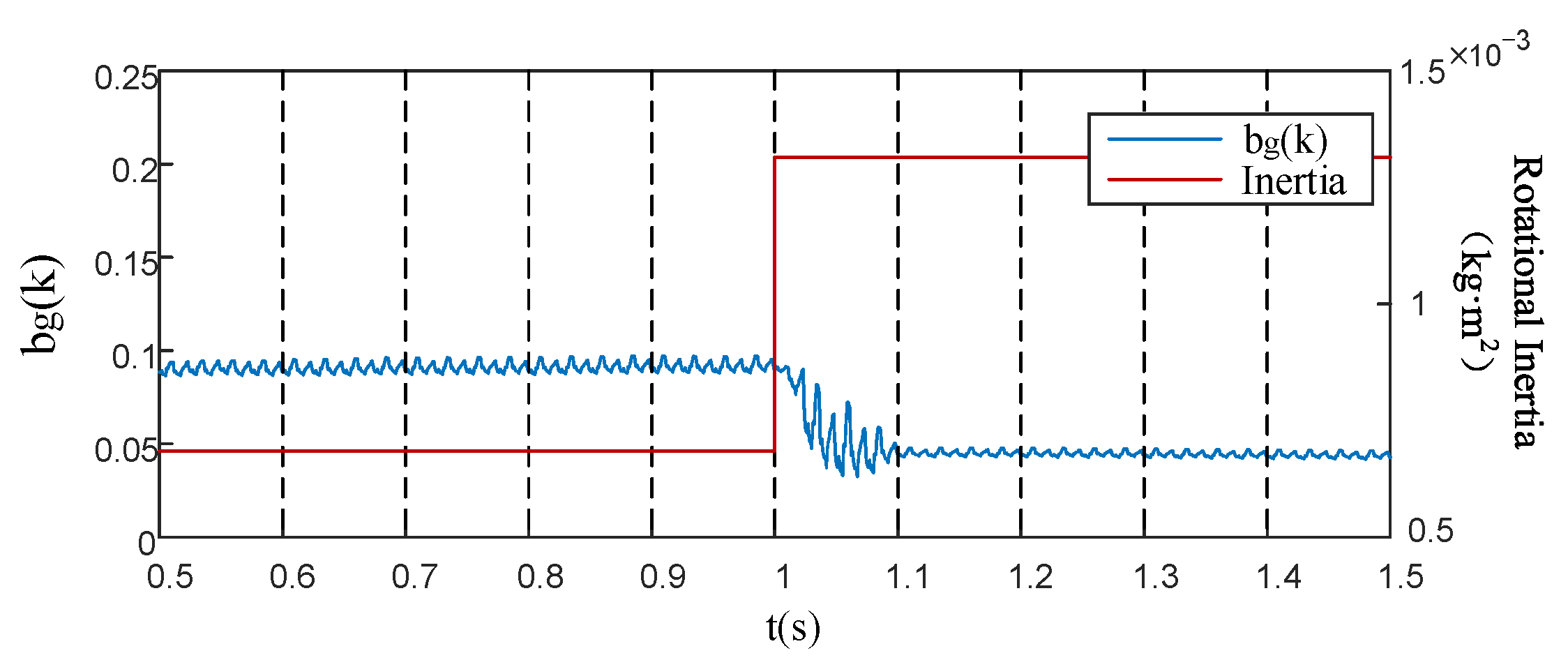
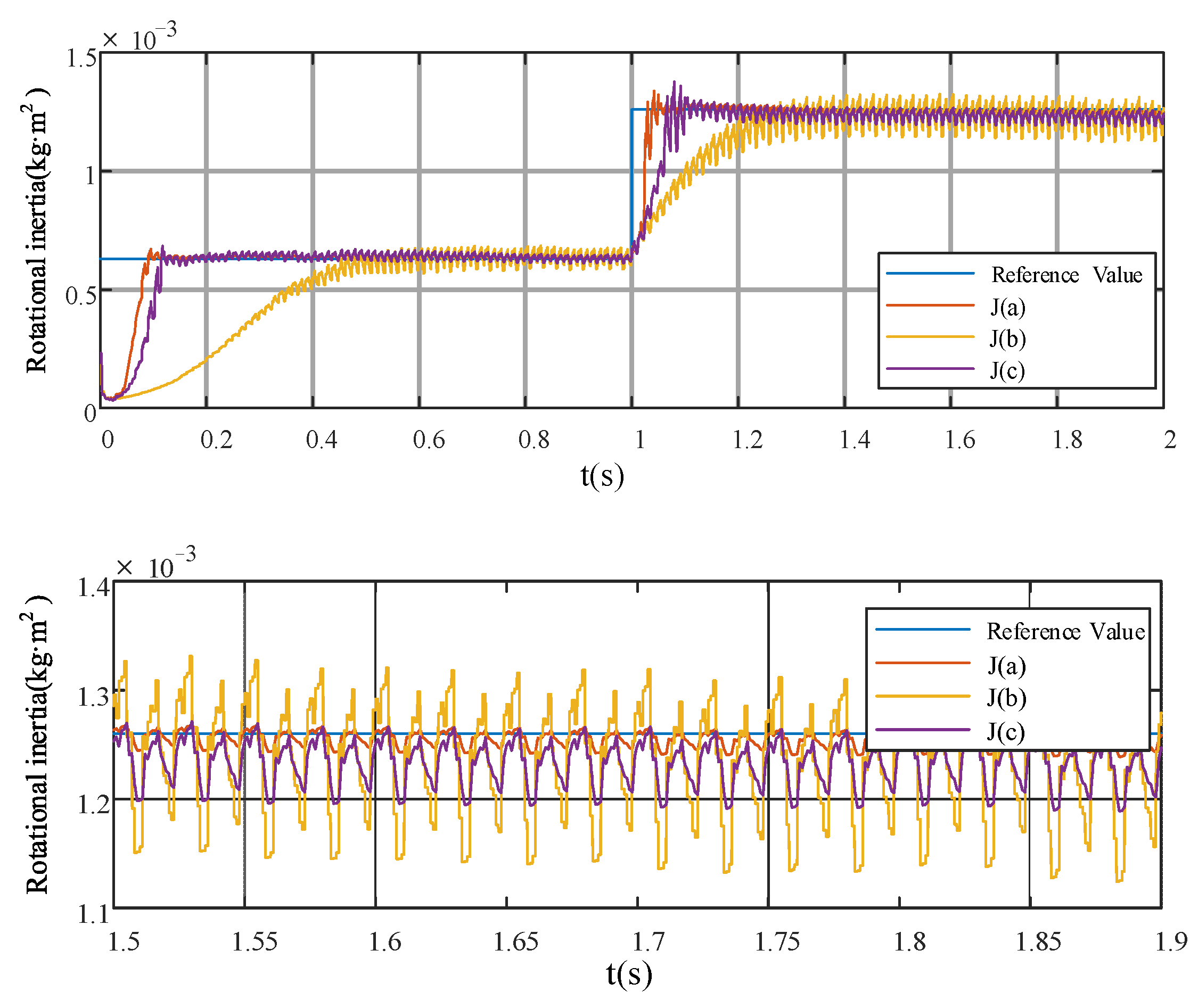
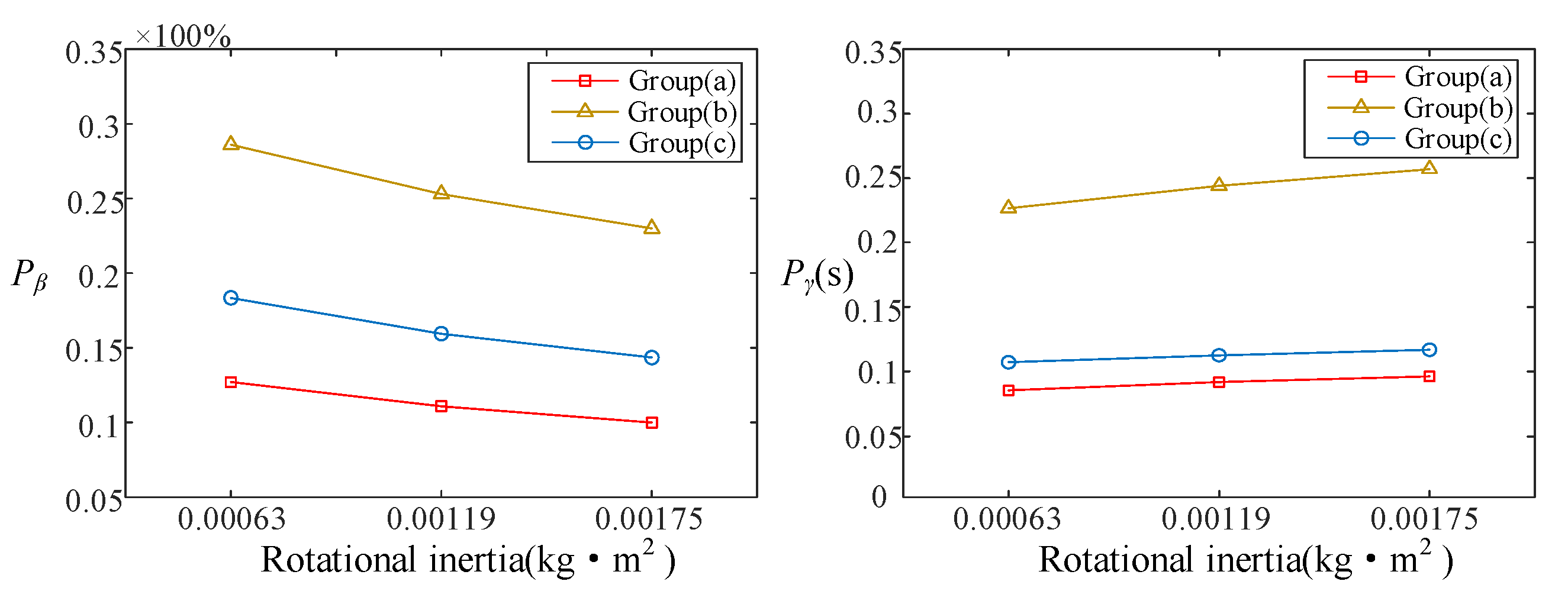
Experiment (iv): Verification experiment under different moment of inertia.
Figure 14 shows the calculation results of parameters
and
under three different moments of inertia. The three abscissa values in the figure represent the standard value of the moments of inertia after 0, 1, and 2 groups of half shaft sleeves are installed on the motor shaft. It shows
,
. In the process of increasing the moment of inertia, the relationship between the accuracy parameters of each algorithm remains unchanged. This proves that the EGF-MRAS algorithm has a better dynamic performance under different working conditions.