Efficient Local Path Planning Algorithm Using Artificial Potential Field Supported by Augmented Reality

Abstract

Mobile robots in industry are commonly used in warehouses and factories. To achieve the highest production rate, requirements for path planning algorithms have caused researchers to pay significant attention to this problem. The artificial potential field algorithm, which is a local path planning algorithm, has been previously modified to obtain higher smoothness of path, to solve the stagnation problem and to jump off the local minimum. The last itemized problem is taken into account in this paper—local minimum avoidance. Most of the modifications of artificial potential field algorithms focus on a mechanism to jump off a local minimum when robots stagnate. From the efficiency point of view, the mobile robot should bypass the local minimum instead of jumping off it. This paper proposes a novel artificial potential field supported by augmented reality to bypass the upcoming local minimum. The algorithm predicts the upcoming local minimum, and then the mobile robot’s perception is augmented to bypass it. The proposed method allows the generation of shorter paths compared with jumping-off techniques, due to lack of stagnation in a local minimum. This method was experimentally verified using a Husarion ROSbot 2.0 PRO mobile robot and Robot Operating System in a laboratory environment.

1. Introduction

In recent years, the path planning problem has been intensively researched due to manufacturing and warehouses robotization [1,2,3]. Numerous mobile robots, robotic arms and human workers in a single workspace lead to logistic problems, due to safety collision-free requirements [4,5]. Global path planning algorithms can provide the optimal collision-free path; however, in a complex environment, the computations to obtain the solution take much more time than the movement of the mobile robot [6]. Satisfactory results with much lower computation times can be obtained by sampling-based rapidly-exploring random tree (RRT) instead of linear search of trajectory points [7,8]. Another problem related to global path planning algorithms is the dynamic environment.

Change of obstacle positions can provide collisions due to the global path planning algorithm, giving the entire path as a result. Any change of environment causes the previous result to be potentially non-executable due to collisions. For these reasons, local path planning algorithms are still being intensively researched. The main difference between the global and local path planning algorithms is the required information about the environment: the global one involves information about the entire environment, while the local one requires information only about the mobile robot’s neighborhood. These algorithms require sensors, such as an RGBD camera, LiDAR, and Time of Flight (ToF), to obtain the necessary information. The application of such algorithms guarantees collision-free operation in a dynamic environment.

The artificial potential field (APF) algorithm is a local path planning algorithm that was proposed by Khatib in 1986 [9]. This method is based on the interaction of the electrostatic particles. The principle is that the goal point is pulling the mobile robot, while the obstacles are pushing. The value of the pushing or pulling force is inversely proportional to the distance between the obstacle or the goal. The basic form of APF algorithm is not immune to a local minimum, e.g., if the object is in line with the mobile robot and the goal, the robot will stagnate and never bypass the obstacle or reach the goal. Such a phenomenon is caused by attractive and repulsive forces with opposite directions and the same values—this is the local minimum. In this situation, the robot stagnates and requires additional actions to jump off the local minimum.

For this reason, the APF algorithm is intensively studied to increase the quality of the movement and reduce the stagnation in local minima. In [10], the APF algorithm was combined with improved black-hole potential field and reinforcement learning to solve the problems, which are scenarios of local minima. The feature of the algorithm is that mobile robots can jump out of local minima without prior knowledge. The concise and reliable path planning method for the autonomous underwater vehicle (AUV) based on the improved APF method was presented in [11]. The regular hexagon-guided method was proposed to improve the local minima problem.

In [12], local path planning of a mobile robot using a novel grid-based potential method was proposed. The generated repulsion field causes a mobile robot to escape from the local minimum. In [13], the adaptive repulsive field function, which improves the artificial potential field, was proposed. The algorithm uses the method of a rolling window to decompose the global path planning problem into the problem of finding local targets in the local window. This allows to solve the problem of local minima effectively. The combination of BUG and APF algorithms was proposed in [14]. In this approach, the ground quality indicator is responsible for detecting the local minimum, and it switches APF to BUG algorithm to jump of the low ground quality.

The potential field force was improved to enhance the stability and robustness of the collision-free path for AUV using the dynamic APF algorithm was proposed in [15]. It was proven that the proposed method can create robust, safe, and stable collision-free path in real time in different encounter scenes of the dynamic airspace, outperform the traditional APF in both safety and stability, and ensure the flyability of the collision-free path. In [16], a new predictive APF was proposed using time information and predictive potential to plan a smoother path. It successfully restricts the maximum turning angle, cuts short the sailing time, and intelligently avoids obstacles. The predictive APF can solve a concave local minimum problem.

Most of these algorithms extend the APF method to jump off a local minimum instead of preventing the robot from stagnating in it. The most important differences between these methods are the energetic efficiency, path length, and robot movement duration. The jump off of the local minimum can be divided into the following phases: (i) going in a local minimum, (ii) stagnation of the robot, and (iii) algorithm to jump off. In the case of preventing the robot from stagnating: (i) the prediction method of an incoming local minimum is required, as well as (ii) an algorithm to prevent the robot from going in it. Due to this, the second method provides a shorter and smoother path and lower power consumption by the motors.

To prevent a mobile robot from going into the local minimum, the additional, a virtual obstacle can be created to extend the mobile robot’s perception. Such an integration of virtual objects into a real-life environment in real-time is called Augmented Reality (AR) [17]. In recent years, AR has been successfully applied in many fields: medicine, military, manufacturing, gaming, visualization, robotics, marketing, tourism, education, path planning, and geospatial and civil engineering [18,19].

AR has been used to ease the programming of a robotic arm task, including trajectory specification, virtual previews of robot motion, visualization of robot parameters, and online reprogramming during simulation and execution [20]. The path planning visualization using AR for a drone was proposed in [21] to make robots more accessible to researchers outside of the technology field. In [22], an AR-based human–robot interaction method was developed with a novel closed loop structure to improve the system response time, compensation accuracy, and other characteristics in manufacturing environment and human–robot collaboration.

In this paper, the authors applied AR to local path planning algorithm for autonomous vehicles, in order to achieve a shorter and smoother path and lower power consumption by the motors. This paper proposes a novel APF supported by augmented reality (AR-APF) to detect an upcoming local minimum and generate a virtual wall to bypass it. Such an approach allows mobile robots to reduce the path length and is more efficient. To the authors’ best knowledge, this is the first time such a solution has been proposed and experimentally verified.

The paper is organized as follows. Section 2 describes the APF algorithm and its limitations. The proposed novel APF supported by augmented reality is presented in Section 3. In this section, the AR-APF is carefully described, including a flowchart and separate subsection for each part of the algorithm. Section 4 describes the laboratory environment and presents results obtained by experimental verification using a Husarion ROSbot 2.0 PRO mobile robot. Finally, Section 5 concludes the paper with a number of suggestions for further research.

2. Artificial Potential Fields Algorithm

One of the most well-known local path planning algorithms for mobile robots is artificial potential fields (APF). APF is based on the electrostatic particles interaction given by the following formula [14]:

$$F=-\frac{k{q}_1{q}_2}{r^2}$$

(1)

where k is the interactions constant, $q_1$ and $q_2$ are the electric charges of the particles, and r is the distance between the particles. In short, the identical particles’ charges push each other, while the opposite particles’ charges pull each other. Based on this information, the goal of a mobile robot has the opposite charge, while the obstacles have the same charge as the mobile robot. The APF algorithm uses the following formula for calculation direction and value of the robot’s movement:

$${\overrightarrow{F}}_w={\overrightarrow{F}}_{goal}+{\overrightarrow{F}}_{obstacles}$$

(2)

with

$${\overrightarrow{F}}_{goal}=-\frac{k_{RT}{q}_R{q}_T}{|{\overrightarrow{r}}_{RT}{|}^2}·\frac{{\overrightarrow{r}}_{RT}}{|{\overrightarrow{r}}_{RT}|}$$

$${\overrightarrow{F}}_{obstacles}=-\sum _{i=1}^N\frac{k_{RO}{q}_R{q}_O}{|{\overrightarrow{r}}_{R{O}_i}{|}^2}·\frac{{\overrightarrow{r}}_{R{O}_i}}{|{\overrightarrow{r}}_{R{O}_i}|}$$

where ${\overrightarrow{F}}_{goal}$ is the attractive force; ${\overrightarrow{F}}_{obstacles}$ is the repulsive force; $k_{RT}$ and $k_{RO}$ is the interaction constant between the mobile robot and the goal, and the mobile robot and obstacles; $q_R$, $q_T$ and $q_o$ is the mobile robot, the goal, and obstacles charge, respectively; and ${\overrightarrow{r}}_{RT}$ and ${\overrightarrow{r}}_{R{O}_i}$ is the directional vector from the mobile robot to the goal and from the mobile robot to i-th obstacle.

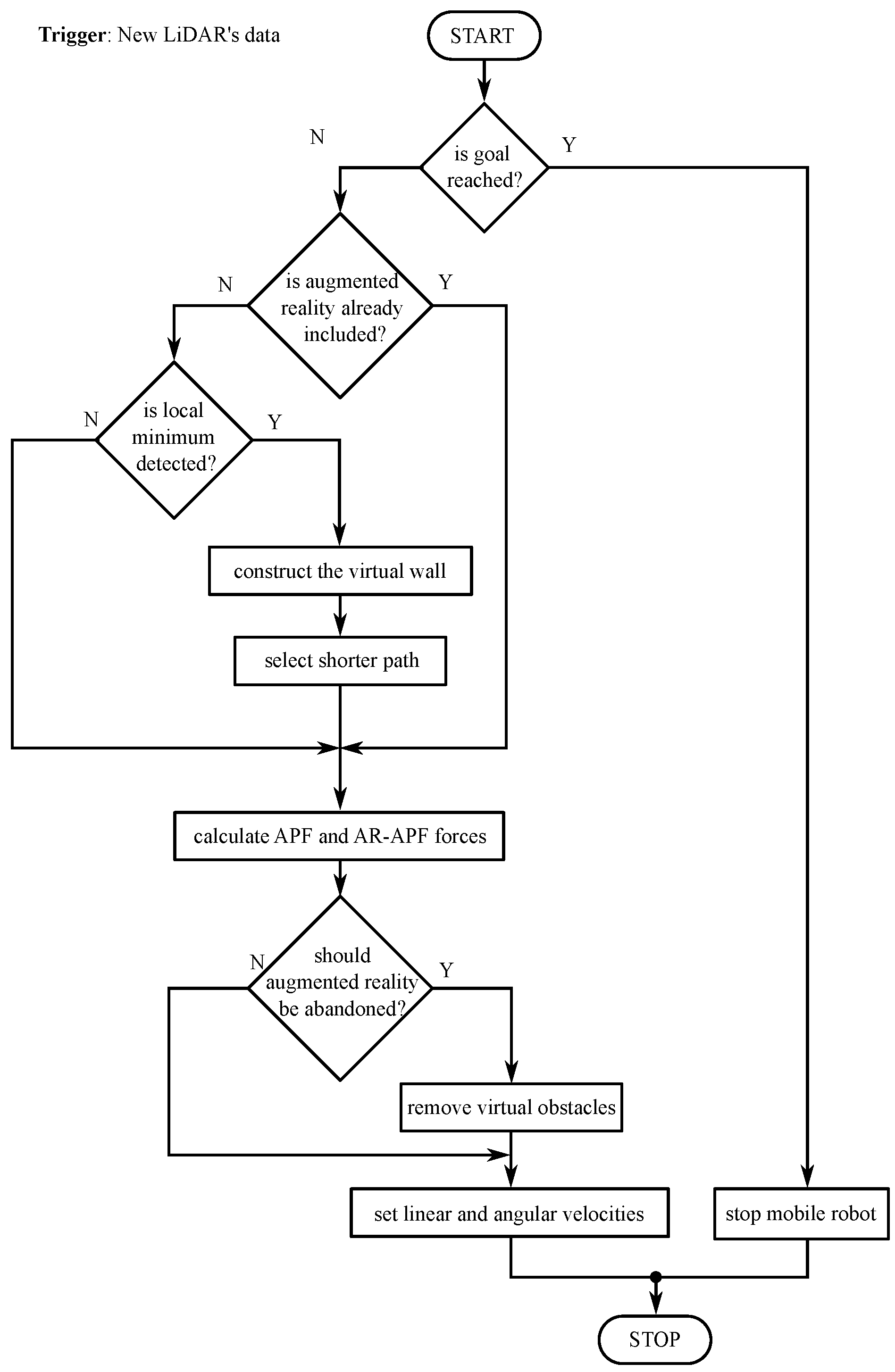
3. Proposed AR-APF Algorithm

As mentioned earlier, the disadvantage of the APF is the lack of local minimum avoidance or bypassing algorithm. In this paper, such a mechanism based on augmented reality is proposed. The idea of the application of augmented reality to extend the mobile robot perception in situation when the local minimum occurs is presented in Figure 1.

First, the algorithm responsible for a local minimum detection is proposed. The information is used to create a virtual wall that allows APF algorithm to avoid it. An additional part is a selection of the shorter path to provide higher efficiency of the mobile robot than the random selection of the future direction. After the detected local minimum is avoided, the virtual wall and obstacle are removed. The flowchart of the proposed augmented reality for APF is presented in Figure 2, while the description of each mentioned part of the algorithm is presented in the next subsections.

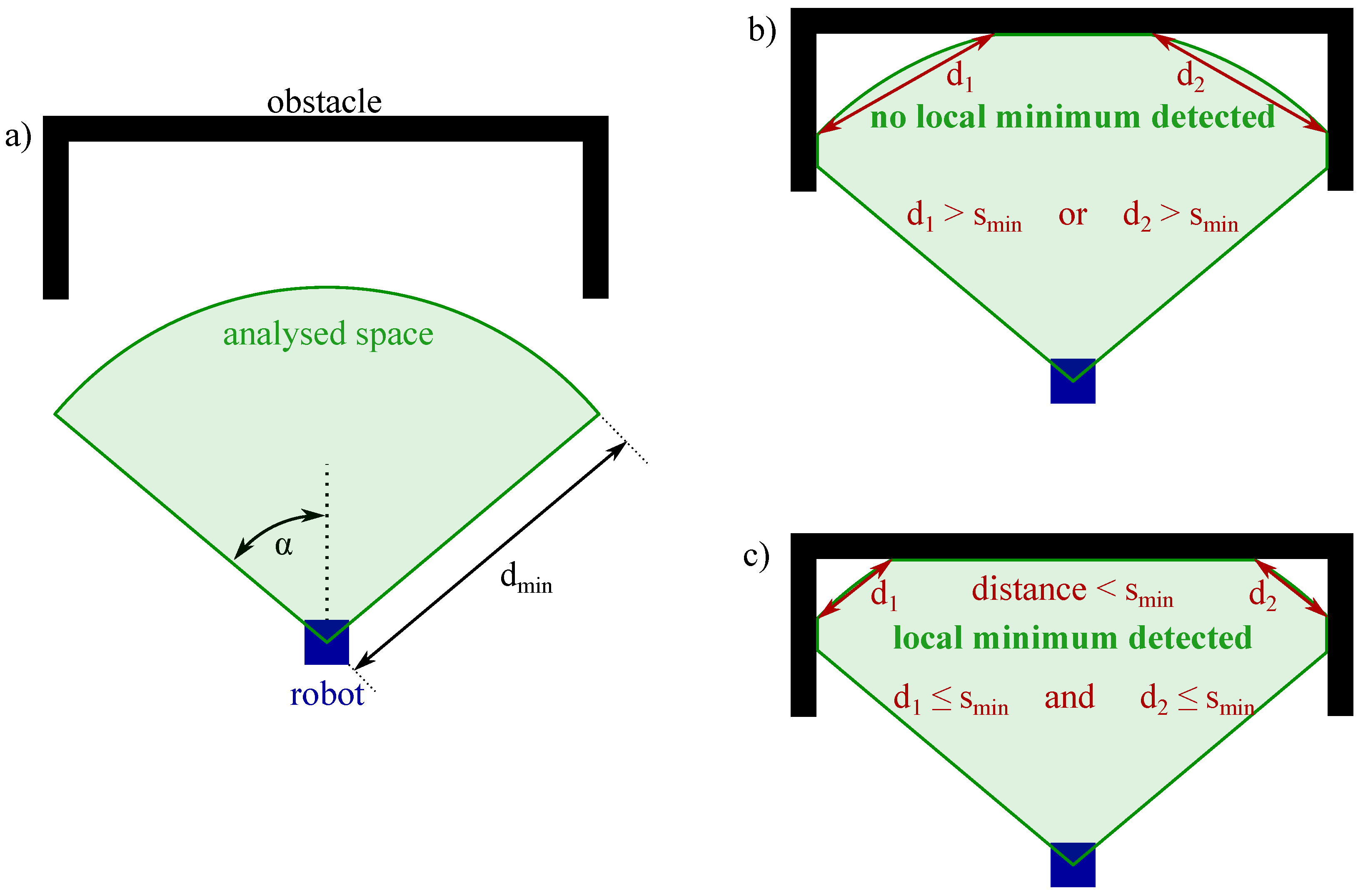
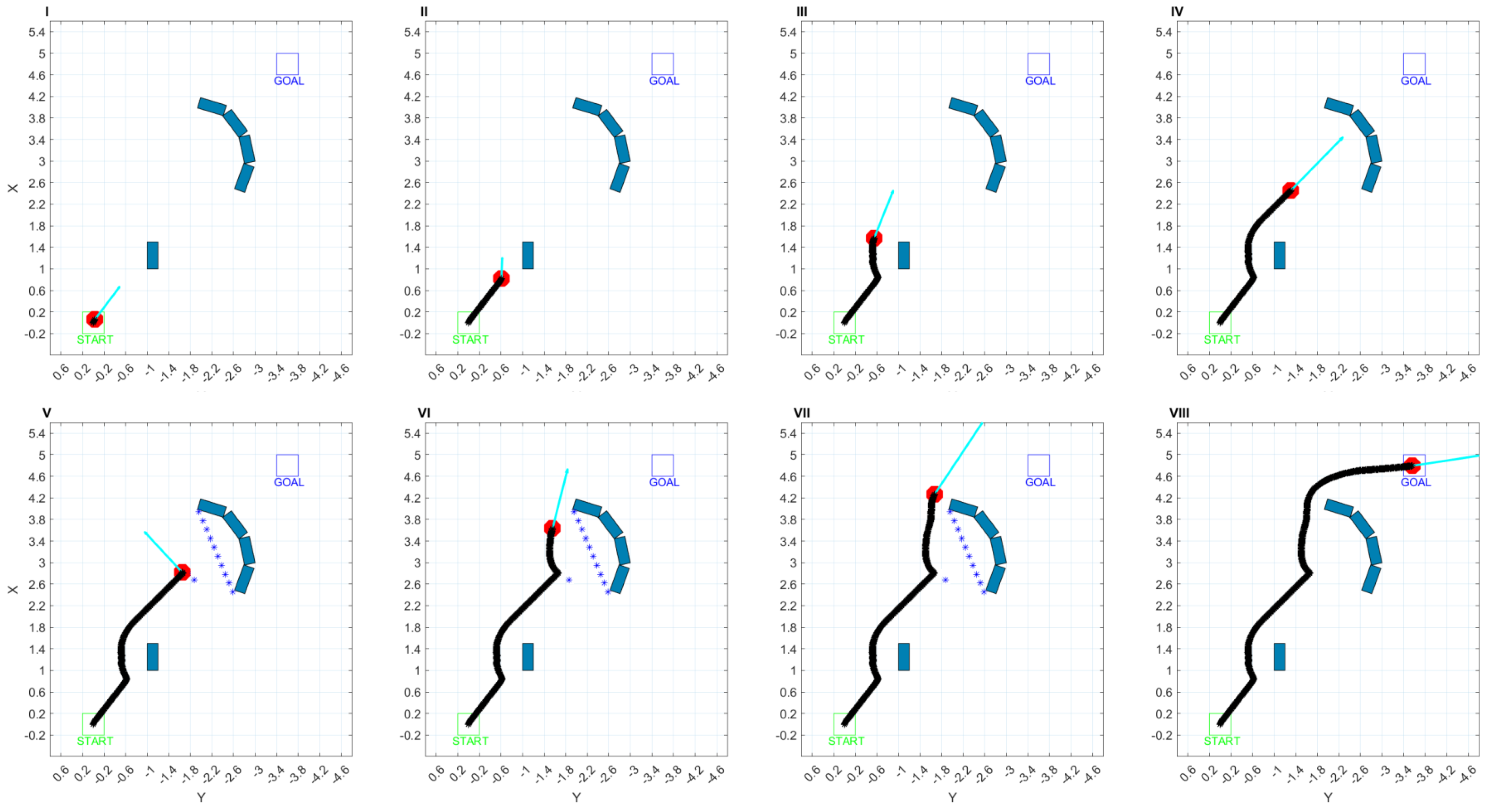
3.1. Detection of the Local Minimum

In the proposed algorithm, the detection of local minimum is based on analysis of LiDAR’s data in range $\pm \alpha$ degrees and $d_{min}$ meters from the robot. The predefined parameters are related to the size of the robot, potential obstacles size, and type of local minimums in the robot’s environments. If in the analyzed range, there is no passage of at least $s_{min}$ meters of width, then the algorithm returns the information about the detection of the local minimum. The passage width is related to the size of the robot. After such detection, the reality of the robot is augmented with virtual obstacles to prevent stagnation in the detected local minimum. The detection of the local minimum is presented in Figure 3.

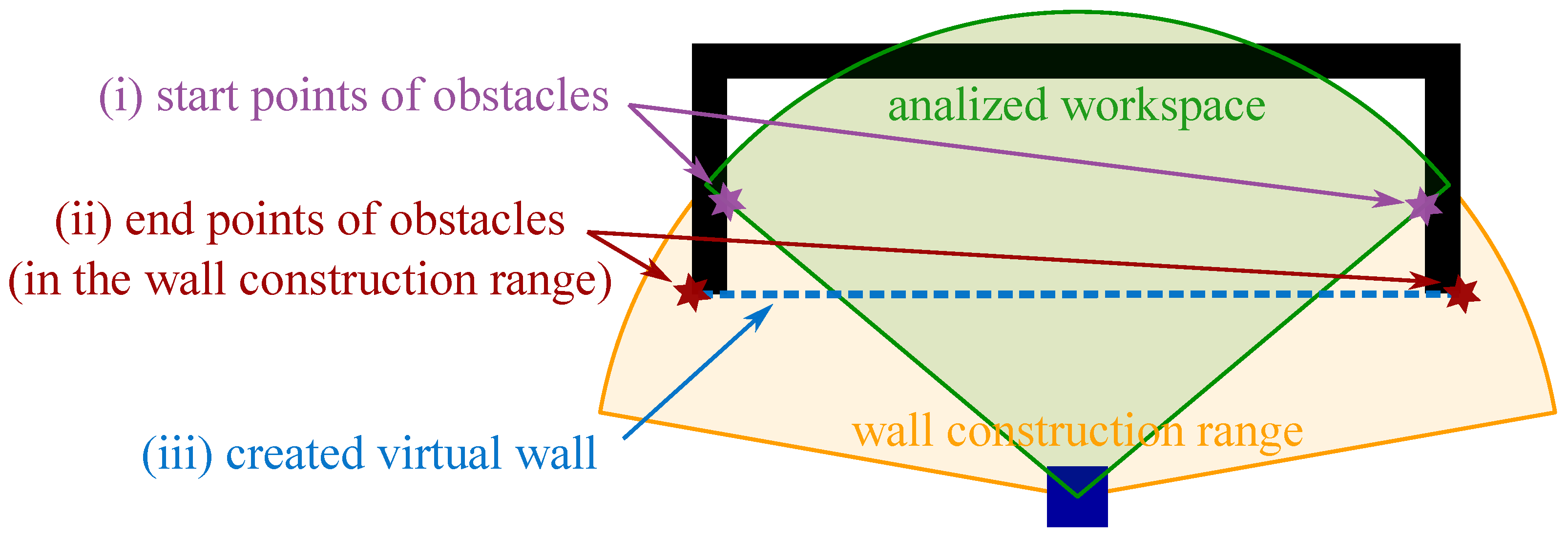
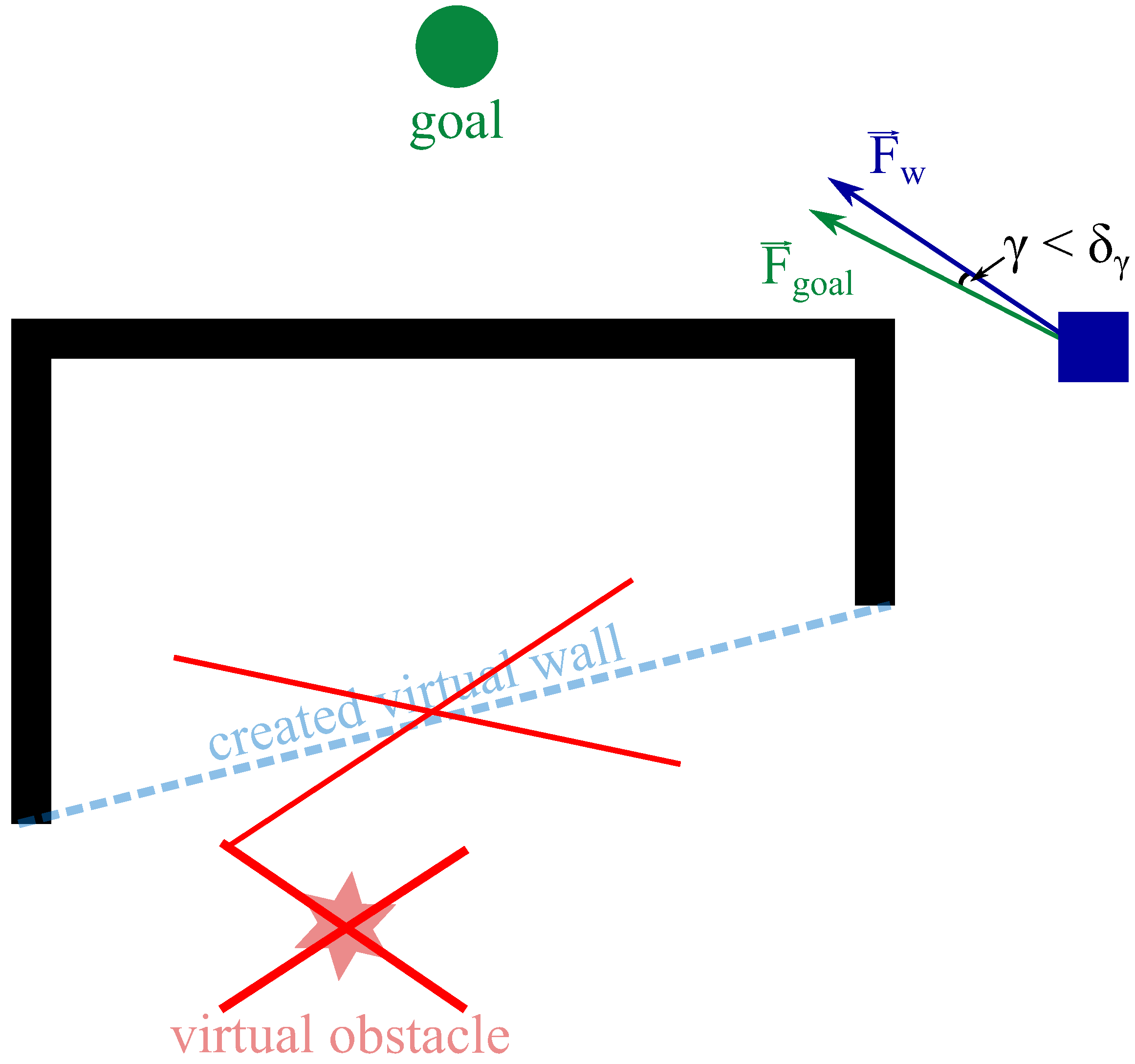
3.2. Construction of the Virtual Wall

To prevent the robot from stagnating at a local minimum, augmented reality provides additional information for the robot. Due to that, the robot does not go into the local minimum and does not have to jump off it. Therefore, indicators, such as theenergetic efficiency, path length, and duration of the robot’s movement, are improved in comparison to jumping-off local minimum algorithms. The virtual wall is created by closing the local minimum with a single line connecting the outer edges of the object. The procedure is as follows:

• start with position determined by the analyzed workspace in the detection of the local minimum part (determined by $\alpha$ and $d_{min}$),
• analyse the LiDAR data going out until the object ends, and
• create a wall using endpoints of the obstacles.

In the proposed procedure, the end of the object is determined as a larger distance between the two subsequent LiDAR samples than $d_{max}$. The value was manually selected, taking into account the robot and obstacles in its environment sizes. The virtual wall is created using $N_{wall}$ points equally spaced on the selected line. The construction of the virtual wall is presented in Figure 4. The wall construction range ($\beta$) is wider than the analyzed workspace to detect the local minimum ($\alpha$) in order to correctly construct the wall, thus, closing the local minimum.

The APF force equation is extended in order to include the virtual wall:

$${\overrightarrow{F}}_w={\overrightarrow{F}}_{goal}+{\overrightarrow{F}}_{obstacles}+{\overrightarrow{F}}_{virtualwall}$$

(3)

with

$${\overrightarrow{F}}_{virtualwall}=-\sum _{i=1}^{N_{wall}}\frac{k_{RW}{q}_R{q}_W}{|{\overrightarrow{r}}_{R{W}_i}{|}^2}·\frac{{\overrightarrow{r}}_{R{W}_i}}{|{\overrightarrow{r}}_{R{W}_i}|}$$

where ${\overrightarrow{F}}_{virtualwall}$ is the repulsive force generated by the virtual wall, $k_{RW}$ is the interaction constant between the mobile robot and virtual wall, $q_W$ is the virtual wall charge, and ${\overrightarrow{r}}_{R{W}_i}$ is the directional vector from mobile robot to i-th virtual wall point.

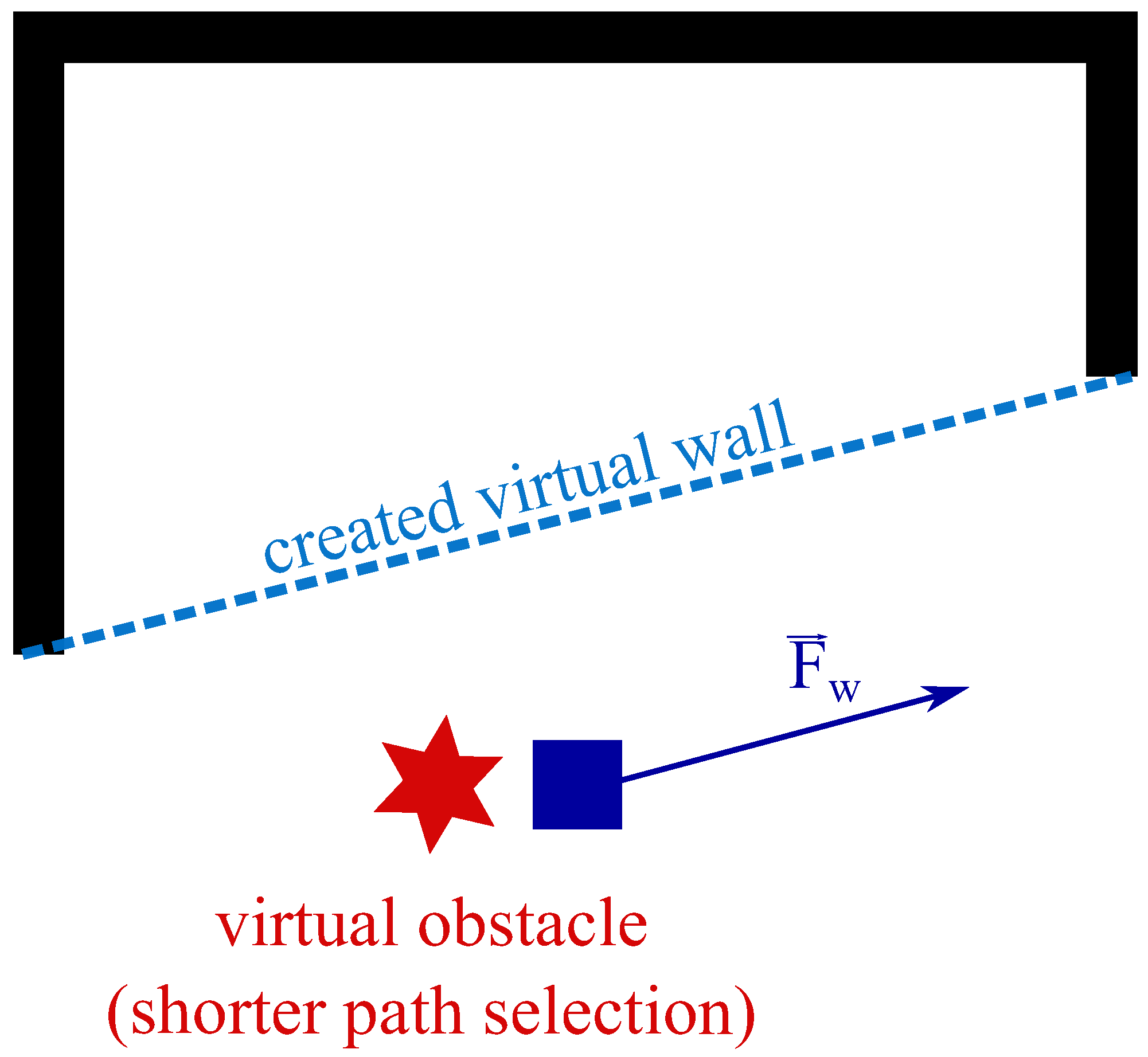
3.3. Naive Shorter Path Selection

To obtain the maximum efficiency of the robot, the shorter path should be selected in the path planning algorithm. In many algorithms, e.g., the BUG algorithm [14], a random selection of the robot’s movement is applied. Due to the usage of the local path planning algorithm, only the naive choice is possible. The naivety comes from the fact that algorithm does not consider another obstacle, because the robot’s perception does not provide additional information about the entire environment.

In order to select the “left” or “right” direction, the distance from the robot to the “left” or “right” endpoints of obstacles is taken into consideration. The higher distance corresponds to the future direction of the robot movement. If the distances are equal, the random direction is selected. The single virtual obstacle with enormous weight is added to the opposite side. The naive shorter path selection is presented in Figure 5.

The final force equation of APF combined with augmented reality is as follows:

$${\overrightarrow{F}}_w={\overrightarrow{F}}_{goal}+{\overrightarrow{F}}_{obstacles}+{\overrightarrow{F}}_{virtualwall}+{\overrightarrow{F}}_{virtualobstacle}$$

(4)

with

$${\overrightarrow{F}}_{virtualobstacle}=-\frac{k_{RD}{q}_R{q}_D}{|{\overrightarrow{r}}_{RD}{|}^2}·\frac{{\overrightarrow{r}}_{RD}}{|{\overrightarrow{r}}_{RD}|}$$

where ${\overrightarrow{F}}_{virtualobstacle}$ is the repulsive force generated by the virtual obstacle, $k_{RD}$ is the interaction constant between the mobile robot and virtual obstacle, $q_D$ is the virtual obstacle charge, and ${\overrightarrow{r}}_{RD}$ is the directional vector from mobile robot to virtual obstacle.

3.4. Abandonment of Augmented Reality

In order to allow the algorithm to achieve proper operations in a non-static environment, the virtual wall and obstacle should be abandoned after the mobile robot avoids the local minimum. For this reason, the known approach from the combination APF and BUG algorithms was applied [14]. In this case, the augmented reality in APF is abandoned when the direction of overall force ${\overrightarrow{F}}_w$ and goal force ${\overrightarrow{F}}_{goal}$ are the same with an allowable difference equal to ${\delta }_{\gamma }$. The abandonment of the augmented reality is presented in Figure 6.

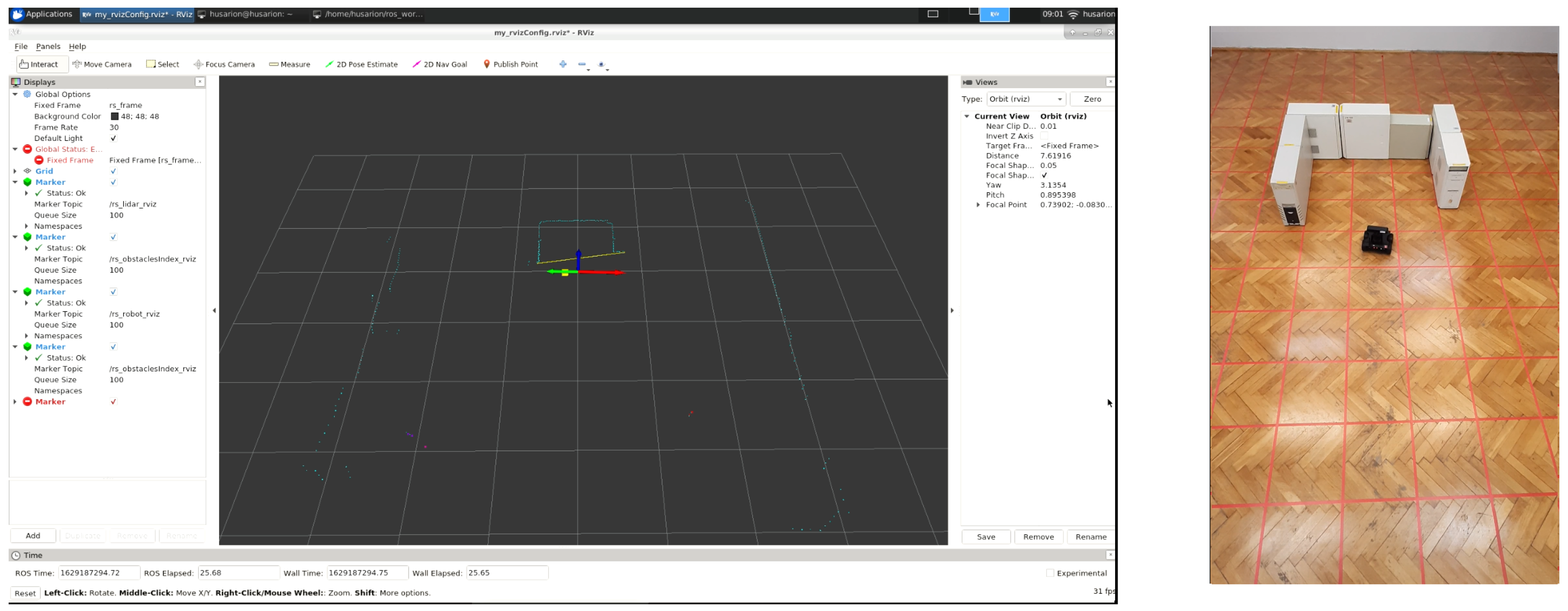
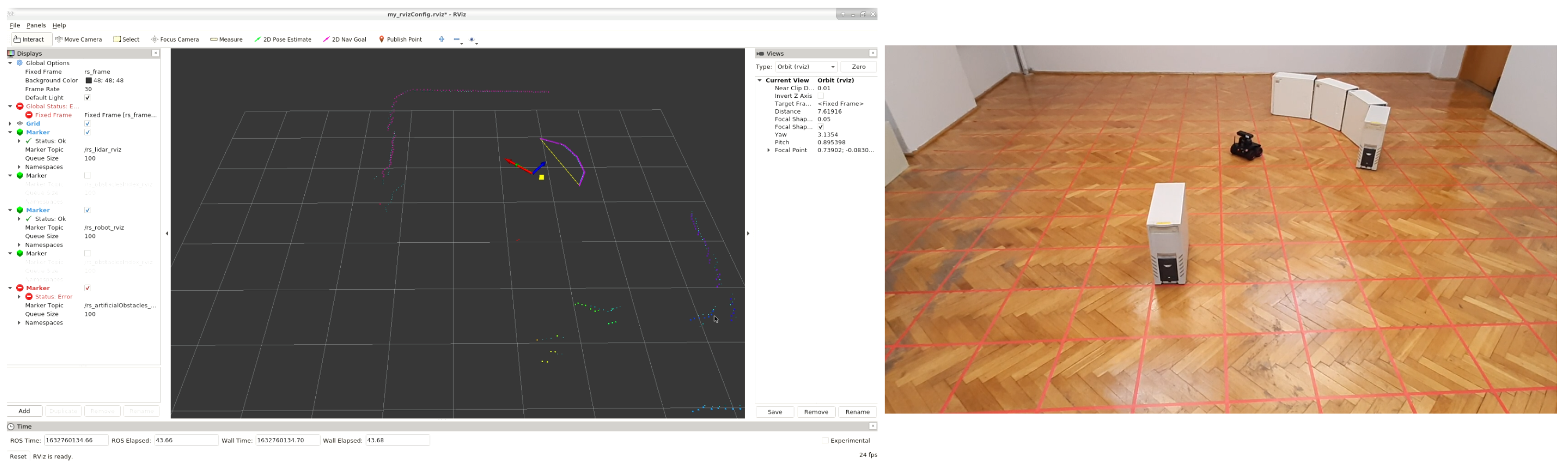
4. Results

Tests were performed on the ROSbot 2.0 PRO (Husarion company) using the Robot Operating System (ROS) [23]. The laboratory environment is presented in Figure 7. The grid resolution is 40 cm, and the robot’s start position is (0, 0) m.

As was mentioned in a previous section, the algorithm uses LiDAR data, and the robot is controlled by linear and angular velocities. An additional preprocessing of LiDAR data is used in order to normalize it to one read per one degree. The graph of data flow in the ROS is presented in Figure 8.

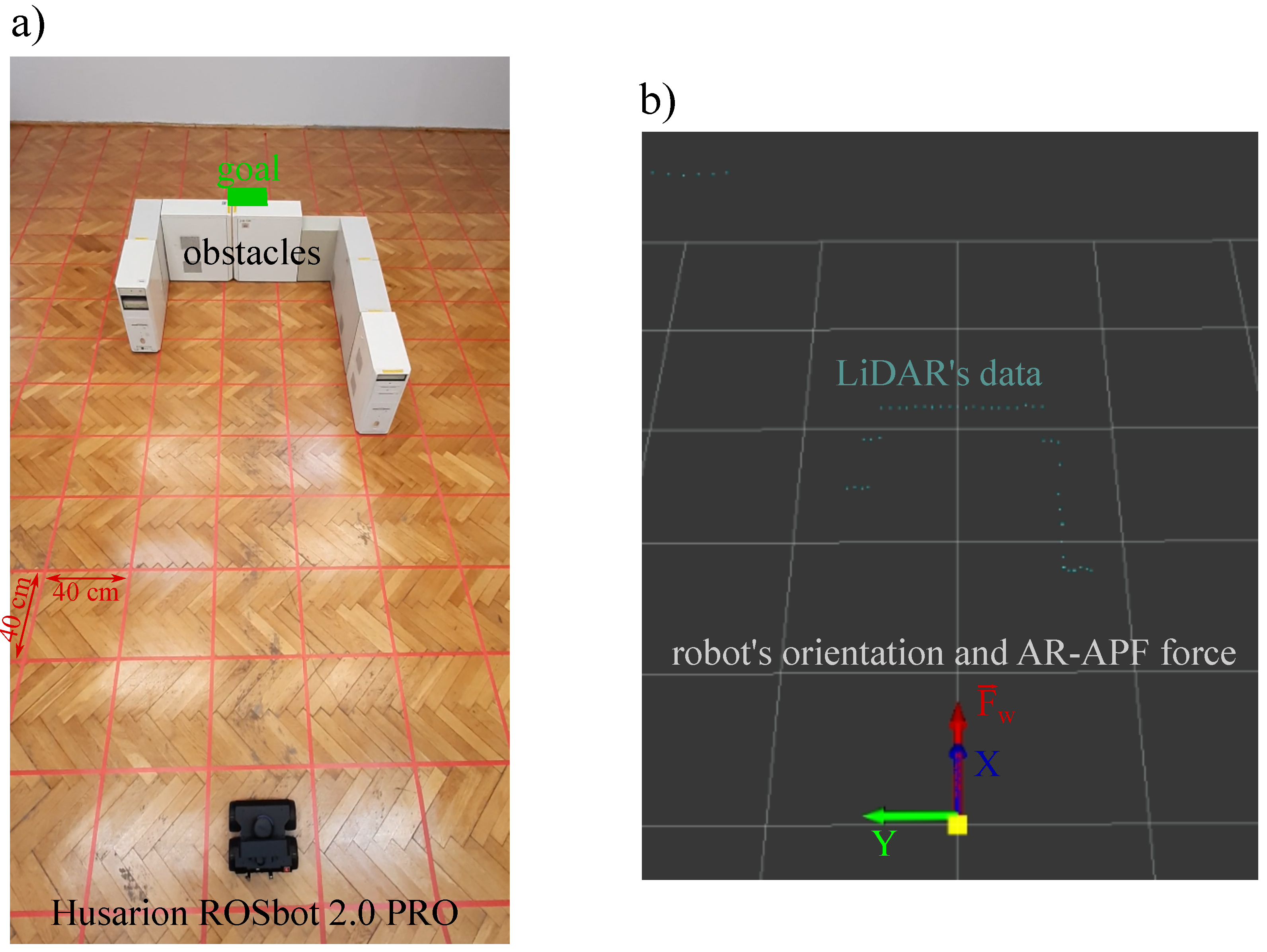
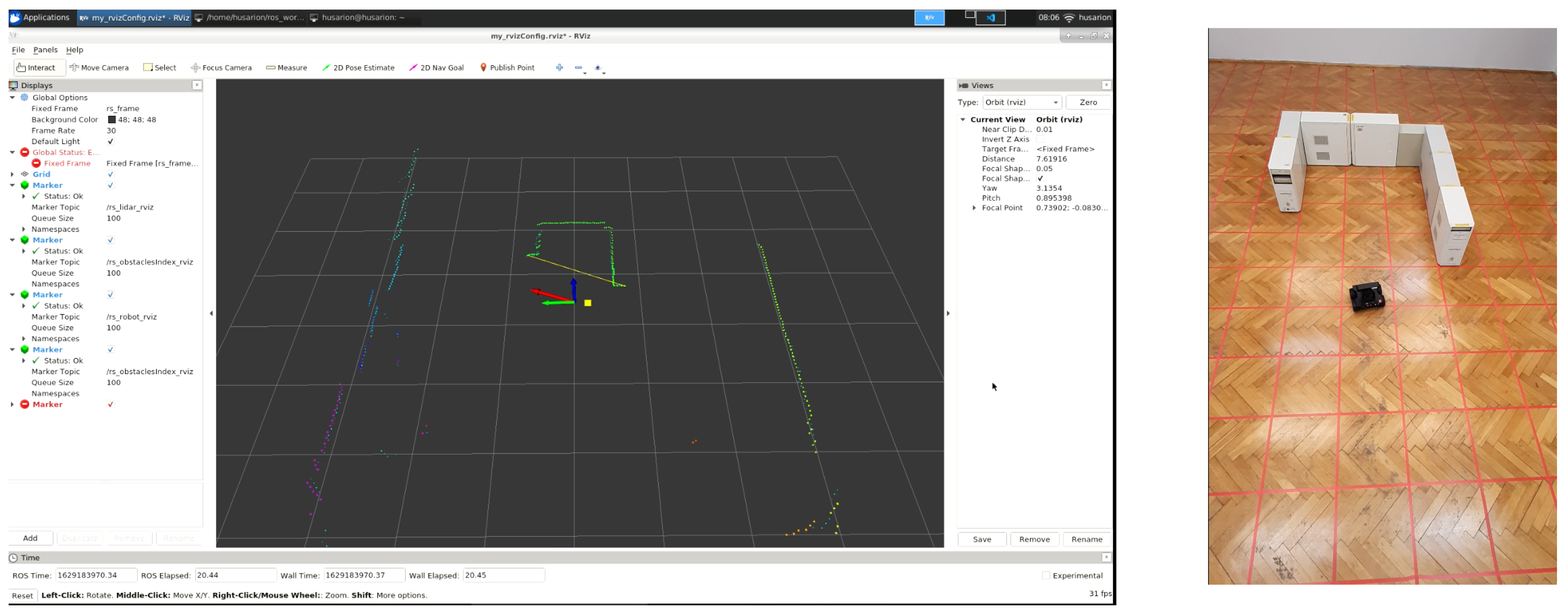
4.1. Experimental Examinations

To prove the correctness of the proposed AR-APF algorithm, we examined it in an environment with a local minimum, which the classical APF algorithm cannot solve. The accuracy of the robot goal position was set to $0.1$ m due to the mobile robot size and its movement accuracy. In both examinations, the mobile robot has, on its path, a local minimum to avoid using the proposed AR-APF algorithm. The parameters of the proposed AR-APF are presented in

Table 1. The parameters of the proposed AR-APF.

Parameter	Value
LiDAR data points (L)	300
$q_R$, $q_O$, $q_W$, $q_D$	$-1$
$q_T$	1
$k_{RT}$	5
$k_{RO}$	$5÷L$
$k_{RW}$, $k_{RD}$	$10\times k_{RO}$
$\alpha$	30 deg
$d_{min}$	$1.2$ m
$s_{min}$	$0.5$ m
$d_{max}$	$0.2$ m
$N_{wall}$	10
$\beta$	75 deg
${\delta }_{\gamma }$	5 deg

. Most of the parameters were selected to fit the laboratory environment, i.e., the robot’s size, obstacles’ sizes, laboratory size, robot sensors. The rest of the parameters, i.e., interaction constants and allowable direction difference of overall force and goal force, were selected by a trial-and-error approach.

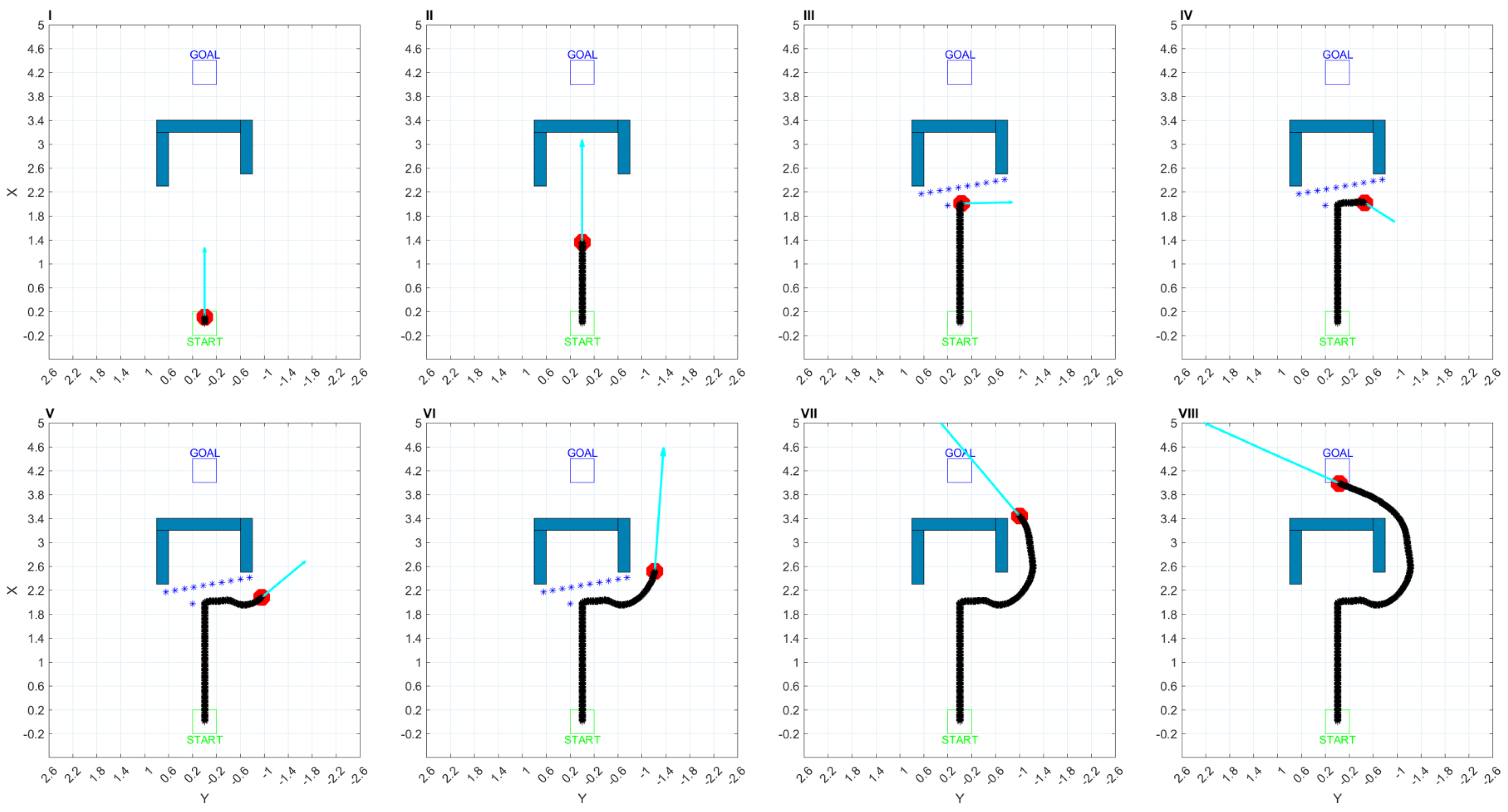
4.1.1. Test (I)

The goal point for Test (I) is $4.2$ m and $0.0$ m in the X and Y axis, respectively. The result of Test (I) is present in Figure 9, and it has the following form: eight important timestamps are presented to show the force calculated using Equation (4), traveled route, obstacles, and virtual obstacles if they exist. In addition, the real photo and RViz visualization at the same timestamp as the image number III in Figure 9 are presented in Figure 10.

The proposed AR-APF algorithm detected a local minimum when the mobile robot approached the obstacles (see images II and III in Figure 9 and Figure 10). Next, the virtual wall was constructed, and the shorter path was selected by putting the virtual obstacle. After the obstacles were avoided, the augmented reality was abandoned (see image VII in Figure 9). The mobile robot successfully avoided the local minimum and reached the goal. The shorter path was selected.

4.1.2. Test (II)

For Test (II), the goal point was $4.2$ m and $0.0$ m in the X and Y axis, respectively. The results of Test (II) are presented in Figure 11, while the photo and RViz visualization at the same timestamp as the image number III in Figure 11 are presented in Figure 12.

The placed virtual wall and obstacle allowed the robot to avoid a local minimum and select the shorter path. The arch passage, which can be seen in images IV–VIII in Figure 11, is related to the force calculated using Equation (4): (i) the artificial obstacle is pushing the robot to right side, goal is pulling the robot upwards, and when the robot is near the real obstacle from the right side, and then is is pushed downside. The force is inversely proportional to the distance from the object. For this reason, the pointed arch in the mobile robot path occurs.

4.1.3. Test (III)

Previous examinations were made to present the AR-APF algorithm. There was no additional obstacles, the local minimum was in front of the robot, and the goal point was in a straight line. In Test (III), an additional obstacle was presented, and the local minimum had no perfect U-shape. The goal point was $4.8$ m and $3.6$ m in the X and Y axis, respectively. In Figure 13, the results of Test (III) are presented. The real photo and RViz visualization are presented in Figure 14.

The proposed AR-APF algorithm successfully avoided obstacles (see images II–IV in Figure 13). No virtual object was placed due to lack of a local minimum. Next, the upcoming local minimum was detected and the AR part of the algorithm placed a virtual wall and obstacle to bypass it (see images V–VII in Figure 13). Finally, the AR-APF reached the goal point.

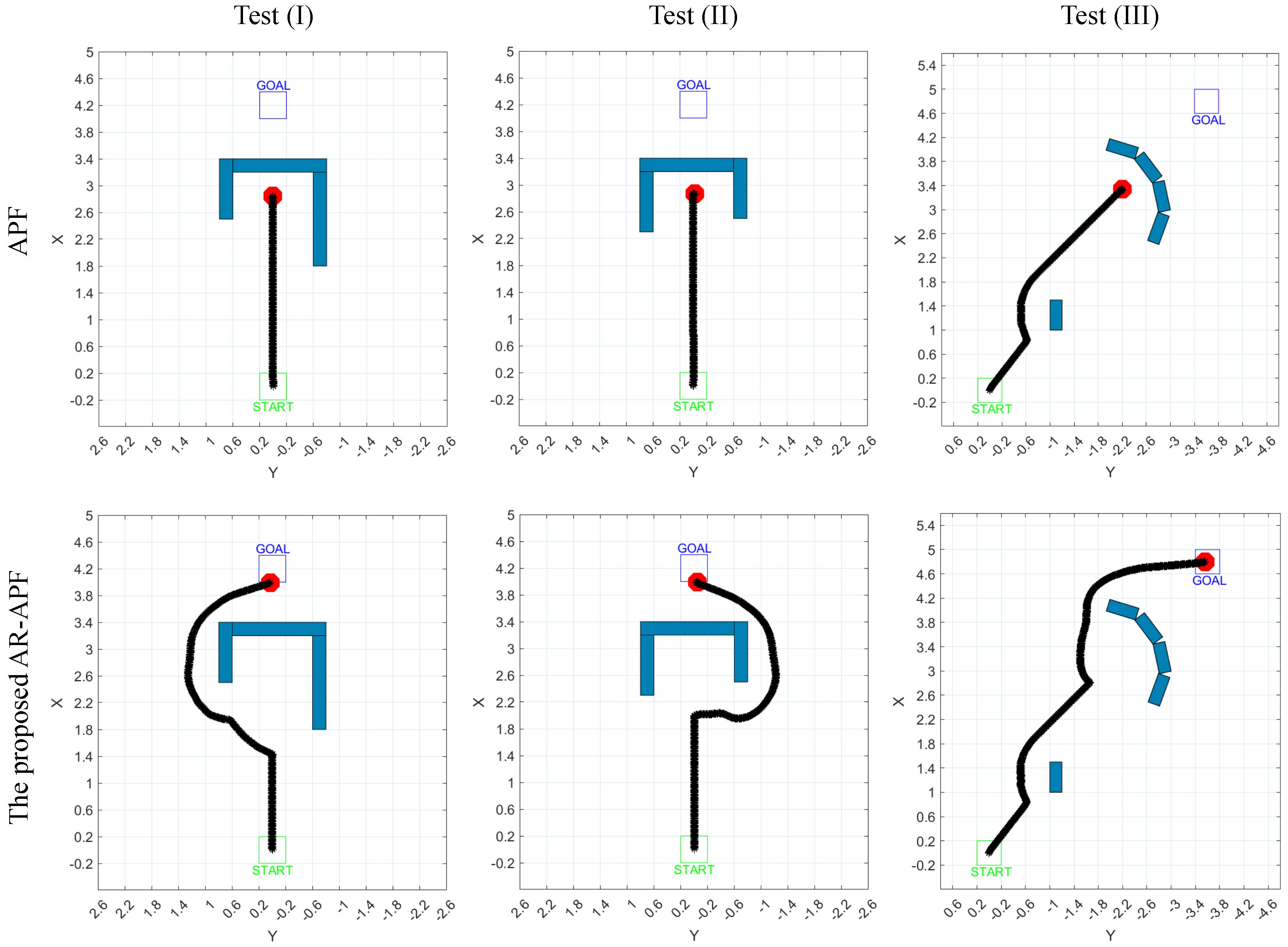
4.1.4. Comparison

The comparison of mobile robot trajectories with implemented classical APF and the proposed AR-APF for Tests (I)–(III) is presented in Figure 15.

The comparison proves that the proposed algorithm successfully bypassed the local minimum and reach the goal, while the APF algorithm stagnated. The behavior of classical APF and the proposed AR-APF were identical in the case of an obstacle in Test (III). This was caused by the fact that these algorithms are identical in the case of a lack of local minimum and virtual wall and obstacle.

5. Conclusions

An extension of the classical APF algorithm was proposed. The main drawback of the classical APF algorithm is the lack of local minimum avoidance or bypassing mechanism. The proposed algorithm uses augmented reality to provide a bypassing mechanism. The detection of the local minimum algorithm based on LiDAR’s data was used as a trigger to create a virtual wall in order to prohibit entry in the local minimum. Next, the artificial obstacle was placed on the left or right side of the robot to push it to the shorter path. After the obstacle with the local minimum was bypassed, the augmented reality was abandoned. The proposed AR-APF algorithm was evaluated experimentally using Husarion ROSbot 2.0. In both examinations, the mobile robot successfully bypassed the obstacle using the shorter path.

The proposed algorithm is still a local path planning algorithm. For this reason, for a more complex local minimum, i.e., a blocked winding hallway, the algorithm may not detect it in advance, due to lacking information about the entire environment. To improve the quality of the path planning algorithm in this case, further research will include AR used for multi-agent systems and collaboration between these to increase the efficiency of the algorithm.