Experimental Energy and Exergy Analysis of an Automotive Turbocharger Using a Novel Power-Based Approach
Abstract
:1. Introduction
2. Materials and Methods
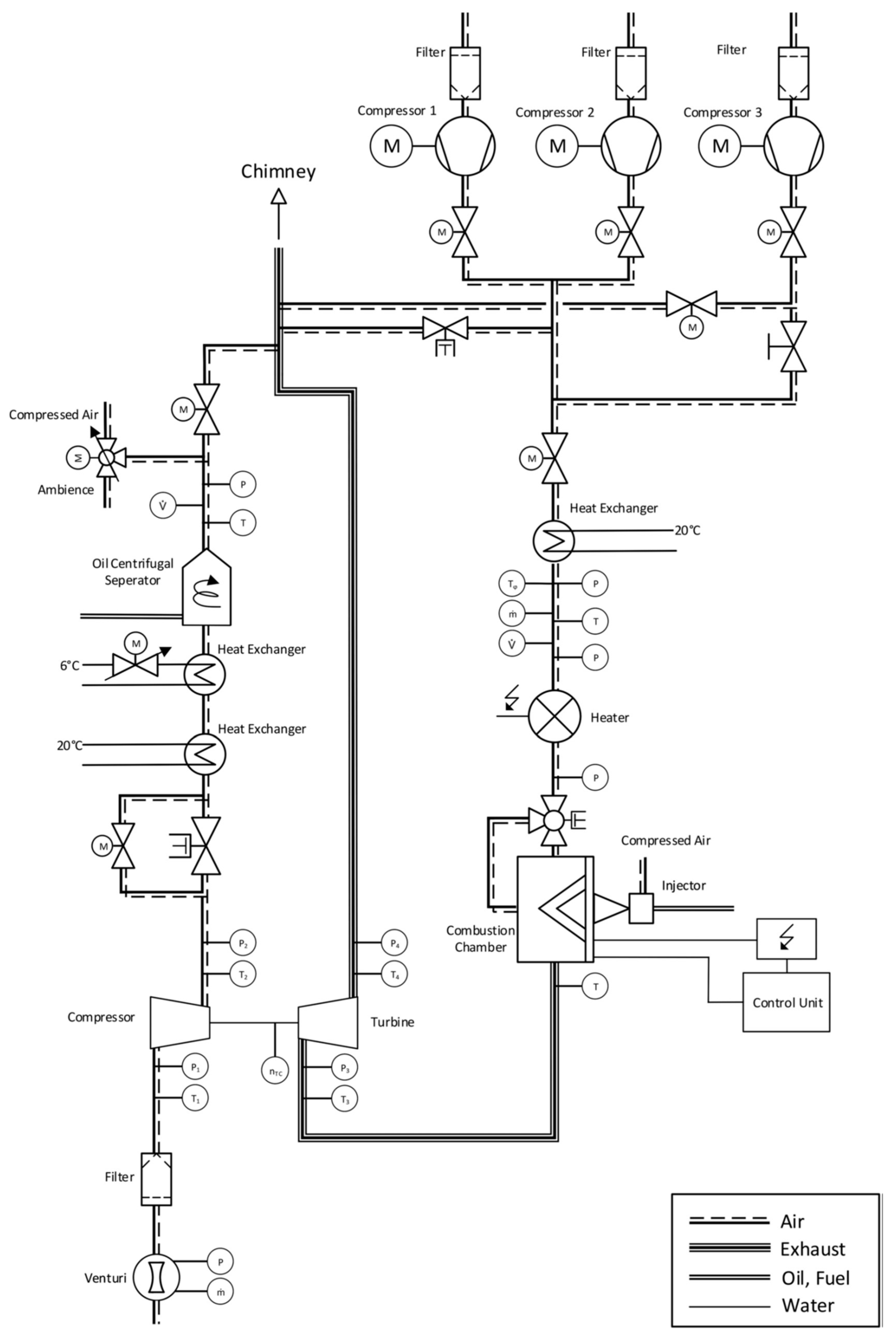
2.1. Experimental Procedure
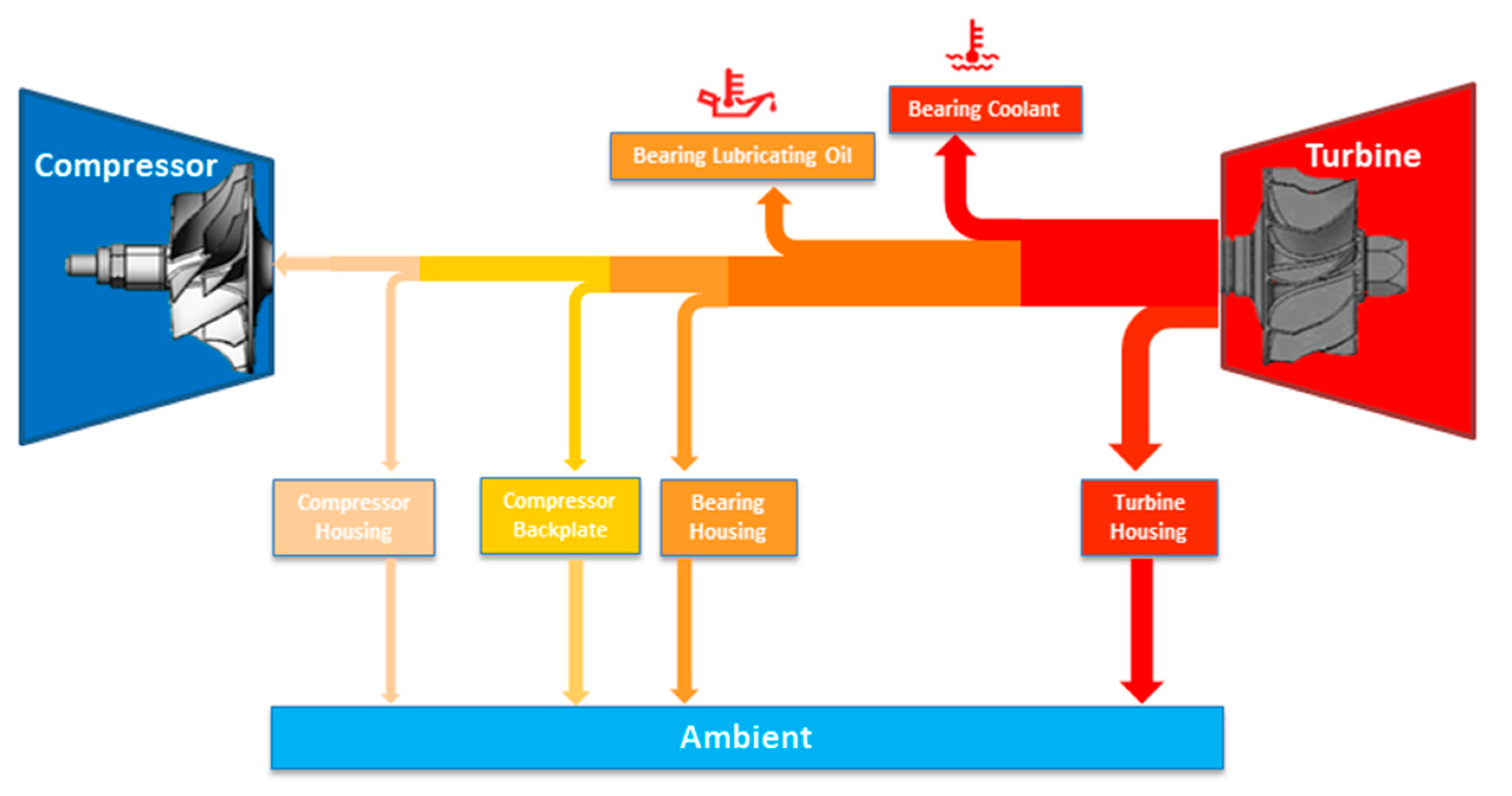
2.1.1. Adiabatic Measurement Conditions
2.1.2. Diabatic (i.e., Non-Adiabatic) Measurement Conditions
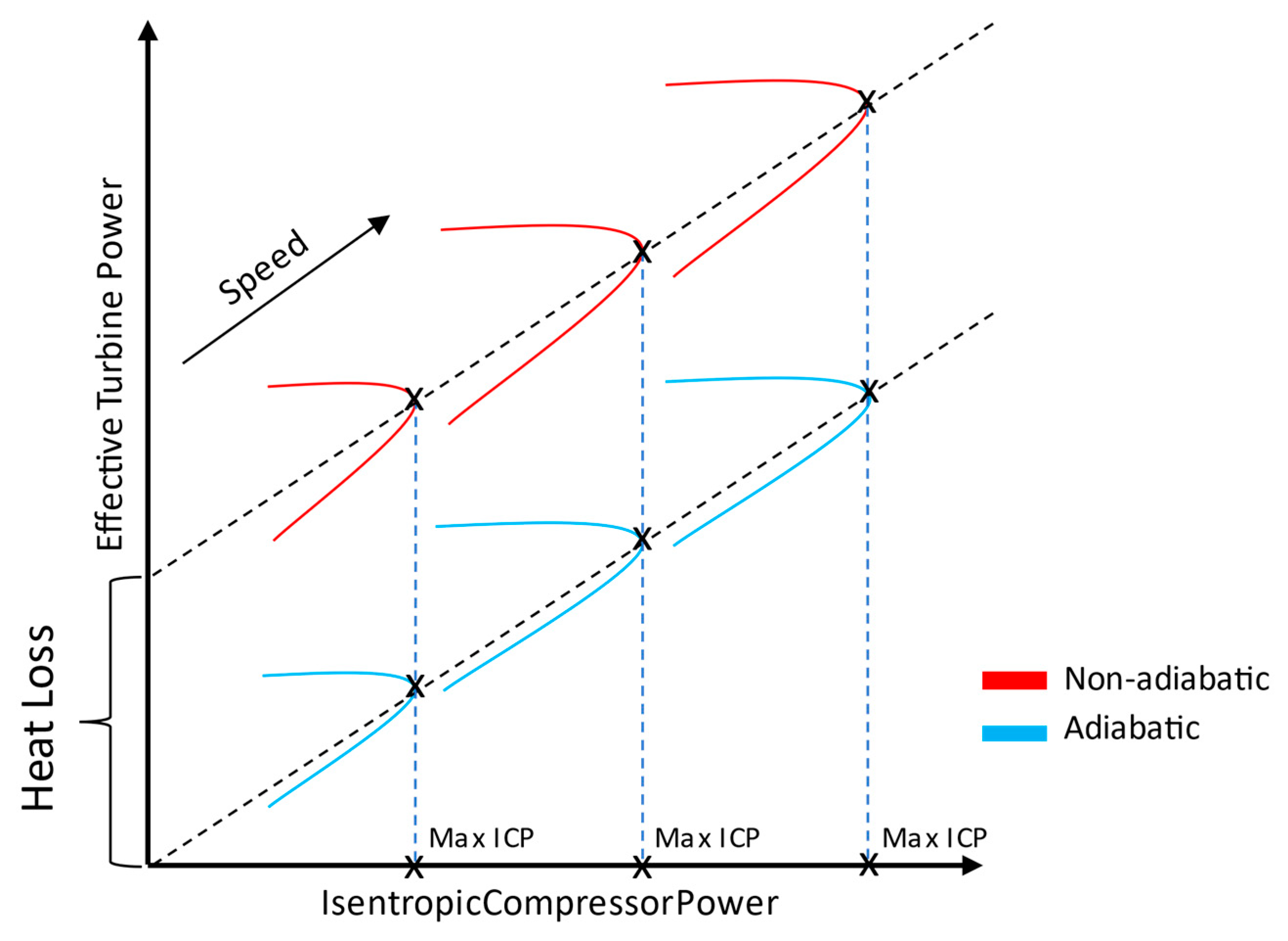
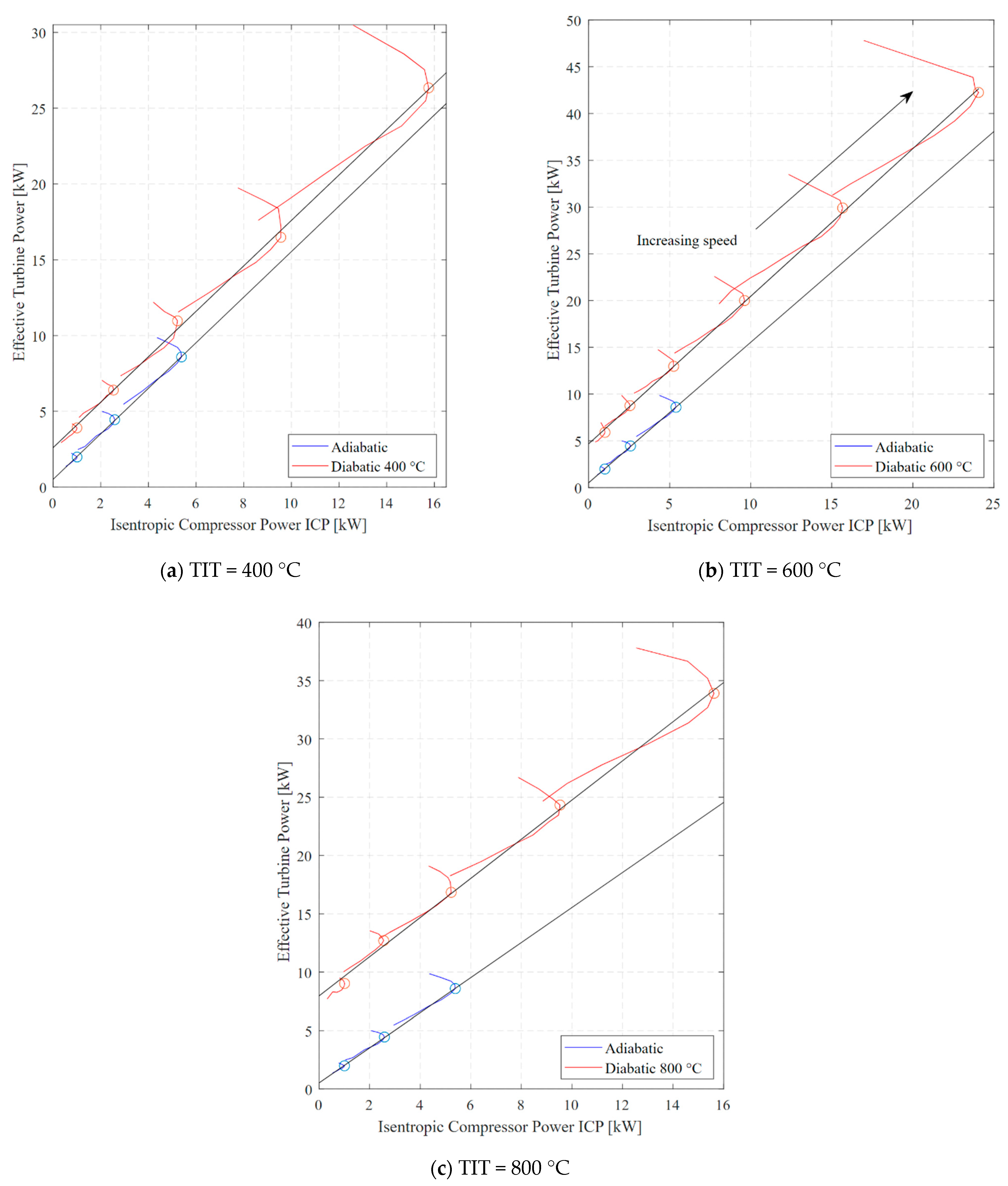
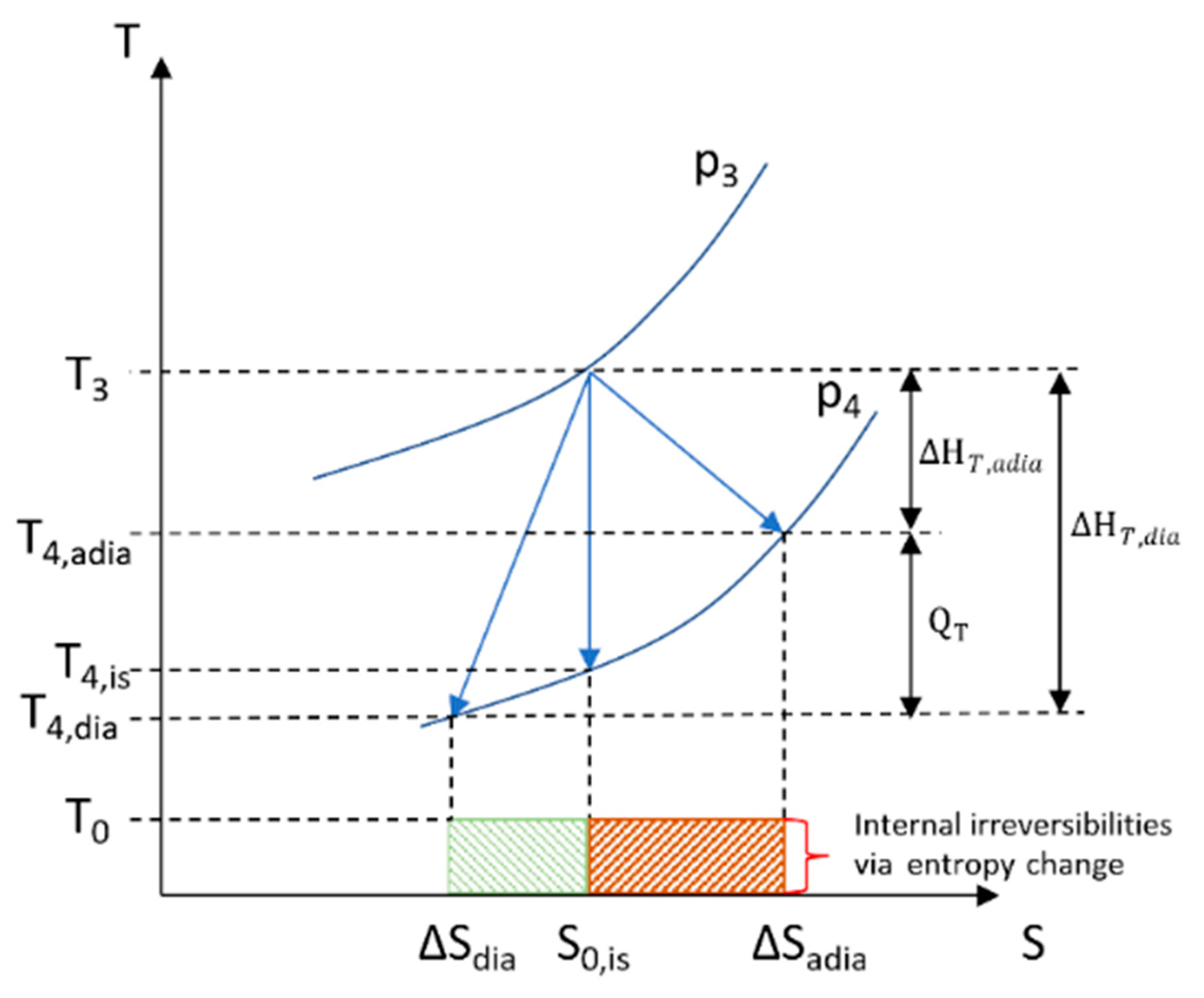
2.2. Power–Based Approach
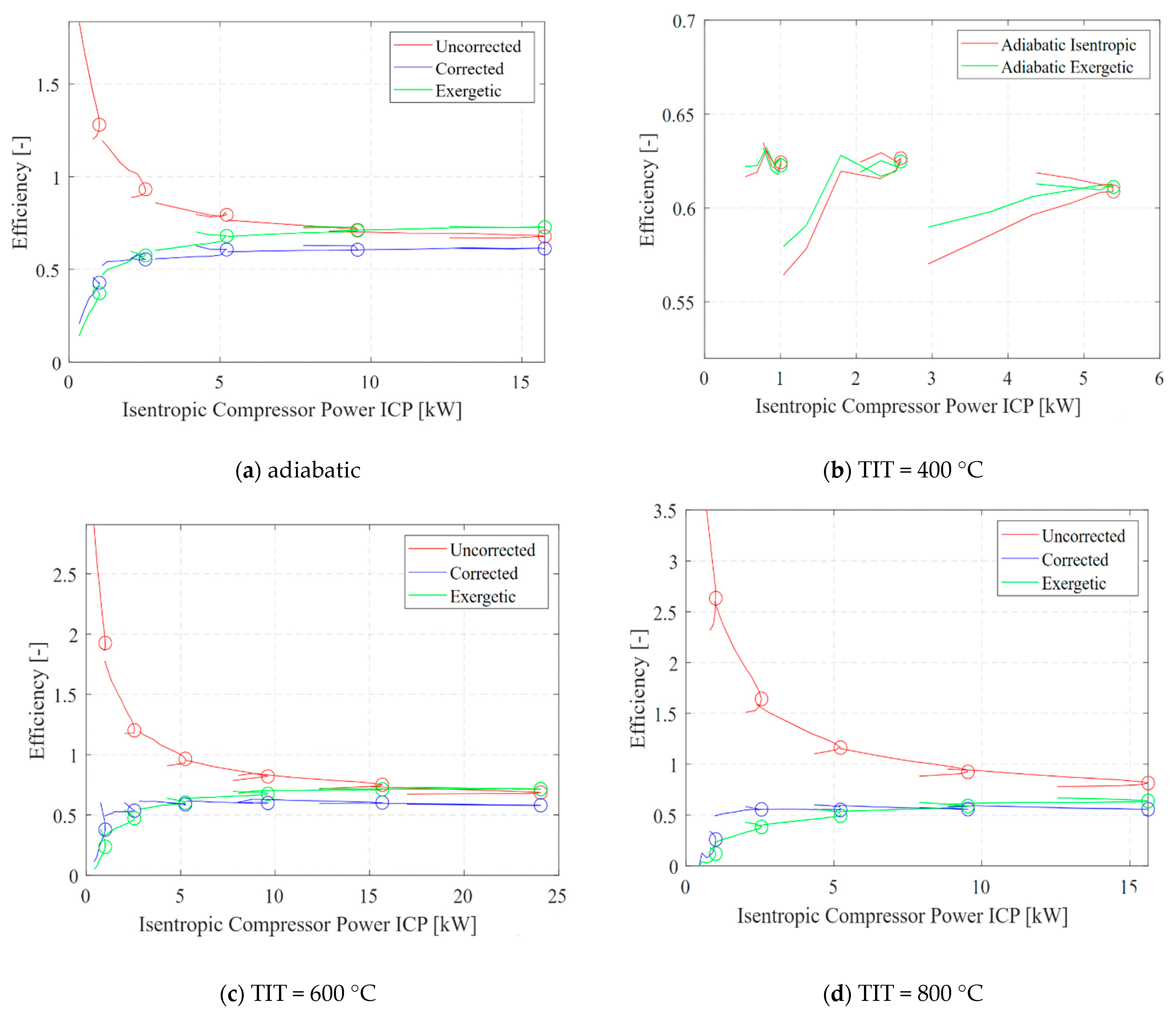
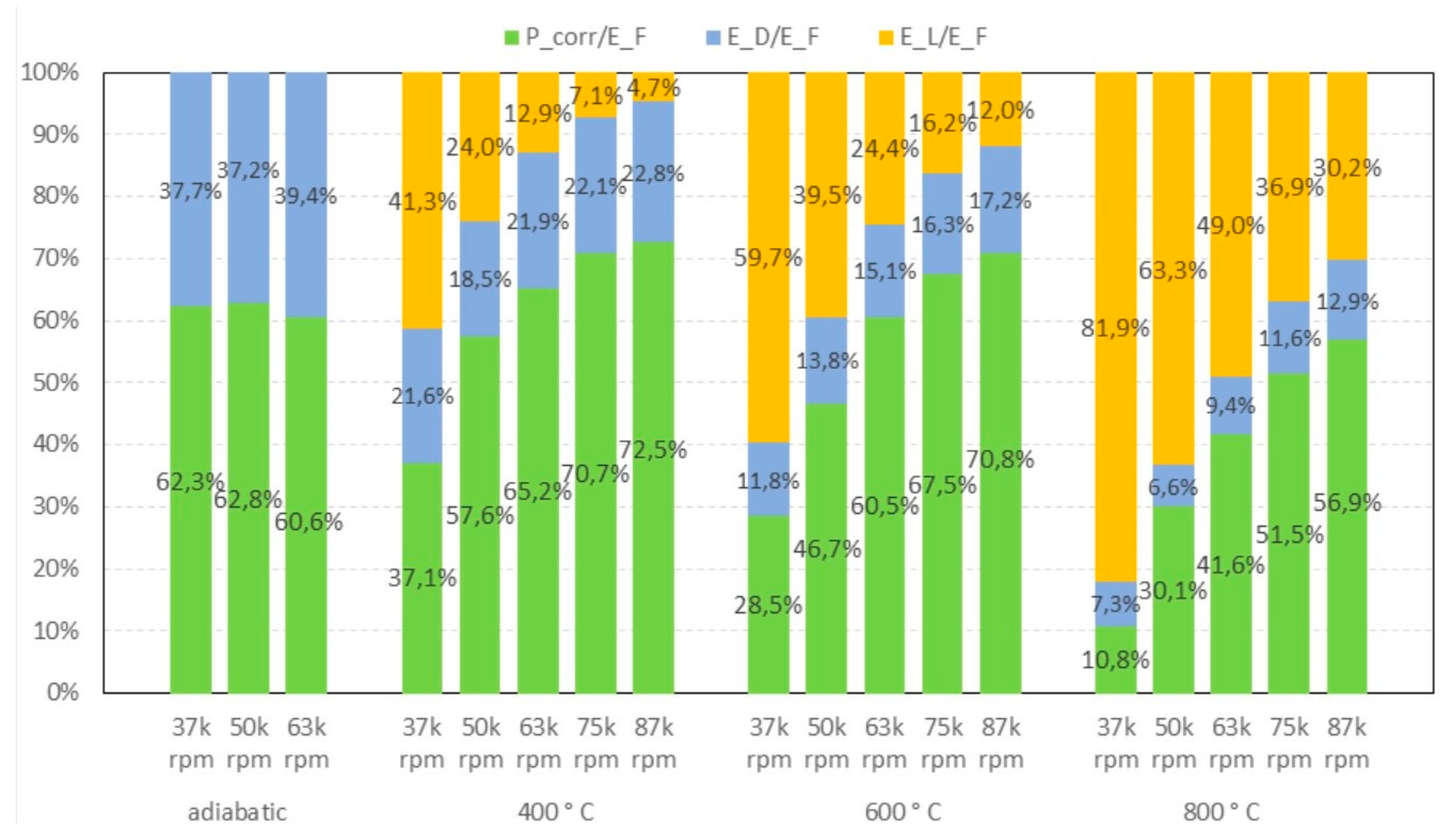
2.3. Experimental Exergy Analysis Methodology
- Product exergy ( the produced (usable) work by a system;
- Exergy destruction ( exergy destruction due to internal irreversibilities;
- Exergy loss (): exergy loss due to heat losses.
3. Results and Discussion
3.1. Turbine Heat Transfer Estimation via a Power-Based Approach
3.2. Exergy Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| CFD | Computational Fluid Dynamics |
| CHT | Conjugate Heat Transfer |
| ETP | Effective Turbine Power |
| IC | Internal Combustion |
| ICP | Isentropic Compressor Power |
| ITE | Isentropic Turbine Efficiency |
| RPM | Rotation per Minute |
| TIT | Turbine Inlet Temperature |
| Notations | |
| T | Temperature |
| Q | Power |
| Heat transfer rate | |
| Mass Flow Rate | |
| Heat capacity at constant pressure | |
| η | Efficiency |
| Pressure ratio | |
| Exergy rate | |
| Enthalpy rate | |
| Entropy rate | |
| p | Pressure |
| Subscripts | |
| 0 | Ambiance |
| 1 | Compressor inlet |
| 2 | Compressor outlet |
| 3 | Turbine inlet |
| 4 | Turbine outlet |
| C | Compressor |
| T | Turbine |
| B | Boundary |
| eff | Effective |
| ex | Exergetic |
| is | isentropic |
| corr | corrected |
| uncorr | uncorrected |
Appendix A
References
- Lim, S.M.; Kazemi Bakhshmand, S.; Biet, C.; Mihaescu, M. Experimental and Numerical Investigation of a Turbocharger Turbine Using Exergy Analysis at Non-Adiabatic Conditions. In SAE Technical Paper Series; SAE Powertrains, Fuels & Lubricants Meeting, SEP. 22, 2020; SAE International400 Commonwealth Drive: Warrendale, PA, USA, 2020. [Google Scholar]
- Gao, X. Model of Aerodynamics and Heat Transfer of a Turbocharger. 2019. Available online: https://www.proquest.com/openview/3c307dead97b5b5ff0b9d15728da16dd/1?cbl=2026366&diss=y&pq-origsite=gscholar&accountid=14264 (accessed on 9 October 2021).
- Aghaali, H.; Ångström, H.-E.; Serrano, J.R. Evaluation of different heat transfer conditions on an automotive turbocharger. Int. J. Engine Res. 2015, 16, 137–151. [Google Scholar] [CrossRef]
- Payri, F.; Olmeda, P.; Arnau, F.J.; Dombrovsky, A.; Smith, L. External heat losses in small turbochargers: Model and experiments. Energy 2014, 71, 534–546. [Google Scholar] [CrossRef]
- Marelli, S.; Gandolfi, S.; Capobianco, M. Heat Transfer Effect on Performance Map of a Turbocharger Turbine for Automotive Application. In SAE Technical Paper Series; WCX™ 17: SAE World Congress Experience, APR. 04, 2017; SAE International400 Commonwealth Drive: Warrendale, PA, USA, 2017. [Google Scholar]
- Marelli, S.; Marmorato, G.; Capobianco, M.; Rinaldi, A. Heat Transfer Effects on Performance Map of a Turbocharger Compressor for Automotive Application. In SAE Technical Paper Series; SAE 2015 World Congress & Exhibition, APR. 21, 2015; SAE International400 Commonwealth Drive: Warrendale, PA, USA, 2015. [Google Scholar]
- Baar, R.; Savic, B.; Zimmermann, R. Ein neues Verfahren zur Bedatung von aerodynamischen, thermischen und mechanischen Turboladermodellen. In Der Verbrennungsmotor—Ein Antrieb mit Vergangenheit und Zukunft; Roß, T., Heine, A., Eds.; Springer: Wiesbaden, Germany, 2018; pp. 37–59. ISBN 978-3-658-19290-7. [Google Scholar]
- Savic, B.; Zimmermann, R.; Jander, B.; Baar, R. New phenomenological and power-based approach for determining the heat flows of a turbocharger directly from hot gas test data. In Proceedings of the 12th European Conference on Turbomachinery Fluid Dynamics and Thermodynamics, Stockholm, Sweden, 3–7 April 2017. [Google Scholar]
- Gao, X.; Savic, B.; Baar, R. Conjugate Heat Transfer Simulation of a Turbocharger Radial Turbine for Gasoline Engines. In Proceedings of the 36th CADFEM ANSYS Simulation Conference, Leipzig, Germany, 10–12 October 2018. [Google Scholar]
- Gao, X.; Savic, B.; Baar, R. A numerical procedure to model heat transfer in radial turbines for automotive engines. Appl. Therm. Eng. 2019, 153, 678–691. [Google Scholar] [CrossRef]
- Zimmermann, R.; Baar, R.; Biet, C. Determination of the isentropic turbine efficiency due to adiabatic measurements and the validation of the conditions via a new criterion. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 4485–4494. [Google Scholar] [CrossRef] [Green Version]
- Lim, S.M.; Dahlkild, A.; Mihaescu, M. Exergy analysis on Turbocharger Radial Turbine with Heat Transfer. In Proceedings of the 12th European Conference on Turbomachinery Fluid Dynamics and Thermodynamics, Stockholm, Sweden, 3–7 April 2017. [Google Scholar]
- Diango, A.; Perilhon, C.; Descombes, G.; Danho, E. Application of exergy balances for the optimization of non-adiabatic small turbomachines operation. Energy 2011, 36, 2924–2936. [Google Scholar] [CrossRef]
- Baar, R.; Biet, C.; Boxberger, V.; Mai, H.; Zimmermann, R. New evaluation of turbocharger components based on turbine outlet temperature measurements in adiabatic conditions. In Proceedings of the 15th International Symposium on Transport Phenomena and Dynamics of Rotating Machinery, ISROMAC 2014, Honolulu, HI, USA; 2014; pp. 24–28. [Google Scholar]
- Baines, N.; Wygant, K.D.; Dris, A. The Analysis of Heat Transfer in Automotive Turbochargers. J. Eng. Gas Turbines Power. Apr. 2010, 132, 042301. [Google Scholar] [CrossRef]
- Bejan, A.; Tsatsaronis, G.; Moran, M.J. Thermal Design and Optimization; Wiley: New York, NY, USA, 1996; ISBN 0471584673. [Google Scholar]
- Savic, B.; Gao, X.; Baar, R. Turbocharger Heat Transfer Determination with a Power-Based Phenomenological Approach and a Conjugate Heat Transfer Validation. J. Turbomach. 2019, 141, 021011. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kazemi Bakhshmand, S.; Luu, L.T.; Biet, C. Experimental Energy and Exergy Analysis of an Automotive Turbocharger Using a Novel Power-Based Approach. Energies 2021, 14, 6572. https://doi.org/10.3390/en14206572
Kazemi Bakhshmand S, Luu LT, Biet C. Experimental Energy and Exergy Analysis of an Automotive Turbocharger Using a Novel Power-Based Approach. Energies. 2021; 14(20):6572. https://doi.org/10.3390/en14206572
Chicago/Turabian StyleKazemi Bakhshmand, Sina, Ly Tai Luu, and Clemens Biet. 2021. "Experimental Energy and Exergy Analysis of an Automotive Turbocharger Using a Novel Power-Based Approach" Energies 14, no. 20: 6572. https://doi.org/10.3390/en14206572
APA StyleKazemi Bakhshmand, S., Luu, L. T., & Biet, C. (2021). Experimental Energy and Exergy Analysis of an Automotive Turbocharger Using a Novel Power-Based Approach. Energies, 14(20), 6572. https://doi.org/10.3390/en14206572





