Abstract
The establishment of the concept of sustainable, decentralised, multi-carrier energy systems, together with the declining costs of renewable energy technologies, has proposed changes in off-grid electrification interventions towards the development of integrated energy systems. Notwithstanding the potential benefits, the optimal capacity planning of such systems with multiple energy carriers—electricity, heating, cooling, hydrogen, biogas—is exceedingly complex due to the concurrent goals and interrelated constraints that must be relaxed. To this end, this paper puts forward an innovative new optimal capacity planning method for a first-of-its-kind stand-alone multiple energy carrier microgrid (MECM) serving the electricity, hot water, and transportation fuel demands of remote communities. The proposed off-grid MECM system is equipped with solar photovoltaic panels, wind turbines, a hydrogen-based energy storage system—including an electrolyser, a hydrogen reservoir, and a fuel cell—a hybrid super-capacitor/battery energy storage system, a hot water storage tank, a heat exchanger, an inline electric heater, a hydrogen refuelling station, and some power converters. The main objective of calculating the optimal size of the conceptualised isolated MECM’s components through minimising the associated lifetime costs is fulfilled by a specifically developed meta-heuristic-based solution algorithm subject to a set of operational and planning constraints. To evaluate the utility and effectiveness of the proposed method, as well as the technical feasibility and economic viability of the suggested grid-independent MECM layout, a numerical case study was carried out for Rakiura–Stewart Island, Aotearoa–New Zealand. Notably, the numeric simulation results highlight that the optimal solution presents a low-risk, high-yield investment opportunity, which is able to save the diesel-dependent community a significant 54% in electricity costs (including electrified space heating)—if financed as a community renewable energy project—apart from providing a cost-effective and resilient platform to serve the hot water and transportation fuel needs.
1. Introduction
Under the Paris Agreement, the New Zealand government has committed to reducing greenhouse gas (GHG) emissions by 30% below 2005 levels, by 2030. Based on this commitment and the Productivity Commission’s report, the Ministry for the Environment (MfE) is driving innovations in clean energy technologies and provisions [1,2,3]. The proliferation of renewable energy sources (RESs) and the penetration of green transportation fleets are two major technological trends among a wide range of clean energy initiatives in the energy sector that the MfE is pursuing to move New Zealand towards a sustainable future [1,2,3].
On a higher level, the International Renewable Energy Agency (IRENA) REmap analysis [4] estimates that the share of electricity in total global energy demand would approximately triple by 2050, where non-dispatchable RESs make up around 66% of total electricity generated (see Figure 1). A considerable portion of the projected increase in electricity demand is attributable to the so-called “end-use sector coupling” interventions that involve the electrification of energy demand across different sectors (mainly heat and transport) with the primary goal of increasing the share of renewable energy in other energy consumption sectors [5].
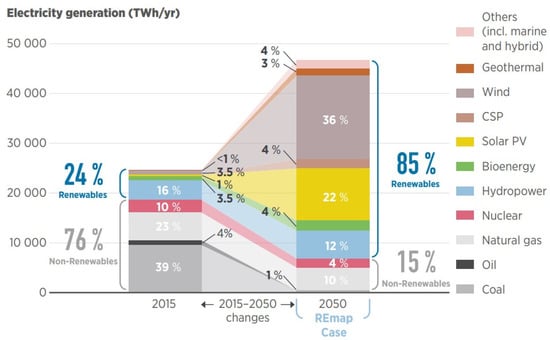
Figure 1.
The 2 °C scenario for electricity generation, REmap case, 2015–2050 [4].
Furthermore, the major shift from synchronous, centralised, fossil-fuel-fired generators to a diversified, heterogeneous combination of renewable energy generation technologies with ever-increasing penetrations of distributed energy resources (DERs) presents potentially significant system balancing challenges given the critical lack of visibility of distribution network operational conditions by system operators in national grids [6,7]—a statement that could similarly be made for the operation of highly renewable off-grid energy systems. In this setting, decentralised smart energy system-based integration of variable renewable energy has been identified as the most promising way of increasing the resilience and reliability of variable renewables-dominated electrical grids—in a cost-optimal manner [8,9]. Moreover, off-grid smart, integrated, renewable energy systems are at the core of “energy for all” initiatives, which are aimed at providing modern energy services to coastal, island, and mountain village communities, as well as, more broadly, rural/peripheral communities [10,11].
In this light, microgrids (MGs) have attracted considerable interest, due to their potential advantages in terms of facilitating the integration of RESs and green transportation technologies into the existing and new energy systems [12]. The so-called multiple energy carrier microgrid (MECM) network refers to an interconnected energy system that provides a platform for linking different energy vectors from varied DERs to meet a variety of energy needs in a region—notably, electricity, heat, and transportation fuel. The MECM model expands on the concept of original electricity demand-oriented MGs with the aspiration of harnessing the interplay between different energy vectors in addressing nearly all the energy needs of communities, whilst improving the resilience, reliability, efficiency, and affordability of renewable energy [13].
Accordingly, this research was motivated by the need to improve the economic viability of smart, integrated renewable energy systems, and particularly off-grid MECMs, which is not only central to the roll-out of variable RESs as part of global efforts to address climate change and energy decentralisation, but is also essential for accelerating universal, democratic, self-sufficient energy access [10].
The optimal equipment capacity planning of an isolated MECM is exceedingly complex due to the underlying intertwined relationships and interactions between several energy carriers. More specifically, it forms a combinational, non-deterministic polynomial time-hard (NP-hard) optimisation problem [14] as a result of: (i) the associated extremely large and non-convex design (search) space, (ii) the presence of several nonlinear constraints involved in its formulation, and (iii) the lack of grid support against the fluctuations of the output powers from RESs—which increases the risk of sub-optimality (oversizing or high excess curtailments). A novel method, based on artificial intelligence-supported meta-heuristic optimisation algorithms, is thus needed to calculate the optimal capacity of stand-alone MECMs’ assets more accurately. Such a method will promote renewable energy systems successfully and effectively in remote areas by reducing the risks of investing in grid-independent renewable energy projects, thereby not only addressing Aotearoa–New Zealand’s climate change and sustainable development policies, but also more broadly as well.
1.1. Literature Review and Knowledge Gaps
A recent, growing body of literature has formulated a range of equipment capacity planning approaches for optimal MECM investment planning modelling frameworks [15,16,17]. The methods in the literature can be broadly categorised into two classes: (1) analytical solution algorithms and (2) meta-heuristic optimisation algorithms. The notable exact mathematical solution algorithms to the optimal MECM sizing problem include linear programming (LP), mixed-integer programming (MIP), mixed-integer linear programming (MILP), and mixed-integer nonlinear programming (MINLP). The major limitation of these solution algorithms is the necessity of several or many decompositions and mean-field approximations, which lead to the loss of parts of the search space—and consequently, a loss of solution fidelity that impairs the solution quality [18]. On the other hand, swarm intelligence-oriented meta-heuristics do not involve any such simplifications of the underlying optimisation problem, but at the cost of relatively substantially higher computational complexities (running times). Yet, despite the fact that the outperformance of meta-heuristics to exact mathematical optimisers has been highlighted in a multitude of energy dispatch and planning optimisation studies [19,20,21,22,23,24,25], the existing meta-heuristic-based approaches in the literature on MECM capacity planning optimisation and, more strikingly, off-grid MECMs, have remained extremely low, as the summary of the most vigorous studies in the literature in Table 1 suggests. The table, furthermore, serves to position this paper within the identified methodological gaps in the mainstream optimal MECM sizing literature.

Table 1.
Summary of the rigorous prior work on the optimal sizing and designing of MECMs.
From Table 1, several methodological and knowledge gaps emerge in the optimal MECM sizing literature, namely:
- A narrow focus on state-of-the-art meta-heuristic-based optimisation algorithms applied to the MECM equipment capacity planning problem;
- General absence of configurations addressing the electricity, space heating, water heating, and e-mobility demands simultaneously, and more particularly, paucity of MECM systems tailored to off-grid applications;
- Negligence of transient power supplies necessary for the stability of MECMs; and
- Lack of multi-energy schemes where the hydrogen energy vector is directly used as a transportation fuel.
1.2. Objective and Novel Contributions
In response to the identified literature gaps, this paper introduces a novel meta-heuristic-based method for the long-term strategic sizing and designing of MECMs. In this context, the main objective of the paper is to generalise the standard MECM designing and capacity planning optimisation problem in several areas to improve the level of the associated analyses, both in terms of the number of energy vectors modelled and energy needs addressed, with a particular focus on applicability in community-scale systems designed for remote areas where grid extensions are not feasible, if not impossible. More specifically, the following novel contributions are made, each addressing one of the above-mentioned four literature gaps:
- Developing a general, meta-heuristic-based solution algorithm for MECMs considering separate reliability indicators for different end-use energy carriers with associated specifically devised rule-based dispatch strategies;
- Conceptualising a fundamentally new off-grid MECM configuration driven by non-dispatchable RESs, and backed by a three-timescale energy storage system to cost-optimally meet nearly all the energy needs of remote and peripheral communities;
- Cost-optimal integration of electric double-layer super-capacitors (SCs) into MECMs, which are associated with high power densities and fast transient response, to serve the transient power load requirements and ensure the stability of such systems; and
- Cost-optimal system integration of a hydrogen refuelling station, where locally-produced green hydrogen is used as an alternative transportation fuel to power fuel cells in various zero-emission vehicles, which benefit from the fast filling time.
1.3. Organisation
The remainder of this paper is organised as follows. Section 2 defines the problem and formulates the specifically developed meta-heuristic-based stand-alone MECM capacity planning optimisation method. Section 3 presents the test-case MECM system and the associated mathematical modelling of its components, whilst additionally providing the input data for the case of Rakiura–Stewart Island, Aotearoa–New Zealand. Subsequently, Section 4 discusses the numeric simulation results obtained from the application of the proposed specifically parametrised method to the test-case system model populated for the site of interest. Finally, conclusions are drawn, and recommended areas for further work are presented in Section 5.
2. Methodology
The proposed meta-heuristic-based MECM capacity planning method seeks to minimise the whole-life cost of the system subject to a set of planning- and operational-level constraints. It provides a platform to ensure the cost-efficiency, sustainability, and reliability of stand-alone MECMs supplying the electricity, transportation fuel, and hot water demands of remote communities. Principally, the proposed method determines the optimum capacity of an MECM’s equipment using the net present cost (NPC) valuations [41], the loss of power supply probability (LPSP) reliability indicator [42], and a state-of-the-art mete-heuristic optimisation algorithm, namely the moth-flame optimisation algorithm (MFOA) [43]. The MFOA is chosen as its superiority to a wide range of well-established and state-of-the-art meta-heuristics in MG capacity planning applications is demonstrated in [25,44], based on rigorous statistical, multi-test-case-oriented analyses. It has also been shown that it is highly stable against the changes in initial guess, and therefore, descriptive statistics analyses, based on several independent simulation runs, are not required [44]. The outperformance of the MFOA can be attributed to its unique search process that uses two types of search agents, moths and flames, enabling it to improve the trade-off between the exploration and exploitation phases by conducting more effective long-range jumps around the global search space and an efficient local search near the global optima.
2.1. Objective Function
The total NPC of the MECM, , is the sum of all the NPCs of the MECM’s components in the candidate pool. The NPC of each component can be calculated by [45]:
where , , , , and denote the optimum capacity, capital cost, replacement cost, operation and maintenance cost, and salvage value of the component, respectively; is the single payment present worth; stands for the capital recovery factor; denotes the real interest rate per annum (6%); and is the expected lifespan of the MECM system (20 years).
The total NPC of the system, , can also be annualised as follows [46]:
Furthermore, the MECM’s levelised cost of energy (NZD/kWh) can be calculated by dividing the total NPC of the system by the total discounted electric, hydrogen, and thermal energy it serves to the customers over the planning horizon [46].
2.2. Constraints
The minimisation of the MECM’s total NPC is carried out subject to the target reliability requirements to supply the electric, heating, and transportation fuel (hydrogen) energy demands. To this end, three separate reliability indices based on the LPSP technique measure the consistency of the supply of electricity, hot water, and hydrogen as a transportation fuel. The LPSP reliability indicator in meeting the electricity/hot water/transportation fuel requirements can be determined by [42]:
where denotes the supplied electric/thermal/hydrogen power, is the demand for electricity/hot water/transportation fuel, and is the total number of hours considered in the operational horizon over which the MECM is representatively dispatched (8760 h). In this study, the LPSP indices are set to 0%; that is, loads are always met.
In addition to the requirement of satisfying the specified reliability criteria, the optimisation problem is subject to a number of other constraints, namely:
- Non-strict equality of the initial and terminal states of energy stored (terminal energy in-store greater than or equal to the initial energy in-store) in the battery bank, the SC bank, and the hydrogen reservoir over an entire representative operational horizon (8760 h); the storage devices are assumed to be half-full-charged at the beginning of simulations to avoid oversizing due to the peaks occurring early in the net load time-series data;
- The demand–supply balance of energy at each time-step of operating the MECM;
- Enforcing the states of energy stored in the SC bank, battery bank, and the hydrogen tank to lie within their pre-defined allowable limits (in percentages) at each time-step of operating the MECM;
- Enforcing the operating points of all the components to lie between zero and the associated rated capacities; and
- Adhering to the pre-specified upper bounds of the design variables (capacity of the MECM’s equipment), in compliance with the target site’s real-world, physical limitations, such as land access.
2.3. Meta-Heuristic Optimisation Algorithm
The non-convexity of the derived objective function, which is subject to several nonlinear constraints, precludes the utilisation of exact mathematical optimisation methods to solve the problem at hand, as illustrated earlier. Accordingly, the MFOA meta-heuristic [43] is utilised to minimise the total NPC of the MECM subject to the formulated constraints. In this study, the population size is considered to be 45 and the maximum number of iterations is set to 300.
2.4. Overview of the Method
Figure 2 shows an overview of the proposed method for the optimum investment planning of the conceptualised stand-alone MECM addressing various energy needs of a remote community. As shown in the figure, first, all input data including the adjusted control parameters of the employed meta-heuristic, hourly forecasts of meteorological and load demand data, techno-economic specifications of the components of the MECM, as well as the project lifetime and real interest rate are loaded. Then, the first estimates of the size of the equipment are determined following the initialisation of the selected meta-heuristic. The system is subsequently operated (Equations (4)–(17)) with an hourly granularity using the first estimates of the equipment size subject to the operational-level constraints, namely the supply–demand balance, as well as the minimum and maximum allowable operating points of the components. At this stage, the LPSP index (Equation (3)) is calculated for each energy carrier and if the associated reliability constraints, as well as the imposed constraints that the terminal energy in-store needs to be greater than or equal to the initial energy in-store for every storage medium, are all satisfied, the algorithm reports the obtained mix of capacities as the cost-optimal choice (Equations (1) and (2)); otherwise, it proceeds to iteratively change the positions of the search agents in the defined solution space (which is bounded by the upper limits of design variables) following the specific rules of the selected meta-heuristic and evaluate the fitness of each design by operating the system for the corresponding size estimates, whilst adhering to the associated dispatch-level constraints, until all the design-loop constraints are relaxed, which yields the desired cost-minimal solution. Accordingly, the inner operational-level if-block is nested within the outer planning-level if-block and, in this way, the overall nested conditional structure ensures that all the constraints that are designed to capture the potential physical, real-world limitations of off-grid MECM installations are adequately met.
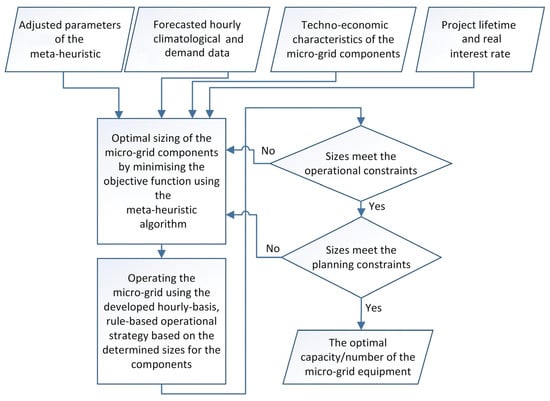
Figure 2.
Flowchart of the proposed optimum MECM investment planning method.
3. Test-Case Off-Grid MECM System
This section mathematically models the components integrated into the conceptualised stand-alone MECM system, the schematic diagram and power flow directions of which are shown in Figure 3.
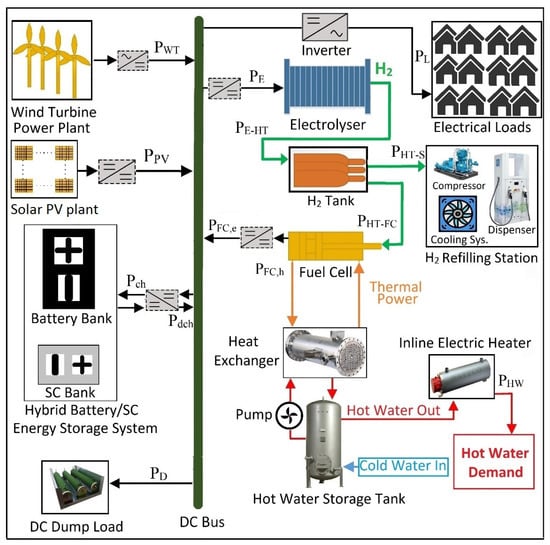
Figure 3.
Schematic diagram and power flow of the conceptualised off-grid MECM system.
3.1. Wind Turbines
Fuhrländer AG’s FL100 (100 kW) wind turbines (WTs) were considered [47]. The output power from the overall WT plant (kW) at different wind speeds is modelled by the following equation [48]:
where is the optimal number of turbines (determined over the course of the iterations of the iterative solution algorithm), is wind speed at time-step , is the turbine’s cut-in wind speed (2.5 m/s), is the turbine’s rated wind speed (13 m/s), is the turbine’s cut-out wind speed (25 m/s), and is the turbine’s rated power (100 kW) [49]. Additionally, the following equation is used to normalise the wind speed profile to the hub height of the selected WT [50]:
where is the reference speed recorded at the height of and is a number in the range (0.1, 0.25) that reflects the status of the terrain on which the turbine is planned for installation. The value of this parameter is 0.25 for the non-flat, tree-covered land considered in this case study [51].
3.2. Solar PV Panels
Canadian Solar’s CS6K-280P (280-W) poly-crystalline solar photovoltaic (PV) panels were considered [52]. The power output from the PV plant at each time-step, (kW), can be calculated as follows [53]:
where is the optimal quantity of panels; is the rated capacity of the panels under the standard test conditions (STC), which equals 0.28 kW; denotes the temperature coefficient of the panel (–0.40%/°C); , , and (25 °C) denote the PV panel temperature, ambient temperature, and the panel temperature at the STC, respectively; and (1 kW/m2) represent the global solar irradiance on the horizontal surface and the solar irradiance at the STC, respectively; and (43 °C) and (85%) denote the nominal module operating temperature and derating factor, respectively. The tilt angle is assumed as 30°. The numeric values 20 and 0.8 represent the ambient temperature (°C) and solar irradiance (kW/m2), respectively, at which the is defined.
3.3. Hybrid SC/Battery System
The energy content of the SC modules and battery packs integrated into the hybrid SC/battery bank at each time-step of the operation of the MECM can be expressed by the following equation:
where is the round-trip efficiency of the SC modules (95%) and battery packs (90%), while and denote the charging power and discharging power of the hybrid SC/battery storage system, respectively.
3.4. Fuel Cell
The electrical output power of the generic polymer electrolyte membrane (PEM) fuel cell unit, which is driven electrically (i.e., it is treated as an electrically lead system) with the associate waste heat considered as a by-product (which is recovered using the heat exchanger), can be calculated by [45]:
where is the fuel cell’s electrical efficiency, which is assumed as 50%, and is the power directed from the hydrogen tank to the fuel cell unit.
The amount of thermal power generated by the fuel cell at a given operating power, , can be determined by [54]:
where is the ratio of the fuel cell’s thermal to electrical output power, which equals 0.8. The water produced by the fuel cell absorbs part of , and the rest of it (here, 65% of ) is used for heat recovery purposes.
The mass of stored hydrogen in the hydrogen reservoir (kg) at time-step can be obtained from:
where is the state of hydrogen energy stored in the tank, is the higher heating value of hydrogen (39.7 kWh/kg [45]), is the power directed from the electrolyser to the tank, is the power directed from the tank to the hydrogen refuelling station, and is the round-trip efficiency of the tank, which is assumed as 98%.
The amount of thermal energy (in the form of hot water) (kW) delivered from the hot water storage tank to the inline electric heater is calculated by [55]:
where is the mass flow rate of the hot water at the tank outlet (kg/h), represents the specific heat capacity of water (4.19 kJ/kg-°C [54]), is the hot water tank’s efficiency (96%), with and denoting the temperature of the water inflowing/outflowing to/from the hot water storage tank, respectively. In this study, is assumed to be constant at 12 °C.
3.5. Other Components
Furthermore, the generic heat exchanger, the inline electric heater, the hydrogen refuelling station, the PEM electrolyser, and the inverter are modelled by their efficiencies, which are set to 90%, 97%, 95%, 60%, and 95%, respectively, in the same way as for the electrical output power of the fuel cell in Equation (10).
The hydrogen refuelling station serves the purpose of refilling the hydrogen fuel cell (HFC)-powered vessels and vehicles. It comprises a high-pressure compressor, a cooling system, and a dispenser, the efficiencies of which are lumped into a single value for the overall system.
3.6. Dispatch Strategy
The output power of the WT and solar PV generation systems, due to their weather-dependent nature, varies temporally—seasonally, monthly, daily, and instantaneously. On the other hand, the variability in electric load demand occurs over a wide range of timescales, from fractions of a second to several months, over a one-year operational planning horizon. Accordingly, three different energy storage systems—the electric double-layer SC bank, the LiFePO4 lithium-ion battery bank, and the stationary hydrogen-based energy storage system—are considered to compensate for the mismatches in supply and demand and meet the net loads (loads minus onsite variable generation). The rationale behind the use of these components lies in their different characteristics in terms of energy and power densities [56]. Specifically, fuel cells and SCs are associated with high energy/power densities, but low power/energy densities; thus, they are best suited to address the mid-to-long-term/instantaneous mismatches in renewable power supply and electricity demand. In addition, batteries bridge the gap between the SCs and fuel cells; they are fit for the purpose of compensating for the daily to weekly fluctuations in supply–demand owing to the intermediary level of both their energy and power densities.
In this light, a rule-based cycle-charging energy dispatch strategy is formalised to decide the operation of the conceptualised off-grid MECM. Accordingly, a low-pass energy filter initially decomposes the non-dispatchable supply–demand mismatch signal into low- and high-frequency components. The low-frequency component is subsequently used to produce hydrogen using the electrolyser or to govern the operation of the fuel cell, depending on the total non-dispatchable power excess or shortage. On the other hand, the high-frequency component is passed through another low-pass energy filter with a higher cut-off frequency, as compared to the previous one. Then, the associated low- and high-frequency components of the second filter’s output are adopted to charge/discharge (depending on the state of the power mismatch) the battery and SC banks, respectively. The corresponding cut-off frequencies of the two filters are optimised by making effective use of a logarithmic transformation in accordance with the technical capabilities of each storage technology, particularly the duration of energy storage capacity per unit of power capacity, whilst additionally leveraging the “roll-off” concept [57]. In mathematical terms, this can be expressed as follows: First, the power mismatch signal is broken down into the low- and high-frequency components using a first-order passive low-pass filter with a transfer function given in Equation (14).
where denotes the cut-off frequency (3.9545 × 10−4 Hz), represents the DC gain (1.586), and identifies the filter quality, with indicating the damping factor (0.707).
By applying the filter, the low-frequency component of the shortage/excess power (addressed by the hydrogen storage system) at time-step can be obtained as follows:
where the value of in the first two time-steps is assumed to be equal to the corresponding value of . That is, and .
The high-frequency component of the excess/shortage signal, which is directed to the hybrid battery/SC bank, can then be obtained as:
A similar process is followed for decomposing the high-frequency component of the mismatch signal to the high and ultra-high sub-components, which are addressed by the respective dedicated battery packs and SC modules. Accordingly, the optimal cut-off frequencies of the first and second filters were determined to be 3.1970 × 10−5 Hz and 8.3331 × 10−4 Hz, respectively. Expectedly, the second filter’s cut-off frequency is greater than that of the first one, as it is geared towards decomposing renewable excess/shortage signals on a finer scale.
The temperature of the hot water demand is enforced to be constant at 40 °C. To this end, an inline electric heater, which is powered by non-dispatchable renewables (solar PV and WT power plants), is used to heat up the water at the tank outlet to the desired temperature of the consumers (40 °C) if the temperature of the water in the tank is below 40 °C. In this way, the inline electric heater acts as a backup to the electrically lead fuel cell for serving the thermal loads. Note that it is by no means optimal to oversize the fuel cell solely for meeting the thermal loads or, more inappropriately, using a thermally lead fuel cell dispatch strategy. This is because both strategies necessitate dumping the excess electric power output from the fuel cell as part of the associated fixed energy management strategies, which would have been indispensable if the inline electric heater was not used as a resource to compensate for any lack of thermal power generation. A dedicated controller also ensures that the temperature of the water stored in the tank does not exceed the acceptable limit of 65 °C, past which curtailing the excess heat is necessary due to the associated technical constraints. Accordingly, it is assumed that the consumers adjust the ratio of cold to hot water to achieve the desired temperature of 40 °C if the temperature of the water outflowing from the hot water storage tank is above 40 °C with a consequent linear decrease in the demand for hot water.
Furthermore, to keep the energy balance of the system, any surplus power beyond the capacity of the electrolyser, hydrogen reservoir, SC bank, and battery bank (across the designated timescales) is used in the inline electric heater to meet the hot water demand—if there exist any as-yet-unsupplied thermal loads. Under this scenario, if the capacity of the heater is not adequate for meeting the thermal demand, the surplus power (beyond the heater’s capacity) is dumped through a DC load consisting of a resistor bank—which increases the loss of thermal power supply probability reliability index. That is, thermal loads are served by a combination of fuel cell generations and inline heater supplies; the former is controlled by electrical loads, whereas the latter is dispatched only during the periods where excess power is present. Moreover, any non-dispatchable power larger than what the overall system can absorb is dissipated in the dump load. On the other hand, when the capacity of the battery bank, SC bank, hydrogen tank, or the fuel cell is not adequate for meeting non-dispatchable power shortages (for electricity supply), load-shedding ensures the MECM system’s power balance, which consequently increases the loss of electric power supply probability.
The power balance problem is solved at an hourly resolution for the baseline year and subsequently, it is assumed that the developed year-long energy dispatch decisions are repeated for each of the ensuing years in the MECM life-cycle. The recurring energy supplies are then discounted in the cash flow (out-years) to the present for the associated levelised cost calculations.
3.7. Data: Techno-Economic Specifications of the Components
The techno-economic specifications of the conceptualised MECM’s components are summarised in Table 2 [25,55,56,58,59,60,61]. The leading brands of equipment in New Zealand’s renewable energy asset market were chosen based on the first author’s judgement of both prevalence and viability, the costs of which are reported in 2019 New Zealand dollars (NZD) in the table—hence, all cost estimates are cited in 2019 NZD throughout this paper (the 2019 annual average exchange rate: NZD 1 = USD 0.69).

Table 2.
Techno-economic specifications of the MECM’s equipment (data sources: [25,55,56,58,59,60,61]).
Table 3 lists the data sources for model scalars.

Table 3.
Data values and sources for model scalars.
3.8. Case Study Site: Rakiura–Stewart Island, Aotearoa–New Zealand
3.8.1. Background
Rakiura–Stewart Island (latitude 46.9973° S, longitude 167.8372° E) is situated approximately 30 km south of the South Island of New Zealand. As of August 2021, it has approximately 405 permanent electricity consumers connected to a distribution network powered by a central diesel power station. The generation plant has a 4(+1) configuration, with a total nameplate capacity of 1646 kW. Several studies have been carried out to examine the economic viability of extending a cable from the port of Bluff on the South Island to Rakiura–Stewart Island, all of which suggested prohibitive capital, replacement, and operation and maintenance (O&M) costs. In this light, the cost of electricity on Rakiura–Stewart Island is higher than that of the national grid electricity provided to customers in the North and South Islands. At around 0.52 NZD/kWh, electricity costs nearly three times that on mainland New Zealand. The current diesel power station operates at an average production efficiency of 4.28 kWh/litre of diesel fuel, while the most recent cost of diesel is approximately 1.75 NZD/kWh. Moreover, each litre of diesel consumed by the existing generators produces 2.7 kg of CO2. Advantageously, local residents believe that reducing the consumption of diesel and developing a renewables-based energy generation system is one of the island’s highest priorities. Collectively, these statistics and facts suggest that using renewable energy rather than fossil fuels to serve the energy needs of the community residing on the ecologically sensitive Rakiura–Stewart Island is of utmost importance [62,63,64].
In this setting, the proposed notional stand-alone MECM could provide clean, reliable, affordable electricity (including space heating loads), transportation fuel, and hot water to the 405-strong remote community residing on Rakiura–Stewart Island. In a systematic study carried out on the assessment of the potentials for the utilisation of RESs on Rakiura–Stewart Island, Mason and McNeil [65] suggested that solar PV and WT power generation technologies are the most technically feasible and cost-effective sources of renewable energy generation among a range of RESs due to the resource abundance and small permanent land and environmental footprints compared to the other options available. This, in retrospect, explains the choice of solar PV and WT generation plants in the proposed stand-alone MECM architecture. However, any other RESs could be readily integrated into the conceptual system, in accordance with the renewable energy potentials of other sites of interest.
3.8.2. Data: Meteorological and Load Demand Forecasts
To forecast the hourly basis, year-round power output profiles for solar PV and WT generation systems, historical solar irradiance, ambient temperature, and wind speed data were first collected from the New Zealand’s National Institute of Water and Atmospheric Research (NIWA) CLiFlo database [66] for Rakiura–Stewart Island for the years 2011 to 2020, and then averaged in intervals of 1 h. The forecasted monthly mean 24-h profiles for solar irradiance (kW/m2), ambient temperature (°C), and wind speed (m/s) are shown in Figure 4, Figure 5 and Figure 6, respectively.
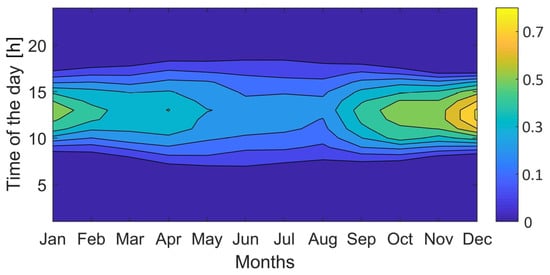
Figure 4.
Monthly mean daily solar irradiance (kW/m2) (data source: [66]).
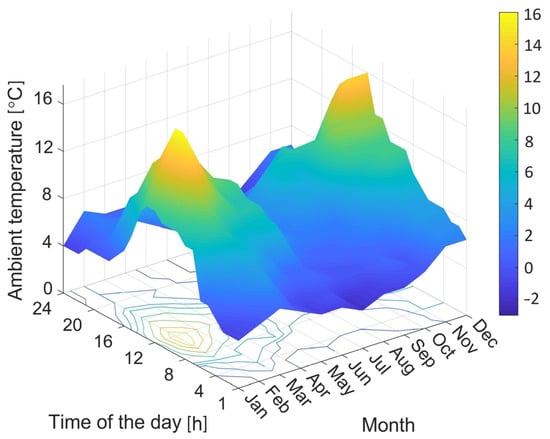
Figure 5.
Monthly mean daily ambient temperature (°C) (data source: [66]).
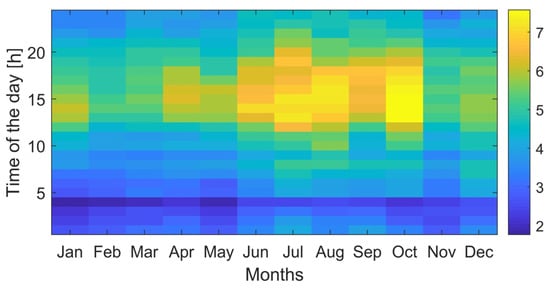
Figure 6.
Monthly mean daily wind speed (m/s) (data source: [66]).
The hourly basis, year-round electrical power load profile is synthesised based on the New Zealand GREEN grid household electricity demand study, which accounts for the space heating energy demand [67]. The hourly basis, year-round thermal load power (hot water demand) profile is synthesised as suggested in [54], assuming that each person uses 44 L of hot water per day. The monthly mean 24-h profiles for the forecasted electric power loads (kW) and thermal power loads (kW) are shown in Figure 7 and Figure 8, respectively. It should be noted that the dispatch decisions are made on an hourly basis and the above-mentioned profiles are presented vs time-of-day (24 h) as averaged over the month only for better visualisation reasons.
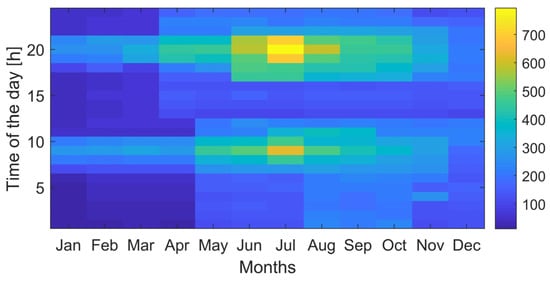
Figure 7.
Monthly mean 24-h electric load (kW) (data source: [67]).
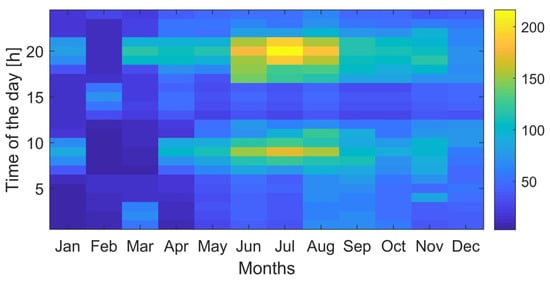
Figure 8.
Monthly mean 24-h heat load (kW) (data source: [54]).
The typical daily profile for hydrogen loads (kg-H2/h) imposed on the conceptualised isolated MECM model—populated for the case of Rakiura–Stewart Island with the goal of decarbonising the transportation sector—is shown in Figure 9. The following assumptions were made in deriving the daily hydrogen load profile:
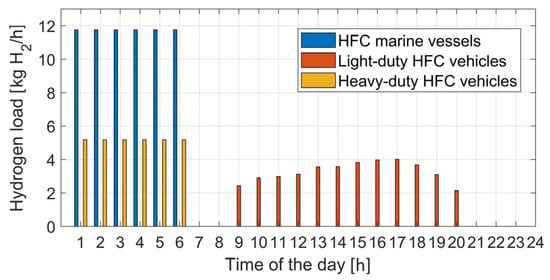
Figure 9.
Typical daily hydrogen load profile (kg-H2/h) (data sources: [68,69]).
- One HFC-powered ferry, five HFC-powered heavy-freight trucks, and five HFC-powered heavy-duty tractors, which can store 208 kg, 32.9 kg, and 8.2 kg of hydrogen, respectively, in their purpose-built carbon composite tanks are considered for integration into the system. The 100-seater marine vessel serves the purpose of transporting the passengers between Rakiura–Stewart Island (at the port of Oban) and the port of Bluff (six crossings per day in summer, and four in winter, and hence, an annual average of five crossings per day), while the trucks and tractors effectively contribute towards achieving the objectives of agricultural sustainability;
- A fleet of thirty 8.5 kW HFC-powered light-duty passenger vehicles also utilise the hydrogen station to refill their 1.5 kg hydrogen tanks;
- A valley-filling energy management scheme that refuels the vessel, heavy-duty tractors, and heavy-freight trucks in the early morning hours (by uniformly distributing their hydrogen loads over the hours 1 a.m. to 6 a.m.) is adopted, while the light-duty passenger vehicles utilise the station randomly during day-time hours (from 9 a.m. to 8 p.m.), following a specifically derived normal distribution; and
- The hydrogen tanks of the light-duty passenger vehicles, heavy-duty tractors, and heavy-freight trucks need to be refuelled from 5% to 100% of their rated capacities every 3, 4, and 5 days, respectively, while the hydrogen tank of the ferry is refuelled from 23% to 100% of its nominal capacity every 2 days [68,69].
4. Numerical Simulation Results and Discussion
The numerical simulation and optimisation of the conceptualised MECM were coded using the MATLAB® software. The optimum combination of the capacity of the MECM’s equipment yielded by solving the formulated problem using the MFOA-based solution algorithm subject to the imposed constraints is presented in Table 4. The minimised total NPC of the MECM system is found to be NZD 7,940,348.

Table 4.
Optimal capacity of the MECM’s equipment.
4.1. Benchmarking the MFOA
To validate the effectiveness of the MFOA in nearing the globally optimum solution of the off-grid MECM design problem, its performance on the test-case under consideration is compared with those of the well-established meta-heuristics in the MG capacity planning literature, namely: the genetic algorithm (GA) [70], the particle swarm optimisation (PSO) [71], the hybrid GA-PSO [72], the artificial bee colony (ABC) algorithm [73], the ant colony optimisation (ACO) [74], and the hybrid ABC-ACO [75]. Table 5 presents the adjusted control parameters of the selected meta-heuristics for the comparative analyses, as suggested by the corresponding developers of the algorithms. The number of search agents (population size) and the maximum number of iterations were fixed at 45 and 300, respectively, for all the meta-heuristics under evaluation.

Table 5.
Developer-suggested parameter settings of the algorithms under comparative analyses.
Table 6 and Table 7 present the comparative results of the efficiency of the meta-heuristics under consideration in nearing the globally optimum MECM design results. Given that the proposed meta-heuristic-based solution algorithm is (inherently) relatively computationally costly to execute, the running times associated with the meta-heuristics of interest were not factored into the comparative analyses. Put differently, the difference in the computational complexity of optimising a solution to the problem at hand using different meta-heuristics is negligible on a percentage basis. In this setting, Table 6 and Table 7 are revealing in the following ways:

Table 6.
Comparative total discounted system cost returned by the evaluated meta-heuristics and the associated CPU usage times.

Table 7.
Comparative resource mix solutions obtained by the evaluated meta-heuristics.
- In the context of off-grid MECM designing and equipment capacity planning optimisation, the performance of the MFOA is superior to the other six meta-heuristics investigated in terms of yielding the least-cost solution. Notably, it outperforms the second-best algorithm (the hybrid GA-PSO) by a significant ~8% (equating to a saving of ~NZD 714,255). The following rank order is achieved for the evaluated algorithms: the MFOA > the hybrid GA-PSO > the GA > the PSO > the hybrid ABC-ACO > the ABC > the ACO.
- Although no significant dependence of the optimal resource portfolio—in terms of the overall configuration and the selected components from the candidate pool—on the chosen meta-heuristic was observed (or in other words, none of the components were rejected and were not even downsized with increases in optimised total system cost due to the sub-optimality of the solutions yielded by the benchmarking meta-heuristics)—to illustrate, in some cases, sub-optimality results in lower than optimum sizes for some of the components at the cost of increases in the size of other components, but this has not occurred here—similar patterns of stagnation in local optima were found in the solution sets returned by the algorithms that have been hybridised. More specifically, although the performance of the hybrid version is slightly better, the GA, the PSO, and the hybrid GA-PSO return practically the same equipment mix (and in turn, practically the same total discounted system cost values), which is also the case for the ABC, the ACO, and the hybrid ABC-ACO. This provides further evidence to support the argument that the hybridisation of meta-heuristics does not necessarily result in improved solution quality in any application.
- The practically unaltered optimal resource mix yielded by the seven meta-heuristics of interest in terms of system configuration indicates that the superiority of the MFOA to the well-established algorithms in off-grid MECM sizing applications stems largely from its well-balanced exploration and exploitation phases, rather than accessing the regions that are invisible to the well-established algorithms. More specifically, the global superiority of the MFOA can be attributed to its unique feature of systematically rebalancing exploration—the early stages of the optimisation process that mimics the long-range movement of individuals—for improved exploitation—the local search around promising regions—of the search space for potential solutions.
Figure 10 displays the comparative convergence patterns of the selected meta-heuristics. As the figure shows, the selected values for the population size and the maximum number of iterations are adequate for the convergence of the studied meta-heuristics. Although the computational speed has not been considered as a criterion for ranking the algorithms, it can be seen from the figure that the MFOA is associated with a comparable convergence point—the iteration after which the meta-heuristic’s returned solution does not change anymore—to the well-established algorithms under consideration. This is the main underlying reason for the observation that the total CPU running (execution) times associated with the algorithms are in the same range as no increased maximum number of iterations is required.
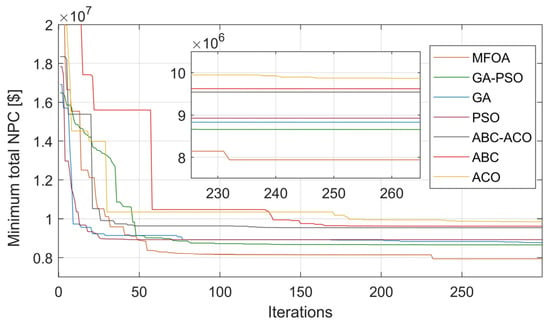
Figure 10.
Comparative running times of the selected meta-heuristics.
4.2. Total Discounted Cost Breakdown
This section presents a breakdown of the total NPC of the simulated MECM system as estimated by the MFOA as the identified superior algorithm. As stated above, the optimal life-cycle cost of implementing the notional MECM on Rakiura–Stewart Island is found to be NZD 7,940,348. The radar chart in Figure 11 shows a breakdown of the total NPC of the MECM into the life-cycle cost incurred by each component in the present value. That is, it depicts the contribution of the associated NPCs of the components to the whole-life cost of the MECM system for the best combination of the component sizes optimised by the MFOA. Although the numbers shown on the graph represent the real NPCs associated with the optimum capacities of the MECM’s components, the chart is plotted on the logarithmic scale for the sake of better visualisation.
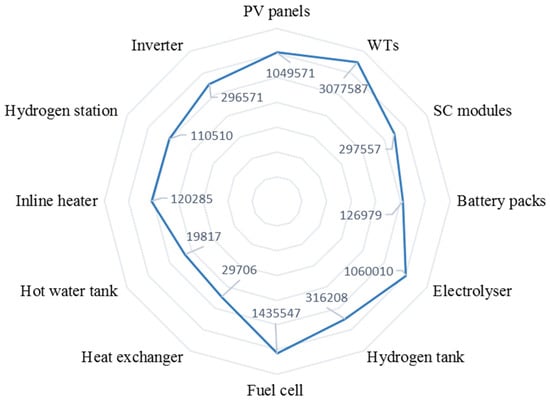
Figure 11.
Breakdown of the optimised total NPC of the conceptualised MECM (NZD).
As can be seen in the figure, the total NPC of non-dispatchable generation systems constitutes the largest cost component (NZD 4,127,158), followed by the aggregate NPC of the hydrogen-based energy storage system’s components: electrolyser, fuel cell, and hydrogen tank (NZD 2,811,765). More specifically, the aggregate NPC of non-dispatchable generation systems (WT and solar PV plants)—as the dominant cost factor for installing the proposed MECM system—comprises approximately 52% of the total NPC of the system, of which 74% is attributable to WTs and 26% is attributable to solar PV panels. The hydrogen-based energy storage system, which represents the second-highest cost factor, accounts for around 35% of the total NPC of the MECM system, of which 51%, 38%, and 11% are occupied by the fuel cell, electrolyser, and hydrogen tank, respectively.
Accordingly, the aggregate NPC of the other components takes up around 13% (equating to NZD 1,001,425) of the expected whole-life cost of the system, with the breakdown as follows: SC bank, 3.7%; loads’ inverter, 3.7%; battery bank, 1.6%; inline heater, 1.5%; hydrogen station, 1.4%; heat exchanger, 0.4%; hot water tank, 0.3%. Note that the (potential) salvage values of the components are factored in the associated component NPC calculations.
It is also noteworthy that the relatively large cost of the fuel cell unit can be explained, in large part, by the observation that it is replaced two times over the lifespan of the project; specifically, in years 8.11 and 16.22 over the 20-year life-cycle of the MECM system. It should be recalled that, unlike all other components, the lifetime of the fuel cell is specified in terms of operating hours. Therefore, the expected number of years of the fuel cell’s service is an output variable, which is determined based on the number of hours it is operated per year, in accordance with the developed dispatch strategy. To illustrate, given that the fuel cell has a lifetime of 10,000 operating hours, the associated expected lifetime of 8.11 years indicates that it operates around 1233 h during one year of the system operation—10,000 h divided by 8.11 years.
4.3. Energy Balance Analyses
This section presents annually resolved energy balance analyses of the conceptualised MECM system, which include an overview of the balance of energy generation and consumption (including energy losses). All the analyses were made based on the least-cost energy mix solution estimated by the proposed MFOA-based method. The resulting values are based on a one-year operational period with hourly granularity under the reliability constraint of maximum LPSP = 0 for all the end-use energy carriers. Note that given the considered 100% energy supply reliability constraint, on any given timescale, the total energy supplied by the onsite DERs is equal to the sum of the total energy demand on the system, the total excess energy curtailed, the total net storage charging energy, and the total losses due to power and energy conversions—and non-ideal characteristics of the associated components. On the other hand, the terminal state-of-charge (SOC) of the storage media are enforced to be greater than or equal to the pre-specified initial energy in-store values (initial SOCs = 50%). Expectedly, the optimal cost solution returns a terminal SOC of 50% for all the storage devices to avoid unnecessary extra allocation (oversizing) of the associated non-dispatchable generation infrastructure. In this light, the annually resolved energy balance analyses could be reduced to the primary energy generation and consumption components. That is, the charging power and discharging power of the storage devices can be excluded from the associated analyses.
The results of the overall energy flow analyses of the conceptual MECM for the generation and consumption components are summarised in Figure 12 in terms of their percentage contributions to the total generation and consumption of energy. Note that, as illustrated above, only the primary sources of energy generation and consumption within the MECM are incorporated in the energy flow analyses. Moreover, while the thermal and hydrogen end-use carriers specifically address the hot water demand and electrified transportation loads on the system, the analysis of energy consumption within the system is not sub-categorised to detail the share of each end-use carrier in the overall energy demand (refer to Figure 7, Figure 8 and Figure 9 for a high-level comparative analysis of the share of each end-use carrier in the overall energy demand), or the specific electrical end-uses of the customers. In the figure, energy generation and consumption are represented by positive and negative signs, respectively. Moreover, the total system losses include: (i) the losses associated with power conversion in power electronics devices (such as the loads’ inverter), (ii) the losses associated with energy conversion due to the non-ideal performances of the energy storage devices and energy conversion components (such as the electrolyser), as well as (iii) the spilled energy in the dump load as a result of producing more non-dispatchable power than the system can absorb. The former two categories of system-wide energy loss are characterised by the associated constant efficiencies of the relevant equipment.
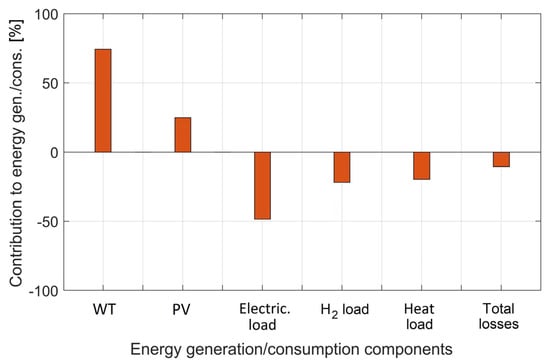
Figure 12.
Breakdown of the generated and consumed energy within the conceptualised MECM.
Accordingly, the results presented in Figure 12 provide an annual energy balance outlook for the notional MECM under consideration. As the figure shows, wind power is the main source of primary energy generation in the system, which makes up around 79% of the total energy supply, whereas the energy generated by the solar PV plant accounts for around 21% of the total supply. On the consumption side, as expected, power loads are the main component of energy use, which account for nearly 48% of the total energy consumption within the system. The other load demand components, namely the hydrogen demand of the station and hot water demand, make up approximately 21% and 19% of the total MECM energy consumption, respectively. Accordingly, the aggregate system-wide energy losses are responsible for approximately 12% of the total energy consumption. The total system losses consist of the energy circulated in the DC dump load as spilled energy (0.9%), the efficiency-dependent power conversion losses in the dedicated power electronics devices (2.7%), as well as the efficiency-dependent energy conversion losses in the energy storage and conversion components (8.4%, in aggregate), with the breakdown as follows: hydrogen-based energy storage system (3.8%), SC bank (1.3%), battery bank (1.1%), inline heater (1.0%), hydrogen station (0.9%), heat exchanger (0.2%), hot water tank (0.1%). Importantly, the negligibly low amount of curtailed energy validates the effectiveness and utility of the devised rule-based energy dispatch algorithm used in the meta-heuristic-based optimal sizing solution algorithm and, more generally, the efficacy of the proposed method in identifying the cost-optimal mix of the assets in the candidate pool—without the overbuilding of non-dispatchable generation technologies.
4.4. Capital Budgeting
To evaluate the financial viability of installing the proposed MECM on Rakiura–Stewart Island, the levelised cost of energy of the MECM model is determined by dividing the estimated total NPC by the total discounted energy it supplies to the electric, heat, and hydrogen loads during its lifespan of 20 years, which is found to be 0.27 NZD/kWh. The levelised cost of energy is then split into the levelised costs of electricity, heat, and hydrogen, considering the fact that only the costs associated with delivering a particular energy service over the MECM’s duty cycle—electricity, heat, or hydrogen—should be factored into the associated carrier-specific levelised cost calculations—and the demand for the other types of energy should be entirely withdrawn from the system. For instance, the hydrogen station, inline heater, and loads’ inverter should only be considered in the calculation of the levelised costs of hydrogen, heat, and electricity. For the components that take part in producing more than one energy type (for example, the fuel cell), the associated NPCs are split according to the percentage of their capacities used to serve the corresponding end-use carriers. Accordingly, the levelised costs of electricity, hot water (for direct use), and hydrogen production using the conceptualised 100% renewable MECM for Stewart Island are determined as 0.24 NZD/kWh, 0.0091 NZD/L, and 6.97 NZD/kg-H2, respectively.
As stated above, presently, the electricity on Rakiura–Stewart Island costs as high as 0.52 NZD/kWh, on average. Furthermore, the most recent studies on renewable hydrogen production in New Zealand have reported the levelised costs of 14 NZD/kg-H2 and 8.91 NZD/kg-H2 for small- and large-scale hydrogen production schemes, respectively [76,77]. Moreover, in general, depending on the availability of RESs, scale of the system, and technologies utilised to heat the water renewably, a litre of hot water is expected to cost between NZD 0.0077 and NZD 0.028 [78].
Based on the above premises, the proposed MECM system, if realised, would impose substantially lower electricity charges on the customers compared to the existing non-renewable power system on the island. It would also produce hydrogen at a levelised cost well below that of the state-of-the-art green hydrogen production schemes, which could facilitate the transition towards a low-carbon transportation system. Moreover, it would be able to satisfy the residential needs for hot water at a levelised cost that is highly competitive with those of the advanced renewables-based technologies and systems for water heating. Thus, it could be concluded that the proposed MECM system introduces a cost-effective plan to realise the targets of decarbonising the island’s energy sector, whilst also improving the site’s energy resilience, reliability, self-sufficiency, security, independence, and adequacy.
In order to further validate the long-term economic viability of implementing the suggested MECM project for Stewart Island, a thorough cost-benefit analysis is carried out using the following three financial sustainability metrics: (1) the discounted payback period (DPP), (2) the profitability index (PI), and (3) the internal rate of return (IRR) [79]. Table 8 presents the obtained values for these economic indicators.

Table 8.
Economic sustainability evaluation of the MECM project under consideration.
The resulting values for the considered financial viability metrics imply that not only is the proposed renewable energy project financially sustainable, but it also could be identified as a low-risk, high-yield opportunity for investment, which creates a steady revenue stream and makes a high return on capital without any subsidies.
5. Conclusions
Energy systems are undergoing a major transition from centralised, top-down structures with a large dependence on fossil fuels to distributed, decentralised, clean energy solutions, in line with efforts on climate change, the depletion of natural resources, and energy security on national and continental scales. The increased focus on renewable energy technologies on such large scales has driven the ever-declining costs of distributed renewable energy generation, storage, and conversion technologies. This, in turn, has facilitated the supply of reliable, affordable, clean energy to millions of people without electricity access living in communities far-removed from national grids through the proliferation of autonomous, low-voltage, low-inertia, local renewable energy networks, in line with the UN’s Sustainable Development Goal 7 towards providing universal sustainable energy access. In this setting, the recent establishment of the concept of renewable multi-carrier MGs has proposed additional changes in the energy industry towards the development of interconnected energy systems tailored to serving nearly all the energy needs of communities in an integrated way.
Accordingly, this paper has demonstrated the economic benefits of developing a sustainable, carbon-neutral, stand-alone MECM system that satisfies nearly all the energy needs—electricity, space heating, hot water, and hydrogen as a transportation fuel—of a remote community residing on Rakiura–Stewart Island, Aotearoa–New Zealand. The conceptualised MECM system is also equipped with a three-timescale energy storage system consisting of an SC bank, a battery bank, and a hydrogen-based energy storage system to support the system in meeting the net load over transient, inter- and intra-day, and seasonal timescales, respectively.
To optimally size the conceptualised system, a novel meta-heuristic-based MECM capacity planning method has been introduced, which considers separate reliability indicators for different energy carriers. A novel rule-based dispatch strategy has also been devised as part of the method to cost-efficiently integrate the fleets of HFC-powered light-duty passenger vehicles, heavy-duty tractors, and heavy-freight trucks, as well as one ferry, into the proposed 100% renewable MECM model, which serves to pave the way towards realising a green transportation system for the island. More specifically, to assist the associated energy planning decision-making processes, the proposed MECM designing method minimises the total discounted system cost subject to the following constraints: (i) the fulfilment of pre-defined reliability levels for supplying the electrical, thermal, and transportation fuel load demands, (ii) the hourly balance between the generated and consumed energy on the MECM’s network over the indicative year-long operational horizon, (iii) the satisfaction of the dynamic stability requirements of the system, (iv) the non-strict equality of the initial and terminal states of energy reserves of the system (terminal energy in-store greater than or equal to the initial energy in-store), and (v) the compliance with the functional and technical characteristics of the employed components.
The proposed energy planning optimisation modelling framework tailored specifically towards small- to medium-scale off-grid MECMs—which is parametrised for the conceptualised test-case system—could be readily adapted for application to other cases, either by incorporating other renewable energy technologies in accordance with the site of interest’s renewable energy potential, or by adding a grid interface for grid-connected systems. Hence, it can provide a credible general path forward in advancing the global transition to a sustainable, low-carbon energy economy.
The effectiveness of the specifically developed MFOA-optimised solution algorithm in yielding the least-cost solutions to the strategic long-term off-grid MECM applications has, furthermore, been validated through comparative analyses of the results with those of the well-established meta-heuristics in the field.
Importantly, the financial appraisal analyses for the case of Rakiura–Stewart Island have indicated that the optimally sized system can save the diesel-dependent community a significant 54% in electricity costs—if financed as a community renewable energy project. However, the contribution of the MECM’s simplified business model and ownership structure to the potential overestimation of the financial viability of the system cannot be ruled out. For example, classifying the consumers as stakeholders would require the system designer to include subsidised costs of hydrogen vehicles/vessels into the model by using appropriate multi-stakeholder business models, which could potentially involve the government, system operator, investors, and consumers. This points to a rich and fruitful ground for future research.
Further work could also seek to add new dimensions to the proposed MECM planning decision-support framework by extending the derived single-objective formulation to a multi-objective optimisation model addressing various conflicting objectives, such as the minimisation of total discounted system cost, maximisation of reliability/resilience/self-sufficiency, minimisation of excess renewable energy generation curtailment, maximisation of system security/adequacy, as well as maximisation of battery utilisation factor and renewables utilisation factor. In addition, future work could seek to systematically quantify the most salient problem-inherent parametric uncertainties, such as the uncertainties in load demand and non-dispatchable (weather-dependent) power generation forecasts.
Author Contributions
Conceptualisation, S.M.; methodology, S.M.; software, S.M.; validation, S.M., A.C.B. and D.B.; formal analysis, S.M., A.C.B. and D.B.; investigation, S.M. and A.C.B.; resources, S.M. and A.C.B.; data curation, S.M.; writing—original draft preparation, S.M.; writing—review and editing, A.C.B. and D.B.; visualisation, S.M.; supervision, A.C.B. and D.B.; project administration, A.C.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mohseni, S.; Brent, A.C.; Burmester, D. A Reliability-Oriented Cost Optimisation Method for Capacity Planning of a Multi-Carrier Micro-Grid: A Case Study of Stewart Island, New Zealand. In Proceedings of the 2019 Electricity Engineers’ Association of New Zealand’s Conference, Auckland, New Zealand, 25–27 June 2019; pp. 1–10, (Preprint version: Arxiv Prepr. 2019, arXiv:1906.09544 [eess.SY]. Available: https://arxiv.org/abs/1906.09544). [Google Scholar]
- New Zealand Ministry for the Environment. About New Zealand’s Emissions Reduction Targets. 2019. Available online: http://www.mfe.govt.nz/climate-change/climate-change-and-government/emissions-reduction-targets/about-our-emissions (accessed on 1 September 2021).
- New Zealand Productivity Commission. Low-Emissions Economy. 2018. Available online: https://www.productivity.govt.nz/assets/Documents/4e01d69a83/Productivity-Commission_Low-emissions-economy_Final-Report.pdf (accessed on 1 September 2021).
- International Renewable Energy Agency (IRENA). Power System Flexibility for the Energy Transition. 2019. Available online: https://www.irena.org/publications/2018/Nov/Power-system-flexibility-for-the-energy-transition (accessed on 1 September 2021).
- Brown, T.; Schlachtberger, D.; Kies, A.; Schramm, S.; Greiner, M. Synergies of sector coupling and transmission reinforcement in a cost-optimised, highly renewable European energy system. Energy 2018, 160, 720–739. [Google Scholar] [CrossRef] [Green Version]
- Power Advisory LLC. Integration of Variable Output Renewable Energy Sources—The Importance of Essential Reliability Services. 2017. Available online: https://www.nrcan.gc.ca/sites/www.nrcan.gc.ca/files/emmc/pdf/17-0071-Essential-Reliability-Services-access-EN.pdf (accessed on 1 September 2021).
- Mohseni, S.; Brent, A.C.; Burmester, D. A Sustainable Energy Investment Planning Model Based on the Micro-Grid Concept Using Recent Metaheuristic Optimization Algorithms. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC 2019), Wellington, New Zealand, 10–13 June 2019; pp. 219–226. [Google Scholar] [CrossRef]
- Burger, C.; Froggatt, A.; Mitchell, C.; Weinmann, J. Decentralised Energy: A Global Game Changer; Ubiquity Press: Berkeley, CA, USA, 2020; ISBN 1911529692. [Google Scholar]
- Mohseni, S.; Brent, A.C.; Burmester, D. Community Resilience-Oriented Optimal Micro-Grid Capacity Expansion Planning: The Case of Totarabank Eco-Village, New Zealand. Energies 2020, 13, 3970. [Google Scholar] [CrossRef]
- Ockwell, D.; Byrne, R. Sustainable Energy for All: Innovation, Technology and Pro-Poor Green Transformations; Taylor & Francis: Abingdon on Thames, UK, 2016; ISBN 131722051X. [Google Scholar]
- Mohseni, S.; Brent, A.C.; Burmester, D.; Chatterjee, A. Optimal Sizing of an Islanded Micro-Grid Using Meta-Heuristic Optimization Algorithms Considering Demand-Side Management. In Proceedings of the 2018 IEEE Australasian Universities Power Engineering Conference (AUPEC), Auckland, New Zeland, 27–30 November 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Phurailatpam, C.; Rajpurohit, B.S.; Wang, L. Planning and optimization of autonomous DC microgrids for rural and urban applications in India. Renew. Sustain. Energy Rev. 2018, 82, 194–204. [Google Scholar] [CrossRef]
- Moghaddas-Tafreshi, S.M.; Mohseni, S.; Karami, M.E.; Kelly, S. Optimal energy management of a grid-connected multiple energy carrier micro-grid. Appl. Therm. Eng. 2019, 152, 796–806. [Google Scholar] [CrossRef]
- Woeginger, G.J. Exact algorithms for NP-hard problems: A survey. In Combinatorial Optimization—Eureka, You Shrink! Springer: Berlin/Heidelberg, Germany, 2003; pp. 185–207. [Google Scholar]
- Klemm, C.; Vennemann, P. Modeling and optimization of multi-energy systems in mixed-use districts: A review of existing methods and approaches. Renew. Sustain. Energy Rev. 2021, 135, 110206. [Google Scholar] [CrossRef]
- Guelpa, E.; Bischi, A.; Verda, V.; Chertkov, M.; Lund, H. Towards future infrastructures for sustainable multi-energy systems: A review. Energy 2019, 184, 2–21. [Google Scholar] [CrossRef]
- Wang, J.; Zhong, H.; Ma, Z.; Xia, Q.; Kang, C. Review and prospect of integrated demand response in the multi-energy system. Appl. Energy 2017, 202, 772–782. [Google Scholar] [CrossRef]
- Bauso, D.; Zhu, Q.; Başar, T. Mixed integer optimal compensation: Decompositions and mean-field approximations. In Proceedings of the 2012 American Control Conference (ACC), Montréal, QC, Canada, 27–29 June 2012; pp. 2663–2668. [Google Scholar] [CrossRef] [Green Version]
- Askarzadeh, A.; dos Santos Coelho, L. A novel framework for optimization of a grid independent hybrid renewable energy system: A case study of Iran. Sol. Energy 2015, 112, 383–396. [Google Scholar] [CrossRef]
- Shang, C.; Srinivasan, D.; Reindl, T. An improved particle swarm optimisation algorithm applied to battery sizing for stand-alone hybrid power systems. Int. J. Electr. Power Energy Syst. 2016, 74, 104–117. [Google Scholar] [CrossRef]
- Mohseni, S.; Moghaddas-Tafreshi, S.M. A multi-agent approach to optimal sizing of a combined heating and power microgrid. arXiv 2018, arXiv:1812.11076. [Google Scholar]
- Mohseni, S.; Brent, A.C.; Burmester, D.; Chatterjee, A. Stochastic Optimal Sizing of Micro-Grids Using the Moth-Flame Optimization Algorithm. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Mohseni, S.; Brent, A.C.; Kelly, S. A hierarchical, market-based, non-cooperative game-theoretic approach to projecting flexible demand-side resources: Towards more realistic demand response-integrated, long-term energy planning models. In Proceedings of the 2020 IEEE 17th International Conference on the European Energy Market (EEM), Stockholm, Sweden, 16–18 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Amir, V.; Jadid, S.; Ehsan, M. Optimal Design of a Multi-Carrier Microgrid (MCMG) Considering Net Zero Emission. Energies 2017, 10, 2109. [Google Scholar] [CrossRef] [Green Version]
- Mohseni, S.; Brent, A.C.; Burmester, D.; Browne, W.N. A Game-Theoretic Approach to Model Interruptible Loads: Application to Micro-Grid Planning. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Ding, X.; Guo, Q.; Qiannan, T.; Jermsittiparsert, K. Economic and environmental assessment of multi-energy microgrids under a hybrid optimization technique. Sustain. Cities Soc. 2021, 65, 102630. [Google Scholar] [CrossRef]
- Ghanbari, A.; Karimi, H.; Jadid, S. Optimal planning and operation of multi-carrier networked microgrids considering multi-energy hubs in distribution networks. Energy 2020, 204, 117936. [Google Scholar] [CrossRef]
- Mansour-Saatloo, A.; Mirzaei, M.A.; Mohammadi-Ivatloo, B.; Zare, K. A Risk-Averse Hybrid Approach for Optimal Participation of Power-to-Hydrogen Technology-Based Multi-Energy Microgrid in Multi-Energy Markets. Sustain. Cities Soc. 2020, 63, 102421. [Google Scholar] [CrossRef]
- Mashayekh, S.; Stadler, M.; Cardoso, G.; Heleno, M. A mixed integer linear programming approach for optimal DER portfolio, sizing, and placement in multi-energy microgrids. Appl. Energy 2017, 187, 154–168. [Google Scholar] [CrossRef] [Green Version]
- Mashayekh, S.; Stadler, M.; Cardoso, G.; Heleno, M.; Madathil, S.C.; Nagarajan, H.; Bent, R.; Mueller-Stoffels, M.; Lu, X.; Wang, J. Security-Constrained Design of Isolated Multi-Energy Microgrids. IEEE Trans. Power Syst. 2018, 33, 2452–2462. [Google Scholar] [CrossRef]
- Ge, S.; Li, J.; Liu, H.; Sun, H.; Wang, Y. Research on Operation–Planning Double-Layer Optimization Design Method for Multi-Energy Microgrid Considering Reliability. Appl. Sci. 2018, 8, 2062. [Google Scholar] [CrossRef] [Green Version]
- Lekvan, A.A.; Habibifar, R.; Moradi, M.; Khoshjahan, M.; Nojavan, S.; Jermsittiparsert, K. Robust optimization of renewable-based multi-energy micro-grid integrated with flexible energy conversion and storage devices. Sustain. Cities Soc. 2021, 64, 102532. [Google Scholar] [CrossRef]
- Wang, J.; Li, K.-J.; Liang, Y.; Javid, Z. Optimization of Multi-Energy Microgrid Operation in the Presence of PV, Heterogeneous Energy Storage and Integrated Demand Response. Appl. Sci. 2021, 11, 1005. [Google Scholar] [CrossRef]
- Lorestani, A.; Gharehpetian, G.B.; Nazari, M.H. Optimal sizing and techno-economic analysis of energy- and cost-efficient standalone multi-carrier microgrid. Energy 2019, 178, 751–764. [Google Scholar] [CrossRef]
- Lorestani, A.; Ardehali, M.M. Optimization of autonomous combined heat and power system including PVT, WT, storages, and electric heat utilizing novel evolutionary particle swarm optimization algorithm. Renew. Energy 2018, 119, 490–503. [Google Scholar] [CrossRef]
- Azimian, M.; Amir, V.; Javadi, S. Economic and Environmental Policy Analysis for Emission-Neutral Multi-Carrier Microgrid Deployment. Appl. Energy 2020, 277, 115609. [Google Scholar] [CrossRef]
- Sanjareh, M.B.; Nazari, M.H.; Gharehpetian, G.B.; Hosseinian, S.H. A novel approach for sizing thermal and electrical energy storage systems for energy management of islanded residential microgrid. Energy Build. 2021, 238, 110850. [Google Scholar] [CrossRef]
- Swaminathan, S.; Pavlak, G.S.; Freihaut, J. Sizing and dispatch of an islanded microgrid with energy flexible buildings. Appl. Energy 2020, 276, 115355. [Google Scholar] [CrossRef]
- Li, R.; Guo, S.; Yang, Y.; Liu, D. Optimal sizing of wind/concentrated solar plant/electric heater hybrid renewable energy system based on two-stage stochastic programming. Energy 2020, 209, 118472. [Google Scholar] [CrossRef]
- Dakir, S.; Boukas, I.; Lemort, V.; Cornélusse, B. Sizing and Operation of an Isolated Microgrid With Building Thermal Dynamics and Cold Storage. IEEE Trans. Ind. Appl. 2020, 56, 5375–5384. [Google Scholar] [CrossRef]
- Rothwell, G.; Gomez, T. Electricity Economics: Regulation and Deregulation; Taylor & Francis: Abingdon-on-Thames, UK, 2016. [Google Scholar]
- Ofry, E.; Braunstein, A. The Loss of Power Supply Probability as a Technique for Designing Stand-Alone Solar Electrical (Photovoltaic) Systems. IEEE Power Eng. Rev. 1983, PER-3, 34–35. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Mohseni, S.; Brent, A.C.; Burmester, D.; Browne, W.N. Lévy-flight moth-flame optimisation algorithm-based micro-grid equipment sizing: An integrated investment and operational planning approach. Energy AI 2021, 3, 100047. [Google Scholar] [CrossRef]
- Hakimi, S.M.; Moghaddas-Tafreshi, S.M. Optimal sizing of a stand-alone hybrid power system via particle swarm optimization for Kahnouj area in south-east of Iran. Renew. Energy 2009, 34, 1855–1862. [Google Scholar] [CrossRef]
- Lotfi, H.; Khodaei, A. Levelized cost of energy calculations for microgrids. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Fuhrländer FL-100 Wind Turbine’s Datasheet. 2019. Available online: https://en.wind-turbine-models.com/turbines/279-fuhrlaender-fl-100-astos (accessed on 1 September 2021).
- Brunetto, C.; Tina, G. Optimal hydrogen storage sizing for wind power plants in day ahead electricity market. IET Renew. Power Gener. 2007, 1, 220–226. [Google Scholar] [CrossRef]
- Li, C.; Liu, Y.; Li, G.; Li, J.; Zhu, D.; Jia, W.; Li, G.; Zhi, Y.; Zhai, X. Evaluation of wind energy resource and wind turbine characteristics at two locations in China. Technol. Soc. 2016, 47, 121–128. [Google Scholar] [CrossRef]
- Amrollahi, M.H.; Bathaee, S.M.T. Techno-economic optimization of hybrid photovoltaic/wind generation together with energy storage system in a stand-alone micro-grid subjected to demand response. Appl. Energy 2017, 202, 66–77. [Google Scholar] [CrossRef]
- Lee, J.; Kim, D.R.; Lee, K.-S. Optimum hub height of a wind turbine for maximizing annual net profit. Energy Convers. Manag. 2015, 100, 90–96. [Google Scholar] [CrossRef]
- Canadian Solar CS6K-270|275|280P PV Module’s Datasheet. 2017. Available online: https://www.collectiu-solar.cat/pdf/2-Panel-Canadian_Solar-Datasheet-CS6K.pdf (accessed on 1 September 2021).
- Patel, M.R. Wind and Solar Power Systems: Design, Analysis, and Operation; CRC Press: Boca Raton, FL, USA, 2005; ISBN 142003992X. [Google Scholar]
- Assaf, J.; Shabani, B. Transient simulation modelling and energy performance of a standalone solar-hydrogen combined heat and power system integrated with solar-thermal collectors. Appl. Energy 2016, 178, 66–77. [Google Scholar] [CrossRef]
- Assaf, J.; Shabani, B. A novel hybrid renewable solar energy solution for continuous heat and power supply to stand-alone applications with ultimate reliability and cost effectiveness. Renew. Energy 2019, 138, 509–520. [Google Scholar] [CrossRef]
- Jacob, A.S.; Banerjee, R.; Ghosh, P.C. Sizing of hybrid energy storage system for a PV based microgrid through design space approach. Appl. Energy 2018, 212, 640–653. [Google Scholar] [CrossRef]
- Mazda, F. Telecommunications Engineer’s Reference Book; Butterworth-Heinemann: Oksford, UK, 2014; ISBN 1483193799. [Google Scholar]
- Sun, S.I.; Smith, B.D.; Wills, R.G.A.; Crossland, A.F. Effects of time resolution on finances and self-consumption when modeling domestic PV-battery systems. Energy Rep. 2020, 6, 157–165. [Google Scholar] [CrossRef]
- Naderi, M.; Bahramara, S.; Khayat, Y.; Bevrani, H. Optimal planning in a developing industrial microgrid with sensitive loads. Energy Rep. 2017, 3, 124–134. [Google Scholar] [CrossRef]
- Erdinc, O.; Paterakis, N.G.; Pappi, I.N.; Bakirtzis, A.G.; Catalão, J.P.S. A new perspective for sizing of distributed generation and energy storage for smart households under demand response. Appl. Energy 2015, 143, 26–37. [Google Scholar] [CrossRef]
- Duman, A.C.; Güler, Ö. Techno-economic analysis of off-grid PV/wind/fuel cell hybrid system combinations with a comparison of regularly and seasonally occupied households. Sustain. Cities Soc. 2018, 42, 107–126. [Google Scholar] [CrossRef]
- Botha, P.; Mills, G. Stewart Island Wind Investigation. Roaring40s Wind Power Limited. 2018. Available online: https://www.mbie.govt.nz/dmsdocument/5768-stewart-island-wind-investigation (accessed on 1 September 2021).
- McNeill, R. A Proposed Way Forward to Deal with Electricity Supply at Stewart Island. Venture Southland. 2007. Available online: https://www.southlanddc.govt.nz/assets/Siesa/docs/11.pdf (accessed on 1 September 2021).
- Stewart Island Electrical Supply Authority (SIESA). What SIESA Does. Available online: https://www.southlanddc.govt.nz/my-southland/siesa-2/what-sieasa-does/ (accessed on 1 September 2021).
- Mason, I.G.; McNeill, R.G. Edging towards sustainability—A 100% renewable electricity system for Stewart Island. In Proceedings of the Electricity Engineers’ Association (EEA) Conference and Exhibition, Wellington, New Zealand, 22–24 June 2016; pp. 1–10. [Google Scholar]
- CliFlo: NIWA’s National Climate Database on the Web. Available online: https://cliflo.niwa.co.nz/ (accessed on 1 September 2021).
- Anderson, B.; Eyers, D.; Ford, R.; Giraldo Ocampo, D.; Peniamina, R.; Stephenson, J.; Suomalainen, K.; Wilcocks, L.; Jack, M. New Zealand GREEN Grid Household Electricity Demand Study 2014–2018; UK Data Service: Colchester, Essex, UK, 2018. [Google Scholar]
- Lee, D.-Y.; Elgowainy, A.; Kotz, A.; Vijayagopal, R.; Marcinkoski, J. Life-cycle implications of hydrogen fuel cell electric vehicle technology for medium-and heavy-duty trucks. J. Power Sources 2018, 393, 217–229. [Google Scholar] [CrossRef]
- Candelaresi, D.; Valente, A.; Iribarren, D.; Dufour, J.; Spazzafumo, G. Comparative life cycle assessment of hydrogen-fuelled passenger cars. Int. J. Hydrogen Energy 2021, in press. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Holland, J.H. Genetic algorithms and machine learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the 1995 IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Kao, Y.T.; Zahara, E. A hybrid genetic algorithm and particle swarm optimization for multimodal functions. Appl. Soft Comput. J. 2008, 8, 849–857. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report-TR06; Erciyes University, Engineering Faculty, Computer Engineering Department: Kayseri, Turkey, 2005. [Google Scholar]
- Dorigo, M.; Di Caro, G.D.; Gambardella, L. Ant Colony Optimization: A New Meta-Heuristic. Proc. Congr. Evol. Comput. 1999, 2, 1470–1477. [Google Scholar] [CrossRef]
- Kefayat, M.; Lashkar Ara, A.; Nabavi Niaki, S.A. A hybrid of ant colony optimization and artificial bee colony algorithm for probabilistic optimal placement and sizing of distributed energy resources. Energy Convers. Manag. 2015, 92, 149–161. [Google Scholar] [CrossRef]
- Watson, M. Could Hydrogen turn Taranaki into the Norway of the Pacific? Available online: https://www.stuff.co.nz/environment/105601987/could-hydrogen-turn-taranaki-into-the-norway-of-the-pacific (accessed on 1 September 2021).
- Concept Consulting Group Ltd. Hydrogen in New Zealand Report 1—Summary. 2019. Available online: http://www.concept.co.nz/uploads/2/5/5/4/25542442/h2_report1_summary_v4.pdf (accessed on 1 September 2021).
- EnergyGuide. How Much Does a Litre of Hot Water Really Cost? Available online: https://www.energuide.be/en/questions-answers/how-much-does-a-litre-of-hot-water-really-cost/2127/ (accessed on 1 September 2021).
- Bierman, J.R.; Smidt, S. The Capital Budgeting Decision: Economic Analysis of Investment Projects; Routledge: London, UK, 2012; ISBN 0203715519. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).