Application of Mobile Energy Storage for Enhancing Power Grid Resilience: A Review

1. Introduction

Natural disasters, such as hurricanes, blizzards, thunderstorms, wildfires, and earthquakes can cause widespread and costly power outages that adversely impact society and the economy. Severe weather is the leading cause of widespread power outages, costing billions of dollars per year due to the dependence of modern society on the uninterrupted supply of electricity. The impact of a power outage increases as more industries move from manual to automated. Many critical infrastructures, such as communication, water, food, defense, transportation, and healthcare rely directly or indirectly on the power grid. A 2012 Congressional Research Service study estimates the inflation-adjusted cost of weather-related outages at $25 to $70 billion annually [1]. The cost of power outages includes lost output and wages, spoiled inventory, delayed production, inconvenience, and damages to the electric grid. Sustained power loss can also affect the provision of health and emergency services during and in the aftermath of the disaster, leading to preventable injury and death. Recent examples of power outages caused by natural disasters include the Hokkaido blackout of 2018 that was due to an earthquake, the South Australian blackout in 2016 caused by a mix of storms, the rolling blackouts in California in 2019 due to wildfires, and the outages in Texas in 2021 due to a winter storm. The number of severe weather events and subsequent power outages is expected to rise as climate change increases their frequency, intensity, and duration. In 2020, the direct economic losses and damage from natural disasters was estimated at $268 billion, stemming from 53-billion-dollar economic loss events around the world, the second highest on record [2].

Beyond weather-related events, distribution systems are increasingly at risk from cyberattacks. The introduction of monitoring and control technologies and the use of advanced communication networks has made the grid more interconnected and hence, more vulnerable to these threats. In 2015, a coordinated cyberattack in Ukraine led to a power outage affecting approximately 225,000 customers and causing a 6-h blackout in and around Kyiv [3,4]. This was the first documented case of a cyberattack bringing down the power grid, and the attack strategy is employable to infrastructures around the world [4].

Improving power grid resilience can help mitigate the damages caused by these events. Power grid resilience has been defined as “the ability to anticipate, resist, absorb, respond to, adapt to, and recover from a disturbance” [5]. According to a 2013 report from the Executive Office of the President, investment in grid resilience will reduce the consequences of a power outage, “saving the economy billions of dollars and reducing the hardship experienced by millions of Americans when extreme weather strikes” [1]. Grid resilience investments include system hardening strategies such as undergrounding wires and upgrading substation components and operational strategies such as deploying microgrids or utilizing distributed energy resources.

Mobile energy storage systems (MESSs) have recently been considered as an operational resilience enhancement strategy to provide localized emergency power during an outage. A MESS is classified as a truck-mounted or towable battery storage system, typically with utility-scale capacity. Referred to as transportable energy storage systems, MESSs are generally vehicle-mounted container battery systems equipped with standardized physical interfaces to allow for plug-and-play operation. Their transportation could be powered by a diesel engine or the energy from the batteries themselves. MESS containers typically hold batteries in addition to systems for thermal management, power conversion, and power control. They may also contain balance-of-system equipment such as transformers [6]. The design, operation, and maintenance of a MESS are governed by IEEE Standard 2030.2.1-2019, which stresses the importance of safety measures including anti-vibration, anti-collision, and waterproof capabilities [7].

Unlike conventional emergency response equipment such as diesel generators, MESSs can operate both during normal conditions and during emergency events. During normal operation, they can provide valuable grid services and capabilities including load leveling, peak shaving, spatiotemporal energy arbitrage, reactive power support, renewable energy integration, and transmission deferral. This ability to provide ancillary services on typical days enables a return-on-investment, which is not common for emergency response equipment. Mobile energy storage does not rely on the availability of fuel supplies, which offers an advantage over portable diesel generators, as fuel supplies may be interrupted or restricted by a disaster. MESSs also do not produce greenhouse gas emissions or create air pollution during operation and can be deployed to help meet clean energy targets. MESSs are typically owned and controlled by utility companies, which offers advantages over other mobile energy resources such as electric vehicle fleets and other resilience enhancement techniques such as demand response. MESSs are not subject to the stochastic behavior and demand of electric vehicle drivers and do not require advanced communication infrastructure, smart meters, or interaction with electricity consumers.

The primary advantage that mobile energy storage offers over stationary energy storage is flexibility. MESSs can be re-located to respond to changing grid conditions, serving different applications as the needs of the power system evolve. For example, during normal operation, a MESS could support an overloaded substation in the summer months, and then move to provide ancillary services in another location once demand drops. This avoids creating stranded assets and saves money compared to multiple stationary energy storage systems [8]. MESSs can also provide energy during emergency conditions and their mobility allows for fast deployment at the location where they are most necessary.

Commercial deployment of MESSs is limited, but expected to increase as the cost of utility-scale batteries continues to fall [6,9]. In 2016, Consolidated Edison of New York announced their plans to develop an 800 kWh MESS unit with Electrovaya, a lithium-ion battery company [10]. Power Edison has deployed mobile energy storage systems for over five years, offering utility-scale plug-and-play solutions [11]. In 2021, Nomad Transportable Power Systems released three commercially available MESS units with energy capacities ranging from 660 kWh to 2 MWh [12]. However, the adoption of MESSs as a resilience resource is hindered by high capital costs, deployment logistics challenges, concerns about interoperability with existing distribution systems, and insufficient connection infrastructure [6]. The capital cost of a standalone, stationary 1 MW/2 MWh battery typically falls between $377/kWh and $831/kWh, depending on the application [6]. The 1 MW/2 MWh Nomad unit has a capital cost of $1,599,000, or ~$800/kWh [13]. In addition to investment costs, battery storage also incurs ongoing operation and maintenance costs. Compared to an ESS, a MESS will likely introduce a cost premium of 5–10% associated with the labor and fuel for transportation [6]. Additionally, the lack of generation during an outage may mean that MESSs are a short-term solution to a long-term problem if they cannot re-charge.

Over the past five years, there has been an increasing interest in using MESSs for resilience enhancement. Researchers have focused on resource allocation to determine the optimal scheduling of a MESS fleet following a resilience event, considering the interactions between MESSs, microgrids, repair crews, and the transportation network. There have been numerous studies that consider the use of MESSs for distribution system resilience enhancement, demonstrating the need for a collective review on the current practices and challenges that face this topic. Review papers on energy storage systems have mentioned MESSs, but to the best of the authors’ knowledge, no comprehensive review exists [14,15]. The remainder of this paper consists of the following sections. Section 2 introduces the concept of power grid resilience and Section 3 describes how MESSs can be used for resilience enhancement. Section 4 presents a review of the current state of the art. Section 5 discusses the gaps in the existing literature and outlines areas of future work, and Section 6 presents the conclusions drawn from this work.

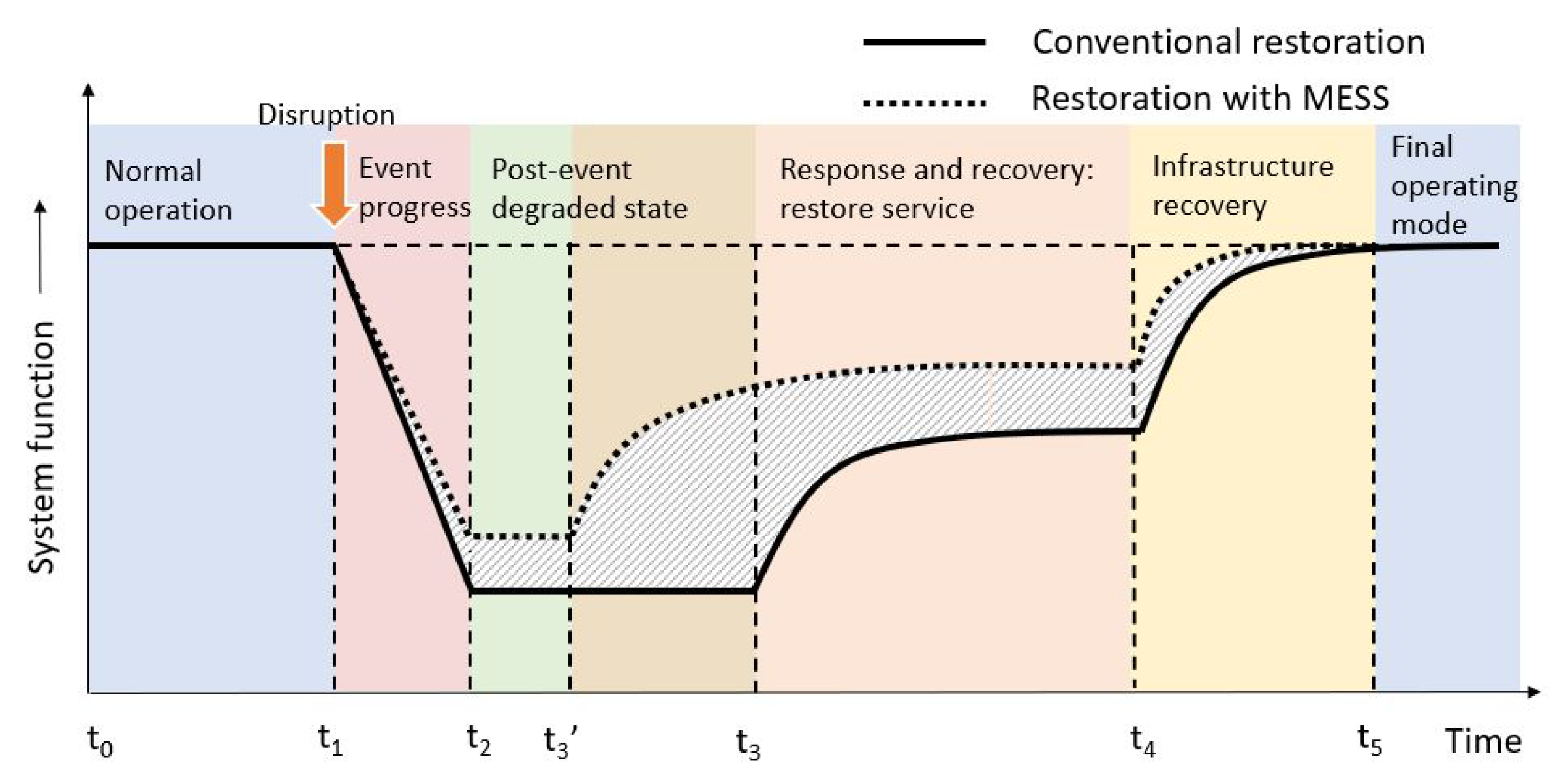
2. Power Grid Resilience

Power grid resilience has recently attracted much attention from both academia and industry. Compared to reliability, which concerns typical, short-term outages, resilience is focused on large-scale disturbances caused by long-duration, high-impact, low-frequency events, such as natural disasters or man-made threats. While reliability definitions and metrics are mature and broadly accepted, resilience definitions vary. Several approaches have been developed to quantify resilience, however, no widely adopted metric is currently in use [16]. While resilience metrics attempt to holistically measure system resilience, resilience evaluation criteria can be used to show how certain measures can enhance total system resilience without having to provide a picture of the overall resilience [17]. Evaluation criteria include performance metrics about the scope and duration of an outage. These include hours of outage, lost load, percentage of customers experiencing an outage, number of critical services without power, and time to recovery [16]. Bhusal et al. [17] and Raoufi et al. [18] provide comprehensive reviews of the current state of the art in power system resilience, detailing potential metrics and evaluation criteria.

Whenever applicable, power grid resilience can be viewed in terms of the timeline of the event under study, i.e., before the event starts, during the course of the event, and during its aftermath. The solutions for each phase, known as preventive, corrective, and restorative mitigation strategies, respectively, need to address different objectives subject to varying types and/or levels of uncertainty. No one-size-fits-all solution exists, and the best resilience strategy may very well vary from one system to another, and from one type of disaster to another.

Preventive strategies are proactive in nature and focus on grid reinforcement to help prevent or minimize the potential impacts of upcoming disasters. These may include hardening substation equipment, hardening control rooms against water hazards or earthquakes, undergrounding lines, deploying distributed energy resources, and/or reconfiguring the network to enable microgrid islanding. Acknowledging the critical role of the control and communication network in maintaining power grid stability during disturbances, some researchers have instead focused on making the IT infrastructure robust [19,20,21]. A downside of these solutions is the normally high costs associated with them, especially given the fact that events of interest are comparatively low frequency (although high impact). Given the constant investments that are needed to maintain utility operations and upkeep, such reinforcement and capacity expansion projects may easily get deprioritized.

Corrective and restorative strategies, on the other hand, are reactive in response to an ongoing or recently terminated event. The goal of both strategies is to utilize the existing power grid resources to maintain connectivity and continue supplying the loads to the extent technically possible. Despite the importance of restoring power once a disturbance has run its course, the power system must continue operating reliably and securely during the event. The colossal amount of destructive energy released by a high-intensity natural disaster event makes it impractical, if not infeasible, to guarantee the availability of all grid components. Hence, the system operator can put in place a predictive control strategy that dispatches the system in anticipation that some sections/resources may become affected by the event and hence may become unavailable. This has been extensively addressed in the literature within the context of security-constrained optimal power flow (SCOPF) [22]. The objective is to ensure that the system remains secure with respect to credible contingencies, and the system constraints are maintained should one of these contingencies happen. While this was traditionally done through performing deterministic contingency analysis and security assessment, utilities are migrating towards more advanced risk-based approaches [23,24]. As opposed to traditional SCOPF-based approaches, risk-based SCOPF attempts to provide a secure solution with less likelihood of exposure to failure by taking into consideration the severity as well as the likelihood of contingency events.

No matter how strong a power system is and how efficiently it is operated once exposed to a natural disaster, it is still possible to be left with large-scale outages due to component failure or damage. This calls for the third category of mitigation strategies: restorative solutions whose goal is to find alternative sources and alternative routes to provide power to as many customers in the outage area as possible while the faulty sections of the grid are being repaired. Grid capabilities, such as microgrid islanding, localized load shedding, and localized power supply through distributed energy resources (DERs), especially units with black start capability, can significantly enhance the chances of a successful restoration of the outage area, whereas the duration of the outage, the expected repair time, the availability of fuel for distributed generators, and the availability of charge in energy storage systems can hinder them.

3. Mobile Energy Storage for Resilience Enhancement

Mobile energy storage increases distribution system resilience by mitigating outages that would likely follow a severe weather event or a natural disaster. This decreases the amount of customer demand that is not met during the outage and shortens the duration of the outage for supported customers. MESSs can be physically dispatched to prioritized locations and critical loads to support emergency response surrounding a natural disaster, providing backup power and black-start services. Mobile energy storage can be used to form a microgrid at a facility or set of facilities with proper connection infrastructure, reducing the amount of lost load during an outage. MESSs can be pre-positioned to vulnerable areas before disaster strikes, be allocated to support outages as the disaster unfolds, or coordinate with repair crews to aid in power system restoration. MESSs can respond quickly to the evolving needs of a community experiencing an outage, providing enhanced resilience and flexibility over stationary technologies [6].

In addition to microgrid support, mobile energy storage can be used to transport energy from an available energy resource to the outage area if the outage is not widespread. A MESS can move outside the affected area, charge, and then travel back to deliver energy to a microgrid. The available resource could be a nearby feeder that is still connected to the transmission system, or a generation resource (such as a utility-scale wind farm or photovoltaic system) that has been stranded due to downed wires or damaged utility infrastructure. This ability to utilize stranded assets could help avoid the economic losses of unused generation. However, if a generation asset or nearby feeder is not available, a MESS is a limited resource, and can only provide backup power with the charge left in its batteries. This may cause customers to lose power once the batteries are depleted, as disaster-related power outages can last days to even weeks. Thus, without the ability to recharge, MESSs are a short-term solution to what may end up being a long-term problem. Additionally, the state of charge of the batteries at the onset of the outage is hard to predict. If the disaster strikes without warning, the batteries may not be fully charged, or worst case may be depleted, rendering the MESS less useful than intended.

Inspired by Bie et al. [5], Mishra et al. [3], and Lei et al. [25], Figure 1 depicts conceptually how MESSs can improve distribution system resilience as an event unfolds. The system function with and without MESSs during the event is shown. For a distribution system, system function in normal operation is the amount of load served, with the highest system function achieved when all demand is met. During an outage, the loads may be weighted by their criticality to give priority to critical infrastructure. The period associated with the event is divided into multiple event stages. These stages begin with normal operation $[t_0,t_1]$, when planning and preventative measures, such as MESS pre-positioning and charging, can take place depending on the advance notice of the disaster. For events, such as hurricanes, blizzards, or wildfires, there may be advance notice of over a day, but for earthquakes or tornadoes there may be less than an hour to prepare [15]. Cyberattacks or other man-made threats may not give any warning.

Following a disruption at $t_1$, the event progresses $[t_1,t_2]$, during which the system function is degraded as damage to the distribution system forces loads to be shed. At $t_2$, the system reaches the post-event degraded state where all system damages have occurred, and no loads are yet restored. In reality, service restoration may begin before all damages have occurred, so the system function after $t_1$ may not be monotonically decreasing. If MESSs are pre-positioned at locations that would otherwise experience an outage, the system function during the event progression and post-event degraded state is improved. Following the degraded state, the response and recovery stage begins where service is restored. With the help of MESSs, service restoration can begin while utility infrastructure is still damaged. Infrastructure recovery begins at $t_4$, where fallen lines or damaged equipment are repaired. At $t_5$, the system has recovered fully and is functioning in its final operating mode. MESSs can improve the system function compared to conventional restoration by energizing loads that would otherwise experience an outage, shown by the dotted line in Figure 1. Additionally, the service restoration time begins earlier (represented by $t_3^{{}^{\prime }}$), and the final operating mode is reached sooner. Overall, the system resilience is improved by reducing the lost load and improving the system function from the solid line to the dotted line. This corresponds to a shorter and less severe outage with MESSs than without.

4. Literature Review

4.1. Scope

This section will review the current state of the art on the use of mobile energy storage for distribution system resilience enhancement and operation in emergency conditions. Along with MESSs, researchers consider the use of other utility-owned and operated technologies including mobile emergency generators (MEGs) and electric buses (EBs) to perform the same resilience enhancement. Coupled together, these technologies are referred to as mobile energy resources (MERs) or mobile power sources (MPSs). MERs all provide backup power during an emergency through the creation of localized microgrids, and their mobility allows for a flexible resilience response. The routing and allocation techniques developed by researchers for any of the MERs can be applied to MESSs. Many of the papers that consider MEGs or EBs have been cited as important related work in studies that consider MESSs. Thus, any paper that includes the use of a utility-scale (100 kW–10 MW) mobile energy resource for distribution system resilience enhancement surrounding a power outage has been included in this review. Vehicle-to-grid strategies that include the use of single or aggregated light-duty electric vehicles for resilience enhancement have been excluded, as they operate on a different scale than MESSs and are not utility-owned or operated resources. MESSs are also studied during normal operating conditions to provide localized ancillary services, such as load leveling, peak shaving, reactive power support, and voltage regulation or to support dispersed renewable energy integration or be used for transmission upgrade deferral [8,26,27]. These cases provide evidence for how MESSs can recoup investment costs during normal operation and provide a benefit beyond resilience but are not included in this study as they do not concern resilience.

4.2. Mobile Energy Resources for Resilience Enhancement

Many studies have investigated the use of MERs for service restoration through proactive pre-positioning and/or real-time allocation. Often, MERs are integrated into service restoration strategies in tandem with network reconfiguration (NR) and the formation of multiple microgrids (MGs), distributed renewable energy generation (DG), and/or demand response programs (DR). Multiple studies also co-optimized and coordinated repair crew (RC) dispatch with MER allocation [28,29,30,31]. Typically, the use of mobile energy storage for distribution system resilience enhancement is approached as a resource allocation problem, the most common formulation being a mixed-integer convex optimization, subject to constraints on MER allocation and operation, network topology and power flow, MER energy capacity, and the transportation system, among others.

Table 1. Survey of previous work on the use of mobile energy resources for resilience enhancement. The arrows indicate that the original formulation is transformed to a more simplified version for better tractability and convergence. The following abbreviations are used: MIQP = mixed integer quadratic program, MILP = mixed integer linear program, MINLP = mixed integer nonlinear program, MISOCP = mixed integer second order cone program, MIQCP = mixed integer quadratically constrained program, MISDP = mixed integer semidefinite program.

Study	MESSs	MEGs	EBs	Formulation	Objective	Coordinated with	Test System Nodes
[32]	-	5	-	MIQP → MILP	Minimize outage duration	-	114
[33]	2	-	3	MINLP → MILP	Maximize resilience	-	123
[34]	4	-	-	MILP	Minimize cost	NR	33
[27]	2, 3	-	-	MISOCP	Minimize cost	MG	15
[25]	1	1	2	MISOCP → MILP	Maximize restored load	NR	33, 123
[35]	-	5	-	MINLP → MILP	Maximize resilience	NR, MG	68
[36]	-	10	-	MILP	Minimize critical load loss	MG	123
[28]	1, 2	1, 2	-	MINLP → MISOCP → MILP	Maximize resilience	RC, NR	33, 123
[37]	4	-	-	MILP	Minimize cost	NR, DG	33
[38]	4	8	25	MILP	Maximize restored load	RC	33
[39]	3, 5	-	-	MILP	Minimize cost	NR, DG	132, 198
[40]	1	1	2	MINLP → MILP	Maximize restored load	NR	33
[29]	-	4	-	MILP	Maximize restored load	DG, RC, NR	123, 8500
[41]	2	-	-	MILP, MISDP, MISOCP	Maximize restored load	DG, NR	33
[30]	-	5	-	MILP	Minimize curtailed energy	NR, RC	47, 123
[42]	1	1	1	MINLP → MILP	Maximize supplied load	NR, DG	33
[43]	4	-	-	Markov decision process	Minimize cost	MG	3 microgrids
[44]	1	2	-	MISOCP	Minimize fuel consumption	DR	37
[31]	2, 3	-	-	MILP	Maximize restored load	RC, MG	33, 69
[45]	-	6	-	MILP	Maximize restored load	-	123
[46]	-	2, 3	-	3-stage stochastic model	Minimize cost	-	13, 123
[47]	-	5	-	MIQCP	Maximize restored load	NR	33
[48]	2, 4	-	-	Non-convex, non-linear → MILP	Maximize the value of supplied load	NR	33, 123
[49]	1	1	-	MILP	Minimize cost	DR, DG	33
[50]	1	1	-	MIQCP	Maximize restored load	RC	15

presents a survey of the previous work on MERs for resilience enhancement, including the formulation, objective, MER technologies considered, and additional technologies that have been coordinated or co-optimized with the MERs.

Researchers have developed multi-stage plans considering proactive pre-positioning and/or real-time allocation of MERs. Lei et al. [32] propose a two-stage restoration plan in which MEGs are proactively pre-positioned before an event and then allocated once after the event strikes to reduce the outage duration of critical loads by forming multiple microgrids. Lei et al. employ the same two-stage framework in [25], which expands the work to also consider EBs, MESSs, network reconfiguration, and dynamic routing and scheduling of mobile resources after a disaster strikes. Instead of minimizing the outage duration, Ref. [25] maximizes the weighted sum of survived or restored loads, which are evaluated using 10,000 Monte Carlo simulations. Lei et al. expand this work once more in [28], which co-optimizes the MER routing with repair crew dispatch and dynamic microgrid formation. In [34,37], Yao et al. develop a two-stage stochastic framework for service restoration after an event strikes to schedule MESSs in coordination with the formation of multiple microgrids. They model the MESS scheduling problem using a time-space network and optimize the service restoration strategy to minimize the total cost, including the customer interruption cost, microgrid generation cost, MESS transportation cost, and battery maintenance cost. Yao et al. extend this work in [39] to implement a rolling optimization framework that dynamically updates road network damage and repair information and coordinates MESS scheduling. Yao et al. adapt the previous works to a deep reinforcement algorithm in [43], using a Markov decision process to formulate the problem instead of the more traditional mixed-integer convex program to increase the computational efficiency. In [34,37,39,43], the charging and discharging patterns of MESSs are modeled as the MESSs move between energized microgrids and those affected by the outage.

Naturally, the costs associated with using MEGs (investment and operation) must be considered to ensure economic viability. Kim and Dvorkin [27] devise a strategy to determine the economic tradeoff between MESSs in normal operating conditions and their economic resilience benefit in emergency response. The two-stage optimization is solved using the progressive hedging algorithm to minimize the operating cost in both conditions, finding that MESSs provide sufficient value in emergency conditions to justify their installation for both types of services. Zhang et al. [46] propose a three-stage stochastic MEG planning model to minimize investment costs and expected penalty costs for load interruptions during outages. Mehrjerdi et al. [49] present a coordinated stochastic plan for MESS operation in integrated electrical and heating networks to minimize operation costs and improve load restoration during electrical or natural gas outages.

Some researchers have proposed solutions for specific types of natural disasters. Gao et al. [33] formulate a stochastic pre-hurricane resource allocation plan to pre-allocate electric buses and MESSs to critical loads to maximize the expected resilience of the system, considering the allocation and transportation costs of each resource. Kavousi-Fard et al. [35] propose a two-stage stochastic post-hurricane strategy again to maximize resilience, considering shortest path and post-hurricane transportation infrastructure constraints. Yang et al. [40] develop a strategy to dispatch MPSs following an earthquake to maximize the total supplied load over the outage period considering the transportation and battery degradation costs. Shi et al. [45] propose a two-stage earthquake-specific restoration plan to maximize the critical load restoration and the restoration path reliability by pre-allocating MEGs in advance and re-allocating them after the earthquake.

As an energy resource, MEG dispatch needs to be coordinated with other energy resources that exist in the distribution system. Ye et al. [29] develop an integrated optimization model for unbalanced distribution system restoration that coordinates distributed energy resources, including renewable energy generation, with MEGs and repair crews. Nazemi et al. [42] formulate a disaster recovery scheme that coordinates network reconfiguration and MPS dispatch while considering the uncertainties of DERs in the system. Nazemi et al. extend this work in [48], developing a plan to coordinate MESS fleets, dynamic network reconfiguration, and renewable energy sources while accounting for their uncertainty and variability. The model maximizes the total value of supplied load as well as the economic value of utilizing renewable energy. Che and Shahidehpour [36] propose a strategy that coordinates MEG dispatch with microgrid formation and load switching sequences to restore critical loads. Bhusal et al. [51] formulate a two-stage framework that determines the minimum MER capacity to perform service restoration when combined with network reconfiguration. Wang et al. [44] describe a plan for an isolated distribution system to survive under limited fossil fuel through the use of MERs, demand response, and renewable energy generation. Prabawa and Choi [41] present a multi-agent system-based approach to coordinate distributed generators, SESSs, and MESSs in a three-layer framework that includes a transportation layer for the MESS routing.

MEGs have also been dispatched in coordination with repair crews for accelerated service restoration. Taheri et al. [30] develop a plan to increase the system survivability through proactive network reconfiguration by utilizing remote-controlled switches, manual switches, and distributed generators, and MEG and repair crew pre-positioning. Ding et al. [31] propose a restoration model that includes repair crews, MESSs, and networked microgrids connected by soft open points, power electronic devices that can replace a traditional tie switch. Xu et al. [38] propose a framework for service restoration considering the dispatch strategy of MPSs and repair crews along with traffic congestion by formulating a weighted dynamic traffic assignment problem to minimize the travel time of the MPSs and the repair crews. For the distribution system, the load restoration problem is formulated to maximize the service time to critical loads subject to unbalanced power flow constraints. Erenoğlu and Erdinç [50] consider traffic congestion when coordinating MEG, MESS, and repair crew dispatch to maximize the power supply continuity and minimizing the battery aging cost of MESSs and the fuel cost of MEGs.

4.3. Power Grid Operational Constraints

The mobility aspect aside, an MER is simply an energy resource. As such, allocating MERs to different load areas within the network would require solving an optimal energy dispatch problem. Such models are solved subject to operational constraints related to active and reactive power flows across the system, MER power output, and node voltages, to name a few. These are modeled as inequality constraints that represent acceptable lower and/or upper bounds for different variables. All papers studied in this survey have included these constraints.

Conventional optimal power flow (OPF) models can be modified to incorporate MERs. Here, the goal is to allocate available energy resources in such a way that it optimizes certain objectives, the most common ones being operation cost and the amount of load served. In [25,39,46], MPSs are modeled as fictitious flows. Kim and Dvorkin [27] and Wang et al. [44] model a computationally tractable second-order cone approximation of the optimal power flow problem for radial topologies based on the work of [52,53,54]. Others use variants of a constrained optimization problem (see Table 1).

Since the problem of allocating MERs is often tied with grid resilience against natural disasters, it is fair to assume that parts of the distribution grid may not be available. This means that network reconfiguration and/or microgrid islanding may be necessary, which can add another layer of complexity to the energy dispatch problem. Kavousi-Fard et al. [35] consider reconfigurable networked microgrids with islanding capability and incorporate switching abilities into the model to determine islanded buses. Ding et al. [31] utilize soft open points, which, during service restoration, can continuously control and regulate power flow and voltage.

In addition to the inequality constraints, some of which are mentioned above, the OPF problem includes equality constraints that represent power flow equations. In the simplest form, this would be a network-wide power balance equation to ensure frequency stability at a high level. However, more realistic OPF models incorporate both active and reactive powers using AC power flow equations. These equations are nonlinear, which can negatively affect both the tractability and the convergence speed of the optimization problem. To address this, many researchers apply linearization techniques to the power flow equations. For instance, in [25,28,30,32,37,39,45,46,50], real and reactive power balance equations at each node are represented based on a linearized DistFlow model. Most studies assume a balanced distribution system, mainly because it can significantly improve the tractability of the optimization problem. However, balanced operation is not necessary a valid assumption for distribution networks, which is why some researchers extend the work to consider more realistic unbalanced three-phase systems. For instance, Gao et al. [33] and Bhusal et al. [51] perform unbalanced three-phase power flow calculations using OpenDSS. Xu et al. [38] consider unbalanced three-phase power flow using a linear approximation model of the optimal power flow problem. Ye et al. [29] use the same approach for dynamically formed microgrids.

4.4. Transportation System

The use of mobile energy resources for distribution system resilience includes two separate problems: the resource allocation problem, and the routing problem. While some studies simply solve the resource allocation problem, i.e., assigning MERs to assist specific loads, a realistic scenario involves an additional routing problem within the transportation network. This imposes additional constraints including travel times, road congestion, and potential road network damage. Researchers have integrated transportation cost into the objective function to minimize the travel time of the MER as redundant travel causes extra cost [25,33,34,37,46]. As the unit transportation cost decreases, the benefit of the MER increases due to their increased allotment [33,37]. Gao et al. [33] assume a constant unit transportation cost of $0.5 per mile per kWh and $10 per mile per bus for MESSs and EBs, respectively. Yao et al. [34,37] assume a constant transportation cost of $80 per transit [37], omitting the important considerations of travel time and distance, road network damage, and road congestion issues which may impact the allocation results. In [43], a unit transportation cost of $80 per hour is used, which accounts for travel time. A measure of transportation cost is helpful when the objective is formulated to minimize the operating cost, but the uncertainties surrounding travel time that stem from possible road damage or congestion cannot be ignored in a realistic scenario.

Multiple studies use Dijkstra’s shortest path algorithm to compute the shortest path from an MER staging location or initial position to the restoration area, which is used to find the optimal routing of the MER [27,32,35,39,41,43,51]. A shorter path corresponds to a shorter traveling time, which allows MERs to serve loads for a longer amount of time, increasing system resilience. Lei et al. [32] and Kim and Dvorkin [27] used Dijkstra’s shortest path algorithm to derive the travel time of each MEG but did not consider potential damage or road congestion issues in the network during real-time allocation. Kavousi-Fard et al. [35] and Prabawa and Choi [41] use Dijkstra’s algorithm to produce the shortest path for MER routing while avoiding damaged roads. As road damage increases, so does MER travel time. In [35], MER travel time is modeled as a random variable by a stochastic framework based on the unscented transform, which can model high uncertainty with less computational burden than the traditional Monte Carlo simulation. Buses with the shortest path from the MER’s initial locations are prioritized for restoration. Bhusal et al. [51] use Dijkstra’s algorithm to determine the optimal routes with which to reach isolated areas, and the resulting travel times are incorporated with a sequential Monte Carlo simulation-based approach to determine the optimal size of MERs for service restoration and reliability enhancement.

Yao et al. [37,39] employ a time-space network model to represent the trips of MESSs including transit and parking arcs but disregarding traffic flow issues or congestion. Wang et al. use the same time-space network to model the travel behavior of MERs in [44]. Additionally, in [39], a scenario-based stochastic model is adopted using the Monte Carlo method to account for road network damage and repair, and Dijkstra’s algorithm is used to calculate the shortest path to minimize travel time. In [43], the transportation network is modeled as a weighted graph and it is assumed that MESSs always take the shortest path as determined by Dijkstra’s algorithm. Ye et al. [29] use a three-dimensional binary variable to represent the temporal-spatial status of a MEG with specific logistics differences between parking and traveling.

Road congestion has been considered in recent studies. Xu et al. [38] consider dynamic traffic flow in the transportation system to inform routing decisions of MPSs and repair crews through a weighted dynamic traffic assignment (WDTA) problem based on the cell transmission model. The WDTA determines the routes and travel times of MERs to minimize the total weighted travel time of all vehicles based on damaged roads and current traffic flow information. MER travel time then determines when they can be used for service restoration. Taheri et al. [30] extracts the required travel time from Google Maps and investigates the sensitivity of the restoration process to traffic congestion through the use of a traffic congestion factor, defined as an after emergency traveling time divided by the normal condition traveling time. Erenoğlu and Erdinç [50] consider traffic congestion and road damage deterministically by assuming that they happen on a specified road in a certain time frame to demonstrate the impacts of traffic congestion on system operation. When making assumptions about the transportation network, uncertainties surrounding travel time, road damage, and congestion should be considered stochastically.

4.5. Resilience Evaluation and Quantification

As discussed, MERs can be allocated to increase power grid resilience through the restoration of critical loads. As mentioned in Section 2, definitions of power system resilience vary and there are no widely adopted metrics in use to measure power system resilience. The concept of power system resilience is mentioned in every paper included in this survey, although the definitions vary between authors. Many researchers claim that their mobile energy resource strategy is resilient, or that it enhances resilience compared to normal operation or other strategies that use different technologies. However, most of these studies fail to include a quantifiable metric with which to measure resilience enhancement. Where data do exist, the use of different metrics makes it hard to compare between studies or against other resilience enhancement strategies. A few papers tailor their strategy to a specific resilience event, which cannot be generalized to any potential outage. Many rely on case studies to test the effectiveness of their proposed plan, Lei et al. [25,32], Gao et al. [33], Kavousi-Fard et al. [35], and Yao et al. [37,39] include a discussion of the conceptual resilience curve presented by Panteli and Mancarella [55], which depicts the change in system performance function during an outage, using the curve to show how mobile energy resources can conceptually improve resilience. Gao et al. [33], Kavousi-Fard et al. [35], and Lei et al. [28] all employ a commonly used metric that measures system resilience, R, as the integral of the system performance function over the outage period minus the allocation cost. The system performance is defined as the total power supplied to critical loads weighted by their priority. Enhanced resilience corresponds to increasing R. This resilience measure is then maximized in the optimization problem to determine the optimal tradeoff between MER allocation and cost. In [29,31], the problem is solved stochastically, hence, R represents the expected value of resilience. In [28], Lei et al. co-optimize distribution system restoration with MER allocation and repair crew dispatch to maximize system resilience.

Malek et al. [47] introduce a set of time-dependent resilience metrics to quantify the resilience enhancement of MEGs combined with network reconfiguration. Three states are considered: the event progression state, the post-event degraded state, and the restorative state. In the event progression state, the severity of load interruption is calculated along with the total time of disturbance, measured in kWh and hours, respectively. In the post-event degraded state, the expected load supply is calculated for a service restoration solution along with the total time taken to execute the restoration plan, measured in kW and hours, respectively. Finally, in the restorative phase, the actual amount of load restored is calculated and measured in kWh along with the restoration period, measured in hours. Malek et al. [47] use these resilience metrics to compare multiple options to determine the optimal restoration plan, finding that the presence of MEGs increased the resilience of the system compared to network reconfiguration alone. While they do not include a measure of overall resilience, [27,30,40,49] employ lost load as a resilience evaluation criteria to show resilience enhancement. A reduction of lost load (measured in kWh or MWh) corresponds to enhanced resilience. In [27], Kim and Dvorkin use the resilience evaluation criteria of lost load to show how their post-disaster allocation of MESSs enhances the distribution system resilience compared to a system without energy storage or one with stationary energy storage.

Related to the concept of resilience is the idea of survivability, discussed in [25,30,33,36,42,44,50]. The Electric Power Research Institute describes survivability as an aspect of resilience, defined as “the ability to maintain a basic level of electricity service to customers” when electricity supply is interrupted [56]. Like resilience, survivability does not have an agreed-upon metric, making it difficult to measure or prove that a strategy can increase survivability. Gao et al. [33] use failure probabilities to estimate the survivability of specific restoration paths, defining a path with high survivability to be likely to maintain function after a hurricane. Paths with high survivability (low failure probability) are preferred when the resource allocation plan is created. However, the authors do not claim that their plan would strengthen the survivability of the system. Conversely, in [25], Lei et al. develop a two-stage restoration plan where the first stage is meant to directly increase survivability through the pre-positioning of mobile power sources (including EBS, MEGs, and MESSs) at critical loads. They measure survivability as the survived electricity supply to critical loads, and their results indicate that pre-positioning MPSs can greatly enhance the system’s survivability. Similarly, Che and Shahidehpour [36] quantify survivability enhancement as a strategy the reduces the loss of critical loads following an outage compared to the base case. Their strategy to restore service using a combination of adaptive microgrid formation, load switching sequences, and mobile emergency resource positioning effectively enhances survivability. The authors extend the result of enhanced survivability to contend that their strategy enhances resilience. However, their work lacks a clear connection between the two terms or a metric for resilience, and that claim is unsubstantiated. Taheri et al. [30] use an increased percentage of served load to represent the increased survivability from their strategy that combines MEG pre-positioning and real-time allocation with network reconfiguration and distributed generation. A metric for survivability was not included in [42,44,50], which makes it difficult to measure the effectiveness of these strategies in reaching that goal.

Some studies develop their strategy around a particular resilience event. In [32,33,35], post-hurricane restoration strategies are developed through the use of failure probabilities and fragility curves to estimate the damage to the distribution system likely caused by a hurricane. In [40,45], the restoration plan is specific to earthquakes. Shi et al. [45] also employ failure probabilities to create a fragility curve for the distribution system to earthquakes. While the use of failure probabilities and fragility curves give a good picture of a specific system’s risk, these case studies cannot be generalized to the effectiveness of the strategy to protect any system from an unexpected resilience event. This limits the results of the studies as resilience can be event-specific, but the events are not well anticipated. A system that is resilient to hurricanes may not respond the same to an earthquake or wildfire, so testing against a generic resilience event is preferred.

Most of the studies considered in this review also use specific case studies to demonstrate the effectiveness of their strategies, assuming that the distribution system is isolated from the rest of the grid [34,38,49], or that specific lines or branches are damaged [28,29,31,36,37,41,42]. In [30], fragility curves are used to determine the failure probability of the distribution system components and predict possible outages from an upcoming disturbance. A more thorough approach is considered in [25], where 10,000 Monte Carlo simulations are conducted to evaluate the effectiveness of their proposed strategy. Similarly, Bhusal et al. [51] used sequential Monte Carlo simulations to model potential outages within the distribution system based on reliability and historical outage data. However, this work considered reliability, not resilience, so the work may not extend to large-scale, long-duration outages.

4.6. The Costs and Benefits of MESSs for Service Restoration

Many researchers have formulated strategies to minimize the cost of the outage and the MESS service restoration plan, including the customer interruption cost, the operation, and maintenance cost of the MESSs, and the transportation costs [27,34,37,39,43,46,49]. These plans attempt to balance the costs and benefits of using MESSs for resilience enhancement. However, while the costs of these technologies are relatively clear (e.g., the capital cost of purchasing a MESS and the operation and maintenance costs of batteries), the benefits are harder to assess.

A MESS generates value under emergency conditions by re-energizing loads during an outage, thereby avoiding the economic losses that those customers would otherwise incur. Thus, to quantify the benefit, it is necessary to understand how customers value uninterrupted electricity. The cost of an outage varies by customer, duration, and magnitude [57]. For example, for industrial or commercial customers, outage costs can be represented by the lost profit during the outage. For residential customers, outage costs are less straightforward, including spoiled food, loss of leisure, and discomfort [57]. Given the increase in home-based therapies (e.g., dialysis), loss of power can at times be life-threatening even for residential customers. Outage costs can accrue over time, growing non-linearly throughout an outage [16,57,58].

Methods to estimate customer interruption costs can be classified as either economy-wide or bottom-up [58]. Economy-wide approaches measure how outages affect economic performance, and while they are useful on a macro level, they cannot be applied to individual customers [57]. Conversely, bottom-up approaches apply to individual customers and assess the value of resilience based on stated or revealed preferences, usually obtained through customer surveys [58]. While surveys are widely seen as the best way to gather data about customer interruption costs, they are expensive and time-intensive to conduct and rely on answers to hypothetical questions [58]. Further, they may not be easily generalizable across different geographical areas and/or demographics. Existing surveys are limited, and often do not consider long-duration outages beyond 24 h [57,58]. Value of lost load (VoLL) is an example of a bottom-up approach commonly used to estimate customer interruption costs. VoLL is a monetary metric based on stated customer preferences, where contingent valuation is used to determine an approximate price that customers are willing to pay for uninterrupted electricity. VoLL is estimated separately for residential, commercial, and industrial customers because the impact of an outage varies significantly between types of customers. For simple analyses, VoLL is often defined as a static $/kWh metric that does not vary with outage duration. However, research suggests that customer outage costs may compound throughout a long-duration outage, so it is important for resilience analysis to consider how VoLL changes with time [16,59]. A static VoLL has been traditionally applied to reliability analysis, and may not be appropriate for resilience, which deals with much longer outages, as research has shown that outage costs compound over time [16,58].

Research on the use of mobile energy resources for resilience enhancement has limited the customer interruption cost to a static VoLL. Gao et al. [33] estimate a “supply benefit” of $50/kWh for critical loads and $10/kWh for non-critical loads. Kim and Dvorkin [27] use a constant $5/kWh in their approach to optimize investments in MESS units. Yao et al. [34,37,39,43] use a value of $2/kWh or $10/kWh, with the higher VoLL representing critical loads. Similarly, Nazemi et al. [48] assign a value between $2/kWh and $10/kWh depending on the customer’s criticality. Zhang et al. [46] vary the VoLL, using values of $4/kWh, $14/kWh, and $57/kWh to determine the sensitivity of MEG planning to VoLL. In no case do the values vary by outage duration, which is inconsistent with the current understanding that outage costs accrue over time. Without an accurate representation of outage costs, it is difficult to accurately estimate the benefit that MESSs can provide, making it difficult for utilities to balance the costs and benefits of the technology or to make an informed investment decision.

5. Discussion

5.1. Research Gaps

While considering the energy dispatch problem of MESSs, the current literature has examined active and reactive power to ensure frequency and voltage stability, respectively. However, if the system has rotating masses in the form of large motors or synchronous generators, dynamic stability needs to be studied as well. Currently, small-signal and transient stability are not considered in the literature as the analysis occurs on the order of every hour and thus allows for the assumption that dynamic stability can be disregarded. However, as the scale of the power system studied decreases, these assumptions may no longer hold; so, it may be necessary to consider dynamic stability for a MESS serving a microgrid or a network of microgrids. Similarly, with MESSs supplying smaller microgrids, voltage and power quality events may become more critical because the system is likely to be less stiff. Additionally, while balanced and unbalanced three-phase systems have been evaluated, no researchers have discussed the potential presence of asymmetry in the distribution system and how that may affect MESS service restoration.

Although MESSs are believed to enhance power grid resilience, the current literature lacks a unified approach to evaluate the effectiveness of their proposed strategies to achieve this goal. It is not enough to state that a measure will enhance resilience, a qualitative analysis is necessary. The absence of agreed-upon resilience metrics makes it challenging to prove resilience enhancement. Additionally, it is difficult to compare existing MESS strategies and to compare MESSs against similar technologies that also increase resilience. Therefore, future work must include a well-defined resilience metric. The same resilience metric can then be used to compare existing strategies such as those presented in this review, or to compare MESSs against stationary energy storage, network reconfiguration, demand response, or distributed energy generators. Often, these technologies may be deployed simultaneously, and a strong resilience metric can help optimize the system of resilience technologies for a specific application. This will create quantifiable results to point towards the best application for MESSs for a given situation. Even when a metric is employed, the method of evaluating the effectiveness of a strategy is often limited to case studies that contain single pre-defined outages, which does not produce a robust measure of the expected resilience enhancement. A stochastic, risk-based approach could improve the measurement of the resilience enhancement for a specific system.

While existing literature has acknowledged the potential costs and benefits of MESSs for resilience enhancement through critical load support, the evaluation is simplistic and unrealistic. The benefits have been evaluated as a reduction in customer interruption costs, which has been modeled using the value of lost load. However, the use of a constant value of lost load does not represent how outage costs evolve and compound throughout a long-duration outage. Additionally, the costs are not representative of the diverse set of customers that could be affected by the outage. Future work should employ duration-dependent outage cost functions that vary based on the customer they represent to better estimate the benefit of increasing resilience and avoiding outage costs. Furthermore, current benefits are calculated based entirely on the monetary costs of an outage. The consequences of a disaster can be exacerbated by social, economic, or political conditions, which are not accounted for in these monetary costs. To properly address issues of equity within MESS power system restoration, it may be necessary to include a social vulnerability index to ensure that non-monetary costs are accounted for. An accurate representation of outage costs can help better estimate the resilience benefit of MESSs, which can help entities make informed investment decisions. Future work can use these benefits in a full cost–benefit analysis of MESSs, considering the stacked benefits achieved from both normal operation and emergency response and the operation cost of a MESS in both situations. Since MESS restoration is limited by the battery capacity and the availability of an energy resource to recharge from, their benefits may only be realized in a small time interval. A cost–benefit analysis is necessary to determine if that time interval is sufficient to offset the costs of deployment.

5.2. MESS Challenges and Opportunities

A primary challenge when deploying MESSs for service restoration is that they are finite energy resources if not recharged. Thus, MESSs may act as short-term solutions to long-term problems in the case of extensive infrastructure damages. Researchers have considered the charging and discharging patterns of a MESS combined with microgrids in specific case studies, but that work could be extended to evaluate where additional reinforcement is necessary to create areas where a MESS can charge during an unexpected outage. Alternatively, MESSs themselves could include integrated renewable generation such as photovoltaic (PV) panels or micro wind turbines to allow for on-site charging.

In either case, the capacity of one MESS may not be sufficient to restore power to the entire outage area. In that case, MESS deployment may need to be coordinated with demand response or load shedding as suggested in [44,49]. Further research could examine how to perform load shedding for residential, non-controllable loads or how to implement programs to reduce power consumption once a customer’s power has been restored by a MESS. Alternatively, a load area could be broken into multiple microgrids so that the MESS capacity can support the entire smaller system. While microgrid formation and MESS deployment have been well studied, the MESS allocation problem could be combined with mobile switching and separation devices to implement network reconfiguration and adaptive microgrid strategies on systems with fixed separation points.

5.3. MESSs vs. Electric Vehicles for Resilience Enhancement

In addition to the mobile energy resources (MESSs, mobile emergency generators, and electric buses) discussed in this review, electric vehicles can act as an energy resource to aid in service restoration [60]. The use of electric vehicles for grid support, or vehicle-to-grid (V2G) technologies, has been well studied, and while V2G can serve the same applications as MESSs, there are several key differences to the deployment strategies. One advantage of V2G over MESSs is that electric vehicles are more dispersed and distributed, and are therefore able to support loads across a wider geographic area. While EVs have much smaller batteries than MESSs, on aggregate, they can represent a resource of a similar scale. However, because EVs are not utility-owned or controlled like MESSs, V2G requires advanced communications and economic incentives to coordinate them for power injection and grid support. In addition, the point of entry to the grid would differ between EVs and MESSs, as MESSs typically connect to a substation, whereas EVs would have to plug in at a dedicated charging station.

6. Conclusions

In the face of natural disasters that are exacerbated by climate change, it has become increasingly important to increase power grid resilience. More resilient power systems can better prepare for, withstand, and recover from disasters, avoiding the social and economic costs of a power outage. Mobile energy resources, specifically MESSs, can increase power grid resilience by restoring power to critical loads following a contingency. Their mobility allows for increased flexibility compared to stationary DERs. MESSs can also provide ancillary services during normal operation, recouping investment decisions, a rare ability for emergency response equipment. As the cost of batteries continues to decrease, commercial deployment of MESSs will likely grow.

This paper provides a comprehensive review of the use of mobile energy resources (including MESSs, EBs, and MEGs) for resilience enhancement. The routing and scheduling optimization problem formulation is discussed along with the constraints imposed by both the power system and the transportation system. Major gaps in the literature stem from a lack of consensus surrounding qualitative metrics with which to measure power grid resilience and subsequent improvements, as well as simplistic and unrealistic models of the customer interruption costs for a long-duration power outage. Risk-based and stochastic analyses are necessary to quantitatively measure resilience enhancement and compare MESSs against other similar technologies. To support informed MESS investment decisions, the customer interruption cost during an outage should be modeled to represent different customers and how costs can accrue throughout a long-duration outage.

This study only considers the use of MESSs in emergency conditions to restore power following an outage, but other applications during normal operation exist. These include load leveling, peak shaving, reactive power support, voltage regulation, the support of dispersed renewable energy integration, and transmission upgrade deferral. MESSs can generate value in both scenarios and implement value stacking to increase their cost-effectiveness. In addition to their use for emergency response, a comprehensive review of the use of MESSs during normal operations for applications is needed for a thorough understanding of the role of MESSs in the future power system.