Application of Mobile Energy Storage for Enhancing Power Grid Resilience: A Review
Abstract
:1. Introduction
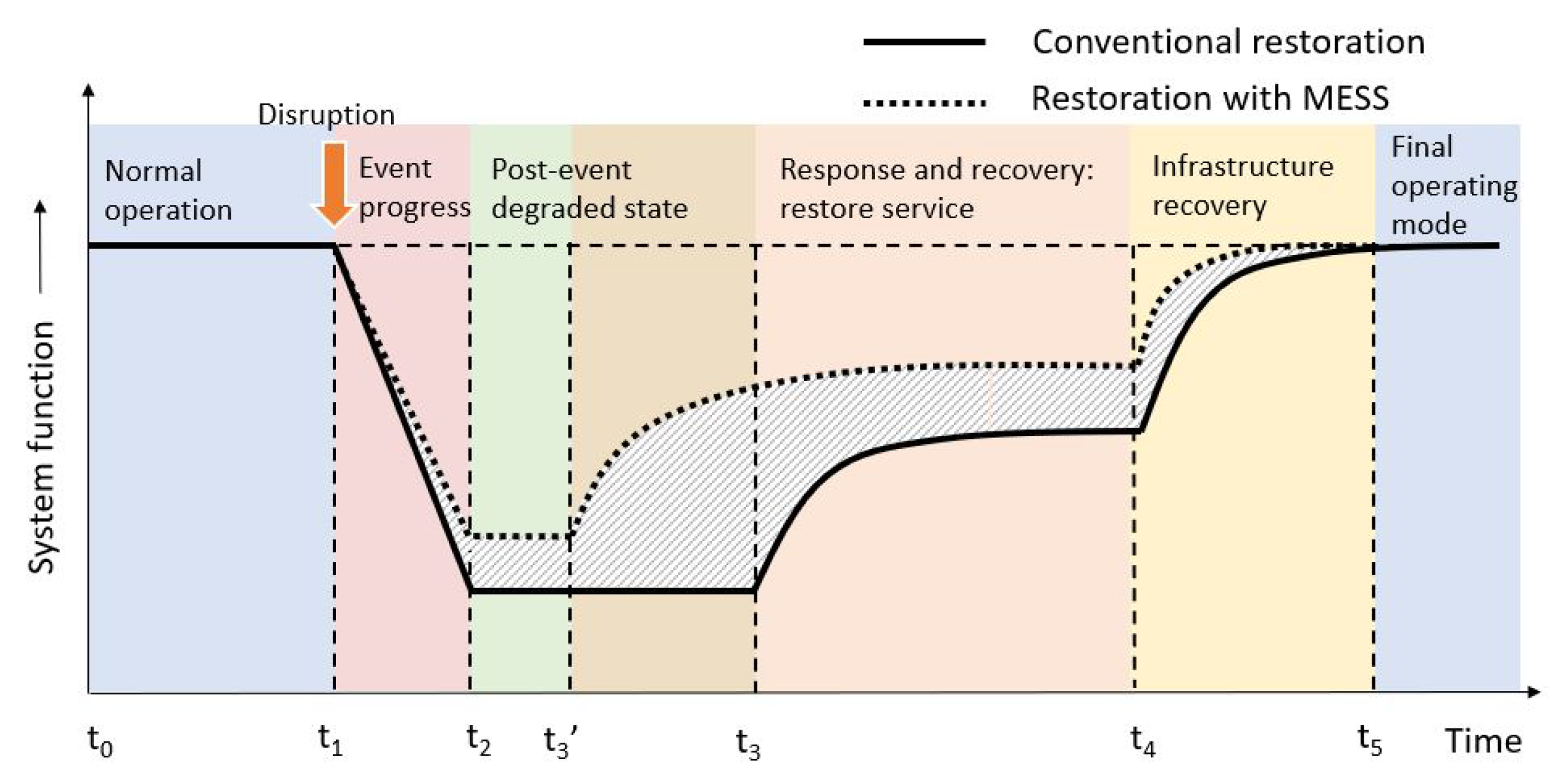
2. Power Grid Resilience
3. Mobile Energy Storage for Resilience Enhancement
4. Literature Review
4.1. Scope
4.2. Mobile Energy Resources for Resilience Enhancement
4.3. Power Grid Operational Constraints
4.4. Transportation System
4.5. Resilience Evaluation and Quantification
4.6. The Costs and Benefits of MESSs for Service Restoration
5. Discussion
5.1. Research Gaps
5.2. MESS Challenges and Opportunities
5.3. MESSs vs. Electric Vehicles for Resilience Enhancement
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MESS | Mobile energy storage system |
| SCOPF | Security constrained optimal power flow |
| DER | Distributed energy resource |
| MEG | Mobile emergency generator |
| EB | Electric bus |
| MER | Mobile energy resource |
| MPS | Mobile power source |
| NR | Network reconfiguration |
| MG | Microgrid |
| DG | Distributed generation |
| RC | Repair crew |
| DR | Demand response |
| MIQP | Mixed integer quadratic program |
| MILP | Mixed integer linear program |
| MINLP | Mixed integer nonlinear program |
| MISOCP | Mixed integer second order cone program |
| MIQCP | Mixed integer quadratically constrained program |
| MISDP | Mixed integer semidefinite program |
| OPF | Optimal power flow |
| WDTA | Weighted dynamic traffic assignment |
| PV | Photovoltaic |
| EV | Electric vehicle |
| V2G | Vehicle-to-grid |
References
- Economic Benefits of Increasing Electric Grid Resilience to Weather Outages; Technical Report; Executive Office of the President: Washington, DC, USA, 2013.
- Podlaha, A.; Lorinc, M.; Srivastava, G.; Bowen, S.; Kerschner, B. Weather, Climate & Catastrophe Insight: 2020 Annual Report; Technical Report; Aon: London, UK, 2021. [Google Scholar]
- Mishra, S.; Anderson, K.; Miller, B.; Boyer, K.; Warren, A. Microgrid resilience: A holistic approach for assessing threats, identifying vulnerabilities, and designing corresponding mitigation strategies. Appl. Energy 2020, 264, 114726. [Google Scholar] [CrossRef] [Green Version]
- Sullivan, J.E.; Kamensky, D. How cyber-attacks in Ukraine show the vulnerability of the U.S. power grid. Electr. J. 2017, 30, 30–35. [Google Scholar] [CrossRef]
- Bie, Z.; Lin, Y.; Li, G.; Li, F. Battling the Extreme: A Study on the Power System Resilience. Proc. IEEE 2017, 105, 1253–1266. [Google Scholar] [CrossRef]
- Mobile Energy Storage Study: Emergency Response and Demand Reduction; Technical Report; Massachusetts Department of Energy Resource: Boston, MA, USA, 2020.
- Institute of Electrical and Electronics Engineers (IEEE). IEEE Guide for Design, Operation, and Maintenance of Battery Energy Storage Systems, both Stationary and Mobile, and Applications Integrated with Electric Power Systems; IEEE: Piscataway, NJ, USA, 2019; pp. 1–45. [Google Scholar] [CrossRef]
- Abdeltawab, H.H.; Mohamed, Y.A.R.I. Mobile Energy Storage Scheduling and Operation in Active Distribution Systems. IEEE Trans. Ind. Electron. 2017, 64, 6828–6840. [Google Scholar] [CrossRef]
- Wilson, M. Lazard’s Levelized Cost of Storage Analysis—Version 6.0; Lazard: New York, NY, USA, 2020; p. 40. [Google Scholar]
- Con Edison Developing Energy Storage System on Wheels. Available online: https://www.coned.com/en/about-us/media-center/news/20160712/energy-storage-on-wheels (accessed on 13 September 2021).
- Mobile Energy Storage. Power Edison. Available online: https://www.poweredison.com (accessed on 13 September 2021).
- Nomad Transportable Power Systems. Available online: https://www.nomadpower.com/ (accessed on 13 September 2021).
- Spittle, B.; Nomad Transportable Power Systems, Waterbury, VT, USA. Personal communication, 2021.
- Abdubannaev, J.; Sun, Y.; Xin, A.; Jan, M.U.; Makhamadjanova, N.; Rakhimov, S. Enhancing Power System Resilience—A review. In Proceedings of the 2019 IEEE 3rd Conference on Energy Internet and Energy System Integration (EI2), Changsha, China, 8–10 November 2019; pp. 2350–2354. [Google Scholar] [CrossRef]
- Wang, Y.; Rousis, A.O.; Strbac, G. On microgrids and resilience: A comprehensive review on modeling and operational strategies. Renew. Sustain. Energy Rev. 2020, 134, 110313. [Google Scholar] [CrossRef]
- Anderson, K.; Li, X.; Dalvi, S.; Ericson, S.; Barrows, C.; Murphy, C.; Hotchkiss, E. Integrating the Value of Electricity Resilience in Energy Planning and Operations Decisions. IEEE Syst. J. 2021, 15, 204–214. [Google Scholar] [CrossRef]
- Bhusal, N.; Abdelmalak, M.; Kamruzzaman, M.; Benidris, M. Power System Resilience: Current Practices, Challenges, and Future Directions. IEEE Access 2020, 8, 18064–18086. [Google Scholar] [CrossRef]
- Raoufi, H.; Vahidinasab, V.; Mehran, K. Power Systems Resilience Metrics: A Comprehensive Review of Challenges and Outlook. Sustainability 2020, 12, 9698. [Google Scholar] [CrossRef]
- Moslehi, K.; Kumar, A.; Shurtleff, D.; Laufenberg, M.; Bose, A.; Hirsch, P. Framework for a self-healing power grid. In Proceedings of the IEEE Power Engineering Society General Meeting, San Francisco, CA, USA, 16 June 2005; Volume 3, p. 3027. [Google Scholar] [CrossRef]
- Deng, C.; Xiao, X.; Fu, Z.; Liu, G.; Yang, H.; Liu, J. Terrestrial-Satellite Hybrid Backbone Communication Network for Smart Power Grid. Energy Procedia 2011, 12, 27–36. [Google Scholar] [CrossRef] [Green Version]
- Sousa, P.; Bessani, A.N.; Dantas, W.S.; Souto, F.; Correia, M.; Neves, N.F. Intrusion-tolerant self-healing devices for critical infrastructure protection. In Proceedings of the 2009 IEEE/IFIP International Conference on Dependable Systems Networks, Lisbon, Portugal, 29 June–2 July 2009; pp. 217–222. [Google Scholar] [CrossRef]
- Capitanescu, F.; Martinez Ramos, J.L.; Panciatici, P.; Kirschen, D.; Marano Marcolini, A.; Platbrood, L.; Wehenkel, L. State-of-the-art, challenges, and future trends in security constrained optimal power flow. Electr. Power Syst. Res. 2011, 81, 1731–1741. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; McCalley, J.D. Risk-based optimal power flow and system operation state. In Proceedings of the 2009 IEEE Power Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, Q.; McCalley, J.D.; Zheng, T.; Litvinov, E. A Computational Strategy to Solve Preventive Risk-Based Security-Constrained OPF. IEEE Trans. Power Syst. 2013, 28, 1666–1675. [Google Scholar] [CrossRef]
- Lei, S.; Chen, C.; Zhou, H.; Hou, Y. Routing and Scheduling of Mobile Power Sources for Distribution System Resilience Enhancement. IEEE Trans. Smart Grid 2019, 10, 5650–5662. [Google Scholar] [CrossRef]
- Kwon, S.Y.; Park, J.Y.; Kim, Y.J. Optimal Operation of Mobile Energy Storage Devices to Minimize Energy Loss in a Distribution System. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/ICPS Europe), Palermo, Italy, 12–15 July 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Kim, J.; Dvorkin, Y. Enhancing Distribution System Resilience With Mobile Energy Storage and Microgrids. IEEE Trans. Smart Grid 2019, 10, 4996–5006. [Google Scholar] [CrossRef]
- Lei, S.; Chen, C.; Li, Y.; Hou, Y. Resilient Disaster Recovery Logistics of Distribution Systems: Co-Optimize Service Restoration With Repair Crew and Mobile Power Source Dispatch. IEEE Trans. Smart Grid 2019, 10, 6187–6202. [Google Scholar] [CrossRef] [Green Version]
- Ye, Z.; Chen, C.; Chen, B.; Wu, K. Resilient Service Restoration for Unbalanced Distribution Systems With Distributed Energy Resources by Leveraging Mobile Generators. IEEE Trans. Ind. Inform. 2021, 17, 1386–1396. [Google Scholar] [CrossRef]
- Taheri, B.; Safdarian, A.; Moeini-Aghtaie, M.; Lehtonen, M. Distribution System Resilience Enhancement via Mobile Emergency Generators. IEEE Trans. Power Deliv. 2021, 36, 2308–2319. [Google Scholar] [CrossRef]
- Ding, T.; Wang, Z.; Jia, W.; Chen, B.; Chen, C.; Shahidehpour, M. Multiperiod Distribution System Restoration With Routing Repair Crews, Mobile Electric Vehicles, and Soft-Open-Point Networked Microgrids. IEEE Trans. Smart Grid 2020, 11, 4795–4808. [Google Scholar] [CrossRef]
- Lei, S.; Wang, J.; Chen, C.; Hou, Y. Mobile Emergency Generator Pre-Positioning and Real-Time Allocation for Resilient Response to Natural Disasters. IEEE Trans. Smart Grid 2018, 9, 2030–2041. [Google Scholar] [CrossRef] [Green Version]
- Gao, H.; Chen, Y.; Mei, S.; Huang, S.; Xu, Y. Resilience-Oriented Pre-Hurricane Resource Allocation in Distribution Systems Considering Electric Buses. Proc. IEEE 2017, 105, 1214–1233. [Google Scholar] [CrossRef]
- Yao, S.; Zhao, T.; Zhang, H.; Wang, P.; Goel, L. Two-stage Stochastic Scheduling of Transportable Energy Storage Systems for Resilient Distribution Systems. In Proceedings of the 2018 IEEE International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Boise, ID, USA, 24–28 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Kavousi-Fard, A.; Wang, M.; Su, W. Stochastic Resilient Post-Hurricane Power System Recovery Based on Mobile Emergency Resources and Reconfigurable Networked Microgrids. IEEE Access 2018, 6, 72311–72326. [Google Scholar] [CrossRef]
- Che, L.; Shahidehpour, M. Adaptive Formation of Microgrids With Mobile Emergency Resources for Critical Service Restoration in Extreme Conditions. IEEE Trans. Power Syst. 2019, 34, 742–753. [Google Scholar] [CrossRef]
- Yao, S.; Wang, P.; Zhao, T. Transportable Energy Storage for More Resilient Distribution Systems With Multiple Microgrids. IEEE Trans. Smart Grid 2019, 10, 3331–3341. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, Y.; He, J.; Su, M.; Ni, P. Resilience-Oriented Distribution System Restoration Considering Mobile Emergency Resource Dispatch in Transportation System. IEEE Access 2019, 7, 73899–73912. [Google Scholar] [CrossRef]
- Yao, S.; Wang, P.; Liu, X.; Zhang, H.; Zhao, T. Rolling Optimization of Mobile Energy Storage Fleets for Resilient Service Restoration. IEEE Trans. Smart Grid 2020, 11, 1030–1043. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Dehghanian, P.; Nazemi, M. Seismic-Resilient Electric Power Distribution Systems: Harnessing the Mobility of Power Sources. IEEE Trans. Ind. Appl. 2020, 56, 2304–2313. [Google Scholar] [CrossRef]
- Prabawa, P.; Choi, D.H. Multi-Agent Framework for Service Restoration in Distribution Systems With Distributed Generators and Static/Mobile Energy Storage Systems. IEEE Access 2020, 8, 51736–51752. [Google Scholar] [CrossRef]
- Nazemi, M.; Dehghanian, P.; Yang, Z. Swift Disaster Recovery for Resilient Power Grids: Integration of DERs with Mobile Power Sources. In Proceedings of the 2020 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Liege, Belgium, 18–21 August 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Yao, S.; Gu, J.; Zhang, H.; Wang, P.; Liu, X.; Zhao, T. Resilient Load Restoration in Microgrids Considering Mobile Energy Storage Fleets: A Deep Reinforcement Learning Approach. In Proceedings of the 2020 IEEE Power Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, W.; Xiong, X.; Xiao, C.; Li, H.; Zhang, B. Integration of Mobile Energy Resources and Demand Response to Strengthen the Survivability of Isolated Distribution Systems. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October–1 November 2020; pp. 1571–1577. [Google Scholar] [CrossRef]
- Shi, W.; Zhuang, P.; Liang, H. Mobile Energy Resource Allocation for Distribution System Resilience Against Earthquakes. In Proceedings of the 2020 IEEE 92nd Vehicular Technology Conference (VTC2020-Fall), Victoria, BC, Canada, 18 November–16 December 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, F.; Zhang, X.; Wang, Z.; Meng, K.; Dong, Z.Y. Mobile Emergency Generator Planning in Resilient Distribution Systems: A Three-Stage Stochastic Model With Nonanticipativity Constraints. IEEE Trans. Smart Grid 2020, 11, 4847–4859. [Google Scholar] [CrossRef]
- Malek, A.F.; Mokhlis, H.; Muhammad, M.A.; Bajwa, A.A.; Mansor, N.N.; Jamian, J.J. Resilience Based Decision Metrics for dispatching Mobile Emergency Truck Generators in Distribution System. In Proceedings of the 2021 IEEE International Conference in Power Engineering Application (ICPEA), Shah Alam, Malaysia, 8–9 March 2021; pp. 233–238. [Google Scholar] [CrossRef]
- Nazemi, M.; Dehghanian, P.; Lu, X.; Chen, C. Uncertainty-Aware Deployment of Mobile Energy Storage Systems for Distribution Grid Resilience. IEEE Trans. Smart Grid 2021, 12, 3200–3214. [Google Scholar] [CrossRef]
- Mehrjerdi, H.; Mahdavi, S.; Hemmati, R. Resilience maximization through mobile battery storage and diesel DG in integrated electrical and heating networks. Energy 2021, 237, 121195. [Google Scholar] [CrossRef]
- Erenoğlu, A.K.; Erdinç, O. Post-Event restoration strategy for coupled distribution-transportation system utilizing spatiotemporal flexibility of mobile emergency generator and mobile energy storage system. Electr. Power Syst. Res. 2021, 199, 107432. [Google Scholar] [CrossRef]
- Bhusal, N.; Gautam, M.; Benidris, M. Sizing of Movable Energy Resources for Service Restoration and Reliability Enhancement. In Proceedings of the 2020 IEEE Power Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Low, S.H. Convex Relaxation of Optimal Power Flow—Part II: Exactness. IEEE Trans. Control. Netw. Syst. 2014, 1, 177–189. [Google Scholar] [CrossRef] [Green Version]
- Farivar, M.; Low, S.H. Branch Flow Model: Relaxations and Convexification—Part I. IEEE Trans. Power Syst. 2013, 28, 2554–2564. [Google Scholar] [CrossRef]
- Taylor, J.A.; Hover, F.S. Convex Models of Distribution System Reconfiguration. IEEE Trans. Power Syst. 2012, 27, 1407–1413. [Google Scholar] [CrossRef]
- Panteli, M.; Mancarella, P. The Grid: Stronger, Bigger, Smarter?: Presenting a Conceptual Framework of Power System Resilience. IEEE Power Energy Mag. 2015, 13, 58–66. [Google Scholar] [CrossRef]
- Electric Power Research Institute. Electric Power System Resiliency: Challenges and Opportunities; Technical Report; Electric Power Research Institute: Washington, DC, USA, 2016. [Google Scholar]
- Ericson, S.; Lisell, L. A flexible framework for modeling customer damage functions for power outages. Energy Syst. 2020, 11, 95–111. [Google Scholar] [CrossRef]
- Rickerson, W.; Gillis, J.; Bulkeley, M. The Value of Resilience for Distributed Energy Resources: An Overview of Current Analytical Practices; Technical Report; National Association of Regulatory Utility Commissioners (NARUC): Washington, DC, USA, 2019. [Google Scholar]
- Sullivan, M.; Schellenberg, J.; Blundell, M. Updated Value of Service Reliability Estimates for Electric Utility Customers in the United States; Technical Report LBNL–6941E; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2015. [CrossRef] [Green Version]
- Mohagheghi, S.; Stoupis, J. Systems and Methods for Restoring Service within Electrical Power Systems. W.O. Petent WO2013066,501A1, 10 May 2013. [Google Scholar]
| Study | MESSs | MEGs | EBs | Formulation | Objective | Coordinated with | Test System Nodes |
|---|---|---|---|---|---|---|---|
| [32] | - | 5 | - | MIQP → MILP | Minimize outage duration | - | 114 |
| [33] | 2 | - | 3 | MINLP → MILP | Maximize resilience | - | 123 |
| [34] | 4 | - | - | MILP | Minimize cost | NR | 33 |
| [27] | 2, 3 | - | - | MISOCP | Minimize cost | MG | 15 |
| [25] | 1 | 1 | 2 | MISOCP → MILP | Maximize restored load | NR | 33, 123 |
| [35] | - | 5 | - | MINLP → MILP | Maximize resilience | NR, MG | 68 |
| [36] | - | 10 | - | MILP | Minimize critical load loss | MG | 123 |
| [28] | 1, 2 | 1, 2 | - | MINLP → MISOCP → MILP | Maximize resilience | RC, NR | 33, 123 |
| [37] | 4 | - | - | MILP | Minimize cost | NR, DG | 33 |
| [38] | 4 | 8 | 25 | MILP | Maximize restored load | RC | 33 |
| [39] | 3, 5 | - | - | MILP | Minimize cost | NR, DG | 132, 198 |
| [40] | 1 | 1 | 2 | MINLP → MILP | Maximize restored load | NR | 33 |
| [29] | - | 4 | - | MILP | Maximize restored load | DG, RC, NR | 123, 8500 |
| [41] | 2 | - | - | MILP, MISDP, MISOCP | Maximize restored load | DG, NR | 33 |
| [30] | - | 5 | - | MILP | Minimize curtailed energy | NR, RC | 47, 123 |
| [42] | 1 | 1 | 1 | MINLP → MILP | Maximize supplied load | NR, DG | 33 |
| [43] | 4 | - | - | Markov decision process | Minimize cost | MG | 3 microgrids |
| [44] | 1 | 2 | - | MISOCP | Minimize fuel consumption | DR | 37 |
| [31] | 2, 3 | - | - | MILP | Maximize restored load | RC, MG | 33, 69 |
| [45] | - | 6 | - | MILP | Maximize restored load | - | 123 |
| [46] | - | 2, 3 | - | 3-stage stochastic model | Minimize cost | - | 13, 123 |
| [47] | - | 5 | - | MIQCP | Maximize restored load | NR | 33 |
| [48] | 2, 4 | - | - | Non-convex, non-linear → MILP | Maximize the value of supplied load | NR | 33, 123 |
| [49] | 1 | 1 | - | MILP | Minimize cost | DR, DG | 33 |
| [50] | 1 | 1 | - | MIQCP | Maximize restored load | RC | 15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dugan, J.; Mohagheghi, S.; Kroposki, B. Application of Mobile Energy Storage for Enhancing Power Grid Resilience: A Review. Energies 2021, 14, 6476. https://doi.org/10.3390/en14206476
Dugan J, Mohagheghi S, Kroposki B. Application of Mobile Energy Storage for Enhancing Power Grid Resilience: A Review. Energies. 2021; 14(20):6476. https://doi.org/10.3390/en14206476
Chicago/Turabian StyleDugan, Jesse, Salman Mohagheghi, and Benjamin Kroposki. 2021. "Application of Mobile Energy Storage for Enhancing Power Grid Resilience: A Review" Energies 14, no. 20: 6476. https://doi.org/10.3390/en14206476
APA StyleDugan, J., Mohagheghi, S., & Kroposki, B. (2021). Application of Mobile Energy Storage for Enhancing Power Grid Resilience: A Review. Energies, 14(20), 6476. https://doi.org/10.3390/en14206476






