Abstract
Harmonic distortion is one of the disturbances that most affects the quality of the electrical system. The widespread use of power electronic systems, especially power converters, has increased harmonic and interharmonic emission in a wide range of frequencies. Therefore, there are new needs in the measurement of harmonic distortion in modern electrical systems, such as measurement in the supra-harmonic range (>2 kHz) and the measurement of interharmonics. The International Electrotechnical Commission (IEC) standards define new total harmonic distortion (THD) rates based on the concept of frequency groupings. However, the rates defined in the IEC standards have shortcomings when measuring signals such as those present in the outputs of power systems with abundant interharmonic content and presence of components in the supra-harmonic range. Therefore, in this work, a comparison is made between the different THD factors currently defined, both in the literature and in the standards, to show which of them are the most suitable for assessing harmonic and interharmonic contamination in power system signals such as those present at the output of inverters.
1. Introduction
The widespread use of power electronic systems and other nonlinear loads is one of the main causes of increasing harmonic distortion, which worsens the quality of electrical systems. Therefore, it is becoming increasingly important for power distribution companies to be concerned with proper reporting of the quality of their electrical product [1,2,3]. Harmonics and interharmonics are caused by nonlinear loads such as the power electronic converters present in adjustable speed drives, switched-mode computer power supplies, and energy-saving lamps, as well as interface converters between renewable energy generators and the power grid. When connected to the grid, power converters affect the increase of harmonic distortion, since consumption and production at frequencies other than the fundamental frequency of the system motivate the increase of harmonic and interharmonic content [4,5]. The report developed by the joint CIGRE/CIRED Working Group C4.24 [6] analyzes the impact that new technologies implemented in electricity systems, both on the demand side and in the system itself, may have on the quality of electricity supply. This report also synthesizes views on new measurement methods and new mitigation techniques and provides important findings and suggestions.
Electronic converters have high-frequency switching circuits which produce distortion above the classical 2 kHz harmonic frequency band, shifting it to the 0–150 kHz range. This wide frequency range is usually divided into low frequencies or harmonics, between 0 Hz and the 40th harmonic (from 0 to 2 kHz, for 50 Hz networks), according to the International Electrotechnical Commission (IEC) standards, and high frequencies or supra-harmonics (from 2 kHz to 150 kHz). The behavior of voltage and current disturbances in this wide range is not uniform in either time or frequency [7,8]. For example, low-frequency distortions usually vary more slowly in time, whereas high-frequency distortions tend to have more variable frequencies and amplitudes. Therefore, suitable time–frequency analysis methods with appropriate sampling windows for each measured frequency range should be used. The high-frequency spectra are often of broadband character. In contrast, spectra at lower frequencies contain mainly discrete or narrowband components at multiples of the power system frequency (harmonics components) or at different frequencies (interharmonics and subharmonics). Another characteristic of low-frequency distortions is their tendency to propagate into the network, whereas high-frequency distortions tend to circulate mainly within the facility [9].
Harmonics and interharmonics, at both low and high frequencies, produce undesired effects such as flicker, overheating of equipment, increased losses in the network, interference in communications systems, and errors in control systems and digital meters [4,10,11]. In addition, interharmonics produce a change in the periodicity of the waveform, with consequent problems due to desynchronization in measurement procedures based on the Discrete Fourier Transform (DFT) [12].
Therefore, it is important to correctly measure the harmonic and interharmonic distortion not exclusively in the electrical network, but additionally in the outputs of power electronic converters in order to characterize the quality of the power supplied. Due to the relevance of electrical energy to all social activity, it is necessary to develop methods for measuring its quality [13,14,15,16,17,18]. Because of the diversity of existing measurement methods, measurement standards become even more necessary for making measurements more systematic and comparable between different equipment, allowing more reliable conclusions to be drawn [19]. Total Harmonic Distortion (THD) is one of the most important measurement indices used in these standards to evaluate quality in power systems systematically and comparably, thus helping to improve power system quality and reduce distortion levels. THD indicates the percentage of signal energy difference from the fundamental component, since the fundamental component is normally the dominant one in power systems, especially for voltage.
Despite the existence of other power quality indices to quantify waveform distortion, such as the measurement of individual harmonics, power factor, etc., it should be noted that international and European standards for renewable energy systems such as grid-connected photovoltaic systems mention only the THD distortion factor when assessing the quantity of harmonic pollution. In addition, many of the current commercial quality measuring instruments measure only the THD factor and do not take into account the total interharmonic distortion or measure in high-frequency ranges. It is therefore convenient to analyze which of the currently defined distortion factors is the most suitable for detecting harmonic and interharmonic contamination in power systems. A correct assessment of the distortion factors that define the power quality is an important step in the task of improving the performance of the power system under analysis.
The objective of this paper is to present a review of the different distortion factors defined both in the standards and in the literature, in order to illustrate the way the new definitions provide a better understanding of harmonic and interharmonic distortion produced by power devices such as inverters. Thus, this paper studies distortion factors that measure harmonic distortion in signals such as those generated by power electronic devices (with a higher interharmonic content and in a wider frequency range) and thus complement those defined in the standards (more suitable for measuring distortion in network signals). Other examples of the use of distortion rates are also presented, including informative work on the quality of analyzed signals as well as the controls on the manner of modulation of the signal by converters and the control of distortion generated by the loads or users.
The rest of the article is structured as follows: Section 2 discusses the main standards that regulate the limits on harmonic distortion and the ways in which it is measured; Section 3 reviews the standardized distortion rates, starting with the most basic such as the traditional THD harmonic distortion factor that measures only harmonics at low frequencies, along with some of its variants and ways of obtaining them according to the related literature. Next, the new concept of spectral bar grouping and the different distortion factors defined in the IEC standards are introduced, which extend the measurement capability of the previous rates but still show shortcomings such as measurement at high frequencies. Within Section 3, other concepts pertaining to the treatment of the distortion indices defined in the standards are also studied, such as the aggregation in time of the distortion factors, the measurement of harmonic distortion at high frequencies, and different procedures for the calculation of distortion indices. Section 4 reviews other distortion factors defined in the literature, which allow for measurements differentiating both harmonic and interharmonic contents at high and low frequencies, and which solve the shortcomings of the previous rates in measuring distortion in more specific applications. Section 5 shows different examples of the application of the distortion rates defined in the previous sections; Section 6 summarizes the characteristics and classifies the main distortion rates studied, including observations and comments derived from this work and tables that synthesize the features of all of the distortion rates considered; finally, Section 7 presents the conclusions derived from this work.
2. Standards that Regulate the Limits and Measurement of Harmonics
The American IEEE (Institute of Electrical and Electronics Engineers) and the European IEC (International Electrotechnical Commission) propose the main standards that define the conditions to be met by the supply signal and the limitations, as well as the means of measuring current and voltage harmonics. Likewise, the IEC establishes standards that are later assumed by the states belonging to the European Union through CENELEC (Comité Européen de Normalisation Electrotechnique). Table 1 lists the main standards established by these organizations for the measurement of power quality and especially for defining the limits and the means of measuring harmonics.

Table 1.
Main standards related to power quality and harmonics limits and measurements.
The IEEE 1159 standard [20] is, at the American level, in charge of establishing the standards related to power quality monitoring. The EN50160 standard [21] establishes, from the European point of view, the voltage limits which the indices characterizing the voltage waveform, including harmonic and interharmonic voltages, must be within. The IEC has defined several Electromagnetic Compatibility (EMC) standards to address power quality problems. The IEC 61000 series covers harmonics and interharmonics as low-frequency electromagnetic phenomena. IEEE 519 [22], unlike IEC 61000 which is divided into six parts which are further subdivided into several parts (see Table 1), deals with harmonic limits and harmonic measurement together. As for power quality standards in the Russian Federation, they are defined in a single interstate standard, GOST 32144–2013 [23]. This standard generally coincides with EN50160, but the limits are somewhat stricter than in the European standard [24].
All these standards have been under revision, since the great level of distortion in voltages and currents has made it essential to improve the definitions of limits in power networks and to standardize measurement procedures that are capable of ensuring accurate control of harmonic and interharmonic distortion in power systems [12].
Regarding limit definitions, standards provide recommended values for limiting harmonic distortion to ensure power quality. For voltage harmonics limits, the majority of nations utilize limits related to the international standards IEEE 519 [22], IEC 61000-2-2 [25], IEC 61000-2-12 [26], and the European standard EN 50160 [21]. Current harmonic emission limits are mainly based on voltage harmonic limits and depend on the size of the installation under consideration [27]. The most restrictive harmonic current limits are for customers with large loads and high voltages, while the most permissive are for small loads and low voltages. Similarly, the limits are more restrictive for generation equipment (harmonics in the voltages supplied by the companies) than for users (harmonic currents injected). To assess these limits, the most universally recognized quality factors utilized today are the global THD factor and a set of limits established for individual harmonics. In the two cases, more severe limits are necessary for continuous events than for short-duration events [27,28]. In practice, these limits are not always respected and consequently, in some systems, the THD percentage could be higher [29].
The American standard IEEE 519 [22] sets the limits for voltage harmonics in Low Voltage (LV) networks at 8% THD, and at 5% in the case of a single harmonic. The European standard EN50160 [21] sets a limit for total harmonic distortion of voltage equal to 8%, considering up to the 40th harmonic; in addition, the same standard sets different single voltage harmonic limits, although only up to the 25th harmonic.
In terms of IEC standards, IEC 61000-2-2 [25] and IEC 61000-2-12 [26] define the margins for compatibility in signal transmission in public low-voltage and medium-voltage supply systems, respectively. These standards specify compatibility limits applicable to the common connection point. Both IEC standards set the limit for total harmonic voltage distortion at 8%, as do IEEE 519 and EN 50160, and also define limits for individual voltage harmonics, in this case up to the 50th harmonic. A more specific standard is IEC 61727 [30], which covers the interface specifications between Photovoltaic (PV) systems and the grid to which they are connected. When defining harmonic limits, the THD factor is always taken into account. Specifically, several limits are provided for current: 5% for total harmonic distortion of current and 2% for total harmonic distortion of voltage, with a maximum of 1% for individual harmonics of voltage.
Table 2 presents a comparison of voltage distortion limits for odd-order harmonics in public Low Voltage (LV) and Medium Voltage (MV) networks, according to the standards. The symbol h represents the order of the harmonic, and the limits indicate the maximum value of the voltage of each harmonic as a percentage of the voltage of the fundamental. In the IEEE 519 standard [22], the medium voltage MV is defined as up to 69 kV; it is defined as up to 35 kV in the other standards.

Table 2.
Voltage distortion limits for THD and odd harmonics in public networks (LV&MV) [20,21,22,23].
As shown in Table 2, the values of the maximum limits in EN 50160 and IEC standards are generally lower or stricter as the order of the harmonic increases. Likewise, the limit values for even-order harmonics are lower or stricter, mainly because the continuous component can cause saturation in motors and transformers, so they are limited to a lower value than the less damaging odd harmonics.
In terms of measurement procedures, IEC 61000-4-30 [31] establishes the techniques for measuring the quality indices of alternate signal supply networks and how to analyze the conclusions found. Similarly, IEC 61000-4-30 points out the need to average over time the measurements found for all power quality indices. This standard, like international standards on testing and measurement techniques for electromagnetic compatibility (EMC) problems and power system networks, references IEC 61000-4-7 [32] to establish harmonics and interharmonics measurements. Thus, for example, in [33] the authors use the frequency groupings of IEC 61000-4-7 to measure the quality of power supplied by wave and tidal energy converters since, although the international technical specification indicated for this type of converters is IEC 62600-30, this standard recommends that the harmonic distortion analysis be based on the aforementioned IEC 61000-4-7 standard. The IEEE 519 standard [22] has also been revised to add criteria analogous to those defined in the IEC standard concerning interharmonics and harmonics measurement methodology, such as the use of a sampling window of about 200 ms per the IEC 61000-4-7 and 61000-4-30 standards, as well as time aggregation intervals of 3 s and 10 min. As for the Russian standards, they also separate into different standards the methods of measuring the quality of electric power [34] and the measurements of harmonics and interharmonics [35], these standards being similar to the European standards [31] and [32], respectively.
IEC 61000-4-7 differentiates between harmonics and interharmonics and considers components above harmonic frequencies up to 9 kHz. In addition, in IEC 61000-4-7, a new concept is presented: the grouping of spectral bars. Four types of spectral line aggregations are defined, which are harmonic groups and subgroups and interharmonic groups and subgroups. These groups and subgroups use the spectral components of the analyzed signal obtained using transforms such as the discrete Fourier transform. In the post-processing phase of the measuring equipment, the necessary operations are carried out for the grouping of these spectral bars, as well as the possible aggregations in time according to the aforementioned IEC 61000-4-30 standard, which is thus related to IEC 61000-4-7. IEC 61000-4-7 also establishes various distortion factors: the popular Total Harmonic Distortion (THD), the Group Total Harmonic Distortion (THDG), and the Subgroup Total Harmonic Distortion (THDS).
Thus, the low-frequency spectrum is currently supported by appropriate standards that define limits and specify measurement procedures for a correct evaluation of these disturbances. On the other hand, the high-frequency range is not yet fully regulated; however, international standardization bodies have created multiple working groups to develop these standards. Likewise, interharmonics measurement standards are evolving, with more and more recommendations in standards such as 61000-4-7.
3. Standardized Distortion Rates
This section reviews the standardized distortion rates defined in standards such as those discussed in the previous section, as well as some of the ways to process them according to the related literature. Special emphasis is given to the new rates defined by the IEC standards, which use the concepts of grouping in frequency and time and also improve the measurability of basic rates, although they still show some shortcomings. Other considerations in the processing of distortion rates defined in the standards are also studied, such as the aggregation in time of the distortion factors previously obtained in the frequency domain, the measurement of harmonic distortion at high frequencies above the harmonic range, and various procedures for the calculation of distortion rates.
3.1. Basic Standardized Distortion Rates
As mentioned in the introduction, due to the adverse effects of harmonics and interharmonics it has been necessary for standards to define limits and ways to measure harmonic distortion. Traditionally, there have been two ways to evaluate harmonic distortion [21]:
- Individually, by finding its relative magnitude yH,h as the ratio of the rms value YH,h of the harmonic component h considered between the rms value YH,1 of the fundamental component: yH,h = YH,h/YH,1 (where Y can be current or voltage, replaced in each case by I or U respectively).
- Globally, using distortion rates such as Total Harmonic Distortion (THD) which relates the rms value of the sum of all harmonic components (YH,h) up to a given order (hmax) to the rms value of the fundamental frequency component (YH,1):
Absolute harmonic distortion rates such as Total Harmonic Content (THC) are also measured. Relative distortion rates (or simply distortion rates) are obtained by normalizing the absolute rates.
The individual form of evaluation can be replaced by grouping methods such as that proposed by IEC 61000-4-7, which in addition to the evaluated harmonic itself also takes into account the existence of nearby interharmonics and the problem of the non-stationarity of all these spectral components. Similarly, rates such as THD can be replaced by other distortion rates.
In the following, we will continue describing other basic or traditional distortion rates that, like THD, allow us to measure harmonic distortion; however, we will not yet differentiate harmonic content from interharmonics at high and low frequencies, as we will later on since it allows us to distinguish other, more specific rates.
3.1.1. Effective Total Harmonic Distortion (THDR)
Total Harmonic Distortion (THD), defined in Equation (1), is used to evaluate the quality of electrical systems such as audio circuits and especially power distribution networks. THD estimates the difference between a real signal, voltage, or current and an ideal sinusoidal reference [22]. THD can also be defined as shown in Equation (2), normalizing by the total rms value of the signal Ytot [36]:
The THDR rate is referred to as the rms or effective THD and is often utilized in audio applications, while the THD rate, also called fundamental THD, is mainly used in power applications. In [37] these two different definitions of THD were examined to avoid possible ambiguities and misinterpretations in measurement. The American standard IEEE 519 [22] also calls THD the harmonic factor or distortion factor. THD is not the same as signal-to-noise ratio (SNR), since SNR compares the energy of the information signal with the energy due to noise (produced by random phenomena). In contrast, THD compares the energy of the fundamental harmonic with other harmonic components of the analyzed signal [38].
3.1.2. Total Waveform Distortion (TWD)
An alternative to the classical THD proposed in standards such as IEEE 519 [22] and IEC 61000-4-7 [32] is to measure the distortion with the Total Waveform Distortion (TWD), the expression of which appears in the IEEE 1459 standard [36]. This distortion factor can be obtained in the time domain:
where Ytot, YH,1, and Ynon_fund are the rms values of the total spectrum of voltage or current signal, its fundamental component, and its high harmonic component, respectively. Alternatively, using Parseval’s relation, we have the definition of the spectral form of this distortion rate in the frequency domain, as a function of the rms values of the spectral components YC,k of each order k separated by the value of the frequency resolution:
In this case, the total waveform distortion TWD rates of voltage and current are measuring all of the distortion, without differentiating between harmonics and interharmonics or between low- and high-frequency zones, unlike classical THD which only measures harmonics at low frequencies. When there is only harmonic content in the analyzed signal, there is no difference between the TWD and THD rates. But if the signal presents both harmonic and interharmonic distortion, then the difference between TWD and THD rates is precisely this interharmonic content, which can be quantified in the Total nonHarmonic Distortion (TnHD) rate [36], expressed in Equation (5).
The TnHD rate is also called “total interharmonic distortion”, and is obtained from the total rms value of the signal Ytot, from which the fundamental and all harmonics (low frequencies) including the continuous component are subtracted, so that this rate measures only the interharmonics at low frequencies, and all components at high frequencies.
3.1.3. Total Demand Distortion (TDD) and Total Rated Distortion (TRD)
A drawback of normalizing by the fundamental is that for low values of the fundamental, the distortion rates normalized by it can take on high values. For this reason, the American standard on harmonics IEEE 519 [22] also defines the Total Demand Distortion (TDD) only for current, which normalizes with respect to the maximum current value (instead of normalizing with respect to the fundamental harmonic I1 with the actual value it has in each measurement, as is done with the THD index):
where THC represents the rms of the measured signal with the fundamental excluded from the sum, and Id is the maximum or peak demand load current of the fundamental component. When the peak current is difficult to determine, the nominal Irated current can be used to normalize. The resulting rate, introduced by IEEE Standard 1547-2018 [39], is referred to as Total Rated Current Distortion, TRD. This rate considers all distortion, harmonic and interharmonic, since it relates the total rms value of the signal Itot from which only the current fundamental I1 is subtracted, as shown in Equation (7):
The benefit of using either peak or nominal current is that it sometimes provides a better estimation of the influence of the distorted current on the network [36]. This is because THD is a property of the signal and does not directly measure the impact of the disturbance, since its level is calculated as a function of the fundamental component. In the case of the voltage waveform in network signals, the variation of the fundamental component is low; therefore, THD can be easily estimated. However, in the case of current distortion, the situation is different: a small THD with a high load can have a greater influence on the power system than a great THD with a small load, which is why TDD is defined [40].
This can also occur when measuring the output voltage of low-power adjustable speed drivers (ASD), which usually have a variable fundamental voltage at the output of the inverter stage, or during events such as voltage dips. For situations with great differences in the fundamental voltage, it may be convenient to utilize a similar rate to describe the voltage distortion, now using the nominal Vrated voltage as a normalizing value [36]:
3.1.4. Weighted Distortion Rates
Investigation of the harmonic composition of voltage and current electrical signals is carried out utilizing both traditional harmonic factors, especially the aforementioned total harmonic distortion, and relatively new indices such as, for instance, a set of weighted total harmonic distortion coefficients for loads such as induction motors whose parameters are frequency-dependent [41]. Within this family of weighted THD factors for inductive loads, developed by [42], the main rate is the basic weighted THD (Weighted Total Harmonic Distortion, WTHD), the expression of which is shown in Equation (9).
The WTHD rate is often interpreted as the normalized current distortion expected in inductive loads (such as motors) fed with the output voltage of an inverter. Weighted THD or WTHD is preferred over THD when the inverter is generating non-sine or square waveforms. THD is intended to express the quality of a sine, so if what is being generated is not a sine the benefit of determining the purity of the output waveform diminishes. The WTHD is intended to predict the distortion in the current, and therefore additional losses. To make an accurate calculation of the WTHD rate it is necessary to take into account the dependence of motor parameters on frequency, especially rotor resistance and leakage inductance, in addition to stator copper losses [42]. The simplest or WTHD rate assumes a total motor leakage inductance that does not vary with frequency.
While the current THD for an inverter with dominant inductive load is the frequency-weighted voltage THD (WTHD) [42,43], the current THD when an LCL filter is present is the triple-frequency weighted THD (W3THD), as demonstrated in [44] for the calculation of the current distortion of a multilevel inverter with LCL filter. This is because integration in time is identical to multiplying by the reverse frequency in the frequency domain.
The weighted distortion rate for capacitive type loads is the Partial Weighted Total Harmonic Distortion (PWHD) [32], in which (contrary to WTHD) more weight is given to high harmonics, as shown in Equation (10).
Other more general indices which encompass the previous WTHD and PWHD are the differential and integral harmonic factors proposed by Zinoviev G.S., which allow for simulating the action of ideal multi-order differentiating and integrating circuits [45]. The differential factors (DFH) and integral factors (IFH) of voltage harmonics of various orders allow for calculating the current distortion rate (THDI) of the related circuits powered by a voltage supply from the known parameters of the load, avoiding the need to obtain and process the mathematical equations of such currents and including the filtering effect of the load on the investigated signals [46]. In Equations (11) and (12) both factors are defined, where the order “q” depends on the type of load.
The integral voltage IFH factor should be considered when the circuit under analysis is inductive, and the differential voltage DFH factor should be used when it is capacitive. The classical voltage THD corresponds to the zeroth order (q = 0) of these factors and can provide an adequate assessment of harmonic content only for circuits with pure active load. A harmonic distortion factor similar to the first-order IFH (q = 1) is the basic weighted total harmonic distortion, or WTHD; see Equation (9). In the opposite case, the partially weighted harmonic distortion rate, PWHD, can be considered a harmonic distortion factor similar to the first order DFH (q = 1).
However, the abovementioned weighted distortion factors require prior knowledge of the type of load (inductive, capacitive, or resistive) and even the type of generator (for current source inverters it is advisable to use current harmonic distortion rates instead of voltage harmonic distortion rates). The use of these factors is therefore limited to the types of loads and generators mentioned. Next, we will review other distortion rates with wider use, such as those proposed by the IEC standards for the measurement of network signals in general.
3.1.5. Group (THDG) and Subgroup (THDS) Distortion Rates
As discussed in Section 2, other international standards such as IEEE 519-2014 [22] adopt the methods defined by the IEC standard for the measurement of harmonics and interharmonics, so it is interesting to review the improvements introduced by this standard for the measurement of harmonic and especially interharmonic distortion. This standard maintains the use of rates such as THD, seen in Equation (1) and used in other standards, and also defines two new distortion rates based on the concepts of grouping in frequency and time: Group Total Harmonic Distortion rate (THDG) and Subgroup Total Harmonic Distortion rate (THDS). Before defining these two new distortion rates, it is useful to study the harmonic groupings which compose these rates and the motivation behind them.
The IEC standard indicates the use of DFT as a basic tool for harmonic analysis, using rectangular windows of 10 periods for 50 Hz networks (12 periods for 60 Hz systems), i.e., about 0.2 s with 5 Hz of resolution. It should be noted that DFT performs an accurate spectral analysis when analyzing stationary signals, and with sampling windows in synchronism with the period of the fundamental frequency of the signal. However, its precision decreases when the duration of the analysis window is not an integer multiple of the period of the fundamental frequency. In case of loss of synchronism or when there are interharmonics, which are common in the presence of power electronic converters, spectral leakage occurs, resulting in inaccurate measurements of the harmonic distortion of the analyzed signal.
One way to decrease the effects of spectral leakage is to use the frequency groupings and time aggregations defined in the IEC standards. IEC 61000-4-7 [32] describes harmonic and interharmonic groups of spectral lines produced by Fourier transform in order to get a more precise estimate of these quantities by reducing the error produced by the dispersion of spectral leakage towards the outside of each frequency group; in other words, by gathering most of the leakage generated inside. Thus, the frequency grouping of spectral bars improves performance in the measurement of leakage-producing interharmonics, and also takes into account the non-stationarity of the signal in aspects such as the amplitude and phase variations of the harmonics. In addition, the frequency groupings obtained (both individually and as distortion rates) should be aggregated over time as indicated in the 61000-4-30 standard [31] in order to reduce the effects of noise and spectral leakage and thus improve the accuracy of measurements generally, as will be discussed in more detail in Section 3.2.
Frequency groupings can be groups and subgroups, of harmonics and interharmonics. Harmonic groups (Yg,h) measure the rms value of a harmonic and of all the spectral bars that are closest to it, while harmonic subgroups (Ysg,h) measure the rms value of the harmonic and of only the two bars that are next to it. The usefulness of the harmonic subgroup is to evaluate the fluctuations in the amplitude and phase of the harmonics in network signals, which cause the appearance of sidebands to these. On the other hand, the interharmonic groups (Yig,h) and the interharmonic subgroups (Yisg,h) measure the rms value contained in the spectral bars between two consecutive harmonics, not including the sidebars to them in the case of the interharmonic subgroups. The symbol Y is replaced as required by the symbol I for current or U for voltage. Figure 1 shows examples of harmonic and interharmonic groups and subgroups for the frequency zone around harmonics 9 and 11.
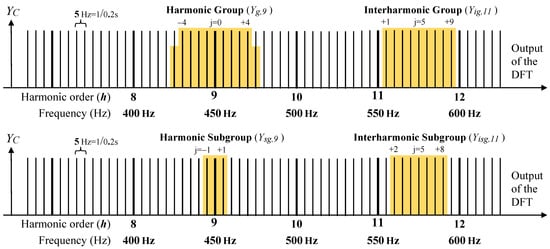
Figure 1.
Illustration of the harmonic group of order 9, Yg,9, the interharmonic group of order 11, Yig,11, the harmonic subgroup of order 9, Ysg,9, and the centered interharmonic subgroup of order 11, Yisg,11, for the case of f1 = 50 Hz.
If the harmonic groupings described above are used, it is necessary to employ other harmonic distortion rates that use the harmonic groups and subgroups, rather than the discrete values of each harmonic, when evaluating each expression. Therefore, in addition to the traditional THD, IEC 61000-4-7 [32] also defines these two other harmonic distortion rates:
- -
- Group Total Harmonic Distortion rate (THDG) is the division of the rms value of the harmonic groups (Yg,h) by the rms value of the fundamental group (Yg,1).
- -
- Subgroup Total Harmonic Distortion rate (THDS) is the ratio of the rms value of the harmonic subgroups (Ysg,h) to the rms value of the fundamental subgroup (Ysg,1).
The value of hmin is equal to 2 and the value of hmax is equal to 40 (2000 Hz for a 50 Hz network) if no other value is defined in a standard related to the limits (in the IEC 61000-3 series); however, for measurements on signals provided by converters, it may be necessary to further increase that figure if it is desired to estimate the high harmonics caused by high switching frequencies and their multiples. This can be done either by raising the value of hmax or by taking into account the recommendations made by this same IEC 61000-4-7 standard in one of its annexes on measurements above the harmonic frequency range, as discussed in Section 3.2.
It should be noted that the THDG group harmonic distortion rate does consider the energy of all interharmonics around every harmonic, since this is included in the definition of the harmonic groups. However, the THDS subgroup harmonic distortion rate only takes into account the energy of the harmonics and their sidebands, mainly due to non-stationarity because of the amplitude and phase fluctuations of the harmonics. Therefore, if it is desired to consider the distortion introduced by all harmonics and interharmonics without distinction, it may be more useful to use the THDG group total harmonic distortion rate. Thus, these THDG and THDS rates complement the already known and traditional THD that did not take into account interharmonics and other measurement problems due to the non-stationarity of the signal.
3.2. Other Considerations on the Processing of Distortion Rates
In this section, other concepts related to the treatment of distortion rates are presented: the necessary aggregation in time of all quality indices, which were previously obtained and grouped in the frequency domain; the special characteristics of harmonic distortion measurement in high-frequency ranges; and, the different ways of processing distortion rates depending on the method used to calculate them and the application for which they are intended.
3.2.1. Aggregation over Time of Distortion Rates and Frequency Groupings
IEC 61000-4-30 [31] states that the measurements found for each power quality index have to be averaged over time. Therefore, the above rates and the rest of the harmonic groupings must also be aggregated over time in a second level of aggregation that improves the results of the first level of frequency grouping. Aggregation over time affords more precision and less variation in the results obtained after DFT against the undesired effects of spectral leaks on the phase angle variations of the interharmonics [47], and, consequently, on the RMS changes of the total vectors resulting from all components that are added in each spectral line [48]. In addition, aggregation in time allows compacting the number of data and reducing the effects of noise present in the signal.
Aggregation over time must be done with both harmonic groupings and distortion rates, which are formed by the above groupings using the square root of the arithmetic mean of the squared input values. Thus, Figure 2 shows a summary of the whole harmonic distortion measurement process according to IEC standards, starting with segmentation in windows of about 0.2 s synchronized with the reference measured signal, subsequently obtaining DFT transforms within each of these windows, obtaining grouping in frequency of the spectral bars, and aggregating in time all of the previously-found groupings.
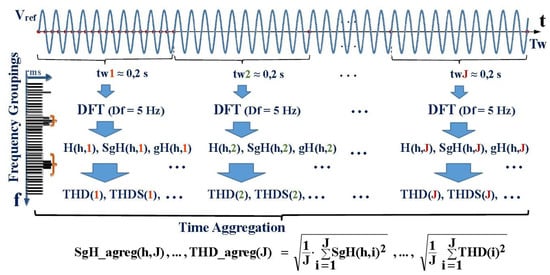
Figure 2.
Illustration of the harmonic distortion measurement process in the IEC standards framework, considering the two levels of grouping, in frequency and in time, and including the harmonic distortion rates defined in the standards among the other groupings.
These frequency and time groupings of the IEC standard and their corresponding parameters (duration of sampling windows and value of aggregation times) are foreseen and are the most suitable for harmonic analysis of general power grid signals. Therefore, aggregation over time can only be performed in periods of 3 s, 10 min, or 2 h [31], and frequency groups are always composed of spectral lines spaced about 5 Hz apart (i.e., a resolution in time or sampling window duration of 0.2 s) [32].
However, when analyzing signals such as those at the outputs of power converters, whose harmonic content differs from that of the network, the aggregation time can be adapted to each particular case according to the conditions of each test, such as the type of converter and connected load, in order to improve the reliability and stability of the measurement results [48]. Similarly, the time resolution also depends on the properties of the analyzed signal and must therefore be adapted to it [49,50]. The choice of a suitable time resolution necessarily affects the resolution in frequency (due to the uncertainty principle [8,36]) and, because of this, can also achieve greater precision in the measurement of harmonic groups and the resultant distortion rates.
3.2.2. Considerations on Measurements above Harmonic Frequencies
New distribution systems, with a greater presence of distributed generation (solar farms, wind farms, etc.) and the use of new technologies (active power factor correctors, connected non-linear loads, etc.), are new causes of harmonic distortion in the harmonic band (<2 kHz) and also in the over harmonic range (>2 kHz), both stationary and nonstationary. On the other hand, commercial power quality measurement devices usually only estimate harmonic distortion at low frequencies.
In earlier studies, such as [51,52,53], the so-called supra-harmonics were studied only in the frequency range between 2 and 9 kHz. Nowadays, the frequency range can be extended up to 150 kHz [54,55,56,57], or even up to 500 kHz [58], as power grid communications used in smart meters and other Power-Line Communications (PLC) in general operate in this area of the spectrum, in addition to frequencies due to electronic devices, PV inverters, etc. This new context demands the use of new measurement methods [58,59,60], new efficient measurement equipment, and the development of new standards [61].
Table 3 shows the main standards for harmonic distortion measurement for all conducted emission spectra. The range analyzed for power system signals is up to 150 kHz. Above 150 kHz, the conducted emissions reach up to 30 MHz, being radiated above that frequency. Measurement in the harmonic frequency range (<2 kHz) is mainly regulated by the IEEE and IEC standards already discussed in Section 2. Above harmonic frequencies, an informative annex to IEC 61000-4-7 [32] defines a relatively new measurement method for frequencies from 2 to 9 kHz, extendable to higher frequencies (up to 150 kHz). In a different informative annex, IEC 61000-4-30 [31] describes a new measurement method for the 9–150 kHz supra-harmonic range. In addition, CISPR-16 (Comité International Spécial des Perturbations Radioélectriques) proposes methods and equipment for measuring disturbances and disturbance immunity for frequencies between 9 kHz and 30 MHz, which are often difficult to implement using on-site measurement systems. The most relevant and widely used information for signal measurements in power systems in the supra-harmonic range (2–150 kHz) is presented in the methods of IEC 61000-4-7 and IEC 61000-4-30 standards. Therefore, the description of these methods, which are necessary to obtain distortion rates including high frequencies, will be explained in more detail below.

Table 3.
Main standards for the measurement of harmonic and conducted emission distortion.
Among these new standards, IEC 61000-4-7 [32] defines in its Annex B the procedure for measuring harmonic distortion up to a range of 9 kHz (approximately the limit of the low-frequency range). However, IEC standards have lately proposed to extend the grouping, initially defined from 2 to 9 kHz, until 150 kHz, for information purposes only. The measurement of these components does not require high-frequency resolution. On the contrary, it is common to regroup the signal energy to analyze it in predefined frequency bands. For frequency analysis, it is recommended to continue using DFT over 200 ms rectangular windows, i.e., with 5 Hz frequency resolution or frequency interval between two consecutive YC,f spectral components. Since the measurement of these components does not require a high-frequency resolution, the DFT output is regrouped in 200 Hz bands, starting with the first band centered above the harmonics range. If the 40th harmonic is the last harmonic, the center frequency of the first group should be equal to 2.1 kHz (40 × 50 Hz + 200 Hz/2) for 50 Hz networks and 2.5 kHz (40 × 60 Hz + 200 Hz/2) for 60 Hz networks. The output YB,b of each band corresponds to the rms value according to Equation (15):
The center frequency b, e.g., 2100 Hz, 2300 Hz, 2500 Hz, designates the grouping or band. The highest center frequency is 8900 Hz (spanning the spectral components from 8900–95 Hz to 8900 + 100 Hz = 9 kHz) for both 50 and 60 Hz networks. The 200 Hz regrouping, in Annex B of IEC 61000-4-7, has been chosen to be consistent with the bandwidth used in CISPR 16-1-2 [62] for frequencies above 9 kHz, in which the same 200 Hz bandwidth was used for the measurement of radiated disturbances.
Another standard such as IEC 61400-21 [63] provides specifications for the measurement of harmonic and interharmonic current emission between 2 kHz and 9 kHz for wind turbines connected to the grid. On the other hand, “IEC SC77A Working Group 9-Power Quality Measurement Method”, in an annex to IEC 61000-4-30 [31], proposes a practical method for on-site power quality applications, in particular for research and studies in the frequency range from 2 to 150 kHz. In this method, an acquisition window of only 0.5 ms is used (so the resolution or distance between spectral bars would be 2 kHz), due to the high sampling frequency (1024 kHz is suggested) and the consequent increase in the amount of data if the window were larger. However, in the latter standard the use of the same method proposed in Annex B of IEC 61000-4-7 is still suggested, for both the measurement of harmonic emissions in the 2 to 9 kHz range and extending the same procedure up to frequencies of 150 kHz. It is also proposed to continue using the 3 s, 10 min, and 2 h time aggregation intervals, already defined in [31], for the whole range of high frequencies in the same way as for low frequencies. However, the IEC standard recognizes that measurement methods for frequencies between 2 and 9 kHz and between 9 and 150 kHz, as well as time-aggregation methods for these frequencies, are still under study.
In [59,64] a comparison is made between the two methods proposed in [31,32], indicating that the one proposed in IEC 61000-4-7 is more robust, accurate, and has a better signal-to-noise ratio than the one suggested in 61000-4-30. On the other hand, it should be noted that measurement intervals of 200 ms are the most common in current standards, so the distance between individual spectral bars before grouping should remain 5 Hz. However, papers such as [65] discuss the implications of using a 0.2 s window for frequencies below 2 kHz and a 0.1 s window (bars spaced 10 Hz apart) for frequencies from 2 to 9 kHz, with the latter ordering the results in 200 Hz frequency bands.
It may also be of interest to measure distortion rates that include clusters corresponding to specific areas in the high part of the spectrum with a large interharmonic content, such as occurs at the outputs of power converters, where the distribution of supraharmonics is related to their switching frequency. For this purpose, the method proposed in Annex B of IEC 61000-4-7 proposes aggregations at 200 Hz frequency, which are larger than those in the lower part of the spectrum. These aggregations can be even larger, 600 or 800 Hz, using three or four groups of 200 Hz, respectively, as suggested in [66]. According to the conclusions of the latter article, the use of aggregations in bands of at least 600 Hz is necessary to give a single value representing more than 99% of the power emitted by a converter (in the case of those used in photovoltaic inverters) in each of the frequency groups around the multiples of the switching frequency. In the same article [66] it is also indicated that in order for these macro-groups, formed by several of the 200 Hz, to be centered around each of the multiples of the switching frequency, it is preferable to use values such as 800 Hz (4 groupings of 200 Hz), rather than values such as 600 Hz. It should also be noted that as the bandwidth of each macro-group increases, more and more noise is combined into a single band and higher levels may be measured that do not correspond to the actual emission. Therefore, the difference between grouping a single 5 Hz bar, several of these in 200 Hz groups, and several of the latter in 800 Hz groups, 2 kHz groups, or other larger values, is a noticeable one for network signals with broadband emissions, though smaller for signals with narrowband emissions [64].
Due to the variety of switching frequencies and ways of emission distribution, the high-frequency harmonic groups must be adjusted with flexibility. Therefore, a switching frequency identification method is proposed in [67,68], in which the bandwidth of each frequency group around multiples of the switching frequency can also be flexibly adjusted according to these frequencies. According to the authors, this flexible supra-harmonic grouping method enhances the proportion of energy collected in each grouping compared to methods such as those proposed in IEC 61000-4-7 [32], IEC 61000-4-30 [31], and [66].
However, the methods proposed in the IEC standards only provide an overall assessment of signal distortions, and do not provide detailed information on each spectral line [9]. Therefore, the IEC standards recommend the development of other methods for the evaluation of the high-frequency range and advise that other techniques could be considered in future versions of the standards. Thus, in [69,70,71,72], new measurement methods for the supra-harmonic frequency range based on the current IEC standards framework are described and compared.
3.2.3. Procedures for Calculating Distortion Rates
Several solutions for calculation of THD and its variants can be found in the literature, both from the frequency domain and from the time domain. Therefore, some of these solutions require spectral analysis to find the harmonic components of the signal, with the consequent computational burden, especially if an online THD measurement is required. The most commonly used method of performing this spectral analysis is the Digital Fourier Transform (DFT) and its optimization in the Fast Fourier Transform (FFT). Table 4 shows the estimation procedures for harmonic distortion indices, classified according to different criteria.

Table 4.
Procedures to estimate harmonic distortion rates.
There are other harmonic and interharmonic measurement methods besides DFT, broadly classified as parametric (for example Kalman, ESPRIT, etc.), nonparametric (such as DFT, FFT, STFT, wavelet, etc.), and hybrid methods [13,15,17]. Comparing these methods, DFT remains the simplest, fastest, and most robust technique for harmonic estimation [14,17]. Because the computational burden of these other methods is usually higher, FFT-based methods are used in real-time applications for power quality monitoring, such as power quality analyzers that measure, among other parameters, THD.
Thus, for example, it has already been seen that in the IEC power quality measurement standards 61000-4-7 [32] and 61000-4-30 [31], the DFT transform is the basis for obtaining the rms values of the harmonic and interharmonic groupings and the distortion rates obtained from these groupings. In [73] a solution is proposed to improve the THD calculation, approximating the value of the fundamental frequency to make a time and frequency synchronized acquisition, and using for this purpose a variant of the DFT based on an interpolation algorithm. In [74] an algorithm is presented to improve the accuracy of the THD calculation by taking better advantage of the capacity of the internal hardware accumulator of the Digital Signal Processor (DSP) used in the calculation of the FFT transform, since the conventional FFT algorithms of the digital processor perform calculations only with the width of the data bus, although the internal hardware accumulator of the DSP presents a greater number of bits.
According to another criterion, rates can be calculated using their general expressions by estimating all their terms if the type of signal analyzed is unknown, or analytically by developing a mathematical expression specifically use with signals generated by devices whose behavior can be modeled (see Table 4 for methods according to type of signal). Thus, other authors propose analytical methods from which specific equations for THD calculation are obtained, but which can only be used under specific conditions. The results of these analytical methods allow us to evaluate the accuracy of the THD obtained but do not always show its dynamic behavior or how THD evolves in time as signal distortion changes [29].
Thus, in [75], the mathematical models of standard non-sinusoidal periodic signals, developed in Fourier series, and their respective total harmonic distortion indices are presented. Based on these models, an analytical calculation of the THD of non-harmonic signals is proposed, focused on quality measurement in communications signals, using bandpass filters and a Cauchy residual technique. Using the above analytical calculation, in [76] the THD measured by power quality analyzers is calibrated using standard non-harmonic periodic signals (such as square wave, triangular, sawtooth) instead of the traditional repertoire of harmonic signals.
In [77], an analytical expression is obtained based on the standard deviation, useful for determining the accuracy of THD measurements for the case of using sinusoidally tuned estimators in general. It is shown that the THD estimation accuracy is proportional to the actual THD value, the signal-to-noise ratio, and the square root of the number of samples. The obtained expression is useful for determining the confidence intervals of the THD estimations and thus for verifying the quality of the measurements performed. Another advantage of the obtained expression is to be able to determine the minimum number of samples to be used and thus optimize the test execution time and memory requirements of the measurement systems.
In [78] a method for finding the THD that improves the performance of industrialized instruments in situations where the fundamental frequency deviates from the rated value, as occurs with network signals, is presented. This method is based on a matrix technique that maps the vector of real harmonics into a vector of pseudo-harmonics achieved by experimental measurement.
In [79] a new approach to THD calculation is described based on the Operator-Matrix State Variable method (OMSV method) instead of the traditional Fourier-based method. In this method, the analyzed electrical circuit is represented as a state-space, described by an m-dimensional vector for each time instant whose components are state variables. This method may be suitable when there are several loads with a nonlinear current-voltage characteristic, due to the inherent advantages of matrix-based calculation methods, as demonstrated analytically and with simulations, although not experimentally.
Many researchers focus primarily on control aspects to ensure stability and performance in power converters; however, for the design of filters for connection to the grid or other loads it is necessary to know the value of harmonic distortion introduced by the converter. Although most researchers use simulation tools employing numerical frequency spectrum computations (FFT), simple current THD equations can be a valuable complement in filtering design procedures to meet power quality standards [44]. Therefore, other analytical methods give specific equations for THD calculation in certain converter topologies. These analytical solutions provide information on the reasons for disturbances and help to reduce them through converter design, but cannot be used to determine the online THD of arbitrary signals.
For example, in [38] a technique is presented to measure THD, especially for inverter signals, using simple high-quality tunable active analog filters, with the drawbacks of taking into account only the 2nd and 3rd harmonics, and requiring manual corrections due to poor filter tuning. In [80] the concept of “interharmonic total harmonic distortion amplification” is presented for the case of Voltage Source Converters (VSC) connected to the network with Phase-Locked Loop (PLL). Through this concept, the grid integration performance of VSCs can be better evaluated, allowing examination of the ability of the VSC to reject the disturbances produced at the common point of grid connection depending on the frequency range in which they occur. In [43,44] the calculation of the current THD of a single-phase multilevel PWM inverter with an LCL filter connected to the grid is addressed, generalizing for this purpose the analytical approach already developed previously for a two-level inverter to the case of a single-phase multilevel inverter with any number of voltage levels. In [29], a computationally accurate and computationally lightweight THD calculation method is proposed which improves the dynamic behavior of other rates and is also robust to grid disturbances such as swells, sags, and frequency variations, thus also being suitable for online evaluation of voltage or current THD. Another analytical algebraic method, based on the line voltage THD formulation but only valid for multilevel inverters, is presented in [81].
The advantages of using analytical THD formulas found for specific situations are the simplicity and speed of the calculations and the improvement of THD accuracy compared to other conventional methods. However, these formulas are not suitable for finding the THD of any signal in general. Moreover, they do not have the flexibility of the methods based on DFT when measuring any harmonic and interharmonic content and in a wider range of frequencies, as occurs with other distortion rates proposed in the literature, such as those studied in Section 4.
4. Distortion Rates for Specific Measurements
Although the above rates have been used and are still used today for the measurement of harmonic distortion in general applications, due to the evolution of technology and the extensive use of power electronics and data communications over the network, which extends both the harmonic and interharmonic content and the range of frequencies to be measured, it is necessary to increase the number of distortion rates to meet these new measurement needs. To this end, in the literature, several authors propose solutions for the measurement of harmonic distortion in specific cases, especially those related to power devices applied to the environment, such as grid connections of photovoltaic and wind power systems, battery chargers, energy-saving lamps, etc. The solutions proposed by these authors can be extended to the measurement of harmonic distortion in similar cases, such as the outputs of inverters or other power converters, giving rise to new rates that, if their use becomes widespread, can later be standardized.
In this section we will review several examples of these types of rates used in the related literature to solve the measurement of harmonic distortion in specific applications, where it is usually necessary to differentiate harmonic and interharmonic contents, cover different frequency ranges, and take into account the stationarity of the signal.
4.1. Limitations of the above Distortion Rates
The following aspects of the distortion rates discussed in the previous section, which limit the possible applications of these rates, should be noted:
- -
- Many of the distortion rates seen in Section 3 cover only harmonics or low frequencies (up to at most the 40th harmonic, in the case of the IEC standard).
- -
- These rates consider the measurement of stationary harmonic distortion but do not consider non-stationary harmonic distortion or the use of the most appropriate harmonic estimation techniques for this purpose.
- -
- The only distortion rate proposed by the IEC that measures total interharmonic content is THDG; the other two measure only spectral bars located at harmonics (THD) or at their adjacent interharmonic frequencies (THDS).
- -
- Moreover, the two IEC rates that include some measure of interharmonics are obtained by dividing or normalizing by the fundamental group/subgroup (including with, if possible, nearby interharmonics); thus, the total value of the THDG and THDS rates could be reduced without giving correct information about interharmonic contamination [12].
- -
- Other rates seen in Section 3, such as voltage and current TWD, or current TRD, measure all the distortion but do so without differentiating between harmonics and interharmonics or between low- and high-frequency zones.
Therefore, none of the above rates discriminate between measurements according to the frequency range (harmonics and supraharmonics) and the type of components that distort the signal (harmonics and interharmonics). It may be convenient for the energy characterization of certain electronic equipment, such as power converters, energy-saving lighting lamps, electric vehicle chargers, and switched-mode power supplies in general, to differentiate between the type of harmonic emissions emitted by using different types of distortion rates.
4.2. Specific Distortion Rates
To solve the above aspects of measurement of harmonics and interharmonics in different frequency ranges and adequate normalization of the obtained rates, several different solutions are proposed in the literature.
Two significant subjects in the measurement of harmonic distortion in modern power systems are addressed in [82]: the measurement of distortion in the range above the harmonics considered low frequency (>2 kHz) and the measurement of stationary as well as non-stationary harmonic distortion. They propose an instrument that measures frequencies up to 2 kHz, using the harmonic and interharmonic groupings described in the IEC standard; frequencies between 2 and 9 kHz in the same way as described in [32] with 200 Hz groupings; and the time-frequency domain behavior of all the above harmonics by using wavelets. In the case of the treatment of the groupings below 2 kHz, the synchronization of the measurements with the fundamental is also required, and in the case of frequencies from 2 to 9 kHz, this synchronization is not necessary; however, a previous bandpass filtering is necessary. In [82] they define a new harmonic distortion rate known as Total High-Frequency Distortion (THFD):
where YB,b represents the rms value of each of the 200 Hz sub-bands calculated in Equation (15) (with b equal to the value of the center frequency of each sub-band, which for a 50 Hz network corresponds to values between bmin = 2100 Hz and bmax = 8900 Hz, in 35 groups of 200 Hz). However, when dividing or normalizing by the fundamental harmonic group Yg,1 the problem raised in [12] due to the possible existence of interharmonics in this group remains, so that the total value of this new rate can be reduced.
Dalali and Jalilian [83] propose a better solution to the previous problem (that is, that the only distortion rate proposed by the IEC standard that can be used for interharmonics analysis, THDG, is not accurate enough because of the existence of interharmonic components around the fundamental); to solve it, they define two new distortion indices similar to THDG, but which already correct the problem of dividing or normalizing by a group with interharmonics. The new distortion indices are named Subgroup Total Harmonic Distortion and improved THDG (THDGS) and Group Total Harmonic Distortion and Improved THDG (ITHDG), and are defined in Equations (17) and (18), respectively, for a fundamental frequency of 50 Hz (with 10 spectral bars Ck between successive harmonics).
The first of the rates defined in [83], THDGS, is similar to the old IEC-defined rate, THDG, but with the fundamental subgroup Csg,1 (fundamental and only its two adjacent spectral bars without the rest of the bars due to interharmonics) in the denominator. In addition, it includes in the numerator the spectral bars (Ck) due to interharmonics around the fundamental (C10), but without the two spectral bars adjacent to the fundamental, nor the fundamental itself.
The second of the rates defined in [83], ITHDG, is normalized only by the fundamental harmonic (C10), without the two lateral spectral bars due to close interharmonics (or due to amplitude/phase changes). In the numerator, the two spectral sidebars to the fundamental are included, so that now all the interharmonic bars are measured.
The new ITHDG distortion rate can better quantify the actual quantity of interharmonic contamination by including all spectral bars close to the fundamental, including contiguous ones. Though it is preferable the other new THDGS index for frequency spectra achieved by sensitive decomposition techniques (like FFT) with severe amplitude or frequency variations that may affect the occurrence of sidebands to the fundamental or its harmonics, and the ITHDG index is recommended to be used together with robust methods such as Kalman filters. However, either of the two distortion rates could be applied in place of the THDG rate (defined by the IEC standard) for the evaluation of contaminated interharmonic waveforms. Nevertheless, the distortion rates proposed in [83] do not define how to measure high frequencies above the 40th harmonic, nor do other rates for the low part that only measure interharmonics.
Alfieri, Bracale, and Larsson [9] propose, among others, the new “Short Time Disturbance Energy” distortion rate for Low- and High-Frequency (STDEL and STDEH) distortion. These distortion indices are founded on the time-frequency performance produced by using the “Sliding-Window Wavelet-Modified ESPRIT Method” (SWWMEM) applied to find the spectral components. STDE rates are a short-time variant of THD; however, unlike THD, they perform the distortion measurement by considering the full spectrum of the signal and not only its harmonics. These indices allow weighting a wide spectrum of frequencies, including high-frequency distortions (from 2 to 150 kHz), and doing so using sliding windows of different lengths, which allows a more adequate quantification of the distortions. On the other hand, the use of these distortion rates in practical real-time applications may be restricted by the large computation time in processing the time-dependent frequency components when there are highly time-varying signal perturbations; there is also an economic cost for the measurement equipment due to the high sampling frequencies required to evaluate the high-frequency spectral components.
Other authors [5,84,85] measure harmonic emissions on the grid side caused by PV inverters, switching power supplies, and other electronic equipment such as electric vehicle chargers. To do so, they use existing waveform distortion indices (Fundamental Factor, FF, and Total Distortion Content, TDC). Also, these authors define two other new waveform distortion indices: Total Harmonic-LF Factor (THFLF), restricted to low harmonics only; and Total Non-Harmonic-LF Distortion Factor (TNHDF), which includes total high and low interharmonics. High harmonics are also considered as interharmonics, because of the very likely loss of synchronism in their estimation concerning the acquisition window synchronizes with the fundamental at a much lower frequency. All these waveform distortion indices are normalized or divided by the total rms value of the measured current:
Using the above indexes, among others, in these same works [5,84,85] it is experimentally verified how the total harmonic content THC increases with power, while the relative THD index decreases at the beginning to end up remaining approximately constant for higher power values. However, the interharmonic current emission increases in the low power operating modes of the electronic equipment evaluated in these papers. The above distortion indices allow for selective measurement of only interharmonics (TNHDF), all harmonic and interharmonic content (TDC), and only harmonics at low frequencies (THF); but they do so by normalizing by the total rms, thereby including the distorted part of the signal. Furthermore, they do not define rates that measure harmonic and interharmonic distortion at only low or only high frequencies.
More recently, [86] considers, among other indices, the instantaneous THD, which measures in this case the whole distortion without discriminating harmonics from interharmonics, and is found using the Hilbert transform and wavelets to consider transient disturbances. Also, in [87], an appropriate technique is proposed to monitor the harmonic distortion in real-time using the Short-Time Fourier Transform (STFT), so that the analyzed signal is represented in the time-frequency domain. From this time-frequency representation, we obtain rates such as instantaneous Total Harmonic Distortion, THD(t), which measures the instantaneous value of THD, instantaneous Total Waveform Distortion, TWD(t), which measures all harmonic and interharmonic content over the entire frequency range, and instantaneous Total Nonharmonic Distortion, TnHD(t), which measures interharmonics at low frequencies and all components at high frequencies. These THD(t), TWD(t), and TnHD(t) rates are normalized by the instantaneous rms value of the fundamental and are obtained based on the definitions of THD, TWD, and TnHD rates seen in Equations (1), (4) and (5), which are now obtained in the time-frequency domain using the STFT and spectrograms for their representation. Thus, these rates also allow for selectively measuring the same harmonic contents as the rates proposed in [5,84,85], now normalizing among the fundamental instead of among the total rms. However, there is still a lack of rates that measure harmonic and interharmonic distortion only at low or only at high frequencies.
In [88] the inrush currents of adjustable-speed drives connected to motors are measured and two new interharmonic distortion rates are defined for this purpose, obtained as the square root of the sum of squares of the rms values of the interharmonics up to 2 kHz (TIHD2kHz) or of only the interharmonics between 2 and 9 kHz (TIHD2–9kHz); both rates are normalized only with the fundamental harmonic I1, without including its close interharmonics. In this paper, it is also experimentally verified that for all distortion rates, both harmonic and interharmonic, their value decreases with the torque of the connected motor in the case of measuring signals produced by frequency inverters (although the absolute total harmonic and interharmonic contents have different behaviors to their related relative rates). It should be noted that in the TIHD2–9kHz rate it does not make sense to consider only interharmonics at high frequencies, since it is normal that, at high frequencies, they are indistinguishable from harmonics. In addition, [88] does not detail how to separate the interharmonics from the assumed harmonics at high frequencies.
But it is in [89] where perhaps a more complete solution to the problem initially posed about distortion rates for measuring interharmonics and for higher frequencies not defined in the standards is given. These authors measure harmonic emissions from PV inverters to the grid using the same THDS subgroup harmonic distortion rate already defined in the standards, to which they add two other rates: Total InterHarmonic Distortion Subgroup (TIHDSYLF), for low frequencies; and Total Harmonic and InterHarmonic Distortion Subgroup (TH&IHDSYHF), for high frequencies. The latter rate includes harmonics and interharmonics, since at high frequencies these are not differentiated. The letter Y in this nomenclature is replaced by either voltage U or current I, as was seen in IEC 61000-4-7 [32]:
The numerators of the (relative) distortion indices give the distortion in absolute values: Total Harmonic Content Subgroup, THCSYLF, (all harmonic subgroups at low frequencies); Total InterHarmonic Content Subgroup, TIHCSYLF, (all interharmonics, except those in the sidebands to harmonics, also at low frequencies); and Total Harmonic and InterHarmonic Content Subgroup, TH&IHCSYHF, (harmonics and interharmonics without distinction, at high frequencies). With the last index, TH&IHDSYHF, the lack of measuring harmonics and interharmonics at high frequencies above those considered harmonics is covered. According to these same authors [89], the TIHDSYLF index (in addition to the THDSYLF defined in the standard itself) has already been referenced in the literature and used in some commercial power quality measurement instruments that meet the class A requirements of IEC 61000-4-30 [31]. The TIHD2kHz rate of [88], cited above, does not provide more information than the TIHDSYLF of [89] if the latter is normalized by the main harmonic.
The rates proposed in [89] are used and improved in later papers. Thus, in [90] the first two rates, THDSYLF and TIHDSYLF, are used again to measure the harmonic distortion produced in the input current of switch-mode power supplies (SMPS’) of desktop PCs. In this case, the authors also consider the first interharmonic subgroups, 0 and 1, in the TIHDS rate, thus including the measurement of interharmonics from 10 Hz to 90 Hz (for a 50 Hz network) that were not included in [89]. Likewise, in [91], the TIHDSYLF rate is used for the measurement of interharmonics, both voltage and current, in a Grid-tied PV Inverter. The TH&IHDSYHF rate is again used in [92,93], in this case extending the frequency range up to 150 kHz (with respect to the 50 kHz in the same rate proposed in [89]) to measure the supra-harmonic distortion produced in SMPS and in the power supply of LED lamps.
5. Applications of Distortion Rates
In the previous sections, different definitions of distortion rates have been reviewed according to the measured contents and the way to obtain these rates, focusing mainly on their application to the characterization of the power quality of the network or devices connected to it. In this section, examples of applications of the distortion rates defined in the previous sections are shown which are not limited only to the informative work of the analyzed signal quality but also have other purposes, such as the control of power converters to optimize the harmonic distortion generated by them, and the observation of the distortion produced by user loads.
The aim of control techniques for power converters, such as those converting renewable energies and grid-connected active filters, is not only to make this conversion with the best possible efficiency but also to do so by controlling the obtained harmonic distortion rates [94,95]. Online measurement of the voltage THD in the power system, with small computational costs, may be suitable for network test applications so that the distortion at different locations in the power network can be controlled online. Thus, optimized modulation methods are shown in the literature to improve the quality of the signals obtained in inverters based on the measurements of their distortion factors in real-time, both for two-level inverters [96] and for multilevel inverters that further optimize the quality of the obtained waveform [97,98]. Other authors [99,100,101] also show the use of the weighted distortion rate WTHD, for the case of inductive loads, as a control parameter of the modulation method for the generation of alternating signals in inverters. In [102,103,104,105] the distortion rate is also used for the design of power converters for high-power LED lamps, so that the harmonic emission of the input current to the grid is reduced.
Distortion rates are also used to measure harmonic pollution produced on the grid by user loads. These loads include environmentally-related power devices such as photovoltaic inverters [5,84,85,89,91,106], wave energy converters [33], wind generators [107,108,109], electric vehicle chargers [110,111,112,113], or energy-efficient lighting devices [93,114,115]. The rates are also used to measure the distortion produced by other general-purpose power converters such as switching power supplies [90,92] and Adjustable speed-drives (ASD), both at their input on the mains side [88,116] and at their output [48].
Likewise, distortion rates could be applied to track the quality of currents drawn by loads on the customer side and for recognition of nonlinear load usage [29,117]. Similarly, THD percentage can be used to identify consumption patterns for various combinations of loads in the network, in real-time, using the Non-intrusive load monitoring (NILM) technique [118,119,120]. Load pattern identification is important for responsible energy consumption, as it makes users aware of power quality and encourages companies to use equipment that emits low levels of harmonics.
A high-accuracy THD measurement system can be used to measure the linearity of the AC behavior of integrated electronic devices operating at very high frequencies. Thus, a high-precision system for measuring very small THD distortion components over a wide frequency range (1–100 MHz) is proposed in [121], which can be used to measure the AC linearity of electronic devices such as operational amplifiers, analog-to-digital converters (ADCs) and digital-to-analog converters (DACs) operating at frequencies up to several tens of megahertz. The distortion rate is also used to measure the quality of audio signals [122,123,124], although in these cases the definition of THD that normalizes by the total rms value of the signal is usually preferred, as given in [37], with the definition of THD that normalizes between the fundamental being preferred for power signals, in which THD can take high values.
Examples of the use of the rates defined in the IEC 61000-4-7 standard [32] can also be found in works such as [83,114,125,126], as well as definitions of different distortion rates proposed by other authors and based on the same standard [59,83,88,89,126,127]. The rates defined in the standard are also used to verify or validate new distortion rates, since they need a recognized method with which to compare their results.
Table 5 shows a summary of references on distortion rates, classified according to their type of application.

Table 5.
Different applications of distortion rates.
6. General Considerations on Distortion Rates
Reviewing what has been discussed in previous sections on distortion rates, as defined both in the literature and in the regulations, the following general considerations can be summarized:
- -
- Distortion measurements can result in absolute rates or rms values of the total harmonics and/or interharmonics within a frequency range (obtained as the square root of the sum of squares of their rms values), and relative rates or distortion rates, found as either of the above normalized absolute rates (usually by dividing by the fundamental or by the fundamental harmonic subgroup).
- -
- The measured frequencies can be low (LF), also called harmonic frequencies, which include up to the 40th harmonic (2 kHz, for 50 Hz networks); and high (HF), from the end of the previous LF up to 9 kHz or even up to 150 kHz if supraharmonic disturbances are measured.
- -
- In the low-frequency range, the measurement of harmonics can be separated from that of interharmonics, or the whole spectral content can be measured together. On the other hand, for high frequencies it does not make sense to separate them (since for high harmonics the synchronism error between the acquisition window and the fundamental is multiplied; thus, high harmonics also behave as interharmonics, generating spectral leakage). Moreover, when measuring the distortion produced by power converters, the separating of harmonics from interharmonics in the high frequencies around the switching frequencies of the converter could lead to very different results in the case of using synchronous modulation (with carrier frequency multiple of the fundamental and therefore also harmonic) or asynchronous modulation. For example, with a carrier of 4 kHz and a fundamental of 60 Hz, the components with frequencies around 4 kHz and their multiples, separated from these by a whole number of times the fundamental, would no longer be harmonic.
- -
- To detect and differentiate each of the harmonics, the most commonly used technique is DFT using short windows of 0.2 s, although when analyzing non-stationary signals it can be replaced by other techniques such as wavelets, sliding window STFT, or even mixing with parametric methods if greater precision is desired. In the latter case, there would be a greater computational burden, and it would be necessary to previously know the harmonic content of the signal to model the parameters of the chosen method.
- -
- Many rates, such as those based on IEC standards, omit the measurement of the spectral bars corresponding to the first interharmonics (included in the interharmonic groups and subgroups 0 and 1, such as between 5 and 45 Hz and between 55 and 95 Hz, for a 50 Hz fundamental). On the other hand, other rates such as TWD, TDC, TnHD, and TNHDF already contain all the interharmonics of the signal, as they are calculated from the total rms value. When measuring the distortion in adjustable speed drivers, components due to motor failures, such as broken bars, eccentricity, and other load imbalances may appear at these frequencies [128,129]. If these interharmonics around the fundamental harmonic are relatively large compared to those around higher harmonics, they can obscure information from the rest of the spectrum, which can be a drawback.
- -
- It may be desirable to remove the continuous component of all distortion rates, as it includes the offsets of all measurement instrumentation and does not provide accurate information.
- -
- The (relative) distortion rates can be divided or normalized in different ways:
- (a)
- By the total rms value of the signal, as is done with the THDR rms rate and with the FF, TDC, THFLF, and TNHDF waveform distortion indices seen in [85]. However, this way of normalizing, at least in the case of the THDR rate, has already been noted to be less accurate for power system signals [37].
- (b)
- There are also rates that normalize by constants, such as maximum values or nominal values. This is due to the disadvantage that when normalizing by the fundamental, for low values of the fundamental, the distortion rates normalized by it can adopt high values. This is the case of Total Demand Distortion (TDD) and Total Rated Distortion (TRD), defined due to the large variation of the current fundamental when varying the connected load. This can also occur when measuring at the output of low-power adjustable speed drivers, which usually have a variable fundamental amplitude at the output of the inverter stage.
- (c)
- By the fundamental harmonic YH,1 when only harmonics (THD) are considered in the numerator or absolute rate, or when all the spectral bars appear (including those adjacent to the fundamental, as in the ITHDG rate of [83] or in the two TIHD rates of [88]). With this solution, it is normalized with respect to the fundamental, without taking into account the effects of its possible amplitude modulation (contained in the spectral bands adjacent to the fundamental), but also without taking into account other nearby frequencies such as those due to motor failures when measuring distortion in these devices.
- (d)
- By the fundamental harmonic subgroup Ysg,1 when only harmonic subgroups (THDS) also appear in the numerator, or all spectral bars except those adjacent to the fundamental (as in the THDGS rate of [83] or in the TIHDS rate of [89]). The utility of the harmonic subgroup is to evaluate fluctuations in the amplitude and phase of harmonics in network signals, which cause the appearance of sidebands to them. Therefore, when normalizing by the fundamental harmonic subgroup, it is intended that the fundamental be considered as the set of that frequency and its nearest spectral bars, to take into account the amplitude variations as being part of that harmonic. According to some authors, it seems more advisable to use this normalization by the fundamental harmonic subgroup when using sensitive methods such as DFT for the treatment of signals susceptible to strong frequency variations, and it can be normalized by the pure fundamental when using more robust methods such as Kalman filters [83,130].
- (e)
- The order of each harmonic considered can also be included in the denominator, as in the weighted total harmonic distortion rate WTHD [42], in which more weight is given to the low harmonics. Another rate in which the order of each harmonic considered is presented is the partially weighted harmonic distortion rate PWHD [32], in which more weight is given to high harmonics, contrary to WTHD.
- -
- In all rates, the fundamental harmonic (and sometimes even the fundamental harmonic subgroup, depending on how the rate is normalized) is always separated from the total spectral content to be evaluated that appears in the numerator of the rate. No spectral content appears in the numerator that is normalized by it, as is the case for the fundamental itself (except for the waveform distortion indices, which normalize by the total rms value of the signal).
- -
- Measurements of groups and subgroups and even individual harmonics and interharmonics (also called “harmonic factors” or HFn) can also be normalized by dividing only by the fundamental, or by dividing by the fundamental and its aggregated sidebands. Papers such as [88,131] normalize by the fundamental for those cases not defined in the standards, while others such as [89] do so by dividing by the fundamental harmonic subgroup (which includes the amplitude modulations of the fundamental).
- -
- Throughout this paper, it has been seen that there is no distortion index better than the others, but rather indexes more suitable than others depending on the intended application and the nature of the signal to be measured, which condition the measurement approach. Thus, to measure only harmonics in the lower part of the spectrum, the most suitable index is THD, but if it is necessary to take into account the effects of amplitude variations of the signal, THDS is preferable, or even WTHD in the case of inductive loads such as motors. On the other hand, to measure the whole harmonic content, indices such as TWD, TRD, or even TDC can be used.
- -
- Therefore, each distortion rate may have different limits, both in the frequency range measured and in the type of harmonic and interharmonic content and the degree of stationarity of the signal to be analyzed, depending on the measurement approach to be covered. For example, to measure harmonic and interharmonic contents in signals generated by inverters, a smaller bandwidth is required if the energy of the components around multiples of the switching frequency is to be evaluated in cases of using PWM type modulations, as opposed to cases of using closed-loop or random type modulations whose high-frequency components are more expanded.
- -
- Regarding the limits when measuring high frequencies, the challenge can be to measure the distortion produced at high frequencies by communication signals in the electrical network, such as PLC (Power-Line Communications) systems, and also by other electronic systems such as switch-mode power supplies (SMPS) present in desktop PCs, energy-saving lamps, electric vehicle chargers, etc. The high-frequency harmonic emissions of these systems are higher than those of the power converters of grid-connected renewable energy equipment and can exceed the limit of 150 kHz considered in the annexes of the standards.
- -
- The CIGRE Joint Working Group (JWG) C4.24 [6] foresees three types of changes in the power system: changes in production (such as the proliferation of distributed generation with more small units connected to LV and MV grids), changes in consumption (proliferation of active power electronics interfaces and small devices such as SMPS), and changes in the grid (with greater use of power line communication equipment and power-electronics equipment). These changes lead to an increase in interharmonic emissions and an increment in the value of emission frequencies (especially due to low power converters and power line communication signals). Actual measurements on the power grid, such as those presented in the annexes of [6], underline the need for further research. Therefore, some challenges for the future are the improvement of the measurement methods of interharmonic and supraharmonic components, and therefore of the distortion rates that evaluate these components.
Due to the above, CIGRE JWG C4.24 [6] makes some findings and recommendations. Measurements at higher frequencies, up to 150 kHz or higher, will require new sensors and transducers, especially in MV and HV networks. Standardized measurement methods and new distortion indices are also needed for high frequencies. Due to the specific signal characteristics in this frequency range, these distortion indices must not only take into account the frequency domain, but also the time-frequency domain. Another recommendation of CIGRE JWG C4.24 is to work with a reduced number of distortion factors in order to simplify power quality reporting.
Table 6 shows a summary of several of the distortion rates analyzed in this work, classified according to how they are normalized, frequency range covered and harmonic and interharmonic content analyzed. Finally, Table 7 synthesizes the main characteristics of each harmonic distortion rate, including their advantages and limitations, and application ranges.

Table 6.
Some distortion rates defined in the regulations and in the literature. For each rate, the bibliographic reference where it has been defined is cited.

Table 7.
Summary table of distortion rates. For each rate, the bibliographic reference where it has been defined is cited.
7. Conclusions
Harmonic distortion rates are indicators that allow systematic and comparable evaluation of the quality of electrical systems, thus helping to improve system quality and to reduce distortion levels. However, due to the connection of various modern equipment based on electronic converters to the electrical network, new needs arise for the measurement of harmonic and interharmonic content, not only in the network but additionally at the output of this equipment.
Measurement standards are necessary to make measurements more systematic and comparable between different equipment, thus allowing more reliable conclusions to be drawn. However, these standards cover the measurement needs mainly of the low-frequency part and, informatively, part of the high-frequency range, being oriented to evaluate only signals in the electrical network. Furthermore, these standards do not always have distortion rates that differentiate the type of distortion according to whether it is harmonic or interharmonic or separate the frequency ranges, or that take into account the stationarity of the signals evaluated. In this sense, several rates are proposed in the literature that are suitable for each type of measurement, many of them based on the new needs of distortion measurement when connecting devices to the grid such as photovoltaic and wind generators, battery chargers for electric vehicles, and other modern electronic equipment.
Therefore, this paper discusses the different total harmonic distortion indices currently defined, both in the literature and in standards, to show which of them are suitable for assessing harmonic and interharmonic contamination in power system signals. In addition to the above, these conclusions can be drawn from this work:
- -
- In this article we have studied the rates proposed in the standards as well as many of the distortion rates proposed by other authors and which are not yet standardized, discussing the performance of each of them and classifying them according to frequency range, type of measured content and means of normalization.
- -
- Likewise, distortion rates have also been reviewed according to their application (i.e., to evaluate the quality of the signal in general, as validators of other rates not yet verified, to control the way of modulating the signal generated by grid-connected inverters, to control the distortion introduced by loads or users, to measure the distortion of a specific type of load as with weighted rates, etc.), as well as according to the way of obtaining them (in the time or frequency domain, experimentally or analytically, and in the latter case, for certain specific measurement situations, optimizing the hardware resources of the digital processors used, measuring distortion rates on-line or in real-time, etc.).
- -
- Most of the rates studied have in common a lack of need for precision in the measurement of high frequencies, being able to cover large bands of frequency components, all considered interharmonic or not synchronized with the analysis window. Therefore, at high frequencies it is not usual to differentiate between harmonic and interharmonic contents, unlike at low frequencies where it is possible to make this distinction if the various rates studied are observed.
- -
- Another consideration common to all the rates analyzed is the means of normalizing, which is usually done by the fundamental harmonic or by its subgroup (if it is desired to consider effects of the non-stationarity of the signal in the form of amplitude changes). Normalizing by the fundamental does not take into account its sidebands, thus avoiding possible amplitude variations; however, it fails to consider other nearby frequency components, such as those due to motor failures, when measuring distortion in equipment.
- -
- Other ways of normalizing can be by the total rms value of the signal (as in distortion factors, which show greater accuracy in the evaluation of audio signals), by constant values such as the peak or nominal value (when analyzing signals with a fundamental that varies considerably between different measurements), or even by taking into account the order of each harmonic evaluated (as in the case of weighted distortion rates). Likewise, in all rates the appearance of spectral contents in the numerator between those to be normalized is avoided, being also convenient to separate the continuous component of all distortion rates, since it may include the offset errors of the measuring equipment.
- -
- We can conclude by saying that there is no distortion index better than the others, but rather indexes more suitable than others for each measurement approach, depending on the intended application and the nature of the signal to be measured.
- -
- Future steps should be to improve existing methods for measuring in the high-frequency range, and for measuring interharmonics, especially with signals that are not completely stationary. Although the effects of supraharmonics are limited to neighboring devices and do not propagate over long distances, they cause adverse effects on the devices, reducing their lifetime and producing interference in communications, so it is also important to improve supraharmonic standards, especially for emissions that exceed the 150 kHz limit considered in the annexes of the standards.
Thus, the new distortion factors make it possible to measure harmonic distortion in signals with a higher interharmonic content and over a wider frequency range, and thus complement those defined in the standards (more suitable for measuring distortion in network signals). However, despite the improvements achieved, and due to the diversity of proposed rates, a standardization of the new rates incorporating the necessary characteristics to evaluate distortion in modern power systems is necessary. It is to be expected that with the new improved distortion rates for measuring interharmonics and higher frequencies, and the revisions and improvements of the standards especially in the part related to the measurement of interharmonics, an increasing number of distortion rates based on standards such as those of the IEC will continue to be used for the measurement of harmonic disturbances and as unifying and validating techniques for other, more innovative ones.
Author Contributions
Conceptualization, A.A.-G., O.D.-P., D.M.-S. and A.Z.-L.; Data curation, A.A-G.; Methodology, A.A.-G., O.D.-P., D.M.-S.; Software, A.A.-G.; Validation, D.M.-S.; Writing—original draft, A.A.-G.; Writing—review and editing, O.D.-P., D.M.-S. and A.Z.-L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| Symbol | Meaning |
| ADC | Analog-to-Digital Converter |
| ASD | Adjustable Speed-Drives (ASD) |
| CENELEC | Comité Européen de Normalisation Electrotechnique |
| CIGRE | Conseil international des grands réseaux électriques |
| CISPR | Comité International Spécial des Perturbations Radioélectriques |
| DAC | Digital-to-Analog Converter |
| DFH | Differential factor of voltage harmonics of various orders |
| DFT | Discrete Fourier Transform |
| DSP | Digital Signal Processor |
| EMC | Electromagnetic Compatibility |
| FF | Fundamental Factor |
| FFT | Fast Fourier Transform |
| HF | High Frequency |
| HFn | Harmonic Factor |
| HV | High Voltage |
| IEC | International Electrotechnical Commission |
| IEEE | Institute of Electrical and Electronics Engineers |
| IFH | Integral factor of voltage harmonics of various orders |
| ITHDG | Group Total Harmonic Distortion and Improved THDG |
| LF | Low Frequency |
| LV | Low Voltage |
| MV | Medium Voltage |
| NILM | Non-Intrusive Load Monitoring technique to identify consumption patterns |
| OMSV | Operator–Matrix State Variable method |
| PLL | Phase-Locked Loop |
| PV | PhotoVoltaic (inverters) |
| PWHD | Partial Weighted Total Harmonic Distortion |
| SMPS | Switch-Mode Power Supplies |
| STDEH | Short Time Disturbance Energy for the High-Frequency |
| STDEL | Short Time Disturbance Energy for the Low-Frequency |
| SWWMEM | Sliding-Window Wavelet-Modified ESPRIT Method |
| TDC | Total Distortion Content |
| TDD | Total Demand Distortion |
| TH&IHDSYHF | Total Harmonic and InterHarmonic Distortion Subgroup |
| THC | Total harmonic content in general, especially total harmonic current |
| THDGS | Subgroup Total Harmonic Distortion and improved THDG |
| THDGY | Group Total Harmonic Distortion |
| THDR | Effective Total Harmonic Distortion |
| THDSY | Subgroup Total Harmonic Distortion |
| THDY | Total Harmonic Distortion |
| THFD | Total High-Frequency Distortion |
| THFLF | Total Harmonic-LF Factor |
| TIHD2–9kHz | Total InterHarmonic Distortion Factor for 2–9 kHz |
| TIHD2kHz | Total InterHarmonic Distortion Factor for 2 kHz |
| TIHDSYLF | Total InterHarmonic Distortion Subgroup |
| TnHD | Total nonHarmonic Distortion or Total interharmonic distortion |
| TNHDF | Total Non-Harmonic-LF Distortion Factor |
| TRD | Total Rated Distortion |
| TWD | Total Waveform Distortion |
| VSC | Voltage Source Converters |
| WTHD | Weighted Total Harmonic Distortion |
| Ck | Spectral component of order k. Also called YC,k |
| h | Harmonic order |
| I1 | Rms value of the fundamental component of current |
| Id | Maximum or peak demand load current of the fundamental component |
| Ih | Rms value of the harmonic component h of current |
| Irated | Nominal current value |
| Itot | Total rms value of current |
| V1 | Rms value of the fundamental component of voltage |
| Vh | Rms value of the harmonic component h of voltage |
| Vrated | Nominal voltage value |
| Vtot | Total rms value of voltage |
| Y | Symbol to be replaced by I for current or by U for voltage |
| YB,b | RMS value of each 200 Hz high-frequency Band centered at frequency b |
| YC,k | Spectral component of order k, where Y can be current or voltage |
| Yg,h | Harmonic group of order h, where Y can be current or voltage |
| YH,1 | Rms value of the fundamental component, where Y can be current or voltage |
| YH,h | Rms value of the harmonic component h, where Y can be current or voltage |
| Yig,h | Interharmonic group of order h, where Y can be current or voltage |
| Yisg,h | Interharmonic subgroup of order h, where Y can be current or voltage |
| Ysg,h | Harmonic subgroup of order h, where Y can be current or voltage |
| Ytot | Total rms value of the signal, where Y can be current or voltage |
References
- Rönnberg, S.; Bollen, M. Power quality issues in the electric power system of the future. Electr. J. 2016, 29, 49–61. [Google Scholar] [CrossRef]
- Ogheneovo Johnson, D. Issues of Power Quality in Electrical Systems. Int. J. Energy Power Eng. 2016, 5, 148. [Google Scholar] [CrossRef]
- Khan, S.; Singh, B.; Makhija, P. A review on power quality problems and its improvement techniques. In Proceedings of the 2017 Innovations in Power and Advanced Computing Technologies (i-PACT), Vellore, India, 21–22 April 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Kalair, A.; Abas, N.; Kalair, A.R.; Saleem, Z.; Khan, N. Review of harmonic analysis, modeling and mitigation techniques. Renew. Sustain. Energy Rev. 2017, 78, 1152–1187. [Google Scholar] [CrossRef]
- Xu, X. Harmonic Modelling and Characterisation of Modern Power Electronic Devices in Low Voltage Networks. Ph.D. Thesis, The University of Edinburgh, Edinburgh, UK, 2018. [Google Scholar]
- JWG-C4. 24/CIRED. Power Quality and Emc Issues With Future Electricity Networks; Eindhoven University of Technology; CIGRE: Eindhoven, The Netherlands, 2018; ISBN 978-2-85873-421-4. [Google Scholar]
- Meyer, J.; Bollen, M.; Amaris, H.; Blanco, A.M.; Gil De Castro, A.; Desmet, J.; Klatt, M.; Kocewiak, Ł.; Rönnberg, S.; Yang, K. Future work on harmonics-Some expert opinions Part II-Supraharmonics, standards and measurements. In Proceedings of the 2014 16th International Conference on Harmonics and Quality of Power (ICHQP), Bucharest, Romania, 25–28 May 2014; pp. 909–913. [Google Scholar] [CrossRef]
- Ribeiro, P.F. Time-Varying Waveform Distortions in Power Systems; John Wiley & Sons: New York, NY, USA, 2009; ISBN 9780470714027. [Google Scholar] [CrossRef]
- Alfieri, L.; Bracale, A.; Larsson, A. New power quality indices for the assessment of waveform distortions from 0 to 150 kHz in power systems with renewable generation and modern non-linear loads. Energies 2017, 10, 1633. [Google Scholar] [CrossRef]
- Arrillaga, J.; Watson, N.R. Power System Harmonics, 2nd ed.; John Wiley & Sons, Ltd: Chichester, UK, 2003; ISBN 0-470-85129-5. [Google Scholar]
- Otcenasova, A.; Bolf, A.; Altus, J.; Regula, M. The Influence of Power Quality Indices on Active Power Losses in a Local Distribution Grid. Energies 2019, 12, 1389. [Google Scholar] [CrossRef]
- Aiello, M.; Cataliotti, A.; Favuzza, S.; Graditi, G. Theoretical and experimental comparison of total harmonic distortion factors for the evaluation of harmonic and interharmonic pollution of grid-connected photovoltaic systems. IEEE Trans. Power Deliv. 2006, 21, 1390–1397. [Google Scholar] [CrossRef]
- Leonowicz, Z.; Lobos, T.; Rezmer, J. Advanced spectrum estimation methods for signal analysis in power electronics. IEEE Trans. Ind. Electron. 2003, 50, 514–519. [Google Scholar] [CrossRef]
- Jain, S.K.; Singh, S.N. Harmonics estimation in emerging power system: Key issues and challenges. Electr. Power Syst. Res. 2011, 81, 1754–1766. [Google Scholar] [CrossRef]
- Chen, C.I.; Chen, Y.C. Comparative study of harmonic and interharmonic estimation methods for stationary and time-varying signals. IEEE Trans. Ind. Electron. 2014, 61, 397–404. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X.; Liu, Y.; Cui, S. Resolution-enhanced harmonic and interharmonic measurement for power quality analysis in cyber-physical energy system. Sensors 2016, 16, 946. [Google Scholar] [CrossRef]
- Stanisavljević, A.M.; Katić, V.A.; Dumnić, B.P.; Popadić, B.P. Overview of voltage dips detection analysis methods. In Proceedings of the 2017 International Symposium on Power Electronics (Ee), Novi Sad, Serbia, 19–21 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Alfieri, L. New Advanced Methods for the Spectral Analysis of Time-Varying Waveforms in Power Systems. Ph.D. Thesis, Department of Electrical Engineering and Information Technology, University of Naples Federico II, Naples, Italy, 2017. [Google Scholar]
- Larsson, A.; Bollen, M. Towards a Standardized Measurement Method for Voltage and Current Distortion in the Frequency Range 2 To 150 Khz. 22nd Int. Conf. Electr. Distrib. 2013, 1052, 1–4. [Google Scholar] [CrossRef]
- IEEE Std 1159-IEEE Recommended Practice for Monitoring Electric Power Quality; IEEE Standard 1159–2009; IEEE: New York, NY, USA, 2009. [CrossRef]
- Standard EN 50160. Voltage Characteristics of Electricity Supplied by Public Distribution Systems; EN 50160; CENELEC: Brussels, Belgium, 2010. [Google Scholar]
- IEEE 519 Recommended Practice and Requirements for Harmonic Control in Electric Power Systems; IEEE Standard 519-2014; IEEE: New York, NY, USA, 2014.
- GOST 32144-2013: Electric Energy. Compatibility of Technical Means is Electromagnetic. Norms of Power Quality in General-Purpose Power Supply Systems; Standartinform; Standardinform Publishers: Moscow, Russia, 2013. [Google Scholar]
- Ded, A.V.; Maltsev, V.N.; Sikorski, S.P. Comparative Analysis of the Specifications on the Power Quality of the European Union and the Russian Federation. J. Phys. Conf. Ser. 2018, 998, 4–10. [Google Scholar] [CrossRef]
- IEC Standard IEC 61000-2-2: Environment-Compatibility Levels for Low-Frequency Conducted Disturbances and Signalling in Public Low-Voltage Power Supply Systems; International Electrotechnical Commission (IEC): Geneva, Switzerland, 2002.
- IEC Standard IEC 61000-2-12: Environment-Compatibility Levels for Low-Frequency Conducted Disturbances and Signalling in Public Medium-Voltage Power Supply Systems; International Electrotechnical Commission (IEC): Geneva, Switzerland, 2003.
- Ćuk, V.; Cobben, J.F.G.; Ribeiro, P.F.; Kling, W.L.; Cobben, J.F.G.; Ribeiro, P.F. A review of international limits for harmonic voltages and currents in public networks. In Proceedings of the 2014 16th International Conference on Harmonics and Quality of Power (ICHQP), Bucharest, Romania, 25–18 May 2014; pp. 621–625. [Google Scholar] [CrossRef]
- Fallows, D.; Nuzzo, S.; Costabeber, A.; Galea, M. Harmonic reduction methods for electrical generation: A review. IET Gener. Transm. Distrib. 2018, 12, 3107–3113. [Google Scholar] [CrossRef]
- Matas, J.; Martin, H.; De La Hoz, J.; Abusorrah, A.; Al-Turki, Y.; Alshaeikh, H. A New THD Measurement Method with Small Computational Burden Using a SOGI-FLL Grid Monitoring System. IEEE Trans. Power Electron. 2020, 35, 5797–5811. [Google Scholar] [CrossRef]
- IEC 61727-2004 Photovoltaic (PV) Systems-Characteristics of the Utility Interface; International Electrotechnical Commission (IEC): Geneva, Switzerland, 2004.
- IEC Standard 61000-4-30: Testing and Measurement Techniques-Power Quality Measurement Methods; International Electrotechnical Commission (IEC): Geneva, Switzerland, 2015.
- IEC Standard 61000-4-7: General Guide on Harmonics and Interharmonics Measurements, for Power Supply Systems and Equipment Connected Thereto; International Electrotechnical Commission (IEC): Geneva, Switzerland, 2010.
- Kelly, J.; Aldaiturriaga, E.; Ruiz-Minguela, P. Applying international power quality standards for current harmonic distortion to wave energy converters and verified device emulators. Energies 2019, 12, 3654. [Google Scholar] [CrossRef]
- GOST 30804. 4.30-2013 Electric Energy. Compatibility of Technical Means is Electromagnetic. Methods for Measuring the Quality of Electrical Energy; Standardinform 51; Standardinform Publishers: Moscow, Russia, 2014. [Google Scholar]
- GOST 30804. 4.7-2013 Compatibility of Technical Means is Electromagnetic. General Guidance on Measuring Instruments and Measurements of Harmonics and Interharmonics for Power Supply Systems and Associated Equipment; Standardinform 33; Standardinform Publishers: Moscow, Russia, 2014. [Google Scholar]
- Bollen, M.H.J.; Gu, I.Y.H. Signal Processing of Power Quality Disturbances; Wiley-IEEE Press: Piscataway, NJ, USA, 2006; ISBN 9780471931317. [Google Scholar] [CrossRef]
- Shmilovitz, D. On the Definition of Total Harmonic Distortion and Its Effect on Measurement Interpretation. IEEE Trans. Power Deliv. 2005, 20, 526–528. [Google Scholar] [CrossRef]
- Sajjad, K.; Kalsoom, G.; Mughal, A. Simplified THD measurement and analysis for electronic power inverters. In Proceedings of the 2015 12th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 13–17 January 2015; pp. 186–191. [Google Scholar] [CrossRef]
- IEEE Std. 1547-2018. Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces; IEEE Standard 1547-2018; IEEE: New York, NY, USA, 2018. [Google Scholar]
- Ingale, R. Harmonic Analysis Using FFT and STFT. Int. J. Signal Process. Image Process. Pattern Recognit. 2014, 7, 345–362. [Google Scholar] [CrossRef]
- Lopatkin, N.N.; Chernov, Y.A. Virtual instrument for non-conventional total harmonic distortion factors evaluation. In Proceedings of the 2016 International Siberian Conference on Control and Communications (SIBCON), Moscow, Russia, 12–14 May 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Holmes, G.; Lipo, T. Pulse Width Modulation for Power Converters: Principles and Practice; Wiley-IEEE Press: Piscataway, NJ, USA, 2003; ISBN 0471208140. [Google Scholar]
- Reznikov, B.; Srndovic, M.; Familiant, Y.L.; Grandi, G.; Ruderman, A. Simple Time Averaging Current Quality Evaluation of a Single-Phase Multilevel PWM Inverter. IEEE Trans. Ind. Electron. 2016, 63, 3605–3615. [Google Scholar] [CrossRef]
- Abdikarimuly, R.; Familiant, Y.L.; Ruderman, A.; Reznikov, B. Calculation of current total harmonic distortion for a single-phase multilevel inverter with LCL-Filter. In Proceedings of the 2016 IEEE International Power Electronics and Motion Control Conference (PEMC), Varna, Bulgaria, 25–28 September 2016; pp. 63–68. [Google Scholar] [CrossRef]
- Lopatkin, N.N.; Chernov, Y.A. Differential and integral factors of harmonics LabVIEW estimation. In Proceedings of the 2016 17th International Conference of Young Specialists on Micro/Nanotechnologies and Electron Devices (EDM), Erlagol, Russia, 30 June–4 July 2016; pp. 493–498. [Google Scholar] [CrossRef]
- Lipko, V.A.; Zinoviev, G.S. The family of extended power quality factors. In Proceedings of the 2015 16th International Conference of Young Specialists on Micro/Nanotechnologies and Electron Devices, Erlagol, Russia, 29 June–3 July 2015; pp. 553–556. [Google Scholar] [CrossRef]
- Peterson, B.; Blanco, A.M.; Rens, J.; Meyer, J.; Botha, G.; Desmet, J. Impact of Aggregation Interval on Harmonic Phase Angle Measurements. In Proceedings of the 2018 IEEE 9th International Workshop on Applied Measurements for Power Systems (AMPS), Bologna, Italy, 26–28 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Arranz-Gimon, A.; Zorita-Lamadrid, A.; Morinigo-Sotelo, D.; Duque-Perez, O. A Study of the effects of time aggregation and overlapping within the framework of IEC standards for the measurement of harmonics and interharmonics. Appl. Sci. 2019, 9, 4549. [Google Scholar] [CrossRef]
- Oliveira, W.R.; Filho, A.L.F.; Cormane, J. A contribution for the measuring process of harmonics and interharmonics in electrical power systems with photovoltaic sources. Int. J. Electr. Power Energy Syst. 2019, 104, 481–488. [Google Scholar] [CrossRef]
- Application Guide to the European Standard EN 50160 on "Voltage Characteristics of Electricity Supplied by Public Distribution Systems". Electricity Product Characteristics and Electromagnetic Compatibility; Union of the Electricity Industry Eurelectric; Eurelectric: Brussels, Belgium, 1995. [Google Scholar]
- Bilik, P. Measurement of voltage and current harmonics for frequencies up to 9 kHz according to IEC61000-4-7. In Proceedings of the 2009 10th International Conference on Electrical Power Quality and Utilisation, Lodz, Poland, 15–17 September 2009; pp. 7–11. [Google Scholar] [CrossRef]
- Barros, J.; De Apráiz, M.; Diego, R.I. Measurement of voltage distortion in the frequency range 2–9 kHz. In Proceedings of the 2010 IEEE International Workshop on Applied Measurements for Power Systems, Aachen, Germany, 22–24 September 2010; pp. 70–73. [Google Scholar] [CrossRef]
- Tarasiuk, T. Method, algorithm and device for estimation of components above the harmonic frequency range up to 9 kHz. Meas. J. Int. Meas. Confed. 2011, 44, 219–229. [Google Scholar] [CrossRef]
- Chicco, G.; Russo, A.; Spertino, F. Supraharmonics: Concepts and experimental results on photovoltaic systems. In Proceedings of the 2015 International School on Nonsinusoidal Currents and Compensation (ISNCC), Lagow, Poland, 15–18 June 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Rönnberg, S.K.; Bollen, M.H.J.; Amaris, H.; Chang, G.W.; Gu, I.Y.H.; Kocewiak, Ł.H.; Meyer, J.; Olofsson, M.; Ribeiro, P.F.; Desmet, J. On waveform distortion in the frequency range of 2–150 kHz-Review and research challenges. Electr. Power Syst. Res. 2017, 150, 1–10. [Google Scholar] [CrossRef]
- Ronnberg, S.K.; Gil-De-Castro, A.; Medina-Gracia, R. Supraharmonics in European and North American Low-Voltage Networks. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Palermo, Italy, 12–15 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Meyer, J.; Khokhlov, V.; Klatt, M.; Blum, J.; Waniek, C.; Wohlfahrt, T.; Myrzik, J. Overview and Classification of Interferences in the Frequency Range 2–150 kHz (Supraharmonics). In Proceedings of the 2018 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Amalfi, Italy, 20–22 June 2018; pp. 165–170. [Google Scholar] [CrossRef]
- Shadmehr, H.; Chiumeo, R.; Belloni, F.R. Beyond FFT algorithm in analyzing harmonics at frequency range of 2 kHz to 500 kHz. In Proceedings of the 2018 18th International Conference on Harmonics and Quality of Power (ICHQP), Ljubljana, Slovenia, 13–16 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Grevener, A.; Meyer, J.; Rönnberg, S. Comparison of Measurement Methods for the Frequency Range 2–150 kHz (Supraharmonics). In Proceedings of the 2018 IEEE 9th International Workshop on Applied Measurements for Power Systems (AMPS), Bologna, Italy, 26–28 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Zhuang, S.; Zhao, W.; Wang, R.; Wang, Q.; Huang, S. New Measurement Algorithm for Supraharmonics Based on Multiple Measurement Vectors Model and Orthogonal Matching Pursuit. IEEE Trans. Instrum. Meas. 2019, 68, 1671–1679. [Google Scholar] [CrossRef]
- Bollen, M.; Olofsson, M.; Larsson, A.; Rönnberg, S.; Lundmark, M. Standards for supraharmonics (2 to 150 kHz). IEEE Electromagn. Compat. Mag. 2014, 3, 114–119. [Google Scholar] [CrossRef]
- CISPR 16-1-2:2014 + A1:2017: Specification for Radio Disturbance and Immunity Measuring Apparatus and Methods-Part 1-2: Radio Disturbance and Immunity Measuring Apparatus-Coupling Devices for Conducted Disturbance Measurements; Comité International Spécial des Perturbations Radioélectriques (CISPR): Geneva, Switzerland, 2017.
- IEC Standard 61400-21:2008: Wind Turbines-Part 21: Measurement and Assessment of Power Quality Characteristics of Grid Connected Wind Turbines; International Electrotechnical Commission (IEC): Geneva, Switzerland, 2008.
- Klatt, M.; Meyer, J.; Schegner, P. Comparison of measurement methods for the frequency range of 2 kHz to 150 kHz. In Proceedings of the 2018 IEEE 9th International Workshop on Applied Measurements for Power Systems (AMPS), Bologna, Italy, 26–28 September 2018; pp. 818–822. [Google Scholar] [CrossRef]
- Bollen, M.H.J.; Ribeiro, P.F.; Larsson, E.O.A.; Lundmark, C.M. Limits for voltage distortion in the frequency range 2 to 9 kHz. IEEE Trans. Power Deliv. 2008, 23, 1481–1487. [Google Scholar] [CrossRef]
- Klatt, M.; Koch, A.; Myrzik, J.; Körner, C.; Darda, T.; Eberl, G. Emission levels above 2 kHz-Laboratory results and survey measurements in public low voltage grids. In Proceedings of the 22nd International Conference and Exhibition on Electricity Distribution (CIRED 2013), Stockholm, Sweden, 10–13 June 2013; pp. 10–13. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Y.; Tao, S.; Siddique, A.; Dong, X. A Flexible Supraharmonic Group Method Based on Switching Frequency Identification. IEEE Access 2020, 8, 39491–39501. [Google Scholar] [CrossRef]
- An, Z.; Wang, T.; Wang, Y.; Tang, S.; Tao, S.; Xu, Y. A variable bandwidth method for supraharmonic band aggregation. In Proceedings of the 2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; pp. 1090–1094. [Google Scholar] [CrossRef]
- Khokhlov, V.; Meyer, J.; Grevener, A.; Busatto, T.; Ronnberg, S. Comparison of measurement methods for the frequency range 2-150 kHz (Supraharmonics) based on the present standards framework. IEEE Access 2020, 8, 77618–77630. [Google Scholar] [CrossRef]
- Mendes, T.; Duque, C.; MansodaSilva, L.; Ferreira, D.; Meyer, J.; Ribeiro, P. Comparative analysis of the measurement methods for the supraharmonic range. Int. J. Electr. Power Energy Syst. 2020, 118, 105801. [Google Scholar] [CrossRef]
- Collin, A.J.; Langella, R.; Testa, A. Assessing Distortion Within the IEC Framework in the Presence of High Frequency Components: Some Considerations on Signal Processing. In Proceedings of the 2018 IEEE 9th International Workshop on Applied Measurements for Power Systems (AMPS), Bologna, Italy, 26–28 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Ritzmann, D.; Lodetti, S.; De La Veg, D.; Khokhlov, V.; Gallarreta, A.; Wright, P.; Meyer, J.; Fernandez, I.; Klingbeil, D. Comparison of Measurement Methods for 2-150-kHz Conducted Emissions in Power Networks. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Mureşan, C.; Drăgan, F.; Zaharia, V.D. Total Harmonic Distortion Computation in Nonsynchronized Sampling conditions. Acta Electroteh. 2011, 52, 114–118. [Google Scholar]
- Mog, G.E.; Ribeiro, E.P. Total harmonic distortion calculation by filtering for power quality monitoring. In Proceedings of the 2004 IEEE/PES Transmision and Distribution Conference and Exposition: Latin America (IEEE Cat. No. 04EX956), Sao Paulo, Brazil, 8–11 November 2004; pp. 629–632. [Google Scholar] [CrossRef]
- Blagouchine, I.V.; Moreau, E. Analytic method for the computation of the total harmonic distortion by the cauchy method of residues. IEEE Trans. Commun. 2011, 59, 2478–2491. [Google Scholar] [CrossRef]
- Tzvetkov, P.M.; Serov, A.N.; Kodjabashev, I.N.; Galabov, K.S. Calibration of power quality analyzers on total harmonic distortion by standard periodic non-harmonic signals. In Proceedings of the 2020 30th International Scientific Symposium'Metrology and Metrology Assurance (MMA), Sozopol, Bulgaria, 7–11 September 2020; pp. 26–29. [Google Scholar] [CrossRef]
- Alegria, F.C. Precision of the sinefitting-based total harmonic distortion estimator. Metrol. Meas. Syst. 2016, 23, 37–46. [Google Scholar] [CrossRef][Green Version]
- Antić, B.M.; Mitrović, Z.L.; Vujičić, V.V. A method for harmonic measurement of real power grid signals with frequency drift using instruments with internally generated reference frequency. Meas. Sci. Rev. 2012, 12, 277–285. [Google Scholar] [CrossRef][Green Version]
- Ivanchenko, M.A.; Dvorkin, D.V. An Alternative Approach for THD Assessment. In Proceedings of the 2020 International Youth Conference on Radio Electronics, Electrical and Power Engineering (REEPE), Moscow, Russia, 12–14 March 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Hou, C.; Zhu, M.; Li, Z.; Li, Y.; Cai, X. Inter Harmonic THD Amplification of Voltage Source Converter: Concept and Case Study. IEEE Trans. Power Electron. 2020, 35, 12651–12656. [Google Scholar] [CrossRef]
- Farokhnia, N.; Vadizadeh, H.; Fathi, S.H.; Anvariasl, F. Calculating the formula of line-voltage THD in multilevel inverter with unequal DC sources. IEEE Trans. Ind. Electron. 2011, 58, 3359–3372. [Google Scholar] [CrossRef]
- Barros, J.; Diego, R.I.; de Apraz, M. A Discussion of New Requirements for Measurement of Harmonic Distortion in Modern Power Supply Systems. IEEE Trans. Instrum. Meas. 2013, 62, 2129–2139. [Google Scholar] [CrossRef]
- Dalali, M.; Jalilian, A. Indices for measurement of harmonic distortion in power systems according to IEC 61000-4-7 standard. IET Gener. Transm. Distrib. 2015, 9, 1903–1912. [Google Scholar] [CrossRef]
- Xu, X.; Collin, A.J.; Djokic, S.Z.; Langella, R.; Testa, A.; Meyer, J.; Moller, F.; Yanchenko, S. On the impact of operating modes and power supply conditions on the efficiency of power electronic devices. In Proceedings of the 2016 IEEE International Workshop on Applied Measurements for Power Systems (AMPS), Aachen, Germany, 28–30 September 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Xiao, X.; Collin, A.J.; Djokic, S.Z.; Yanchenko, S.; Moller, F.; Meyer, J.; Langella, R.; Testa, A. Analysis and Modelling of Power-Dependent Harmonic Characteristics of Modern PE Devices in LV Networks. IEEE Trans. Power Deliv. 2017, 32, 1014–1023. [Google Scholar] [CrossRef]
- Yu, Y.; Zhao, W.; Li, S.; Huang, S. A Two-Stage Wavelet Decomposition Method for Instantaneous Power Quality Indices Estimation Considering Interharmonics and Transient Disturbances. IEEE Trans. Instrum. Meas. 2021, 70, 1–13. [Google Scholar] [CrossRef]
- Basir, M.S.S.M.; Ismail, R.C.; Yusof, K.H.; Katim, N.I.A.; Isa, M.N.M.; Naziri, S.Z.M. An implementation of Short Time Fourier Transform for Harmonic Signal Detection. J. Phys. Conf. Ser. 2021, 1755, 012013. [Google Scholar] [CrossRef]
- Soltani, H.; Blaabjerg, F.; Zare, F.; Loh, P.C. Effects of Passive Components on the Input Current Interharmonics of Adjustable-Speed Drives. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 152–161. [Google Scholar] [CrossRef]
- Langella, R.; Testa, A.; Meyer, J.; Moller, F.; Stiegler, R.; Djokic, S.Z. Experimental-Based Evaluation of PV Inverter Harmonic and Interharmonic Distortion Due to Different Operating Conditions. IEEE Trans. Instrum. Meas. 2016, 65, 2221–2233. [Google Scholar] [CrossRef]
- Xu, X.; Collin, A.J.; Djokic, S.Z.; Langella, R.; Testa, A. Operating cycle performance, lost periodicity, and waveform distortion of switch-mode power supplies. IEEE Trans. Instrum. Meas. 2018, 67, 2434–2443. [Google Scholar] [CrossRef]
- Ravindran, V.; Ronnberg, S.K.; Busatto, T.; Bollen, M.H.J. Inspection of interharmonic emissions from a grid-tied PV inverter in North Sweden. In Proceedings of the 2018 18th International Conference on Harmonics and Quality of Power (ICHQP), Ljubljana, Slovenia, 13–16 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Xiao, X.; Djokic, S.; Langella, R.; Testa, A. Performance comparison of three main SMPS types under sinusoidal and distorted supply voltage. In Proceedings of the 2017 IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Xu, X.; Collin, A.; Djokic, S.Z.; Langella, R.; Testa, A.; Drapela, J. Experimental evaluation and classification of LED lamps for typical residential applications. In Proceedings of the 2017 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Turin, Italy, 26–29 September 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Alhafadhi, L.; Teh, J. Advances in reduction of total harmonic distortion in solar photovoltaic systems: A literature review. Int. J. Energy Res. 2020, 44, 2455–2470. [Google Scholar] [CrossRef]
- Martinek, R.; Rzidky, J.; Jaros, R.; Bilik, P.; Ladrova, M. Least mean squares and recursive least squares algorithms for total harmonic distortion reduction using shunt active power filter control. Energies 2019, 12, 1545. [Google Scholar] [CrossRef]
- Albatran, S.; Khalaileh, A.R.; Allabadi, A.S. Minimizing Total Harmonic Distortion of a Two-Level Voltage Source Inverter Using Optimal Third Harmonic Injection. IEEE Trans. Power Electron. 2020, 35, 3287–3297. [Google Scholar] [CrossRef]
- Muthukuri, N.K.; Mopidevi, S. A Novel Switching Sequence for Asymmetrical 15-Level Packed U Cell Inverter Topology with Improved Total Harmonic Distortion. J. Control Autom. Electr. Syst. 2021, 32, 721–734. [Google Scholar] [CrossRef]
- Noroozi, M.; Abrishamifar, A.; Rezaierad, G. A New Carrier-Based Pulse Width Modulation Scheme with Reduced Output Voltage Total Harmonic Distortion for Multi-Level Inverters. IETE J. Res. 2020, 1–12. [Google Scholar] [CrossRef]
- Srndovic, M.; Familiant, Y.L.; Grandi, G.; Ruderman, A. Time-Domain Minimization of Voltage and Current Total Harmonic Distortion for a Single-Phase Multilevel Inverter with a Staircase Modulation. Energies 2016, 9, 815. [Google Scholar] [CrossRef]
- Barbie, E.; Rabinovici, R.; Kuperman, A. Analytical formulation and optimization of Weighted Total Harmonic Distortion in three-phase staircase modulated multilevel inverters. Energy 2021, 215, 119137. [Google Scholar] [CrossRef]
- Rettner, C.; Schiedermeier, M.; Apelsmeier, A.; Marz, M. Fast DC-link capacitor design for Voltage Source Inverters based on weighted total harmonic distortion. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020; pp. 3520–3526. [Google Scholar] [CrossRef]
- Kavci, M.; Tekin, A.; Tarhan, C. Total Harmonic Distortion and Power Factor Improvement Technique for CRM Flyback PFC Converters. In Proceedings of the 2019 IEEE 62nd International Midwest Symposium on Circuits and Systems (MWSCAS), Dallas, TX, USA, 4–7 August 2019; pp. 399–402. [Google Scholar] [CrossRef]
- Pal, S.; Singh, B.; Shrivastava, A. An efficient wide input wide output CrCM flyback converter in high-power LED lighting. Int. Trans. Electr. Energy Syst. 2020, 30, 1–17. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, J.; Wu, X. An improved variable on-time control strategy for a CRM flyback PFC converter. IEEE Trans. Power Electron. 2017, 32, 915–919. [Google Scholar] [CrossRef]
- Yan, T.; Xu, J.; Zhang, F.; Sha, J.; Dong, Z. Variable-On-Time-Controlled Critical-Conduction-Mode Flyback PFC Converter. IEEE Trans. Ind. Electron. 2014, 61, 6091–6099. [Google Scholar] [CrossRef]
- Elvira-Ortiz, D.A.; Morinigo-Sotelo, D.; Duque-Perez, O.; Osornio-Rios, R.A.; Romero-Troncoso, R.J. Study of the harmonic and interharmonic content in electrical signals from photovoltaic generation and their relationship with environmental factors. J. Renew. Sustain. Energy 2019, 11, 43502. [Google Scholar] [CrossRef]
- Patel, D.; Varma, R.K.; Seethapathy, R.; Dang, M. Impact of wind turbine generators on network resonance and harmonic distortion. In Proceedings of the CCECE 2010, Calgary, AB, Canada, 2–5 May 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Memon, S.H.; Kumar, M.; Memon, A.H.; Memon, Z.A.; Soomro, S.A. Total Harmonic Distortion (THD) Analysis of Grid Integrated Permanent Magnet Synchronous Generator ( PMSG ) With Full Scale Converter (FSC) Based Wind Farm. IJCSNS Int. J. Comput. Sci. Netw. Secur. 2018, 18, 232–238. [Google Scholar]
- Misra, R.; Paudyal, S. Analysis and reduction of total harmonic distortions in distribution system with electric vehicles and wind generators. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Bosak, A.; Bosak, A.; Kulakovskyi, L.; Oboronov, T. Impact of EV Chargers on Total Harmonic Distortion in the Distribution System Network. In Proceedings of the 2019 IEEE 6th International Conference on Energy Smart Systems (ESS), Kyiv, Ukraine, 17–19 April 2019; pp. 329–333. [Google Scholar] [CrossRef]
- Ahmed, A.; Iqbal, A.; Khan, I.; Al-Wahedi, A.; Mehrjerdi, H.; Rahman, S. Impact of EV charging Station Penetration on Harmonic Distortion Level in Utility Distribution Network: A Case Study of Qatar. In Proceedings of the 2021 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 2–5 February 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Guo, J.; Yang, J.; Ivry, P.; Serrano, C. Analysis of the Impacts of V2G Chargers on LV Grid Harmonics. In Proceedings of the ICRERA 2020 9th International Conference on Renewable Energy Research and Applications, Glasgow, UK, 27–30 September 2020; pp. 88–92. [Google Scholar] [CrossRef]
- Zagrajek, K.; Paska, J.; Kłos, M.; Pawlak, K.; Marchel, P.; Bartecka, M.; Michalski, Ł.; Terlikowski, P. Impact of electric bus charging on distribution substation and local grid in Warsaw. Energies 2020, 13, 1210. [Google Scholar] [CrossRef]
- Alfieri, L.; Bracale, A.; Carpinelli, G.; Larsson, A. Accurate assessment of waveform distortions up to 150 kHz due to fluorescent lamps. In Proceedings of the 2017 6th International Conference on Clean Electrical Power (ICCEP), Santa Margherita Ligure, Italy, 27–29 June 2017; pp. 636–644. [Google Scholar] [CrossRef]
- Brusil, C.; Arcos, H.; Espin, F.; Velasquez, C. Analysis of harmonic distortion of led luminaires connected to utility grid. In Proceedings of the 2020 IEEE ANDESCON, Quito, Ecuador, 13–16 October 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Soltani, H.; Davari, P.; Kumar, D.; Zare, F.; Blaabjerg, F. Effects of DC-link filter on harmonic and interharmonic generation in three-phase adjustable speed drive systems. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 675–681. [Google Scholar] [CrossRef]
- Domagk, M.; Gu, I.Y.H.; Meyer, J.; Schegner, P. Automatic identification of different types of consumer configurations by using harmonic current measurements. Appl. Sci. 2021, 11, 3598. [Google Scholar] [CrossRef]
- Devarapalli, H.P.; Siva Sarma Dhanikonda, V.S.S.; Gunturi, S.B. Non-intrusive identification of load patterns in smart homes using percentage total harmonic distortion. Energies 2020, 13, 4628. [Google Scholar] [CrossRef]
- Sadeghianpourhamami, N.; Ruyssinck, J.; Deschrijver, D.; Dhaene, T.; Develder, C. Comprehensive feature selection for appliance classification in NILM. Energy Build. 2017, 151, 98–106. [Google Scholar] [CrossRef]
- Dong, M.; Meira, P.C.M.; Xu, W.; Chung, C.Y. Non-intrusive signature extraction for major residential loads. IEEE Trans. Smart Grid 2013, 4, 1421–1430. [Google Scholar] [CrossRef]
- Komuro, T.; Sobukawa, S.; Sakayori, H.; Kono, M.; Kobayashi, H. Total harmonic distortion measurement system of electronic devices up to 100 MHz with remarkable sensitivity. IEEE Trans. Instrum. Meas. 2007, 56, 2360–2368. [Google Scholar] [CrossRef]
- Huang, J.; Feng, X.; Chen, S.; Shen, Y. Analysis of total harmonic distortion of miniature loudspeakers used in mobile phones considering nonlinear acoustic damping. J. Acoust. Soc. Am. 2021, 149, 1579–1588. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.; Pawar, S.J.; Weng, S.; Shiah, Y.C.; Huang, J.H. Effect of nonlinear stiffness on the total harmonic distortion and sound pressure level of a circular miniature loudspeaker-experiments and simulations. IEEE Trans. Consum. Electron. 2012, 58, 212–220. [Google Scholar] [CrossRef]
- Wei, C.; Wu, J.; Wei, R.; He, M. High-Fidelity and High-Efficiency Digital Class-D Audio Power Amplifier. J. Electr. Comput. Eng. 2021, 2021, 5533745. [Google Scholar] [CrossRef]
- Spertino, F.; Chicco, G.; Ciocia, A.; Malgaroli, G.; Mazza, A.; Russo, A. Harmonic distortion and unbalance analysis in multi-inverter photovoltaic systems. In Proceedings of the 2018 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Amalfi, Italy, 20–22 June 2018; pp. 1031–1036. [Google Scholar] [CrossRef]
- Collin, A.J.; Djokic, S.Z.; Drapela, J.; Langella, R.; Testa, A. Proposal of a desynchronized processing technique for assessing high-frequency distortion in power systems. IEEE Trans. Instrum. Meas. 2019, 68, 3883–3891. [Google Scholar] [CrossRef]
- Chicco, G.; Pons, E.; Russo, A.; Spertino, F.; Porumb, R.; Postolache, P.; Toader, C. Assessment of unbalance and distortion components in three-phase systems with harmonics and interharmonics. Electr. Power Syst. Res. 2017, 147, 201–212. [Google Scholar] [CrossRef]
- Merizalde, Y.; Hernández-Callejo, L.; Duque-Perez, O. State of the art and trends in the monitoring, detection and diagnosis of failures in electric induction motors. Energies 2017, 10, 1056. [Google Scholar] [CrossRef]
- Gangsar, P.; Tiwari, R. Signal based condition monitoring techniques for fault detection and diagnosis of induction motors: A state-of-the-art review. Mech. Syst. Signal Process. 2020, 144, 106908. [Google Scholar] [CrossRef]
- Köse, N.; Salor, Ö.; Leblebicioǧlu, K. Interharmonics analysis of power signals with fundamental frequency deviation using Kalman filtering. Electr. Power Syst. Res. 2010, 80, 1145–1153. [Google Scholar] [CrossRef]
- Testa, A.; Akram, M.F.; Burch, R.; Carpinelli, G.; Chang, G.; Dinavahi, V.; Hatziadoniu, C.; Grady, W.M.; Gunther, E.; Halpin, M.; et al. Interharmonics: Theory and Modeling. IEEE Trans. Power Deliv. 2007, 22, 2335–2348. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).