Power Quality Phenomena, Standards, and Proposed Metrics for DC Grids
Abstract
1. Introduction
- high-performance control uses information on current not only to improve performance with feed-forward control, but also to control impedance [22];
- distorted current is a cause of induced disturbance through cables, in particular for common-mode components that are often the result of large capacitance to ground (as resulting either by the distributed capacitance of the source or load, such as PV panels or battery banks, or by purposely inserted capacitors to reduce EMI) [20]; common-mode current is not evaluated by the commonly used PQ indexes, being usually ascribed to EMC, and those uncontrolled common-mode currents, aside from interference, may also increase the overall human exposure to magnetic field right where limits are particularly low [37];
- distorted current may also directly cause disturbance for specific signaling systems using the return circuit or ground wire as an active conductor; examples may be found in metros and railways (track circuits using the running rails as part of a coded signal transmission to detect the presence of trains) and in the automotive sector (negotiation of the charging profile of an electric vehicle following SAE J2836-1 [38] and IEC 61851-1 [39] standards, using pulse-width-modulated signals).
2. Relevant Power Quality Phenomena
- interference to sources and loads as an EMC (electromagnetic compatibility) problem, affecting e.g., measurement and control quantities;
- interference to sources and loads as an operational problem, resulting in poor voltage quality (fluctuations and variations) disrupting source or load operation, causing flicker, torque variation, etc.; in this respect, DC grids intrinsically perform better thanks to a large amount of local storage;
- issues of network instability and low-frequency oscillations (LFOs), in particular when stressed by major transients, that trigger undamped response of sources and loads; by convention, LFOs in AC networks are confined below the fundamental; here, without loss of generality, LFO may be considered to occur up to a hundred Hz;
- resonances occurring at higher frequency (often named high-frequency oscillations, HFO, or harmonic resonances, HR), above usual control bandwidths, related to network resonances, influenced by the physical extension and interaction with parasitics and reactive elements; and
- impact in terms of overheating and accelerated aging, as for filter capacitors, cables, storage devices, and transformer insulation; ripple current and in general the rms value and the number of charging/discharging cycles are the parameters of the electrical interface considered for quantification of stress and aging of batteries and supercapacitors, in addition to environmental conditions and in particular temperature.
2.1. EMC and Interference
- Residual current devices (RCDs), a class of devices common to AC and DC applications, relying on current measurements for detection of fault conditions with a wide range of fault impedance values. Type B of AC RCDs could be used for DC applications, although they are not fully specified for it; such devices may have an unspecified sensitivity to high-frequency components [43,44]. Conversely, RCDs for DC applications are required to be immune from high-frequency ripple (see section 8.17 in [45]), but the amplitude and frequency of such ripple are not better specified. Coordinated solutions are being proposed complementing the limited immunity of single devices to a wide range of disturbance with an increased information set collected by distance protections and networked devices [46].
- DC leakage monitors: the latest IEC 62020-1 [47] does not yet include DC devices, but they are covered by the EN 61557-8 [48], considering their application to “pure DC IT systems”. Practically speaking, a pure DC IT grid does not exist as some amount of differential- and common-mode ripple is always present. Such devices have been available on the market for a long time (such as Bender [49], Danisense [50] or THIIM [51] brands) with sensitivities that expose them to unwanted tripping, as caused by current ripple, that may also occur on the earth conductors due to unavoidable potential difference between remote locations (in particular when switching power converters are used). In some cases, a selectable filter [50] allows to limit the bandwidth, but the real susceptibility to high-frequency ripple is rarely declared, nor disciplined by any kind of standard. Personal experience with one of these devices indicates susceptibility (and unwanted tripping at the DC threshold of about 10 mA) in the range 50–70 mArms for ripple occurring at some kHz.
- Series arcs detection methods [4,52]. The method in [4] is based on the comparison of current drop estimates in successive short time intervals (50 μs) and with running average values on longer intervals (50 ms), showing a factor of 2 of difference in the indicators with and without arc; the required sampling is 200 kSa/s, thus potentially exposed to high-frequency pollution from static converters, then reduced by successive averaging. Similarly, in [53], min and max current values are run over optimized window lengths (5 to 25 ms), whose difference is an indicator of intermittence; the influence of system noise was not investigated, although the number of consecutive windows used in estimates can be used to filter out grid transients such as load steps, avoiding them being detected as arcs. A much lower sampling of 1440 Sa/s is required in [52], thus less exposed to system noise and high-frequency switching components. Commercially available AFDDs/AFCIs are mainly focused on AC grids (the EN 62606 [54] considers only AC distribution, whereas the UL 1699B [55] specifically addresses arcs in DC grids and PV systems), but the extensive deployment of PV systems has fostered the design of some specific devices [56,57]. The detection method is not detailed, but the monitored frequency range is reported as above 20 kHz [57] and between 20 and 40 kHz [56]. In both cases, this detection range would be exposed to distortion from the AC network (for transformerless PV systems), transient responses to, e.g., step changes [58], and most of all to supraharmonics originating from converters, as it is evident in [56], where the 16 kHz-spaced switching harmonics have almost the same amplitude of the targeted arc noise (and there are cases of noise profiles dominated by such harmonic peaks). Tests of effectiveness and performance indicated by the UL 1699B include a change of distance from the arc to detect (farther by 66 m) to check sensitivity and the verification of correct operation with an inverter connected. A quantitative framework would be welcome, specifying the minimum signal-to-noise ratio with respect to supraharmonics, that should be in any case subject to limitations.
- DC protections for large-power installations are implemented as assisted circuit breakers (called “hybrid”) [11] or fully static semiconductor-based devices [10], driven by detection algorithms. Various techniques have been proposed and applied to DC railways [3,59] and distributed generation DC grids [60,61], exploiting various methods and monitored grid quantities: (i) methods based on autonomous signal injection and impedance estimation [3,59] are rather immune to distortion, as ideally, the applied intensity may increase until a satisfactory operation is achieved; (ii) the criterion proposed for the DC side of a wind power system in [60] is based on DC ripple, that in normal conditions must be low (0.2%) for the method to work; (iii) the robust technique correlating internal current waveforms to separate faults of internal and external origin [61] was tested against uncorrelated Gaussian noise, but not with signal distortion, which is highly correlated as well.
2.2. Voltage Fluctuations and Variations
2.3. Network Instability, Oscillations, and Resonances
2.3.1. High-Frequency Oscillations (HFOs)
2.3.2. Low-Frequency Oscillations (LFOs)
2.4. Stress, Heating, and Aging of Components
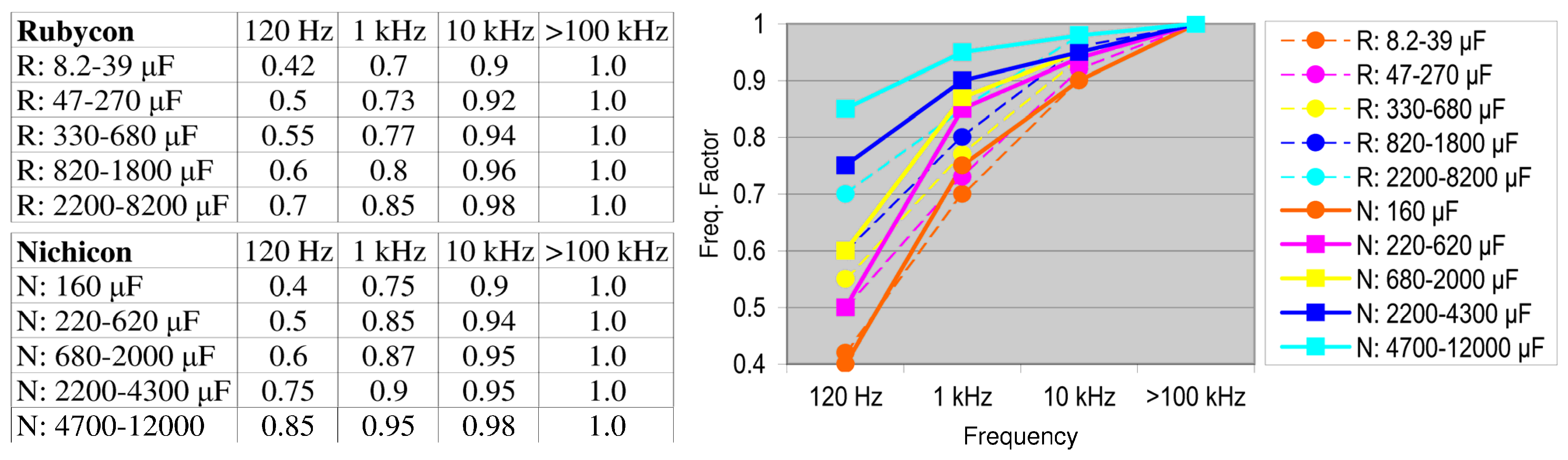
2.4.1. Capacitors
- the peak value of the electric field (or voltage) indicates the stress on dielectric;
- the total rms value compared to the fundamental weights the overall distortion of the waveform and this is applicable in general to voltage and current;
- components at higher frequency cause additional heating not only for more pronounced skin effect in conductors (and possibly proximity effect), but also increased dielectric losses, and this is indicated by Ks; this index was derived focusing on the impact of signals with a large derivative, weighting thus each component by its harmonic order; the harmonic order h is in general recognized as related to increased power losses, although they do not go necessarily linearly with h.
2.4.2. Supercapacitors
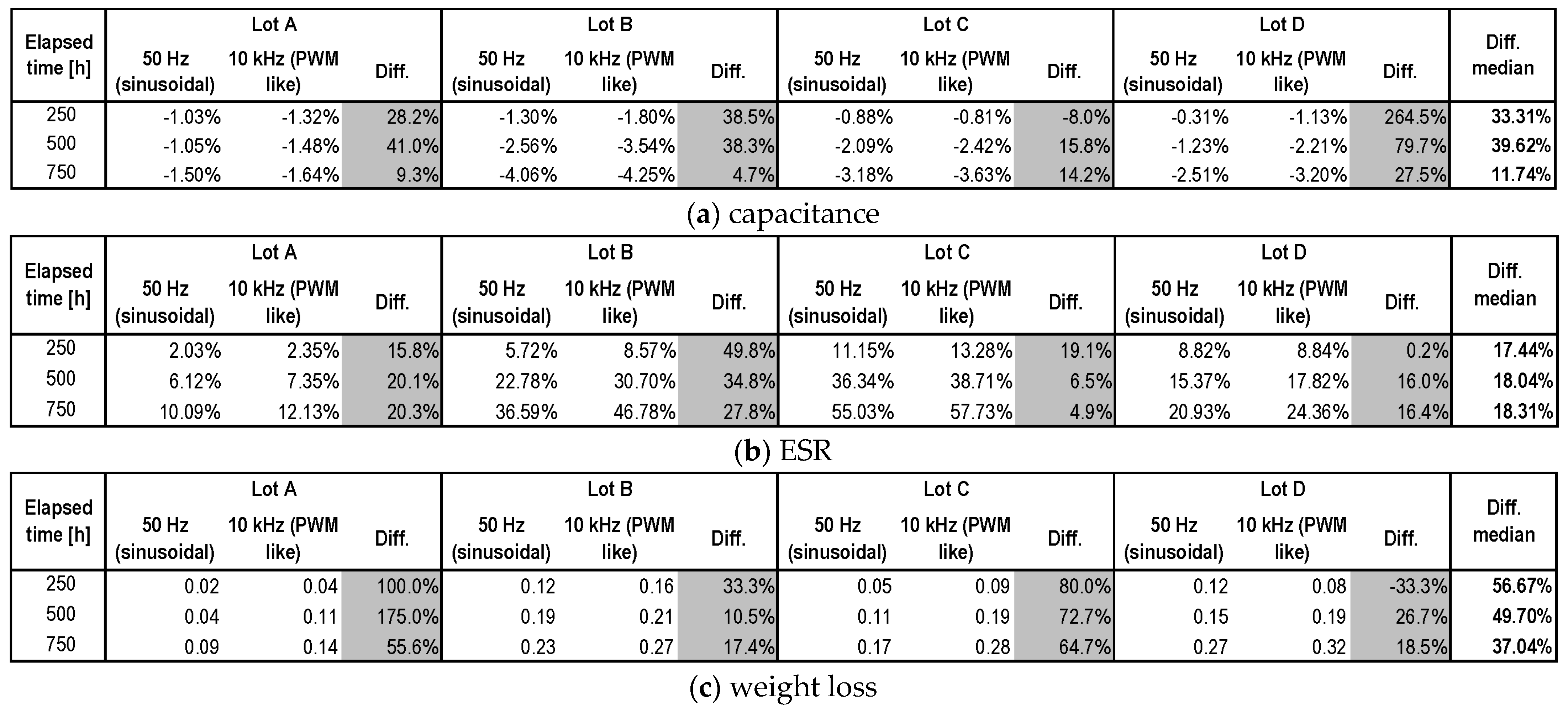
- the effect of 100 Hz and 100 kHz in [34] is the same;
- aging due to the amount of current ripple is evident when above about 20% [33];
- the aging figures with respect to ESR and capacitance obtained by [89] are similar/lower than those appearing in [34] for the same time interval; observing that the difference is in the ripple frequency, we may conclude that high frequency would contribute to the aging factors moderately, but up to a factor of 2 for capacitance reduction (although in contrast to [34], this is in agreement with what was observed for aluminum capacitors and commented on in Section 2.4.1).
2.4.3. Batteries
2.4.4. Photovoltaic Panels
2.4.5. Fuel Cells
3. Standard Classification of Power Quality Phenomena
3.1. Voltage Swells, Sags, and Interruptions
3.2. Fast Transients (Spikes and Surges)
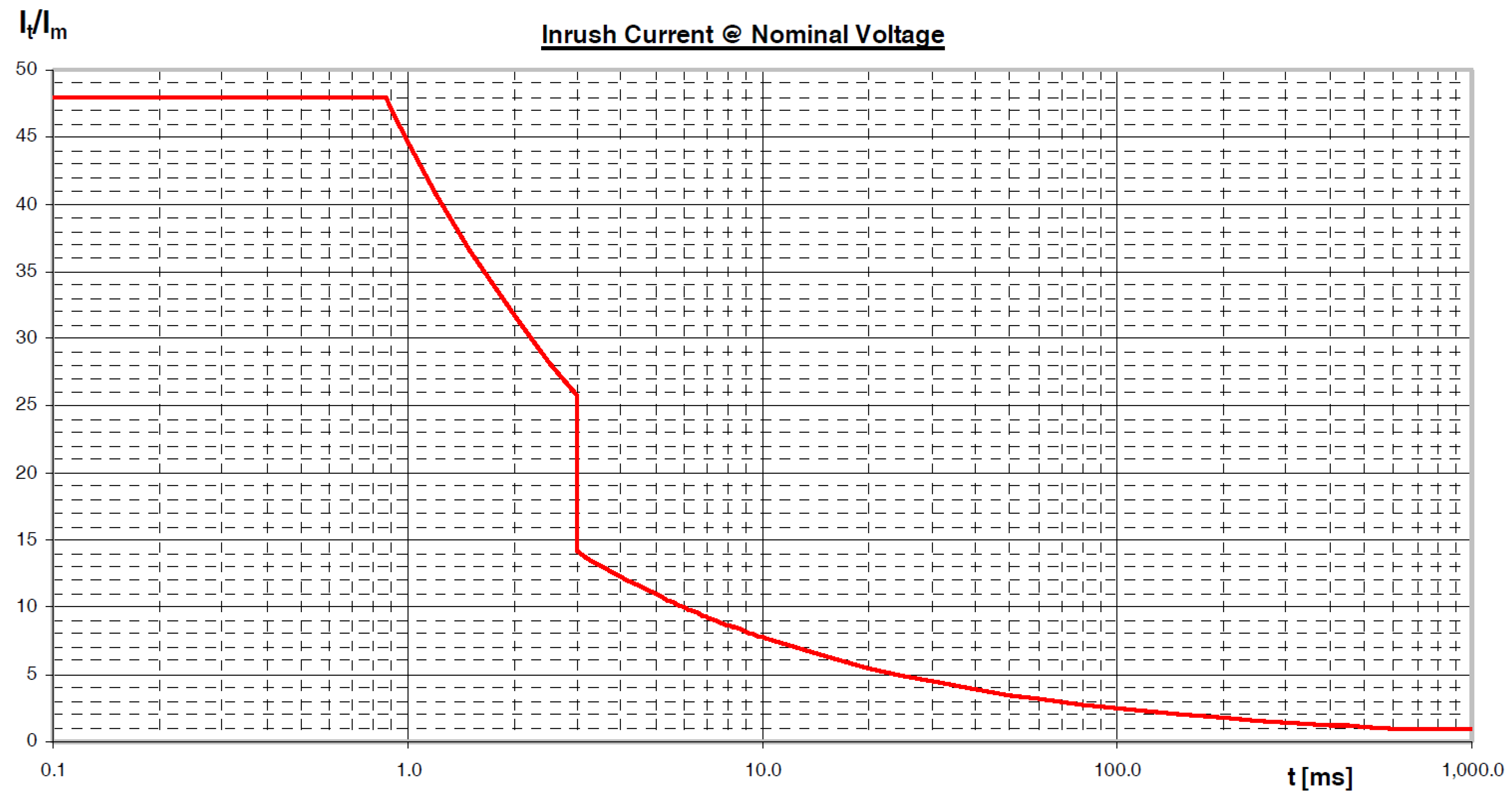
3.3. Inrush Current and Short-Circuit Current
3.4. Harmonics, Ripple, and Periodic Variations
3.4.1. Harmonics
3.4.2. Supraharmonics
- primary emissions, whose sources are recognized in the switching components of various kinds of converters, interfacing, and regulating sources and loads; primary emissions are caused by the identified sources in relation to the network impedance, often substituted by the LISN during laboratory tests;
- secondary emissions are caused instead by the loading of nearby sources and loads, including in particular EMI filters, modifying as a matter of fact the overall network impedance seen at the measurement terminals; this phenomenon has been recently considered as a significant source of variability and deviation of measurement results from those referred to the network alone [20,127];
- a quite general third type of emission can be identified in the interaction of low-frequency network distortion with mechanisms of emission for non-linear loads, for which the behavior in real use conditions would be different from ideal lab testing in controlled supply condition.
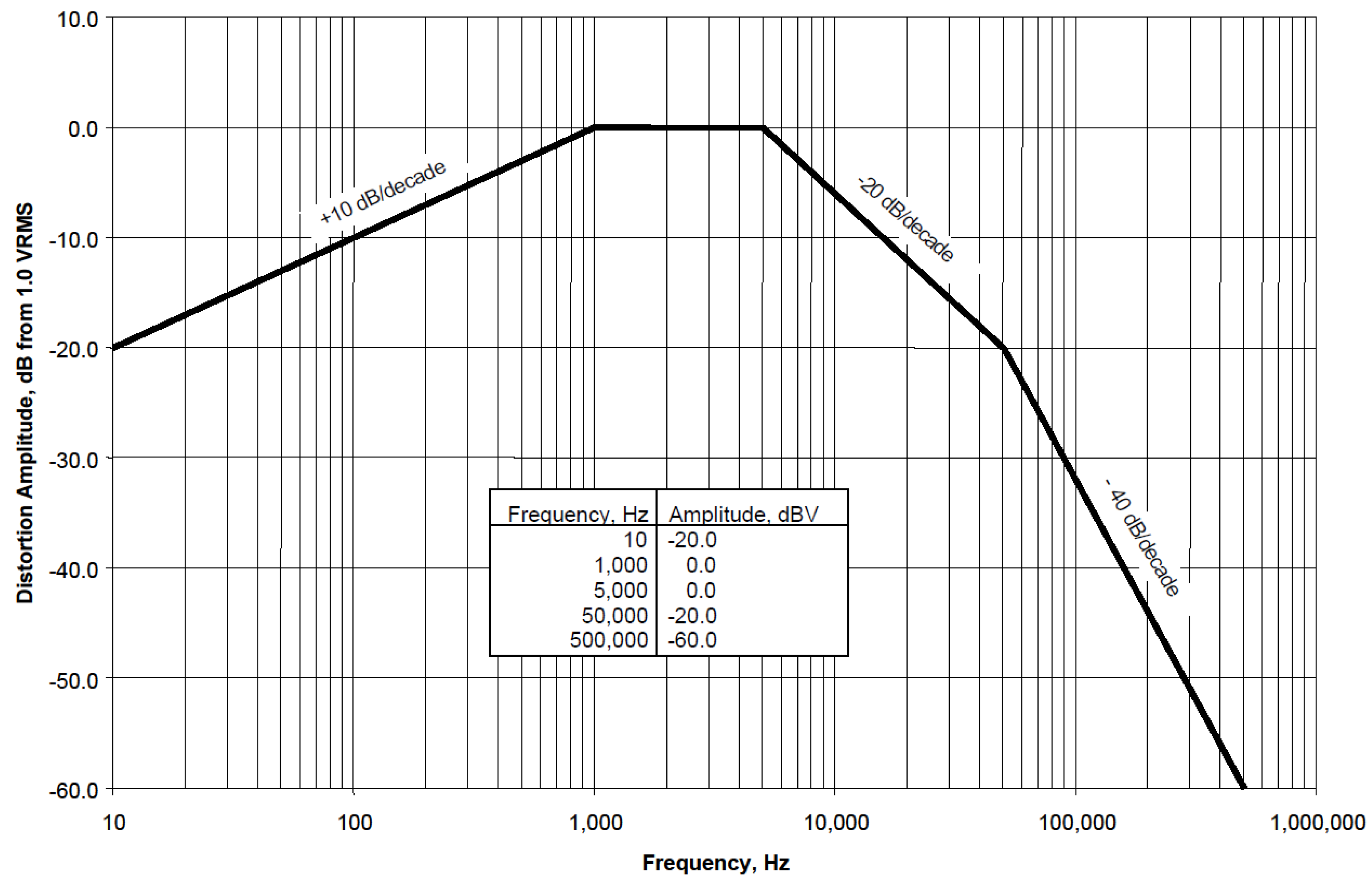
- Combined disturbance of N equipment of the same type connected to the same distribution area would increase by √N, assuming a random distribution of the phase for emission components at the same frequency; already at N = 4 the margin is reached, and compatibility would not be ensured.
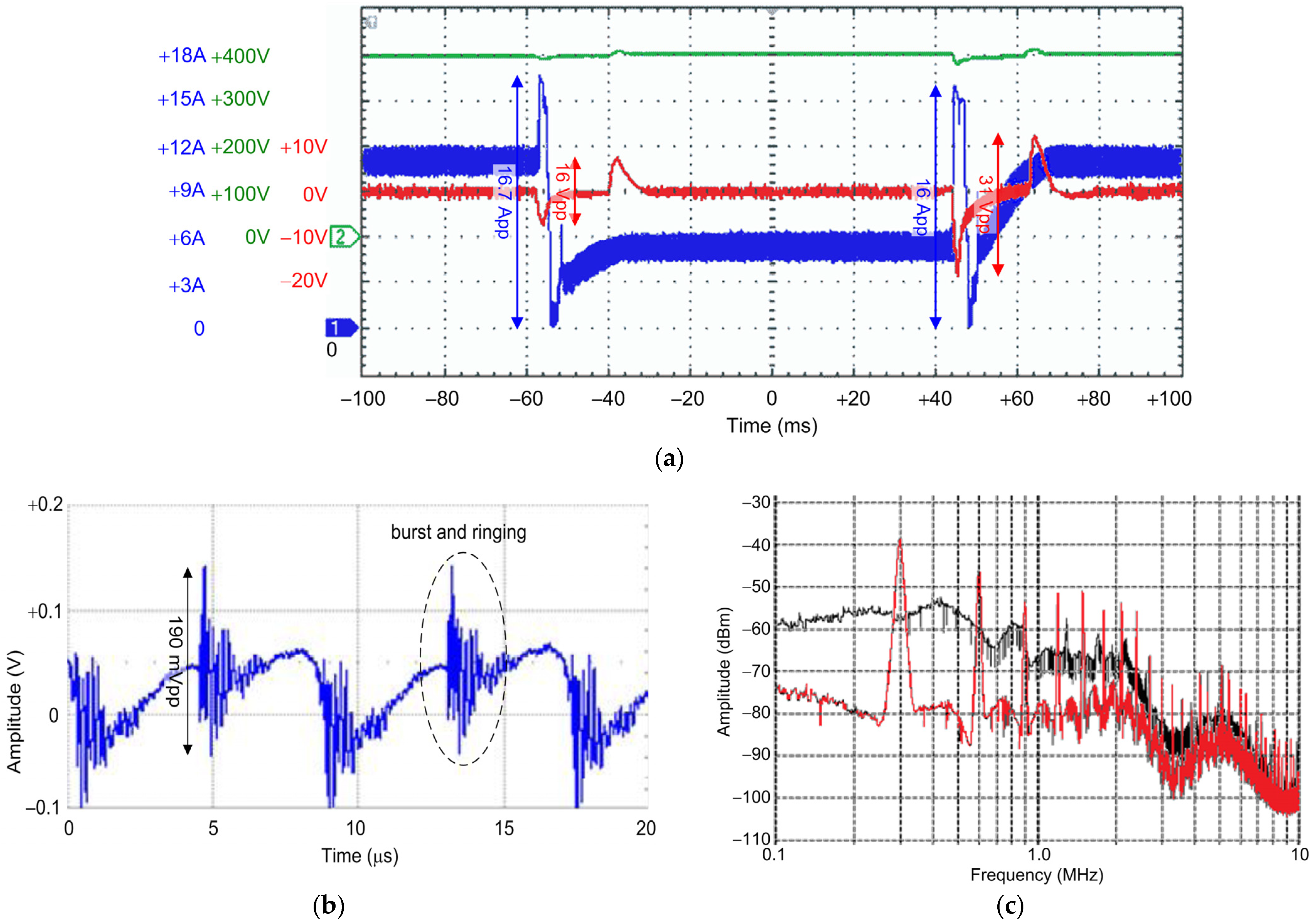
- Different types of equipment are likely to position their emissions at different frequencies, thus not summing for the determination of the overall spectrum of emissions, but all concurring for the determination of the overall distortion D. In this case, the margin with respect to D values discussed in Section 3.4.3 is much wider, as by summing all components of Figure 8, we would get a contribution of about 0.2 Vrms.
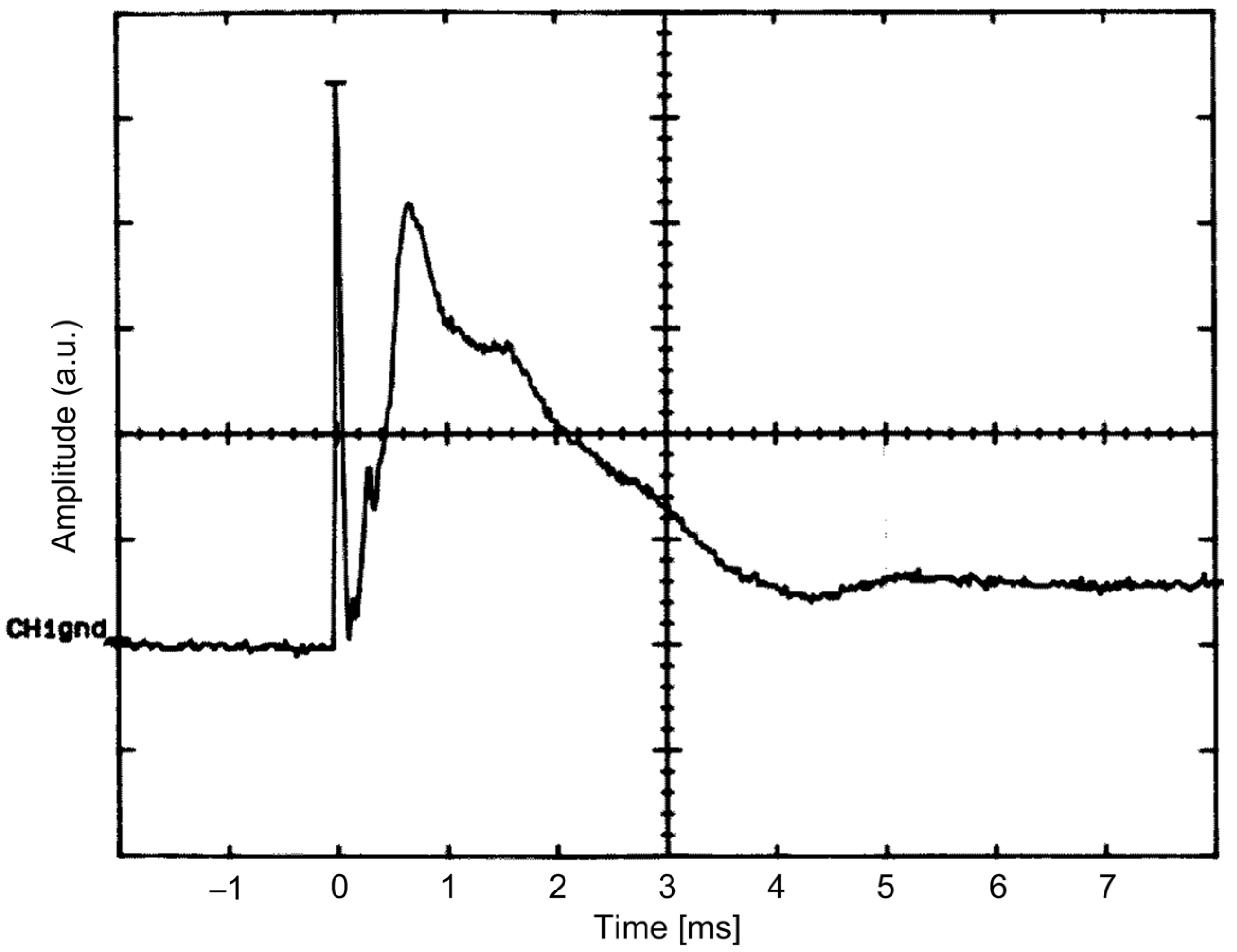
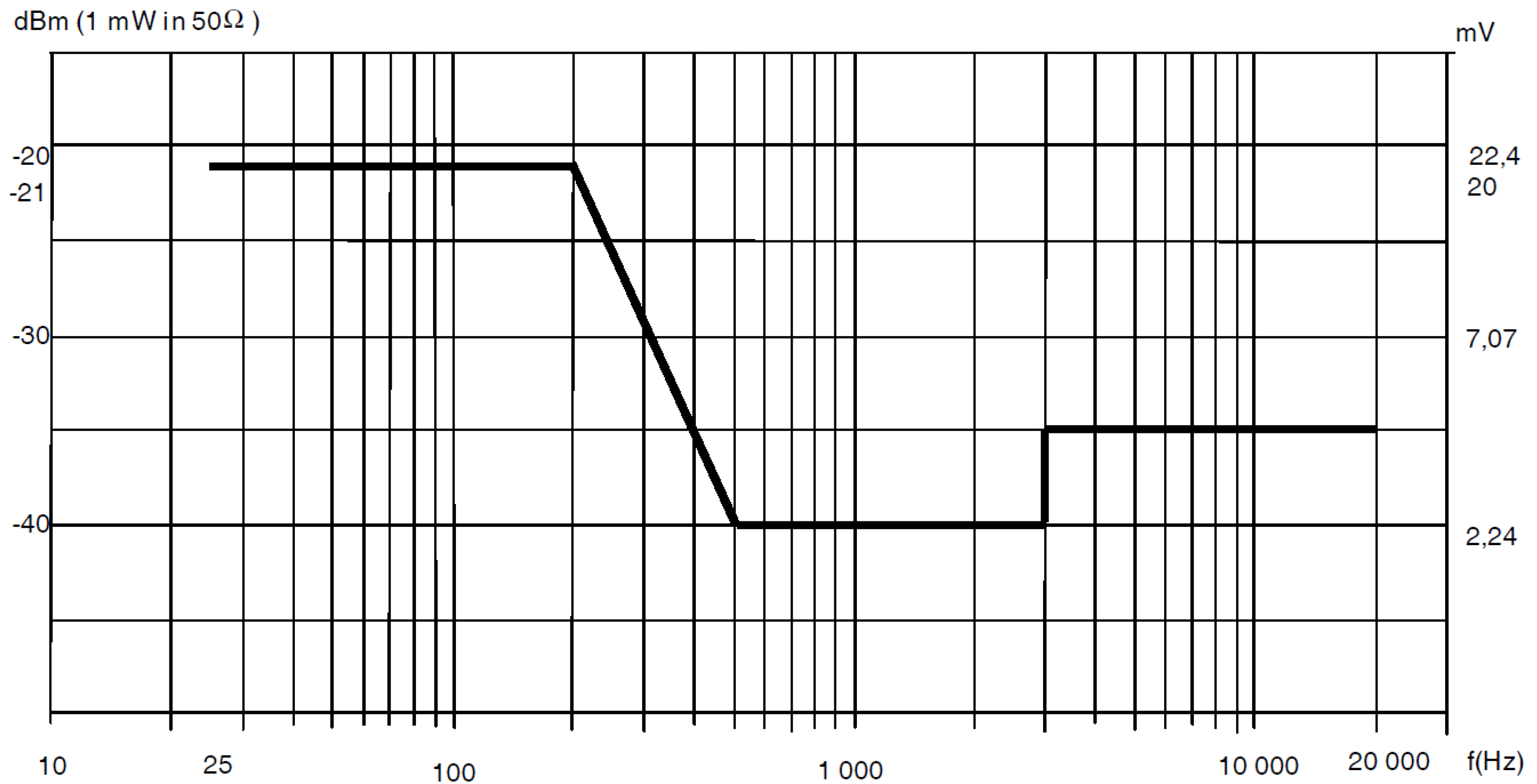
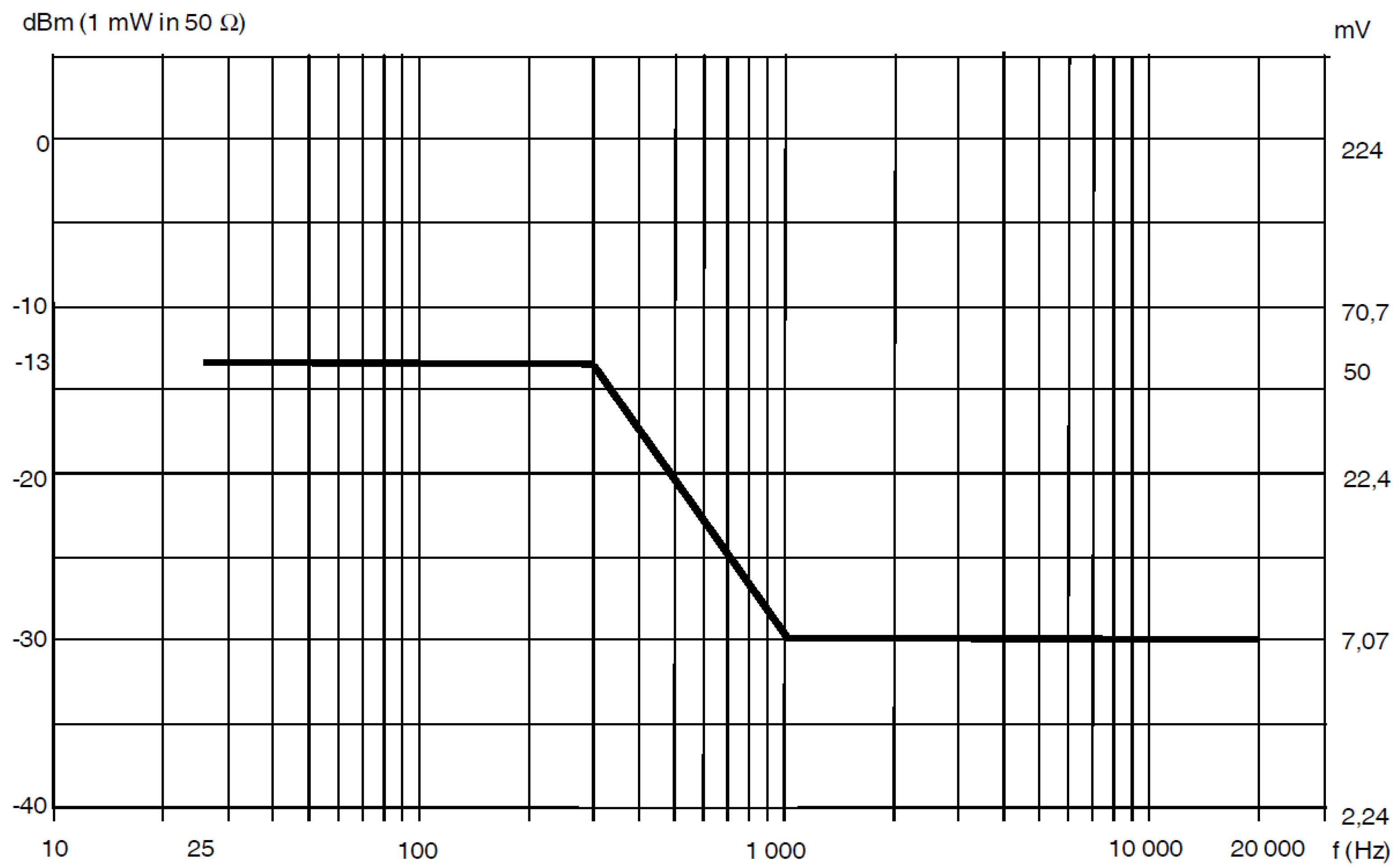
- Network resonances amplify network distortion and as discussed for the inrush case, resonance occurred in the kHz range for cables in the order of 50 m of length, including the effect of the significant amount of deployed capacitance. The factor of merit taking into consideration resistance and inductance of cables in [124] would be in the order of 1.5–1.7. The shallow profile between 500 Hz and 3 kHz in Figure 8, compared to the profile in Figure 9, seems to indicate that a margin of 5 dB was taken, possibly right for resonance phenomena.
3.4.3. Ripple and Voltage Fluctuations
3.5. Common-Mode Disturbance
4. PQ Indexes for Quantification of Phenomena
4.1. Spectrum Components, Harmonic/Supraharmonic Analysis, and Aggregation
- the IEC 61000-4-30 indicates a rms approach, so that , where N = 10 min/3 s = 200;
- the statistical distribution of index results may be more informative, provided that a compact representation is provided, such as mean and dispersion, median, percentile, or similar (as applied to ripple in Section 4.2.2).
- The IEC 61000-4-7 for AC systems requires grouping of inter-harmonic components, in principle not applicable to DC systems and also does not transfer well to higher frequency intervals above 9 kHz.
- The IEC 61000-4-30 hints at the use of CISPR 16-1-2 frequency scan method, which has a major drawback: the resolution bandwidth (RBW) is 200 Hz for frequencies up to 150 kHz and this is inadequate to capture highly localized emissions caused by switching by-products, as shown in [142]; a larger RBW should be used, losing, however, the major strength pointed out in the IEC 61000-4-30, that is the direct comparison with limits or reference levels of IEC/CENELEC standards.
- A band limited method using 2 kHz spacing is also proposed by the IEC 61000-4-30, using a time-domain acquisition followed by Fourier analysis, but alternative methods may be implemented, such as a bank of filters or multiresolution signal decomposition (MSD) algorithms (e.g., wavelet packet decomposition and variational or empirical mode decomposition [142,143,144]). The 2 kHz resolution matches the observations in [142], where 0.5–1 ms time localization was identified as optimal for the accurate estimate of non-stationary components related to switching pulses. A broader frequency resolution is also in line with the broadband characteristics of the mechanisms of interference and the minimum channel width of PLC systems.
4.2. Ripple
4.2.1. Band-Limited Ripple Index
4.2.2. Statistics and Time-Series Analysis
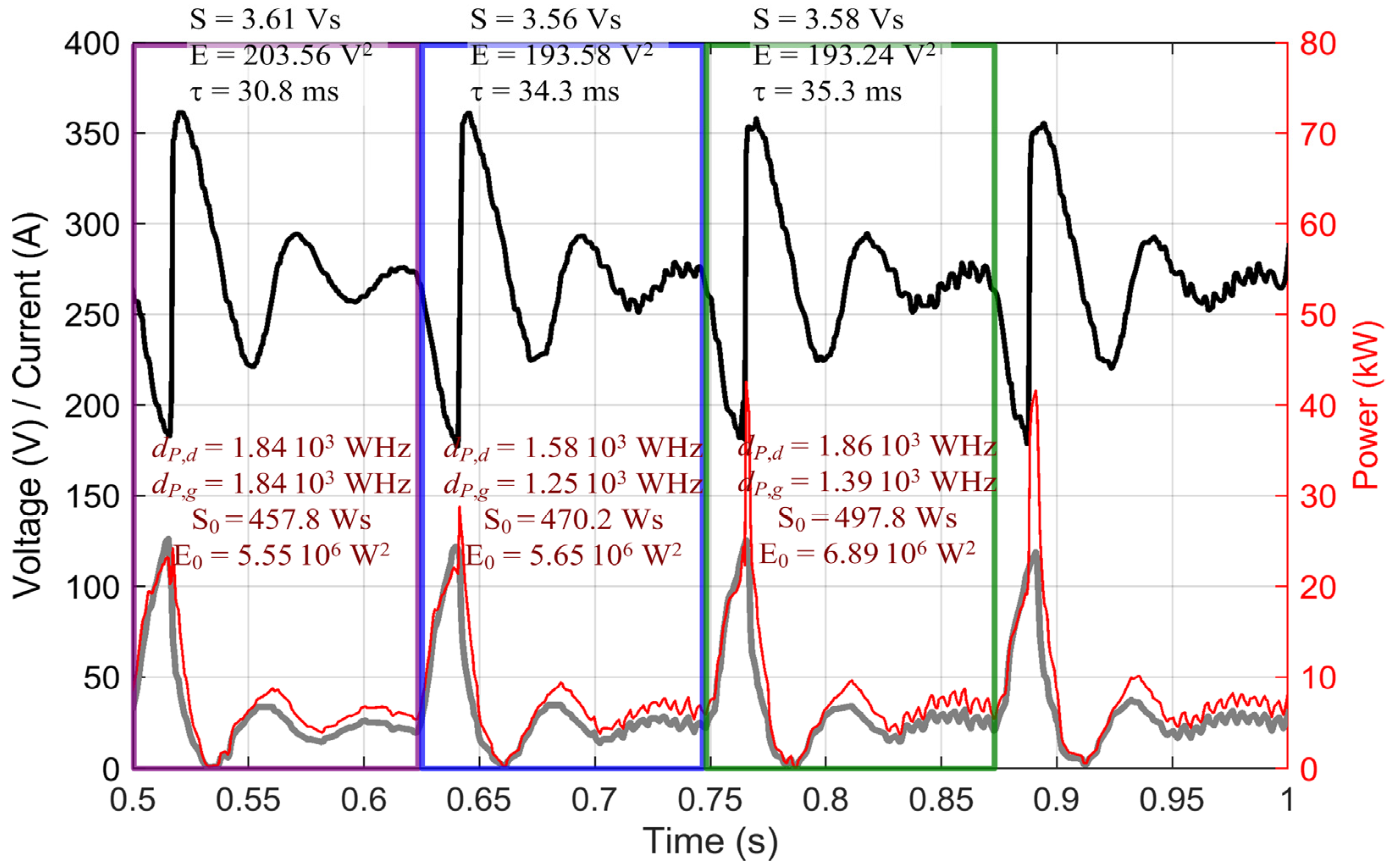
4.3. Transients and Pulsed Loads: Area, Energy, Duration, and Power Trajectory
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| AFCI | arc-fault circuit interrupter |
| AFFD | arc fault detection device |
| BPL | broadband over power line |
| Cchem | electrochemical capacitance |
| Cgeo | geometrical capacitance |
| D | distortion |
| DF | distortion factor |
| EMC | electromagnetic compatibility |
| ESR | equivalent series resistance |
| FC | fuel cell |
| FCC | federal communication commission |
| FF | form factor |
| HFO | high-frequency oscillation |
| Iavg | average (DC steady) current |
| Ipp | peak-peak ripple current |
| Irms | current rms value |
| IPV,sc | short-circuit current PV panel |
| LFO | low-frequency oscillation |
| LV | low voltage |
| MPPT | maximum power point tracking |
| MV | medium voltage |
| PEM | proton exchange membrane |
| PLC | power line communication |
| PQ | power quality |
| PV | photovoltaic |
| RCD | residual current devices |
| Rp | peak ripple |
| Rpp | peak–peak ripple |
| Rrms | rms ripple |
| SPD | surge protecting device |
| THD | total harmonic distortion |
| VLRA | valve regulated lead acid |
| XLPE | cross-link poly ethylene |
References
- Nuutinen, P.; Peltoniemi, P.; Silventoinen, P. Short-Circuit Protection in a Converter-Fed Low-Voltage Distribution Network. IEEE Trans. Power Electron. 2013, 28, 1587–1597. [Google Scholar] [CrossRef]
- Li, C.; Zhao, Y.; Wu, F.; Jia, K.; Chen, C. A Single-Ended Protection for Multi-terminal Flexible DC Distribution System. In Proceedings of the 4th International Conference on Power and Energy Engineering (ICPEE), Xiamen, China, 19–21 November 2020. [Google Scholar] [CrossRef]
- Park, J.-D. Ground Fault Detection and Location for Ungrounded DC Traction Power Systems. IEEE Trans. Veh. Technol. 2015, 64, 5667–5676. [Google Scholar] [CrossRef]
- Lu, Q.; Ye, Z.; Su, M.; Li, Y.; Sun, Y.; Huang, H. A DC Series Arc Fault Detection Method Using Line Current and Supply Voltage. IEEE Access 2020, 8, 10134–10146. [Google Scholar] [CrossRef]
- Crotti, G.; Delle Femine, A.; Gallo, D.; Giordano, D.; Landi, C.; Luiso, M.; Mariscotti, A.; Roccato, E. Pantograph-to-OHL Arc: Conducted Effects in DC Railway Supply System. In Proceedings of the IEEE 9th International Workshop on Applied Measurements for Power Systems (AMPS), Bologna, Italy, 26–28 September 2018. [Google Scholar] [CrossRef]
- Seferi, Y.; Blair, S.M.; Mester, C.; Stewart, B.G. A novel arc detection method for dc railway systems. Energies 2021, 14, 444. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, X.; Al-Akayshee, M. A Reliable Medium-Voltage High-Power Conversion System for MWs Wind Turbines. IEEE Trans. Sustain. Energy 2020, 11, 859–867. [Google Scholar] [CrossRef]
- Chen, L.; Shao, S.; Xiao, Q.; Tarisciotti, L.; Wheeler, P.W.; Dragicevic, T. Model Predictive Control for Dual-Active-Bridge Converters Supplying Pulsed Power Loads in Naval DC Micro-Grids. IEEE Trans. Power Electron. 2020, 35, 1957–1966. [Google Scholar] [CrossRef]
- Maqsood, A.; Corzine, K.A. Integration of Z-Source Breakers into Zonal DC Ship Power System Microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 269–277. [Google Scholar] [CrossRef]
- Cairoli, P.; Qi, L.; Tschida, C.; Ramanan, V.R.R.; Raciti, L.; Antoniazzi, A. High Current Solid State Circuit Breaker for DC Shipboard Power Systems. In Proceedings of the IEEE Electric Ship Technologies Symposium (ESTS), Washington, DC, USA, 14–16 August 2019. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, W.; Li, X.; Pang, S.; Wang, M.; Zhang, H. Research on Topology of Medium Voltage Hybrid DC Circuit Breaker Based on IGCT. In Proceedings of the 4th International Conference on HVDC (HVDC), Xi’an, China, 6–9 November 2020. [Google Scholar] [CrossRef]
- Swierczynski, B.; Gonzalez, J.J.; Teulet, P.; Freton, P.; Gleizes, A. Advances in low-voltage circuit breaker modelling. J. Phys. D Appl. Phys. 2004, 37, 595–609. [Google Scholar] [CrossRef]
- Whaite, S.; Grainger, B.; Kwasinski, A. Power Quality in DC Power Distribution Systems and Microgrids. Energies 2015, 8, 4378–4399. [Google Scholar] [CrossRef]
- Kaleybar, H.J.; Brenna, M.; Foiadelli, F. Compatibility of Present 3 kV DC and 2 × 25 kV AC High-Speed Railway Power Supply Systems Towards Future MVDC System. In Proceedings of the 12th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tabriz, Iran, 2–4 February 2021. [Google Scholar]
- Aatif, S.; Yang, X.; Hu, H.; Maharjan, S.K.; He, Z. Integration of PV and Battery Storage for Catenary Voltage Regulation and Stray Current Mitigation in MVDC Railways. J. Mod. Power Syst. Clean Energy 2021, 9, 585–594. [Google Scholar] [CrossRef]
- Ferrari, P.; Mariscotti, A.; Pozzobon, P. Reference curves of the pantograph impedance in DC railway systems. In Proceedings of the IEEE International Conference on Circuits and Systems, Geneva, Switzerland, 28–31 May 2000. [Google Scholar] [CrossRef]
- TR 102 532. Environmental Engineering (EE)—The Use of Alternative Energy Solutions in Telecommunications Installations; ETSI: Sophia Antipolis, France, 2009. [Google Scholar]
- Prabhala, V.; Baddipadiga, B.; Fajri, P.; Ferdowsi, M. An Overview of Direct Current Distribution System Architectures and Benefits. Energies 2018, 11, 2463. [Google Scholar] [CrossRef]
- Meyer, J.; Khokhlov, V.; Klatt, M.; Blum, J.; Waniek, C.; Wohlfahrt, T.; Myrzik, J. Overview and Classification of Interferences in the Frequency Range 2–150 kHz (Supraharmonics). In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Amalfi, Italy, 20–22 June 2018. [Google Scholar] [CrossRef]
- Bollen, M.; Shyar, H.H.; Rönnberg, S. Spread of high frequency current emission. In Proceedings of the 22nd International Conference and Exhibition on Electricity Distribution (CIRED), Stockholm, Sweden, 10–13 June 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Mariscotti, A. Characterization of Active Power Flow at Harmonics for AC and DC Railway Vehicles. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Hanoi, Vietnam, 14–17 October 2019. [Google Scholar] [CrossRef]
- Gu, Y.; Li, W.; He, X. Frequency-Coordinating Virtual Impedance for Autonomous Power Management of DC Microgrid. IEEE Trans. Power Electron. 2015, 30, 2328–2337. [Google Scholar] [CrossRef]
- Xiangchen, Z.; Guohui, Z.; Jinbin, Z. Impedance Detection Based on Ripple Analysis and Current Sharing Control in DC Microgrid. IEEE Access 2020, 8, 43554–43562. [Google Scholar] [CrossRef]
- Feng, X.; Xiong, Q.; Wardell, D.; Gattozzi, A.L.; Strank, S.M.; Hebner, R.E. Extra-Fast DC Distribution System Protection for Future Energy Systems. IEEE Trans. Ind. Appl. 2019, 55, 3421–3430. [Google Scholar] [CrossRef]
- Artale, G.; Cataliotti, A.; Cosentino, V.; Privitera, G. Experimental characterization of series arc faults in AC and DC electrical circuits. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Montevideo, Uruguay, 12–15 May 2014. [Google Scholar] [CrossRef]
- Mariscotti, A.; Giordano, D. Experimental characterization of pantograph arcs and transient conducted phenomena in DC railways. Acta Imeko 2020, 9, 10–17. [Google Scholar] [CrossRef]
- Signorino, D.; Giordano, D.; Mariscotti, A.; Gallo, D.; Delle Femine, A.; Balic, F.; Quintana, J.; Donadio, L.; Biancucci, A. Dataset of measured and commented pantograph electric arcs in DC railways. Data Brief 2020, 31, 105978. [Google Scholar] [CrossRef]
- Zheng, D.; Chen, L.; Nian, H.; Sun, D.; Chen, L. Low-frequency Stability Analysis of the DC-link in Dual Active Bridge (DAB) Based Microgrid. In Proceedings of the IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Macao, 1−4 December 2019. [Google Scholar] [CrossRef]
- Rashidirad, N.; Hamzeh, M.; Sheshyekani, K.; Afjei, E. High-Frequency Oscillations and their Leading Causes in DC Microgrids. IEEE Trans. Energy Convers. 2017, 32, 1479–1491. [Google Scholar] [CrossRef]
- Habibullah, M.; Mithulananthan, N.; Zare, F.; Sharma, R. Impact of Control Systems on Power Quality at Common DC Bus in DC Grid. In Proceedings of the IEEE PES GTD Grand International Conference and Expo. Asia, Bangkok, Thailand, 20−23 March 2019. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, Y.; Geng, G.; Jiang, Q.; Liu, W.; Li, L. Suppression Strategy of Ultra-Low Frequency Oscillation in Yunnan Power Grid with BESS. In Proceedings of the North American Power Symposium (NAPS), Wichita, KS, USA, 13−15 October 2019. [Google Scholar] [CrossRef]
- Wen, H.; Xiao, W.; Wen, X.; Armstrong, P. Analysis and Evaluation of DC-Link Capacitors for High-Power-Density Electric Vehicle Drive Systems. IEEE Trans. Veh. Technol. 2012, 61, 2950–2964. [Google Scholar] [CrossRef]
- Sarr, C.T.; Camara, M.B.; Dakyo, B. Influence of Cycles Number and RMS Value of DC-current Ripple on Supercapacitors Aging. In Proceedings of the International Conference on Clean Electrical Power (ICCEP), Otranto, Italy, 2−4 July 2019. [Google Scholar] [CrossRef]
- German, R.; Sari, A.; Venet, P.; Briat, O.; Vinassa, J.M. Study of static converters related ripple currents effects on supercapacitors ageing within DC networks. In Proceedings of the IEEE 24th International Symposium on Industrial Electronics (ISIE), Búzios, Rio de Janeiro, Brazil, 3−5 June 2015. [Google Scholar] [CrossRef]
- Breucker, S.D.; Engelen, K.; D’hulst, R.; Driesen, J. Impact of current ripple on Li-ion battery ageing. In Proceedings of the World Electric Vehicle Symp. and Exhib. (EVS27), Barcelona, Spain, 17−20 November 2013. [Google Scholar] [CrossRef]
- Han, X.; Lu, L.; Zheng, Y.; Feng, X.; Li, Z.; Li, J.; Ouyang, M. A review on the key issues of the lithium ion battery degradation among the whole life cycle. eTransportation 2019, 1, 100005. [Google Scholar] [CrossRef]
- Mariscotti, A. Assessment of Human Exposure to Electromagnetic Field in Modern Microgrids, Power Systems and Electric Transports. Energies 2021, 14, accepted. [Google Scholar]
- SAE J2836-1. Use Cases for Communication between Plug-in Vehicles and the Utility Grid; SAE: Warrendale, PA, USA, 2019. [Google Scholar]
- IEC 61851-1. Electric Vehicle Conductive Charging System—Part 1: General Requirements; IEC: Geneva, Switzerland, 2017. [Google Scholar]
- Den Broeck, G.V.; Stuyts, J.; Driesen, J. A critical review of power quality standards and definitions applied to DC microgrids. Appl. Energy 2018, 229, 281–288. [Google Scholar] [CrossRef]
- Barros, J.; de Apráiz, M.; Diego, R. Power Quality in DC Distribution Networks. Energies 2019, 12, 848. [Google Scholar] [CrossRef]
- Kumar, D.; Zare, F.; Ghosh, A. DC Microgrid Technology: System Architectures, AC Grid Interfaces, Grounding Schemes, Power Quality, Communication Networks, Applications, and Standardizations Aspects. IEEE Access 2017, 5, 12230–12256. [Google Scholar] [CrossRef]
- Freschi, F. High-Frequency Behavior of Residual Current Devices. IEEE Trans. Power Deliv. 2012, 27, 1629–1635. [Google Scholar] [CrossRef]
- Czapp, S.; Tariq, H. Behaviour of Residual Current Devices at Frequencies 2 up to 50 kHz. Energies 2021, 14, 1785. [Google Scholar] [CrossRef]
- EN 60755-2. General Safety Requirements for Residual Current Operated Protective Devices—Part 2: Residual Current Operated Protective Devices for DC Systems; CENELEC: Brussels, Belgium, 2019. [Google Scholar]
- Chandra, A.; Sigh, G.K.; Pant, V. Protection techniques for DC microgrid—A review. Electr. Power Syst. Res. 2020, 187, 106439. [Google Scholar] [CrossRef]
- IEC 62020-1. Electrical Accessories—Residual Current Monitors (RCMs)—Part 1: RCMs for Household and Similar Uses; IEC: Geneva, Switzerland, 2021. [Google Scholar]
- EN 61557-8. Electrical Safety in Low Voltage Distribution Systems Up to 1000 Vac and 1500 Vdc—Equipment for Testing, Measuring or Monitoring of Protective Measures—Part 8: Insulation Monitoring Devices for IT Systems; CENELEC: Brussels, Belgium, 2015. [Google Scholar]
- Bender, LINETRAXX RCMB300 Series, AC/DC Sensitive Residual Current Monitoring Modules with an Integrated Measuring Current Transformer. 2020. Available online: https://www.benderinc.com/products/ground-fault-monitoring-grounded/linetraxx_rcmb300-series (accessed on 15 July 2021).
- Danisense, RCMH070IB+ Datasheet. 2020. Available online: https://www.danisense.com/images/pdf/RCMH070IBv8.pdf (accessed on 15 July 2021).
- Thiim, Earth Leakage Monitor for DC Unearthed IT Systems Mod. DDEA. Available online: https://www.thiim.com/datasheets/ddea.pdf (accessed on 15 July 2021).
- Ananthan, S.N.; Feng, X.; Penney, C.; Gattozzi, A.; Hebner, R.; Santoso, S. Voltage Differential Protection for Series Arc Fault Detection in Low-Voltage DC Systems. Inventions 2021, 6, 5. [Google Scholar] [CrossRef]
- Yao, X.; Herrera, L.; Ji, S.; Zou, K.; Wang, J. Characteristic Study and Time-Domain Discrete- Wavelet-Transform Based Hybrid Detection of Series DC Arc Faults. IEEE Trans. Power Electron. 2014, 29, 3103–3115. [Google Scholar] [CrossRef]
- EN 62606. General Requirements for Arc Fault Detection Devices; CENELEC: Brussels, Belgium, 2019. [Google Scholar]
- UL 1699B. Photovoltaic (PV) DC Arc-Fault Circuit Protection; Underwriter Laboratories: Northbrook, IL, USA, 2018. [Google Scholar]
- Siemens, 5SM Arc Fault Detection Unit for Photovoltaics. 2015. Available online: https://cache.industry.siemens.com/dl/files/961/109476961/att_846525/v1/manual_5SM_ADU_for_photovoltaic_en_en-US.pdf (accessed on 15 July 2021).
- Huawei, Arc Fault Circuit Interrupter for PV Systems. 2020. Available online: https://solar.huawei.com/en-GB/download?p=%2F-%2Fmedia%2FSolar%2Fnews%2Fwhitepaper%2FAFCI-whitepaper.pdf (accessed on 15 July 2021).
- Johnson, J.; Armijo, K.M.; Avrutsky, M.; Eizips, D.; Kondrashov, S. Arc-fault unwanted tripping survey with UL 1699B-listed products. In Proceedings of the IEEE 42nd Photovoltaic Specialist Conference (PVSC), New Orleans, LA, USA, 14–19 June 2015. [Google Scholar] [CrossRef]
- Boler, O.; Ibrahem, A.; Ali, A.A.; Granger, M.G.; Abdelgabir, H.; Sozer, Y.; De Abreu-Garcia, J.A. A Novel High Frequency Impedance Analysis Method to Protect DC Electrical Railway Systems. IEEE Trans. Ind. Appl. 2020, 56, 669–677. [Google Scholar] [CrossRef]
- Lee, W.-S.; Kang, S.-H. Protection for distributed generations in the DC micro-grid. In Proceedings of the IEEE PES International Conference and Exhibition on Innovative Smart Grid Technologies, Manchester, UK, 5–7 December 2011. [Google Scholar] [CrossRef]
- Jia, K.; Wang, C.; Bi, T.; Feng, T.; Zhu, R. Transient Current Correlation Based Protection for DC Distribution System. IEEE Trans. Ind. Electron. 2020, 67, 9927–9936. [Google Scholar] [CrossRef]
- EN 55014-1. Electromagnetic Compatibility—Requirements for Household Appliances, Electric Tools and Similar Apparatus—Part 1: Emission; CENELEC: Brussels, Belgium, 2020. [Google Scholar]
- Pinomaa, A.; Ahola, J.; Kosonen, A.; Nuutinen, P. Applicability of narrowband power line communication in an LVDC distribution network. In Proceedings of the IEEE International Symposium on Power Line Communications and Its Applications, Glasgow, UK, 30 March–2 April 2014. [Google Scholar] [CrossRef]
- Devolo G3-PLC Modem 500k. Available online: https://www.devolo.global/fileadmin/Web-Content/DE/products/sg/g3-plc-modem-500K/documents/en/Produktblatt_G3-Modem_0219_EN.pdf (accessed on 30 July 2021).
- EN 50065-1. Signalling on Low-Voltage Electrical Installations in the Frequency Range 3 kHz to 148.5 kHz—Part 1: General Requirements, Fequency Bands and Electromagnetic Disturbances; CENELEC: Brussels, Belgium, 2011. [Google Scholar]
- IEC 61851-21-2. Electric Vehicle Conductive Charging System—Part 21-2: Electric Vehicle Requirements for Conductive Connection to an AC/DC Supply—EMC Requirements for off Board Electric Vehicle Charging Systems; IEC: Geneva, Switzerland, 2018. [Google Scholar]
- Sayed, W.E.; Lezynski, P.; Smolenski, R.; Moonen, N.; Crovetti, P.; Thomas, D.W.P. The Effect of EMI Generated from Spread-Spectrum-Modulated SiC-Based Buck Converter on the G3-PLC Channel. Electronics 2021, 10, 1416. [Google Scholar] [CrossRef]
- IEC 61000-4-17. Electromagnetic Compatibility (EMC)—Part 4-17: Testing and Measurement Techniques—Ripple on d.c. Input Power Port Immunity Test; IEC: Geneva, Switzerland, 2009. [Google Scholar]
- IEC 61000-4-16. Electromagnetic Compatibility (EMC)—Part 4-16: Testing and Measurement Techniques—Test for Immunity to Conducted, Common Mode Disturbances in the Frequency Range 0 Hz to 150 kHz; IEC: Geneva, Switzerland, 2015. [Google Scholar]
- MIL-STD-461. Requirements for the Control of Electromagnetic Interference Characteristics of Subsystems and Equipment; US Department of Defense: Washington, DC, USA, 2015. [Google Scholar]
- Mok, K.-T.; Wang, M.-H.; Tan, S.-C.; Hui, S.Y.R. DC Electric Springs—A Technology for Stabilizing DC Power Distribution Systems. IEEE Trans. Power Electron. 2017, 32, 1088–1105. [Google Scholar] [CrossRef]
- Mariscotti, A. Characterization of Power Quality transient phenomena of DC railway traction supply. Acta Imeko 2012, 1, 26–35. [Google Scholar] [CrossRef][Green Version]
- Mariscotti, A.; Sandrolini, L. Detection of harmonic overvoltage and resonance in AC railways using measured pantograph electrical quantities. Energies 2021, 14, 5645. [Google Scholar] [CrossRef]
- Kwasinski, A.; Onwuchekwa, C.N. Dynamic Behavior and Stabilization of DC Microgrids with Instantaneous Constant-Power Loads. IEEE Trans. Power Electron. 2011, 26, 822–834. [Google Scholar] [CrossRef]
- Sun, J. Impedance-Based Stability Criterion for Grid-Connected Inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Guo, J.; Chen, T.; Chaudhuri, B.; Hui, S.Y.R. Stability of Isolated Microgrids with Renewable Generation and Smart Loads. IEEE Trans. Sust. Energy 2020, 11, 2845–2854. [Google Scholar] [CrossRef]
- Amin, M.; Molinas, M. Understanding the Origin of Oscillatory Phenomena Observed between Wind Farms and HVDC Systems. IEEE Trans. Emerg. Sel. Top. Power Electron. 2017, 5, 378–392. [Google Scholar] [CrossRef]
- Ahmed, M.; Meegahapola, L.; Vahidnia, A.; Datta, M. Analysis and mitigation of low-frequency oscillations in hybrid AC/DC microgrids with dynamic loads. IET Gener. Transm. Distrib. 2019, 13, 1477–1488. [Google Scholar] [CrossRef]
- Rashidirad, N.; Hamzeh, M.; Sheshyekani, K.; Afjei, E. An Effective Method for Low-Frequency Oscillations Damping in MultiBus DC Microgrids. IEEE Trans. Emerg. Sel. Top. Circuits Syst. 2017, 7, 403–412. [Google Scholar] [CrossRef]
- Wang, H.; Blaabjerg, F. Reliability of Capacitors for DC-Link Applications in Power Electronic Converters—An Overview. IEEE Trans. Ind. Appl. 2014, 50, 3569–3578. [Google Scholar] [CrossRef]
- Buiatti, G.M.; Cruz, S.M.A.; Cardoso, A.J.M. Lifetime of Film Capacitors in Single-Phase Regenerative Induction Motor Drives. In Proceedings of the IEEE Intern. Symp. on Diagnostics for Electric Machines, Power Electronics and Drives, Cracow, Poland, 6–8 September 2007. [Google Scholar] [CrossRef]
- Montanari, G.; Fabiani, D. The effect of nonsinusoidal voltage on intrinsic aging of cable and capacitor insulating materials. IEEE Trans. Dielectr. Electr. Insul. 1999, 6, 798–802. [Google Scholar] [CrossRef]
- AVX, High-Power Capacitors—Calculation Form. Available online: https://www.avx.com/docs/techinfo/FimGuide.pdf (accessed on 30 July 2021).
- Parler, S.G. Deriving Life Multipliers for Electrolytic Capacitors. IEEE Power Electron. Soc. Newsl. 2004, 16, 11–12. [Google Scholar]
- Albertsen, A. Electrolytic Capacitor Lifetime Estimation; Technical report; Jianghai Europe GmbH: Krefeld, Germany, 2010. [Google Scholar]
- Nichicon. Aluminum Electrolytic Capacitors, UBY 2011. Available online: https://www.nichicon.co.jp/english/products/pdfs/e-uby.pdf (accessed on 13 September 2021).
- Rubycon. Radial Lead Aluminum Electrolytic Capacitors ZLJ 2011. Available online: http://www.rubycon.co.jp/en/catalog/e_pdfs/aluminum/e_ZLJ.pdf (accessed on 13 September 2021).
- Enisz, K.; Kohlrusz, G.; Fodor, D.; Kovacs, L.; Marschalko, R. Degradation analysis of DC-link aluminium electrolytic capacitors operating in PWM power converters. Adv. Electr. Electron. Eng. 2020, 18, 85–91. [Google Scholar] [CrossRef]
- Bellache, K.; Bailo Camara, M.; Dakyo, B. Supercapacitors Characterization and Modeling Using Combined Electro-Thermal Stress Approach Batteries. IEEE Trans. Ind. Appl. 2019, 55, 1817–1827. [Google Scholar] [CrossRef]
- Rafik, F.; Gualous, H.; Gallay, R.; Crausaz, A.; Berthon, A. Frequency, thermal and voltage supercapacitor characterization and modeling. J. Power Sources 2007, 165, 928–934. [Google Scholar] [CrossRef]
- Hammar, A.; Venet, P.; Lallemand, R.; Coquery, G.; Rojat, G. Study of Accelerated Aging of Supercapacitors for Transport Applications. IEEE Trans. Ind. Electron. 2010, 57, 3972–3979. [Google Scholar] [CrossRef]
- Jossen, A. Fundamentals of battery dynamics. J. Power Sources 2006, 154, 530–538. [Google Scholar] [CrossRef]
- Savoye, F.; Venet, P.; Millet, M.; Groot, J. Impact of Periodic Current Pulses on Li-Ion Battery Performance. IEEE Trans Ind. Electron. 2012, 59, 3481–3488. [Google Scholar] [CrossRef]
- Karden, E.; Buller, S.; Doncker, R.W.D. A frequency-domain approach to dynamical modeling of electrochemical power sources. Electrochim. Acta 2002, 47, 2347–2356. [Google Scholar] [CrossRef]
- Smith, M.J.; Gladwin, D.T.; Stone, D.A. Experimental analysis of the influence of high-frequency ripple currents on dynamic charge acceptance in lead-acid batteries. In Proceedings of the 43rd Annual Conference of the IEEE Industrial Electronics Society (IECON), Beijing, China, 29 October–1 November 2017. [Google Scholar] [CrossRef]
- Karvonen, A.; Thiringer, T. Parameter analysis of current and voltage ripple in a hybrid vehicle traction system. In Proceedings of the IEEE International Electric Machines & Drives Conference (IEMDC), Coeur d’Alene, ID, USA, 10–13 May 2015. [Google Scholar] [CrossRef]
- Wang, J.; Zou, K.; Chen, C.; Chen, L. A high frequency battery model for current ripple analysis. In Proceedings of the 25th Annual IEEE Applied Power Electronics Conference and Expo. (APEC), Palm Springs, CA, USA, 21–25 February 2010. [Google Scholar] [CrossRef]
- Harting, N.; Wolff, N.; Röder, F.; Krewer, U. Nonlinear Frequency Response Analysis (NFRA) of Lithium-Ion Batteries. Electrochim. Acta 2017, 248, 133–139. [Google Scholar] [CrossRef]
- Jespersen, J.; Tønnesen, A.; Nørregaard, K.; Overgaard, L.; Elefsen, F. Capacity Measurements of Li-Ion Batteries using AC Impedance Spectroscopy. World Electr. Veh. J. 2009, 3, 127–133. [Google Scholar] [CrossRef]
- Buller, S.; Thele, M.; DeDoncker, R.; Karden, E. Impedance-Based Simulation Models of Supercapacitors and Li-Ion Batteries for Power Electronic Applications. IEEE Trans. Ind. Appl. 2005, 41, 742–747. [Google Scholar] [CrossRef]
- Lehner, S.; Baumhöfer, T.; Sauer, D.U. Disparity in initial and lifetime parameters of lithium-ion cells. IET Electr. Syst. Transp. 2016, 6, 34–40. [Google Scholar] [CrossRef]
- Benavides, N.D.; Chapman, P.L. Modeling the Effect of Voltage Ripple on the Power Output of Photovoltaic Modules. IEEE Trans. Ind. Electron. 2008, 55, 2638–2648. [Google Scholar] [CrossRef]
- Choi, W.; Enjeti, P.N.; Howze, J.W. Development of an Equivalent Circuit Model of a Fuel Cell to Evaluate the Effects of Inverter Ripple Current. In Proceedings of the 19th IEEE Applied Power Electronics Conference and Exposition, Anaheim, CA, USA, 22–26 February 2004. [Google Scholar] [CrossRef]
- Fontes, G.; Turpin, C.; Astier, S.; Meynard, T.A. Interactions between Fuel Cells and Power Converters: Influence of Current Harmonics on a Fuel Cell Stack. IEEE Trans. Power Electron. 2007, 22, 670–678. [Google Scholar] [CrossRef]
- Gemmen, R.S. Analysis for the Effect of Inverter Ripple Current on Fuel Cell Operating Condition. Trans. ASME 2003, 125, 576–585. [Google Scholar] [CrossRef]
- Mariscotti, A. Methods for Ripple Index evaluation in DC Low Voltage Distribution Networks. In Proceedings of the IEEE Intern. Meas. Techn. Conf. IMTC, Warsaw, Poland, 1–3 May 2007. [Google Scholar] [CrossRef]
- MIL-STD-704F. Interface Standard—Aircraft Electric Power Characteristics; US Department of Defense: Washington, DC, USA, 2004. [Google Scholar]
- IACS E5. Requirements concerning Electrical And Electronic Installations, Rev. 1; IACS: London, UK, 2005. [Google Scholar]
- Rules and Regulations for the Classification of Ships; Lloyd Register of Shipping: London, UK, 2016.
- EN 50163. Railway Applications—Supply Voltages of Traction Systems; CENELEC: Brussels, Belgium, 2020. [Google Scholar]
- EN 300 132-2. Environmental Engineering (EE)—Power Supply Interface at the Input of Information and Communication Technology (ICT) Equipment—Part 2: −48 V Direct Current (DC); ETSI: Sophia Antipolis, France, 2019. [Google Scholar]
- ITU-T Std. L.1200. Direct Current Power Feeding Interface Up to 400 V at the Input to Telecommunication and ICT Equipment; International Telecommunication Union: Geneva, Switzerland, 2012. [Google Scholar]
- IEC 61000-4-11. Electromagnetic Compatibility (EMC)—Part 4-11: Testing and Measurement Techniques—Voltage Dips, Short Interruptions and Voltage Variations Immunity Tests; IEC: Geneva, Switzerland, 2020. [Google Scholar]
- IEC 61000-4-14. Electromagnetic Compatibility (EMC)—Part 4-14: Testing and Measurement Techniques—Voltage Fluctuation Immunity Test for Equipment with Input Current Not Exceeding 16 a Per Phase; IEC: Geneva, Switzerland, 2009. [Google Scholar]
- IEC 61000-4-29. Electromagnetic Compatibility (EMC)—Part 4-29: Testing and Measurement Techniques—Voltage Dips, Short Interruptions and Voltage Variations on d.c. Input Power Port Immunity Tests; IEC: Geneva, Switzerland, 2000. [Google Scholar]
- EN 50155. Railway Applications—Rolling Stock—Electronic Equipment; CENELEC: Brussels, Belgium, 2017. [Google Scholar]
- IEEE Std. 1159. IEEE Recommended Practice for Monitoring Electric Power Quality; IEEE: Piscataway, NJ, USA, 2009. [Google Scholar]
- IEC 61000-4-30. Electromagnetic Compatibility (EMC)—Part 4-30: Testing and Measurement Techniques—Power Quality Measurement Methods; IEC: Geneva, Switzerland, 2015. [Google Scholar]
- IEC 61000-6-2. Electromagnetic Compatibility (EMC)—Part 6-2: Generic Standards—Immunity Standard for Industrial Environments; IEC: Geneva, Switzerland, 2019. [Google Scholar]
- EN 62920. Photovoltaic Power Generating Systems—EMC Requirements and Test Methods for Power Conversion Equipment; CENELEC: Brussels, Belgium, 2017. [Google Scholar]
- EN 50124-2. Railway Applications—Insulation Coordination—Part 2: Overvoltages and Related Protection; CENELEC: Brussels, Belgium, 2017. [Google Scholar]
- Mariscotti, A.; Giordano, D.; Delle Femine, A.; Signorino, D. Filter Transients onboard DC Rolling Stock and Exploitation for the Estimate of the Line Impedance. In Proceedings of the Intern. Instrum. and Meas. Techn. Conf., Dubrovnik, Croatia, 25–28 May 2020. [Google Scholar] [CrossRef]
- Asakimori, K.; Murai, K.; Tanaka, T.; Babasaki, T. Effect of inrush current flowing into EMI filter on the operation of ICT equipment in HVDC system. In Proceedings of the IEEE 36th International Telecommunications Energy Conference (INTELEC), Vancouver, BC, Canada, 28 September–2 October 2014. [Google Scholar] [CrossRef]
- IEC 61000-3-3. Electromagnetic Compatibility (EMC)—Part 3-3: Limits—Limitation of Voltage Changes, Voltage Fluctuations and Flicker in Public Low-Voltage Supply Systems, for Equipment with Rated Current <= 16 A per Phase and Not Subject to Conditional Connection; IEC: Geneva, Switzerland, 2019. [Google Scholar]
- EN 300 132-3-1. Environmental Engineering (EE)—Power Supply Interface at the Input of Information and Communication Technology (ICT) Equipment—Part 3: Operated by Rectified Current Source, Alternating Current Source or Direct Current Source Up to 400 V—Sub-Part 1: Direct Current Source Up to 400 V; ETSI: Sophia Antipolis, France, 2011. [Google Scholar]
- IEC 61000-4-7. Electromagnetic Compatibility (EMC)—Part 4-7: Testing and Measurement Techniques—General Guide on Harmonics and Interharmonics Measurements and Instrumentation, for Power Supply Systems and Equipment Connected Thereto; IEC: Geneva, Switzerland, 2002. [Google Scholar]
- Bollen, M.; Olofsson, M.; Larsson, A.; Ronnberg, S.; Lundmark, M. Standards for supraharmonics (2 to 150 kHz). IEEE Electrom. Comp. Mag. 2014, 3, 114–119. [Google Scholar] [CrossRef]
- IEC 61000-4-19. Electromagnetic Compatibility (EMC)—Part 4-19: Testing and Measurement Techniques—Test for Immunity to Conducted, Differential Mode Disturbances and Signalling in the Frequency Range 2 kHz to 150 kHz at a.c. Power Ports; IEC: Geneva, Switzerland, 2014. [Google Scholar]
- EN 50155. Railway Applications—Rolling Stock—Electronic Equipmen; CENELEC: Brussels, Belgium, 2019. [Google Scholar]
- IEEE Std. 1662. IEEE Recommended Practice for the Design and Application of Power Electronics in Electrical Power Systems; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- IEC 61851-23. Electric Vehicle Conductive Charging System Part 23: DC Electric Vehicle Charging Station; IEC: Geneva, Switzerland, 2014. [Google Scholar]
- IEC 60479-1. Effects of Current on Human Beings and Livestock—Part 1: General Aspects; IEC: Geneva, Switzerland, 2018. [Google Scholar]
- IEC 60479-5. Effects of Current on Human Beings and Livestock—Part 5: Touch Voltage Threshold Values for Physiological Effects; IEC: Geneva, Switzerland, 2007. [Google Scholar]
- Mariscotti, A. Electrical Safety and Stray Current Protection with Platform Screen Doors in DC Rapid Transit. IEEE Trans. Transp. Electrif. 2021, 7, 1724–1732. [Google Scholar] [CrossRef]
- SMA Solar Technology. Leading Leakage Currents. Available online: https://files.sma.de/downloads/Ableitstrom-TI-en-26.pdf (accessed on 18 July 2021).
- Yu, S.; Wang, J.; Zhang, X.; Li, F. Complete Parasitic Capacitance Model of Photovoltaic Panel Considering the Rain Water. Chin. J. Electr. Eng. 2017, 3, 77–84. [Google Scholar] [CrossRef]
- IEC 63053. General Requirements for Residual Current Operated Protective Devices for DC Systems; IEC: Geneva, Switzerland, 2017. [Google Scholar]
- Zhou, M.; Yang, M.; Wu, X.; Fu, J. Research on Composite Control Strategy of Quasi-Z-Source DC–DC Converter for Fuel Cell Vehicles. Appl. Sci. 2019, 9, 3309. [Google Scholar] [CrossRef]
- Joung, M.; Kim, H.; Baek, J. Dynamic analysis and optimal design of high efficiency full bridge LLC resonant converter for server power system. In Proceedings of the 27th Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012. [Google Scholar] [CrossRef]
- Maxim Integrated. DC-to-DC Converter Combats EMI, App. Note 1077, 28 May 2002. Available online: https://pdfserv.maximintegrated.com/en/an/AN1077.pdf (accessed on 30 July 2021).
- Sandrolini, L.; Mariscotti, A. Impact of Short-Time Fourier Transform Parameters on the Accuracy of EMI Spectra Estimates in the 2–150 kHz Supraharmonics Interval. Electr. Power Syst. Res. 2021, 195, 107130. [Google Scholar] [CrossRef]
- Mariscotti, A.; Sandrolini, L. Time-Frequency Transforms for the Analysis of Supraharmonics caused by Switched-Mode Power Supplies. Electronics 2020, 9, 2088. [Google Scholar] [CrossRef]
- Luo, D.; Wu, T.; Li, M.; Yi, B.; Zhuo, H. Application of VMD and Hilbert Transform Algorithms on Detection of the Ripple Components of the DC Signal. Energies 2020, 13, 935. [Google Scholar] [CrossRef]
- Lodetti, S.; Bruna, J.; Melero, J.J.; Sanz, J.F. Wavelet Packet Decomposition for IEC Compliant Assessment of Harmonics under Stationary and Fluctuating Conditions. Energies 2019, 12, 4389. [Google Scholar] [CrossRef]
- Magro, M.C.; Mariscotti, A.; Pinceti, P. Definition of Power Quality Indices for DC Low Voltage Distribution Networks. In Proceedings of the IEEE Instrumentation and Measurement Technology Conference Proceedings, Sorrento, Italy, 24–27 April 2006. [Google Scholar] [CrossRef]
- Ciornei, I.; Albu, M.; Sanduleac, M.; Hadjidemetriou, L.; Kyriakides, E. Analytical derivation of PQ indicators compatible with control strategies for DC microgrids. In Proceedings of the IEEE PES PowerTech, Manchester, UK, 18–22 June 2017. [Google Scholar] [CrossRef]
- Mariscotti, A. Discussion of Power Quality Metrics suitable for DC Power Distribution and Smart Grids. In Proceedings of the 23rd Imeko TC4 International Symposium, Xi’an, China, 17–20 September 2019. [Google Scholar]
- Giordano, D.; Clarkson, P.; Gamacho, F.; Van Den Brom, H.E.; Donadio, L.; Fernandez-Cardador, A.; Spalvieri, C.; Gallo, D.; Istrate, D.; De Santiago Laporte, A.; et al. Accurate Measurements of Energy, Efficiency and Power Quality in the Electric Railway System. In Proceedings of the Conference on Precision Electromagnetic Measurements (CPEM), Paris, France, 8–13 July 2018. [Google Scholar] [CrossRef]
- Liang, J.; Ng, S.K.K.; Kendall, G.; Cheng, J.W.M. Load Signature Study—Part I: Basic Concept, Structure, and Methodology. IEEE Trans. Power Deliv. 2010, 25, 551–560. [Google Scholar] [CrossRef]
- EN 50160. Voltage Characteristics of Electricity Supplied by Public Distribution Networks; CENELEC: Brussels, Belgium, 2011. [Google Scholar]
- IEC 61000-2-2. Electromagnetic Compatibility (EMC)—Part 2-2: Environment—Compatibility Levels for Low-Frequency Conducted Disturbances and Signalling in Public Low-Voltage Power Supply Systems; IEC: Geneva, Switzerland, 2019. [Google Scholar]
- IEC 61000-2-4. Electromagnetic Compatibility (EMC)—Part 2-4: Environment—Compatibility Levels in Industrial Plants for Low-Frequency Conducted Disturbances; IEC: Newark, NY, USA, 2020. [Google Scholar]
- Crider, J.M.; Sudhoff, S.D. Reducing Impact of Pulsed Power Loads on Microgrid Power Systems. IEEE Trans. Smart Grid 2010, 1, 270–277. [Google Scholar] [CrossRef]
- Mariscotti, A. Power Quality Metrics for DC Grids with Pulsed Power Loads. Acta Imeko 2021, 10, 153–161. [Google Scholar] [CrossRef]
- IEC 61000-4-5. Electromagnetic Compatibility (EMC)—Part 4-5: Testing and Measurement Techniques—Surge Immunity Test; IEC: Geneva, Switzerland, 2014. [Google Scholar]
- MIL-STD-1399-300. Interface Standard Section 300—Part 1: Low Voltage Electric Power, Alternating Current; US Department of Defense: Washington, DC, USA, 2018. [Google Scholar]

| Sources and Loads (1) (Increase Number or Rated Power) | Grid Parameters | ||||
|---|---|---|---|---|---|
| Stability (2) | Impedance | Main Res. Freq. | Main Res. Damping | ||
| Sources | Voltage controlled (VCS) | ↑ | ↓ | ↑↑ | ↑↑ |
| Current controlled (CCS) | ↓ | ↑ | ↓ | ↓↓ | |
| Loads | Constant current (CCL) | ↑ | — | ↑↑ | ↑↑ |
| Constant impedance (CIL) | ↑ | — | ↑↑ | ↑↑ | |
| Constant power (CPL) (3) | ↓ | — | ↓ | ↓↓ | |
| Ripple | ESR | Capacitance | Ref. |
|---|---|---|---|
| 20% rms, 0.1 Hz (±5 Apk sin. on 30 Adc) | linear +50% at 0–60% ripple | −5% at ≥20% ripple | Sarr * et al. [33] |
| 10% rms, 100 and 10 kHz (12 Arms sin. on 120 Adc) | +2/+20% at 1000 h, +25/+70% at 5000 h | −10/−16% at 1000 h, −25/−30% at 5000 h | German et al. [34] |
| 16.7% p-p (9.6% rms), 0.1–0.5 Hz (±5 Apk triang. on 30 Adc) | 0% at 0.2 Hz, +15% at 0.5 Hz +8% at 1000 cy (110 h), +8% at 8000 cy (900 h), +12% at 14,000 cy (1550 h) | −2% at 0.2 Hz, −3% at 0.5 Hz −2% at 1000 cy (110 h), −5% at 8000 cy (900 h), −6% at 14,000 cy (1550 h) | Bellache et al. [89] |
| Efficiency % | Ripple Amplitude (mA) | Ripple Frequency (kHz) | ||
|---|---|---|---|---|
| 5 | 10 | 25 | ||
| Low insolation 0.07 kW/m2 IPV,sc = 175 mA | 50 | >99 | >99 | 98 |
| 100 | 98.5 | 96 | 91.5 | |
| 150 | 97 | 87 | 74 | |
| High insolation 0.193 kW/m2 IPV,sc = 483 mA | 100 | >99 | 99 | 98 |
| 200 | 99 | 94 | 92 | |
| 400 | — | 81 | 75 | |
| Test Type | Operating Point % | Ripple Factor % | Ripple Frequency (kHz) | |||
|---|---|---|---|---|---|---|
| 30 | 60 | 120 | 1250 | |||
| Hydrogen concentration | ≤80 | >99 | >99 | >99 | >99 | |
| 98 | 91 | 96 | — | — | ||
| Oxygen concentration | 25 | 3 | >99 | >99 | >99 | >99 |
| 9 | >99 | >99 | >99 | >99 | ||
| 30 | 97 | 98.5 | 99 | >99 | ||
| 62 | 3 | >99 | >99 | >99 | >99 | |
| 9 | 98 | 99 | 99 | >99 | ||
| 30 | 93 | 95 | 96.5 | 99 | ||
| 98 | 3 | 99 | >99 | >99 | >99 | |
| 9 | 95 | 97.5 | 98 | >99 | ||
| 30 | 85 | 87 | 91 | 97.5 | ||
| Standard | Phenomenon | Type | Nom. Volt. Un [V] | Ref. Values | |
|---|---|---|---|---|---|
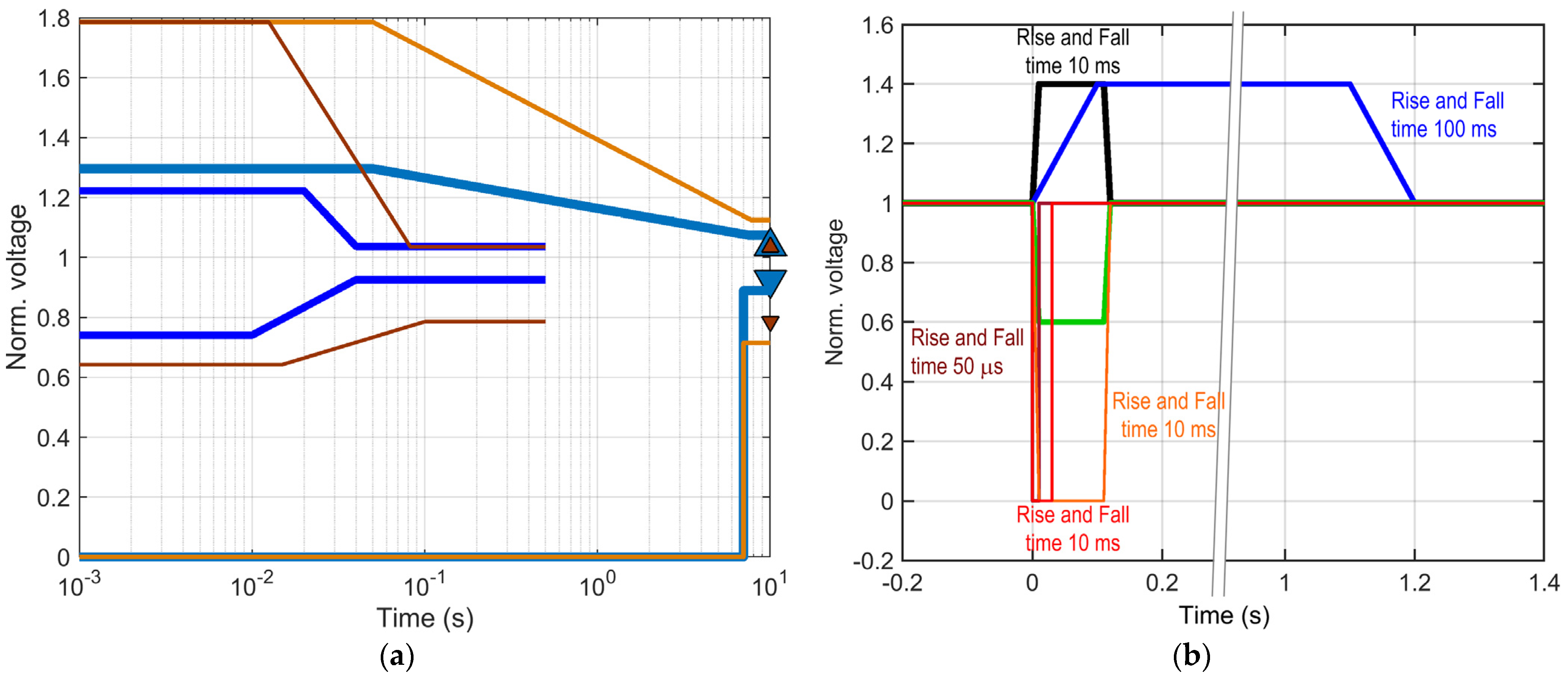
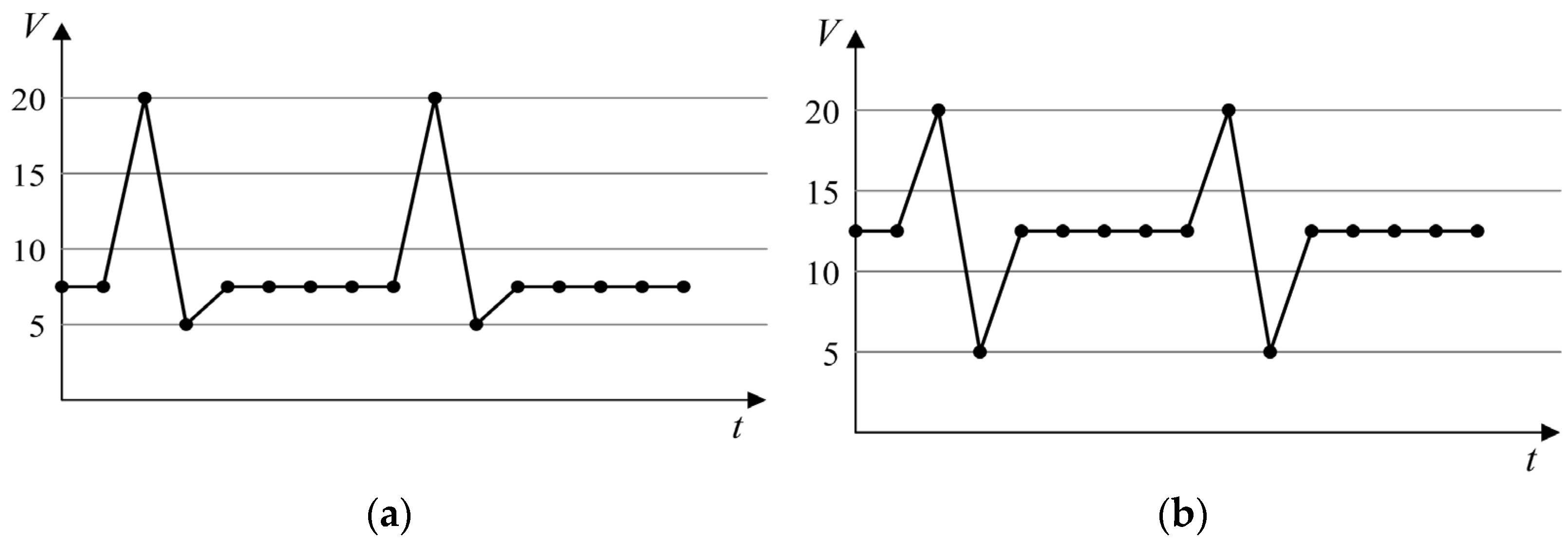
| MIL-STD-704F | Voltage var. | A | 28, 270 | see Figure 3a | |
| EN 61000-4-29 | Voltage var. | I | 24–110 | 85–120%, 0.1–10 s | |
| EN 61000-4-29 | Voltage dip | I | 24–110 | 40, 70%, 0.01–1 s | |
| EN 61000-4-29 | Voltage interr. HiZ and LoZ | I | 24–110 | 0%, 0.001–1 s | |
| IACS | Voltage var. | I | ≤1kV | 95–105% | |
| Lloyd Reg. | Voltage var. | I | LV & MV | 90–110% | |
| EN 50155 | Voltage var. | I | 24–110 | see Figure 3b | |
| EN 50155 | Voltage interr. | I | 24–110 | 0%, 0.01–0.03 s | |
| L.1200 | Voltage var. | A | 300, 380 | Un→400→Un, 1 min Un→260→Un, 1 min Un→410→Un, 1 s Un→420→Un, 10 ms | |
| L.1200 | Voltage dip | I | 300, 380 | 40%, 0.01 s | |
| L.1200 | Voltage interr. HiZ & LoZ | I | 300, 380 | 0%: 0.01 s (LoZ), 1 s (HiZ) | |
| Standard | Type | Nom. Volt. Un (V) | Ref. Values | |
|---|---|---|---|---|
| MIL-STD-704F | A | 28 | DF < 3.5%; Rp,1 < 1.5/28 V | |
| MIL-STD-704F | A | 270 | DF < 1.5%; Rp,1 < 6/270 V | |
| EN 61000-4-17 | G | ≤360 V | Vrip-gen = Rpp = 2, 5, 10, 15% | |
| IACS | I | ≤1 kV | Rrms < 10% (1) | |
| EN 50155 | I | 24–110 | Rp,2, Rp,3 < 5% | |
| IEEE Std. 1662 | I | LV & MV (2) | Rrms < 10% (1) | |
| IEC 61851-23 (3) | A,E | LV | Rp,1 < 5 V | |
| Lloyd Reg. | I | LV & MV | Rrms < 10% (1) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mariscotti, A. Power Quality Phenomena, Standards, and Proposed Metrics for DC Grids. Energies 2021, 14, 6453. https://doi.org/10.3390/en14206453
Mariscotti A. Power Quality Phenomena, Standards, and Proposed Metrics for DC Grids. Energies. 2021; 14(20):6453. https://doi.org/10.3390/en14206453
Chicago/Turabian StyleMariscotti, Andrea. 2021. "Power Quality Phenomena, Standards, and Proposed Metrics for DC Grids" Energies 14, no. 20: 6453. https://doi.org/10.3390/en14206453
APA StyleMariscotti, A. (2021). Power Quality Phenomena, Standards, and Proposed Metrics for DC Grids. Energies, 14(20), 6453. https://doi.org/10.3390/en14206453






