Heat Loss Due to Domestic Hot Water Pipes
Abstract
:1. Introduction
- It is possible to estimate accurately enough the length of DHW piping based on the general characteristics of the building at the early design stage of the building.
- Based on the data of the early design stage, it is possible to calculate DHW circulation losses with sufficient accuracy and to propose a corresponding supplement to the calculation method.
2. Methods
2.1. Research Scheme to Investigate DHW and DHW Circulation Heat Losses
- Detailed calibrated dynamic indoor climate and energy simulation model for a nZEB apartment building (nZEB case building in Table 1) to determine heat loss factors on room (21 °C heated and unheated basement) and water temperature, insulation (0, 20, 40 mm with and without valve insulation) and length of pipes and water circulation strategy (continuous circulation, clock based);
- Design DHW pipe length from 15 apartment buildings (Test building in Table 1);
- Generating a method for calculating pipe length and heat loss from pipes to be used in early stages of design;
- Validating of pipe length equation in7 reference apartment buildings (Reference buildings in Table 1);
- Validation of DHW heat loss with earlier studied 23 buildings measured heat losses.
2.2. nZEB Case Building
2.3. Test Buildings and Reference Buildings
2.4. Determining DHW Pipe Length
2.5. Indoor Climate and Energy Performance by nZEB Case Building Calibration
2.6. Heat Losses Calculations from DHW and DHW Circulation Pipes
2.7. The Influence of DHW and DHW Circulation Heat Loss on the Whole Building Energy Performance and Indoor Climate
3. Results
3.1. Measured and Calculated DHW Circulation Losses in Case Building
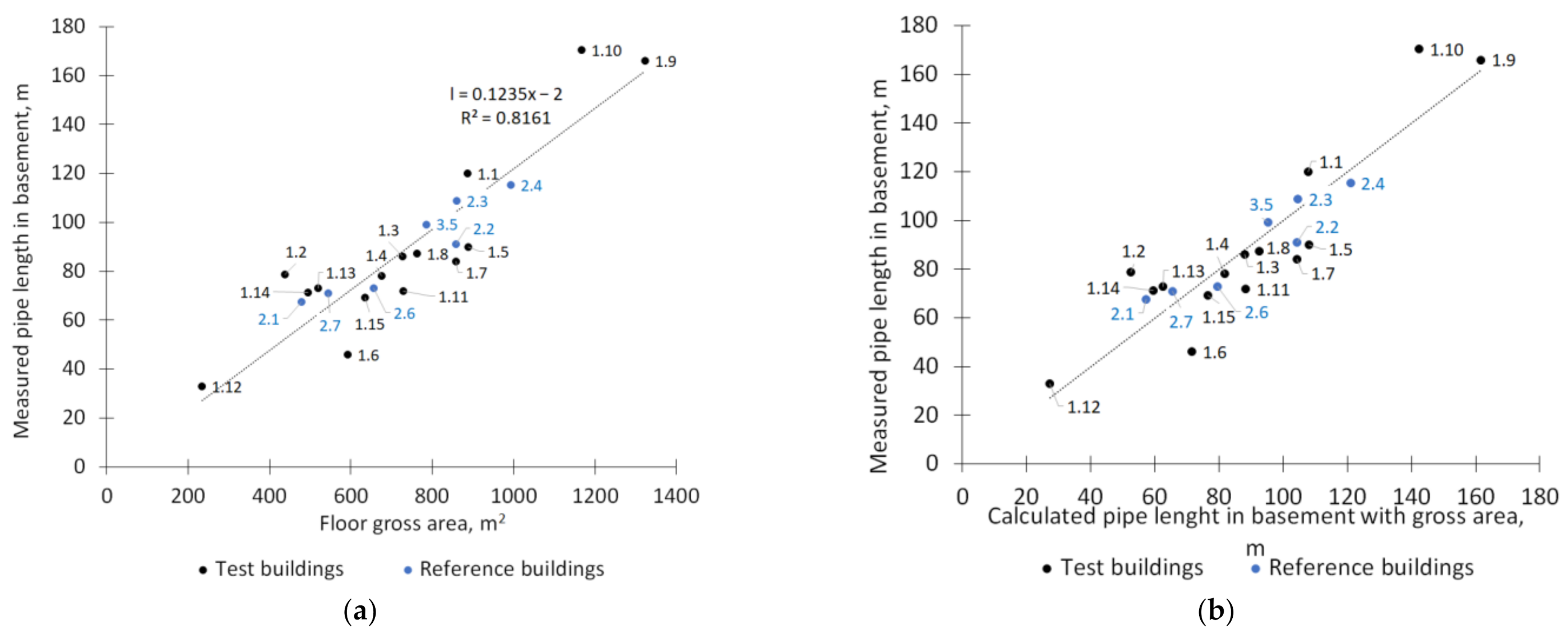
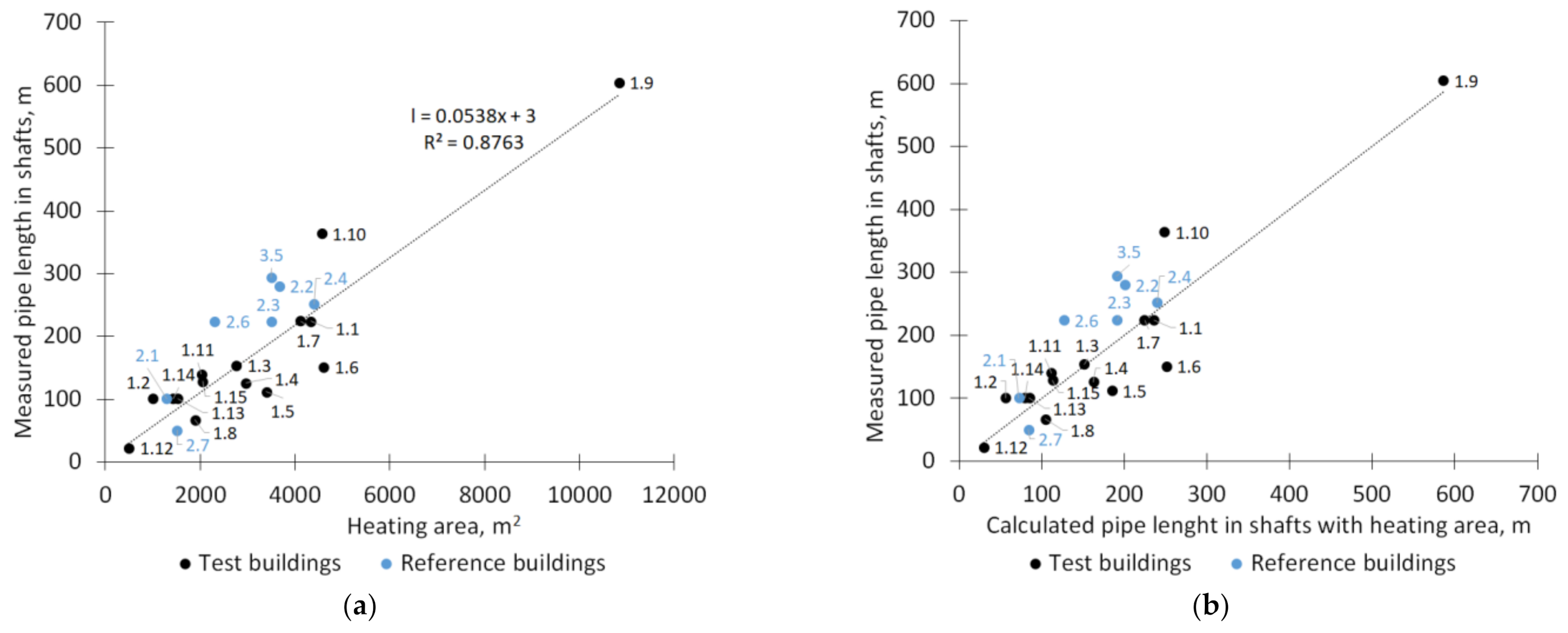
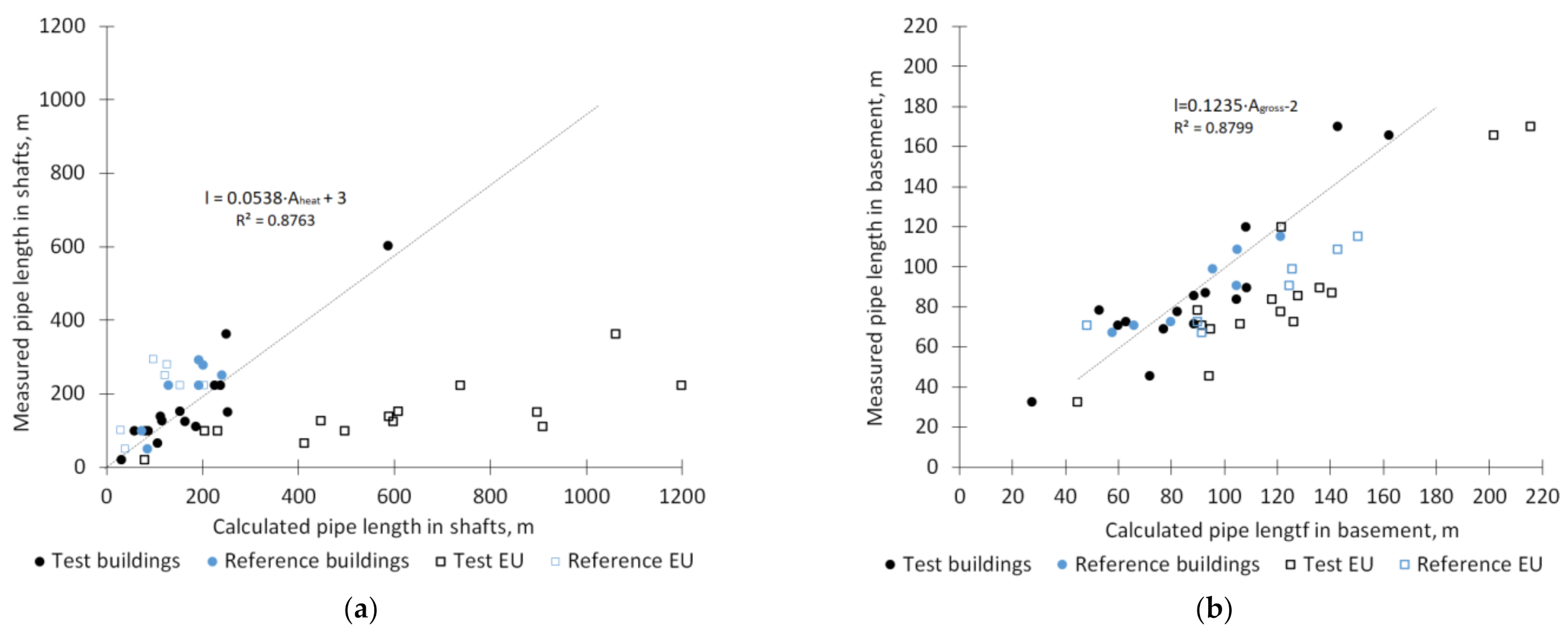
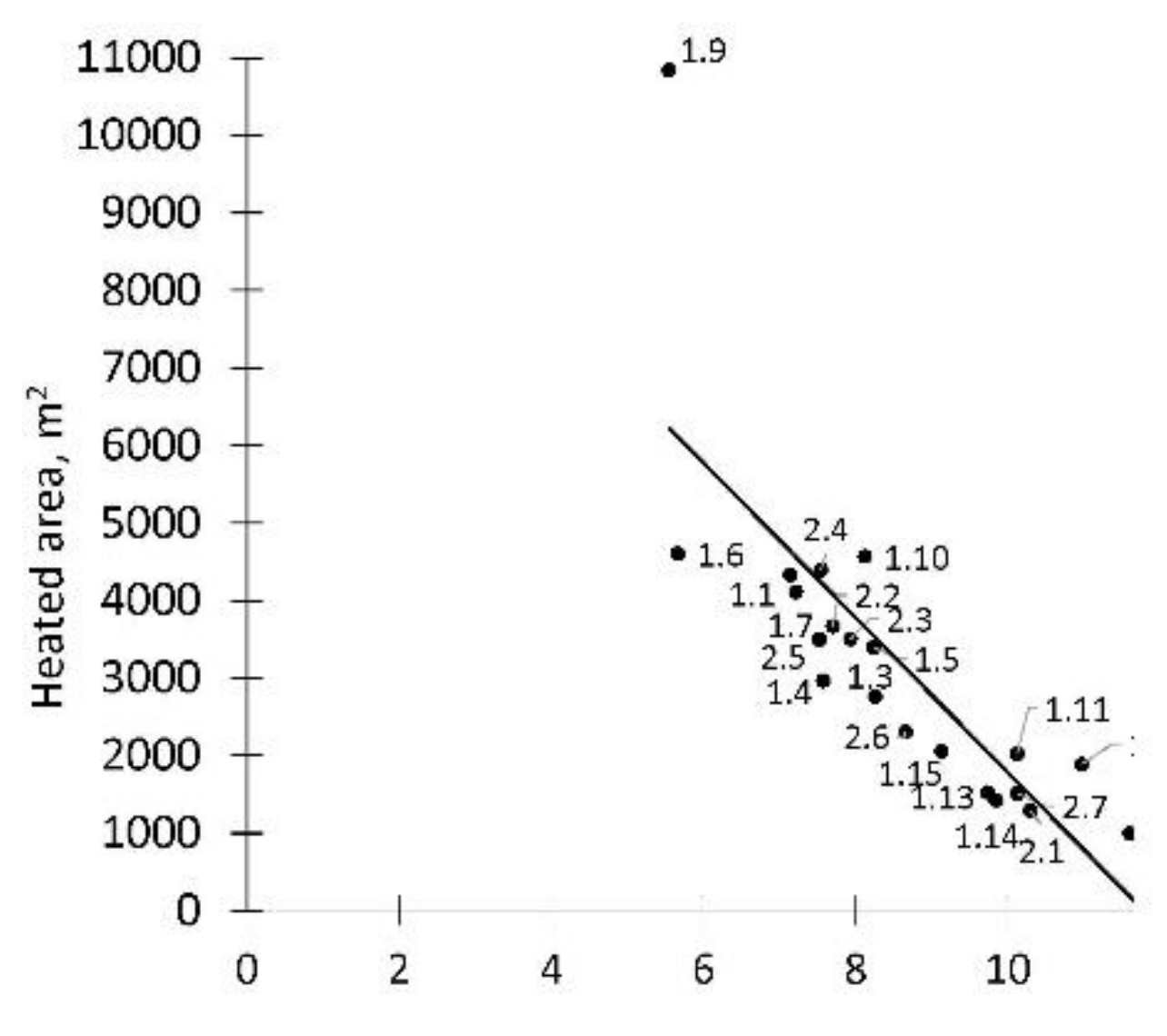
3.2. Pipe Length Calculation
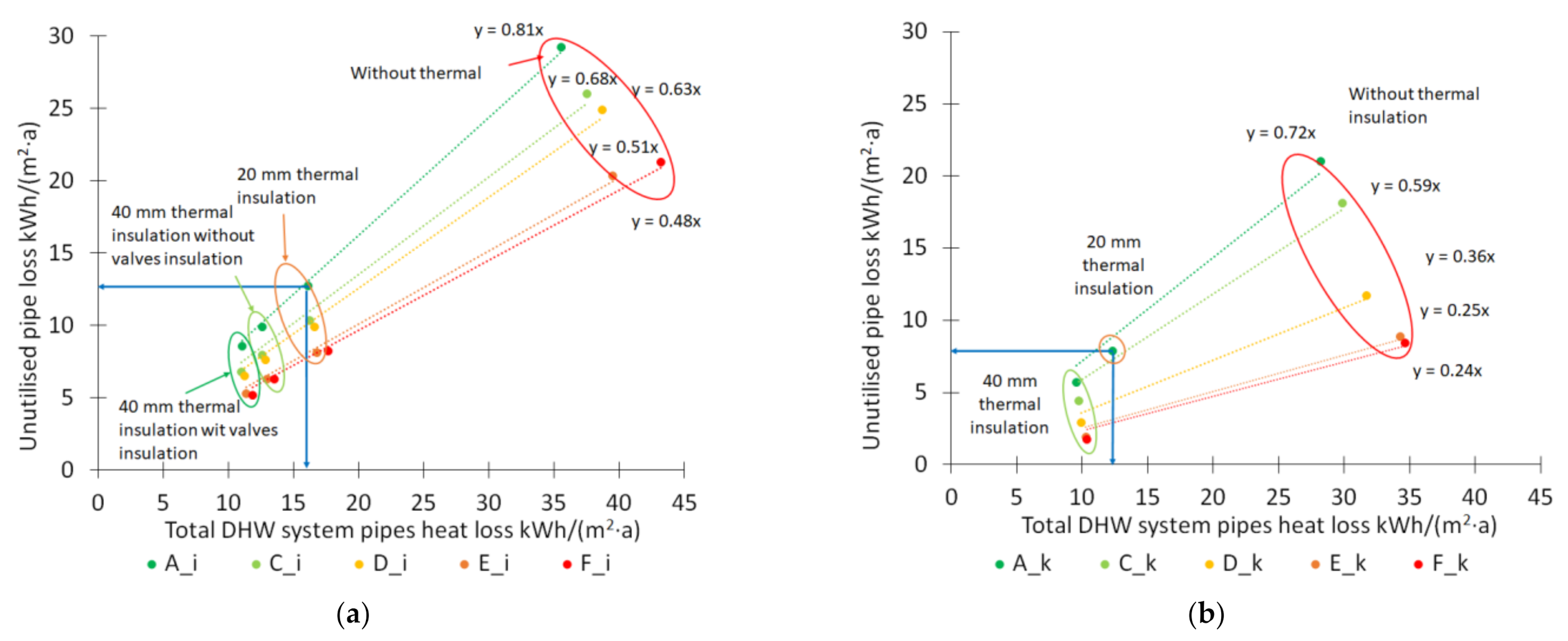
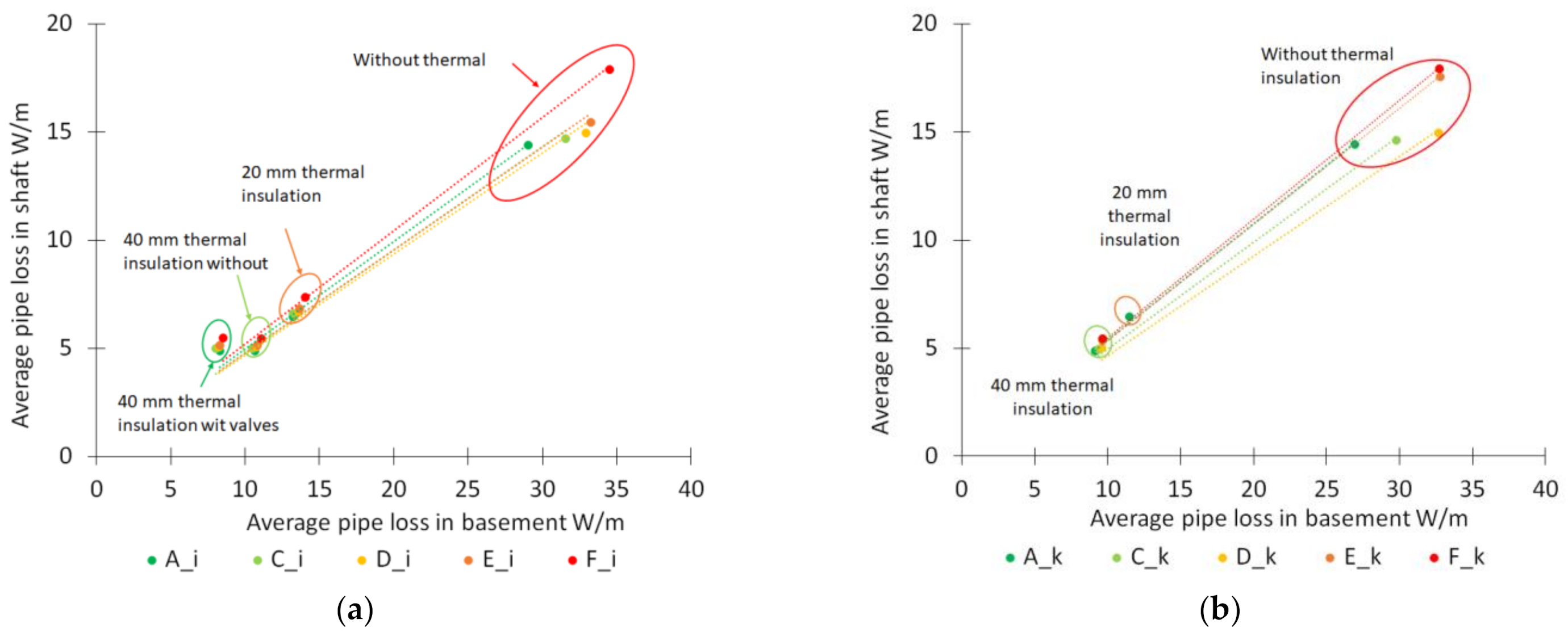
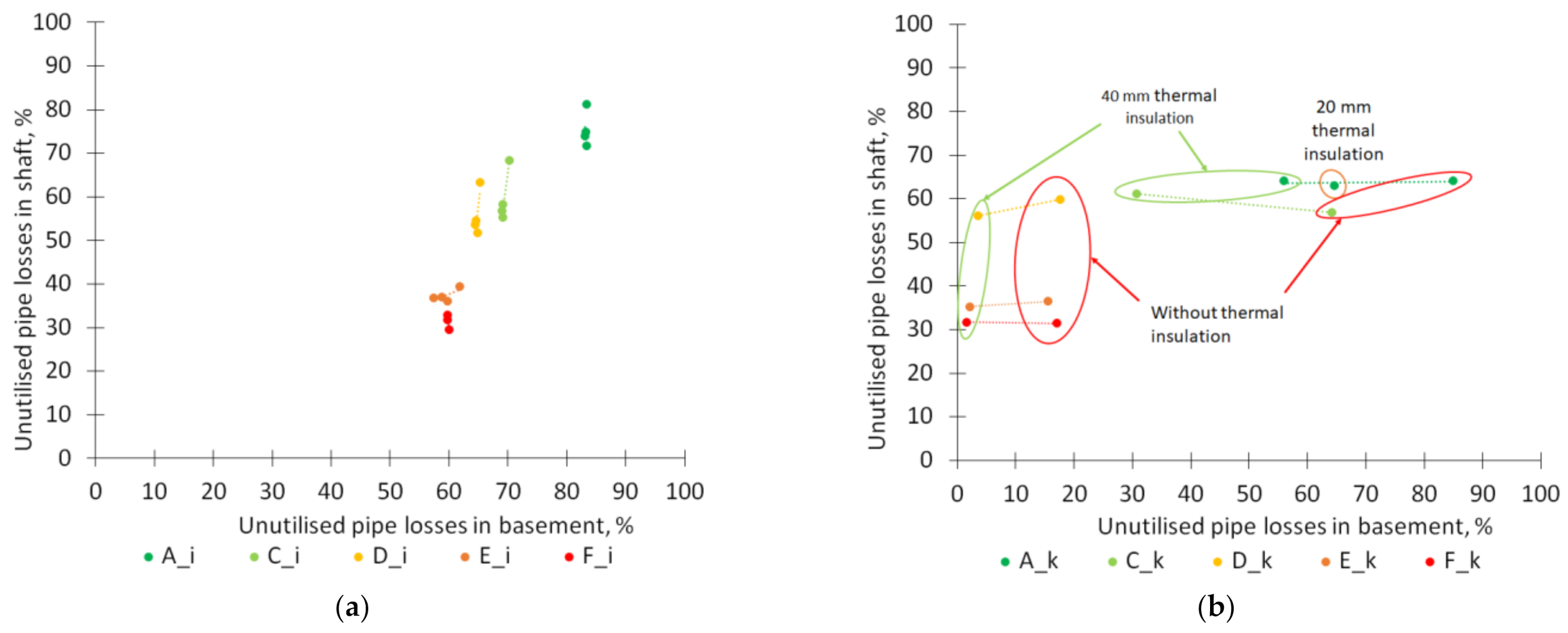
3.3. Parameters Influencing Heat Loss from DHW Circulation Piping
- With different thickness of thermal insultation (0, 20 and 40 mm);
- With and without DHW circulation balancing valve insulation;
- Temperature in basement 21 °C or unheated;
- With different energy performance classes (EPC) (A, C, D, E, and F);
- Circulation pump working time.
3.4. Heat Loss from DHW Piping in Earlier Studied Buildings
3.5. Generating Heat Loss Equation from DHW Piping
4. Discussion
5. Conclusions
- Pipe length is the most important value to use when assessing pipe heat losses in apartment buildings;
- ○
- Pipe length with EN standard equation is not relevant for Estonian apartment buildings:
- ■
- Length and width of buildings in the Estonian Registry of Buildings database is presented as a maximum and is not useful for nonrectangular shaped buildings;
- ■
- Length according to EN 15316-3 standard for pipe gives over-long pipe lengths compared to Estonian apartment buildings;
- ○
- Using floor gross area for calculating basement pipe length gave an average 14% difference from measured pipe length in all buildings;
- ○
- Using the building heating area for calculating vertical shaft pipe lengths gave an average 28.3% difference from measured pipe length in all buildings;
- ○
- With 40 mm thermal insulation on the pipes, heat losses from pipes in an EPC C class basement were 10.8 W/m and in shafts 5.1 W/m, and with 20 mm thermal insulation heat losses were 13.6 W/m in the basement and 6.5 W/m in the shafts.
- Pipe heat loss calculations in the reference building showed that the difference between thermal insulation levels on pipes did not affect how much heat loss from pipes can be utilised as internal heat gain;
- ○
- For EPC class C buildings without basement heating, utilised pipe heat losses were in total 33%, and separately, in basements 30% and in shafts 40%.
- Heat loss from calculated lengths compared between the different thicknesses of thermal pipe insulation was more or less the same in buildings with different EPC classes and the actual value itself was more or less the same, which enables our equations to be used in all EPC classes of buildings.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bøhm, B.; Danig, P. Monitoring the energy consumption in a district heated apartment building in Copenhagen, with specific interest in the thermodynamic performance. Energy Build. 2004, 36, 229–236. [Google Scholar] [CrossRef]
- Bøhm, B. Production and distribution of domestic hot water in selected Danish apartment buildings and institutions. Analysis of consumption, energy efficiency and the significance for energy design requirements of buildings. Energy Convers. Manag. 2013, 67, 152–159. [Google Scholar] [CrossRef]
- Gassel, A. Beiträge zur Berechnung Solarthermischer und Exergieeffizienter Energiesysteme. Ph.D. Thesis, TU Dresden, Dresden, Germany, 1999. [Google Scholar]
- Horváth, M.; Hrabovszky-Horvath, S.; Csoknyai, T. Parametric analysis of solar hot water production in “commi-block” buildings. In Proceedings of the 5th International Youth Conference on Energy (IYCE), Pisa, Italy, 27–30 May 2015; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2015; pp. 1–5. [Google Scholar]
- Zhang, Y.; Bonneville, C.; Wilson, S.; Maroney, M.; Staller, J.; Yun Wei, J. Using Energy Flow Analysis to Assess Energy Savings from Recirculation Controls in Multi-Family Central Domestic Hot Water System. ASHRAE Trans. 2012, 118, 357–366. [Google Scholar]
- Marszal-Pomianowska, A.; Zhang, C.; Pomianowski, M.; Heiselberg, P.; Gram-Hanssen, K.; Hansen, A.R. Simple methodology to estimate the mean hourly and the daily profiles of domestic hot water demand from hourly total heating readings. Energy Build. 2019, 184, 53–64. [Google Scholar] [CrossRef]
- Huhn, R.; Davids, A. Savings potential: Decrease of the circulation losses in centralized drinking water heating systems Einsparpotenziale: Senkung der Zirkulationsverluste in Zentralen Trinkwassererwärmungsanlagen. Euroheat Power/Fernwarme Int. 2008, 37, 38–39. [Google Scholar]
- Kitzberger, T.; Kilian, D.; Kotik, J.; Pröll, T. Comprehensive analysis of the performance and intrinsic energy losses of centralized Domestic Hot Water (DHW) systems in commercial (educational) buildings. Energy Build. 2019, 195, 126–138. [Google Scholar] [CrossRef]
- Mühlbacher, H.; Carter, J. Warmwasserbereitung-Vergleich Zentraler und Dezentraler Warmwasserversorgung; Forschungsstelle für Energiewirtschaft eV (FfE): München, Germany, 2002. [Google Scholar]
- Cholewa, T.; Siuta-Olcha, A.; Anasiewicz, R. On the possibilities to increase energy efficiency of domestic hot water preparation systems in existing buildings—Long term field research. J. Clean. Prod. 2019, 217, 194–203. [Google Scholar] [CrossRef]
- Adam, M.; Walter, D.; Backes, K.; Steinweg, J. Classification of hydraulic designs and hardware-in-the-loop-tests of solar assisted heating systems for multi-family houses. In Proceedings of the 2016 International Energy and Sustainability Conference (IESC), Cologne, Germany, 30 June–1 July 2016; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Ahmed, K.; Pylsy, P.; Kurnitski, J. Hourly consumption profiles of domestic hot water for different occupant groups in dwellings. Sol. Energy 2016, 137, 516–530. [Google Scholar] [CrossRef]
- Navalón, P.S. Evaluation of Heat Losses from a Domestic Hot Water Circulation System. Ph.D. Thesis, University of Gävle, Gävle, Sweden, 2015. [Google Scholar]
- Brand, M. Heating and Domestic Hot Water Systems in Buildings Supplied by Low-Temperature District Heating. Ph.D. Thesis, Technical University of Denmark, Copenhagen, Denmark, 2013. [Google Scholar]
- Grasmanis, D.; Talcis, N.; Greķis, A. Heat Consumption assessment of the domestic hot water systems in the apartment buildings. In Proceedings of the REHVA Annual Conference 2015 “Advanced HVAC and Natural Gas Technologies”, Riga, Latvia, 6–9 May 2015; RTU Press, Riga Technical University Press: Riga, Latvia, 2015; pp. 167–176. [Google Scholar]
- Rocheron, C. Domestic Hot Water—An Energy Approach Application of Heat Pumps for Residential Apartment Buildings. Master’s Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2012. [Google Scholar]
- Hamburg, A.; Kalamees, T. The Influence of Energy Renovation on the Change of Indoor Temperature and Energy Use. Energies 2018, 11, 3179. [Google Scholar] [CrossRef] [Green Version]
- Hamburg, A.; Kalamees, T. Improving the Indoor Climate and Energy Saving in Renovated Apartment Buildings in Estonia. In Proceedings of the Cold Climate HVAC Conference, Kiruna, Sweden, 12–15 March 2018; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2018; pp. 243–251. [Google Scholar]
- Hamburg, A.; Kalamees, T. How well are energy performance objectives being achieved in renovated apartment buildings in Estonia? Energy Build. 2019, 199, 332–341. [Google Scholar] [CrossRef]
- Raide, I.; Kalamees, T.; Mauring, T. Lessons learnt from the first public buildings in Estonia intended to be passive houses. Proc. Estonian Acad. Sci. 2015, 64, 157. [Google Scholar] [CrossRef]
- Arumägi, E.; Kalamees, T. Design of the first net zero energy buildings in Estonia. Sci. Technol. Built Environ. 2016, 22, 1039–1049. [Google Scholar] [CrossRef]
- Attia, S.G.; de Herde, A. Early design simulation tools for net zero energy buildings: A comparison of ten tools. In Proceedings of the 12th International Building Performance Simulation Association, Sydney, Australia, 14–16 November 2011. [Google Scholar]
- European Standards. EN 15316-3. Energy Performance of Buildings—Method for Calculation of System Energy Requirements and System Efficiencies—Part 3: Space Distribution Systems (DHW, Heating and Cooling), Module M3-6, M4-6, M8-6; European Standards: Brussels, Belgium, 2017. [Google Scholar]
- Kuusk, K.; Kalamees, T. nZEB Retrofit of a Concrete Large Panel Apartment Building. Energy Procedia 2015, 78, 985–990. [Google Scholar] [CrossRef] [Green Version]
- Journal of Physics: Conference Series; IOPscience: Bristol, UK, 2013; Volume 132, pp. 1006–1011. [CrossRef]
- Majandus-ja Kommunikatsiooniministeerium. Estonian Registry of Buildings Database. 2021. Available online: www.ehr.ee (accessed on 2 September 2021).
- Davison, A.C.; Hinkley, D.V. Bootstrap Methods and Their Application; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Shalin, P. Modelling and Simulation Methods for Modular Continuous System in Buildings; KTH: Stockholm, Sweden, 1996. [Google Scholar]
- Björsell, N.; Bring, A.; Eriksson, L.; Grozman, P.; Lindgren, M.; Sahlin, P.; Shapovalov, A. IDA indoor climate and energy. In Proceedings of the IBPSA Building Simulation 99 Conference, Kyoto, Japan, 13–15 September 1999; pp. 1–8. [Google Scholar]
- ISO. ISO/DIS 12241 Thermal Insulation for Building Equipment and Industrial Installations—Calculation Rules; ISO: Geneva, Switzerland, 2008. [Google Scholar]
- Hamburg, A.; Kalamees, T. The influence of heat loss from pipes in an unheated basement on the heating energy consumption of an entire typical apartment building. E3S Web Conf. 2020, 172, 12005. [Google Scholar] [CrossRef]
- Ympäristöministeriö, Energiatehokkuus, Rakennuksen energiankulutuksen ja lämmitystehontarpeen laskenta, (Ministry of the Environment, Energy efficiency, Calculation of building energy consumption and heating power demand), Regulation, Helsinki, Finland. 2018.
- 7 RT I, 19.01.2018. MKM määrus nr. 58, Hoonete energiatõhususe arvutamise metoodika (Minister of Economic Affairs and Communications regulation nr. 58, Methodology for calculating the energy performance of buildings). 2018.
- Himpe, E.; Rebollar, J.V.; Janssens, A. Heat losses in collective heat distribution systems: Comparing simplified calculation methods with dynamic simulations. In Proceedings of the 13th International Conference of the International Building Performance Simulation Association (Building Simulation 2013), Chambéry, France, 26–28 August 2013; International Building Performance Simulation Association (IBPSA): Chambery, France, 2013; pp. 3432–3439. [Google Scholar]

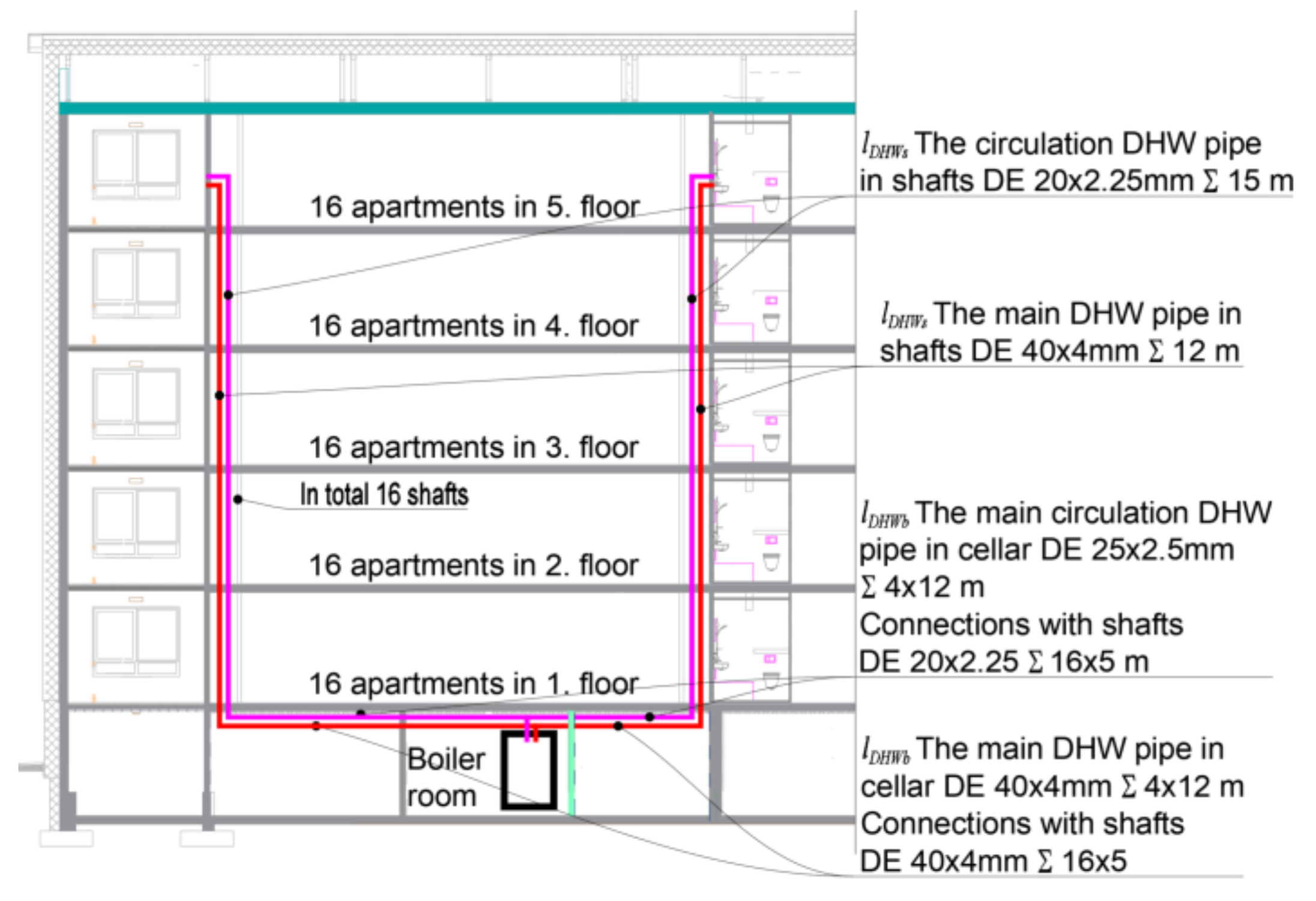
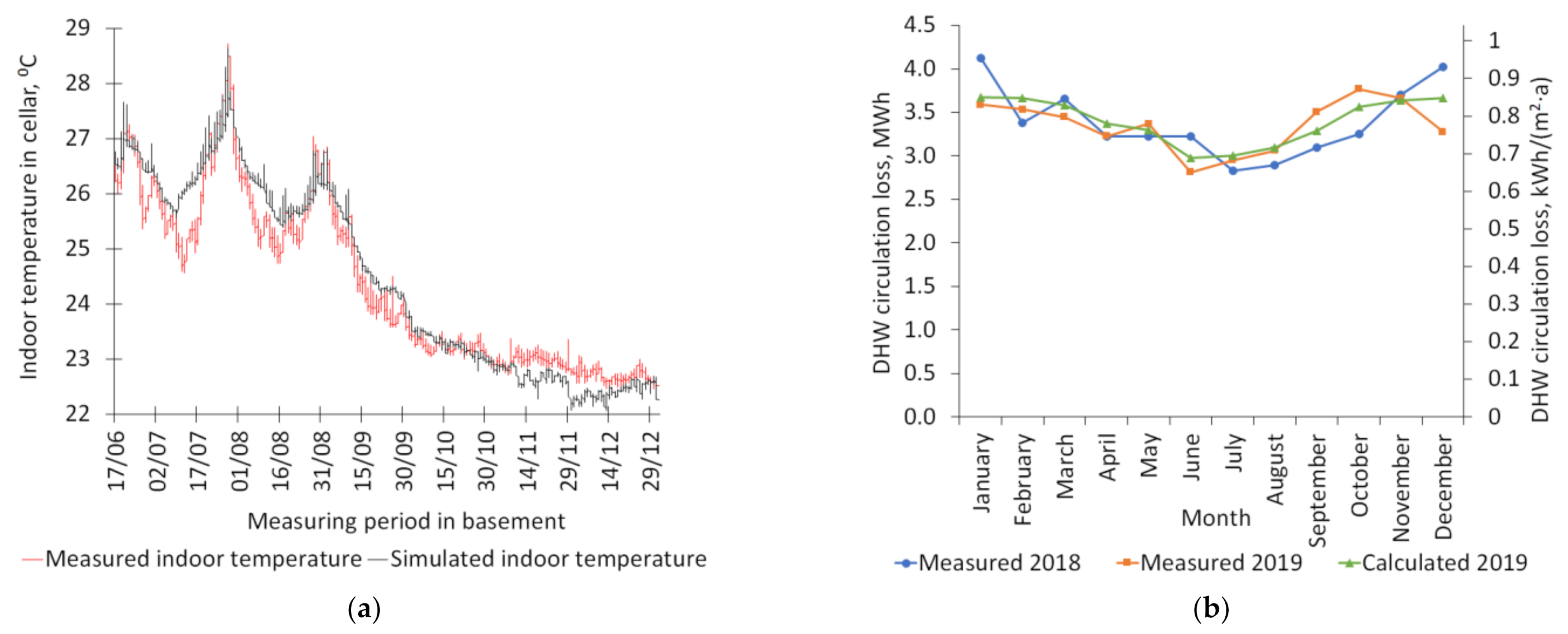

| Characteristic | nZEB Case Building | Test Buildings | Reference Buildings | Earlier Studied Buildings |
|---|---|---|---|---|
| Target | Calibration of model and energy use of DHW | Determination of pipe length equations | Validating of pipe length equation | Validating of DHW heat loss |
| Description | ||||
| No. of buildings | 1 | 15 | 7 | 23 |
| Building’s basic data | Heated area, net area, layout area (floor gross area), volume, length, width, height, number of: floors, apartments, DHW shafts. | |||
| Building pipe length | Detailed 3D BIM and energy simulation model with real length of pipes | Measured length of pipes from 2D-design drawings + onsite survey | Measured length of pipes from 2D-design drawings + onsite survey | |
| A. Length of DHW and DHW circulation pipes | ||||
| Pipe lengths | Detailed simulation with measured pipe lengths | Generating of Equation with real pipe length | Validation of the performance of Equation with real pipe length | Calculated pipe length with generated Equations |
| B. Heat loss of DHW pipes | ||||
| DHW and DHW circulation heat loss | Detailed simulation model, calibrated based on detailed field measurements | Calculated pipe heat loss with measured length, calculated length and assumed measured losses from earlier study | Calculated pipe heat loss with measured length, calculated length and assumed measured losses from earlier study | Measured DHW system energy losses |
| The influence of DHW system heat loss. | Calibrated model calculations with different renovation scenarios | Calculated DHW system unutilised heat loss | Calculated DHW system unutilised heat loss | Calculated DHW system heat loss comparison with measured consumption |
| Code | Construction Material for Walls | Construction Year | Volume | Heating Area | Net Area | Building Gross Area | Length | Width | Apartments per Floor | No. Shafts | No. of Apartments | Perimeter | DHW Pipe Length in Basement | DHW Pipe Length in Shafts |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m3 | m2 | m2 | m2 | m | m | m | m | m | ||||||
| nZEB case building | ||||||||||||||
| 1.1 | Concrete | 1986 | 15757 | 4330 | 4330 | 887 | 57.5 | 16.2 | 16 | 16 | 80 | 147 | 120 | 224 |
| Test buildings | ||||||||||||||
| 1.2 | LWC block | 1974 | 3283 | 998 | 1306 | 438 | 49.0 | 8.8 | 6 | 12 | 18 | 116 | 79 | 101 |
| 1.3 | Concrete | 1975 | 12017 | 2763 | 3378 | 727 | 65.7 | 11.7 | 11 | 11 | 55 | 155 | 86 | 154 |
| 1.4 | Concrete | 1966 | 10696 | 2968 | 3519 | 676 | 61.7 | 12.2 | 12 | 12 | 60 | 148 | 78 | 126 |
| 1.5 | Brick | 1983 | 14252 | 3393 | 4110 | 888 | 61.7 | 18.6 | 10 | 10 | 50 | 161 | 90 | 112 |
| 1.6 | Concrete | 1970 | 16114 | 4606 | 5030 | 593 | 46.8 | 13.4 | 8 | 8 | 72 | 121 | 46 | 151 |
| 1.7 | Concrete | 2017 | 15967 | 4112 | 4112 | 859 | 43.1 | 32.8 | 15 | 15 | 75 | 152 | 84 | 225 |
| 1.8 | LWC block | 1986 | 7944 | 1887 | 2415 | 762 | 72.0 | 12.0 | 8 | 8 | 24 | 168 | 87 | 67 |
| 1.9 | Concrete | 1981 | 35403 | 10840 | 10840 | 1323 | 101.0 | 13.2 | 16 | 24 | 144 | 228 | 166 | 605 |
| 1.10 | Concrete | 1979 | 18400 | 4567 | 5933 | 1167 | 109.9 | 12.2 | 18 | 26 | 90 | 244 | 171 | 364 |
| 1.11 | Brick | 1977 | 11143 | 2022 | 3211 | 728 | 51.9 | 14.3 | 10 | 10 | 50 | 132 | 72 | 140 |
| 1.12 | Brick | 1970 | 1844 | 498 | 498 | 234 | 23.4 | 10.5 | 4 | 4 | 8 | 68 | 33 | 23 |
| 1.13 | Brick | 1972 | 5495 | 1526 | 1172 | 520 | 57.7 | 18.1 | 6 | 12 | 18 | 152 | 73 | 101 |
| 1.14 | LWC block | 1979 | 5211 | 1426 | 1036 | 495 | 48.8 | 9.9 | 6 | 12 | 18 | 117 | 71 | 101 |
| 1.15 | LWC block | 1975 | 8945 | 2054 | 2448 | 634 | 49.2 | 11.2 | 9 | 9 | 45 | 121 | 69 | 129 |
| Reference buildings | ||||||||||||||
| 2.1 | Concrete | 1977 | 3959 | 1291 | 1959 | 478 | 48.8 | 9.9 | 6 | 12 | 18 | 117 | 68 | 101 |
| 2.2 | Concrete | 1986 | 12763 | 3669 | 3669 | 859 | 62.3 | 13.1 | 12 | 20 | 60 | 151 | 91 | 280 |
| 2.3 | Concrete | 1964 | 13833 | 3501 | 4494 | 861 | 73.0 | 12.0 | 16 | 16 | 80 | 170 | 109 | 224 |
| 2.4 | Concrete | 1977 | 16412 | 4399 | 4399 | 993 | 75.9 | 12.7 | 12 | 18 | 60 | 177 | 115 | 252 |
| 2.5 | Brick | 1976 | 13341 | 3495 | 3495 | 786 | 62.3 | 13.6 | 9 | 21 | 45 | 152 | 99 | 294 |
| 2.6 | Brick | 1975 | 10484 | 2309 | 2868 | 657 | 33.2 | 32.0 | 8 | 16 | 40 | 130 | 73 | 224 |
| 2.7 | LWC block | 1987 | 5979 | 1508 | 1862 | 545 | 23.8 | 13.5 | 6 | 6 | 18 | 75 | 71 | 50 |
| Pipe’s Outer Diameter, mm | 50 | 40 | 25 | 20 |
|---|---|---|---|---|
| Thermal pipe insulation thickness, mm | Pipe’s linear thermal transmittance Ψ (W/m·K) | |||
| 40 | 0.25 | 0.22 | 0.17 | 0.15 |
| 20 | 0.37 | 0.32 | 0.23 | 0.21 |
| 0 | 1.22 | 0.98 | 0.62 | 0.50 |
| Energy Performance of Building—Primary Energy (PE) Use and Energy Performance Certificate (EPC) Class | ||||||
|---|---|---|---|---|---|---|
| EPC “A *” and “B” PE ≤ 125 kWh/(m2·a) | EPC “C” PE ≤ 150 kWh/(m2·a) | EPC “D” PE ≤ 180 kWh/(m2·a) | EPC “E” PE ≤ 220 kWh/(m2·a) | EPC “F” PE ≤ 280 kWh/(m2·a) | ||
| Thermal transmittance of building envelope U, W/(m2·K) | External wall | 0.13 | 0.17 | 0.22 | 0.22 | 1.0 |
| Basement wall | 0.10 | 0.21 | 0.61 | 0.61 | 0.61 | |
| Basement floor | 0.23 | 0.38 | 0.39 | 0.39 | 0.39 | |
| Roof | 0.11 | 0.17 | 0.17 | 0.22 | 0.76 | |
| Window | 0.82 | 1.0 | 1.2 | 1.4 | 1.7 | |
| Ventilation strategy | Apartments | Mechanical ventilation 0.5 L/(s·m2), ventilation heat recovery (VHR) 0.8. | 0.5 L/(s·m2) no VHR | 0.35 L/(s·m2) no VHR | ||
| Common rooms and heated basement | Mechanical ventilation 0.5 L/(s·m2), VHR 0.8. | No VHR 0.5 L/(s·m2) | ||||
| In unheated room | 0.15 L/(s·m2) without heat recovery | |||||
| Factor | Equation to Calculate the Pipe Length, m | R2 | Difference between Measured and Calculated, % | MBE (Mean Bias Error) | RMSE (Root Mean Square Error) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Test Buildings | Test Buildings | Reference Buildings | All Buildings Average | Test Buildings | Reference Buildings | All Buildings Average | Test Buildings | Reference Buildings | All Buildings Average | ||
| One parameter model | Pipe length in basement | ||||||||||
| x = Volume | l = 0.0034·x + 46 | 0.56 | 23.8 | 9.2 | 19.2 | −0.57 | −5.8 | −2.2 | 24.4 | 9.5 | 20.8 |
| x = Heating area | l = 0.0109·x + 53 | 0.52 | 23.2 | 6.8 | 18.0 | −0.04 | −4.6 | −1.5 | 25.4 | 9.2 | 21.6 |
| x = Net area | l = 0.0112·x + 49 | 0.57 | 24.6 | 7.8 | 19.2 | 0.03 | −4.5 | −1.4 | 23.9 | 9.4 | 20.5 |
| x = Gross area | l = 0.1235·x − 2 | 0.82 | 17.1 | 8.4 | 14.4 | −0.01 | 0.2 | 0.1 | 15.7 | 7.7 | 13.6 |
| x = Apartments per floor | l = 7.2845·x + 13 | 0.68 | 22.5 | 14.5 | 19.9 | 0.00 | −4.6 | −1.5 | 1.0 | 14.6 | 18.9 |
| x = No. shafts | l = 6.1258·x + 11 | 0.89 | 13.0 | 28.7 | 18.0 | 0.00 | 17.1 | 5.4 | 12.3 | 28.4 | 18.9 |
| x = Perimeter of building | l = 0.8015·x − 31 | 0.85 | 15.6 | 11.8 | 14.4 | 0.00 | −8.9 | −2.8 | 14.1 | 16.4 | 14.9 |
| One parameter model | Pipe length in shafts | ||||||||||
| x = Volume | l = 0.0163·x − 24 | 0.87 | 33.9 | 31.6 | 33.2 | −0.1 | −48.4 | −15.5 | 50.7 | 65.2 | 55.7 |
| x = Heating area | l = 0.0538·x + 3 | 0.88 | 26.8 | 31.6 | 28.3 | 0.1 | −45.8 | −14.5 | 48.7 | 65.0 | 54.4 |
| x = Net area | l = 0.0522·x − 11 | 0.87 | 33.9 | 29.9 | 32.6 | −0.1 | −54.1 | 11.3 | 50.7 | 71.9 | 60.0 |
| x = Gross area | l = 0.4471·x − 151 | 0.74 | 55.9 | 32.5 | 48.5 | 0.0 | −23.8 | −7.6 | 69.9 | 56.8 | 66.0 |
| x = Apartments per floor | l = 25.768·x − 91 | 0.59 | 36.9 | 34.7 | 36.2 | 0.0 | −41.1 | −13.1 | 88.2 | 85.8 | 87.4 |
| x = Tot apartments | l = 3.6964·x − 24 | 0.86 | 34.7 | 34.7 | 34.7 | 0.0 | −58.2 | −18.5 | 53.5 | 83.3 | 64.5 |
| x = No shafts | l = 21.648·x − 98 | 0.77 | 36.5 | 25.1 | 32.8 | 0.0 | 35.5 | 11.3 | 66.1 | 44.4 | 60.0 |
| x = Perimeter | l = 2.5985·x − 211 | 0.62 | 59.3 | 37.4 | 52.3 | 0.0 | −54.1 | −17.2 | 85.0 | 71.9 | 81.1 |
| Two parameter model | Pipe length in basement | ||||||||||
| x = Gross area and y = No. shafts | l = 1.04236·x + 3.56701·y | 0.94 | 9.7 | 18.4 | 12.5 | 0.8 | 10.9 | 4.0 | 9.4 | 18.9 | 13.2 |
| x = No. shafts and y = Perimeter | l = 3.02566·x + 0.44814·y − 16 | 0.96 | 10.3 | 18.4 | 12.9 | 0.5 | 4.1 | 1.7 | 9.7 | 18.2 | 13.0 |
| EN 15316-3 | 42.6 | 30.6 | 38.8 | 33.3 | 20.6 | 29.3 | 36.8 | 27.9 | 34.2 | ||
| Two parameter model | Pipe length in shafts | ||||||||||
| x = no. shafts and y = heating area | l = 10.1399·x + 0.03717·y − 67 | 0.94 | 23.8 | 14.3 | 9.8 | 0.0 | −5.7 | −1.8 | 20.2 | 20.6 | 20.4 |
| EN 15316-3 | 325.3 | 144.7 | 267.8 | 515.2 | −94.6 | 321.2 | 610.3 | 114.3 | 508.0 | ||
| Insulation of Pipes | Basement is Unheated | |||
|---|---|---|---|---|
| Basement losses | qa.basement, W/m | Qunut. basement, % | ||
| EPC “A” | EPC “C” | |||
| 40 mm (insulated valves) | 8.3 | 83 | 70 | |
| 40 mm (uninsulated valves) | 10.8 | |||
| 20 mm | 13.6 | |||
| Basement is heated +21 °C | ||||
| qa.basement, W/m | Qunut. basement, % | |||
| 40 mm (insulated valves) | 7.0 | 56 | 48 | |
| 40 mm (uninsulated valves) | 9.2 | |||
| 20 | 11.5 | |||
| Shaft losses | qa.shaft, W/m | Qunut. shaft, % | ||
| 40 mm | 5.1 | 69 | 59 | |
| 20 mm | 6.8 | |||
| 0 mm | 15.5 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamburg, A.; Mikola, A.; Parts, T.-M.; Kalamees, T. Heat Loss Due to Domestic Hot Water Pipes. Energies 2021, 14, 6446. https://doi.org/10.3390/en14206446
Hamburg A, Mikola A, Parts T-M, Kalamees T. Heat Loss Due to Domestic Hot Water Pipes. Energies. 2021; 14(20):6446. https://doi.org/10.3390/en14206446
Chicago/Turabian StyleHamburg, Anti, Alo Mikola, Tuule-Mall Parts, and Targo Kalamees. 2021. "Heat Loss Due to Domestic Hot Water Pipes" Energies 14, no. 20: 6446. https://doi.org/10.3390/en14206446
APA StyleHamburg, A., Mikola, A., Parts, T.-M., & Kalamees, T. (2021). Heat Loss Due to Domestic Hot Water Pipes. Energies, 14(20), 6446. https://doi.org/10.3390/en14206446






