1. Introduction
Among the Sustainable Development Goals (SDGs) established by the United Nations General Assembly in 2015 [
1], SDG 7 aims at affordable, reliable, sustainable and modern energy access for all. Microgrids are a key technology to this end, and have seen recently remarkable expansion in isolated rural areas around the world with limited or no access to the main electric grid. The typical standalone microgrid utilizes renewable or other local energy sources to provide electricity in places where long-distance power transmission and substantial grid investments are deemed uneconomical [
2]. An irreplaceable component of these miniature power grids is the energy storage system (ESS), whose main role is to ensure power quality and energy balance between the intermittent supply and demand [
3,
4]. Batteries are the most widely used energy storage technology in microgrids, mainly due to their scalability, modularity and limited maintenance needs. Lead–acid batteries, in particular, remain to this day the most commonly found battery technology in operating microgrids, being the most commercially mature. A big challenge in these ESS, however, is battery degradation due to deep discharge and surge currents often found in standalone microgrids supplied by intermittent renewables supply, such as solar [
5]. For example, lead–acid batteries under high charge/discharge rates suffer from the formation of smaller sulphate crystals that lead to inhomogeneous current distribution and increased internal resistance, all of which have a negative impact on battery life [
6]. To this day, the longevity and associated replacement costs of batteries remain one of the most critical factors for the economic viability of an off-grid microgrid investment.
To overcome these challenges, the scientific community has explored in the last decade how to hybridize a battery ESS with other storage technologies, such as supercapacitors [
7,
8,
9,
10,
11,
12,
13,
14], fuel cells [
15,
16] and flywheels [
17], to come up with a more reliable hybrid energy storage system (HESS) that features longer lifespan and higher resistance to degradation. Supercapacitors (or ultracapacitors) are deemed among the most suitable coupling candidates, as they exhibit high power density (though low energy density) and complementary characteristics to electrochemical batteries [
18,
19]. They can readily support high charge/discharge rates as often as required with negligible impact to their life, which typically exceeds a decade [
20]. For this reason, they couple nicely with batteries in absorbing the sudden changes in power demand that allows for a smoother power profile to the batteries and reduced deterioration. Furthermore, the two energy storage technologies exhibit relatively similar operating principles as they are both electrochemical devices, which translates to similar low set-up costs [
2]. Furthermore, the long-term operation and maintenance (O&M) costs of supercapacitors are lower than those of batteries [
21]. This paper takes a deep look on how to hybridize an ESS with lead–acid batteries and supercapacitors, providing recommendations for the topology selection, the design of the control scheme, the battery degradation modeling and economic viability analysis of the investment.
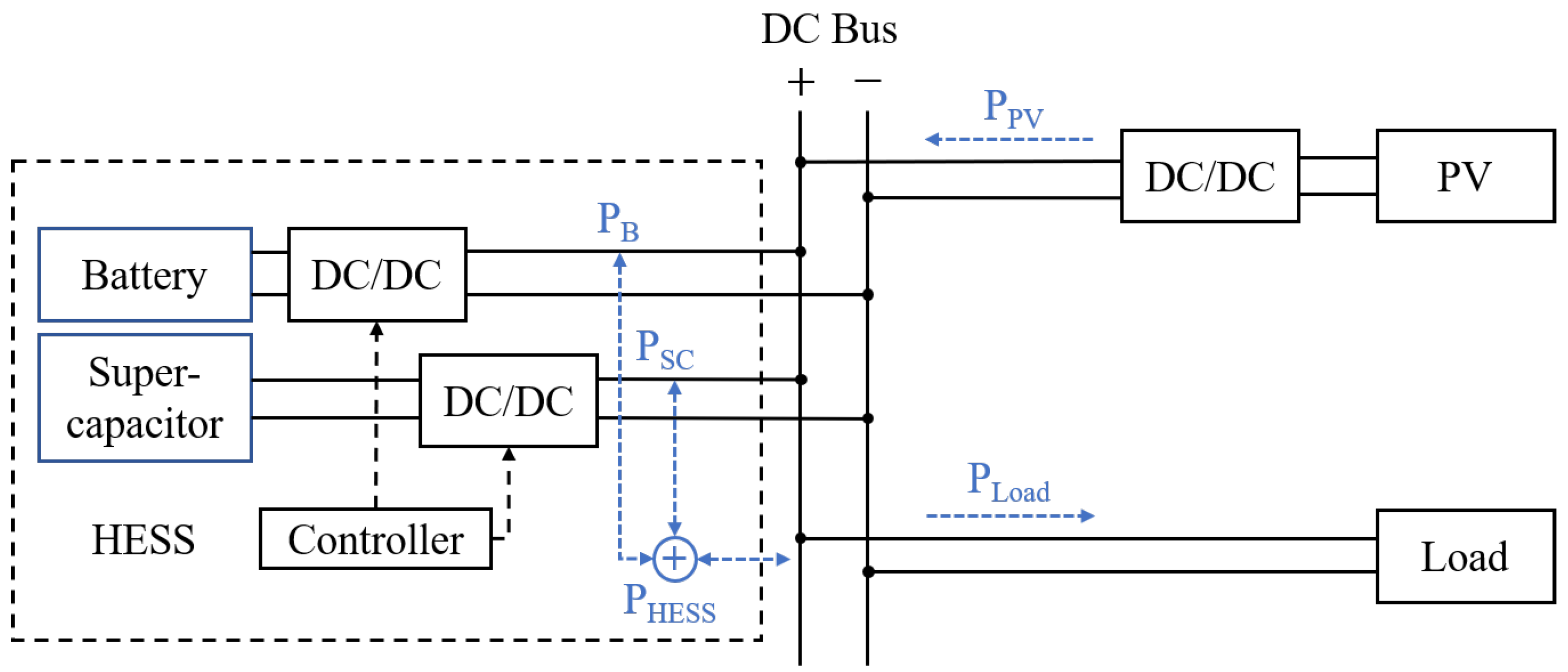
The state of the art in HESS topologies involves mainly three different configurations of batteries and supercapacitors: passive, semi-active and fully active [
2,
7]. The most appropriate topology for an application is selected based on factors such as the set-up cost, efficiency, controllability, system complexity and utilization rate. The passive HESS is the simplest and cheapest topology, according to which the batteries and supercapacitors are directly coupled in parallel at the DC link without any power electronics or control [
8,
9]; this approach is widely applied in high voltage ESS, benefiting from low internal losses and reduced system complexity. However, this way the supercapacitors voltage varies little and their capacity is severely underutilized, which entails only limited extension of the battery life. Furthermore, this approach faces also challenges related to impedance matching between the batteries and supercapacitors. The semi-active configuration, on the other hand, employs power electronics in either batteries or supercapacitors—not both—to expand the operating region of the latter [
10,
11]. With this approach, one of the two storage devices is effectively isolated, thus allowing for more flexible power allocation between the two. Nonetheless, the passive element may suffer from surge currents—if it is the battery—or cause bus voltage fluctuation and negatively impact the power quality—if it is the supercapacitors. The third option of fully active configuration tackles all these issues. Usually a parallel connection is adopted [
5,
12,
13,
14], but cascade implementations are also reported [
22]. The big gain with this topology is effective decoupling of the two components permitting independent control during operation and separate sizing at the design phase. Especially for DC standalone microgrids, this is a viable option for getting the energy storage mix right and extending the HESS lifespan as much as possible. It is worth noting that there are some recent alternatives that involve distributed hybridization combined with active balancing, achieved by incorporating supercapacitors into the balancing bus in order to enable cell-level hybridization [
23]. However, this is still a new and more complex solution, so far targeted only at Li-ion batteries in e-mobility applications. Therefore, this paper adopts the fully active HESS method as the most appropriate for isolated DC microgrids.
Various philosophies exist in the literature regarding the control strategy of fully active HESS to allocate the power flows between the batteries and supercapacitors and maintain the system stability. These control strategies, commonly referred to as energy management systems (EMS), may involve power filtering [
5,
14,
24,
25,
26], deterministic rule-based control [
13,
27], fuzzy logic [
10,
28] and optimization-based control [
29,
30,
31]. In [
28], a fuzzy logic rule-based control is applied to a HESS to ensure that the ESS elements operate in the safe region. Alternatives employing neural networks [
29] and model predictive control [
30,
31] are based on multi-objective or cost functions that aim to optimize the power allocation. A combination of the rule-based concept with optimization algorithms is proposed in [
27]. However, the aforementioned approaches employ sophisticated algorithms that require large amounts of input data and complex mathematical calculations, which have acted as barriers towards wider adoption. By contrast, the power filtering approach has proven quite popular, as it is both effective and easy to implement. It has been also shown that a simple filter-based control is effective in off-line sizing applications as well, yielding very similar results to more complex, non-causal, optimization control approaches as long as battery model accounts for sufficiently complex dynamics [
32]. Given these considerations, this paper focuses on the power filtering method.
There are many studies on power filtering in the literature. Somayajula et al. in [
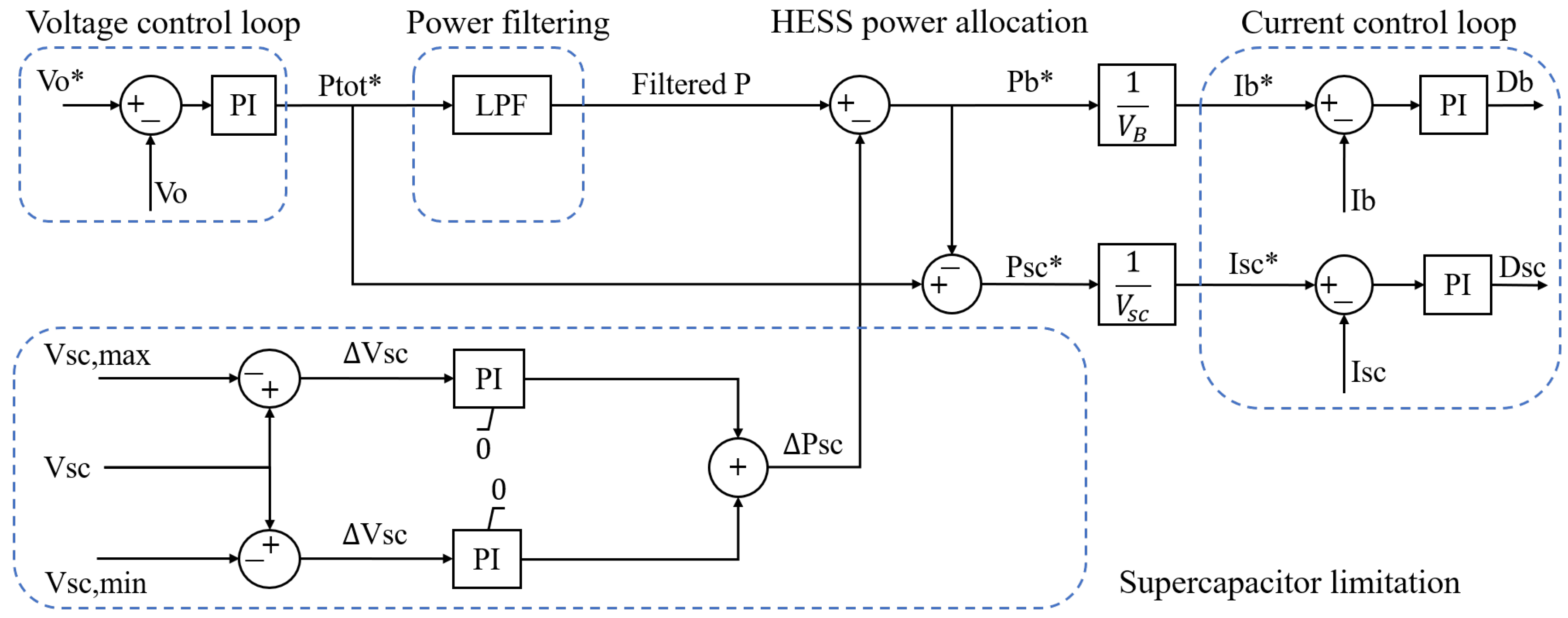
33] demonstrated an active supercapacitor control scheme to achieve smoothing of intermittent renewables generation; the adopted cascade control comprising an outer voltage loop and an inner current loop has been also applied to battery-supercapacitor hybrid systems to ensure power quality. Decoupling the high frequency part of the power control using a first-order low-pass filter (LPF) is proposed in [
5,
14,
24,
25]. However, these studies do not properly consider the safe operating region of the ESS components. Especially for the supercapacitors, their low energy density and high charge/discharge rates lead to highly volatile voltage; if not properly contained within the safety limits, this may result in irreversible damage if overcharged (e.g., voltage exceeding the structural limits) or power converter malfunction if left uncharged (e.g., power converter not managing to step-up the low input voltage). To this end, State of Charge (SoC) controllers are proposed in [
26,
34], which however aim to maintain the energy of the supercapacitors around the reference level and do not directly control the voltage. This may occasionally result in voltage out of limits due to SoC miscalculation caused by various factors, such as parasitic resistances or capacitance deviation due to aging and deterioration. To this day, a complete control scheme for hybrid batteries-supercapacitors systems based on power filtering that strictly adheres to the supercapacitor voltage limits is missing from the literature.
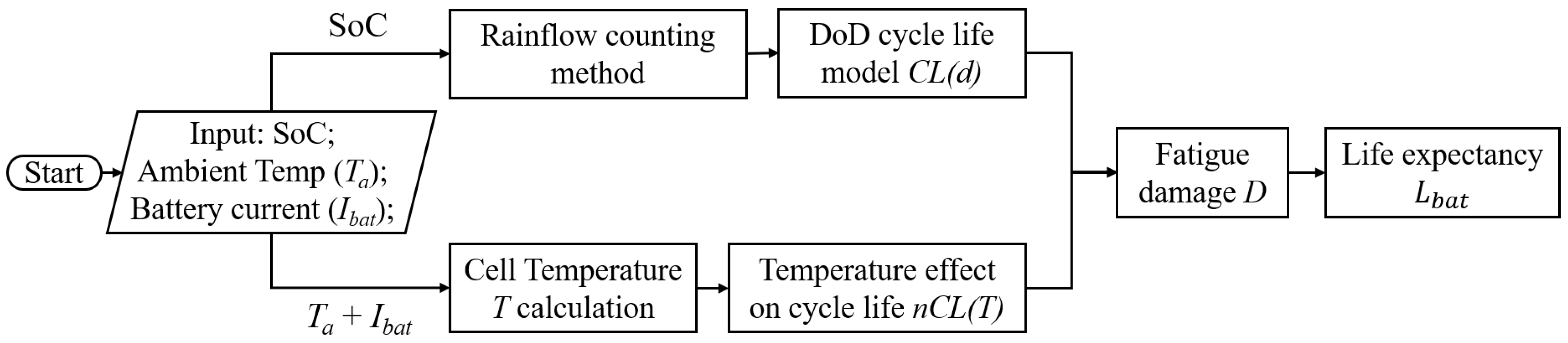
To evaluate the contribution of the hybridization to the battery lifespan, the battery degradation needs to be captured and modeled. There are three different degradation modeling philosophies in the literature: physical-mechanistic models, empirical models and data-driven models [
35,
36,
37]. Physical-mechanistic models are generally based on electrochemical aging processes inside the battery and involve physics-inspired differential equations. For example, Dufo-López et al. in [
35] consider the phenomena of internal corrosion of the battery and aging of the active material to quantify the capacity loss. Although very well-aligned with the physics, these models require many unknown parameters and laborious computations that limit their applicability only to research purposes. The empirical models, on the other hand, entail simpler mathematical functions and coefficients extracted from fitting to experimental results. This makes this approach more effective and practical, except that it requires lots of experimental data to capture a wide range of operating conditions and degradation factors. Making assumptions for untested conditions, to make up for missing data, may introduce uncertainty in the results [
36]. A popular extension of this category are the cycle-counting models [
38]; by adopting the principle of fatigue damage, these models measure the degradation for each cycle of use assuming that the aging factors are independent and cumulative. This allows for a more abstract and universal model structure that relies on limited empirical information usually available in the manufacturer datasheet. Examples of such quantitative cycle-counting models may be found in [
6,
14,
22,
39,
40,
41,
42]. The third category of data-driven degradation models apply statistical analysis and machine learning on a large database to predict the battery status and extract patterns to quantify the lifespan [
37,
43]. These methods are not yet widely used due to their dependence on large datasets and sophisticated implementation. This paper, therefore, adopts the cycle-counting empirical approach due to practicality and wide acceptance in the field.
The battery ages and degrades over time mainly due to (i) calendar aging, i.e., capacity decrease under idle conditions, and (ii) cycle life aging, i.e., degradation during usage [
44]. In standalone microgrids, the ESS is in continuous operation and the latter type of aging prevails; this is why the degradation model of this paper focuses on cycle life aging, as generally done in HESS studies. This type of deterioration can be manifested as corrosion of positive grid, hard/irreversible sulfation and shedding [
45]. The most prevalent failure mode for lead–acid batteries in standalone stationary systems is the former, also known as anodic corrosion [
46], which used to be a major problem in early design, thereafter overcome by the adoption of improved grid alloys. The corrosion rate is accelerated by high temperatures, extreme voltages and cycling operation (versus constant current operation) [
46]. Primary factors of this degradation are the depth of discharge (DoD) (i.e., how deeply the battery is discharged), the charge/discharge rates and the battery’s operating temperature [
6]. Most relevant models take into account only the DoD factor and employ a cycle-counting method, such as the rainflow counting method [
6,
40], to capture the number and depth of the cycles [
42,
47]. However, these models are designed for moderate and deep discharge cycles (e.g., more than 10%) and may fail to accurately capture the effect of smaller cycles, i.e., microcycles, often found in off-grid microgrids with irregular power flows due to intermittent supply and demand [
14,
22]. The case study of this paper show that it is imperative to employ a microcycles DoD model when there is access to high time-resolution electricity data (e.g., second resolution) in order to accurately capture the DoD degradation. Furthermore, battery temperature is also an important stress factor to battery degradation, usually studied separately from the DoD effect [
48]. The investigation in this paper demonstrates that the two factors are strongly related in the presence of microcycles and rapidly changing battery currents. Narayan et al. [
38] have proposed a model that combines both DoD and temperature effects, albeit following an alternative dynamic capacity fading approach that is too complicated for classical cycle counting and fundamentally differs from the aforementioned mainstream DoD models. There is still a need in the literature for a lead–acid battery degradation model that accounts for the combined effect of microcycles DoD and temperature.
In applications of lead–acid battery and supercapacitor hybrid systems, the selection of energy storage components mainly depends on the availability, system size and cost. Lead–acid batteries are the industry standard for small-scale standalone photovoltaic (PV) systems, both in valve-regulated and flooded deep-cycle designs [
49]. The batteries are usually connected in series to meet the system voltage requirements, and then several strings are added in parallel to meet the required capacity. Twelve-volt batteries are considered the most cost-effective solution for systems comprising up to 4–6 parallel strings, and two-volt batteries are usually preferred for larger systems. Suggestions on the selection of lead–acid battery types in different scenarios are given in [
49], where there is a need to strike a balance between lifespan, cost and energy density. The supercapacitors are commercially available in modules, consisting of several cells connected in series; the maximum voltage of a single cell is usually 2.7 V. For the selection of supercapacitors, the capacity is determined by the maximum energy variation required by the system and its operating voltage range [
26]. As supercapacitors are much more expensive than batteries, a thorough cost-benefit analysis should take place to come up with the appropriate size of the two components.
The aim of this paper is to propose a complete methodology to hybridize a lead–acid battery ESS with supercapacitors for standalone DC microgrids. A new power allocation control scheme and battery degradation model are proposed to accurately capture and maximize the battery life extension due to hybridization. A thorough techno-economic analysis takes place based on a 90-day electricity dataset from a real-life 4.8 kW standalone microgrid installed in rural India, to determine the viability of the hybridization at six different scenarios. The main novel points of this study are as follows:
A complete ESS hybridization methodology is developed, including the control design, battery degradation and economic viability analysis, while the results are based on data from a real-life DC microgrid.
A new power allocation control scheme is proposed, based on power filtering that strictly abides by the supercapacitors’ voltage operating limits.
A new degradation mechanism model for lead–acid batteries (or simply "battery degradation model") is introduced that accounts for the combined effect of microcycles DoD and battery temperature, appropriate for high time-resolution profiles.
The structure of the paper is as follows.
Section 2 presents the control scheme and power filtering method that respects the supercapacitors’ voltage limits, while the new battery degradation model that accounts for both DoD and temperature impact is given in
Section 3. In
Section 4, the real-life case study of this paper is detailed, followed by a sensitivity analysis on the thermal parameters.
Section 5 discusses the economic benefit from the hybridization at six different scenarios and
Section 6 concludes this study.
5. Economic Analysis and Discussion
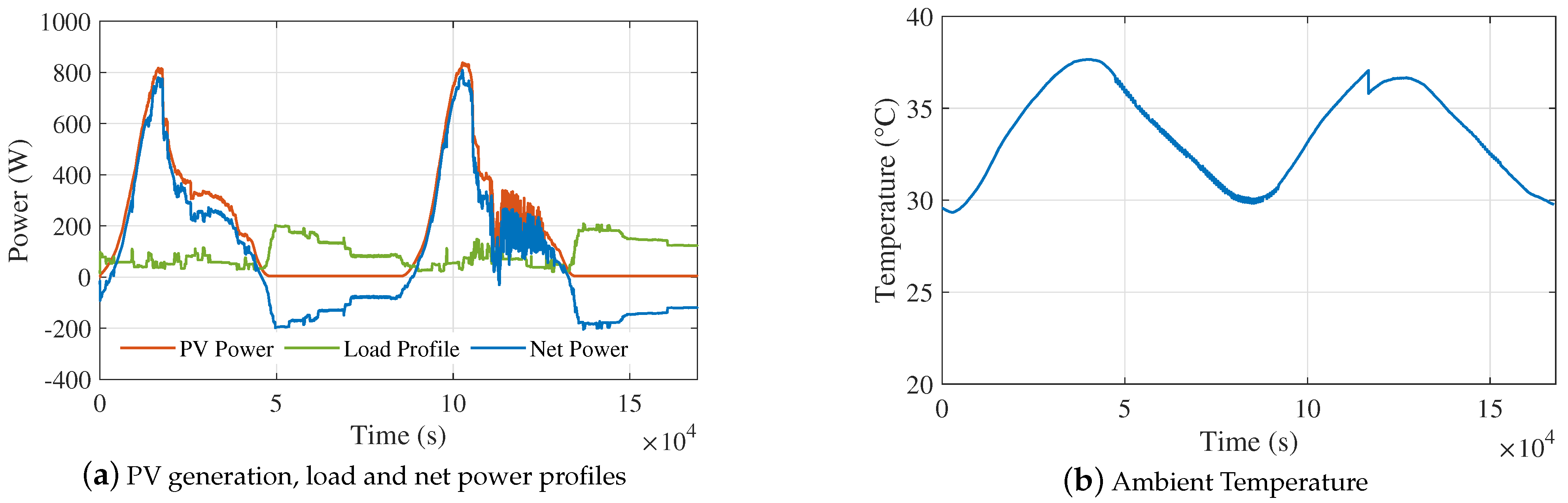
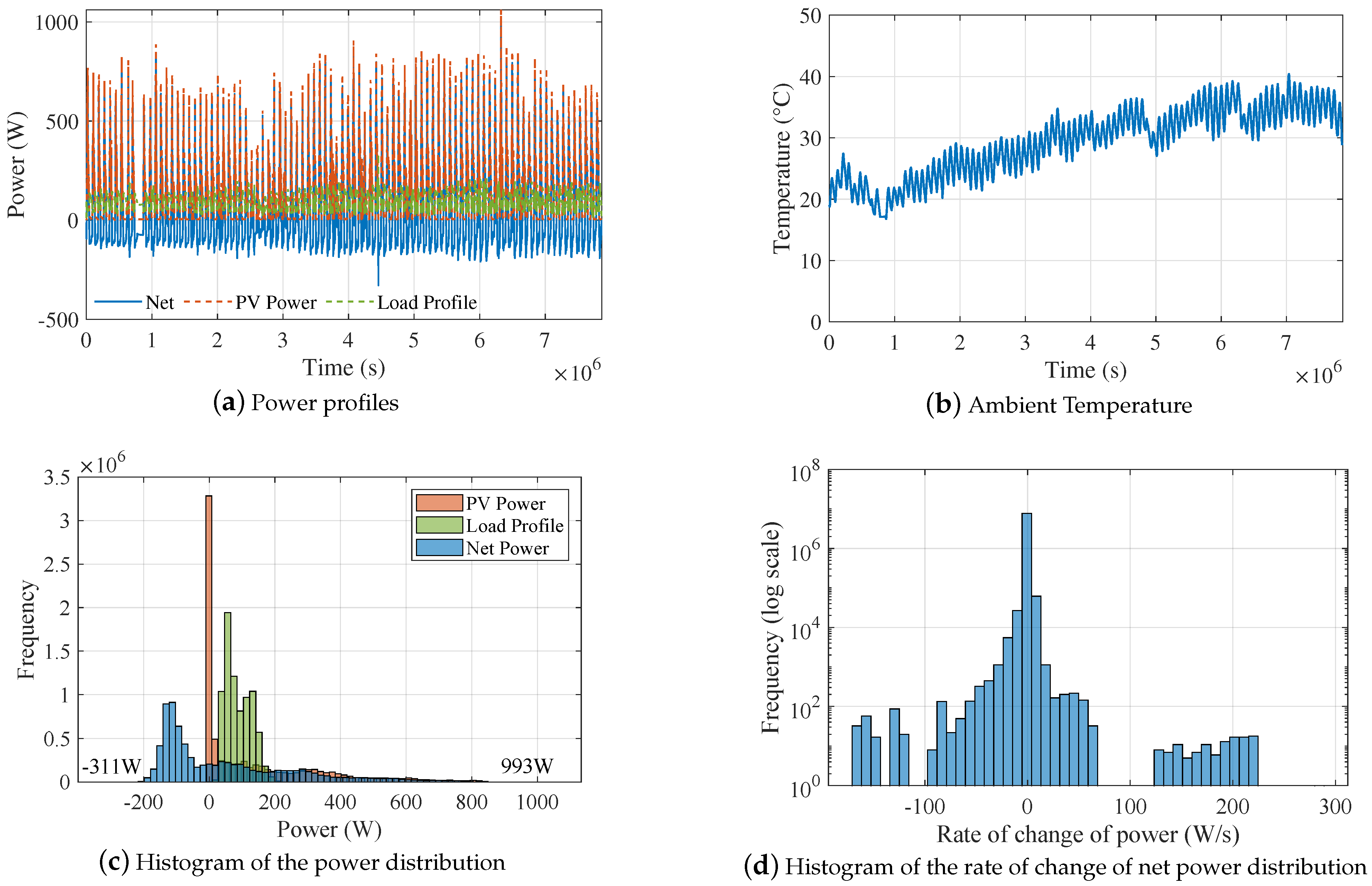
Although the previous section shows that hybridization is more or less beneficial to the battery’s life, it is not clear when it makes sense in terms of economic viability. Here, the benefit of more long-lived batteries is weighted against the additional investment burden of the supercapacitors and their power converter to evaluate the overall economic benefit of the hybridization. The case study of the previous section is used as an example, assessed in six different scenarios to understand when the investment is viable and when it is not.
The net present cost (NPC) metric is adopted in this paper to evaluate the total investment required for the two alternative ESS over the entire project life. NPC involves the initial one-time investment
, any replacement costs
R and operation and maintenance (O&M) costs
during the lifetime of the project [
22,
68]:
In the battery-alone system,
comprises the costs for the batteries
and their converter
, while the HESS involves additionally the supercapacitors costs
and their own converter costs
. Equation (
16) shows the full picture for the HESS case.
The parameters used in this paper are given in
Table 5. The capital cost accounts for the main investment. According to [
21], the capital cost of lead–acid batteries in 2018 was approximately 260
$/kWh and it was predicted to drop to 220
$/kWh by 2025. Assuming that this project starts in 2020, a battery capital cost of 250
$/kWh is considered, with a discount rate of 2.4%. The capital cost of supercapacitors is typically 10,000
$/kWh [
69], as adopted for example in the case study of [
70]. The O&M costs of supercapacitors are generally lower than that of batteries, selecting here 0.1% and 0.45% of the investment, respectively, based on [
21]. The cost of the power converters is taken from [
21,
68].
Assuming a project lifetime of 15 years, the replacement costs
R in both battery-alone ESS and HESS refer only to the batteries, since the supercapacitors and converters lifespan typically reaches or exceeds 15 years [
21,
68]. Given the battery lifespan
calculated in years by the proposed degradation model in
Section 3, the batteries need to be replaced
times during the project lifetime; every replacement will cost
adjusted by the annual market discount rate
that reflects the fact that technology becomes cheaper over time. As
r may not be an integer, the equation below involves the cost of full replacements
(rounded down) plus the cost of the final replacement that accounts only for the remaining years and is adjusted by
. The latter intervention is a simple way to account for capital recovery after the project life.
Finally, the O&M costs increase every year due to aging of the equipment, reflected in the actual discount rate
d. During the first battery lifetime, the annual maintenance costs will be an adjusted version of
based on
d, where
is a percentage of the initial investment (see
Table 5). When the batteries are replaced, the maintenance costs will be a discounted value of
, which is again a percentage but of the respective replacement cost (see Equation (
17)). The final O&M expression is given below for the HESS.
It is worth noting that the O&M costs of the hybridized system will not fundamentally differ from the battery-alone ESS. Being both electrochemical storage devices, the battery and supercapacitor require simple and straightforward maintenance, i.e., keeping the surface clean and the connectors sealed etc. [
71]. The skillset required by the local technicians for installation, operation and maintenance is practically the same in the two systems, which does not create any additional barriers in adopting the HESS in isolated rural communities. However, it should be noted that supercapacitors consumables are not as readily available as lead–acid batteries in local markets in rural India, although currently the market size of Indian supercapacitor manufacturing industry grows steadily every year [
72].
5.1. Base Scenario
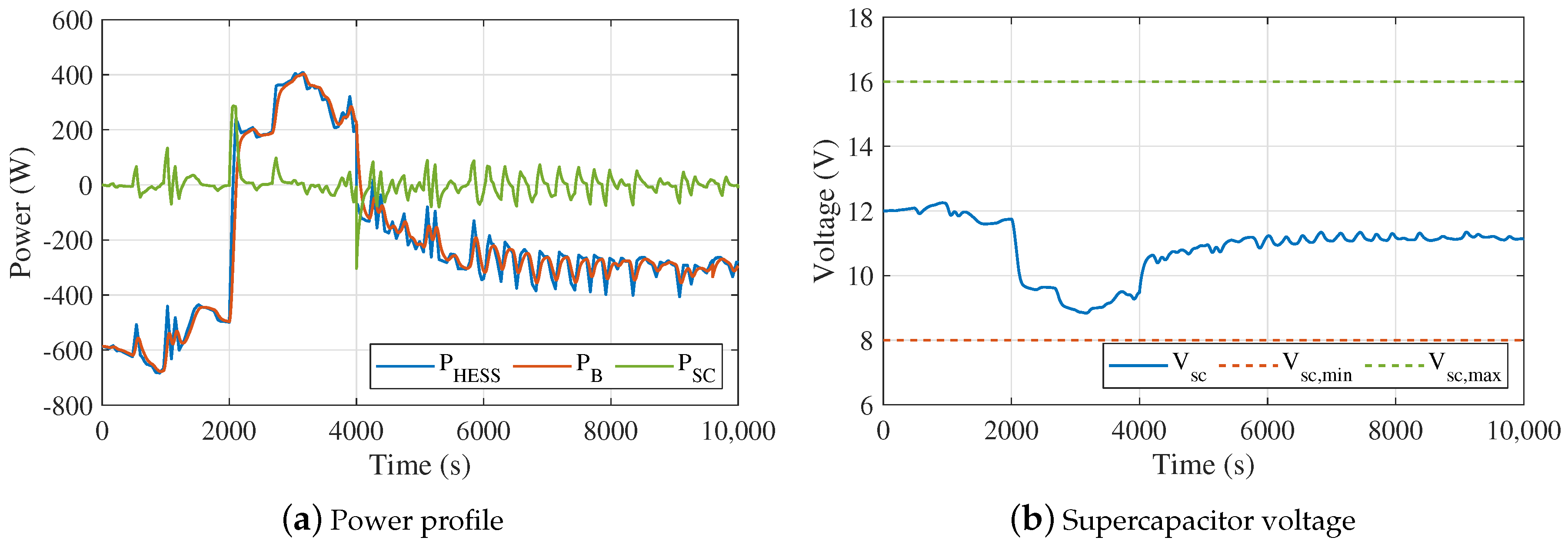
The base scenario refers to the default HESS parameters of
Table 3 and the economic considerations of
Table 5. This includes a set of reasonable assumptions corresponding to a realistic system, used thereafter as a benchmark for the remaining scenarios. The results of the techno-economic analysis are given in
Table 6. The battery life in the basic scenario is estimated to be 5–5.5 years, which is well-aligned with industry’s expectations for real-life microgrids [
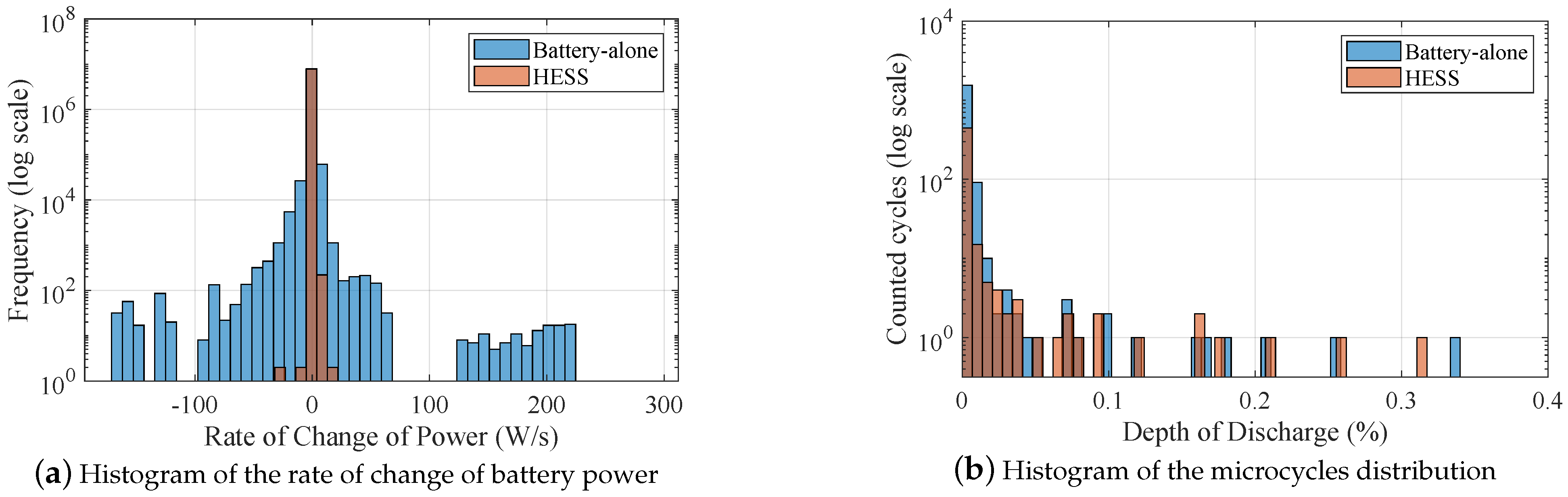
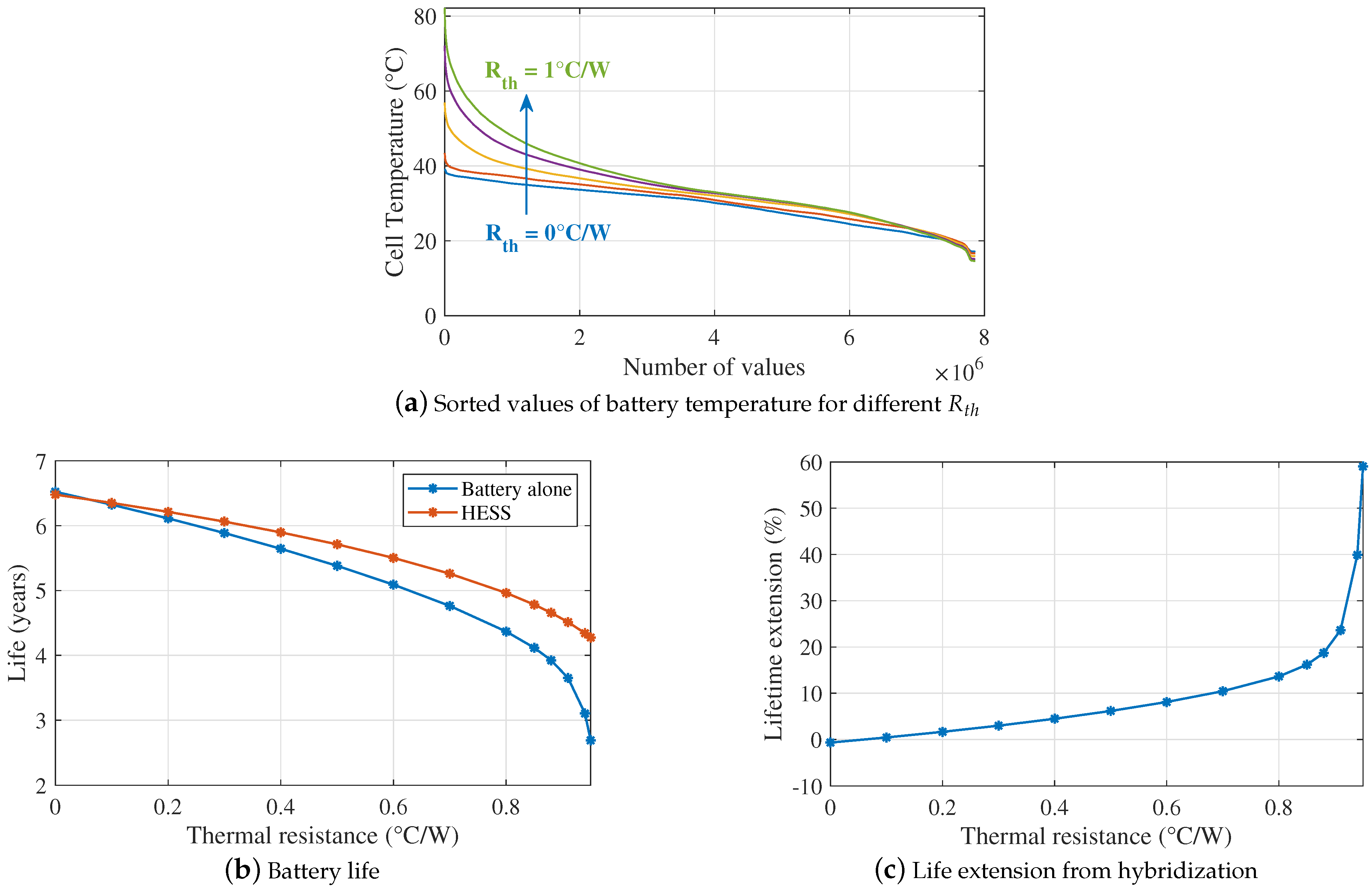
71]. The supercapacitors’ contribution reduces the total number of cycles by 2/3, mainly the microcycles, which translates to about 8% longer lifespan for the batteries. However, given the additional investment costs in the HESS, the economic benefit is much more limited at 1.9%. This makes the hybridization economically viable, albeit very marginally. The following scenarios explore how these numbers change for different thermal and economic considerations.
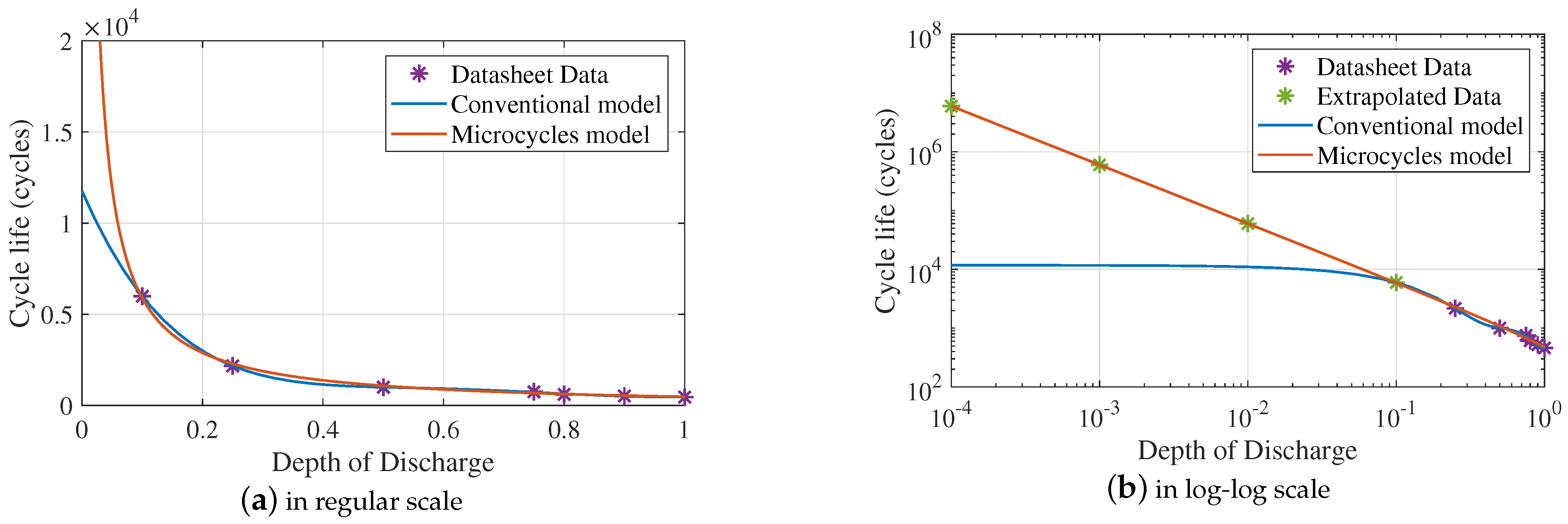
5.2. Scenario 2: Conventional Cycle Life DoD Model
The discussion in
Section 3.1.2 outlines two cycle life models that evaluate the DoD degradation effect: the conventional model designed for cycles with substantial DoD, and the microcycle model that accounts also for the cycles with very little DoD. Given that the case-study electricity profile is of high time-resolution and the numerous microcycles are visible, it is of paramount importance to use the latter model in all analyses, as has been done throughout this paper. To support this claim, scenario 2 employs the conventional model instead, with the results given in
Table 7. Clearly, the battery degradation is severely overestimated, yielding about 1 year lifespan for the battery-alone and 3 years for the HESS. Although, hybridization seems very beneficial indeed in this case, the results of 1–3 years are not realistic [
71], highlighting that this type of model can not reflect reality and should not be used to inform an investment. In fact, the main conclusion from this scenario is how important is to use a microcycles life model when the SoC profile is of high time-resolution and the microcycles are visible. In cases that a microcycle model is not available, it is preferable to completely disregard the microcycles from the profile when evaluating the DoD degradation.
5.3. Scenario 3: Poor Thermal Characteristics
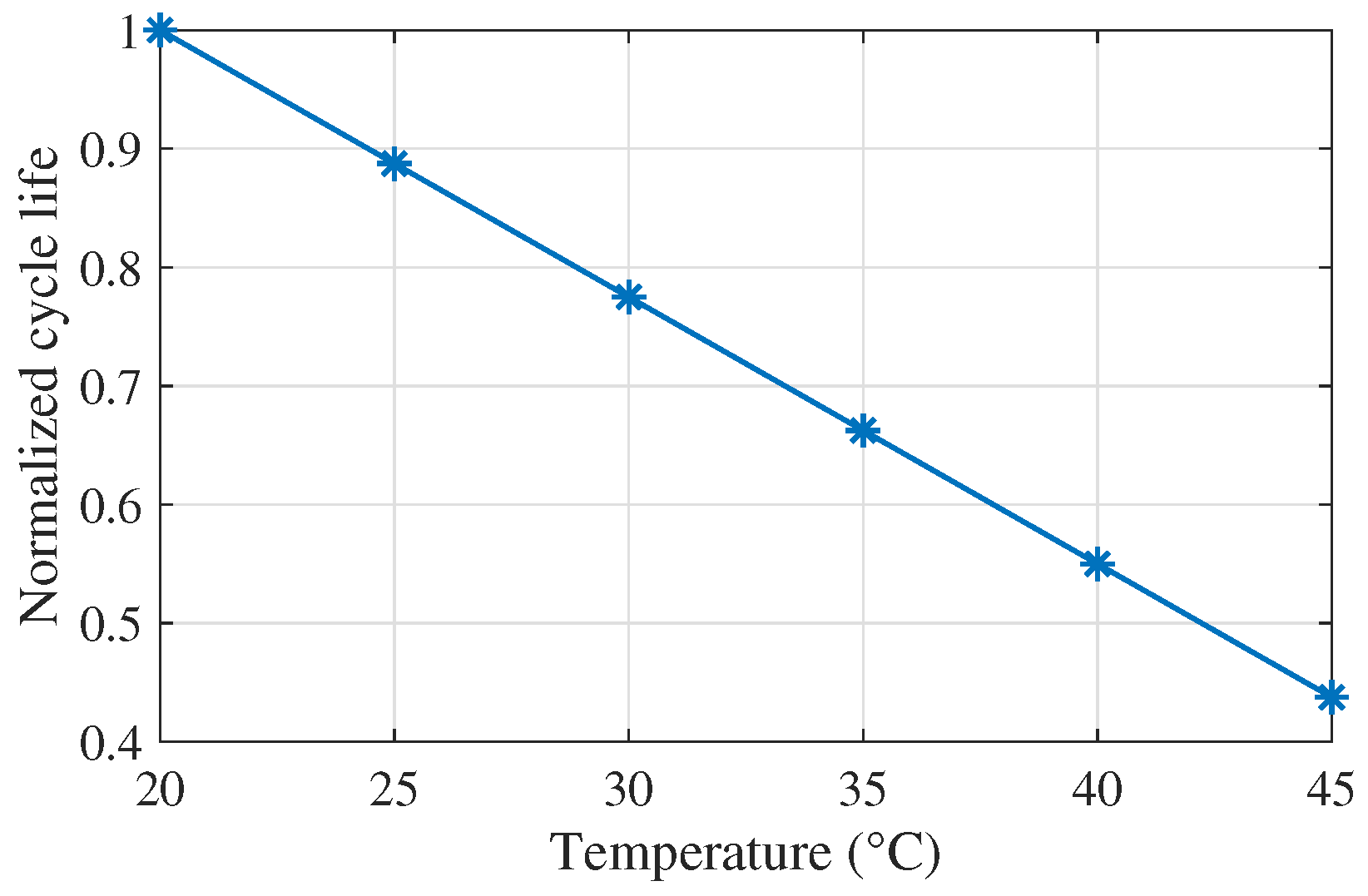
The thermal parameters of
Table 3 are indicative and strongly depend on the specific system and environment. Their influence on the battery life is discussed in
Section 4.3; here, the respective economic impact is assessed in a scenario with worse thermal characteristics (e.g., poor ventilation and thermal management system): thermal resistance 0.8
C/W, thermal time constant 14,400 s (4 h) and converter losses 8%. For example, [
66] shows that the thermal resistance can be in some cases as high as 1.1
C/W and the thermal constant around 3–4 h. The results of
Table 8 show a lifespan reduction of more than a year in both systems compared to the base scenario due to the higher battery temperature. These severe thermal conditions result in a battery life falling short of the industrial targets [
71], but hybridization manages to mitigate this impact to a large extent. The contribution of the hybridization is considerable indeed, extending the battery longevity by more than 20%, which translates to about 12% economic benefit. Clearly, hybridization is highly beneficial in this case, which indicates that a HESS is a good solution under poor thermal conditions.
5.4. Scenario 4: Good Thermal Characteristics
On the other hand, improved thermal characteristics should affect the results in the opposite way. Here, the thermal parameters are: thermal resistance 0.4
C/W; thermal time constant 21,600 s (6 h); [
67,
73] and converter losses remain at 5%. For example, [
73] shows that with a properly designed cooling system, the thermal resistance will almost be lower than 0.4
C/W, or even be reduced to 0.2
C/W.
Table 8 shows that the battery life of the only-battery system meets and exceeds the industry expectations, which entails marginal only life improvement from hybridization and a negative economic benefit indeed. In other words, the hybridization contribution is too little to overcome the relevant financial overhead. This highlights once again the importance to consider both temperature and DoD factors in a battery degradation model to yield reliable conclusions.
5.5. Scenario 5: Economic Parameters in Favor of Hybridization
In order to assess the influence of the economic parameters on the viability of the hybridization, this section repeats the analysis assuming conditions more favorable to the supercapacitors. Specifically, the supercapacitors’ capital cost is reduced by 20% to 8000
$/kWh, the batteries are priced 12% higher at 280
$/kWh, the market discount rate
drops to 0.4% and the O&M discount rate
d is assumed to be −1% (see
Table 5 for comparison). The resulting
Table 9 differs from the base case
Table 6 only in the financial figures, now increasing the economic benefit of the hybridization to 3.6%. Apparently, this is not fundamentally different from the 1.9% in the base case, which entails that the hybridization viability is more sensitive on the thermal parameters, rather than the economic ones.
5.6. Scenario 6: Economic Parameters against Hybridization
By contrast, this scenario explores economic parameters that stand against the hybridization: supercapacitors cost
$12,000/kWh, battery costs
$220/kWh, 5% battery market discount rate and −10% O&M discount rate.
Table 9 shows a slightly negative economic benefit which renders the hybridization marginally inviable. Still, a drop from 1.9% in the base case to −0.6% here is very limited considering the substantial variations in the capital costs, which essentially confirms the relative insensitivity of the hybridization to the economic parameters.
In fact, the main conclusion from this investigation is that the main factors to assess whether a lead–acid battery ESS should be hybridized with supercapacitors are the thermal parameters, rather than the economic ones. The poorest the thermal conditions, the more likely the hybridization to be beneficial.
6. Conclusions
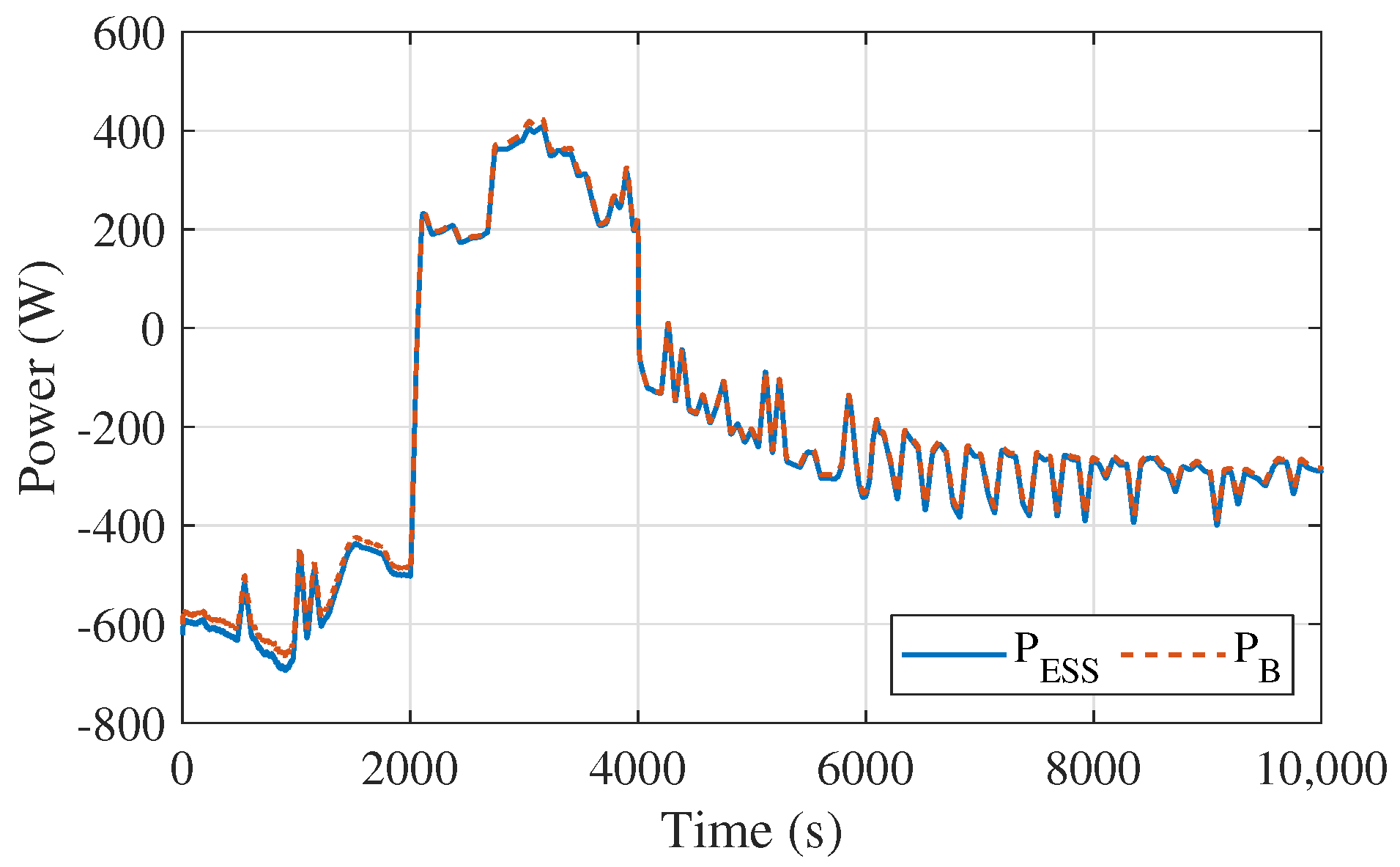
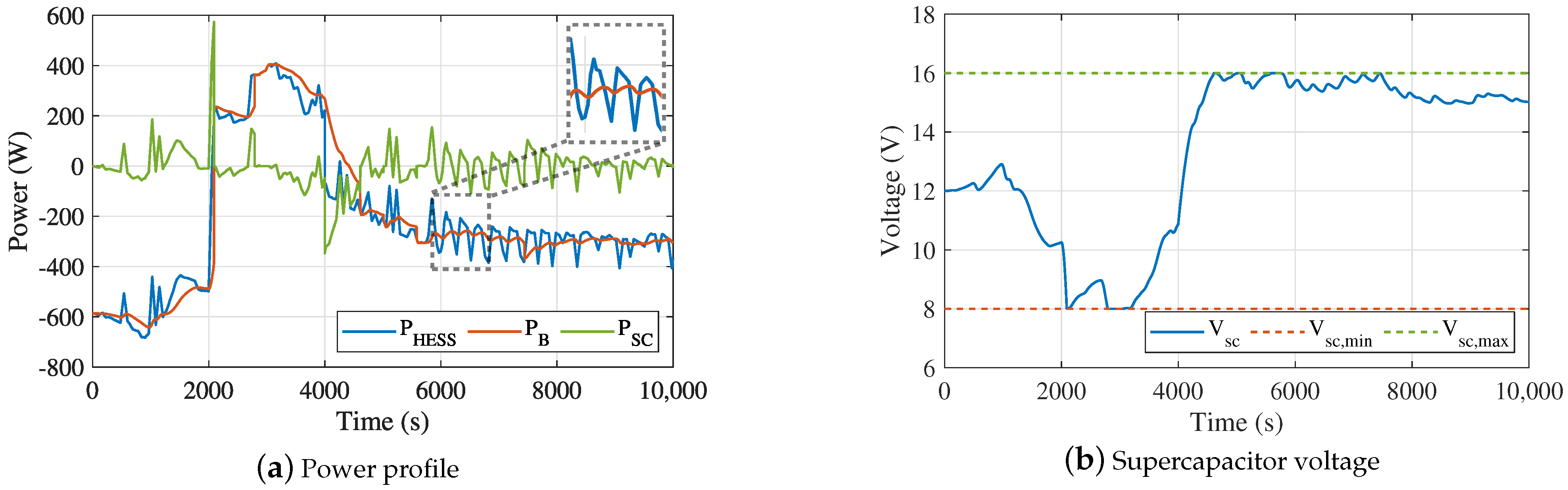
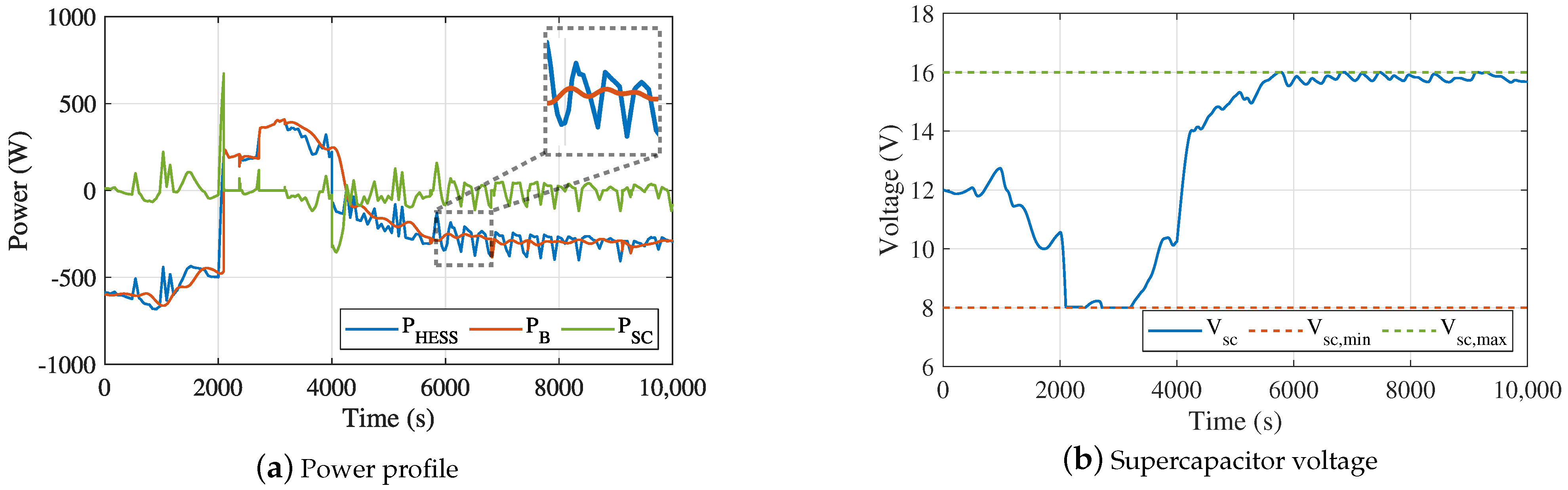
This paper describes a methodology to hybridize a battery-based energy storage system using supercapacitors for a smoother power profile, presenting a new control scheme, a new battery degradation mechanism model and an economic viability analysis. Compared to a system with only lead–acid batteries, the hybrid system features longer battery life. The results showed that a simple first-order low-pass filter is an effective and reliable solution for the power filtering, performing more favorably than higher order FIR filters given the limited supercapacitors capacity and strict voltage limits. Apparently, the supercapacitors result in fewer microcycles, but also in lower average battery temperature due to the smoother current profile that yields less power losses compared to a fluctuating current in the battery-alone case. This also highlights the importance in capturing both DoD and temperature effects in a battery degradation model, such as in the one proposed.
Especially when there is access to second-resolution time series that allows visibility to numerous microcycles, an appropriate microcycles cycle life DoD model should be used; if not available, the microcycles should instead be completely disregarded from the profile to avoid erroneous battery life estimation. A sensitivity analysis showed that the thermal parameters of the system not only affect the battery life, but play a major role in the hybridization benefit: poorer or better thermal conditions render the hybridization more or less useful respectively. This is confirmed by the economic analysis, which concludes that the financial benefit of the hybridization depends more on the thermal conditions rather than the economic parameters of the investment.
The methodology and findings of this study may be useful when exploring hybridization options for battery ESS in standalone microgrids. In addition, this type of hybrid ESS has great grid-connected potential as well, mainly in facilitating high levels of renewables integration. It is nowadays seen as a credible way to absorb generation and load intermittency and provide ancillary services to the power system, such as frequency response and inertia emulation, functions that again result in irregular charge/discharge battery profiles that hint towards a hybrid ESS.
Furthermore, it is worth noting that the core of the proposed methodology applies to Li-ion battery systems as well, which is increasingly gaining popularity due to longer life, smaller size and less weight. Most steps of this paper’s methodology will be common in this case, but with substantially different characteristics and parameters that do not allow for straightforward extrapolation of this study findings to Li-ion battery systems.