Mitigating the Piston Effect in High-Speed Hyperloop Transportation: A Study on the Use of Aerofoils
Abstract
1. Introduction
1.1. Studies on Airflow around High-Speed Systems
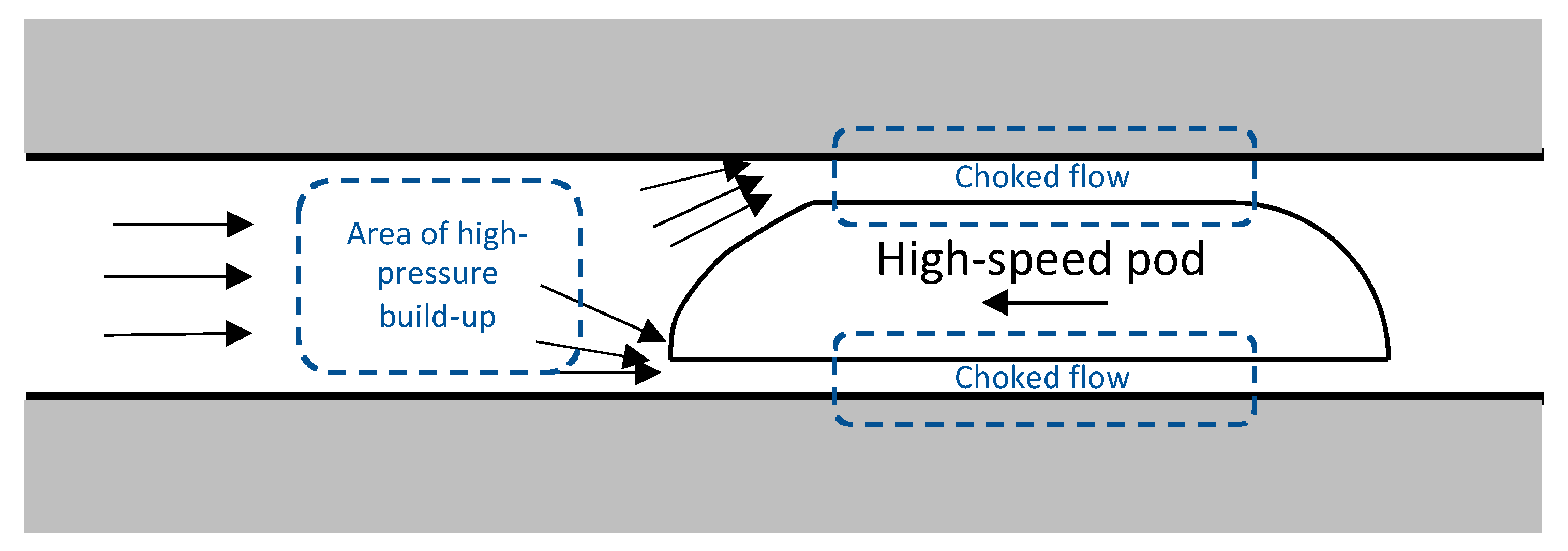
1.2. Kantrowitz Limit
1.3. Aerodynamic Studies on the Hyperloop
1.4. Research Questions
- How does the piston effect influence the performance of a Hyperloop pod in a partially vacuum tunnel?
- Does the addition of aerofoil-shaped fins improve the aerodynamic performance of a Hyperloop pod?
2. Method
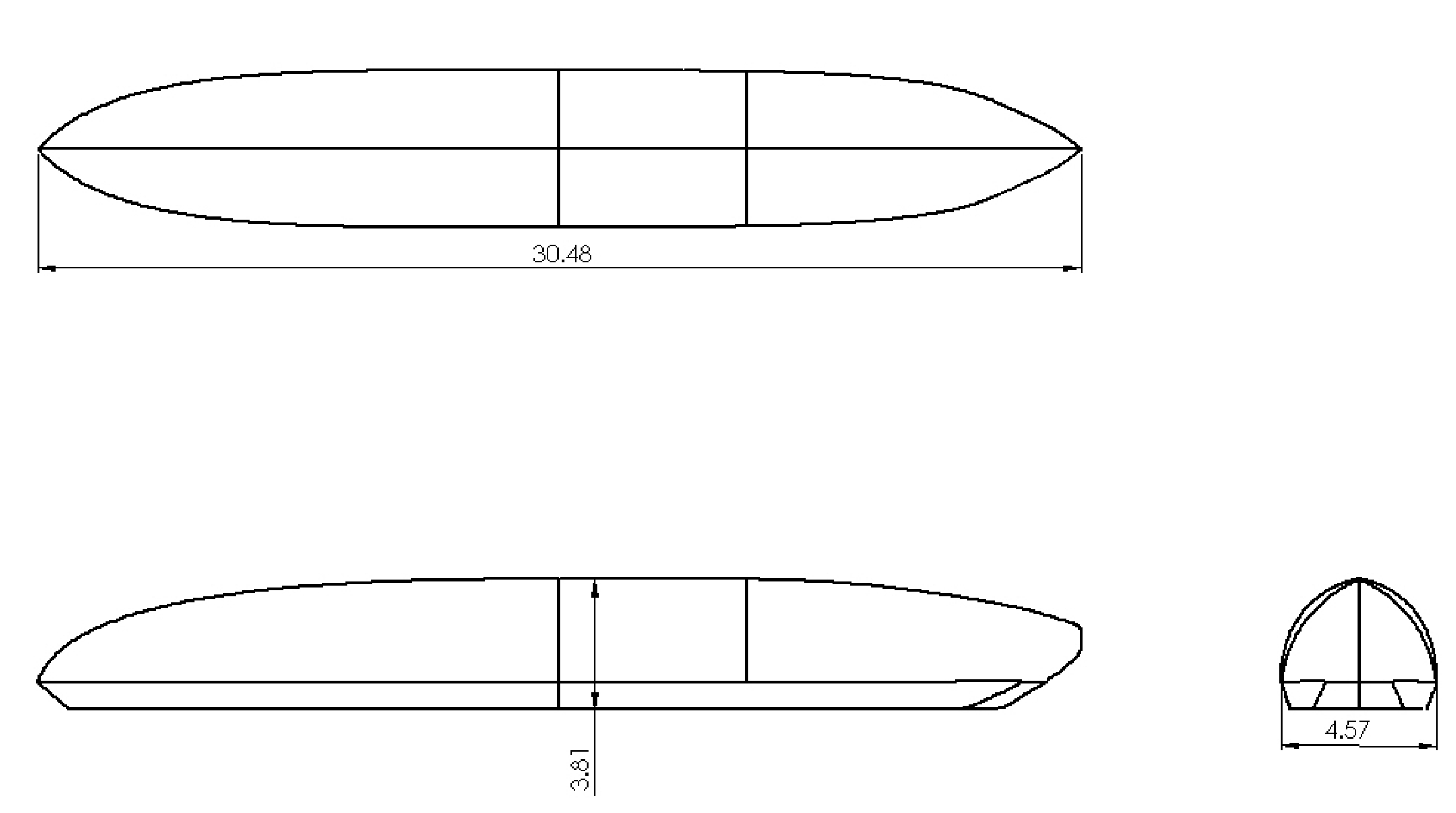
2.1. Model Dimensions
2.2. Computational Modeling
- k-ω closure: σk1 = 0.85, σω1 = 0.65, β1 = 0.075
- k-ε closure: σk2 = 1.00, σω2 = 0.85, β2 = 0.082
- SST closure: β* = 0.09, a1 = 0.31
2.3. Materials
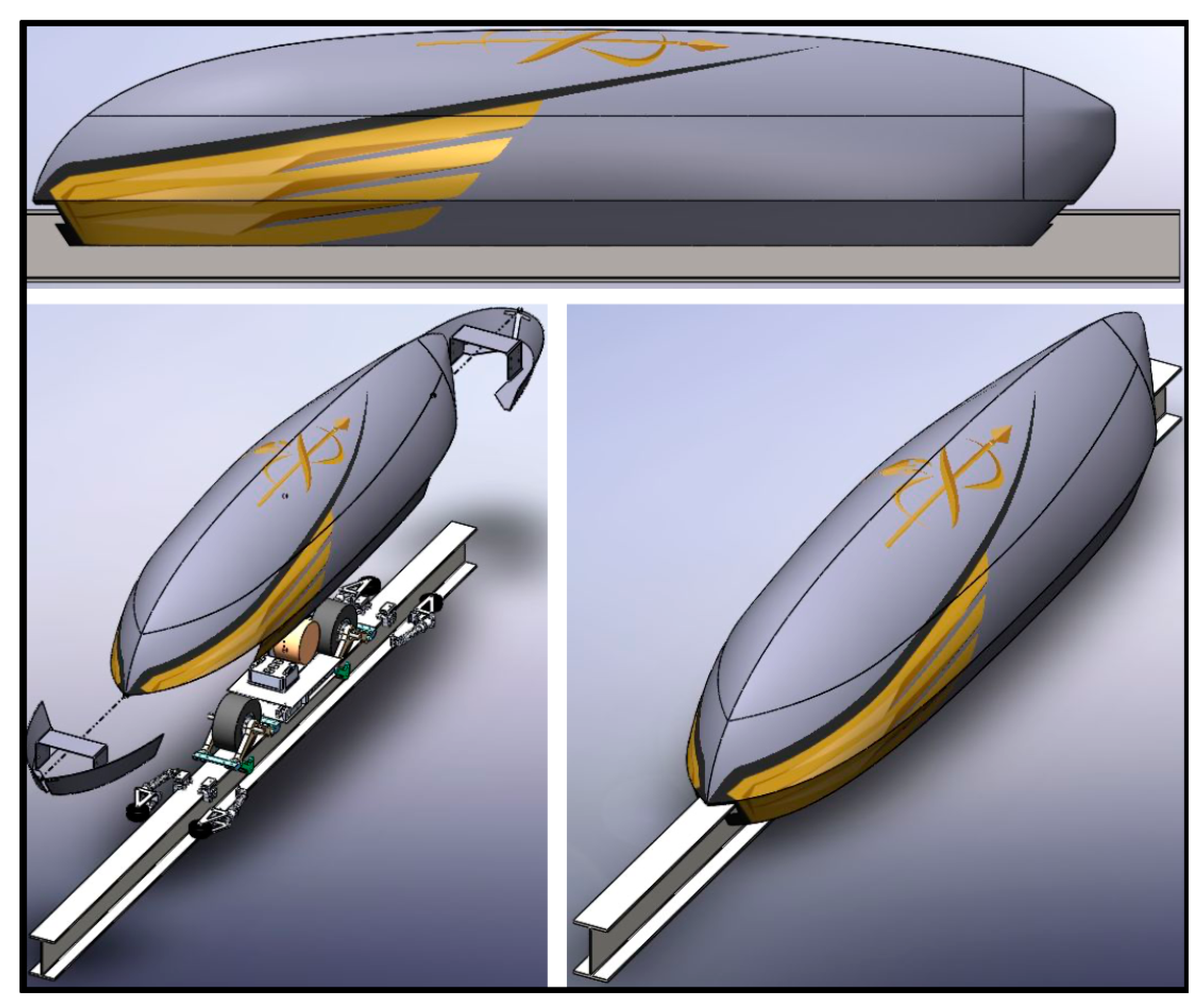
2.4. Phase I Model—Investigation of the Plunger Effect
2.5. Mesh Generation and Grid Convergence
2.6. Phase II Model—With Aerofoils to Mitigate the Plunger Effect
3. Results
3.1. Verification and Validation of the Model Used
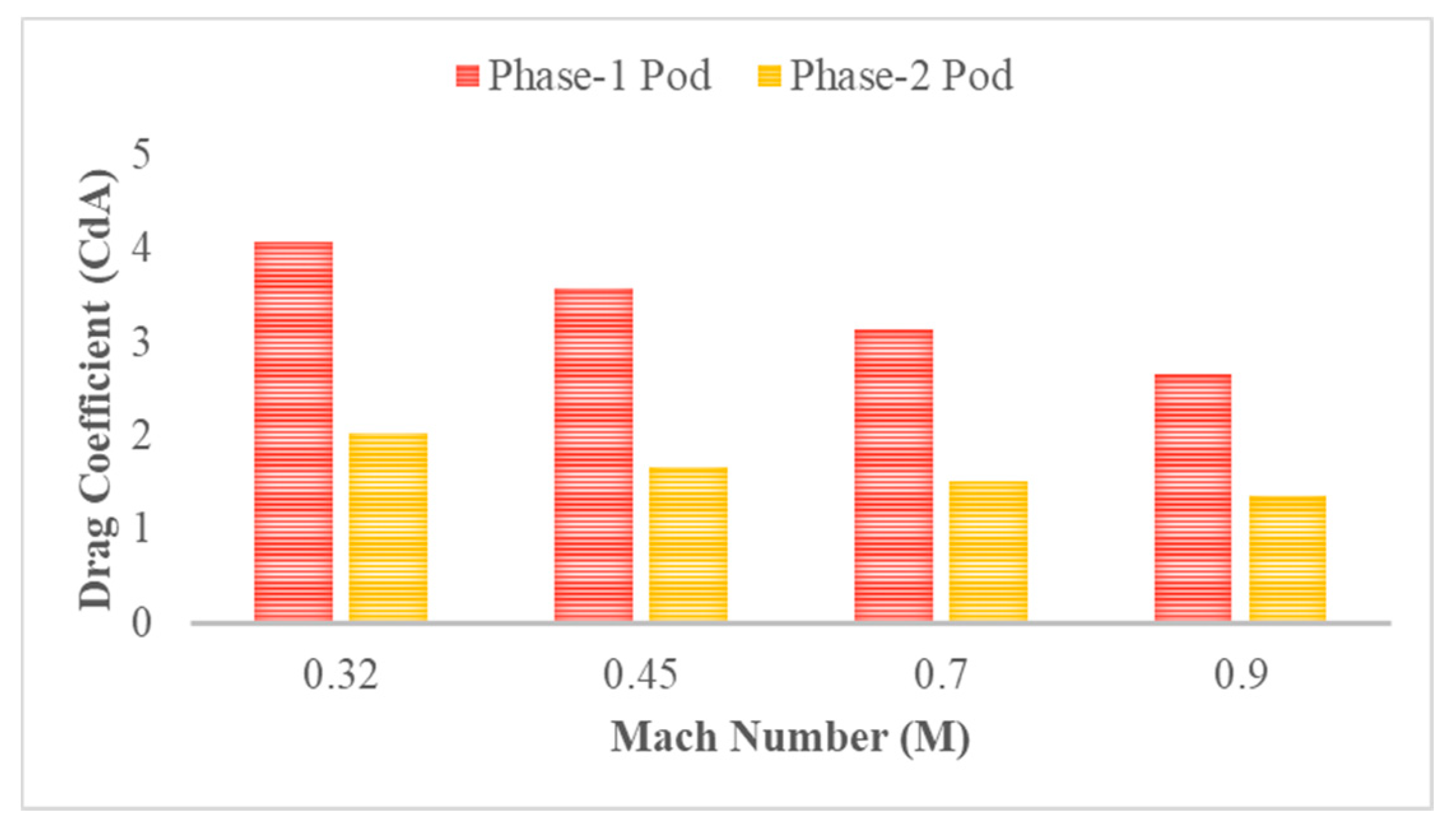
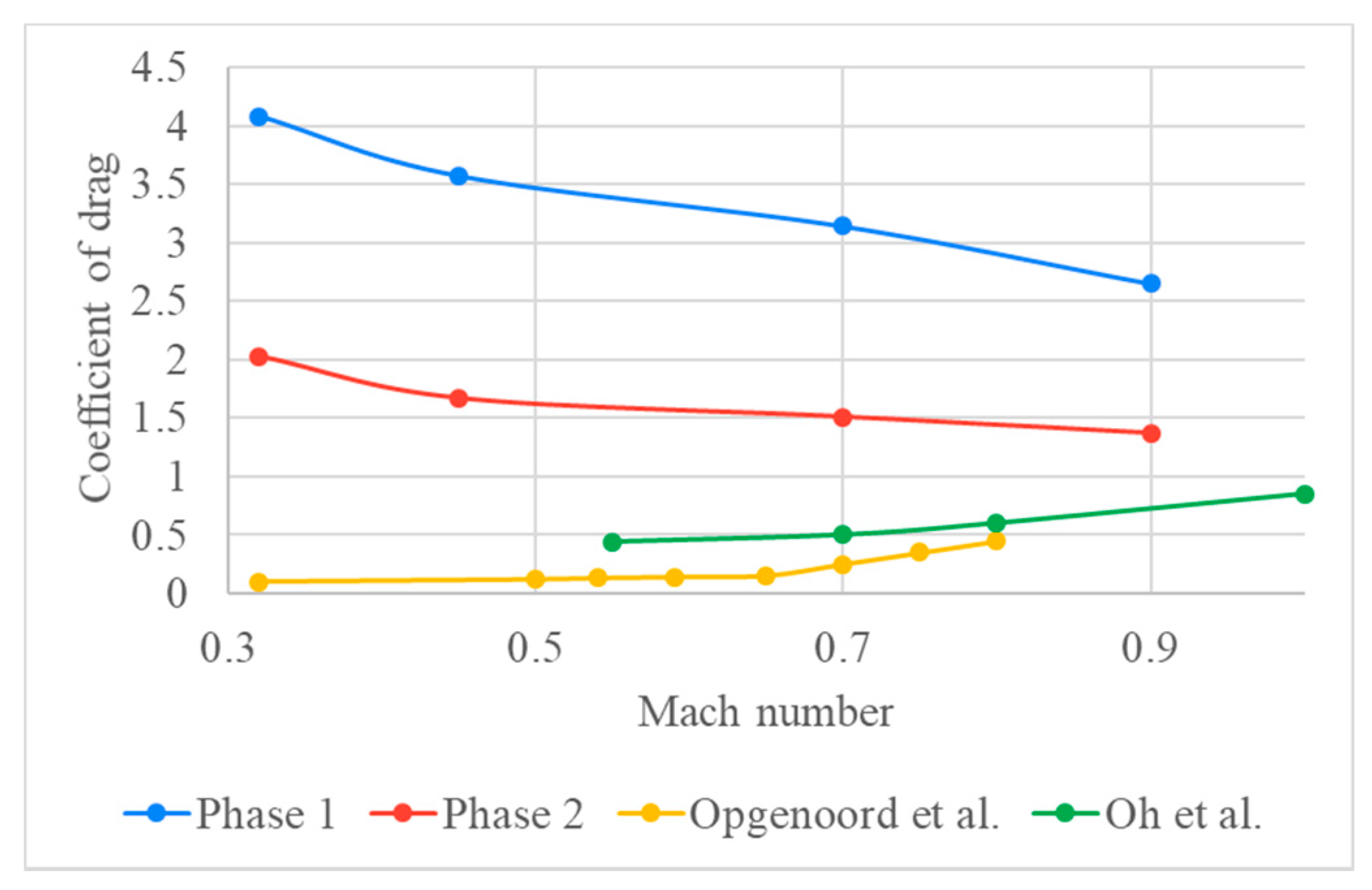
3.2. Drag Coefficient
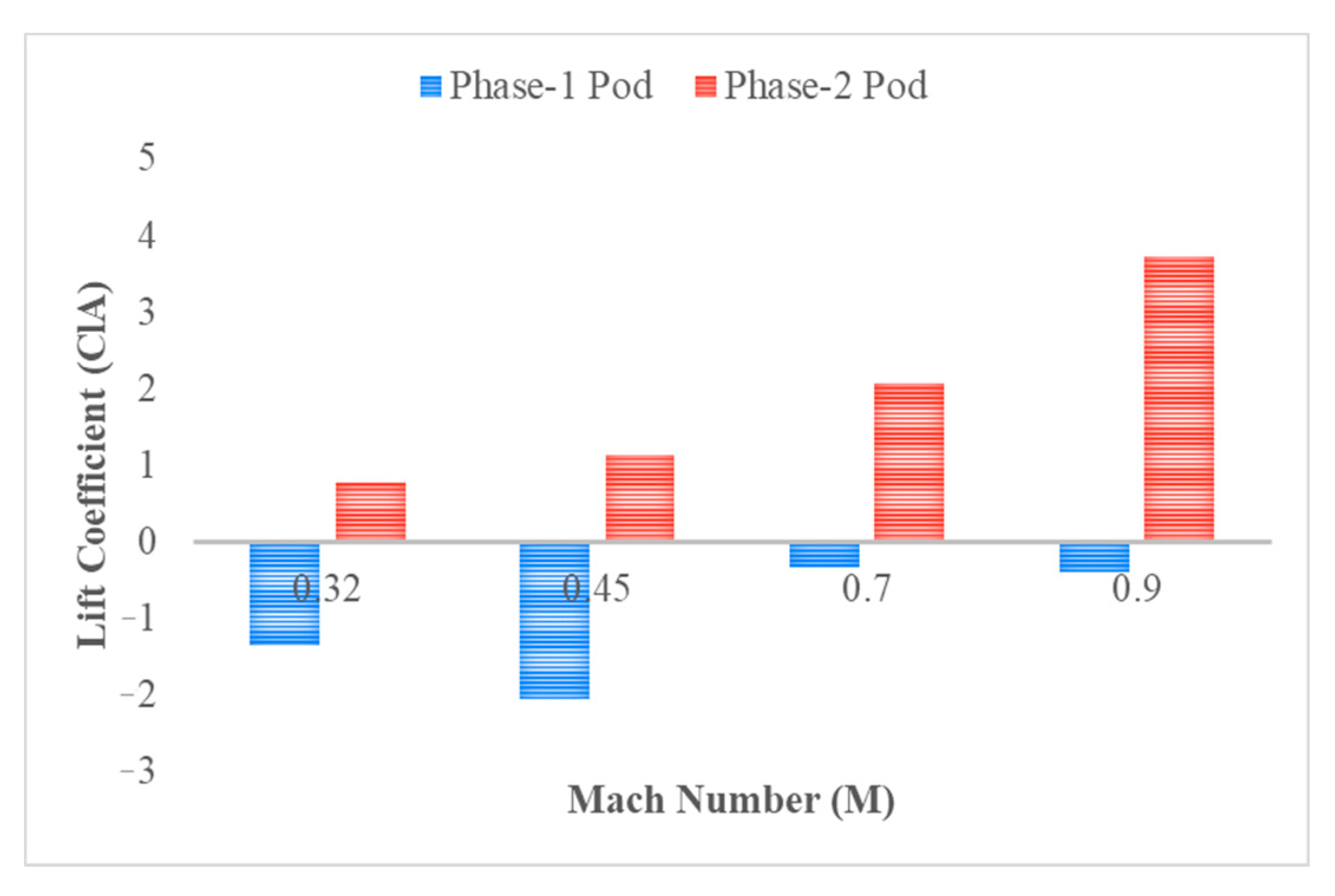
3.3. Lift Coefficient
3.4. Formation of Eddy Currents
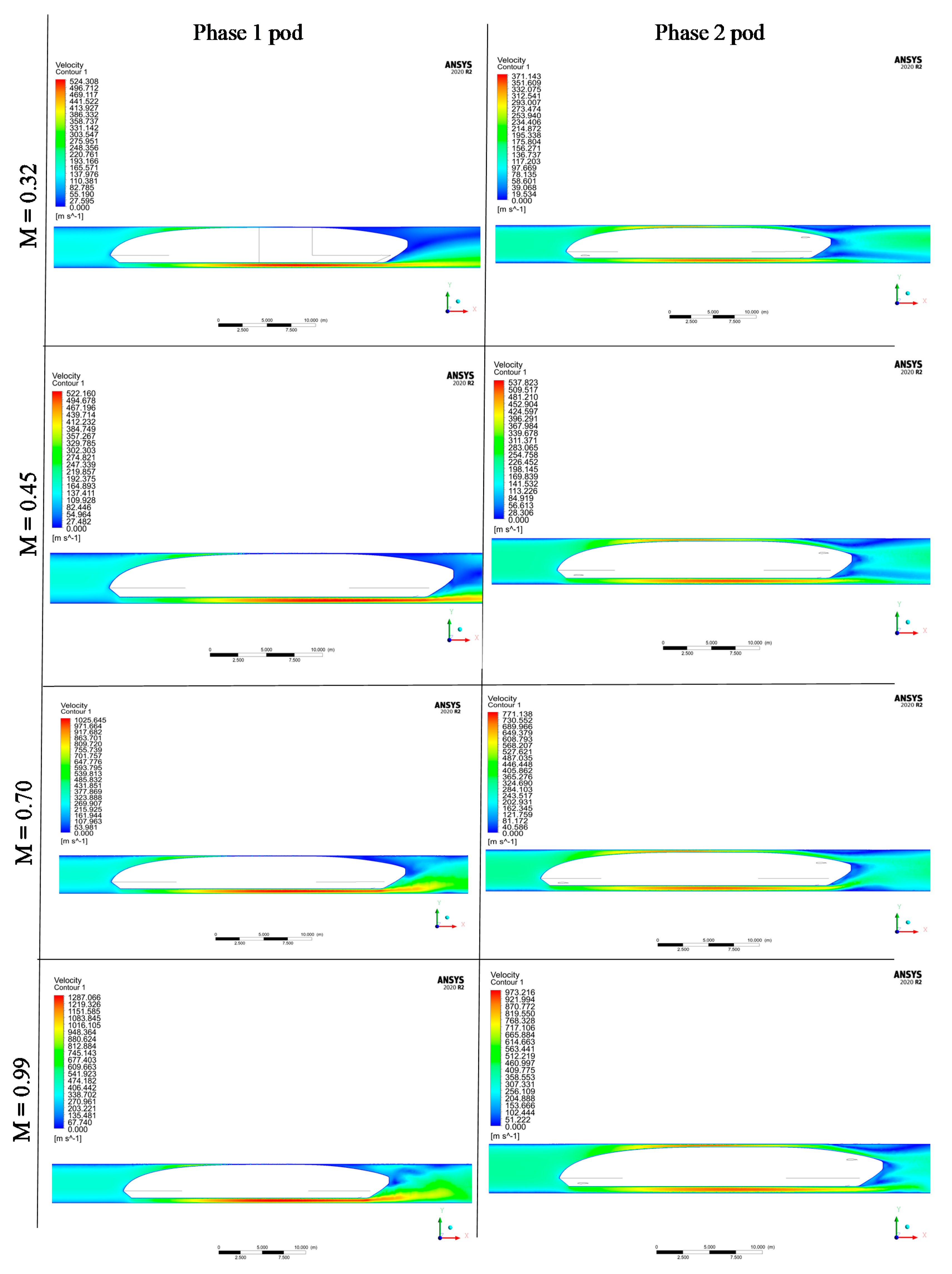
3.5. Velocity Contours
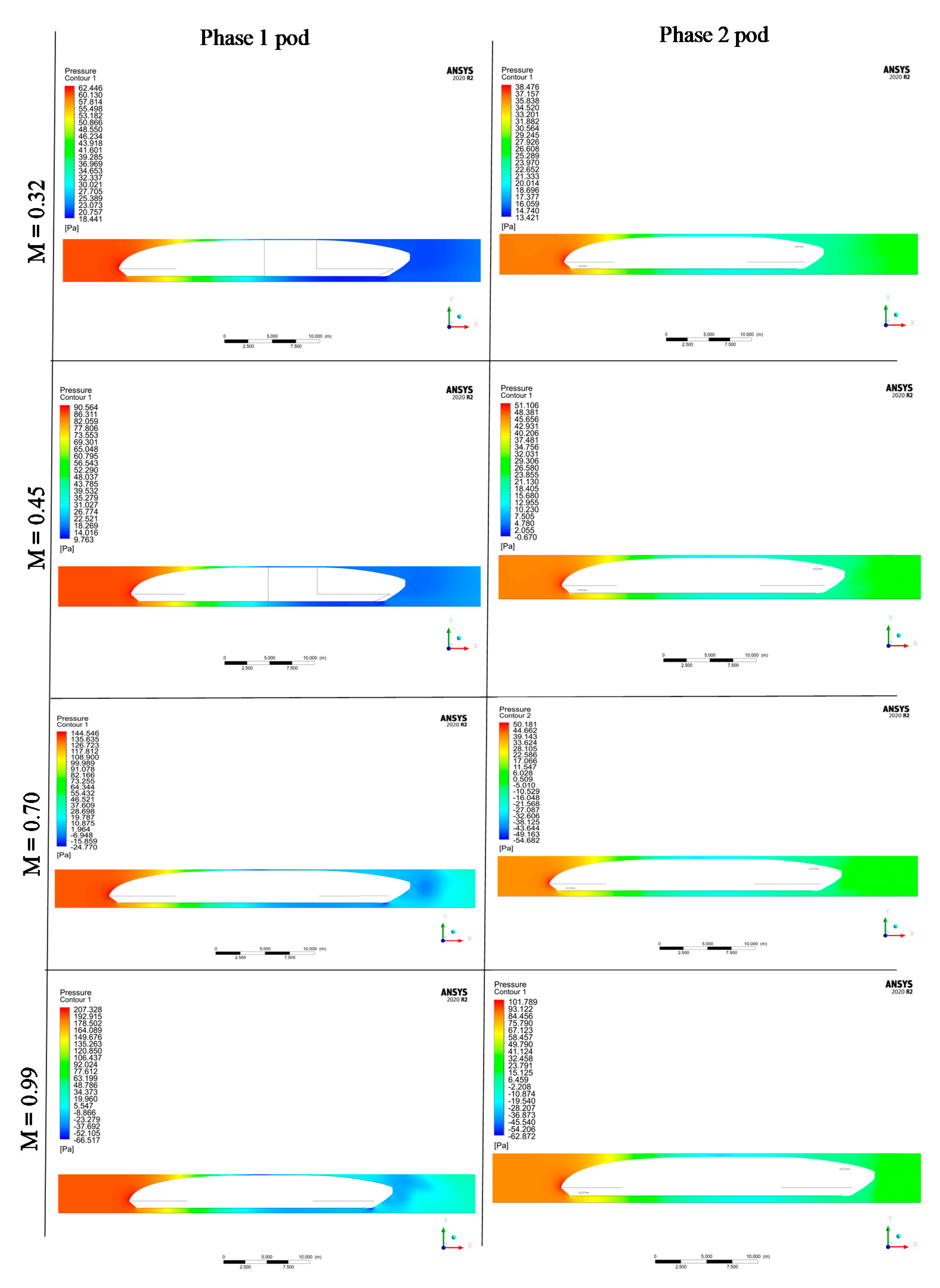
3.6. Pressure Contours
4. Discussion
4.1. Plunger Effect inside the Vacuum Tube
4.2. Use of Aerofoil Fins on Hyperloop Pods
4.3. Limitations of the Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sakowski, M. The Next Contender in High Speed Transport Elon Musks Hyperloop. J. Undergrad. Res. Univ. Ill. Chic. 2016, 9, 47–49. [Google Scholar] [CrossRef]
- Clary, D.A. Rocket Man: Robert H. Goddard and the Birth of the Space Age; Hachette: London, UK, 2003. [Google Scholar]
- Goddard, E.C. Vacuum Tube Transportation System. U.S. Patent No. 2,511,979, 20 June 1950. [Google Scholar]
- Yaghoubi, H. The Most Important Maglev Applications. J. Eng. 2013, 2013, 537986. [Google Scholar] [CrossRef]
- Powell, J.; Danby, G.T.; Jordan, J.C. The Fight for Maglev: Making America the World Leader in 21st Century Transport; CreateSpace: Scotts Valley, CA, USA, 2012. [Google Scholar]
- van Goeverden, K.; Milakis, D.; Janic, M.; Konings, R. Analysis and modelling of performances of the HL (Hyperloop) transport system. Eur. Transp. Res. Rev. 2018, 10, 41. [Google Scholar] [CrossRef]
- Musk, E. Hyperloop Alpha; Spacex: Hawthorne, CA, USA, 2013. [Google Scholar]
- Chaidez, E.; Bhattacharyya, S.P.; Karpetis, A.N. Levitation Methods for Use in the Hyperloop High-Speed Transportation System. Energies 2019, 12, 4190. [Google Scholar] [CrossRef]
- Opgenoord, M.M.; Caplan, P.C. Aerodynamic design of the Hyperloop concept. AIAA J. 2018, 56, 4261–4270. [Google Scholar] [CrossRef]
- Pan, S.; Fan, L.; Liu, J.; Xie, J.; Sun, Y.; Cui, N.; Zhang, L.; Zheng, B. A review of the piston effect in subway stations. Adv. Mech. Eng. 2013, 5, 950205. [Google Scholar] [CrossRef]
- Bonnett, C.F. Practical Railway Engineering; Imperial College Press: London, UK, 2005. [Google Scholar]
- Takayama, K.; Sasoh, A.; Onodera, O.; Kaneko, R.; Matsui, Y. Experimental investigation on tunnel sonic boom. Shock Waves 1995, 5, 127–138. [Google Scholar] [CrossRef]
- Auvity, B.; Bellenoue, M.; Kageyama, T. Experimental study of the unsteady aerodynamic field outside a tunnel during a train entry. Exp. Fluids 2001, 30, 221–228. [Google Scholar] [CrossRef]
- Baker, C. Train aerodynamic forces and moments from moving model experiments. J. Wind Eng. Ind. Aerodyn. 1986, 24, 227–251. [Google Scholar] [CrossRef]
- Baker, C.; Brockie, N. Wind tunnel tests to obtain train aerodynamic drag coefficients: Reynolds number and ground simulation effects. J. Wind Eng. Ind. Aerodyn. 1991, 38, 23–28. [Google Scholar] [CrossRef]
- Brockie, N.; Baker, C. The aerodynamic drag of high speed trains. J. Wind Eng. Ind. Aerodyn. 1990, 34, 273–290. [Google Scholar] [CrossRef]
- Watkins, S.; Saunders, J.; Kumar, H. Aerodynamic drag reduction of goods trains. J. Wind Eng. Ind. Aerodyn. 1992, 40, 147–178. [Google Scholar] [CrossRef]
- Xia, C.; Shan, X.; Yang, Z. Wall interference effect on the aerodynamics of a high-speed train. Procedia Eng. 2015, 126, 527–531. [Google Scholar] [CrossRef]
- Lee, Y.; Kim, K.H.; Rho, J.H.; Kwon, H.B. Investigation on aerodynamic drag of Korean high speed train (HEMU-430X) due to roof apparatus for electrical device. J. Mech. Sci. Technol. 2016, 30, 1611–1616. [Google Scholar] [CrossRef]
- Li, Z.-w.; Yang, M.-z.; Huang, S.; Liang, X. A new method to measure the aerodynamic drag of high-speed trains passing through tunnels. J. Wind Eng. Ind. Aerodyn. 2017, 171, 110–120. [Google Scholar] [CrossRef]
- Yang, Q.-S.; Song, J.-H.; Yang, G.-W. A moving model rig with a scale ratio of 1/8 for high speed train aerodynamics. J. Wind Eng. Ind. Aerodyn. 2016, 152, 50–58. [Google Scholar] [CrossRef]
- Catanzaro, C.; Cheli, F.; Rocchi, D.; Schito, P.; Tomasini, G. High-speed train crosswind analysis: CFD study and validation with wind-tunnel tests. In Proceedings of the International Conference on the Aerodynamics of Heavy Vehicles, Potsdam, Germany, 12–17 September 2010; pp. 99–112. [Google Scholar]
- Paradot, N.; Talotte, C.; Garem, H.; Delville, J.; Bonnet, J.-P. A comparison of the numerical simulation and experimental investigation of the flow around a high speed train. In Proceedings of the Fluids Engineering Division Summer Meeting, Montreal, QC, Canada, 14–18 July 2002; pp. 1055–1060. [Google Scholar]
- Shin, C.-H.; Park, W.-G. Numerical study of flow characteristics of the high speed train entering into a tunnel. Mech. Res. Commun. 2003, 30, 287–296. [Google Scholar] [CrossRef]
- Li, X.-H.; Deng, J.; Chen, D.-W.; Xie, F.-F.; Zheng, Y. Unsteady simulation for a high-speed train entering a tunnel. J. Zhejiang Univ. Sci. A 2011, 12, 957–963. [Google Scholar] [CrossRef]
- Wang, D.; Li, W.; Zhao, W.; Han, H. Aerodynamic Numerical Simulation for EMU Passing Each Other in Tunnel. In Proceedings of the 1st International Workshop on High-Speed and Intercity Railways, Hong Kong, 19–22 July 2011; pp. 143–153. [Google Scholar]
- Chu, C.-R.; Chien, S.-Y.; Wang, C.-Y.; Wu, T.-R. Numerical simulation of two trains intersecting in a tunnel. Tunn. Undergr. Space Technol. 2014, 42, 161–174. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Krajnović, S.; Ringqvist, P.; Nakade, K.; Basara, B. Large eddy simulation of the flow around a simplified train moving through a crosswind flow. J. Wind Eng. Ind. Aerodyn. 2012, 110, 86–99. [Google Scholar] [CrossRef]
- Zhuang, Y.; Lu, X. Numerical investigation on the aerodynamics of a simplified high-speed train under crosswinds. Theor. Appl. Mech. Lett. 2015, 5, 181–186. [Google Scholar] [CrossRef]
- Khayrullina, A.; Blocken, B.; Janssen, W.; Straathof, J. CFD simulation of train aerodynamics: Train-induced wind conditions at an underground railroad passenger platform. J. Wind Eng. Ind. Aerodyn. 2015, 139, 100–110. [Google Scholar] [CrossRef]
- García, J.; Muñoz-Paniagua, J.; Crespo, A. Numerical study of the aerodynamics of a full scale train under turbulent wind conditions, including surface roughness effects. J. Fluids Struct. 2017, 74, 1–18. [Google Scholar] [CrossRef]
- Muld, T.W.; Efraimsson, G.; Henningson, D.S. Flow structures around a high-speed train extracted using proper orthogonal decomposition and dynamic mode decomposition. Comput. Fluids 2012, 57, 87–97. [Google Scholar] [CrossRef]
- Xia, C.; Wang, H.; Shan, X.; Yang, Z.; Li, Q. Effects of ground configurations on the slipstream and near wake of a high-speed train. J. Wind Eng. Ind. Aerodyn. 2017, 168, 177–189. [Google Scholar] [CrossRef]
- Wang, S.; Bell, J.R.; Burton, D.; Herbst, A.H.; Sheridan, J.; Thompson, M.C. The performance of different turbulence models (URANS, SAS and DES) for predicting high-speed train slipstream. J. Wind Eng. Ind. Aerodyn. 2017, 165, 46–57. [Google Scholar] [CrossRef]
- Mei, Y.; Zhou, C. The One-Dimensional Unsteady Flow Prediction Method and Applications on the Pressure Waves Generated by High-Speed Trains Passing through a Tunnel. In Proceedings of the 1st International Workshop on High-Speed and Intercity Railways, Hong Kong, 19–22 July 2011; pp. 397–405. [Google Scholar]
- Kantrowitz, A.; Donaldson, C. Preliminary investigations of supersonic diffuser, duP. Naca WR L 1945, 713, 2–11. [Google Scholar]
- Chin, J.C.; Gray, J.S. Open-source conceptual sizing models for the hyperloop passenger pod. In Proceedings of the 56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 5–9 January 2015; p. 1587. [Google Scholar]
- Braun, J.; Sousa, J.; Pekardan, C. Aerodynamic design and analysis of the hyperloop. AIAA J. 2017, 55, 4053–4060. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, H.; Benedict, M.; Coleman, D. Aerodynamic simulation of high-speed capsule in the Hyperloop system. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, Denver, CO, USA, 5–9 June 2017; p. 3741. [Google Scholar]
- Oh, J.-S.; Kang, T.; Ham, S.; Lee, K.-S.; Jang, Y.-J.; Ryou, H.-S.; Ryu, J. Numerical analysis of aerodynamic characteristics of hyperloop system. Energies 2019, 12, 518. [Google Scholar] [CrossRef]
- Biadgo, A.M.; Simonović, A.; Svorcan, J.; Stupar, S. Aerodynamic characteristics of high speed train under turbulent cross winds: A numerical investigation using unsteady-RANS method. Fme Trans. 2014, 42, 10–18. [Google Scholar] [CrossRef]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries: La Cañada, CA, USA, 1998; Volume 2. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Taylor, R.E. Specific Heat of Carbon/Carbon Composites; Airforce Office of Scientific Research: West Lafayette, IN, USA, 1981. [Google Scholar]
- Palaniappan, K.; Jameson, A. Bodies having Minimum Pressure Drag in Supersonic Flow—Investigating Nonlinear Effects. J. Aircr. 2010, 47, 1451–1454. [Google Scholar] [CrossRef]
- Nathman, J. The Solution of the Prandtl-Glauert Equation around Non-slender Bodies. Anal. Method Rep. 1987, 8, 7–15. [Google Scholar]
- Nasa/Langley. LS(1)-0413 (GA(W)-2) Airfoil. Available online: https://m-selig.ae.illinois.edu/ads/coord/ls413.dat (accessed on 27 October 2020).
- Moin, P.; Mahesh, K. Direct numerical simulation: A tool in turbulence research. Annu. Rev. Fluid Mech. 1998, 30, 539–578. [Google Scholar] [CrossRef]
- Graham, C. Evaluation of the Performance of Various Turbulence Models for Accurate Numerical Simulation of a 2D Slot Nozzle Ejector; Washington University at St. Louis: St. Louis, MO, USA, 2014. [Google Scholar]
- Rinard, G. Vehicle Drag Reduction System. U.S. Patent No. 5,280,990, 8 July 2014. [Google Scholar]
- Lin, C.J.; Chuah, Y.K.; Liu, C.W. A study on underground tunnel ventilation for piston effects influenced by draught relief shaft in subway system. Appl. Therm. Eng. 2008, 28, 372–379. [Google Scholar] [CrossRef]



| Case | Number of Elements | Drag (n) (Relative Error) | Lift (n) (Relative Error) | Pressure (pa) (Relative Error) | Velocity (m/s) (Relative Error) |
|---|---|---|---|---|---|
| Type 1 | 3,081,385 | 2793.89 (34.95%) | −185.27 (0%) | 227.81 (27.05%) | 1374.77 (19.55%) |
| Type 2 | 2,236,054 | 2070.32 (180.95%) | −185.27 (5.29%) | 179.31 (15.88%) | 1149.87 (14.70%) |
| Type 3 * | 1,601,627 | 736.9 | −195.07 | 207.8 | 1319 |
| Material of the pod | 3k Twill weave carbon fiber |
| Material of the tube | Steel |
| Material for the fluid | Air |
| Speeds considered (m/s) | 112, 154, 241, 309 |
| Tube pressure (Pa) | 25 |
| Tube temperature (°C) | 49 |
| Density of fluid (kg/m3) | 0.000270 |
| Density of the pod material (kg/m3) | 1760 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bose, A.; Viswanathan, V.K. Mitigating the Piston Effect in High-Speed Hyperloop Transportation: A Study on the Use of Aerofoils. Energies 2021, 14, 464. https://doi.org/10.3390/en14020464
Bose A, Viswanathan VK. Mitigating the Piston Effect in High-Speed Hyperloop Transportation: A Study on the Use of Aerofoils. Energies. 2021; 14(2):464. https://doi.org/10.3390/en14020464
Chicago/Turabian StyleBose, Aditya, and Vimal K. Viswanathan. 2021. "Mitigating the Piston Effect in High-Speed Hyperloop Transportation: A Study on the Use of Aerofoils" Energies 14, no. 2: 464. https://doi.org/10.3390/en14020464
APA StyleBose, A., & Viswanathan, V. K. (2021). Mitigating the Piston Effect in High-Speed Hyperloop Transportation: A Study on the Use of Aerofoils. Energies, 14(2), 464. https://doi.org/10.3390/en14020464





