Author Contributions
Conceptualization, S.C. and S.M.; methodology, S.C. and S.M.; software, S.C.; validation, S.C.; formal analysis, S.C., S.M., H.K.; investigation, S.C. and M.B.; resources, S.R., T.S., and W.S.; data curation, S.C.; writing—original draft preparation, S.C.; writing—review and editing, S.C., M.B., S.M., S.R., T.S., W.S. and H.K.; visualization, S.C. and S.M.; supervision, S.M.; project administration, S.M. and T.S.; funding acquisition, S.M., T.S. and H.K. All authors have read and agreed to the published version of the manuscript.
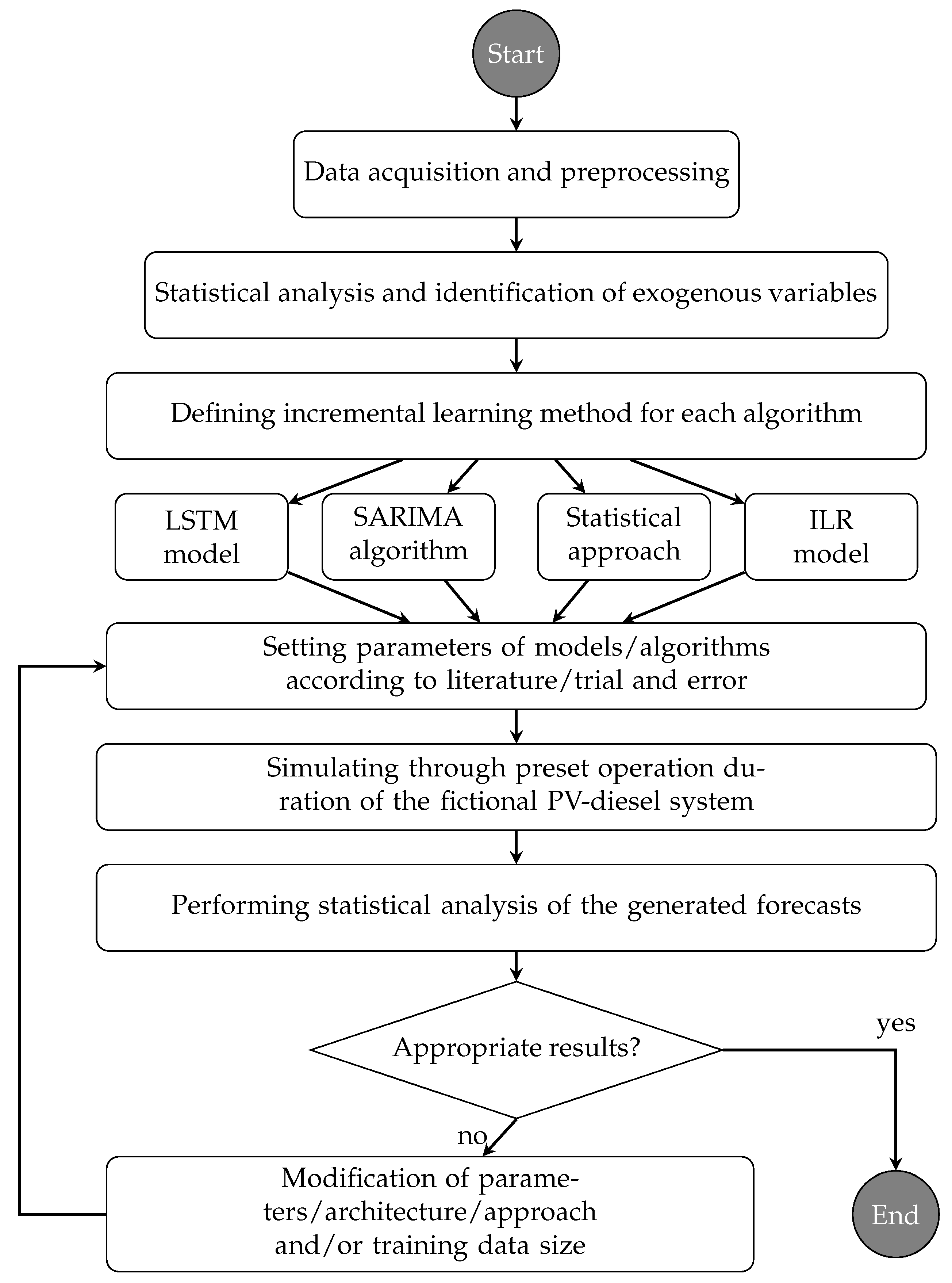
Figure 1.
Flowchart of the research steps conducted in this study.
Figure 1.
Flowchart of the research steps conducted in this study.
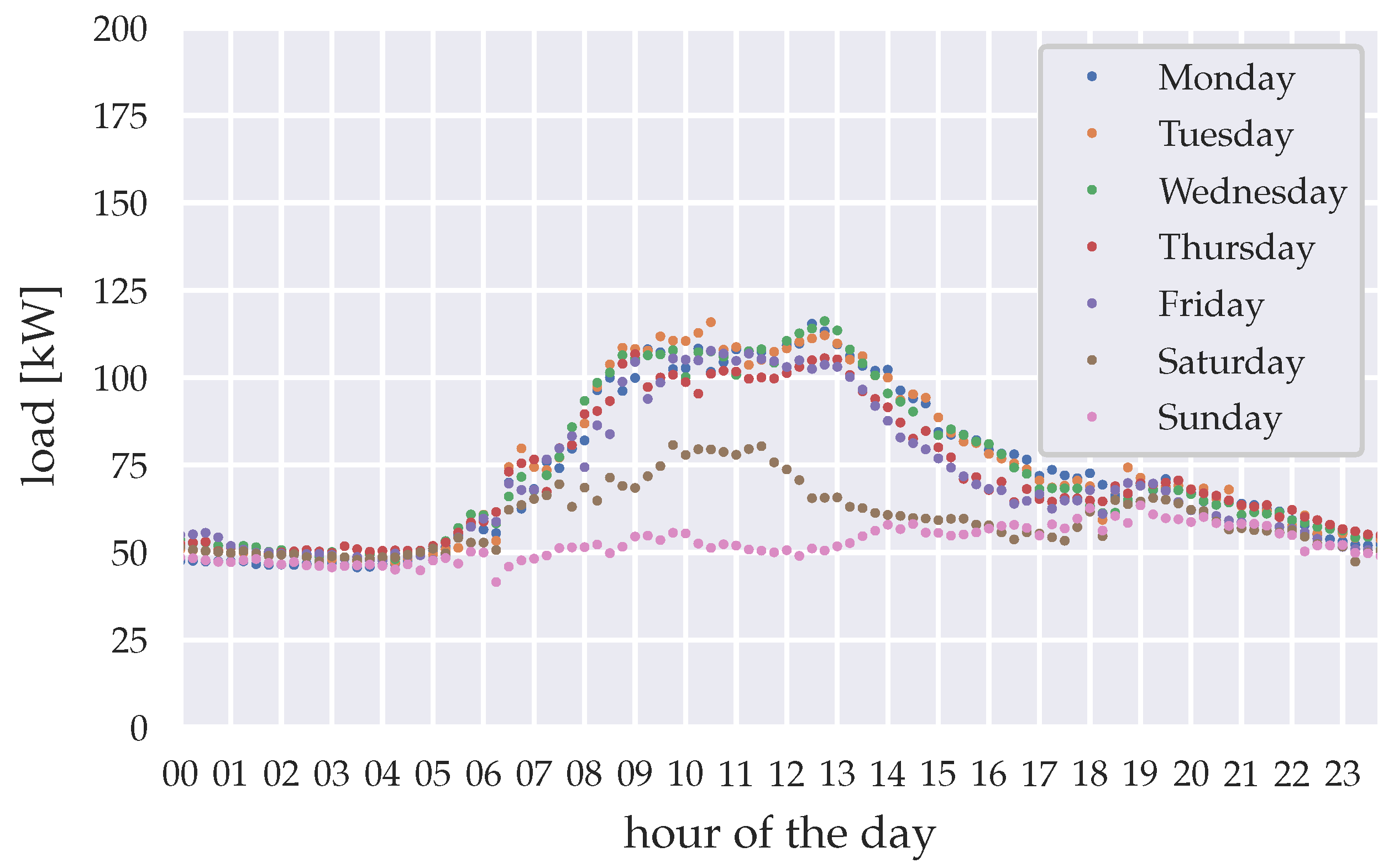
Figure 2.
Mean load for the wet season 2015 (April–October), clustered by weekday.
Figure 2.
Mean load for the wet season 2015 (April–October), clustered by weekday.
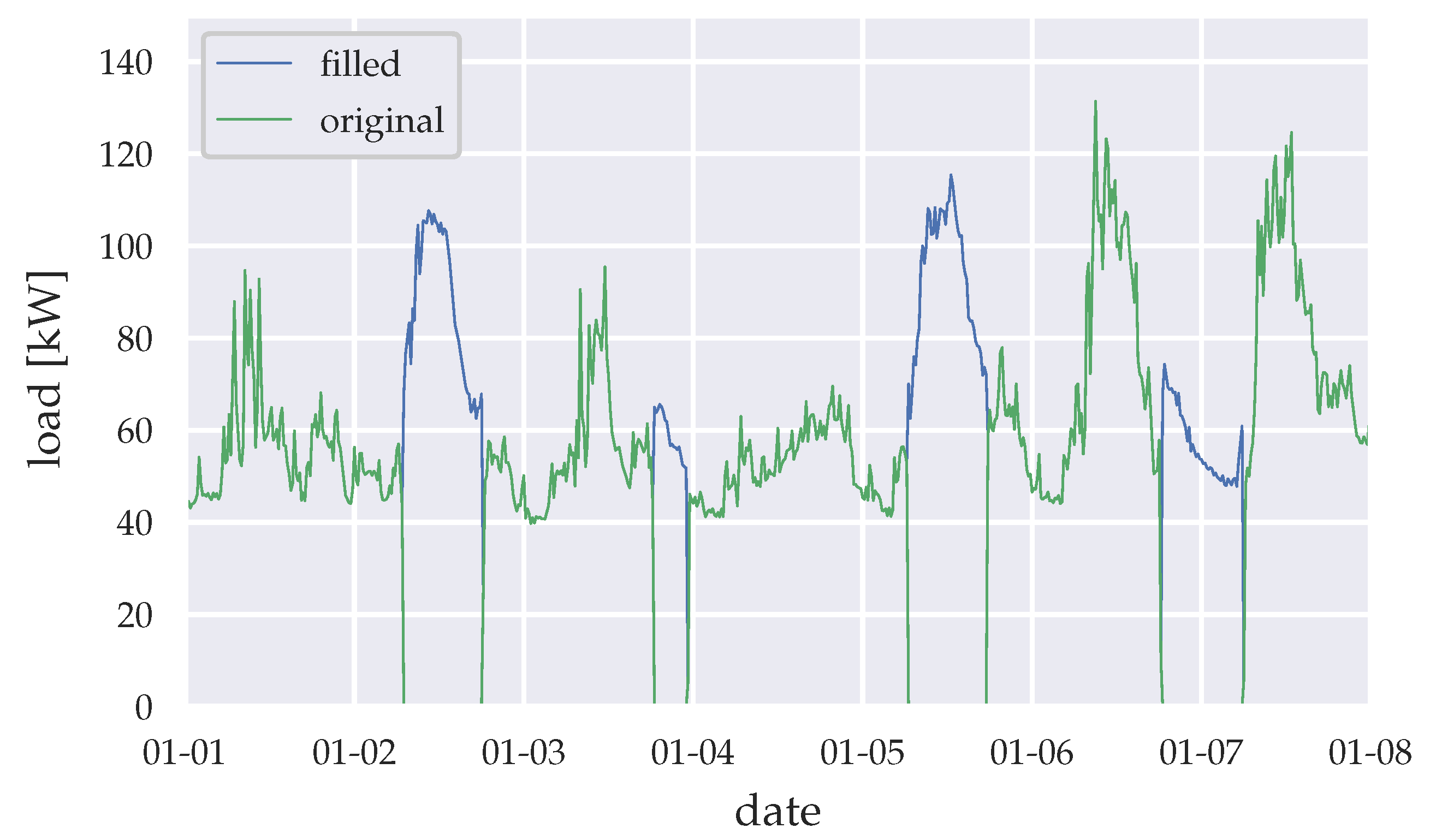
Figure 3.
Data filling (example for the first week of 2015).
Figure 3.
Data filling (example for the first week of 2015).
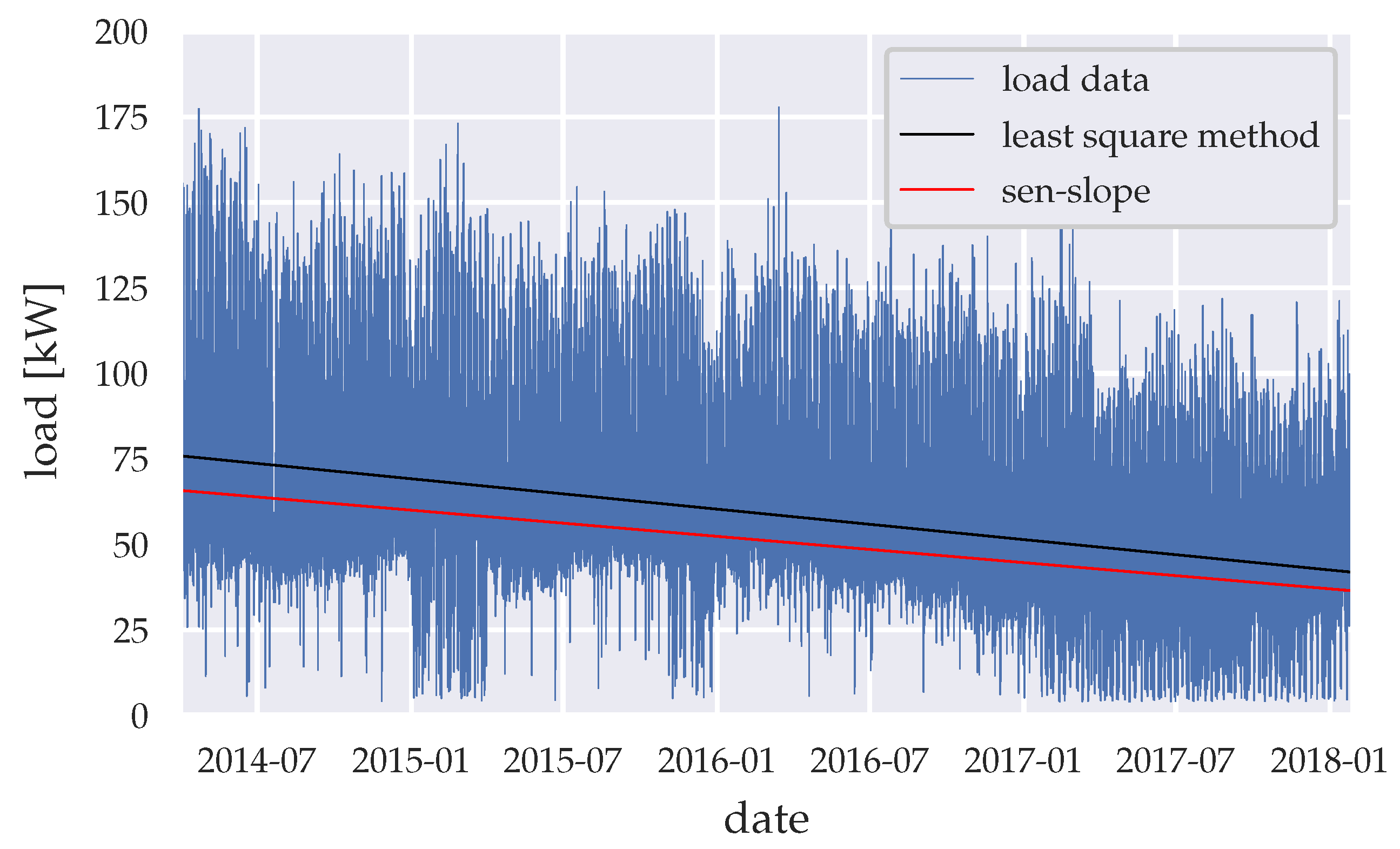
Figure 4.
Load trend throughout the whole time-series period.
Figure 4.
Load trend throughout the whole time-series period.
Figure 5.
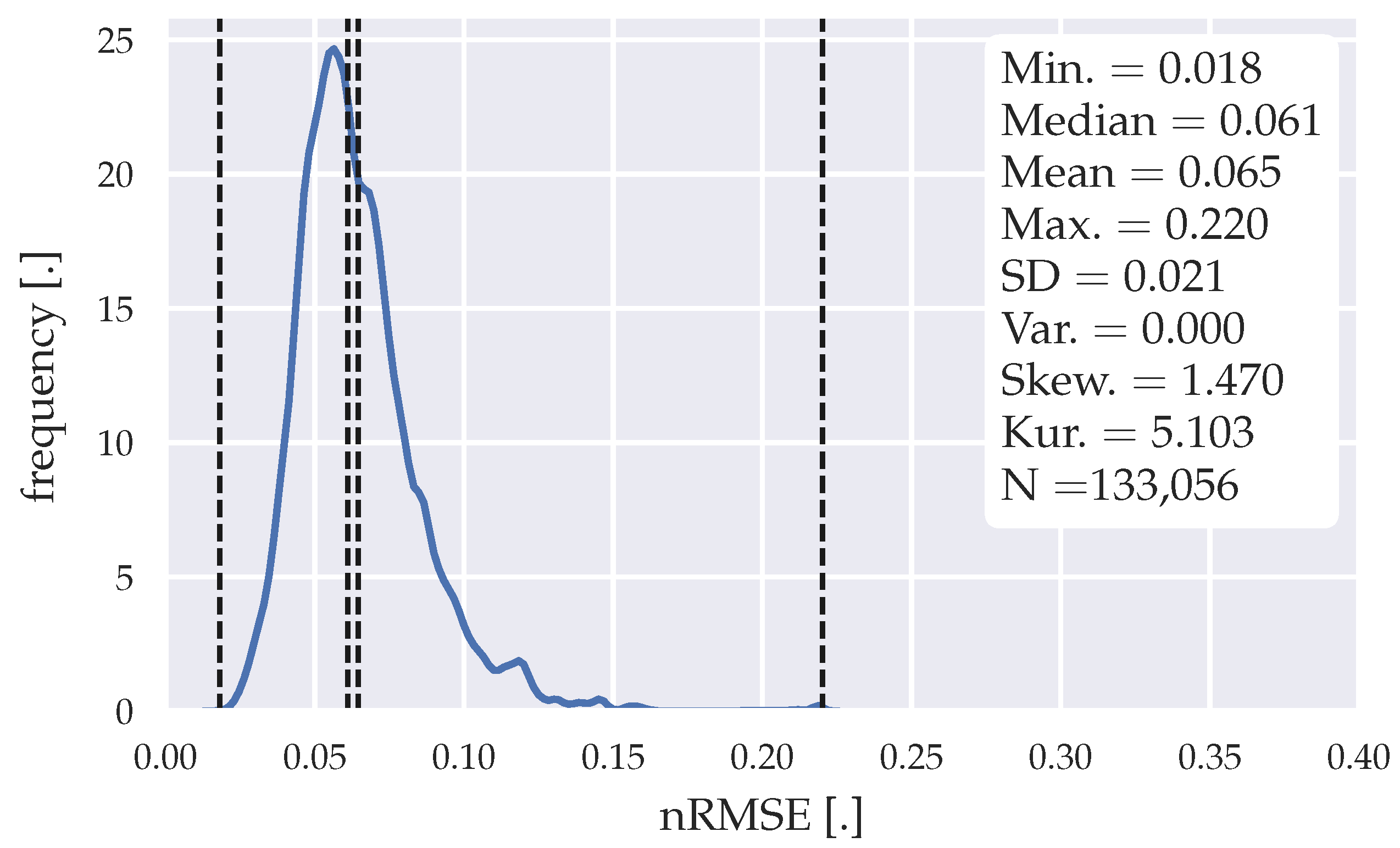
Error distribution of the forecasts generated with the statistical forecasting algorithm.
Figure 5.
Error distribution of the forecasts generated with the statistical forecasting algorithm.
Figure 6.
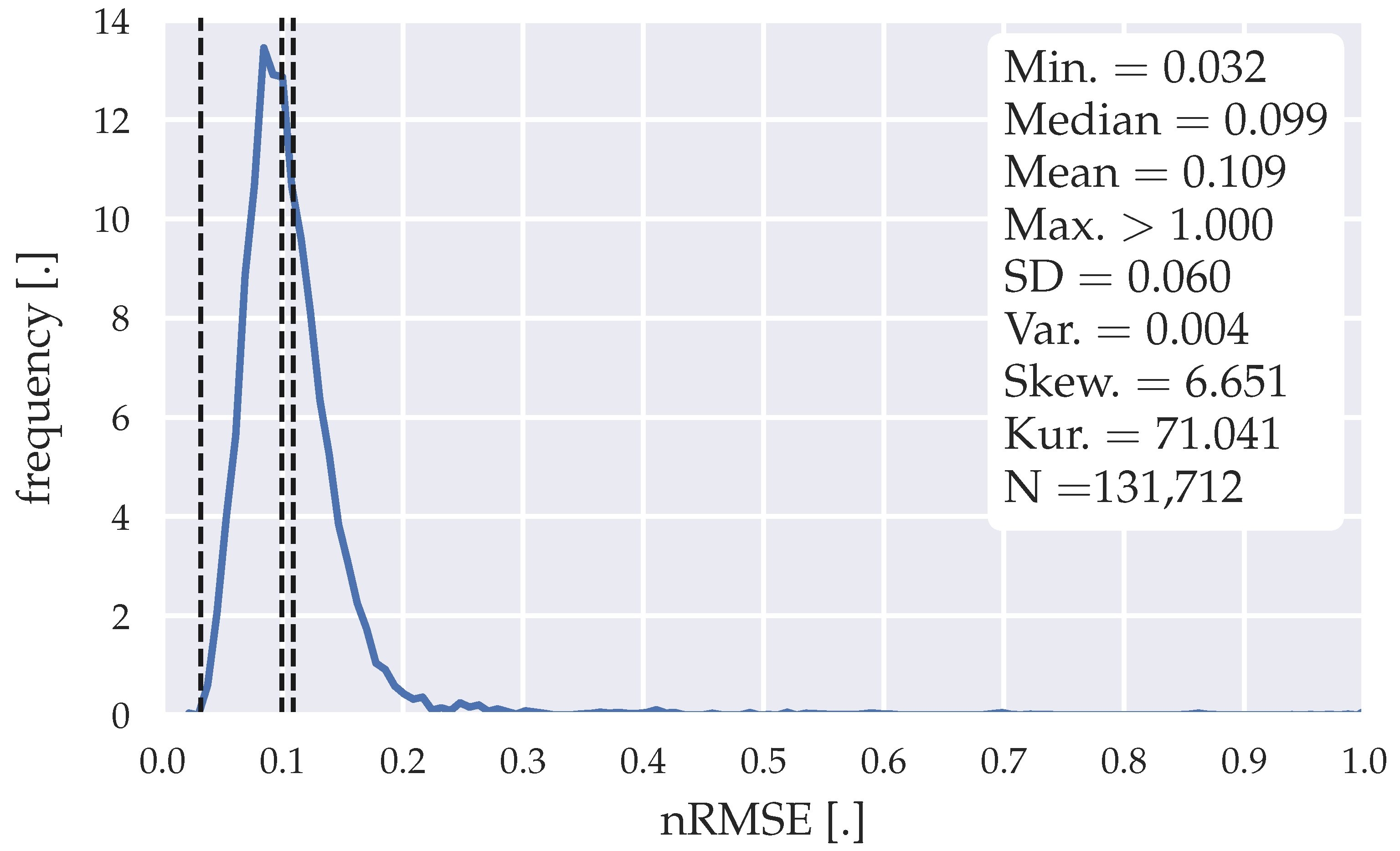
Error distribution of the forecasts generated with the SARIMA algorithm| SARIMA(1,1,1)(1,1,2)96 model.
Figure 6.
Error distribution of the forecasts generated with the SARIMA algorithm| SARIMA(1,1,1)(1,1,2)96 model.
Figure 7.
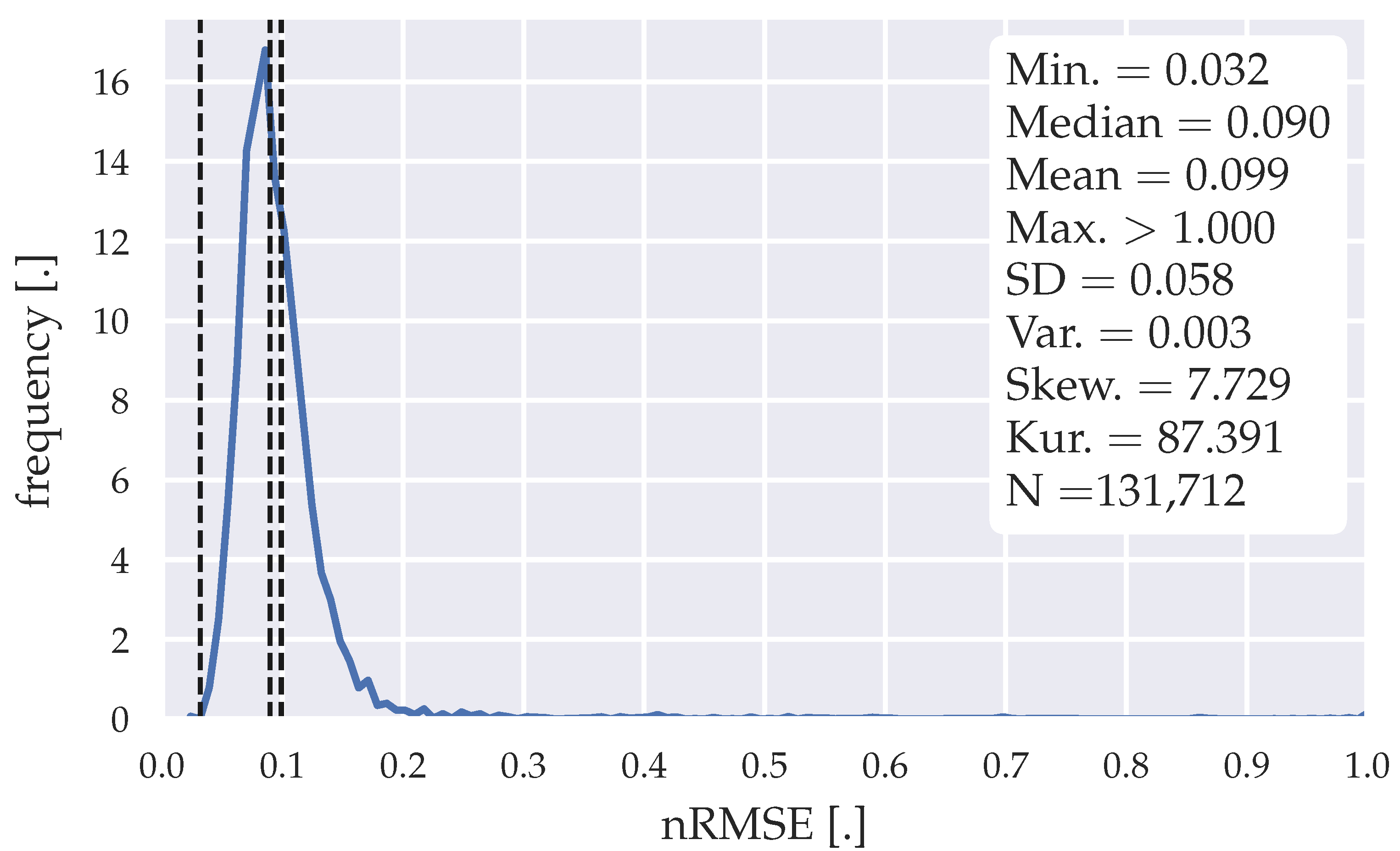
Error distribution of the forecasts generated with the SARIMA algorithm| SARIMA(3,1,1)(0,1,2)96 model.
Figure 7.
Error distribution of the forecasts generated with the SARIMA algorithm| SARIMA(3,1,1)(0,1,2)96 model.
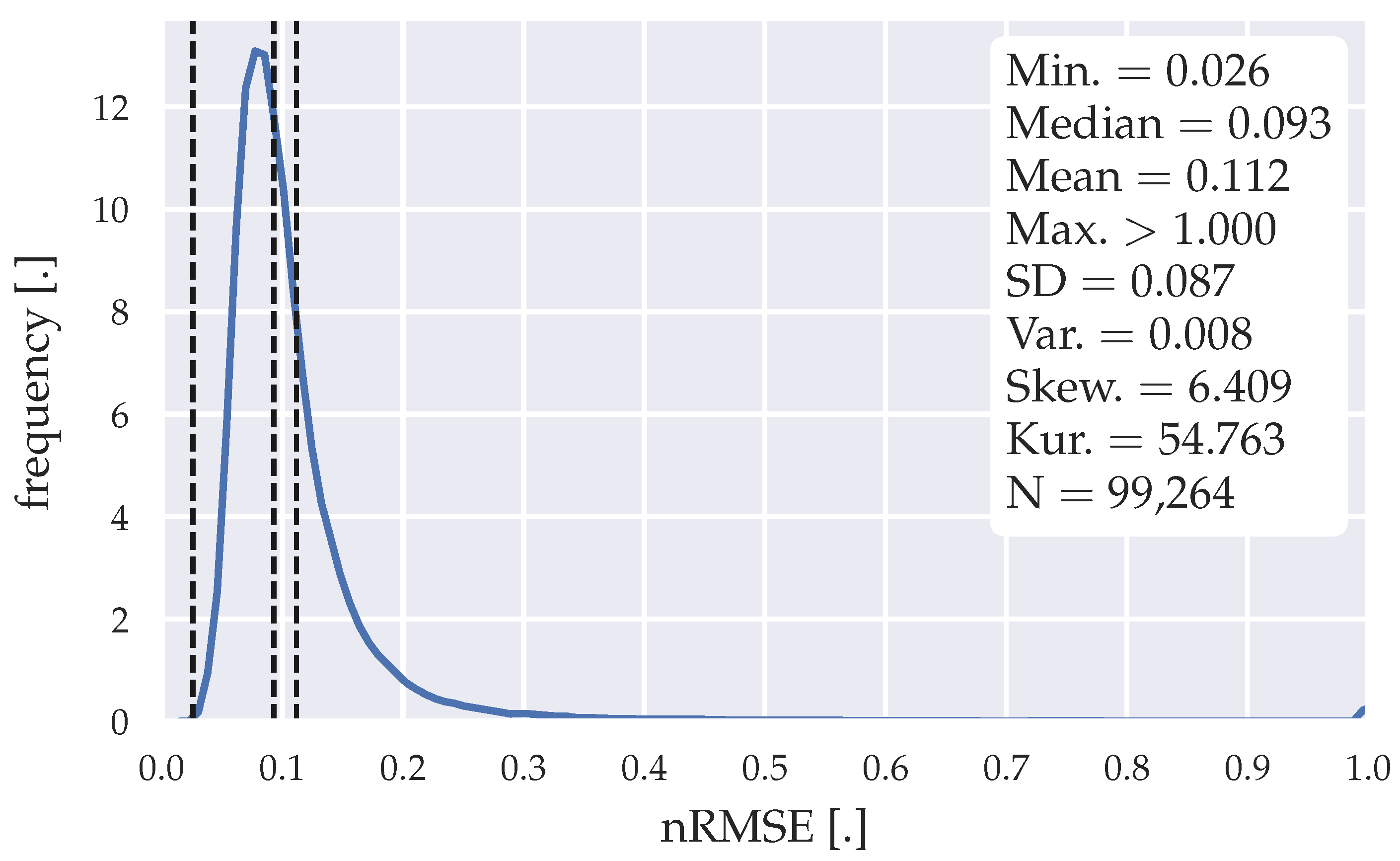
Figure 8.
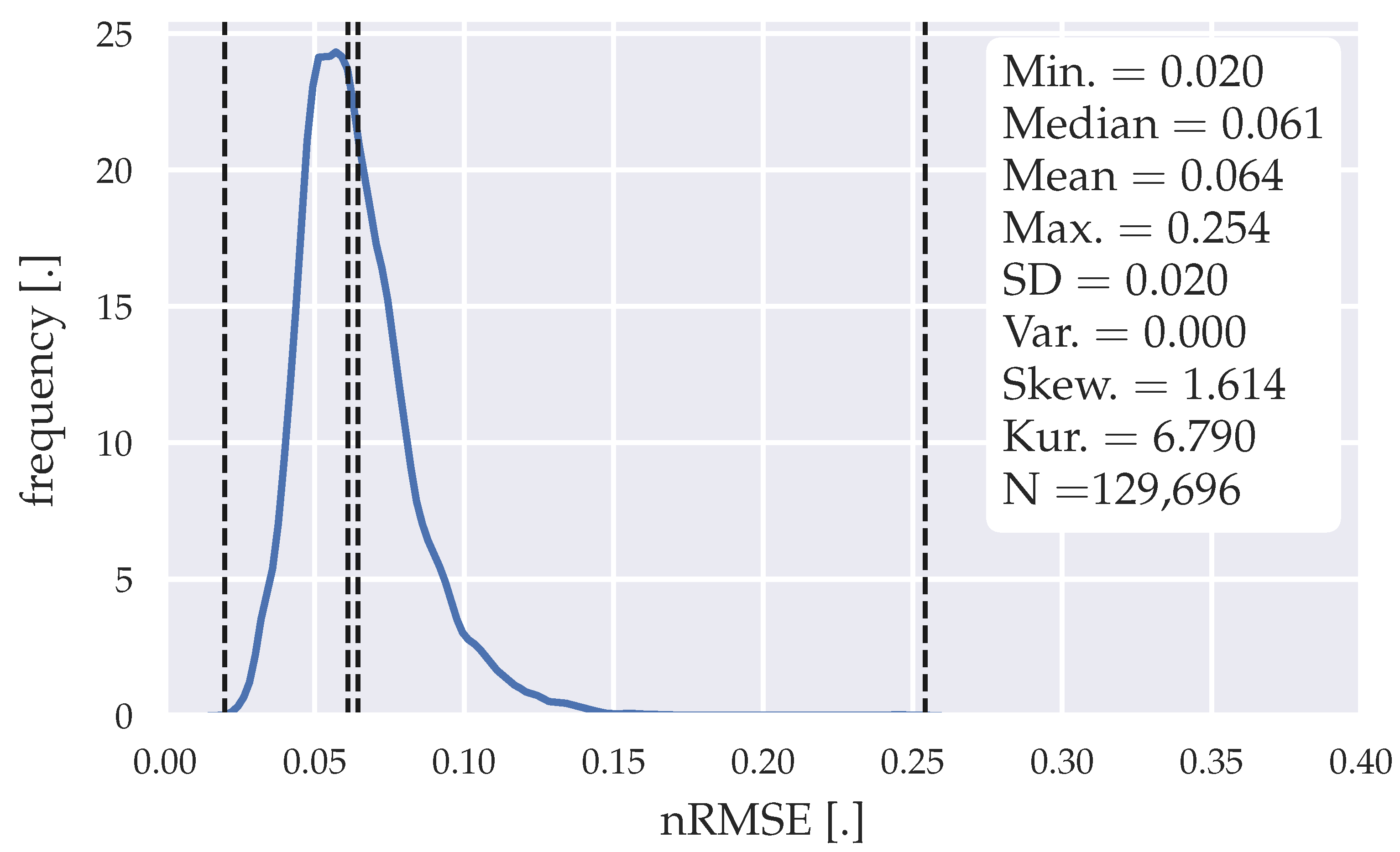
Error distribution of the forecasts generated with the LSTM model.
Figure 8.
Error distribution of the forecasts generated with the LSTM model.
Figure 9.
Error distribution of the forecasts generated with the ILR model.
Figure 9.
Error distribution of the forecasts generated with the ILR model.
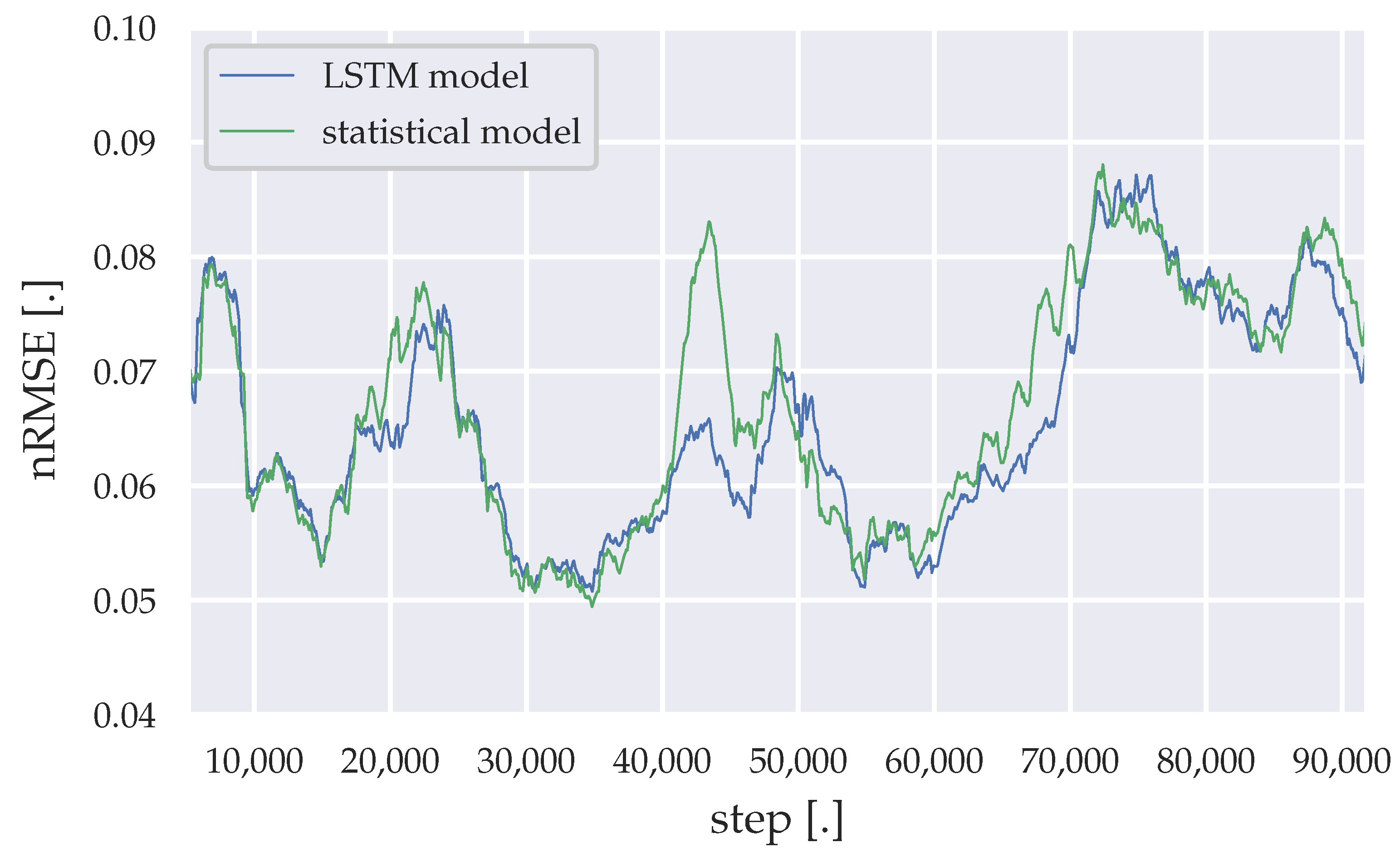
Figure 10.
Moving average of the nRMSE generated by the LSTM model and the statistical algorithm (weekdays).
Figure 10.
Moving average of the nRMSE generated by the LSTM model and the statistical algorithm (weekdays).
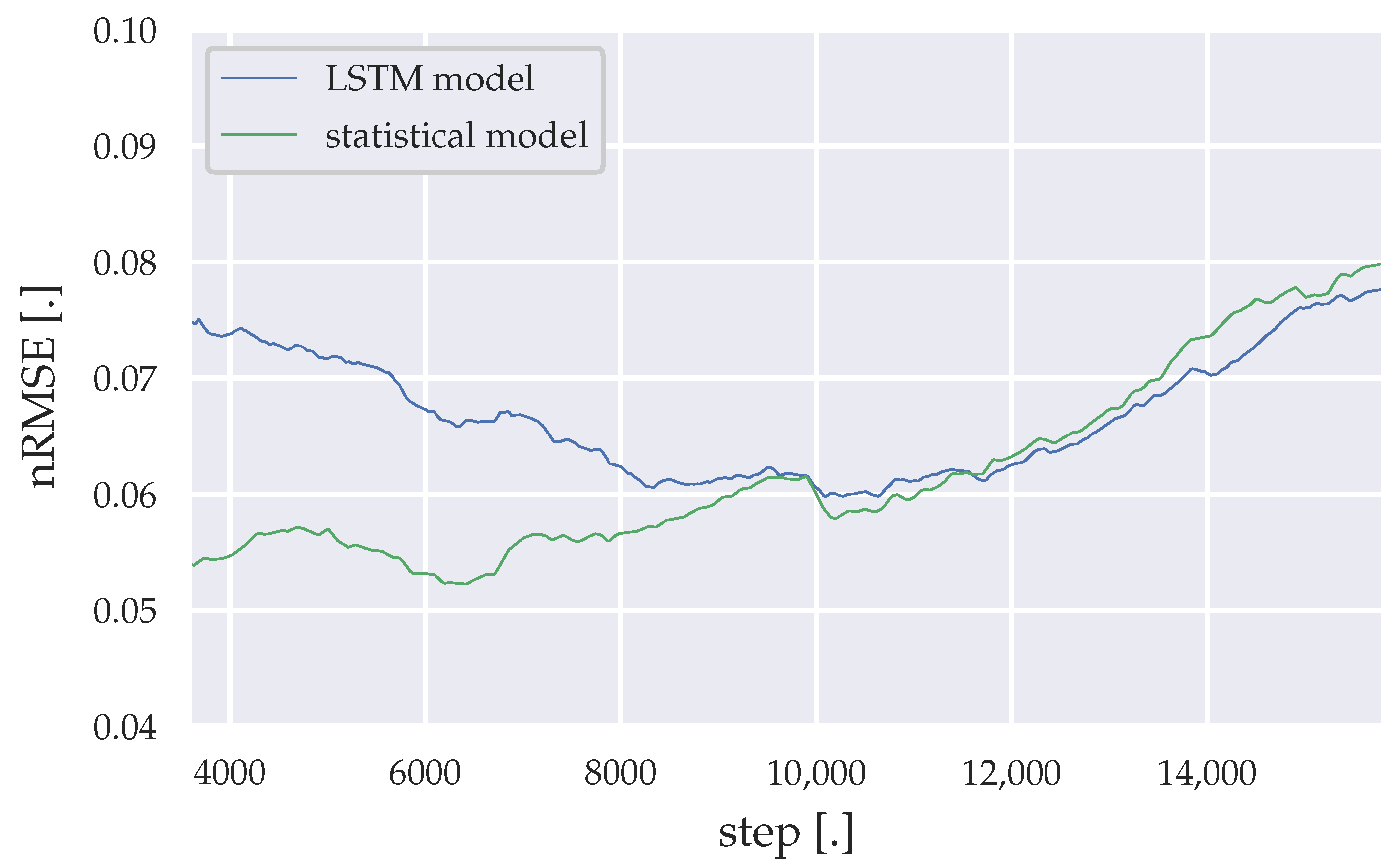
Figure 11.
Moving average of the nRMSE generated by the LSTM model and the statistical algorithm (Saturdays).
Figure 11.
Moving average of the nRMSE generated by the LSTM model and the statistical algorithm (Saturdays).
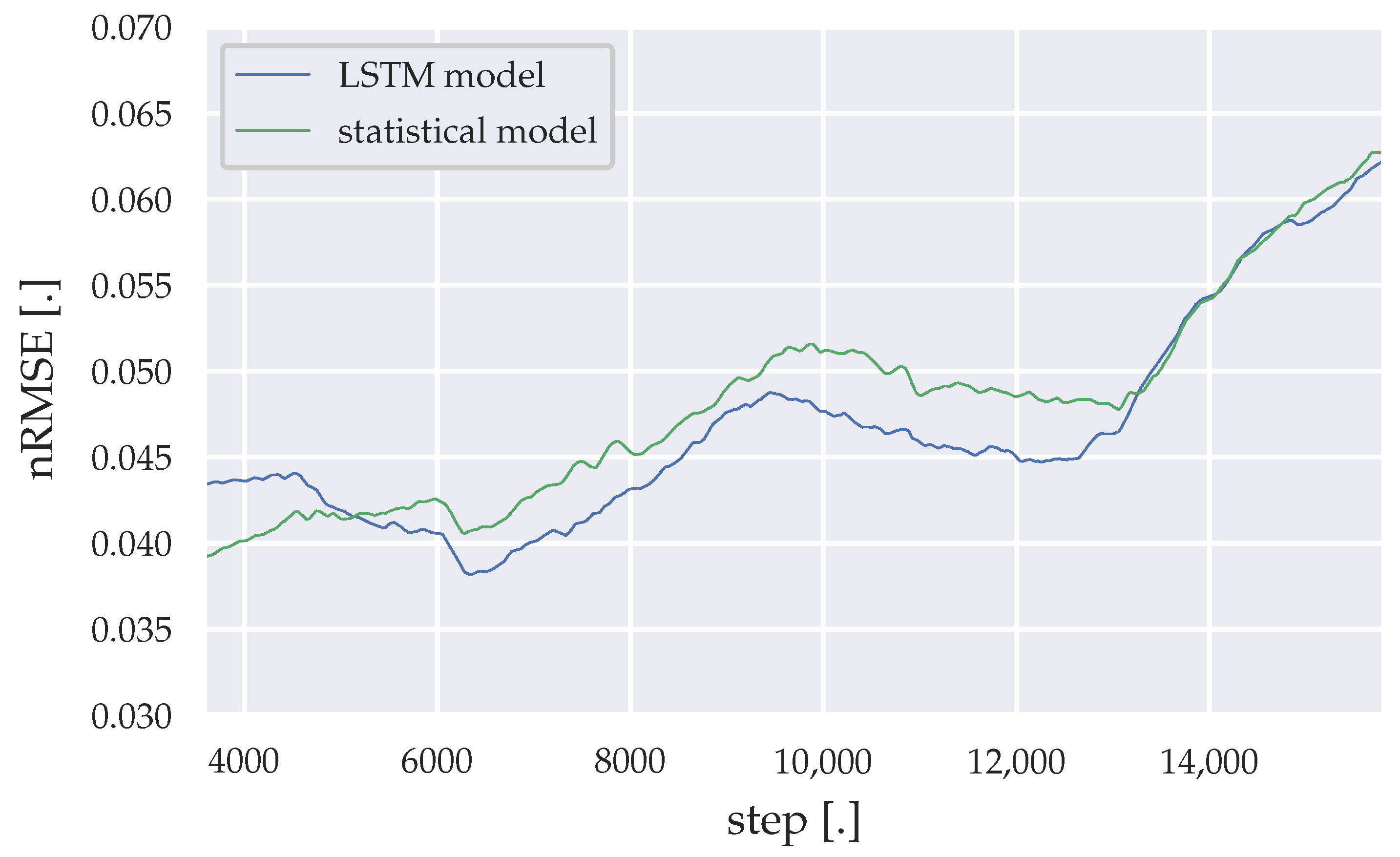
Figure 12.
Moving average of the nRMSE generated by the LSTM model and the statistical algorithm (Sundays).
Figure 12.
Moving average of the nRMSE generated by the LSTM model and the statistical algorithm (Sundays).
Table 1.
Quantitative statistical evaluation, divided by years and seasons (wet: April–October|dry: November–March). “SD” stands for standard deviation. Values in kW, except variance.
Table 1.
Quantitative statistical evaluation, divided by years and seasons (wet: April–October|dry: November–March). “SD” stands for standard deviation. Values in kW, except variance.
| Year | Period | Min. | Max. | Median | Mean | Q0.05 | Q1 | Q3 | Q0.95 | SD | Var. |
|---|
| 2014 | Mar.–Dec. | 4.2 | 177.36 | 61.28 | 69.52 | 42.88 | 51.08 | 81.48 | 121.96 | 24.99 | 624.51 |
| wet season | 5.68 | 177.36 | 60.68 | 68.90 | 42.40 | 50.32 | 80.88 | 121.71 | 24.09 | 629.60 |
| dry season | 4.2 | 175 | 63.04 | 71.62 | 45.51 | 53.52 | 83.17 | 123.4 | 24.52 | 601.33 |
| 2015 | Jan.–Dec. | 4.4 | 173 | 59.75 | 66.57 | 42.44 | 50.25 | 77.77 | 111.63 | 22.10 | 488.58 |
| wet season | 4.44 | 154.5 | 58.86 | 65.78 | 42.38 | 50.09 | 76.19 | 109.5 | 21.29 | 453.13 |
| dry season | 4.4 | 173 | 61.06 | 67.69 | 42.59 | 50.47 | 79.63 | 115.06 | 23.17 | 536.70 |
| 2016 | Jan.–Dec. | 5.68 | 177.75 | 53.49 | 58.87 | 33.41 | 43.72 | 70.25 | 100.81 | 20.78 | 431.75 |
| wet season | 5.68 | 155.5 | 53.4 | 59.01 | 35.84 | 43.75 | 70.19 | 99.81 | 20.17 | 406.87 |
| dry season | 6.16 | 177.75 | 53.69 | 58.66 | 30.84 | 43.59 | 70.44 | 101.88 | 21.60 | 466.74 |
| 2017 | Jan.–Dec. | 4.0 | 154.88 | 41.19 | 44.31 | 23.56 | 33.15 | 52.38 | 77.63 | 16.67 | 278.00 |
| wet season | 4.04 | 121.81 | 40.69 | 43.36 | 22.48 | 32.44 | 51.53 | 75.01 | 16.10 | 259.23 |
| dry season | 4.0 | 154.88 | 41.88 | 45.65 | 25.08 | 34.03 | 53.56 | 81.18 | 17.37 | 301.55 |
| 2018 | Jan.–Feb. | 4.32 | 121.16 | 40.92 | 43.49 | 23.78 | 33.76 | 49.69 | 75.76 | 15.78 | 249.04 |
Table 2.
Mann–Kendall significance test, divided by years.
Table 2.
Mann–Kendall significance test, divided by years.
| Year | Period | p-Value | z-Value |
|---|
| 2014 | Mar.–Dec. | 0.089 | 1.7 |
| 2015 | Jan.–Dec. | <<0.05 | −14.13 |
| 2016 | Jan.–Dec. | <<0.05 | −52.84 |
| 2017 | Jan.–Dec. | <<0.05 | −17.26 |
| 2018 | Jan.–Feb. | <<0.05 | 8.35 |
Table 3.
Statistical results with different time frames, divided into the photovoltaic geographical information system (PVGIS) data set and the European center for medium-range weather forecasts 5th generation (ERA5) data set.
Table 3.
Statistical results with different time frames, divided into the photovoltaic geographical information system (PVGIS) data set and the European center for medium-range weather forecasts 5th generation (ERA5) data set.
| Data Set | Timeframe | Pearson’s r-Value | p-Value |
|---|
| PVGIS | whole day | 0.54 | <<0.05 |
| PVGIS | day-time | 0.2 | <<0.05 |
| PVGIS | night-time | 0.49 | <<0.05 |
| ERA5 | whole day | 0.5 | <<0.05 |
| ERA5 | day-time | 0.27 | <<0.05 |
| ERA5 | night-time | 0.28 | <<0.05 |
Table 4.
Statistical results of both data sets with the cooling degree day (CDD).
Table 4.
Statistical results of both data sets with the cooling degree day (CDD).
| Data Set | Timeframe | Pearson’s r-Value | p-Value |
|---|
| PVGIS | whole day | −0.14 | <<0.05 |
| ERA5 | whole day | 0.01 | 0.61 |
Table 5.
Comparison of the normalized root-mean-square error (nRMSE), with different horizon configurations.
Table 5.
Comparison of the normalized root-mean-square error (nRMSE), with different horizon configurations.
| Horizon Configuration | Min. nRMSE | Med. nRMSE | Mean nRMSE | Max. nRMSE |
|---|
| 4 weeks | 0.023 | 0.065 | 0.068 | 0.2 |
| 8 weeks | 0.018 | 0.065 | 0.061 | 0.22 |
| 12 weeks | 0.016 | 0.065 | 0.061 | 0.232 |
| 16 weeks | 0.018 | 0.065 | 0.062 | 0.234 |
Table 6.
Long short-term memory (LSTM) neural network architecture.
Table 6.
Long short-term memory (LSTM) neural network architecture.
| Layer-Type | Amount of Cells | Parameters | Activation Function |
|---|
| LSTM | 96 | 37,632 | rectified linear unit |
| LSTM | 192 | 221,962 | rectified linear unit |
| fully connected neural network | 192 | 37,056 | rectified linear unit |
| fully connected neural network | 96 | 18,528 | rectified linear unit |
Table 7.
Fitting settings for each neural network.
Table 7.
Fitting settings for each neural network.
| Type | Epochs | Batch Size | Loss Function | Optimizer |
|---|
| initial weekday | 5 | 12 | mean squared error | adaptive moment estimation |
| initial saturday | 5 | 12 | mean squared error | adaptive moment estimation |
| initial sunday | 5 | 6 | mean squared error | adaptive moment estimation |
| continous weekday | 2 | 12 | mean squared error | adaptive moment estimation |
| continous saturday | 2 | 12 | mean squared error | adaptive moment estimation |
| continous sunday | 2 | 6 | mean squared error | adaptive moment estimation |
Table 8.
nRMSE with different prediction horizons|statistical forecasting algorithm.
Table 8.
nRMSE with different prediction horizons|statistical forecasting algorithm.
| Prediction Horizon | Min. nRMSE | Median nRMSE | Mean nRMSE | Max. nRMSE |
|---|
| 3 h | 0.003 | 0.047 | 0.056 | 0.41 |
| 6 h | 0.004 | 0.051 | 0.058 | 0.385 |
| 9 h | 0.005 | 0.054 | 0.060 | 0.338 |
| 12 h | 0.009 | 0.056 | 0.062 | 0.302 |
| 15 h | 0.011 | 0.058 | 0.063 | 0.272 |
| 18 h | 0.015 | 0.060 | 0.064 | 0.25 |
| 21 h | 0.018 | 0.061 | 0.064 | 0.234 |
| 24 h | 0.018 | 0.061 | 0.065 | 0.220 |
Table 9.
Computational effort for the statistical forecasting method, divided in weekday, Saturday, and Sunday batching, clustered in training and prediction efforts.
Table 9.
Computational effort for the statistical forecasting method, divided in weekday, Saturday, and Sunday batching, clustered in training and prediction efforts.
| Type | Data Batching | Median Computation Time | Overall Computation Time |
|---|
| training | weekday | 0.067 ms | 131.428 ms |
| Saturday | 0.064 ms | 12.229 ms |
| Sunday | 0.014 ms | 2.763 ms |
| prediction | weekday | 0.032 ms | 2.905 s |
| Saturday | 0.029 ms | 0.446 s |
| Sunday | 0.029 ms | 0.452 s |
Table 10.
nRMSE with different prediction horizons|SARIMA(1,1,1)(1,1,2)96 model.
Table 10.
nRMSE with different prediction horizons|SARIMA(1,1,1)(1,1,2)96 model.
| Prediction Horizon | Min. nRMSE | Median nRMSE | Mean nRMSE | Max. nRMSE |
|---|
| 3 h | 0 | 0.070 | 0.086 | >1 |
| 6 h | 0 | 0.075 | 0.09 | >1 |
| 9 h | 0.002 | 0.081 | 0.094 | >1 |
| 12 h | 0.005 | 0.087 | 0.098 | >1 |
| 15 h | 0.021 | 0.091 | 0.102 | >1 |
| 18 h | 0.028 | 0.095 | 0.105 | >1 |
| 21 h | 0.029 | 0.097 | 0.107 | >1 |
| 24 h | 0.032 | 0.099 | 0.109 | >1 |
Table 11.
nRMSE with different prediction horizons|SARIMA(3,1,1)(0,1,2)96 model.
Table 11.
nRMSE with different prediction horizons|SARIMA(3,1,1)(0,1,2)96 model.
| Prediction Horizon | Min. nRMSE | Median nRMSE | Mean nRMSE | Max. nRMSE |
|---|
| 3 h | 0 | 0.066 | 0.081 | >1 |
| 6 h | 0.002 | 0.071 | 0.085 | >1 |
| 9 h | 0.002 | 0.076 | 0.088 | >1 |
| 12 h | 0.003 | 0.080 | 0.091 | >1 |
| 15 h | 0.018 | 0.084 | 0.094 | >1 |
| 18 h | 0.026 | 0.086 | 0.096 | >1 |
| 21 h | 0.029 | 0.088 | 0.098 | >1 |
| 24 h | 0.032 | 0.09 | 0.099 | >1 |
Table 12.
Computational effort for both SARIMA configurations, divided in weekday, Saturday, and Sunday batching, clustered in training and prediction efforts.
Table 12.
Computational effort for both SARIMA configurations, divided in weekday, Saturday, and Sunday batching, clustered in training and prediction efforts.
| Configuration | Type | Data Batching | Median Computation Time | Overall Computation Time |
|---|
| SARIMA 1,1,1, 1,1,2 | training | weekday | 17.580 s | 4.787 h |
| Saturday | 22.403 s | 1.221 h |
| Sunday | 17.075 s | 0.931 h |
| prediction | weekday | 0.488 ms | 46.440 s |
| Saturday | 0.510 ms | 8.546 s |
| Sunday | 0.490 ms | 10.505 s |
| SARIMA 3,1,1, 0,1,2 | training | weekday | 20.141 s | 5.484 h |
| Saturday | 22.323 s | 1.216 h |
| Sunday | 17.041 s | 0.928 h |
| prediction | weekday | 0.460 ms | 45.660 s |
| Saturday | 0.499 ms | 8.678 s |
| Sunday | 0.481 ms | 8.348 s |
Table 13.
nRMSE with different prediction horizons|LSTM model.
Table 13.
nRMSE with different prediction horizons|LSTM model.
| Prediction Horizon | Min. nRMSE | Median nRMSE | Mean nRMSE | Max. nRMSE |
|---|
| 3 h | 0.002 | 0.048 | 0.058 | 0.376 |
| 6 h | 0.006 | 0.053 | 0.06 | 0.287 |
| 9 h | 0.007 | 0.056 | 0.062 | 0.26 |
| 12 h | 0.011 | 0.058 | 0.063 | 0.279 |
| 15 h | 0.018 | 0.059 | 0.064 | 0.281 |
| 18 h | 0.019 | 0.06 | 0.064 | 0.276 |
| 21 h | 0.02 | 0.061 | 0.064 | 0.266 |
| 24 h | 0.02 | 0.061 | 0.064 | 0.254 |
Table 14.
Computational effort for the LSTM model, divided in weekday, Saturday, and Sunday batching, clustered in training and prediction efforts.
Table 14.
Computational effort for the LSTM model, divided in weekday, Saturday, and Sunday batching, clustered in training and prediction efforts.
| Type | Data Batching | Median Computation Time | Overall Computation Time |
|---|
| training | weekday | 6.941 s | 22.115 min |
| Saturday | 4.783 s | 26.326 min |
| Sunday | 4.784 s | 26.272 min |
| prediction | weekday | 39.987 ms | 61.786 min |
| Saturday | 40.106 ms | 25.761 min |
| Sunday | 40.108 ms | 25.696 min |
Table 15.
nRMSE with different prediction horizons|ILR method.
Table 15.
nRMSE with different prediction horizons|ILR method.
| Prediction Horizon | Min. nRMSE | Median nRMSE | Mean nRMSE | Max. nRMSE |
|---|
| 3 h | 0.003 | 0.063 | 0.086 | >1 |
| 6 h | 0.007 | 0.075 | 0.096 | >1 |
| 9 h | 0.012 | 0.082 | 0.102 | >1 |
| 12 h | 0.017 | 0.087 | 0.105 | >1 |
| 15 h | 0.018 | 0.090 | 0.108 | >1 |
| 18 h | 0.021 | 0.092 | 0.11 | >1 |
| 21 h | 0.025 | 0.093 | 0.111 | >1 |
| 24 h | 0.026 | 0.093 | 0.112 | >1 |
Table 16.
Computational effort for the ILR method, clustered in initial training, training, and prediction efforts.
Table 16.
Computational effort for the ILR method, clustered in initial training, training, and prediction efforts.
| Type | Median Computation Time | Overall Computation Time |
|---|
| initial training | - | 0.125 ms |
| training | 0.126 ms | 12.630 s |
| prediction | 21.406 ms | 31.584 min |
Table 17.
nRMSE comparison of all algorithms, with a forecasting horizon of 24 h.
Table 17.
nRMSE comparison of all algorithms, with a forecasting horizon of 24 h.
| Algorithm | Min. nRMSE | Median nRMSE | Mean nRMSE | Max. nRMSE |
|---|
| LSTM model | 0.02 | 0.061 | 0.064 | 0.376 |
| statistical algorithm | 0.018 | 0.061 | 0.065 | 0.22 |
| SARIMA 1,1,1 1,1,2 | 0.032 | 0.099 | 0.109 | >1 |
| SARIMA 3,1,1 0,1,2 | 0.032 | 0.09 | 0.099 | >1 |
| ILR algorithm | 0.018 | 0.090 | 0.108 | >1 |
Table 18.
Descriptive statistics of the moving average nRMSE, generated by the LSTM model and the statistical algorithm (weekdays).
Table 18.
Descriptive statistics of the moving average nRMSE, generated by the LSTM model and the statistical algorithm (weekdays).
| Model | Min. | Max. | Mean | Median |
|---|
| LSTM model | 0.051 | 0.087 | 0.065 | 0.063 |
| statistical algorithm | 0.049 | 0.088 | 0.067 | 0.066 |
Table 19.
Descriptive statistics of the moving average nRMSE, generated by the LSTM model and the statistical algorithm (Saturdays).
Table 19.
Descriptive statistics of the moving average nRMSE, generated by the LSTM model and the statistical algorithm (Saturdays).
| Model | Min. | Max. | Mean | Median |
|---|
| LSTM model | 0.060 | 0.078 | 0.067 | 0.066 |
| statistical algorithm | 0.052 | 0.079 | 0.061 | 0.059 |
Table 20.
Descriptive statistics of the moving average nRMSE, generated by the LSTM model and the statistical algorithm (Sundays).
Table 20.
Descriptive statistics of the moving average nRMSE, generated by the LSTM model and the statistical algorithm (Sundays).
| Model | Min. | Max. | Mean | Median |
|---|
| LSTM model | 0.038 | 0.062 | 0.047 | 0.046 |
| statistical algorithm | 0.039 | 0.061 | 0.048 | 0.048 |