A DCM Single-Controlled Three-Phase SEPIC-Type Rectifier
Abstract
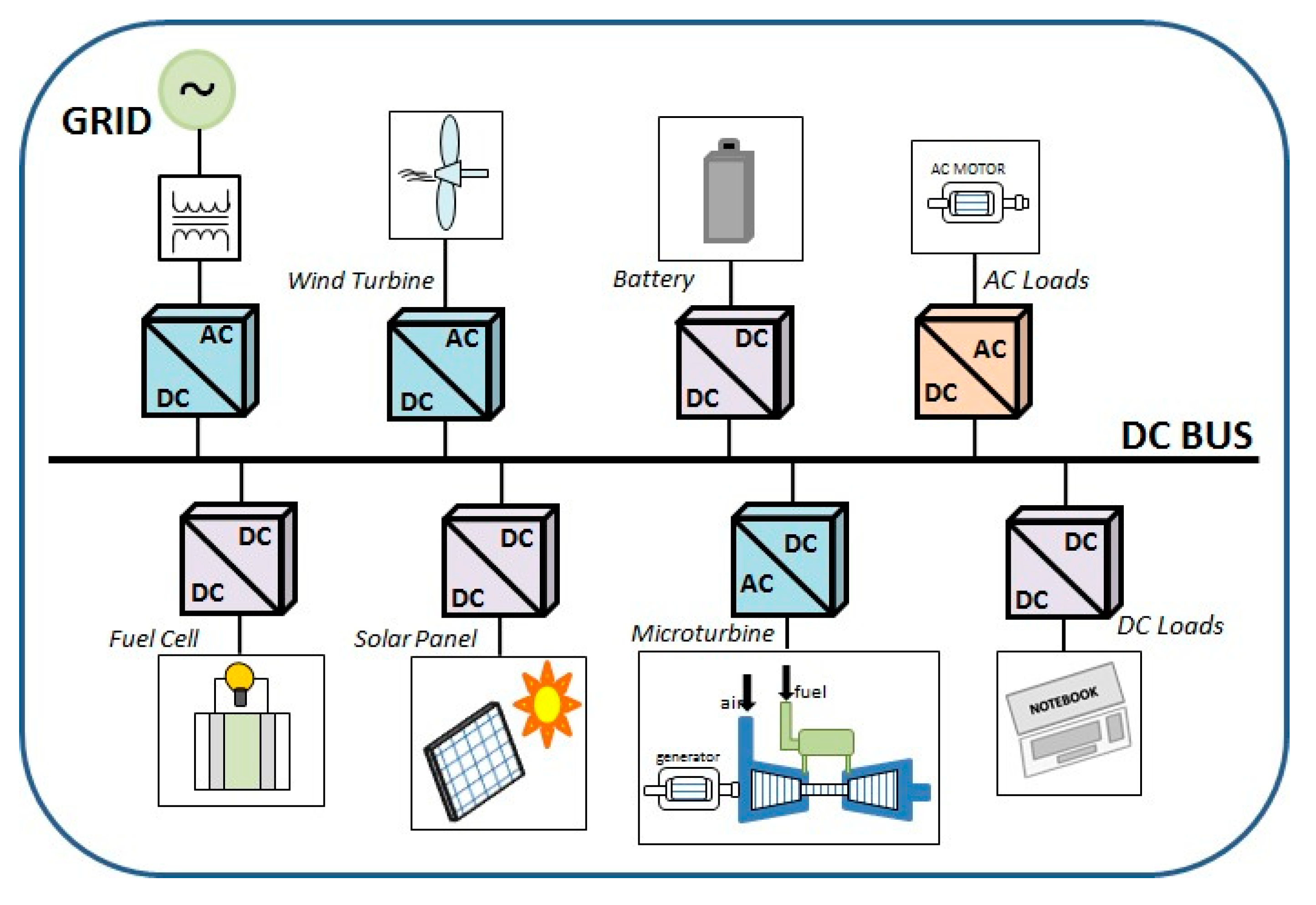
1. Introduction
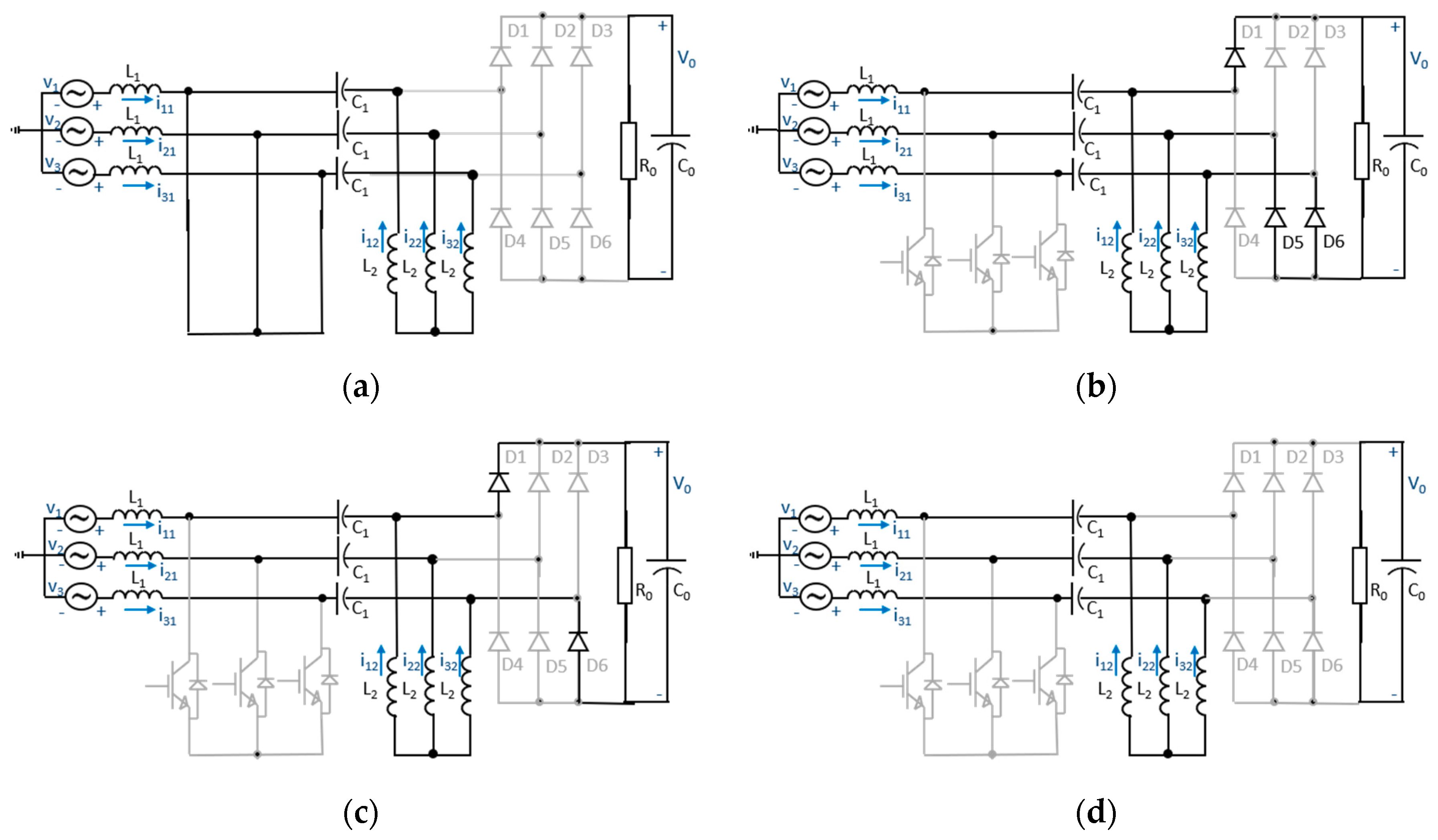
2. Proposed Converter
2.1. SEPIC-Type Rectifier Operation Principle
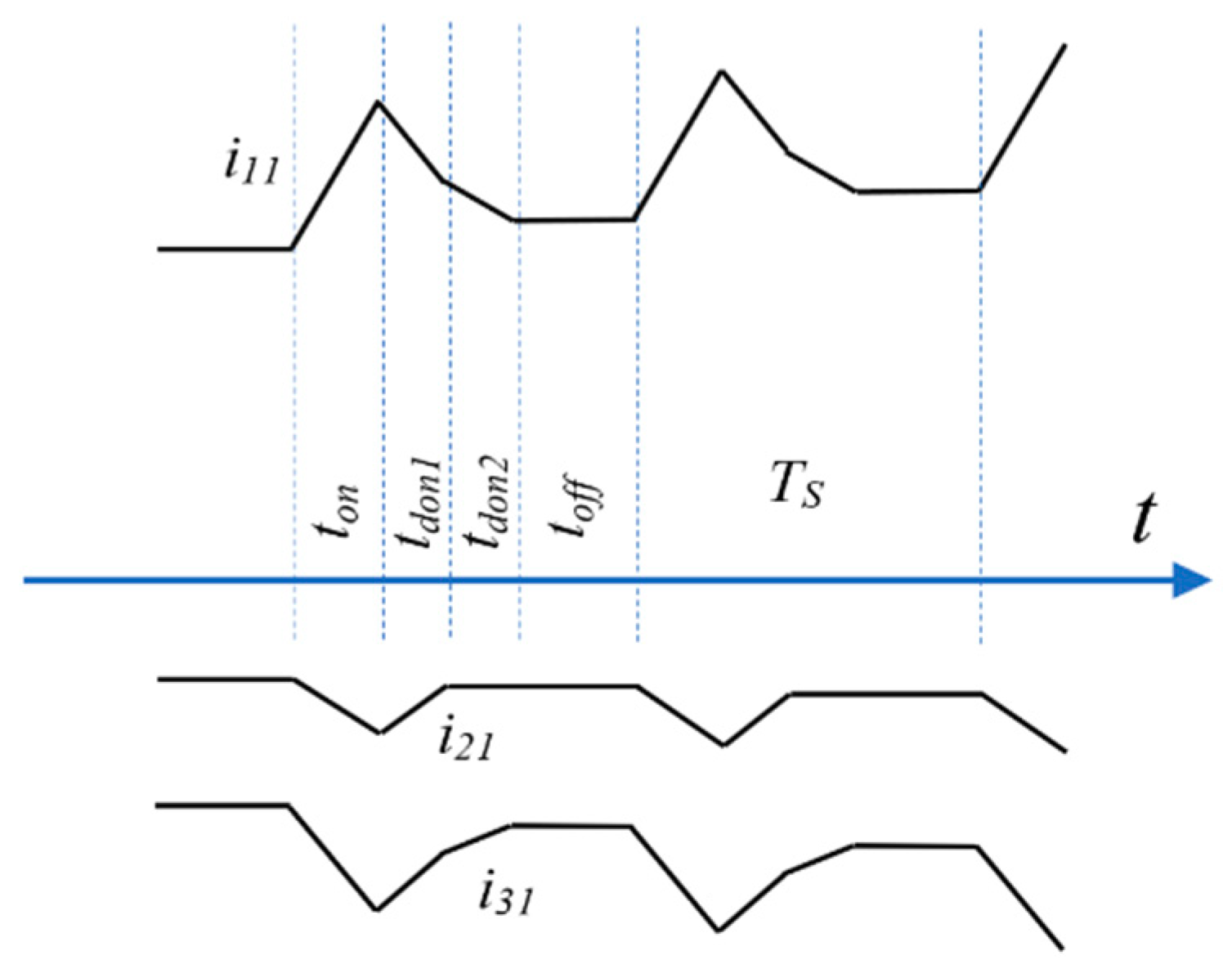
2.1.1. First Stage—Switches Turned on (ton)
2.1.2. Second Stage (tdon1)
2.1.3. Third Stage (tdon2)
2.1.4. Fourth Stage—Freewheeling (toff)
2.2. Theoretical Converter Analysis
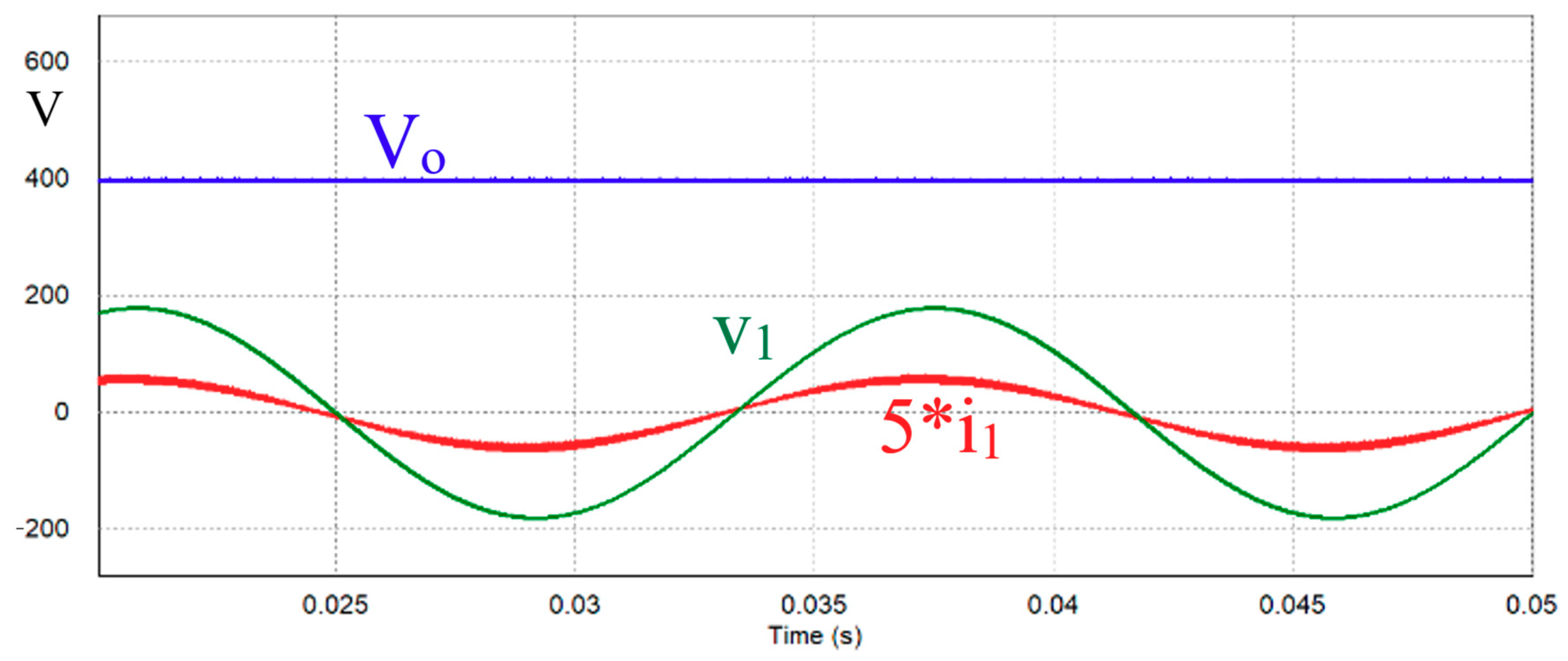
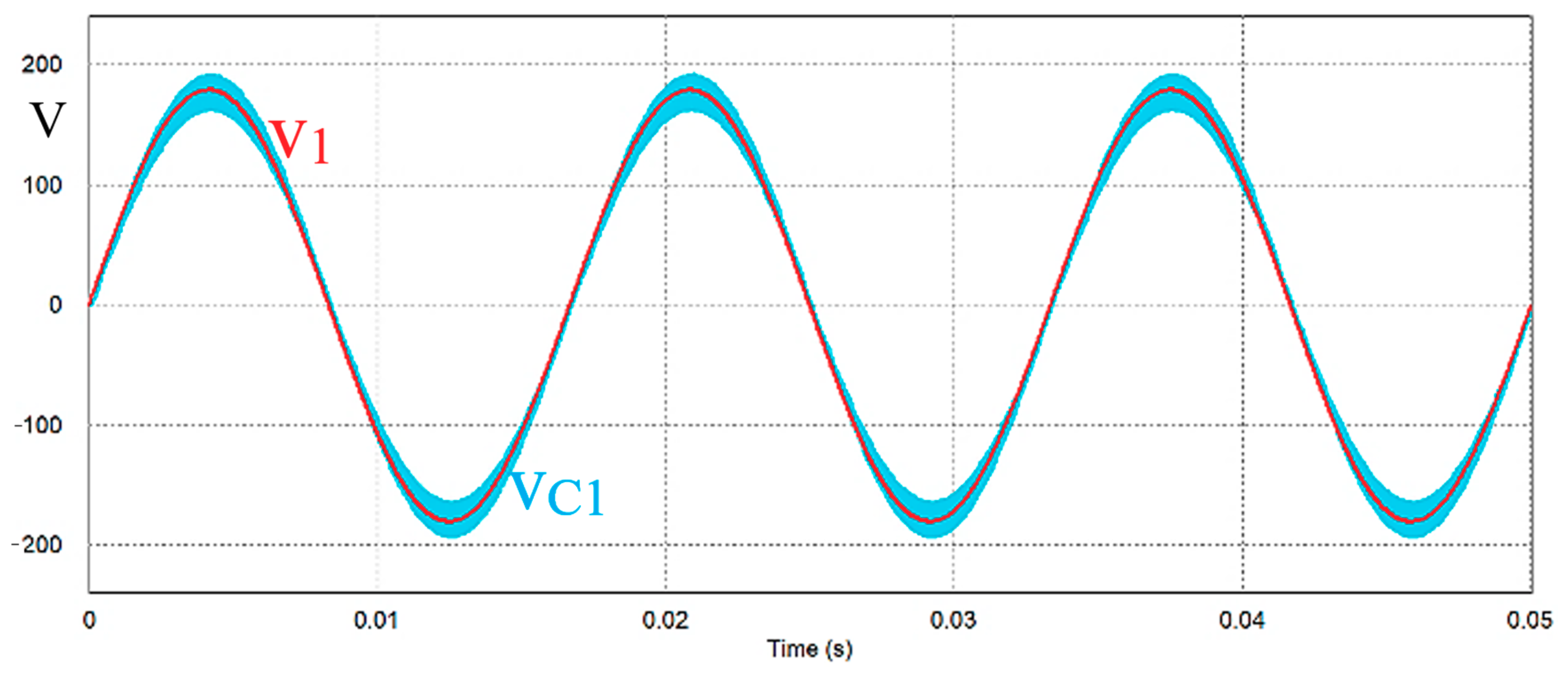
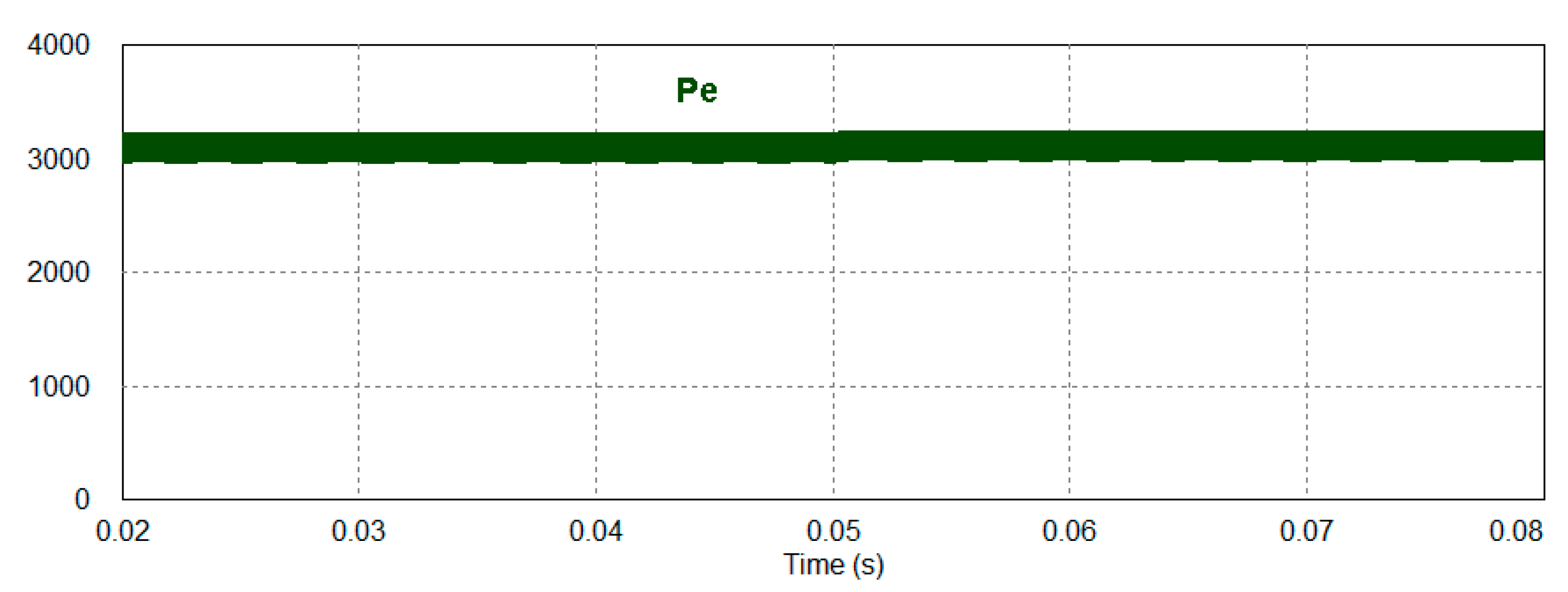
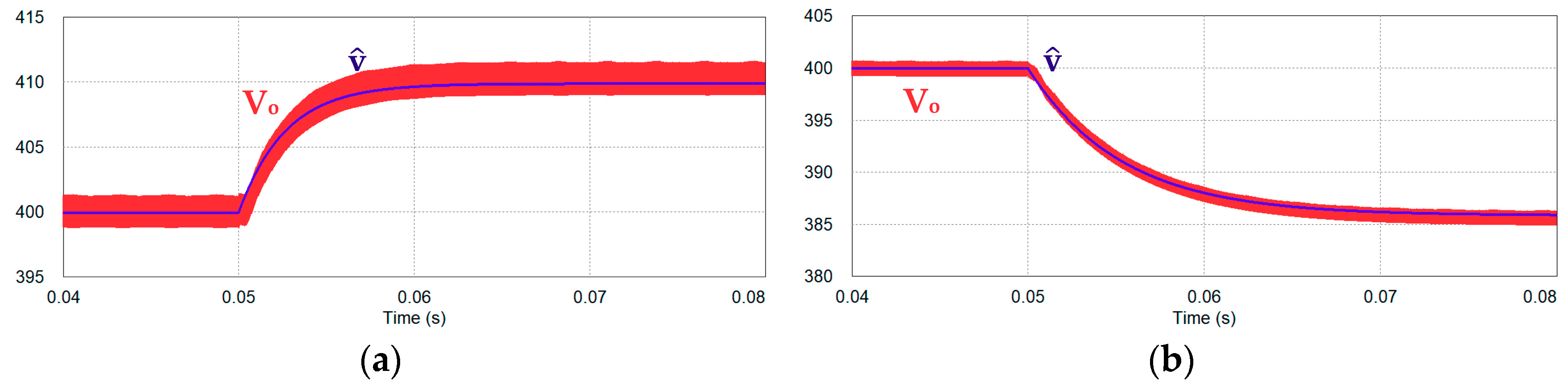
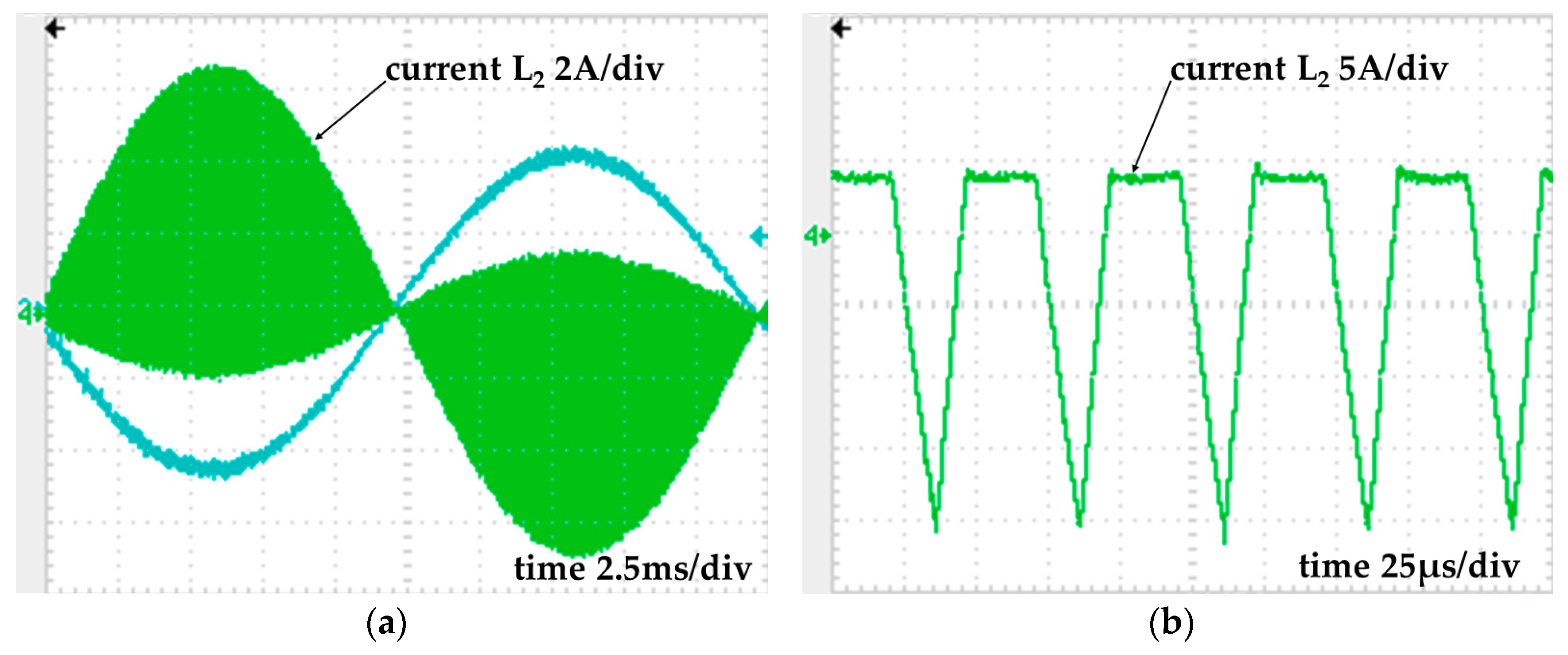
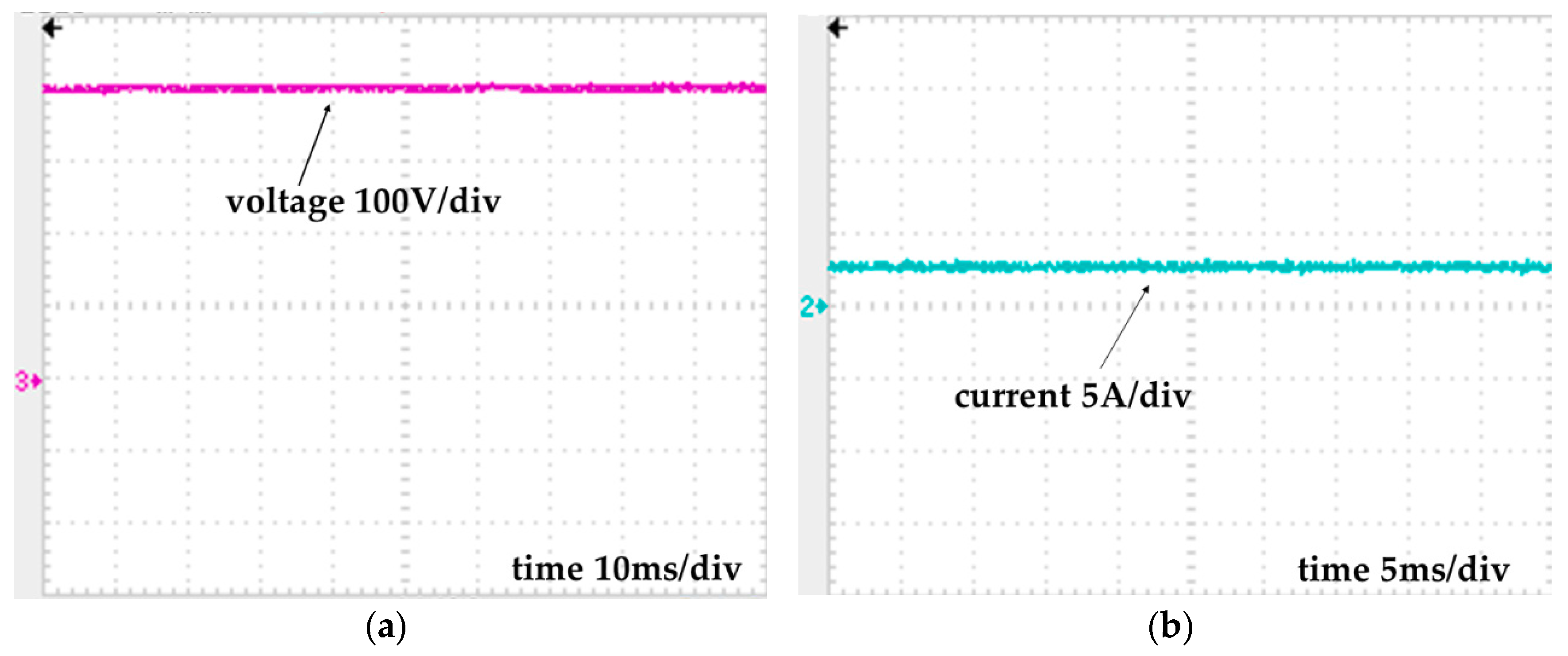
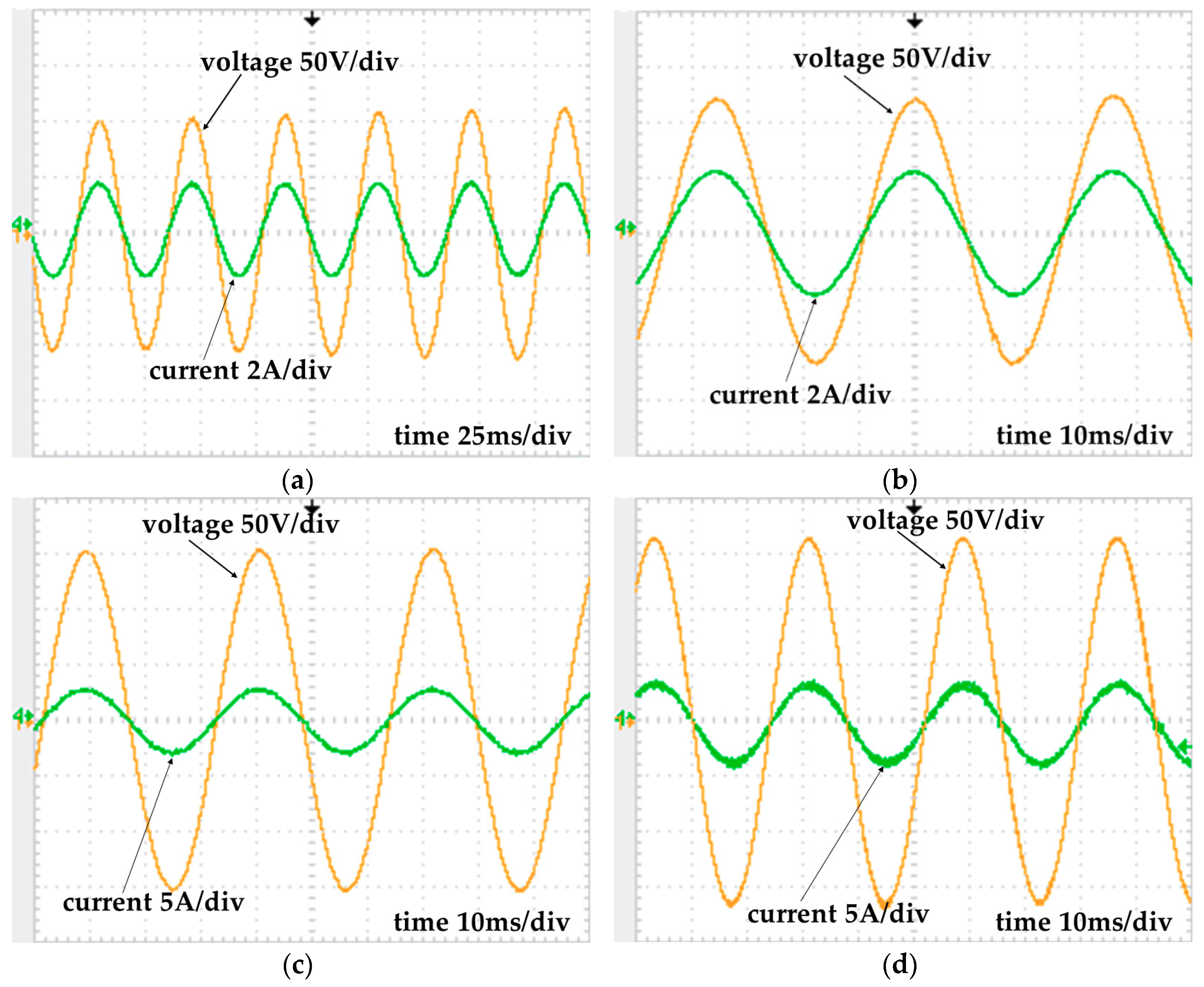
3. Simulation Results
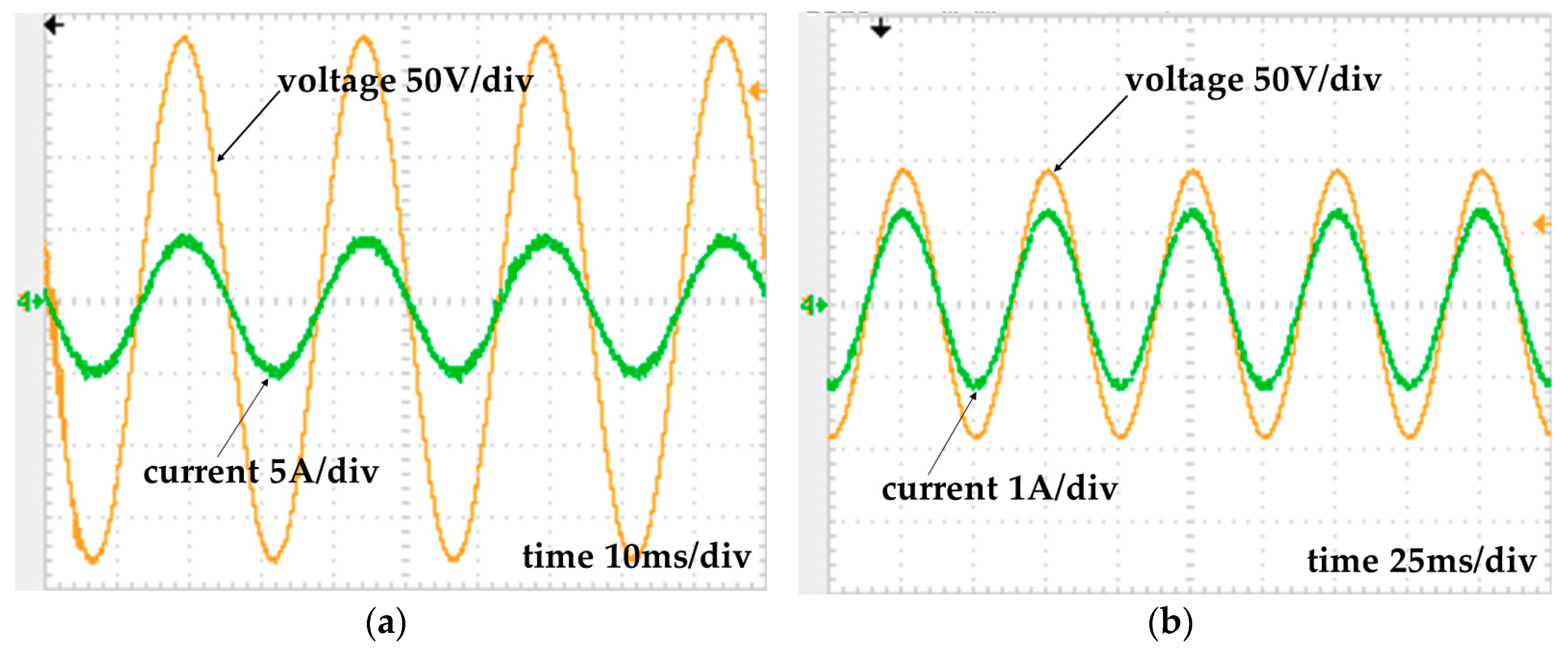
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ghareeb, A.T.; Mohamed, A.A.; Mohammed, O.A. DC microgrids and distribution systems: An overview. In Proceedings of the IEEE Power and Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013. [Google Scholar]
- Han, Y.; Ning, X.; Yang, P.; Xu, L. Review of Power Sharing, Voltage Restoration and Stabilization Techniques in Hierarchical Controlled DC Microgrids. IEEE Access 2019, 7, 149202–149223. [Google Scholar] [CrossRef]
- Mackay, L.; van der Blij, N.H.; Ramirez-Elizondo, L.; Bauer, P. Toward the Universal DC Distribution System. Electr. Power Compon. Syst. 2017, 45, 1032–1042. [Google Scholar] [CrossRef]
- Noroozian, R.; Abedi, M.; Gharehpetian, G.B.; Hosseini, S.H. Distributed resources and DC distribution system combination for high power quality. Int. J. Electr. Power Energy Syst. 2010, 32, 769–781. [Google Scholar] [CrossRef]
- Patrao, I.; Figueres, E.; Garcerá, G.; González-Medina, R. Microgrid architectures for low voltage distributed generation. Renew. Sustain. Energy Rev. 2015, 43, 415–424. [Google Scholar] [CrossRef]
- Lee, J.-Y.; Heo, K.-W.; Kim, K.-T.; Jung, J.-H. Analysis and Design of Three-Phase Buck Rectifier Employing UPS to Supply High Reliable DC Power. Energies 2020, 13, 1704. [Google Scholar] [CrossRef]
- Yao, K.; Meng, Q.; Bo, Y.; Hu, W. Three-Phase Single-Switch DCM Boost PFC Converter with Optimum Utilization Control of Switching Cycles. IEEE Trans. Ind. Electron. 2016, 63, 60–70. [Google Scholar] [CrossRef]
- Foroozeshfar, R.; Adib, E. Three-phase ripple free DCM boost converter with low THD. IET Power Electron. 2019, 12, 120–128. [Google Scholar] [CrossRef]
- Granza, M.H.; Gules, R.; Font, C.H.I. Hybrid and Three-Level Three-Phase Rectifiers Using Interleaved DCM Boost Converters. IEEE Access 2019, 7, 160168–160176. [Google Scholar] [CrossRef]
- Yao, K.; Meng, Q.; Yang, F.; Yang, S. A Novel Control Scheme of Three-Phase Single-Switch Quasi-CRM Boost Rectifier. IEEE Trans. Power Electron. 2017, 32, 6236–6244. [Google Scholar] [CrossRef]
- Azazi, H.Z.; Ahmed, S.M.; Lashine, A.E. Single-stage three-phase boost power factor correction circuit for AC–DC converter. Int. J. Electron. 2018, 105, 30–41. [Google Scholar] [CrossRef]
- Liu, J.; Xu, W.; Chan, K.W.; Liu, M.; Zhang, X.; Chan, N.H.L. A Three-Phase Single-Stage AC-DC Wireless-Power-Transfer Converter with Power Factor Correction and Bus Voltage Control. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1782–1800. [Google Scholar] [CrossRef]
- Foroozeshfar, R.; Adib, E. Unity power factor three-phase AC-DC converter applying two switch DCM SEPIC converter with coupled inductors. IET Power Electron. 2018, 11, 945–951. [Google Scholar] [CrossRef]
- Gangavarapu, S.; Rathore Gae, A.K. A Three-Phase Single-Stage Isolated Flyback-Based PFC Converter with Leakage Energy Recovery Clamping Circuit. IEEE Trans. Transp. Electrif. 2019, 5, 1155–1168. [Google Scholar] [CrossRef]
- Gangavarapu, S.; Rathore, A.K.; Fulwani, D.M. Three-Phase Single-Stage-Isolated Cuk-Based PFC Converter. IEEE Trans. Power Electron. 2019, 34, 1798–1808. [Google Scholar] [CrossRef]
- Metwaly, M.K.; Azazi, H.Z.; Deraz, S.A.; Dessouki, M.E.; Zaky, M.S. Power Factor Correction of Three-Phase PWM AC Chopper Fed Induction Motor Drive System Using HBCC Technique. IEEE Access 2019, 7, 43438–43452. [Google Scholar] [CrossRef]
- Lan, D.; Das, P.; Ye, C.; Sahoo, S.K.; Srinivasan, D. High Frequency Link Matrix Rectifier in Discontinuous Conduction Mode with Reduced Input Current Distortion. IEEE Trans. Ind. Electron. 2020. [Google Scholar] [CrossRef]
- Miniböck, J.; Mauerer, M.; Huber, J.E.; Kolar, J.W. Three-phase buck–boost PFC rectifier with common-mode free output voltage and low semiconductor blocking voltage stress. IET Power Electron. 2019, 12, 2022–2030. [Google Scholar] [CrossRef]
- Zhang, Q.; Na, T.; Song, L.; Dong, S. A Novel Modulation for Soft-Switching Three-Phase Quasi-Z-Source Rectifier without Auxiliary Circuit. IEEE Trans. Ind. Electron. 2018, 65, 5157–5166. [Google Scholar] [CrossRef]
- Aiello, G.; Cacciato, M.; Scarcella, G.; Scelba, G.; Gennaro, F.; Aiello, N. Real-time emulation of a three-phase Vienna rectifier with DC voltage control and power factor correction. Electr. Eng. 2020, 102, 97–106. [Google Scholar] [CrossRef]
- Prakash, P.S.; Kalpana, R.; Singh, B. Third Harmonic Current Injection Based Front-End AC-DC Converter for Power Quality Improvement in DC Distribution Systems. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Smart Grid and Renewable Energy (PESGRE2020), Cochin, India, 2–4 January 2020; pp. 1–6. [Google Scholar]
- Abdelsalam, I.; Alajmi, B.N.; Marei, M.I.; Alhajri, M.F. Wind energy conversion system based on open-end winding three-phase PMSG coupled with ac−dc buck-boost converter. J. Eng. 2019, 2019, 4336–4340. [Google Scholar] [CrossRef]
- Chub, A.; Husev, O.; Blinov, A.; Vinnikov, D. Novel Isolated Power Conditioning Unit for Micro Wind Turbine Applications. IEEE Trans. Ind. Electron. 2017, 64, 5984–5993. [Google Scholar] [CrossRef]
- Chen, Z.; Guerrero, J.M.; Blaabjerg, F. A review of the state of the art of power electronics for wind turbines. IEEE Trans. Power Electron. 2009, 24, 1859–1875. [Google Scholar] [CrossRef]
- Tofoli, F.L.; de Oliveira, D.S.; Barreto, L.H.S.C.; Oliveira, E.F.; Praça, P.P.; Antunes, F.M. Low cost wind energy conversion system based on the discontinuous conduction mode three-phase semi-controlled rectifier. IET Power Electron. 2015, 8, 851–859. [Google Scholar] [CrossRef]
- Jenisha, C.M.; Ammasaigounden, N.; Kumaresan, N.; BhagyaSri, K. Power electronic interface with de-coupled control for wind-driven PMSG feeding utility grid and DC load. IET Power Electron. 2018, 11, 329–338. [Google Scholar] [CrossRef]
- Rahimi, M. Modeling, control and stability analysis of grid connected PMSG based wind turbine assisted with diode rectifier and boost converter. Int. J. Electr. Power Energy Syst. 2017, 93, 84–96. [Google Scholar] [CrossRef]
- Aubrée, R.; Auger, F.; Macé, M.; Loron, L. Design of an efficient small wind-energy conversion system with an adaptive sensorless MPPT strategy. Renew. Energy 2016, 86, 280–291. [Google Scholar] [CrossRef]
- Zhang, S.; Tseng, K.-J.; Vilathgamuwa, D.M.; Nguyen, T.D.; Wang, X.-Y. Design of a Robust Grid Interface System for PMSG-Based Wind Turbine Generators. IEEE Trans. Ind. Electron. 2011, 58, 316–328. [Google Scholar] [CrossRef]
- Yaramasu, V.; Dekka, A.; Durán, M.J.; Kouro, S.; Wu, B. PMSG-based wind energy conversion systems: Survey on power converters and controls. IET Electr. Power Appl. 2017, 11, 956–968. [Google Scholar] [CrossRef]
- Carranza, O.; Figueres, E.; Garcerá, G.; González, L.G. A Control Circuit Small Wind Turbines with Low Harmonic Distortion and Improved Power Factor. In Proceedings of the International Conference on Renewable Energies and Power Quality (ICREPQ’09), Valencia, Spain, 15–17 April 2009; pp. 447–452. [Google Scholar]
- Tonkoski, R.; Lopes, L.A.C.; Dos Reis, F. A single-switch three-phase boost rectifier to reduce the generator losses in wind energy conversion systems. In Proceedings of the 2009 IEEE Electrical Power & Energy Conference (EPEC), Montreal, QC, Canada, 22–23 October 2009; pp. 1–8. [Google Scholar]
- Dos Reis, F.S.; Tan, K.; Islam, S. Using PFC for harmonic mitigation in wind turbine energy conversion systems. In Proceedings of the IECON Proceedings (Industrial Electronics Conference), Busan, Korea, 2–6 November 2004; Volume 3, pp. 3100–3105. [Google Scholar]
- Singer, S. Realization of Loss-Free Resistive Elements. IEEE Trans. Circuits Syst. 1990, 37, 54–60. [Google Scholar] [CrossRef]



| Ve (V) | P (kW) | Vo(V) |
|---|---|---|
| 220 | 1 | 400 |
| fs (kHz) | d 40 Hz(%) | d 20 Hz(%) | L1 (mH) | L2 (µH) | C1 (µF) | C0 (µF) |
|---|---|---|---|---|---|---|
| 20 | 28 | 20 | 12 | 95 | 4.7 | 100 |
| IGBT | Diode | Capacitor 4.7 µF | L1 (12 mH) | L2 (95 µH) | Capacitor C0 (100 µF) |
|---|---|---|---|---|---|
| HGTG11N120CND (FAIRCHILD) | HFA50PA60C (International Rectifier) | 940C12P47K-F (Cornell Dubilier) | Made of silicon steel | Built with ferrite core | 450 V Eletrolytic (Epcos) |
| Wind Speed | Power Factor | Current TDH |
|---|---|---|
| 12 m/s | 0.998 | 5.7% |
| 6 m/s | 0.993 | 4.8% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Freitas, T.; Caliman, J.; Menegáz, P.; dos Santos, W.; Simonetti, D. A DCM Single-Controlled Three-Phase SEPIC-Type Rectifier. Energies 2021, 14, 256. https://doi.org/10.3390/en14020256
Freitas T, Caliman J, Menegáz P, dos Santos W, Simonetti D. A DCM Single-Controlled Three-Phase SEPIC-Type Rectifier. Energies. 2021; 14(2):256. https://doi.org/10.3390/en14020256
Chicago/Turabian StyleFreitas, Tiara, João Caliman, Paulo Menegáz, Walbermark dos Santos, and Domingos Simonetti. 2021. "A DCM Single-Controlled Three-Phase SEPIC-Type Rectifier" Energies 14, no. 2: 256. https://doi.org/10.3390/en14020256
APA StyleFreitas, T., Caliman, J., Menegáz, P., dos Santos, W., & Simonetti, D. (2021). A DCM Single-Controlled Three-Phase SEPIC-Type Rectifier. Energies, 14(2), 256. https://doi.org/10.3390/en14020256








