A Probabilistic Conductor Size Selection Framework for Active Distribution Networks
Abstract
:1. Introduction
- New technologies—new load types, such as EVs and ESS, and distributed generation from PV, wind, and arbitrage systems introduce new considerations in the network planning process [1].
- Combination of uncertainties—the capacity and location, often termed allocation, of DERs, is out of the control of DNOs and is mostly random. Furthermore, stochastic factors influence the DER power exports and imports.
- Dynamic operation of DERs—the time-of-use characteristic for DERs, mainly EVs and ESSs, is more complicated than for standard residential loads
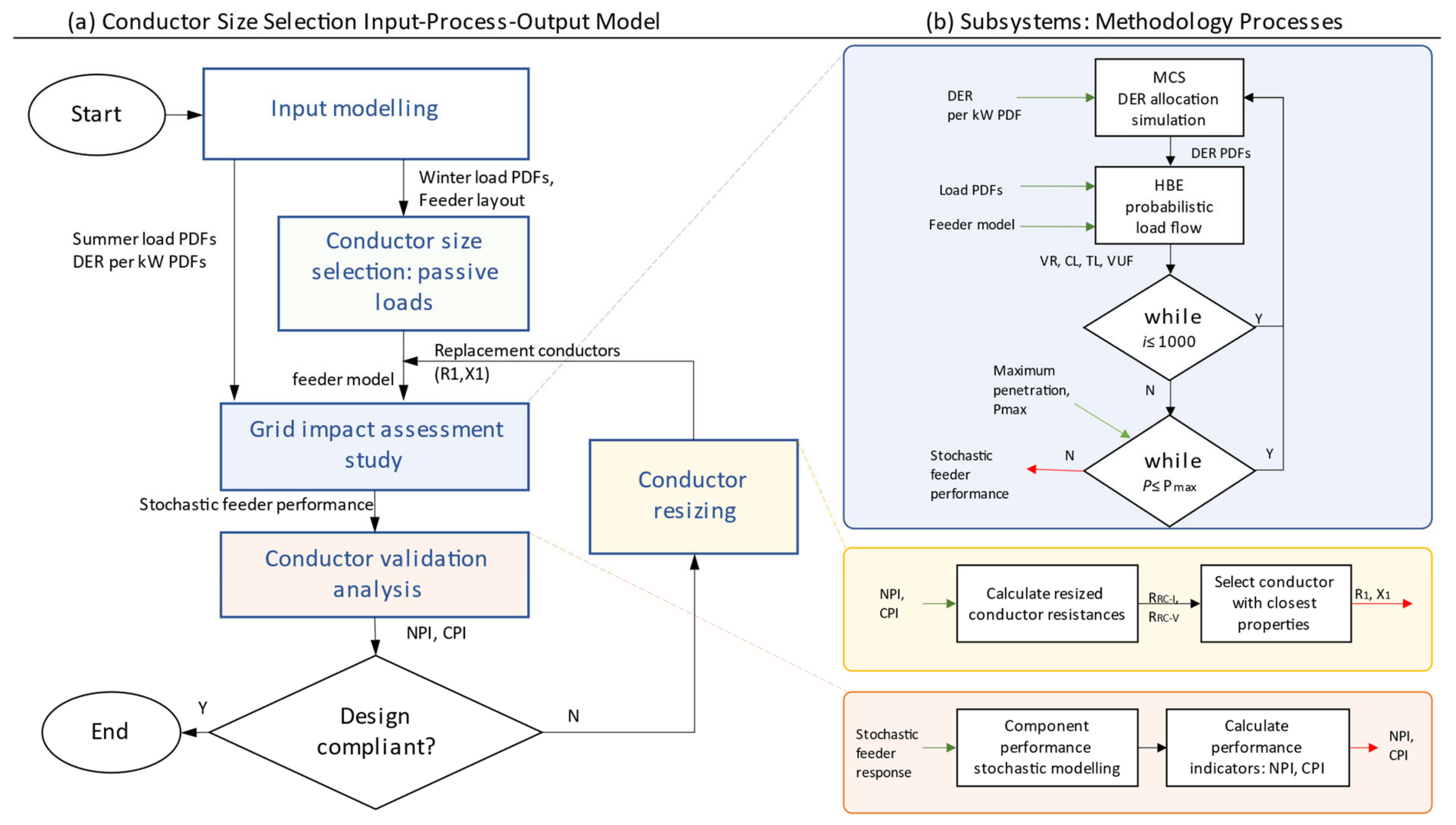
2. A Stochastic-Probabilistic CSS Methodology
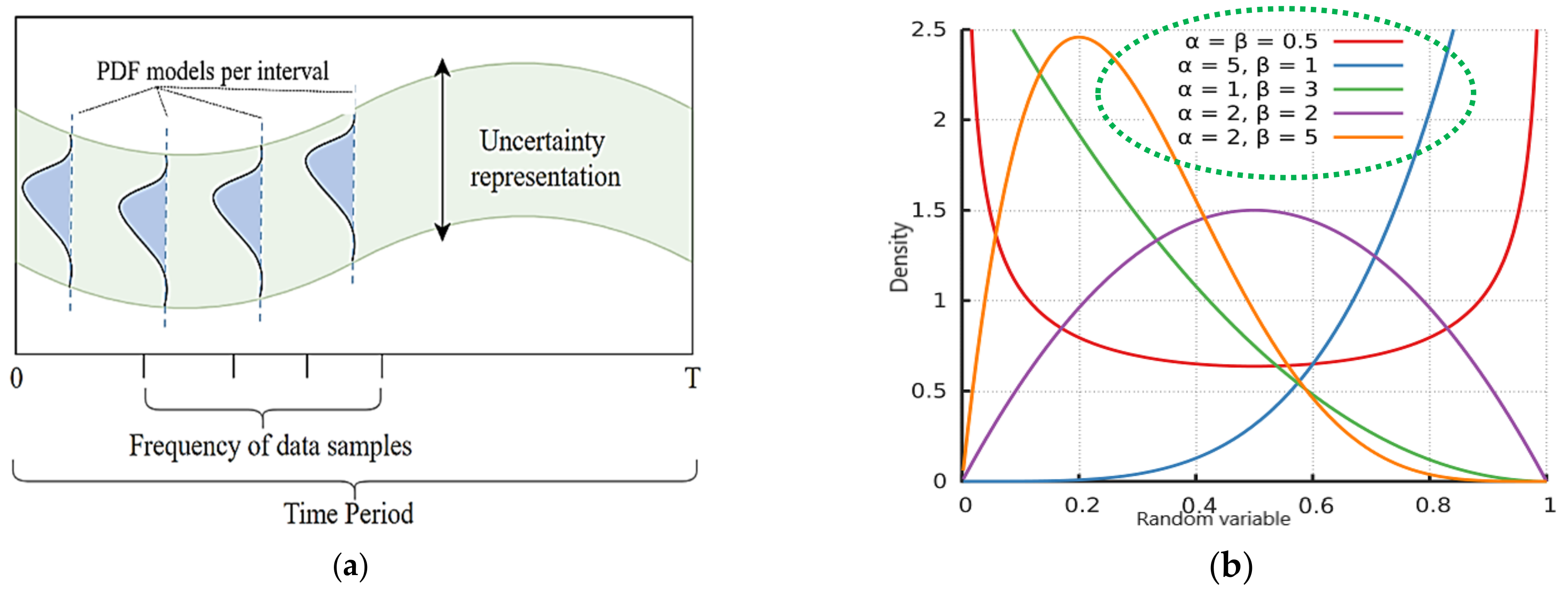
2.1. Input Modelling
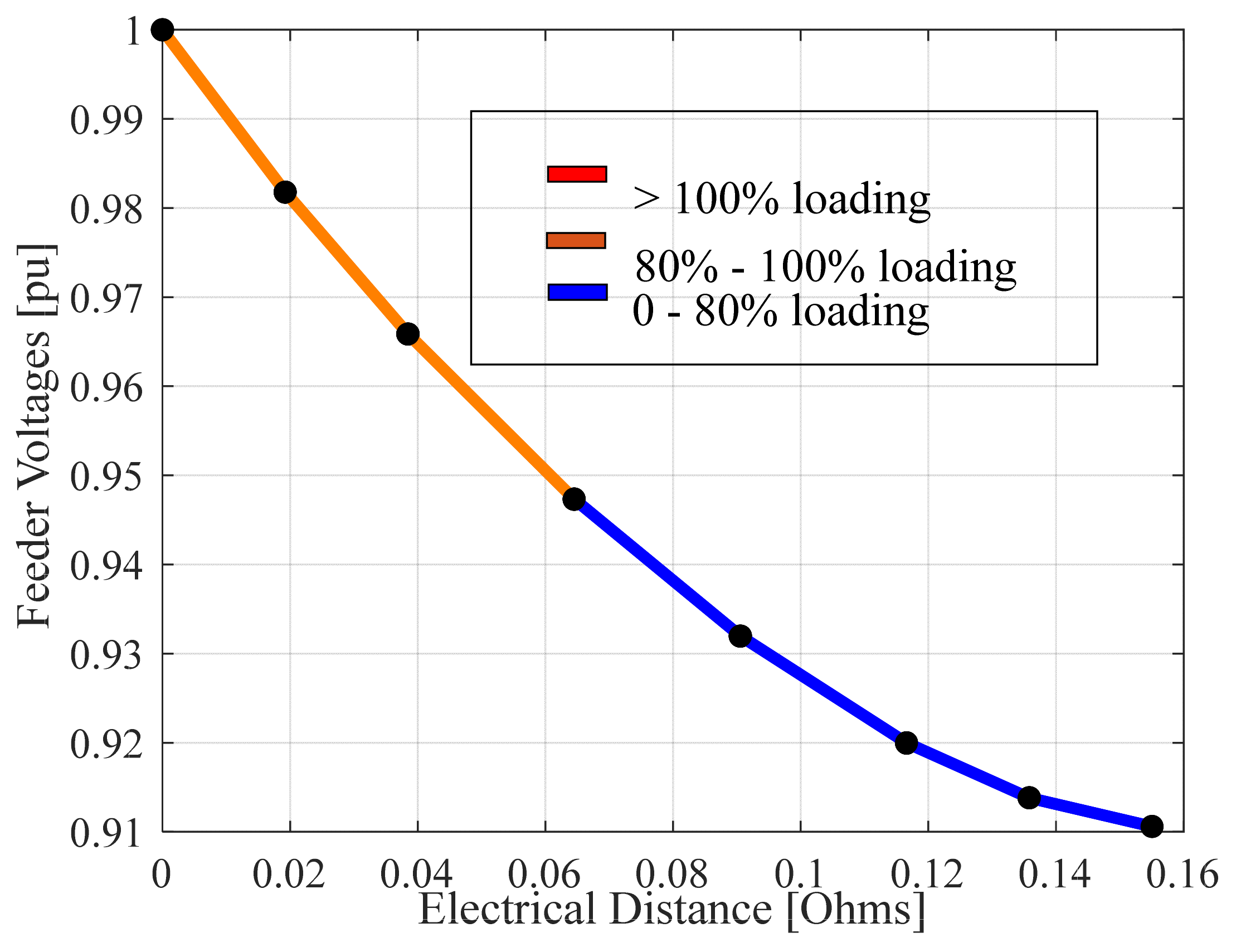
2.1.1. Distribution Feeder
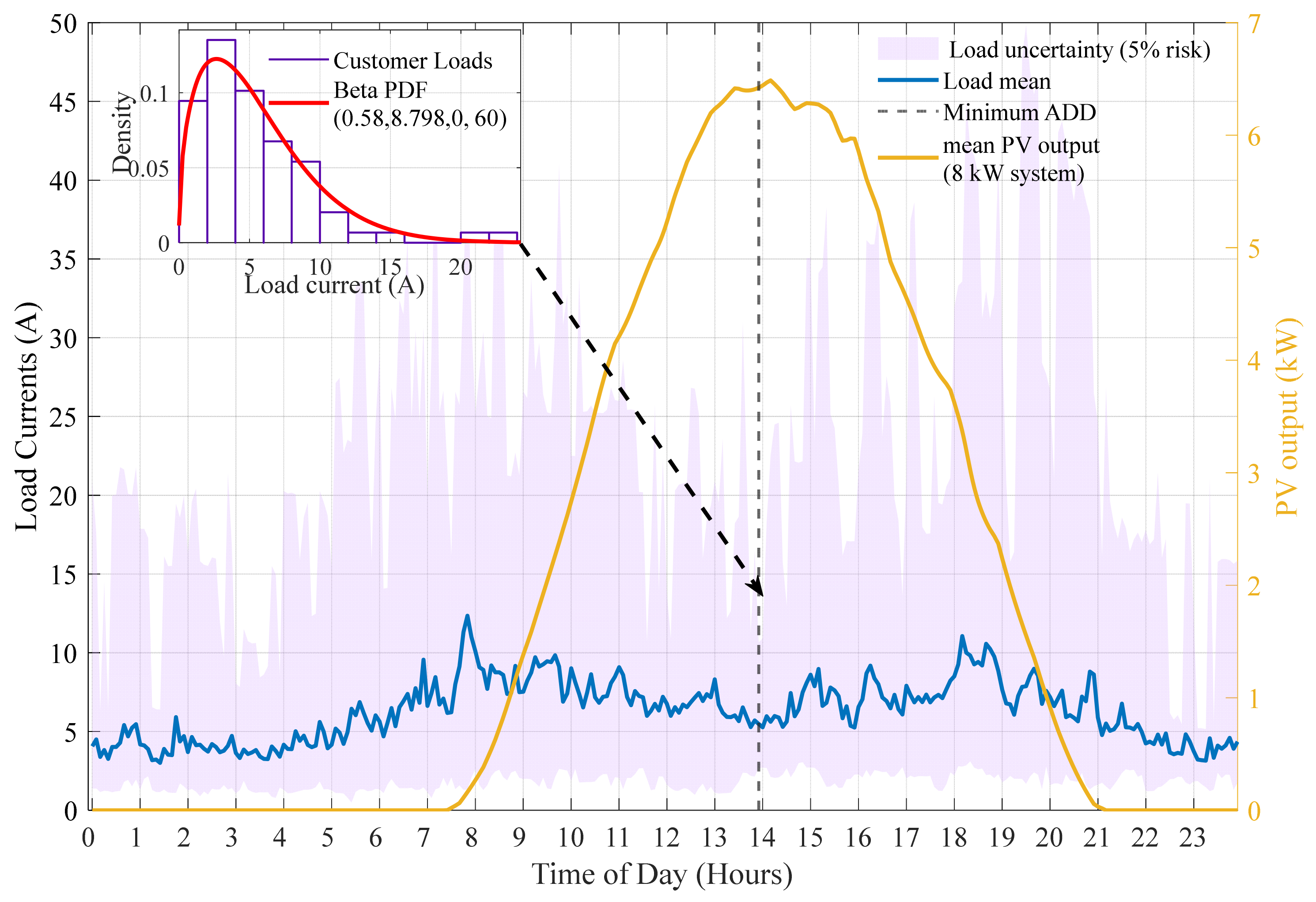
2.1.2. Customer Loads
2.1.3. Distributed Energy Resources
2.2. Process Modelling
2.2.1. Grid Impact Assessment Study
- Voltage-rise (VR);
- Voltage-drop (VD);
- Conductor loading (CL);
- Transformer loading (TL), calculated as the three-phase aggregated loading;
- Voltage unbalance factor (VUF), calculated as the ratio between the maximum voltage deviation across the phases and the mean node voltage.
2.2.2. Conductor Validation Analysis
- i.
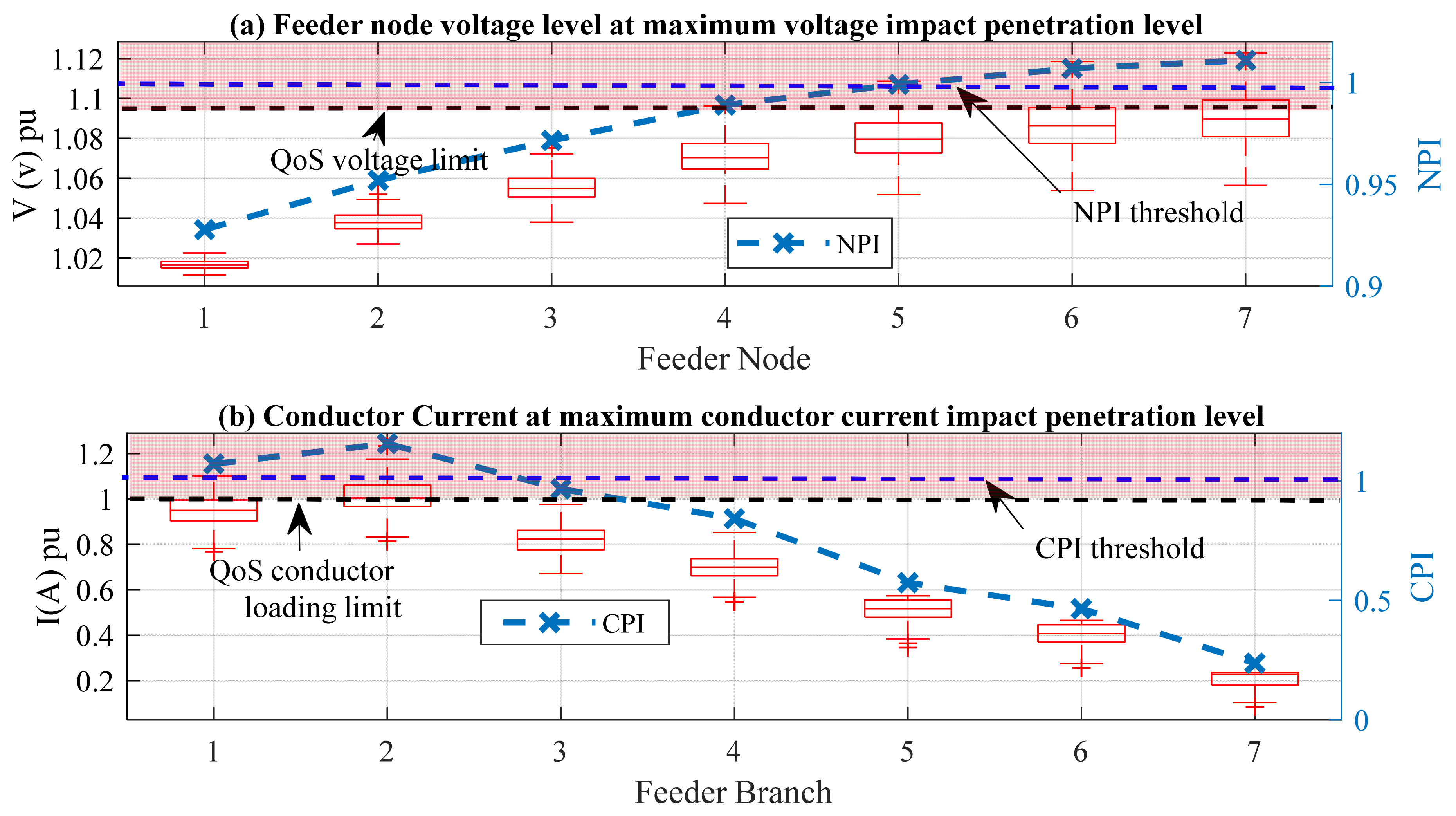
- Based on the load flow results obtained from the grid assessment study, we identify the penetration level recording the maximum impact on voltage, p_v, and conductor loading, p_i.
- ii.
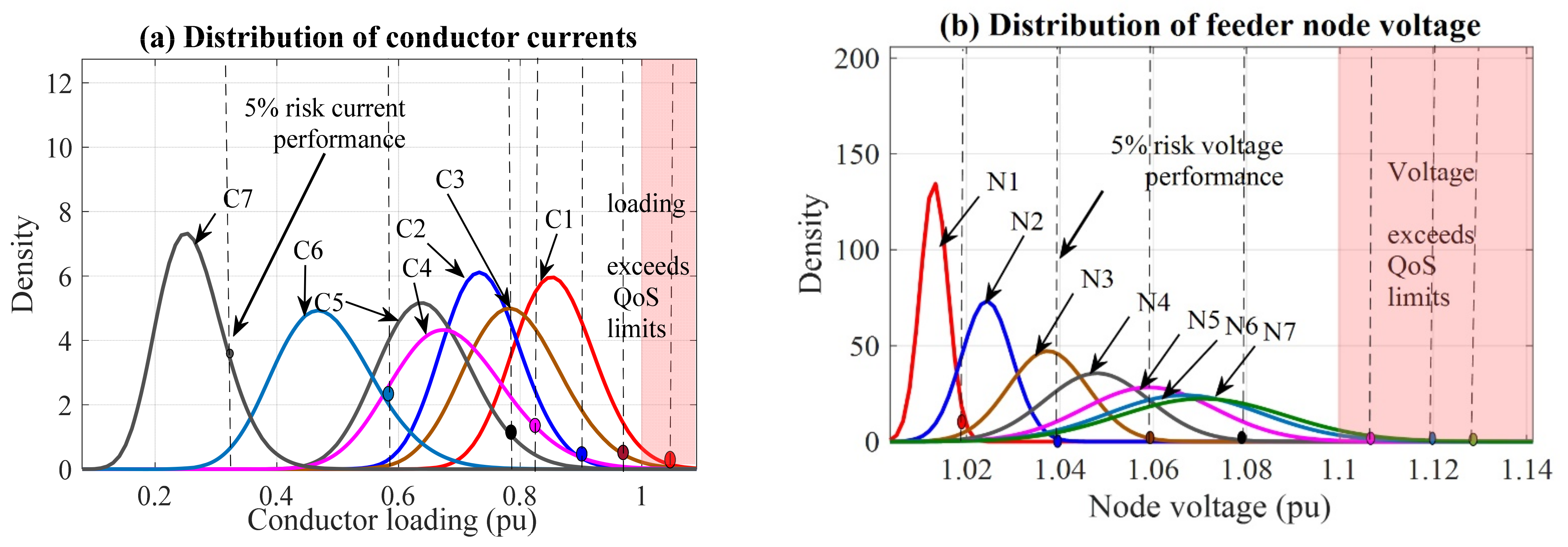
- At these maximum impact penetration levels, we characterize using beta PDFs the stochastic performance of the conductor loading, CLBp_i, and node voltage, VRNp_q, results corresponding to the 1000 MCS DER allocation scenarios, for all branches, B, and nodes, N.
- iii.
- From the beta PDFs, risk-adjusted performance indices are determined by extracting the 97.5th percentile, reflecting a 2.5% risk level. Compounded with the 2.5% risk applied in the HBE load flow analysis, the overall design process’s risk becomes 5%, which satisfies feeder design standards [43]. The calculation of the conductor performance index (CPI) and the node performance index (NPI) are given in Equations (7) and (8).
2.2.3. Output Processing–Iterative Resizing
- i.
- We estimate the resistance per km of the replacement conductor by scaling down the initial (or previous) per km resistance, R0, using the CPI and NPI indices. Equations (9) and (10) show the calculation of the resized conductor resistance, RRC-V, and RRC-I. RRC-V and RRC-I indicate the resized conductors based on voltage and conductor loading performance, respectively.RRC-V = R0/NPIRRC-I = R0/CPI
- ii.
- A replacement conductor with the closest and lower resistance per km to that of the resized conductors from Equations (9) and (10) is selected from a directory of available conductors, such as Table 2.
- iii.
- Once a conductor is selected, the feeder model is updated with the new conductor properties (R1, X1) and fed back as modified inputs for another iteration of the CSS simulation. The stop criterion is based on the compliance of all components (NPI, CPI ≤ 1) or the convergence of conductor selection, resulting from the unavailability of appropriate conductors in the available directory.
3. Case Study Simulation, Results, and Analysis
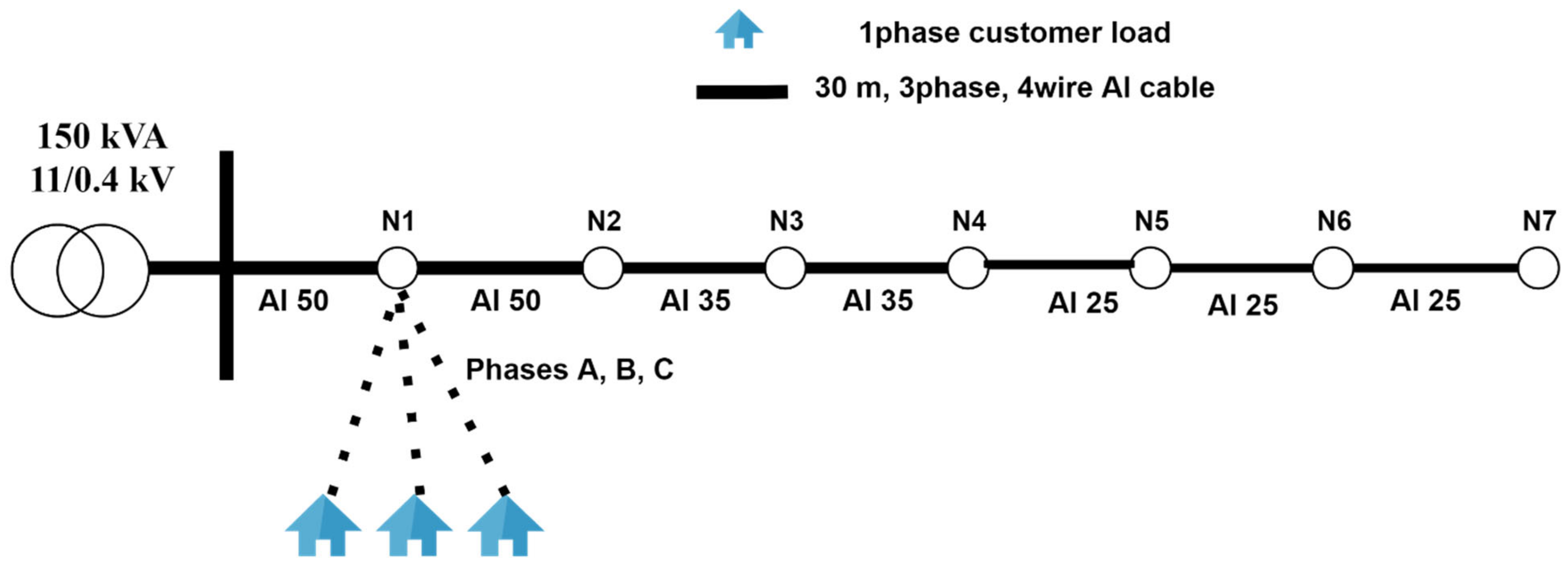
3.1. Feeder Model
3.2. Load and DER Models
3.3. Initial Feeder Design
3.4. Grid Impact Assessment and Conductor Validation Analysis for the Initial Design
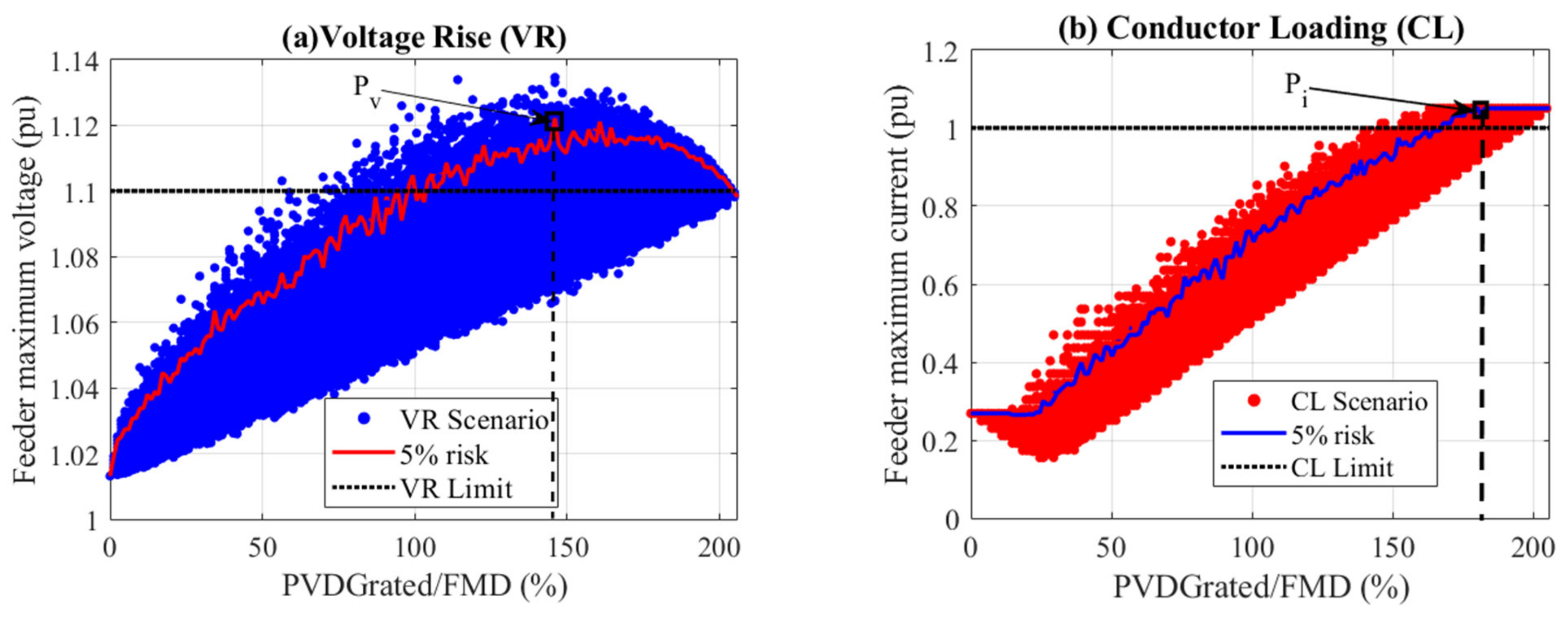
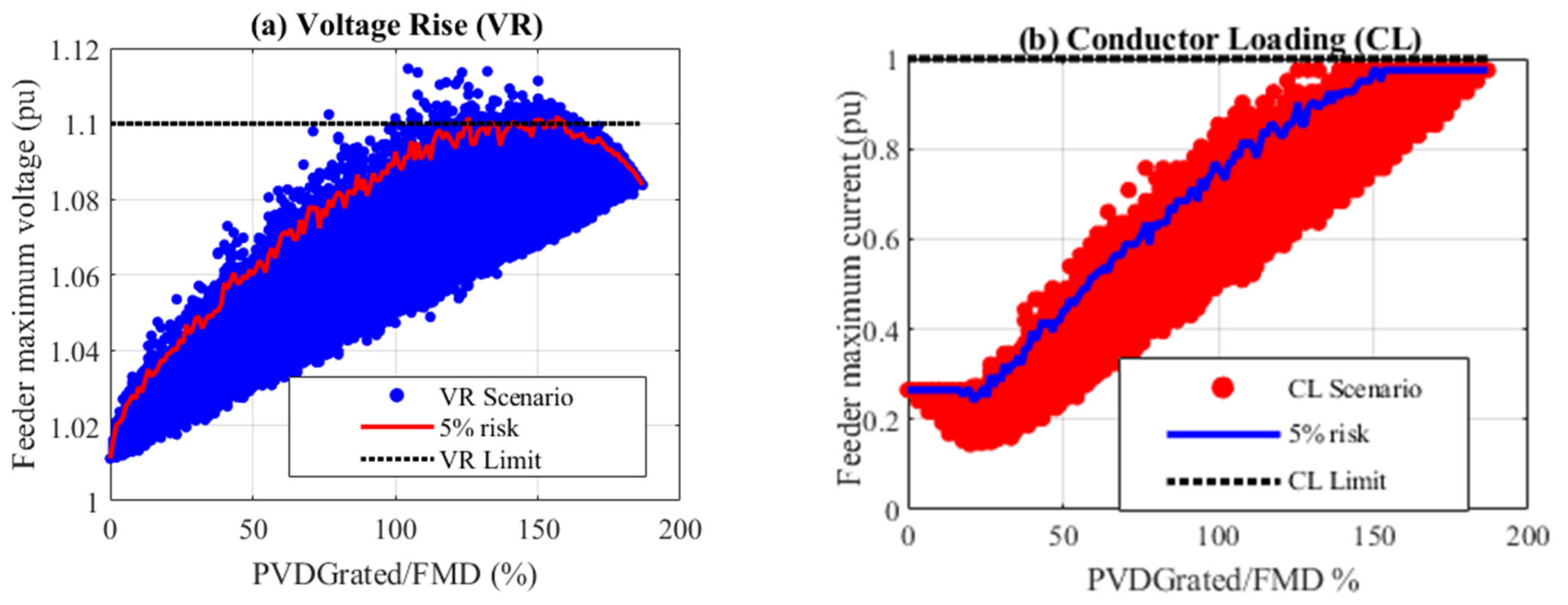
3.4.1. Interpretation of Scatterplots
3.4.2. Discussion of the Performance of the Initial System Design
- i.
- Based on voltage impacts (Figure 6a), the feeder can accommodate penetration up to 100% of FMD (81.5 kWp) and between 205% (162 kWp) and the simulated maximum (162 kWp). The feeder violates voltage limits between 125% and 205% penetration, which indicates that future penetration scenarios falling in this range have a high likelihood for overvoltage conditions.
- ii.
- Based on conductor loading impacts (Figure 6b), the feeder can accommodate a PV capacity of up to 160% of FMD (130.5 kWp). All penetration scenarios above this limit violate thermal loading limits.
- iii.
- Combining the limits, the feeder can only host penetrations up to 100% (81.5 kWp), which corresponds to 48.5% of the desired penetration.
3.4.3. Conductor Validation Analysis
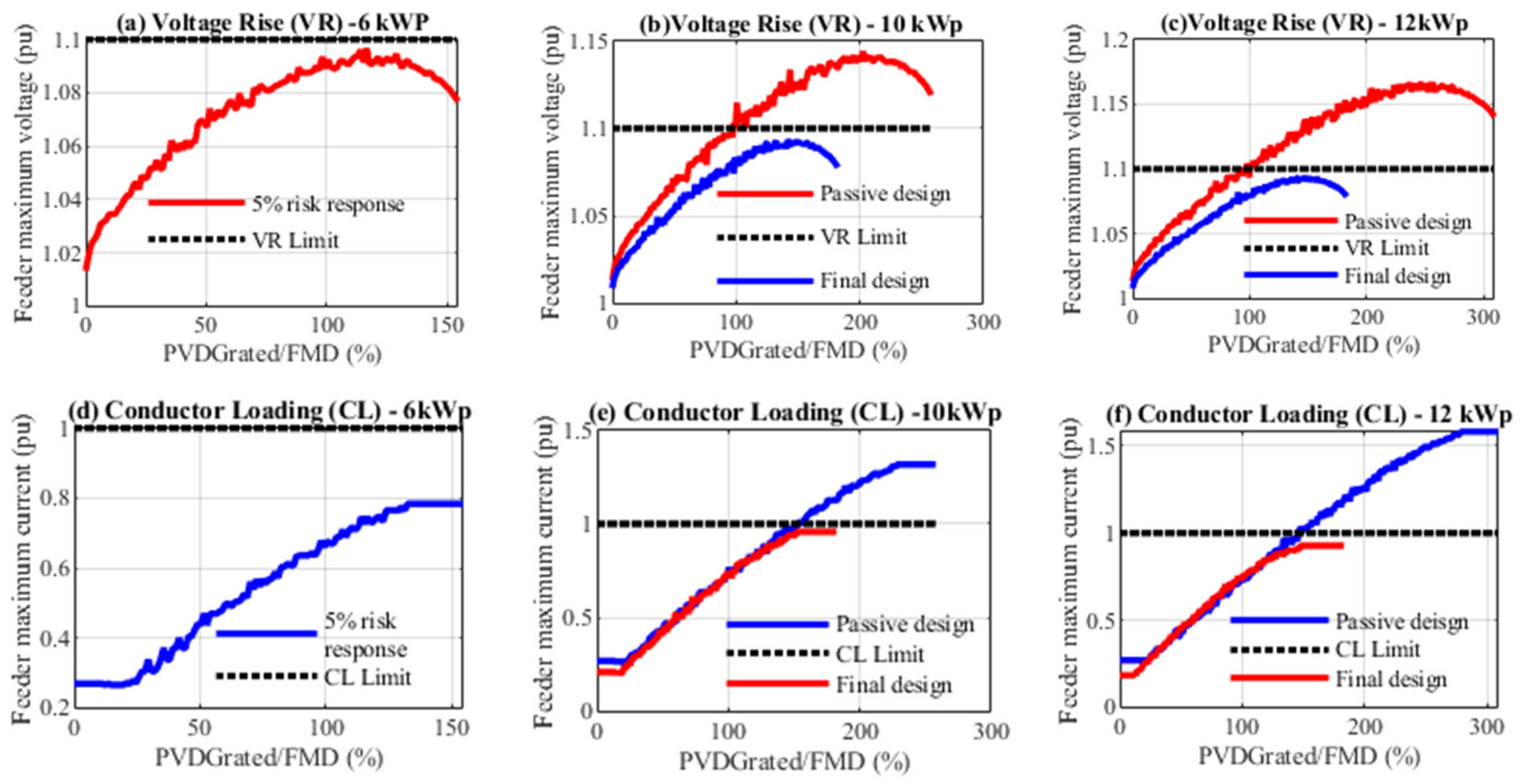
3.5. Conductor Resizing and Performance Validation
Discussion of the Performance of the Final System Design
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chihota, M.J.; Bekker, B. New planning principles for distribution networks with penetration of distributed energy resources. In Proceedings of the 6th IEEE International Energy Conference, ENERGYCon 2020, Gammarth, Tunisia, 28 September–1 October 2020; IEEE Explore: Gamath, Tunisia, 2020; Volume 2, pp. 643–648. [Google Scholar]
- Waswa, L.S.; Bekker, B. Impact of PV small scale embedded generation on South Africa’s system demand profile. In Proceedings of the South African Solar Energy Conference, Durban, South Africa, 25–27 June 2018. [Google Scholar]
- Gaunt, C.T.; Herman, R.; Namanya, E.; Chihota, J. Voltage modelling of LV feeders with dispersed generation: Probabilistic analytical approach using Beta PDF. Electr. Power Syst. Res. 2017, 143, 25–31. [Google Scholar] [CrossRef]
- Masters, C.L.; Mutale, J.; Strbac, G.; Curcic, S.; Jenkins, N. Statistical evaluation of voltages in distribution systems with embedded wind generation. IEE Proc. Gener. Transm. Distrib. 2000, 147, 207–211. [Google Scholar] [CrossRef]
- Walling, R.A.; Saint, R.; Dugan, R.C.; Burke, J.; Kojovic, L.A. Summary of distributed resources impact on power delivery systems. IEEE Trans. Power Deliv. 2008, 23, 1636–1644. [Google Scholar] [CrossRef]
- Vita, V.; Alimardan, T.; Ekonomou, L. The impact of distributed generation in the distribution networks’ voltage profile and energy losses. In Proceedings of the 2015 IEEE European Modelling Symposium (EMS), Madrid, Spain, 6–8 October 2015; pp. 260–265. [Google Scholar]
- Ismael, S.M.; Abdel Aleem, S.H.E.; Abdelaziz, A.Y.; Zobaa, A.F. State-of-the-art of hosting capacity in modern power systems with distributed generation. Renew. Energy 2019, 130, 1002–1020. [Google Scholar] [CrossRef]
- Schwaegerl, C.; Joos, G.; Hatziargyriou, N. Active distributed systems and distibuted energy resources. In Electricity Supply Systems of the Future; Springer: Berlin/Heidelberg, Germany, 2020; pp. 519–567. [Google Scholar]
- Rylander, M.; Smith, J.; Sunderman, W. Streamlined Method for Determining Distribution System Hosting Capacity. Pap. Present. Annu. Conf. Rural Electr. Power Conf. 2015, 2015, 3–9. [Google Scholar]
- Herman, R.; Gaunt, C.T. A practical probabilistic design procedure for LV residential distribution systems. IEEE Trans. Power Deliv. 2008, 23, 2247–2254. [Google Scholar] [CrossRef]
- NRS. NRS 034-1:2007 Electricity Distribution—Guidelines for the Provision of Electricity Distribution Networks in Residential Areas Part 1: Planning and Design of Distribution Networks; NRS: Decatur, TX, USA, 2007. [Google Scholar]
- Franco, J.F.; Rider, M.J.; Lavorato, M.; Romero, R. Optimal conductor size selection and reconductoring in radial distribution systems using a mixed-integer LP approach. IEEE Trans. Power Syst. 2013, 28, 10–20. [Google Scholar] [CrossRef]
- Rao, R. Optimal conductor selection for loss reduction in radial distribution systems using differential evolution. Int. J. Eng. Sci. Technol. 2010, 2, 2829–2838. [Google Scholar]
- Zhao, Z.; Mutale, J. Optimal conductor size selection in distribution networks with high penetration of distributed generation using adaptive genetic algorithm. Energies 2019, 12, 2065. [Google Scholar] [CrossRef] [Green Version]
- Sellick, R.L.; Gaunt, C.T. Comparing methods of calculating voltage drop in low voltage feeders. Trans. South African Inst. Electr. Eng. 1995, 86, 96–111. [Google Scholar]
- Chihota, M.J.; Bekker, B.; Gaunt, C. Technical Assessment of the impact of Distributed energy resources on distribution feeders. In Uncertainties in Modern Power Systems; Zobaa, A.F., Shady, E., Aleem, A., Eds.; Elsevier: Oxford, UK, 2021; pp. 398–436. [Google Scholar]
- Wang, C.; Song, G.; Li, P.; Ji, H.; Zhao, J.; Wu, J. Optimal siting and sizing of soft open points in active electrical distribution networks. Appl. Energy 2017, 189, 301–309. [Google Scholar] [CrossRef]
- Pakdel, D.; Ramezani, M. Enhancement of distribution network performance in the presence of uncertain parameters. IET Renew. Power Gener. 2020, 14, 515–525. [Google Scholar] [CrossRef]
- Abul’Wafa, A.R. Multi-conductor feeder design for radial distribution networks. Electr. Power Syst. Res. 2016, 140, 184–192. [Google Scholar] [CrossRef]
- Funkhouser, A.; Huber, R. A method for determining economical ACSR Conductor sizes for the distribution systems. IEEE Explor. 1955, 74, 479–484. [Google Scholar]
- Farrag, M.A.; Khalil, A.H.; Omran, S. Optimal conductor selection and capacitor placement in radial distribution system using nonlinear AC load flow equations and dynamic load model. Int. Trans. Electr. Energy Syst. 2020, 30, 1–19. [Google Scholar] [CrossRef]
- Khalil, T.M.; Gorpinich, A.V. Optimal conductor selection and capacitor placement for loss reduction of radial distribution systems by selective particle swarm optimization. Proc. ICCES 2012 2012 Int. Conf. Comput. Eng. Syst. 2012, 215–220. [Google Scholar]
- Mendoza, F.; Requena, D.; Bemal-Agustín, J.L.; Domínguez-Navarro, J.A. Optimal conductor size selection in radial power distribution systems using evolutionary strategies. In Proceedings of the 2006 IEEE/PES Transmission & Distribution Conference and Exposition: Latin America, Caracas, Venezuela, 15–18 August 2006; pp. 6–10. [Google Scholar]
- Falaghi, H.; Singh, C. Optimal Conductor Size Selection in Distribution Systems with Wind Power Generation. In Wind Power Systems-Application of Computational Intelligence; Wang, L., Singh, C., Kusiak, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 25–51. ISBN 9783642132490. [Google Scholar]
- Falaghi, H.; Ramezani, M.; Haghifam, M.R.; Milani, K.M. Optimal selection of conductors in radial distribution systems with time varying load. Proceedings of the CIRED 18th International Conference and Exhibition on Electricity Distribution 1–4.
- Rao, R.S.; Satish, K.; Narasimham, S.V.L. Optimal conductor size selection in distribution systems using the harmony search algorithm with a differential operator. Electr. Power Compon. Syst. 2011, 40, 41–56. [Google Scholar] [CrossRef]
- Sivanagaraju, S.; Rao, J.V. Optimal conductor selection in radial distribution system using discrete Particle Swarm Optimization. World J. Model. Simul. 2009, 5, 183–191. [Google Scholar]
- Rao, P.S.N. An extremely simple method of determining optimal conductor sections for radial distrbution feeders. IEEE Trans. Power Appar. Syst. 1985, 104, 1439–1442. [Google Scholar] [CrossRef]
- Kaur, D.; Sharma, J. Optimal conductor sizing in radial distribution systems planning. Int. J. Electr. Power Energy Syst. 2008, 30, 261–271. [Google Scholar] [CrossRef]
- Martínez-Gil, J.F.; Moyano-García, N.A.; Montoya, O.D.; Alarcon-Villamil, J.A. Optimal Selection of Conductors in Three-Phase Distribution Networks Using a Discrete Version of the Vortex Search Algorithm. Computation 2021, 9, 80. [Google Scholar] [CrossRef]
- Ismael, S.M.; Abdel Aleem, S.H.E.; Abdelaziz, A.Y.; Zobaa, A.F. Practical Considerations for Optimal Conductor Reinforcement and Hosting Capacity Enhancement in Radial Distribution Systems. IEEE Access 2018, 6, 27268–27277. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, H.; Yu, D.C.; Wang, X.; Song, H. A practical approach to the conductor size selection in planning radial distribution systems. IEEE Trans. Power Deliv. 2000, 15, 350–354. [Google Scholar] [CrossRef]
- Montoya, G.O.D.; Grajales, A.; Hincapié, I.R.A. Optimal selection of conductors in distrbution systems using tabu search algorithms. Ingeniare. Rev. Chil. Ing. 2018, 26, 283–295. [Google Scholar]
- Montoya, O.D.; Garces, A.; Castro, C.A. Optimal conductor size selection in radial distribution networks using a mixed-integer non-linear programming formulation. IEEE Lat. Am. Trans. 2018, 16, 2213–2220. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Grisales-Noreña, L.F. On the mathematical modeling for optimal selecting of calibers of conductors in DC radial distribution networks: An MINLP approach. Electr. Power Syst. Res. 2021, 194, 107072. [Google Scholar] [CrossRef]
- Samani, E.; Aminifar, F. Tri-Level Robust Investment Planning of DERs in Distribution Networks with AC Constraints. IEEE Trans. Power Syst. 2019, 34, 3749–3757. [Google Scholar] [CrossRef]
- Chihota, M.J. Extending the Herman-Beta Transform for Probabilistic Load Flow Analysis of Radial Feeders; University of Cape Town: Cape Town, South Africa, 2019. [Google Scholar]
- Herman, R.; Kritzinger, J. The statistical description of grouped domestic electrical load currents. Electr. Power Syst. Res. 1993, 27, 43–48. [Google Scholar] [CrossRef]
- Herman, R.; Heunis, S.W. General probabilistic voltage drop calculation method for LV distribution networks based on a beta p.d.f. load model. Electr. Power Syst. Res. 1998, 46, 45–49. [Google Scholar] [CrossRef]
- Gaunt, C.T.; Herman, R.; Dekenah, M.; Sellick, R.L.; Heunis, S.W. Data collection, load modelling and probabilistic analysis for LV domestic electrification. In Proceedings of the 15th International Conference on Electricity Distribution, Nice, France, 1–4 June 1999. [Google Scholar]
- University of Cape Town, Domestic Electrical Load Survey Secure Data 1994:2014. version 1. Available online: https://www.datafirst.uct.ac.za/dataportal/index.php/catalog/757/study-description (accessed on 30 September 2021).
- IEEE Load representation for dynamic performance analysis. IEEE Trans. Power Syst. 1993, 8, 472–482. [CrossRef]
- NRS. NRS 048-2: Electricity Supply-Quality of Supply Part 2: Voltage Characteristics, Compatibility Levels, Limits and Assessment Methods; NRS: Decatur, TX, USA, 2003. [Google Scholar]
- NRS. NRS 097-2-3: 2014-A Simplified Utility Connection Criteria for Low-Voltage Connected Generators; NRS: Decatur, TX, USA, 2014; p. 27. [Google Scholar]
| Technical Constraint | Constraint Limit | Confidence Intervals |
|---|---|---|
| Voltage drop | >0.9 pu | 2.5% |
| Voltage rise | <1.1 pu | 97.5% |
| Loading of conductors | <1 pu | 2.5% |
| Cable Size | Current Rating | Resistance | Reactance | Impedance |
|---|---|---|---|---|
| mm2 | (A) | Ω/km | Ω/km | Ω/km |
| 25 | 105 | 1.200 | 0.096 | 1.493 |
| 35 | 144 | 0.868 | 0.096 | 1.082 |
| 50 | 183 | 0.641 | 0.090 | 0.801 |
| 70 | 228 | 0.443 | 0.089 | 0.557 |
| 95 | 277 | 0.320 | 0.086 | 0.406 |
| 120 | 322 | 0.253 | 0.084 | 0.325 |
| 150 | 350 | 0.206 | 0.082 | 0.269 |
| Input Type | Input Model Parameters | ||||||
|---|---|---|---|---|---|---|---|
| Period | Probabilistic Model | ADMD (kVA) | pf | ||||
| α | β | C (A) | σ (A) | ||||
| Load | Winter | 1.67 | 4.07 | 60 | 10.50 | 4.015 | 0.95 |
| Summer | 0.58 | 8.78 | 60 | 4.423 | 0.855 | 0.95 | |
| PV | Summer | 255.5 | 255.5 | 6.96 | 0.150 | 0.800 | 1 |
| Conductor Properties | Feeder Section | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| Case 1: (Initial design) | Cross-section (mm2) | 50 | 50 | 35 | 35 | 25 | 25 | 25 |
| Resistance (ohms/km) | 0.641 | 0.641 | 0.868 | 0.868 | 1.20 | 1.20 | 1.20 | |
| Case 2: (Final design) | Cross-section (mm2) | 70 | 50 | 35 | 35 | 35 | 35 | 35 |
| RRC-I (Ω/km) | 0.610 | 0.712 | 0.894 | 1.095 | 1.44 | 2.07 | 3.13 | |
| RRC-V (Ω/km) | 0.697 | 0.674 | 0.894 | 0.876 | 1.192 | 1.173 | 1.16 | |
| Resistance (ohms/km) | 0.443 | 0.641 | 0.868 | 0.868 | 0.868 | 0.868 | 0.868 | |
| Deterministic–active design | Cross-section (mm2) | 70 | 70 | 50 | 50 | 35 | 35 | 35 |
| Feeder Design | Permissible Penetration Range (% of FMD) | ||
|---|---|---|---|
| Voltage Rise | Cond. Loading | Overall | |
| Case 1 (Initial, passive design) | 0–100% | 0–160% | 0–100% |
| 205%–full uptake | |||
| Case 2 (Final, active design) | Full range | Full range | Full range |
| Capacity (kWp) | Conductor Size (mm2) | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Passive Design | 50 | 50 | 35 | 35 | 25 | 25 | 25 |
| 6 kWp | 50 | 50 | 35 | 35 | 25 | 25 | 25 |
| 8 kWp | 70 | 50 | 35 | 35 | 35 | 35 | 35 |
| 10 kWp | 95 | 70 | 50 | 35 | 35 | 50 | 50 |
| 12 kWp | 120 | 95 | 70 | 50 | 35 | 50 | 50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Waswa, L.; Chihota, M.J.; Bekker, B. A Probabilistic Conductor Size Selection Framework for Active Distribution Networks. Energies 2021, 14, 6387. https://doi.org/10.3390/en14196387
Waswa L, Chihota MJ, Bekker B. A Probabilistic Conductor Size Selection Framework for Active Distribution Networks. Energies. 2021; 14(19):6387. https://doi.org/10.3390/en14196387
Chicago/Turabian StyleWaswa, Lewis, Munyaradzi Justice Chihota, and Bernard Bekker. 2021. "A Probabilistic Conductor Size Selection Framework for Active Distribution Networks" Energies 14, no. 19: 6387. https://doi.org/10.3390/en14196387
APA StyleWaswa, L., Chihota, M. J., & Bekker, B. (2021). A Probabilistic Conductor Size Selection Framework for Active Distribution Networks. Energies, 14(19), 6387. https://doi.org/10.3390/en14196387






