Abstract
Dynamic analysis of magnetic fluids with the combined effect of heat sink and chemical reactions based on their physical properties demonstrates strong shock resistance capabilities, low-frequency response, low energy consumption, and high sensitivity. Therefore, the applied magnetic field always takes diamagnetic, ferromagnetic, and paramagnetic forms. The influence of radiation is considered in the temperature profile. This manuscript investigates an analytic solution of incompressible and magnetic Casson fluid in Darcy’s medium subjected to temperature and concentration dependence within a porous-surfaced plate with generalized boundary conditions. The substantial mathematical technique of the Laplace transform with inversion is invoked in the governing equations of the magnetic Casson fluid. The analytic results are transformed into a special function for the plate with a constant velocity, a plate with linear velocity, a plate with exponential velocity, and a plate with sinusoidal velocity. Graphical illustrations of the investigated analytic solutions at four different times are presented. Our results suggest that the velocity profile decreases by increasing the value of the magnetic field, which reflects the control of resistive force. The Nusselt number remains constant at a fixed Rd and is reduced by raising the Rd value.
1. Introduction
Heat transfer is mainly observed due to variation in the temperature of bodies. This process plays a vital role in mechanization and industries such as climate engineering, device cooling, nuclear power plants, and energy acquisition. The well-known Fourier law for heat transfer [1] and Fick’s law for mass transfer have been widely used in the literature. The fragility of Fourier law is that the initial bugging is immediately perceived by the medium, which is impractical. The classical Fourier law was amended by adding relaxation time to heat flux by Cattaneo [2]. Christov [3] further modified Cattaneo’s law by incorporating a Lie derivative for the heat flux. The Cattaneo–Christov theory has been applied to both Newtonian and non-Newtonian fluids with various physiological effects. The Cattaneo–Christov model was discussed by Straughan for the thermal convection of a viscous fluid [4]. Salahuddin et al. [5] applied the theory given in [3] to Williamson fluid. The flow of Eyring–Powell fluid over an exponentially stretching surface in three dimensions was reported by Hayat and Nadeem [6] following [3]. With the same theory, Maxwell fluid flow with an expanding sheet with changeable thickness was studied by Hayat et al. [7]. Moreover, Hashim and Khan [8] considered Carreau fluid with a slender sheet under the effect of the model in [3]. Oldroyd-B fluid was analyzed employing [3] by Abbasi et al. [9]. Hayat et al. [10] presented a comparative study of viscoelastic fluids through [3]. Unsteady and nonlinear convection of micro- and nanofluids under [3] was recently stated by Upadhya et al. [11].
Non-Newtonian fluids have extensive use in industrial and engineering processes such as the production of paper, polymer processing, geological flows in the earth mantle, ink printing, paint suspensions, and biological flows. Thus, the analysis of such fluids is of substantial research interest and significant importance. Typical characteristics of the flow of non-Newtonian fluids have become a crucial area of research for scientists, mathematicians, engineers, and researchers. Strain rate and stress are a combination of linear and nonlinear relations characterized by Newtonian fluid and non-Newtonian fluids, respectively. With the relationship between strain rate and stress, non-Newtonian fluids, polymer solutions, slurries, and pastes, to mention just a few, are difficult for developing mathematical modeling in terms of differential equations. Due to this reason, non-Newtonian fluids give rise to an abundance of rheological mathematical models of fluids. We classify such fluids models by century: 18th century, from 1867 to 1893 (Barus and Maxwell model), and 19th century, from 1922 to 1995 (Blatter model, Ellis model, Giesekus model, Phan–Thien–Tanner model, Johnson–Tevaarwerk model, Carreau–Yasuda model, Carreau model, Cross model, Rivlin–Ericksen model, Oldroyd-8 constants model, Oldroyd-B model, Rivlin model, generalized Burgers, Eyring, and Williamson fluid model), among others. Among these fluid models, which are the most accurate and treated fluid models in the biofield, is the so-called Casson fluid model (1959). The main significance of this model is to characterize the pseudoplastic properties of yield stress. Common, useful examples of the Casson model are concentrated fruit juices, jelly, tomato sauce, and honey, among others [12,13,14,15,16]. To characterize the rheology of Casson fluid, several authors have adopted different research directions.
Magneto fluid dynamics has become an important topic in recent years. The study of magnetohydrodynamics has assisted real-life applications. For instance, electromagnetic forces can be used to pump liquid metals without the need for any moving parts. The concept of MHD has significant importance in stellar and planetary processes and has also boosted engineering applications, such as direct conversion generators and flow problems of ionized gasses. MHD unsteady flow in a porous channel with convective heat conditions at the surface was explored by Makinde [17], whose study concludes that the presence of a magnetic field strengthens flow control. The boundary layer flow of MHD Maxwell nanofluid was discussed with numerical assistance [18]. Ellahi et al. [19] numerically inquired about the Couette flow of heat transfer in magnetohydrodynamics. Thermal radiation is a ruling factor in the thermodynamic analysis of high-temperature systems such as boilers and solar connectors. Heat and mass relocation analysis with thermal radiation plays a vital role in manufacturing industries, such as the design of flippers, gas motors, and cooling towers; various propulsion devices for aircraft, energy utilization, and food processing; and diverse agricultural, military, and health applications. As a result, a lot of work has been conducted on fluid flow considering radiation in thermal radiation. The effect of thermal radiation has been analyzed for viscoelastic fluids. The Rosseland approximation was applied to characterize the heat flux in a heat equation by Qasim et al. [20]. Ayub et al. [21] discussed the influence of a wall shield on the radiation of a transverse electromagnetic wave. The solution was obtained by the Wiener–Hopf technique.
Maleque [22] described the porous effects of Casson fluid flow with an axial uniform magnetic field in which similarity parameters were applied to reduce nonlinear ordinary differential equations. In order to determine the angular velocity approximately, the numerical shooting method was used. Abd El-Aziz and Afify [23] numerically analyzed the slippage of Casson nanofluid to enhance the warmth transfer of an overextended sheet. Their main emphasis was to validate their obtained results by comparing them with existing literature. Casson fluid over a steady spinning plane based on three-dimensional, thin-film, nanofluid flow was examined by Anwar et al. [24]. They used the homotopy analysis method to calculate the governing equation and Mathematica software (Wolfram Mathematica, New Jersey, NJ, United State) to provide a graphical illustration of the velocity gradient, temperature, and concentration gradient of the Casson model. Although research on the Casson model is ongoing, we include some related studies based on heat transfer [25,26,27,28,29], fractional models of fluids with magnetic field [30,31,32,33,34,35,36,37,38,39,40], and some others [41,42,43,44,45,46,47,48,49,50,51,52,53,54] herein. Motivated by the above discussion, we analyzed an analytic solution of incompressible and magnetic Casson fluid subjected to temperature and concentration dependence within a porous-surfaced plate.
The intention of this manuscript is to develop exact symmetric solutions of MHD Casson fluid with chemically reactive flow with the help of generalized boundary conditions. A substantial mathematical technique of Laplace transforms with inversion is applied to magnetic Casson fluid. In Section 2, dimensionless governing equations are developed. In Section 3, exact solutions of concentration, temperature, and velocity field are developed with the help of the Laplace transformation. In Section 4, analytic solutions are transformed into special functions for a plate with constant velocity, a plate with linear velocity, a plate with exponential velocity, and a plate with sinusoidal velocity. In Section 5, graphical illustrations of the investigated analytic solutions at four different times are presented. Finally, concluding observations are listed in Section 6.
2. Mathematical Formulation
Let us consider incompressible MHD Casson fluid with a permeable surface with inclination angle and magnetic field normal to the plate. At the plate started to move with velocity , having its concentration and temperature depend upon time as , and . The physical model describing flow is given in Figure 1. We suppose that the rheological equation for incompressible Casson fluid [12,13] is
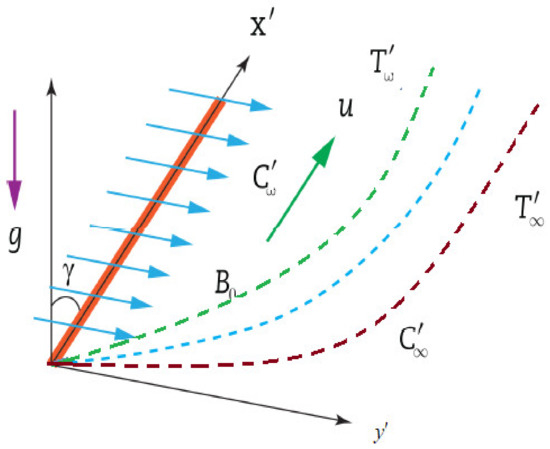
Figure 1.
Geometrical presentation of Casson fluid.
Some necessary assumptions considered to formulate the mathematical model are described as:
- (a)
- The pressure gradient is absent on the boundary.
- (b)
- No external electric fields exist because of the neglected polarization effect.
- (c)
- Due to the consideration of an infinitely long plate, the governing equations only involve time t and axial coordinate y.
- (d)
- It is assumed that the induced magnetic field is sufficiently weak and has no significant role in the flow process.
Following these assumptions, primary flow, temperature, and concentration equations are derived under Rosseland and Boussinesq’s approximation.
The initial boundary conditions are
Radiative flux is defined by using the Rosseland approximation [32],
is a linear function and expressed by the Taylor expansion. By neglecting higher powers, we have
Substituting Equations (7) and (8) into Equation (2), the required form of the temperature profile is given as:
For the simplification of the governing equations, Equations (1)–(3), we introduce the dimensionless variable among the governing equations of Casson fluid. We define them as described below:
After invoking the dimensionless quantities in Equations (1)–(3), we simplify the governing equations of Casson fluid as:
with imposed conditions
3. Method of Solution
3.1. Analyticity of Temperature Profile
The analyticity of the temperature distribution can be derived for the coupled equation by utilizing the Laplace transform on (13). Using appropriate conditions (15)–(17), we have
Equation (18) is a homogenous linear differential equation that can be evaluated by means of elementary approaches with appropriate conditions (15)–(17). The solution for Equation (18) is obtained as
Taking inverse (19) by means of the Laplace transformation, we obtain a suitable result as
Nusselt Number
To estimate the heat transfer rate, the Nusselt number is used, which is calculated as:
3.2. Analyticity of Concentration Profile
The analyticity of the concentration field can be derived for the coupled equation by utilizing the Laplace transform on (14) using appropriate conditions (15)–(17). We arrive at
Equation (21) is a homogenous linear differential equation that can be evaluated by means of elementary approaches with appropriate conditions (15)–(17). The solution of Equation (21) is obtained as
Taking inverse (22) by means of the Laplace transformation, we obtain a suitable result as
where the property of special function used on (23) is defined as
Sherwood Number
To estimate the mass transfer rate from plate to fluid, the Sherwood number is used, which is calculated as:
3.3. Analyticity of Velocity Profile
The analyticity of the velocity field can be derived for coupled equations, and by utilizing the Laplace transform on (12) using appropriate conditions (15)–(17), we arrive at
The general solution of (26) after the substitution of (19) and (22) is
Using boundary conditions, the final form of the velocity profile is
Here, we generate some letting parameters to avoid lengthy and cumbersome calculations
Taking inverse (27) by means of the Laplace transformation, we obtain a suitable result as
4. Special Cases
It is further noted that some interesting solutions can be recovered from Equation (30), which represents the final solution of velocity with the generalized boundary conditions on temperature, concentration, and velocity. For the sake of new solutions on the basis of generalized boundary conditions, we consider in Equation (28), and we arrive at
The inverse Laplace of Equation (31) using (24) and (25) is
The different cases of the velocity field can be considered using Equation (31).
4.1. Motion of Plate with Constant Velocity
The solution for the motion of plate can be achieved by setting . We recover the solution as
4.2. Motion of Plate with Linear Velocity
The solution for the motion of the plate can be achieved by setting . We recover the solution as
4.3. Motion of Plate with Exponential Acceleration
The solution for the motion of the plate can be achieved by setting . We recover the solution as
4.4. Motion of Plate with Sinusoidal Oscillation
The solution for the motion of the plate can be achieved by setting . We recover the solution as
5. Results and Discussion
This section is devoted to the physical interpretation of the heat and mass transfer executed on the motion of free-convection MHD Casson fluid through a limitless plate with porous medium. The impact of thermal radiation, chemical reactions, and magnetic fields are also analyzed via the Laplace transformation to obtain a unique solution. The impact of physical parameters such as on the energy velocity profile is discussed with a graphical approach using MATHCAD-15.
Figure 2 investigates the domination of M on the velocity components. With an increase in M, the velocity decreases due to force. It behaves as a drag force. By enhancing the value of M, the Lorentz force also increases. Fluid flow on the boundary layer is slowed down due to this force. It is perceived that the behavior of the fluid profile is effective in the classical model.
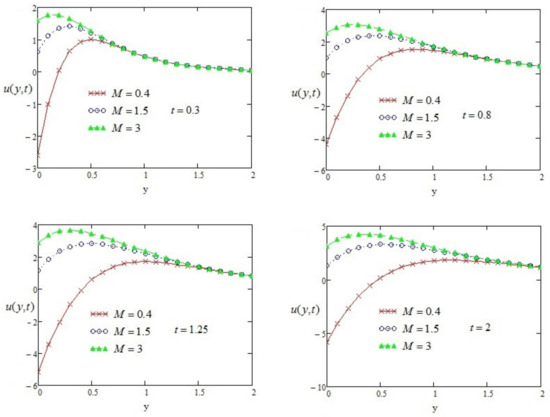
Figure 2.
Velocity profile of with variation of time effect and other parameters such as .
Figure 3 analyzes the effect of Casson parameter on the velocity field. The magnitude of the velocity field enlarges with a small value of . For a large value of , the boundary layer thickness is minimized, which helps to reduce the velocity.
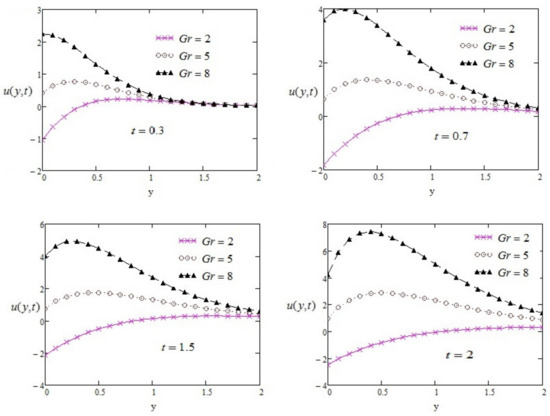
Figure 3.
Velocity profile of with variation of time effect and other parameters such as .
Thermal and isothermal conditions represent the domination of , as shown in Figure 4. Physically, shows the relation between thermal and viscous forces. For the variation of time, the behavior of the velocities is unique. The influence of is illustrated in Figure 5. It can be noticed that the resultant velocity increases by enhancing . It can also be seen that velocity increases with an increase in time. The behaviors of and on the velocity profile are the same. Figure 6 analyzes the variation of on the velocity with the help of time. The large value of radiation parameter causes an increase in fluid flow. The rate of energy transport of the fluid increases due to an increase in the intensity of the radiation parameter and a decrease in viscosity. Due to such behavior, the fluid moves faster and enhances the fluid velocities. The domination of chemical reaction on the concentration field is discussed in Figure 7. With a large value of , the concentration profile decreases. The positive value of is analyzed as destructive, and the negative value behaves as productive. Figure 8 displays the Nusselt number Nu against time, varying the radiation parameter. It is clear that with a fixed value of Rd, Nu remains constant when changing the value of t. By increasing the value of Rd, Nu drops to smaller values, maintaining the same constant trend with increasing t. This shows that the changing radiation parameter values decrease the convective thermal energy flow. Figure 9 shows the effect of skin friction with the variation of time. By increasing the value of time, skin friction drops to a smaller value. This shows that skin friction remains constant with the effect of the variation of time. The existence of the Prandtl number may reflect the control of the thickness of the momentum and the enlargement of thermal conductivity. The value of Prandtl number is fixed. The Prandtl number for water at 17 °C is 7.56 and for air at room temperature is 0.7. The Prandtl number is for non-Newtonian fluid.
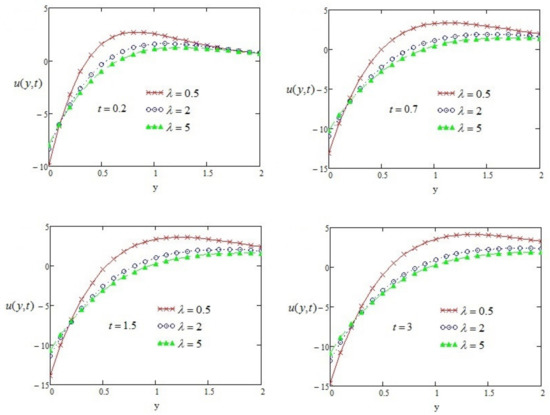
Figure 4.
Velocity profile of with variation of time effect and other parameters such as .

Figure 5.
Velocity profile of with variation of time effect and other parameters such as .

Figure 6.
Temperature profile of with variation of time effect and other parameters such as .

Figure 7.
Concentration profile of with variation of time effect and other parameters such as .
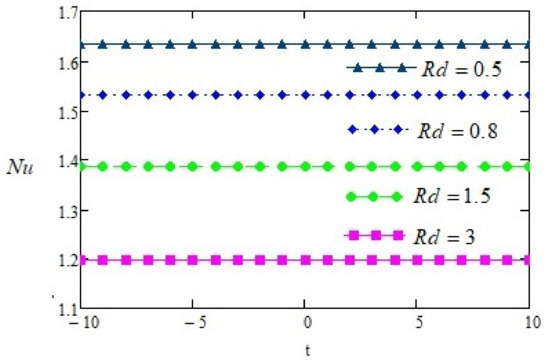
Figure 8.
Graph displaying Nu dependence on Rd.

Figure 9.
Graph displaying kin friction dependence on time.
6. Conclusions
The exact symmetrical and closed-form solution of MHD Casson fluid with chemically reactive flow was analyzed by the Laplace transformation. Generalized boundary conditions along the infinite plate were taken. The graphical approach was used to discuss the influence of the dimensionless parameter on fluid velocity. Key points can be taken from the graphical discussion:
- (a)
- Velocity can be elevated to enhance the values of the thermal Grashof number (Gr) and the mass Grashof number (Gc).
- (b)
- Thermal radiation plays a significant role in the development of thermal and momentum boundary layers.
- (c)
- Velocity can be de-accelerated to enhance the values of the magnetic field (M).
- (d)
- Temperature can be elevated to enhance the values of the radiation parameter (Rd).
- (e)
- The concentration field can be reduced by enhancing the value of the chemical reaction parameter Kc.
- (f)
- The magnitude of the velocity field is enhanced with a small value of .
- (g)
- The Nusselt number shows the opposite behavior with a higher value of Rd.
- (h)
- The value of the Prandtl number is 12 for non-Newtonian fluids.
Author Contributions
Conceptualization, S.T.S. and M.B.R.; data collection, S.T.S. and H.A.; formal analysis, S.T.S. and M.B.R.; investigation, S.T.S.; methodology, S.T.S.; software, S.T.S. and M.B.R.; writing—original draft preparation, S.T.S. and J.A.; review, M.B.R. and J.A. funding, M.B.R.; J.A.; writing—review and editing, J.A. and H.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been supported by the Polish National Science Centre under the grant OPUS 18 No. 2019/35/B/ST8/00980.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
My manuscript has no associated data.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Fourier, J.B.J. Théorie Analytique De La Chaleur; Chez Firmin Didot, Père et Fils: Paris, France, 1822. [Google Scholar]
- Cattaneo, C. Sulla conduzione del calore. Atti Semin. Mat. Fis. Univ. Modena Reggio Emilia 1948, 3, 83–101. [Google Scholar]
- Christov, C.I. On frame indifferent formulation of the Maxwell-Cattaneo model of finite-speed heat conduction. Mech. Res. Commun. 2009, 36, 481–486. [Google Scholar] [CrossRef]
- Straughan, B. Thermal convection with the Cattaneo-Christov model. Int. J. Heat Mass Transf. 2010, 53, 95–98. [Google Scholar] [CrossRef]
- Salahuddin, T.; Malik, M.Y.; Hussain, A.; Bilal, S.; Awais, M. Mhd flow of Cattanneo–Christov heat flux model for williamson fluid over a stretching sheet with variable thickness:using numerical approach. J. Magn. Magn. Mater. 2016, 401, 991–997. [Google Scholar] [CrossRef]
- Hayat, T.; Nadeem, S. Flow of 3D Eyring-Powell fluid by utilizing Cattaneo-Christov heat flux model and chemical processes over an exponentially stretching surface. Results Phys. 2018, 8, 397–403. [Google Scholar] [CrossRef]
- Hayat, T.; Farooq, M.; Alsaedi, A.; Al-Solamy, F. Impact of Cattaneo-Christov heat flux in the flow over a stretching sheet with variable thickness. AIP Adv. 2015, 5, 087159. [Google Scholar] [CrossRef]
- Hashim; Khan, M. On Cattaneo-Christov heat flux model for Carreau fluid flow over a slendering sheet. Results Phys. 2017, 7, 310–319. [Google Scholar] [CrossRef]
- Abbasi, F.M.; Shehzad, S.A.; Hayat, T.; Alsaedi, A.; Hegazy, A. Influence of Cattaneo-Christov heat flux in flow of an Oldroyd-B fluid with variable thermal conductivity. Int. J. Numer Methods Heat Fluid Flow 2016, 26, 2271–2282. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Alsaedi, A.; Mustafa, M. A comparative study for flow of viscoelastic fluids with Cattaneo-Christov heat flux. PLoS ONE 2016, 11, e0155185. [Google Scholar] [CrossRef] [Green Version]
- Upadhya, S.M.; Raju, C.S.K.; Mahesha; Saleem, S. Nonlinear unsteady convection on micro and nanofluids with Cattaneo-Christov heat flux. Results Phys. 2017, 9, 779–786. [Google Scholar] [CrossRef]
- Meral, F.C.; Royston, T.J.; Magin, R. Fractional calculus in viscoelasticity: An experimental Study. Comm. Non-Linear Sci. Num. Simu. 2010, 15, 939–945. [Google Scholar] [CrossRef]
- Khalid, A.; Khan, I.; Khan, A.; Shafie, S. Unsteady MHD free convection flow of Casson fluid past over an oscillating vertical plate embedded in a porous medium. Eng. Sci. Tech. Int. J. 2015, 18, 309–317. [Google Scholar] [CrossRef] [Green Version]
- Akbar, N.S.; Nadeem, S. Characteristics of heating scheme and mass transfer on the peristaltic flow for an Eyring–Powell fluid in an endoscope. Int. J. Heat Masstransf. 2012, 55, 375–383. [Google Scholar] [CrossRef]
- Ali, F.; Sheikh, N.A.; Khan, I.; Saqib, M. Magnetic field effect on blood flow of Casson fluid in an axisymmetric cylindrical tube: A fractional model. J. Magne. Mag. Mater. 2017, 423, 327–336. [Google Scholar] [CrossRef]
- Malik, M.Y.; Hussain, A.; Nadeem, S. Boundary layer flow of an Eyring-Powell model fluid due to a stretching cylinder with variable viscosity. Sci. Iran. 2013, 20, 313–321. [Google Scholar]
- Makinde, O.D.; Khan, Z.H.; Ahmad, R.; Haq, R.U.; Khan, W.U. Unsteady MHD flow in a porous channel with thermal radiation and heat source/ sink. Int. J. Appl. Comput. Math. 2019, 5, 1–21. [Google Scholar] [CrossRef]
- Nadeem, S.; Akhtar, S.; Abbas, N. Heat transfer of Maxwell base fluid flow of nanomaterial with MHD over a vertical moving surface. Alex. Eng. J. 2020, 59, 1847–1856. [Google Scholar] [CrossRef]
- Ellahi, R.; Shivanian, E.; Abbasbandy, S.; Hayat, T. Numerical study of magnetohydrodynamics generalized Couette flow of Eyring-Powell fluid with heat transfer and slip condition. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 1433–1445. [Google Scholar] [CrossRef]
- Qasim, M.; Hayat, T.; Obaidat, S. Radiation effect on the mixed convection flow of a viscoelastic fluid along an inclined stretching sheet. Z. Nat. 2012, 67, 195–202. [Google Scholar] [CrossRef]
- Ayub, M.; Khan, T.A.; Jilani, K. Effect of cold plasma permittivity on the radiation of the dominant TEM-wave by an impedance loaded parallel-plate waveguide radiator. Math. Methods App. Sci. 2016, 39, 134–143. [Google Scholar] [CrossRef]
- Maleque, A. Unsteady MHD Non-Newtonian Casson Fluid Flow due to a Porous Rotating Disk with Uniform Electric Field. Fluid Mech. Open Acc. 2016, 3, 123–131. [Google Scholar]
- El-Aziz, M.A.; Afify, A.A. Effect of Hall current on MHD slip flow of Casson nanofluid over a stretching sheet with zero nanoparticle mass flux. Thermophys. Aeromech. 2019, 26, 429–443. [Google Scholar] [CrossRef]
- Anwar, S.; Zahir, S.; Saeed, I.; Muhammad, J.; Ullah, A.; Taza, G.; Poom, K. Three-Dimensional Casson Nanofluid Thin Film Flow over an Inclined Rotating Disk with the Impact of Heat Generation/Consumption and Thermal Radiation. Coatings 2019, 9, 248. [Google Scholar]
- Mernonr, A.V.; Mazumdar, J.N.; Lucas, S.K. A mathematical study of peristaltic transport of a Casson fluid. Math. Comput. Model 2002, 35, 895–912. [Google Scholar] [CrossRef]
- Shaw, S.; Gorla, R.S.R.; Murthy, P.; Ng, C.O. Pulsatile Casson fluid flow through a stenosed bifurcated artery. Int. J. Fluid Mech. 2009, 36, 43–63. [Google Scholar] [CrossRef]
- Mustafa, M.; Hayat, T.; Pop, I.; Aziz, A. Unsteady boundary layer flow of a Casson fluid due to an impulsively started moving flat plate. Heat Transf. Asian Res. 2011, 40, 563–576. [Google Scholar] [CrossRef]
- Saeed, S.T.; Bilal, M.B.; Baleanu, D. A fractional study of generalized Oldroyd-B fluid with ramped conditions via local and non-local kernels. Nonlinear Eng. Model. Appl. 2021, 10, 177–186. [Google Scholar] [CrossRef]
- Bilal, M.B.; Atangana, A.; Saeed, S.T. MHD free convection flow over a vertical plate with ramped wall temperature and chemical reaction in view of non-singular kernel. Fract. Order Anal. Theory Methods Appl. 2020, 253–279. [Google Scholar] [CrossRef]
- Abro, K.A.; Ilyas, K. Effects of CNTs on magnetohydrodynamic flow of methanol based nanofluids via Atangana-Baleanu and Caputo-Fabrizio fractional derivatives. Therm. Sci. 2019, 23, 883–898. [Google Scholar]
- Abro, K.A.; Gomez-Aguilar, J.F. A comparison of heat and mass transfer on a Walter’s-B fluid via Caputo-Fabrizio versus Atangana- Baleanu fractional derivatives using the Fox-H function. Eur. Phys. J. Plus 2019, 134, 101. [Google Scholar] [CrossRef]
- Saeed, S.T.; Khan, I.; Riaz, M.B.; Husnine, S.M. Study of Heat Transfer under the Impact of Thermal Radiation, Ramped Velocity, and Ramped Temperature on the MHD Oldroyd-B Fluid Subject to non-integer Differentiable Operators. J. Math. 2020, 2020, 1–14. [Google Scholar] [CrossRef]
- Saeed, S.T.; Abro, K.A.; Almani, S. Role of single slip assumption on the viscoelastic liquid subject to non-integer differentiable operators. Math. Methods Appl. Sci. 2021, 44, 6005–6020. [Google Scholar] [CrossRef]
- Iftikhar, N.; Saeed, S.T.; Riaz, M.B. Fractional study of heat and mass transfer of MHD Oldroyd-B fluid with ramped velocity and temperature. Comp. Methods Diff. Eqs. 2021, 1–28. [Google Scholar] [CrossRef]
- Riaz, M.B.; Saeed, S.T.; Baleanu, D. Role of Magnetic field on the Dynamical Analysis of Second Grade Fluid: An Optimal Solution subject to Non-integer Differentiable Operators. J. Appl. Comp. Mech. 2021, 7, 54–68. [Google Scholar]
- Abdeljawad, T.; Riaz, M.B.; Saeed, S.T.; Iftikhar, N. MHD Maxwell Fluid with Heat Transfer Analysis under Ramp Velocity and Ramp Temperature Subject to Non-Integer Differentiable Operators. Comp. Model Eng. Sci. 2021, 126, 821–841. [Google Scholar]
- Riaz, M.B.; Saeed, S.T. Comprehensive analysis of integer order, Caputo-Fabrizio and Atangana-Baleanu fractional time derivative for MHD Oldroyd fluid with slip effect and time dependent boundary condition. Disc. Cont. Dyn. Syst. 2021, 14, 3719–3746. [Google Scholar] [CrossRef]
- Saeed, S.T.; Riaz, M.B.; Baleanu, D.; Abro, K.A. A Mathematical Study of Natural Convection Flow through a Channel with nonsingular Kernels: An Application to Transport Phenomena. Alex. Eng. J. 2020, 59, 2269–2281. [Google Scholar] [CrossRef]
- Khan, I.; Saeed, S.T.; Riaz, M.B.; Abro, K.A.; Husnine, S.M.; Nisar, K.S. Influence in a Darcy’s Medium with Heat Production and Radiation on MHD Convection Flow via Modern Fractional Approach. J. Mater. Res. Tech. 2020, 9, 10016–10030. [Google Scholar] [CrossRef]
- Riaz, M.B.; Siddiqui, M.; Saeed, S.T.; Atangana, A. MHD Oldroyd-B Fluid with Slip Condition in view of Local and Nonlocal Kernels. J. Appl. Comp. Mech. 2021, 7, 116–127. [Google Scholar]
- Riaz, M.B.; Saeed, S.T.; Baleanu, D.; Ghalib, M. Computational results with non-singular & non-local kernel flow of viscous fluid in vertical permeable medium with variant temperature. Front. Phys. 2020, 8, 275. [Google Scholar]
- Saeed, S.T.; Riaz, M.B.; Baleanu, D.; Akgul, A.; Husnine, S.M. Exact Analysis of Second Grade Fluid with Generalized Boundary Conditions. Intel. Auto. Soft Comp. 2021, 28, 547–559. [Google Scholar] [CrossRef]
- Rehman, A.U.; Riaz, M.B.; Akgul, A.; Saeed, S.T.; Baleanu, D. Heat and mass transport impact on MHD second grade fluid: A comparative analysis of fractional operators. Heat Trans. Asian Res. 2021. [Google Scholar] [CrossRef]
- Rehman, A.U.; Riaz, M.B.; Saeed, S.T.; Yao, S. Dynamical analysis of radiation and heat transfer on MHD second grade fluid. Comp. Model Eng. Sci. 2021. [Google Scholar] [CrossRef]
- Rehman, A.U.; Riaz, M.B.; Awrejcewicz, J.; Baleanu, D. Exact solutions of thermomagetized unsteady non-singularized Jeffrey fluid: Effect of ramped velocity, concentration with Newtonian heating. Results Phys. 2021, 26, 104367. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Tamnanloo, J.; Mousavi, S.H.; Miandoab, E.S.; Hosseini, E.; Ghasem, H.; Mozaffari, S. Discrete-Continuous genetic algorithm for designing a mixed refrigerant cryogenic process. Ind. Eng. Chem. Res. 2021, 60, 7700–7713. [Google Scholar] [CrossRef]
- Tesema, T.E.; Kookhaee, H.; Habteyes, T.G. Extracting electronics transition bands of adsorbates from Molecule-Plasmon excitation coupling. J. Phys. Chem. Lett. 2020, 11, 3507–3514. [Google Scholar] [CrossRef]
- Ghasemi, H.; Mozaffari, S.; Mousavi, S.H.; Aghabarari, B.; Abu-Zahra, N. Decolonization of wastewater by heterogeneous Fenton reaction using MnO2-Fe3O4/CuO hybrid catalysts. J. Enviro. Chem. Eng. 2021, 9, 105091. [Google Scholar] [CrossRef]
- Wang, C.F.; Kafle, B.; Tesema, T.E.; Kookhaee, H.; Habteyes, T.G. Molecular sensitivity of near field vibrational infrared imaging. J. Phys. Chem. C 2020, 124, 21018–21026. [Google Scholar] [CrossRef]
- Alberghi, C.; Candido, L.; Testoni, R.; Utili, M.; Zucchetti, M. Verification and validation of COMSOL magnetohydrodynamic models for liquid metal breeding blankets technologies. Energies 2021, 14, 5413. [Google Scholar] [CrossRef]
- Melchiorri, L.; Narcisi, V.; Giannetti, F.; Caruso, G.; Tassone, A. Development of a RELAP5/MOD3.3 module for MHD pressure drop analysis in liquid metals loops: Verification and validation. Energies 2021, 14, 5538. [Google Scholar] [CrossRef]
- Bilal, S.; Majeed, A.H.; Mahmood, R.; Khan, I.; Sheikh, A.H.; Sherif, E.-S.M. Heat and mass transfer in hydromagnetic second grade fluid past a porous inclined cylinder under the effects of thermal dissipation, diffusion and Radiative heat flux. Energies 2020, 13, 278. [Google Scholar] [CrossRef] [Green Version]
- Bilal, S.; Rehman, M.; Noeiaghdam, S.; Ahmed, H.; Akgul, A. Numerical analysis of natural convection driven flow of a non-Newtonian power-law fluid in a Trapezoidal enclosure with a U-shaped constructal. Energies 2021, 14, 5355. [Google Scholar] [CrossRef]
- Sarris, E.; Gravanis, E. Flow regime analysis of the pressure build up during CO2 injection in saturated porous rock formation. Energies 2019, 12, 2972. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).