1. Introduction
The majority of the inverter-based generation (IBG) connected to the grid is presently based on grid following (GFL) technology. These devices have a phase locked loop (PLL) in order to synchronize with the grid voltage and behave as current sources. As the share of IBG increases, large parts of the system may be operated without synchronous machines.
In such a scenario, grid-forming (GFM) controls may be required to endow the converter with a voltage source behaviour and so provide the reference for frequency and voltage. However, this change comes at a price: the current exchanged with the grid depends on the impedance between the grid and the converter (two voltage sources). For large voltage differences (amplitude or phase) between both voltage sources, the current can be higher than the converter nominal value for a determined period of time. Compared to synchronous machines that can support several times its rated current, power electronics can only hold small over currents (20–40%). Therefore, inverters need to be protected against any event leading to over currents such as short circuits, phase shifts or even connection of large loads.
Many current limiting strategies have been proposed in the technical literature for GFM converters. One simple option consists in adding saturations to the cascaded proportional-integral (PI) inner control loops. Other authors have proposed to switch the control to a PLL-based current control during grid faults in order to keep the synchronism with the system while still limiting the current [
1]. The main drawback of this method is the requirement of a complex algorithm for fault detection and triggering conditions setting.
Recently, some concepts based on Threshold Virtual Impedance (TVI) have been proposed for current limiting purposes [
2,
3]. The idea is to implement a control structure capable of emulating the effect of a physical impedance when the current exceeds a pre-selected trigger value. The TVI limits the output current of the inverter by virtually increasing the impedance between the limited inverter and the grid, using a control algorithm. In short, a virtual impedance is basically an estimated voltage difference, proportional to the amount of current injected by the inverter. So, by applying this voltage difference at the output, the behaviour of the system will be similar to a voltage source in series with a variable impedance. Usually, TVI controls are divided into three steps [
4]:
- (1)
Overcurrent detection and virtual impedance activation,
- (2)
Virtual impedance calculation and
- (3)
AC voltage droop estimation.
Once all the three steps are performed, the estimated AC voltage droop is applied at the output voltage following different strategies depending on the grid forming algorithm. Some grid forming controls have a virtual impedance per each phase [
5], others control only in the voltage module [
6], while the majority of them implement the algorithm in DQ reference frame [
1,
7,
8].
Indeed, many different implementations have been proposed to achieve grid forming capability. In the present paper the grid forming control is implemented in DQ reference frame without sequence separation [
9]. However, this DQ reference frame can also be implemented with separated sequences: positive (PS), negative (NS) and zero [
10]. The TVI current limiting strategy can be implemented in many ways related to sequences and independently of the main control strategy. Some of these ways are enumerated below:
Positive and negative sequences completely separated in DQ frame [
10];
Without sequence separation in unsaturated mode but the TVI activation with separated sequences;
With separated sequences at the outer control loops (and TVI activation) but without separating sequences at the inner control loops;
With separated sequences but using a current source for the NS (PI control loop).
In the present paper, from a solution based on a DQ reference frame without sequence separation (unsaturated mode), a new TVI with separated and configurable thresholds and gains for each sequence is proposed.
2. Requirements for Current Limiting Methods
In addition to protecting the inverter from any damage, current limitation control must comply with certain stability and performance requirements. They are related to low-voltage or fault ride through (LVRT or FRT) specifications that usually include a certain withstand capability together with droop characteristics and dynamic requirements on the injected current as well as prioritization strategies and fast power recovery. On top of it, when a safe and stable operation is achieved, the inverter should contribute to minimize disturbances and ensure grid power quality, limiting voltage variations and countering unbalance and harmonic distortion. In order to assess the different methods to limit the inverter current, several basic criteria can be listed:
The ability to limit the output current below the inverter maximum value without disconnection by internal protections;
The ability to remain synchronized to other inverters/generation units during transients. Transition between normal and current limiting mode must be as smooth as possible to ensure stability;
The ability to support the grid providing inertial response, system strength, reducing unbalances and absorbing harmonic currents.
The first two features are mandatory, and the correct behaviour of the current limitation strategy is relatively easy to assess from the control design perspective considering standard FRT profiles and worst-case scenarios for grid conditions. However, the power quality characteristic and the expected behaviour during faults may vary depending on national implementations of grid codes and even location. Although there are no grid codes for utility scale grid forming inverters in force at this moment (June, 2021), some proposals are under discussion [
11,
12].
References [
12,
13] point out in the same direction regarding voltage unbalances or asymmetries. According to both, the GFM should provide a low negative-sequence impedance and therefore provide unbalanced currents to counteract asymmetric voltages in the grid. However, what happens when the inverter current limit is reached is not clear. Based on the existing grid codes drafts and literature, in this work the following requirements are considered relevant when an inverter faces unbalanced voltage dips:
In normal operation, the capacity of the inverter to reduce voltage unbalances depends on the negative sequence impedance, which should then be as low as possible. If the negative sequence current is below the NS TVI threshold (current limit), the grid forming inverter should compensate a large part of the unbalanced voltage at its terminals (depending on the system impedance).
When current limiting control is active, the ability to support the grid voltage at the event of unbalanced voltages can be interpreted as a prioritization of the negative sequence current over the positive sequence one.
User defined setting should allow to define the share of positive and negative sequence contribution.
3. Implemented Grid Forming Control and Sequence Model
Grid forming inverters are synchronised measuring only local electrical values, without any communication. The active power—frequency droop control allows a simple synchronisation process between several pieces of equipment operating in parallel. This droop control is usually implemented with a low-pass filter (LPF) to eliminate the measurement noise, but more importantly it also enables inertia provision. The LPF can be implemented at two different locations: at the active power measurement or on the droop error signal (measured active power—reference active power). The second option gives an exact equivalent of the swing equation of a synchronous machine [
4].
From the variety of control strategies proposed for grid-forming inverters, only few studies are focused in high-power applications. However, these type of power ratings can be crucial in the 100% renewable energy power system. If the grid forming control is oriented to high-power systems, low switching frequencies are likely to cause large AC voltage response times, a poorly damped system or a strong transient coupling between the AC voltage and the active power. In such conditions, slow dynamics, restrained stability regions or interactions between control loops can appear.
In order to improve the control performance, an inner control loop is used in many control structures [
14]. So, the aim of the inner control loop is to enhance the AC voltage dynamics. In the present paper, cascaded voltage and current loops represented in the
dq synchronous rotating frame (SRF) [
2,
15] are used. Each loop consists of proportional-integral controllers (PI), feed-forward decoupling terms and compensations. First, the AC voltage loop generates the current reference for the current control loop, whose outputs are the voltage references for the modulation. More details about the tuning method of these controls can be found in [
2,
15,
16].
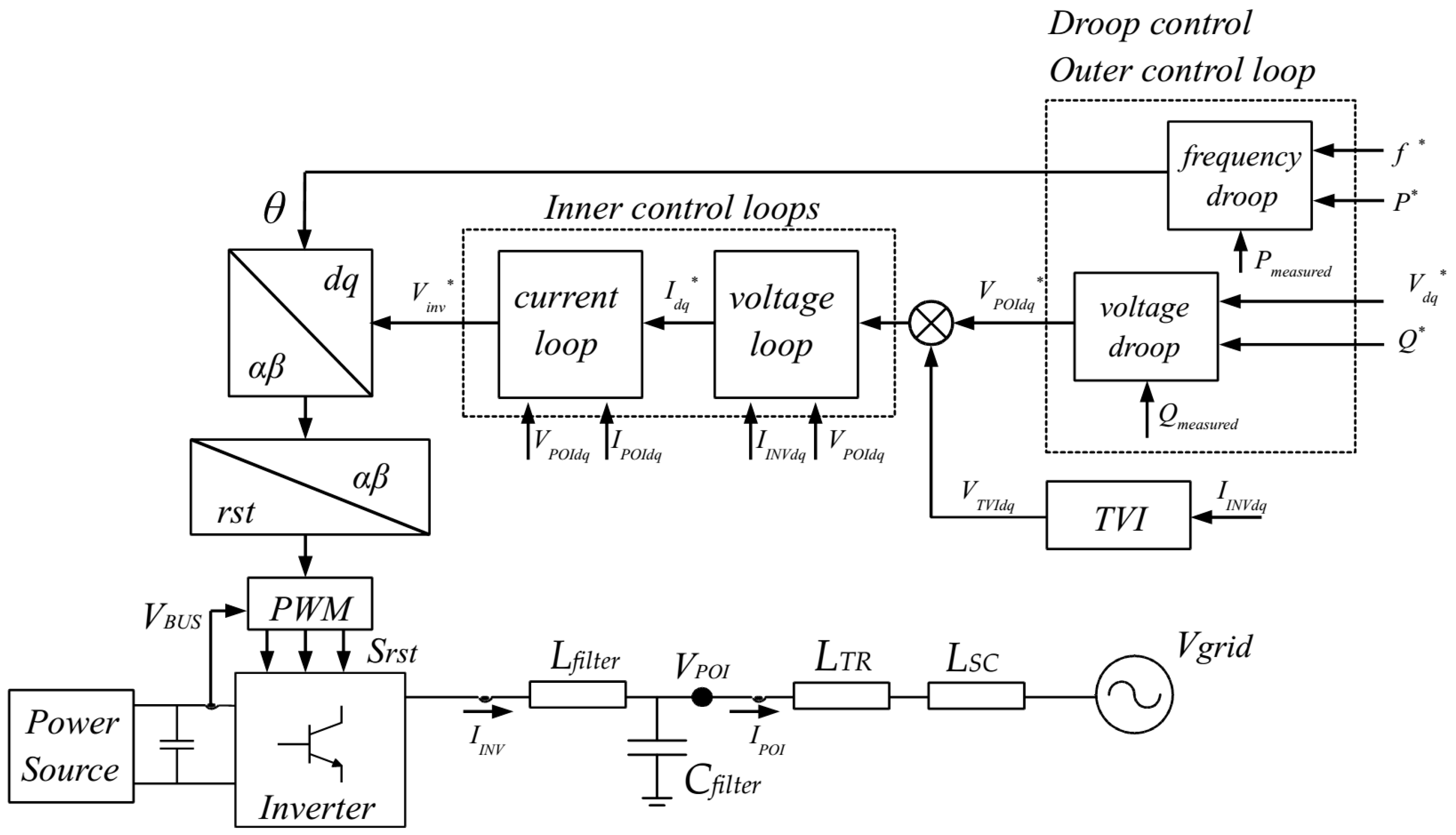
The three-phase voltage source inverter is connected to the point of interconnection (POI) through an LC filter. An ideal three-phase voltage source is considered as the main grid with an inductance (LSC) limiting the short circuit current. A step-up transformer with Δ-Y (Dy11) connections is also considered (LTR). So, zero sequence currents cannot flow through the transformer. Even though all the inductances have been considered with a small resistive part, the resistive part is assumed to be very small.
Regarding the DC side, a primary power source is connected to the DC bus through a DC-DC converter. The general overview of the system is shown in
Figure 1.
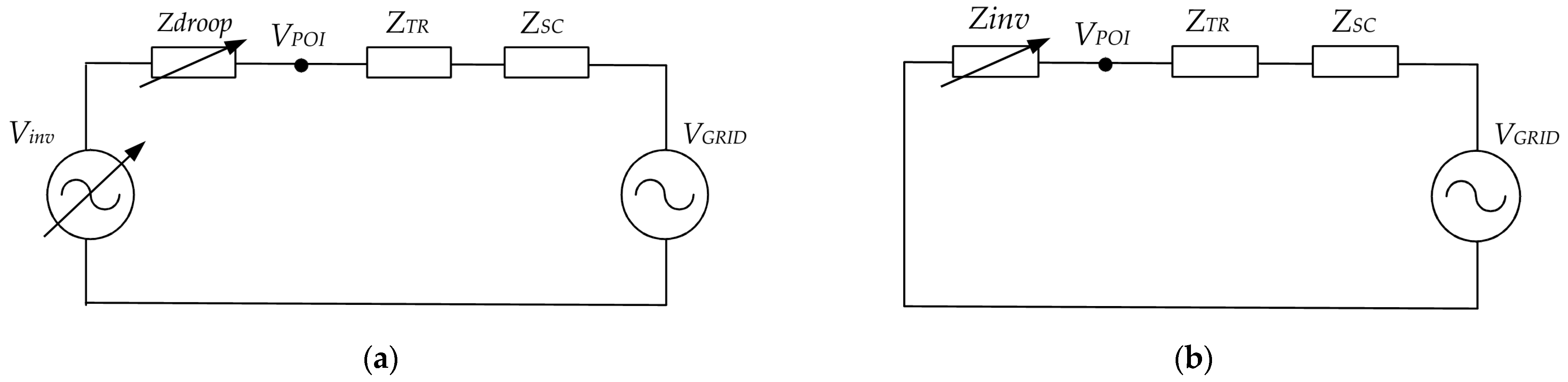
The system presented in
Figure 1 can be modelled in sequences as depicted in
Figure 2. The zero sequence model is neglected due to transformer connections. The inner voltage of the grid forming control should be positive sequence and fundamental frequency only. Thus, in negative sequence the inverter does not present any voltage source behaviour.
The output of the droop voltage control is sent to a voltage regulator (inner voltage control loop); this value is imposed at the controlled point (
VPOI). As a consequence, in steady state, all the impedances behind the voltage-controlled point are not seen by the droop control [
17]. Of course, the physical impedances are still there, but they will not take part in the steady-state because the voltage drop will be compensated by the controller. Along with the control algorithm, they will nonetheless determine the device transient impedance, which is not the case of the primary voltage control of synchronous machines. Indeed, the control of fast acting devices such as VSC impacts the system response at the transient (around 100 ms) time scales, which is generally defined exclusively by the electromagnetic design in synchronous generators (transient impedances
xd’ and
xq’) [
18]. As will be shown in the next section, a GFM VSC can reach steady-state at 100ms following reasonable voltage or load disturbances (not leading to current limitation).
For the positive sequence voltage, a grid forming control with droop and inner voltage loop can be represented as a controlled voltage source in series with an impedance imposed by the droop control. On the other hand, the negative sequence circuit can be represented just as an impedance presented by the grid forming inverter, which does not depend only on physical elements (output power filter). It also relies on the control structure and parameters. The whole system (control and power elements) can be represented in sequences as depicted in
Figure 2.
This way of modelling reduces the inverter and its control into a source (voltage or current source), and an impedance. This Norton/Thevenin equivalent model can be derived based on its control block diagram, by measuring directly the impedance of a real equipment [
19] or by simulation analysis of an accurate model [
20], as will be shown in the next section.
This impedance will determine the negative sequence current absorption and voltage reduction during unsaturated mode, while the inverter does not reach the current limit. Depending on the grid requirements, this impedance can be low enough or not. If it is not enough, control structures oriented to reduce this impedance should be implemented.
In a more general way, for other frequencies different to the fundamental, from the controlled voltage point only an equivalent inner impedance is seen, as the voltage source is only at fundamental frequency. Even more, for high frequencies, beyond the bandwidth of the VSC control, only the physical elements (filter) become relevant.
4. Simulation Model Description and Negative Sequence Impedance Model Validation
In real equipment with digital control units, several delays appear related to the implementation of the control algorithm. For example, the ADC (analog to digital converter) modules to measure the current and voltage need a certain amount of time to convert the data from analog to digital. Even more, to prevent the aliasing effect, usually ADCs are associated to digital filters. So, the phase of the measured signals is not immediately converted at the beginning of the algorithm execution, and the sampled signals at the previous time are used at the start of the next algorithm execution. A control execution time delay appears.
The simulation model has been implemented in the Matlab-simulink platform. The inverter control described in
Section 3 is implemented in programming Matlab language and C++. In order to get a closer representation of the real equipment, the inverter model block is implemented in discrete time frame with a control execution time of 200 μs, which is two times faster than the switching frequency.
Voltage and current transductions along with the ADC are also modelled with an equivalent delay and respective digital filters [
21]. In short, the considered system model is related to the OSMOSE WP3 demonstrator [
9,
22], which has been validated during FATs [
23]. The main electrical characteristics are summarized in
Table 1.
The non-saturated mode negative impedance presented by the inverter is computed by applying a voltage at the desired component (negative sequence in this case) and measuring the current that flows to the inverter. As the grid impedances are known (
Table 2), the inverter impedance can be estimated based on Ohm’s law.
4.1. Positive Sequence Model Validation
Looking at
Figure 2a, it is possible to see that the droop control and the voltage set point have an influence in the circuit. Thus, in order to make the validation simpler, the effect of both is eliminated. If the voltage set point of the grid forming inverter is 1 pu (Qset = 0) and the grid voltage drops to 0.9 pu, for a 0% droop static gain (
Zdroop = 0), the voltage at the POI (
VPOI) is the same as the set point (1 pu). As this voltage depends on the actuation of a PI regulator, transiently an impedance can appear, but after 100 ms (in fact in less than <50 ms) the measured voltage is 1 pu.
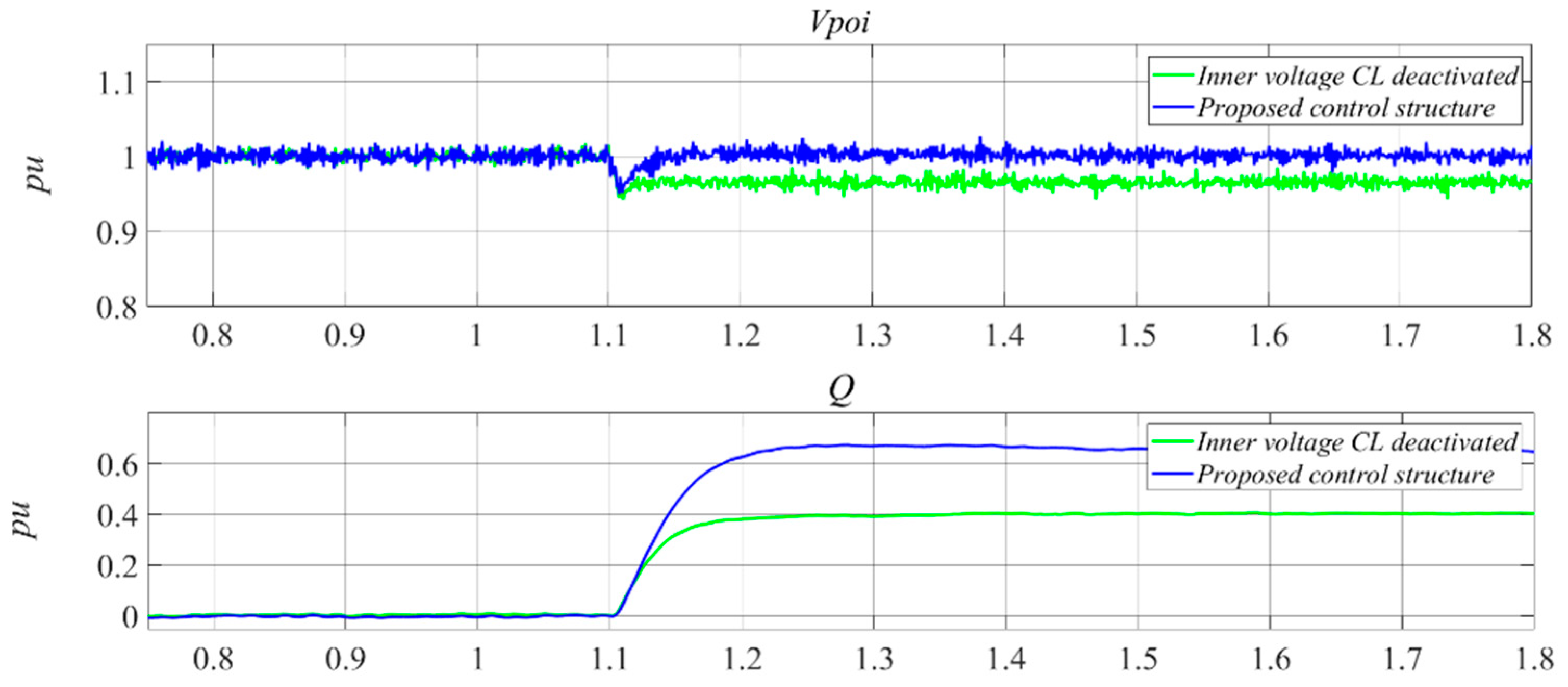
Figure 3 shows a comparison of simulation results for the grid forming inverter with the proposed control with inner control loops activated and deactivated. When inner control loops are deactivated, as the droop controls are also simplified (static gain zero) the inverter impedance is the same as the filter impedance. There is no control implemented, only voltage/frequency set points.
However, with the proposed grid forming control, the physical impedances lose relevance, and the system behaves as modelled in
Figure 2a making the inverter transient impedance (after around 100 ms) settable (droop gain) [
24]. It is then worth noticing that a GFM VSC can provide large system strength (low impedance) at the transient time frame. At the first instants (sub-transient regime), the voltage drop is strongly influenced by the filter impedance (physical impedance).
4.2. Negative Sequence Model Validation
To validate the NS model (
Figure 2b), a 0.2 pu negative sequence voltage is applied with a 0° phase shift, while the inverter is connected. According to the proposed model, the measured negative sequence current will be determined by the grid short circuit impedance (
ZSC = 0.043 + 0.076 jpu), the transformer impedance (
ZTR = 0.028 + 0.063 jpu) and the inverter impedance. This last impedance depends on the implemented control and output power filter.
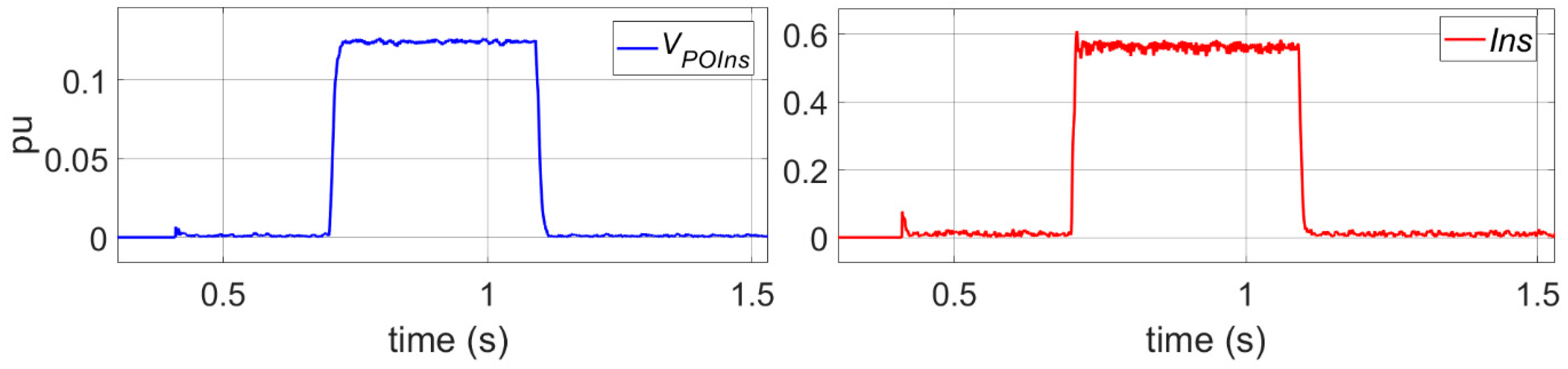
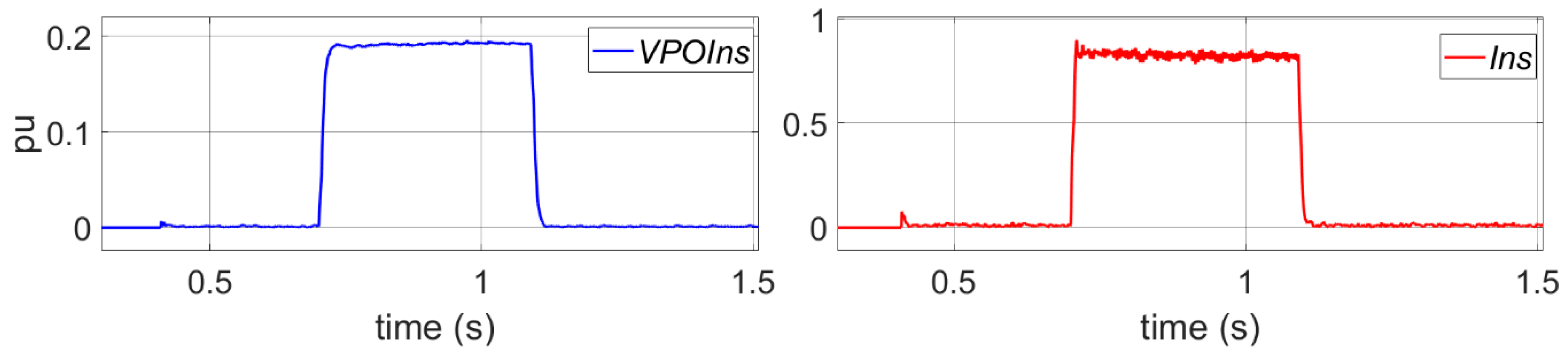
After applying this NS voltage, the measured current is
Ins = 0.56 pu, and the measured NS voltage
VPOIns = 0.127 pu, see
Figure 4.
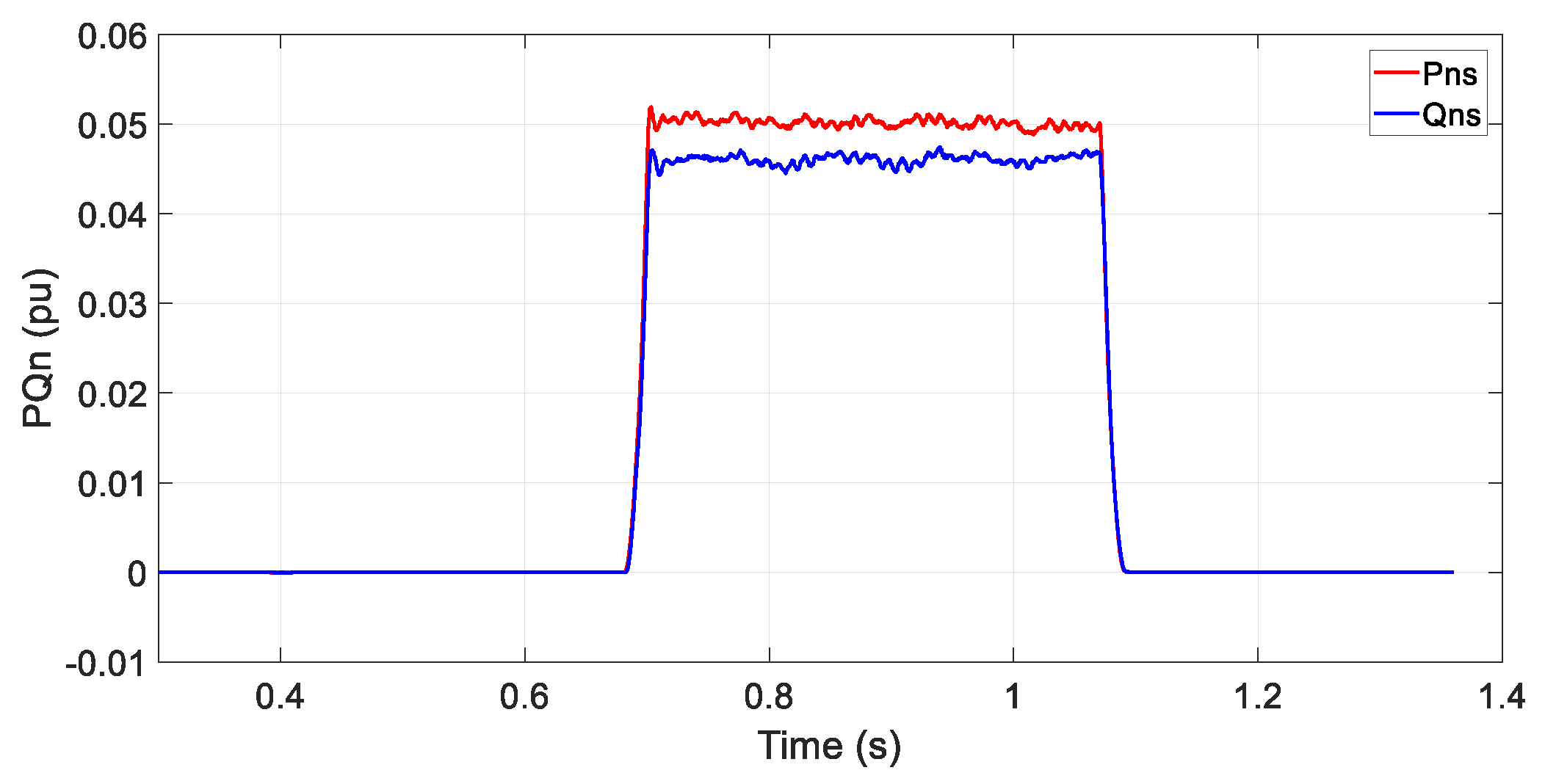
Measured apparent power is 0.07 pu (
Sns =
Ins ·
VPOIns). Active power is
Pns = 0.049 pu, and reactive power is
Qns = 0.047 pu (
Figure 5). From measured voltage and current, it is possible to estimate the absolute value of the inverter impedance, Equation (1), and total system impedance (2).
The same way, it is possible to estimate the real and imaginary part of the inverter impedance (Equations (3) and (4)), based on the measured NS active and reactive power:
The measured impedance is not the same as the output filter. The control algorithm has an impact on the impedance presented by the inverter. To verify the impedance measurement, the negative sequence voltage is applied with 4 different phase shifts: 0°, 90°, 180° and 270° phase shift to the positive sequence voltage,
Table 3.
In the next step, the linearity of the estimated impedance is tested. To analyse the linearity of the impedance, in a second step the applied NS voltage (
Vgns) is increased to 0.3 pu. After applying this NS voltage, the measured current is
Ins = 0.84 pu, and the measured NS voltage
VPOIns = 0.19 pu, see
Figure 6.
Assuming the same impedances for
Zinv_ns and
Ztotal_ns the theoretical
VPOIns and
Ins should be:
Looking at the simulation results, the measured NS voltage and current have the same value as described in Equations (5) and (6). So, the internal impedance of the inverter can be considered constant for different phase shifts (
Table 3) and linear with the voltage amplitude.
5. Threshold Virtual Impedance Method for Current Limiting
In the present paper, three different TVI-based current limiting methods are analysed. The first method is the simplest and is oriented to balanced faults or events. This method can be found in several studies [
4,
25] and has proven effective in many cases. However, to the knowledge of the authors, it is always used in balanced voltage events.
The current module is estimated in
dq [
4] or in
αβ [
25] reference frame without considering sequence separation, Equation (7).
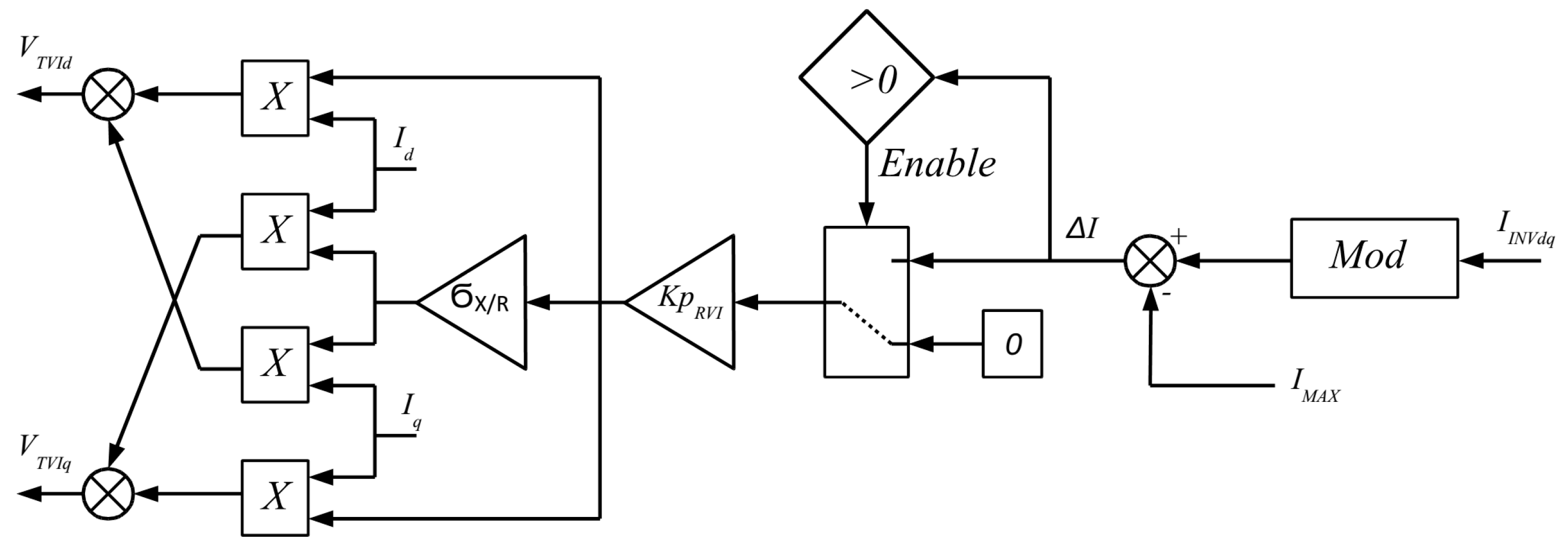
If the current injected by the inverter is below the maximum trigger value (
Imax), the virtual impedance value is zero. However, when the output current is bigger than the maximum value, the impedance increases linearly with the current. The impedance has two terms: the virtual impedance proportional gain
KpRVI and the virtual impedance ratio σ
X/R. The first one is related to steady state current limitation and the second to system dynamics. The tuning method of these parameters can be found in [
26]. A general control diagram of this method is depicted in
Figure 7.
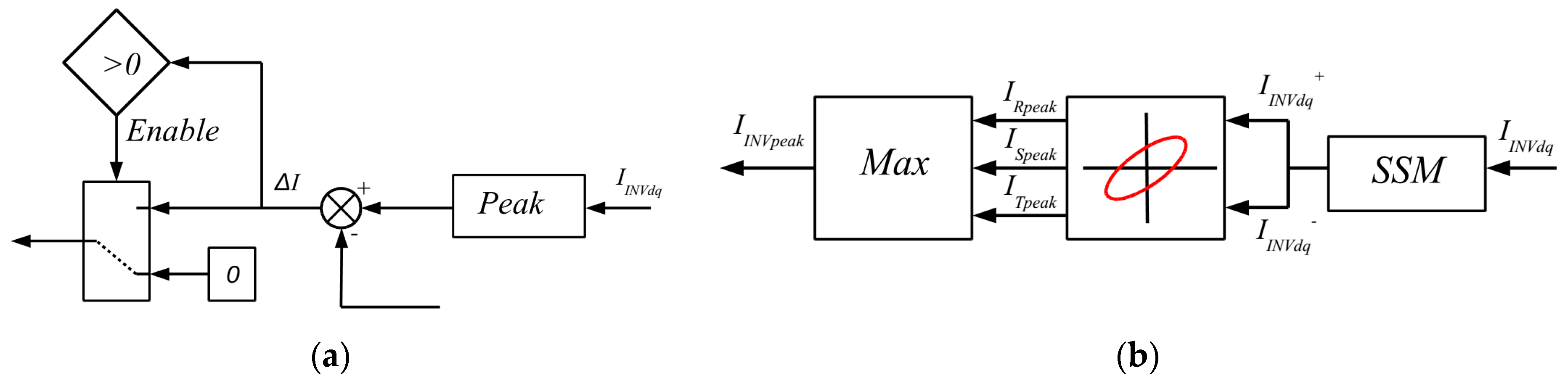
The second method is an evolution from the first method, and the only difference is related to the way the maximum current is estimated. This method takes into account inverter limitations when it is injecting a current with non-fundamental components, such as positive and negative sequences [
27]. Thus, in order to consider current limitations, sequence elliptical maximums are considered. The general control diagram of this method is shown in
Figure 8.
An example similar to this method can be found in [
28], and details about how to estimate the current limit with positive and negative sequence components are in [
29].
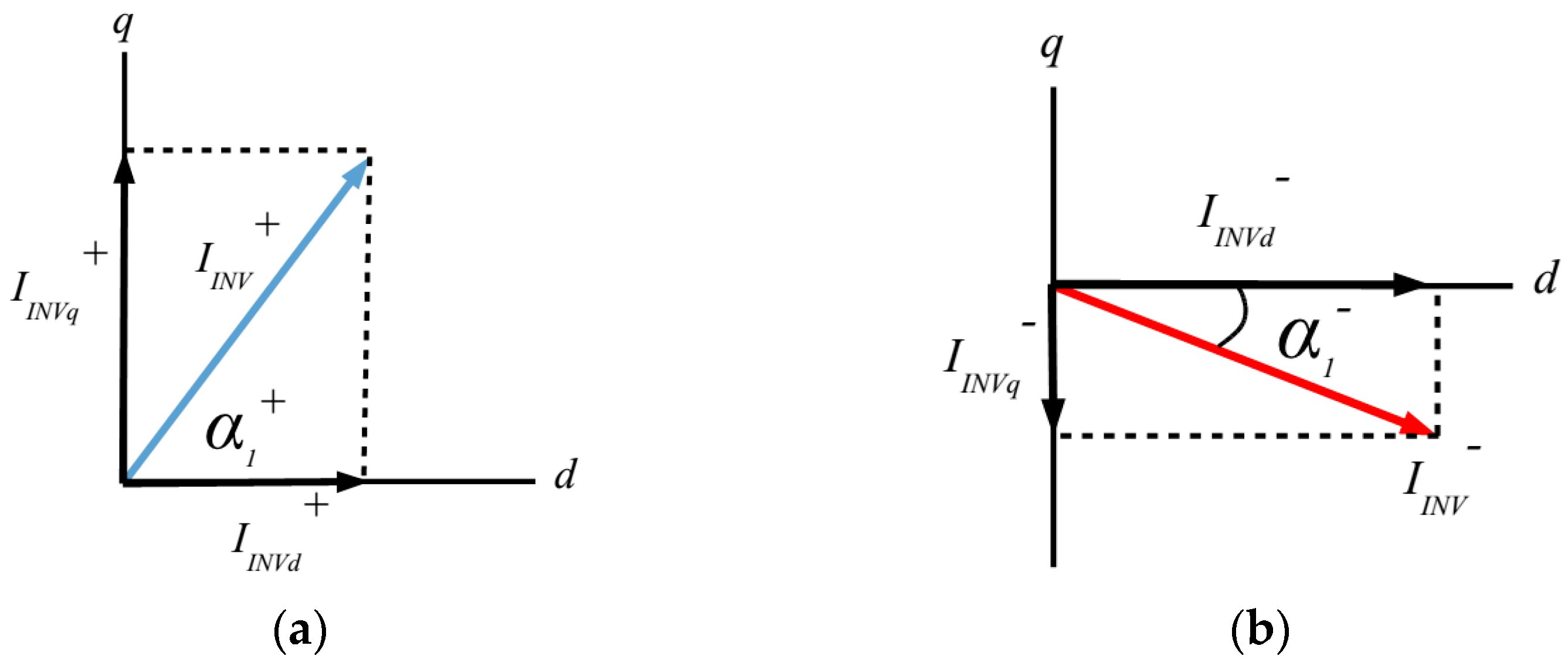
In this second method, first the current is separated in sequences using a sequence separation method (SSM). Then, with the current separated in sequences, the module of each sequence is estimated, Equations (8) and (9).
Along with the module, the angle of each sequence is also estimated, Equations (10) and (11)
This information provides the positions of the positive and negative sequence current vectors, as shown in
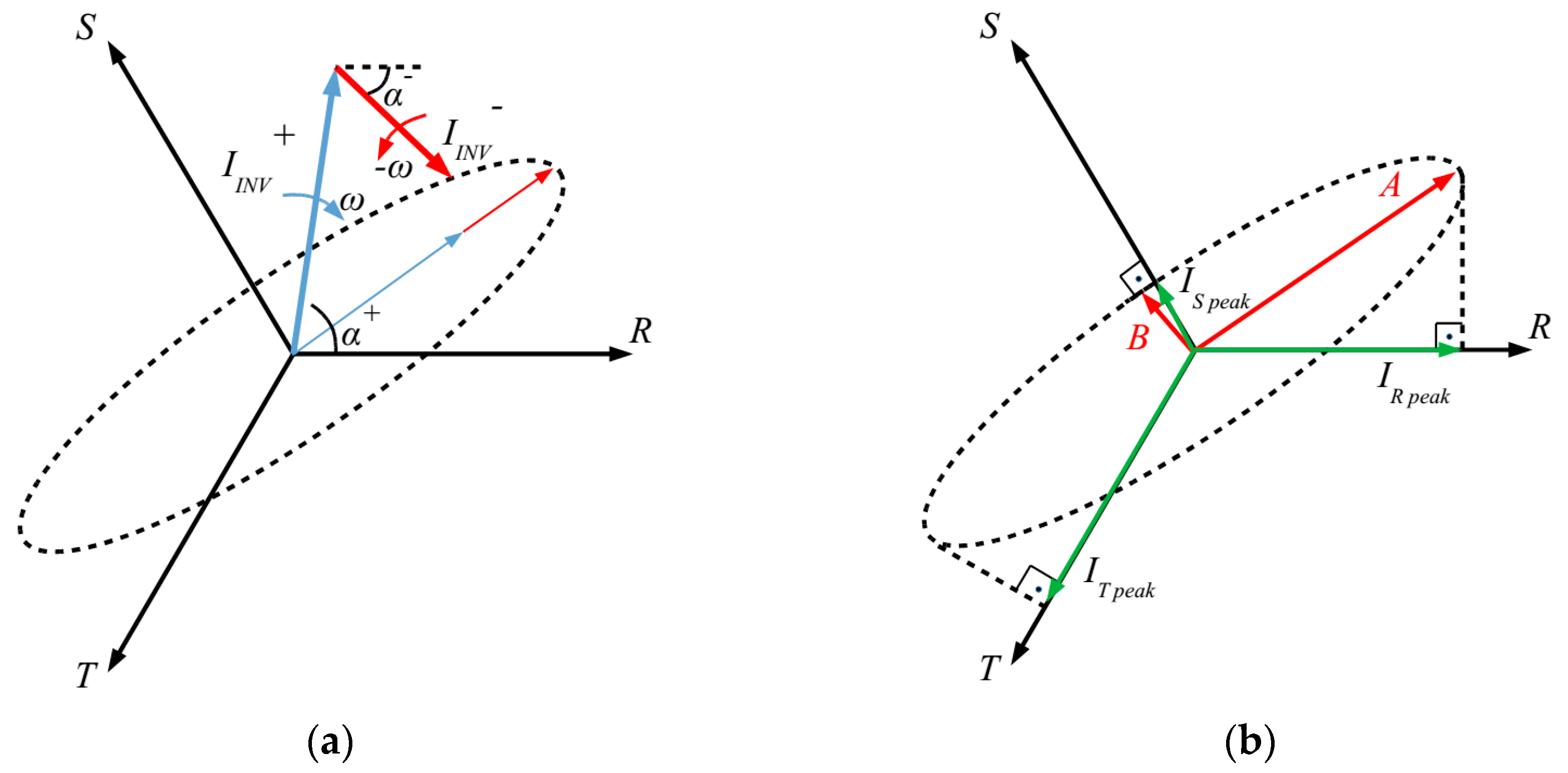
Figure 9. These two vectors are rotating in the opposite direction from each other, and in each period they draw an ellipse,
Figure 10a.
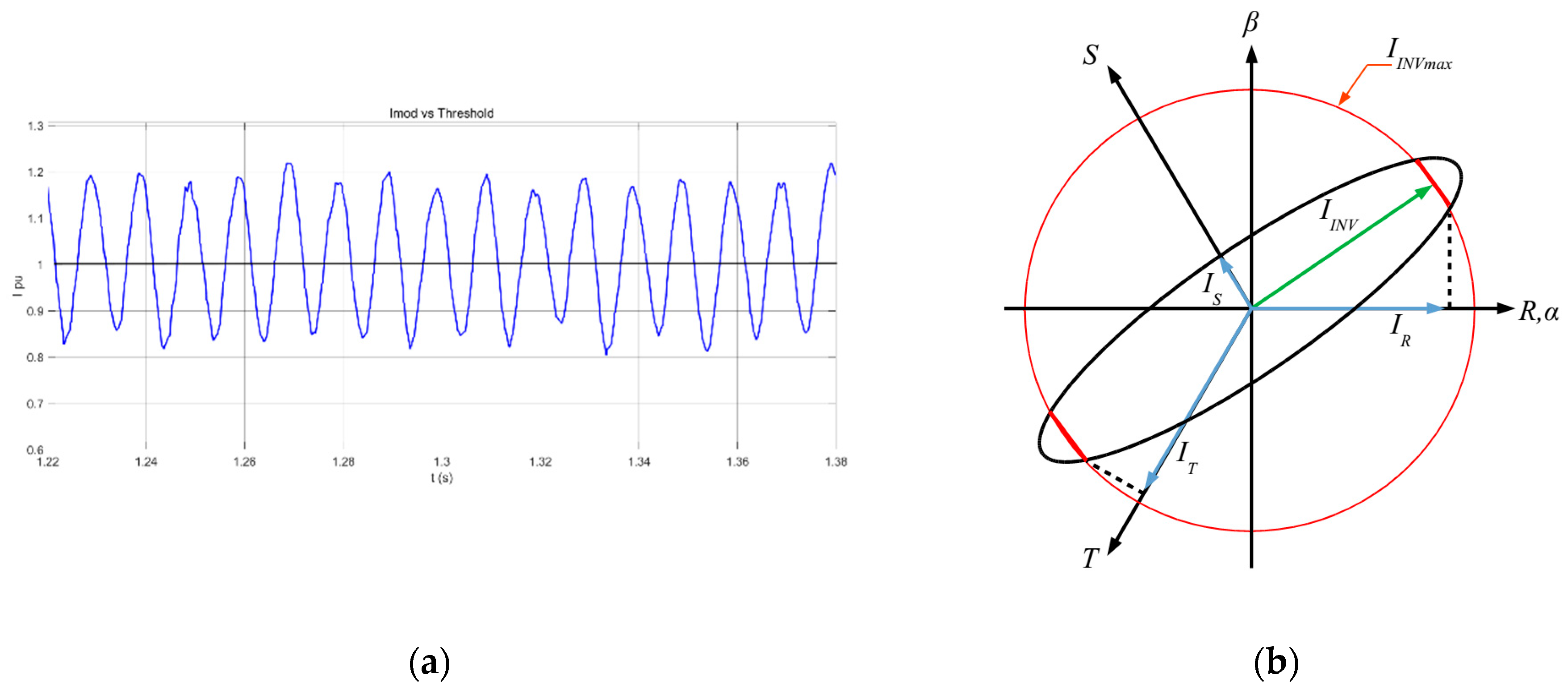
The width and height parameters of an ellipse are called the semi-major (A) and semi-minor (B) axes. The semi-major axis is the longest semi-diameter, while the semi-minor axis is a line segment that is at right angles with the semi-major axis. Considering the ellipse positive and negative vectors drawn in each period, the semi-major axis (A) and the semi-minor axis (B) that define the ellipse will be the sum of the positive and negative sequences when the vectors are in phase and in counter-phase, respectively, Equations (12) and (13).
Finally, the angle of the ellipse (α
1) is the angle of the semi-major axis (A), where the two sequences align (14).
The projections of the ellipse in each phase (RST) define the maximum current flowing through each of them in a period,
Figure 10b.
The projection on the horizontal axis is related to the phase R. For the estimation of the projections in phases S and T, the ellipse is rotated 120° and −120°; thus, it is possible to obtain the expressions of the projections of each phase:
Finally, the peak value is obtained by comparing the maximum of each three phases and selecting the biggest value:
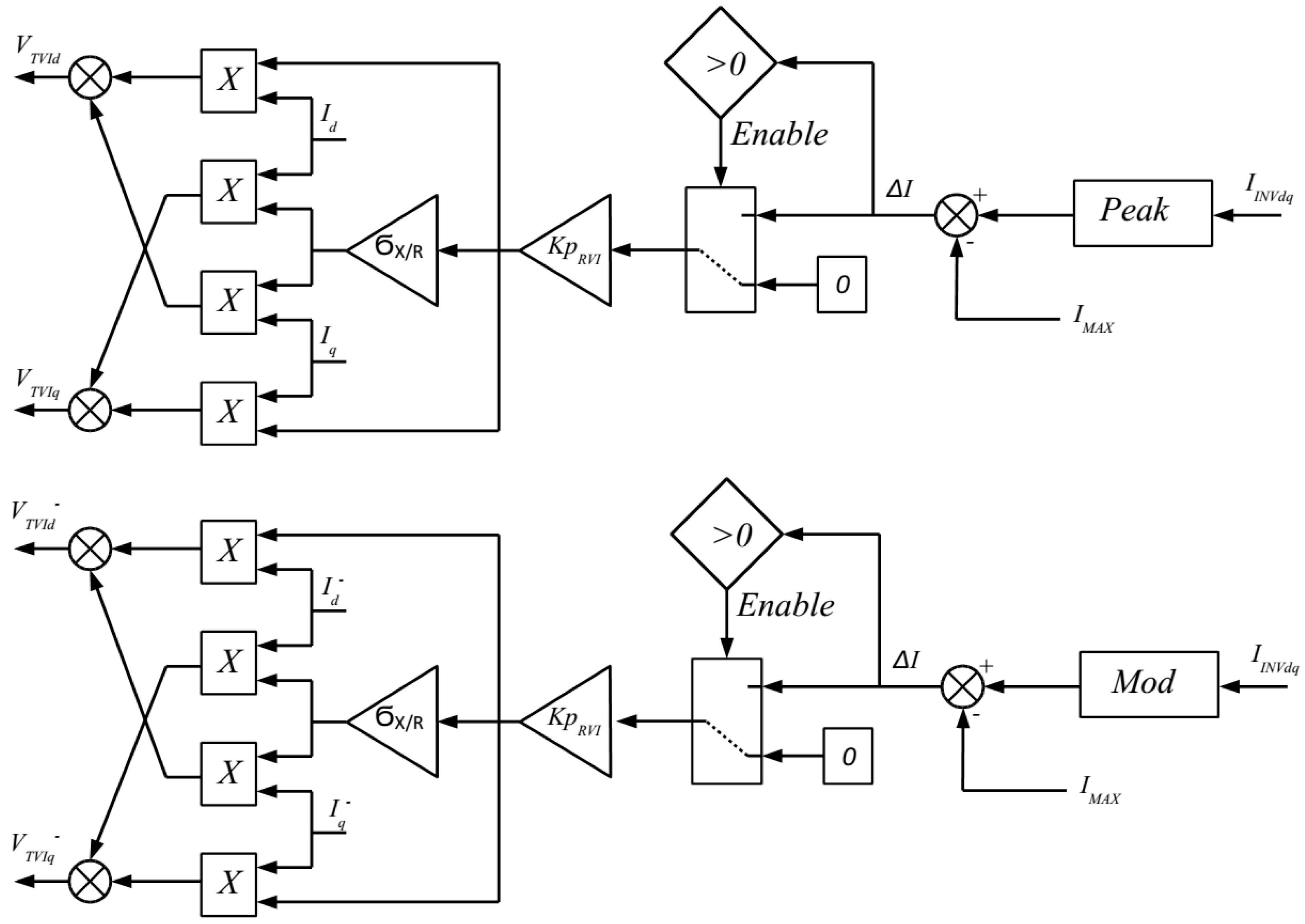
The last method proposes a novel control structure for the TVI with separated and configurable thresholds and gains for each sequence. As the negative sequence has the priority, a threshold
(INEG_MAX) for the negative sequence to activate a negative sequence impedance is added. For the positive sequence, the same peak value as for the second method is used. This peak threshold value considers also the injected negative current; so, by setting a negative current threshold lower than the maximal value, the negative priority is limited to that value. As a result, the positive sequence current is not limited directly, and it will pass through the headroom capacity left out by the NS current. The control diagram of the proposed method is depicted in
Figure 11.
6. Simulation Results
In this section, the three different methods for current limiting a grid forming inverter presented in the previous section are compared under unbalanced voltages and faults. Thus, based on the inverter control presented
Figure 1 and control parameters shown in
Table 4, two different events have been simulated: a 6% continuous unbalanced voltage and a type C fault.
For the continuous unbalanced voltage, an operation point with low voltage (0.88 pu) at normal operation is selected arbitrarily in order to have a significant, positive sequence current when the unbalance starts. If the method shows good results at permanent unbalance, as the next step, the method is tested under a type C fault with a 0.5 pu depth. This is equivalent to a single-phase fault at the high-voltage side of the transformer, or a two-phase fault at the inverter terminals [
30].
A type C fault with a depth “
h” generates positive and negative components described in
Table 5, where
V is the pre fault voltage module.
The three TVI methods have been evaluated under the first event. However, as the first method does not show good enough results, the type C fault is not applied to this method.
6.1. Simulation Results: TVI Threshold without Sequence Separation (First Method)
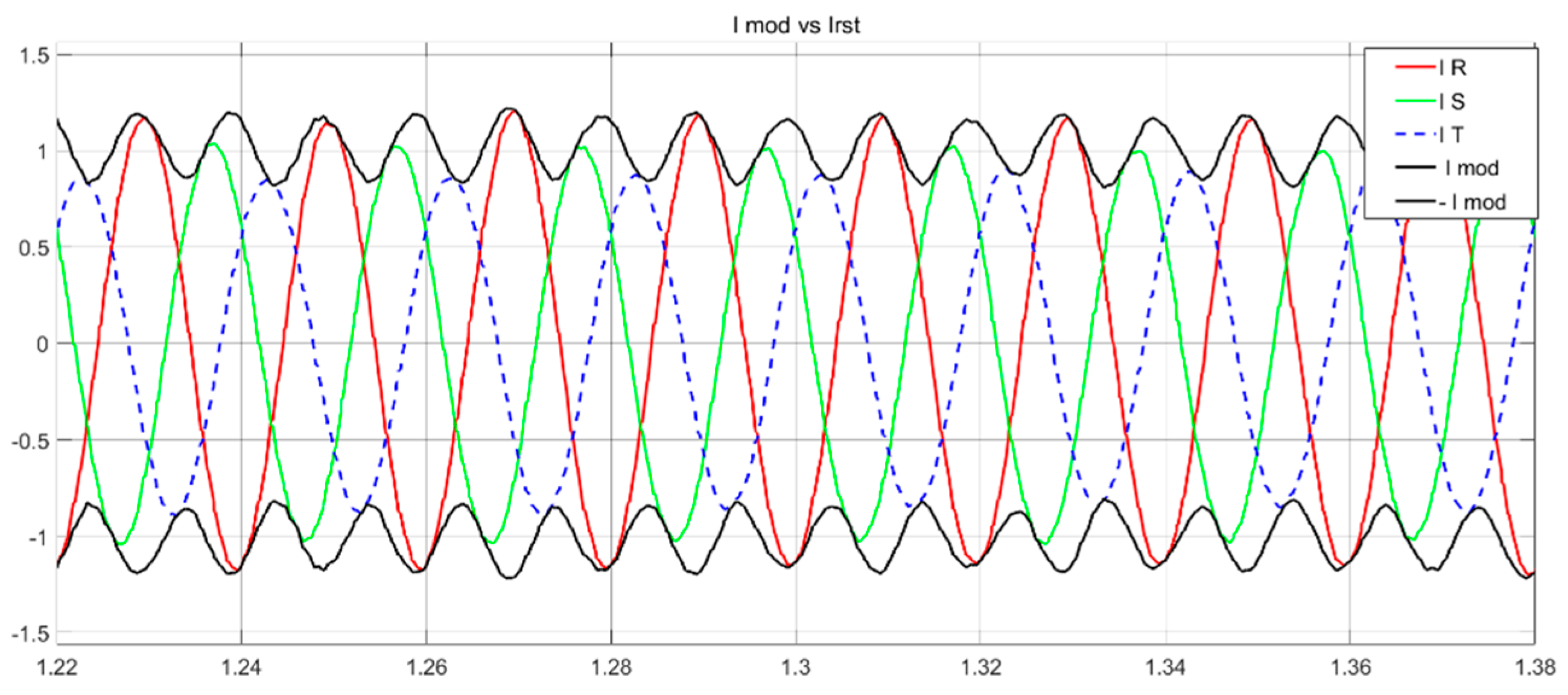
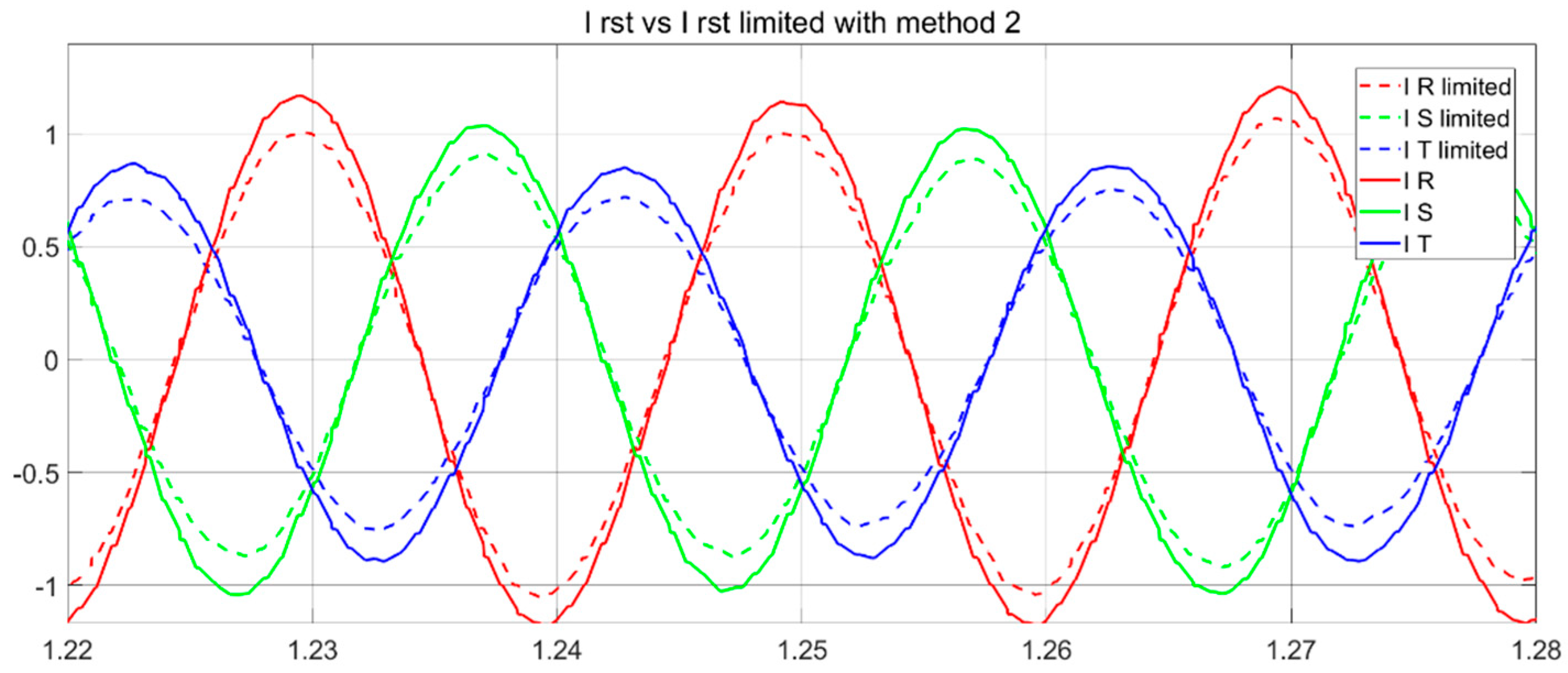
With this method, the injected current at unbalances is not controlled. It depends on the inverter and the line impedance. This negative sequence can be seen as a 100 Hz oscillation at the current module (two times faster than the RST frequency) in
Figure 12.
So, when the maximum current surpasses the TVI current threshold with a 100 Hz oscillation (
Figure 13a), the virtual impedance actuates intermittently (
Figure 14b), behaving as a non-linear load.
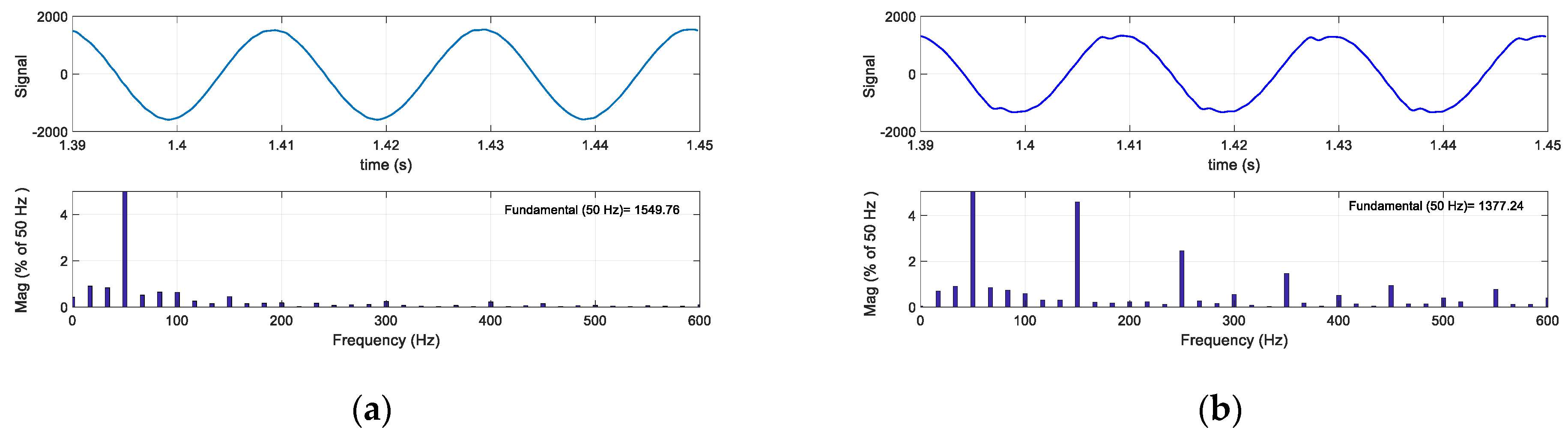
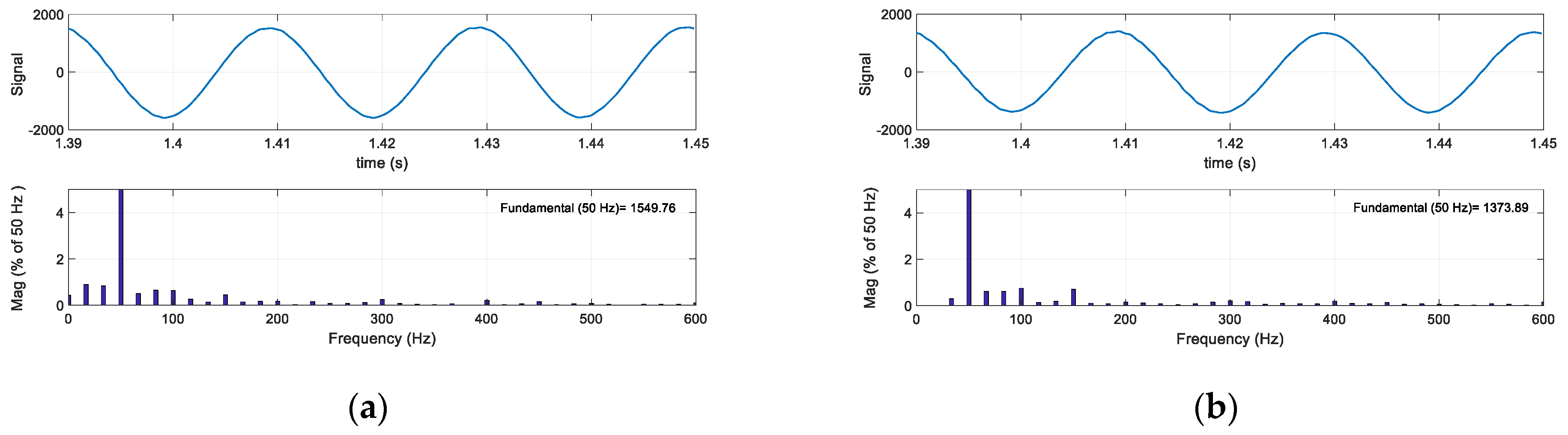
This non-linear behaviour injects non-desired harmonics to the grid. In
Figure 14 it is possible to see the FFT of the current without the TVI actuation and when the TVI is actuating. This solution does limit the current but generates perturbations. Looking at the THD, this solution changes the THD of the phase R current from <2% to 5.9%.
Looking at the FFT, the virtual impedance behaves very similar to a non-linear square signal (components at all the odd harmonics with a decreasing amplitude, Equation (19)).
The three-phase RST current signals related to the FFT (
Figure 14b) are shown in
Figure 15. The amplitude of the perturbation generated by the TVI depends on the impedance module and the unbalanced currents.
6.2. Simulation Results: TVI Threshold with Ipeak Based Sequence Separation (Second Method)
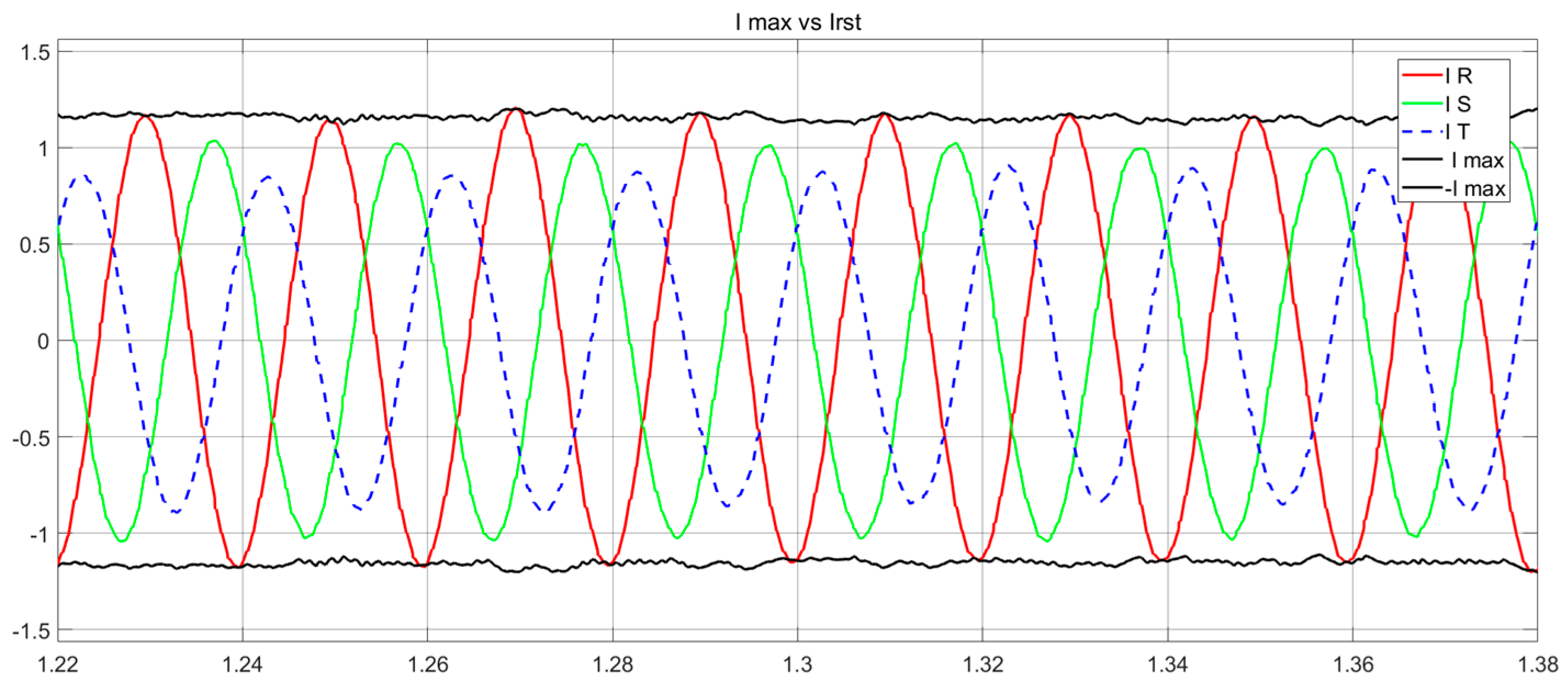
With this second method, the injected current at unbalance is not controlled either; it also depends on the inverter impedance and the line impedance. However, the peak current is estimated taking into account the negative sequence, and the peak current is relatively constant independently of the amount of negative sequence current,
Figure 16.
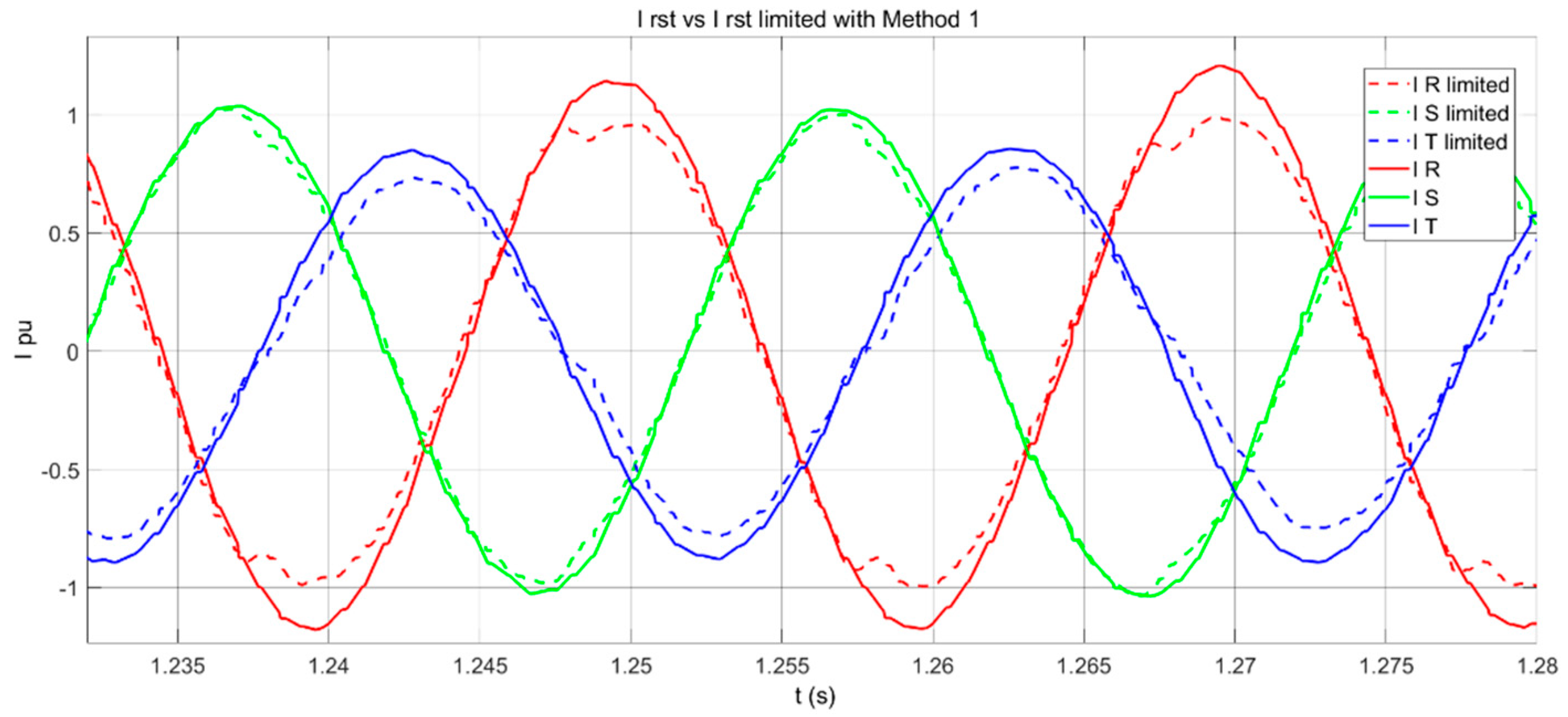
The TVI actuation is linear with the peak current, and the 100 Hz oscillation is not seen. The three-phase RST current signals are shown in
Figure 17. The amplitude of the current reduction is similar in all the phases, and it is possible to see the same sinusoidal shape when the TVI is activated.
This solution does not cause further perturbations while limiting the current. Looking at the FFT of the current without the TVI actuation and when the TVI is actuating, the FFT confirms a similar harmonic content in both cases,
Figure 18.
Once the ability to limit the output current below the inverter maximum value with smooth transition, stable operation and without generating further disturbances is validated, the ability to support the grid voltage reducing unbalances is evaluated. To evaluate this characteristic, the grid forming inverter model is tested against the second event: a 0.5 pu type C fault,
Figure 19.
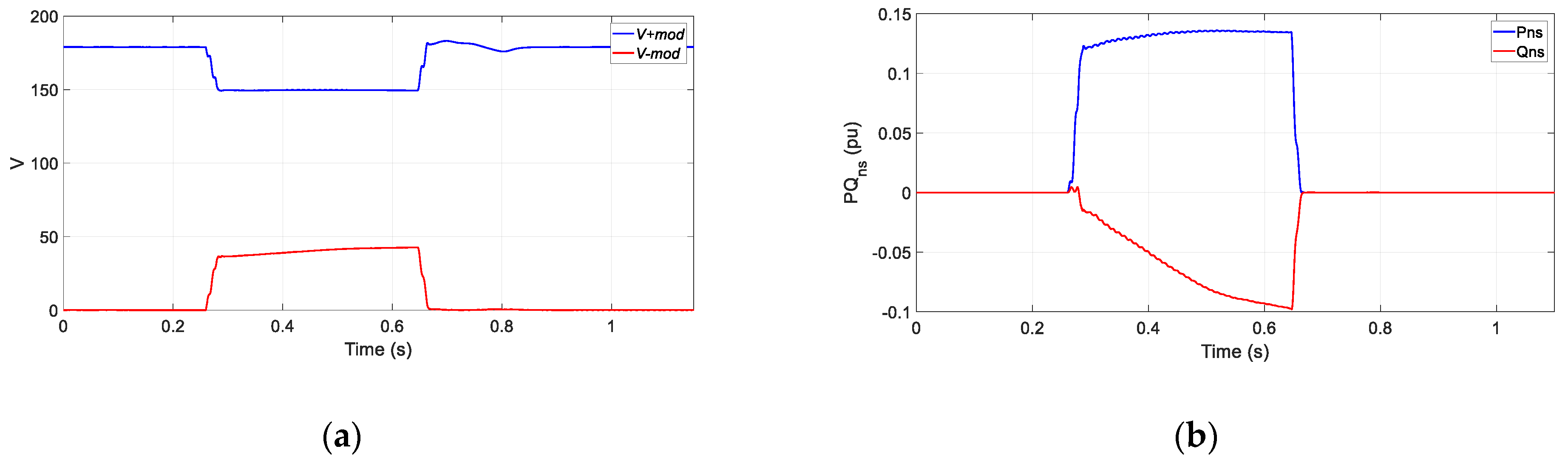
Looking at
Figure 19b it is possible to see how the injected negative reactive power is increasing during the fault, but the negative sequence voltage increases in amplitude during the fault as well instead of being reduced (
Figure 19a).
So, apart from the current limitation, a grid-connected inverter should have voltage support capability when faults occur at the grid in terms of positive sequence voltage increase and negative sequence voltage elimination [
31]. This last requirement is not met in this case.
6.3. Simulation Results: Proposed Novel TVI Solution (Third Method)
With the proposed method, the TVI has two different threshold values:
A maximum negative current, below this value the negative current flows to the inverter depending on the inverter impedance and the line impedance;
A maximum peak current value. This peak current is the same as in the previous method and takes into account the negative sequence current also.
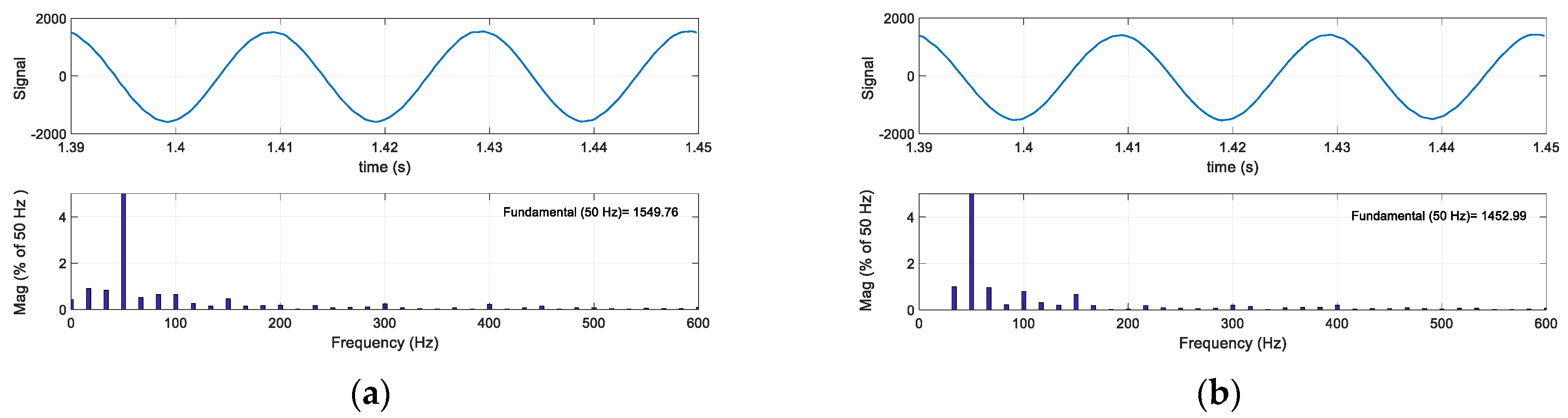
Thus, the TVI actuation is linear with the peak current, and the harmonic content of the current is not modified significantly with the TVI,
Figure 20.
So, once ensured that this method limits adequately the output current, as with the previous method, the ability to support the grid voltage reducing unbalances is evaluated. The simulation results of the grid forming inverter against a 0.5 pu type C fault are shown in
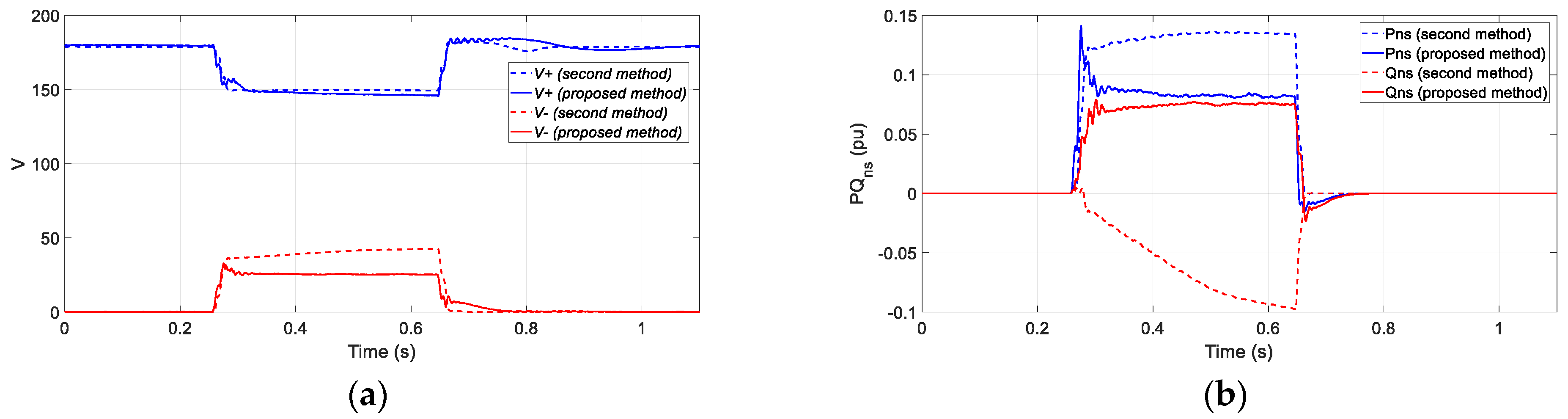
Figure 21.
This time, the negative sequence voltage is not increased during the fault, and the negative reactive power has the opposite sign. During the fault, the inverter injects positive and negative sequence currents supporting the positive sequence voltage (by increasing it) and reducing the negative sequence voltage.
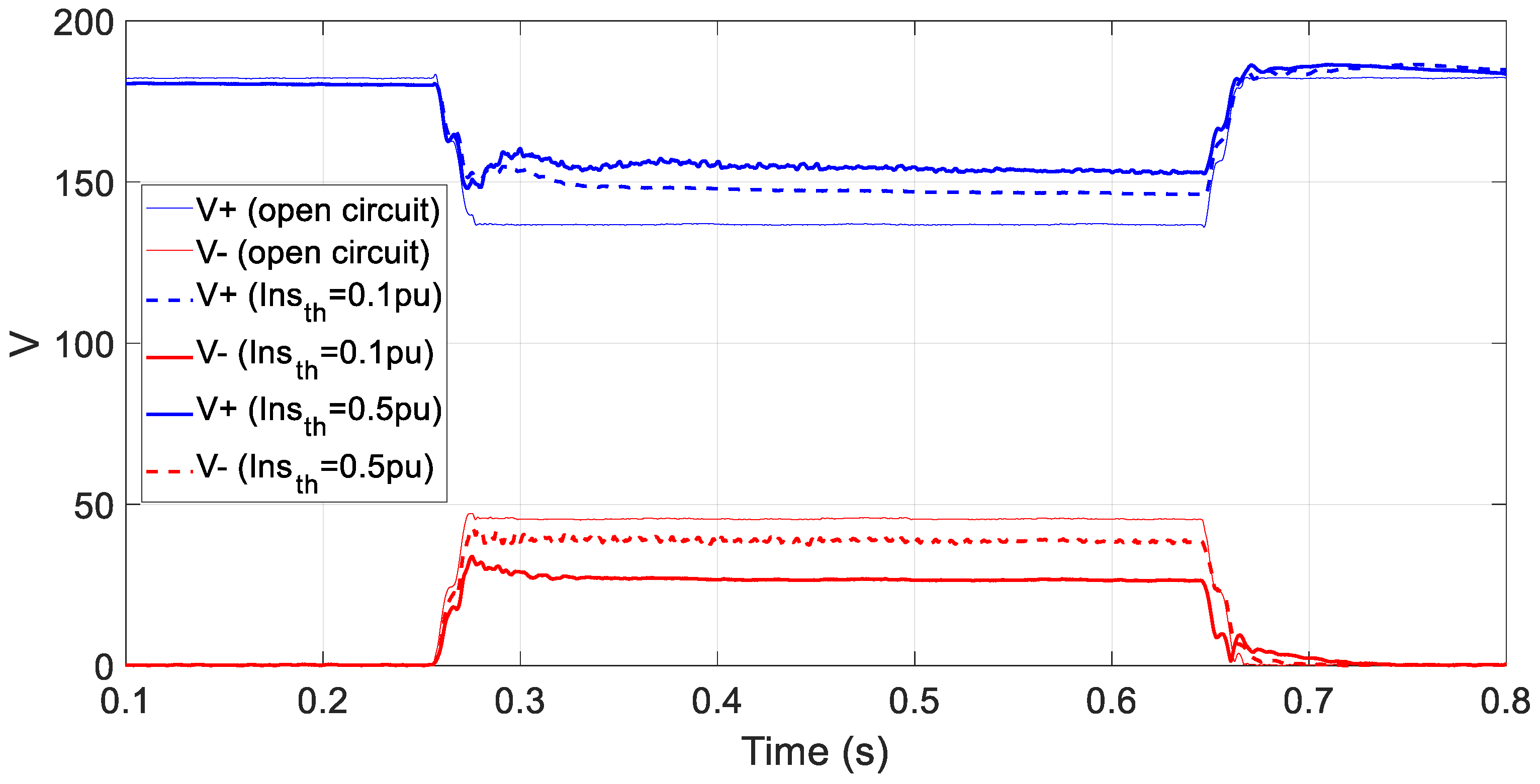
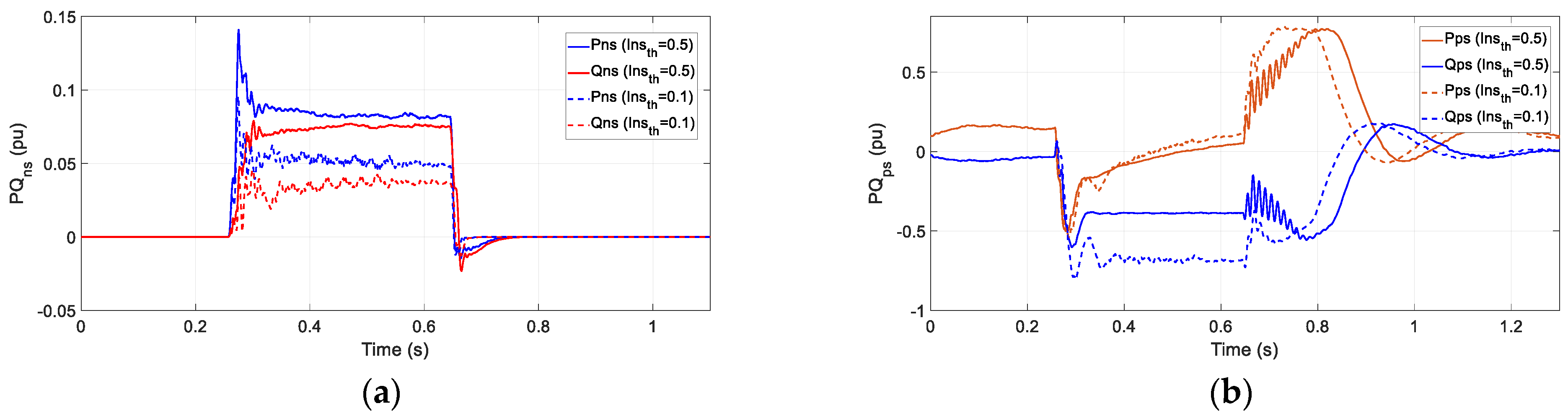
Furthermore, as this new TVI strategy has two independent TVI thresholds and two independent virtual impedance values, it provides to the grid forming inverter the ability to shape the desired performance during faults. In
Figure 22 and
Figure 23, for the same type C fault, two different TVI settings are shown in order to show the different performances during faults. The higher the negative sequence current threshold, the larger the negative current. However, as the total output current is thermally limited, the share of the negative sequence current is increased at the expenses of the positive sequence current reduction. As a consequence, the positive sequence voltage is supported with less current, and the positive voltage drop is deeper. So, the configuration should find a compromise between positive voltage support and the negative sequence voltage reduction.
Looking at
Figure 23b it is possible to see that both settings inject to the grid similar positive sequence active power during faults. However, the positive reactive power shows a significant reduction when the negative sequence threshold is higher, i.e., when the available current is mainly directed to the negative sequence.
7. Conclusions
The use of the peak current instead of the current module for the TVI activation avoids its non-linear behaviour when limiting unbalanced currents. This change is almost transparent and can be used with any TVI control structure.
Many virtual impedance methods use two components to control the performance of the impedance during faults, such as the virtual impedance proportional gain RVI and the virtual impedance ratio XVI. In a similar manner, this new TVI strategy provides to the grid forming inverter the ability to shape the desired performance during unbalanced faults by adding new variables. These new variables allow a more accurate control of the TVI in sequences to define the share of current directed to support positive and negative sequence voltage. This division is not made directly; a negative current threshold and an absolute current threshold are used. Both of them are coordinated with negative sequence current priority. The absolute threshold value considers also the injected negative current; so, by setting a negative current threshold to the absolute value, the negative priority is achieved.
The reactive power behaviour during faults and permanent unbalanced voltages showed the desired performance in simulation. However, this paper does not pay special attention to the active power behaviour during faults. So, the proposed method should be tested more extensively in order to verify its correct performance related to the active power. Regarding the required active power behaviour during faults, there are still open points, such as the de-synchronization problem when limiting the output current and the post fault re-synchronization time. Ideally, the TVI should also address those issues.
Author Contributions
M.Z.: conceptualization, formal analysis, investigation, software, writing—original draft preparation. C.C.: conceptualization, formal analysis, investigation, writing—review and editing. T.P.: conceptualization, formal analysis, investigation. A.S.-R.: conceptualization, formal analysis, investigation, writing—review and editing. E.O.: conceptualization, formal analysis, investigation, writing—review and editing. P.I.: conceptualization, formal analysis, investigation, writing—review and editing. S.H.K.: conceptualization, formal analysis, investigation, writing—review and editing. J.A.: conceptualization, formal analysis, investigation. All authors have read and agreed to the published version of the manuscript.
Funding
This work is part of the OSMOSE project. The project has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No. 773406. This article reflects only the author views, and the European Commission is not responsible for any use that may be made of the information it contains.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cardozo, C.; Vernay, Y.; Denis, G.; Prevost, T.; Zubiaga, M.; Valera, J.J. OSMOSE: Grid-Forming performance assessment within multiservice storage system connected to the transmission grid. In Proceedings of the CIGRE Session 48, Paris, France, 25 August–3 September 2020. [Google Scholar]
- Qoria, T.; Gruson, F.; Colas, F.; Oue, K.; Li, C.; Prevost, T.; Guillaud, X. Tuning of AC voltage-controlled VSC based Linear Quadratic Regulation. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Henninger, S.; Jaeger, J. Advanced classification of converter control concepts for integration in electrical power systems. Int. J. Electr. Power Energy Syst. 2020, 123, 106210. [Google Scholar] [CrossRef]
- Qoria, T.; Gruson, F.; Colas, F.; Denis, G.; Prevost, T.; Guillaud, X. Critical clearing time determination and enhancement of grid-forming converters embedding virtual impedance as current limitation algorithm. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1050–1061. [Google Scholar] [CrossRef] [Green Version]
- Gurule, N.S.; Hernandez-Alvidrez, J.; Darbali-Zamora, R.; Reno, M.J.; Flicker, J.D. Experimental Evaluation of Grid-Forming Inverters Under Unbalanced and Fault Conditions. In Proceedings of the IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 4057–4062. [Google Scholar] [CrossRef]
- Taul, M.G.; Wang, X.; Davari, P.; Blaabjerg, F. Current Limiting Control with Enhanced Dynamics of Grid-Forming Converters During Fault Conditions. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1062–1073. [Google Scholar] [CrossRef] [Green Version]
- Denis, G. Les nouvelles stratégies de contrôle d’onduleurs pour un système électrique 100% interfacé par électronique de puissance. Ph.D. Thesis, Ecole Centrale de Lille, Villeneuve-d’Ascq, France, 2017. [Google Scholar]
- Raza, M. Offshoregrid Control of Voltage Source Converters for Integrating Offshore Wind Power Plants. Doctoral thesis, UPC, Departament d’Enginyeria Elèctrica, Barcelona, Spain, 2017. Available online: http://hdl.handle.net/2117/114452 (accessed on 4 August 2021).
- Qoria, T.; Cossart, Q.; Li, C.; Guillaud, X.; Gruson, F.; Kestelyn, X. Deliverable 3.2: Local Control and Simulation tools for Large Transmission Systems. MIGRATE proyect. Available online: https://www.h2020-migrate.eu/_Resources/Persistent/5c5beff0d5bef78799253aae9b19f50a9cb6eb9f/D3.2%20-%20Local%20control%20and%20simulation%20tools%20for%20large%20transmission%20systems.pdf (accessed on 10 August 2021).
- Ortjohann, E.; Arias, A.; Morton, D.; Mohd, A.; Hamsic, N.; Omari, O. Grid-Forming Three-Phase Inverters for Unbalanced Loads in Hybrid Power Systems. In Proceedings of the 2006 IEEE 4th World Conference on Photovoltaic Energy Conference, Waikoloa, HI, USA, 7–12 May 2006; pp. 2396–2399. [Google Scholar] [CrossRef]
- National Grid, Draft Grid Code—Grid Forming Converter Specification. [Online]. Available online: https://www.nationalgrideso.com/document/159296/download (accessed on 4 August 2021).
- ENTSO-E. Technical Report: High Penetration of Power Electronic Interfaced Power Sources and the Potential Contribution of Grid forming Converters. January 2020. Available online: https://eepublicdownloads.entsoe.eu/clean-documents/Publications/SOC/High_Penetration_of_Power_Electronic_Interfaced_Power_Sources_and_the_Potential_Contribution_of_Grid_Forming_Converters.pdf (accessed on 12 April 2021).
- Denninger, R.; Reichert, S.; Rogalla, S.; Jalili, K. Testing Characteristics of Grid Forming Converters Part II: Voltage Source Properties and Contribution to Power Quality. In Proceedings of the 19th Wind Integration Workshop, Virtual, 11–13 November 2020. [Google Scholar]
- Qoria, T.; Li, C.; Oue, K.; Gruson, F.; Colas, F.; Guillaud, X. Direct AC voltage control for grid-forming inverters. J. Power Electron. 2019, 20, 198–211. [Google Scholar] [CrossRef]
- Qoria, T.; Gruson, F.; Colas, F.; Guillaud, X.; Debry, M.; Prevost, T. Tuning of Cascaded Controllers for Robust Grid-Forming Voltage Source Converter. In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; pp. 1–7. [Google Scholar] [CrossRef] [Green Version]
- Qoria, T. Grid-forming control to achieve a 100% power electronics interfaced power transmission systems. Ph.D. Thesis, Ecole Doctorale Sciences et Metiers de L’ingenieur L2EP–Campus de Lille, Lille, France, 2020. [Google Scholar]
- Du, W.; Chen, Z.; Schneider, K.P.; Lasseter, R.H.; Nandanoori, S.P.; Tuffner, F.K.; Kundu, S. A Comparative Study of Two Widely Used Grid-Forming Droop Controls on Microgrid Small-Signal Stability. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 963–975. [Google Scholar] [CrossRef]
- Lepour, D.; Paolone, M.; Denis, G.; Cardozo, C.; Prévost, T.; Guiu, E. Performance assessment of Synchronous Condensers vs Voltage Source Converters providing grid-forming functions. In Proceedings of the 2021 IEEE Madrid PowerTech, Madrid, Spain, 28 June–2 July 2021. [Google Scholar]
- Shamseh, M.B.; Inzunza, R.; Kinoshita, M.; Ambo, T. Comparison between Norton Impedance Model and Frequency Scan Analysis of 3.36MW Inverter. In Proceedings of the 2019 8th International Conference on Renewable Energy Research and Applications (ICRERA), Brasov, Romania, 3–6 November 2019; pp. 827–832. [Google Scholar] [CrossRef]
- Sowa, I. Impedance Analysis of Harmonic Resonance in HVDC Connected Wind Power Plants. Master’s Thesis, Universitat Politecnica de Catalunya (UPC), Barcelona, Spain, 2016. [Google Scholar]
- Kang, J.-W.; Hyun, S.-W.; Kan, Y.; Lee, H.; Lee, J.-H. A Novel Zero Dead-Time PWM Method to Improve the Current Distortion of a Three-Level NPC Inverter. Electronics 2020, 9, 2195. [Google Scholar] [CrossRef]
- Prevost, T.; Vernay, Y.; Cardozo, C.; Denis, G.; Zuo, Y.i.; Zecchino, A.; Yuan, Z.; Cherkaoui, R.; Paolone, M.; Zubiaga, M.; et al. Deliverable D3.2 Overall Specifications of the Demonstrations. OSMOSE Project. Available online: https://www.osmose-h2020.eu/downloads/?wpdmc=wp3-deliverables (accessed on 10 July 2021).
- Cardozo, C.; Denis, G.; Prevost, T.; Zubiaga, M.; Sanchez-Ruiz, A.; Valera, J.J.; Vernay, Y. OSMOSE WP3: Factory Acceptance Test of the grid forming demonstrator. In Proceedings of the 10th Solar Integration Workshop, Virtual Conference, 5 November 2020. [Google Scholar]
- Li, Y.; Gu, Y.; Zhu, Y.; Junyent-Ferré, A.; Xiang, X.; Green, T.C. Impedance Circuit Model of Grid-Forming Inverter: Visualizing Control Algorithms as Circuit Elements. IEEE Trans. Power Electron. 2021, 36, 3377–3395. [Google Scholar] [CrossRef]
- Karthikeyan, A.; Krishna, D.G.A.; Nagamani, C. Virtual Impedance based DFCL for DVR during Downstream Faults. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 18–21 December 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Paquette, A.D.; Divan, D.M. Virtual Impedance Current Limiting for Inverters in Microgrids With Synchronous Generators. IEEE Trans. Ind. Appl. 2015, 51, 1630–1638. [Google Scholar] [CrossRef]
- Zubiaga, M.; Sanchez-Ruiz, A.; Olea, E.; Unamuno, E.; Bilbao, A.; Arza, J. Power Capability Boundaries for an Inverter Providing Multiple Grid Support Services. Energies 2020, 13, 4314. [Google Scholar] [CrossRef]
- Freytes, J.; Li, J.; de Préville, G.; Thouvenin, M. Grid-Forming Control with Current Limitation for MMC Under Unbalanced Fault Ride-Through. IEEE Trans. Power Deliv. 2021, 36, 1914–1916. [Google Scholar] [CrossRef]
- Milikua, A. Estrategias de Control de un Compensador Paralelo de Reactiva en Redes con Tensiones Desequilibradas. Ph.D. Thesis, University of Mondragon, Mondragón, Spain, 2015. [Google Scholar]
- Guasch, L. Efectos de los Huecos de Tensión en las Máquinas de Inducción y en los Transformadores Trifásicos. Ph.D. Thesis, Universitat politecnica de Catalunya, Barcelona, Spain, 2006. [Google Scholar]
- Paspatis, A.G.; Konstantopoulos, G.C. Voltage Support under Grid Faults with Inherent Current Limitation for Three-Phase Droop-Controlled Inverters. Energies 2019, 12, 997. [Google Scholar] [CrossRef] [Green Version]
Figure 1.
Power conversion system configuration.
Figure 1.
Power conversion system configuration.
Figure 2.
Sequence separated power system considering GFM with droop and inner voltage control loops (a) positive and (b) negative.
Figure 2.
Sequence separated power system considering GFM with droop and inner voltage control loops (a) positive and (b) negative.
Figure 3.
Grid forming inverter with the proposed control (blue) and with inner control loops deactivated (green) for a 10% grid voltage drop.
Figure 3.
Grid forming inverter with the proposed control (blue) and with inner control loops deactivated (green) for a 10% grid voltage drop.
Figure 4.
Simulation results, negative sequence voltage and current at VPOI applying a 0.2 pu negative sequence voltage at the grid (Vgns).
Figure 4.
Simulation results, negative sequence voltage and current at VPOI applying a 0.2 pu negative sequence voltage at the grid (Vgns).
Figure 5.
Simulation results, negative active and reactive power at VPOI applying a 0.2 pu negative sequence voltage at the grid (Vgns).
Figure 5.
Simulation results, negative active and reactive power at VPOI applying a 0.2 pu negative sequence voltage at the grid (Vgns).
Figure 6.
Simulation results, negative sequence voltage and current at VPOI applying a 0.3 pu negative sequence voltage at the grid (Vgns).
Figure 6.
Simulation results, negative sequence voltage and current at VPOI applying a 0.3 pu negative sequence voltage at the grid (Vgns).
Figure 7.
First method TVI control scheme.
Figure 7.
First method TVI control scheme.
Figure 8.
TVI control scheme considering sequence separation for the activation (a) focus on the differences with the first method and (b) details on peak current estimation.
Figure 8.
TVI control scheme considering sequence separation for the activation (a) focus on the differences with the first method and (b) details on peak current estimation.
Figure 9.
Positive (a) and negative (b) sequence current vectors.
Figure 9.
Positive (a) and negative (b) sequence current vectors.
Figure 10.
Representation of the ellipse drawn by positive and negative current vectors (a) RST current projections of the ellipse and semi-major (A) and semi-minor (B) axes (b).
Figure 10.
Representation of the ellipse drawn by positive and negative current vectors (a) RST current projections of the ellipse and semi-major (A) and semi-minor (B) axes (b).
Figure 11.
Proposed TVI control scheme. For the positive sequence the scheme is the same as shown in
Figure 8, and for the negative sequence the same as in
Figure 7.
Figure 11.
Proposed TVI control scheme. For the positive sequence the scheme is the same as shown in
Figure 8, and for the negative sequence the same as in
Figure 7.
Figure 12.
RST currents and current module under a permanent 6% unbalanced voltage.
Figure 12.
RST currents and current module under a permanent 6% unbalanced voltage.
Figure 13.
Current module under a permanent 6% unbalanced voltage and TVI threshold value (a) and the associated ellipse (b).
Figure 13.
Current module under a permanent 6% unbalanced voltage and TVI threshold value (a) and the associated ellipse (b).
Figure 14.
FFT of the R phase current under a permanent 6% unbalanced voltage (a) without TVI activation and (b) first method TVI activation.
Figure 14.
FFT of the R phase current under a permanent 6% unbalanced voltage (a) without TVI activation and (b) first method TVI activation.
Figure 15.
RST currents under a permanent 6% unbalanced voltage (solid line) without TVI activation and (dashed line) first method TVI activation.
Figure 15.
RST currents under a permanent 6% unbalanced voltage (solid line) without TVI activation and (dashed line) first method TVI activation.
Figure 16.
RST currents and peak current under a permanent 6% unbalanced voltage.
Figure 16.
RST currents and peak current under a permanent 6% unbalanced voltage.
Figure 17.
RST currents under permanent 6% unbalanced voltage (solid line) without TVI activation and (dashed line) second method TVI activation.
Figure 17.
RST currents under permanent 6% unbalanced voltage (solid line) without TVI activation and (dashed line) second method TVI activation.
Figure 18.
FFT of the R phase current under permanent 6% unbalanced voltage (a) without TVI activation and (b) second method TVI activation.
Figure 18.
FFT of the R phase current under permanent 6% unbalanced voltage (a) without TVI activation and (b) second method TVI activation.
Figure 19.
Grid forming inverter at a 50% type C asymmetric fault, 350 ms. (a) Positive and negative voltage modules; (b) positive and negative active and reactive power.
Figure 19.
Grid forming inverter at a 50% type C asymmetric fault, 350 ms. (a) Positive and negative voltage modules; (b) positive and negative active and reactive power.
Figure 20.
FFT of the R phase current under permanent 6% unbalanced voltage (a) without TVI activation and (b) proposed TVI method activation.
Figure 20.
FFT of the R phase current under permanent 6% unbalanced voltage (a) without TVI activation and (b) proposed TVI method activation.
Figure 21.
Grid forming inverter at a 50% type C asymmetric fault, 350 ms. (a) Positive and negative voltage modules (comparative between second and proposed TVI method). (b) Positive and negative active and reactive power.
Figure 21.
Grid forming inverter at a 50% type C asymmetric fault, 350 ms. (a) Positive and negative voltage modules (comparative between second and proposed TVI method). (b) Positive and negative active and reactive power.
Figure 22.
Simulation results for a 50% asymmetric fault, 350 ms. Two different settings for the proposed TVI.
Figure 22.
Simulation results for a 50% asymmetric fault, 350 ms. Two different settings for the proposed TVI.
Figure 23.
Simulation results for a 50% asymmetric fault, 350 ms. Two different settings for the proposed TVI. (a) Negative sequence active and reactive power. (b) Positive sequence active and reactive power.
Figure 23.
Simulation results for a 50% asymmetric fault, 350 ms. Two different settings for the proposed TVI. (a) Negative sequence active and reactive power. (b) Positive sequence active and reactive power.
Table 1.
Main electrical characteristics of the system.
Table 1.
Main electrical characteristics of the system.
| Parameter | Value | Unite |
|---|
| Grid nominal voltage | 0.6 | kV |
| Rated current | 1000 | A |
| Snom | 1 | MVA |
| Vdc BUS | 1100 | V |
| Inverter Switching Frequency | 2.5 | kHz |
| Inverter output inductance (Lfilter) | 100 | µH |
| Inverter output capacitance (Cfilter) | 660 | µF |
| Transformer leakage inductance (LTR) | 70 | µH |
| Grid impedance (LSC) | 84 | µH |
Table 2.
Grid impedance values.
Table 2.
Grid impedance values.
| SI | ZTR (±50 Hz) | ZSC (±50 Hz) |
|---|
| | SI | PU | SI | PU |
|---|
| Reactance | 70 μH | 0.063 | 84 μH | 0.076 |
| Resistance | 0.01 Ω | 0.028 | 0.015 Ω | 0.043 |
Table 3.
Summary of estimated negative sequence impedances based on simulation results.
Table 3.
Summary of estimated negative sequence impedances based on simulation results.
| | VPOIns | Igns | Pns/Qns | Igns |
|---|
| Case 2-a: 0° | d | −0.127 | d | 0.34 | Pns | −0.051 | active | −203 A |
| q | 0.017 | q | −0.39 | Qns | −0.04 | reactive | −164 A |
| Case 2-b: 90° | d | 0.128 | d | −0.34 | Pns | −0.051 | active | −203 A |
| q | −0.019 | q | 0.39 | Qns | −0.04 | reactive | −164 A |
| Case 2-c: 180° | d | 0.127 | d | −0.34 | Pns | −0.051 | active | −203 A |
| q | 0.017 | q | −0.39 | Qns | −0.04 | reactive | −164 A |
| Case 2-d: 270° | d | −0.128 | d | 0.34 | Pns | −0.051 | active | −203 A |
| q | −0.019 | q | 0.39 | Qns | −0.04 | reactive | −164 A |
Table 4.
Inverter controller main parameters.
Table 4.
Inverter controller main parameters.
| Parameter | Value | Unite |
|---|
| Active power droop gain (mp) | 0.01 | - |
| Reactive power droop gain (nq) | 0.01 | - |
| KpRVI | 1.8 | pu |
| σX/R | 0.8 | pu |
| Kp Inner voltage loop | 7 | pu |
| Ki Inner voltage loop | 1.16 | pu |
| Kp Inner current loop | 0.14 | pu |
| Ki Inner current loop | 0.6 | pu |
Table 5.
Fault C components in sequences depending on the fault depth.
Table 5.
Fault C components in sequences depending on the fault depth.
| Fault Type | Zero | Positive | Negative |
|---|
| C | V0 = 0 | V+ = V · (1 + h)/2 | V− = V · (1 − h)/2 |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).