Study on the Motion Characteristics of 10 MW Superconducting Floating Offshore Wind Turbine Considering 2nd Order Wave Effect
Abstract
1. Introduction
2. Model Description
2.1. Wind Turbine
2.2. Floating Platform
2.3. Scale Model (1:90)
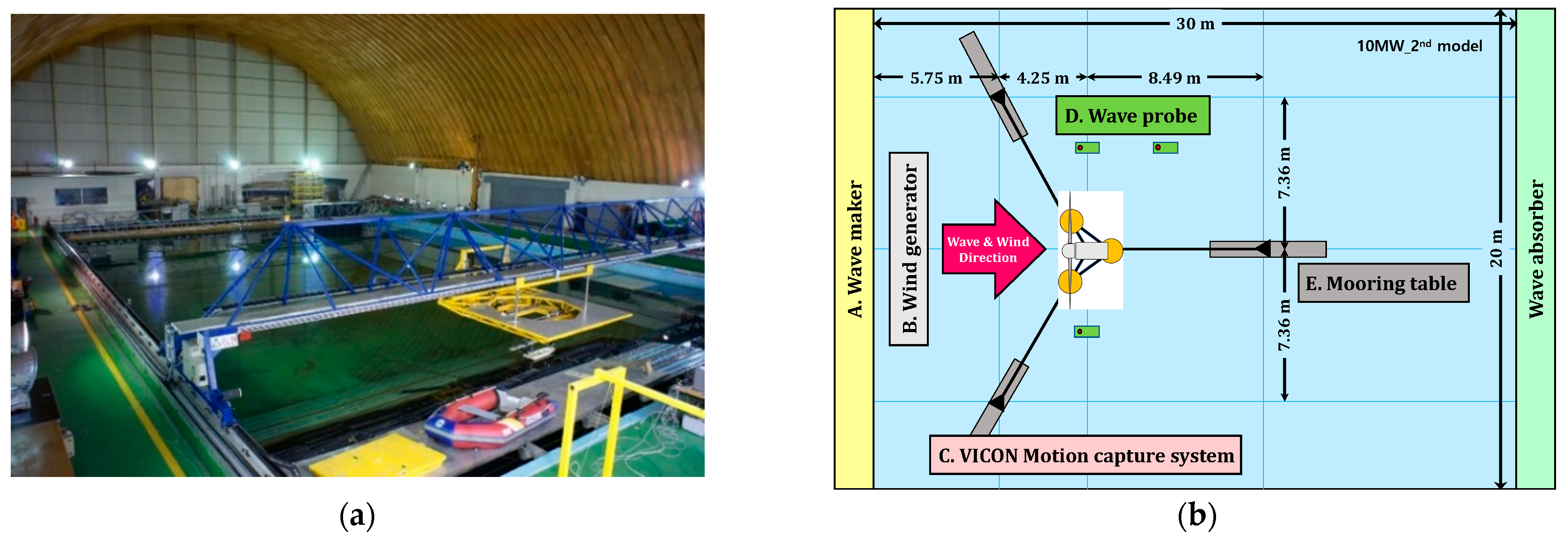
3. Model Test
3.1. Model Test Facilities
3.2. Model Test Condition
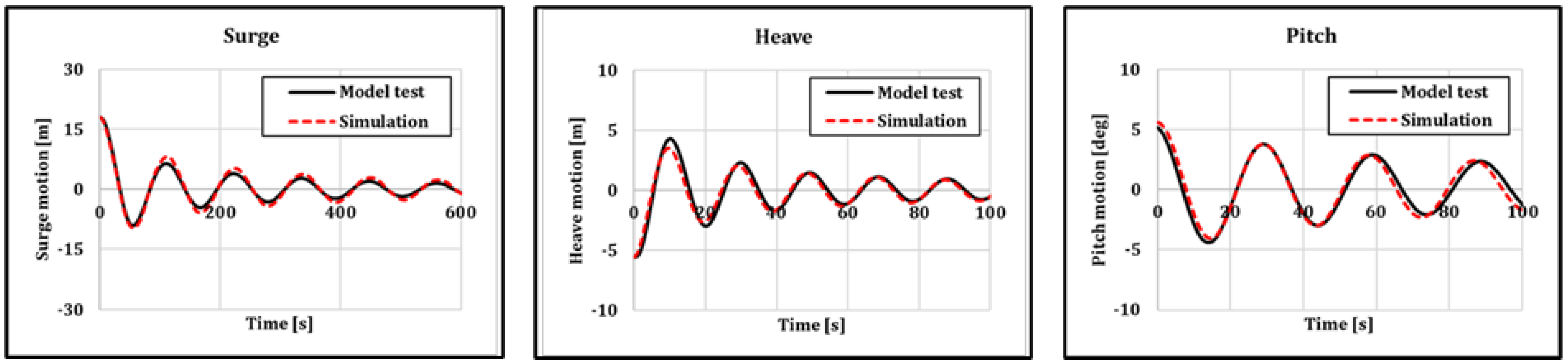
3.3. Model Calibration: Free-Decay Test
4. Model Test Result Validation and Verification
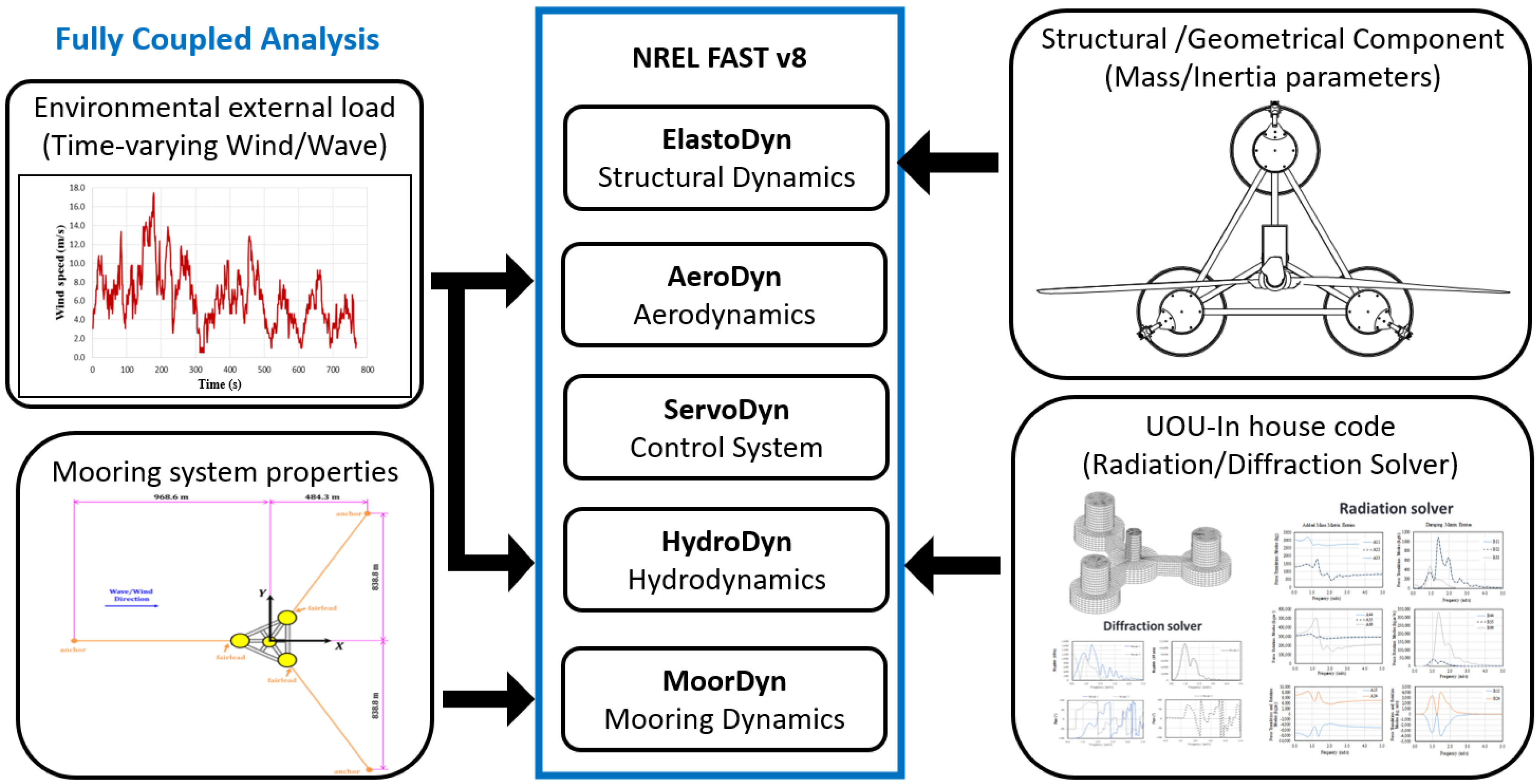
4.1. Numerical Analysis Approach
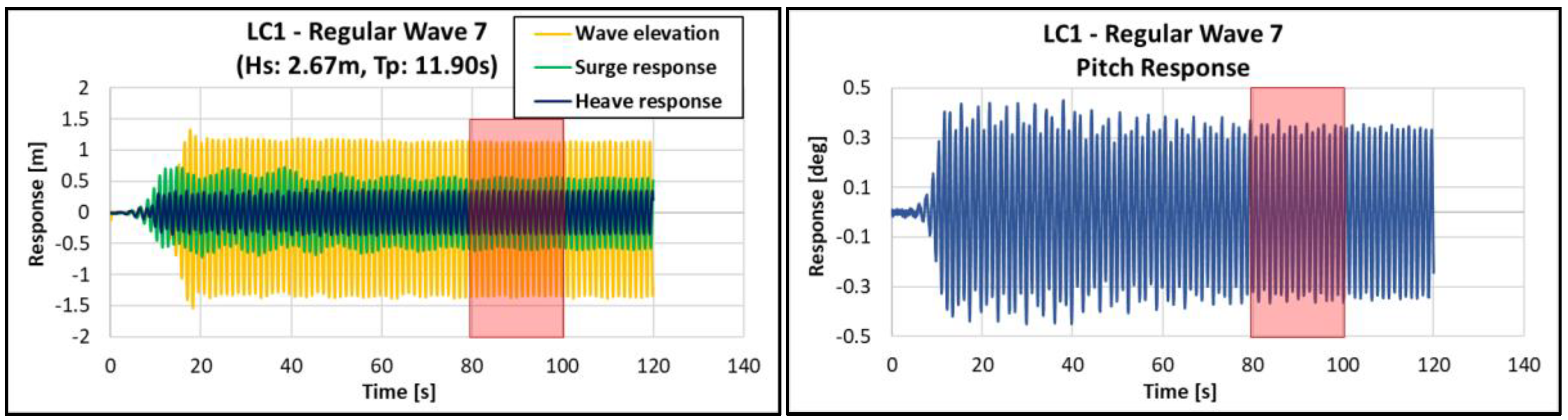
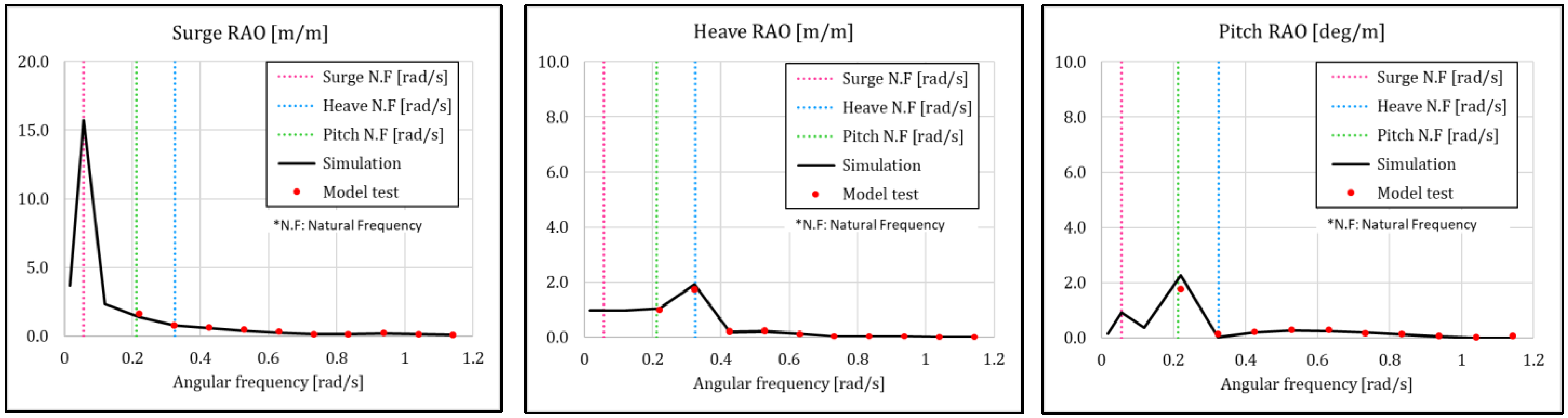
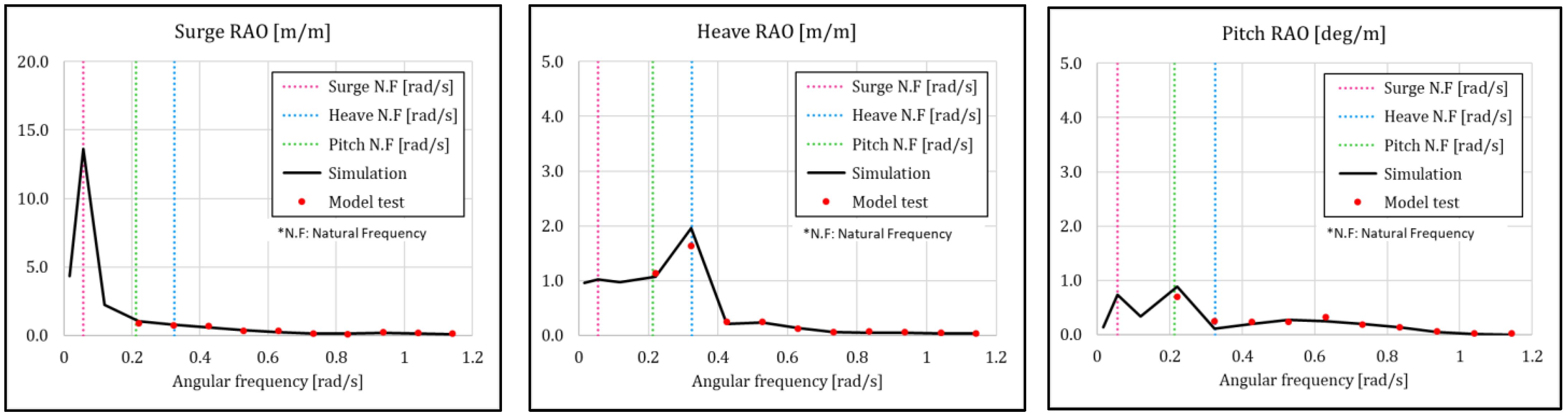
4.2. LC1 & LC2: RAO Result in Regular Wave
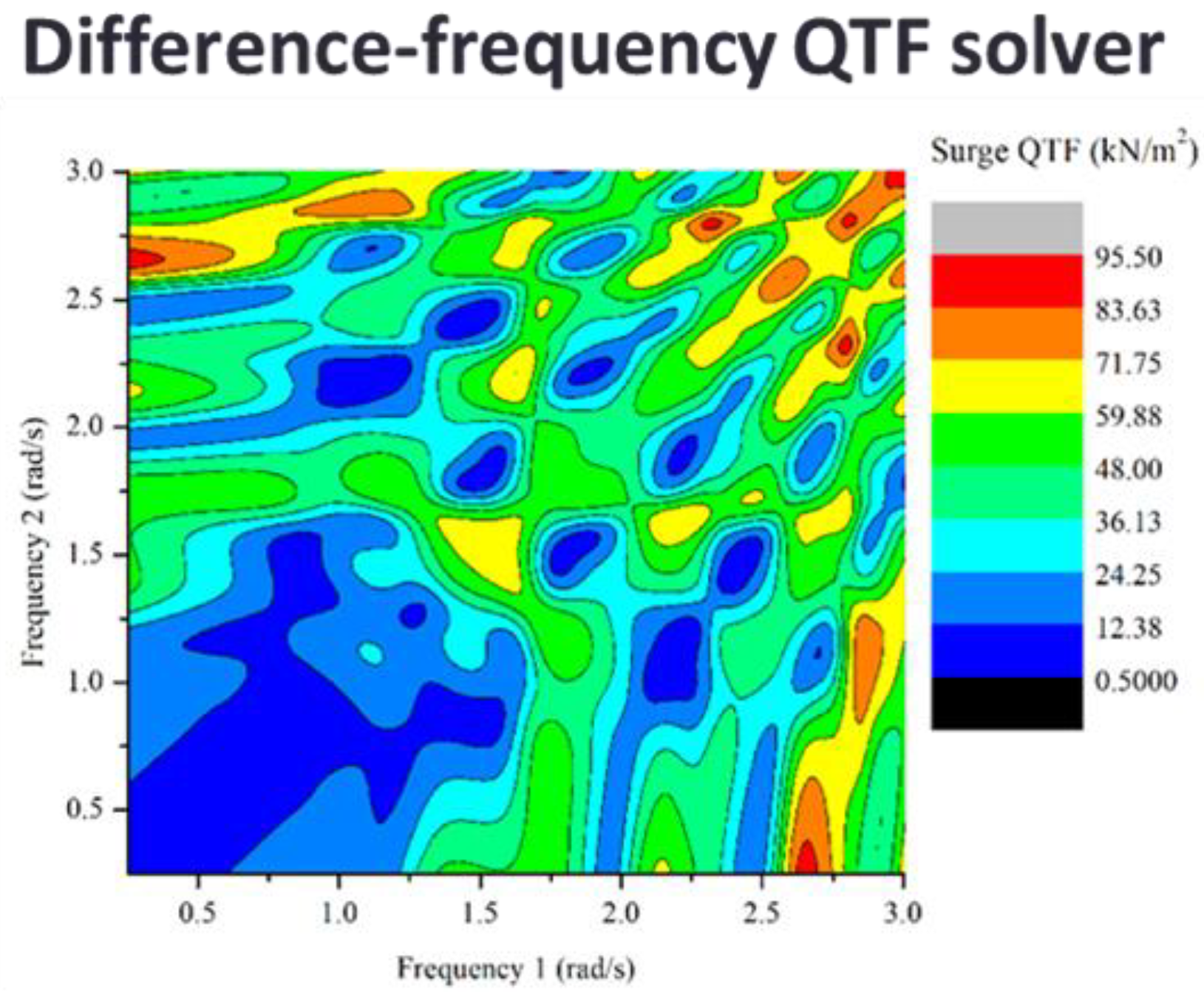
4.3. QTF Solver for 2nd Order Wave Load
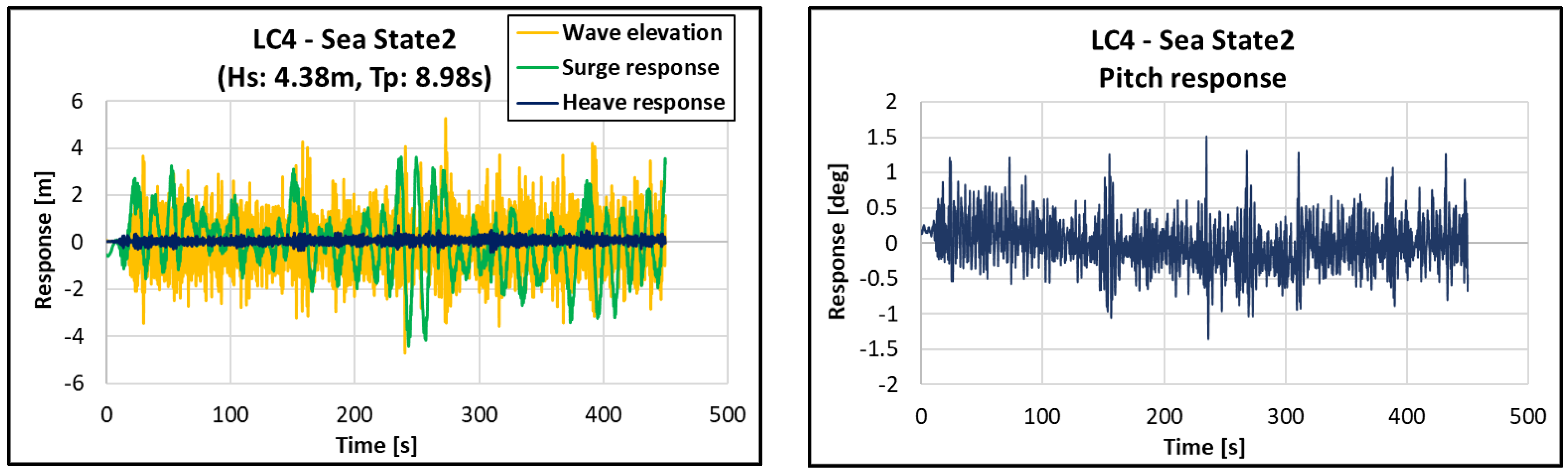
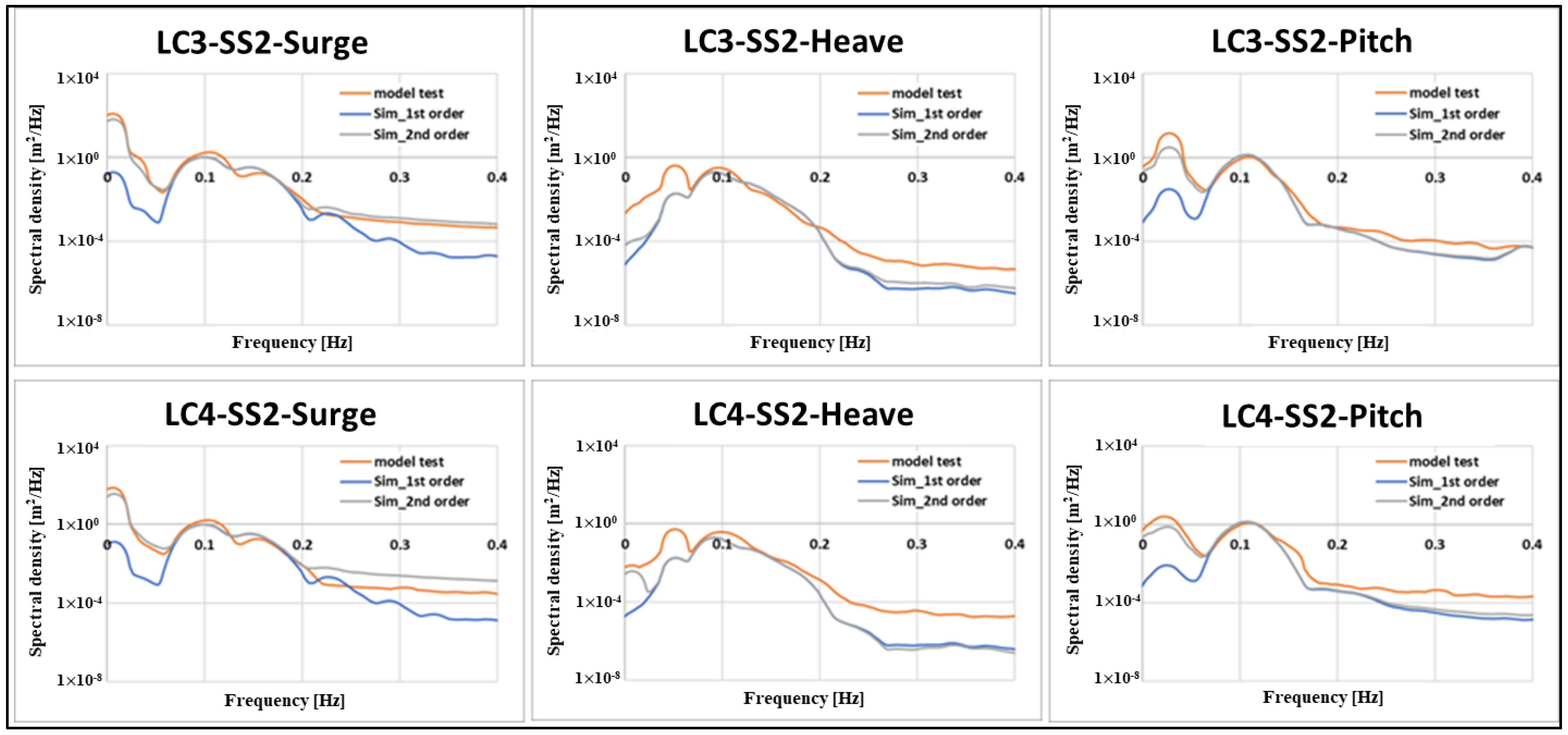
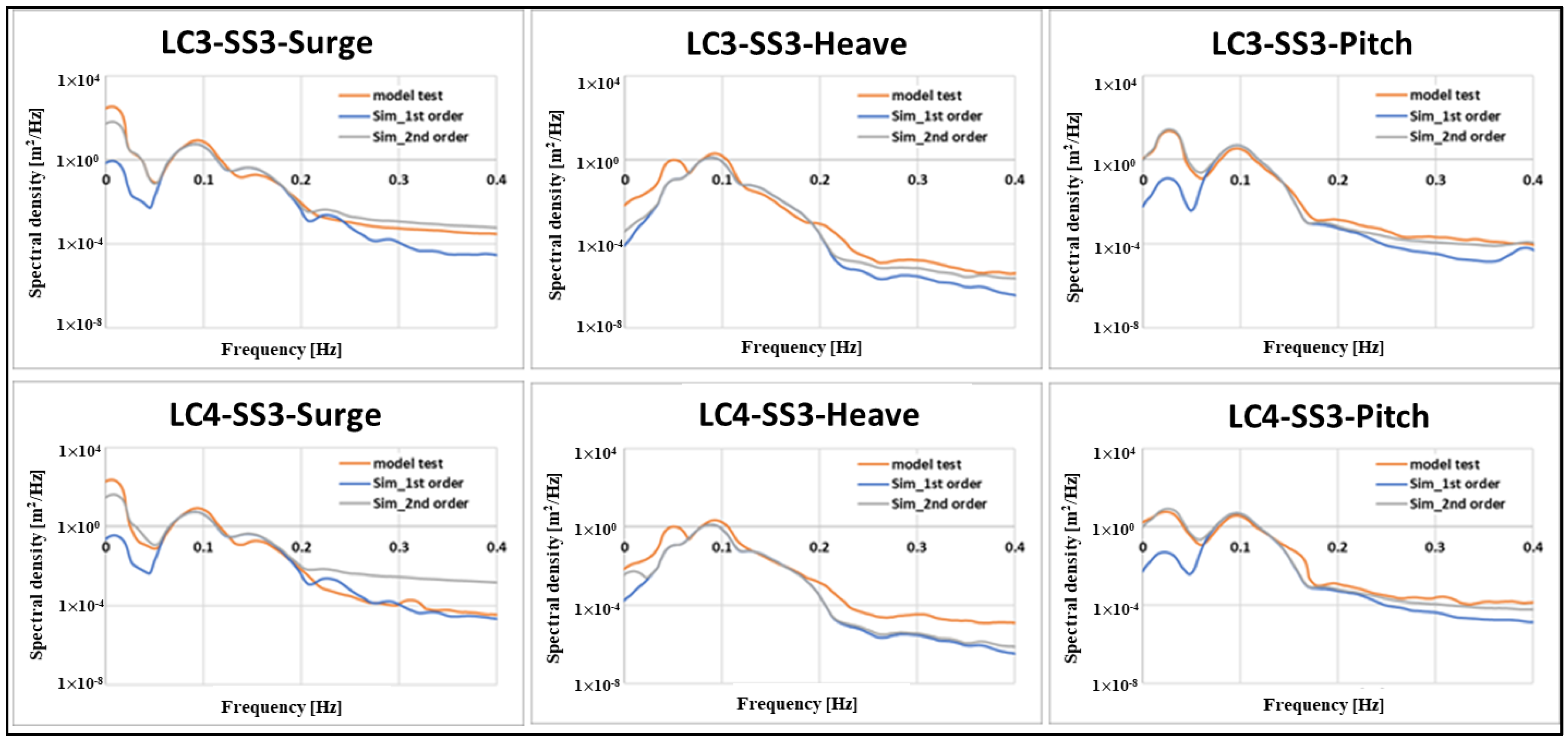
4.4. LC3 & LC4: FFT Result in Irregular Wave
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| CM | Center of Mass |
| FFT | Fast Fourier Transform |
| FOWT | Floating Offshore Wind Turbine |
| JONSWAP | Joint North Sea Wave Project |
| N.F. | Natural Frequency |
| PM | Pierson-Moskowitz |
| QTF | Quadratic Transfer Function |
| RAO | Response Amplitude Operator |
| RWTS-FOWT | Reference Wind TurbineSuperconducting Floating Offshore Wind Turbine |
| SWL | Still Water Level |
| UOU | University of Ulsan |
References
- Vestas, V236-15.0MW. Available online: https://www.vestas.com/en/products/offshore%20platforms/v236_15_mw#! (accessed on 9 June 2021).
- EcoSwing (Energy Cost Optimization using Superconducting Wind Generators)—World’s First Demonstration of a3.6MW Low-Cost Lightweight DD Superconducting Generator on a Wind Turbine. Available online: https://cordis.europa.eu/project/id/656024 (accessed on 9 June 2021).
- US DoE Backs Push for Wind Turbines up to 15 MW. Available online: https://www.rechargenews.com/wind/us-doe-backs-push-for-wind-turbines-up-to-15mw/2-1-597387 (accessed on 9 June 2021).
- First Floating Foundation for Kincardine 9.6 MW Turbines Arrives in Rotterdam. Available online: https://www.offshorewind.biz/2020/10/15/first-floating-foundation-for-kincardine-9-6-mw-turbines-arrives-in-rotterdam/ (accessed on 10 June 2021).
- Hoang, T.-K.; Queval, L.; Berriaud, C.; Vido, L. Design of a 20 MW Fully Superconducting Wind Turbine Generator to Minimize the Levelized Cost of Energy. In Proceedings of the 13th European Conference on Applied Superconductivity (EUCAS2017), Geneva, Switzerland, 17–21 September 2017. [Google Scholar]
- Pan, Y.; Gu, D. Superconducting Wind Turbine Generators. Trans. Environ. Electr. Eng. 2016, 1, 9–15. [Google Scholar] [CrossRef][Green Version]
- Abrahamsen, A.B.; Magnusson, N.; Jensen, B.B.; Runde, M. Large Superconducting Wind Turbine Generators. Energy Procedia 2012, 24, 60–67. [Google Scholar] [CrossRef][Green Version]
- Equinor, Offshore Wind in South Korea. Available online: https://www.equinor.com/en/where-we-are/south-korea.html (accessed on 10 June 2021).
- Coulling, A.J.; Goupee, A.; Robertson, A.; Jonkman, J.M.; Dagher, H.J. Validation of a FAST semi-submersible floating wind turbine numerical model with DeepCwind test data. J. Renew. Sustain. Energy 2013. [Google Scholar] [CrossRef]
- Bayati, I.; Jonkman, J.; Robertson, A.; Platt, A. The Effects of Second-Order Hydrodynamics on a Semisubmersible Floating Offshore Wind Turbine. Presented at the Science of Making Torque from Wind Technical University of Denmark, Copenhagen, Denmark, 17–20 June 2014. NREL/CP-5000-61752. [Google Scholar]
- Pham, T.D.; Shin, H.K. The Effect of the Second-Order Wave Loads on Drift Motion of a Semi-Submersible Floating Offshore Wind Turbine. J. Mar. Sci. Eng. 2020, 8, 859. [Google Scholar] [CrossRef]
- Jung, G.E.; Sung, H.J.; Dinh, M.C.; Park, M.W.; Shin, H.K. A Comparative Analysis of Economics of PMSG and SCSG Floating Offshore Wind Farms. Energies 2021, 14, 1386. [Google Scholar] [CrossRef]
- Bak, C.; Zahle, F.; Bitsche, R.; Kim, T.; Yde, A.; Henriksen, L.C.; Hansen, M.H.; Blasques, J.P.A.A.; Gaunaa, M.; Natarajan, A. The DTU 10-MW Reference Wind Turbine; DTU Library: Kongens Lyngby, Denmark, 2013. [Google Scholar]
- Robertson, A.; Jonkman, J.; Masciola, M.; Goupee, A.; Coulling, A.; Luan, C. Definition of the Semisubmersible Floating System for Phase II of OC4; NREL Technical Report; NREL/TP-5000-60601; NREL: Golden, CO, USA, 2014.
- Ahn, H.J.; Shin, H.K. Experimental and Numerical Analysis of a 10 MW Floating Offshore Wind Turbine in Regular Waves. Energies 2020, 13, 2608. [Google Scholar] [CrossRef]
- Bin, W.; Yougang, T.; Yan, L.; Runbo, C. Effects of Second-Order Sum-and Difference-Frequency Wave Forces on the Motion Response of a Tension-Leg Platform Considering the Set-down Motion. J. Ocean Univ. China 2018, 17, 311–319. [Google Scholar]
- Jonkman, J.M.; Robertson, A.N.; Hayman, G.J. HydroDyn User’s Guide and Theory Manual; NREL Technical Report; NREL/TP-xxxx-xxxx; NREL: Golden, CO, USA, 2015.
- Jonkman, J.M.; Buhl, M.L. FAST User’s Guide; NREL Technical Report; NREL/EL-500-38230; NREL: Golden, CO, USA, 2005.
- Robertson, A.N.; Gueydon, S.; Bachynski, E.; Wang, L.; Jonkman, J.; Alarcon, D.; Amet, E.; Beardsell, A.; Bonnet, P.; Boudet, B.; et al. OC6 Phase I: Investigating the underprediction of low-frequency hydrodynamic loads and responses of a floating wind turbine. J. Phys. Conf. Ser. 2020, 1618, 032033. [Google Scholar] [CrossRef]
- Valamanesh, V.; Myers, A.T. Aerodynamic Damping and Seismic Response of Horizontal Axis Wind Turbine Towers. J. Struct. Eng. 2014, 140, 04014090. [Google Scholar] [CrossRef]
- Salzmann, D.J.C.; Tempel, J.V.D. Aerodynamic Damping in the Design of Support Structures for Offshore Wind Turbine; TU Delft: Delft, The Netherlands, 2005. [Google Scholar]
- Coulling, A.J.; Goupee, A.J.; Robertson, A.; Jonkman, J. Importance of Second-Order Difference-Frequency Wave Diffraction Forces in the Validation of a Fast Semi-Submersible Floating Wind Turbine Model. In Proceedings of the ASME 2013 32th International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013. [Google Scholar]
- Zhang, L.; Shi, W.; Karimirad, M.; Michailides, C.; Jiang, Z. Second-Order Hydrodynamic Effects on the Response of Three Semisubmersible Floating Offshore Wind Turbines. Ocean Eng. 2020, 207, 107371. [Google Scholar] [CrossRef]
- Pinkster, J.A. Low Frequency Second Order Wave Exciting Forces on Floating Structures. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1980. [Google Scholar]
- Shin, H.K.; Yu, Y.J.; Pham, T.D.; Ahn, H.J.; Seo, B.C.; Kim, J.B. Analysis of Environmental Conditions for the Conceptual Design of a 200MW Floating Offshore Wind Farm in the East Sea, Korea. In Proceedings of the 2nd International Offshore Wind Technical Conference IOWTC 2019, St. Julian’s, Malta, 3–6 November 2019. [Google Scholar]
- Xu, K.; Shao, Y.; Gao, Z.; Moan, T. A study on fully nonlinear wave load effects on floating wind turbine. J. Fluids Struct. 2019, 88, 216–240. [Google Scholar] [CrossRef]





| Parameter | RWT DTU 10 MW Class | Superconducting 10 MW Class |
|---|---|---|
| Hub height [m] | 119 | 120 |
| Rotor diameter | 178.3 | 178.2 |
| Cut-in, Rated, Cut-out wind speed [m/s] | 4, 11.4, 25 | 3, 11.3, 25 |
| Blade mass, 1ea [kg] | 41,000 | 32,512 |
| Hub mass [kg] | 106,000 | 80,000 |
| Nacelle mass [kg] | 446,000 | 335,000 |
| Tower mass [kg] | 605,000 | 610,084 |
| Total mass [kg] | 1,280,000 | 1,113,097 |
| Parameter | Value |
|---|---|
| Depth to platform base below SWL [m] | 24.6 |
| Elevation to platform top above SWL [m] | 15.7 |
| Volume of displacement, V0 [m3] | 25,889 |
| Platform total mass (Including ballast) [kg] | 24,977,000 |
| Center of mass of platform [m] | −16.56 |
| Platform roll inertia about CM [kg·m2] | 1.92 × 1010 |
| Platform pitch inertia about CM [kg·m2] | 1.92 × 1010 |
| Platform yaw inertia about center [kg·m2] | 3.75 × 1010 |
| Parameter | Value |
|---|---|
| Number of mooring lines | 3 |
| Depth to anchors below SWL [m] | 150 |
| Depth to fairleads below SWL [m] | 17.46 |
| Unstretched mooring line length [m] | 950 |
| Mooring line mass density in air [kg/m] | 443.2 |
| Mooring line pretension [kN] | 2932 |
| Axial stiffness (1EA) [kN] | 1,815,000 |
| MBL (Minimum breaking load) [kN] | 14,677 |
| Parameter | Ideal Model (1:90) | Actual Model (1:90) | Deviation |
|---|---|---|---|
| Rotor and nacelle mass [kg] | 0.704 | 0.720 | 2.32% |
| Tower mass [kg] | 0.837 | 0.820 | −1.70% |
| Platform mass [kg] | 34.30 | 34.62 | 1.32% |
| Platform Center of mass from SWL [m] | 0.184 | 0.184 | 0.00% |
| Ixx of the Platform [kg·m2] | 3.624 | 3.450 | −4.80% |
| Iyy of the Platform [kg·m2] | 3.624 | 3.450 | −4.80% |
| Total wind turbine mass [kg] | 35.80 | 35.50 | −3.02% |
| 1 Mooring line mass density [kg/m] | 0.067 | 0.068 | 1.49% |
| 1 Mooring nominal diameter [mm] | 1.578 | 1.570 | −0.51% |
| Mooring line length [m] | 10.56 | 10.56 | 0.00% |
| Load Case | Wind | Wave | Rotor |
|---|---|---|---|
| LC1 | No wind | Regular wave | Fixed |
| LC2 | Rated wind speed | Regular wave | Rotating |
| LC3 | No wind | Irregular wave | Fixed |
| LC4 | Rated wind speed | Irregular wave | Rotating |
| Parameter | Ideal Condition | Actual Condition | Deviation [%] |
|---|---|---|---|
| Rated wind speed [m/s] | 1.19 | 1.00 | −15.97 |
| Rated rotor speed [rpm] | 88.8 | 90.0 | 1.35 |
| Rated thrust force [N] | 2.272 | 2.22 | −0.67 |
| Parameter | Model Test | Simulation | Conformity [%] |
|---|---|---|---|
| Surge natural period [s] | 112.0 | 112.3 | 99.7 |
| Heave natural period [s] | 19.4 | 19.4 | 100.0 |
| Pitch natural period [s] | 29.6 | 28.9 | 102.4 |
| Wave No. | Full Scale (1:1) | Model Scale (1:90) | ||||
|---|---|---|---|---|---|---|
| Wave Height | Wave Period | Wave Length | Wave Height | Wave Period | Wave Length | |
| [m] | [s] | [m] | [m] | [s] | [m] | |
| Regular wave 1 | 2.67 | 5.50 | 47.25 | 0.03 | 0.580 | 0.525 |
| Regular wave 2 | 2.67 | 6.04 | 57.06 | 0.03 | 0.637 | 0.634 |
| Regular wave 3 | 2.67 | 6.70 | 70.20 | 0.03 | 0.707 | 0.780 |
| Regular wave 4 | 2.67 | 7.53 | 88.38 | 0.03 | 0.793 | 0.982 |
| Regular wave 5 | 2.67 | 8.58 | 114.84 | 0.03 | 0.904 | 1.276 |
| Regular wave 6 | 2.67 | 9.97 | 155.25 | 0.03 | 1.051 | 1.725 |
| Regular wave 7 | 2.67 | 11.90 | 221.22 | 0.03 | 1.255 | 2.458 |
| Regular wave 8 | 2.67 | 14.77 | 337.50 | 0.03 | 1.557 | 3.750 |
| Regular wave 9 | 2.67 | 19.45 | 548.46 | 0.03 | 2.050 | 6.094 |
| Regular wave 10 | 2.67 | 28.46 | 941.67 | 0.03 | 3.000 | 10.463 |
| Sea State No. | Full Scale (1:1) | Model Scale (1:90) | ||
|---|---|---|---|---|
| Wave Height | Wave Period | Wave Height | Wave Period | |
| [m] | [s] | [m] | [s] | |
| SS1 | 2.67 | 7.66 | 0.02967 | 0.80743 |
| SS2 | 4.38 | 8.98 | 0.04867 | 0.94658 |
| SS3 | 6.18 | 10.36 | 0.06867 | 1.09204 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Pham, T.D.; Shin, H.; Ha, K. Study on the Motion Characteristics of 10 MW Superconducting Floating Offshore Wind Turbine Considering 2nd Order Wave Effect. Energies 2021, 14, 6070. https://doi.org/10.3390/en14196070
Yu Y, Pham TD, Shin H, Ha K. Study on the Motion Characteristics of 10 MW Superconducting Floating Offshore Wind Turbine Considering 2nd Order Wave Effect. Energies. 2021; 14(19):6070. https://doi.org/10.3390/en14196070
Chicago/Turabian StyleYu, Youngjae, Thanh Dam Pham, Hyunkyoung Shin, and Kwangtae Ha. 2021. "Study on the Motion Characteristics of 10 MW Superconducting Floating Offshore Wind Turbine Considering 2nd Order Wave Effect" Energies 14, no. 19: 6070. https://doi.org/10.3390/en14196070
APA StyleYu, Y., Pham, T. D., Shin, H., & Ha, K. (2021). Study on the Motion Characteristics of 10 MW Superconducting Floating Offshore Wind Turbine Considering 2nd Order Wave Effect. Energies, 14(19), 6070. https://doi.org/10.3390/en14196070







