Impact of Control Loops on the Passivity Properties of Grid-Forming Converters with Fault-Ride through Capability †
Abstract
:1. Introduction
2. System Representation
3. System Modeling and Input-Admittance Derivation
4. Passivity Characterization of the Converter System
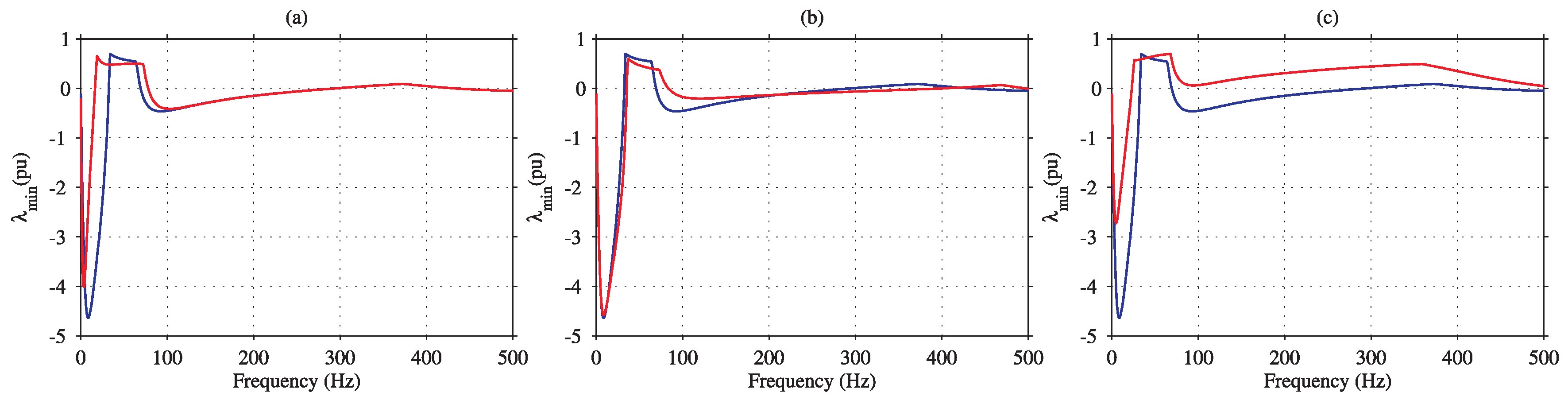
4.1. Impact of Operating Point
4.2. Impact of Control Parameters
4.3. Simulation Study
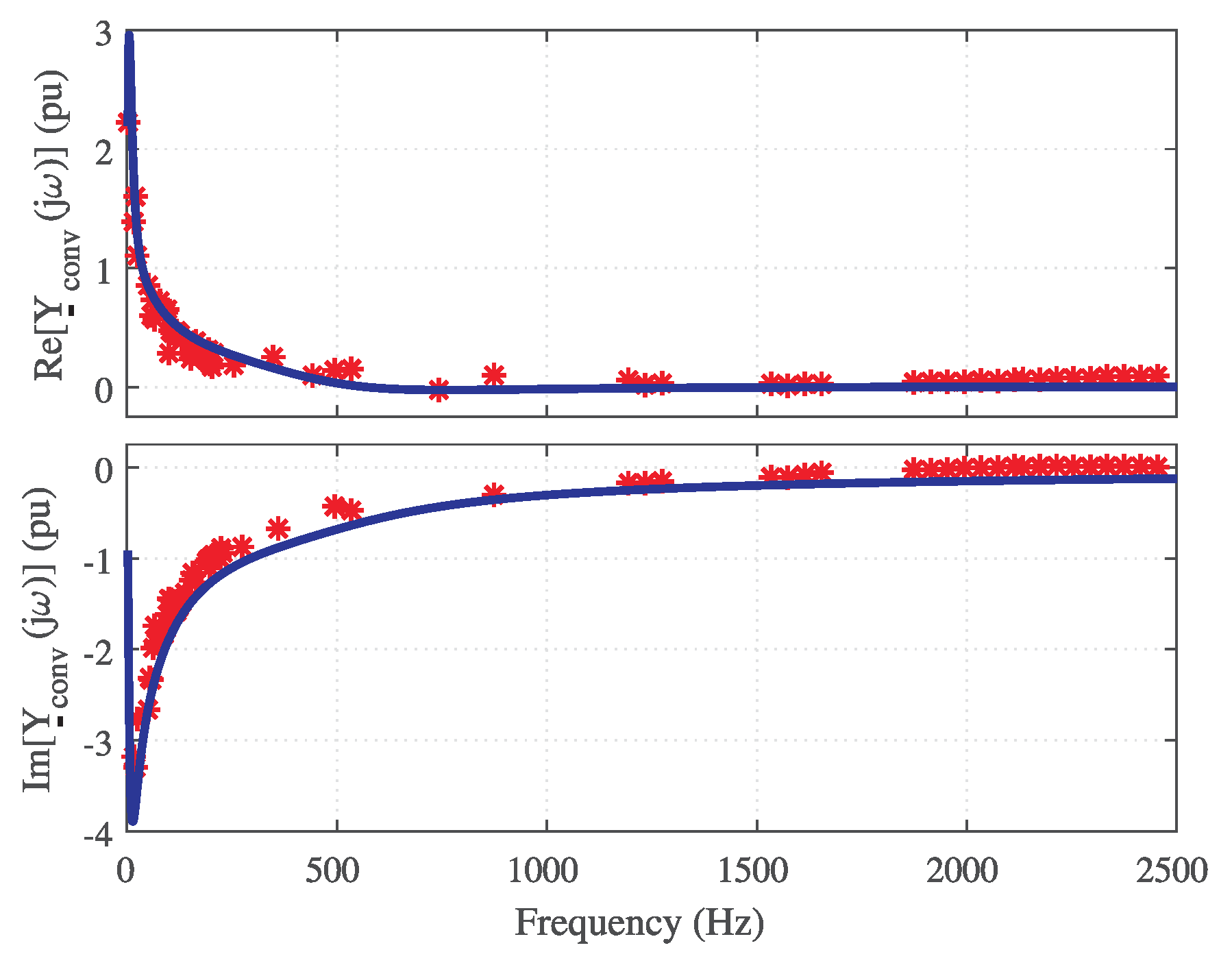
5. Experimental Validation
5.1. Input-Admittance Verification
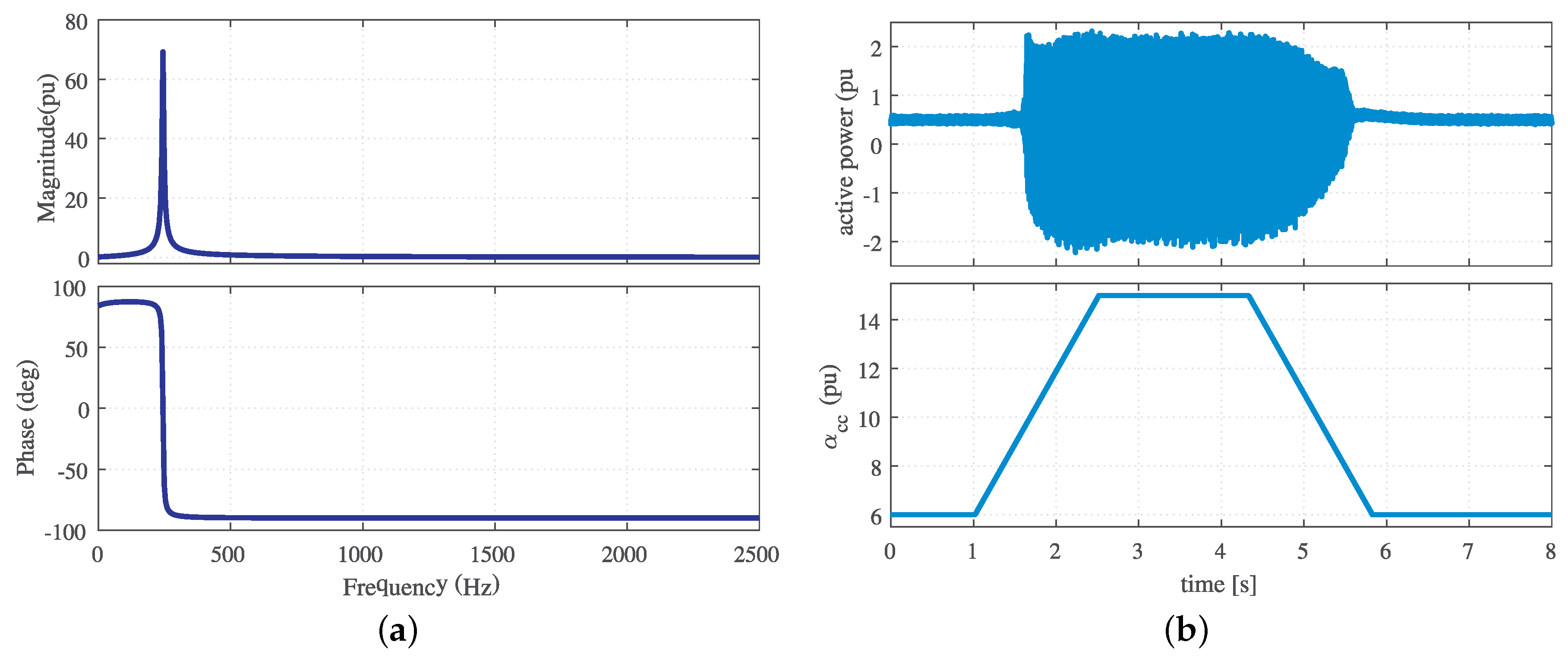
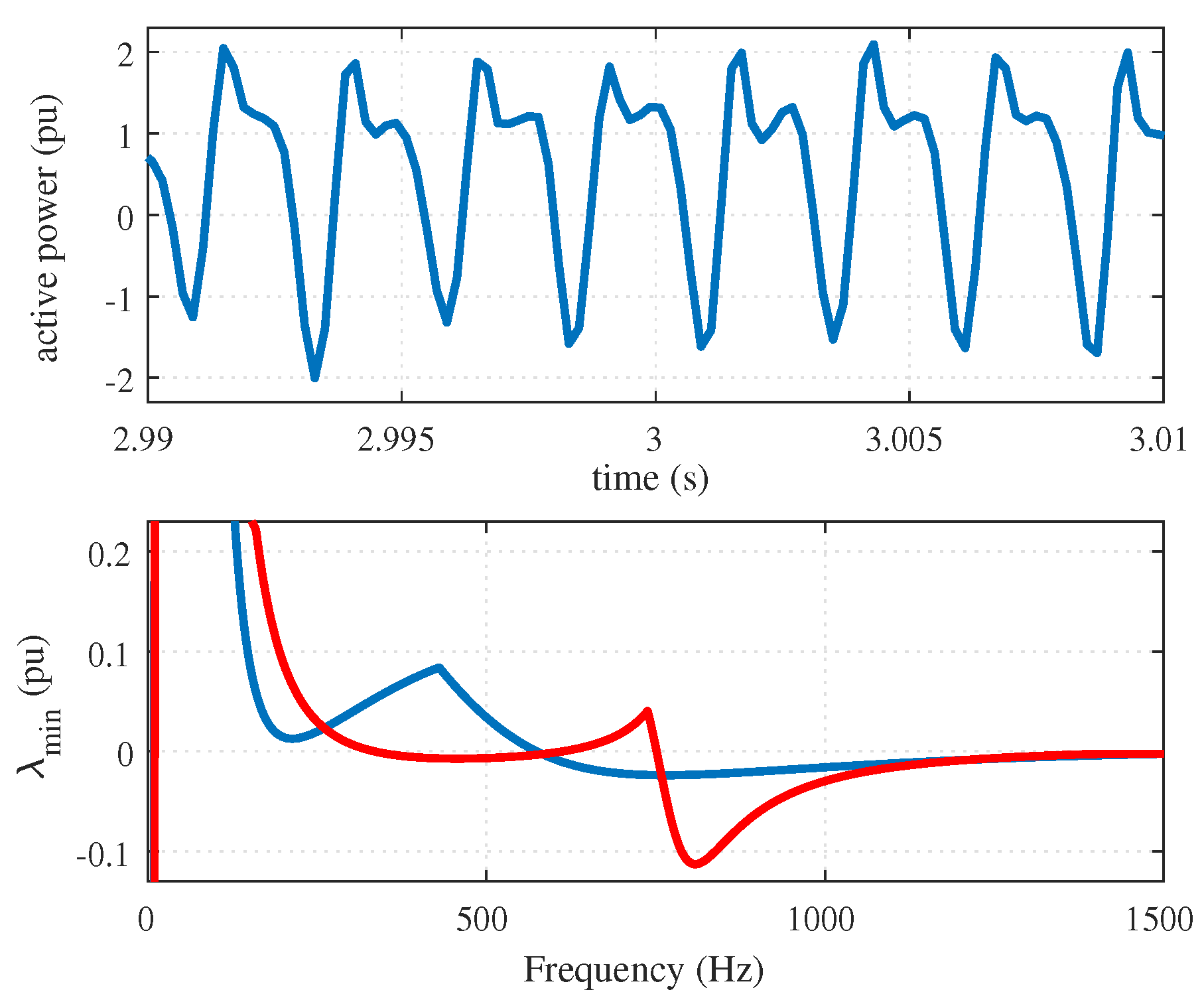
5.2. Resonance Instability Study
6. Passivity Improvement through Tuning of Virtual-Impedance Parameters
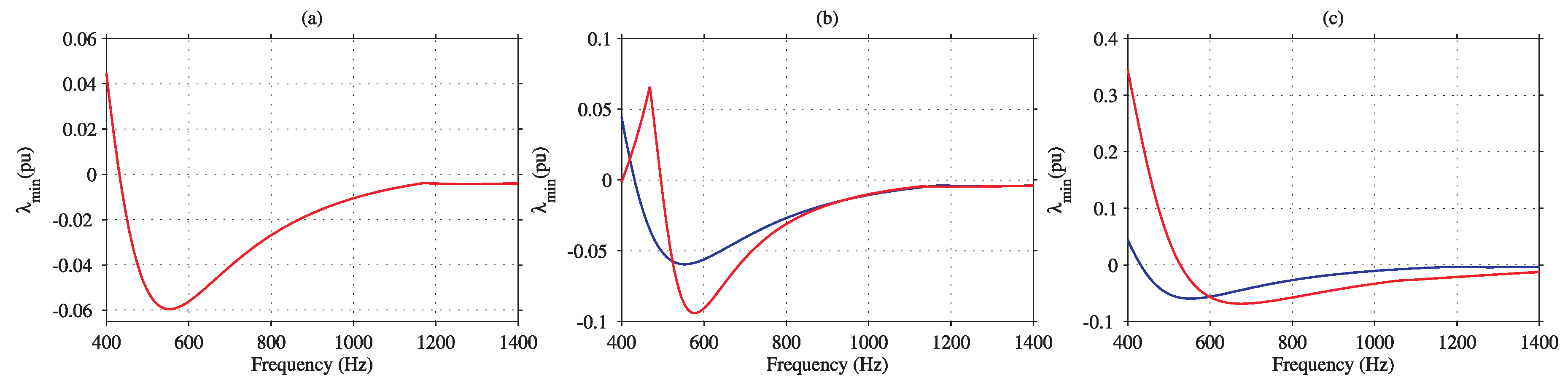
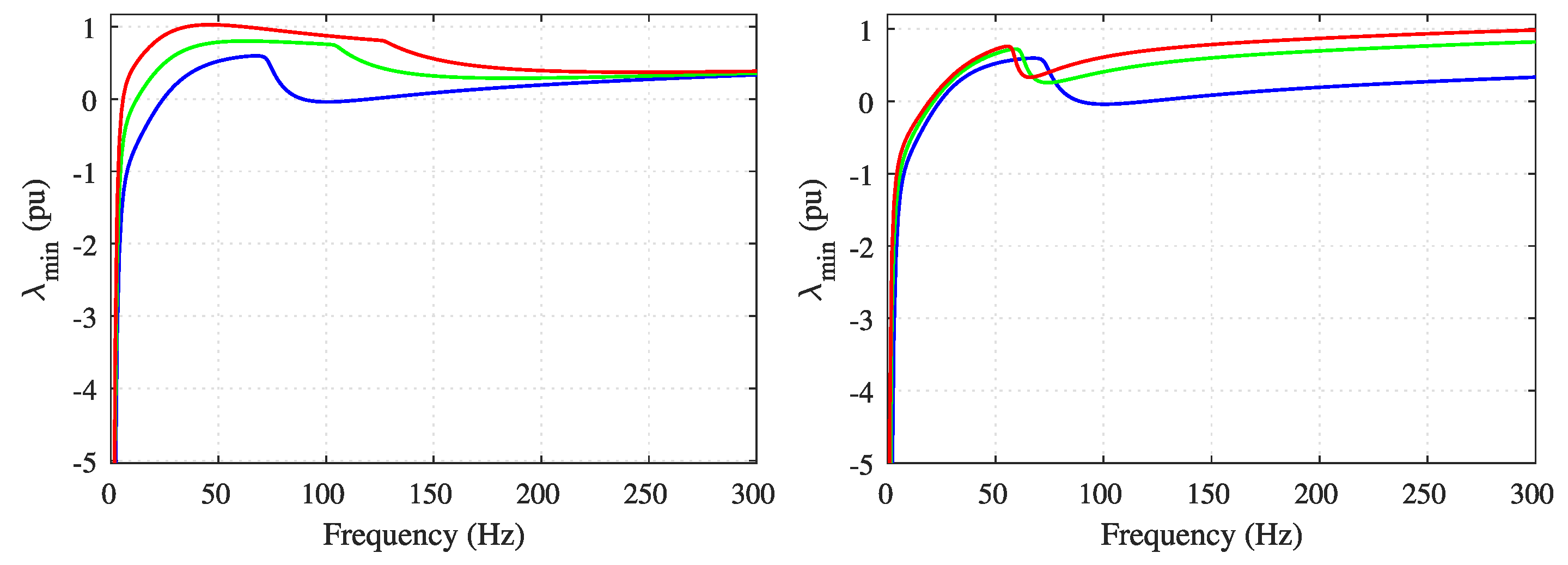
6.1. Low-Frequency Passivity Enhancement
6.2. Medium- and High-Frequency Passivity Enhancement
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.; Harnefors, L.; Nee, H.-P. Power-Synchronization Control of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Syst. 2010, 25, 809–820. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Weiss, G. Synchronverters: Inverters That Mimic Synchronous Generators. IEEE Trans. Ind. Electron. 2011, 54, 1259–1267. [Google Scholar] [CrossRef]
- Rodriguez, P.; Candela, I.; Citro, C.; Rocabert, J.; Luna, A. Control of grid-connected power converters based on a virtual admittance control loop. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–10. [Google Scholar]
- Kkuni, K.; Mohan, S.; Yang, G.; Xu, W. Comparative assessment of typical control realizations of grid forming converters based on their voltage source behavior. arXiv 2021, arXiv:2106.10048v1. [Google Scholar]
- Rodriguez, P.; Candela, I.; Luna, A. Control of PV generation systems using the synchronous power controller. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, Colorado, 15–19 September 2013; pp. 993–998. [Google Scholar]
- Watson, J.; Ojo, Y.; Lestas, I.; Spanias, C. Stability of power networks with grid-forming converters. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar]
- Ray, I. Review of Impedance-Based Analysis Methods Applied to Grid-Forming Inverters in Inverter-Dominated Grids. Energies 2021, 14, 2686. [Google Scholar] [CrossRef]
- Beza, M.; Bongiorno, M. Impact of converter control strategy on low-and high-frequency resonance interactions in power-electronic dominated systems. Int. J. Electr. Power Energy Syst. 2020, 120, 105978. [Google Scholar] [CrossRef]
- Beza, M.; Bongiorno, M.; Narula, A. Impact of control loops on the low-frequency passivity properties of grid-forming converters. In Proceedings of the 2020 22nd European Conference on Power Electronics and Applications (EPE’20 ECCE Europe), Lyon, France, 7–11 September 2020; pp. 1–10. [Google Scholar]
- Harnefors, L.; Yepes, A.G.; Vidal, A.; Doval-Gandoy, J. Passivity-Based Controller Design of Grid-Connected VSCs for Prevention of Electrical Resonance Instability. IEEE Trans. Ind. Electron. 2015, 62, 702–710. [Google Scholar] [CrossRef]
- Liu, H.; Sun, J. Voltage Stability and Control of Offshore Wind Farms with AC Collection and HVDC Transmission. IEEE J. Emerg. Sel. Topics Power Electron. 2014, 2, 1181–1189. [Google Scholar]
- Amin, M.; Molinas, M. Understanding the Origin of Oscillatory Phenomena Observed Between Wind Farms and HVdc Systems. IEEE J. Emerg. Sel. Topics Power Electron. 2017, 5, 378–392. [Google Scholar] [CrossRef] [Green Version]
- Beza, M.; Bongiorno, M. Identification of resonance interactions in offshore-wind farms connected to the main grid by MMC-based HVDC system. Int. J. Electr. Power Energy Syst. 2019, 111, 101–113. [Google Scholar] [CrossRef]
- Li, C.; Liang, J.; Cipcigan, L.; Ming, W.; Colas, F.; Guillaud, X. DQ Impedance Stability Analysis for the Power-Controlled Grid-Connected Inverter. IEEE Trans. Energy Convers. 2020, 2020 35, 1762–1771. [Google Scholar] [CrossRef]
- Liao, Y.; Wang, X.; Blaabjerg, F. Passivity-Based Analysis and Design of Linear Voltage Controllers For Voltage-Source Converters. IEEE Open J. Ind. Electron. Soc. 2020, 2020 1, 114–126. [Google Scholar] [CrossRef]
- Liao, Y.; Wang, X. Passivity Analysis and Enhancement of Voltage Control for Voltage-Source Converters. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 5424–5429. [Google Scholar]
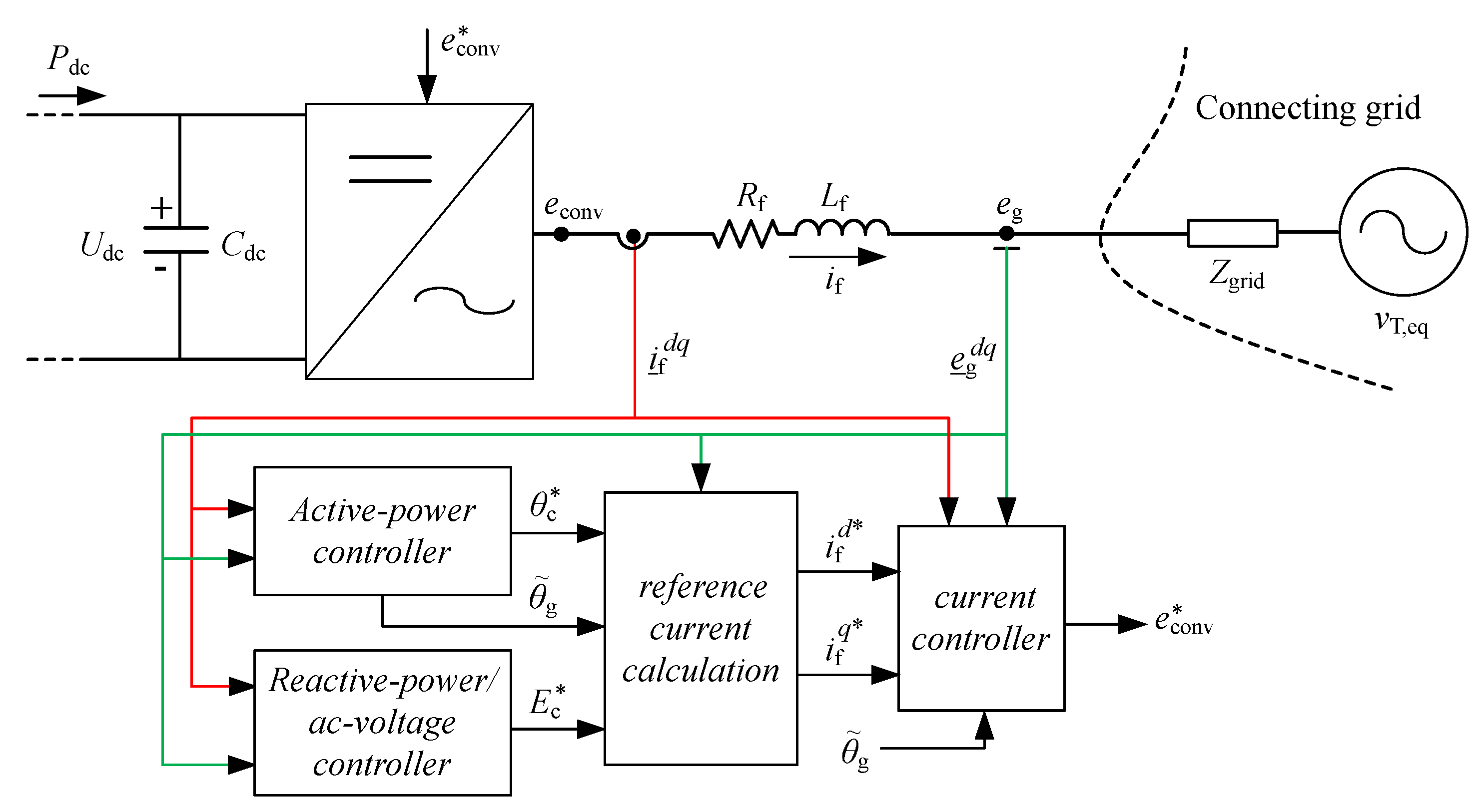
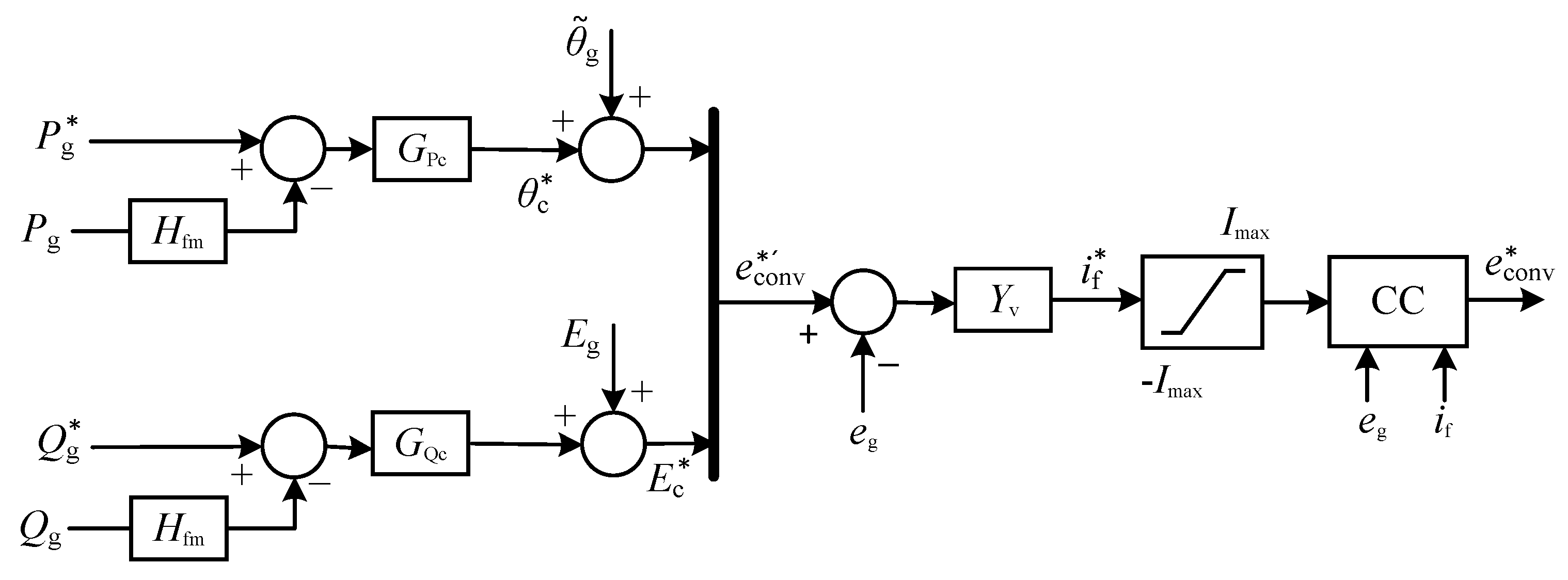







| active-power controller: |
| reactive-power controller: |
| power-measurement filter: |
| current controller: |
| voltage feed-forward filter: |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beza, M.; Bongiorno, M.; Narula, A. Impact of Control Loops on the Passivity Properties of Grid-Forming Converters with Fault-Ride through Capability. Energies 2021, 14, 6036. https://doi.org/10.3390/en14196036
Beza M, Bongiorno M, Narula A. Impact of Control Loops on the Passivity Properties of Grid-Forming Converters with Fault-Ride through Capability. Energies. 2021; 14(19):6036. https://doi.org/10.3390/en14196036
Chicago/Turabian StyleBeza, Mebtu, Massimo Bongiorno, and Anant Narula. 2021. "Impact of Control Loops on the Passivity Properties of Grid-Forming Converters with Fault-Ride through Capability" Energies 14, no. 19: 6036. https://doi.org/10.3390/en14196036
APA StyleBeza, M., Bongiorno, M., & Narula, A. (2021). Impact of Control Loops on the Passivity Properties of Grid-Forming Converters with Fault-Ride through Capability. Energies, 14(19), 6036. https://doi.org/10.3390/en14196036







