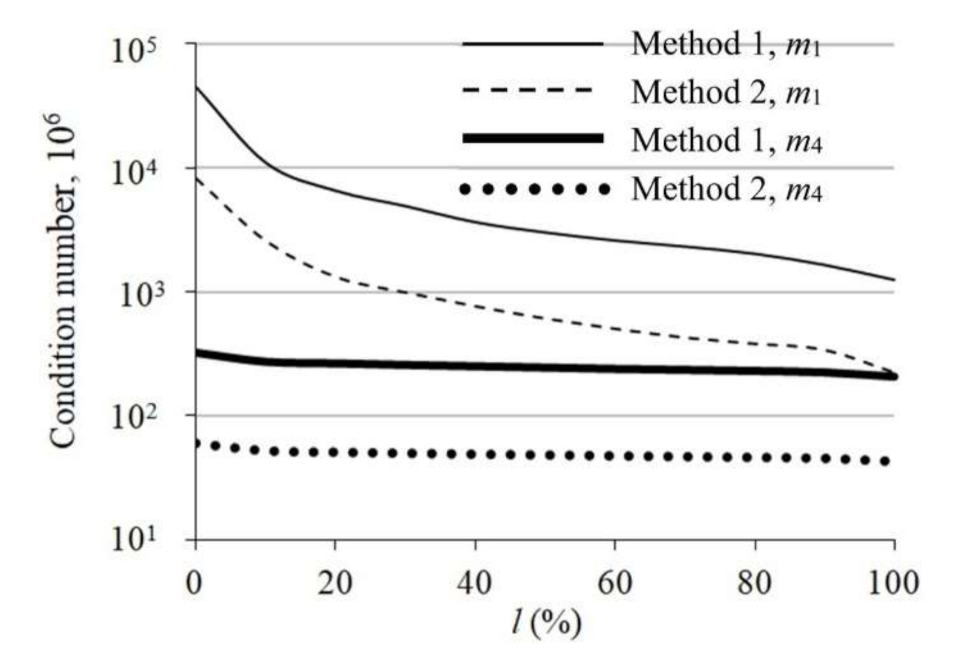
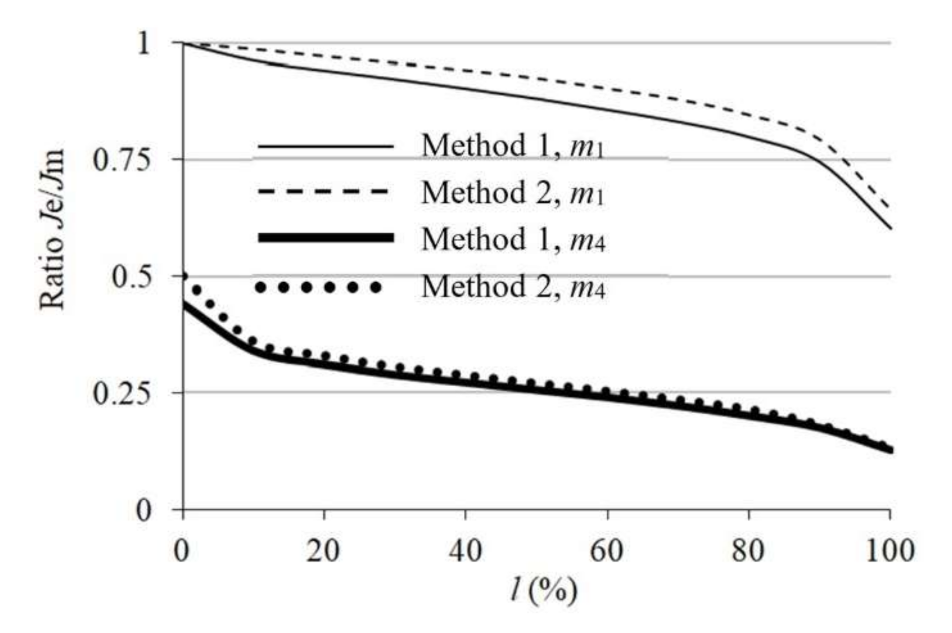
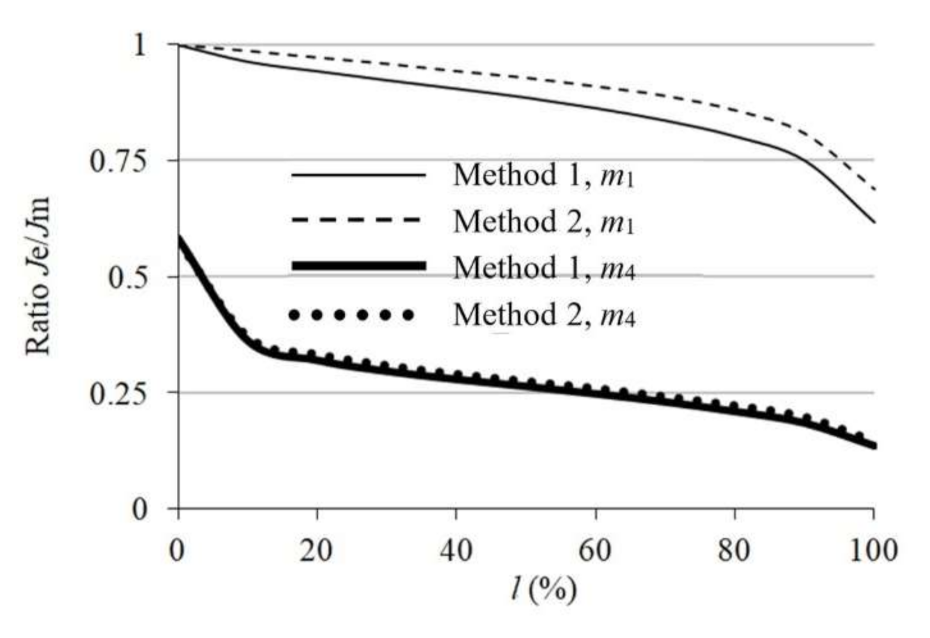
3.1. The Classical State Estimation
In this paper, the term of “the classical state estimation” is understood as a state estimation for a power system without a quadrature booster.
In the paper, the weighted-least-squares power-system state-estimation method is considered [
17]. For that method, an objective function is following:
where:
x is a power-system state vector;
z is a vector of measurements;
h(
x) is a vector of functions of vector
x, representing dependence of measured quantities on the state vector; and
R is a diagonal matrix of measurement-data covariances.
State vector
x in polar coordinate system is defined as:
where: δ
i i = 2, 3, …,
n are phase angles of voltages at nodes 2, 3, …,
n;
Vi i = 1, 2, …,
n are magnitudes of voltages at nodes 1, 2, …,
n; and
n is a number of all nodes in a power system.
Node 1 is considered as a reference node. The phase angle for that node is equal to zero.
The number of state-vector elements (
nx) is as follows:
The relationships among measured quantities and elements of the state vector are as follows [
18]:
where:
Pi and
Qi are an active and reactive power injections at
i-th node, respectively;
Pij Qij are an active and reactive power flows, respectively, between
i-th and
j-th node, measured at
i-th node;
is an admittance of the series branch connecting
i-th and
j-th node;
is an admittance of the shunt branch at
i-th node; and
Yrow i is the
i-th row of an admittance matrix for the considered system:
i, l = 1, 2, …,
n are elements of the admittance matrix and
V is a vector:
The relationships (11)–(13) are used for definition of elements of function vector
h(
x). Vector
h(
x) can be presented as follows:
Formula (16) assumes that: PAC_i = Pi, QAC_i = Qi i ∈ {1, 2, …, n}; Pf_j and Qf_j are, respectively, an active and reactive power flow at the end of the appropriate branch, j ∈ {1, 2, …, 2g}; and g is a number of all branches in a power system. The power flows are numbered according to the adopted rule.
The number of elements of vector
h(
x) (
mz) is as follows:
where:
m is the number of measured quantities (the number of measurement data) and
mz_0 is the number of quantities, of which values are known (the number of pseudo-measurements).
A pseudo-measurement is treated as a measurement of high accuracy. We assume that
mz_0 is calculated using the formula:
where:
n0 is the number of zero-injection nodes.
Note, for the zero-injection node, there are two pseudo-measurements, i.e., an active and reactive power flow. Each of those power is equal to zero.
The vector defined in Formula (16) has the maximal possible number of elements. That number is equal to 3n + 4g. In fact, often the number of elements of the vector h(x) is smaller because not all nodal powers, power flows as well as nodal voltage magnitudes are measured, or if they are measured they are not available.
The characterized estimation method assumes iteratively searching for a solution to the state-estimation problem. During this computational process, the normal-equation set is solved:
where:
k is a number of iteration and
xk is a solution of the state vector at
k-th iteration,
G(x) is called a gain matrix.
Jacobian matrix H(x) can be presented as follows:
Matrix H(x) (like vector h(x) before) is presented under the assumption of the maximum number of measured quantities. When the number of these quantities is smaller, the number of rows of the vector h(x) and also of the matrix H(x) is smaller than previously assumed.
We can formulate the following algorithm for the considered case of the state estimation:
Determine the parameters of the power system elements.
Determine measurement vector z and measurement-data covariance matrix R.
Set vector x0, i.e., a vector whose elements are the initial values of the elements of state vector x.
k = 0.
Calculate elements of Jacobian matrix H(x) and vector h(x) for xk.
Calculate xk + 1, i.e., new approximation of vector x using (19).
k = k + 1.
If stopping criteria are fulfilled, calculate unmeasured quantities, else go to step 5.
A flow chart of the state estimation process is in
Figure 4.
The necessary condition of existence of a solution of the state estimation is
nx ≥
mz, i.e.,
r ≥ 1, where
r is an index defining the data redundancy in the state estimation. Index
r is calculated using formula:
3.2. The State Estimation with the Use of the Considered Model of the Quadrature Booster—Method 1
In the considered case of the state estimation, the state vector is as following
where:
is a magnitude of source voltage
;
and
are a magnitude and a phase angle of source voltage
, respectively.
For Method 1, the number of state-vector elements (
nx_1) is given by the formula
where
nQB is the number of sources in the quadrature booster model and
nQB = 2.
Comparing to the state vector (9), additional elements of the state vector (23) are the magnitudes and phase angles of voltages
and
. In turn, in the vector of measured quantities
h(
x), additional quantities are
,
(5) and
(7). In Equation (25), in vector
h(
x), only quadrature-booster-related quantities are distinguished.
For the considered case,
mz_0 is calculated as follows:
where
m0_QB is the number of scalar equations describing the quadrature booster model that can be used to determine quantities taking known values and
m0_QB = 3 (equations resulting from (5) and (7)).
Due to the differences in the content of vectors
h(
x) and
x for the considered case of the state estimation and for the state estimation described in
Section 3.1, there is also a difference in the form of Jacobian matrix
H(
x) between the mentioned cases of the state estimation. Formula (27) shows the elements of this matrix related with the quadrature booster:
An algorithm for Method 1 assumes realization of the same steps as for the classical state estimation (see
Figure 4). Vector
h(
x) and matrix
H(
x) that are used in the algorithm are different from those considered in the classical state estimation.
3.3. The State Estimation with the Switching off of the Quadrature Booster in a Power System Model—Method 2
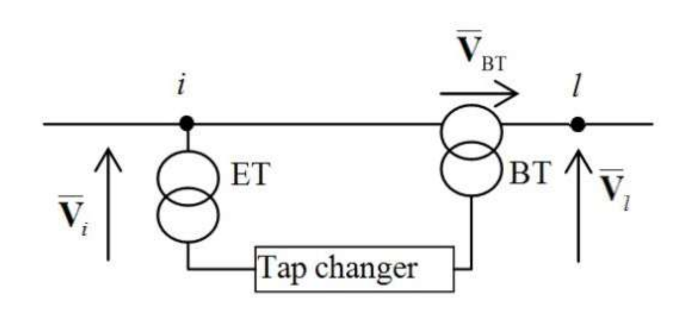
Unlike in Method 1, in Method 2 of the state estimation, the quadrature booster is switched off in the used power system model. This is illustrated in
Figure 5.
Figure 5 presents the branch between nodes
i and
k, in which in the real power system there is the phase shifter (the quadrature booster).
Figure 5 shows two cases considered in the paper. The case in
Figure 5a is taken into account in Method 1, and the case in
Figure 5b—in Method 2.
It should be noted, that node
l is a virtual one, for which
Pl = 0 and
Ql = 0. While in Method 1,
Pl and
Ql are used as measured quantities, in Method 2,
Pl and
Ql are no longer such quantities. For bus
l, it is not possible to formulate the power balance equation because the quadrature booster is off. This means that the number of the zero-injection nodes (i.e.,
n0) decreases by 1. There is the same reason of removal of the powers
Pi and
Qi from measured-quantities vector
h(
x) as in the case of the powers
Pl and
Ql. Removal of the powers
Pi and
Qi from vector
h(
x) entails a further reduction of
mz by 2 as either
n0 decreases by 1 when node
i is a zero-injection node in a real system, or
m decreases by 2 when
Pi and
Qi are measured. Note that in Method 2, the quadrature booster model is not considered. Thus, Equations (5) and (
7), with which 3 (
mz_QB) elements of the vector
h(
x) are related, are not taken into account. In effect:
where
mz_1 and
mz_2 are parameters
mz for Method 1 and Method 2, respectively.
In Method 2, the state vector is the same as for the classical state estimation (
nx_2 = 2
n − 1), that is
where
nx_1 and
nx_2 are parameters
nx for Method 1 and Method 2, respectively.
Measured-quantities vector h(x) differs from the vector (16) for the classical state estimation in that the powers PAC_i, QAC_i, PAC_l, and QAC_l are not present in it. This means that in Method 2, there are no rows in Jacobian matrix H(x) related to the powers PAC_i, QAC_i, PAC_l, and QAC_l. A number of columns in that matrix is the same as in the classical state estimation.
An algorithm for Method 2 assumes realization of the same steps as for Method 1 (see
Figure 4) and additionally calculation of the magnitudes and phase angles of voltages
and
. Vector
h(
x) and matrix
H(
x), which are used in the algorithm, are different for the considered methods.
In the case of Method 2, results of iterative estimation calculations do not include estimates of the magnitudes and phase angles of voltages
and
. Those voltages characterize the operational state of the quadrature booster. It should be noted, that they are calculated in iterative estimation calculations in the case of Method 1. The mentioned voltages can be calculated on the base of results of iterative estimation calculations of Method 2. For purposes of those calculations the following formulas can be used:
where:
i,
l, and
k are the numbers of nodes, shown in
Figure 5;
is an impedance of the series branch between nodes
l and
k;
is an admittance of the shunt branch at node
l; and
and
are a magnitude and a phase angle of node voltage
, respectively;