1. Introduction
The energy yield of floating photovoltaics (FPVs) is in the spotlight, as offshore photovoltaic (PV) installations present significant advantages over corresponding onshore ones (see [
1,
2]). These, among others, include the ample surface available for arrangements in farms, the nearshore/coastal regions and the open sea, including locations that are already licensed for offshore wind parks (in the area between wind turbines), as well as the potential of hybridization with offshore wind energy. The development of offshore FPV parks is particularly important for southern European regions, e.g., in the Mediterranean Sea, since solar radiation in southern latitudes is relatively high, nearly 150–200% greater than that of the Atlantic Sea Ocean, the North Sea and Baltic Sea regions [
3], while wind and wave potentials are comparatively low. Furthermore, offshore PV installations present increased efficiency due to the cooling effects of water and wind, which are triggered by the interaction of airflow with the solar panels [
4]. It is worth mentioning here that, according to a recent report from DNV GL, it is expected that offshore FPVs will reach maturity by 2030 (see also DNVGL-RP-0584-Edition 2021-03).
On the other hand, although several solar farms have been developed on closed water basins, such as lakes, reservoirs and dams, implementing installations in the open sea is a challenging task, as their interaction with several environmental factors is not yet fully understood [
5]. In the offshore and nearshore region, safety and viability require the design and construction of resilient FPV structures that can withstand the harsh marine environment. Regarding the deployment of floating structures of relatively large dimensions in nearshore and coastal areas, it is also expected that bathymetric variations will have significant effects on their responses under wave loads, which also affect the performance of the power output due to oscillatory motions of the structure and the panels arranged on the deck. Stability requirements, in conjunction with a lightweight structure with a center of gravity at a relatively increased height above the keel, led to the consideration of a twin hull structure with a more complicated response pattern and resonance characteristics. In this study, a hydrodynamic model is developed to predict the dynamic responses of a floating structure supporting photovoltaic panels on a deck while being subject to wave loads. For the treatment of complicated resonance phenomena, as well as the effects of finite and possibly variable bathymetry, which characterizes nearshore and coastal regions, a general model based on boundary element methods (BEM) is developed, which is capable of modeling the involved phenomena. The model is then systematically applied in selected examples to produce preliminary results, which are illustrative of the effect of dynamic motions on the energy efficiency of a floating unit.
The interaction of free surface gravity waves with floating bodies at intermediate depths in areas that are characterized by non-uniform seabed topographies is a mathematically interesting problem, which can be used to analyze a wide range of applications, such as the design and performance evaluation of ships and other floating structures operating in nearshore areas. Theoretical aspects of the problem of small-amplitude water waves propagating in a finite water depth and their interaction with floating and/or submerged bodies have been presented under various geometric assumptions by many authors [
6,
7,
8] regarding the existence of trapped modes in a channel with obstructions. Furthermore, shallow-water conditions are frequently encountered in marine applications. When floating structures or docks are moored in shallow-water areas, accurate predictions of the motions induced by the prevailing sea state are needed, not only for optimizing the mooring system, depending on the stability needs of each configuration, but also for ensuring that the under-keel clearance remains sufficient for the structure to avoid grounding in extreme (for the area under study) weather and sea conditions. In many applications, the water depth is assumed to be constant, which is practically valid in cases where there are small depth variations or the floating body’s dimensions are small compared to the bottom variation length. However, in applications involving the utilization of floating bodies in coastal waters, the variations of bathymetry may cause significant effects on the hydrodynamic behavior of ships and structures, especially concerning the wave-induced responses. Under the assumption of slowly varying bathymetry, mild-slope model have been developed for the analysis of wave-induced floating body motion [
9]. To treat environments that are characterized by steeper bathymetric variations, e.g., near the coast or the entrances of ports and harbors, extended models are required (see, e.g., Ohyama and Tsuchida [
10]).
In the present work, a novel method based on BEM is used for the hydrodynamic analysis of twin-hull floating structures with PV systems; the method is capable of treating the effects of varying bathymetry without any mild-slope assumptions. In particular, a low-order panel based on linear wave theory is developed and verified. Following the hybrid formulation by Yeung [
11], the present method utilizes the simplicity of Rankine sources, in conjunction with appropriate representations of the wavefield in the exterior semi-infinite domain, as presented by Nestegard and Sclavounos [
12] for 2D radiation problems in deep water and by Drimer and Agnon [
13] in the case of finite water depth. Τhe far field is modeled using complete (normal-mode) series expansions, which are derived using separation of variables in the two constant-depth half-strips separating the variable bathymetry region from the regions of wave incidence and wave transmission (see
Figure 1). Numerical results are presented concerning twin-hull floating bodies of simple geometry over uniform and sloping seabeds. With the aid of systematic comparisons, the effects of bottom slope on the hydrodynamic characteristics (hydrodynamic coefficients and responses) are presented and discussed. Finally, results are presented regarding the effect of wave-induced motions on floating PV performance, indicating significant variations in the performance index ranging from 0 to 15%, depending on the sea state.
2. Mathematical Formulation
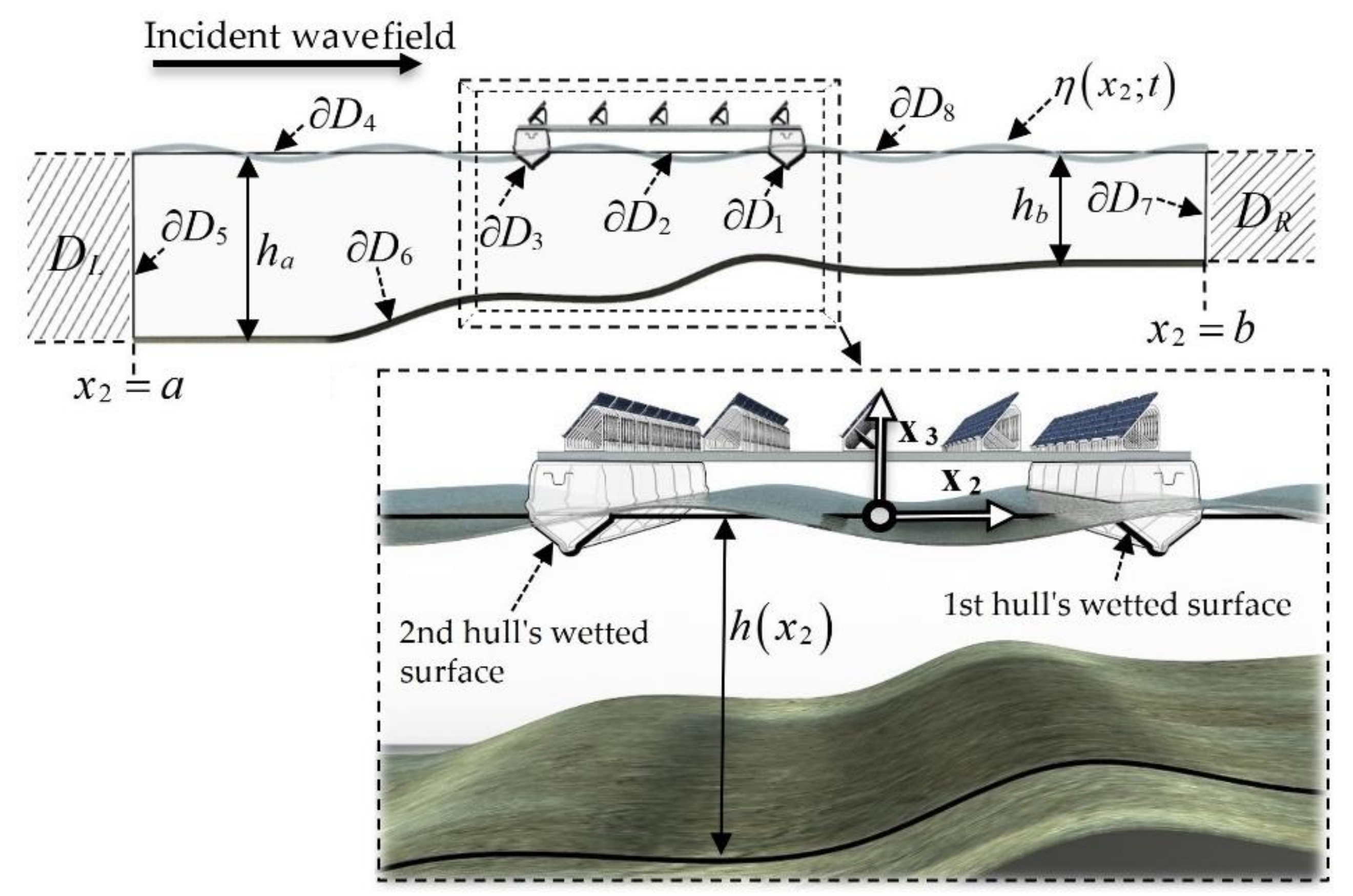
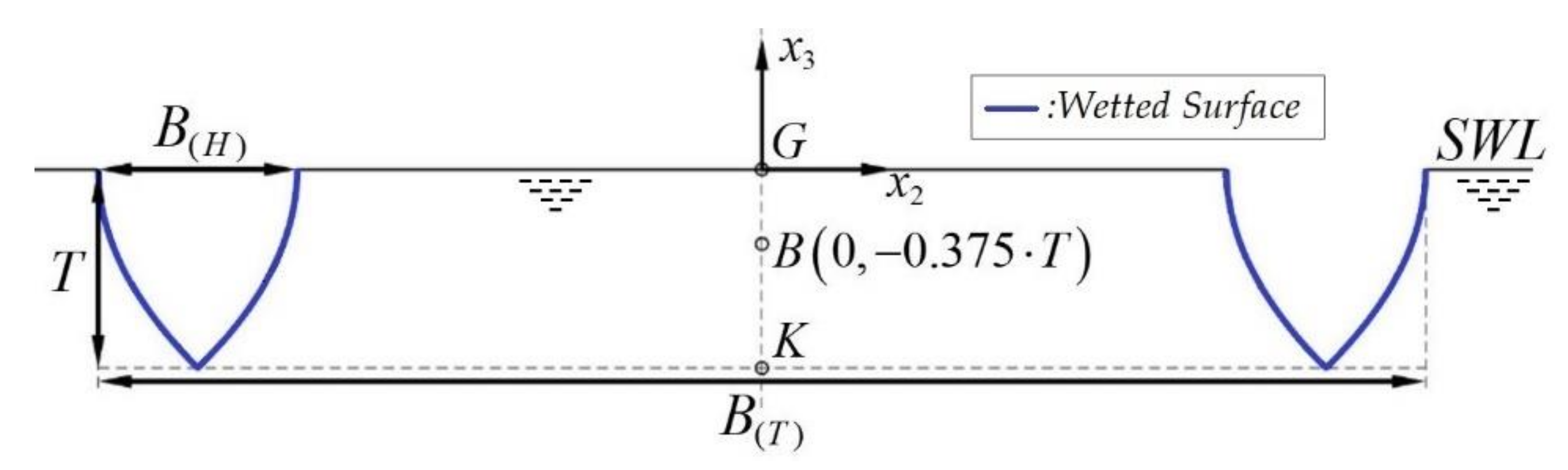
The 2D problem concerning the hydrodynamic behavior of a twin hull floating body of arbitrary cross-section in a coastal–marine environment is considered, as illustrated in
Figure 1. A Cartesian coordinate system
is introduced, with the origin placed at the mean water level, coinciding with the structure’s center of flotation, with the
-axis pointing upwards. The configuration is considered unchanged in the
-direction and, therefore, the analysis is limited to the
plane, modeling a two-dimensional cross-section.
The environment comprises a water layer bounded by the free surface at
and the rigid bottom at depth
. It is assumed that
exhibited a general variation, i.e., the corresponding bathymetry is defined by parallel, straight contours lying between two regions of constant but different water depths:
in the region of wave incidence and
in the region of transmission. The fluid is assumed to be homogeneous, inviscid and incompressible and its motion irrotational with a small width. The wavefield in the region is excited by a harmonic incident field, with propagation direction normal to the depth contours (along the
-axis). Without loss of generality, a left-incident wave field is assumed (see
Figure 1). Thus, in the context of linearized wave theory, the fluid motion is fully described by the 2D wave potential
, with the velocity field being equal to
Assuming that the free-surface elevation and the wave velocities are small, the potential function
satisfies the linearized wave equations (see, e.g., [
14,
15]). Under these assumptions, the wavefield is time-harmonic and its potential function can be represented by the time-independent (normalized) complex potential function
as:
where
is the incident wave height,
is the acceleration of gravity,
is the frequency parameter and
. The free surface elevation is obtained in terms of the wave potential at
as follows:
In addition to the physical boundaries (floating body, free surface, seabed), we further introduce two vertical interfaces on either side of the body, serving as incidence/radiation/transmission boundaries. Therefore, the boundary
of the two-dimensional domain
, occupied by the fluid, is decomposed into eight subsections
as illustrated in
Figure 1, so that
is enclosed by the curve
, with
and
being the right- and left-hand sides, respectively, of the twin-hull’s wetted surface. The sections of
numbered 2, 4 and 8 correspond to the water-free surface, while
is the impermeable seabed. Finally, the wave incidence occurs via
, which also serves, along with
as a radiation interface for the diffracted field due to the presence of the (fixed) body, as well as the radiation fields that develop due to the wave-induced body’s motions.
Apart from the non-uniform domain
containing the floating body, the total flow field is considered to be of infinite length and, therefore, also comprises the uniform semi-infinite subdomains
and
, where the depth is constant and equal to
and
, respectively. Hence, the function
is of the form:
The function
appearing in Equation (1) is the normalized potential in the frequency domain, which will hereafter be simply written as
. Using standard floating body hydrodynamic theory [
15,
16], the potential is decomposed as follows:
where
is the propagating field, with
being the incident field, which corresponds to the solution of the wave propagation problem across the non-uniform subdomain in the absence of the floating structure and
being the diffraction potential, which accounts for the presence of the body, fixed in its mean position. Moreover, the functions
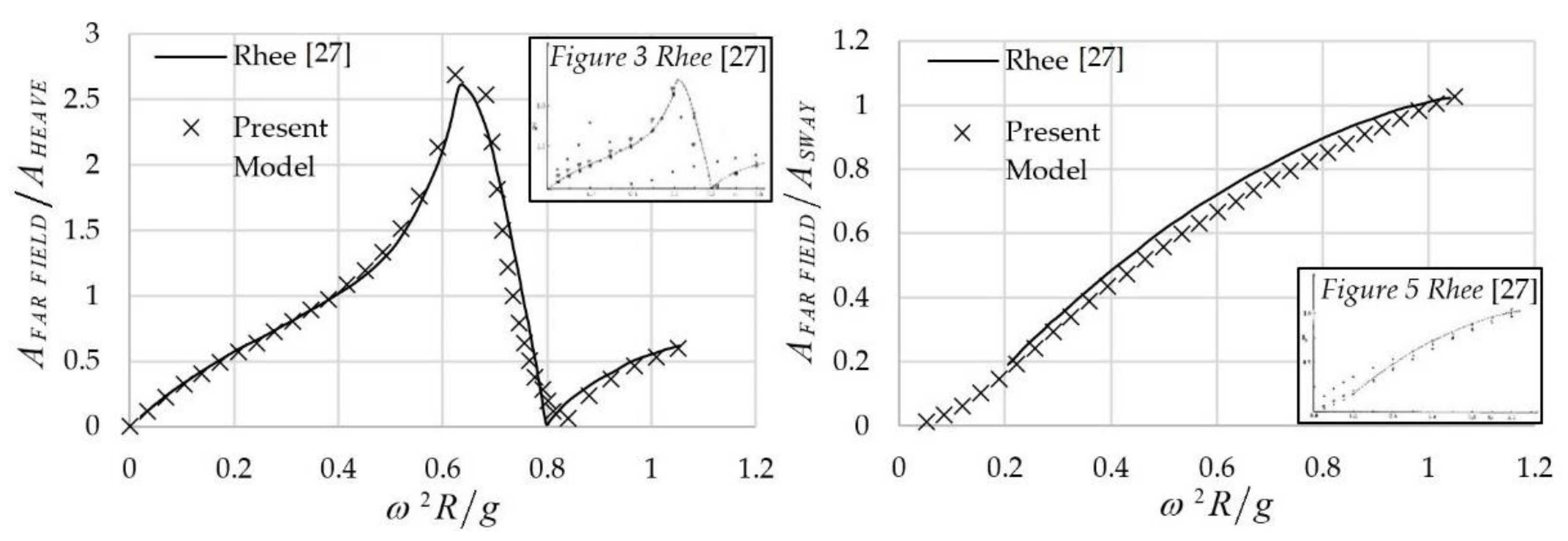
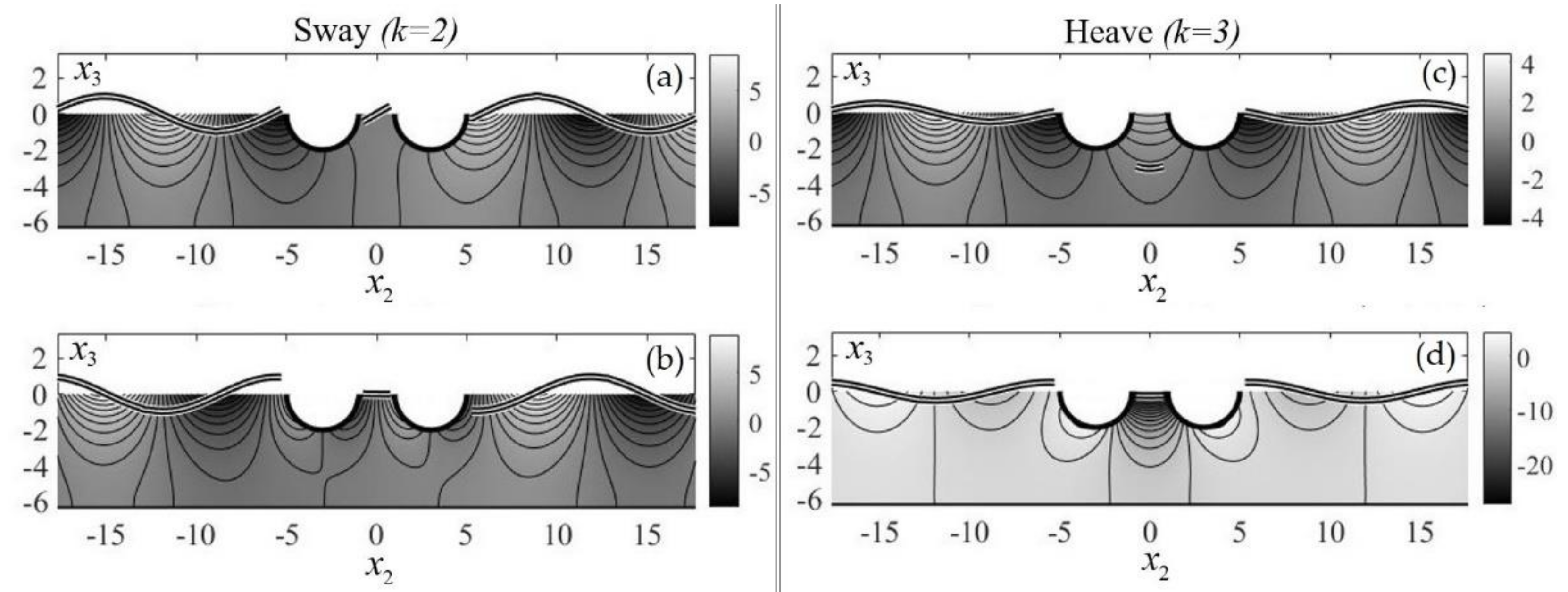
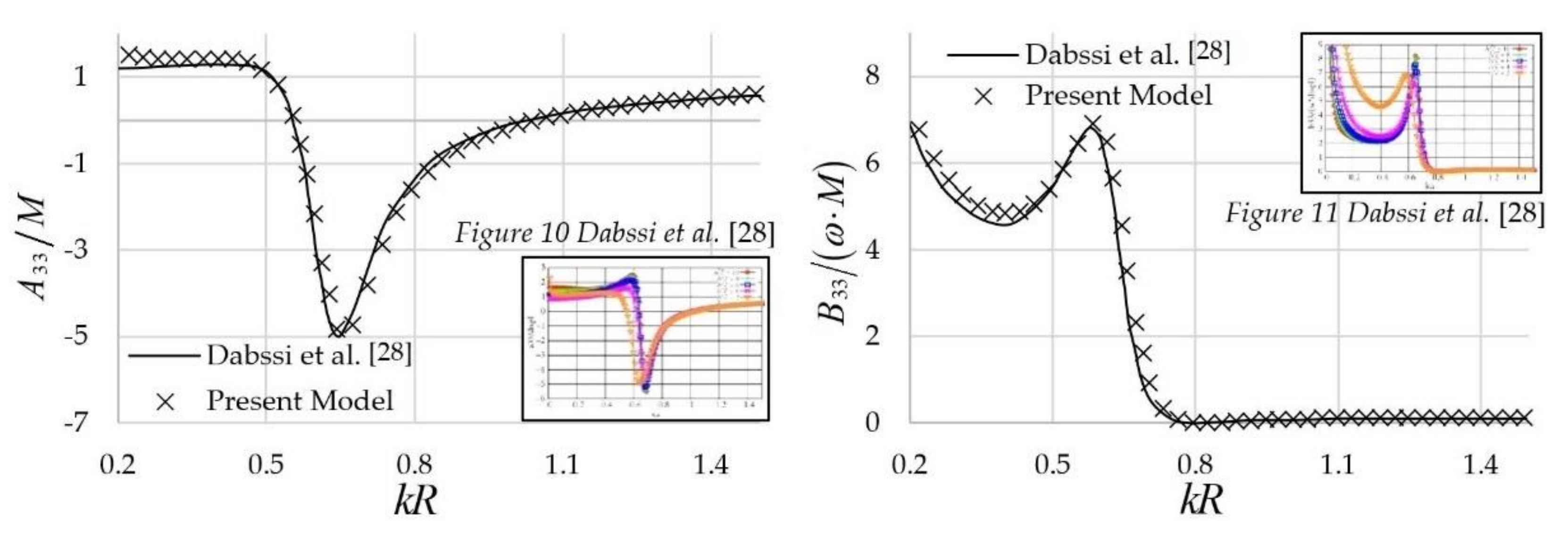
, denote the radiation potentials associated with the motion of the twin-hull structure, corresponding to its three degrees of freedom (DOF), i.e., the linear transverse motion (sway:
k = 2), the linear vertical motion (heave:
k = 3) and the rotation about the longitudinal (
) axis (roll:
k = 4). Finally,
, stand for the complex amplitudes of the corresponding wave-induced motions.
The sub-problems, whose solutions provide the potential functions
, in the variable bathymetry region, were formulated as radiation-type problems in the bounded subdomain
, with the aid of the following general representations of the wave potential
in the left- and right-side semi-infinite strips
and
, which are obtained using separation of variables (see, e.g., [
17]):
The first term
in the series Equations (5) is the propagating mode, while the remaining ones
are the evanescent modes with
being the corresponding coefficients. The first term of
is further separated into a unit-amplitude mode propagating toward
D, playing the role of the incident field, and the additional mode
, propagating toward
in the
-direction, which is the reflected field coming from the diffraction potential
In the above expansions, the functions
are defined as
and are obtained using separation of variables via the vertical Sturm–Liouville problem, to which Laplace’s equation reduces in the constant depth strips
and
. The corresponding eigenvalues
and
are respectively obtained as the real root and the imaginary roots of the dispersion relation:
where
denotes the acceleration due to gravity. The completeness of the expansions derives from the standard theory of regular eigenvalue problems (see, e.g., [
18]). Based on the above representations, the hydrodynamic problems concerning the propagating and radiation potentials
were formulated as radiation-type problems, satisfying the following systems of equations, boundary conditions and matching conditions for
:
The above boundary sections are also illustrated in
Figure 1. Moreover, in Equations (6a)–(6f),
denotes the unit normal vector to the boundary
, directed to its exterior. The boundary data
appearing on the right-hand side of Equation (6d) are defined by the components of the generalized normal vector on the wetted surface boundary section
:
,
and
, and constitute the (unit-amplitude) excitations of the system in Equation (6a)–(6f) for each
k.
is set to 0 so that the solution of the propagating field is obtained by treating the floating body as an impermeable, immobile solid boundary. Finally, the operators
and
are appropriate Dirichlet-to-Neumann (DtN) maps (see, e.g., [
19]), ensuring the complete matching of the fields
, on the vertical interfaces
and
, respectively. These operators are derived from Equations (5a)–(5c), exploiting the completeness properties of the vertical bases
. More details are provided in
Appendix A.
5. Effects of Floating Structure Response in Waves on Floating PV Performance
The energy efficiency of a floating photovoltaic (FPV) unit is based on several parameters, many of which are the result of the surrounding marine environment. Some of the factors that affect the energy efficiency of FPV are common with corresponding land-based units, with similar power output levels, while others are absent in land installations.
In open seas, there is generally a higher level of humidity than inland, as well as lower ambient temperatures. The decreased temperatures are a result of various factors, which among others, include [
29] the water’s transparency, which results in the incoming solar radiation being transmitted to inner layers of the medium rather than just the surface layer, as well as the fraction of incident irradiation that is naturally used for evaporation. Furthermore, the wind speed is usually higher due to long fetch distances compared to land. The above parameters can help to maintain a low operating temperature of the solar cells, which, in turn, leads to close-to-optimal performance of the solar panel. The latter’s efficiency decreases with increasing temperatures. More importantly, PV efficiency is strongly dependent on the angle of incidence (AOI) of solar irradiation, which, in offshore FPV installations, is directly affected by the dynamic wave-induced motions. In particular, the power output of photovoltaic cells is strongly affected by the angle of incidence (AOI) of solar irradiation and the plane of array (POA) irradiance, which is given by the following equation:
where
DNI, DHI and
RI are the direct, diffuse and reflected irradiance components on a tilted surface, respectively. To provide indicative results regarding the effect of wave-induced motions of the floating structure on the power output, we considered an offshore installation in the geographical sea area of the southern Aegean Sea. For the latter area, the optimized values for tilt and azimuth angles of the photovoltaic installations, respectively, are
and
using data extracted from the Sandia Module Database, which is provided by the PV_LIB toolbox (
https://pvpmc.sandia.gov/applications/pv_lib-toolbox/ (accessed on 12 August 2021)).
In this work, a preliminary assessment of a floating photovoltaic system’s energy efficiency is made for twin-hull structures, taking into account data regarding the dynamic motions of the floating unit carrying the panels, as derived by the hydrodynamic model presented earlier, while the interesting effects of temperature and humidity will be studied in future work. The linear motions, i.e., sway (k = 2) and heave (k = 3), are considered to have no important effect on the tilt angle of the panels and, therefore, the angle of incidence. Hence the effect of the unit’s mobility is limited to the angular oscillation i.e., the roll motion (k = 4) under excitation from the beam incident waves.
For this purpose, response data was simulated by assuming specific sea conditions. The latter are characterized by a frequency spectrum used to describe the incident waves. We considered the floating twin-hull structure of total breadth
examined in the previous section in constant water depth
The sea state is described by a Brettschneider spectrum model (see [
30], Chapter 2.3), as follows:
where
is the significant wave height,
is the peak frequency and
the corresponding peak period.
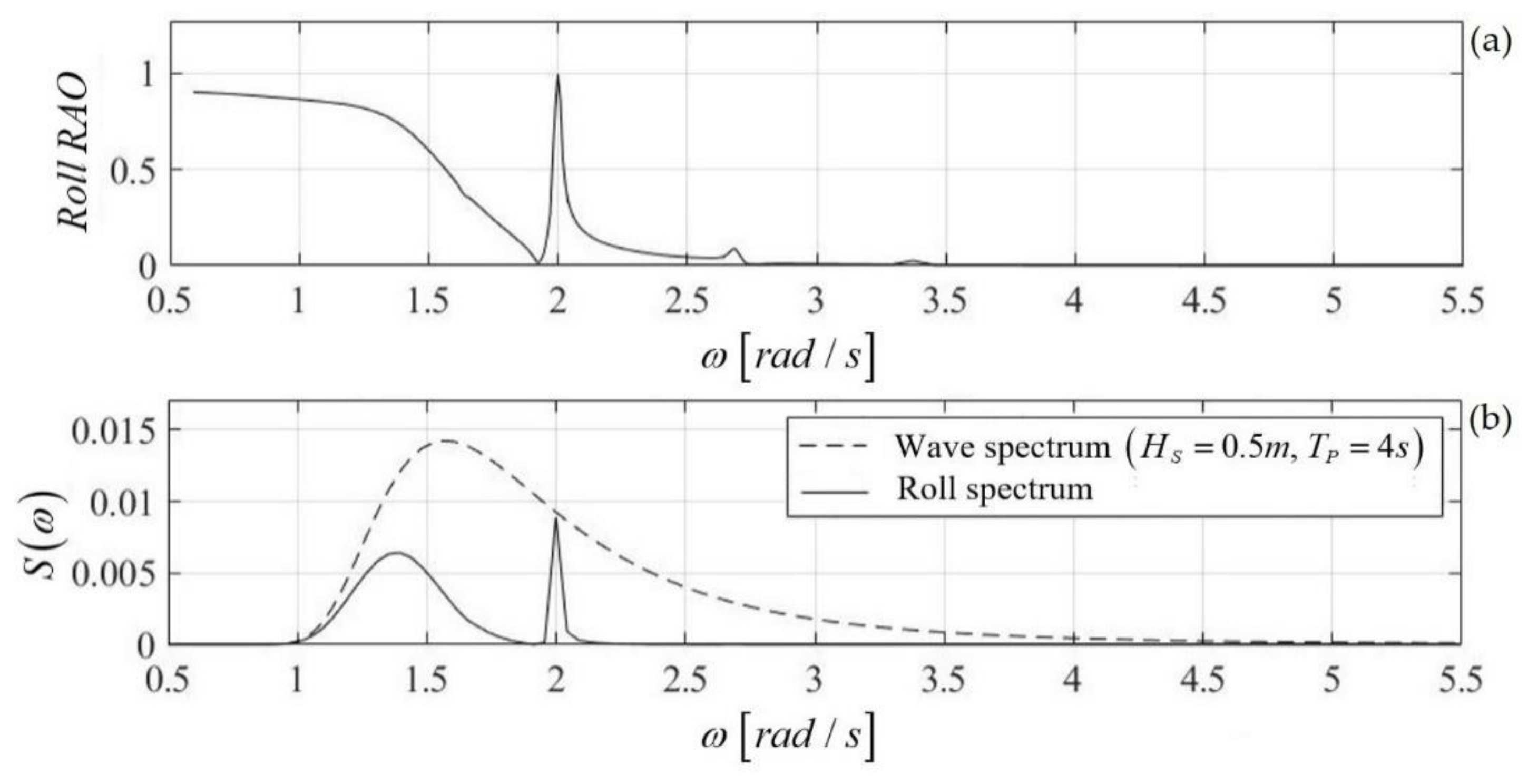
The roll responses calculated by the present model, as discussed in the previous section, were used to evaluate the fluctuations of the AOI and the effect on the power output performance of a PV system consisting of panels, with the aforementioned values of tilt (relative to the horizontal deck of the structure) and azimuth angles. Specifically, the roll spectrum was calculated using the RAO of the roll motion (see
Figure 7a) of the twin-hull structure using:
where the wavenumber
k is given by the dispersion relation of water waves for the water depth considered. Based on the calculated roll spectrum, time series of the roll motion
of the above floating twin-hull structure were simulated, for the considered configuration (structure and coastal environment) and incident waves, characterized by the parameters
using the random-phase model [
30], Chapter 8.2, (see also [
31]).
The results were normalized using the value corresponding to calm water (flat horizontal deck of the structure) in the same sea environment, which results in the following definition of the performance index:
where
and
for the geographical area and sea environment considered, respectively, and
is a representative value for the angle of incidence.
As an example, the numerical results concerning the calculated roll response of a floating twin-hull structure of breadth
at depth
with an incident wave spectrum (dashed line) and roll angle spectrum (solid line) of the structure in the case of incident waves of significant wave height
and peak period
are presented in
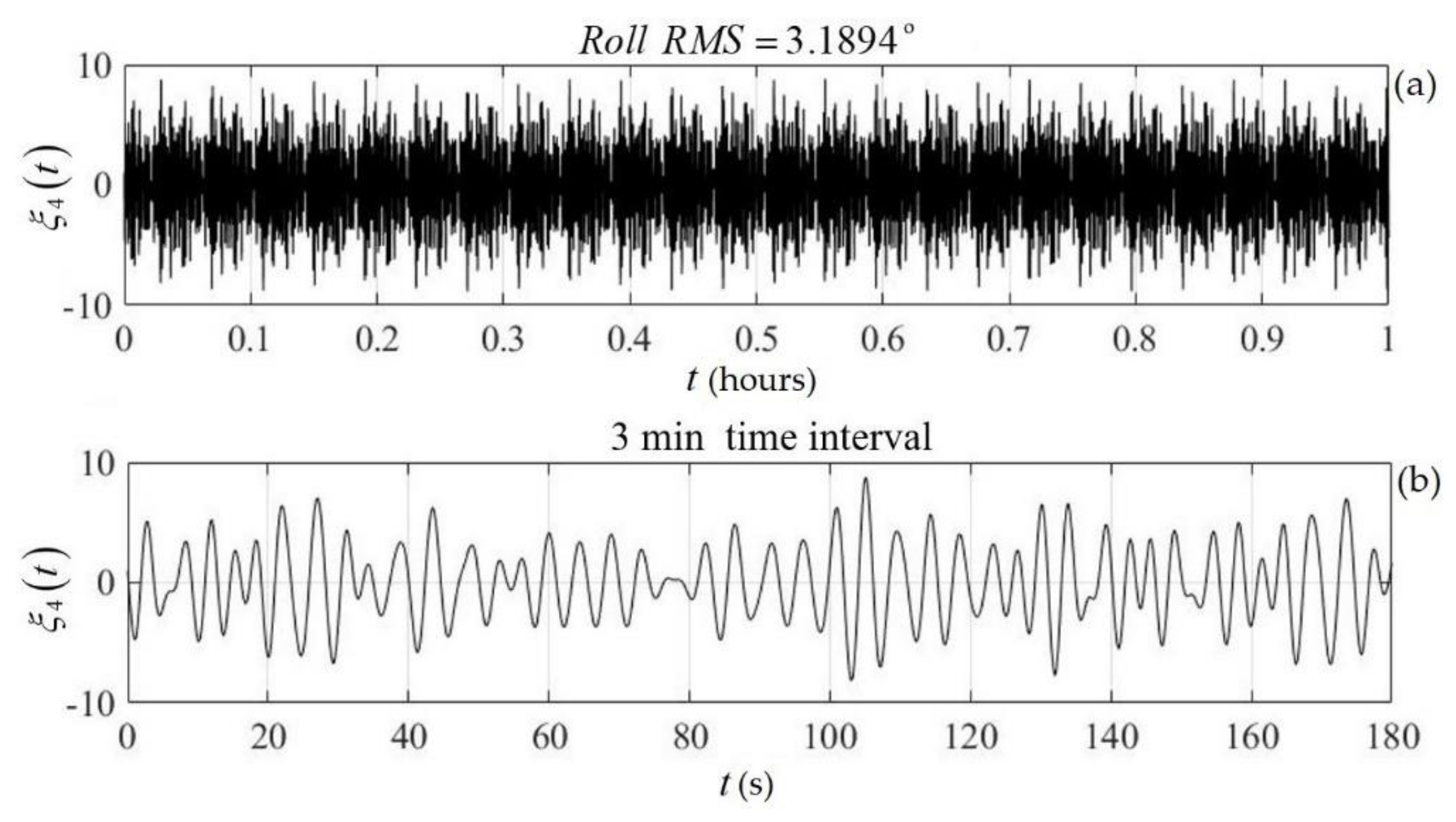
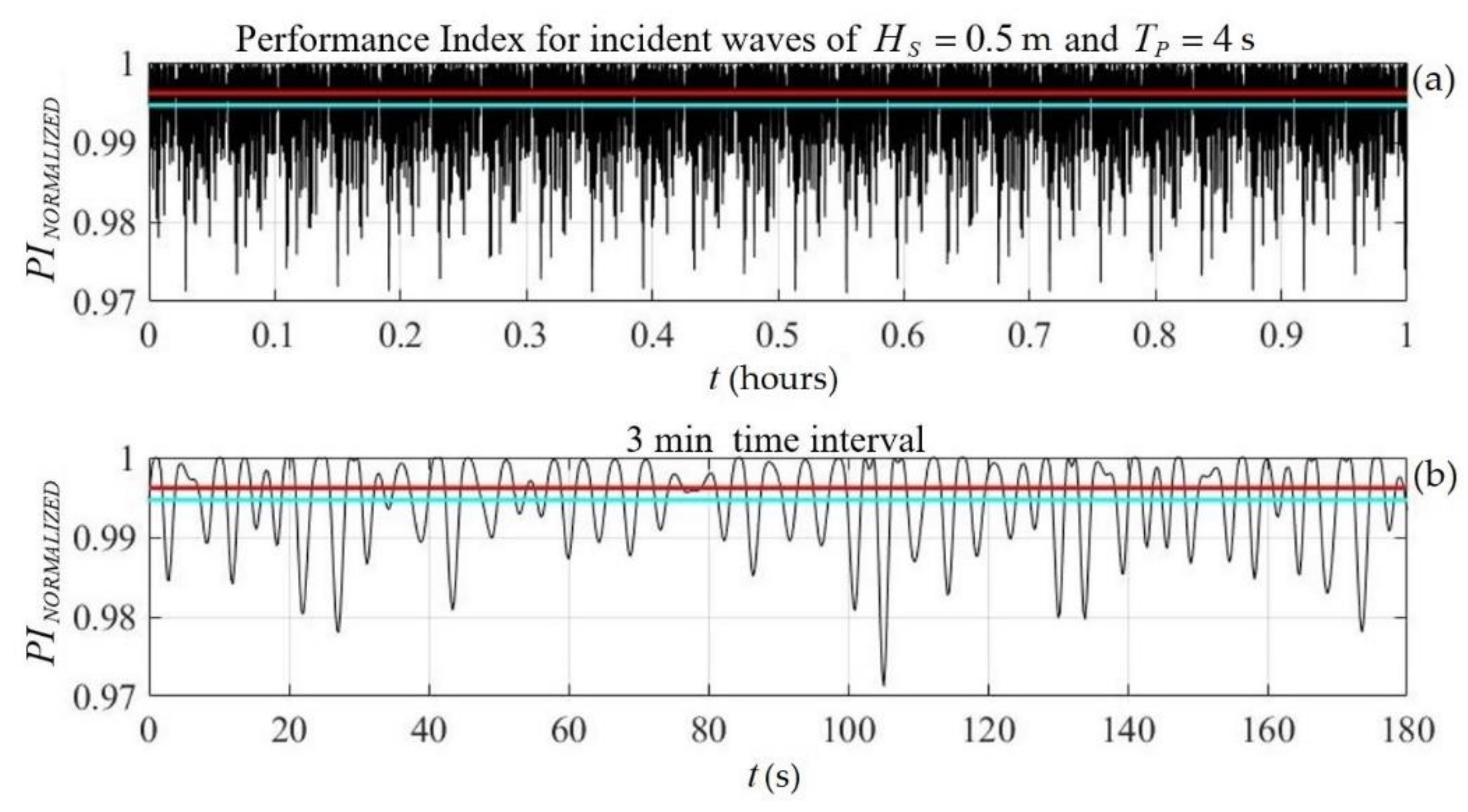
Figure 9. Based on the calculated roll spectrum, the simulated time series of the roll motion of the above floating twin-hull structure for the considered coastal environment and incident waves are shown in
Figure 10 for a time interval of 1 h. Furthermore, in the same figure, a representative small interval of 3 min was obtained using the random-phase model [
30,
31] for a sea state that was characterized by significant wave height
and peak period
, as generated by winds corresponding to the Beaufort scale levels
. In this case, indicative results concerning the effect of waves and roll responses of the structure on the performance index are shown in
Figure 11, as calculated by Equation (20) using a representative value of the mean angle of incidence
and omitting, as a first approximation, the effect of diffuse and reflected irradiance components
. The value of the performance index in calm water was
. In the considered case of incident waves, which were characterized by a very low energy content, the
value of the estimated performance index dropped to
. The latter’s mean value, as well as the corresponding calm-water value, are shown in
Figure 11 using cyan and red lines, respectively.