Forecasting and Assessment of the Energy Security Risk in Fuzzy Environment

Abstract

Energy security is of key importance for states and international organizations. An important issue in energy security is the assessment of current and future energy security methods. While the assessment of the current methods is relatively easy, since it is based on recent information, the assessment of the future methods is burdened with uncertainty and is therefore much more difficult. Therefore, the aim of the article is to develop a new approach for assessing current and future energy security issues based on a complex security index, supported by the computationally transparent fuzzy multi-criteria decision analysis (MCDA) method. The use of the fuzzy MCDA methods allows one to capture the uncertainty of assessments and forecasts, and the forecasts themselves were based on the Holt’s method; the international energy security risk index (IESRI) was used as the source of the data to generate the forecasts. The research compared two data sources for forecasts (IESRI categories and metrics) and two methods of forecast fuzzification. As a result, the forecasted assessments and rankings of energy security for the 2020–2030 period were obtained. On the basis of these forecasts, general trends shaping energy security were also indicated.

1. Introduction

On the one hand, energy policy is one of the most complex processes and challenges of the modern world [1]. On the other hand, energy security is a fundamental condition for sustainable development, which is a goal pursued by all countries in the world. Analyzing the situation, forecasting, and making decisions in this area is of interest to researchers who propose various measures and conduct numerous studies, striving to obtain reliable measurements and interpretable results. It is important since the obtained results can be used by decision-makers to make responsible decisions. The literature emphasizes the importance of methods of energy supply and related costs, as well as the important role of energy in economic development and the impact it has on the progress of individual countries, especially in the industrial sector [2]. It is recognized that an affordable and adequate energy supply plays a key role in economic development [3]. Energy is an important factor contributing to the achievement of sustainable development goals, since energy consumption is necessary for economic, environmental, and social reasons [4]. Therefore, energy security is of key importance for states, international organizations, and also for individual consumers [5]. It should be mentioned that the discussion on energy security has a long history, while papers containing scientific analyses in accordance with current research principles and standards were published only occasionally until recently [6,7,8]. However, in recent years, this issue has been noticed and has become one of the most important topics discussed today [9] since, according to many authors, energy affects every aspect of life (not only economic, but also social) [10].

An important aspect related to energy security is the assessment of its current and future status. Simple approaches can be used to assess the state of energy security, based, for example, on the technical analysis of the stability of the energy system or the economic analysis of energy imports. However, much more interesting, and at the same time methodologically justified, are complex approaches taking into account various technical, commercial, economic, environmental, etc. factors [1]. Such a complex assessment is more reliable when it is supported by an analysis of uncertainty and sensitivity [11]. In addition to assessing the current state of energy security, an important aspect that is often ignored in research is forecasting and analyzing future scenarios [12]. Forecasts allow one to react in advance to threats to energy security and support decision-making processes, limiting the occurrence of adverse effects [13]. It should be noted that both in the context of the current assessment and forecasting, it is important that energy security is measured using reliable methods that allow for an objective numerical assessment [14]. Therefore, multi-criteria decision analysis (MCDA) methods are used here, allowing for the construction of complex indexes based on a reliable and widely recognized methodology [15]. MCDA methods have been developed to deal with complex decision problems in which there are many, often conflicting, criteria and uncertainties [16]. They allow for dealing with such problems in a structured, transparent, and credible way. Moreover, MCDA methods are often used in ex-ante decision problems, where the decision maker or analyst is not able to fully determine all consequences of the decision [17] and thus also allow uncertainty to be analyzed. MCDA methods that deal well with uncertainties related to both input data and decision consequences are methods based on fuzzy set theory [18]. Unfortunately, many such methods are computationally very complicated, which means that they are treated by stakeholders as a ‘black box’. This undermines the confidence in the fuzzy MCDA methods and the credibility of the recommendations generated by these methods [19].

A research gap is visible here, consisting in the need for a complex assessment and forecasting of energy security with the use of an appropriate research methodology. The methodology used should allow for a systematic analysis of uncertainty. At the same time, it should be relatively uncomplicated in terms of calculations and give results easy to interpret. Therefore, the aim of this research and, at the same time, our methodological contribution, is to develop a new approach to assessing the current and future energy security based on a complex safety index, supported by the computationally transparent fuzzy MCDA method. The proposed approach will allow for forecasting future energy security based on the methodology derived from econometrics, management, and decision sciences. The practical aspect of the research is the implementation of the developed methodological approach and the determination of energy security forecasts for countries that are significant energy users in the world. Section 2 provides an overview of the literature on energy security and its measurement. Section 3 provides an extensive discussion of the methodological details of the proposed approach and research procedure. Section 4 presents the research results in the form of energy security forecasts and a discussion. The article ends with conclusions from the conducted research and an indication of further directions of work.

2. Literature Review

There are opinions in the literature that, for many years of dealing with the subject of energy, no generally accepted definition of energy security has been developed and that such action is extremely difficult to implement [20]. On the other hand, the term promoted by the International Energy Agency (IEA) is commonly cited, according to which energy security should be defined as the uninterrupted availability of energy sources at an affordable price [21]. At the same time, it has a long and short-term dimension. In the longer term, it concerns investments in energy supply in line with economic development and sustainable environmental needs, while in the short term it focuses on controlling supply and demand changes. With this approach to the issue of energy security, the associated uncertainty that many countries feel is the result of a lack of physical availability of energy sources or inaccessible prices.

The literature proposes three positions towards understanding the essence of energy security, namely the approach taking into account:

• Technical and technological parameters, i.e., technical stability and resistance of the energy system;
• Only the questions of whether and how much energy is imported by a given country (using the energy dependence index);
• Comprehensive approach to the discussed issues, including a number of variables (technical, market, economic, environmental, etc.) in order to assess and forecast energy security. An example of such a comprehensive approach is the international energy security risk index (IESRI), a composite aggregated measure based on 29 individual variables divided into eight groups. IESRI started to be used in research from 2012 as a new tool designed to facilitate a better understanding of global energy markets [1].

Azzuni and Breyer (2020) [14] believe that measuring energy security by means of appropriate methods is of great importance as it allows for an objective assessment using reliable numerical indicators. The authors presented methodological gaps in their work. In their conclusions, they pointed out that there is no single way to develop and increase energy security, but there are various alternatives and options. The literature on the subject indicates that it is difficult to measure energy security with a simple measure [8]. An example of a proposal is the use of MCDA methods, which will enable the combination of indicators into one index [15]. With Saisana et al. (2005), [11] indicates that such a complex measure is more reliable if the analysis of uncertainty, sensitivity, and robustness is also performed.

Gasser (2020) [12] pointed out that the interest in using energy security indicators has increased recently. He also indicated their usefulness for comparing countries in terms of energy. In his work, he presented the results of a detailed analysis of 63 quantitative indicators measuring the level of energy security of at least one country. In their conclusions, the author of the review indicated the lack of transparency, especially in areas such as selection of a set of indicators, standardization methods, weighting of indicators, and aggregation functions. He also noted weaknesses in data processing and multivariate analysis. According to Gasser [12], only a few studies provide analyses of uncertainty, sensitivity, or robustness, which may increase confidence in the final results. Additionally, the author noted that in most studies, indexes are constructed on the basis of historical data. Few provide forecasts or scenario analyses which are tools to show future trends that can support policymakers in making the right decisions about future energy policy.

Podbregar et al. (2020) [1] emphasize that the usual methodological approach (i.e., the selection of indicators to measure energy security, cannot be used). According to the authors, the collection of the data used and its subsequent processing takes place using a differentiated approach, which affects the correct analysis of energy security, which is associated with a high degree of risk, uncertainty, and ambiguity. The literature discusses and proposes many tools for assessing the level of energy security, including Kanchana and Unesaki (2014) [22]; Lu et al. (2014) [23]; and Phdungsilp (2015) [24]. Noteworthy are the studies by Azzuni and Breyer (2017) [25], continued in 2020 [14], who developed a 15-dimensional analysis of energy security which included: availability, diversity, cost, technology and efficiency, location, time frame, resilience, environment, health, culture, literacy, employment, politics, military, and cyber security. The authors emphasized that this is one of the most comprehensive and detailed approaches. They also noted that there is a need to develop an appropriate tool to quantify the level of energy security that will support appropriate policy in this area and the need for a holistic but sufficiently detailed approach for individual countries in a global context. In 2020, Azzuni and Breyer [14] proposed an energy security assessment using an indicator covering the sustainable development of the energy system. This index is built on 15 dimensions and parameters discussed in the publication from 2017 [25], and according to the authors, the newly introduced energy security index completes the existing research gaps in energy issues.

The literature on the subject shows methodological diversity, the results of interesting research and the use of interesting measures used to assess the level of energy security. An example is the risky external energy supply (REES) index used by Le Coq et al. (2009) [26] to assess the security of the EU’s external energy supply (oil, natural gas, and coal), whereas Delgado (2011) [27] proposed the socioeconomic energy risk index, and Munoza et al. (2015) [28] used the geopolitical energy supply risk index (GESRI) in their research to quantify geopolitical energy risk. The ordered weighted average for the EU countries was the methodological basis for the complex indicators of energy supply security, which was proposed by Badea et al. (2011) [29]. Another proposal for measuring energy security is an indicator constructed with the use of the five most common dimensions of this issue, developed by Erahman et al. (2016) [30]. The proposal to use the proprietary index of energy security covering the environment and social aspects in EU countries was proposed by Radovanovic et al. (2017) [31]. However, Augutis et al. (2020) [32] stated that this proposal does not provide any threshold values and the results are difficult to interpret, which undermines the information credibility in terms of energy security of the proposed measure.

The article by Chernyak et al. (2018) [33] containing analyses and forecasts of the energy security risk index for eleven European countries in the period between 1992 and 2016 is noteworthy. Taking into account various approaches to defining energy security discussed in the literature, the authors proposed a regressive model for assessing the energy security risk index, which takes into account the levels of economic, technical and technological, environmental, social, and resource components. Earlier, they classified the countries under study into three groups according to IESRI, and in their final research they focused on calculating the forecast of the energy security risk index based on data from 1992 to 2014. According to the authors, this made it possible to learn about the shaping of the energy market in the near future, especially for Ukraine, which needs to develop a new energy security strategy.

Li et al. (2019) [34] believe that among the works published recently, it is worth paying a lot of attention to discussing the current situation, forecasts and proposed decisions in the field of energy security. Interesting considerations on energy demand, its supply and import as well as costs, energy security, CO2 emissions in connection with the state and environmental development of Pakistan were presented by Lin and Raz (2020) [35]. The authors estimated eleven indicators of energy security for long-term energy supply using the MARKAL framework and obtained proposals for solutions to improve the energy security of their country. Augutis et al. (2020) [32] presented a study on the energy security of the small Baltic countries (Estonia, Latvia, and Lithuania), which is essential for ensuring energy independence and is a driving force for economic development. In their work, they presented the research results obtained on the basis of a system of indicators, which took into account the technical, economic, geopolitical, and socio-political aspects of energy security. The main goal of the work of Podbregar et al. (2020) [1] was an analysis of the methodological environment of the IESRI. In the presented study, the authors used stepwise regression, principal component analysis, and Promax oblique rotation. Critical evaluation of the Index suggested design changes to it and the removal of variables that do not contribute to its precision.

Table 1. Studies that measured countries’ energy security (ES) and risk using various methods and energy indices.

Research Objective	Research Subject	Applied Index/Methodology	No. of Indicators	No. of Countries	Ref.
Analysis of the model settings of IESRI	25 countries over 26 years	International ES Risk Index	29	25	[1]
ES index that is comprehensive on a global scale	All countries in the world	ES Index *	78	229	[14]
Assessment of the security of energy supply	Nine ASEAN member states	ES using indicator-cased analysis	35	9	[22]
Future ES assessment in the three energy scenarios	Thailand	ES indicators to track the impact of changes in the energy system	9	1	[24]
Assessment of the security of energy supply	EU member states	REES—Risky External Energy Supply index	7	24	[26]
Estimation of the geopolitical risk of energy supplies	122 countries in the world	Geopolitical Energy Supply Risk Index	47	122	[28]
Applying family of complex indicators to assess threats to ES	EU member states	Ordered Weighted Averaging method	8	27	[29]
Assessment of the state of ES	Indonesia and 70 other countries	ES Index *	14	71	[30]
Defining a new ES index with long-term stability	EU member states	ES Index *	6	28	[31]
Analysis of the implementation of the ES level over time	Baltic countries	ES Level	67	3	[32]
ES risk index analysis and forecasting	11 European countries	International ES Risk Index	29	11	[33]
Universal, multidimensional index system and comparing ES systems of different countries	19 G20 countries	ES Index *	14	19	[34]
Estimation of ES indicators for long-term energy supply	Pakistan	MARKAL model for ES	11	1	[35]

* Different indexes with the same name.

includes studies that measured countries’ energy security and risk using various methods and energy indices. In turn,

Table 2. Other research in the field of energy security (ES).

Research Objective	Research Subject	Applied Methods or Techniques	Main Conclusions	Ref.
Review of ES indicators, among others, in terms of scope and geographic coverage	63 indicators quantifying the level of ES of countries	Multivariate analysis, normalization, weighting and aggregation of indicators and assessment of uncertainty, sensitivity and resilience	The results show a significant lack of transparency, especially with regard to the selection of the set of indicators, the standardization method, the indicator weighting scheme and the aggregation function	[12]
Identify and classify the most commonly used parameters and associated weights to make ES decisions	10 Swedish energy-intensive industrial companies	Combination of a structured questionnaire and interview, analysis of surveys using the Likert scale	While the potential is huge, energy management programs are not fully implemented and adopted by industries	[20]
The assessment of ES (especially the security of oil supplies)	China	A proprietary network model based on ecological analysis	The security of crude oil supplies in China has increased. North and South America contributed the most	[23]

includes other interesting research in the field of energy security.

The discussed studies indicate the importance of energy policy and energy security. They propose a complex approach to energy security and risk assessment, while signaling that it is important to properly capture uncertainty, sensitivity, and robustness in such analyses. Additionally, great attention should be paid to forecasts and scenarios relating to the future. A research gap is visible here, indicated, among others, by Gasser [12], related to paying too little attention to the analysis of the future. Therefore, in this study, we propose a forecasting framework for energy security assessment. It forecasts future energy security using the Holt’s method. As discussed above, our framework takes into account the uncertainty of forecasts based on fuzzy set theory, and at the same time provides a comprehensive safety assessment through the use of the complex IESRI index and the MCDA methodology.

3. Materials and Methods

The methodological approach proposed in the article is based on four foundations: data available in the International Index of Energy Security Risk report [36], Holt’s forecasting method [37], fuzzy set theory [38], and the fuzzy weighted sum method (FWSM) [39].

3.1. International Index of Energy Security Risk

The empirical material used in the research came from a report [36] on the IESRI. It is a tool designed to better understand global energy markets. The report contains information on the trends in the field of threats to energy security and the energy market in the period from 1980 to 2018. The published lists concerned 25 countries that make up the group of significant energy users: Australia, Brazil, Canada, China, Denmark, France, Germany, India, Indonesia, Italy, Japan, Mexico, the Netherlands, New Zealand, Norway, Poland, Russian Federation, South Africa, South Korea, Spain, United States, Thailand, Turkey, Ukraine, and Great Britain.

IESRI is a complex indicator that measures threats to energy security in relation to the base average of countries belonging to the Organization for Economic Cooperation and Development (OECD). The primary source material for the index is the U.S. Energy Information Administration’s database of international energy statistics, which is compiled from hundreds of other documents and data. Key information comes from, among others, the World Bank, IEA, British Petroleum or OECD. These include, for example: energy prices, transport and energy generation, and the use of refineries. Selected information on energy security has been concentrated in eight categories: (1) Global Fuel, (2) Fuel Import, (3) Energy Expenditure, (4) Price & Market Volatility, (5) Energy Use Intensity, (6) Electric Power Sector, (7) Transportation Sector, (8) Environmental. They represent and balance some key and often competing aspects of energy security. Using these categories as guidance, 29 individual metrics were developed covering a wide range of energy sources, energy end-use, generation capacity, operations and emissions. The individual metrics and categories along with the assigned values of the weighting factors are presented in

Table 3. Metrics Used to Create International Index of Energy Security Risk.

Category	Metric	Weight [%]
Global Fuel Metrics	Security of World Oil Reserves	2
	Security of World Oil Production	3
	Security of World Natural Gas Reserves	2
	Security of World Natural Gas Production	3
	Security of World Coal Reserves	2
	Security of World Coal Production	2
Fuel Import Metrics	Petroleum Import Exposure	3
	Natural Gas Import Exposure	3
	Coal Import Exposure	2
	Total Energy Import Exposure	4
	Fossil Fuel Import Expenditures per GDP	5
Energy Expenditure Metrics	Energy Expenditure Intensity	4
	Energy Expenditures per Capita	3
	Retail Electricity Prices	6
	Crude Oil Prices	7
Price & Market Volatility Metrics	Crude Oil Price Volatility	5
	Energy Expenditure Volatility	4
	World Oil Refinery Utilization	2
	GDP per Capita	4
Energy Use Intensity Metrics	Energy Consumption per Capita	4
	Energy Intensity	7
	Petroleum Intensity	3
Electric Power Sector Metrics	Electricity Diversity	5
	Non-CO2 Emitting Share of Electricity Generation	2
Transportation Sector Metrics	Transportation Energy per Capita	3
	Transportation Energy Intensity	4
Environmental Metrics	CO2 Emissions Trend	2
	Energy-Related Carbon Dioxide Emissions per Capita	2
	Energy-Related Carbon Dioxide Emissions Intensity	2

[36].

Due to the different measurement units that accompany the variables that take part in the index construction, they were transformed into a comparable form. In order for the indicator to provide information on both changes in energy security risk in a given country and changes in risk compared to other countries over time, an international benchmark has been created. A complete description of the methodology, IESRI values obtained for individual countries participating in the study, and the ranking obtained on this basis were published in the International Index of Energy Security Risk report [36].

It should be noted that, in practice, IESRI is a MCDA model. Metrics correspond to criteria, categories correspond to groups of criteria, individual countries and the OECD group are decision alternatives, and the calculation procedure used in IESRI is a practical implementation of the weighted sum method (WSM). In turn, the performances of alternatives are the values of the metrics for individual countries.

3.2. Holt’s Forecasting Method

The two-parameter Holt’s model is the exponential smoothing method [37], which is used when significant change in the development tendency of the forecast variable is found [40]. This model belongs to the group of adaptive forecasting methods and is used when there is a time series in which there is a distinct systematic component in the form of a linear trend with random fluctuations.

Due to the popularity of the Holt’s method, a significant number of its applications in various fields have been reported in the literature. Among the recent publications, the work of Poonia and Azad (2020) [41] on short-term COVID-19 forecasts for 28 Indian states and five union territories deserves attention. Martinez et al. (2020) [42] were also interested in the topic and applied the Holt’s model to predict daily reported COVID-19 cases in Brazil and three Brazilian states. Another application of the mentioned procedure for forecasting electricity consumption in Malaysia is presented in the work of Ahmad and Nor (2020) [43]. On the other hand, the research by Soebandrija et al. (2020) [44] focused on forecasting the demand for laboratory equipment, and the work of Huard et al. (2020) [45] includes sales forecasts based on Cdiscount e-commerce data. There is also great interest in the Holt–Winters model, which is one of the adaptive models of forecasting variables with seasonal fluctuations. The work of Trull et al. (2020) [46] discusses electricity demand forecasts in Spain. On the other hand, the article by Almazrouee (2020) [47] presents a comparison of the Prophet model with the Holt-Winters model in order to assess the long-term forecasting of electrical loads in Kuwait.

The Holt’s method involves smoothing using a moving average of the time series. Thanks to this action, we obtain information about the properties of the series that can be used to calculate the forecast. Holt’s method for a time series without seasonal fluctuations can be written by the Formulas (1) and (2):

$$\{\begin{array}{r}\hfill {\widehat{L}}_t=y_t \\ \hfill {\widehat{L}}_t=\alpha y_t+\left(1-\alpha \right)\left({\widehat{L}}_{t-1}+{\widehat{T}}_{t-1}\right) \end{array} \begin{array}{c} if t=1\\ if t>1\end{array}$$

(1)

$$\{\begin{array}{r}\hfill {\widehat{T}}_t=y_t-y_{t-1}\\ \hfill {\widehat{T}}_t=\beta ({\widehat{L}}_t-{\widehat{L}}_{t-1})+\left(1-\beta \right){\widehat{T}}_{t-1}\end{array}\begin{array}{c} if t=1\\ if t>1\end{array}$$

(2)

where:

${\widehat{L}}_t$—the level is a smoothed estimate of the value of the data at the end of the t period (t = 0,1, …, n),

${\widehat{T}}_t$—the trend is a smoothed estimate of the average growth at the end of the t period,

$\alpha , \beta$—smoothing parameters, $\alpha , \beta \in \left[0, 1\right]$.

Finding the optimal values of α and β is looking for a combination of these parameters that minimizes the sum of squared prediction errors one step ahead, according to the Formula (3) [48]:

$${{\displaystyle \sum }}_{t=2}^n{\left(y_t-{\widehat{y}}_t\right)}^2, where {\widehat{y}}_{t+1}={\widehat{L}}_t+{\widehat{T}}_t$$

(3)

In Formula (1), the starting point is to take the corresponding actual value as the evaluation of the trend value in the first period. The Holt’s method takes into account the dependence (2) of the increase in the assessments of the trend value in the t period on the change (increase) in the assessments of the trend value in the previous period, i.e., t−1. The β parameter expresses the effect of the previous increment. The force is greater as β approaches zero. Thus, the forecast can be written as the Formula (4):

$$y_h^{*}={\widehat{y}}_n+h{\widehat{T}}_n$$

(4)

where:

${\widehat{y}}_n$—the last (latest) evaluation of the trend value,

h—forecast horizon [37].

Expired forecasts can be compared with the actual values of the time series. The obtained differences are errors of expired forecasts provided by the model for the adopted parameters α and β. The linear mean of the expired forecast errors is taken as a general measure of the quality of the Holt model, according to the Formula (5):

$$J_1=\frac{1}{n-1}{{\displaystyle \sum }}_{t=2}^n\left|y_t-{\widehat{y}}_t\right|$$

(5)

3.3. Fuzzy Set Theory and Fuzzy Weighted Sum Method

The fuzzy set theory was developed by Zadeh [38], and one of its practical implementations are trapezoidal fuzzy numbers (TFNs) [49,50]. The advantages of TFNs, compared to more complex implementations, are: ease of use, ease of interpretation [51], computational efficiency and easier data acquisition [52]. It is believed that the trapezoidal approximation is a reasonable compromise between the tendency to lose too much information and the tendency to introduce too complicated forms of approximation [52]. TFN $\tilde{a}=\left(a_1,a_2,a_3,a_4\right)$ is described by the Formula (6) [53]:

$$\tilde{a}\left(x\right)=\{\begin{array}{r}\hfill \begin{array}{c}0 if x\le a_1\\ \frac{x-a_1}{a_2-a_1} if a_1\le x\le a_2\end{array}\\ \hfill 1 if a_2\le x\le a_3\\ \hfill \begin{array}{c}\frac{a_4-x}{a_4-a_3} if a_3\le x\le a_4\\ 0 if x\ge a_4\end{array}\end{array}$$

(6)

with $a_1\le a_2\le a_3\le a_4.$ The basic mathematical operations performed on TFNs and used in the developed research procedure are adding two TFNs $\tilde{a},\tilde{b}$ and multiplying TFN by the crisp number $r$, according to the Formulas (7) and (8) [54]:

$$\tilde{a}\oplus \tilde{b}=\left(a_1,a_2,a_3,a_4\right)\oplus \left(b_1,b_2,b_3,b_4\right)=\left(a_1+b_1,a_2+b_2,a_3+b_3,a_4+b_4\right)$$

(7)

$$\tilde{a}\otimes \mathrm{r}=\left(a_1,a_2,a_3,a_4\right)\otimes \mathrm{r}=\left(a_1\times \mathrm{r},a_2\times \mathrm{r},a_3\times \mathrm{r},a_4\times \mathrm{r}\right)$$

(8)

Fuzzy numbers can be generated from the set of crisp numbers. This process is called fuzzification [55]. In the fuzzification process, TFN elements can be constructed on the basis of at least two approaches, which we have defined as: (1) the population standard deviation approach [13], and (2) the half distance approach between max./min. and the mean [56]. In both approaches, the $a_1,a_2,a_3,a_4$ values of TFN are generated from the formulas shown in

Table 4. Mathematical details of the two approaches to fuzzification.

Population Standard Deviation Approach	Half Distance Approach between Min./Max. and the Mean
$a_1=\underset{i=1\dots k}{\min }{y}_i^{*}$	$a_1=\underset{i=1\dots k}{\min }{y}_i^{*}$
$a_2=\overline{M}-\sigma$	$a_2=a_1+\frac{\overline{M}-a_1}{2}$
$a_3=\overline{M}+\sigma$	$a_3=a_4-\frac{a_4-\overline{M}}{2}$
$a_4=\underset{i=1\dots \mathrm{k}}{\max }{y}_i^{*}$	$a_4=\underset{i=1\dots \mathrm{k}}{\max }{y}_i^{*}$
$\overline{M}=\frac{{{\displaystyle \sum }}_{i=1}^k{y}_i^{*}}{k}$	$\overline{M}=\frac{{{\displaystyle \sum }}_{i=1}^k{y}_i^{*}}{k}$
$\sigma =\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^k{\left(y_i^{*}-\overline{M}\right)}^2}{k}}$

, where $y_i^{*}$ is the i-th sample in the form of crisp number, and k is the number of samples.

In the approach based on population standard deviation, in extreme cases, and in particular when $a_1=0$, the variable $a_2$ may become negative. In that case, the negative value should be replaced by assigning $a_2=0$. Based on the above-mentioned elements of the fuzzy set theory, the FWSM was implemented, which in practice is a fuzzy extension of the MCDA model used in IESRI.

WSM in its classic version [57] is also called the weighted scoring method or simple additive weighting (SAW) method [58]. Although WSM defines the data normalization procedure [59], data normalization is already implemented in IESRI and all data is provided in a normalized form [36]. Therefore, in our approach, we decided to use FWSM without a built-in standardization procedure. Thanks to this, we avoided additional scaling of the data, and as a result, the obtained numerical results of forecasts are fully consistent with the scale used in IESRI. Consequently, the current IESRI results (2018) can be compared with the forecasts obtained in the study. The use of other MCDA methods, such as AHP [60] or PROMETHEE, would not allow direct comparison of the status quo with the forecast values, as the results would be expressed on scales other than the scale used in IESRI.

FWSM, as with other MCDA methods, allows one to consider a discrete decision problem that includes a set of decision alternatives $A=\left\{\tilde{a},\tilde{b},\dots ,\tilde{m}\right\}$. Each alternative is considered in terms of n criteria belonging to the set $C=\left\{c_1,c_2,\dots ,c_n\right\}$, and the criteria are assigned weights $W=\left\{w_1,w_2,\dots ,w_n\right\}$, where ${\displaystyle \sum }_{i=1}^n{w}_i=1$ [61]. FWSM calculates the sum of the products of the criteria weights and the performance of alternatives for each criterion, according to the Formula (9) [62]:

$$\widetilde{V\left(a\right)}={\displaystyle \sum }_{i=1}^n{c}_i\left(\tilde{a}\right)\otimes w_i$$

(9)

Then, the obtained values are defuzzified using the Formula (10) [39,62]:

$$Df\left(\widetilde{V\left(a\right)}\right)=\frac{V{\left(a\right)}_1+V{\left(a\right)}_2+V{\left(a\right)}_3+V{\left(a\right)}_4}{4}$$

(10)

In our FWSM implementation, the alternatives are ranked from minimum to maximum, so the better alternative has a lower $Df\left(\tilde{V}\right)$.

3.4. Research Procedure

The data available in the 2020 edition of the International Index of Energy Security Risk report [36] were obtained for the research. The data included 29 metrics, grouped into 8 categories. The metrics covered five-year periods from 1980 to 2015, and their values were given for twenty-five countries and for the OECD group in total. The IERSI report was also used to derive the weights of individual metrics and categories. It should be clarified here that the use of five-year periods caused that the most recent data (i.e., data from 2016, 2017, and 2018 were ignored). The use of these data would disrupt the five-year trend due to the non-cyclical nature of the time series. In other words, the latest trends would be determined in the one-year time frame, not in the five-year frame, disturbing the dynamics of changes in the time series. As a result, this would lead to the incorrect behavior of the forecasting model.

Based on data from 1980 to 2015, Holt’s forecast models for each country and OECD group were built. These models made it possible to determine the projected values of individual metrics and categories in 2020, 2025, and 2030 (see Formulas (1)–(4)). While the forecast for 2020 seems to be overdue already, it should be noted that research data for this year are not yet available, as the IESRI report for 2020 will not be available until 2022. It should be indicated that for the forecasts for 2020–2030, the forecast horizon value was h = 1, 2, 3. Moreover, it should be clarified that in the case of a downtrend, in some cases the Holt’s method generated negative values. Since the IESRI values are ≥0, negative values were converted to 0. For metrics, these were 14 negative forecasts for 2020, 51 forecasts for 2025 and 63 forecasts for 2030 (see Tables S2 and S3 in Supplementary Materials). In turn, in the case of the category, these were 2 forecasts for 2020, 3 forecasts for 2025 and 5 forecasts for 2030 (see Tables S4 and S5 in Supplementary Materials).

Then, based on the forecasted metric/category values for 2020, 2025, 2030, TFNs were generated. These numbers were constructed separately using both approaches indicated in Table 4. TFNs generated for individual countries were input data for the multi-criteria procedure based on FWSM.

The FWSM procedure was carried out using Formulas (9) and (10) with the use of arithmetic operations defined by Formulas (7) and (8) on TFNs determined by Formula (6). As a result, defuzzified forecasted IESRI values were obtained. The $Df\left(\tilde{V}\right)$ values are in ascending order, so the best alternative has the lowest risk described by the IESRI value.

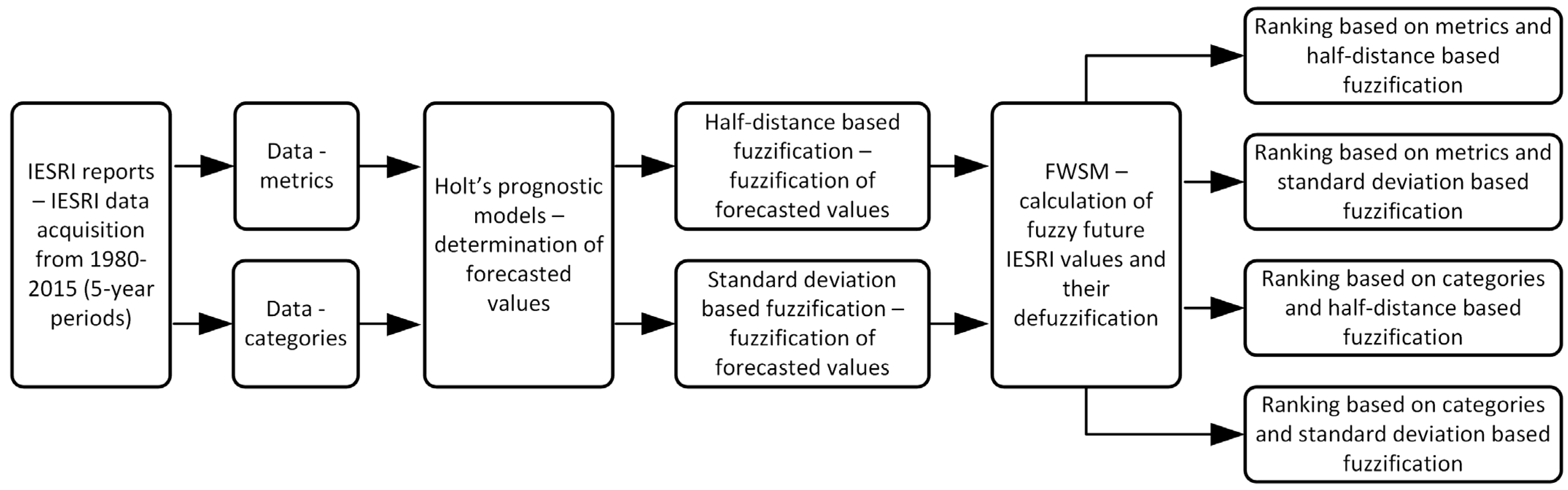
The diagram of the test procedure is presented in Figure 1.

It should be noted that the procedure was carried out in two variants. The first was to use the detailed metrics used by IESRI. However, the second option was based on categories, which made it possible to make slightly more generalized forecasts relating to averaging the values of the metrics included in a given category. In this way, the forecasts were to some extent independent of detailed metrics. In this variant, the values of a given category were calculated as the weighted sum of the metrics that make up this category. Then, on the basis of these averaged values of the categories, category forecasts for the years 2020, 2025, 2030 were generated. As a result, a total of four rankings were obtained, based on metrics or categories of metrics and one of the two fuzzification methods. It allowed us to verify the forecasts and examine the sensitivity of the obtained solution depending on the selected level of generalization of the criteria (metrics or categories) and depending on the selected fuzzification method.

4. Results

All of the obtained results were based on the data published in the International Index of Energy Security Risk report (2020 edition) [36]. Based on this data, the projected future IESRI values were calculated. At the beginning, the category values were calculated based on the values of individual metrics. Then, for the categories and for the detailed metrics, forecasts for the year 2020, 2025, and 2030 were determined, using the Holt’s method for this purpose. Source data for each country in the form of metric values, as well as calculated category values and forecasts, are presented in the Supplementary Materials, Table S1.

Based on the value of the forecasts, fuzzification was performed using two approaches and the TFNs aggregating the forecasts for the years 2020, 2025, and 2030 were determined into one fuzzy number for each metric/category describing a given country. These TFNs are also featured in the Supplementary Materials, in Table S2 (metrics, standard deviation based fuzzification), Table S3 (metrics, half distance based fuzzification), Table S4 (categories, standard deviation based fuzzification), and Table S5 (categories, half distance based fuzzification). In this way, four different scenarios presented in Tables S2–S5 were defined, the solutions of which were different variants of the IESRI forecast for the period 2020–2030.

As a result of the research, for each of the scenarios considered, a country ranking was obtained, based on the aggregated IESRI values forecasted for the 2020–2030 period. Figure 2 shows the rankings obtained on the basis of the forecasted metric values, using TFNs constructed using standard deviation based fuzzification (Figure 2a) and half distance based fuzzification (Figure 2b). In turn, Figure 3 shows the rankings generated using the forecasted values of the categories, based on TFNs constructed using standard deviation based fuzzification (Figure 3a) and half distance based fuzzification (Figure 3b). The rankings with the numerical values of the forecasts are also presented in

Table 5. IESRI rankings obtained using forecasted values of metrics and categories, as well as various fuzzification methods.

Country (Alternative)	Metrics				Categories				Energy Security Risk 2018 (IESRI)
	Standard Deviation Based Fuzzification		Half Distance Based Fuzzification		Standard Deviation Based Fuzzification		Half Distance Based Fuzzification
	Score	Rank	Score	Rank	Score	Rank	Rank	Rank	Score	Rank
A1-OECD	913.2	9	913.3	9	880.2	8	880.2	8	884	8
A2-Australia	863.8	5	863.9	5	782.9	4	782.9	4	805	4
A3-Brazil	1077.9	14	1078.0	14	1107.7	14	1107.7	14	1059	14
A4-Canada	825.5	4	825.6	4	873.6	7	873.6	7	802	3
A5-China	876.8	7	878.0	7	883.5	9	883.9	9	912	9
A6-Denmark	886.5	8	886.6	8	843.5	5	843.5	5	864	5
A7-France	1217.1	15	1217.2	15	1219.7	15	1219.7	15	1128	16
A8-Germany	1241.8	16	1241.9	16	1319.6	19	1319.6	19	1085	15
A9-India	1337.9	20	1338.0	20	1375.0	22	1375.0	22	1144	17
A10-Indonesia	865.5	6	867.0	6	886.1	10	887.5	10	932	10
A11-Italy	1336.8	19	1336.9	19	1346.1	21	1346.1	21	1240	21
A12-Japan	1486.8	23	1486.9	23	1434.5	23	1434.5	23	1281	23
A13-Mexico	1003.6	11	1003.7	11	995.8	13	995.8	13	966	12
A14-Netherlands	1358.2	21	1358.3	21	1260.6	16	1260.6	16	1147	18
A15-New Zealand	770.9	3	771.1	3	744.9	3	744.9	3	757	2
A16-Norway	665.6	1	665.7	1	657.7	2	657.7	2	869	6
A17-Poland	1011.3	12	1011.5	12	845.3	6	845.3	6	967	13
A18-South Africa	1324.0	18	1324.1	18	1320.9	20	1320.9	20	1156	19
A19-South Korea	1618.4	24	1618.5	24	1560.4	24	1560.4	24	1453	25
A20-Spain	1246.4	17	1246.5	17	1319.4	18	1319.4	18	1189	20
A21-Thailand	1660.2	25	1660.3	25	1594.0	25	1594.0	25	1396	24
A22-Turkey	1375.8	22	1375.9	22	1273.7	17	1273.7	17	1267	22
A23-United Kingdom	1042.2	13	1042.3	13	962.1	12	962.1	12	944	11
A24-United States	693.0	2	693.1	2	650.5	1	650.5	1	727	1
A25-Russian Federation	1001.1	10	1001.1	10	897.5	11	897.5	11	875	7
A26-Ukraine	1788.2	26	1788.7	26	1634.7	26	1634.7	26	1463	26

, against the background of the current state taken from the International Index of Energy Security Risk 2020 edition report [36]. Additionally,

Table A1. IESRI fuzzy values forecasted for the 2020–2030 period, obtained using the forecasted metric values.

Country	Standard Deviation Based Fuzzification				Half Distance Based Fuzzification
	${\mathit{a}}_{\mathbf{1}}$	${\mathit{a}}_{\mathbf{2}}$	${\mathit{a}}_{\mathbf{3}}$	${\mathit{a}}_{\mathbf{4}}$	${\mathit{a}}_{\mathbf{1}}$	${\mathit{a}}_{\mathbf{2}}$	${\mathit{a}}_{\mathbf{3}}$	${\mathit{a}}_{\mathbf{4}}$
A1-OECD	832.3977	846.0811	979.0481	995.4487	832.3977	872.0008	953.5263	995.4487
A2-Australia	769.6321	785.6849	940.4262	959.3635	769.6321	815.8339	910.6996	959.3635
A3-Brazil	944.1213	967.4906	1186.956	1213.1099	944.1213	1010.1919	1144.6863	1213.1099
A4-Canada	764.4488	774.5047	875.1912	887.9645	764.4488	794.168	855.9259	887.9645
A5-China	723.207	743.3968	1001.6417	1039.0546	723.207	795.883	953.8068	1039.0546
A6-Denmark	813.0532	824.6541	946.1028	962.1228	813.0532	848.4346	922.9695	962.1228
A7-France	1113.2199	1131.0511	1301.6227	1322.3394	1113.2199	1164.2683	1268.8281	1322.3394
A8-Germany	1134.194	1152.7804	1329.3799	1350.6836	1134.194	1187.1567	1295.4015	1350.6836
A9-India	1132.3003	1168.7979	1505.4819	1544.8464	1132.3003	1234.2398	1440.5128	1544.8464
A10-Indonesia	697.2061	718.7536	1002.2936	1043.6366	697.2061	777.0207	950.236	1043.6366
A11-Italy	1223.5005	1243.1313	1429.0235	1451.3715	1223.5005	1279.3086	1393.2441	1451.3715
A12-Japan	1344.8402	1369.6706	1602.507	1630.2179	1344.8402	1414.9553	1557.6441	1630.2179
A13-Mexico	919.8995	934.1061	1071.7288	1088.6527	919.8995	960.9281	1045.3047	1088.6527
A14-Netherlands	1227.6302	1250.4449	1464.671	1490.203	1227.6302	1292.1137	1423.4001	1490.203
A15-New Zealand	694.7673	707.2584	832.9529	848.7984	694.7673	731.9485	808.964	848.7984
A16-Norway	607.4212	616.9461	712.9204	725.1654	607.4212	635.6967	694.5688	725.1654
A17-Poland	923.4354	938.0494	1082.8788	1100.9019	923.4354	966.4518	1055.185	1100.9019
A18-South Africa	1201.3036	1222.6752	1424.0595	1448.1484	1201.3036	1261.8551	1385.2775	1448.1484
A19-South Korea	1492.7511	1514.6541	1720.7673	1745.3876	1492.7511	1554.7505	1681.0688	1745.3876
A20-Spain	1153.8347	1169.6715	1321.8022	1340.3563	1153.8347	1199.3054	1292.5663	1340.3563
A21-Thailand	1475.7783	1508.4648	1810.5798	1845.9932	1475.7783	1567.1682	1752.2757	1845.9932
A22-Turkey	1260.5705	1280.5719	1469.7624	1492.481	1260.5705	1317.3885	1433.3438	1492.481
A23-United Kingdom	898.0399	923.2161	1159.6197	1187.7952	898.0399	969.1987	1114.0763	1187.7952
A24-United States	635.9304	644.8348	739.3368	751.9444	635.9304	663.3535	721.3604	751.9444
A25-Russian Federation	890.3076	910.6433	1091.6111	1111.9469	890.3076	945.7174	1056.5371	1111.9469
A26-Ukraine	1542.3707	1585.1603	1988.8882	2036.3462	1542.3707	1664.606	1911.5937	2036.3462

and

Table A2. IESRI fuzzy values forecasted for the 2020–2030 period, obtained using the forecasted values of the category.

Country	Standard Deviation Based Fuzzification				Half Distance Based Fuzzification
	${\mathit{a}}_{\mathbf{1}}$	${\mathit{a}}_{\mathbf{2}}$	${\mathit{a}}_{\mathbf{3}}$	${\mathit{a}}_{\mathbf{4}}$	${\mathit{a}}_{\mathbf{1}}$	${\mathit{a}}_{\mathbf{2}}$	${\mathit{a}}_{\mathbf{3}}$	${\mathit{a}}_{\mathbf{4}}$
A1-OECD	831.4374	840.3937	920.0952	929.0514	831.4374	855.8409	904.6479	929.0514
A2-Australia	699.1546	714.5241	851.297	866.6665	699.1546	741.0326	824.7885	866.6665
A3-Brazil	1030.7758	1044.8999	1170.5895	1184.7135	1030.7758	1069.2602	1146.2291	1184.7135
A4-Canada	837.7398	844.317	902.8471	909.4243	837.7398	855.6609	891.5032	909.4243
A5-China	744.4394	765.555	996.3319	1027.8495	744.4394	810.8526	952.5576	1027.8495
A6-Denmark	774.3862	787.0637	899.88	912.5575	774.3862	808.929	878.0147	912.5575
A7-France	1133.3773	1149.2168	1290.172	1306.0114	1133.3773	1176.5359	1262.8529	1306.0114
A8-Germany	1206.964	1227.637	1411.6056	1432.2786	1206.964	1263.2927	1375.95	1432.2786
A9-India	1207.4172	1238.1646	1511.7852	1542.5326	1207.4172	1291.196	1458.7538	1542.5326
A10-Indonesia	778.1757	791.1529	974.0302	1001.0908	778.1757	829.567	941.0245	1001.0908
A11-Italy	1281.8593	1293.6391	1398.4674	1410.2473	1281.8593	1313.9563	1378.1503	1410.2473
A12-Japan	1311.1069	1333.7532	1535.2819	1557.9282	1311.1069	1372.8122	1496.2229	1557.9282
A13-Mexico	918.2761	932.5056	1059.1333	1073.3628	918.2761	957.0478	1034.5911	1073.3628
A14-Netherlands	1169.3791	1186.1115	1335.0131	1351.7456	1169.3791	1214.9707	1306.1539	1351.7456
A15-New Zealand	691.8613	701.5972	788.2367	797.9726	691.8613	718.3891	771.4448	797.9726
A16-Norway	607.9194	617.0456	698.26	707.3862	607.9194	632.7861	682.5195	707.3862
A17-Poland	756.3206	772.6446	917.9118	934.2359	756.3206	800.7994	889.757	934.2359
A18-South Africa	1217.2855	1236.3044	1405.5536	1424.5725	1217.2855	1269.1073	1372.7507	1424.5725
A19-South Korea	1483.0743	1497.2559	1623.4571	1637.6387	1483.0743	1521.7154	1598.9976	1637.6387
A20-Spain	1234.5697	1250.1412	1388.711	1404.2824	1234.5697	1276.9979	1361.8543	1404.2824
A21-Thailand	1482.6642	1503.1038	1684.9952	1705.4347	1482.6642	1538.3569	1649.7421	1705.4347
A22-Turkey	1179.635	1196.8915	1350.4566	1367.7131	1179.635	1226.6545	1320.6936	1367.7131
A23-United Kingdom	832.0374	855.9119	1068.3708	1092.2454	832.0374	897.0894	1027.1934	1092.2454
A24-United States	589.6243	600.7888	700.1408	711.3052	589.6243	620.0445	680.885	711.3052
A25-Russian Federation	826.588	839.5939	955.3338	968.3397	826.588	862.0259	932.9018	968.3397
A26-Ukraine	1488.6189	1515.4311	1754.0321	1780.8443	1488.6189	1561.6752	1707.788	1780.8443

(Appendix A) show the values of TFNs $\widetilde{V\left(a\right)}$ (see Formula (9)), the defuzzified values of which in Table 5 were the basis for determining the order of countries in the rankings. The same TFNs shown in Table A1 and Table A2 are also shown in Figure 2 and Figure 3 and represent the fuzzy values of the IESRI forecasts for the 2020–2030 period.

When analyzing the results presented in Table 5, it should be noted that both in the case of forecasts based on metrics and categories, the fuzzification method hardly affects the obtained forecasts. Depending on the selected fuzzification method, differences appear in the case of the TFN core, which results from the formulas shown in Table 4 and is shown in Table A1 and Table A2. It can also be seen from Figure 2 and Figure 3 that using standard deviation based fuzzification a wider TFN core is obtained than using half distance based fuzzification. However, after the defuzzification of TFNs presented in Table A1 and Table A2, the differences between standard deviation based fuzzification and half distance based fuzzification almost always concern only the decimal part of the score, as shown in Table 5. Slightly larger differences, at the level of 1.5 score points, appear only in the case of Indonesia (A10). Nevertheless, the fuzzification method does not affect the order of countries in the rankings.

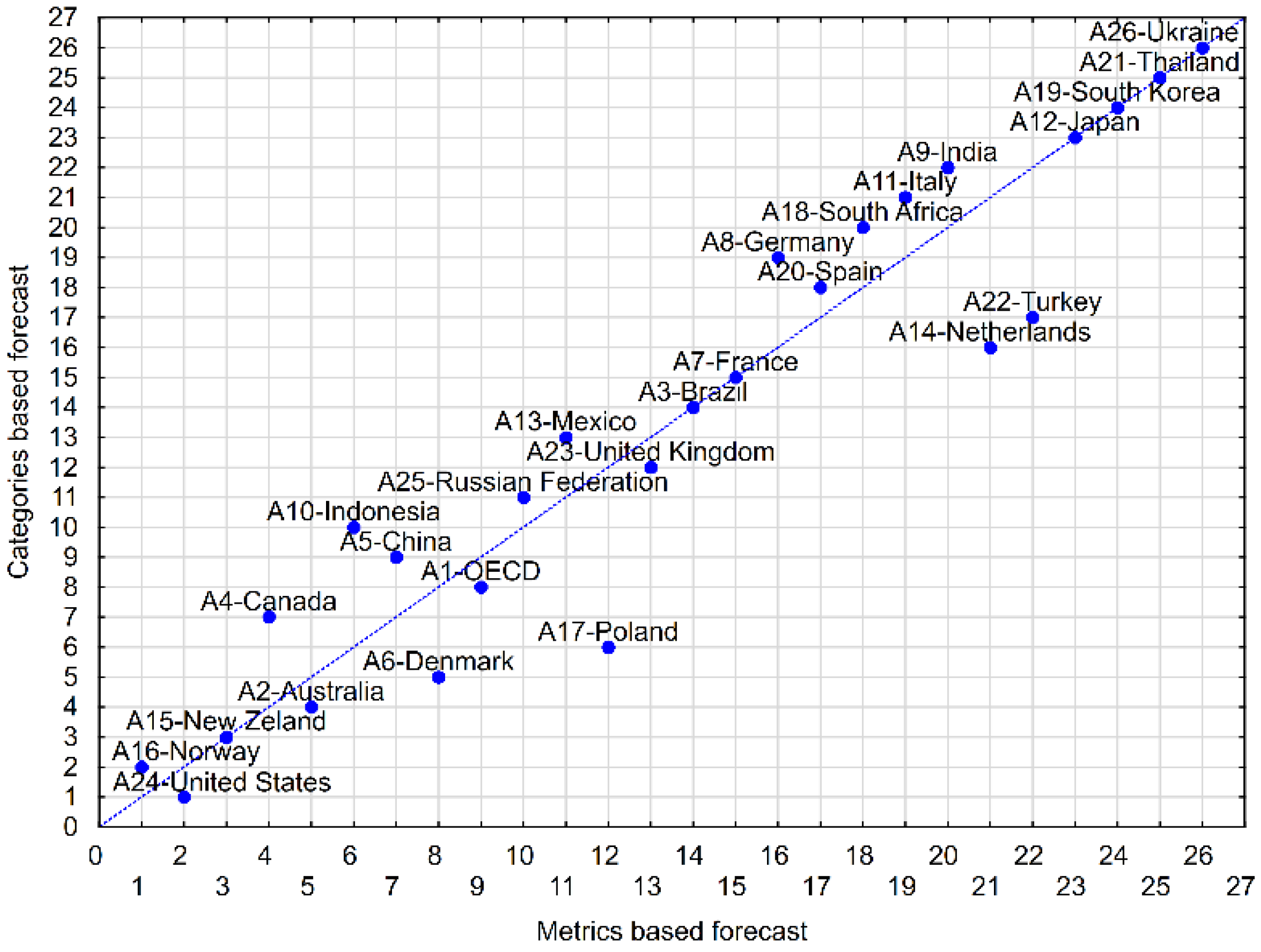
When it comes to comparing forecasts based on metrics and categories, they differ to some extent. The smallest differences between the forecast scores obtained on the basis of metrics and categories are in the case of A5-China, A7-France, and A18-South Africa. These differences are at the level of about 4–6 score points. In turn, the largest differences, exceeding 100 points, appear in the case of A17-Poland, A22-Turkey, A25-Russian Federation, and A26-Ukraine. The analysis of the dispersion between the forecast rankings based on metrics and categories is shown in Figure 4. Table 5 and Figure 4 show that the considered rankings overlap for seven countries: A15-New Zealand (3rd place), A3-Brazil (14), A7-France (15), A12-Japan (23), A19-South Korea (24), A21-Thailand (25), and A26-Ukraine (26). For most countries, the differences in the rankings are 1–3 places, and there are bigger differences only in the case of A10-Indonesia (4 places), A17-Poland (6), A14-Netherlands (5), A22-Turkey (5). The Kendall’s tau correlation coefficient, which is recommended when examining the similarity of rankings [63], for rankings based on metrics and categories was 0.84, which indicates a significant similarity. On the other hand, some countries show that the differences in forecasts based on metrics and categories can be significant.

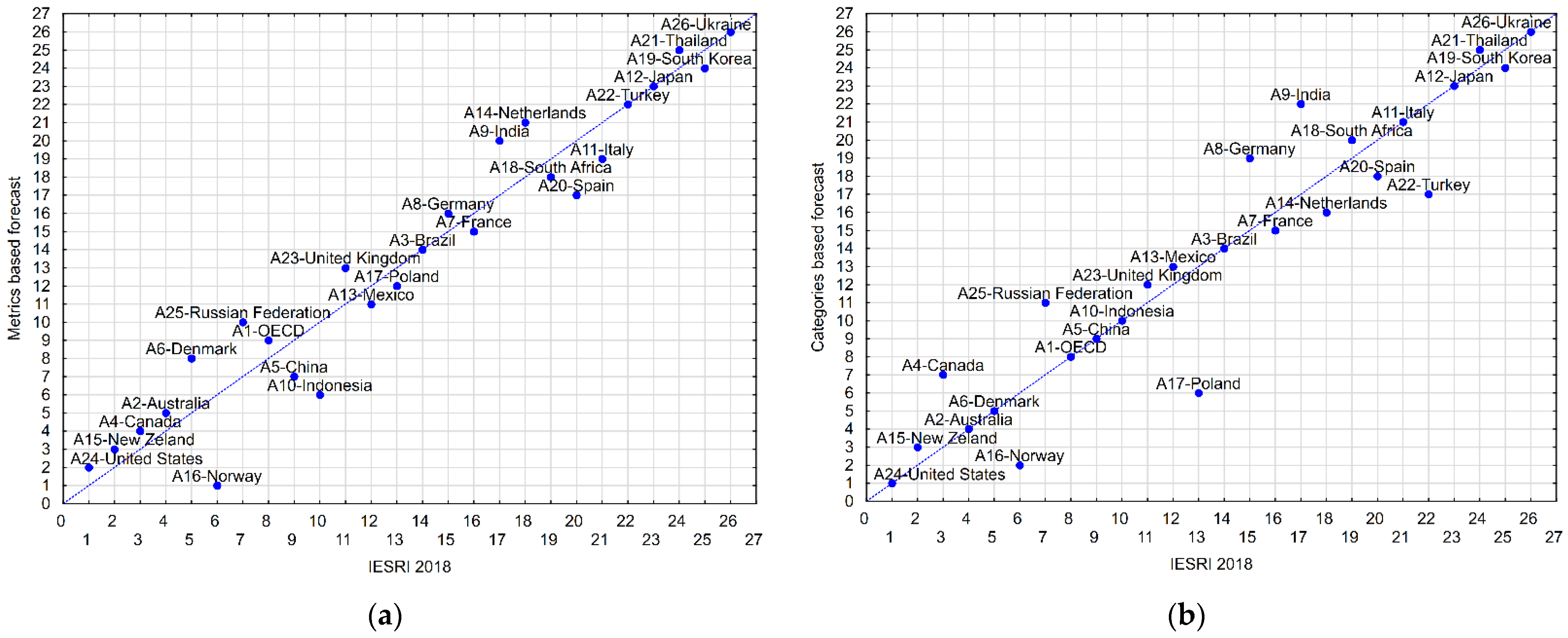
The most important element of the analysis is the comparison of the current (Energy Security Risk 2018) scores and the current ranking with the forecasts. Figure 5 shows the scattering between the current IESRI 2018 ranking and the projected rankings based on metrics and categories. If a country is below the diagonal of the graph, it means that the forecast predicts its rise in the ranking in the period 2020–2030 in relation to 2018.

Based on Figure 5a and Table 5, it is easy to see that in the case of the metric-based forecast, the promotion of the following countries is predicted: A16-Norway (by 5 places), A5-China (2), A10-Indonesia (4), A20-Spain (3), and A11-Italy (2), as well as a promotion by one place for A13-Mexico, A17-Poland, A7-France, A18-South Africa, and A19-South Korea. In turn, the biggest loss, by as many as three places, is expected in the case of A6-Denmark, A9-India, A14-Netherlands and A25-Russian Federation. Other countries will report losses as well, and the forecast shows no change in the ranking for A3-Brazil, A22-Turkey, A12-Japan, and A26-Ukraine. According to the metric-based forecast, the most significant advance of A16-Norway will make it overtake A24-United States between 2020 and 2030 and become a leader in the IESRI ranking. However, taking into account the uncertainty expressed by the fuzzy scores and presented in Figure 2 and in Table A1, it should be noted that the change of the leader is not certain. Moreover, based on Figure 2 and Table A1, A15-New Zealand and A10-Indonesia also have a minimum chance of being first in the ranking. On the other hand, A15-New Zealand may even drop to position nine in the 2020–2030 ranking, behind the OECD average (A1). On the other hand, A10-Indonesia could drop to position 14 behind A3-Brazil. The greatest uncertainty is characterized by the forecast A26-Ukraine score, which is in the last place in the 2018 ranking and in the 2020–2030 ranking. However, despite this, it is only allowed to be in the 23rd place and getting ahead of A12-Japan in the forecasted ranking based on metrics.

When analyzing Figure 5b together with Table 5 (i.e., the forecasts based on categories), it should be noted that A16-Norway (by four places), as well as A17-Poland (7), A22-Turkey (5), A14-Netherlands (2), A20-Spain (2), A7-France (1), A19-South Korea (1) are expected to rise in the ranking. This forecast shows that A24-United States, A2-Australia, A6-Denmark, A1-OECD, A5-China, A10-Indonesia, A3-Brazil, A11-Italy, A12-Japan, and A26-Ukraine have maintained their position in the ranking. The biggest drops in the ranking, by as much as 3 places, are expected for: A9-India (by 5 places), A4-Canada (4), A8-Germany (4), and A25-Russian Federation (4). For the remaining countries, a decrease by one place is forecasted. In the case of the category-based forecast, A24-United States is expected to remain at the top of the ranking, but an uncertainty analysis based on Figure 3 and Table A2 indicates that there is a high probability that the United States will be overtaken by A16-Norway. In turn, the A15-New Zealand and A2-Australia have only a minimal chance of overtaking these two countries. The lowest uncertainty is characteristic of the 14th place of the A3-Brazil alternative, which with low probability may change places in the ranking with A13-Mexico, A23-United Kingdom, A7-France, and with minimal probability it may be overtaken by A14-Netherlands and A22-Turkey. As in the metric-based forecast, also here the last place is predicted for A26-Ukraine, which, after taking uncertainty into account, could move up a maximum of 4 places and overtake A9-India. It should be noted here that due to the different methodology (averaging the values of metrics in categories and forecasting the value of categories), the predicted ranking based on categories is less reliable than the forecast based on metrics.

5. Conclusions

Summarizing the obtained results from the methodological point of view, it should be stated that the forecasts presented in Table 5 are not completely certain. Therefore, a very important contribution of this article concerns the consideration of the uncertainty captured with the fuzzy set theory and represented by TFNs. This uncertainty indicates some acceptable prediction error and informs about alternative possible IESRI score values and positions in the predicted rankings (see Figure 2 and Figure 3 and Table A1 and Table A2). Additionally, thanks to the forecast aggregation method consisting in the construction of a fuzzy number based on forecasts for 2020, 2025, and 2030, the resulting forecast takes into account the uncertainty of time. Thanks to this, in practice, the possible time of occurrence of the event (obtaining the predicted IESRI score value) was obtained in the 2020–2030 period without a strong determination of the exact time.

Despite the uncertainty, the forecasts indicate certain trends, the observation of which, together with the obtained numerical values of the forecasts, constitutes a practical contribution of the article. The observed trends include: dynamic increase in energy security by Norway (decrease of the IESRI score by over 200 points in the perspective of 2020–2030 in relation to 2018), stability of energy security in the case of the United States, or no chance for improvement of Ukraine’s energy security. Analyzing Table 5, one can also notice a generalized conclusion that countries such as China, Indonesia, Norway and the United States will increase their energy security. However, in the case of other countries, the security will decline (IESRI score will increase) even in the case of anticipated promotions in the IESRI ranking.

As for the limitations of the methodology used, it should be remembered that the presented forecasts are based on Holt’s method taking into account linear trends with random fluctuations. This means that this method does not take into account seasonal fluctuations, unlike the Holt-Winters method. On the other hand, in the perspective of the five-year periods 1980–2015, it is difficult to find such seasonal fluctuations, since if they did occur, they would probably have been included and smoothed out within the five-year periods. Also, the use of TFNs may raise the objection that there are much more advanced fuzzy set implementations. However, as noted earlier, TFNs have numerous advantages over other more complex implementations. The biggest limitation of the applied forecasting methodology is the fact that it is only a mathematical model that may not take into account real events and situations in the political, economic or social context. On the other hand, the mathematical model was based on a reliable, complex IESRI. In turn, the numerical data contained in the IESRI 2020 edition constitute a reliable basis for the developed model and determine its numerical reliability. As for the directions of further work, an interesting issue may be the use of other MCDA methods to forecast energy security risk such as VMCM [64], Fuzzy ANP [65], or Fuzzy TOPSIS [18].