Analysis of Hybrid and Plug-In Hybrid Alternative Propulsion Systems for Regional Diesel-Electric Multiple Unit Trains
Abstract
:1. Introduction
- A method to support a hypothetical conversion of a conventional regional DMU vehicle to its hybrid and plug-in hybrid counterparts, equipped with the prominent ESS technologies and newly developed causal and easy-to-implement real-time power control, allowing for a realistic estimation of fuel savings;
- A comparative analysis of alternative propulsion systems in a case study of a selected benchmark vehicle and railway line in the northern Netherlands, providing the railway undertaking with an assessment of potential benefits in terms of reduction of produced GHG emissions and energy costs.
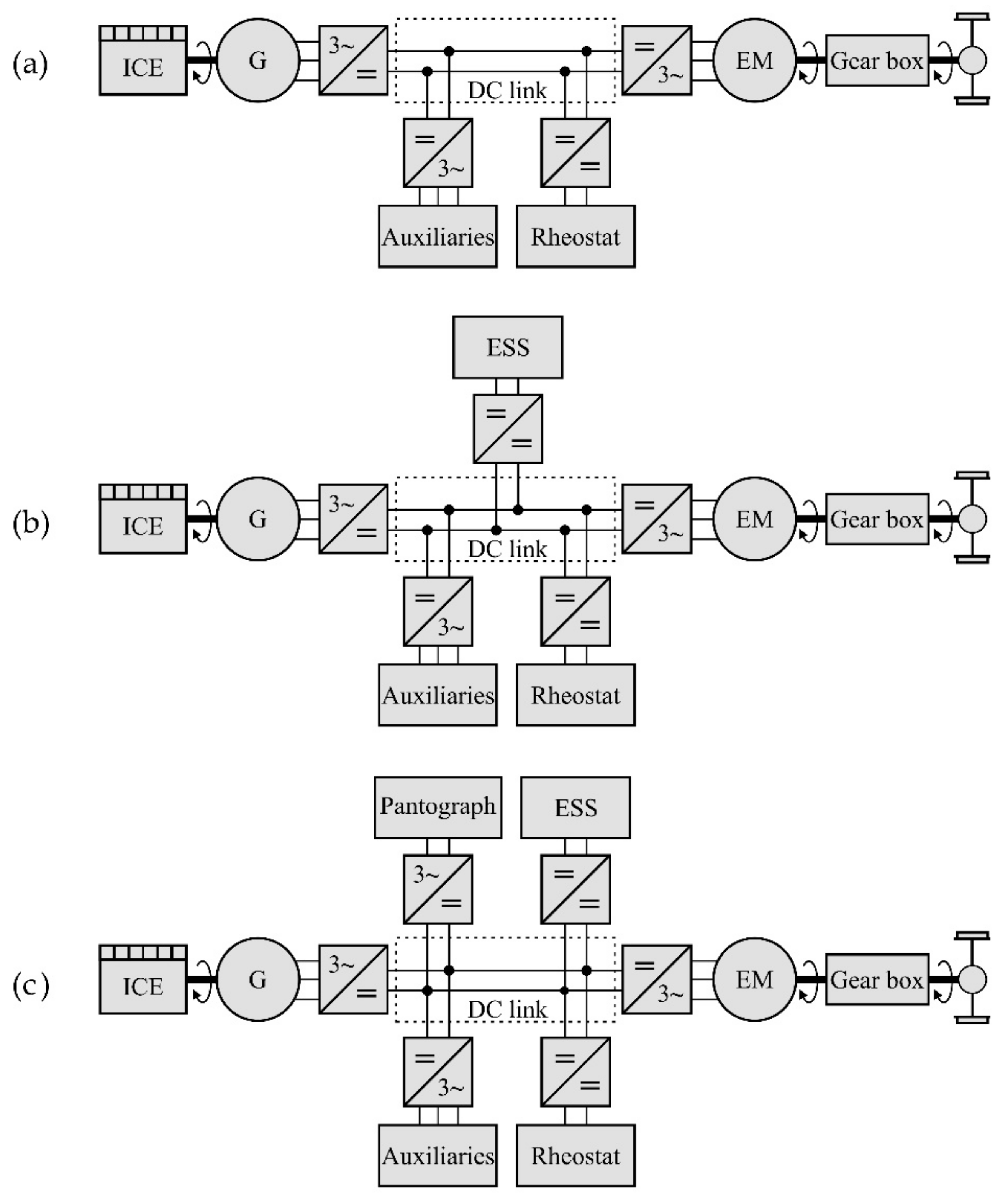
2. Configuration of Standard, Hybrid, and Plug-In Hybrid Propulsion Systems
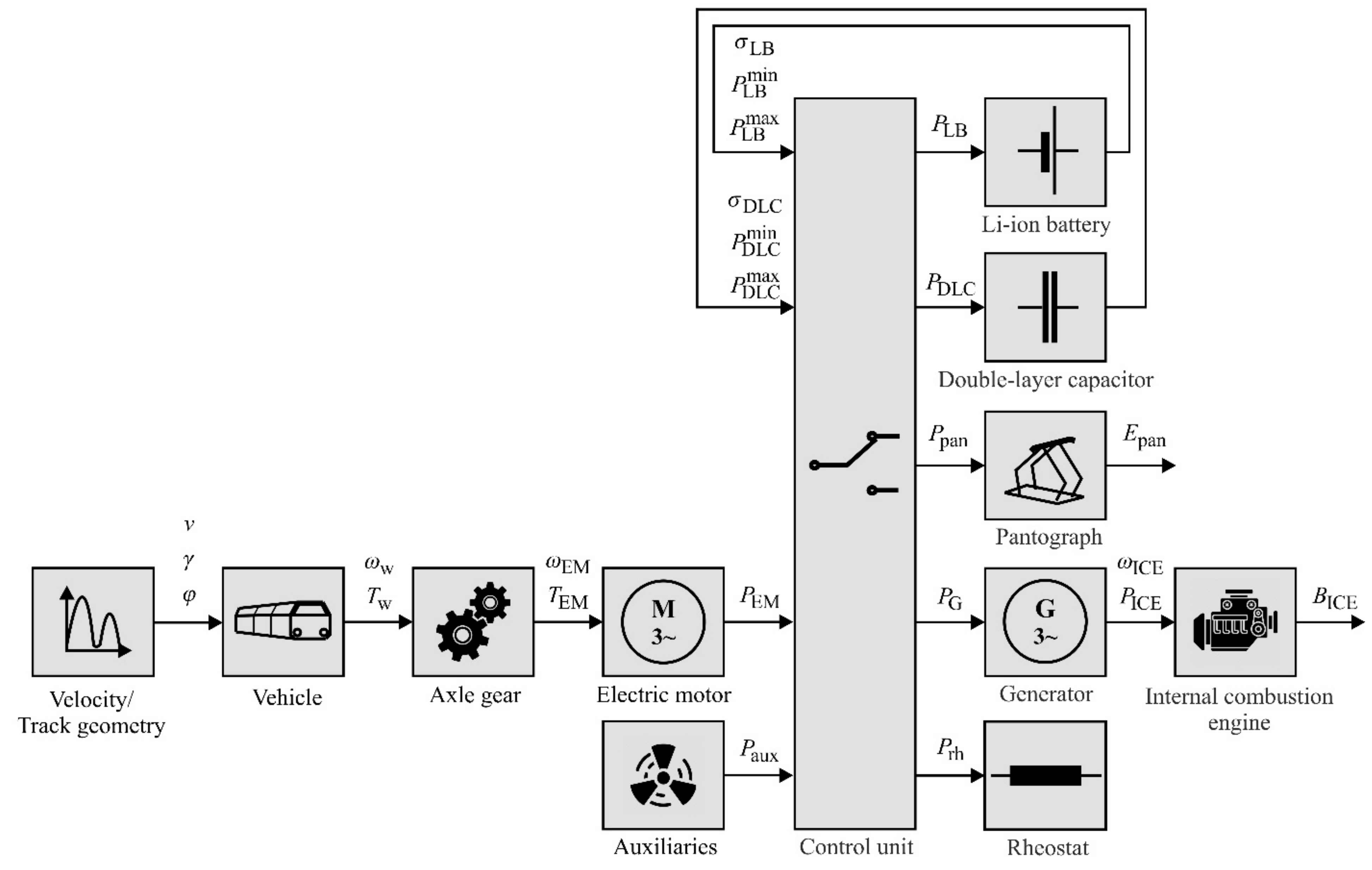
3. Modeling and Control of Alternative Propulsion Systems
3.1. Simulation Model
3.1.1. Vehicle
3.1.2. Axle Gear
3.1.3. Electric Motor
3.1.4. Auxiliaries
3.1.5. Diesel Generator Set
3.1.6. Pantograph
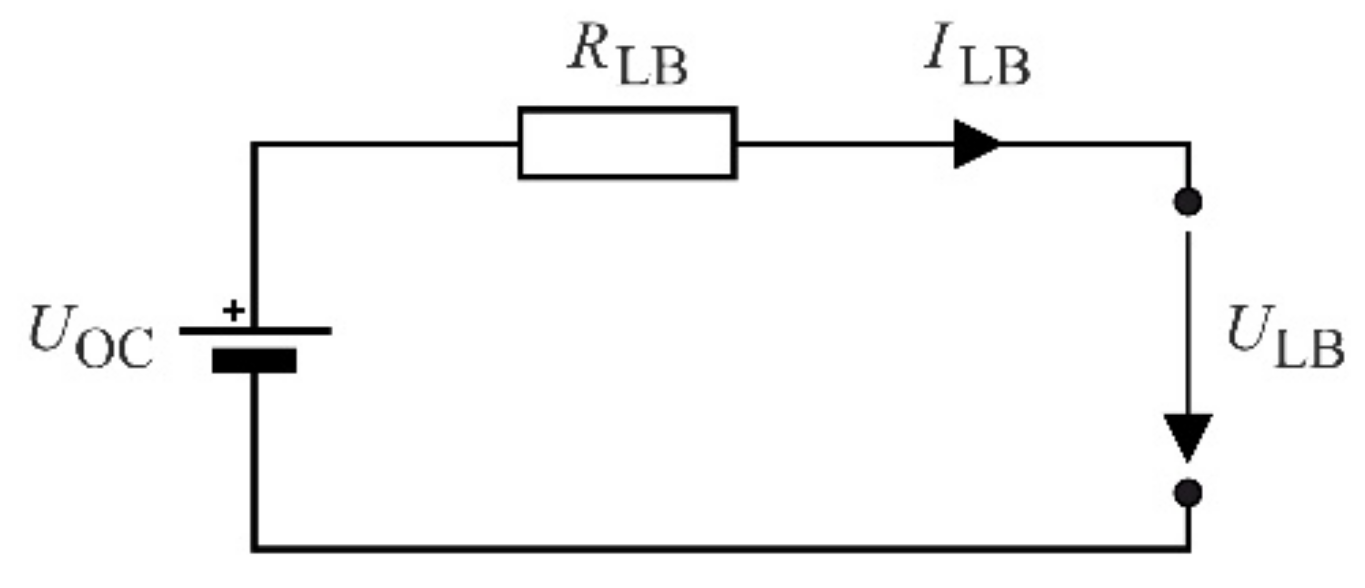
3.1.7. Lithium-Ion Battery
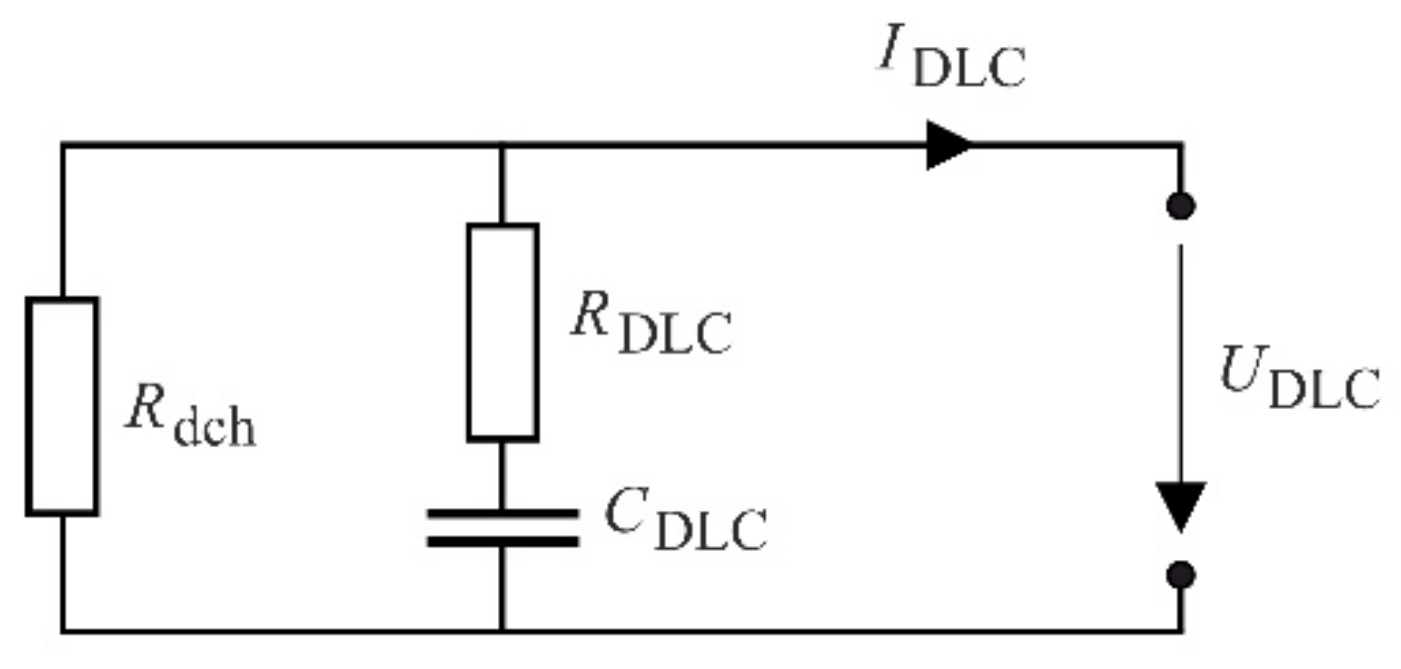
3.1.8. Double-Layer Capacitor
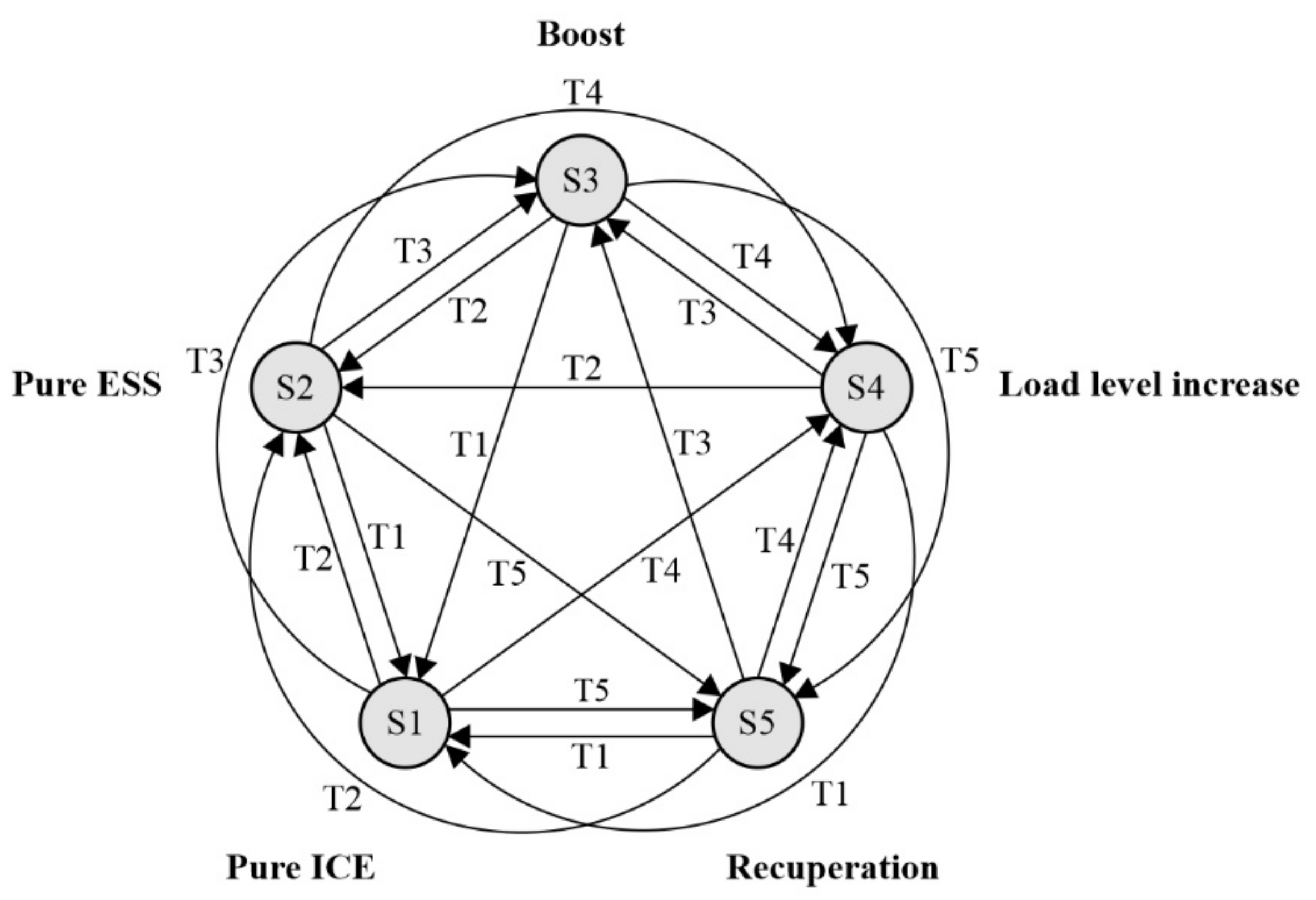
3.2. Energy Management Strategy
- Removing emissions and noise in terminal stops by switching off the ICE and supplying auxiliary systems from an ESS or electric power grid;
- Improving fuel economy by maximizing regenerative braking energy and its later use in powering traction and auxiliary systems;
- Increasing overall ICE-G efficiency by avoiding low load operation;
- Supporting ICE-G by an ESS during high power demand phases (acceleration).
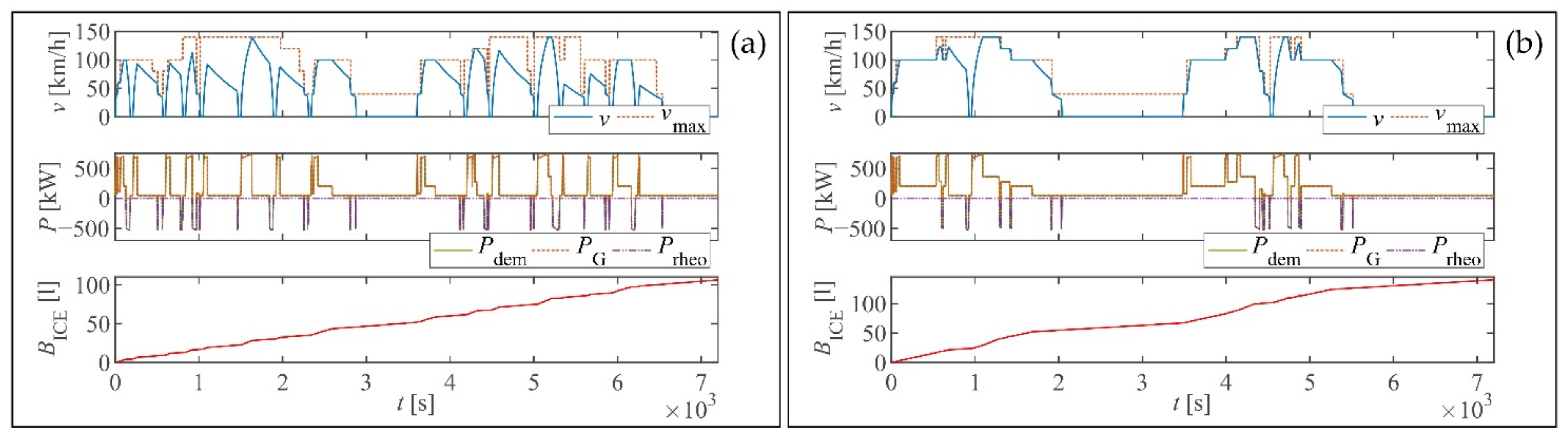
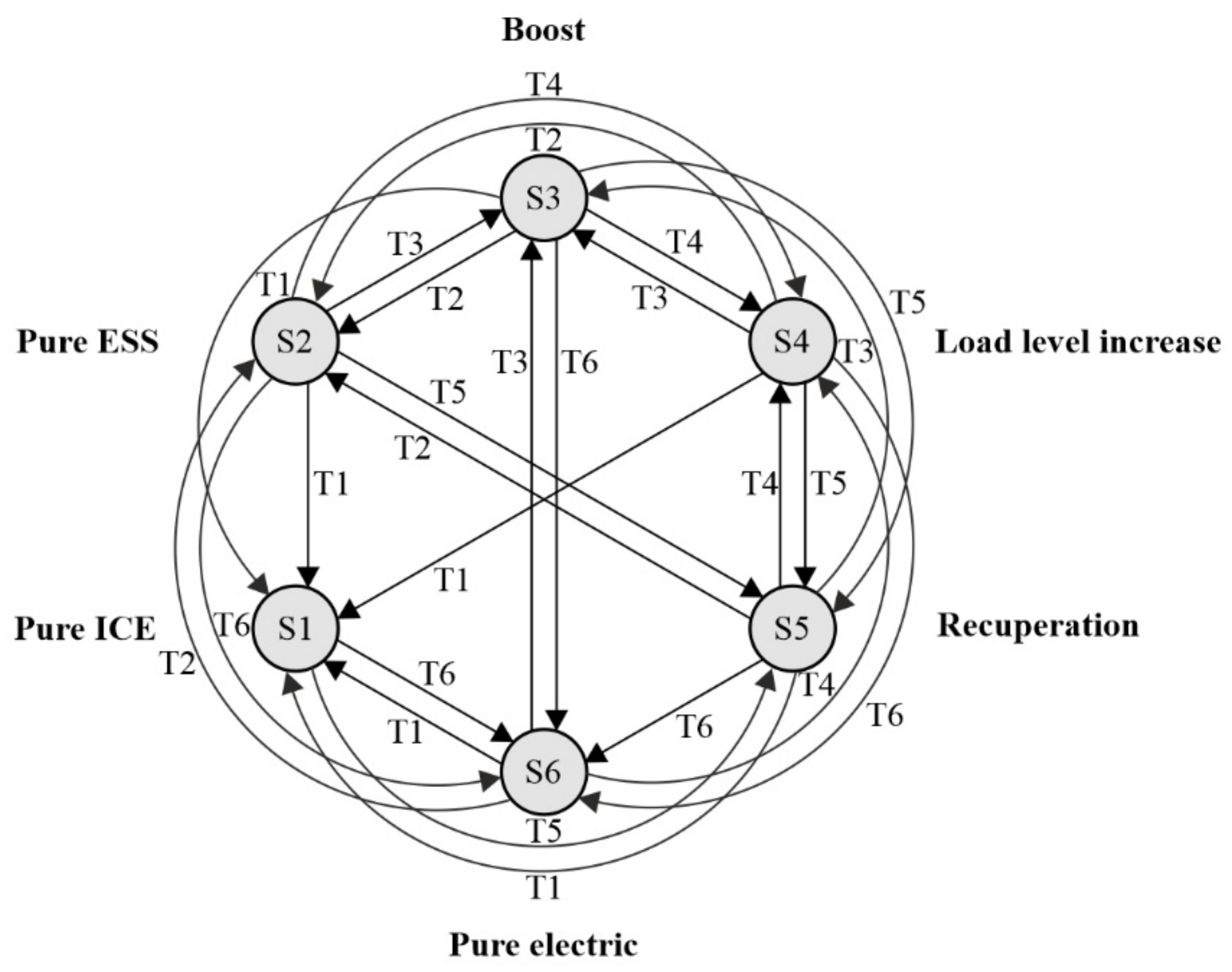
3.2.1. FSM Control for HDEMU Vehicle
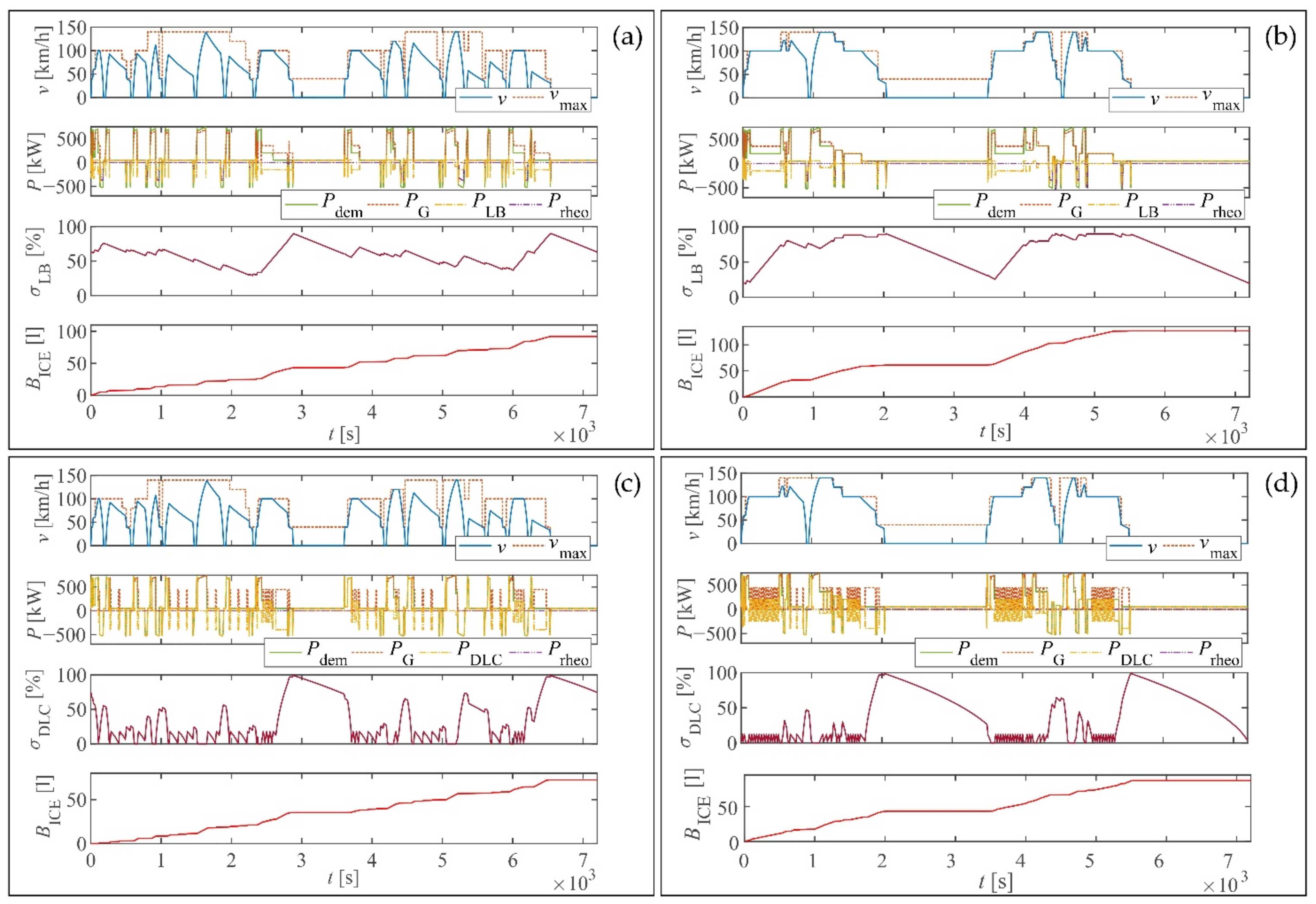
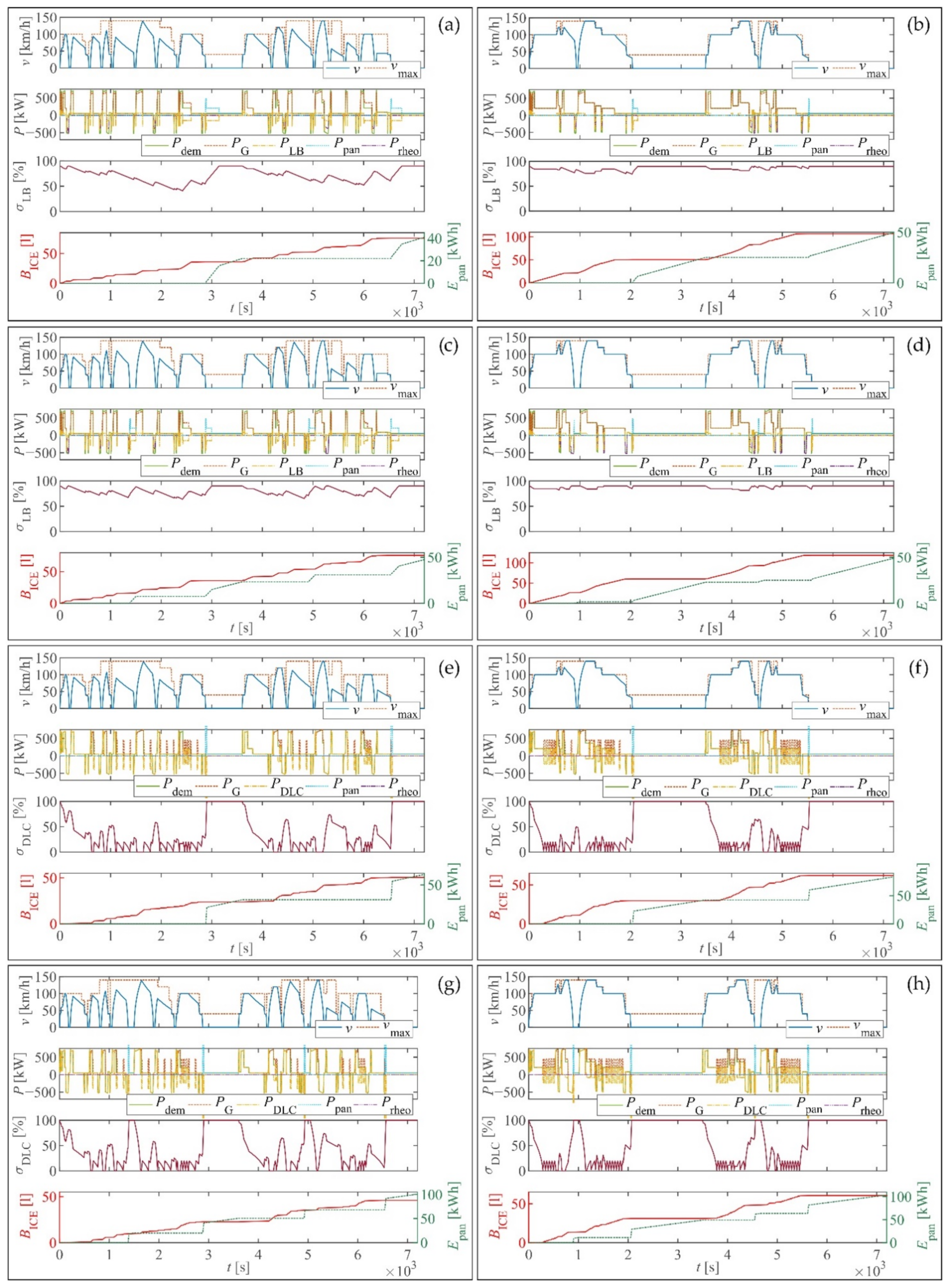
3.2.2. FSM Control for PHDEMU Vehicle
4. Case Study of the Dutch Northern Regional Railway Lines
4.1. Benchmark Railway Vehicle
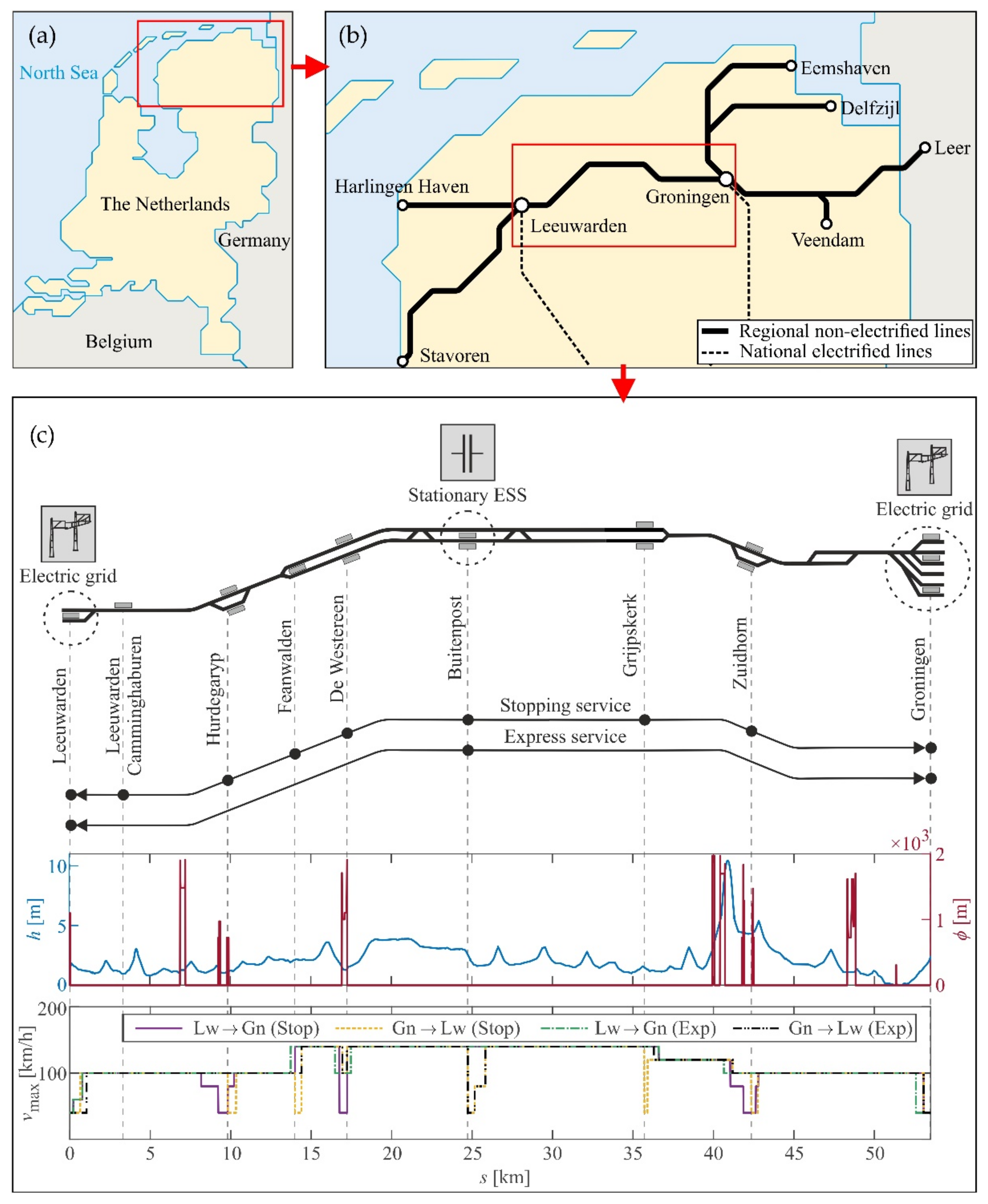
4.2. Benchmark Railway Line Selection
- Charging facilities located only in terminal stations with long layover times;
- Charging facilities located in terminal stations and an additional fast charging facility located in Buitenpost, a common short stop for the two services.
4.3. Comparative Assessment Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviations | |
| AC | Alternating current |
| BEMU | Battery-electric multiple unit |
| DC | Direct current |
| DEMU | Diesel-electric multiple unit |
| DLC | Double-layer capacitor |
| DMU | Diesel multiple unit |
| DP | Dynamic programming |
| ECMS | Equivalent consumption minimization strategy |
| EM | Electric motor |
| EMS | Energy management strategy |
| ESS | Energy storage system |
| EVSE | Electric vehicle supply equipment |
| FCMU | Fuel-cell multiple unit |
| FSM | Finite state machine |
| G | Generator |
| GHG | Greenhouse gasses |
| GTW | Gelenktriebwagen |
| HDEMU | Hybrid diesel-electric multiple unit |
| HEV | Hybrid electric vehicle |
| HVAC | Heating, ventilation, and air conditioning |
| ICE | Internal combustion engine |
| IS | Intermediate stop |
| LB | Lithium-ion battery |
| LCA | Life cycle assessment |
| LCC | Life cycle costs |
| LTO | Li titanium oxide |
| NMC | Nickel manganese cobalt |
| PHDEMU | Plug-in hybrid diesel-electric multiple unit |
| PHEV | Plug-in hybrid electric vehicle |
| PMP | Pontryagin’s minimum principle |
| RB | Rule-based |
| RU | Railway undertaking |
| SoC | State-of-charge |
| TS | Terminal stop |
| Parameters | |
| Maximum acceleration | |
| Maximum deceleration | |
| Capacitance of the double-layer capacitor | |
| Wheel diameter | |
| Energy content of the double-layer capacitor | |
| Energy content of the battery | |
| Usable energy content of the battery | |
| Maximum (starting) tractive effort at the wheel | |
| Gravitational acceleration | |
| Constant gear ratio | |
| Allowed maximum charging current for double-layer capacitor | |
| Allowed maximum discharging current for double-layer capacitor | |
| Allowed maximum continuous charging current of the battery | |
| Allowed maximum continuous discharging current of the battery | |
| Allowed peak (pulse) charging current of the battery | |
| Allowed peak (pulse) discharging current of the battery | |
| Weight of the double-layer capacitor | |
| Weight of the battery | |
| Total weight of passengers | |
| Empty vehicle mass | |
| Total vehicle mass | |
| Constant auxiliaries power | |
| Cooling power coefficient | |
| Rated power of the electric motor | |
| Optimal level of electrical power from the diesel generator | |
| Rated power of the internal combustion engine | |
| Maximum power from the charging grid | |
| Nominal capacity of the battery | |
| Self-discharging resistance of the double-layer capacitor | |
| Internal resistance of the double-layer capacitor | |
| Battery internal resistance during charging | |
| Battery internal resistance during discharging | |
| Davis equation coefficient (constant term) | |
| Davis equation coefficient (linear term) | |
| Davis equation coefficient (quadratic term) | |
| Line-specific critical track section | |
| Position of the terminal stop | |
| Time limit for the allowed battery pulse charging current | |
| Time limit for the allowed battery pulse discharging current | |
| Maximum voltage of the double-layer capacitor | |
| Minimum voltage of the double-layer capacitor | |
| Maximum battery voltage | |
| Minimum battery voltage | |
| Maximum velocity | |
| Simulation (integration) time step | |
| Constant efficiency of the gearbox | |
| Rotating mass factor | |
| Fuel density | |
| Energy storage system hysteresis cycle for the state-of-charge | |
| State-of-charge limit for the energy storage system | |
| Minimum state-of-charge for the energy storage system | |
| Maximum battery state-of-charge | |
| Minimum battery state-of-charge | |
| Dynamic variables | |
| Vehicle acceleration | |
| Binary indicator for the track electrification status | |
| Total fuel consumption | |
| Total electrical energy consumption | |
| Binary indicator for the state-of-charge hysteresis cycle | |
| Tractive/braking effort at the wheel | |
| Current of the double-layer capacitor | |
| Maximum current of the double-layer capacitor | |
| Minimum current of the double-layer capacitor | |
| Battery current | |
| Maximum battery current | |
| Maximum battery charging current defined by the manufacturer | |
| Maximum battery discharging current defined by the manufacturer | |
| Minimum battery current | |
| Total auxiliaries power | |
| Total requested power for traction and auxiliaries | |
| Power of the double-layer capacitor | |
| Maximum power of the double-layer capacitor | |
| Minimum power of the double-layer capacitor | |
| Electric power of the electric motor | |
| Maximum power of the energy storage system | |
| Minimum power of the energy storage system | |
| Electrical output power of the generator | |
| Mechanical output power of the internal combustion engine | |
| Power of the battery | |
| Maximum power of the battery | |
| Minimum power of the battery | |
| Electric power received via pantograph | |
| Curve resistances | |
| Grade resistances | |
| Battery internal resistance | |
| Vehicle resistances | |
| Distance traveled | |
| Time | |
| Battery pulse charging time counter | |
| Battery pulse discharging time counter | |
| Torque at the mechanical output of the electric motor | |
| Torque at the wheel | |
| Terminal voltage of the double-layer capacitor | |
| Battery terminal voltage | |
| Battery open circuit voltage | |
| Vehicle velocity | |
| Angle of the slope | |
| Efficiency of the electric motor | |
| Efficiency of the generator | |
| State-of-charge of the double-layer capacitor | |
| Battery state-of-charge | |
| Curve radius | |
| Specific fuel consumption | |
| Rotational speed of the electric motor | |
| Rotational speed of the internal combustion engine | |
| Rotational speed of the wheel | |
Appendix A
References
- UN. Kyoto Protocol to the United Nations Framework Convention on Climate Change, Kyoto. 1998. Available online: https://unfccc.int/resource/docs/convkp/kpeng.pdf (accessed on 22 January 2021).
- UN. Paris Agreement, Paris. 2015. Available online: https://unfccc.int/sites/default/files/english_paris_agreement.pdf (accessed on 22 January 2021).
- Di Domenico, G.C.; Dick, C.T. Methods of Analyzing and Comparing Energy Efficiency of Passenger Rail Systems. Transp. Res. Rec. 2015, 2475, 54–62. [Google Scholar] [CrossRef] [Green Version]
- UIC; CER. Moving Towards Sustainable Mobility: A Strategy for 2030 and Beyond for the European Railway Sector, Paris. 2012. Available online: http://www.cer.be/sites/default/files/publication/CER-UIC_Sustainable_Mobility_Strategy_-_SUMMARY.pdf (accessed on 28 January 2021).
- RailwayTechnology. Bombardier Talent 3 Battery Train. Available online: https://www.railway-technology.com/projects/bombardier-talent-3-battery-train/ (accessed on 5 April 2021).
- Siemens. Desiro ML ÖBB Cityjet eco for ÖBB Personenverkehr AG. Available online: https://assets.new.siemens.com/siemens/assets/api/uuid:b26911b1-2b0e-48b4-b593-81adbf032d75/db-desiro-ml-oebb-cityjet-eco-e.pdf (accessed on 5 April 2021).
- Siemens. Mireo Plus B Ortenau for SFBW, Baden-Württemberg, Germany. Available online: https://assets.new.siemens.com/siemens/assets/api/uuid:636c61e0-bd2d-4f97-a2c7-78e690792a44/mors-b10022-00dbmireoplusortenauenus-72_original.pdf (accessed on 5 April 2021).
- RailTech. Stadler Gets First Order for Akku Battery-Powered Trains. Available online: https://www.railtech.com/rolling-stock/2019/06/20/stadler-gets-first-order-for-akku-battery-powered-trains/?gdpr=accept (accessed on 5 April 2021).
- Alstom. Alstom’s Hydrogen Train Enters Regular Passenger Service in Austria. Available online: https://www.alstom.com/press-releases-news/2020/9/alstoms-hydrogen-train-enters-regular-passenger-service-austria (accessed on 5 April 2021).
- FuelCellWorks. Siemens Mireo Plus H Fuel Cell Hydrogen Train—The Middle Distance Champion. Available online: https://fuelcellsworks.com/news/siemens-mireo-plus-h-fuel-cell-hydrogen-train-the-middle-distance-champion/ (accessed on 5 April 2021).
- IRJ. Zillertalbahn Hydrogen Train Design Revealed. Available online: https://www.railjournal.com/fleet/zillertalbahn-hydrogen-train-design-revealed/ (accessed on 5 April 2021).
- Bai, S.; Liu, C. Overview of energy harvesting and emission reduction technologies in hybrid electric vehicles. Renew. Sustain. Energy Rev. 2021, 147, 111188. [Google Scholar] [CrossRef]
- Fuhs, A. Hybrid Vehicles, 1st ed.; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar] [CrossRef]
- Doucette, T.T.; McCulloch, M.D. Modeling the prospects of plug-in hybrid electric vehicles to reduce CO2 emissions. Appl. Energy 2011, 88, 2315–2323. [Google Scholar] [CrossRef]
- Orecchini, F.; Santiangeli, A. Automakers’ powertrain options for hybrid and electric vehicles. In Electric and Hybrid Vehicles; Elsevier: Amsterdam, The Netherlands, 2010; pp. 579–636. [Google Scholar]
- Orecchini, F.; Santiangeli, A.; Dell’Era, A. EVs and HEVs using lithium-ion batteries. In Lithium-Ion Batteries; Elsevier: Amsterdam, The Netherlands, 2014; pp. 205–248. [Google Scholar]
- Williamson, S.S. Energy Management Strategies for Electric and Plug-in Hybrid Electric Vehicles; Springer: New York, NY, USA, 2013. [Google Scholar]
- EC. Public Report: Ultra Low Emission Vehicle—Transport Using Advanced Propulsion 2 (ULEV-TAP II); EC: Erlangen, Germany, 2005. [Google Scholar]
- Marsilla, M. CleanER-D Deliverable 7.5.4: Future Scenarios and Recommendations for Implementation of Hybrid Solutions. 2013. Available online: http://www.cleaner-d.eu/deliverables.htm (accessed on 9 February 2021).
- Hillmansen, S.; Roberts, C.; Mcgordon, A.; Jennings, P. Concept Validation for Hybrid Trains. Final Report DfTRG/0078/2007, Birmingham. 2008. Available online: https://www.birmingham.ac.uk/Documents/college-eps/railway/Hybirdconceptfinal5.pdf (accessed on 14 February 2021).
- Hillmansen, S.; Roberts, C.; Mcgordon, A.; Jennings, P. DMU Hybrid Concept Evaluation. Final Report DfTRG/0078/2007, Birmingham. 2009. Available online: https://www.birmingham.ac.uk/Documents/college-eps/railway/HybridRailReportDMUV1.pdf (accessed on 14 February 2021).
- Railway Gazette International. Hybrid Drive Demonstrates 15% Fuel Saving. Available online: https://www.railwaygazette.com/news/traction-rolling-stock/single-view/view/hybrid-drive-demonstrates-15-fuel-saving.html (accessed on 17 May 2021).
- Fujii, T.; Teraya, N.; Osawa, M. Special edition paper Development of an NE train. JR EAST Tech. Rev. 2004, 4, 62–70. Available online: https://www.jreast.co.jp/e/development/tech/pdf_4/Tech-no.4-62-70.pdf (accessed on 2 April 2021).
- Shiraki, N.; Satou, H.; Arai, S. A hybrid system for diesel railcar series Ki-Ha E200. In Proceedings of the 2010 International Power Electronics Conference—ECCE ASIA, Sapporo, Japan, 21–24 June 2010; pp. 2853–2858. [Google Scholar] [CrossRef]
- Engel, B.; Soefker, C. The Innovative Traction System with the Flywheel of the LIREXTM. In Proceedings of the World Congress on Railway Research, Cologne, Germany, 25–29 November 2001. [Google Scholar]
- Research and Technology Centre of Deutsche Bahn AG. Applications for energy storage flywheels in vehicles of Deutsche Bahn AG. In Proceedings of the World Congress on Railway Research, Cologne, Germany, 25–29 November 2001. [Google Scholar]
- INSIDEEVs. Meet Audi’s Plug-In Hybrid Locomotive. Available online: https://insideevs.com/news/328130/meet-audis-plug-in-hybrid-locomotive/ (accessed on 1 June 2021).
- Alstom. Alstom to Supply Two H3 Hybrid Shunting Locomotives for Audi. Available online: https://www.alstom.com/press-releases-news/2015/2/alstom-to-supply-two-h3-hybrid-shunting-locomotives-for-audi (accessed on 1 June 2021).
- Alstom. Alstom to Deliver Two Prima H3 Shunting Locomotives to Metrans. Available online: https://www.alstom.com/press-releases-news/2016/2/alstom-to-deliver-two-prima-h3-shunting-locomotives-to-metrans (accessed on 1 June 2021).
- Railcolor News. Romania’s First Hybrid Locomotive Design Plugs-in to Sustainability. Available online: https://railcolornews.com/2018/02/28/ro-romanias-first-hybrid-locomotive-design-plugs-in-to-sustainability/ (accessed on 1 June 2021).
- Masatsuki, I. Development of the Battery Charging System for the New Hybrid Train that Combines Feeder Line and the Storage Battery. In Proceedings of the 2010 International Power Electronics Conference—ECCE ASIA, Sapporo, Japan, 21–24 June 2010; pp. 3128–3135. [Google Scholar] [CrossRef]
- Masatsuki, I. Development of Catenary and Battery powered hybrid railcar system. In Proceedings of the 9th World Congress on Railwau Reearch, Lille, France, 22–26 May 2011. [Google Scholar]
- Hirose, H.; Yoshida, K.; Shibanuma, K. Development of catenary and storage battery hybrid train system. In Proceedings of the 2012 Electrical Systems for Aircraft, Railway and Ship Propulsion, Bologna, Italy, 16–18 October 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Kono, Y.; Shiraki, N.; Yokoyama, H.; Furuta, R. Catenary and storage battery hybrid system for electric railcar series EV-E301. In Proceedings of the 2014 International Power Electronics Conference (IPEC-Hiroshima 2014—ECCE ASIA), Hiroshima, Japan, 18–21 May 2014; pp. 2120–2125. [Google Scholar] [CrossRef]
- Shiraki, N.; Tokito, K.; Yokozutsumi, R. Propulsion system for catenary and storage battery hybrid electric railcar series EV-E301. In Proceedings of the 2015 International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles (ESARS), Aachen, Germany, 3–5 March 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Mwambeleko, J.J.; Kulworawanichpong, T. Battery electric multiple units to replace diesel commuter trains serving short and idle routes. J. Energy Storage 2017, 11, 7–15. [Google Scholar] [CrossRef]
- Kapetanović, M.; Núñez, A.; van Oort, N.; Goverde, R.M.P. Reducing fuel consumption and related emissions through optimal sizing of energy storage systems for diesel-electric trains. Appl. Energy 2021, 294, 117018. [Google Scholar] [CrossRef]
- Sorrentino, M.; Serge Agbli, K.; Hissel, D.; Chauvet, F.; Letrouve, T. Application of dynamic programming to optimal energy management of grid-independent hybrid railcars. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2021, 235, 236–247. [Google Scholar] [CrossRef]
- Ogawa, T.; Yoshihara, H.; Wakao, S.; Kondo, K.; Kondo, M. Energy consumption analysis of FC-EDLC hybrid railway vehicle by dynamic programming. In Proceedings of the European Conference on Power Electronics and Applications, Aalborg, Denamrk, 2–5 September 2007; pp. 1–8. [Google Scholar] [CrossRef]
- Leska, M.; Aschemann, H. Fuel-optimal combined driving strategy and energy management for a parallel hybrid electric railway vehicle. In Proceedings of the 20th International Conference on Methods and Models in Automation and Robotics, MMAR 2015, Miedzyzdroje, Poland, 24–27 August 2015; pp. 1127–1132. [Google Scholar] [CrossRef]
- Peng, H.; Li, J.; Thul, A.; Deng, K.; Ünlübayir, C.; Lowenstein, L.; Hameyer, K. A scalable, causal, adaptive rule-based energy management for fuel cell hybrid railway vehicles learned from results of dynamic programming. eTransportation 2020, 4, 100057. [Google Scholar] [CrossRef]
- Leska, M.; Prabel, R.; Aschemann, H.; Rauh, A. Optimal Operating Strategy for Hybrid Railway Vehicles based on a Sensitivity Analysis. IFAC Proc. Vol. 2014, 47, 942–947. [Google Scholar] [CrossRef] [Green Version]
- Leska, M.; Aschemann, H.; Melzer, M.; Meinert, M. Comparative Calculation of the Fuel-Optimal Operating Strategy for Diesel Hybrid Railway Vehicles. Int. J. Appl. Math. Comput. Sci. 2017, 27, 323–336. [Google Scholar] [CrossRef] [Green Version]
- Torreglosa, J.P.; Jurado, F.; García, P.; Fernández, L.M. Hybrid fuel cell and battery tramway control based on an equivalent consumption minimization strategy. Control. Eng. Pract. 2011, 19, 1182–1194. [Google Scholar] [CrossRef]
- Peng, H.; Li, J.; Löwenstein, L.; Hameyer, K. A scalable, causal, adaptive energy management strategy based on optimal control theory for a fuel cell hybrid railway vehicle. Appl. Energy 2020, 267, 114987. [Google Scholar] [CrossRef]
- Liu, J.; Wu, X.; Li, H.; Qi, L. An optimal method of the energy consumption for fuel cell hybrid tram. Int. J. Hydrogen Energy 2020, 45, 20304–20311. [Google Scholar] [CrossRef]
- Zhang, W.; Li, J.; Xu, L.; Ouyang, M. Optimization for a fuel cell/battery/capacity tram with equivalent consumption minimization strategy. Energy Convers. Manag. 2017, 134, 59–69. [Google Scholar] [CrossRef]
- Li, H.; Ravey, A.; N’Diaye, A.; Djerdir, A. Online adaptive equivalent consumption minimization strategy for fuel cell hybrid electric vehicle considering power sources degradation. Energy Convers. Manag. 2019, 192, 133–149. [Google Scholar] [CrossRef]
- Lanneluc, C.; Pouget, J.; Poline, M.; Chauvet, F.; Gerbaud, L. Optimal Energy Management of a Hybrid Train: Focus on Saving Braking Energy. In Proceedings of the 2017 IEEE Vehicle Power and Propulsion Conference (VPPC), Belfort, France, 11–14 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Dittus, H.; Hülsebusch, D.; Ungethüm, J. Reducing DMU fuel consumption by means of hybrid energy storage. Eur. Transp. Res. Rev. 2011, 3, 149–159. [Google Scholar] [CrossRef] [Green Version]
- García-Garre, A.; Gabaldón, A. Analysis, Evaluation and Simulation of Railway Diesel-Electric and Hybrid Units as Distributed Energy Resources. Appl. Sci. 2019, 9, 3605. [Google Scholar] [CrossRef] [Green Version]
- Spiryagin, M.; Cole, C.; Sun, Y.Q.; McClanachan, M.; Spiryagin, V.; McSweeney, T. Design and Simulation of Rail Vehicles, 1st ed.; Taylor & Francis Group, LLC: Boca Raton, FL, USA, 2014. [Google Scholar]
- Vazquez, S.; Lukic, S.M.; Galvan, E.; Franquelo, L.G.; Carrasco, J.M. Energy storage systems for transport and grid applications. IEEE Trans. Ind. Electron. 2010, 57, 3881–3895. [Google Scholar] [CrossRef] [Green Version]
- Ghaviha, N.; Campillo, J.; Bohlin, M.; Dahlquist, E. Review of Application of Energy Storage Devices in Railway Transportation. Energy Procedia 2017, 105, 4561–4568. [Google Scholar] [CrossRef]
- Meinert, M.; Prenleloup, P.; Schmid, S.; Palacin, R. Energy storage technologies and hybrid architectures for specific diesel-driven rail duty cycles: Design and system integration aspects. Appl. Energy 2015, 157, 619–629. [Google Scholar] [CrossRef]
- Xu, L.; Mueller, C.D.; Li, J.; Ouyang, M.; Hu, Z. Multi-objective component sizing based on optimal energy management strategy of fuel cell electric vehicles. Appl. Energy 2015, 157, 664–674. [Google Scholar] [CrossRef]
- Cipek, M.; Pavković, D.; Kljaić, Z.; Mlinarić, T.J. Assessment of battery-hybrid diesel-electric locomotive fuel savings and emission reduction potentials based on a realistic mountainous rail route. Energy 2019, 173, 1154–1171. [Google Scholar] [CrossRef]
- Pröhl, L. OPEUS Deliverable DO2.1—OPEUS Simulation Methodology, EU-Project OPEUS (S2R-OC-CCA-02-2015); University of Rostock: Rostock, Germany, 2017. [Google Scholar]
- Pröhl, L. OPEUS Deliverable DO2.2—OPEUS Simulation Tool, EU-Project OPEUS (S2R-OC-CCA-02-2015); University of Rostock: Rostock, Germany, 2017. [Google Scholar]
- Davis, W.J. The tractive resistance of electric locomotives and cars. Gen. Electr. Rev. 1926, 29, 685–707. [Google Scholar]
- Brünger, O.; Dahlhaus, E. Running time estimation. In Railway Timetabling & Operations; Hansen, I.A., Pachl, J., Eds.; Eurailpress: Hamburg, Germany, 2014; pp. 65–89. [Google Scholar]
- Huerlimann, D.; Nash, A. Opentrack-Simulation of Railway Networks, User Manual Version 1.3.; ETH Zurich, Institute for Transportation Planning and Systems: Zurich, Switzerland, 2003. [Google Scholar]
- Leska, M.; Gruning, T.; Aschemann, H.; Rauh, A. Optimization of the longitudinal dynamics of parallel hybrid railway vehicles. In Proceedings of the 2012 IEEE International Conference on Control Applications, Dubrovnik, Croatia, 3–5 October 2012; pp. 202–207. [Google Scholar] [CrossRef]
- Prohl, L.; Aschemann, H. Grey Wolf optimisation of an operating strategy for energy storage systems in electrically driven railway vehicles. In Proceedings of the 18th European Control Conference ECC, Naples, Italy, 25–28 June 2019; pp. 1908–1913. [Google Scholar] [CrossRef]
- Schmid, S.; Ebrahimi, K.; Pezouvanis, A.; Commerell, W. Model-based comparison of hybrid propulsion systems for railway diesel multiple units. Int. J. Rail Transp. 2017, 6, 16–37. [Google Scholar] [CrossRef] [Green Version]
- Han, Y.; Meng, X.; Zhang, G.; Li, Q.; Chen, W. An energy management system based on hierarchical control and state machine for the PEMFC-battery hybrid tramway. In Proceedings of the IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Harbin, China, 7–10 August 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Yan, Y.; Huang, W.; Liu, J.; Li, Q.; Chen, W. The Control Strategy of Fuel Cell Hybrid Tram Based on State Machine Control. In Proceedings of the IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 21–23 November 2019; pp. 699–703. [Google Scholar] [CrossRef]
- Li, Q.; Yang, H.; Han, Y.; Li, M.; Chen, W. A state machine strategy based on droop control for an energy management system of PEMFC-battery-supercapacitor hybrid tramway. Int. J. Hydrogen Energy 2016, 41, 16148–16159. [Google Scholar] [CrossRef]
- Paukert, H. CleanER-D Deliverable 7.2.1: Detailed Specification: Parameters Definition. 2011. Available online: http://www.cleaner-d.eu/deliverables.htm (accessed on 9 January 2021).
- Pourabdollah, M.; Murgovski, N.; Grauers, A.; Egardt, B. Optimal Sizing of a Parallel PHEV Powertrain. IEEE Trans. Veh. Technol. 2013, 62, 2469–2480. [Google Scholar] [CrossRef] [Green Version]
- Giro Batalla, R.; Feenstra, M. Energy Consumption in GTW DMU Trains—ECO Driving; Project Statement; Arriva Nederland: Sunderland, UK, 2012. [Google Scholar]
- Stadler Bussnang AG. GTW DMU-2 2/6 and GTW 2/8 Low-Floor for Arriva, Netherlands. Available online: https://www.stadlerrail.com/media/pdf/garr1008e.pdf (accessed on 15 January 2021).
- Takami, N.; Inagaki, H.; Tatebayashi, Y.; Saruwatari, H.; Honda, K.; Egusa, S. High-power and long-life lithium-ion batteries using lithium titanium oxide anode for automotive and stationary power applications. J. Power Sources 2013, 244, 469–475. [Google Scholar] [CrossRef]
- Toshiba. SCiBTM Rechargeable Battery. Available online: https://www.global.toshiba/ww/products-solutions/battery/scib.html (accessed on 16 February 2021).
- SAFT; UNEW. OPEUS Deliverable D6.1—Innovative Technologies Outlook Update. EUproject OPEUS (S2R-OC-CCA-02-2015). 2017. Available online: https://projects.shift2rail.org/s2r_ip4_n.aspx?p=OPEUS (accessed on 16 February 2021).
- Maxwell. 125 Volt Transportation Module. 2021. Available online: https://www.maxwell.com/products/ultracapacitors/125v-tran-modules# (accessed on 16 February 2021).
- ProRail. Network Statement 2020. Available online: https://www.prorail.nl/siteassets/homepage/samenwerken/vervoerders/documenten/network-statement-2020-prorail-version-1.6.pdf (accessed on 21 March 2021).
- Leska, M.; Gruning, T.; Aschemann, H.; Rauh, A. Optimal trajectory planning for standard and hybrid railway vehicles with a hydro-mechanic transmission. In Proceedings of the European Control Conference ECC, Zurich, Switzerland, 17–19 July 2013; pp. 4550–4555. [Google Scholar] [CrossRef]
- Kirschstein, T.; Meisel, F. GHG-emission models for assessing the eco-friendliness of road and rail freight transports. Transp. Res. Part B Methodol. 2015, 73, 13–33. [Google Scholar] [CrossRef]
- Hoffrichter, A.; Miller, A.R.; Hillmansen, S.; Roberts, C. Well-to-wheel analysis for electric, diesel and hydrogen traction for railways. Transp. Res. Part D Transp. Environ. 2012, 17, 28–34. [Google Scholar] [CrossRef]
- CEN. Standard EN 16258: Methodology for Calculation and Declaration of Energy Consumption and GHG Emissions of Transport Services (Freight and Passengers). Available online: https://standards.cen.eu/dyn/www/f?p=204:110:0::::FSP_PROJECT:32935&cs=12646506D5D79DADCB74CA2C32A2DAA45 (accessed on 3 March 2021).
- CO2emissiefactoren. 2020 List of CO2 Emission Factors [in Dutch]. Available online: https://www.co2emissiefactoren.nl/wijzigingen-overzicht/ (accessed on 9 May 2021).
- EcoWatch. Dutch Trains Are World’s First to Run on 100% Wind Power. Available online: https://www.ecowatch.com/dutch-trains-wind-energy-2187547588.html (accessed on 29 March 2021).
- CBS. Pump Prices for Motor Fuels; Location Gas Station, Fuel Type [in Dutch]. Available online: https://opendata.cbs.nl/statline/?ts=1585295852166#/CBS/nl/dataset/81567NED/table (accessed on 1 May 2021).
- Scheepmaker, G.M.; Goverde, R.M.P.; Kroon, L.G. Review of energy-efficient train control and timetabling. Eur. J. Oper. Res. 2017, 257, 355–376. [Google Scholar] [CrossRef] [Green Version]
- Hoffrichter, A.; Roberts, C.; Hillmansen, S. Conceptual propulsion system design for a hydrogen-powered regional train. IET Electr. Syst. Transp. 2016, 6, 56–66. [Google Scholar] [CrossRef] [Green Version]
- CEN. EN 15528: Railway Applications—Line Categories for Managing the Interface Between Load Limits of Vehicles and Infrastructure. 2015. Available online: https://www.en-standard.eu/din-en-15528-railway-applications-line-categories-for-managing-the-interface-between-load-limits-of-vehicles-and-infrastructure/ (accessed on 21 February 2021).
- Peng, F.; Zhao, Y.; Chen, T.; Zhang, X.; Chen, W.; Zhou, D.; Li, Q.F. Development of robust suboptimal real-time power sharing strategy for modern fuel cell based hybrid tramways considering operational uncertainties and performance degradation. Appl. Energy 2018, 226, 503–521. [Google Scholar] [CrossRef]
- Esters, T.; Marinov, M. An analysis of the methods used to calculate the emissions of rolling stock in the UK. Transp. Res. Part D Transp. Environ. 2014, 33, 1–16. [Google Scholar] [CrossRef]
- Romare, M.; Dahllöf, L. The Life Cycle Energy Consumption and Greenhouse Gas Emissions from Lithium-Ion Batteries. 2017. Available online: http://www.energimyndigheten.se/globalassets/forskning--innovation/transporter/c243-the-life-cycle-energy-consumption-and-co2-emissions-from-lithium-ion-batteries-.pdf (accessed on 20 June 2021).
- Ellingsen, L.A.W.; Singh, B.; Strømman, A.H. The size and range effect: Lifecycle greenhouse gas emissions of electric vehicles. Environ. Res. Lett. 2016, 11, 054010. [Google Scholar] [CrossRef]
- Jones, H.; Moura, F.; Domingos, T. Life cycle assessment of high-speed rail: A case study in Portugal. Int. J. Life Cycle Assess. 2017, 22, 410–422. [Google Scholar] [CrossRef]
- García Márquez, F.P.; Lewis, R.W.; Tobias, A.M.; Roberts, C. Life cycle costs for railway condition monitoring. Transp. Res. Part E Logist. Transp. Rev. 2008, 44, 1175–1187. [Google Scholar] [CrossRef]



| Parameter | Unit | Value | Description |
|---|---|---|---|
| t | 70.4 | Tare weight 1 | |
| - | 0.05 | Rotating mass factor 2 | |
| t | 7 | Total passengers weight 3 | |
| N | 1001 | Davis equation coefficient (constant term) 2 | |
| N/(km/h) | 22.3 | Davis equation coefficient (linear term) 2 | |
| N/(km/h)2 | 0.1 | Davis equation coefficient (quadratic term) 2 | |
| m | 0.86 | Powered wheel diameter 4 | |
| - | 1.7218 | Axle gear ratio 5 | |
| - | 0.97 | Axle gear efficiency 6 | |
| km/h | 140 | Maximum velocity 4 | |
| m/s2 | 1.05 | Maximum acceleration 2 | |
| m/s2 | −1 | Maximum deceleration 2 | |
| kN | 80 | Maximum (starting) tractive effort at the wheel 4 | |
| kW | 600 | Maximum power at the wheel 4 | |
| kW | 2 × 400 | EM rated power 1 | |
| kW | 2 × 390 | ICE rated power 1 | |
| kW | 50 | Constant auxiliaries power 3 | |
| - | 0.01 | Cooling power coefficient 3 | |
| g/L | 825 | Fuel density (diesel) 6 |
| Parameter | Unit | Value | Description |
|---|---|---|---|
| LB module 1 | |||
| Ah | 45 | Nominal capacity | |
| A | −160/160 | Minimum/maximum continuous current | |
| A | −350/350 | Minimum/maximum pulse current | |
| s | 10 | Allowed time for pulse current | |
| V | 18/32.4 | Minimum/maximum voltage | |
| Ω | 0.006 | Internal resistance charge/discharge | |
| % | 10/90 | Minimum/maximum SoC 2 | |
| kWh | 1.24 | Energy content | |
| kWh | 0.922 | Usable energy content 3 | |
| kg | 15 | Weight | |
| DLC module 4 | |||
| F | 63 | Rated capacitance | |
| A | −240/240 | Minimum/maximum continuous current | |
| V | 12.5/125 | Minimum/maximum voltage | |
| Ω | 0.018 | Internal resistance | |
| kWh | 0.14 | Energy content | |
| kg | 61 | Weight |
| Station | Distance (km) | Departure Time (hh:mm) | |||
|---|---|---|---|---|---|
| Stopping Service 1 | Express Service | ||||
| Lw → Gn | Gn → Lw | Lw → Gn | Gn → Lw | ||
| Leeuwarden | 0 | hh: 51 | hh + 2:40 (arrival) | hh: 44 | hh + 2:16 (arrival) |
| Leeuwarden C. | 3.34 | hh: 54 | hh + 2:35 | - | - |
| Hurdegaryp | 9.83 | hh + 1:01 | hh + 2:30 | - | - |
| Feanwalden | 14.00 | hh + 1:05 | hh + 2:25 | - | - |
| De Westereen | 17.24 | hh + 1:08 | hh + 2:20 | - | - |
| Buitenpost | 24.74 | hh + 1:16 | hh + 2:15 | hh + 1:00 | hh + 2:00 |
| Grijskerk | 35.71 | hh + 1:23 | hh + 2:06 | - | - |
| Zuidhorn | 42.35 | hh + 1:30 | hh + 2:01 | - | - |
| Groningen | 54.05 | hh + 1:39 (arrival) | hh + 1:51 | hh + 1:18 (arrival) | hh + 1:42 |
| Service | Configuration | ESS | Charging Option 1 | Energy Consumption | GHG Emissions 2 [kgCO2e] | Energy Costs [EUR] | |
|---|---|---|---|---|---|---|---|
| Fuel [L] | Electricity [kWh] | ||||||
| Stopping | DEMU | - | - | 106.31 | - | 343.38 | 131.51 |
| HDEMU | LB | - | 92.01 | - | 297.19 | 113.82 | |
| DLC | - | 72.43 | - | 233.95 | 89.60 | ||
| PHDEMU | LB | TSs | 75.77 | 41.01 | 267.54 (244.74) | 94.72 | |
| TSs + IS | 75.84 | 47.44 | 271.34 (244.96) | 94.96 | |||
| DLC | TSs | 50.38 | 63.43 | 197.99 (162.73) | 63.85 | ||
| TSs + IS | 46.04 | 100.55 | 204.62 (148.71) | 59.38 | |||
| Express | DEMU | - | - | 140.40 | - | 453.49 | 173.67 |
| HDEMU | LB | - | 126.80 | - | 409.56 | 156.85 | |
| DLC | - | 87.11 | - | 281.37 | 107.76 | ||
| PHDEMU | LB | TSs | 106.61 | 49.61 | 371.93 (344.35) | 133.07 | |
| TSs + IS | 118.58 | 49.84 | 410.72 (383.01) | 147.89 | |||
| DLC | TSs | 61.98 | 83.48 | 246.61 (200.20) | 78.68 | ||
| TSs + IS | 60.49 | 104.81 | 253.66 (195.38) | 77.36 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kapetanović, M.; Vajihi, M.; Goverde, R.M.P. Analysis of Hybrid and Plug-In Hybrid Alternative Propulsion Systems for Regional Diesel-Electric Multiple Unit Trains. Energies 2021, 14, 5920. https://doi.org/10.3390/en14185920
Kapetanović M, Vajihi M, Goverde RMP. Analysis of Hybrid and Plug-In Hybrid Alternative Propulsion Systems for Regional Diesel-Electric Multiple Unit Trains. Energies. 2021; 14(18):5920. https://doi.org/10.3390/en14185920
Chicago/Turabian StyleKapetanović, Marko, Mohammad Vajihi, and Rob M. P. Goverde. 2021. "Analysis of Hybrid and Plug-In Hybrid Alternative Propulsion Systems for Regional Diesel-Electric Multiple Unit Trains" Energies 14, no. 18: 5920. https://doi.org/10.3390/en14185920
APA StyleKapetanović, M., Vajihi, M., & Goverde, R. M. P. (2021). Analysis of Hybrid and Plug-In Hybrid Alternative Propulsion Systems for Regional Diesel-Electric Multiple Unit Trains. Energies, 14(18), 5920. https://doi.org/10.3390/en14185920






