Towards Understanding the Structure of Subcritical and Transcritical Liquid–Gas Interfaces Using a Tabulated Real Fluid Modeling Approach
Abstract
:1. Introduction
1.1. Review on Supercritical Fluids and Transcritical Injection
1.2. Review on Numerical and Thermodynamic Models for Two-Phase Flows
1.3. Subcritical, Transcritical, and Supercritical Real Fluid Mixing Injection

1.4. Review on the VLE Tabulation Approach
1.5. Outline of the Present Study
2. The Real-Fluid Model (RFM)
2.1. Governing Equations of the Flow Solver
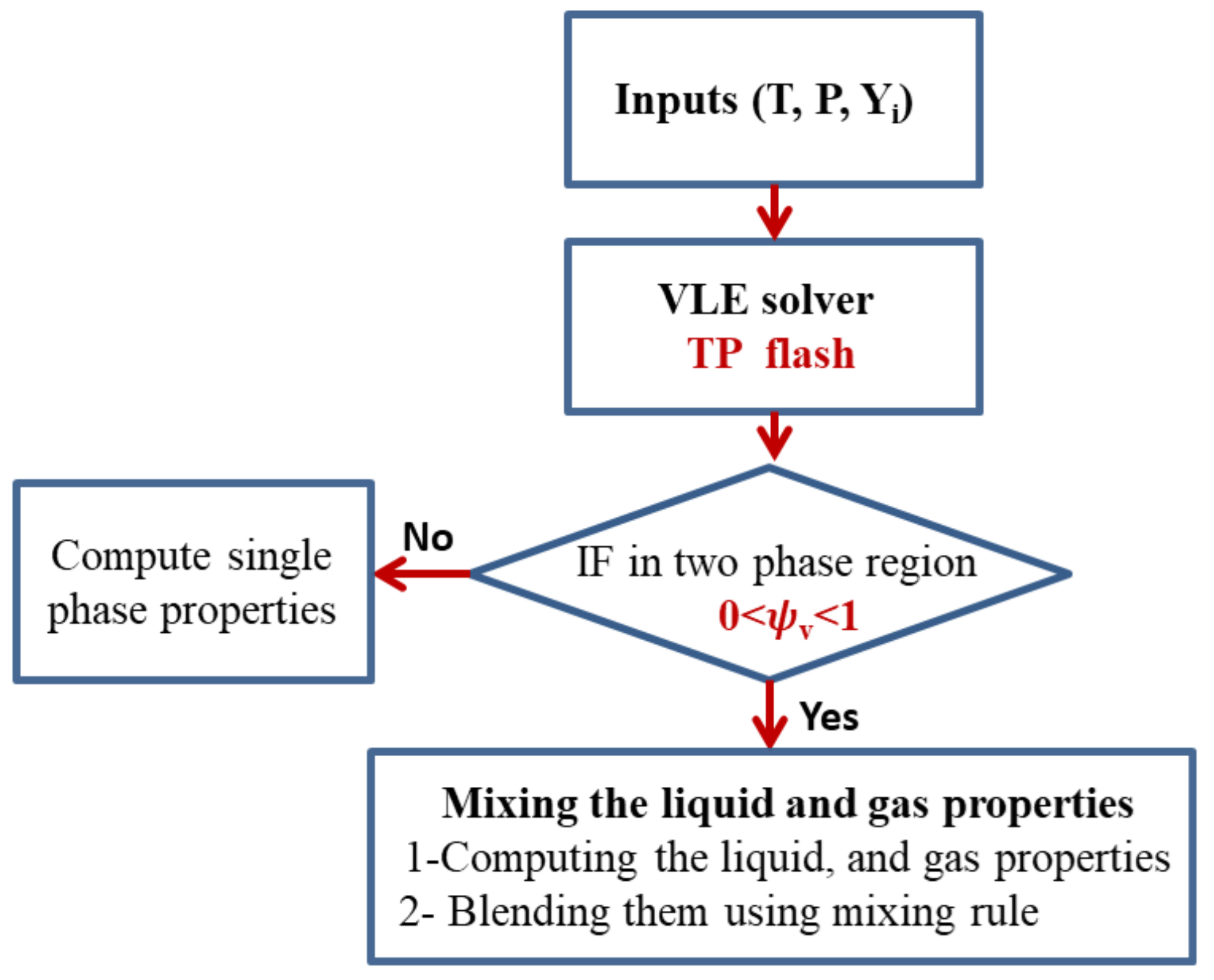
2.2. Equilibrium Thermodynamic Closure of the Flow Solver, and the Tabulation Look-Up
- A Table look-up function:Compute the thermal, transport properties as well as the phase state using the input parameters.
- A Reverse look-up function:Compute/Update the temperature using the inputs .
- Inputs: , where is the initial (feed) mass fraction of species and , where is the total number of species.
- Solve the VLE problem: () = VLE , where , , , are species the initial feed (in mole fraction), species molar fraction in the liquid and gas phase, respectively. is the vapor molar fraction. See [8].
- If the mixture is in single phase liquid or single phase vapor , then the single phase properties are directly computed. In this configuration, if the density is less than 400 kg/m, then the phase is assumed to be vapor, and if it is greater than 400 kg/m, it is assumed to be liquid.
- If the mixture is in a two phase state , compute both the liquid and gas phase properties, then the two-phase mixture properties are evaluated through Equations (A1)–(A7). In (A1)–(A7), is the phase volume fraction and () stands for liquid and vapor phases, respectively. The vapor volume fraction is computed from the vapor mole fraction as . are the mixture’s density, specific internal energy, and Wood speed of sound.
- Repeat steps (2 and 3) or (2 and 4), until the specified input ranges for are completed for the desired number of points in the table.

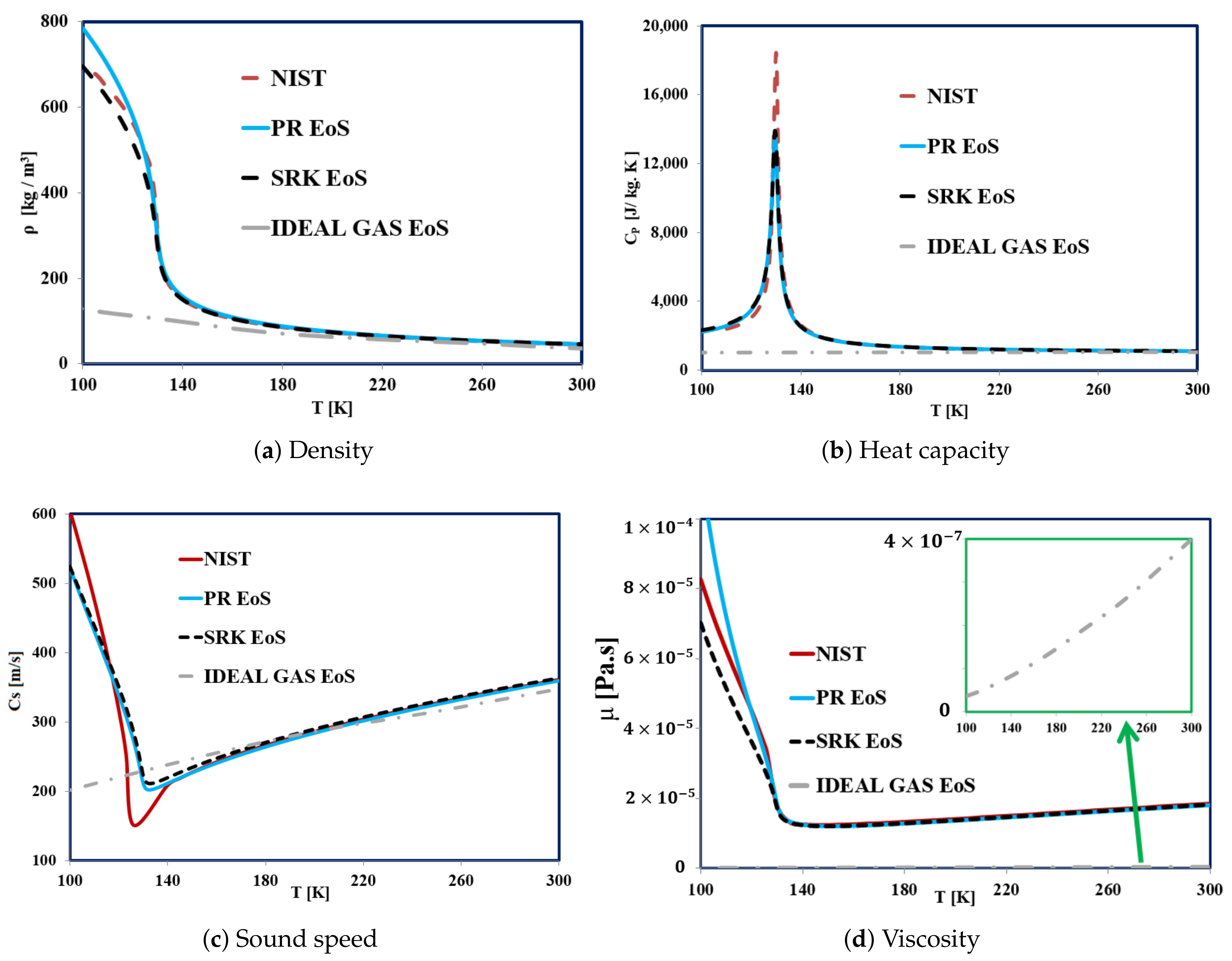
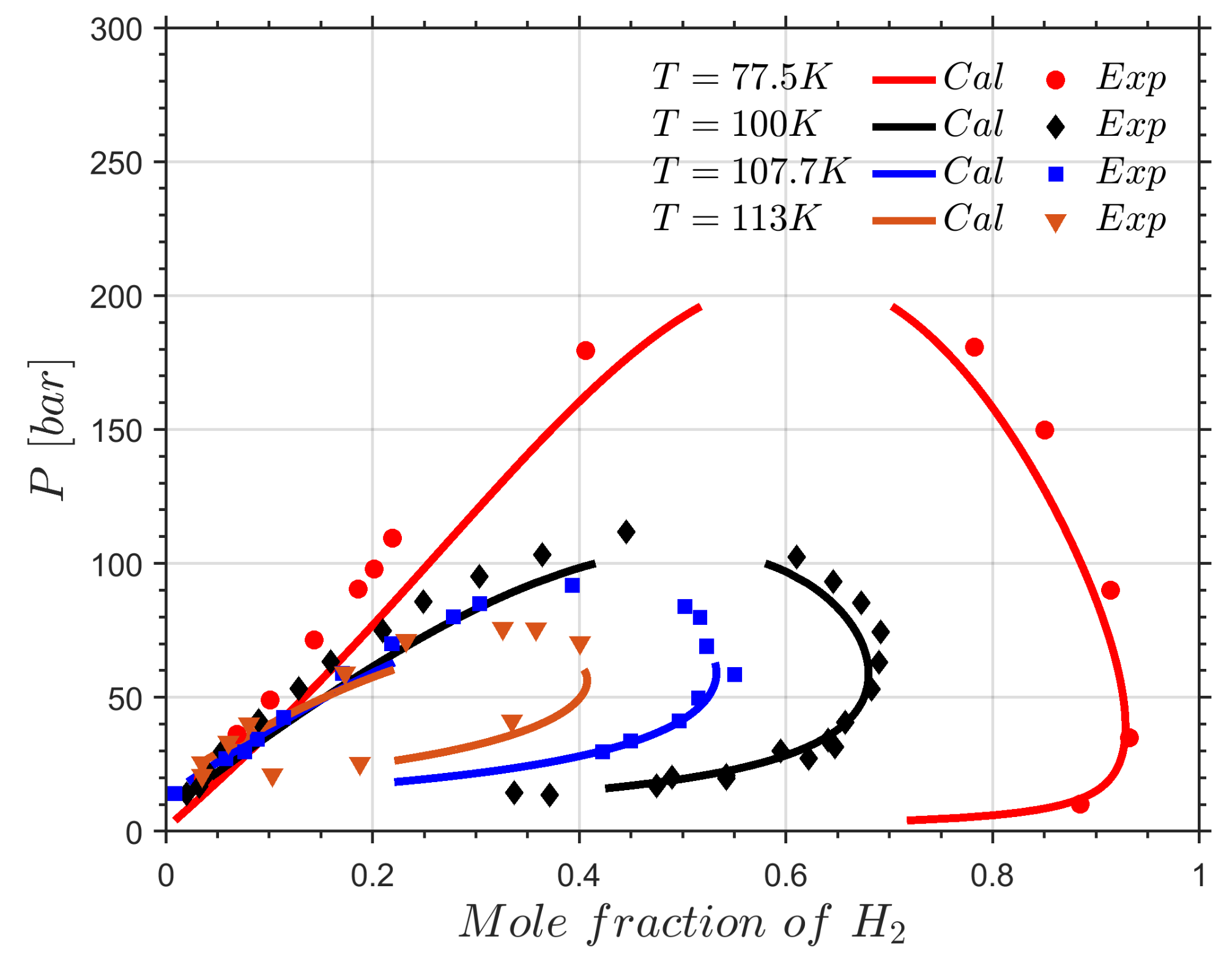
2.3. Validation of the VLE Solver
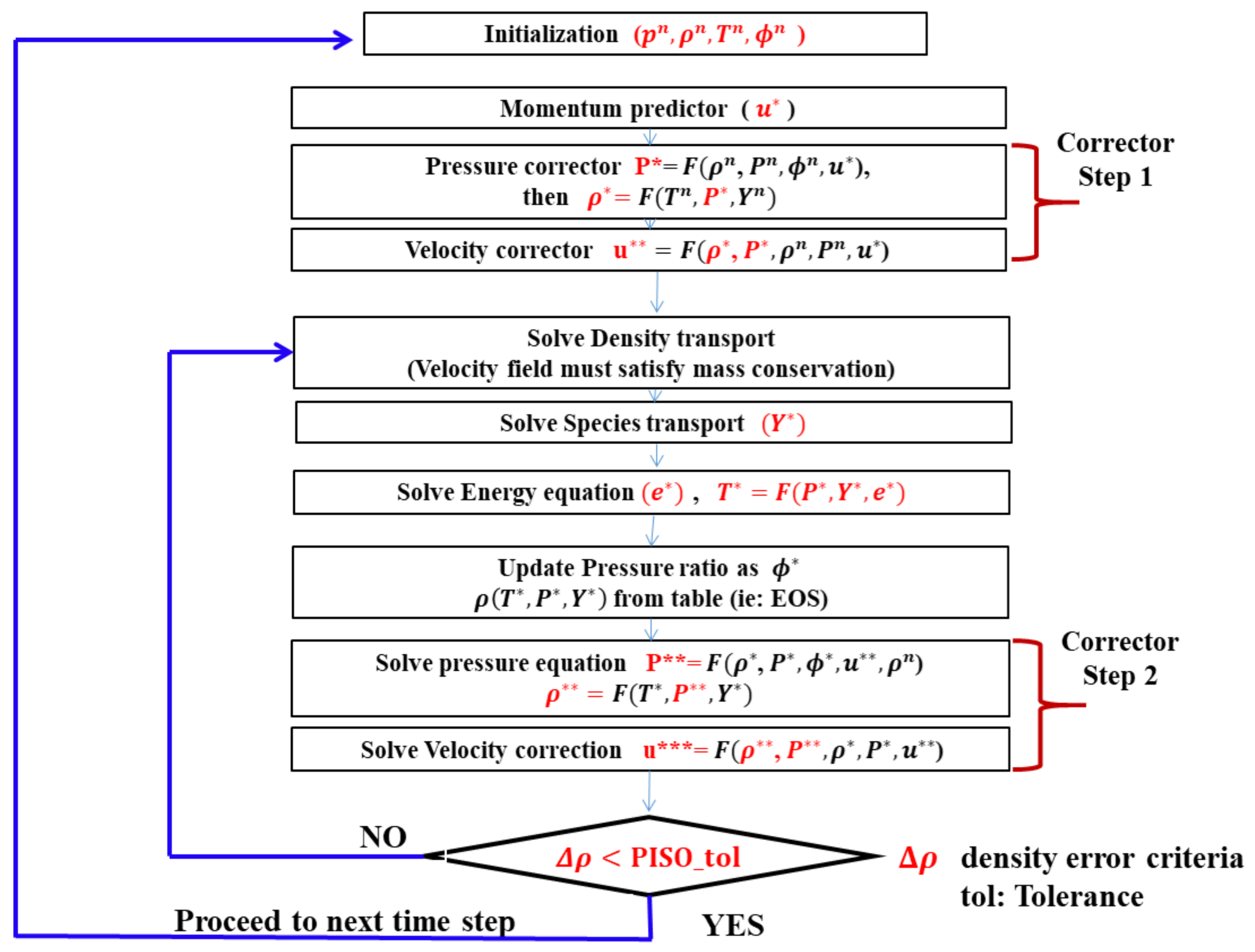
2.4. Coupling the Flow Solver with the Thermodynamic Solver
- Read the thermodynamic table during the simulation setup and initialize the thermal and transport properties as well as the phase state based on the temperature , pressure , and species mass fraction in the domain, where the exponent (n) denotes the current time step.
- Solve the momentum predictor, and then the first corrector step.
- Solve the transport equations in the order shown in the flow chart, as depicted in Figure 8b.
- At the end of each iteration loop, the convergence is checked based on the density correction error for density based solver, where : the current correction for the density, is the previous value of the density correction, and for pressure based solver, where : the current correction for the pressure, and is the previous value of the pressure correction. If the specified loop tolerance error is reached, the values of the previous time step are updated before proceeding to the next time step, otherwise a new SIMPLE or PISO loop is performed.
3. Transcritical Mixing and Evaporation Study
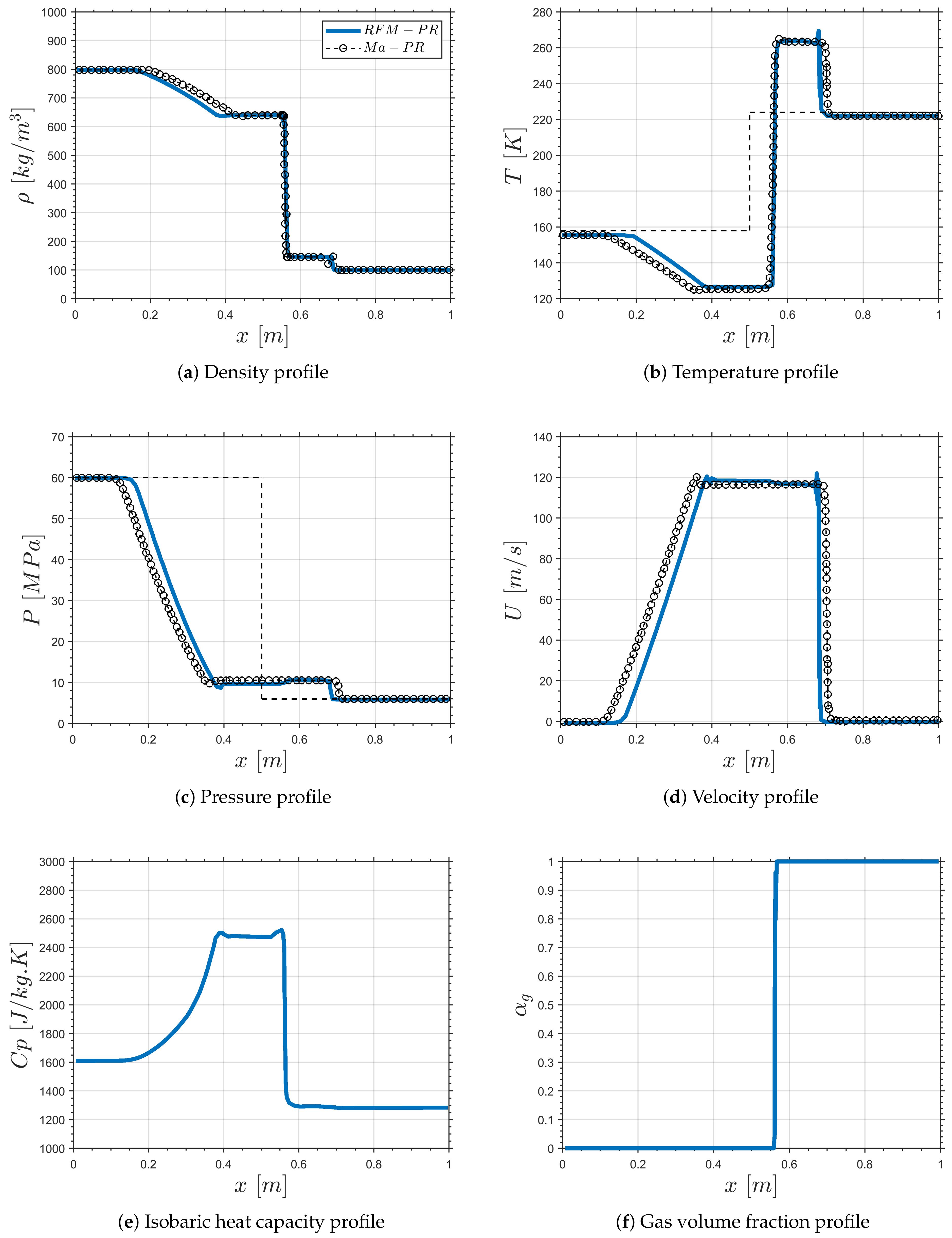
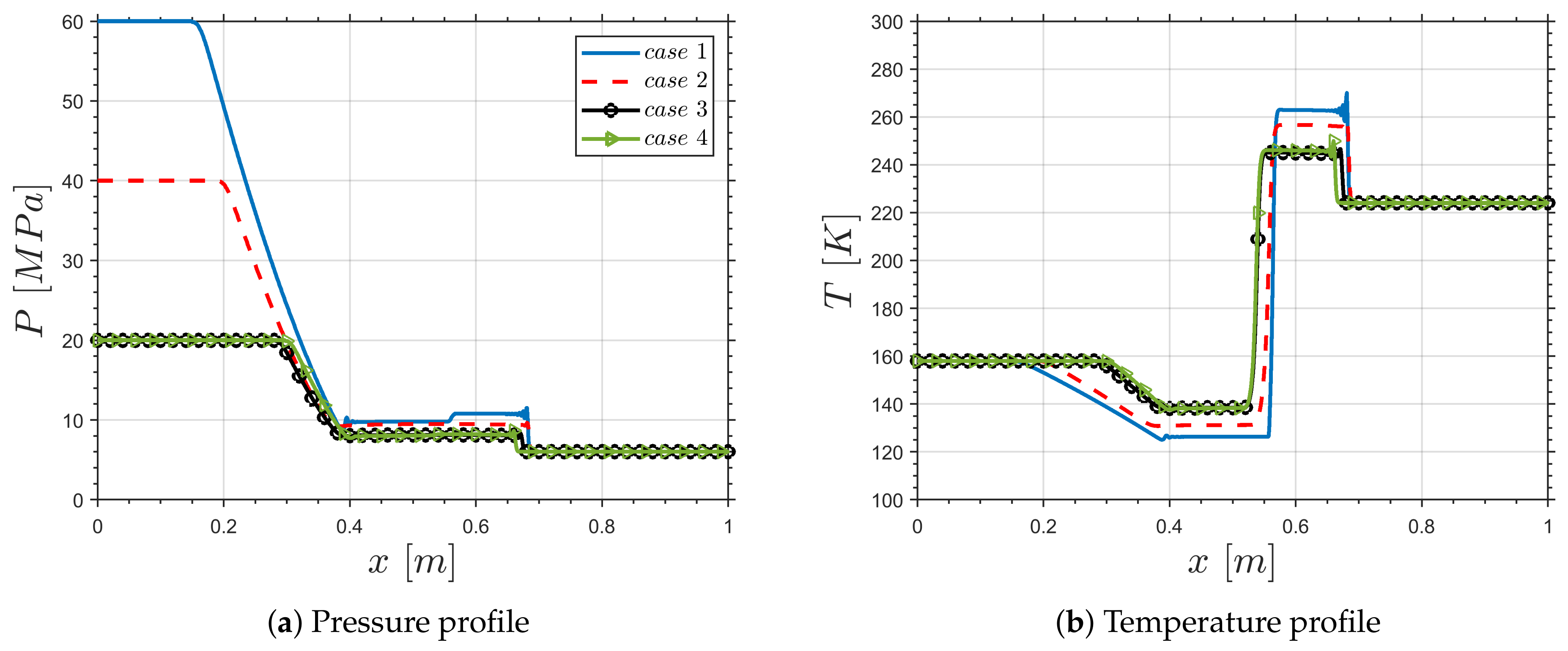
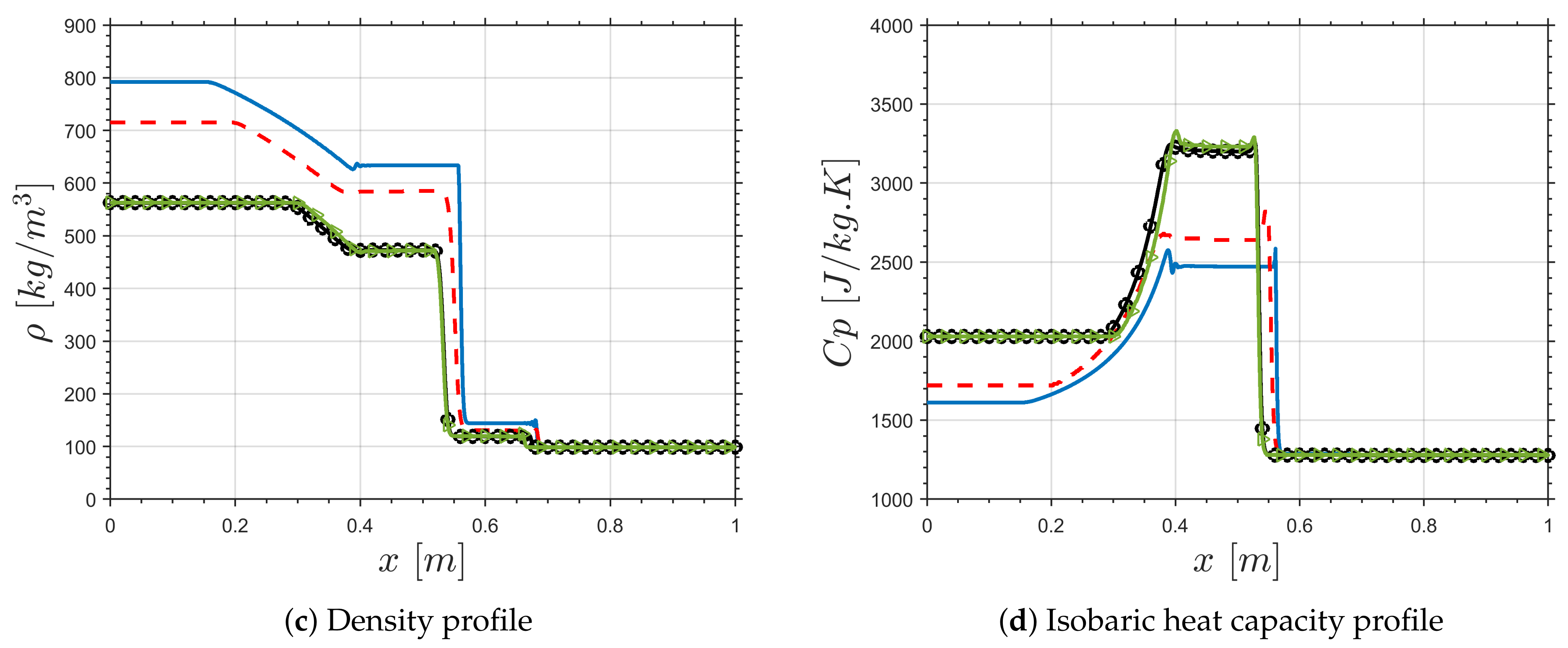
3.1. 1-D Transcritical Shock Tube Test Cases
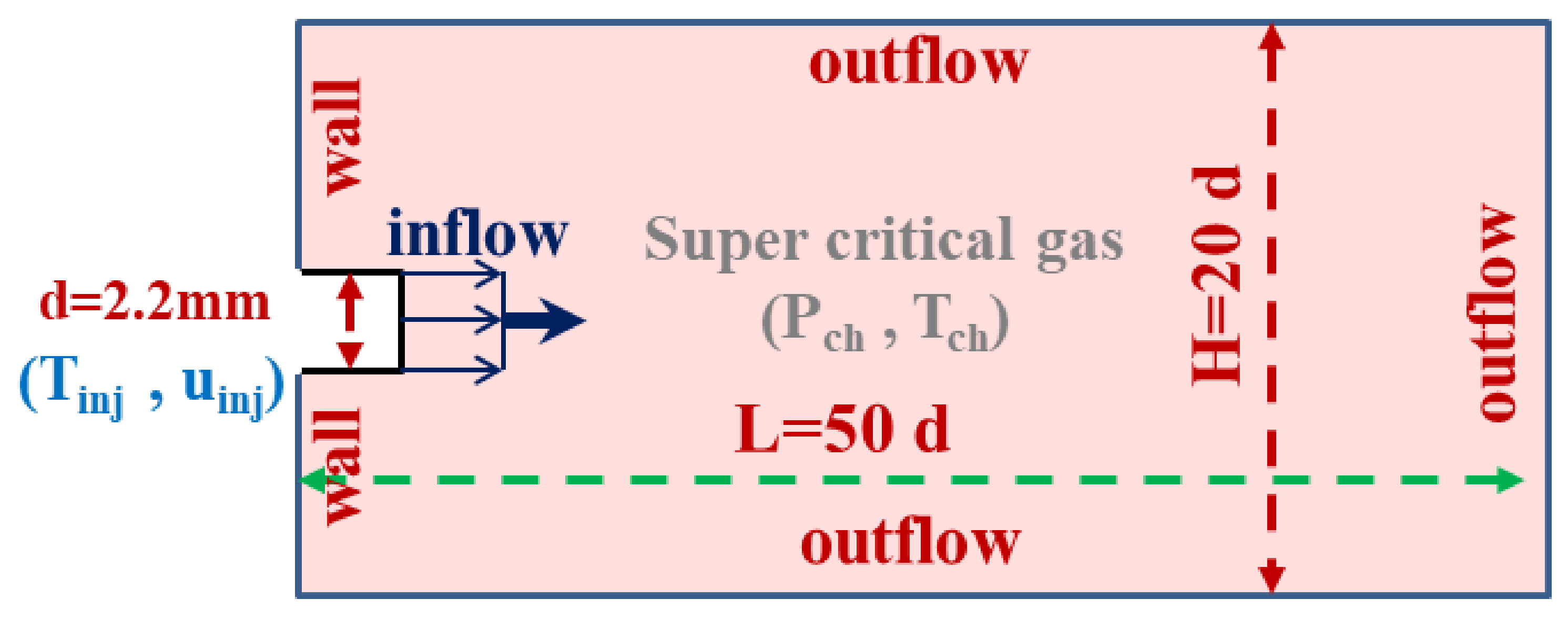
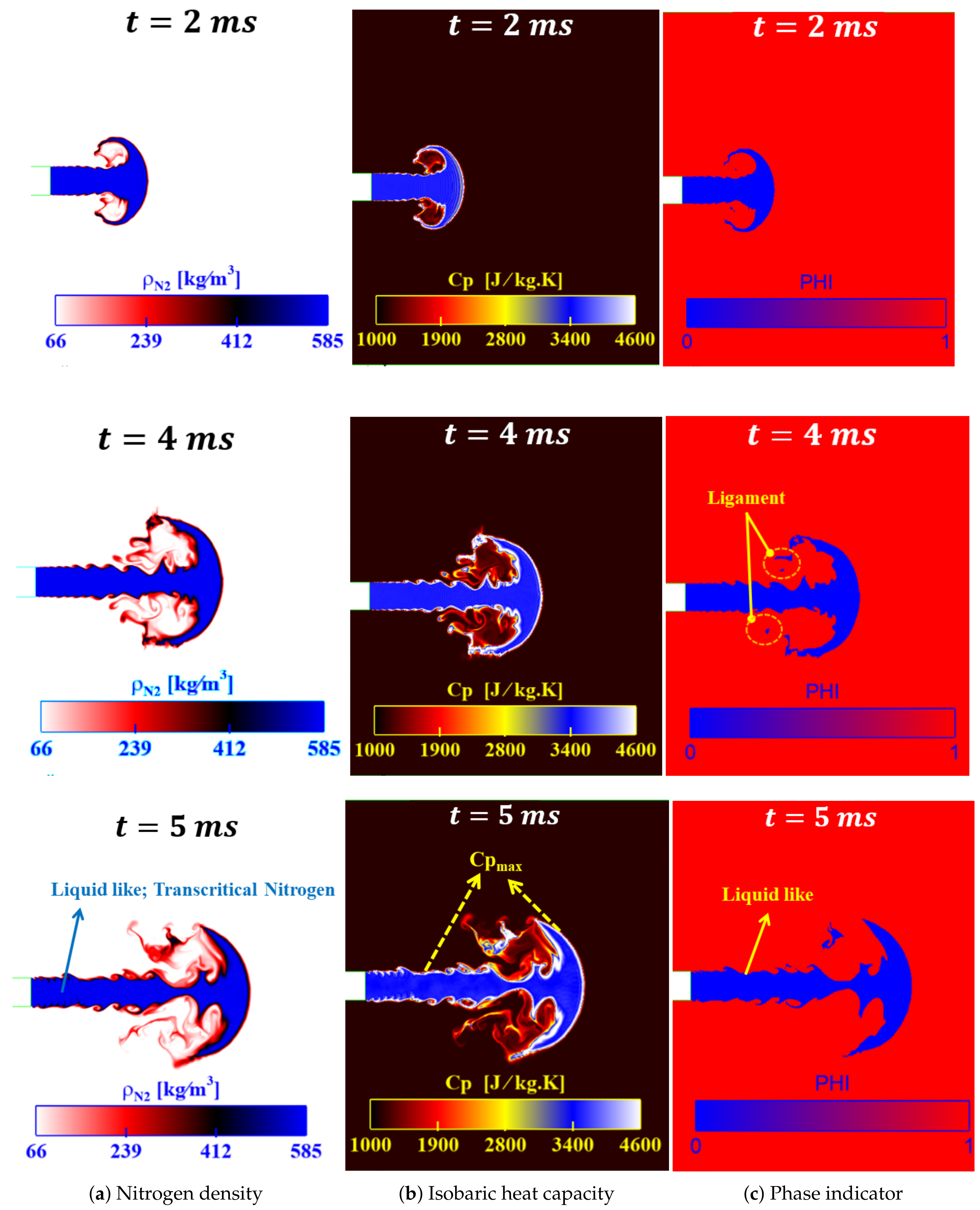
3.2. Transcritical Single-Component Cryogenic Injection
3.3. Binary Coaxial Injection of L with Hot G
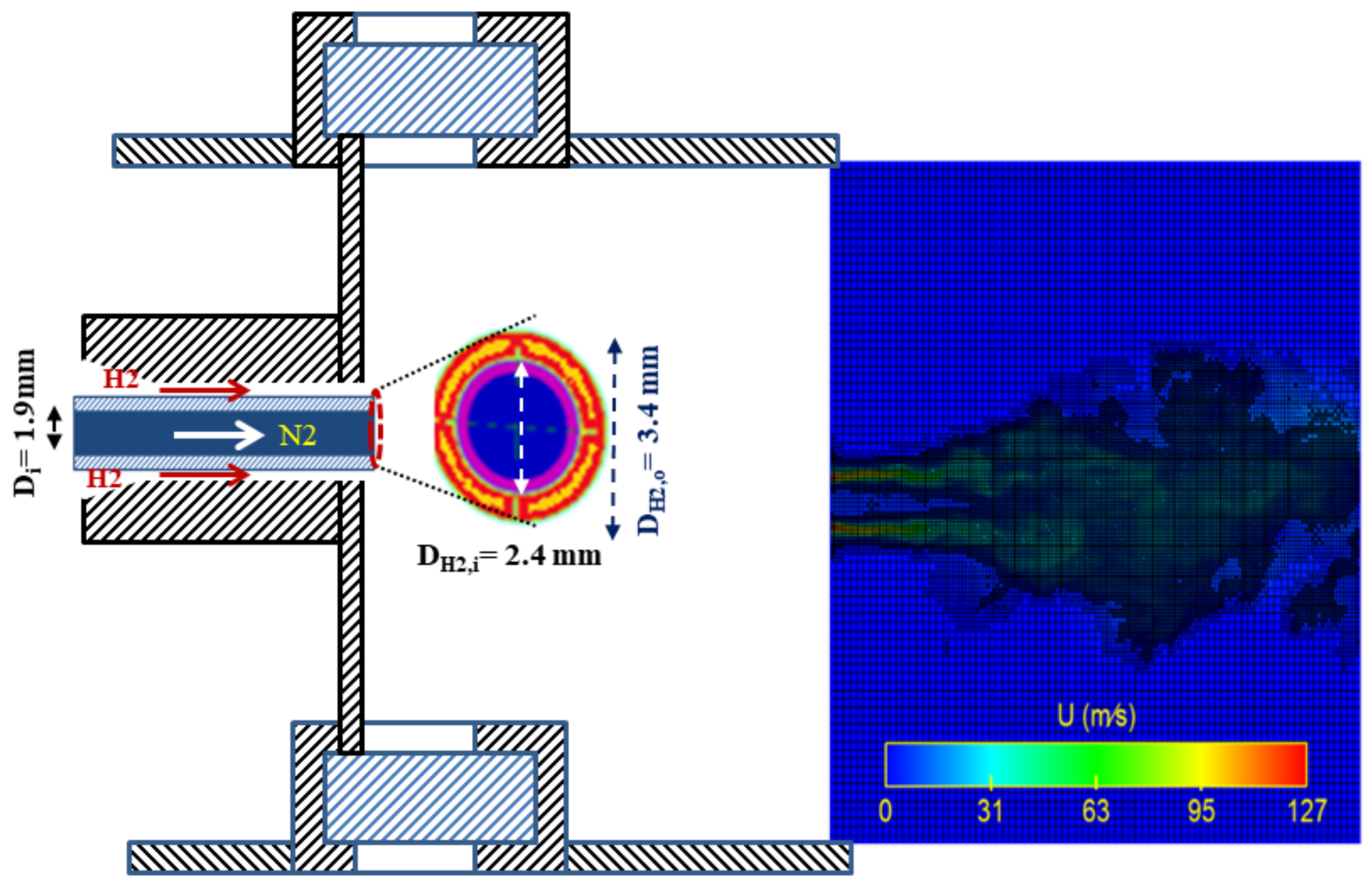
3.3.1. Configuration Description and Numerical Methods (Case 8)
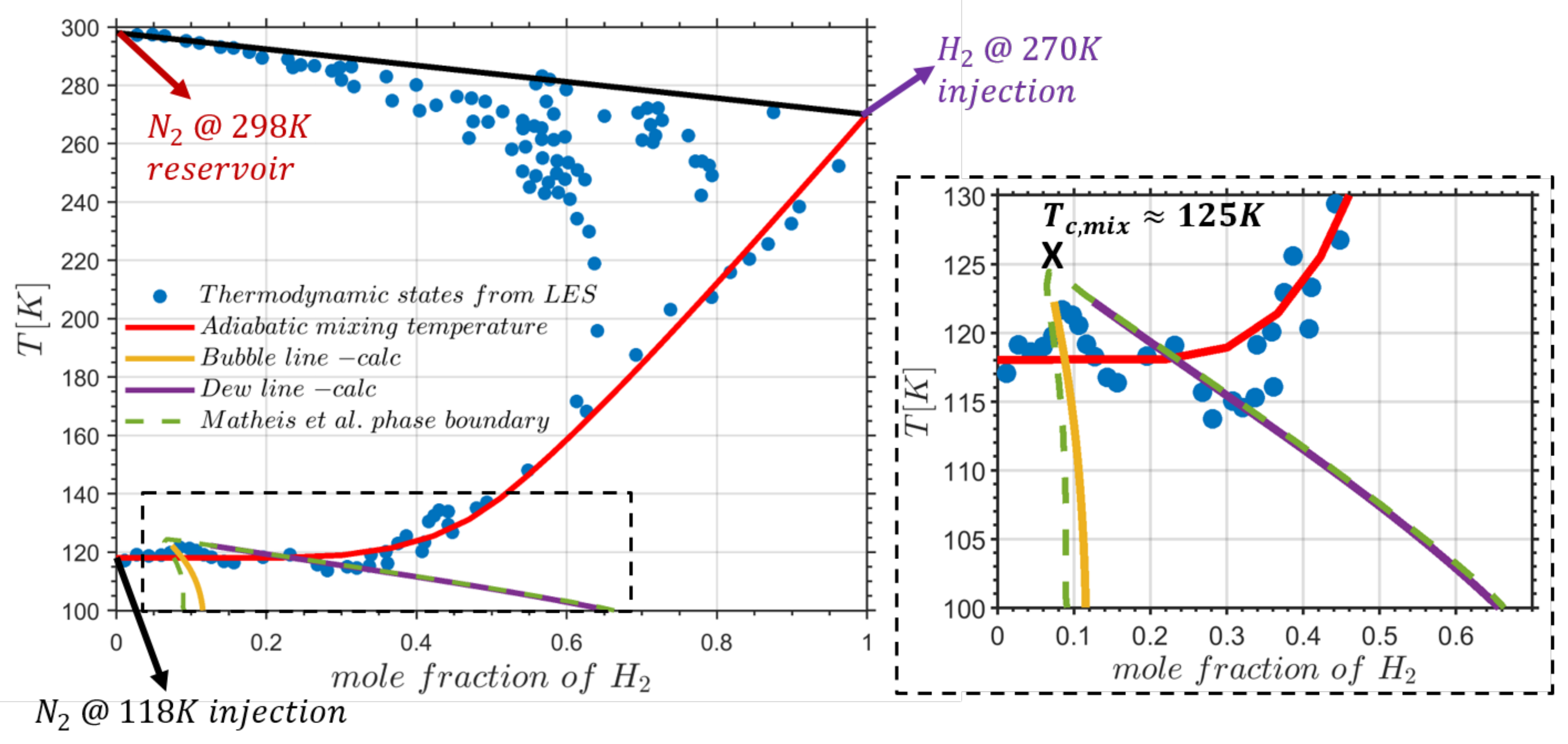
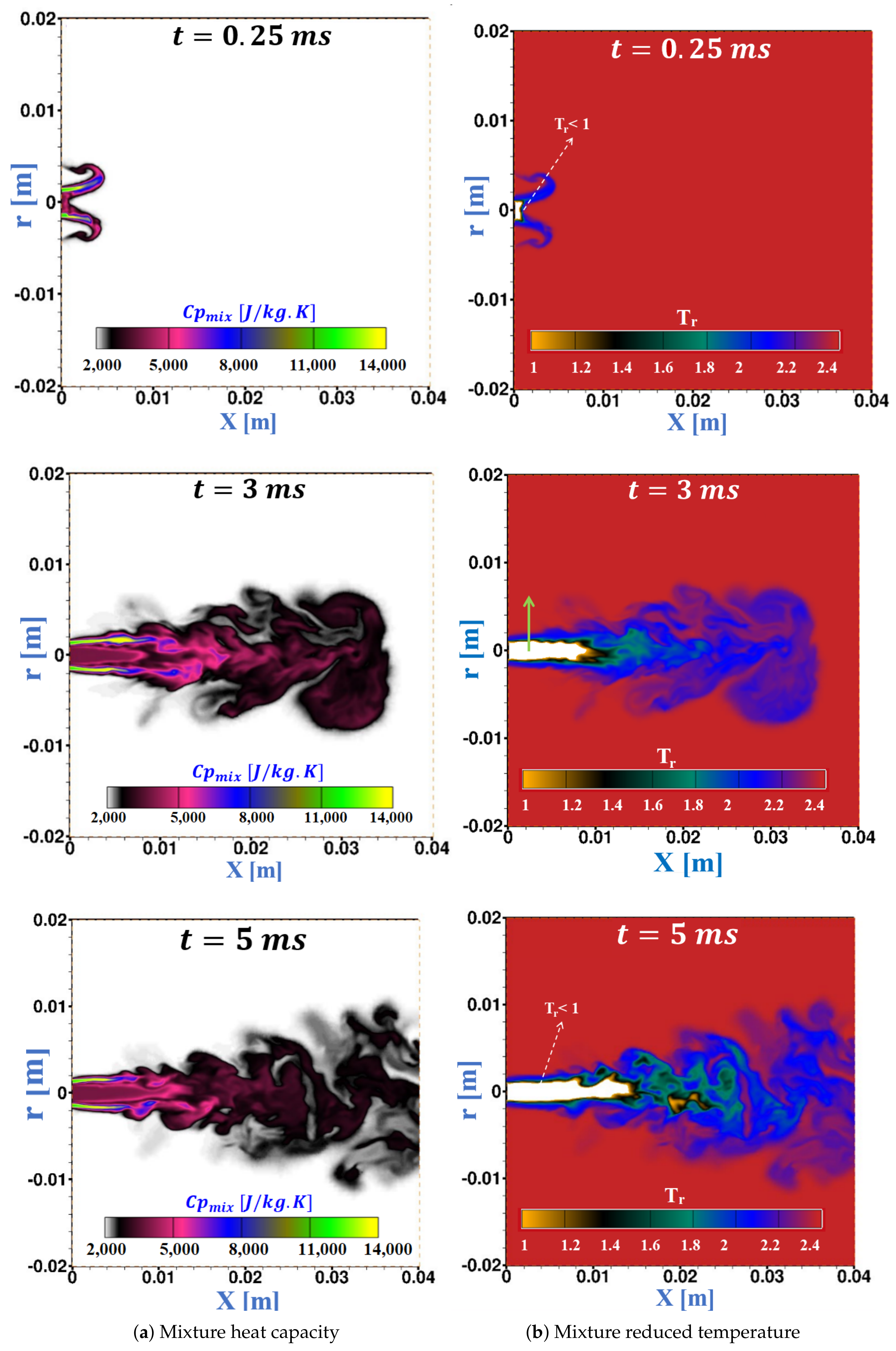
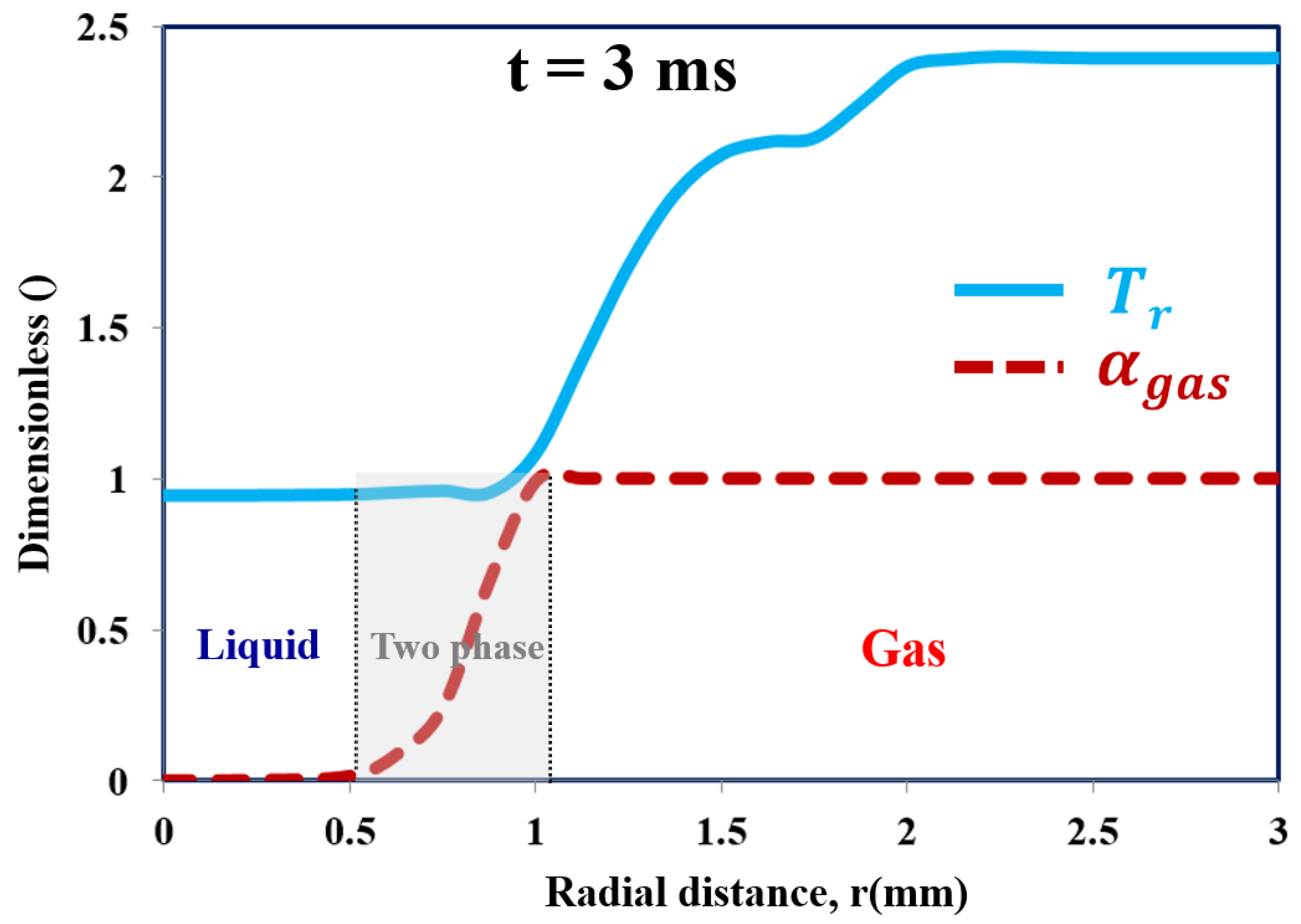
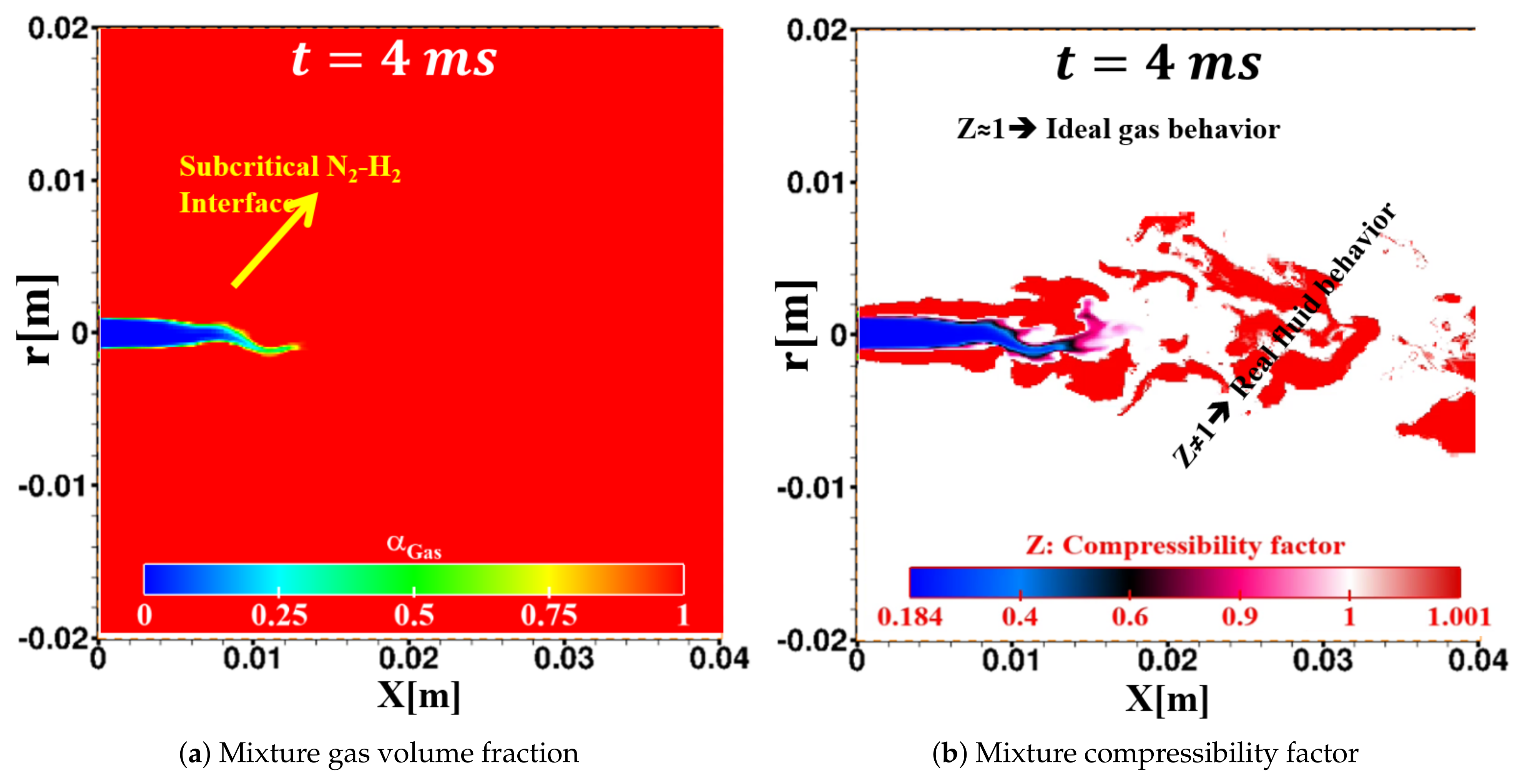
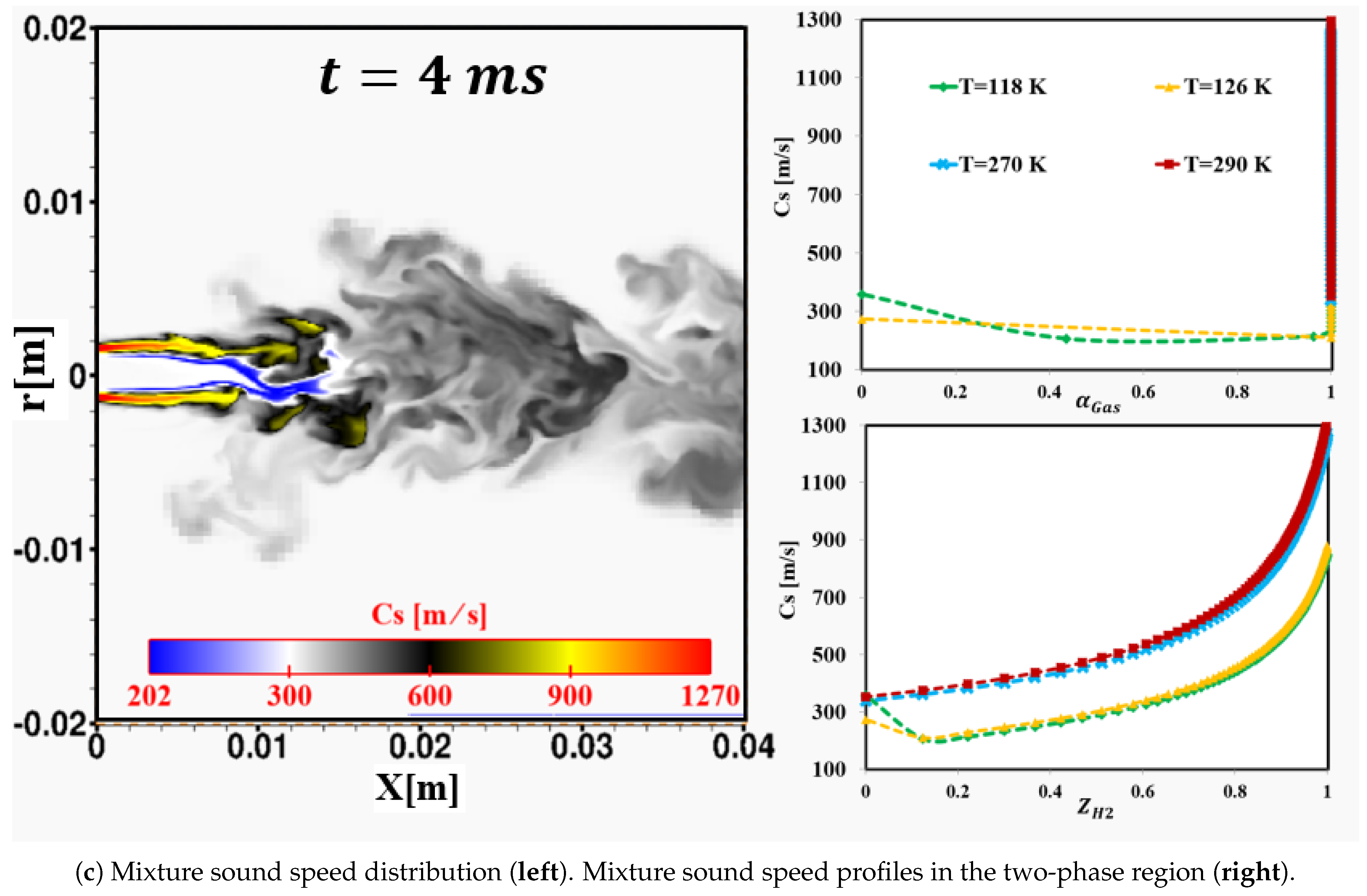
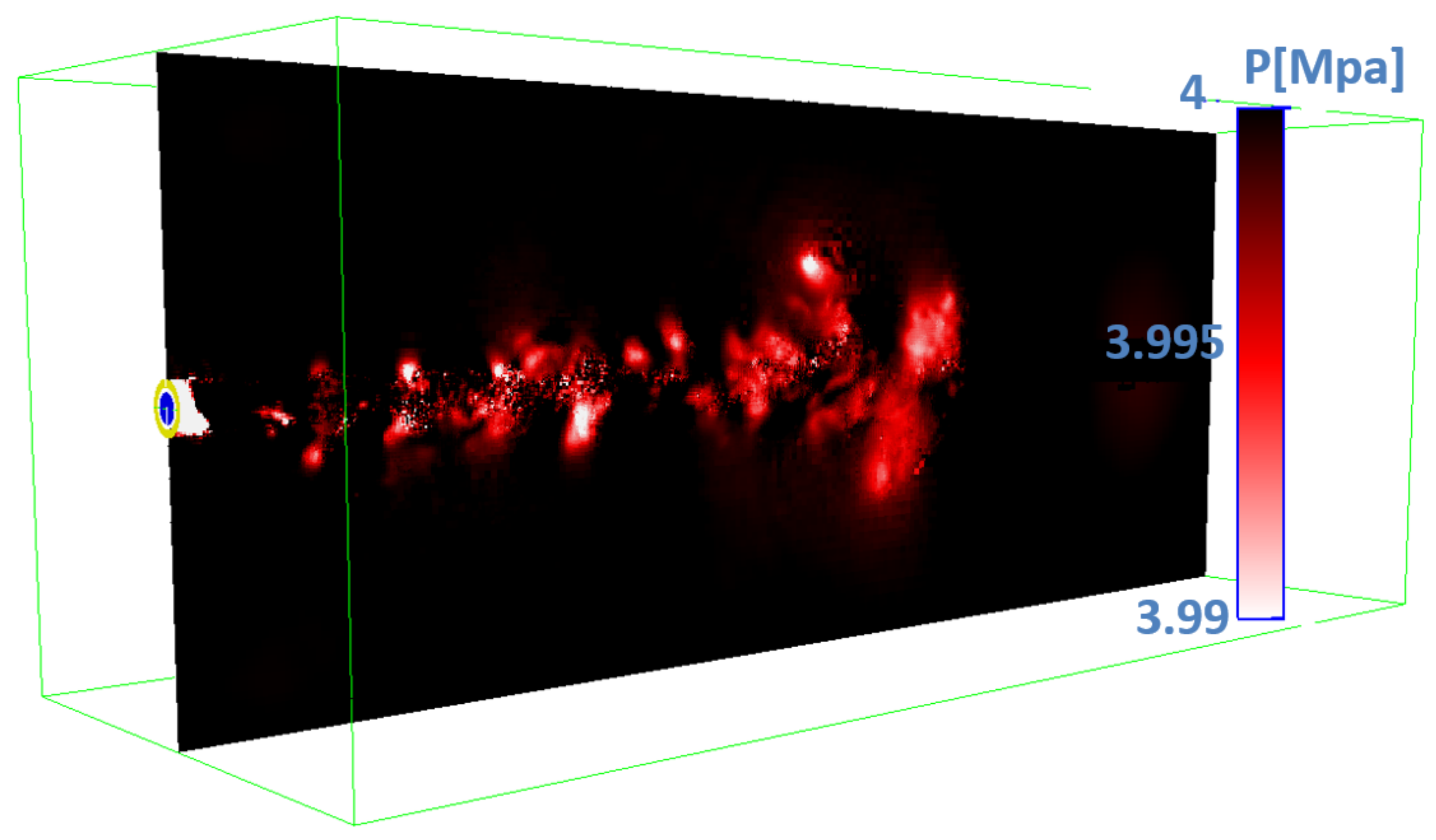
3.3.2. Results and Discussion
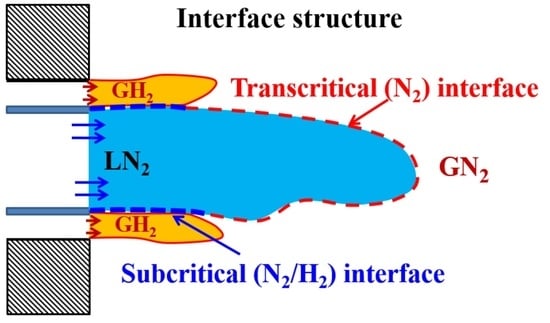
Flow Mixing Hydro-Thermodynamics and Interface Features
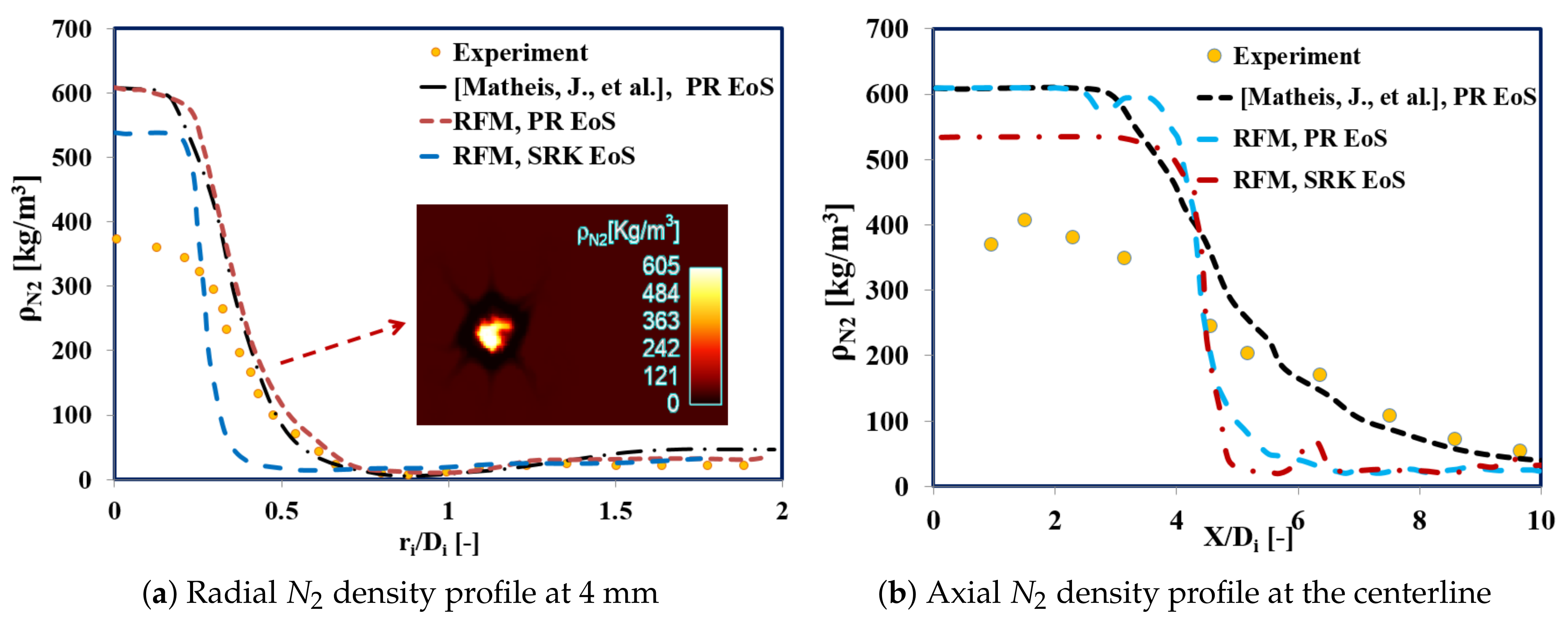
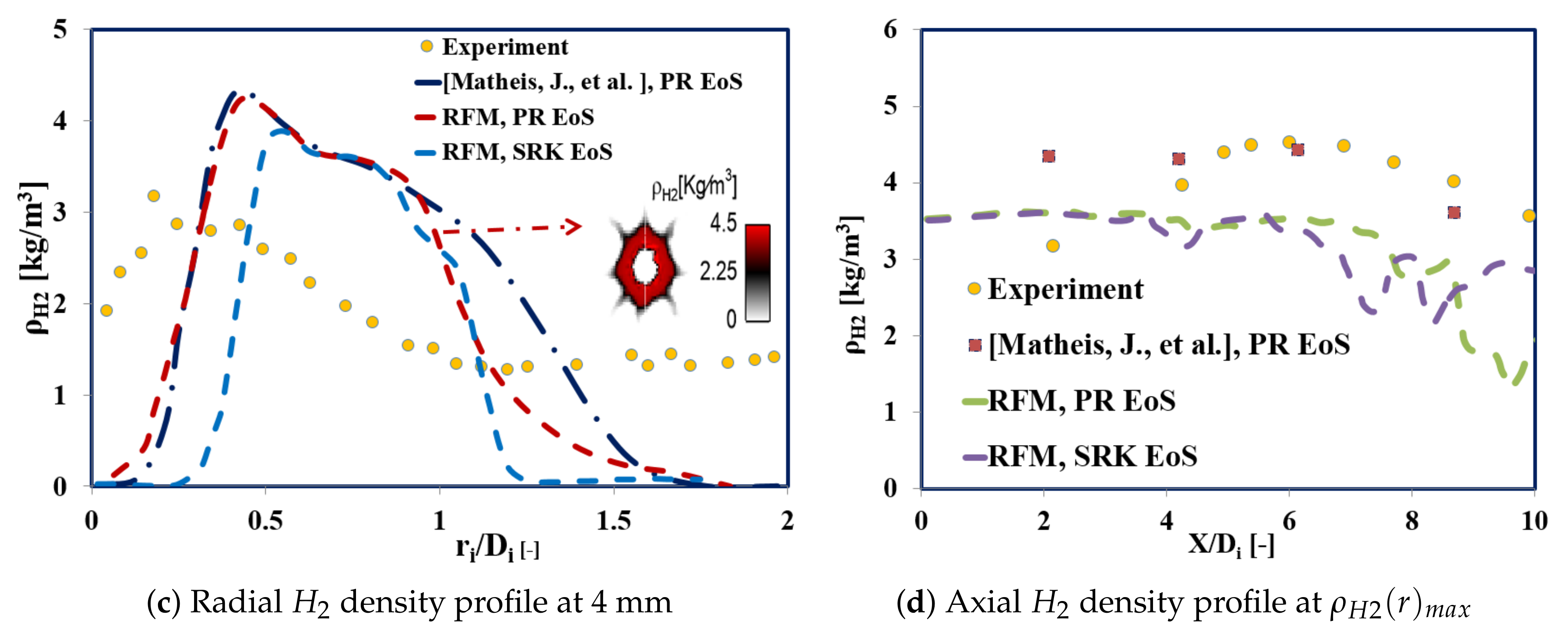
Experimental Validation
4. Conclusions
- The 1-D studies, cases (1–4), for transcritical shock tube test cases confirmed that the modified SIMPLE and PISO algorithms for the RFM model were in good agreement compared to the available data in the literature.
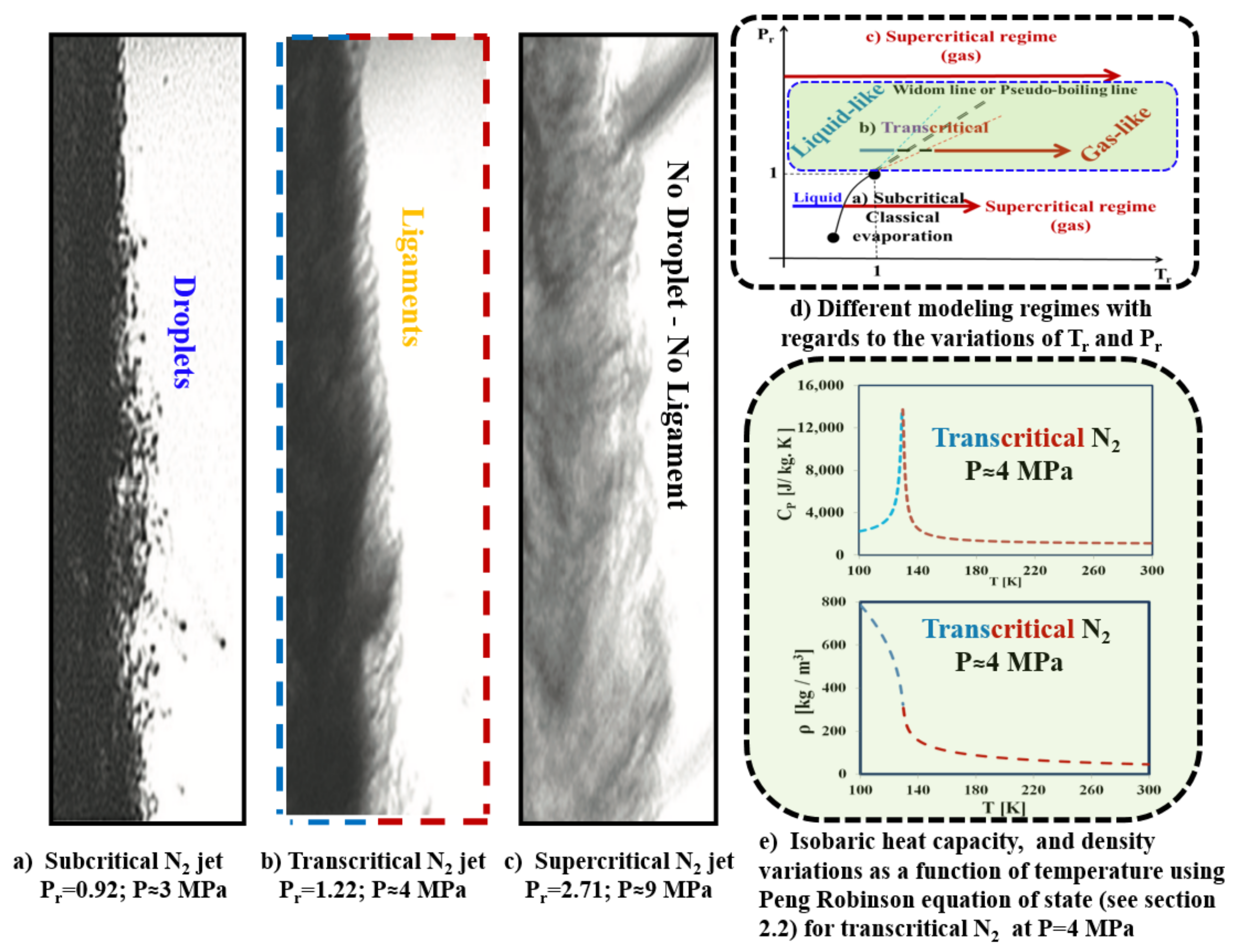
- The LES studies of cryogenic single-component case, cases (5–7), (liquid-like nitrogen injected into gas nitrogen) demonstrated its transcritical interface features by exhibiting the well known thermal shield, as a layer of large isobaric heat capacity separating the liquid-like and the gas-like regions..
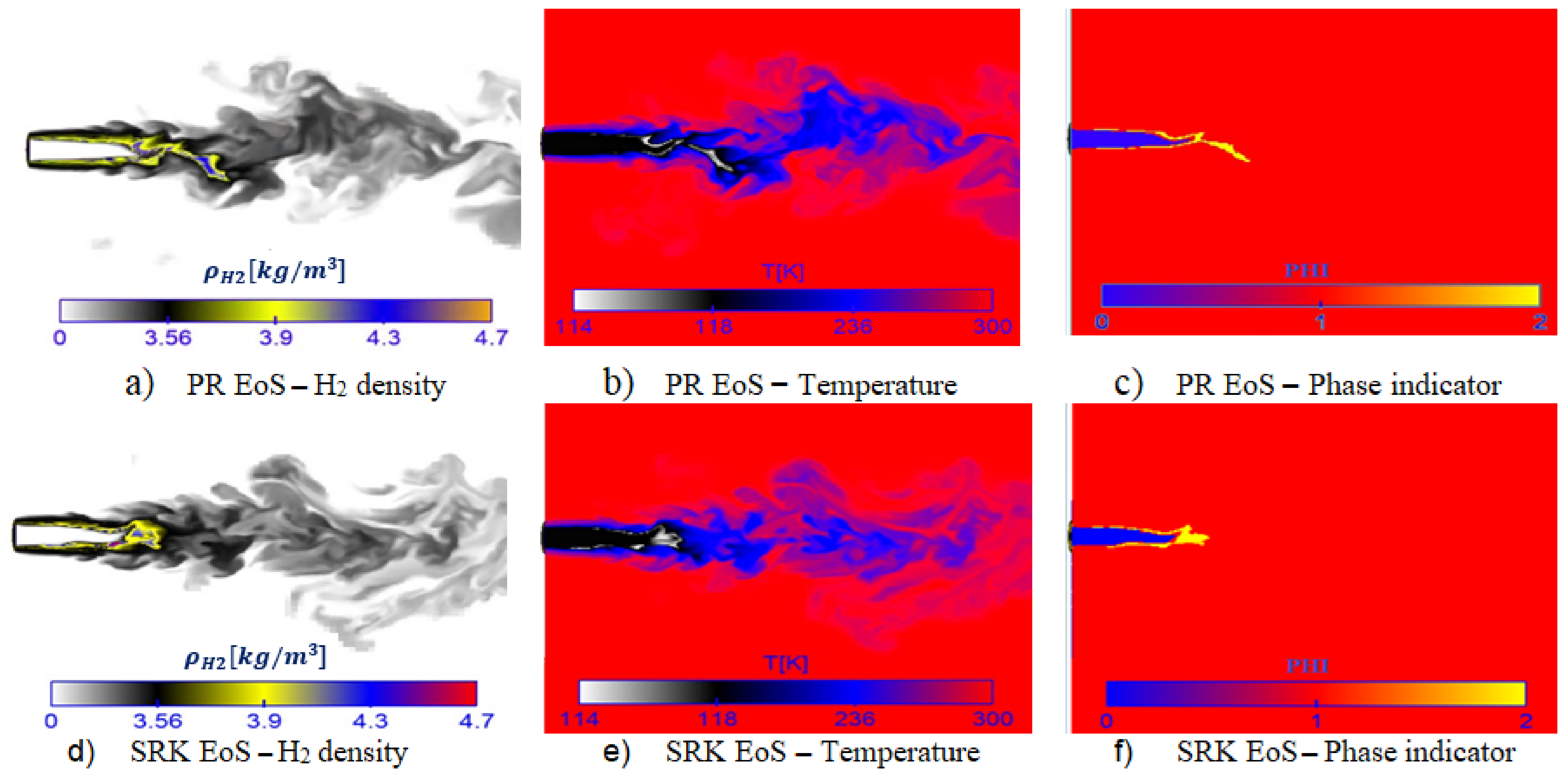
- The LES study of classical cryogenic injection of liquid nitrogen injected coaxially with warm hydrogen jet, case 8, showed some interesting thermodynamic phenomena, such as the condensation of as well as cooling effects in the two-phase layer around the liquid core, which demonstrates the subcritical nature of the interface.
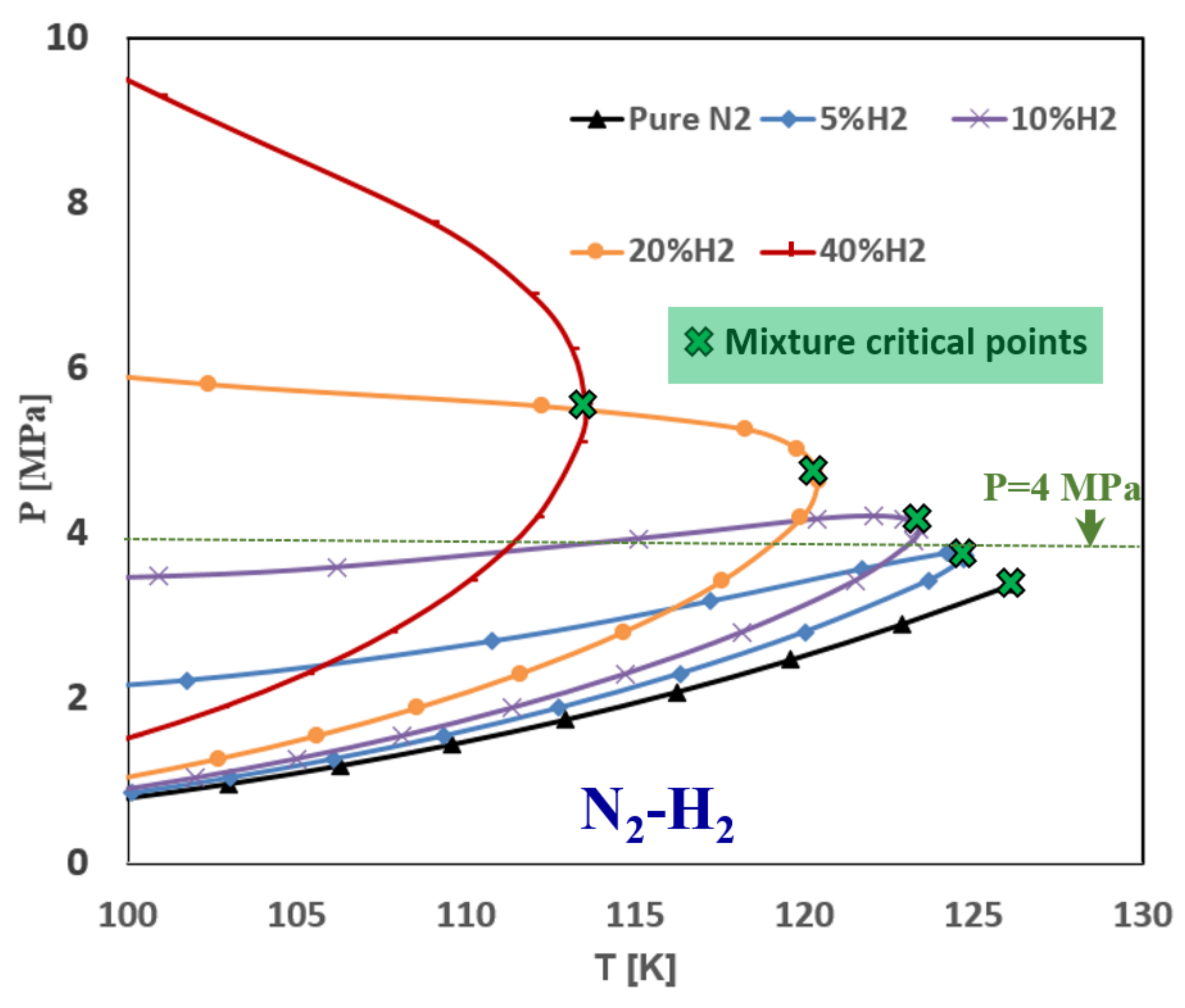
- Another interesting observed phenomenon for case 8 is related to the mixing of and , which led to locally increased mixture critical points. Therefore, due to the mixing process around the liquid core interface, some flow zones may move from the supercritical mixing regime to the subcritical phase change regime inducing condensation and evaporation.
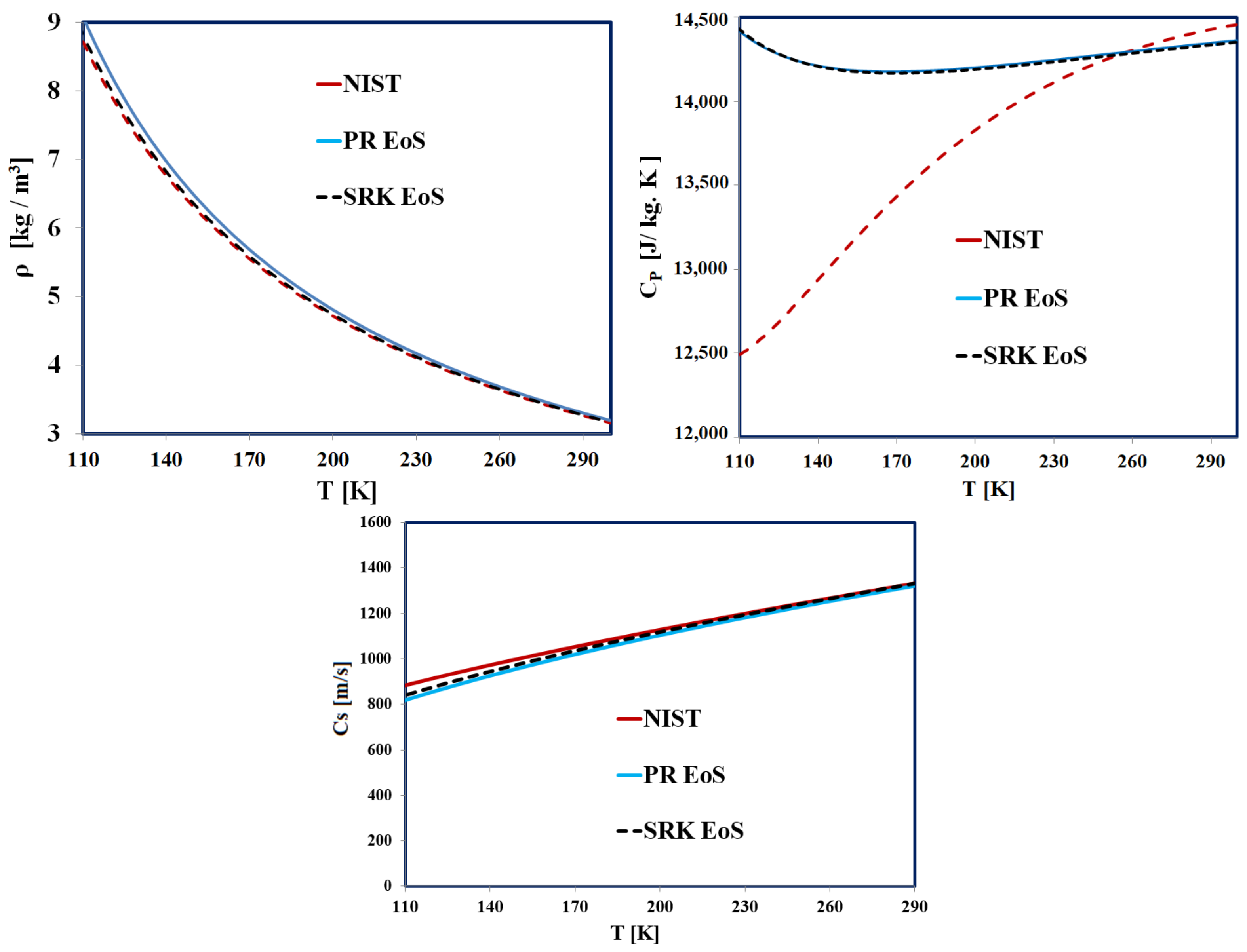
- The numerical results were finally compared with available experimental data [43] and published numerical studies [40], with satisfactory agreement. Moreover, we confirmed the importance of using a powerful real fluid EoS. The current investigations illustrated that the SRK EoS had a better prediction of the fluid density compared to the PR EoS, corroborating the results reported by [40].
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Sirignano, W.A.; Delplanque, J.P. Transcritical vaporization of liquid fuels and propellants. J. Propul. Power 1999, 15, 806–902. [Google Scholar]
- Chehroudi, B.; Talley, D.; Mayer, W.; Branam, R.; Smith, J.J.; Schik, A.; Oschwald, M. Understanding Injection into High Pressure Supercritical Environments. In Proceedings of the Fifth International Symposium on Liquid Space Propulsion, Long Life Combustion Devices Technology, Huntsville, AL, USA, 27–30 October 2003; NASA Marshall Spaceflight Center: Huntsville, AL, USA, 2003. [Google Scholar]
- Mayer, W.O.; Schik, A.; Schaffler, M.; Tamura, H. Injection and mixing processes in high-pressure liquid oxygen/gaseous hydrogen rocket combustors. J. Propul. Power 2000, 16, 823–828. [Google Scholar] [CrossRef]
- Crua, C.; Manin, J.; Pickett, L.M. On the transcritical mixing of fuels at diesel engine conditions. Fuel 2017, 208, 535–548. [Google Scholar] [CrossRef] [Green Version]
- Jofre, L.; Urzay, J. Transcritical diffuse-interface hydrodynamics of propellants in high-pressure combustors of chemical propulsion systems. Prog. Energy Combust. Sci. 2021, 82, 100877. [Google Scholar] [CrossRef]
- Banuti, D.T. Crossing theWidom-line—Supercritical pseudo-boiling. J. Supercrit. Fluids 2015, 98, 12–16. [Google Scholar] [CrossRef]
- Bellan, J. Supercritical (and subcritical) fluid behavior and modeling: Drops, streams, shear and mixing layers, jets and sprays. Prog. Energy Combust. Sci. 2000, 26, 329–366. [Google Scholar] [CrossRef] [Green Version]
- Yi, P.; Yang, S.; Habchi, C.; Lugo, R. A multicomponent real-fluid fully com- pressible four-equation model for two-phase flow with phase change. Phys. Fluids 2019, 31, 026102. [Google Scholar] [CrossRef]
- Yang, S.; Yi, P.; Habchi, C. Real-fluid injection modeling and LES simulation of the ECN Spray A injector using a fully compressible two-phase flow approach. Int. J. Multiph. Flow 2020, 122, 103145. [Google Scholar] [CrossRef]
- Dahms, R.N.; Oefelein, J.C. On the transition between two-phase and single-phase interface dynamics in multicomponent fluids at supercritical pressures. Phys. Fluids 2013, 25, 092103. [Google Scholar] [CrossRef]
- Ma, P.C.; Lv, Y.; Ihme, M. An entropy-stable hybrid scheme for simulations of transcritical real-fluid flows. J. Comput. Phys. 2017, 340, 330–357. [Google Scholar] [CrossRef]
- Ma, P.C.; Wu, H.; Banuti, D.T.; Ihme, M. On the numerical behavior of diffuse-interface methods for transcritical real-fluids simulations. Int. J. Multiph. Flow 2019, 113, 231–249. [Google Scholar] [CrossRef]
- Andrews, T. The Bakerian Lecture—On the Continuity of the Gaseous and Liquid States of Matter. Philos. Trans. R. Soc. Lond. 1869, 159, 575. [Google Scholar]
- Lapenna, P.E. Thermodynamic Small Scales in Transcritical Turbulent Jets. AIAA J. 2021. [Google Scholar] [CrossRef]
- Doehring, A.; Kaller, T.; Schmidt, S.J.; Adams, N.A. Large-eddy simulation of turbulent channel flow at transcritical states. Int. J. Heat Fluid Flow 2021, 89, 108781. [Google Scholar] [CrossRef]
- Ningegowda, B.M.; Rahantamialisoa, F.N.Z.; Pandal, A.; Jasak, H.; Im, H.G.; Battistoni, M. Numerical Modeling of Transcritical and Supercritical Fuel Injections Using a Multi-Component Two-Phase Flow Model. Energies 2020, 13, 5676. [Google Scholar] [CrossRef]
- Gallo, P.; Corradini, D.; Rovere, M. Widom line and dynamical crossovers as routes to understand supercritical water. Nat. Commun. 2014, 5, 5806. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.; Kumar, P.; Buldyrev, S.V.; Chen, S.-H.; Poole, P.H.; Sciortino, F.; Stanley, H.E. Relation between the Widom line and the dynamic crossover in systems with a liquid–liquid phase transition. Proc. Natl. Acad. Sci. USA 2005, 102, 16558–16562. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Michelsen, M.L. The isothermal flash problem, Part I. Phase split calculation. Fluid Phase Equilib. 1982, 9, 1–19. [Google Scholar] [CrossRef]
- Ayyappan, D.; Vaidyanathan, A.; Muthukumaran, C.K.; Nandakumar, K. Transition of subcritical liquid jets in single and multicomponent systems. Phys. Fluids 2018, 30, 104106. [Google Scholar] [CrossRef]
- Mirjalili, S.; Jain, S.S.; Dodd, M. Interface-Capturing Methods for Two-Phase Flows: An Overview and Recent Developments; Center for Turbulence Research Annual Research Briefs, Stanford University: Stanford, CA, USA, 2017; pp. 117–135. [Google Scholar]
- Saurel, R.; Pantano, C. Diffuse-Interface Capturing Methods for Compressible Two-Phase Flows. Annu. Rev. Fluid Mech. 2018, 50, 105–130. [Google Scholar] [CrossRef] [Green Version]
- Cahn, J.; Hilliard, J. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Baer, M.; Nunziato, J. A two-phase mixture theory for the deflagration-to-detonation transition (DDT) in reactive granular materials. Int. J. Multiph. Flow 1986, 12, 861–889. [Google Scholar] [CrossRef]
- Pantano, C.; Saurel, R.; Schmitt, T. An oscillation free shock-capturing method for compressible van der Waals supercritical fluid flows. J. Comput. Phys. 2017, 335, 780–811. [Google Scholar] [CrossRef] [Green Version]
- Hirt, C.W.; Nichols, B.D. Volume of uid (vof) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Scardovelli, R.; Zaleski, S. Analytical relations connecting linear interfaces and volume fractions in rectangular grids. J. Comput. Phys. 2000, 164, 228–237. [Google Scholar] [CrossRef]
- Mastrone, M.N.; Hartono, E.A.; Chernoray, V.; Concli, F. Oil distribution and churning losses of gearboxes: Experimental and numerical analysis. Tribol. Int. 2020, 151, 106496. [Google Scholar] [CrossRef]
- Peng, Q.; Gui, L.; Fan, Z. Numerical and experimental investigation of splashing oil flow in a hypoid gearbox. Eng. Appl. Comput. Fluid Mech. 2018, 12, 324–333. [Google Scholar] [CrossRef] [Green Version]
- Chiapolino, A.; Boivin, P.; Saurel, R. A simple phase transition relaxation solver for liquid-vapor flows. Int. J. Numer. Methods Fluids 2017, 83, 583–605. [Google Scholar] [CrossRef] [Green Version]
- Zein, A.; Hantke, M.; Warnecke, G. Modeling phase transition for compressible two-phase flows applied to metastable liquids. J. Comput. Phys. 2010, 229, 2964–2998. [Google Scholar] [CrossRef]
- Mirjalili, S.; Ivey, C.B.; Mani, A. Comparison between the diffuse interface and volume of fluid methods for simulating two-phase flows. Int. J. Multiph. Flow 2019, 116, 221–238. [Google Scholar] [CrossRef] [Green Version]
- Osher, S.; Fedkiw, R.P. Level set methods: An overview and some recent results. J. Comput. Phys. 2001, 169, 463–502. [Google Scholar] [CrossRef] [Green Version]
- Sethian, J.A.; Smereka, P. Level set methods for fuid interfaces. Annu. Rev. Fluid Mech. 2003, 35, 341–372. [Google Scholar] [CrossRef] [Green Version]
- Umemura, A.; Shinjo, J. Detailed SGS atomization model and its implementation to two-phase flow LES. Combust. Flame 2018, 195, 232–252. [Google Scholar] [CrossRef]
- Legier, J.P.; Poinsot, T.; Veynante, D. Dynamically thickened flame LES model for premixed and non-premixed turbulent combustion. In Proceedings of the Summer Program, Stanford, CA, USA, 2–27 July 2000; Center for Turbulence Research, NASA Ames/Stanford University: Stanford, CA, USA, 2000; pp. 157–168. [Google Scholar]
- Devassy, B.M.; Habchi, C.; Daniel, E. Atomization Modelling of Liquid Jets Using a Two-Surface-Density Approach. At. Sprays 2015, 25, 47–80. [Google Scholar] [CrossRef]
- Linstrom, P; Mallard, W. The NIST Chemistry WebBook: A Chemical Data Resource on the Internet. J. Chem. Eng. Data 2001, 46, 1059–1063. [Google Scholar] [CrossRef]
- Banuti, D.; Hannemann, K. Efficient multiphase rocket propellant injection model with high quality equation of state. In Proceedings of the 4th Space Propulsion Conference, Cologne, Germany, 19–22 May 2014. [Google Scholar]
- Matheis, J.; Müller, H.; Hickel, S.; Pfitzner, M. Large-Eddy Simulation of Cryogenic Jet Injection at Supercritical Pressures. High-Press. Flows Propuls. Appl. 2020, 260, 531–570. [Google Scholar]
- Multi-component vapor-liquid equilibrium model for LES and application to ECN spray A. arXiv 2016, arXiv:1609.08533.
- Lacaze, G.; Schmitt, T.; Ruiz, A.; Oefelein, J.C. Comparison of energy, pressure-and enthalpy-based approaches for modeling supercritical flows. Comput. Fluids 2019, 181, 35–56. [Google Scholar] [CrossRef] [Green Version]
- Oschwald, M.; Schik, A.; Klar, M.; Mayer, W. Investigation of coaxial LN2/GH2-injection at supercritical pressure by spontaneous Raman scattering. In Proceedings of the 35th Joint Propulsion Conference and Exhibit, Los Angeles, CA, USA, 20–24 June 1999. [Google Scholar]
- Michelsen, M.L. The isothermal flash problem, Part II. Phase split calculation. Fluid Phase Equilib. 1982, 9, 21–40. [Google Scholar] [CrossRef]
- Koukouvinis, P.; Vidal-Roncero, A.; Rodriguez, C.; Gavaises, M.; Pickett, L. High pressure/high temperature multiphase simulations of dodecane injection to nitrogen: Application on ECN Spray—A. Fuel 2020, 275, 117871. [Google Scholar] [CrossRef]
- Yi, P.; Jafari, S.; Yang, S.; Habchi, C. Numerical analysis of subcritical evaporation and transcritical mixing of droplet using a tabulated multicomponent vapor-liquid equilibrium model. In Proceedings of the ILASS—Europe 2019, 29th Conference on Liquid Atomization and Spray Systems, Paris, France, 2–4 September 2019. [Google Scholar]
- Brown, S.; Peristeras, L.; Martynov, S.; Porter, R.T.J.; Mahgerefteh, H.; Nikolaidis, I.; Boulougouris, G.; Tsangaris, D.; Economou, I. Thermodynamic interpolation for the simulation of two-phase flow of non-ideal mixtures. Comput. Chem. Eng. 2016, 95, 49–57. [Google Scholar] [CrossRef]
- Azimian, A.R.; Arriagada, J.; Assadi, M. Generation of steam tables using artificial neural networks. Heat Transf. Eng. 2004, 25, 41–51. [Google Scholar] [CrossRef]
- Lorenzo, M.; De Lafon, P.; Di Matteo, M.; Pelanti, M.; Seynhaeve, J.M.; Bartosiewicz, Y. Homogeneous two-phase flow models and accurate steam-water table look-up method for fast transient simulations. Int. J. Multiph. Flow 2017, 95, 199–219. [Google Scholar] [CrossRef]
- Fang, Y.; De Lorenzo, M.; Lafon, P.; Poncet, S.; Bartosiewicz, Y. An Accurate and Efficient Look-up Table Equation of State for Two-phase Compressible Flow Simulations of Carbon Dioxide. Ind. Eng. Chem. Res. 2018, 57, 7676–7691. [Google Scholar] [CrossRef]
- Foll, F.; Hitz, T.; Muller, C.; Munz, C.-D.; Dumbser, M. On the use of tabulated equations of state for multi-phase simulations in the homogeneous equilibrium limit. Shock Waves 2019, 29, 769–793. [Google Scholar] [CrossRef]
- Praneeth, S.; Hickey, J.-P. Uncertainty quantification of tabulated supercritical thermodynamics for compressible Navier–Stokes solvers. arXiv 2018, arXiv:1801.06562. [Google Scholar]
- Saha, S.; Carroll, J.J. The isoenergetic-isochoric flash. Fluid Phase Equilib. 1997, 138, 23–41. [Google Scholar] [CrossRef]
- Richards, K.J.; Senecal, P.K.; Pomraning, E. Converge 3.0; Convergent Science: Madison, WI, USA, 2021; Available online: https://convergecfd.com/ (accessed on 15 January 2019).
- Chung, T.H.; Ajlan, M.; Lee, L.L.; Starling, K.E. Generalized multi-parameter correlation for non-polar and polar fluid transport properties. Ind. Eng. Chem. Res. 1988, 27, 671–679. [Google Scholar] [CrossRef]
- Sagaut, P. Large-Eddy Simulation for Incompressible Flows, 3rd ed.; Scientific Computation; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2005. [Google Scholar]
- Peng, D.-Y.; Robinson, D.B. A new two-constant equation of state. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Soave, G. Equilibrium constants from a modified redlichkwong equation of state. Chem. Eng. Sci. 1972, 27, 1197–1203. [Google Scholar] [CrossRef]
- Ware, C.; Knight, W.; Wells, D. Memory intensive statistical algorithms for multibeam bathymetric data. Comput. Geosci. 1991, 17, 985–993. [Google Scholar] [CrossRef]
- Streett, W.B.; Calado, J.C.G. Liquid-vapour equilibrium for hydrogen + nitrogen at temperatures from 63 to 110 k and pressures to 57 mpa. J. Chem. Thermodyn. 1978, 10, 1089–1100. [Google Scholar] [CrossRef]
- Boyd, B.; Jarrahbashi, D. A diffuse-interface method for reducing spurious pressure oscillations in multicomponent transcritical flow simulations. Comput. Fluids 2021. [Google Scholar] [CrossRef]
- Issa, R.I.; Gosman, A.D.; Watkins, A.P. The Computation of Compressible and Incompressible Recirculating Flows by a Non-Iterative Implicit Scheme. J. Comput. Phys. 1986, 62, 66–82. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Hemisphere Publishing Corporation: Washington, DC, USA, 1980. [Google Scholar]
- Poormahmood, A.; Farshchi, M. Numerical study of the mixing dynamics of trans- and supercritical coaxial jets. Phys. Fluids 2020, 32, 125105. [Google Scholar] [CrossRef]
- Yang, S. Modeling of Diesel Injection in Subcritical and Supercritical Conditions. Ph.D. Thesis, University of Paris-Saclay, Gif-sur-Yvette, France, 2019. [Google Scholar]
- Yang, S.; Habchi, C. Real-fluid phase transition in cavitation modeling considering dissolved non-condensable gas. Phys. Fluids 2020, 32, 032102. [Google Scholar]
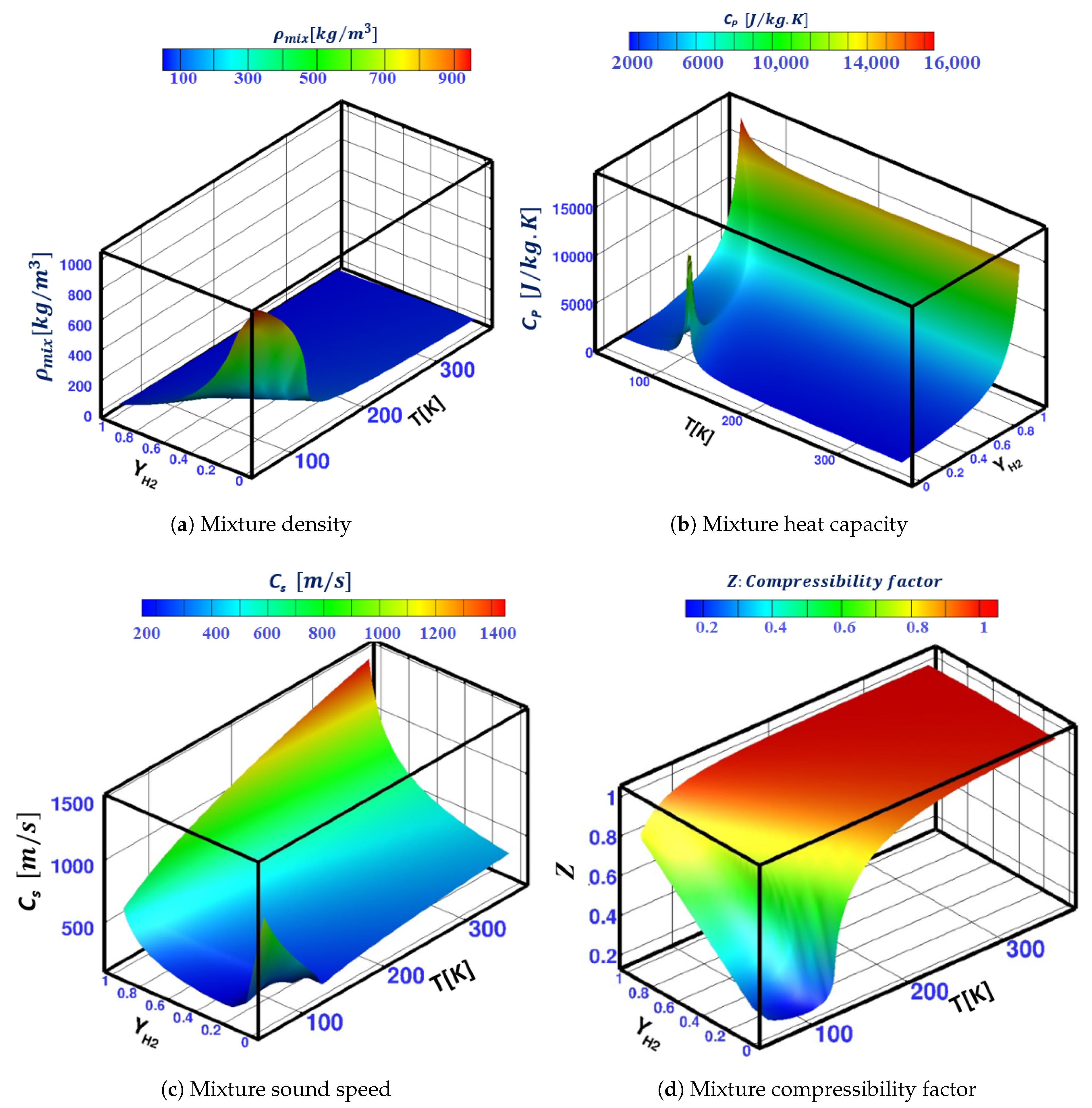





| EOS | |||||
|---|---|---|---|---|---|
| PR | 1+ | ||||
| SRK | 1 | 0 |
| (MPa) | (MPa) | (K) | (K) | (m/s) | Numerical Scheme | |
|---|---|---|---|---|---|---|
| Case 1 | 60 | 6 | 158 | 224 | 0 | |
| Case 2 | 40 | 6 | 158 | 224 | 0 | |
| Case 3 | 20 | 6 | 158 | 224 | 0 | |
| Case 4 | 20 | 6 | 158 | 224 | 0 |
| (K) | (K) | (MPa) | |
|---|---|---|---|
| Case 5 | 126.9 | 298 | 6 |
| Case 6 | 150 | 298 | 6 |
| Case 7 | 135 | 298 | 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jafari, S.; Gaballa, H.; Habchi, C.; de Hemptinne, J.-C. Towards Understanding the Structure of Subcritical and Transcritical Liquid–Gas Interfaces Using a Tabulated Real Fluid Modeling Approach. Energies 2021, 14, 5621. https://doi.org/10.3390/en14185621
Jafari S, Gaballa H, Habchi C, de Hemptinne J-C. Towards Understanding the Structure of Subcritical and Transcritical Liquid–Gas Interfaces Using a Tabulated Real Fluid Modeling Approach. Energies. 2021; 14(18):5621. https://doi.org/10.3390/en14185621
Chicago/Turabian StyleJafari, Sajad, Hesham Gaballa, Chaouki Habchi, and Jean-Charles de Hemptinne. 2021. "Towards Understanding the Structure of Subcritical and Transcritical Liquid–Gas Interfaces Using a Tabulated Real Fluid Modeling Approach" Energies 14, no. 18: 5621. https://doi.org/10.3390/en14185621
APA StyleJafari, S., Gaballa, H., Habchi, C., & de Hemptinne, J.-C. (2021). Towards Understanding the Structure of Subcritical and Transcritical Liquid–Gas Interfaces Using a Tabulated Real Fluid Modeling Approach. Energies, 14(18), 5621. https://doi.org/10.3390/en14185621