Application of the Harmonic Balance Method for Spatial Harmonic Interactions Analysis in Axial Flux PM Generators
Abstract
:1. Introduction
2. Harmonic Balance Method for Modeling PM Machines
2.1. General Assumptions
2.2. Aplication of HBM for Modeling Spatial Harmonic Interaction in 3-Phase PM Generators
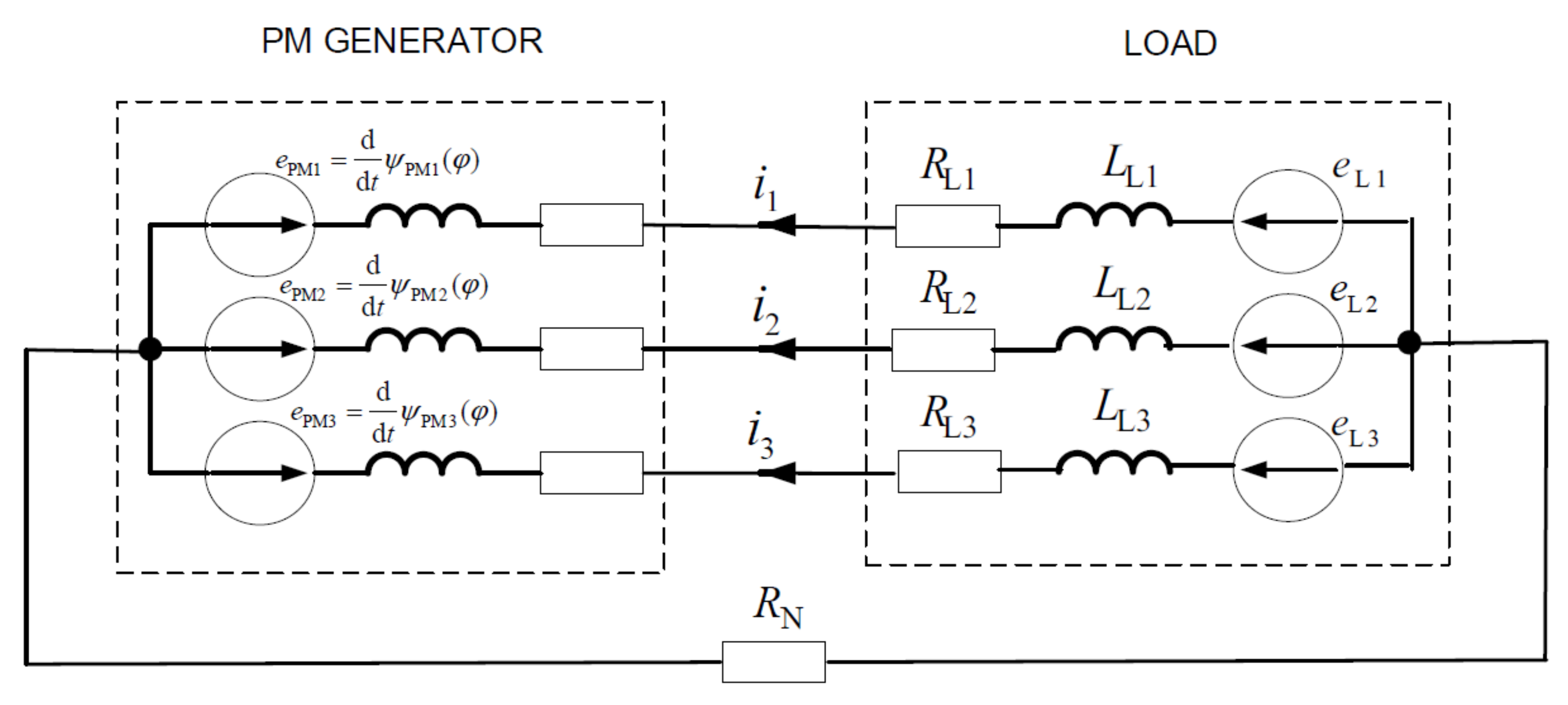
3. Model of AFPMG in Steady State Operation
3.1. Parameters of AFPMG Mathematical Model
3.2. Spatial Harmonic Interaction Model for AFPMG
4. Laboratory Tests and Model Verifications
4.1. Description of Tested Generators
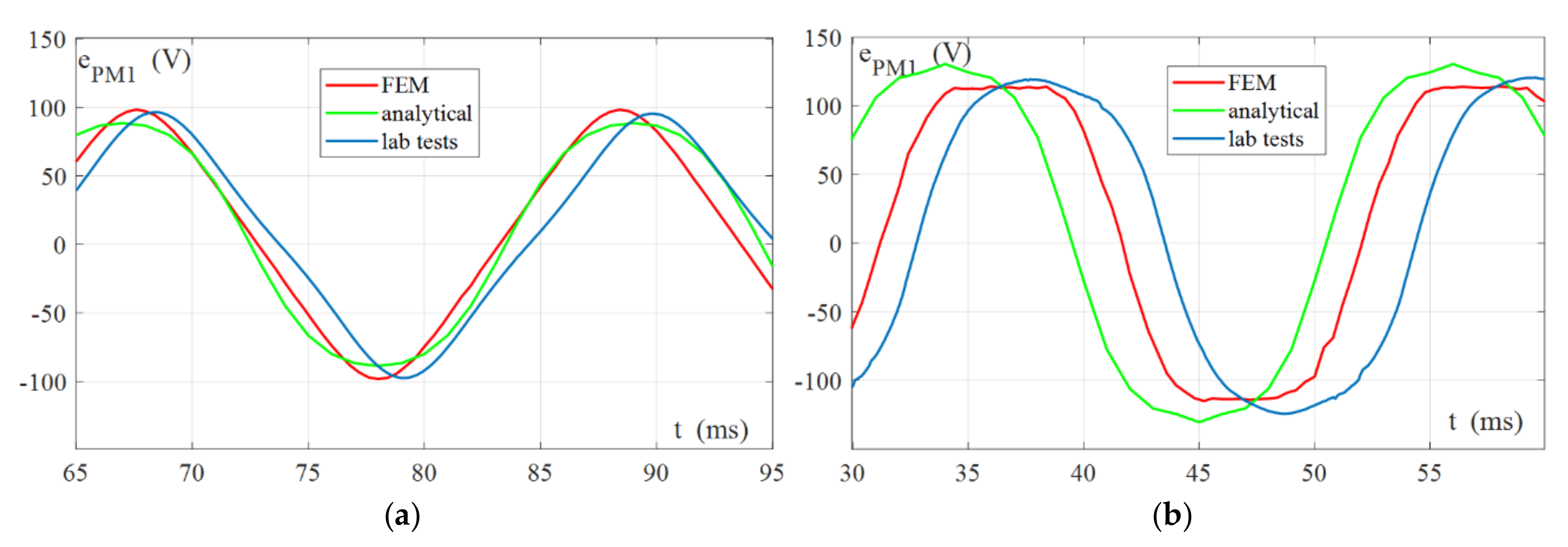
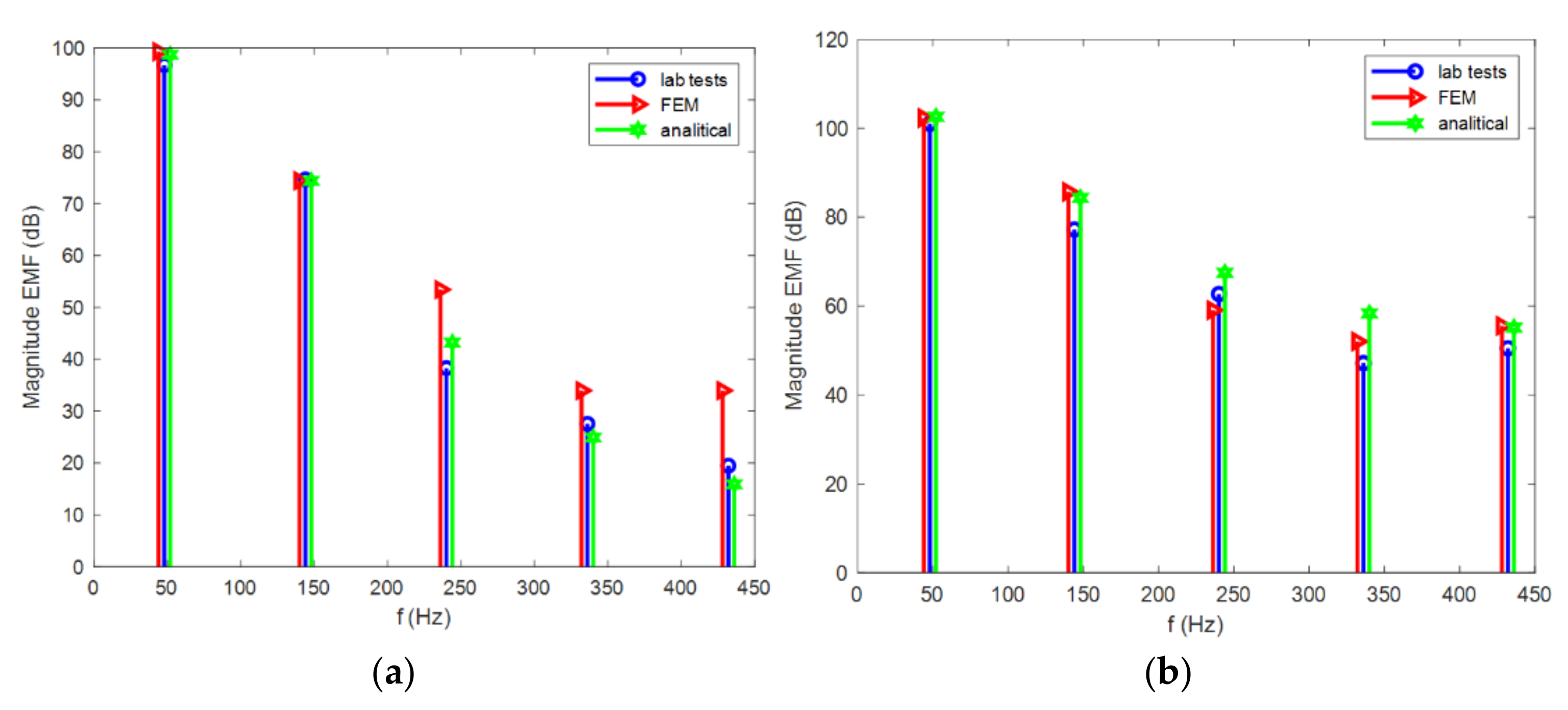
4.2. Verification of Spatial Harmonic Interactions Models
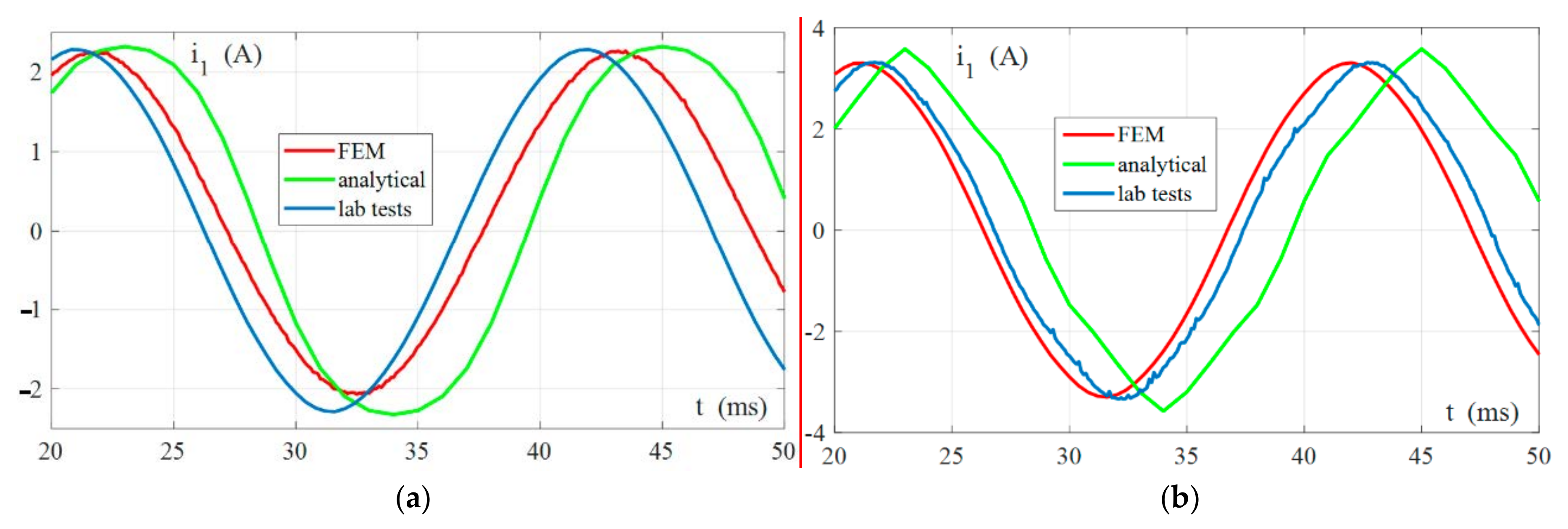
4.2.1. Verification of the Stator Currents
4.2.2. Verification of the Electromagnetic Torque
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chalmers, B.; Spooner, E. An axial-flux permanent-magnet generator for a gearless wind energy system. IEEE Trans. Energy Convers. 1999, 1z4, 251–257. [Google Scholar] [CrossRef]
- Caricchi, F.; Crescimbini, F. Modular Axial-Flux Permanent-Magnet Motor for Ship Propulsion Drives. IEEE Trans. Energy Convers. 1999, 14, 673–679. [Google Scholar] [CrossRef]
- Chen, Y.; Pillay, P.; Khan, A. PM Wind Generator Topologies. IEEE Trans. Ind. Appl. 2005, 41, 1619–1626. [Google Scholar] [CrossRef] [Green Version]
- Chan, T.F.; Lai, L.L. An Axial-Flux Permanent-Magnet Synchronous Generator for a Direct-Coupled Wind-Turbine System. IEEE Trans. Energy Convers. 2007, 22, 86–94. [Google Scholar] [CrossRef]
- Park, Y.-S.; Jang, S.-M.; Choi, J.-H.; Choi, J.-Y.; You, D.-J. Characteristic Analysis on Axial Flux Permanent Magnet Synchronous Generator Considering Wind Turbine Characteristics According to Wind Speed for Small-Scale Power Application. IEEE Trans. Magn. 2012, 48, 2937–2940. [Google Scholar] [CrossRef]
- Kirtley, J.L. Permanent Magnets in Electric Machines. Electric Power Principle; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2019. [Google Scholar]
- Gieras, J.; Wang, R.; Kamper, M. Axial Flux Permanent Magnet Brushless Machines; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Aydin, M.; Huang, S.; Lipo, T.A. Axial Flux Permanent Magnet Disc Machines: A Review; Wisconsin Electric Machines & Power Electronics Consortium: Madison, WI, USA, 2004. [Google Scholar]
- Radwan-Pragłowska, N.; Borkowski, D.; Węgiel, T. Model of Coreless Axial Flux Permanent Magnet Generator. In Proceedings of the 2017 International Symposium on Electrical Machines (SME), Naleczow, Poland, 18–21 June 2017. [Google Scholar] [CrossRef]
- Radwan-Pragłowska, N.; Węgiel, T.; Borkowski, D. Parameters identification of coreless axial flux permanent magnet generator. Arch. Electr. Eng. 2020, 67, 391–402. [Google Scholar]
- Radwan-Pragłowska, N.; Węgiel, T.; Borkowski, D. Modeling of Axial Flux Permanent Magnet Generators. Energies 2020, 13, 5741. [Google Scholar] [CrossRef]
- Kamper, M.J.; Wang, R.-J.; Rossouw, F.G. Analysis and performance of axial flux permanent-magnet machine with air-cored nonoverlapping concentrated stator windings. IEEE Trans. Ind. Appl. 2008, 44, 1495–1504. [Google Scholar] [CrossRef]
- Zhilichev, Y.N. Three-dimensional analytic model of permanent magnet axial flux machine. IEEE Trans. Magn. 1998, 34, 3897–3901. [Google Scholar] [CrossRef]
- Parviainen, A.; Niemelä, M.; Pyrhönen, J. Modeling of axial flux permanent-magnet machines. IEEE Trans. Ind. Appl. 2004, 40, 1333–1340. [Google Scholar] [CrossRef]
- Azzouzi, J.; Barakat, G.; Dayko, B. Quasi-3D analytical modeling of the magnetic field of an axial flux permanent-magnet synchronous machine. IEEE Trans. Energy Conv. 2005, 20, 746–752. [Google Scholar] [CrossRef]
- Wang, R.J.; Kamper, M.J.; Van der Westhuizen, K.; Gieras, J.F. Optimal design of a coreless stator axial flux permanent-magnet generator. IEEE Trans. Magn. 2005, 41, 55–64. [Google Scholar] [CrossRef]
- Virtic, P.; Pisek, P.; Marcic, T.; Hadziselimovic, M.; Bojan, S. Analytical Analysis of Magnetic Field and Back Electromotive Force Calculation of an Axial-Flux Permanent Magnet Synchronous Generator with Coreless Stator. IEEE Trans. Magn. 2008, 44, 4333–4336. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Agha-Mirsalim, M.; Mirzaei, M. Design, prototyping, and analysis of a low cost axial-flux coreless permanent-magnet generator. IEEE Trans. Magn. 2008, 44, 75–80. [Google Scholar] [CrossRef]
- Choi, J.-Y.; Lee, S.-H.; Ko, K.-J.; Jang, S.-M. Improved Analytical Model for Electromagnetic Analysis of Axial Flux Machines with Double-Sided Permanent Magnet Rotor and Coreless Stator Windings. IEEE Trans. Magn. 2011, 47, 2760–2763. [Google Scholar] [CrossRef]
- Sung, S.-Y.; Jeong, J.-H.; Park, Y.-S.; Choi, J.-Y.; Jang, S.-M. Improved Analytical Modeling of Axial Flux Machine with a Double-Sided Permanent Magnet Rotor and Slotless Stator Based on an Analytical Method. IEEE Trans. Magn. 2012, 48, 2945–2948. [Google Scholar] [CrossRef]
- Stamenkovic, I.; Milivojevic, N.; Schofield, N.; Krishnamurthy, M.; Emadi, A. Design, Analysis, and Optimization of Ironless Stator Permanent Magnet Machines. IEEE Trans. Power Electron. 2013, 28, 2527–2538. [Google Scholar] [CrossRef]
- Jin, P.; Yuan, Y.; Minyi, J.; Shuhua, F.; Heyun, L.; Yang, H.; Ho, S.L. 3-D Analytical Magnetic Field Analysis of Axial Flux Permanent-Magnet Machine. IEEE Trans. Magn. 2014, 50, 11. [Google Scholar] [CrossRef]
- Huang, Y.K.; Zhou, T.; Dong, J.N.; Lin, H.Y.; Yang, H.; Cheng, M. Magnetic equivalent circuit modeling of yokeless axial flux permanent magnet machine with segmented armature. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Maryam, S.; Naghi, R.; Vahid, B.; Juha, P.; Majid, R. Comparison of Performance Characteristics of Axial-Flux Permanent-Magnet Synchronous Machine with Different Magnet Shapes. IEEE Trans. Magn. 2015, 51, 1–6. [Google Scholar]
- Węgiel, T. Cogging torque analysis based on energy approach in surface-mounted PM machines. In Proceedings of the 2017 International Symposium on Electrical Machines (SME), Naleczow, Poland, 18–21 June 2017. [Google Scholar] [CrossRef]
- Sobczyk, T. A reinterpretation of the Floquet solution of the ordinary differential equation system with periodic coefficients as a problem of infinite matrix. Compel 1986, 5, 1–22. [Google Scholar] [CrossRef]
- Gilmore, R.J.; Steer, M.B. Nonlinear Circuit Analysis Using the Method of Harmonic Balance—A Review of the Art. Part, I. Introductory Concepts. Int. J. Microw. Millim.-Wave Comput.-Aided Eng. 1991, 1, 22–37. [Google Scholar] [CrossRef]
- Gilmore, R.J.; Steer, M.B. Nonlinear Circuit Analysis Using the Method of Harmonic Balance—A Review of the Art. Part II. Advanced Concepts. Int. J. Microw. Millim.-Wave Comput.-Aided Eng. 1991, 1, 159–180. [Google Scholar] [CrossRef]
- Sobczyk, T. Direct determination of two-periodic solution for nonlinear dynamic systems. Compel 1994, 13, 509–529. [Google Scholar] [CrossRef]
- Rusek, J. Category, slot harmonics and the torque of induction machines. Compel 2003, 22, 388–409. [Google Scholar] [CrossRef]
- Wegiel, T. Space Harmonic Interactions in Permanent Magnet Generator; Cracow University of Technology: Cracow, Poland, 2013. [Google Scholar]
- Esparza, M.; Segundo-Ramirez, J.; Kwon, J.B.; Wang, X.; Blaabjerg, F. Modeling of VSC-based power systems in the extended harmonic domain. IEEE Trans. Power Electron. 2017, 32, 5907–5916. [Google Scholar] [CrossRef]
- Ludowicz, W.; Wojciechowski, R.M. Analysis of the Distributions of Displacement and Eddy Currents in the Ferrite Core of an Electromagnetic Transducer Using the 2D Approach of the Edge Element Method and the Harmonic Balance Method. Energies 2021, 14, 3980. [Google Scholar] [CrossRef]

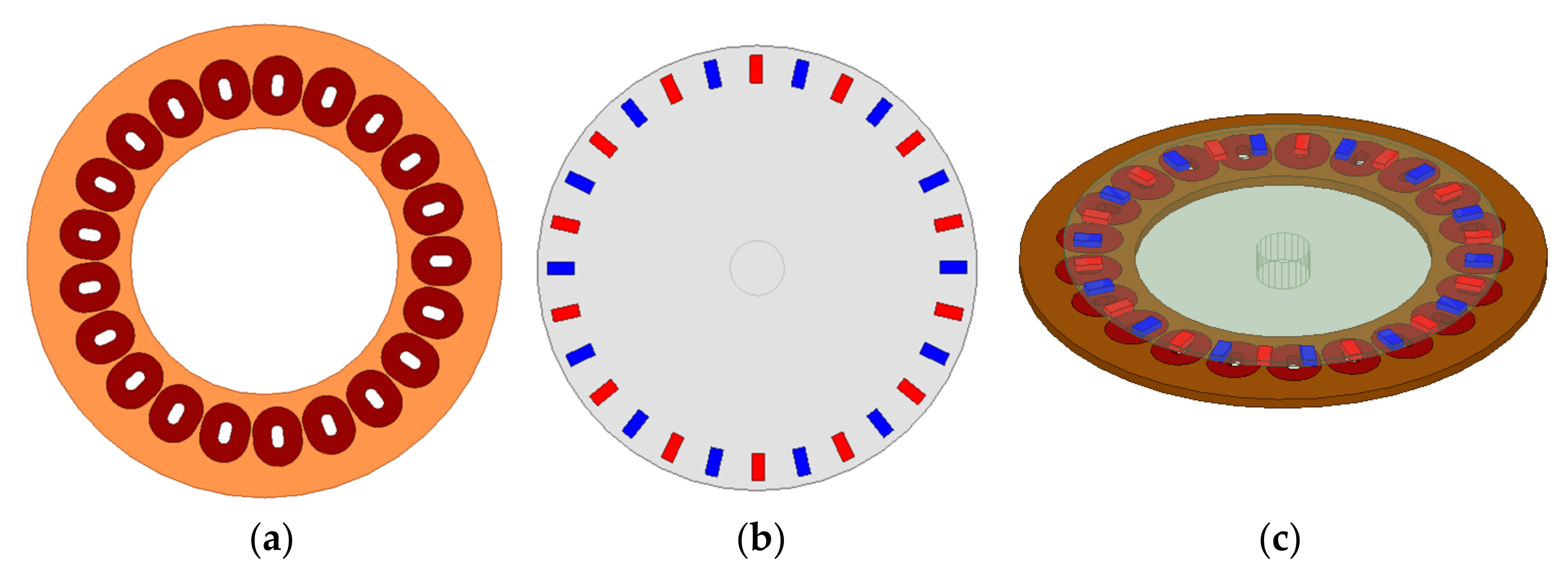





| Parameters and Dimensions of the Permanent Magnets of AFPM Generators |
|
| Construction of the Stators in AFPM Generators |
|
| AFPMG | Inductances | PM Flux Linkage Harmonics ; | ||||||
|---|---|---|---|---|---|---|---|---|
| (a) | coreless stator | 4.7 mH | 6.2 mH | 0.897 Wb | 18.2 mWb | 0.30 mWb | 0.03 mWb | 0.007 mWb |
| (b) | stator with cores | 6.0 mH | 6.2 mH | 1.398 Wb | 57.2 mWb | 4.9 mWb | 1.2 mWb | 0.7 mWb |
| AFPMG | THDEMF | EMF(RMS) | ||||
|---|---|---|---|---|---|---|
| Analytical Calculations | Measure | Analytical Calculations | Measure | |ΔEMF(%)| | ||
| (a) | coreless stator | 6.1% | 6.5% | 61.3 V | 62.6 V | 2.1% |
| (b) | stator with cores | 6.0% | 7.3% | 101.3 V | 95.8 V | 5.7% |
| AFPMG | THDI | I(RMS) | ||||
|---|---|---|---|---|---|---|
| Analytical Calculations | Measure | Analytical Calculations | Measure | |∆I(%)| | ||
| (a) | coreless stator | 0.16% | 0.23% | 1.65 A | 1.69 A | 2.4% |
| (b) | stator with cores | 1.67% | 1.95% | 2.29 A | 2.23 A | 2.6% |
| AFPMG | Tem(AV) | |||
|---|---|---|---|---|
| Analytical Calculations | Measure | |Tem(%)| | ||
| (a) | coreless stator | 11.9 Nm | 12.3 Nm | 3.3% |
| (b) | stator with cores | 31.1 Nm | 29.3 Nm | 6.1% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radwan-Pragłowska, N.; Węgiel, T.; Borkowski, D. Application of the Harmonic Balance Method for Spatial Harmonic Interactions Analysis in Axial Flux PM Generators. Energies 2021, 14, 5570. https://doi.org/10.3390/en14175570
Radwan-Pragłowska N, Węgiel T, Borkowski D. Application of the Harmonic Balance Method for Spatial Harmonic Interactions Analysis in Axial Flux PM Generators. Energies. 2021; 14(17):5570. https://doi.org/10.3390/en14175570
Chicago/Turabian StyleRadwan-Pragłowska, Natalia, Tomasz Węgiel, and Dariusz Borkowski. 2021. "Application of the Harmonic Balance Method for Spatial Harmonic Interactions Analysis in Axial Flux PM Generators" Energies 14, no. 17: 5570. https://doi.org/10.3390/en14175570
APA StyleRadwan-Pragłowska, N., Węgiel, T., & Borkowski, D. (2021). Application of the Harmonic Balance Method for Spatial Harmonic Interactions Analysis in Axial Flux PM Generators. Energies, 14(17), 5570. https://doi.org/10.3390/en14175570








