Advanced Flexibility Market for System Services Based on TSO–DSO Coordination and Usage of Distributed Resources

Abstract

The high and growing share of renewable sources and the more important role of Distributed Energy Resources (DERs) in the Distribution System (DS) is leading to a need for more efficient coordination of those sources. In future power systems, TSO–DSO coordination will play a key role in providing flexibility services. Lack of proper coordination of sources may lead to congestion in the network or to a lack of possibility to generate or consume energy on a requested level. The crucial aspect is that the TSO–DSO coordination must be based on an active role of all participants: TSO, DSO, generation units and the demand. This paper presents the possible application of the TSO–DSO coordination by providing the flexibility services from DS to the Transmission System (TS). The paper presents the complex optimization of TS, DS and its coordination. The main goal of the paper is to show the possibility of the application of the flexibility market into the current system design. It requires the creation of a new platform, where the offers of the flexibility services could be submitted and then exchanged between entities. The paper shows that the usage of flexibility services may decrease the operational cost of the system, and the DERs providing those services may benefit from an additional source of income.

1. Introduction

Nowadays, changes in the electricity sector are creating a need for new developments, mainly due to substantial increase of Renewable Energy Sources (RES) generation, but also due to growth in Energy Storage (ES), demand response and demand from the growing sector of electric vehicles. The increase of renewable sources is mainly driven by the European Union target of 32% share of renewable energy [1]. The main issue that arises is variability and uncertainty of the operation of renewable sources and Electric Vehicles (EVs). In the case of variability of renewable energy sources the operator has no possibility to store energy generated simultaneously, whereas in the case of EVs it is possible to manage the load on the level of particular facility or a group of facilities. An example of EVs facility management is presented in [2]. The operation of energy storage and the demand response may be planned and executed with high certainty. A large number of renewable sources and other distributed sources will be located in the distribution grid. With the growth of power generated by renewable sources, the TSO may not be able to plan and balance accurately the operation of the whole network. That is the reason why the distribution network will have to participate in future flexibility services. The large field in novelties will be related to the distribution grid, which will be forced to go through a transformation. The distribution grid is now mainly the sink of the network, where large power plants are the source. Shortly, this paradigm may change, due to growth in power generated within the distribution grid. It may turn out that instead of the transfer of energy from TS to DS, which usually occurs, DS will transfer energy to TS, due to surplus of generation over demand.

The main goal of the future system is to maximize the use of intermittent renewable energy sources, which produce energy only in specific conditions, whereas the large power plants at this time will be able to cover residual demand. When the conditions will be less favorable, then the large power plants will cover most of the demand. At this time the distribution grid is not prepared for the flow in both directions; what is more, most of the lines are not monitored in real-time. This presents a great challenge to maintain and handle the data of thousands of lines and other equipment. It requires a large amount of financial effort and years of well thought out investments. The other issue is an aspect of the operation of the distribution system; there is a need to treat it as an area that can be balanced to some extent. Moreover, there is a need to use flexible resources located in DS, when there is a need from a technical or economical point of view. What is more, now the distribution system is working in a “fit-and-forget” approach [3], which is related to the state in which infrastructure is oversized, to be able to cover peak values of the flow. This approach probably will exist and gain importance in the future, due to an increase in installed power of distributed generation and changes within the power system.

The article is organized as follows: At first, the literature review is presented; the following part presents an introduction of the mathematical formulation of the problem; the next section shows the model identification and case studies. The paper ends with the conclusions followed by appendixes.

2. Literature Review

The main goal of TSO in TSO–DSO coordination is to ensure balance and to manage congestion. The main application of the flexibility services may be found in voltage and frequency control, as well as in congestion management [4]. There are services in TS such as spinning reserve that can provide a large amount of energy in a short period. There are some other services as flexible ramping products, which can increase or decrease the power to some extent. The flexibility at the TSO level is usually based on large generators, although the flexibility can be achieved by usage of renewable sources, aggregators, Virtual Power Plants (VPPs) and demand side response. Those sources can adapt to TSOs’ flexibility needs; nonetheless frequently their costs are higher than large generators. The large customer may react to the price signals sent by TSO and reduce or increase its demand, while there is a space for such an action. The other solution is to perform a curtailment of the renewable sources; however, it is mostly used in menacing situations that may threaten system security [5]. Nonetheless, the future power system will be facing the need for curtailment more frequently.

The DSOs own the same types of flexible resources, although they are smaller in power and their number is larger. The main services that may be provided by DERs are voltage control and local congestion management [4]. DERs from DS may be curtailed to decrease the generation from DS; thus, it will allow to smooth the profile on the TS–DS interface. The largest incentive to DERs and also to demand side response will be to implement dynamic tariffs as an impulse to adapt to system needs. This will encourage a change in the demand based on the price signals [5]. There are multiple issues connected with the integration of Distributed Resources (DRs) into the system: The challenges of charging and discharging electric vehicles [6], finding an appropriate optimization technique in wind farms [7], finding an adequate optimization technique in EVs [2] or coordination of wind energy and pumped storage power plants [8]. Contracting strategies of renewable sources and hybrid power sources are strongly investigated in the research [9]. DSOs may be responsible for optimization and managing congestion in their grid; additionally, they may provide some additional services to TSO. This may include the flexibility services, ancillary services, balancing, etc.

There are ideas to apply the active generation from TS in the congestion management by the concept of traffic lights [3,10]. Reference [11] proposed to assign each state from the traffic light concept to the proper state of congestion. The green state is associated with congestion pricing, the yellow state with redispatching and the red one with the curtailment either of generators or loads. The green state embraces results from auctioning process, which can relieve the congestion. If not, the TSO applies the redispatch and if the issue is still present, the TSO is forced to curtail the sources. The amount of redispatch performed by TSO depends on the market transactions, and the market design connected with congestion pricing and also with the stage of grid development. The same approach may be applied in DS; it may consist of a similar pricing system and curtailment of the sources in DS. Shortly, one of the actions taken by DSO may be the prequalification and validation of the flexibility services. The prequalification means the verification whether any of the constraints are not violated in DS. There is an interesting approach, in which DSO may in the future consist of many microgrid structures, which will be controlled independently and the DSO will take care of the coordination of interconnected DS grids [12].

Usage of services from active sources has to be properly managed without creating additional congestion in the distribution grid. Due to that, the verification process has to be performed, in which DSO will confirm which services and to what extent they can be performed without violating any of the constraints. Flexibility services that can be offered for TSO will be aggregated. In Particular, possibility of curtailment of small renewable generation or possible decrease in demands of consumers will be accumulated in an offer. The impact of services may differ in significance due to the amount of power produced by the particular power plant. The solution to this may be the aggregation of a large number of small resources into more significant offers. This is one of the main prospects, which will have the highest chance to be successful in TSO–DSO coordination. TSO operates on large volumes of energy; that is why it is important to aggregate power from distribution system offers. The other advantage to using aggregated power in TSO–DSO coordination is that the renewable sources may not be properly predicted and such risk can be mitigated by aggregation. Then it may be possible to use the other source with higher predictability such as energy storage or demand response, which can be easily planned with high accuracy. Most TSO networks are meshed, whereas most DSO networks are radial. Due to that, they need to be described by different power flow methods. The meshed networks tend to be more reliable, whereas in DS, due to its radial connections, outages may appear [13].

The main challenge which confronted by DSO is the reinforcement of the network and equipping it with real-time measurement devices. The other challenge for the DSO may be the prequalification process, which if applied may be computationally intensive. DSOs will have to move investments into smart grids, which will be fully adapted to bidirectional flow. DSOs will have to perform a more active operation in their system. The key question is how to properly integrate the flexible sources within the system. Potential solutions may be found in [10], where the integrated scheme of TSO–DSO coordination is presented as Active System Management (ASM). Nowadays, the DSO has to integrate the resources in its network, whereas in the future it will have to interconnect them as well as manage their operation. An important part will be played by the aggregation of resources by an aggregator or in VPP [14,15]. The main goal of the future flexibility market will be to provide a power profile to TSO, with deviations in plus and minus, given by aggregators and resources in DS.

TSO–DSO coordination may be performed in different concepts; the probable schemes of this coordination, resulting from [16], are presented in detail below. It divides the responsibility between TSO and DSO and creates a few kinds of markets. Some projects, taken into consideration, give new approaches to the TSO–DSO coordination. There are some projects taking place on how to properly integrate the flexible sources within the system. There is a concept called “web of cells”, which is an approach not based on the existing architecture. It is a division of the area into smaller ones, to ensure the maximization of usage of distributed sources locally [10]. The other project, which is based on existing systems and real-time monitoring is “IDE4L”. It is based on creating a common platform, which can be easily connected to already existing systems. Another project, LINK-Solution, focuses on creating the smart power grid in which every component connected to the grid may be modeled.

SmartNet is one of the most promising projects, due to having coordination between TSO–DSO on two levels: Technical and market. Additionally, it integrates distributed resources in one platform. It proposes a few different coordination schemes between TSO and DSO, which may be implemented in the ancillary services, but it may be expanded further into balancing and the energy market. There are centralized ancillary services (ASs), shared balancing responsibility, common TSO–DSO, local AS market and integrated flexibility market model [16]. Centralized ancillary services is a model in which the TSO is active and the DSO is passive. It is a common market, in which only TSO buys the energy from resources from the DS and is the one that is operating the whole system. The DSO role is limited only to provide the prequalification of the power flow within the grid. The shared balancing market is similar to the previous scheme, although the main difference is that both markets are operated separately and sources from DS cannot be used in the general market. The responsibility of balancing the grid rests on a particular participant. The role of the operators is to balance their grids. The Common TSO–DSO AS market model is one common market in TS and DS, in which TSO and DSO operate simultaneously. The model takes into consideration constraints of the whole transmission system, as well as distribution constraints. The local AS market model consists of two separate markets, one local operated by DSO, in which DSO has the priority to use resources from DS. After that, the rest of the offers not applied in the market are transferred to the general market operated by TSO. The integrated flexibility model is a common market for TSO and DSO. What is more, the non-regulated parties will have a chance to participate in the flexibility market. In this scheme, there is a need to provide an independent market operator to ensure neutrality [4]. Detailed descriptions of the different coordination schemes and their advantages and disadvantages may be found in [4,17,18]. The practical models of the following coordination schemes may be found in [19,20,21]. The other view on the flexibility market may be found in [22], where the coordination between three parties is taken into consideration: TSO–DSO–retailer. Reference [23] considers the comparison of only two schemes, TSO central ancillary services and DSO local services market. The conclusions are drawn into more potential to maximize the social welfare of DSO local services market over TSO central ancillary services.

The coordination between parties in the power system may implement a new way to manage congestion. Instead of using costly redispatch and producing power in a power plant with a higher cost, there is an idea to use DERs, at a lower cost. However, it may occur that for some periods or areas the redispatch will be the cheapest solution. After the prequalification, there is a need to collect the offers, sort them in the merit order and choose the cost-effective ones, which will manage congestion. The framework of the congestion management by TSO and DSO is shown in detail in [10]. Prequalification is one of the first steps in the TSO–DSO coordination process described in papers, although the scheme presented in this research does not require the prequalification of the units. While it is very important to check if the offers accepted do not violate any constraints in the network.

There are various solution methods regarding the modeling of TSO and DSO networks, starting from linear based models, through non-linear, mixed integer and mixed integer non-linear programming ending with quadratic programming. However, the most convenient and appropriate method may be mixed integer linear programming due to the simplicity and convergence [14]. Another subject is consideration of reactive power in the model of the DS and another one is the decision on how to model the power flow. There are some models that resolve the issue of TSO–DSO coordination using AC optimal power flow as in [24,25]. To reflect the real power flow the most appropriate method would be to use it in modeling AC power flow on two levels. However, simplified DC power flow with losses was established as equally efficient in TS [26]. An interesting approach to TSO–DSO coordination is shown in [27], although it may be extended with power flow in DS and flexible choice of offers on the interface TS–DS. An interesting approach is shown in [28], which considers two systems, DSO and TSO with real modeling of the system including the full power flow in both systems. The DC power flow is taken into consideration in both systems. Regarding the offers from DERs or generation sources, reference [24] used a bid function, whereas reference [25] presented the linear cost function for thermal generators. As has been previously presented, reference [26] uses set of fixed profiles for 24 h differentiated by cost. The current paper presents another approach in which the offers are established separately for periods. The model applied in the article considers three binary approaches, according to [29,30]; there are some two-binary [31] or single binary [32] approaches, although the three-binary approach was applied.

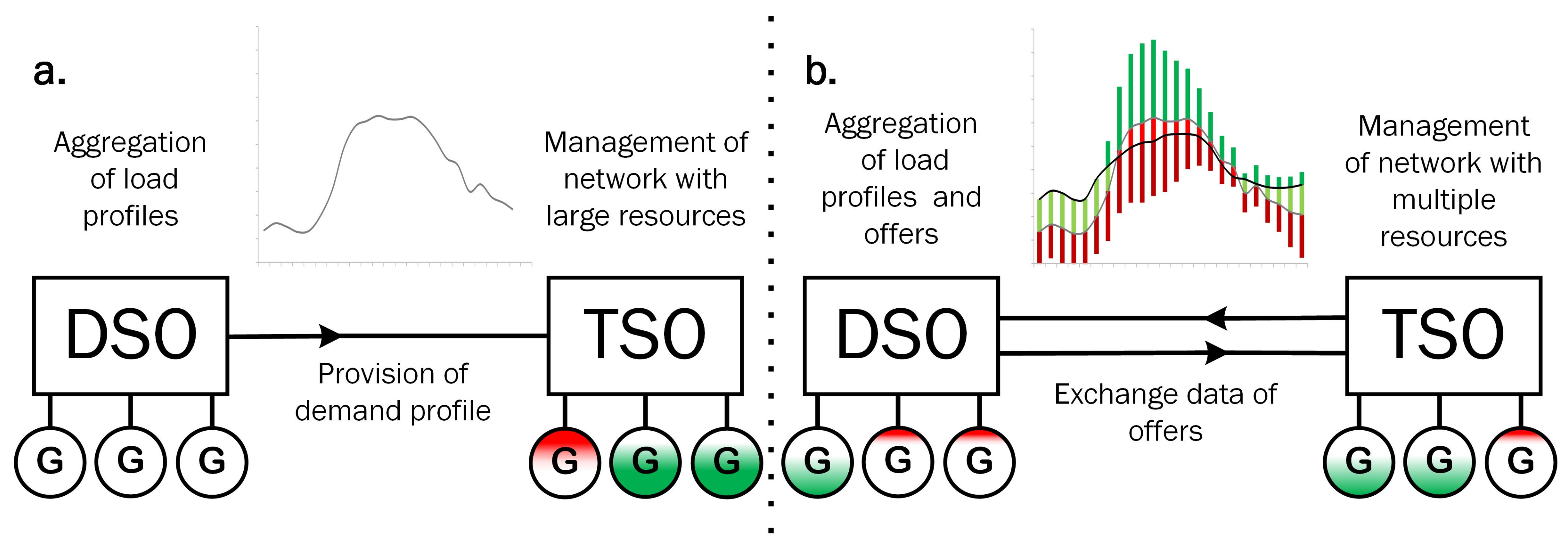
The key point of this paper is the strategy for coordination of operation between entities TSO and DSO. The current approach is that TSO maintains the sources from its grid, whereas resources from DS are not coordinated and do not provide any services to the operator, as shown in Figure 1a in red, green and white. Their output is based on the dispatch resulting from the day ahead market, although DERs do not participate in balancing market and the large ones may be curtailed. The main rule is that the TSO maintains TS by resources connected to its grid and the other ones are visible to TS as a constant profile in the TS–DS interface.

This paper establishes a new approach to coordination of sources from DS for purposes of TS. There is a need for proper coordination between entities to make this feasible and economically justified. The coordination of sources by TSO not only embraces the sources from TS but also allows using resources from DS. Its purpose is to decrease the operation costs of the power system, by extending the range of offers. The new approach of TSO–DSO coordination is given in Figure 1b, the usage of offers is lower and distributed among the most cost-efficient ones.

The concept of taking into consideration the TS and DS to show the coordination in complete form is applied in the article. The network constraints are considered in TS as well as in DS. The concept includes variable resources (DERs) in DS and other resources (RES and ES) in TS. The networks include renewable generation (solar and wind), other sources (like biogas power plants), ES and active and passive load. In the article, TS is modeled by DC power flow similarly to [29,30] extended by losses, whereas DS is modeled by AC power flow according to [33].

The main advantages of this paper are:

• Complete formulation of the coordination concept.
• Representation of networks in detailed form with constraints included.
• Presentation of offers for periods separately, instead of a fixed profile for the whole planning period.

The novelties in comparison to other studies are:

• Introduction of the five phase cycle of coordination between TSO and DSO instead of prequalification process. The cycle verifies the possibility of fulfilment of already chosen offers.
• The formulation of energy storage with initial dispatch included

3. Mathematical Formulation of the Problem

3.1. Transmission System Model

The model presented below allows to define commitment and dispatch of generation units connected directly to TS. It is based on initial load profiles, offers of generation units, Active Industrial Loads (AILs) and ES. TSO model for unit commitment and economic dispatch is based on [29,30] in terms of unit commitment, power system and thermal unit constraints.

3.1.1. Unit Commitment and Economic Dispatch of Conventional Sources

An essential element of the model is the formulation of constraints for large centrally dispatched units, presented in Equations (1)–(10).

$$U_{{}_{t,n}}-U_{{}_{t-1,n}}=V_{{}_{t,n}}-W_{{}_{t,n}}$$

(1)

$$P_{{}_{t,n}}+R_{{}_{t,n}}\le (p_{ma{x}_n}-p_{mi{n}_n})·U_{{}_{t,n}}-(p_{ma{x}_n}-p_{r{d}_n})·W_{{}_{t+1,n}}+(p_{r{u}_n}-p_{ma{x}_n})·V_{{}_{t,n}}$$

(2)

$$P_{{}_{t,n}}-R_{{}_{t,n}}\ge 0$$

(3)

Equation (1) is a basic binary constraint for a three-binary formulation with on and off states, turning on and turning off variables. Next, Equation (2) describes the maximal power constraint, which considers the reserve $R_{{}_{t,n}}$ and states of the unit $U_{{}_{t,n}},V_{{}_{t,n}},W_{{}_{t,n}}$. Equation (3) determines minimal power constraint for unit with consideration of reserve.

$$\sum _{i=t-t{u}_n+1}^t{V}_{{}_{i,n}}\le U_{{}_{t,n}}$$

(4)

$$\sum _{i=t-t{d}_n+1}^t{W}_{{}_{i,n}}\le 1-U_{{}_{t,n}}$$

(5)

Equation (4) restricts a start up of the unit, if the unit was in operation in the last $t{u}_n$ hours before the planned start up. Correspondingly, the down time of unit $t{d}_n$ is specified by Equation (5).

$$P_{{}_{t,n}}+R_{{}_{t,n}}-P_{{}_{t-1,n}}\ge p_{r{u}_n}$$

(6)

$$-P_{{}_{t,n}}+P_{{}_{t-1,n}}\ge p_{r{d}_n}$$

(7)

$$PS{T}_{{}_{t,n}}=\sum _{i=1}^I\left(p_{u_{n,i}}·V_{{}_{t+i,n}}\right)+p_{d_{n,i}}·W_{{}_{t,n}}$$

(8)

$$S{I}_{{}_{t,n,s}}\le \sum _{i=0}^{t_{hcs{u}_n}-1}{W}_{{}_{t-i,n}}$$

(9)

$$\sum _{s=1}^{S}S{I}_{{}_{t,n,s}}=V_{{}_{t,n}}$$

(10)

Equations (6) and (7) define, respectively, ramp up and ramp down of large units. Equation (8) determines the amount of energy generated during starts and shutdowns of large units. Finally, Equations (9) and (10) present variables of hot and cold starts of the unit to allow differentiation between them.

3.1.2. Generation from Other Resources in TS

Additionally, the TS model consists of renewable sources: Wind and solar. The power output of both is defined by Equation (11). Equation uses variables $CU{R}_{P{V}_{t,n}}$ and $CU{R}_{WN{D}_{t,n}}$ to allow curtailment of those resources. Equation (12) defines the limits of maximal and minimal curtailment.

$$RE{S}_{{}_{t,n}}=p{v}_{{}_t}·p_{p{v}_n}·(1-CU{R}_{P{V}_{t,n}})+\sum _{q=1}^Q(wn{d}_{{}_{t,q}}·wndlo{c}_{{}_{n,q}})·p_{wn{d}_n}·(1-CU{R}_{WN{D}_{t,n}})$$

(11)

$$0\le CU{R}_{P{V}_{t,n}}\le cur;0\le CU{R}_{WN{D}_{t,n}}\le cur$$

(12)

The model may use active industrial load, which is directly connected to transmission grid. Loads may be reduced by the certain factor, which must be compensated for in other periods of time. The limits of maximal reduction and increase are presented in Equations (13) and (14). Equation (15) determines the final profile of the industrial load connected in the node, on the basis of profile, installed power and activation of load shift. The whole reduction of the load must be covered by load increase. In other words, the whole shifted load is compensated for in other periods of time. It is implemented by usage of Equation (16).

$$0\le AL{N}_{{}_{t,n}}\le aln$$

(13)

$$0\le AL{P}_{{}_{t,n}}\le alp$$

(14)

$$AI{L}_{{}_{t,n}}=al{o}_{{}_t}·p_{a{l}_n}+al{o}_{{}_t}·p_{a{l}_n}·AL{P}_{{}_{t,n}}-al{o}_{{}_t}·p_{a{l}_n}·AL{N}_{{}_{t,n}}$$

(15)

$$\sum _{t=1}^T(al{o}_{{}_t}·p_{a{l}_n}·AL{P}_{{}_{t,n}})=\sum _{t=1}^T(al{o}_{{}_t}·p_{a{l}_n}·AL{N}_{{}_{t,n}})$$

(16)

The Energy Storage System (ESS) in TS is described in a similar manner as in [15,27,34,35,36]. Firstly, Equation (17) determines the output of energy storage in a time period in a particular node. The State Of Charge (SOC) is limited by the minimum and maximum values, as shown in Equation (18). Equation (19) defines SOC of a particular energy storage system on the basis of the previous state, operation of discharging and charging in a considered period of time. At this point, it is important to emphasize that the model allows to define the energy $e{s}_{e_n}$ and power $e{s}_{p_n}$ of particular ESSs separately. Equations (20)–(22) provide a constraint that only one of the operation modes is possible per one period. In other words ESS may either charge or discharge in one period. Decision variables in (20) are restricted to binaries and the equation determines that only one of the variables may be a non-zero.

$$E{S}_{t,n}=(e{s}_{p_n}·P_{DI{S}_{t,n}}-e{s}_{p_n}·P_{CH{A}_{t,n}})$$

(17)

$$so{c}_{mi{n}_n}\le SO{C}_{{}_{t,n}}\le so{c}_{ma{x}_n}$$

(18)

$$SO{C}_{{}_{t,n}}·e{s}_{e_n}=SO{C}_{{}_{t-1,n}}·e{s}_{e_n}-e{s}_{p_n}·\frac{P_{DI{S}_{t,n}}}{e{s}_{e{f}_n}}+e{s}_{p_n}·P_{CH{A}_{t,n}}·e{s}_{e{f}_n}$$

(19)

$$DI{S}_{{}_{t,n}}^B+CH{A}_{{}_{t,n}}^B\le 1$$

(20)

$$0\le P_{DI{S}_{t,n}}\le DI{S}_{{}_{t,n}}^B$$

(21)

$$0\le P_{CH{A}_{t,n}}\le CH{A}_{{}_{t,n}}^B$$

(22)

3.1.3. Power Flow in TS

The power flow is described based on [26] with the extension of power losses. It is a simplification of AC power flow represented by DC power flow with linearized losses in lines. Equation (23) describes the transmission capacity limits of the line flow. Equation (24) allows to define a positive and negative component of nodal angle difference and Equation (25) limits the value of angles. Equation (26) defines flow in line in TS based on nodal angle difference. Equation (27) determines the sum of flows from and to the particular node. Equations (28) and (29) allow to calculate nodal angle difference divided into segments for linearization purposes.

$$-f_{{}_{max}}·top{o}_{{}_{n,m}}\le F{L}_{{}_{t,n,m}}\le f_{{}_{max}}·top{o}_{{}_{n,m}}$$

(23)

$$AN{G}_{P_{t,n,m}}-AN{G}_{N_{t,n,m}}=AN{G}_{{}_{t,m}}-AN{G}_{{}_{t,n}}$$

(24)

$$AN{G}_{P_{t,n,m}}\ge 0;AN{G}_{N_{t,n,m}}\ge 0$$

(25)

$$F{L}_{{}_{t,n,m}}=-dis{t}_{{}_{n,m}}·b·top{o}_{{}_{n,m}}·(AN{G}_{P_{t,n,m}}-AN{G}_{N_{t,n,m}})$$

(26)

$$NE{T}_{{}_{t,n}}=\sum _{m=1}^{N}F{L}_{{}_{t,n,m}}$$

(27)

$$DI{F}_{{}_{t,n,m,z}}\le se{c}_{{}_z}+(1-top{o}_{{}_{n,m}})·c$$

(28)

$$AN{G}_{P_{t,n,m}}+AN{G}_{N_{t,n,m}}=\sum _{z=1}^{Z}DI{F}_{{}_{t,n,m,z}}$$

(29)

Equation (30) determines linearized losses in line and Equation (31) allows to calculate the sum of losses from lines connected to the considered node.

$$LOS{S}_{{}_{t,n,m}}=dis{t}_{{}_{n,m}}·g·\sum _{z=1}^Z(DI{F}_{{}_{t,n,m,z}}·alp{h}_{{}_z})·top{o}_{{}_{n,m}}$$

(30)

$$N{L}_{{}_{t,n}}=\sum _{m=1}^{N}LOS{S}_{{}_{t,n,m}}$$

(31)

Finally, the section of power flow is finished with cross border exchange. Equation (32) presents inflows and outflows on the basis of a given profile and declared power of interconnection. It results in a simple formulation, which corresponds to the real case, where day-ahead market cross boarder exchange may be considered as a parameter of balancing market realized by TSO.

$$c{b}_{{}_{t,n}}=c{b}_{e{x}_{t,n}}·c{b}_{ca{p}_n}$$

(32)

3.1.4. Nodal Balance of Production and Consumption

Equation (33) provides a nodal balance of production and consumption. The first component consists of power produced in large centrally dispatched units, then RES, ES followed by not served energy for flexibility of formulation and finally profile of cross-border exchange. On the other side, consumption is represented by demand in TS, large AILs, DS load profile, network flow and the sum of line losses in node. Components such as cross-border exchange, ES and network flow may represent positive and negative values, though their allocation depends on the formulation.

$$(p_{mi{n}_n}·U_{{}_{t,n}}+P_{{}_{t,n}}+PS{T}_{{}_{t,n}})+RE{S}_{{}_{t,n}}+E{S}_{{}_{t,n}}+NS{E}_{{}_{t,n}}+c{b}_{{}_{t,n}}=d_{{}_{t,n}}+AI{L}_{{}_{t,n}}+ODS{O}_{{}_{n,t}}+NE{T}_{{}_{t,n}}+N{L}_{{}_{t,n}}$$

(33)

3.1.5. Objective Function and Its Components

Conventional unit cost is based on no-load costs, costs of starts depending on the state of the unit, generation cost and $C{O}_2$ allowance price component. The formulation is presented in Equation (34).

$$C_{Con{v}_{t,n}}=U_{{}_{t,n}}·c_{n{l}_n}+C_{cs{u}_n}·S{I}_{{}_{t,n,1}}+C_{hs{u}_n}·S{I}_{{}_{t,n,2}}+(U_{{}_{t,n}}·p_{mi{n}_n}+P_{{}_{t,n}})·(c_{ge{n}_n}+pr{i}_{CO2})$$

(34)

In the model RES may be curtailed; however, it is connected with an additional cost of curtailment. Equation (35) determines cost of curtailment on the basis of amount of power curtailed and price, equally for both technologies, photovoltaic (PV) and wind generation.

$$C_{Cur{t}_{t,n}}=p{v}_{{}_t}·p_{p{v}_n}·c_{curp{v}_n}·CU{R}_{P{V}_{t,n}}+\sum _{q=1}^Q(wn{d}_{{}_{t,q}}·wn{d}_{lo{c}_{n,q}}·p_{wn{d}_n}·c_{curwn{d}_n}·CU{R}_{WN{D}_{t,n}})$$

(35)

Component of energy storage in the objective function covers costs of charging and its reduction by power injected into the TS during discharging; this formulation is presented in Equation (36).

$$C_{E{S}_{t,n}}=-pr{i}_{{}_t}·e{s}_{p_n}·P_{DI{S}_{t,n}}+pr{i}_{{}_t}·e{s}_{p_n}·P_{CH{A}_{t,n}}$$

(36)

In the case of active industrial loads, TSO covers costs of load shift. Thus, in Equation (37) power is calculated twice; it is multiplied by the price and divided by two.

$$C_{A{L}_{t,n}}=(al{o}_{{}_t}·p_{a{l}_n}·AL{P}_{{}_{t,n}}+al{o}_{{}_t}·p_{a{l}_n}·AL{N}_{{}_{t,n}})·\frac{c_{al}}{2}$$

(37)

Equation (38) determines the cost of non-served energy. Moreover, this component gives flexibility to the model calculation. If the input parameters are chosen appropriately, then $NS{E}_{{}_{t,n}}$ is equal to zero.

$$C_{NS{E}_{t,n}}=NS{E}_{{}_{t,n}}·c_{{}_{nse}}$$

(38)

Finally, Equation (39) defines the sum of all components—total cost. The objective function is minimized.

$$min\left(TotalCost\right)=\sum _{n=1}^N\sum _{t=1}^T(C_{Con{v}_{t,n}}+C_{Cur{t}_{t,n}}+C_{E{S}_{t,n}}+C_{A{L}_{t,n}}+C_{NS{E}_{t,n}})$$

(39)

3.2. DS Model

This section describes the DS model. It considers not only active power but also reactive power to better reflect real power flow in DS. It is delivered based on DistFlow methodology, applied in [33]. DistFlow methodology is widely applied in problems describing power flow in radial networks of DS [37,38].

3.2.1. Point of Common Coupling (PCC)

The equations below describe the limits of energy transferred between TS and DS in both directions. Equations (40) and (41) create limits for solely active and reactive power, respectively. Then Equations (42) and (43) cover areas, where active and reactive power is transmitted; reactive power is limited to a certain level according to the needed level of active power.

$$-pcc\le P_{PC{C}_t}\le pcc$$

(40)

$$-pcc\le Q_{PC{C}_t}\le pcc$$

(41)

$$-o·pcc+P_{PC{C}_t}\le Q_{PC{C}_t}\le o·pcc+P_{PC{C}_t}$$

(42)

$$-o·pcc-P_{PC{C}_t}\le Q_{PC{C}_t}\le o·pcc-P_{PC{C}_t}$$

(43)

3.2.2. Distributed Generation (DG)

Firstly, the power output of DG is defined by the modification of initial self-dispatch by accepted increase and decrease offers; it is realized with Equation (44). Constraints for active and reactive power are constructed in the same manner as in the case of PCC. Those formulations of generation limits are defined for active and reactive power, respectively, in Equations (45) and (46). Additionally, mixed generation of both active and reactive power is determined in Equation (47).

$$P_{D{G}_{t,n}}=po{w}_{{}_{n,t}}·p_{ma{x}_n}+D{G}_{P_{t,n}}-D{G}_{N_{t,n}}$$

(44)

$$p_{mi{n}_n}·U_{{}_{t,n}}\le P_{D{G}_{t,n}}\le p_{ma{x}_n}·U_{{}_{t,n}}$$

(45)

$$-p_{ma{x}_n}·U_{{}_{t,n}}\le Q_{D{G}_{t,n}}\le p_{ma{x}_n}·U_{{}_{t,n}}$$

(46)

$$-o·p_{ma{x}_n}+P_{D{G}_{t,n}}\le Q_{D{G}_{t,n}}\le o·p_{ma{x}_n}-P_{D{G}_{t,n}}$$

(47)

3.2.3. Active Demand of Load

Demands are divided into commercial, residential and industrial types. All of the equations given below to commercial load can be easily adapted to residential or industrial type. Equation (48) exemplifies final demand of commercial loads, which is modified by accepted offers: $CO{M}_{P_{t,n}}$ and $CO{M}_{N_{t,n}}$. Equations (49) and (50) describe, respectively, maximal level of demand shift and equality between increased and decreased demand. Reactive power of demand is calculated by using constant power factor, as in Equation (51). The total amount of power shifted in the commercial demand is limited by Equation (52). Industrial and residential loads are described in the same manner; thus, they are not described in this section.

$$CO{M}_{{}_{t,n}}=p_{co{m}_n}·co{m}_{{}_t}·(1+CO{M}_{P_{t,n}}-CO{M}_{N_{t,n}})$$

(48)

$$CO{M}_{P_{t,n}}\le c{o}_{{}_{cr}};CO{M}_{N_{t,n}}\le c{o}_{{}_{cr}}$$

(49)

$$\sum _{t=1}^T(p_{co{m}_n}·co{m}_{{}_t}·CO{M}_{P_{t,n}})=\sum _{t=1}^T(p_{co{m}_n}·co{m}_{{}_t}·CO{M}_{N_{t,n}})$$

(50)

$$Q_{CO{M}_{t,n}}=t{g}_{co{m}_1}·CO{M}_{{}_{t,n}}$$

(51)

$$CO{M}_{P_{t,n}}\le m·c{o}_{{}_{cr}}$$

(52)

3.2.4. Generation from Other DERs

Generation from DERs embraces PV, wind generation and ES, which will be described below.

• Photovoltaic generation

  $$P{V}_{{}_{t,n}}=p{v}_{{}_t}·p_{p{v}_n}·(1-CU{R}_{P{V}_{t,n}})$$

  (53)

  $$CU{R}_{P{V}_{t,n}}\le cur$$

  (54)
  The power output of PV is calculated based on generation profile, installed power and activated curtailment, as presented in Equation (53). Maximal curtailment activation is limited by Equation (54).
• Wind generation

  $$WIN{D}_{{}_{t,n}}=\sum _{q=1}^Q(wn{d}_{{}_{t,q}}·wn{d}_{lo{c}_{n,q}}·p_{wn{d}_n})\dot{(}1-CU{R}_{WN{D}_{t,n}})$$

  (55)

  $$CU{R}_{WN{D}_{t,n}}\le cur$$

  (56)
  Equations that describe wind generation are shown as Equations (55) and (56). The first one differs from the formulation for PV, whereas the second one is identical. The difference between the generation form of PV and wind generation has the source in the usage of multiple wind generation profiles. Wind generation profile allows to differentiate generation between a few locations. In the case of PV, the generation profile is identical.
• Energy Storage
  Firstly, in modelling energy storage Equations (57) and (58) are presented in identical form as in TS model. Further, formulation of reactive power is presented in Equations (59)–(61). Reactive power is limited in accordance with the level of active power generation scheduled for the considered period of time.

  $$so{c}_{mi{n}_n}\le SO{C}_{{}_{t,n}}\le so{c}_{ma{x}_n}$$

  (57)

  $$DI{S}_{t,n}^B+CH{A}_{t,n}^B\le 1$$

  (58)

  $$-e{s}_{p_n}\le Q_{E{S}_{t,n}}\le e{s}_{p_n}$$

  (59)

  $$-o·e{s}_{p_n}+E{S}_{{}_{t,n}}\le Q_{E{S}_{t,n}}\le o·e{s}_{p_n}-E{S}_{{}_{t,n}}$$

  (60)

  $$-o·e{s}_{p_n}-E{S}_{{}_{t,n}}\le Q_{E{S}_{t,n}}\le o·e{s}_{p_n}+E{S}_{{}_{t,n}}$$

  (61)
  The equations below differ from the formulation presented for the TS model. The main difference is in the usage of $in{i}_{di{s}_{t,n}}$ and $in{i}_{ch{a}_{t,n}}$, which defines a level of initial operation plan of ESS. The initial plan may be considered as a result of the day ahead market, which may be treated as a starting point for this model. Moreover, this formulation is original and is presented for the first time in this publication. None of the considered references presented a formulation with an initial state and binary restriction of charge and discharge. Details and advantages of this formulation are presented in Appendix A. Equation (62) represents formulation of the power output of ESS based on flexibility services provided by ES ( $P_{DI{S}_{t,n}}$ and $P_{CH{A}_{t,n}}$) and its initial plan. State of charge is defined based on the previous state of charge, used flexibility services and initial plan, as shown in Equation (63). Finally, Equations (64) and (65) limit the operation of charge and discharge in the same period with proper selection of binary indicator from Equation (58).

  $$E{S}_{{}_{t,n}}=e{s}_{p_n}·(P_{DI{S}_{t,n}}+in{i}_{di{s}_{t,n}})-e{s}_{p_n}·(P_{CH{A}_{t,n}}+in{i}_{ch{a}_{t,n}})$$

  (62)

  $$SO{C}_{{}_{t,n}}·e{s}_{e_n}=SO{C}_{{}_{t-1,n}}·e{s}_{e_n}-\frac{e{s}_{p_n}·P_{DI{S}_{t,n}}}{e{s}_{ef}}+e{s}_{p_n}·P_{CH{A}_{t,n}}·e{s}_{ef}+in{i}_{chat,n}·e{s}_{p_n}·e{s}_{ef}-\frac{in{i}_{di{s}_{t,n}}·e{s}_{p_n}}{e{s}_{ef}}$$

  (63)

  $$in{i}_{di{s}_{t,n}}+P_{DI{S}_{t,n}}-P_{CH{A}_{t,b}}\le DI{S}_{t,n}^B+in{i}_{ch{a}_{t,n}}$$

  (64)

  $$in{i}_{ch{a}_{t,n}}+P_{CH{A}_{t,n}}-P_{DI{S}_{t,b}}\le CH{A}_{t,n}^B+in{i}_{di{s}_{t,n}}$$

  (65)

3.2.5. Power Flow in DS

The next subset of equations defines the formulation of power flow in DS. Equations (66) and (67) describe inflow or outflow in a particular node, based on line flows. Equations (68) and (69) limit solely active and reactive power flow in particular lines, respectively. Reactive power is limited by the level of transmitted active power in Equations (70) and (71). Finally, the square of nodal voltage is limited as in Equation (72) and voltage drop along the line is determined as in Equation (73).

$$NE{T}_{{}_{t,n}}=\sum _{l=1}^L(a_{{}_{n,l}}·P_{L_{l,t}})$$

(66)

$$QE{T}_{{}_{t,n}}=\sum _{l=1}^L(a_{{}_{n,l}}·Q_{L_{l,t}})$$

(67)

$$-flow\le P_{L_{l,t}}\le flow$$

(68)

$$-flow\le Q_{L_{l,t}}\le flow$$

(69)

$$-o·flow+P_{L_{l,t}}\le Q_{L_{l,t}}\le o·flow-P_{L_{l,t}}$$

(70)

$$-o·flow-P_{L_{l,t}}\le Q_{L_{l,t}}\le o·flow+P_{L_{l,t}}$$

(71)

$$v{q}_{min}\le VN{Q}_{{}_{t,n}}\le v{q}_{max}$$

(72)

$$\sum _{n=1}^N(VN{Q}_{{}_{t,n}}·a_{{}_{n,l}})=2·(r·P_{L_{l,t}}+x·Q_{L_{l,t}})$$

(73)

3.2.6. Balance

The consecutive section defines balance in nodes for active and reactive power separately. The active power balance in Equation (74) takes into account all resources available in the network, demands of load and inflows or outflows in a particular node. Equation (75) provides a reactive power balance; it is similar to active power balance excluding wind generation and PV generation, which in this concept do not contribute to reactive power. Both equations are presented in general form, where $P_{PCC}$ and $Q_{PCC}$ are not presented; thus, those are taken into account only for one node for each DS.

$$P{V}_{{}_{t,n}}+WIN{D}_{{}_{t,n}}+P_{D{G}_{t,n}}+E{S}_{{}_{t,n}}+NS{E}_{{}_{t,n}}=DE{M}_{{}_{t,n}}+NE{T}_{{}_{t,n}}$$

(74)

$$Q_{D{G}_{t,n}}+Q_{E{S}_{t,n}}+Q_{NS{E}_{t,n}}=Q_{DE{M}_{t,n}}+QE{T}_{{}_{t,n}}$$

(75)

3.2.7. Objective Function

The section below describes components of the objective function and its final form. Firstly, the cost of distributed generation flexibility services is defined in Equation (76). The cost is defined as the cost of activation of flexibility service.

$$C_{D{G}_{t,n}}=D{G}_{P_{t,n}}·c_{pdg}+D{G}_{Nt,n}·c_{ndg}$$

(76)

Then, Equation (77) exemplifies the cost of flexibility services provided by active loads. Components are divided into sums for each type of load. The price of flexibility provided by loads is differentiated according to load type; price is defined as the cost of load shift between considered periods.

$$C_{DE{M}_{n,t}}=p_{co{m}_n}·co{m}_{{}_t}·(CO{M}_{N_{t,n}}+CO{M}_{P_{t,n}})+p_{in{d}_n}·in{d}_{{}_t}·(IN{D}_{N_{t,n}}+IN{D}_{P_{t,n}})+p_{re{s}_n}·re{s}_{{}_t}·(RE{S}_{N_{t,n}}+RE{S}_{P_{t,n}})$$

(77)

The cost of curtailment has two components; the first corresponds with PV curtailment and the second with wind generation curtailment. The total cost of curtailment for both items is shown in Equation (78). The cost of curtailment for both PV and wind generation is defined as a share of day ahead market price, which results in a minor reduction of income for RES in the case of provision of flexibility services.

$$C_{Cur{t}_{t,n}}=p{v}_{{}_t}·p_{p{v}_n}·c_{cur}·pr{i}_{{}_t}·CU{R}_{P{V}_{t,n}}+\sum _{q=1}^Q(wn{d}_{{}_{t,q}}·wn{d}_{lo{c}_{n,q}}·p_{wn{d}_n}·c_{cur}·pr{i}_{{}_t}·CU{R}_{WN{D}_{t,n}})$$

(78)

The cost of flexibility services provided by ESS is presented in Equation (79). Similar to the cost of services provided by DG, ESSs are paid for when energy is activated concerning an offer in the flexibility market.

$$C_{E{S}_{t,n}}=c_{pes}·e{s}_{p_n}·P_{DI{S}_{t,n}}+c_{nes}·e{s}_{p_n}·P_{CH{A}_{t,n}}$$

(79)

The model takes into account the possibility of not served energy, which should not be present in the normal state. Equations (80) and (81) define the cost of not served energy regarding active and reactive power.

$$C_{NS{E}_{t,n}}=NS{E}_{{}_{t,n}}·c_{{}_{nse}}$$

(80)

$$C_{QNS{E}_{t,n}}=Q_{NS{E}_{t,n}}·c_{qnse}$$

(81)

Equation (82) determines the objective function as the sum of previously presented components. The objective function is minimized to obtain minimal cost of operation.

$$min\left(Obj\right)=\sum _{n=1}^N\sum _{t=1}^T(C_{D{G}_{t,n}}+C_{DE{M}_{t,n}}+C_{Cur{t}_{t,n}}+C_{E{S}_{t,n}}+C_{NS{E}_{t,n}}+C_{QNS{E}_{t,n}})$$

(82)

3.3. TSO–DSO Coordination

The TSO–DSO coordination introduced in this paper embraces the usage of distributed sources in DS. The proposed balancing market is extended by resources from DS or, in other words, it presents the idea of a future flexibility market. Advancement in the energy market requires tight coordination and data exchange at every step due to mutual relations between parties involved and dependencies between participants. The proposed design of a flexibility market with a balancing market included is shown in Figure 2.

The coordination introduced in this paper is divided into five phases in which offers from DERs are collected, aggregated, selected, verified and finally accepted by TSO and included in the final operation plan of the grid. The coordination between TSO and DSO models introduces the following stages: Preparation of self-dispatch, a collection of offers from DERs and initial power flow in DS, selection of the offers by TSO, verification of the requests by DSO and the final operation plan presented by TSO and sent back to DSO, Large Dispatchable Units (LDUs) and the distributed resources in DS. The charts shown in Figure 2 present a profile with offers of reduction and increase of output power in every stage. Moreover, in the figure, accepted and rejected offers are differentiated by color. During stage four, the chart is extended by the final profile and on stage five initial and final profiles are presented with accepted offers.

A more detailed view of the first three steps is shown in Figure 3. All stages from Figure 3 correspond with the ones shown before. Step $2c$ in Figure 3 was not included previously, since currently it is already a part of the balancing market. Offers and already contracted outputs from LDUs are crucial for balancing the market since those are the core that allows to balance the demand in the power system.

In the first phase, the initial point of operation and offers are collected from DERs by DSO. The self-dispatch of DERs is created on the grounds of the day ahead market or other contracts. DERs send possible offers of increase or decrease regarding their capabilities for flexibility offer.

The second stage is focused on power flow in DS. Based on the information from DERs, DSO optimizes network operation with sources located in DS. Currently, this is limited only to small corrective actions; however, in the future with high penetration of RES such an action will play a key role in grid management. DERs may have the possibility to increase energy produced or decrease the generation in the flexibility market. The values of available power possible to be offered as flexibility may be used by DSO for DS management or by TSO for purposes of congestion management or optimization of energy cost in TS.

The general equations expressing the possibility to modify the actual generation level are presented below. Equation (83) defines maximal power that a source may offer for increase; Equation (84) determines the power to decrease the output.

$$P_{Offi}=p_{ma{x}_n}-P_{outpu{t}_{t,n}}$$

(83)

$$P_{Offd}=P_{outpu{t}_{t,n}}-p_{mi{n}_n}$$

(84)

The third stage embraces the TSO model balancing market, where offers of LDUs are corrected to provide electricity to the final user with affordable price and without violating network constraints. Moreover, the model takes into consideration offers collected by DSO. The TSO model optimizes resources in TS based on offers submitted by them and in DS based on offers collected and aggregated by DSO. The variable of acceptance (1) or rejection (0) of offer $V_{of{f}_i}$ is introduced. The Equation (85) of cost formulation is presented below.

$$Cos{t}_{off}=\sum _{i=1}^I(P_{Off{i}_i}·V_{off{i}_i}·pric{e}_{off{i}_i}+P_{Off{d}_i}·V_{off{d}_i}·pric{e}_{off{d}_i})$$

(85)

The TSO role is to choose offers of increase or decrease, which will reduce total cost of system operation. The acceptance is multiplied by the power offered and their cost, resulting in components of, respectively, balance and objective function. The accepted offers in Figure 4 are presented in brighter colors on the chart, green for increase and red for reduction of generation. Furthermore, offers chosen by TSO are named as “requested offers” from DSO by TSO. The results of the third phase cover preparation of the schedule with requested–accepted offers and exchange this data with DSOs for final verification.

In some instances, there is a need to extend the TSO model by equations to reflect a better modelled environment. Regarding the possible shift provided by the active load, there is an added equality constraint, where the decrease of demand has to be equal to the increase of demand in another period of time. Equation (86) presents this example. It is based on an active industrial load.

$$\sum _{t=1}^T(p_{pl{i}_{t,c}}·v_{pl{i}_{t,c}})=\sum _{t=1}^T(p_{nl{i}_{t,c}}·v_{nl{i}_{t,c}})$$

(86)

A more detailed view of the two last steps is shown in the Figure 4. Both phases continue the coordination and a detailed description of the phases is presented below.

The fourth stage includes the verification process by DSO. The operator performs power flow studies considering requested offers by TSO. The requested offers from TSO are considered in the model in the equations, which verifies whether the requested value ($p_{re{q}_t}$) may be realized and whether it will not result in violation of the network constraints. An example of an equation is presented below. The equation ensures that resource type i will provide a volume that is greater or equal to the already planned values ($p_{use{d}_t}$), increased by the additional TSO’s request. Supplementary variable $X_{{}_t}$ allows to not satisfy the criteria only if network constraints will be violated by the chosen offer.

$$p_{re{q}_t}+p_{use{d}_t}-X_{{}_t}\le \sum _{n=1}^N{p}_{ac{t}_t}$$

(87)

The necessity of such verification increases due to the model formulation. Initially, DSO collects offers from DERs and eventually uses them to solve network constraints within DS. DSO passes offers to TSO without feasibility studies. Prequalification is computationally intensive or impossible to analyze in all possible options of offers potentially accepted by TSO. However, DSO verifies feasibility on the stage, where the request is known and only the feasibility of the chosen offers is confirmed. In other words, it is needed since in the first step DSO sends all the possible use of the resources without checking whether the offers do not violate the network constraints. Therefore this verification needs to be performed in the third step. Before the next phase, the verified offers with the final profile at PCC are sent back to TSO. The fifth stage embraces the final plan optimized by TSO including offers that are verified and able to be applied. The final plan is distributed among interested agents.

The pseudocode of the whole concept is presented in Figure 5 for clarification purposes. The code reflects phases presented above on charts.

4. Model Identification

The model consists of simple TS and three different DSs, which are connected to the third, fifth and eighth nodes of the transmission network. For simplification purposes, TS and DSs are analyzed on the single voltage level for each one. Both systems are designed straightforwardly and thus are relatively small; however, their size is sufficiently large to analyze the operation and verify the presented coordination scheme.

4.1. Transmission System Model

The purpose of the following subsection is to describe the TS used in the case studies. The system is presented in Figure 6. It consists of eight nodes; in each of them LDU and load are located. The load type for each node is defined in Appendix B.1. In the majority of nodes, generation facilities—wind generation, PV and energy storage—are located, beside typical distributed dispatchable generation and load. In two nodes large active industrial loads are located. The system is built out of twelve lines, which create multiple loops within the network. In line with the previous section, the system is based on a single voltage level.

4.2. Distribution System Model

In the following subsection three different DSs are presented in Figure 7. Each of the DSs consists of seven nodes and six lines, but in different arrangement. The first DS is connected to third node of the TS, the second DS is connected to fifth node of the TS and the third DS is connected to the eighth node of the TS. The data regarding parameters of sources, demand and network are presented in Appendix B.2. In the DSs the following units are considered: Demand, active demand, DG, PV, wind energy generation and ES.

5. Case Studies

The case studies are divided into two parts: Comparison of business as usual (S1) and the operation with flexibility market offers (S2). The second part embraces comparison between the same scenarios (S3—business as usual; S4—flexibility market) differing in the share of renewable energy. RESs are tripled in installed power when compared to initial scenarios S1 and S2.

The concept requires two platforms of data exchange: First to collect and exchange data between DSOs and DERs located in DS and second to exchange data between TSO and DSO. The needs in the area of software and hardware are to be clarified on further steps of implementation. Authors suggest that DSO should coordinate the first platform, whereas the second should be managed by TSO.

5.1. Comparison of Different Scenarios S1 and S2

The first part of case studies embraces comparison between business as usual and operation with flexibility services provided by DR. The decrease of system operation costs in scenario S2 compared to business as usual is −0.32%. This value added was obtained by the use of three DSs connected to TS. The important thing is that those networks represent less than 10% of the total demand in the network. If the share of active market participants will be more significant, then higher benefits of the flexibility market should be expected.

The income of resources participating in flexibility services was investigated. The increase of income in distributed generation, which provides flexibility services, grew by 3.87% in comparison to the income in business as usual. In the case of ES, the income was increased by 4.96%. To conclude, the resources may benefit from the existence of an additional market, in parallel to income from the energy market.

The distribution of the income of DG in DS 1 regarding the regular operation (initial income from energy market) and the final one including income from flexibility market is shown in Figure 8. The income of DG is computed according to Equation (76). The usage of the flexibility offers influences the distribution of income by increasing it in high demand periods when the price of DERs is lower than the price of LDU.

Table 1. Energy transferred in PCCs in the 3rd (initial) and 5th (final) steps in scenario S2.

	Initial (3rd Step)			Final (5th Step)
	DS 1	DS 2	DS 3	DS 1	DS 2	DS 3
Sum	952.72	780.62	143.26	860.73	697.22	21.94
Average	39.70	32.53	5.97	35.86	29.05	0.91
Min	−237.66	−104.56	−147.21	−211.19	−66.38	−90.46
Max	212.93	166.02	134.84	199.99	132.65	111.68

presents the parameters of energy transferred in PCC after the third and fifth steps. It presents four parameters of profile: Sum of energy transferred and average, minimum and maximum values for each DS. The sum of energy is reduced in the final flow for each network: −9.65% in the case of DS1, −10.68% in the case of DS2 and −84.68% in the case of DS3. The exchange is reduced by DERs located in DS. Generally, resources generate more in peak hours to reduce the cost of the whole network. The maximum flow of energy between TS and DS decreased, similarly to the average. In the case of minimal flow, the index grew. The positive sign of flow in PCC means that the energy is transferred from TS to DS, whereas the negative sign of flow in PCC means the opposite transfer.

The chart in Figure 9 shows the profile of exchange in PCC for DS 3 in a 24 h period. It presents that the values differ the most when demand or price are on the extreme points. In other words, the model smooths exchange between TS and DS, the peaks are shaved and the valleys are filled.

The following graph Figure 10 presents the value of the energy transmitted from TSO to demand, including active DS. The sum of the profile decreased by 0.93% in the scenario using flexibility services S2 in comparison to scenario S1. It can be concluded that the distribution systems in the future will be able to smooth the profile and reduce the exchange with TSO.

The other comparison embraces the operation of ES in node 6 in DS 1, as shown in Figure 11. It shows the initial energy plan, which is performed by ES initially on the base of its participation in the energy market. Additionally, it presents the operation plan with flexibility activation from DSO, which is the result of the third step in scenario S2 using flexibility services. Finally, it shows the plan after the fifth step in the same scenario. The ES operation plan shows the change in ES operation, taking into consideration firstly the activation of flexibility from DSO and secondly services activation from both TSO and DSO.

5.2. Analysis of Influence in the Case of High Renewable Installed Power

This section encompasses the comparison of the base scenario shown before and the scenario of probable future power systems with high RES penetration. This scenario will consist of an increased amount of renewable energy along with an increased amount of ES. The scenario takes into consideration tripled power of RES and ES. In scenario S4, the whole system costs are decreased by 3.32% in comparison with using a business as usual approach. The overview of four scenarios is presented below in

Table 2. Cost comparison between scenarios.

	S1	S2	S3	S4
Operation cost of DS 1	843	8208	10,031	14,568
Operation cost of DS 2	644	10,794	21,874	25,589
Operation cost of DS 3	864	12,150	10,972	16,107
Operation cost of TS	1,279,928	1,247,015	283,935	259,697
Sum	1,282,278	1,278,167	326,812	315,961

. The first scenarios, S1 and S2, involve the base case regarding power in renewable sources, whereas scenarios S3 and S4 involve an increased amount of renewable energy. Due to the different amount of installed power of renewable energy sources, the pair of scenarios S1 and S2 should not be compared directly with pair S3 and S4. Scenario S1 shows the results of business as usual, similarly to scenario S3, whereas scenarios S2 and S4 present the cases based on flexibility services offered in both networks.

6. Conclusions

Future power systems consisting of a large number of renewable sources and DERs will need strong TSO–DSO cooperation to provide better utilization of those sources and lower operation cost of the network with flexibility services. TSO–DSO coordination will play a key role in system operation and congestion management in future power systems.

Therefore, the paper presented the framework of TSO–DSO coordination, which will be focused on the creation and usage of the flexibility market. To efficiently use renewable sources and DERs from DS, it will be necessary to provide flexibility offers from those sources that can be possibly used for TSO and DSO purposes. The paper introduced the entire optimization of the TSO system, the DSO system and its coordination. The main goal of the paper was to show the possibility of application of the flexibility market into the existing system and a comparison between them.

The case studies presented that TSO–DSO coordination decreased the operational costs of the whole system in comparison to business as usual—power system management system using corrective measures. The paper showed that this coordination brings benefits to the sources that offer their services in a flexibility market, in the form of an additional income. Due to the design of the coordination, the offers are used only if those are more beneficial than conventional corrective measures in the TS network. The case studies demonstrated that, using flexibility services, the transfer from TS to DS is reduced. On account of that, it can be concluded that in the future DS will be able to smooth the profile on the TS–DS interface and reduce the exchange with TS, by reason of increased usage of flexibility services. Finally, the study presented that the flexibility services may decrease system operation cost, especially if the system has a high share of RES.

The next steps of the research may cover areas such as different pricing mechanisms and the influence of the evolution of energy mix on the future flexibility of the system and an extended analysis of different scenarios of network development.