Output Temperature Predictions of the Geothermal Heat Pump System Using an Improved Grey Prediction Model
Abstract
1. Introduction
2. Materials and Methods
2.1. GM (1,1) Model
2.2. Improved IGM (1,1) Model
3. Experimental Design
3.1. Data Description
3.2. Model Evaluation
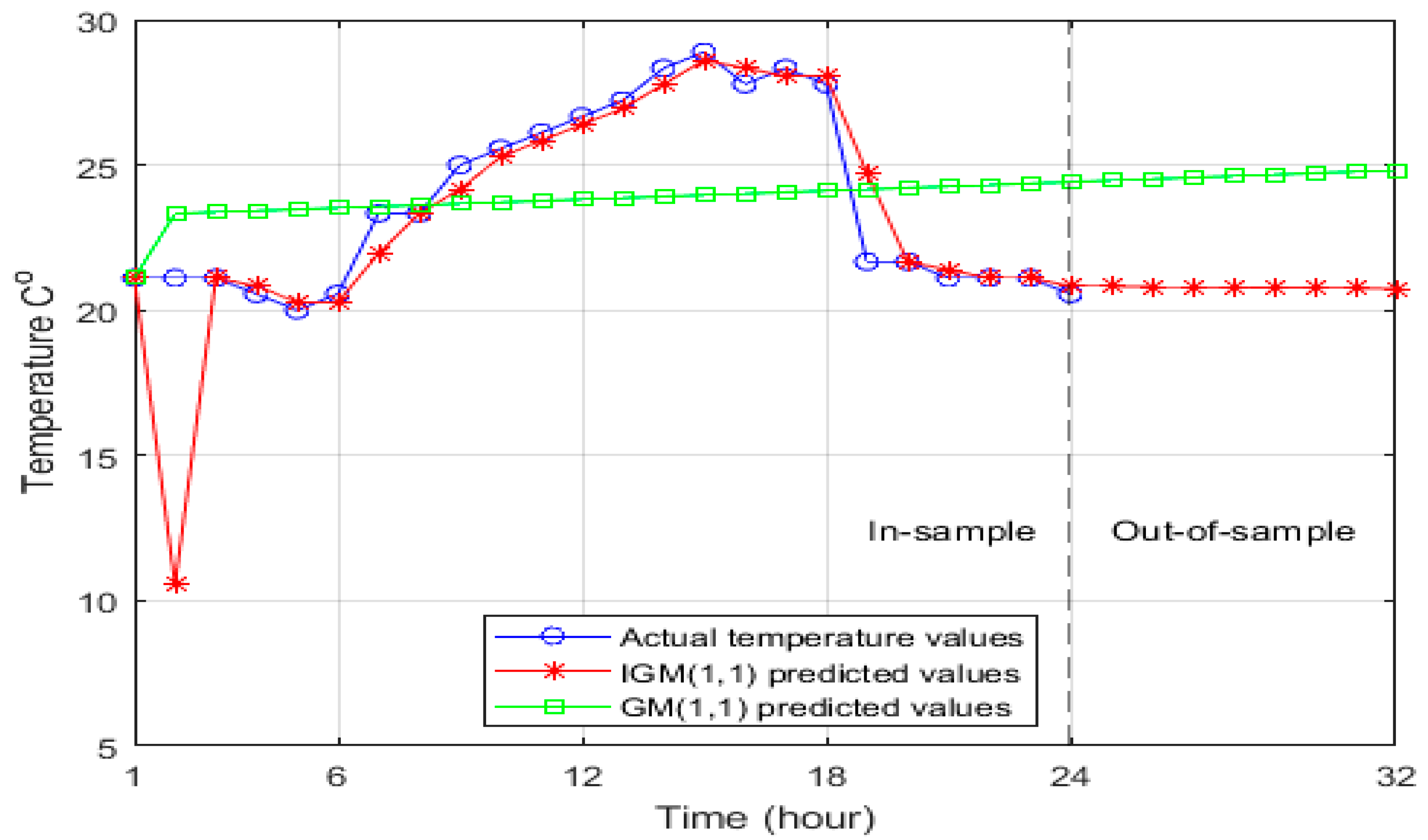
4. Result and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nagano, K.; Katsura, T.; Takeda, S. Development of a design and performance prediction tool for the ground source heat pump system. Appl. Therm. Eng. 2006, 26, 1578–1592. [Google Scholar] [CrossRef]
- Sfeir, A.; Million, T.; Bernier, M.A.; Joly, A. A methodology to evaluate pumping energy consumption in GSHP systems. ASHRAE Trans. 2005, 111, 714–729. [Google Scholar]
- Omer, A.M. Ground-source heat pumps systems and applications. Renew. Sustain. Energy Rev. 2008, 12, 344–371. [Google Scholar] [CrossRef]
- Kakac, S.; Liu, H.; Pramuanjaroenkij, A. Heat Exchangers: Selection, Rating, and Thermal Design; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Katsunori, N.; Katsura, T. Performance Prediction Program and Performance Prediction System for Ground Source Heat Pump System. U.S. Patent No. 7,113,888, 26 September 2006. [Google Scholar]
- Esen, H.; Inalli, M.; Sengur, A.; Esen, M. Performance prediction of a ground-coupled heat pump system using artificial neural networks. Expert Syst. Appl. 2008, 35, 1940–1948. [Google Scholar] [CrossRef]
- Gang, W.; Wang, J. Predictive ANN models of ground heat exchanger for the control of hybrid ground source heat pump systems. Appl. Energy 2013, 112, 1146–1153. [Google Scholar] [CrossRef]
- Baruque, B.; Porras, S.; Jove, E.; Calvo-Rolle, J.L. Geothermal heat exchanger energy prediction based on time series and monitoring sensors optimization. Energy 2019, 171, 49–60. [Google Scholar] [CrossRef]
- Michopoulos, A.; Κyriakis, N. Predicting the fluid temperature at the exit of the vertical ground heat exchangers. Appl. Energy 2009, 86, 2065–2070. [Google Scholar] [CrossRef]
- Quan, Q.; Hao, Z.; Xifeng, H.; Jingchun, L. Research on water temperature prediction based on improved support vector regression. Neural Comput. Appl. 2020, 1–10. [Google Scholar] [CrossRef]
- Thiyagarajan, K.; Kodagoda, S.; Ulapane, N. Short-term Time Series Forecasting of Concrete Sewer Pipe Surface Temperature. In Proceedings of the 2020 16th International Conference on Control, Automation, Robotics and Vision (ICARCV), Shenzhen, China, 13–15 December 2020; pp. 1194–1199. [Google Scholar] [CrossRef]
- Mehrmolaei, S.; Mohammad, R.K. Time series forecasting using improved ARIMA. In Proceedings of the 2016 Artificial Intelligence and Robotics (IRANOPEN), Qazvin, Iran, 9 April 2016. [Google Scholar]
- Toharudin, T.; Pontoh, R.S.; Caraka, R.E.; Zahroh, S.; Lee, Y.; Chen, R.C. Employing long short-term memory and Facebook prophet model in air temperature forecasting. Commun. Stat. Simul. Comput. 2021, 1–24. [Google Scholar] [CrossRef]
- Ju-Long, D. Control problems of grey systems. Syst. Control. Lett. 1982, 1, 288–294. [Google Scholar] [CrossRef]
- Liu, S.; Lin, Y. Grey Information: Theory and Practical Applications; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Deng, J.L. The Basis of Grey Theory; Press of Huazhong University of Science & Technology: Wuhan, China, 2002; pp. 35–41. [Google Scholar]
- Yousuf, M.U.; Al-Bahadly, I.; Avci, E. A modified GM (1,1) model to accurately predict wind speed. Sustain. Energy Technol. Assess. 2021, 43, 100905. [Google Scholar]
- Wang, Y.; Wei, F.; Sun, C.; Li, Q. The Research of Improved Grey GM (1,1) Model to Predict the Postprandial Glucose in Type 2 Diabetes. BioMed Res. Int. 2016, 2016, 6837052. [Google Scholar] [CrossRef][Green Version]
- Zhou, W.; He, J.-M. Generalized GM (1,1) model and its application in forecasting of fuel production. Appl. Math. Model. 2013, 37, 6234–6243. [Google Scholar] [CrossRef]
- Qian, W.; Wang, J. An improved seasonal GM (1,1) model based on the HP filter for forecasting wind power generation in China. Energy 2020, 209, 118499. [Google Scholar] [CrossRef]
- Julong, D. Introduction to grey system theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Akay, D.; Atak, M. Grey prediction with rolling mechanism for electricity demand forecasting of Turkey. Energy 2007, 32, 1670–1675. [Google Scholar] [CrossRef]
- Wu, L.; Liu, S.; Yao, L.; Yan, S. The effect of sample size on the grey system model. Appl. Math. Model. 2013, 37, 6577–6583. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, H.; Guo, Y. Wind Power Prediction Based on PSO-SVR and Grey Combination Model. IEEE Access 2019, 7, 136254–136267. [Google Scholar] [CrossRef]
- Hsu, L.-C.; Wang, C.-H. Forecasting the output of integrated circuit industry using a grey model improved by the Bayesian analysis. Technol. Forecast. Soc. Chang. 2007, 74, 843–853. [Google Scholar] [CrossRef]
- Urrutia, J.D.; Antonil, F.E. A Markov chain grey model: A forecasting of the Philippines electric energy demand. AIP Conf. Proc. 2019, 2192, 090013. [Google Scholar] [CrossRef]
- Wang, Y.; Dang, Y.; Li, Y.; Liu, S. An approach to increase prediction precision of GM (1,1) model based on optimization of the initial condition. Expert Syst. Appl. 2010, 37, 5640–5644. [Google Scholar] [CrossRef]
- Jia, Z.; Fan, Z.; Li, C.; Jiang, M. The application of improved grey GM (1,1) model in power system load forecast. In Future Wireless Networks and Information Systems; Springer: Berlin/Heidelberg, Germany, 2012; pp. 603–608. [Google Scholar]
- Madhi, M.H.; Mohamed, N. An improved GM (1,1) model based on modified background value. Inf. Technol. J. 2017, 16, 11–16. [Google Scholar] [CrossRef][Green Version]
- Hsu, L.-C. Using improved grey forecasting models to forecast the output of opto-electronics industry. Expert Syst. Appl. 2011. [Google Scholar] [CrossRef]
- Beier, R.; Smith, M.D.; Spitler, J.D. Reference data sets for vertical borehole ground heat exchanger models and thermal response test analysis. Geothermics 2011, 40, 79–85. [Google Scholar] [CrossRef]
- Ruiz-Calvo, F.; Cervera-Vázquez, J.; Montagud, C.; Corberán, J. Reference data sets for validating and analyzing GSHP systems based on an eleven-year operation period. Geothermics 2016, 64, 538–550. [Google Scholar] [CrossRef]
- Leidel, J. Human Health Science Building Geothermal Heat Pump Systems; No. EE0002970-Final-Revised; Oakland University: Rochester, MI, USA, 2014. [Google Scholar]


| Time (Hours) k | Actual Temperature Values °C | IGM (1,1) Predicted Values °C | GM (1,1) Predicted Values °C |
|---|---|---|---|
| 25 | 37.72778 | 37.664 | 38.8703 |
| 26 | 37.76667 | 37.6669 | 39.1248 |
| 27 | 37.82222 | 37.6698 | 39.3809 |
| 28 | 37.87778 | 37.6727 | 39.6387 |
| 29 | 37.90556 | 37.6756 | 39.8982 |
| 30 | 37.94444 | 37.6785 | 40.1594 |
| 31 | 38 | 37.6814 | 40.4223 |
| 32 | 38.04444 | 37.6843 | 40.6869 |
| Time (Hours) k | Actual Temperature Values °C | IGM (1,1) Predicted Values °C | GM (1,1) Predicted Values °C |
|---|---|---|---|
| 25 | 19.31 | 19.389 | 20.1565 |
| 26 | 19.29 | 19.3879 | 20.263 |
| 27 | 19.31 | 19.3869 | 20.3701 |
| 28 | 19.25 | 19.3858 | 20.4777 |
| 29 | 19.18 | 19.3848 | 20.5859 |
| 30 | 19.25 | 19.3837 | 20.6947 |
| 31 | 19.18 | 19.3827 | 20.804 |
| 32 | 18.74 | 19.3817 | 20.9139 |
| Time (Hours) k | Actual Temperature Values °C | IGM (1,1) Predicted Values °C | GM (1,1) Predicted Values °C |
|---|---|---|---|
| 25 | 21.11 | 20.8235 | 24.4642 |
| 26 | 20 | 20.8121 | 24.5149 |
| 27 | 20.56 | 20.8006 | 24.5658 |
| 28 | 20 | 20.7892 | 24.6167 |
| 29 | 20.56 | 20.7777 | 24.6678 |
| 30 | 20.11 | 20.7662 | 24.7189 |
| 31 | 23.33 | 20.7548 | 24.7702 |
| 32 | 22.78 | 20.7433 | 24.8216 |
| Geothermal Heat Pump System Output Temperature Prediction at Eight Hours | GM (1,1) | IGM (1,1) | ||||
|---|---|---|---|---|---|---|
| RMSE | MAE | MAPE (%) | RMSE | MAE | MAPE (%) | |
| Oklahoma University | 1.96 | 0.24 | 4.98 | 0.23 | 0.027 | 0.56 |
| University Politècnica de València | 1.402 | 0.17 | 7.02 | 0.263 | 0.025 | 1.033 |
| Oakland University | 3.625 | 0.144 | 16.66 | 1.243 | 0.038 | 4.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salhein, K.; Ashraf, J.; Zohdy, M. Output Temperature Predictions of the Geothermal Heat Pump System Using an Improved Grey Prediction Model. Energies 2021, 14, 5075. https://doi.org/10.3390/en14165075
Salhein K, Ashraf J, Zohdy M. Output Temperature Predictions of the Geothermal Heat Pump System Using an Improved Grey Prediction Model. Energies. 2021; 14(16):5075. https://doi.org/10.3390/en14165075
Chicago/Turabian StyleSalhein, Khaled, Javed Ashraf, and Mohamed Zohdy. 2021. "Output Temperature Predictions of the Geothermal Heat Pump System Using an Improved Grey Prediction Model" Energies 14, no. 16: 5075. https://doi.org/10.3390/en14165075
APA StyleSalhein, K., Ashraf, J., & Zohdy, M. (2021). Output Temperature Predictions of the Geothermal Heat Pump System Using an Improved Grey Prediction Model. Energies, 14(16), 5075. https://doi.org/10.3390/en14165075






