1. Introduction
In a heat transfer problem, the accuracy of thermophysical properties and boundary conditions is critical to obtain an accurate numerical simulation. As a boundary condition, convective heat transfer depends on different parameters such as time, surface geometry, and surface temperature, to name a few. The accurate determination of the convective heat transfer coefficient is a difficult task as convection is a very complicated phenomenon and expensive experiments with sophisticated instruments are required to appropriately unravel its dynamics [
1].
The advent of high-speed and high-capacity computers and the development of different regularization methods over the past decades have played significant roles in successful applications of numerical inverse methods, as inexpensive alternatives to costly and time-consuming experiments with sophisticated instruments, to appropriately estimate unknown heat transfer quantities such as the heat transfer coefficient [
2,
3,
4,
5,
6,
7,
8,
9,
10]. Inverse heat transfer problems are mathematically challenging problems because they are ill-posed and the accuracy of the estimation of an unknown quantity is very sensitive to measurement errors [
11,
12,
13]. If the unknown quantity to be estimated (in this study, the heat transfer coefficient) can be expressed as a constant parameter [
14,
15] or represented by a few parameters [
16], a parameter estimation approach may be used to estimate the parameters thereby estimating the unknown quantity. However, a function estimation approach should be used to estimate the unknown functional form of the unknown quantity when there is no information available on the functional form of the unknown quantity. In the function estimation approach, the
sensitivity and
adjoint problems are required to obtain the gradient of objective function with respect to unknown functional form which impose additional mathematical developments and computational costs on the inverse analysis. In this study, based on the numerical procedure employed in [
17], a two-dimensional transient inverse heat conduction problem is considered. The thermophysical properties are assumed constant, the geometry of heat-conducting body is irregular, and the body is subject to Neumann and Robin boundary conditions at its boundary surface parts. Using the parameter estimation approach initially developed in [
17] for the estimation of unknown functional form of a time-dependent heat flux (a boundary condition of second kind) imposed at a boundary surface, here the unknown functional form of a time-dependent heat transfer coefficient(a third-kind boundary condition) is estimated efficiently and accurately without involving the solution of the sensitivity and adjoint problems. Thus, the mathematical development effort and the computational cost are reduced significantly.
To do so, the heat-conducting body (the physical domain) is mapped onto a regular computational domain in order to take advantage of the ease of implementation of the finite-difference method to explicitly solve the transient heat conduction equation and the associated boundary conditions. As the body shape is irregular, a body-fitted (elliptic) grid generation method is used to mesh the irregular domain which makes the proposed method general and applicable to any irregular domain as long as it can be mapped onto a regular computational domain. Using the chain rule to relate the temperature at sensor place and the time-dependent heat transfer coefficient applied on the part of the body boundary, explicit expressions are derived to compute sensitivity coefficients during the solution of the transient heat conduction equation without the need for solving the sensitivity and adjoint equations. The steepest-descent method, as an iterative regularization method, with a stopping criterion specified by discrepancy principle is used to minimize the objective function and reach the solution accurately. A test case with three complicated functional forms of timewise variation of the heat transfer coefficient is presented to reveal the accuracy, efficiency, and robustness of the inverse analysis. Moreover, two different measurement errors are considered. It is shown that the inverse analysis is not strongly affected by the errors involved in the temperature measurements and the unknown functional forms of the timewise variation of the heat transfer coefficient can be recovered with excellent accuracy. As stated before, the objective of this study is to present a parameter estimation approach to estimate the unknown functional form of a time-dependent heat transfer coefficient efficiently and accurately.
2. Governing Equation
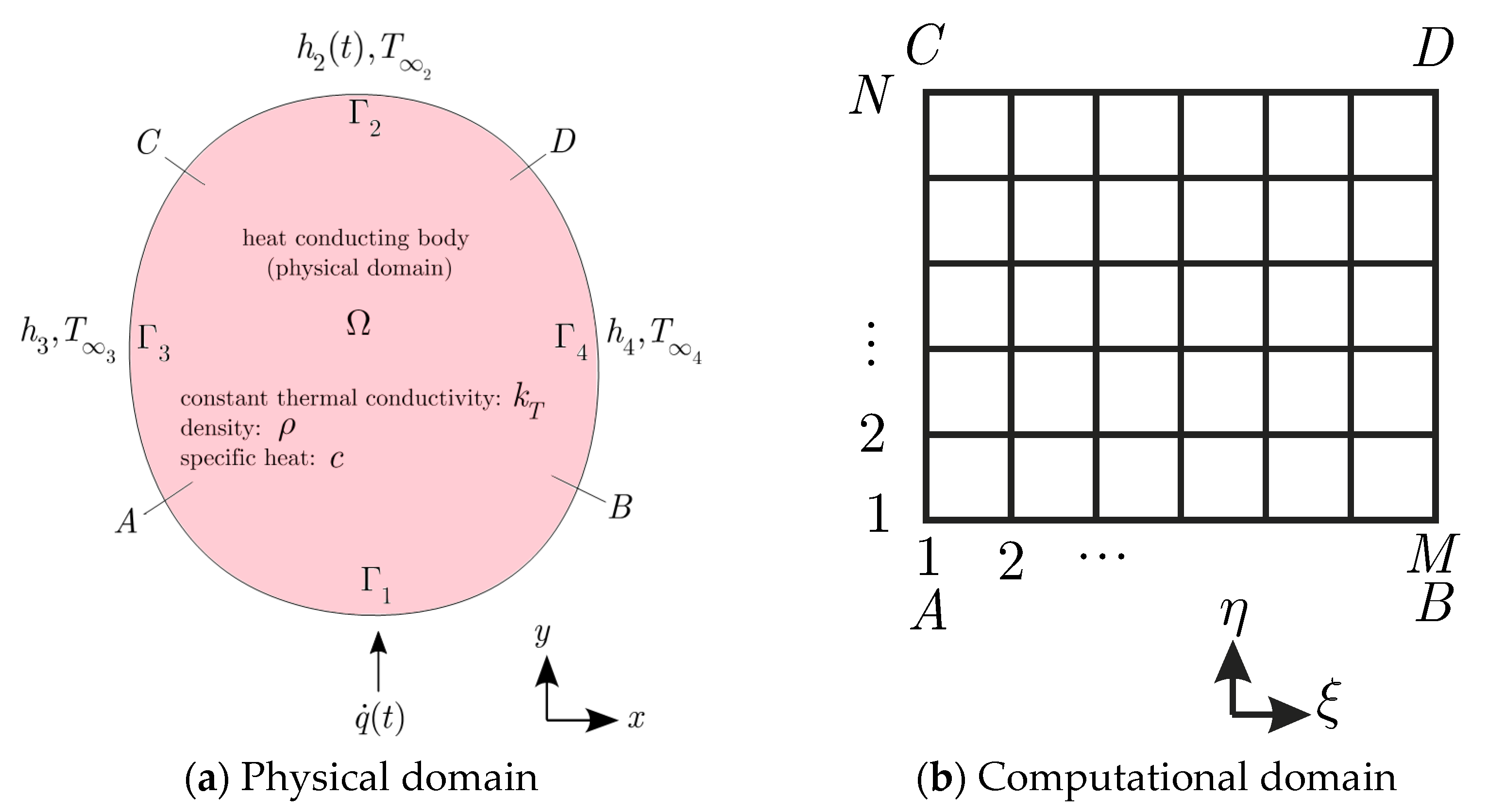
The body shown in
Figure 1a is initially at the temperature
. At time
, it is exposed to a time-dependent heat flux
at boundary surface
and convective heat transfer on boundary surfaces
with corresponding heat transfer coefficients
,
, and
and surrounding temperatures
. The thermal conductivity, density, and specific heat of the body are
,
, and
, respectively.
The governing equation for a two-dimensional transient heat conduction problem with no heat generation can be expressed as [
17,
18]
with the boundary and initial conditions
where
is the time. Since the heat-conducting body is irregular, it (the
and
physical domain) can be mapped onto a regular one (the
and
computational domain). The elliptic grid generation method is employed to generate a grid over the physical domain. Then the heat conduction equation and its associated boundary and initial conditions can be transformed from the (
) to the (
) variables [
12,
18]. The transformation results in
where
and
are grid control functions. If
, then a smooth grid over the physical domain is obtained. Therefore, Equation (6) becomes
where
The transformed boundary and initial conditions can be expressed as
where the initial condition
is rewritten as
in terms of the variables
and
. Now the finite-difference method can be employed to discretize the derivatives present in the above equations in the regular computational domain, as follows (assuming
)
where
. One-sided forward and one-sided backward relations are used to discretize the boundary condition equations. The explicit method can be used to solve the resulting transient heat conduction equation, Equation (7). Using forward-time-central-space (FTCS) discretization and the relations in Equation (14), we get
where
is the time step. Taking into account the stability criterion, the time-marching procedure can be used to solve Equation (15) and obtain
. That is, the nodal temperatures at the time level
,
, can be determined from the knowledge of nodal temperatures at the previous time level
,
, as follows
4. Results
A test case with three different complicated functional forms of variation of the heat transfer coefficient with time is presented to investigate the accuracy, efficiency, and robustness of the proposed sensitivity analysis method to estimate the time-dependent heat transfer coefficient on part of the boundary of a heat conducting body. Initially the heat transfer coefficient is assumed to be known, the transient heat conduction problem is then solved to calculate the temperature at the sensor place at times
(
). Then, the calculated temperatures are used as
simulated measured ones to recover the initially used heat transfer coefficient. The three different forms of timewise variation of the heat transfer coefficient considered are as follows (
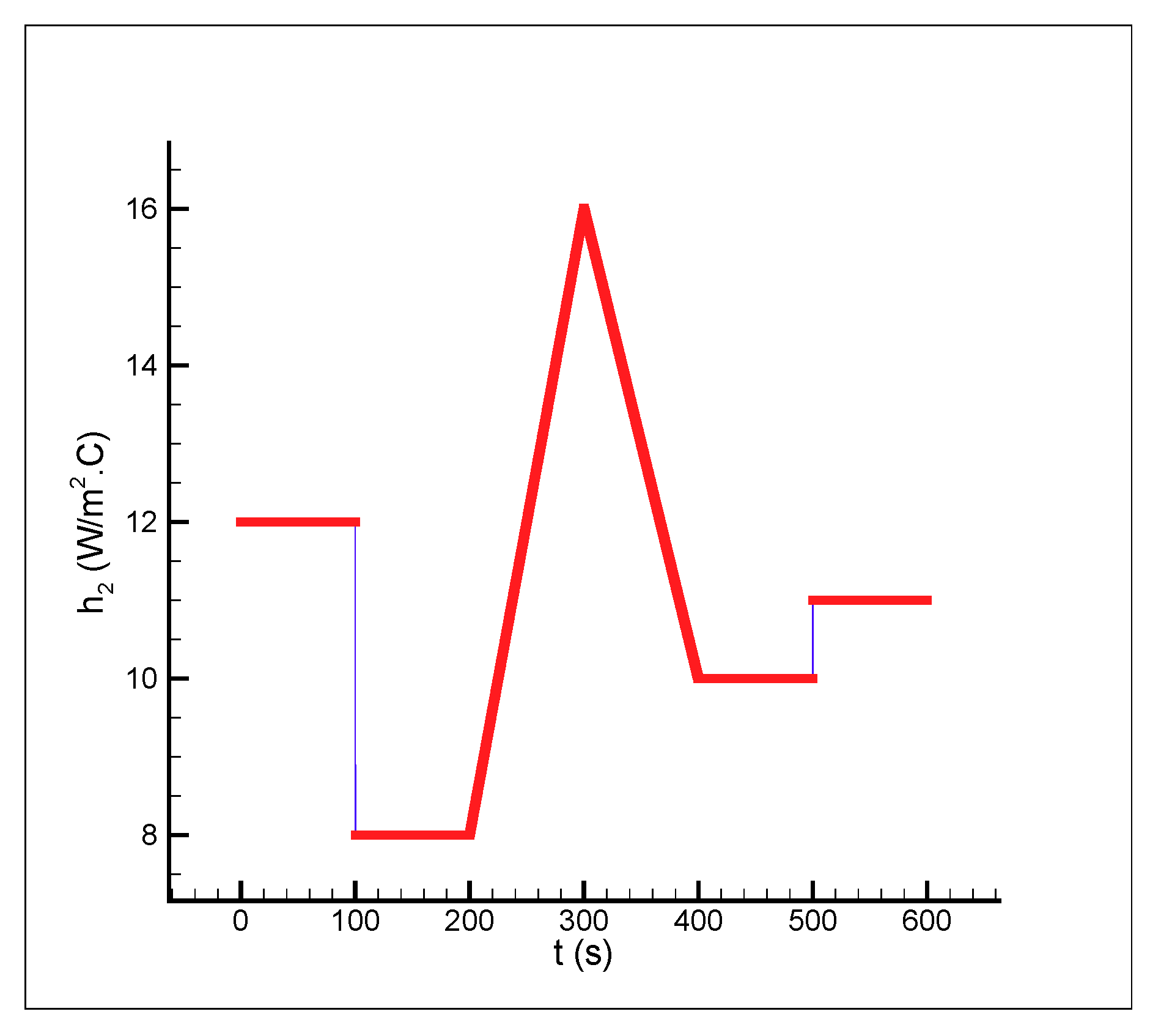
Figure 2,
Figure 3 and
Figure 4)
and
which is an arbitrary waveform generated in MATLAB used here to model the variation of the heat transfer coefficient with time.
Assuming the heat conducting body is made of stainless steel (type 304), the numerical values of the coefficients involved in the test case are listed in
Table 1.
In all simulations in this study, the heat conducting body is meshed using a grid size of
, the temperature measurement sensor is placed at node
(close to the boundary subject to convective heat transfer with the convective heat transfer coefficient
to obtain sensible sensitivity coefficients) (
Figure 5), the initial temperature is
, the final time is
, and the time step is
. Thus, the number of transient readings of the single sensor
is
. This means that that the number of unknown parameters is
. Thus, the estimation of such a large number of unknown parameters using the parameter estimation approach commonly used in the literature is not feasible. However, using the proposed sensitivity analysis, one can handle the estimation of the large number of unknown parameters accurately and efficiently. In this study, two different measurement errors of
and
are considered. The stopping criteria for the test case with the following measurement errors are
As the size of Jacobian matrix is
, we will deal in this study with a Jacobian matrix of size
. Once the temperature at the sensor place is obtained at the time
, the elements of the Jacobian matrix can be calculated during the transient solution using the obtained expression for the sensitivity coefficients; that is, during the solution of the direct problem, the terms
,
and
,
are computed from Equations (21) and (23), respectively, and then the sensitivity coefficients can be obtained using the following pseudo-code
Initially, the implementation of the direct problem solver is validated with the results obtained from the commercial finite element software COMSOL. To do so, using the data given in
Table 1,
, and the body shown in
Figure 5, the temperature distribution in the body is calculated by the two methods (our finite-difference explicit code, Equation (16), using two different time steps of 0.1 and 0.001 s and the finite element software COMSOL) which is shown in
Figure 6. Moreover, the temperature history of the place of the sensor,
, obtained by both methods is shown in
Figure 7. The comparison between the results reveals a very good agreement hereby verifying the correct implementation of the explicit solver.
In this inverse heat conduction problem, three different and complicated functional forms of timewise variations (including the variations which are difficult to be recovered by an inverse analysis such as discontinuities and sharp corners [
12]) for the heat transfer coefficient are chosen to examine the accuracy, efficiency, and robustness of the inverse analysis presented in this study. A comparison of the initial (guessed), final, and desired heat transfer coefficients is shown in
Figure 8a,
Figure 9a and
Figure 10a (for the case of no measurement error,
),
Figure 8c,
Figure 9c and
Figure 10c (for the measurement error of
), and
Figure 8e,
Figure 9e and
Figure 10e (for the measurement error of
). By comparing the desired and final functional forms shown in the above figures, it can be seen that the desired functional forms are recovered accurately which implies that the inverse analysis is not strongly affected by the errors involved in the temperature measurements due to the accuracy of the proposed sensitivity analysis scheme. When measurement errors exist, some oscillatory behaviors are observed around the exact values due to the ill-posed nature of the inverse heat transfer problem. The convergence histories of the objective function for the three functional forms of interest are shown in
Figure 8b,
Figure 9b and
Figure 10b (for the case of no measurement error,
),
Figure 8d,
Figure 9d and
Figure 10d (for the measurement error of
), and
Figure 8f,
Figure 9f and
Figure 10f (for the measurement error of
). The details of the results, including the initial and desired values for the unknown time-dependent heat transfer coefficient, the initial and final values of the objective function, and the number of iterations required to reach the solutions are given in
Table 2. The computation time for each iteration (the direct and inverse solutions) is about 4 s. In spite of large unknown variables (6000 in the test case) and large final time,
, this short computation time confirms that the employed inverse analysis based on the proposed sensitivity analysis is very efficient. The results are obtained by a FORTRAN compiler and computations are run on a PC with Intel Core i5 and 6G RAM.
From the above figures, we can also see that the estimated heat transfer coefficient deviates from the exact one in a neighborhood of
and approaches the initially guessed heat transfer coefficient. The mathematical reason is that by approaching the final time
, the number of the zero elements in the column vectors of the sensitivity matrix
also increases so that there exists only one nonzero element in the last column vector because the sensitivity matrix is a lower-triangular matrix (see Equation (26)). Thus, the last column vector can be written as
From Equation (19), (
), we can write the gradient of the objective function
with respect to
at the final time
as
which is a very small number. Substituting a very small value for
into Equation (28),
, results in a very small value for
. Likewise, substituting a very small number for
into Equation (27),
, results in
, as observed. In other words, by approaching the final time
, there is no significant modification in the value of
during the minimization process and the heat transfer coefficient retains its initially guessed value until the end of the minimization process.