Multi-Period Fast Robust Optimization for Partial Distributed Generators (DGs) Providing Ancillary Services
Abstract
:1. Introduction
2. Robust Model for Partial DGs Providing Ancillary Services
2.1. Deterministic Optimization Model
2.2. Robust Optimization Model
3. Solving Method
3.1. Master Problem
3.2. Sub-Problem
3.3. Solution Steps
4. Numerical Analysis
4.1. Case 1
4.2. Case 2
4.3. Case 3
4.4. Case 4
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, J.; Cui, M.; Li, B.; Fang, H.; He, Y. Fast solving method based on linearized equations of branch power flow for coordinated charging of EVs (EVCC). IEEE Trans. Veh. Technol. 2019, 68, 4404–4418. [Google Scholar] [CrossRef]
- Farivar, M.; Clarke, C.R.; Low, S.H.; Chandy, K.M. Inverter VAR control for distribution systems with renewable. In Proceedings of the IEEE International Conference on Smart Grid Communications, Brussels, Belgium, 17–20 October 2011; pp. 457–462. [Google Scholar] [CrossRef] [Green Version]
- Dommel, H.W.; Tinney, W.F. Optimal power flow solutions. IEEE Trans. Power Appar. Syst. 1968, 87, 1866–1876. [Google Scholar] [CrossRef]
- Baran, M.E.; Wu, F.F. Optimal capacitor placement on radial distribution systems. IEEE Trans. Power Deliv. 1989, 4, 725–734. [Google Scholar] [CrossRef]
- Baran, M.; Wu, F. Optimal sizing of capacitors placed on a radial distribution system. IEEE Trans. Power Deliv. 1989, 4, 735–743. [Google Scholar] [CrossRef]
- Lavaei, J.; Low, S.H. Zero duality gap in optimal power flow problem. IEEE Trans. Power Syst. 2012, 27, 92–107. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Tse, D. Geometry of injection regions of power networks. IEEE Trans. Power Syst. 2013, 28, 788–797. [Google Scholar] [CrossRef] [Green Version]
- Lavaei, J.; Tse, D.; Zhang, B. Geometry of power flows and optimization in distribution networks. IEEE Trans. Power Syst. 2014, 29, 572–583. [Google Scholar] [CrossRef] [Green Version]
- Farivar, M.; Low, S.H. Branch flow model: Relaxations and convexification-Part I. IEEE Trans. Power Syst. 2013, 28, 2554–2564. [Google Scholar] [CrossRef]
- Farivar, M.; Low, S.H. Branch flow model: Relaxations and convexification-Part II. IEEE Trans. Power Syst. 2013, 28, 2565–2572. [Google Scholar] [CrossRef]
- Li, N.; Chen, L.; Low, S.H. Exact convex relaxation of OPF for radial networks using branch flow model. In Proceedings of the IEEE 3rd International Conference on Smart Grid Communications, Tainan, Taiwan, 5–8 November 2012; pp. 7–12. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.; Wu, Q.; Wang, J.; Zhao, H. A sufficient condition on convex relaxation of AC optimal power flow in distribution networks. IEEE Trans. Power Syst. 2017, 32, 1359–1368. [Google Scholar] [CrossRef] [Green Version]
- Gan, L.; Li, N.; Topcu, U.; Low, S.H. Exact convex relaxation of optimal power flow in radial networks. IEEE Trans. Autom. Control 2015, 60, 72–87. [Google Scholar] [CrossRef] [Green Version]
- Nick, M.; Cherkaoui, R.; Le Boudec, J.-Y.; Paolone, M. An exact convex formulation of the optimal power flow in radial distribution networks including transverse components. IEEE Trans. Autom. Control 2018, 63, 682–697. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, Q.H.; Padullaparti, H.V.; Lao, K.-W.; Santoso, S.; Ke, X.; Samaan, N.A. Exact optimal power dispatch in unbalanced distribution systems with high PV penetration. IEEE Trans. Power Syst. 2019, 34, 718–728. [Google Scholar] [CrossRef]
- Robbins, B.A.; Zhu, H.; Dominguez-Garcia, A.D. Optimal tap setting of voltage regulation transformers in unbalanced distribution systems. IEEE Trans. Power Syst. 2016, 31, 256–267. [Google Scholar] [CrossRef]
- Dall’Anese, E.; Zhu, H.; Giannakis, G. Distributed optimal power flow for smart microgrids. IEEE Trans. Smart Grid 2013, 4, 1464–1475. [Google Scholar] [CrossRef] [Green Version]
- Zafar, R.; Ravishankar, J.; Fletcher, J.E.; Pota, H.R. Optimal Dispatch of Battery Energy Storage System Using Convex Relaxations in Unbalanced Distribution Grids. IEEE Trans. Ind. Inform. 2020, 16, 97–108. [Google Scholar] [CrossRef]
- Xiang, Y.; Liu, J.; Liu, Y. Robust energy management of microgrid with uncertain renewable generation and load. IEEE Trans. Smart Grid 2016, 7, 1034–1043. [Google Scholar] [CrossRef]
- Lee, C.; Liu, C.; Mehrotra, S.; Bie, Z. Robust distribution network reconfiguration. IEEE Trans. Smart Grid 2015, 6, 836–842. [Google Scholar] [CrossRef]
- Ding, T.; Liu, S.; Yuan, W.; Bie, Z.; Zeng, B. A two-stage robust reactive power optimization considering uncertain wind power integration in active distribution networks. IEEE Trans. Sustain. Energy 2016, 7, 301–311. [Google Scholar] [CrossRef]
- Zeng, B.; Zhao, L. Solving two-stage robust optimization problems using a column-and-constraints generation method. Oper. Res. Lett. 2013, 41, 457–461. [Google Scholar] [CrossRef]
- Gao, H.; Liu, J.; Wang, L. Robust coordinated optimization of active and reactive power in active distribution systems. IEEE Trans. Smart Grid 2017, 9, 4436–4447. [Google Scholar] [CrossRef]
- Ding, T.; Li, C.; Yang, Y.; Jiang, J.; Bie, Z.; Blaabjerg, F. A two-stage robust optimization for centralized-optimal dispatch of photovoltaic inverters in active distribution networks. IEEE Trans. Sustain. Energy 2017, 8, 744–754. [Google Scholar] [CrossRef]
- Wei, W.; Wang, J.; Li, N.; Mei, S. Optimal Power Flow of Radial Networks and Its Variations: A Sequential Convex Optimization Approach. IEEE Trans. Smart Grid 2017, 8, 2974–2987. [Google Scholar] [CrossRef]
- Zhang, J.; Cui, M.; He, Y.; Li, F. Multi-period fast robust optimization of active and reactive power in active distribution networks. TechRxiv 2020. [Google Scholar] [CrossRef]
- Cui, M.; Wang, J. Deeply hidden moving-target-defense for cybersecure unbalanced distribution systems considering voltage stability. IEEE Trans. Power Syst. 2021, 36, 1961–1972. [Google Scholar] [CrossRef]
- Chunyu, C.; Mingjian, C.; Xin, F.; Bixing, R.; Yang, C. Load altering attack-tolerant defense strategy for secondary frequency control system. Appl. Energy 2020, 280, 116015. [Google Scholar] [CrossRef]
- Abdelouadoud, S.; Girard, R.; Neirac, F.; Guiot, T. Optimal power flow of a distribution system based on increasingly tight cutting planes added to a second order cone relaxation. Int. J. Electr. Power Energy Syst. 2015, 69, 9–17. [Google Scholar] [CrossRef]



| Objective Function Values (p.u.) | ||||
|---|---|---|---|---|
| Improved CCG | Proposed Method | |||
| MP | SP | MP | SP | |
| 0.1 | −0.0933 | −0.0934 | −0.0934 | −0.0934 |
| 0.2 | 0.0072 | 0.0072 | 0.0072 | 0.0072 |
| 0.3 | 0.1194 | 0.1194 | 0.1184 | 0.1184 |
| 0.4 | 0.2408 | 0.2409 | 0.2408 | 0.2409 |
| 0.5 | 0.3754 | 0.3755 | 0.3754 | 0.3755 |
| 0.6 | 0.5231 | 0.5232 | 0.5231 | 0.5232 |
| Improved CCG | Proposed Method | |||
|---|---|---|---|---|
| Iterations | Time (s) | Iterations | Time (s) | |
| 0.1 | 3 | 46.155 | 2 | 35.662 |
| 0.2 | 2 | 33.772 | 2 | 36.256 |
| 0.3 | 5 | 100.713 | 2 | 33.577 |
| 0.4 | 2 | 19.926 | 2 | 35.015 |
| 0.5 | 2 | 19.734 | 2 | 33.844 |
| 0.6 | 2 | 21.128 | 2 | 28.190 |
| Objective Function Values (p.u.) | ||||
|---|---|---|---|---|
| Improved CCG | Proposed Method | |||
| MP | SP | MP | SP | |
| 0.1 | −0.0660 | −0.0661 | −0.0660 | −0.0661 |
| 0.2 | 0.0270 | 0.0269 | 0.0269 | 0.0267 |
| 0.3 | 0.1464 | 0.1462 | 0.1440 | 0.1439 |
| 0.4 | 0.2694 | 0.2692 | 0.2656 | 0.2654 |
| 0.5 | 0.4080 | 0.4072 | 0.4016 | 0.4014 |
| 0.6 | 0.5561 | 0.5544 | 0.5502 | 0.5501 |
| Improved CCG | Proposed Method | |||
|---|---|---|---|---|
| Iterations | Time (s) | Iterations | Time (s) | |
| 0.1 | 2 | 65.025 | 2 | 77.585 |
| 0.2 | 2 | 75.127 | 2 | 82.130 |
| 0.3 | 3 | 110.968 | 2 | 69.863 |
| 0.4 | 3 | 113.343 | 2 | 69.791 |
| 0.5 | 5 | 264.499 | 4 | 139.552 |
| 0.6 | 5 | 272.656 | 3 | 111.973 |
| Objective Function Values (p.u.) | ||||||
|---|---|---|---|---|---|---|
| Improved CCG | CCG | Proposed Method | ||||
| MP | SP | MP | SP | MP | SP | |
| 0.1 | −2.0870 | −2.0466 | −2.1100 | −2.0377 | −2.0633 | −2.0634 |
| 0.2 | −2.0613 | −2.0277 | −2.0645 | −2.0213 | −2.0403 | −2.0403 |
| 0.3 | −2.0101 | −2.0061 | −2.0135 | −1.9599 | −2.0159 | −2.0164 |
| 0.4 | −1.9388 | −1.9072 | −1.9418 | −1.8868 | −1.9240 | −1.9240 |
| 0.5 | −1.8582 | −1.8268 | −1.8617 | −1.8068 | −1.8447 | −1.8450 |
| 0.6 | −1.7764 | −1.7321 | −1.7752 | −1.7144 | −1.7568 | −1.7573 |
| Improved CCG | CCG | Proposed Method | ||||
|---|---|---|---|---|---|---|
| Iterations | Time (s) | Iterations | Time (s) | Iterations | Time (s) | |
| 0.1 | 10 | 3524.916 | 10 | 3810 | 2 | 183.664 |
| 0.2 | 10 | 3152.919 | 10 | 4248 | 2 | 195.945 |
| 0.3 | 10 | 3318.348 | 10 | 4258 | 2 | 193.753 |
| 0.4 | 10 | 3151.459 | 10 | 4606 | 2 | 192.636 |
| 0.5 | 10 | 3091.671 | 10 | 4017 | 2 | 192.460 |
| 0.6 | 10 | 3010.364 | 10 | 4154 | 3 | 299.966 |
| 33-Bus System | 69-Bus System | 123-Bus System | |
|---|---|---|---|
| 0.1 | 6.3948 × 10−9 | 7.9871 × 10−7 | 6.4669 × 10−8 |
| 0.2 | 8.8074 × 10−9 | 3.6889 × 10−8 | 5.0020 × 10−9 |
| 0.3 | 7.8910 × 10−9 | 4.1979 × 10−8 | 1.3896 × 10−8 |
| 0.4 | 8.4152 × 10−9 | 5.3522 × 10−8 | 3.1927 × 10−8 |
| 0.5 | 9.4049 × 10−9 | 8.7201 × 10−7 | 7.4779 × 10−8 |
| 0.6 | 8.0618 × 10−9 | 7.3739 × 10−7 | 7.8610 × 10−8 |
| Time | PV Bus Number | Time | PV Bus Number | Time | PV Bus Number |
|---|---|---|---|---|---|
| 1 | 7, 23, 26, 31, 32 | 9 | 7, 23, 26, 31, 32 | 17 | 7, 23, 26, 31, 32 |
| 2 | 7, 23, 26, 31, 32 | 10 | 7, 23, 26, 31, 32 | 18 | 6, 7, 26, 31, 32 |
| 3 | 20, 23, 26, 31, 32 | 11 | 7, 23, 26, 31, 32 | 19 | 6, 7, 26, 31, 32 |
| 4 | 14, 20, 26, 31, 32 | 12 | 7, 23, 26, 31, 32 | 20 | 6, 7, 26, 31, 32 |
| 5 | 14, 20, 26, 31, 32 | 13 | 7, 23, 26, 31, 32 | 21 | 7, 23, 26, 31, 32 |
| 6 | 14, 20, 26, 31, 32 | 14 | 7, 23, 26, 31, 32 | 22 | 7, 23, 26, 31, 32 |
| 7 | 20, 23, 26, 31, 32 | 15 | 7, 23, 26, 31, 32 | 23 | 7, 23, 26, 31, 32 |
| 8 | 7, 23, 26, 31, 32 | 16 | 7, 23, 26, 31, 32 | 24 | 7, 23, 26, 31, 32 |
| Time | PV Bus Number | Time | PV Bus Number | Time | PV Bus Number |
|---|---|---|---|---|---|
| 1 | 39, 44, 48, 52, 54 | 9 | 39, 44, 48, 52, 53 | 17 | 44, 48, 52, 53, 54 |
| 2 | 25, 39, 44, 48, 52 | 10 | 44, 48, 52, 53, 54 | 18 | 44, 48, 52, 53, 54 |
| 3 | 25, 39, 44, 48, 52 | 11 | 44, 48, 52, 53, 54 | 19 | 44, 48, 52, 53, 54 |
| 4 | 25, 39, 44, 48, 52 | 12 | 44, 48, 52, 53, 54 | 20 | 44, 48, 52, 53, 54 |
| 5 | 15, 39, 44, 48, 52 | 13 | 44, 48, 52, 53, 54 | 21 | 39, 48, 52, 53, 54 |
| 6 | 25, 39, 44, 48, 52 | 14 | 44, 48, 52, 53, 54 | 22 | 39, 48, 52, 53, 54 |
| 7 | 25, 39, 44, 48, 52 | 15 | 44, 48, 52, 53, 54 | 23 | 39, 48, 52, 53, 54 |
| 8 | 25, 39, 44, 48, 52 | 16 | 44, 48, 52, 53, 54 | 24 | 44, 48, 52, 53, 54 |
| Time | WT Bus Number | Time | WT Bus Number | Time | WT Bus Number |
|---|---|---|---|---|---|
| 1 | 71, 85, 104, 107, 114 | 9 | 70, 71, 104, 107, 114 | 17 | 33, 48, 56, 66, 122 |
| 2 | 70, 71, 104, 107, 114 | 10 | 48, 56, 66, 78, 122 | 18 | 39, 48, 56, 66, 122 |
| 3 | 71, 85, 104, 107, 114 | 11 | 33, 48, 56, 66, 122 | 19 | 39, 48, 56, 66, 122 |
| 4 | 71, 85, 104, 107, 114 | 12 | 33, 48, 56, 66, 122 | 20 | 39, 48, 56, 66, 122 |
| 5 | 71, 85, 104, 107, 114 | 13 | 33, 48, 56, 66, 122 | 21 | 39, 48, 56, 66, 122 |
| 6 | 71, 85, 104, 107, 114 | 14 | 48, 56, 66, 78, 122 | 22 | 39, 48, 56, 66, 122 |
| 7 | 70, 71, 104, 107, 114 | 15 | 33, 48, 56, 66, 122 | 23 | 48, 56, 66, 78, 122 |
| 8 | 70, 71, 104, 107, 114 | 16 | 33, 48, 56, 66, 122 | 24 | 48, 56, 66, 78, 122 |
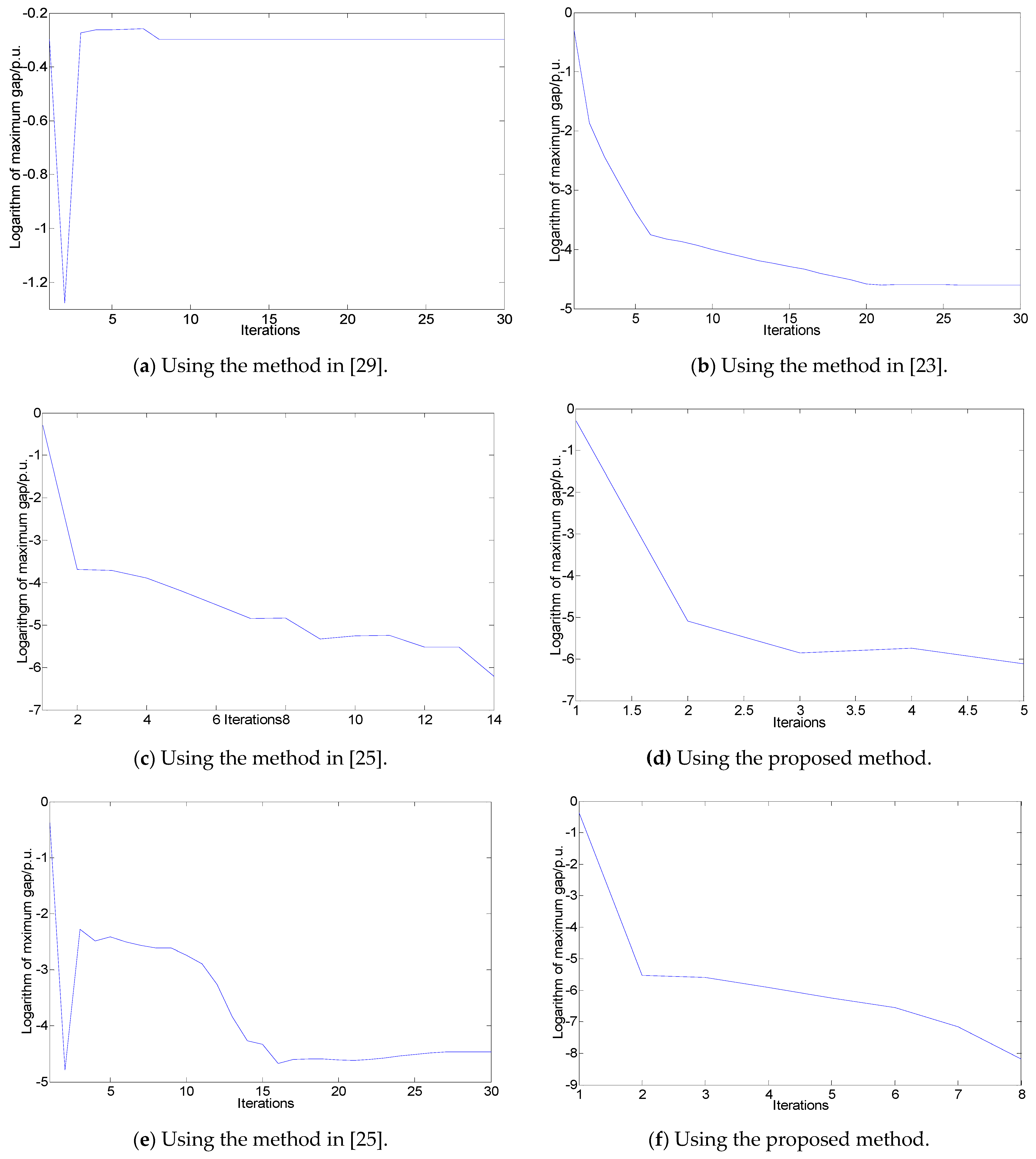
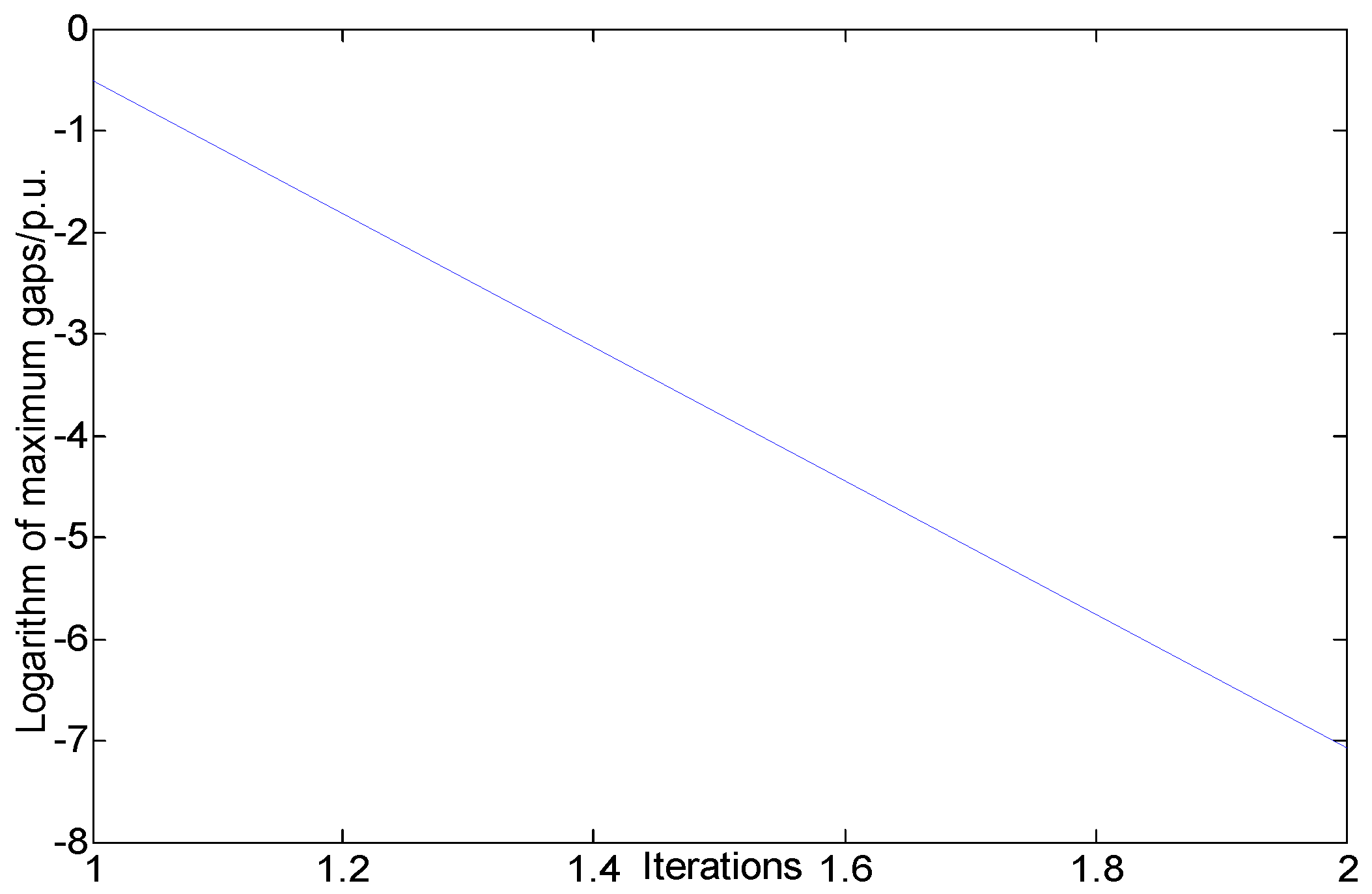
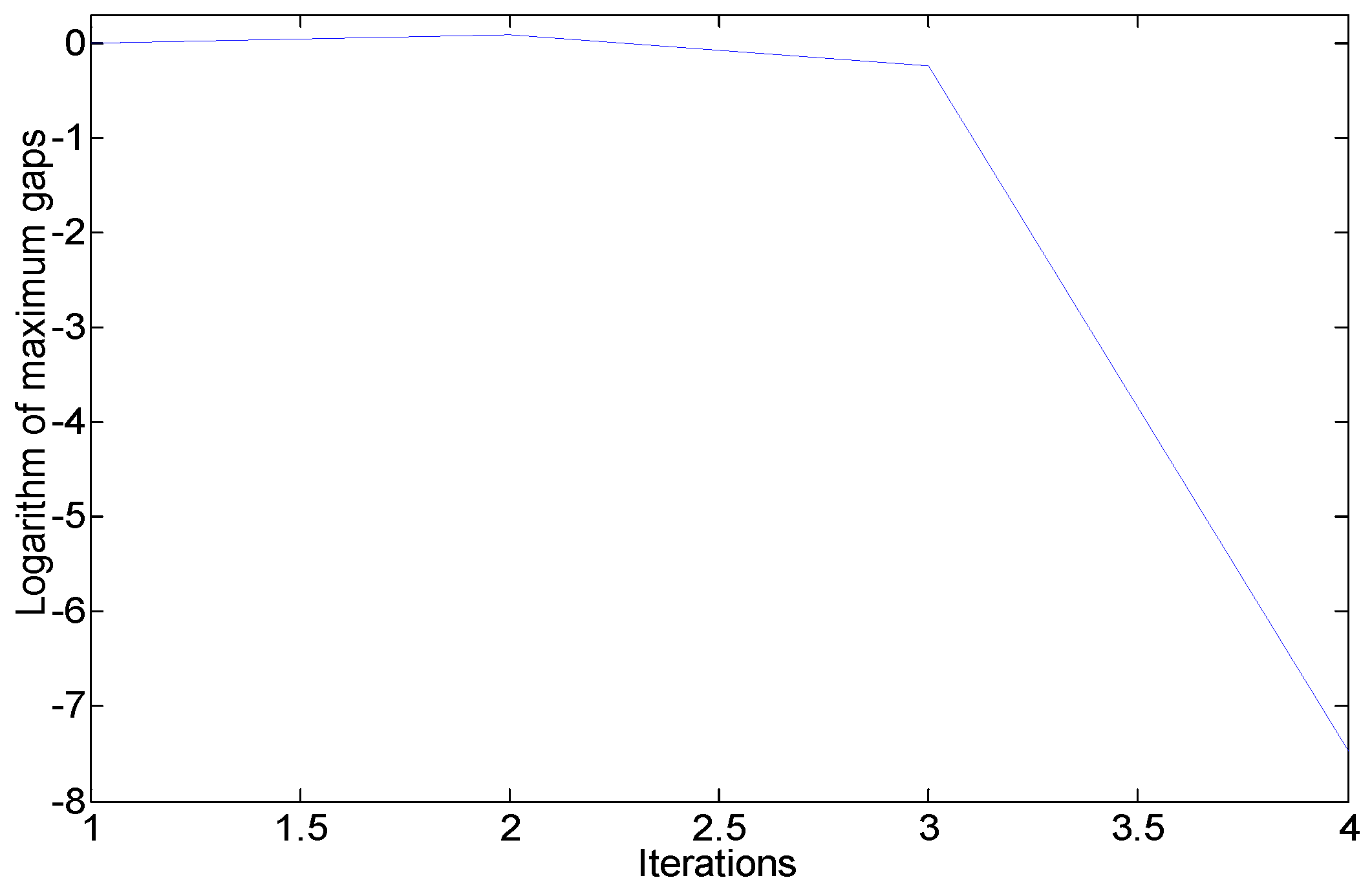
| Active Power of Each PV (MW) | Proposed Method | Method in [23] | Method in [25] | Method in [29] |
|---|---|---|---|---|
| 1.5 | 5 | 30 | 14 | 30 |
| 2.5 | 5 | 30 | 30 | 30 |
| 3.5 | 4 | 30 | 30 | 30 |
| 4.5 | 5 | 30 | 30 | 30 |
| 5.5 | 4 | 30 | 30 | 30 |
| 6.5 | 4 | 30 | 30 | 30 |
| Objective Function (p.u.) | ||||
|---|---|---|---|---|
| Method in [25] | Proposed Method | |||
| MP | SP | MP | SP | |
| 0.1 | −0.7654 | −0.7654 | −0.7655 | −0.7655 |
| 0.2 | −0.7323 | −0.7323 | −0.7323 | −0.7323 |
| 0.3 | −0.6992 | −0.6992 | −0.6992 | −0.6992 |
| 0.4 | −0.6660 | −0.6660 | −0.6660 | −0.6660 |
| 0.5 | −0.6329 | −0.6329 | −0.6329 | −0.6329 |
| 0.6 | −0.5997 | −0.5997 | −0.5997 | −0.5997 |
| Method in [25] | Proposed Method | |||
|---|---|---|---|---|
| Iterations | Time (s) | Iterations | Time (s) | |
| 0.1 | 2 | 31.433 | 2 | 13.896 |
| 0.2 | 2 | 31.894 | 2 | 15.148 |
| 0.3 | 2 | 31.938 | 2 | 11.402 |
| 0.4 | 2 | 29.879 | 2 | 13.179 |
| 0.5 | 2 | 31.046 | 2 | 11.724 |
| 0.6 | 2 | 33.076 | 2 | 11.168 |
| Objective Function Values (p.u.) | ||||
|---|---|---|---|---|
| Method in [23] | Method in [29] | |||
| MP | SP | MP | SP | |
| 0.1 | −0.7619 | −0.7655 | Infeasible | −0.7655 |
| 0.2 | Infeasible | 58.4681 | Infeasible | −0.7323 |
| 0.3 | Infeasible | 60.6725 | Infeasible | −0.6992 |
| 0.4 | Infeasible | 62.8792 | Infeasible | −0.6660 |
| 0.5 | Infeasible | 65.0870 | Infeasible | −0.6329 |
| 0.6 | Infeasible | 67.2952 | Infeasible | −0.5997 |
| Method in [23] | Method in [29] | |||
|---|---|---|---|---|
| Iterations | Time (s) | Iterations | Time (s) | |
| 0.1 | 5 | 46.240 | 2 | 57.417 |
| 0.2 | 5 | 20.606 | 2 | 56.451 |
| 0.3 | 5 | 23.765 | 2 | 53.611 |
| 0.4 | 5 | 22.276 | 2 | 56.217 |
| 0.5 | 5 | 20.324 | 2 | 56.976 |
| 0.6 | 5 | 20.741 | 2 | 56.599 |
| Objective Function Values (p.u.) | ||||
|---|---|---|---|---|
| 69-Bus System | 123-Bus System | |||
| MP | SP | MP | SP | |
| 0.5 | −1.2676 | −1.2679 | −3.7354 | −3.7379 |
| 69-Bus System | 123-Bus System | |||
|---|---|---|---|---|
| Iterations | Time (s) | Iterations | Time (s) | |
| 0.5 | 3 | 495.609 | 3 | 1985.721 |
| Time | PV Bus Number | Time | PV Bus Number | Time | PV Bus Number |
|---|---|---|---|---|---|
| 1 | 15, 39, 44, 48, 52 | 9 | 15, 26, 27, 39, 52 | 17 | 39, 44, 48, 52, 53 |
| 2 | 15, 39, 44, 48, 52 | 10 | 15, 19, 25, 26, 27 | 18 | 15, 39, 44, 48, 52 |
| 3 | 15, 39, 44, 48, 52 | 11 | 15, 19, 25, 26, 27 | 19 | 33, 39, 44, 48, 52 |
| 4 | 15, 39, 44, 48, 52 | 12 | 15, 19, 25, 26, 27 | 20 | 33, 39, 44, 48, 52 |
| 5 | 15, 39, 44, 48, 52 | 13 | 15, 19, 25, 26, 27 | 21 | 15, 39, 44, 48, 52 |
| 6 | 15, 39, 44, 48, 52 | 14 | 15, 19, 25, 26, 27 | 22 | 15, 39, 44, 48, 52 |
| 7 | 15, 39, 44, 48, 52 | 15 | 19, 25, 26, 27, 39 | 23 | 15, 39, 44, 48, 52 |
| 8 | 39, 48, 52, 53, 54 | 16 | 15, 27, 39, 48, 52 | 24 | 15, 39, 44, 48, 52 |
| Time | Reactive Power (kvar) | Time | Reactive Power (kvar) |
|---|---|---|---|
| 1 | 175, 588, 128, 232, 590 | 13 | −106, −172, −426, −480, −508 |
| 2 | 151, 540, 108, 211, 489 | 14 | −106, −173, −430, −484, −512 |
| 3 | 130, 498, 92, 192, 401 | 15 | −181, −442, −495, −522, 19 |
| 4 | 120, 480, 85, 184, 363 | 16 | 88, −406, −415, 175, 415 |
| 5 | 117, 474, 83, 182, 350 | 17 | 253, −240, 491, 544, −8.9 × 10−4 |
| 6 | 124, 400, 87, 187, 376 | 18 | 263, 598, 51, 598, 598 |
| 7 | 95, 496, 61, 180, 369 | 19 | 43, 600, 32, 600, 600 |
| 8 | −513, 252, 537, −268, 45 | 20 | 71, 600, 57, 600, 600 |
| 9 | −275, −393, −415, 29, −275 | 21 | 237, 600, −29, 531, 600 |
| 10 | −107, −175, −435, −489, −517 | 22 | 230, 600, −35, 500, 600 |
| 11 | −106, −172, −427, −481, −509 | 23 | 206, 600, −58, 376, 600 |
| 12 | −105, −171, −425, −478, −507 | 24 | 182, 599, −80, 253, 600 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Cui, M.; He, Y. Multi-Period Fast Robust Optimization for Partial Distributed Generators (DGs) Providing Ancillary Services. Energies 2021, 14, 4911. https://doi.org/10.3390/en14164911
Zhang J, Cui M, He Y. Multi-Period Fast Robust Optimization for Partial Distributed Generators (DGs) Providing Ancillary Services. Energies. 2021; 14(16):4911. https://doi.org/10.3390/en14164911
Chicago/Turabian StyleZhang, Jian, Mingjian Cui, and Yigang He. 2021. "Multi-Period Fast Robust Optimization for Partial Distributed Generators (DGs) Providing Ancillary Services" Energies 14, no. 16: 4911. https://doi.org/10.3390/en14164911
APA StyleZhang, J., Cui, M., & He, Y. (2021). Multi-Period Fast Robust Optimization for Partial Distributed Generators (DGs) Providing Ancillary Services. Energies, 14(16), 4911. https://doi.org/10.3390/en14164911







