Land Subsidence Estimation for Aquifer Drainage Induced by Underground Mining

Abstract

Land subsidence caused by groundwater withdrawal induced by mining is a relatively unknown phenomenon. This is primarily due to the small scale of such movements compared to the land subsidence caused by deposit extraction. Nonetheless, the environmental impact of drainage-related land subsidence remains underestimated. The research was carried out in the “Bogdanka” coal mine in Poland. First, the historical impact of mining on land subsidence and groundwater head changes was investigated. The outcomes of these studies were used to construct the influence method model. With field data, our model was successfully calibrated and validated. Finally, it was used for land subsidence estimation for 2030. As per the findings, the field of mining exploitation has the greatest land subsidence. In 2014, the maximum value of the phenomenon was 0.313 cm. However, this value will reach 0.364 m by 2030. The spatial extent of land subsidence caused by mining-induced drainage extends up to 20 km beyond the mining area’s boundaries. The presented model provided land subsidence patterns without the need for a complex numerical subsidence model. As a result, the method presented can be effectively used for land subsidence regulation plans considering the impact of mining on the aquifer system.

1. Introduction

Natural Earth factors such as neotectonics [1], volcanic eruptions [2], earthquakes [3] and anthropogenic activities including surface and subsurface urban building [4,5], oil and groundwater extraction [6,7] and mining [8] can all cause land subsidence. This type of phenomenon has been witnessed in various regions around the world for decades [7]. Nonetheless, the growing demand for natural resources is the primary cause of ground subsidence worldwide [9].

Globally, the demand for fresh water, and thus excessive groundwater pumping, is the leading cause of aquifer deformation [10,11,12,13,14]. Groundwater is primarily used for domestic purposes, agriculture and industry. The overexploitation of groundwater can cause land subsidence of up to a few m [15]. Land surface deformation endangers human lives and property by causing severe damage to both buildings and transportation infrastructure. As a result, aquifer deformation contributes to various socioeconomic effects and high infrastructure-related repair costs [16,17,18,19,20].

Severe aquifer system compaction is observed due to its drainage, particularly in densely populated metropolitan areas. Los Angeles [21], New Orleans [22], Las Vegas [23], Mexico [24], Venice [25], Tehran [26], Ho Chi Minh City [27], Shanghai [28], Bangkok [29] and Beijing [30] are among them. The problem, however, is especially critical in South-East Asia’s large coastal cities, which are located in river deltas [31]. Most coastal cities are built on unconsolidated, fine-grained, shallow alluvial deposits that are highly compressible. Unfortunately, drainage-related land subsidence may be associated with the occurrence of many geohazards. Floods [32], earth fissures [33] and infrastructure damage [34] are examples of these. However, land subsidence due to the compression of alluvial deposits has been monitored, documented and widely acknowledged for many years. As a result, remediation plans that allow for the long-term management of land subsidence in such prone areas have been developed [35,36,37].

In contrast to the well-known compaction process of the fine-grained, shallow aquifer system, deeper rock layer compaction remains a significant research challenge [38,39]. Specifically, it is underground mining that necessitates deep rock layer drainage [40,41]. Underground exploitation of mineral resources is typically carried out at great depths of up to a few km in complex geological and hydrogeological conditions. As a result, studying rock mass deformation and related phenomena, including land subsidence, is typically challenging.

Mining activity harms the natural environment and, as a result, has a negative or burdensome impact on humans [42,43,44,45]. However, in most cases, there is a need for economic activity in a clearly defined production area, which forces the transformation of the natural environment. The most visible and distinguishing changes in the mining environment are the deformation of the Earth’s crust. Land subsidence due to mining is mainly caused by removing a deposit from a rock mass and forming a post-mining void [46]. This type of land subsidence can damage the surface and underground infrastructure and endanger surface users’ safety [8,47,48,49,50,51]. Land subsidence’s spatial extent and value are primarily determined by the depth of exploitation, seam thickness, panel dimensions, overlying rock mass geomechanical conditions, geological defects, surface topography, production methods and post-mining void reclamation method [30,52,53]. Many research papers have been presented in recent years documenting the land subsidence phenomenon caused by mining [47,49,54,55,56,57,58,59,60,61,62,63]. As a result, one can be stated that the spatial extent of the phenomenon can range from several km² [49] to tens of km² [15], while its values can range from a few mm/year [64] to several cm/day [65].

Nevertheless, underground mining is also associated with the drainage of rock layers for both technological and safety reasons [46]. Mine drainage typically starts during the mine construction stage. It is carried out continuously throughout the mine’s life cycle and usually lasts until the mine is closed. Nonetheless, in many cases, even after the closure of mining operations, mine drainage maintenance is still required for safety reasons [66]. Due to the long-life cycle of underground mines, which can range from a few to several dozen years, the volume of groundwater pumped out of the rock mass is significant and, in many cases, exceeds billions of m³ [67]. Such a substantial volume of groundwater withdrawn and a long-term process of mining-induced drainage results in a permanent change in the aquifer system’s hydraulic conductivity and storage properties. Therefore, a decrease in hydrostatic pressure is observed at the large-scale depression cone [67,68]. The decrease in the groundwater head causes consolidation and compaction of the drained aquifer and the propagation of rock mass deformation to the terrain surface [25,69]. As a result, land subsidence caused by groundwater withdrawal occurs, and, therefore, watercourses and surface reservoirs may be impacted [7,15,25].

The spatial extent of the depression cone, and thus the area of land subsidence caused by aquifer drainage, is generally much larger than the direct impact of underground mining [67,68,70]. As a result, groundwater-related land subsidence frequently extends beyond mining boundaries [70]. These are the places on and beneath the ground where the mining company is responsible for the occurrence of underground mining’s negative effects [68,70,71,72]. Even if the value of land subsidence is relatively small, the phenomenon may pose a threat to the environment [70]. Land subsidence caused by mining-induced rock mass drainage is, unfortunately, still a poorly understood research topic. Furthermore, observed land subsidence in underground mining usually imposes direct and indirect mining exploitation impacts, that is to say, land subsidence due to void propagation and compaction of aquifer due to mining-induced dewatering. Furthermore, in analyses of rock mass deformation and subsidence prediction due to underground mining, indirect influences are frequently overlooked or misinterpreted [71,73]. Given the preceding, numerous efforts are being made to monitor ground deformation during underground mining and groundwater exploitation. Land subsidence was initially monitored primarily through well observations [74,75], extensometers [76,77], fiber optics sensing [78,79], levelling [80,81] and GNSS [82,83]. Although ground-based monitoring allows for high accuracy in measuring land surface deformation in a small area, due to low spatial resolution and high cost, providing a more detailed map of ground deformation at a regional scale is difficult. As a result, in recent years, remote sensing techniques such as LIDAR, InSAR and UAV have been widely used in land subsidence research. These techniques have the potential to overcome the limitations of traditional geodetic measurements for surface deformation, allowing them to be used to monitor ground subsidence over large areas [84]. There has also been a significant amount of research carried out on using LIDAR, InSAR and UAV techniques in monitoring land subsidence in mining areas [50,85,86,87,88,89,90,91,92]. However, these are primarily focused on analyzing temporal changes land subsidence [93] and horizontal ground movements [94,95,96], investigating sinkholes near former mine workings and shafts [97], studying mining-induced tremors [8,47,98,99,100,101,102,103] and updating elevation maps for administrative purposes [51,102].

Once land subsidence data is combined with hydrological observations, a qualitative correlation between groundwater level variation and land subsidence can be established. Therefore, the monitoring of ground surface displacements is used to model the land subsidence associated with rock mass drainage. Many geomechanical [104,105,106,107,108,109], stochastic [110,111,112,113,114,115,116,117,118], GIS-based analysis [119,120,121,122,123,124,125,126,127,128,129] and, more recently, AI (Artificial Intelligence)-based models [130,131,132,133] can accurately predict mining-induced ground movements. The influence function method is, however, most widely used [112]. The method allows for reliable forecast and, as a result, the spatial extent and value of land subsidence to be successfully determined without requiring a large amount of labor or calculation power and input data [112].

Nonetheless, research on groundwater head changes in complex aquifer systems necessitates a multifaceted approach [25]. To date, the techniques used have primarily focused on models, the implementation of which required a thorough identification of the characteristics of the rock mass deformation mechanism. However, due to the difficulty of the problem and the limited data availability data, parametrization of the models used so far and the results of the simulations contributed to high uncertainties. Furthermore, modelling this phenomenon remains a challenging research issue due to the multitude of factors involved and the nonlinear relationship between land subsidence and groundwater head decrease in heterogeneous aquifers affected by underground mining [48,49,50,70,121,134,135,136,137].

The literature presents a variety of methods for modelling ground surface displacements caused by rock mass drainage. However, very little research has been carried out on the land subsidence resulting from underground mining-related groundwater pumping. Hejmanowski et al. [138] attempted to investigate the direct and indirect effects of mining on the occurrence of land subsidence. In the conducted research, various combinations of the Knothe model parameters were analyzed, which would improve the accuracy of prediction of rock mass deformation. According to the authors, the proposed methodology for conducting this type of analysis must be closely tailored to the local mining and geological conditions, which necessitates a thorough understanding of the study area through in-situ measurements. Witkowski and Hejmanowski [71] used a multilayer perceptron network and the supporting vectors method to analyze and simulate a large-scale subsidence trough near one of the underground mines in Poland. The neural network was given the task of processing measurement data to determine the mapping process. The authors obtained satisfactory simulation results, indicating and recommending empirical data to validate the modelling outcomes. Malinowska et al. [70] investigated the spatiotemporal distribution of ground movements caused by groundwater head changes induced by copper ore and anhydrite mining in Poland. Traditional surveying methods and persistent scatterer Satellite Radar Interferometry were used to determine ground movements in the study. Based on these findings, a comparative analysis of the dynamics of ground movements, the rock mass’s mine life and hydrogeological conditions was carried out. These analyses enabled the time factor for land uplift modelling to be determined.

Considering the small number of studies on rock layer drainage caused by underground mining, it appears justified to conduct additional research on this topic. Furthermore, the study’s findings would allow for a comprehensive assessment of the environmental impact of underground mining to meet long-term sustainable management plans of prone areas.

Given the foregoing, the main goals of the paper are as follows:

(1)

to model the entire field of land subsidence related to mining-induced drainage of an aquifer system;

(2)

to separate land subsidence related to direct mining impact from the imposing influence of drainage-related land subsidence;

(3)

to analyze the regional-scale impact of mining-induced drainage on the environment considering prone surface water reservoirs.

The presented research was conducted in the “Bogdanka” underground hard coal mine in Poland. First, based on the geodetic measurement and remote sensing data, land subsidence in mining exploitation’s direct and indirect impact was examined in 1959–2014. Then, the previous research work results concerning the determination of the spatio-temporal drop in the groundwater head due to mining drainage in 1980–2020 were utilized. The results of these works were used to build the influence function method model (IF). This model was then employed to estimate nonlinear and spatially varying land subsidence. The model was successfully calibrated and validated based on the land subsidence and groundwater head changes data. Based on the calibrated and validated model, a forecast of the drainage-related land subsidence for 2030 was made. The impact of rock mass drainage on the water environment was also assessed, emphasizing the rich hydrographic network of the study area.

The IF model provided land subsidence patterns using the relationship between groundwater head decrease, the spatial distribution of the drained aquifer and subsequent subsidence without requiring comprehensive calibration or an elaborate numerical subsidence model. Therefore, the research results indicate that the method provided can be used effectively for land subsidence control and regulation plans. Consequently, our results can pave the way for a more reliable assessment of the impact of underground mining exploitation on the aquifer system.

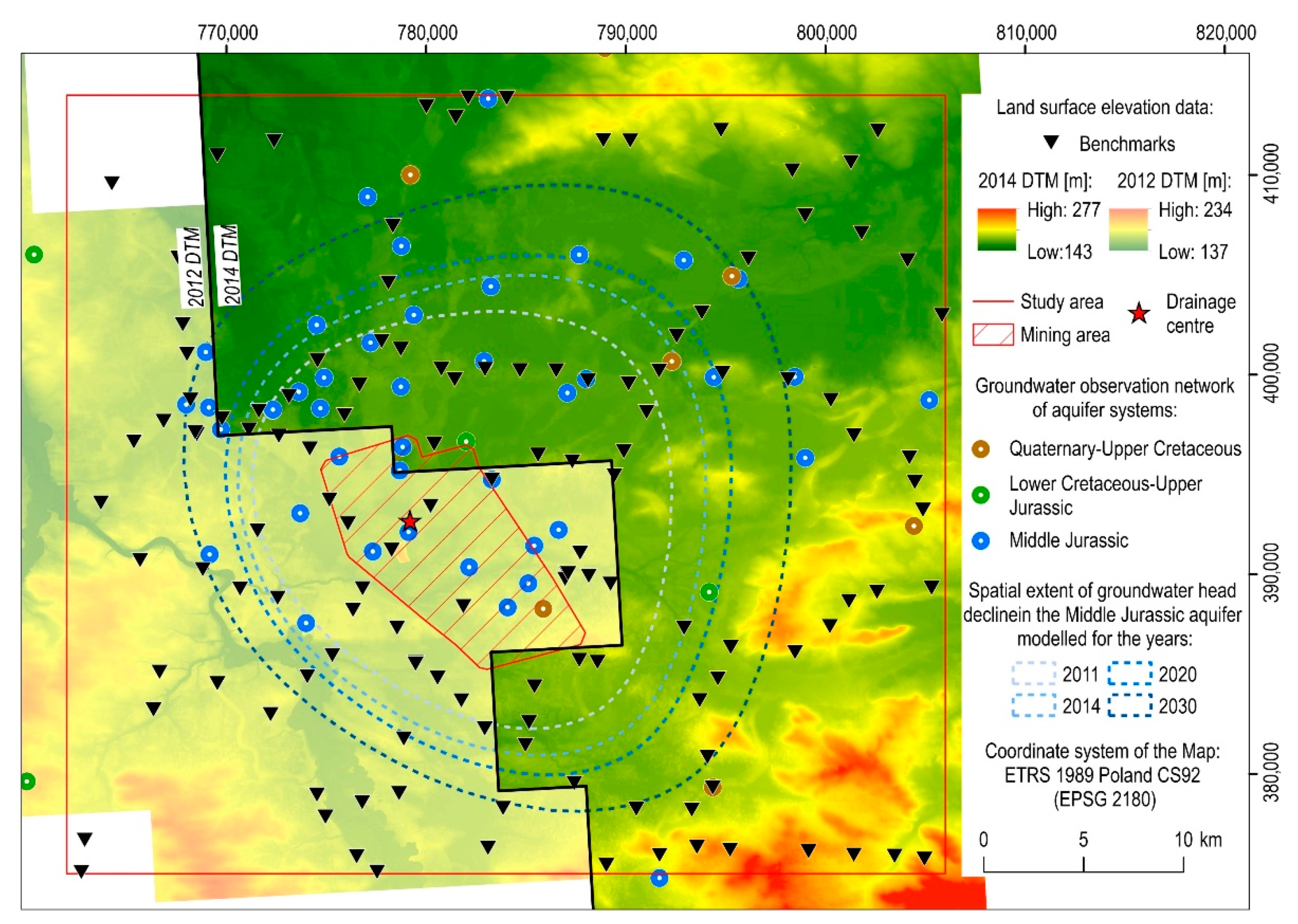
2. Study Area and Materials

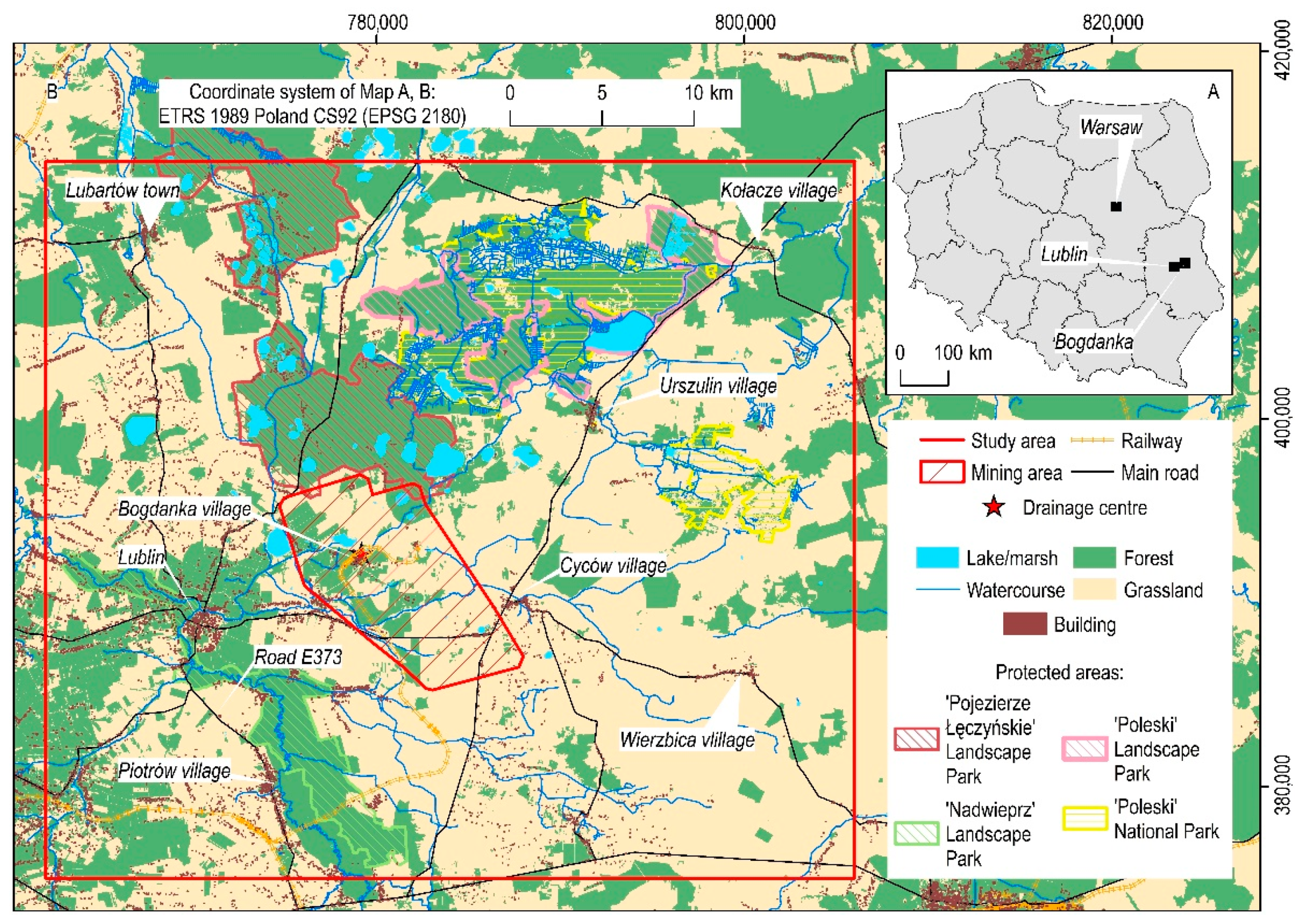
2.1. Study Area

The study was conducted in the mining area and near the “Bogdanka” mine. The area is approximately 1800 km² and is located in the south-eastern part of Poland, 30 km northeast of Lublin (Figure 1A). The area of interest encompasses a part of the “Western Polessye” macro-region, a subregion of the “East European Plain” mega-region. It is situated at an elevation between 170 to 191 masl (meters above sea level) [139].

Most of the research area is used for agriculture. Therefore, arable fields, forests and grasslands dominate the landscape. The buildings are primarily concentrated in small villages and towns with populations under 20,000 inhabitants [140]. Moreover, surface and underground infrastructure are both underdeveloped. The research area is traversed by the European road E373, linking Lublin, Poland, to Kyiv, Ukraine (Figure 1B) [139].

The presence of numerous peat bogs, wetlands and natural water reservoirs of karst origin characterizes the research area due to its lowland nature. They are legally protected habitats for diverse flora and fauna, as well as valuable aquatic ecosystems. Among these ecosystems is the “Poleski” National Park, part of the Natura 2000 network of nature protection areas on the European Union territory. Furthermore, three landscape parks were established in the area of interest: “Poleski”, “Nadwieprzański” and “Pojezierze Łęczyńskie”. There are also many smaller protected areas, such as nature reserves, nature monuments, ecological areas and nature and landscape complexes (Figure 1B) [139,141,142,143,144].

The research area is drained by strongly meandering minor-drainage rivers and numerous smaller watercourses (Figure 1B). Due to the presence of marshes, a dense network of drainage ditches was built in the study area in the past [141,142]. However, they no longer serve their original purpose.

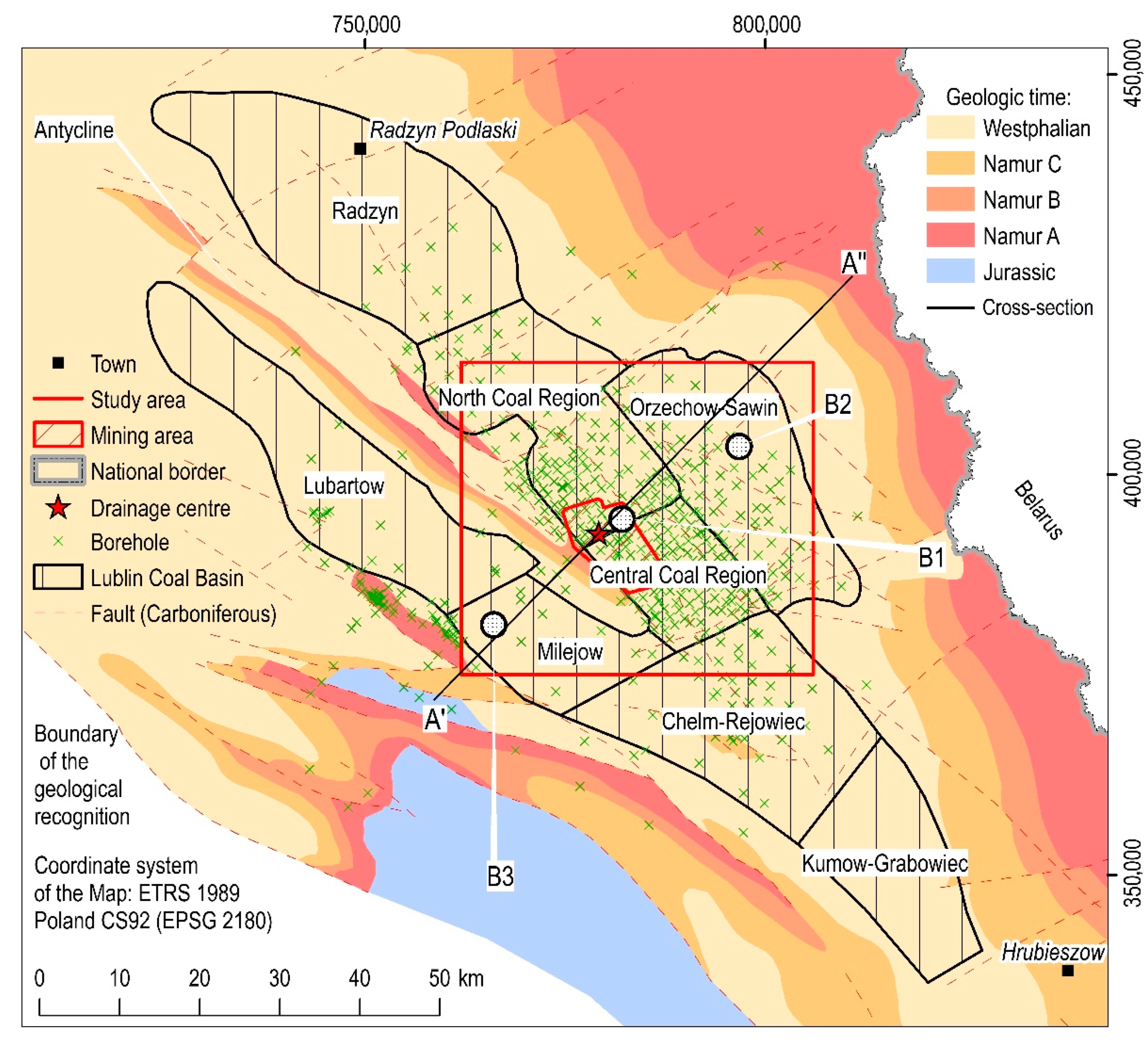
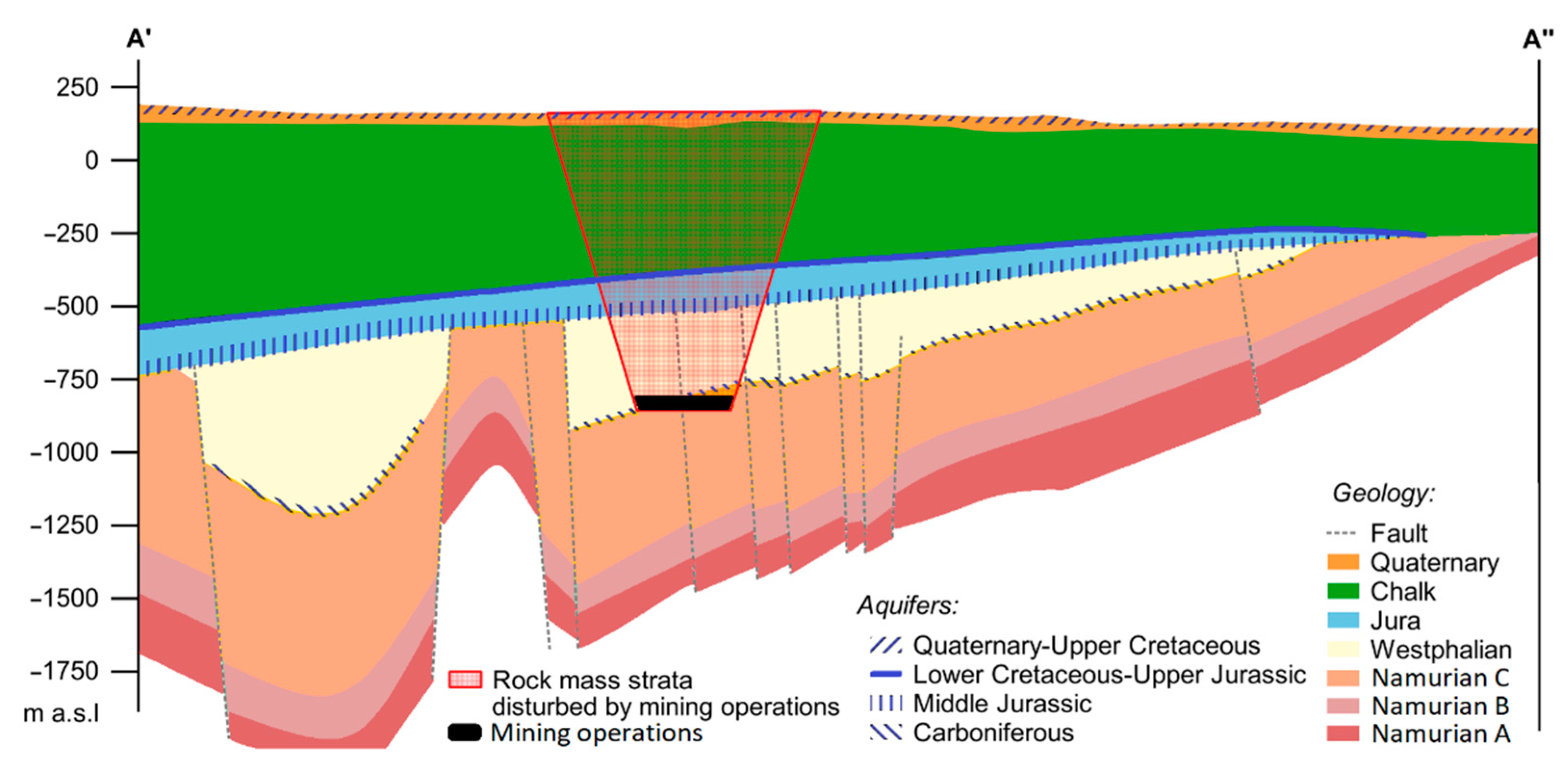
2.1.1. Geology

The study area is in the western, lateral part of the Precambrian East European Platform (Figure 2). Therefore, the dislocation zone of Precambrian origin runs along this border. The area of interest is located within a large syncline structure that extends from Radzyń Podlaski through Bogdanka to Hrubieszów. Precambrian rocks can be identified in the substrate of the study area. They range in depth from approximately 3500 m in the west to approximately 1800 m in the east. During the Variscan orogeny, Paleozoic rocks folded. The Mesozoic layer tectonics strongly refers to the Paleozoic substrate. Mesozoic formations are inclined to the southwest. The final structural shape of the area of interest was formed as a result of Alpine orogeny. The Cenozoic formations are loosely layered on top of the Mesozoic sediments and show no tectonic differentiation [141,145] (Figure 2 and Figure 3).

The hard coal deposit can be found in the synclinorium, which has a flat bottom and asymmetrical wings. Small dip angles distinguish the synclinorium in the northeast wing and a very steep course in the southwest wing. The tectonic faults are minor, and stratigraphic throws are only a few m [141,145] (

Table 1. Stratigraphy and depth of geological strata and aquifers in the area of interest in chosen boreholes. Note that borehole B1 is located in the drainage center, whereas boreholes B2 and B3 are placed in the northeast, small dip angle wing and southwest steep dip angle wing of the synclinorium, respectively (see Figure 2 for the location of boreholes). Source of data: the Polish Geological Institute-National Research.

Type	Era	Unit	Depth [m]
			B1	B2	B3
Geologic Time	Cenozoic	Quaternary	55	64	71
	Mesozoic	Cretaceous	55–578	64–496	71–725
		Jurassic	578–698	496–586	725–901
		Westphalian	698–1268	586–1103	901–1163
	Paleozoic	Namur C	1268–1672	1103–1457	1163–1322
		Namur B	1672–1731	1457–1511	1322–1380
		Namur A	1731-	1511-	1380-
Aquifer	Cenozoic—Mesozoic	Quaternary—Upper Cretaceous	2–12	3–9	3–15
	Mesozoic	Lower Cretaceous—Upper Jurassic	577–579	495–497	724–727
	Mesozoic	Middle Jurassic	631–692	537–584	798–872
	Paleozoic	Carboniferous	755~770	649~665	965~980

).

The Precambrian crystalline base is composed of metamorphosed granitoids and crystalline rocks. Cambrian, Ordovician, Silurian and Devonian deposits form the Paleozoic bedrock. It is primarily composed of Cambrian siltstones and sandstones, Ordovician limestones, claystones and siltstones, clay-silt facies and limestone-dolomitic facies of Silurian and Old Devonian origin. The upper Devonian deposits were eroded and denuded [141,145].

Carboniferous formations can be found throughout the research area. Their thickness varies between 600 and 1600 m. Visen (lower Carboniferous) and Westphalian (upper Carboniferous) formations were formed in three cycles: Namur A, Namur B and Namur C. Carbonate, clastic and volcanic rocks constitute the Visen strata. Namur A is primarily composed of carbonate, fine-clastic and phytogenic rocks. Namur B contains deposits of silt and sandstone, siltstones with interbedded limestone, coal and coal shale. Mining exploitation is carried out in the upper Westphalian. These rock layers are composed of silt and clay sediments with spheroidicity concretions, hard coal and sandstone deposits [141,145].

The Mesozoic, Tertiary and Quaternary strata are distinguished in the overburden of the hard coal deposit. Mesozoic sedimentation followed a stratigraphic gap that spanned the Triassic and Lower Jurassic periods. Middle Jurassic sediments are composed of limestones and dolomites with thicknesses ranging from 80 to 120 m. The Cretaceous deposits are 400 m to 600 m thick and constitute the majority of the Carboniferous overburden. They are formed by chalk, marls, marly limestones and carbonate-silicate limestones. The Cretaceous surface was heavily eroded during the Alpine orogeny. Therefore, there are no Paleocene sediments in the study area. Instead, quartz and clay sands represent the Neogene formations. These deposits vary in thickness, ranging from a few to several m. In the study area, the thickness of the Pleistocene is also variable. It ranges from zero m in Cretaceous outcrops to several dozen m in more extensive tectonic valleys. Sand, gravel and clay constitute Pleistocene sediments. River and lake sediments from the Holocene periods include peat and organic sludge [141,145].

2.1.2. Hydrogeology

There are four aquifers in the research area. These include unconfined Quaternary-Upper Cretaceous aquifer and confined Lower Cretaceous-Upper Jurassic, Middle Jurassic and Carboniferous aquifers [141,146,147] (Figure 3, Table 1).

The first aquifer contains sediments of a thickness of a few m of Quaternary and Upper Cretaceous origin. The groundwater is primarily associated with the clastic sediments that fill the valleys indented within the chalk rocks. The aquifer has significant horizontal and vertical lithological variability. Therefore, its hydraulic conductivity varies substantially throughout the study area. The groundwater table of the Quaternary-Upper Cretaceous aquifer occurs relatively shallow, at a depth of several mbsl. Precipitation and surface water inflow are the primary sources of groundwater recharge. As a result, the aquifer is highly vulnerable to seasonal fluctuations in the groundwater table. Over 1400 wells in the research area pump water from the Quaternary-Upper Cretaceous aquifer primarily for domestic use. However, the aquifer drainage is relatively small and does not form a depression cone [141,146,147].

The second aquifer is comprised of Lower Cretaceous and Upper Jurassic sediments. These are primarily sands, sandstones and karst limestones with several m of thickness. Therefore, in the study area, the aquifer is not a significant groundwater reservoir. A 400 m thick layer of impermeable chalk separates the Lower Cretaceous-Upper Jurassic aquifer from the Quaternary-Upper Cretaceous aquifer. As a result, there are no hydraulic connections between these groundwater reservoirs [141,146,147].

Low permeable limestones up to 100 m thick separate the Middle Jurassic aquifer from the Lower Cretaceous-Upper Jurassic aquifer. Hence, the two aquifers have only a few hydraulic connections. The Middle Jurassic aquifer is primarily made up of sandstones, limestones and dolomites that reach a thickness of 100 m. Thus, regional groundwater inflow associated with Jurassic sediments recharges the aquifer primarily. Notably, in the study area, the third aquifer serves as the primary groundwater reservoir. It is also subject to heavy mining drainage since it is located on the roof of mining excavations [141,146,147].

The Carboniferous aquifer is formed of Upper Carboniferous rocks. This aquifer is characterized by low storativity and the dominance of impermeable clays over permeable sandstones. Moreover, only minor hydraulic connections exist between the Carboniferous and Middle Jurassic aquifers. However, those connections are not well recognized due to the substantial depth and poor hydrogeological reconnaissance of the Carboniferous aquifer [141,146,147].

Since the current study is focused on land subsidence modelling due to groundwater head changes rather than hydrogeological modelling of groundwater head decrease due to mining-induced drainage, please refer to our previously published paper for a more detailed description of the hydrogeological conditions in the study area [67].

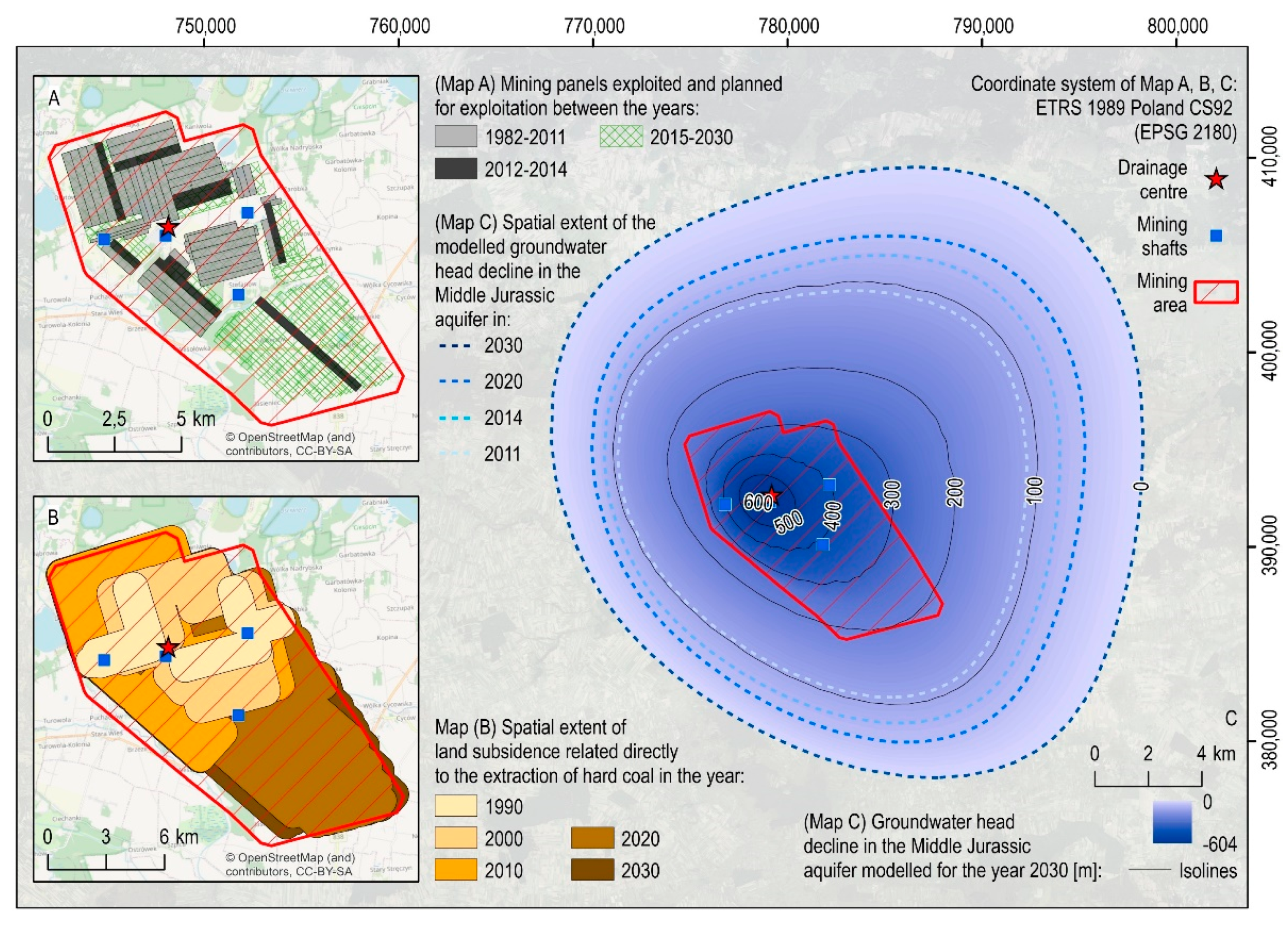
2.1.3. Underground Mining Exploitation and Its Past, Current and Future Impact on Aquifer System and Terrain Surface

The research area includes a part of the Lublin Coal Basin (LZW). This basin is a 180-kilometre-long and 20–40-km-wide belt that extends from the Polish-Ukrainian border to Radzyń Podlaski. The total area of the basin is approximately 9100 km² [141]. Hard coal balance resources in the LZW account for approximately 21.5 per cent of total resources in Poland [140]. According to the Polish Geological Institute, the LZW contains 11 hard coal deposits with total reserves of 9,250,000,000 tons. Only one of these deposits is fully operational. It is extracted within the “Bogdanka” mine and covers 799,000,000 tons of hard coal balance resources [141,144] (Figure 2).

The “Bogdanka” mine is situated in the Central Coal Region (CRW), which is located in the northeastern part of the LZW. The construction of the mine began in 1976, and it has been extracting hard coal continuously since 1982. The mining is carried out in a longwall system with surface protection provided by a hydraulic backfill [144]. It is worth noting that the “Bogdanka” mine is currently Poland’s most profitable underground hard coal mine [140].

The mine is permitted to exploit three coal deposits: “Bogdanka”, “K-3” and “Ostrów”. The “Bogdanka” field, located in the center of the research area, has been already mined (Figure 4A). The thickness of deposits exploited varies from 0.9 m to 3.2 m. The exploitation depth ranges from 860 to 1100 m. The hard coal deposit is nearly horizontal, accompanied by low-strength rocks and favorable tectonic conditions [141,144,148]. The mining operations future scenario assumes that hard coal mining will also be carried out in the southern part of the analyzed area, in the “Ostrów” field, by the end of 2030 [143,144]. The mine has three extraction shafts that are approximately 1 km deep. Two of them are located in Bogdanka and were put into service at the start of the mine’s operation. In addition, in 2011, a new shaft in Stefanów was put into operation in connection with the planned exploitation of hard coal in the southern part of the mine [144] (Figure 4A).

The surface impact of mining operations was particularly evident in the form of land subsidence [144]. According to our previous research [67], the total area of direct effects of underground mining, estimated with the use of the Knothe influence function method, was approximately 16, 33, 53 and 82 km² in 1990, 2000, 2010 and 2020, respectively (Figure 4B). Between 1982 and 2013, the total value of land subsidence caused directly by hard coal mining was 3.5 m, according to Hejmanowski et al. [138]. This value was calculated via an interpretation and analysis of geodetic measurements, specifically precise levelling, carried out in the mine area. According to the findings of this study, land subsidence occurred within the current mining area, primarily on grasslands that had been temporarily flooded by meltwater and had numerous traces of peat exploitation. In the mining area, two extensive post-mining floodplains have formed. The first occurred to the north of the main shafts of the “Bogdanka” field, covering approximately 100 ha and the second occurred in the vicinity of Nadrybie village, covering approximately 30 ha [144,149,150] (Figure 1). The flooded land in the Nadrybie region has been assigned to the Natura 2000 network. Notably, no significant threat to surface infrastructure occurred due to the direct impact of hard coal mining. Moreover, the mining entrepreneur has consistently repaired minor damage to surface infrastructure [144]. However, as the planned mining operation in the southeast progresses, similar issues are expected to arise in the area under consideration.

The impact on the hydrosphere of the “Bogdanka” mine is related to groundwater drainage in the amount required for the mine’s safe operation [144]. The pumping of groundwater began in 1976. Initially, only rock mass near the drilled mine shafts was drained. However, the aquifer drainage was extended to the mine-induced area and the cracked zones overlying mining panels as the opening-up work progressed and hard coal extraction developed. The implemented mine drainage scheme assumes deep drainage of the Middle Jurassic aquifer via boreholes drilled from the roof of mining panels and mining shafts. The groundwater is then pumped out of mining workings through the shafts [144,148,149,150]. In the years 1976–2016, the total amount of groundwater pumped out exceeded 180 million m³. The rate of groundwater inflow, however, varied over time. As a result, the annual groundwater outflow from the “Bogdanka” mine drainage is approximately 24,140 m³/day [141,144].

According to previous research and the results of numerical modelling of groundwater head changes in the “Bogdanka” mine, the Middle Jurassic aquifer was heavily drained between 1976 and 2020 [67] (Figure 4C). The drainage center in the vicinity of the mine shafts had the most significant decrease in groundwater head, 604 m. The depression cone had been expanding in the northeast and southeast directions. As a result, a large drainage center related to the mine shafts was identified in 2020. The groundwater head in this area was approximately 400 mbsl. The depression cone’s spatial extent was approximately 8 km to the southwest, 16 km to the northeast, 11 km to the northwest and 14 km southeast of the drainage center. In 2020, the depression cone covered an area of about 548 km². According to the groundwater model predictions, the depression cone will continue to develop in the coming years as hard coal mining progresses [67]. In 2030, the maximum decrease in groundwater head will be 644 m in the drainage center area. The depression cone will extend approximately 15 km north, 20 km northeast and 12 km south of the drainage center. In 2030, the total area of the depression cone will be around 756 km² (Figure 4C).

The “Bogdanka” mine prioritizes the economic use of groundwater from rock mass drainage and, in some cases, limits the drainage of the Middle Jurassic aquifer. In addition, a part of the groundwater is used for technical purposes in mine workings, such as providing fire protection and climatic installations and the surface, primarily to replenish water in a closed cycle in the hard coal enrichment process. Eventually, unused mine water is cleaned before being discharged into surface watercourses [144].

2.2. Materials

2.2.1. Land Subsidence Data

The terrain surface elevation in the research area was determined using geodetic and remote sensing data provided by the Main Office of Geodesy and Cartography of Poland (Figure 5).

The geodetic data set included 150 benchmarks, which was determined as part of nationwide measurement campaigns in Poland carried out in 1959, 1981 and 2011. Benchmarks were chosen to regularly cover the entire research area and ensure geodetic measurements’ continuity throughout the analyzed period. Furthermore, for the study, only benchmarks with the highest elevation accuracy were chosen.

The altitude of selected benchmarks was determined using precision levelling (1959, 1981 and 2011) and GNSS measurements (2011). Normal heights were determined using the PL-KRON60-NH and PL-KRON86-NH coordinate systems in 1959 and 1986, 2011, respectively. In all years, the average measurement error of 1 km of precision levelling was less than 4 mm/km, while the vertical accuracy of the benchmarks was smaller than 2 cm [142,151].

In Poland, precise levelling of the highest accuracy class is performed once every 20 years [142]. However, despite its high accuracy, such a measurement technique is time-consuming and costly compared to novel measurement methods. As a result, different measurement campaigns have been conducted in Poland since 2010 to determine the current elevation of the terrain surface. These measurements are carried out using Airborne Laser Scanning (ALS) as part of the IT System of Country Protection (ISOK) project [152].

The Digital Terrain Model (DTM) is one of the ALS products. It is created from an ALS point cloud classified into points on the ground and areas underwater. This means that the process of filtering out points that do not belong to the terrain, such as buildings and vegetation, must meet strict requirements. Before generating the resulting DTM, the areas of the obtained point cloud that lack data are filled in with an appropriate interpolation algorithm. The DTM retrieved from ALS products is a raster with a 1 m mesh size. It generates a continuous area database composed of individual archiving modules. The archiving module has a coverage area of about 1 km per 1 km. The ALS point cloud has an elevation accuracy of at least 10 cm. The point cloud’s normal heights were determined using the PL-KRON86-NH coordinate system [142].

Due to high cost, large area and therefore time-consuming, ALS measurements were gradually taken in the study area from 2011 to 2018 [142,152] (Figure 5). As a result, the spatial coverage of ALS data is heterogeneous and often extremely limited. Consequently, the current study only uses the ALS-retrieved DTM, which was obtained in 2012 and 2014. It includes the vast majority of the research area, particularly its northern, eastern and southern parts.

2.2.2. Groundwater Data

The findings of our previous research were incorporated into the current study. These research results sought to determine the environmental impact of the “Bogdanka” mine on the aquifer system. A numerical hydrogeological model was developed for this purpose, allowing us to assess past and current impacts and predict future changes in the aquifer system under underground hard coal mining conditions. Guzy and Malinowska provide a thorough summary of the research carried out and a description of the hydrogeological model [67].

In particular, data presenting the groundwater head in the Middle Jurassic aquifer in 1976 (before groundwater pumping start date), 2011, 2014 and 2030 was used in the current study (Figure 4, see Section 2.1.3). The groundwater hydrogeological model was of regular shape with a dimension of 60 km by 60 km. It covered 3600 km² and was divided into a regular mesh of 240 rows and 240 columns [67]. Therefore, the size of the resulting groundwater head raster cell was 250 m by 250 m.

The model was created using data from geographical, geological, hydrogeological and mining sources. Field data from the Polish Geological Institute-National Research Institute [141], the Mine and Surveying Department of the Bogdanka mine [144] and the Main Office of Geodesy and Cartography of Poland [142] were included. Data from the literature were also used in the study. The use of groundwater head measurements, which are carried out within a dense network of piezometers, is particularly noteworthy. It comprises 56 piezometers located in the Lower Cretaceous-Upper Jurassic and Middle Jurassic aquifers (Figure 5). To reflect the existing hydrogeological conditions, the hydrogeological model had to be simplified significantly. These simplifications are the result of a low recognition of hydrogeological conditions, as well as the modelling goals assumed. Nonetheless, the findings of our previous study show that the groundwater numerical model provides reliable information on the impact of mining drainage on the aquifer system in the study area.

The previously published work contains a more detailed description of the groundwater hydrogeological model of the “Bogdanka” mine [67].

2.2.3. Geological and Geographic Data

The geological boreholes were used to determine the elevation data of the top and bottom of the Middle Jurassic aquifer. These boreholes were primarily drilled by the Polish Geological Institute-National Research Institute in the 1950s, 1960s and 1970s during the geological reconnaissance of the study area, which was associated with the discovery of hard coal deposits (see also Section 2.1.3) [141].

Data from 532 boreholes distributed regularly across the study area were used in the study (Figure 2). The vast majority of boreholes are several hundred m deep and thus cover the entire hard coal deposit’s overburden. The geological data included the depths of individual complexes of rock layers, as well as their geomechanical parameters. Discreet data, as well as profiles and cross-sections, are digitally saved and shared [141]. A large amount of measurement data, in particular, allowed for precise identification of the spatial location of the principal aquifer in the study area [67].

Geographical data used in the study specifically concerned the distribution of the hydrographic network, including lakes, lagoons, rivers and smaller watercourses (Figure 1B). These data come from the Database of Geographical Objects, managed by the Main Office of Geodesy and Cartography of Poland [142]. They mainly were obtained through direct geodetic measurements and are constantly updated applying the most recent measuring techniques, including the ISOK project’s results [153]. However, OpenStreetMap was also used to determine the distribution of geographical objects in the study area [139].

3. Methodology

The research methodology presented in the article was divided into three sections (Figure 6).

The first part of the research determined land subsidence due to mining-induced drainage in the area of interest (Section 3.1). In the second part of the study, previous research on the impact of mine drainage on groundwater head change in the Middle Jurassic aquifer was used [67]. The findings of these studies, along with data on mining-induced land subsidence, were used to develop an influence method-based model of ground movements related to mining drainage (Section 3.2). Finally, in the third section of the study, the impact of mining drainage on surface water reservoirs was evaluated using calculated values of aquifer-drainage related land subsidence (Section 3.3).

The research presented here was conducted between 1959 and 2030. This time span includes the period before mining exploitation, and rock layer drainage began (1959–1981), the time of the most severe drainage of the rock mass due to mining exploitation (1981–2014), and the most recent and planned hard coal exploitation (2014–2030). The research area was determined based on the groundwater head change modelling results in the Main Jurassic aquifer due to mining drainage for 2030. As a result, the maximum predicted spatial extent of the depression cone in the principal aquifer and thus the maximum forecasted spatial extent of land subsidence due to mining drainage could be included in the presented study. This area is a rectangle 40 by 45 km in size, with a total area of 1800 km².

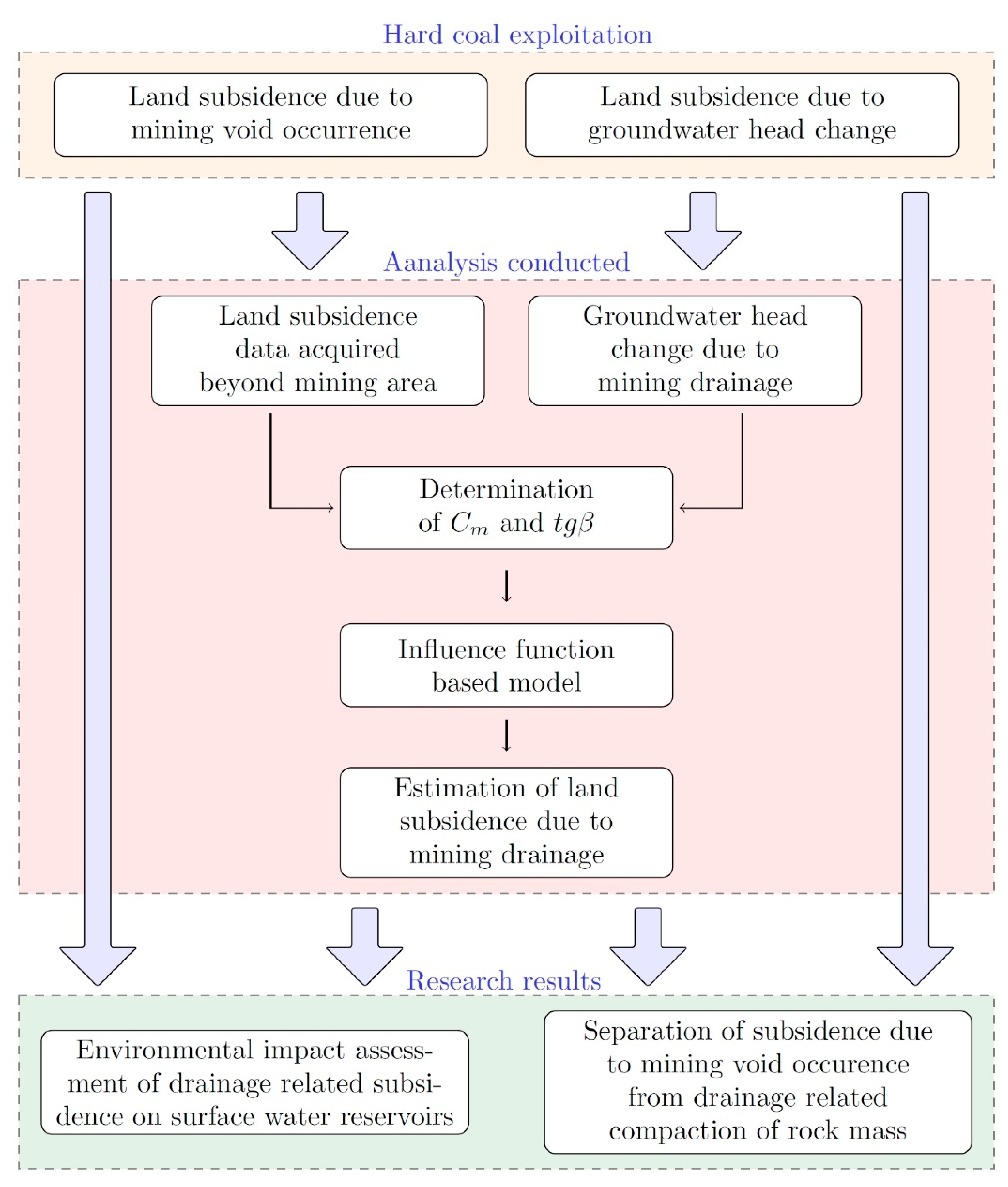
3.1. Estimation of Past and Current Land Subsidence Due to Mining-Induced Drainage

Land subsidence resulting from mining operations is revealed in the form of direct and indirect impacts, as mentioned in Section 2.1.3. Direct impacts include extracting hard coal, forming a post-mining void, and its migration to the ground surface. On the other hand, indirect influences result from the drainage of the rock mass that occurs during hard coal extraction. Nonetheless, direct and indirect impacts overlap and form a single land subsidence trough above the mining area and within the immediate range of the impact of hard coal extraction.

To determine land subsidence caused solely by rock mass drainage, defining an area directly influenced by hard coal mining was necessary. According to Polish law, the mining entrepreneur is required to define the spatial extent of the mining area at the stage of the procedure for granting a concession for mining mineral resources. Furthermore, the general public has access to information about its location and spatial extent. As a result, the mining area was determined in this study using the Polish Geological Institute-National Research Institute data. Nonetheless, the current study used previous research on determining the spatial extent of direct mining influences using the Knothe influence function.

With the progress of mining in the following fields of exploitation, the mining area of the “Bogdanka” mine has been changed over the years. According to available data from the Polish Geological Institute-National Research Institute, the mining area covered approximately 76 km² in 2020. However, according to previous research, the total area of direct effects of underground mining in 1990, 2000, 2010 and 2020 was approximately 16, 33, 53 and 82 km² (Section 2.1.3).

Given the previous, estimates of land subsidence caused by mining-induced drainage were made at points outside the mining area. Therefore, we used the maximum spatial extent of the mining area, which was estimated to be 82 km² in 2020, in our calculations.

Since mining drainage began in 1976 and coal mining started in 1982, estimation of land subsidence due to mining-induced drainage was conducted over three time periods. The first lasted from 1959 to 1981 and covered the time between the start of mining operations. The second and third periods covered 1981–2011 and 2011–2014, respectively. These included both active mining exploitation and rock layer drainage.

Due to the different coordinate systems of the normal heights of geodetic network points determined in 1959 compared to other measurement periods, the elevation of points defined in the PL-KRON60-NH system had to be transformed to the PL-KRON86-NH system [154,155]. This transformation was carried out by calculating the average value of the reference constant $\overline{T}$ on 134 points of the geodetic network using Equation (1):

$$\overline{T}={{\displaystyle \sum }}_{i=1}^n\frac{H_{1986}{}_i-H_{1960}{}_i}{n},$$

(1)

where $H_{1986}$ and $H_{1960}$ are the normal heights of the benchmarks $i$ to $n$ in the PL-KRON86-NH and PL-KRON60-NH coordinate systems, respectively.

The transformation constant $\overline{T}$ had a value of −0.006 m, with $\sigma$ = ±0.0005 m. As a result, it should be assumed that the normal height differences between the reference systems in the studied area are constant and have been correctly determined. As a result, the normal heights of the geodetic control points in the PL-KRON86-NH system in 1959 were determined using Equation (2):

$$H_{1960}{}_i=H_{1986}+\overline{T}.$$

(2)

Furthermore, the normal heights of the benchmarks in 2014 were determined using the elevation extracted from the DTM obtained from ALS measurements. This procedure was based on a spatial analysis performed with ArcGIS software.

3.2. Influence Function Model for Groundwater-Related Land Subsidence Estimation

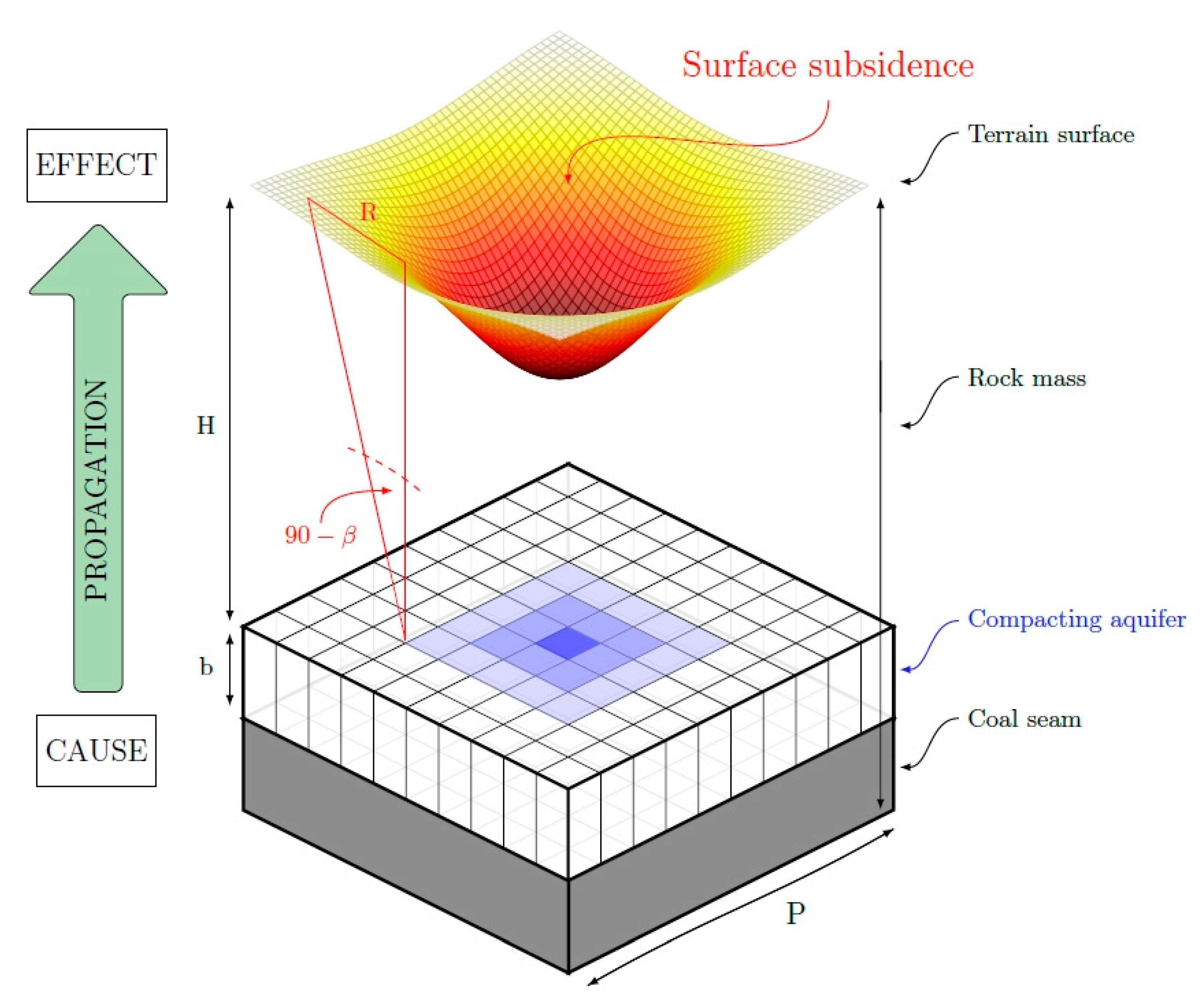
3.2.1. Development of the Mathematical Model

In the present study, the groundwater-related land subsidence influence function model was developed using the stochastic Knothe-Budryk theory. In this geometrical-integral approach, the change in the volume of the post-mining void is assumed to be the process causing land subsidence [156,157]. Since the original version of the Knothe-Budryk theory was intended to forecast rock mass deformation caused by mining deformations, the filling of the post-mining void is demonstrated by a random movement of rock particles towards the interior of the void [112].

To simplify the mathematical model of the deformation process, the conceptualization of the rock mass was required. Therefore, the Knothe-Budryk model assumes that this medium is homogeneous, continuous, anisotropic vertically and isotropic horizontally. Consequently, the geomechanical properties of the rock mass are averaged, and the complex structure of the medium can be significantly reduced.

Moreover, the Knothe-Budryk theory is based on the assumption of elementary influences. This means that removing an elementary element from the rock mass with a volume $dV$ causes a proportional elementary increase in land subsidence $d{S}_A$ at point A. The cause and effect of the process are linked by a relationship in which the proportionality coefficient is the influence function. This function is known as the surface of influence $f\left(x,y\right)$ and can be expressed using Equation (3) [156]:

$$d{S}_A=f\left(x,y\right)·dV,$$

(3)

where $x$ and $y$ are the Cartesian coordinates.

In the case of mining a deposit with a thickness $g$, the elementary volume $dV$ of a deposit is defined by Equation (4):

$$dV=dx·dy·dz=dx·dy·\left(a·g\right),$$

(4)

where $a$ is the parameter indicating the degree of filling of the post-mining void, ranging between $\langle 0;1\rangle$, and $z$ is the Cartesian coordinate.

The model thus only describes the change in the volume of the post-exploitation void, which is the actual cause of the deformation process, by the change in the vertical dimension of this void. As a result, the relationship between the primary cause of rock mass deformation and its effect in the form of land subsidence takes the form of Equation (5):

$$d{s}_A=\left(a·g\right)·f\left(x,y\right)dxdy.$$

(5)

To determine the total impact of the exploitation field with finite dimensions on land subsidence, the elementary influences of all deposit elements comprising this field must be added up. In the Knothe-Budryk model, the elementary impacts of the exploitation with the volume $dV$ are summed up using the integral operator and the rule of linear superposition. As a result, a total land subsidence $S_A$ at point A derived from all elementary volumes in the exploitation field with a $P$ area is obtained. It is expressed by Equation (6):

$$s_A=\left(a·g\right)·{{\displaystyle \iint }}_{P}f\left(x,y\right)dxdy.$$

(6)

The value of $s_A$ should be interpreted as the final land subsidence in point A after the field has been exploited and all ground movements have ceased. According to the Knothe-Budryk model, Equation (6) is the most general formula for calculating land subsidence at any point on the terrain surface. However, the surface of influence $f\left(x,y\right)$ in Equation (6) can also be defined in the model by parameterizing the normal Gaussian distribution function, as shown in Equation (7):

$$f\left(x\right)=\frac{h}{\sqrt{\pi }}exp\left(-h^2·x\right),$$

(7)

where $h$ is the parameter of the normal Gaussian distribution function.

In the Knothe-Budryk model, the h parameter was replaced by the radius of influence $R$. This radius corresponds to the influence angle $\beta$, the value of which is determined by the structural and geomechanical conditions of the rock mass and is expressed by Equation (8):

$$\tan \beta =\frac{H}{R},$$

(8)

where $H$ is the depth of mining exploitation.

The $\tan \beta$ parameter is also called the rock mass parameter. The value of $\tan \beta$ is most commonly in the range $\langle 1;3\rangle$.

The Knothe-Budryk theory is further parameterized by replacing the Gaussian function with a triangle with the base $2R$ and an area equal to the area under the Gaussian curve, as shown in Equation (9):

$${{\displaystyle \int }}_{-\infty }^{+\infty }f\left(x\right)dx=1.$$

(9)

Afterwards, the area of this triangle is calculated, and the value of the parameter h is determined using Equation (10):

$$h=\frac{\sqrt{\pi }}{R}.$$

(10)

By substituting (10) to (7), the influence function is obtained in the form expressed by Equation (11):

$$f\left(x\right)=\frac{1}{R}exp\left(-\frac{\pi ·x^2}{R^2}\right).$$

(11)

Additionally, by rotating function (11) around the axis of symmetry, it is possible to obtain the surface of influence $f\left(x,y\right)$, which is expressed by Equation (12):

$$\phi \left(x,y\right)=\frac{1}{R^2}exp\left(-\pi \frac{x^2+y^2}{R^2}\right).$$

(12)

Once (12) is substituted into (6), the following Equation (13) is obtained for calculating the land subsidence of any point A on the land surface:

$$s_A=\frac{\left(a·g\right)}{R^2}{{\displaystyle \iint }}_{P}exp\left(-\pi \frac{x^2+y^2}{R^2}\right)dxdy.$$

(13)

The assumptions of the original Knothe-Budryk method, developed for hard coal deposits, remain unchanged. However, in subsequent years, the theory was modified to forecast land surface deformation caused by the exploitation of other mineral deposits, such as iron ores, rock salt deposits and oil and gas deposits. Given the preceding, according to Equation (4), in the case of rock mass deformation caused by mining drainage, the change in the elementary volume of the deposit $dV$ can be defined by Equation (14):

$$dV=dx·dy·dz=dx·dy·\left(C_m·b\right),$$

(14)

where $C_m$ is the compaction coefficient of the aquifer, and $b$ is the primary thickness of the aquifer.

The $C_m$ reflects the change in effective pressure in the rock layers caused by pore pressure changes. It is expressed by Equation (15) [158]:

$$C_m=\frac{\Delta b}{b}·\frac{1}{\Delta p},$$

(15)

where $\Delta b=b-b_t$ and $\Delta p=p-p_t$ are the changes in the thickness of the aquifer corresponding to the change in the hydrostatic pressure in the aquifer in the given time $t$, respectively.

According to the Knothe-Budryk theory, the compaction coefficient $C_m$ corresponds to the parameter $a$, whereas the primary thickness of the aquifer $b$ correlates with the thickness $g$ of the deposit. By substituting $C_m$ and $b$ into Equation (13), it is possible to define Equation (16):

$$s_A=\left(C_m·b\right)·R^{-2}{{\displaystyle \iint }}_{P}exp\left(-\pi \frac{x^2+y^2}{R^2}\right)dxdy.$$

(16)

This formula can be used to estimate land subsidence due to mining-induced drainage using the Knothe-Budryk theory.

3.2.2. Conceptualization and Numerical Representation of the Model

The development of a mathematical model that can assess the impact of mining drainage on aquifer compaction and, as a result, the occurrence of land subsidence necessitates many simplifications that reflect the existing mining, geological, hydrogeological and geomechanical conditions in the area of interest. These simplifications result from an inability to fully recognize the geological structure of rock layers, limited empirical data (and often the availability of this data) and significant computational difficulties associated with complex mathematical models of physical phenomena occurring in nature.

According to Section 2, mining drainage has a direct impact on the Middle Jurassic aquifer. A series of impermeable Cretaceous layers with a thickness of approximately 400 m separates this aquifer from the Quaternary-Upper Cretaceous aquifer. As a result, these groundwater reservoirs have no hydraulic connections. Furthermore, the Middle Jurassic aquifer is separated from the Lower Cretaceous-Upper Jurassic aquifer by low permeable limestones up to 100 m thick. As a result, only a few hydraulic connections exist between the two aquifers. Finally, groundwater inflow from the Carboniferous aquifer into mine voids is presumed to be negligible. Importantly, the geological recognition of this aquifer is relatively poor.

The overburden of the hard coal deposit in the research area consists of numerous deposits with a diverse stratigraphic profile in both vertical and horizontal cross-sections. The genesis and geomechanical parameters of rock formations differ, which have only been partially recognized in boreholes. World experience has shown that it is impossible to fully recognize the geomechanical structure of rock formations and thus build a very detailed mathematical model of these rock formations over such a large area as presented in the study.

Keeping in mind the initial conceptualization, the following research area schematization was used in this study:

• The research area was determined based on the groundwater head change modelling results in the Main Jurassic aquifer due to mining drainage in 2030. As a result, the maximum predicted spatial extent of the depression cone in the main aquifer and thus the maximum forecasted spatial extent of land subsidence due to mining drainage could be included in the presented study.
• Mining drainage was assumed to cause direct compaction of the Middle Jurassic aquifer. Furthermore, since there is no direct hydraulic connection with the Middle Jurassic aquifer, the remaining aquifers do not undergo compaction due to changes in groundwater head due to mining-induced drainage. As a result, it is assumed that these aquifers do not directly contribute to the formation of drainage-related land subsidence.
• According to the assumptions of the Knothe-Budryk theory, the propagation of the Middle Jurassic aquifer deformation occurs through a homogeneous rock mass adjacent to this aquifer. As a result, the rock mass deformation process is revealed in discontinuous land surface deformation.

In the study presented, SubCom v.1., an OpenSource GUI-based program implemented in the Scilab environment, was used to compute land subsidence due to mining-induced drainage [73]. The software allows for calculating model parameters for compaction layers in oil, gas and groundwater extraction areas. The SubCom is based on a stochastic model and employs the Knothe-Budryk influence function theory discussed in Section 3.2.1. Witkowski and Hejmanowski provide a more detailed description of the software in the mathematical implementation of the Knothe-Budryk theory [73].

Computation of land subsidence using Equation (16) necessitates knowledge of the aquifer system compaction parameters. These include the spatial dimension $P$ and thickness $b$ of the aquifer, as well as the compaction coefficient $C_m$ and the characteristics of the overlying rock layers, which are described by the parameter $\tan \beta$.

Consequently, the model consisted of one layer and parameters that reflect the compacting Middle Jurassic aquifer. The model area $P$ is a rectangle 40 by 45 km in size, with a total area of 1800 km². It was divided into a regular mesh of 400 rows and 450 columns. The size of the cell was 100 m by 100 m, whereas the total number of cells was 180,000 (Figure 7).

The thickness of the Middle Jurassic aquifer was retrieved as the difference between the elevation layers of the top and bottom of this aquifer. The elevation data were computed using laboratory tests on geological cores performed by the Polish Geological Institute-National Research Institute. They were derived from 532 geological profiles almost evenly distributed across the entire study area (Figure 2). Elevation maps of the model layers were generated using kriging interpolation of discrete points for accounting for the geostatistical dependencies of the hydrogeological strata.

The basic parameters of the model include both $\tan \beta$ and the compaction coefficient $C_m$. Their values should correspond to the local environmental conditions of the rock mass. As a result, determining these parameters is a fundamental requirement for reliable modelling of land subsidence caused by mining-induced drainage.

The values of the $C_m$ and $\tan \beta$ parameters in the presented study were calculated using Equation (16). However, since the integral in (16) does not have an effective solution, this type of equation should be solved using numerical methods, as discussed in Section 3.2.3. In such cases, the initial values of the parameters to be determined must be provided. As a result, the input values of $C_m$ and $\tan \beta$ were defined using literature data and laboratory tests of sandstone compaction and the findings of studies in the fields of gas, oil and groundwater exploitation [159,160,161,162].

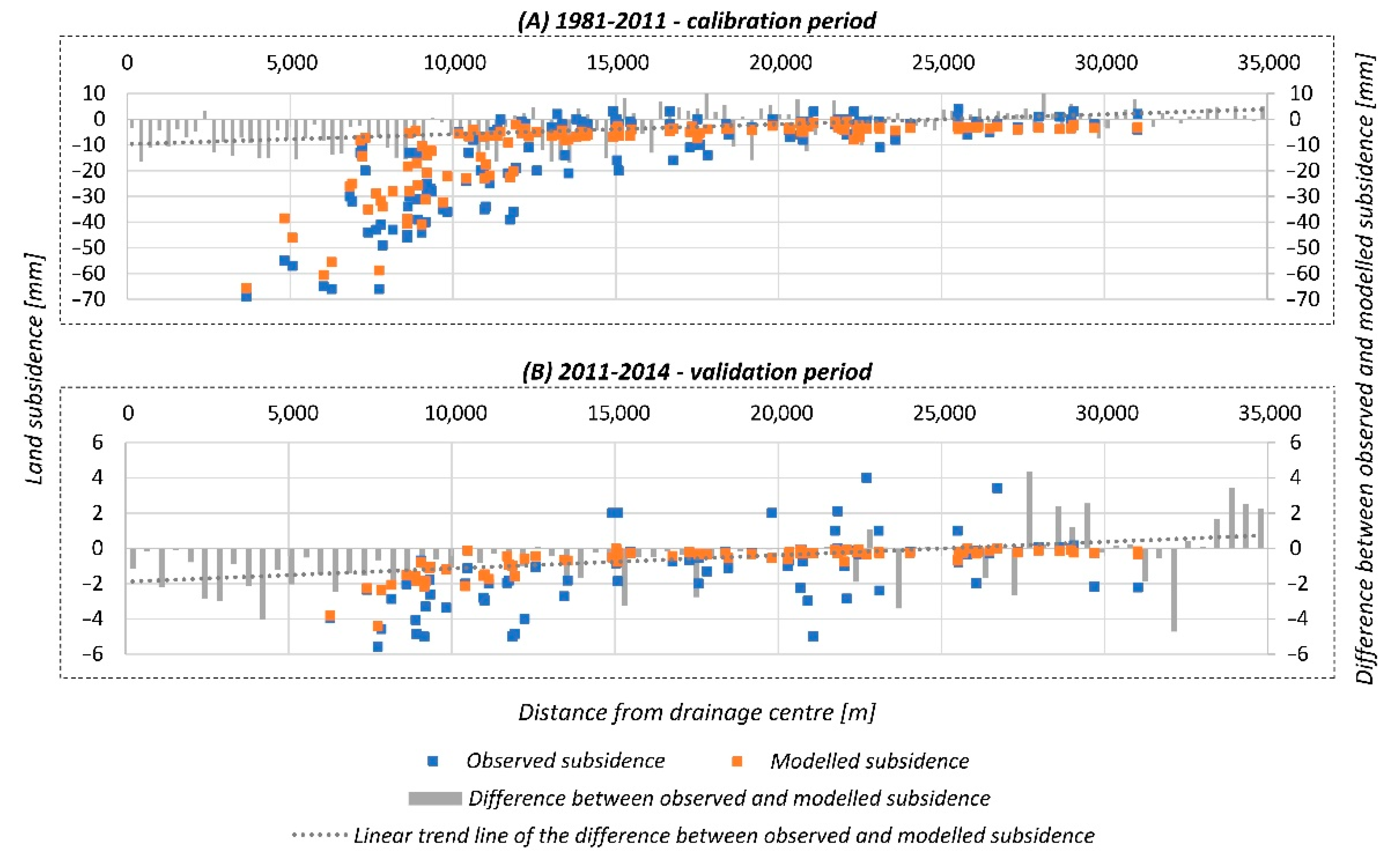
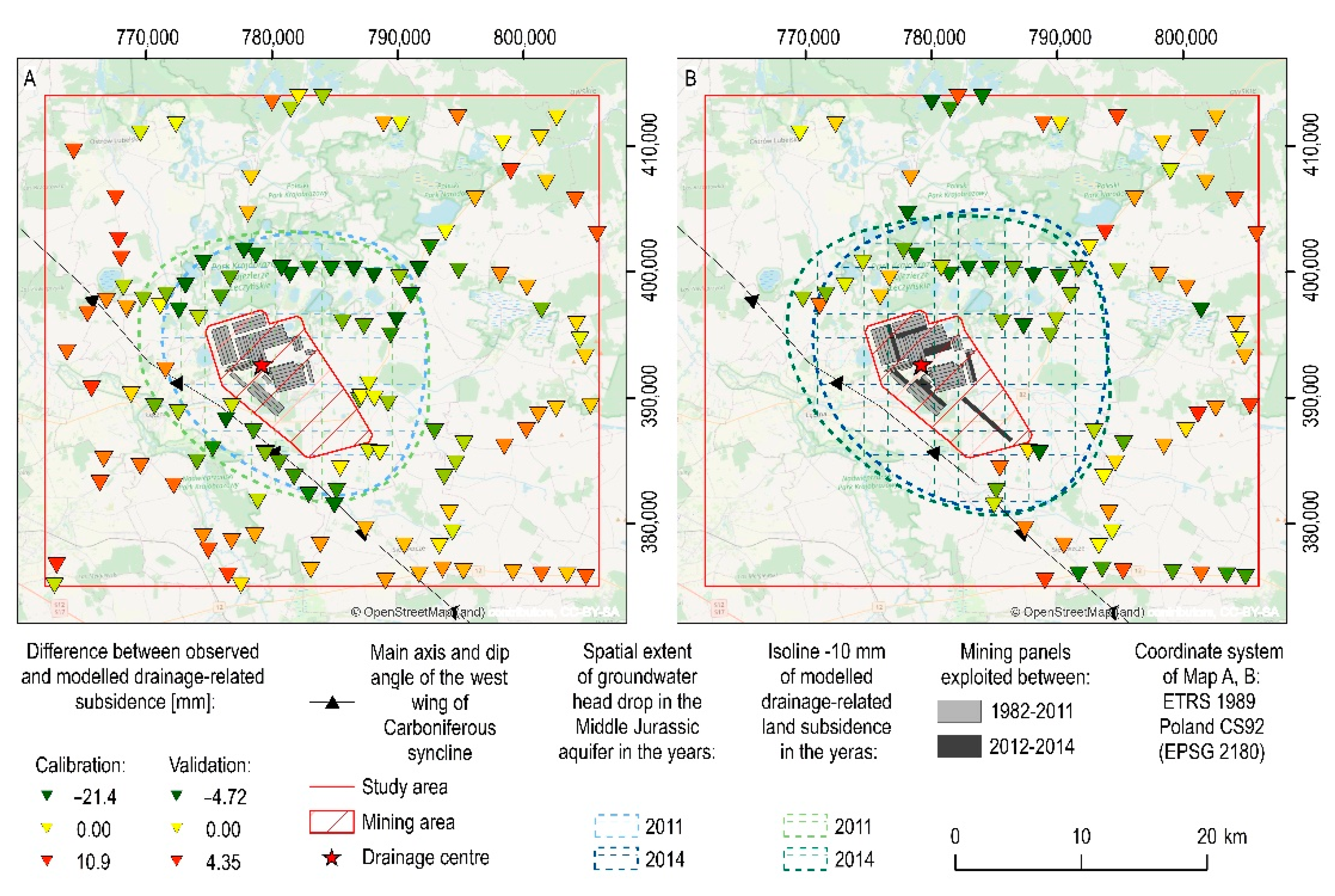
3.2.3. Model Calibration, Validation and Future Scenario

Calibration and validation of each model should begin with developing a target with an acceptable margin of error. The purpose of the modelling process primarily determines the error range. Moreover, during calibration, the user should concentrate on parameters with less certainty and only slightly modify parameters with greater confidence. The majority of the other parameters are less sensitive and can be adjusted within a reasonable range.

Given the previous, the presented model was calibrated and validated by determining the parameters $C_m$ and $\tan \beta$ for local conditions using data on land subsidence changes in the study area. Since these parameters define the average characteristics of the aquifer’s compaction and the propagation of the deformation process through the rock mass and are determined based on empirical data, $C_m$ and $\tan \beta$ are the most uncertain variables. Therefore, the remaining parameters of the model presented were assumed to be constant values with high determination accuracy.

Taking the uncertainty of the integral in (16) into account, the model parameters $C_m$ and $\tan \beta$ were calculated using the Gauss-Newton method for nonlinear equation systems. The main idea behind this method is to express the original nonlinear equation in a linear form using the Taylor series expansion, as shown in Equation (17) [73]:

$$S_A^o-S_A^t=\frac{d{S}_A^t\left(C_m,\tan \beta \right)}{d{C}_m}d{C}_m+\frac{d{S}_A^t\left(C_m,\tan \beta \right)}{d\tan \beta }d\tan \beta +\delta ,$$

(17)

where $S_A^o$ and $S_A^t$ are the observed and theoretical land subsidence at point A, respectively, and $\delta$ is the model error.

When a large amount of data with a relatively high degree of accuracy is available, the presented method is commonly used to determine the values of the parameters of nonlinear equations. Furthermore, the least square method can be used to assume a minimization of the model error $\delta$ for observations $i$ to $n$, as expressed by Equation (18):

$$M={\displaystyle \sum }_{i=1}^n{\delta }_i{\delta }_i\to min.$$

(18)

Finally, the iterative minimization of the $M$ function from (18) can be accomplished using Equation (19):

$$A\hat{X}=L\to \hat{X}={\left(A^{T}A\right)}^{-1}{A}^{T}L,$$

(19)

where $A=\left[\begin{array}{cc}\frac{d{S}_{A,1}^t\left(C_m,\tan \beta \right)}{d{C}_m}& \frac{d{S}_{A,1}^t\left(C_m,\tan \beta \right)}{d\tan \beta }\\ ⋮& ⋮\\ \frac{d{S}_{A,n}^t\left(C_m,\tan \beta \right)}{d{C}_m}& \frac{d{S}_{A,n}^t\left(C_m,\tan \beta \right)}{d\tan \beta }\end{array}\right]$, $\hat{X}=\left[\begin{array}{c}{C}_m\\ \tan \beta \end{array}\right]$ and $L=\left[\begin{array}{c}{S}_{A,1}^o-S_{A,1}^t\\ ⋮\\ S_{A,n}^o-S_{A,n}^t\end{array}\right]$.

The variance-covariance matrix for Equation (19) can also be used to calculate the standard deviation of the model parameters $\sigma C_m$ and $\mathsf{\sigma }\tan \beta$ as well as the correlation coefficient R².

Calibration and validation of the model was performed by determining the values of the $C_m$ and $\tan \beta$ parameters for local conditions, using the procedure described in Equations (17)–(19). The model was calibrated using changes in the normal heights of 125 benchmarks from 1981 to 2011. The initial condition was the estimated groundwater head and land surface elevation before hard coal mining. The model was run a few times to determine the optimal values for its parameters.

The calculated value of the $C_m$ coefficient in the model calibration procedure was 7.11 × 10⁻⁴, with $\sigma C_m$ = ±6.41 × 10⁻⁵, whereas the value of the $\tan \beta$ parameter was 0.38, with $\mathsf{\sigma }\tan \beta$ = ±0.049. The values of these parameters are consistent with data obtained from other research sites and laboratory tests for the compaction of sandstone aquifers and the determination of the spatial range of impacts of fluids deposit exploitation [159,160,161,162]. The determination coefficient R² of the model was 0.71, which was considered satisfactory.

In general, the calculated and observed land subsidence trends were similar (Figure 8A). The mean difference was 6.07 mm, with a standard deviation of ±7.73 mm. Given the maximum value of land subsidence between 1981 and 2011, these results were considered acceptable since the mean error of calculated land subsidence was less than 10%. Nonetheless, due to the parameterization of the developed model, the values of land subsidence in the mining drainage’s center are slightly underestimated and overestimated in the research area’s periphery (Figure 9A). The main issue is with the $C_m$ and $\tan \beta$ parameters, which are assumed to reflect the overall geomechanical properties of the modelling area. It should also be noted that when the rock mass is drained, the aquifer compaction process does not begin immediately. The delay in drainage-induced rock mass deformation is related to the amount of decrease in groundwater head. However, determining the groundwater head decrease threshold value at which compaction of rock layers begins remains a significant research challenge and was not the immediate goal of the study presented.

Due to ALS data temporal coverage, the model validation procedure used 77 geodetic points. The validation was carried out for the change in land surface elevation from 2011 to 2014. Simultaneously, the estimated groundwater head for 2011 and 2014 was used as the initial and final conditions. Satisfactory model results concerning observed values of land subsidence were obtained during model validation (Figure 8B). Due to the shorter measurement period, the mean difference between these values was 0.80 mm, with a standard deviation of ±1.30 mm, which is less than 20%. In analogy with the model calibration results, there is a slight asymmetry in the values of the modelled land subsidence concerning empirical observations in the case of model validation. This asymmetry is observable as a function of distance from the drainage center (Figure 9B). Even though the model validation results show a similar trend to the model calibration results, they cannot be considered statistically significant due to the very small land subsidence values, which are lower than the accuracy of ALS measurements. As a result, the obtained model validation results should only be regarded as indicative.

A prediction of land subsidence due to mining-induced drainage was made using the calibrated and validated model. It was completed for the year 2030. The initial conditions for the calculations were the results of the 2014 model validation.

3.3. Assessment of the Impact of Land Subsidence Induced by Mining Drainage on Surface Water Reservoirs

The elevation of the ground surface is affected by land subsidence caused by rock mass drainage. As a result, this phenomenon may have an impact on the flow of surface watercourses. Primary hydraulic drops along watercourses may be disturbed, resulting in local surface water runoff or the formation of floodplains.

We used DTMs specified for 2014 and 2030 to automatically delineate a drainage system and quantify its characteristics to determine the environmental impact of drainage-induced land subsidence in the area of interest. DTM for 2014 was calculated using CODGIK data, whereas 2030 DTM was estimated by adding the values of land subsidence due to mining drainage specified in the research for 2030 to the 2014 DTM. Since the spatial resolution of the DTMs was 10 m per 10 m, the following procedure could be applied to both DTMs simultaneously in the ArcGIS environment using the Hydrology Toolbox [163].

First, any sinks in the original DTMs were identified using the Sink tool. A sink is typically a value that is incorrectly lower than the values of its surroundings. These depressions are problematic since any water that flows into them cannot flow out. Therefore, they were filled with the Fill tool to ensure proper drainage mapping [164]. Then, using appropriately prepared DTMs as input to the Flow Direction tool, we determined which direction water would flow out of each cell. Next, the D8 flow method was used to model the flow direction from each cell to its steepest downslope neighbor [165,166]. Following that, we used the Flow Accumulation tool to calculate the number of upslope cells flowing to a location to create a stream network. As inputs, the previous step’s output flow direction rasters were used [166,167]. As the first stage in defining the stream network system, a threshold was specified on the rasters derived from the Flow Accumulation tool. Therefore, it was possible to delineate a stream network and calculate a set of linear raster features to be represented as values on a background of “NoData” [166,167]. This task was completed using the CON tool applied by Equation (20):

$$stream=\mathrm{CON}\left(accumulation>1000,1\right),$$

(20)

where $stream$ and $accumulation$ are the rasters representing stream network and accumulation flow, respectively.

As a result, the stream network included all cells with more than 1000 cells flowing into them. Furthermore, given the spatial resolution of the DTMs used as inputs, it was assumed that a stream would accumulate a flow from at least 100,000 m². Finally, the stream network rasters were converted into polylines to calculate 2014 and 2030 elevation profiles for selected streams [163].

4. Results and Discussion

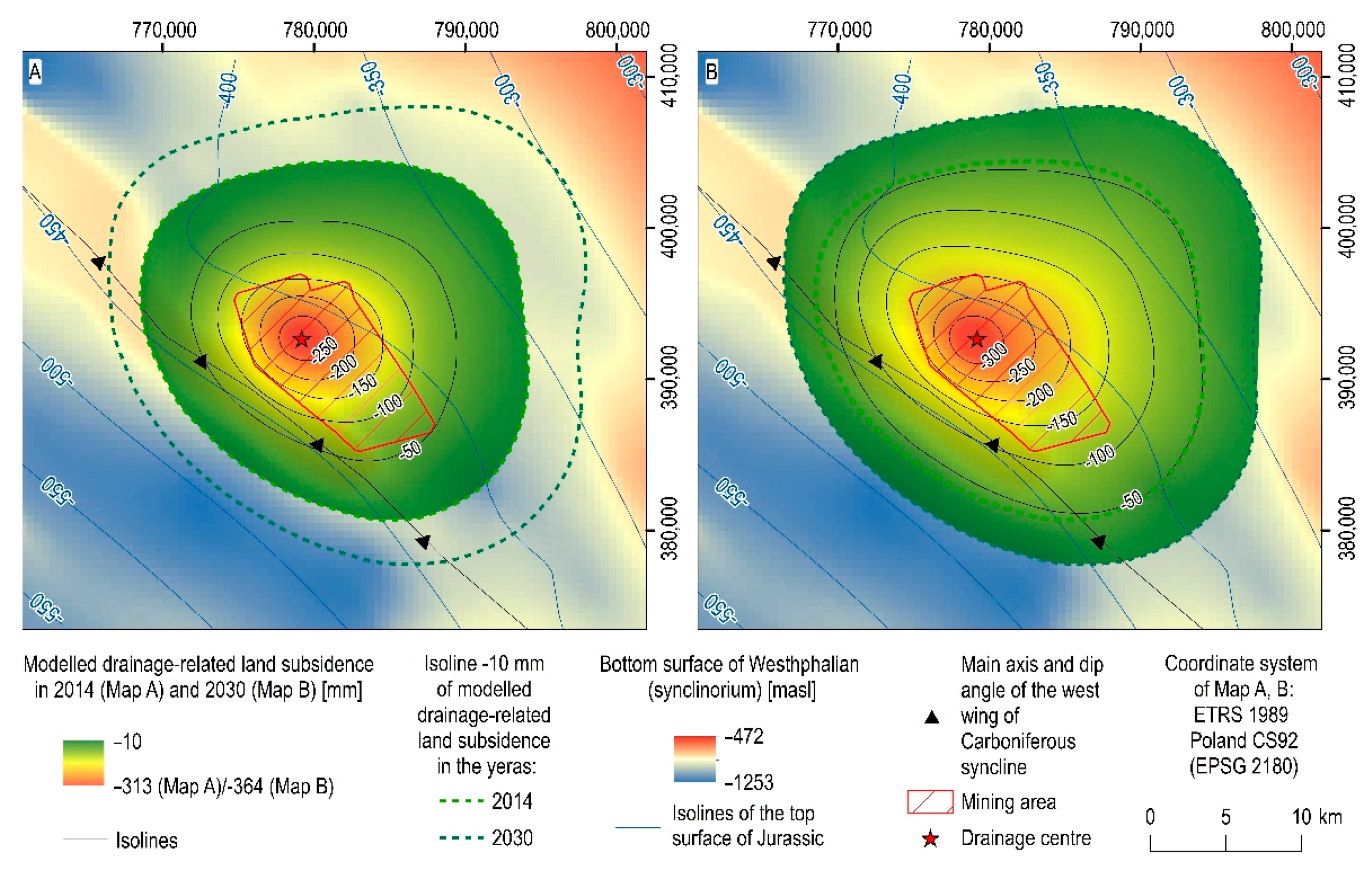
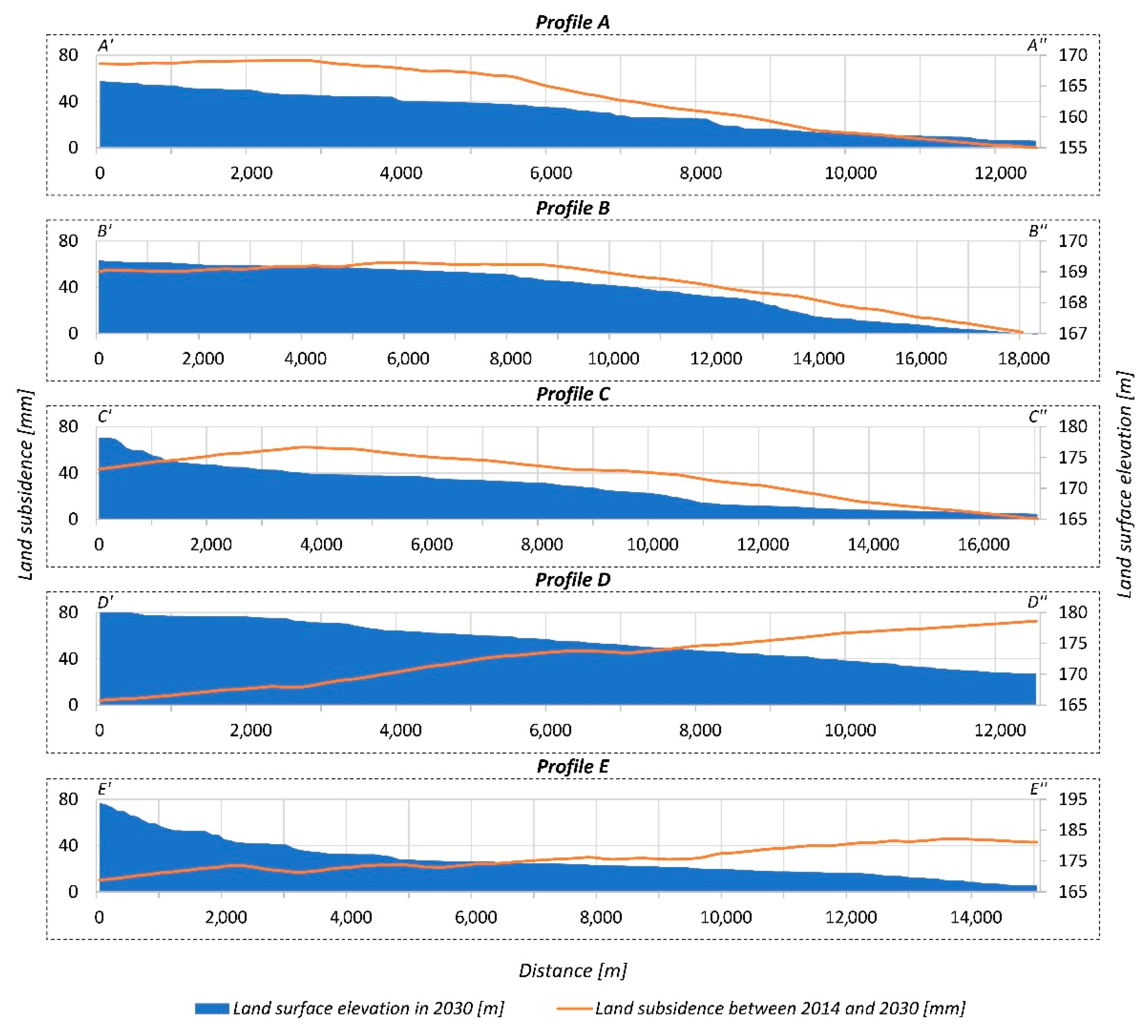
4.1. Spatial and Temporal Distribution of Drainage-Related Land Subsidence

The calculated values of land subsidence due to mining-induced drainage reached a maximum of 0.313 m and 0.369 m, respectively, in 2014 and 2030 (Figure 10). The shape of the subsidence troughs is similar, indicating a degree of asymmetry. They have a gentler and larger range of NE and NS and a narrower range to the W and SW. The maximum spatial extent of subsidence troughs towards the NE in 2014 and 2030 is 15.2 km and 20.3 km, respectively. In 2014, the total area of the bowl was 483.1 km², and it is expected to increase to 770.3 km² by 2030. As a result, these bowls are about 6 and 9 times larger than the maximum area of the Bogdanka mine, as determined solely by the direct impacts of hard coal exploitation. Drainage-induced subsidence trough asymmetry is related to regional geological and hydrogeological conditions. The phenomenon has a greater spatial extent in areas where the Middle Jurassic aquifer is located at shallower depths. Lower values of land subsidence are most likely related to the greater depth of the Middle Jurassic aquifer and the steep wing of the synclinorium in which the exploited hard coal deposit is located in the S and SW parts of the study area (see Section 2.1).

Land subsidence caused by drainage is most evident near mining shafts (Figure 10). This is the most extensive and long-lasting mining-induced drainage area. The mining area had the relatively highest values of land subsidence in 2014. This zone encompasses the most severe disintegration of the rock mass structure caused by hard coal mining. Therefore, strong fractures and fissures propagating to the ground surface characterize the rock mass in this area, providing convenient pathways for groundwater migration from the Middle Jurassic aquifer into mining voids. Within the limits of the mining area, drainage-related land subsidence amounted to no less than 0.133 m. This is about 42 per cent of the maximum values of land subsidence due to groundwater withdrawal estimated this year. This trend is expected to continue in the coming years. In 2030, the values of the analyzed phenomena in the mining area will be no less than 0.206 m, which corresponds to 52% of the maximum values of predicted land subsidence in that year.

Given the previous, it is reasonable to conclude that land subsidence caused by rock mass drainage has relatively low values, especially outside of the mining area. Importantly, the estimated land subsidence in 2014 and 2030 exceeds the mining area boundaries and covers the area where no negative effects of hard coal mining should occur, according to Polish law (Figure 10). Despite this, the small magnitude of the phenomenon and the large area where land subsidence has been estimated indicates that no discontinuous deformations due to horizontal stresses in the Earth’s crust’s subsurface layer should be expected. As a result, the analyzed phenomena could not endanger infrastructure or affect the safety of surface users.

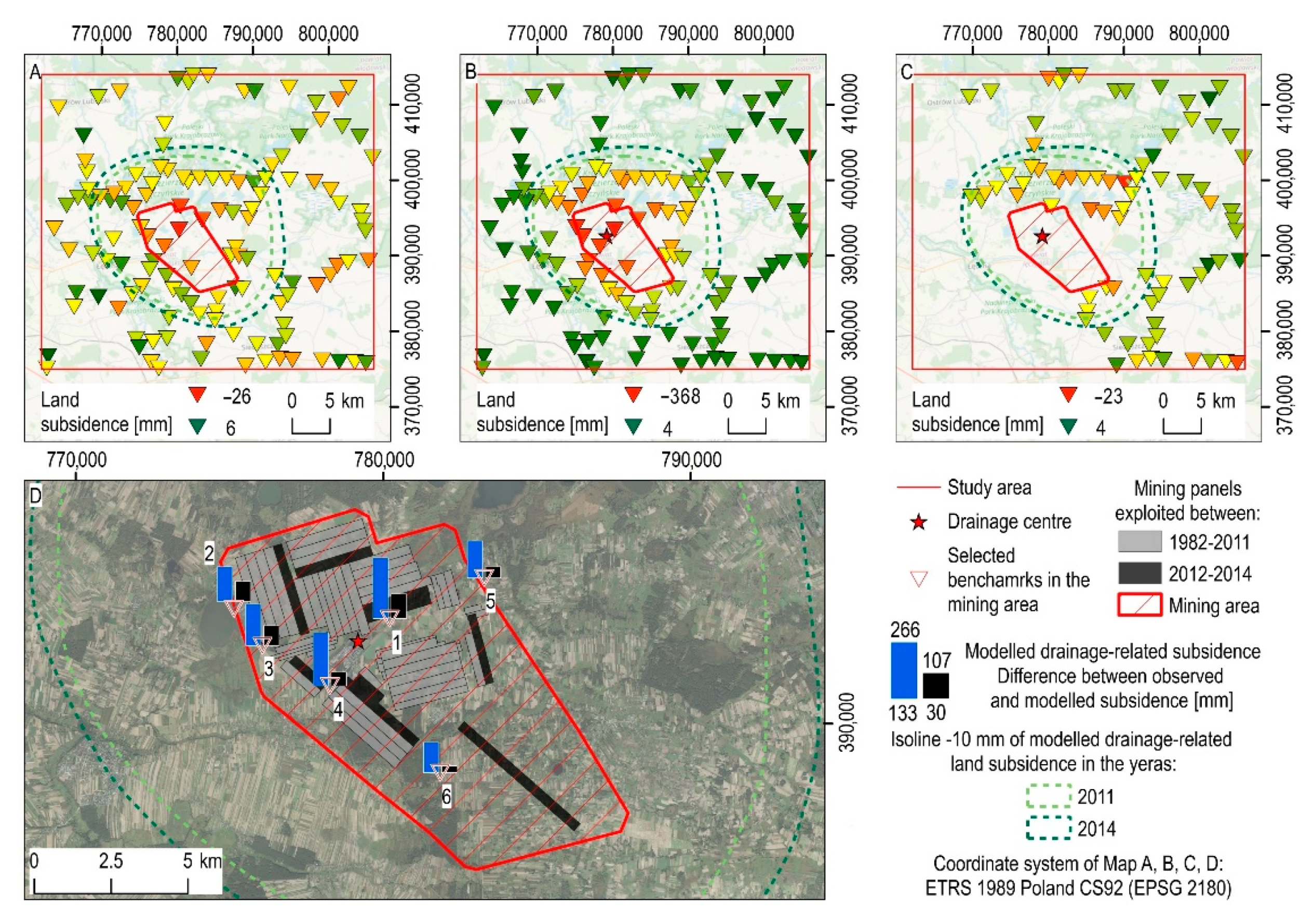
4.2. Separation of Direct Mining-Related Land Subsidence from the Imposing Influence of Drainage-Related Land Subsidence

Based on the analyses of the change in elevation of the geodetic network points, it is possible to conclude that no significant movements of the land surface were observed in the entire area of research between 1959 and 1981, i.e., before the start of mining operations (Figure 11A). The mean value of land subsidence outside the mining area during this period was −3.06 mm, with σ = ±3.29 mm, and the extreme values of the phenomenon were −8 mm and +4 mm. Due to the lowland nature of the research area and numerous wetlands and surface floodplains, a drainage network was established in the area of interest in the second half of the 20th century. As a result, a slight trend of land subsidence could be attributed to the progressive drainage carried out to increase agricultural area during this period. As a result, minor compaction of the loose Quaternary formations could occur as a result of dewatering.

Nonetheless, due to the small values of land subsidence observed during this period, they can be equated, at least partially, with measurement errors and the accuracy of determining the elevation of the benchmarks. Land subsidence in the mining area reached a maximum of −26 mm between 1959 and 1981, with an average value of −13.14 mm and σ = ±7.36 mm. Maximum subsidence values were measured near the mining shafts (Figure 11A).

Intensive expansion of hard coal exploitation in the central part of the mine was carried out during the following measurement period, i.e., 1981–2011 (Figure 11B). As a result, the values of land subsidence during this period were the highest in the mining area, averaging −254.86 mm, with σ = ±62.23 mm. Drastic decreases in land surface occurred in the drainage center area, as in the previous time interval, and totaled 368 mm. This value most likely corresponded partly to the direct impact of mining operations and the formation of the post-mining void, which propagates towards the ground surface. Importantly, land subsidence outside the mining area was much lower between 1981 and 2011 (Figure 11B). It decreased with increasing distance from the boundaries of the mining area, reaching a maximum of several dozen mm, with an average value of −14.54 mm and σ = ±17.81. As described in Section 4.1, these changes in surface elevation are most likely due to the drainage of rock layers and the compaction of the Middle Jurassic aquifer.

Land subsidence in the north and east part of the study area was relatively small between 2011 and 2014, the last analyzed measurement period, due to the short time interval (Figure 11C). The phenomenon averaged −1.32 mm with σ = ±3.05 mm outside the mining area. These values indicate further slow compaction of the drained Middle Jurassic aquifer. Nonetheless, given the accuracy of their determination, the obtained values of land subsidence are as small that a broader inference about the phenomenon’s characteristics during this measurement period should be regarded as uncertain. Note that it was impossible to determine land subsidence in the remaining part of the area of interest due to data scarcity.

Considering the results of the analysis of changes in land surface elevation, as well as the modelling results described in Section 4.1, it is possible to conclude that land subsidence observed outside the mining area during the entire analyzed period is most likely related to the drainage of rock layers as a result of hard coal mining. The observed values of ground surface subsidence in the mining area, on the other hand, are the result of overlapping direct and indirect impacts of hard coal mining, namely the migration of the post-mining void and the drainage of rock layers.

The observed and modelled values of land subsidence in selected “1–6” benchmarks were analyzed to distinguish the effects of land subsidence resulting from hard coal mining and void propagation from mining-induced drainage (Figure 11D,

Table 2. Land subsidence in imposing direct and indirect impacts of hard coal exploitation in the Bogdanka mine estimated based on changes in the elevation of the benchmarks observed and modelled in 1981–2012.

Benchmark	ΔH Observed [mm]	ΔH Modelled [mm]	Difference between Observed and Modelled Change in the Elevation [mm]
1	−374.0	−266.5	−107.5
2	−240.0	−152.3	−87.7
3	−269.0	−181.7	−87.3
4	−295.0	−234.4	−60.6
5	−211.0	−162.4	−48.6
6	−163.0	−133.0	−30.0

). These benchmarks are located directly in the hard coal mining area and were measured by ALS in April 2012 (see Section 2.2.1). However, due to the short time lag between the modelled drainage-related land subsidence for 2011 and the observed value of land subsidence, it was decided to compare these data because it was the only way to distinguish between direct and indirect effects of mining exploitation. The maximum observed values of land subsidence from 1981 to 2012 were −374 mm and occurred in the central part of the mine. The observed values of land-surface subsidence in the marginal parts of the mining area ranged from −163 mm to −295 mm. The “1” benchmark had the largest difference between the observed and modelled value of the phenomenon, which was −107.5 mm. To sum up, the greater the distance from the drainage center, the smaller the difference in the analyzed values of land subsidence.

It should be noted that while the analyzed benchmarks are distributed in the mining area, they are not located directly above the mining fields (Figure 11D). As a result, the observed values of land surface subsidence do not fully reflect the maximum scale of displacements associated with hard coal exploitation. Admittedly, more than one m of land subsidence is observed in post-mining troughs located directly above exploited fields.

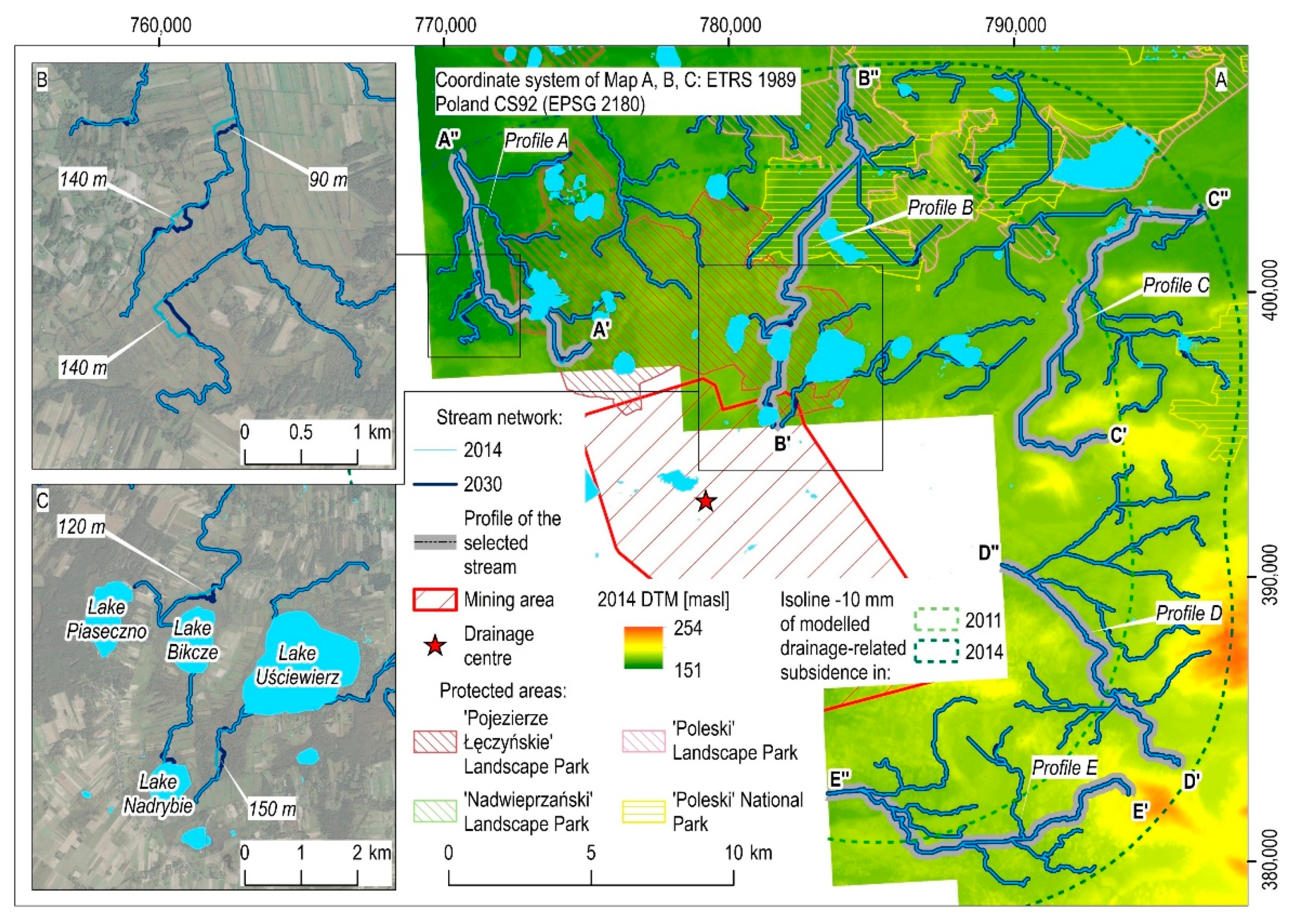
4.3. Regional-Scale Impact of Land Subsidence Due to Mining-Induced Drainage on Surface Water Reservoirs

The network of surface watercourses determined as a result of the research is dense and covers the entire study area (Figure 12A). On the other hand, the stream network is primarily made up of small watercourses with low water flow that can be several kilometers long. Therefore, the stream network determined for 2014 and 2030 does not vary significantly across most of the research area (Figure 12A). This means that mining-drainage land subsidence does not affect the direction and shape of the surface hydrographic network. Nonetheless, changes in several watercourses near the mining area’s boundaries are expected. The most significant changes in the stream network’s spatial distribution will occur to the east of Lake Nadrybie and the north of Lake Bikcze (Figure 12B). These changes will occur for approximately 200 m along the watercourses. The analyzed area is part of the “Pojezierze Łęczyńskie” Landscape Park and is mostly made up of wetlands, peat bogs and lakes. On the other hand, the forecast changes should have no negative impact on the natural environment in this area due to their small magnitude. Small changes in the course of the surface hydrographic network will also occur east of Lake Krzecze-Krasne (Figure 12C). They will cover a few dozen m of selected watercourses. However, it should be noted that such changes will occur in lowland and wetland areas with a dense network of drainage ditches.

The land surface elevation profiles of five watercourses were investigated to understand better the impact of mining-drainage land surface subsidence on the stream network. Selected watercourses are located within the predicted land surface elevation changes for 2030. The maximum subsidence along A–E streams is estimated to be 75, 61, 62, 73 and 46 mm, respectively (Figure 13A–E). Since watercourses A, B and C have a longitudinal course and a decrease in surface elevation to the north, the greatest values of land subsidence will be observed in their initial fragments (Figure 13A–C). Due to the horizontal course of the remaining streams and the slope of the land surface towards the west, the greatest values of subsidence along the D and E watercourses are forecasted in their middle and end sections (Figure 13D,E).

In 2014, there were minor primary hydraulic drops observed along the analyzed watercourses (Figure 14). In that year, the maximum drops for the A-E streams were −6, −1, −8, −4 and −16 mm/m, respectively. Changes in land surface elevation predicted from 2014 to 2030 will have little effect on hydraulic drops along the selected watercourses. The hydraulic drop differences for all streams will be between 0.02 and −0.01 mm/m (Figure 14). As a result, these values will be orders of magnitude lower than the original 2014 hydraulic drops calculated. As a result, drainage-induced land subsidence will not cause any unexpected outflow or inflow of surface water in the study area. To conclude, it is reasonable to predict that there will be no substantial changes in the surface distribution of protected wetlands in the coming years. Noticeably, surface watercourses and specially protected areas in the Poleski National Park, which is part of the Natura 2000 network, will be exempt from adverse impacts of mining-related land subsidence.

5. Conclusions

Land subsidence is a common occurrence in many parts of the world. Both natural and man-made events can cause this. Nonetheless, groundwater withdrawal is one of the primary causes of land subsidence. In most cases, freshwater extraction for domestic purposes induces drainage and subsequent compaction of rock layers. However, this type of land subsidence is widely observed, monitored and thus recognized around the world [15,25]. As a result, it is possible to mitigate the negative effects of such land subsidence.

Nonetheless, land subsidence caused by mining-induced groundwater withdrawal is a relatively unknown phenomenon. This is because underground mineral resource extraction occurs primarily at great depths in complex geological and hydrogeological conditions. As a result, studying rock mass deformation and related phenomena such as land subsidence remains a difficult research problem.

Given the scarcity of research on rock layer drainage caused by underground mining, the current study sought to determine the extent of land subsidence caused by mining drainage and the impact of this phenomenon on the aquatic environment, specifically surface water reservoirs. The research was carried out at the Bogdanka underground coal mine in Poland.

First, land subsidence in mining exploitation’s direct and indirect impact was investigated using geodetic measurement and remote sensing data from 1959 to 2014. The previous research on determining the spatio-temporal drop in groundwater head due to mining drainage in 1981–2014 was then analyzed. The outcomes of these studies were used to develop the influence function method model. The model was successfully calibrated and validated using land subsidence data from 1981 to 2011 and 2011 to 2014. Finally, this model was used to estimate nonlinear and spatially varying land subsidence due to rock mass drainage across the entire study area for 2030. Based on the findings, it was possible to determine the direct mining influences in the study area and the environmental impact of hard coal exploitation considering surface water reservoirs.

The following are the main conclusions:

• In 2014 and 2030, the calculated values of land subsidence due to mining-induced drainage reached a maximum of 0.313 m and 0.369 m, respectively. The highest values of land subsidence due to mining drainage were calculated in the vicinity of shafts, representing the drainage center. Subsidence troughs have a similar shape but are asymmetrical. As a result, the maximum spatial extent of subsidence troughs is 15.2 km and 20.3 km, respectively, with the greatest extent to the northeast. Our findings show that the environmental impact of underground mining is much broader than direct land subsidence. What is more, the spatial extent of the drainage-related land subsidence significantly exceeds the mine’s boundaries, which cover approximately 80 km². The total area of the subsidence trough caused by aquifer compaction was 483.1 km² in 2014, and it is expected to increase to 770.3 km² by 2030.
• The mining area had the greatest disparity between observed and modelled ground surface subsidence values. They reached a maximum of −107.5 mm, compared to the modelled value of −266.5 mm. This result demonstrates that the direct effects of coal exploitation, namely the propagation of the post-mining void and the results of drainage-related rock layer compaction, overlap in the central part of the mine. However, it was impossible to determine the extreme difference between land subsidence caused by hard coal extraction and aquifer system compaction due to a lack of measurement data distributed directly above the hard coal mining fields. Only at six benchmarks could observed land subsidence be compared to modelled drainage-related land subsidence in the area above mining panels. As a result, the obtained results should be regarded as understated and inadequate. However, due to a lack of data, we were unable to conduct a more thorough analysis.
• Due to the relatively low values, land subsidence caused by rock mass drainage will not cause significant disturbances in the course of surface streams in the study area. Only a few small sections of the selected streams will experience a change in the spatial course up to several hundred m long. These changes, however, will occur in areas that are already heavily flooded or are peat bogs. Furthermore, the research indicates that natural hydraulic drops of watercourses will be unaffected by land subsidence. As a result, rapid surface water runoff or flooding is not expected to occur. Therefore, surface water reservoirs in the research area, including particularly protected areas, will be unaffected by the negative effects of mining.
• Without requiring extensive calibration or an elaborate numerical subsidence model, the influence-function model provided land subsidence patterns based on the relationship between groundwater head decrease, the spatial distribution of the drained aquifer and subsequent subsidence, as well as geological data. In general, the obtained modelling results agree well with the empirical data. Nonetheless, the model has some inaccuracies, such as a slight underestimation of the value of land subsidence in the central drainage region and an overestimation of these values in the marginal part of the area of interest. Despite this, the research findings show that the method presented can be used effectively for land subsidence control and regulation plans and that it could be widely used for land subsidence estimation based solely on land subsidence and groundwater head data and geological recognition of the study area. As a result, our findings may pave the way for a more reliable assessment of the impact of underground mining on the aquifer system.