A Multimodal Smart Quantum Particle Swarm Optimization for Electromagnetic Design Optimization Problems
Abstract
1. Introduction
2. The Proposed Work
2.1. Process Analysis of Smart Particle of the Swarm
| Pseudocode of updating rule ofin the archive |
| If do |
| Clear the previous of |
| Store the new as in the archive |
| elseif |
| Ignore the new and upheld the previous one |
| end if |
| declare the global best from the updated archive. |
2.2. Optimal Strategy for Parameter Setting
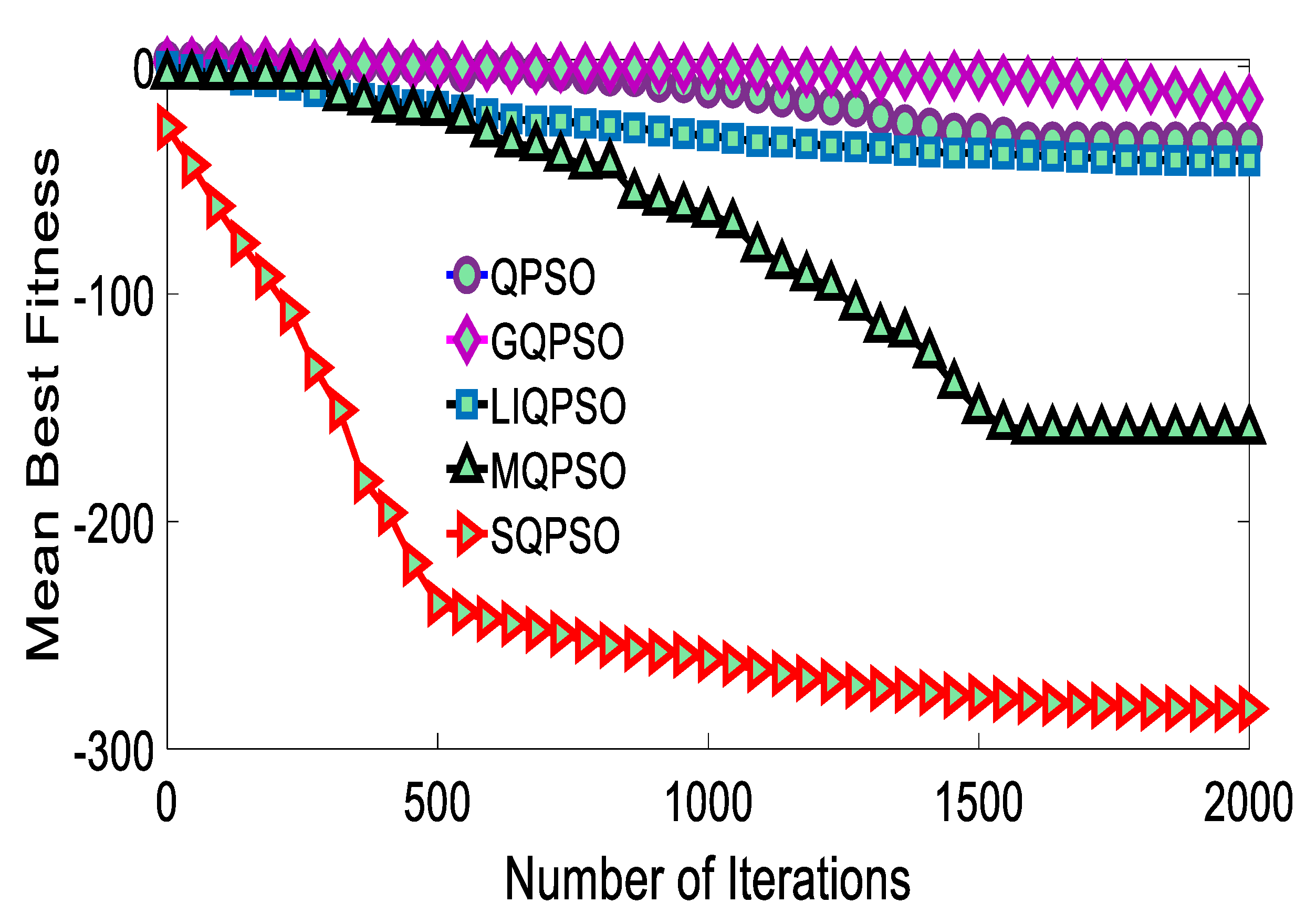
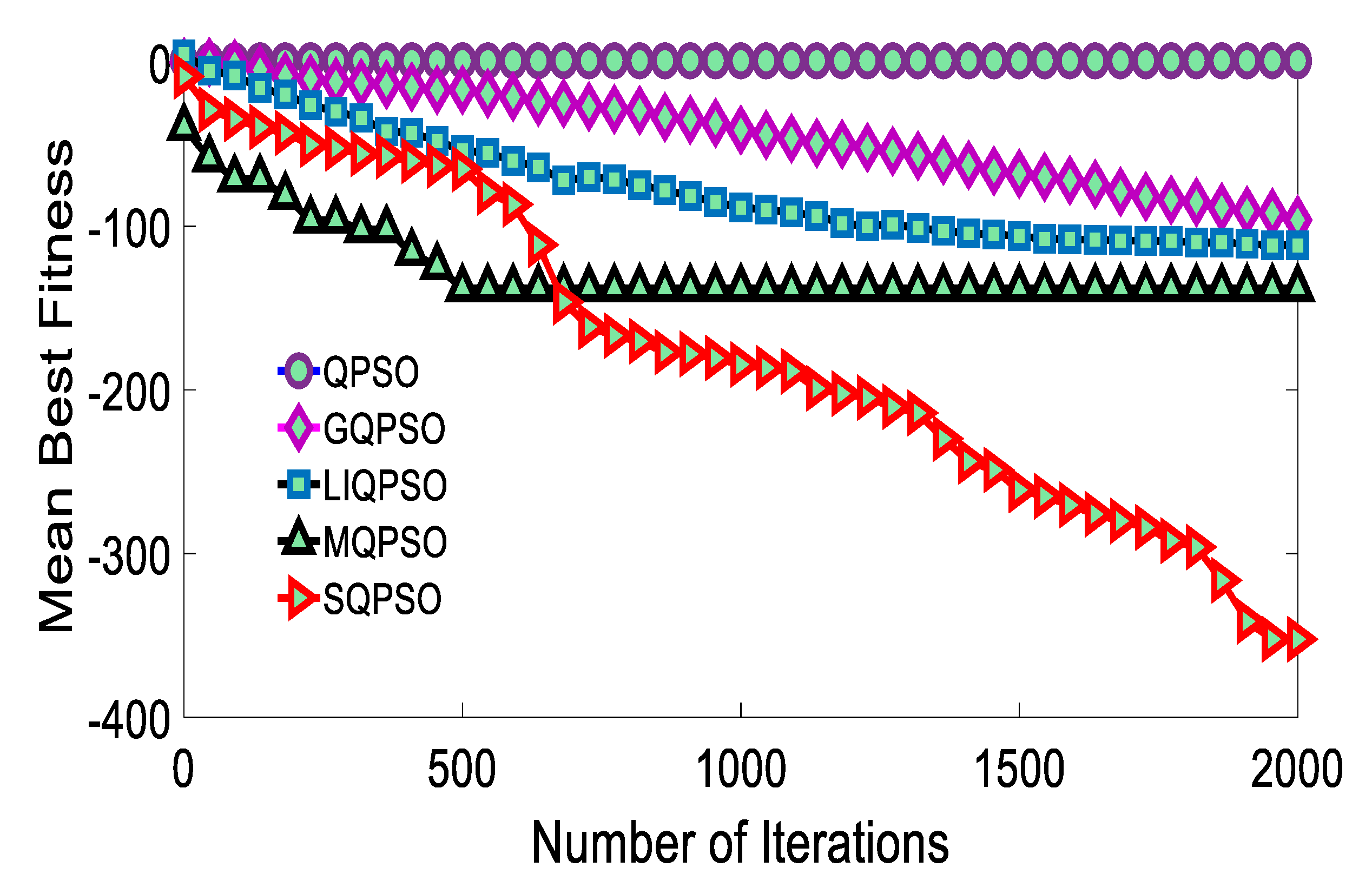
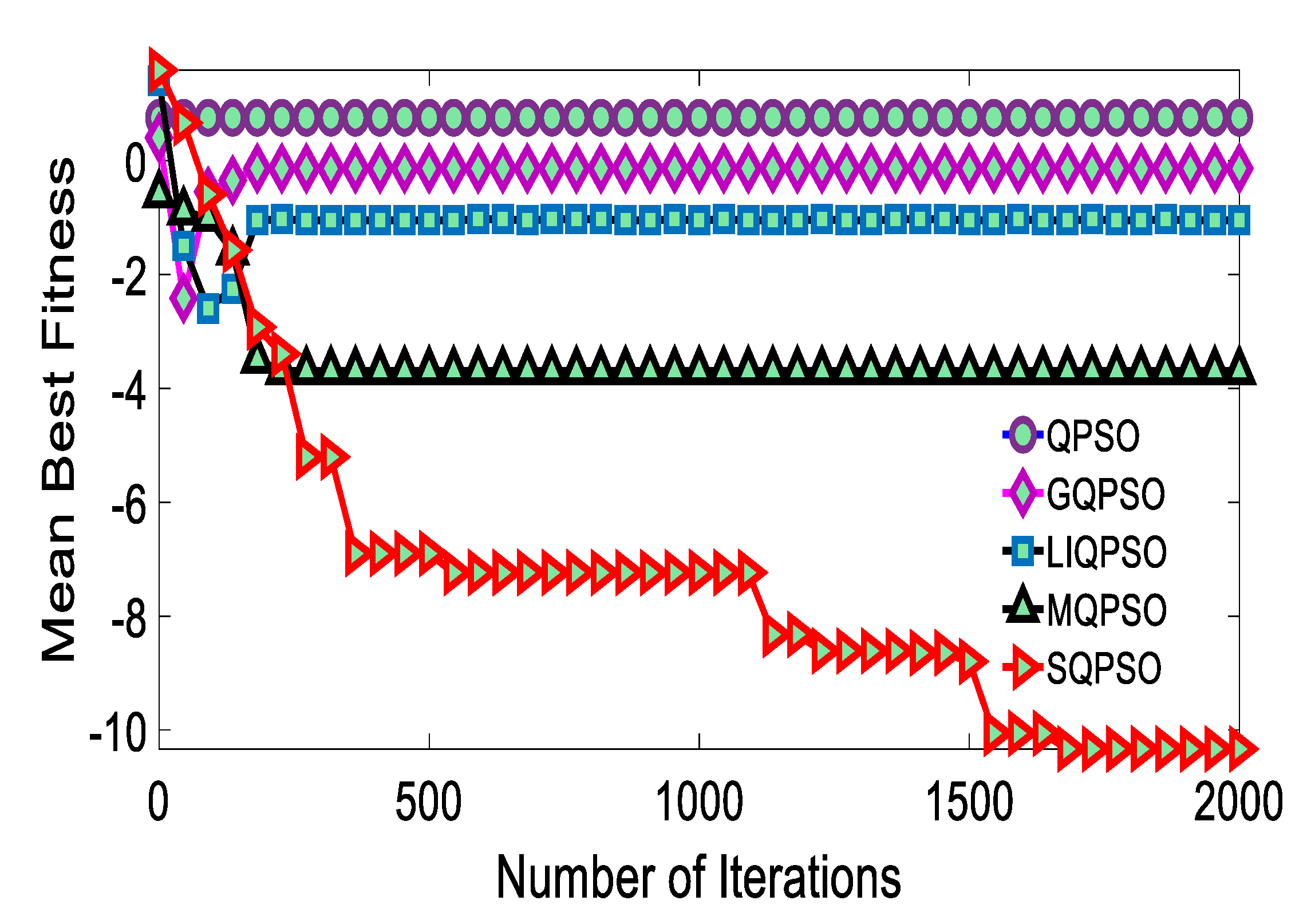
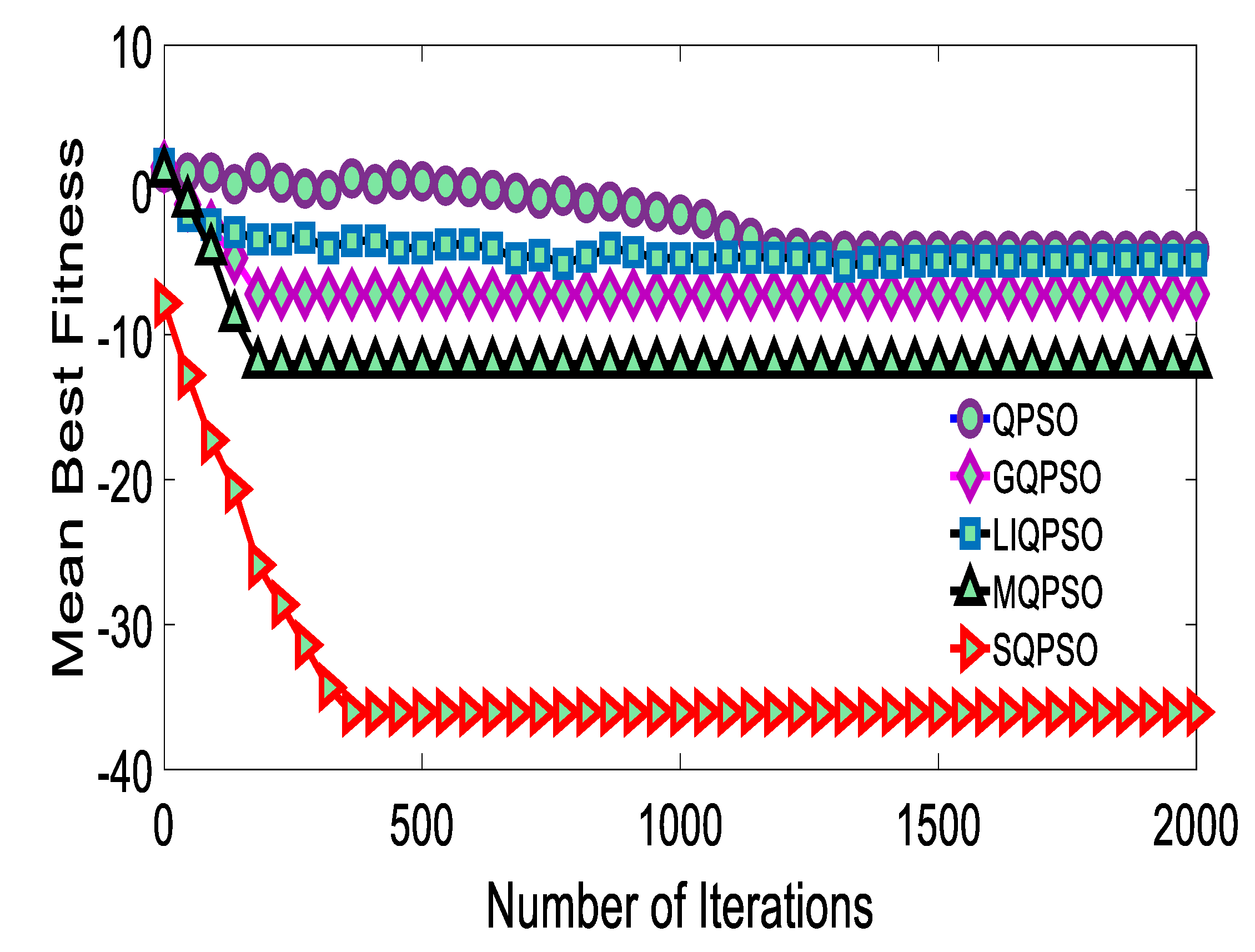
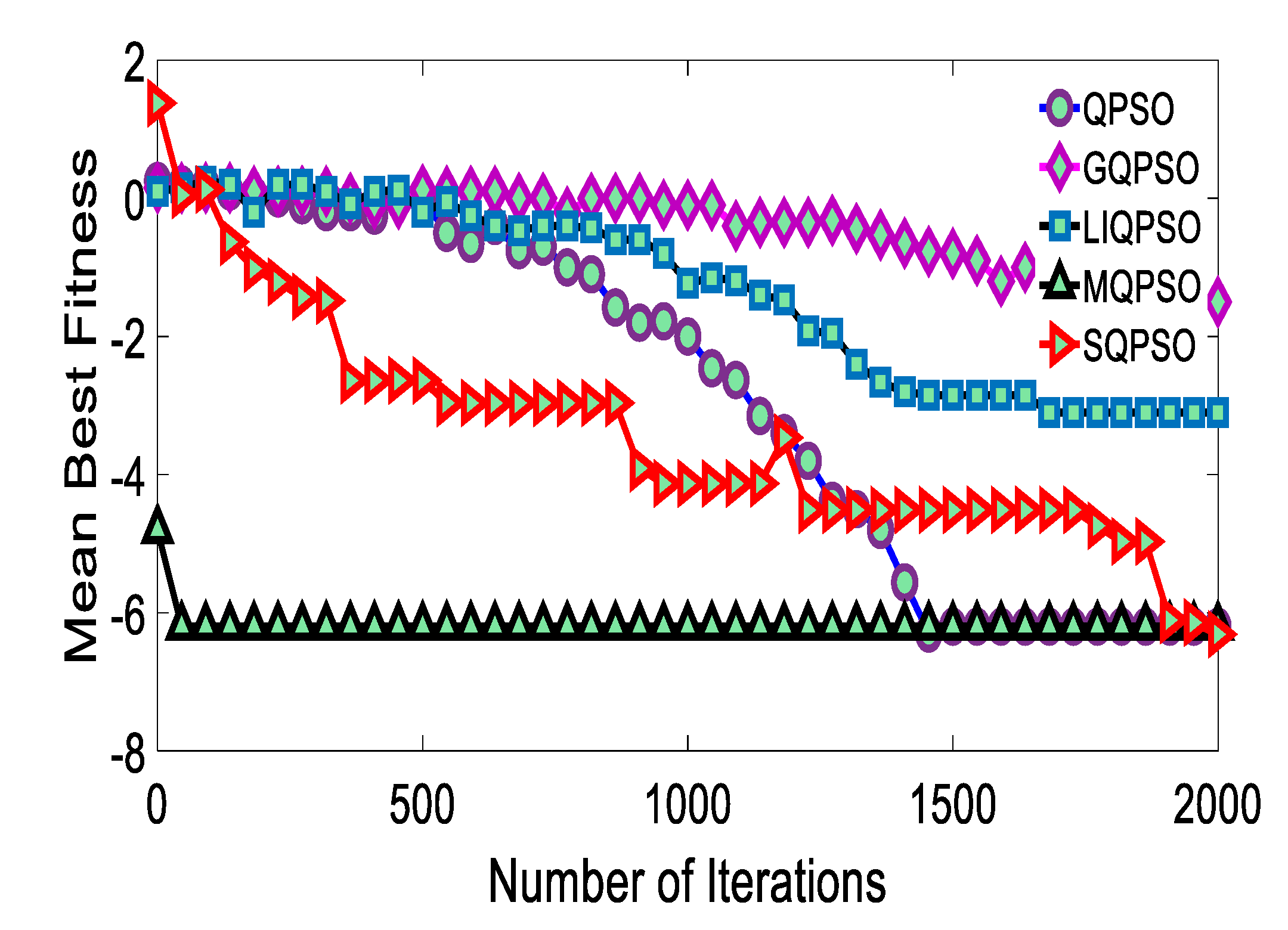
3. Numerical Result Analysis
4. Result and Discussion
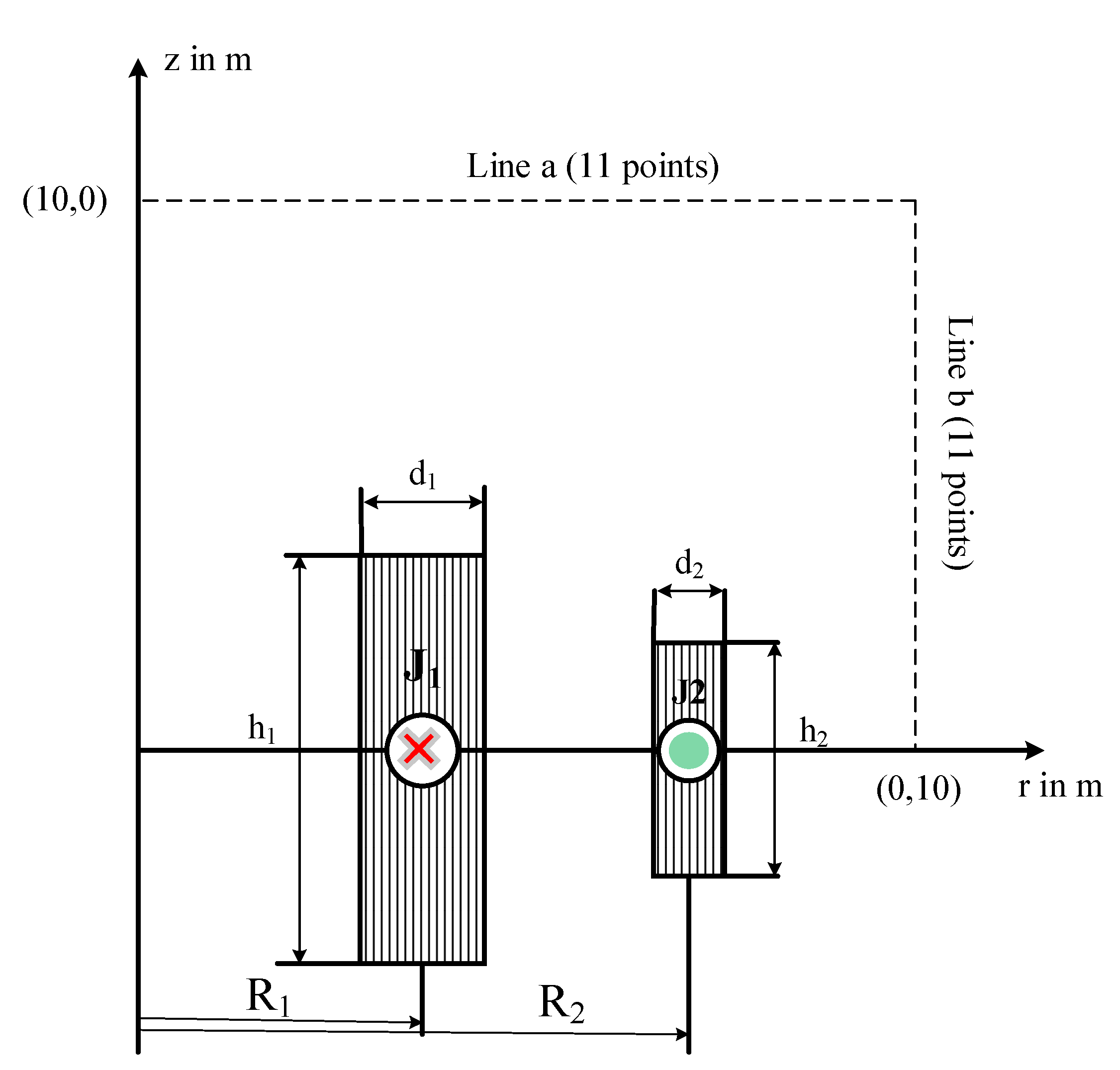
5. Numerical Validation for Engineering Problems
Objective Function of the TEAM Problem 22
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Xiao, M.; Gao, L.; Pan, Q. Queuing search algorithm: A novel metaheuristic algorithm for solving engineering optimization problems. Appl. Math. Model. 2018, 63, 464–490. [Google Scholar] [CrossRef]
- Ab Wahab, M.N.; Nefti-Meziani, S.; Atyabi, A. A Comprehensive Review of Swarm Optimization Algorithms. PLoS ONE 2015, 10, e0122827. [Google Scholar] [CrossRef]
- Coello, C.C. Use of a self-adaptive penalty approach for engineering optimization problems. Comput. Ind. 2000, 41, 113–127. [Google Scholar] [CrossRef]
- Garg, H. Solving structural engineering design optimization problems using an artificial bee colony algorithm. J. Ind. Manag. Optim. 2014, 10, 777–794. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 11, pp. 111–117. [Google Scholar]
- van den Bergh, F. An Analysis of Particle Swarm Optimizers. Ph.D. Thesis, South Africa University, Pretoria, South Africa, 2001. [Google Scholar]
- Ozcan, E.; Mohan, C.K. Particle swarm optimization: Surfing the waves. In Proceedings of the IEEE 1999 Congress on Evolutionary Computation-CEC99, Washington, DC, USA, 6–9 July 1999. [Google Scholar] [CrossRef]
- Jain, N.K.; Nangia, U.; Jain, J. A Review of Particle Swarm Optimization. J. Inst. Eng. Ser. B 2018, 99, 407–411. [Google Scholar] [CrossRef]
- Dong, J.; Yang, S.; Ni, G.; Ni, P. An improved particle swarm optimization algorithm for global optimizations of electromagnetic devices. Int. J. Appl. Electromagn. Mech. 2007, 25, 723–728. [Google Scholar] [CrossRef]
- Coco, S.; Laudani, A.; Fulginei, F.R.; Salvini, A. TEAM problem 22 approached by a hybrid artificial life method. COMPEL—Int. J. Comput. Math. Electr. Electron. Eng. 2012, 31, 816–826. [Google Scholar] [CrossRef]
- Xuerong, Y.; Hao, C.; Huimin, L.; Xinjun, C.; Jiaxin, Y. Multi-Objective Optimization Design for Electromagnetic Devices with Permanent Magnet Based on Approximation Model and Distributed Cooperative Particle Swarm Optimization Algorithm. IEEE Trans. Magn. 2017, 54, 8000604. [Google Scholar] [CrossRef]
- Khan, S.U.; Yang, S.; Wang, L.; Liu, L. A Modified Particle Swarm Optimization Algorithm for Global Optimizations of Inverse Problems. IEEE Trans. Magn. 2015, 52, 7000804. [Google Scholar] [CrossRef]
- Ho, S.L.; Yang, S.; Ni, G.; Wong, H. A particle swarm optimization method with enhanced global search ability for design optimizations of electromagnetic devices. IEEE Trans. Magn. 2006, 42, 1107–1110. [Google Scholar] [CrossRef][Green Version]
- Hantash, N.; Khatib, T.; Khammash, M. An Improved Particle Swarm Optimization Algorithm forOptimal Allocation of Distributed Generation Units in Radial Power Systems. Appl. Comput. Intell. Soft Comput. 2020, 2020, 8824988. [Google Scholar] [CrossRef]
- Wu, T.; Shi, X.; Liao, L.; Zhou, C.; Zhou, H.; Su, Y. A Capacity Configuration Control Strategy to Alleviate Power Fluctuation of Hybrid Energy Storage System Based on Improved Particle Swarm Optimization. Energies 2019, 12, 642. [Google Scholar] [CrossRef]
- Zaharis, Z.D.; Gravas, I.P.; Yioultsis, T.V.; Lazaridis, P.I.; Glover, I.A.; Skeberis, C.; Xenos, T.D. Exponential log-periodic antenna design using improved particle swarm optimization with velocity mutation. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Liu, J.; Yang, D.; Lian, M.; Li, M. Research on Intrusion Detection Based on Particle Swarm Optimization in IoT. IEEE Access 2021, 9, 38254–38268. [Google Scholar] [CrossRef]
- Khan, R.A.; Yang, S.; Fahad, S.; Khan, S.U. Kalimullah A Modified Particle Swarm Optimization with a Smart Particle for Inverse Problems in Electromagnetic Devices. IEEE Access 2021, 9, 99932–99943. [Google Scholar] [CrossRef]
- Tu, S.; Rehman, O.U.; Rehman, S.U.; Ullah, S.; Waqas, M.; Zhu, R. A Novel Quantum Inspired Particle Swarm Optimization Algorithm for Electromagnetic Applications. IEEE Access 2020, 8, 21909–21916. [Google Scholar] [CrossRef]
- Coelho, L.D.S. Gaussian quantum-behaved particle swarm optimization approaches for constrained engineering design problems. Expert Syst. Appl. 2010, 37, 1676–1683. [Google Scholar] [CrossRef]
- Rehman, O.U.; Yang, S.; Khan, S.; Rehman, S.U. A Quantum Particle Swarm Optimizer With Enhanced Strategy for Global Optimization of Electromagnetic Devices. IEEE Trans. Magn. 2019, 55, 1–4. [Google Scholar] [CrossRef]
- Jiang, S.; Yang, S. An improved quantum-behaved particle swarm optimization algorithm based on linear interpolation. IEEE Congr. Evol. Comput. 2014, 769–775. [Google Scholar] [CrossRef]
- Sun, J.; Feng, B.; Xu, W. Particle swarm optimization with particles having quantum behavior. In Proceedings of the 2004 Congress on Evolutionary Computation, Portland, OR, USA, 19–23 June 2004; Volume 1, pp. 325–331. [Google Scholar]
- Alotto, P.; Baumgartner, U.; Freschi, F.; Jaindl, M.; Kostinger, A.; Magele, C.; Renhart, W.; Repetto, M. SMES Optimization Benchmark Extended: Introducing Pareto Optimal Solutions Into TEAM22. IEEE Trans. Magn. 2008, 44, 1066–1069. [Google Scholar] [CrossRef]
- Schonwetter, G.; Magele, C.; Preis, K.; Paul, C.; Renhart, W.; Richter, K. Optimization of SMES solenoids with regard to their stray fields. IEEE Trans. Magn. 1995, 31, 1940–1943. [Google Scholar] [CrossRef]

| Modal | Name | Benchmark Functions | Search Space | |
|---|---|---|---|---|
| Unimodal | Sphere | 0 | ||
| Schwefel’s 2.22 | 0 | |||
| Multimodal | Rosenbrock | 0 | ||
| Griewank | 0 | |||
| Complex | Schwefel’s Problem 1.2 | and = −450 | 0 | |
| Griewank | and = −180 | 0 |
| Sphere f1 | |||||
| QPSO | GQPSO | LIQPSO | MQPSO | SQPSO | |
| Max | 3.00 | 2.00 | 0.00 | −4.00 | −26.66 |
| Min | −32.60 | −14.40 | −41.50 | −160.00 | −282.40 |
| Std | 13.95 | 4.43 | 12.69 | 60.38 | 72.92 |
| Mn | −13.43 | −2.88 | −27.17 | −78.82 | −230.27 |
| Schwefel’s 2.22 f2 | |||||
| QPSO | GQPSO | LIQPSO | MQPSO | SQPSO | |
| Max | 1.00 | 0.00 | 5.00 | −39.80 | −8.58 |
| Min | 1.00 | −96.30 | −111.67 | −138.01 | −352.19 |
| Std | 0.00 | 29.18 | 34.63 | 25.14 | 99.77 |
| Mn | 1.00 | −43.47 | −75.96 | −125.62 | −175.87 |
| Rosenbrock f3 | |||||
| QPSO | GQPSO | LIQPSO | MQPSO | SQPSO | |
| Max | 0.75 | 0.40 | 1.40 | −0.60 | 1.59 |
| Min | 0.75 | −2.42 | −2.60 | −3.70 | −10.33 |
| Std | 0.00 | 0.36 | 0.48 | 0.78 | 2.92 |
| Mn | 0.75 | −0.19 | −1.06 | −3.46 | −7.30 |
| Griewank f4 | |||||
| QPSO | GQPSO | LIQPSO | MQPSO | SQPSO | |
| Max | 1.20 | 1.60 | 1.80 | 1.20 | −7.83 |
| Min | −4.20 | −7.20 | −5.30 | −12.01 | −36.04 |
| Std | 2.17 | 1.74 | 1.19 | 2.79 | 6.47 |
| Mn | −1.91 | −6.71 | −4.21 | −11.22 | −33.61 |
| Schwefel’s Problem 1.2 f5 | |||||
| QPSO | GQPSO | LIQPSO | MQPSO | SQPSO | |
| Max | 0.10 | 0.05 | 0.12 | −1.70 | 6.04 |
| Min | −7.48 | −3.20 | −5.90 | −7.10 | −8.38 |
| Std | 2.89 | 0.95 | 1.80 | 1.32 | 4.31 |
| Mn | −3.09 | −0.89 | −1.48 | −6.59 | −5.14 |
| Complex Griewank f6 | |||||
| QPSO | GQPSO | LIQPSO | MQPSO | SQPSO | |
| Max | 0.25 | 0.15 | 0.25 | −4.80 | 1.38 |
| Min | −6.30 | −1.50 | −3.10 | −6.20 | −6.31 |
| Std | 2.61 | 0.58 | 1.30 | 0.21 | 1.68 |
| Mn | −2.84 | −0.41 | −1.35 | −6.17 | −3.42 |
| Algorithm | R2 | h2/2 | d2 | OF |
|---|---|---|---|---|
| QPSO | 3.0786 | 0.2414 | 0.3795 | 0.1077 |
| GQPSO | 3.1723 | 0.2319 | 0.3892 | 0.1222 |
| LI-QPSO | 3.0214 | 0.2732 | 0.3419 | 0.0959 |
| MQPSO | 3.1396 | 0.3160 | 0.2871 | 0.0716 |
| SQPSO | 3.0245 | 0.2561 | 0.2871 | 0.0278 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fahad, S.; Yang, S.; Khan, R.A.; Khan, S.; Khan, S.A. A Multimodal Smart Quantum Particle Swarm Optimization for Electromagnetic Design Optimization Problems. Energies 2021, 14, 4613. https://doi.org/10.3390/en14154613
Fahad S, Yang S, Khan RA, Khan S, Khan SA. A Multimodal Smart Quantum Particle Swarm Optimization for Electromagnetic Design Optimization Problems. Energies. 2021; 14(15):4613. https://doi.org/10.3390/en14154613
Chicago/Turabian StyleFahad, Shah, Shiyou Yang, Rehan Ali Khan, Shafiullah Khan, and Shoaib Ahmed Khan. 2021. "A Multimodal Smart Quantum Particle Swarm Optimization for Electromagnetic Design Optimization Problems" Energies 14, no. 15: 4613. https://doi.org/10.3390/en14154613
APA StyleFahad, S., Yang, S., Khan, R. A., Khan, S., & Khan, S. A. (2021). A Multimodal Smart Quantum Particle Swarm Optimization for Electromagnetic Design Optimization Problems. Energies, 14(15), 4613. https://doi.org/10.3390/en14154613







