Energy and Exergy Analyses of a Flat Plate Solar Collector Using Various Nanofluids: An Analytical Approach
Abstract
:1. Introduction
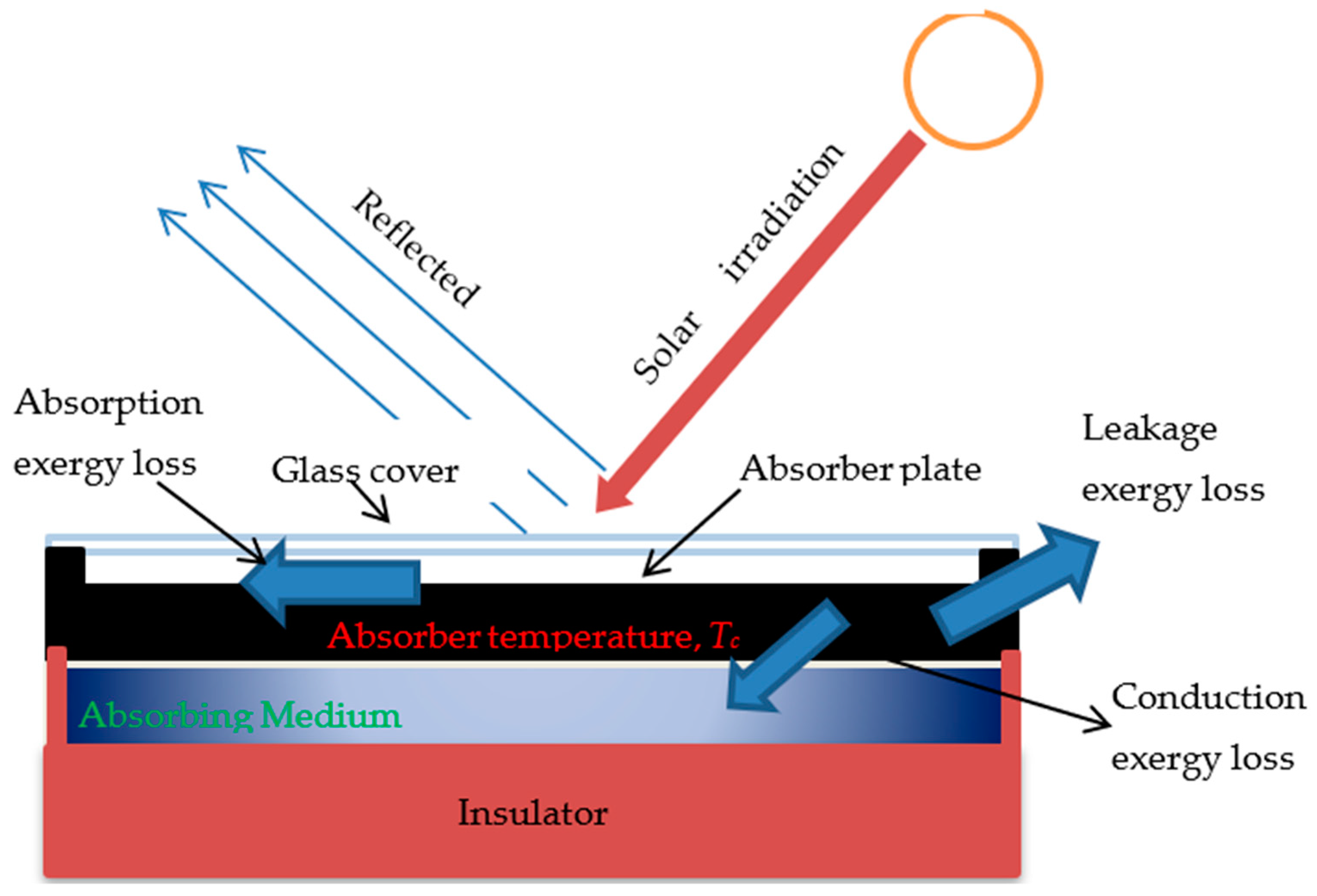
2. Analytical Approach
2.1. The First Law of Thermodynamics for Energy Efficiency
2.2. The Second Law of Thermodynamics for Exergy Efficiency
- ✓
- eopt: Optical loss percent solar energy absorbed owing to glazing transmissiveness and amorphous absorption.
- ✓
- erp: When solar radiation at Ts is absorbed by the absorber at Tc, there is a loss fraction. (Absorption at low temperatures degrades the high-quality energy).
- ✓
- epa: A portion of the exergy lost by the absorber to the environment.
- ✓
- epf: The heat transfer from the absorber to the fluid is accompanied by a heat-conduction loss percentage.
3. Input Data and Methodology
3.1. Input Data
3.2. Methodology
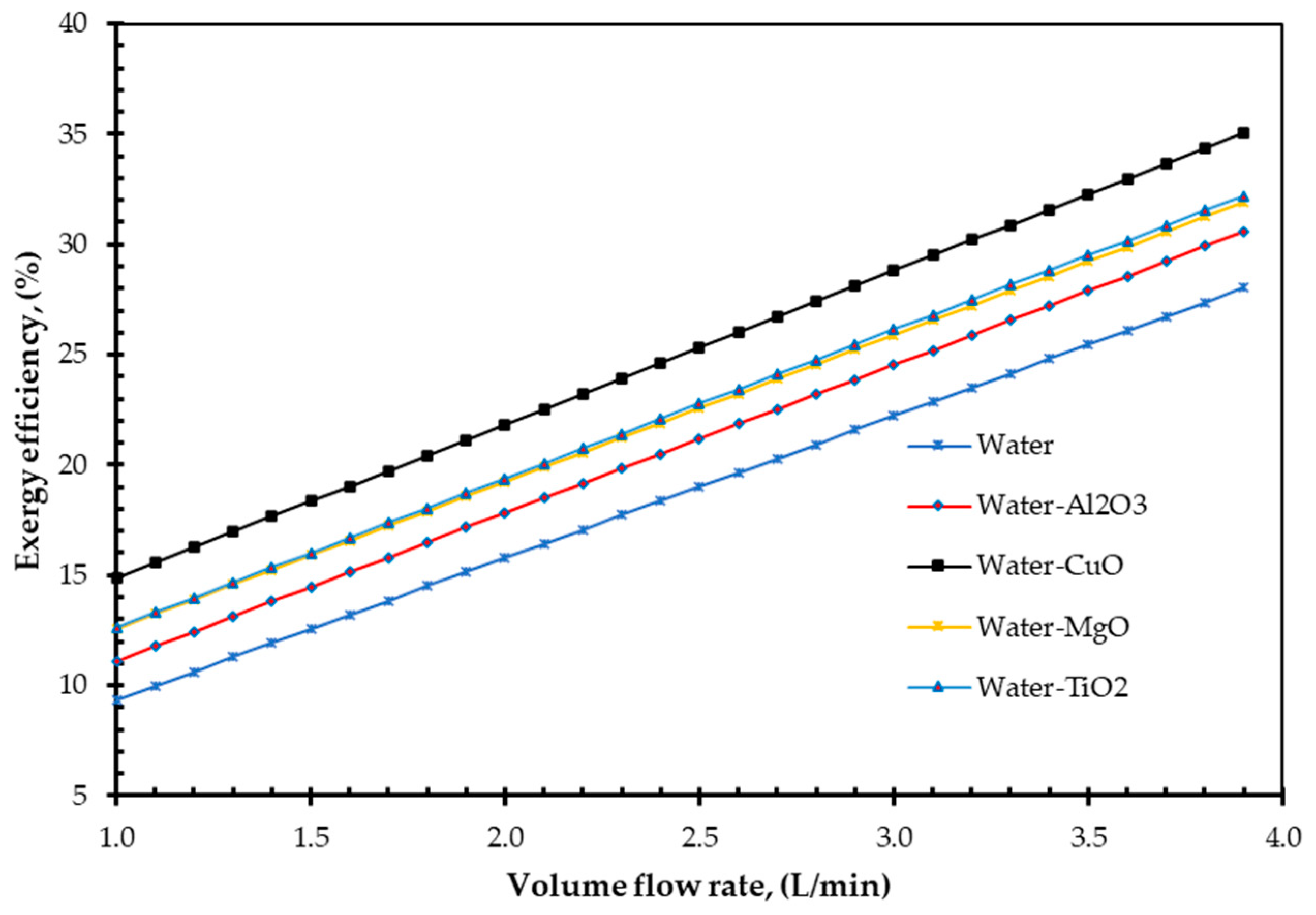
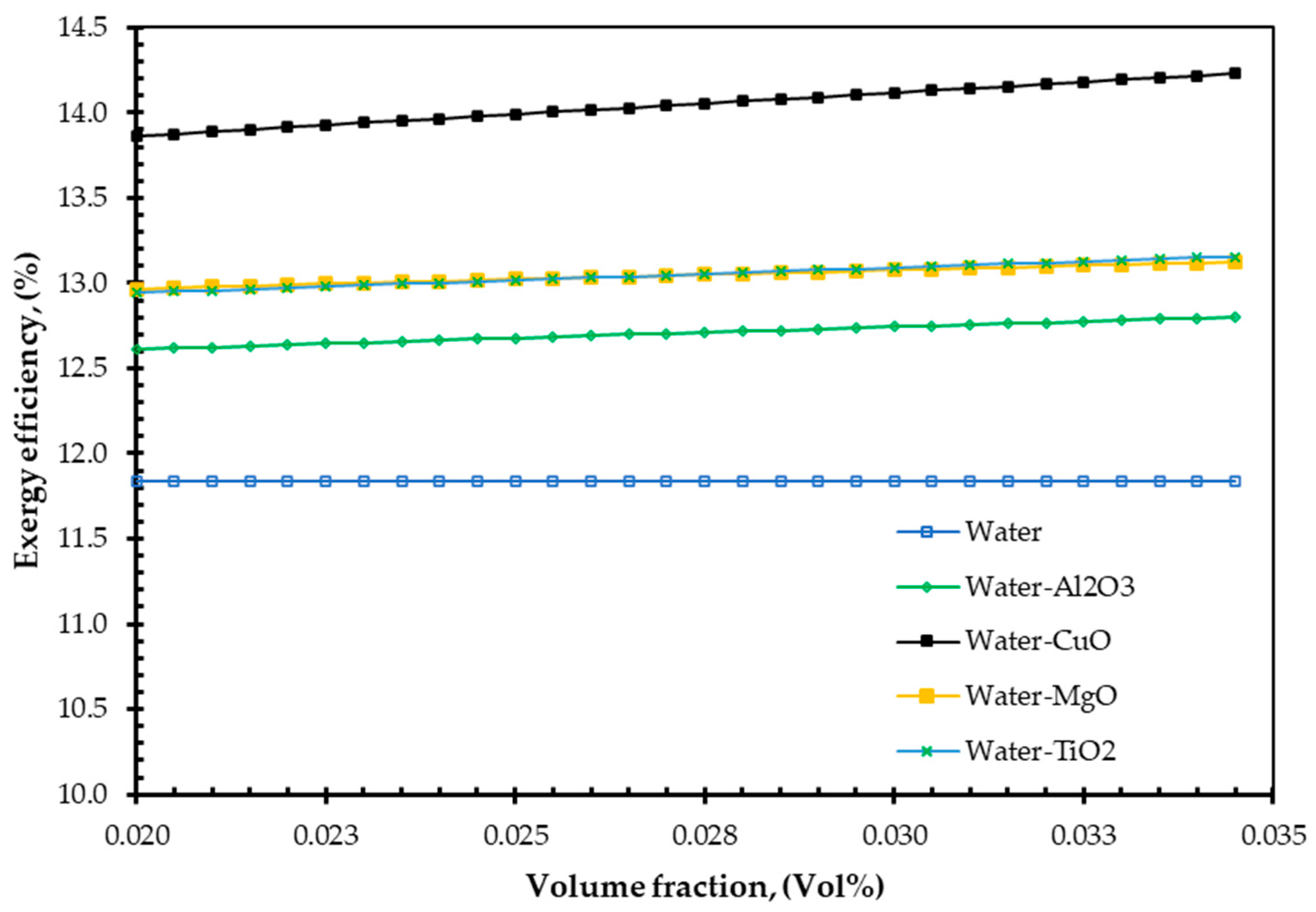
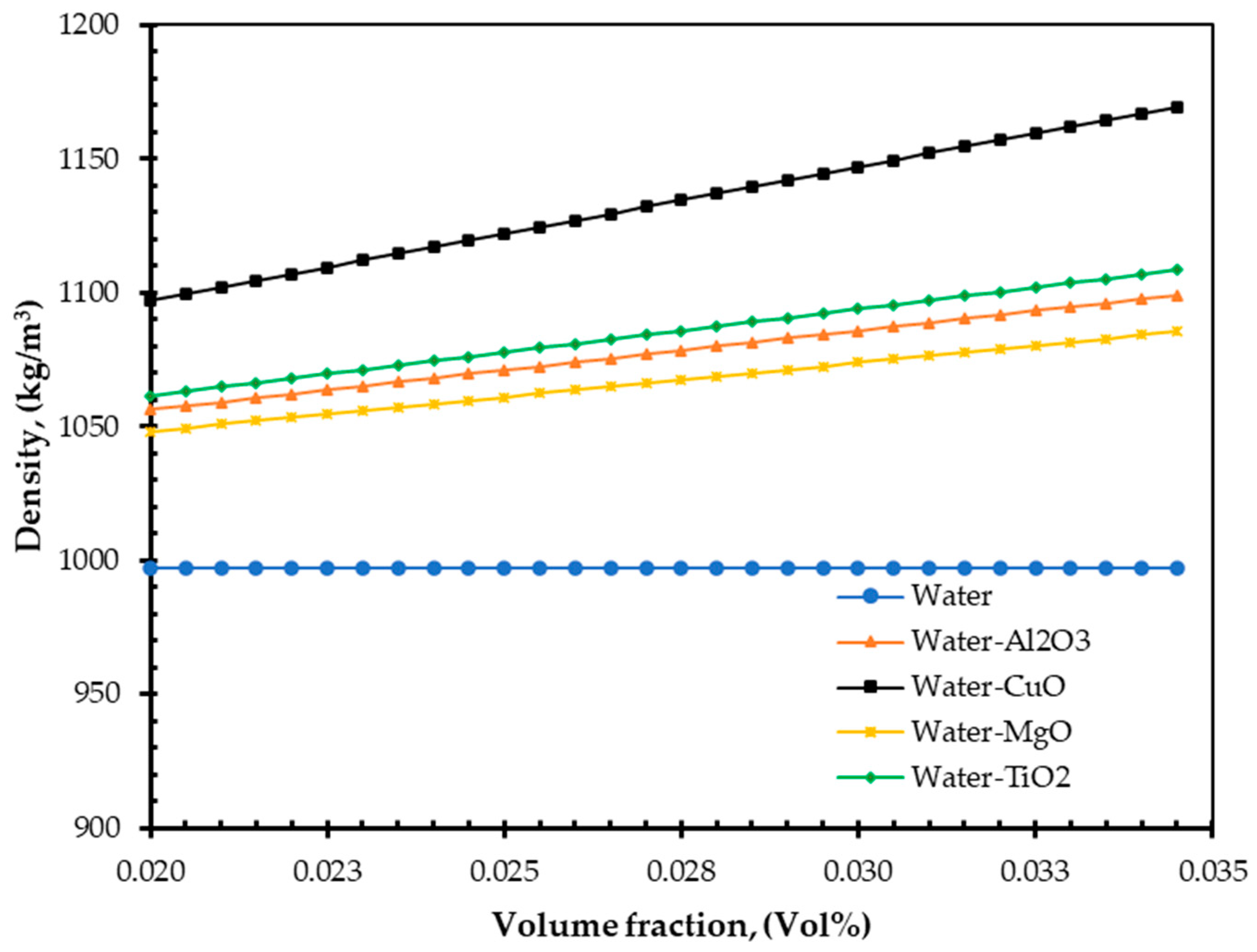
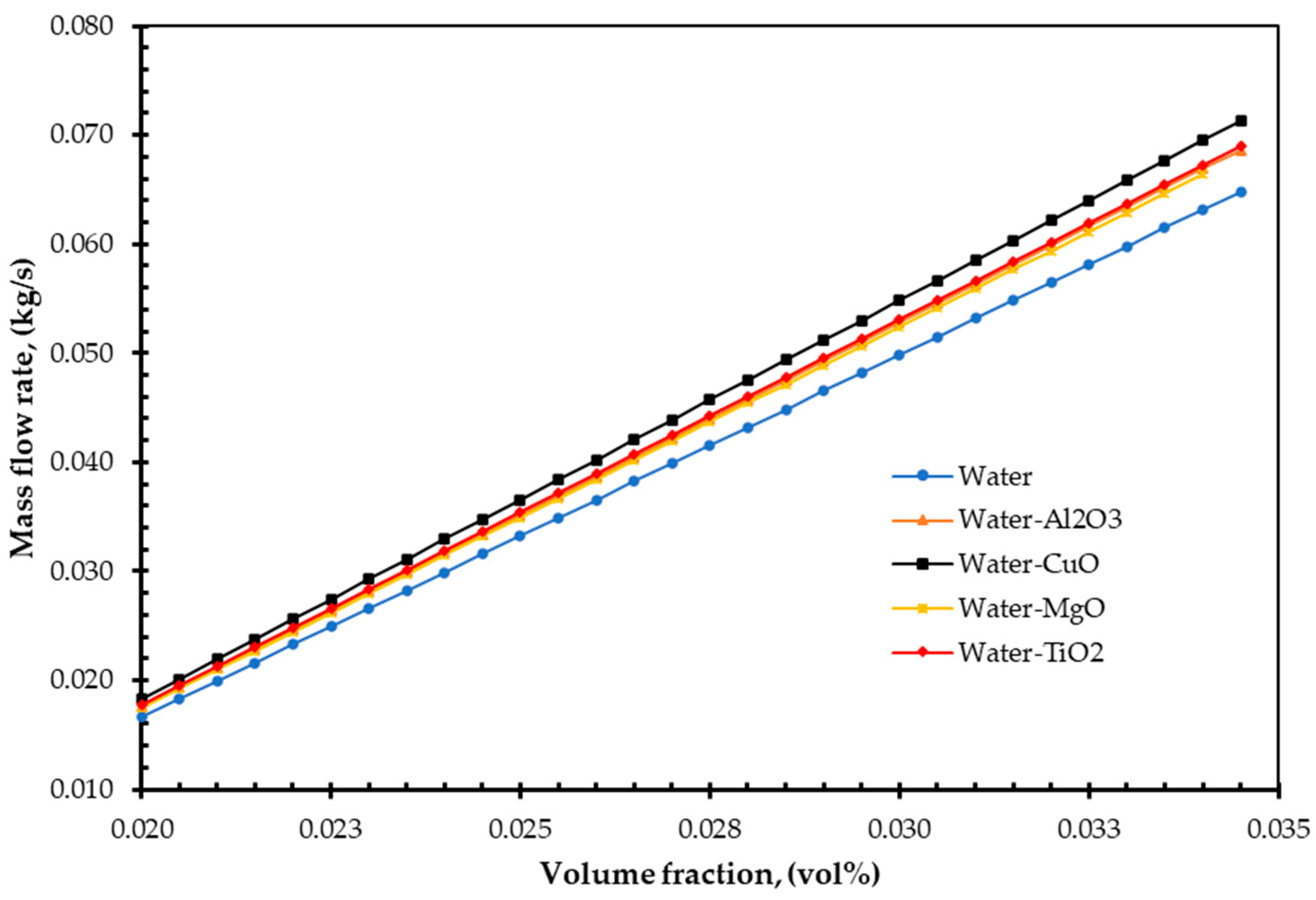
4. Results and Discussions
- ✓
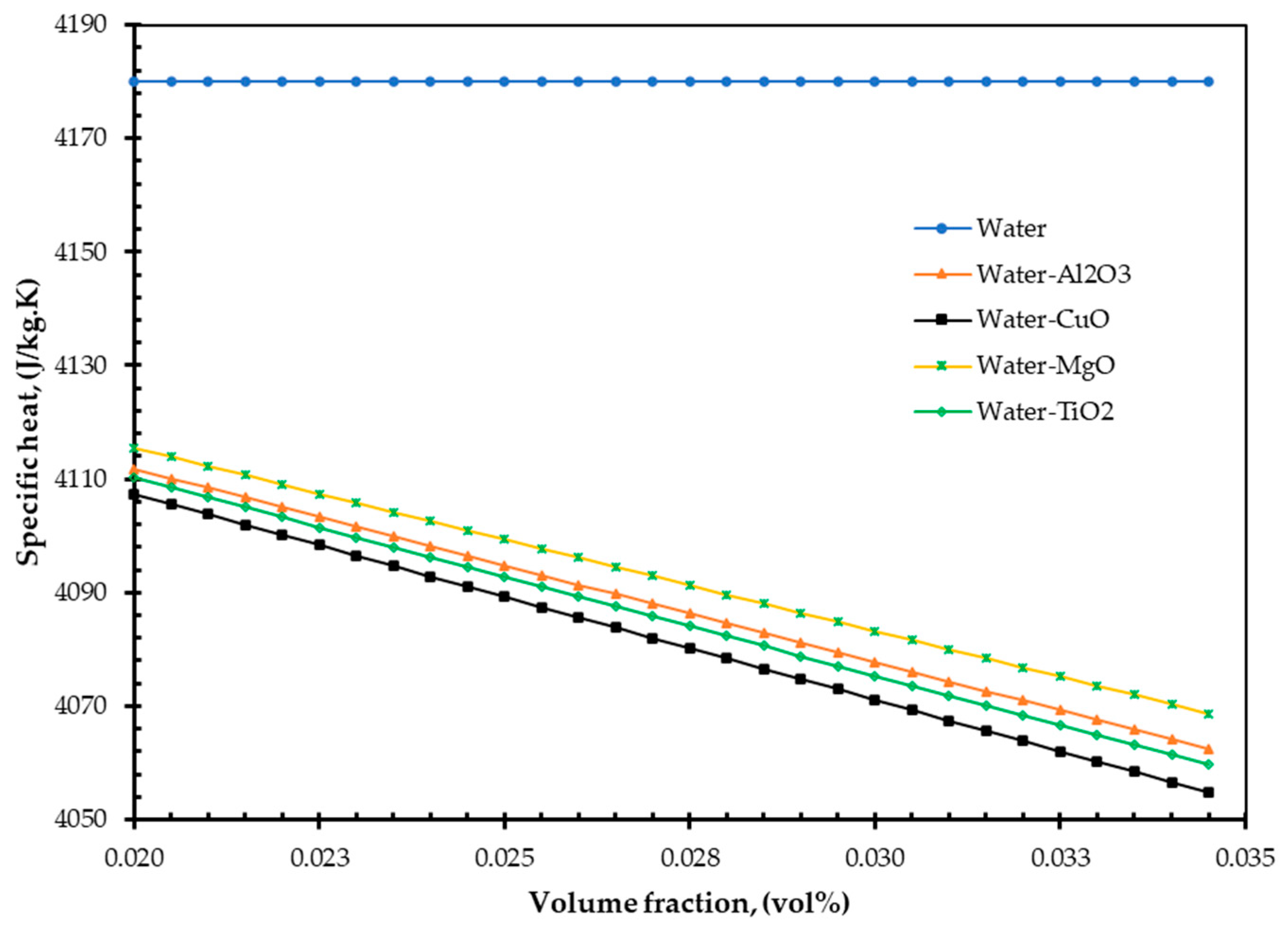
- As nanofluids replace water as an absorbing medium, the nanofluids’ viscosity, density, and TC increase, but its specific heat decreases compared to the base fluid (water). Interestingly, these findings are in agreement with those of Pandey et al. [50].
- ✓
- To gain exergy, the entropy generation number is typically expected to decrease. The entropy generation number decreases when nanofluids are used as agent fluids [51].
- ✓
- With an increase in particle concentration, the heat transfer rate is increased [56].
5. Conclusions
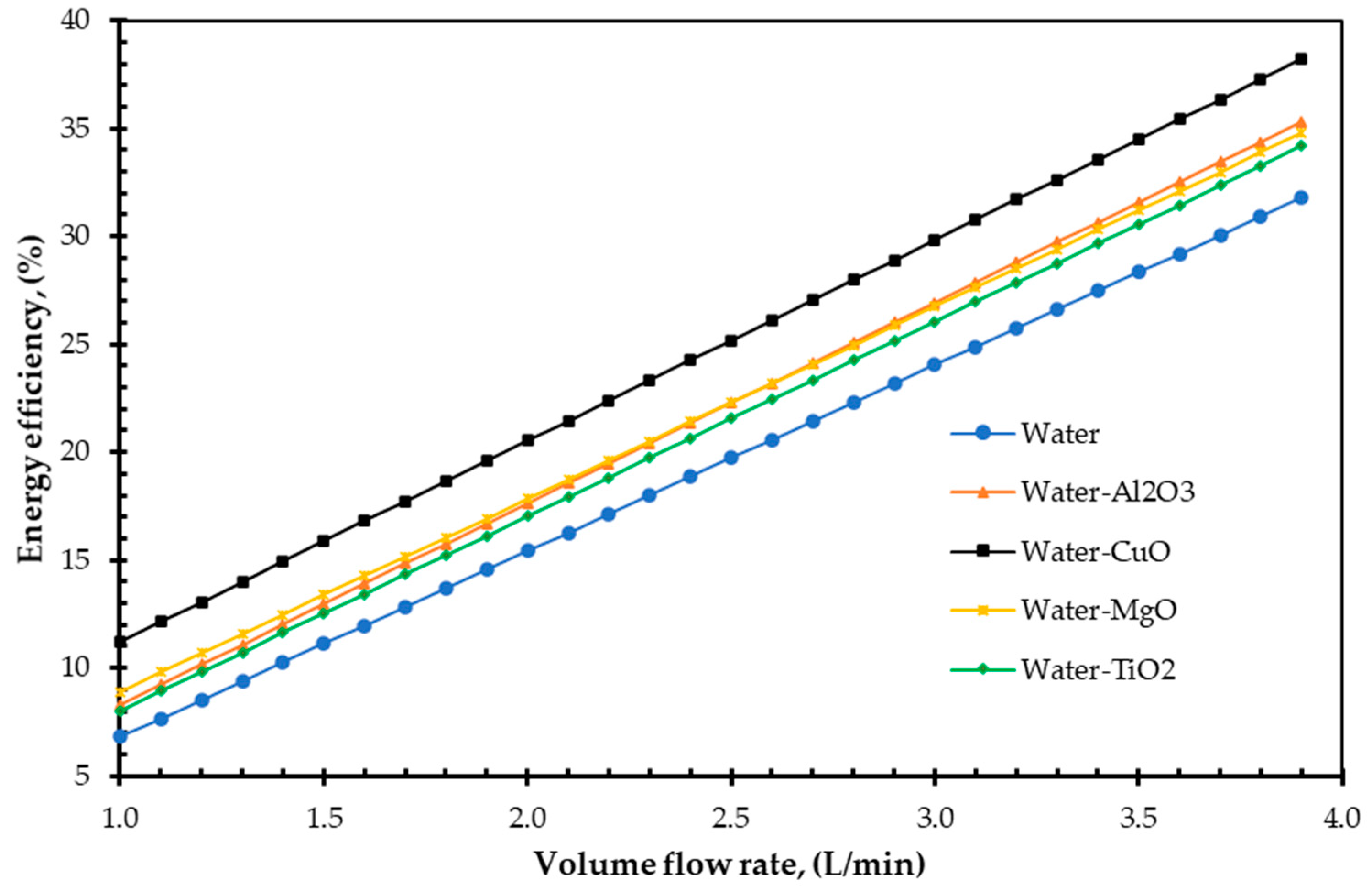
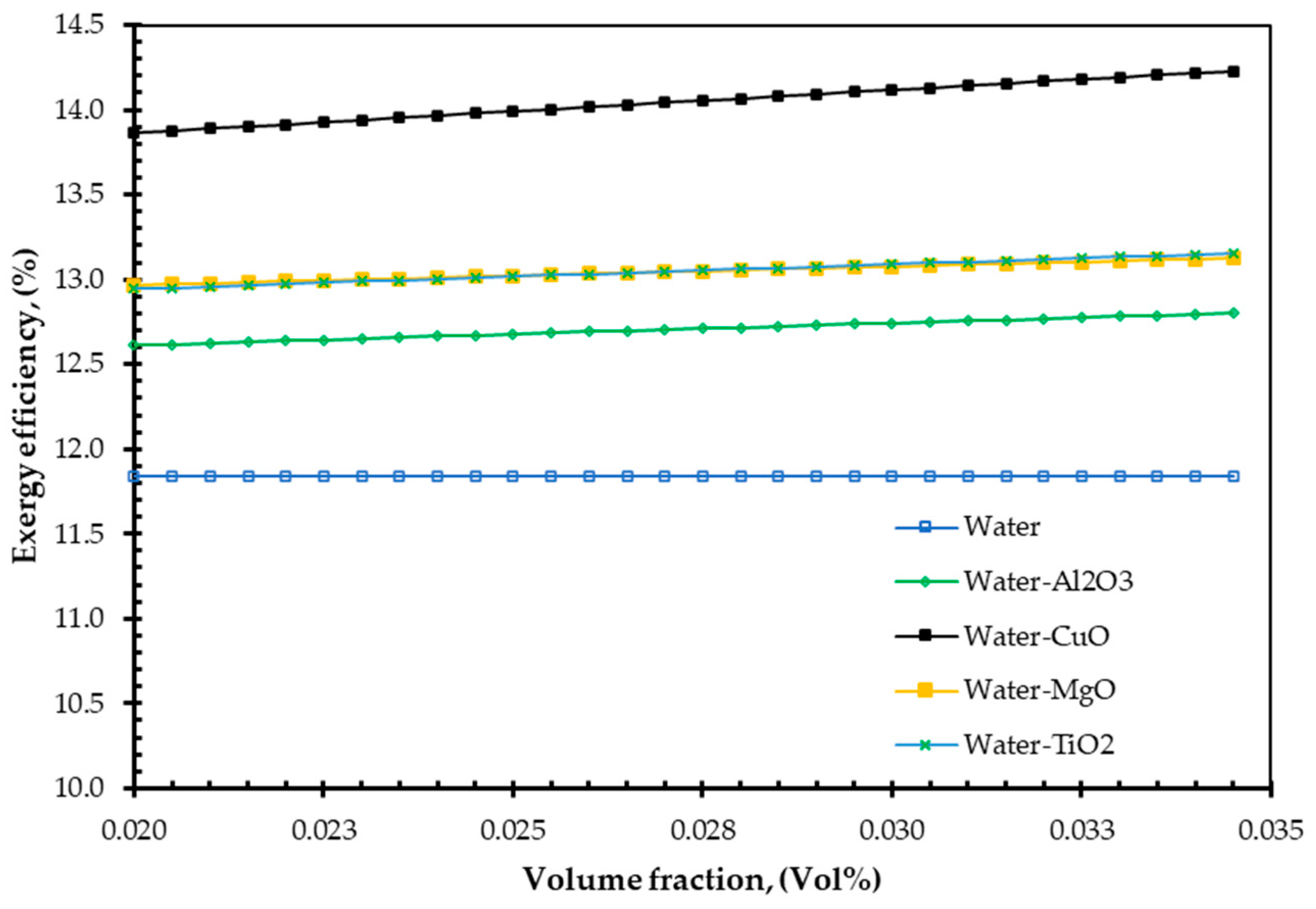
- The analytical result shows CuO nanofluid increased the EnE efficiency of a FPSC by 38.21% and 14.86%, respectively.
- Additionally, the study demonstrated that increasing volume fraction, mass flow rate, and density could improve EnE efficiency. Whenever the volume flow rate remains constant, the mass flow rate can be increased by adding nanoparticles into the base fluid, which has higher efficiency. Specific heat is one of the essential parameters for efficiency improvement. By reducing the specific heat of a fluid, the efficiency of a FPSC can be improved. It is simple to do so by suspending a small number of nanoparticles.
- CuO nanofluid is a better option for increasing both the EnE efficiency of FPSC.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Ap | absorption area, m2 |
| Cp | specific heat, J/kg·K |
| e | exergy loss |
| exergy gain rate per unit area, W/m2 | |
| FR | heat removal factor |
| F’ | collector efficiency factor |
| g | gravitational acceleration, m/s2 |
| IT | incident solar energy per unit area, W/m2 |
| k | heat conductivity, W/m·K |
| ṁ | mass flow rate, kg/s |
| P | mechanical power, W |
| thermal energy rate, W | |
| energy gain rate, W | |
| s | entropy per unit mass, J/kg·K |
| S | absorbed irradiation, W/m2 |
| T | temperature, K |
| Tc | absorber plate temperature, K |
| U1 | overall heat loss, W/m2 K |
| V | volume flow rate, L/min |
| z | height from reference level, m |
| EnE | energy and exergy |
| FPSC | flat plate solar collector |
| DAC | directive solar collector |
| CNT | carbon nanotube |
| TC | Thermal conductivity |
| ηEn | energy efficiency |
| ηEx | exergy efficiency |
| ηo | optical efficiency |
| τ | transmittance |
| α | absorptance |
| φ | nanoparticles volume fraction, % |
| ρ | density, kg/m3 |
| σ | overall entropy production, J/kg·K |
| Subscript | |
| a | ambient |
| bf | base fluid |
| dest | destruction |
| fin | inlet fluid |
| fout | outlet fluid |
| np | nanoparticles |
| nf | nanofluid |
References
- Dziadik, P.C. Solar energy collection system and components. Google Patents Patent No. US 8,173,888B2, 8 May 2012. [Google Scholar]
- Mahian, O.; Kianifar, A.; Kalogirou, S.A.; Pop, I.; Wongwises, S. A review of the applications of nanofluids in solar energy. Int. J. Heat Mass Transf. 2013, 57, 582–594. [Google Scholar] [CrossRef]
- Kostić, L.T.; Pavlović, Z.T. Optimal position of flat plate reflectors of solar thermal collector. Energy Build. 2012, 45, 161–168. [Google Scholar] [CrossRef]
- Otanicar, T.P. Direct Absorption Solar Thermal Collectors Utilising Liquid-Nanoparticle Suspensions; Arizona State University: Tempe, AZ, USA, 2009. [Google Scholar]
- Yousefi, T.; Shojaeizadeh, E.; Veysi, F.; Zinadini, S. An experimental investigation on the effect of pH variation of MWCNT–H2O nanofluid on the efficiency of a flat-plate solar collector. Sol. Energy 2012, 86, 771–779. [Google Scholar] [CrossRef]
- Wang, X.-Q.; Mujumdar, A.S. Heat transfer characteristics of nanofluids: A review. Int. J. Therm. Sci. 2007, 46, 1–19. [Google Scholar] [CrossRef]
- Xuan, Y.; Li, Q. Heat transfer enhancement of nanofluids. Int. J. Heat Fluid Flow 2000, 21, 58–64. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab.: Lemont, IL, USA, 1995. [Google Scholar]
- Fotukian, S.; Esfahany, M.N. Experimental investigation of turbulent convective heat transfer of dilute γ-Al2O3/water nanofluid inside a circular tube. Int. J. Heat Fluid Flow 2010, 31, 606–612. [Google Scholar] [CrossRef]
- Natarajan, E.; Sathish, R. Role of nanofluids in solar water heater. Int. J. Adv. Manuf. Technol. 2009, 1–5. [Google Scholar] [CrossRef]
- Tyagi, H.; Phelan, P.; Prasher, R. Predicted efficiency of a low-temperature nanofluid-based direct absorption solar collector. J. Sol. Energy Eng. 2009, 131, 041004. [Google Scholar] [CrossRef]
- Yousefi, T.; Veysi, F.; Shojaeizadeh, E.; Zinadini, S. An experimental investigation on the effect of Al2O3–H2O nanofluid on the efficiency of flat-plate solar collectors. Renew. Energy 2012, 39, 293–298. [Google Scholar] [CrossRef]
- Otanicar, T.P.; Golden, J.S. Comparative environmental and economic analysis of conventional and nanofluid solar hot water technologies. Environ. Sci. Technol. 2009, 43, 6082–6087. [Google Scholar] [CrossRef]
- Otanicar, T.P.; Phelan, P.E.; Prasher, R.S.; Rosengarten, G.; Taylor, R.A. Nanofluid-based direct absorption solar collector. J. Renew. Sustain. Energy 2010, 2, 033102. [Google Scholar] [CrossRef] [Green Version]
- Ziyadanogullari, N.B.; Yucel, H.; Yildiz, C. Thermal performance enhancement of flat-plate solar collectors by means of three different nanofluids. Therm. Sci. Eng. Prog. 2018, 8, 55–65. [Google Scholar] [CrossRef]
- Said, Z.; Saidur, R.; Rahim, N. Energy and exergy analysis of a flat plate solar collector using different sizes of aluminium oxide based nanofluid. J. Clean. Prod. 2016, 133, 518–530. [Google Scholar] [CrossRef]
- Said, Z.; Saidur, R.; Sabiha, M.; Hepbasli, A.; Rahim, N. Energy and exergy efficiency of a flat plate solar collector using pH treated Al2O3 nanofluid. J. Clean. Prod. 2016, 112, 3915–3926. [Google Scholar] [CrossRef]
- Sundar, L.S.; Singh, M.K.; Punnaiah, V.; Sousa, A.C. Experimental investigation of Al2O3/water nanofluids on the effectiveness of solar flat-plate collectors with and without twisted tape inserts. Renew. Energy 2018, 119, 820–833. [Google Scholar] [CrossRef]
- Hawwash, A.; Rahman, A.K.A.; Nada, S.; Ookawara, S. Numerical investigation and experimental verification of performance enhancement of flat plate solar collector using nanofluids. Appl. Therm. Eng. 2018, 130, 363–374. [Google Scholar] [CrossRef]
- Moghadam, A.J.; Farzane-Gord, M.; Sajadi, M.; Hoseyn-Zadeh, M. Effects of CuO/water nanofluid on the efficiency of a flat-plate solar collector. Exp. Therm. Fluid Sci. 2014, 58, 9–14. [Google Scholar] [CrossRef]
- Genc, A.M.; Ezan, M.A.; Turgut, A. Thermal performance of a nanofluid-based flat plate solar collector: A transient numerical study. Appl. Therm. Eng. 2018, 130, 395–407. [Google Scholar] [CrossRef]
- Nasrin, R.; Alim, M. Semi-empirical relation for forced convective analysis through a solar collector. Sol. Energy 2014, 105, 455–467. [Google Scholar] [CrossRef]
- Shojaeizadeh, E.; Veysi, F.; Kamandi, A. Exergy efficiency investigation and soptimisation of an Al2O3–water nanofluid based Flat-plate solar collector. Energy Build. 2015, 101, 12–23. [Google Scholar] [CrossRef]
- Kiliç, F.; Menlik, T.; Sözen, A. Effect of titanium dioxide/water nanofluid use on thermal performance of the flat plate solar collector. Solar Energy 2018, 164, 101–108. [Google Scholar] [CrossRef]
- Said, Z.; Sabiha, M.; Saidur, R.; Hepbasli, A.; Rahim, N.A.; Mekhilef, S.; Ward, T. Performance enhancement of a flat plate solar collector using titanium dioxide nanofluid and polyethylene glycol dispersant. J. Clean. Prod. 2015, 92, 343–353. [Google Scholar] [CrossRef]
- Jouybari, H.J.; Saedodin, S.; Zamzamian, A.; Nimvari, M.E.; Wongwises, S. Effects of porous material and nanoparticles on the thermal performance of a flat plate solar collector: An experimental study. Renew. Energy 2017, 114, 1407–1418. [Google Scholar] [CrossRef]
- Faizal, M.; Saidur, R.; Mekhilef, S.; Hepbasli, A.; Mahbubul, I. Energy, economic, and environmental analysis of a flat-plate solar collector operated with SiO2 nanofluid. Clean Technol. Environ. Policy 2015, 17, 1457–1473. [Google Scholar] [CrossRef] [Green Version]
- Meibodi, S.S.; Kianifar, A.; Niazmand, H.; Mahian, O.; Wongwises, S. Experimental investigation on the thermal efficiency and performance characteristics of a flat plate solar collector using SiO2/EG–water nanofluids. Int. Commun. Heat Mass Transf. 2015, 65, 71–75. [Google Scholar] [CrossRef]
- Cengel, Y.A.; Boles, M.A. Thermodynamics: An Engineering Approach 6th Editon (SI Units); The McGraw-Hill Companies, Inc.: New York, NY, USA, 2007. [Google Scholar]
- Saidur, R.; BoroumandJazi, G.; Mekhlif, S.; Jameel, M. Exergy analysis of solar energy applications. Renew. Sustain. Energy Rev. 2012, 16, 350–356. [Google Scholar] [CrossRef]
- Farahat, S.; Sarhaddi, F.; Ajam, H. Exergetic soptimisation of flat plate solar collectors. Renew. Energy 2009, 34, 1169–1174. [Google Scholar] [CrossRef]
- Alim, M.A.; Abdin, Z.; Saidur, R.; Hepbasli, A.; Khairul, M.A.; Rahim, N.A. Analyses of entropy generation and pressure drop for a conventional flat plate solar collector using different types of metal oxide nanofluids. Energy Build. 2013, 66, 289–296. [Google Scholar] [CrossRef]
- Ge, Z.; Wang, H.; Wang, H.; Zhang, S.; Guan, X. Exergy Analysis of Flat Plate Solar Collectors. Entropy 2014, 16, 2549–2567. [Google Scholar] [CrossRef]
- Akram, N.; Sadri, R.; Kazi, S.; Zubir, M.N.M.; Ridha, M.; Ahmed, W.; Soudagar, M.E.M.; Arzpeyma, M. A comprehensive review on nanofluid operated solar flat plate collectors. J. Therm. Anal. Calorim. 2020, 139, 1309–1343. [Google Scholar] [CrossRef]
- Zayed, M.; Zhao, J.; Du, Y.; Kabeel, A.; Shalaby, S. Factors affecting the thermal performance of the flat plate solar collector using nanofluids: A review. Sol. Energy 2019, 182, 382–396. [Google Scholar] [CrossRef]
- Said, Z.; Hachicha, A.A.; Aberoumand, S.; Yousef, B.A.; Sayed, E.T.; Bellos, E. Recent advances on nanofluids for low to medium temperature solar collectors: Energy, exergy, economic analysis and environmental impact. Prog. Energy Combust. Sci. 2021, 84, 100898. [Google Scholar] [CrossRef]
- Alawi, O.A.; Kamar, H.M.; Mallah, A.; Mohammed, H.A.; Kazi, S.; Sidik, N.A.C.; Najafi, G. Nanofluids for Flat Plate Solar Collectors: Fundamentals and Applications. J. Clean. Prod. 2020, 291, 125725. [Google Scholar] [CrossRef]
- Henning, H.-M. Solar Air Conditioning and Refrigeration. Task 38 of the IEA (International Energy Agency) Solar Heating and Cooling Program. Available online: http://lmora.free.fr/task38/pdf/matin/Henning.pdf (accessed on 10 May 2011).
- Xuan, Y.; Roetzel, W. Conceptions for heat transfer correlation of nanofluids. Int. J. Heat Mass Transf. 2000, 43, 3701–3707. [Google Scholar] [CrossRef]
- Zhou, S.-Q.; Ni, R. Measurement of the specific heat capacity of water-based Al2O3 nanofluid. Appl. Phys. Lett. 2008, 92, 093123. [Google Scholar] [CrossRef]
- Struckmann, F. Analysis of a Flat-Plate Solar Collector. 2008. Available online: http://www.ht.energy.lth.se/fileadmin/ht/Kurser/MVK160/Project_08/Fabio.pdf (accessed on 10 May 2021).
- Sukhatme, S.P.; Nayak, J. Solar Energy; McGraw-Hill Education: New York, NY, USA, 2017. [Google Scholar]
- Luminosu, I.; Fara, L. Determination of the optimal operation mode of a flat solar collector by exergetic analysis and numerical simulation. Energy 2005, 30, 731–747. [Google Scholar] [CrossRef]
- Sarhaddi, F.; Farahat, S.; Ajam, H.; Behzadmehr, A. Exergetic performance assessment of a solar photovoltaic thermal (PV/T) air collector. Energy Build. 2010, 42, 2184–2199. [Google Scholar] [CrossRef]
- Suzuki, A. A fundamental equation for exergy balance on solar collectors. J. Sol. Energy Eng. 1988, 110, 102–106. [Google Scholar] [CrossRef]
- Jafarkazemi, F.; Ahmadifard, E. Energetic and exergetic evaluation of flat plate solar collectors. Renew. Energy 2013, 56, 55–63. [Google Scholar] [CrossRef]
- Jeter, S.M.; Stephens, J.H. Systems and methods of thermal energy storage and release. Google Patents Patent No. US 2012/0132398 A1, 31 May 2012. [Google Scholar]
- Bejan, A. Entropy Generation through Heat and Fluid Flow; Wiley: New York, NY, USA, 1982; Volume 1. [Google Scholar]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Pandey, S.D.; Nema, V. Experimental analysis of heat transfer and friction factor of nanofluid as a coolant in a corrugated plate heat exchanger. Exp. Therm. Fluid Sci. 2012, 38, 248–256. [Google Scholar] [CrossRef]
- Moghaddami, M.; Mohammadzade, A.; Esfehani, S.A.V. Second law analysis of nanofluid flow. Energy Convers. Manag. 2011, 52, 1397–1405. [Google Scholar] [CrossRef]
- Amini, M.; Kianifar, A. An Analytical Study on Energy and Exergy of a Minichannel-Based Solar Collector Using Fe3O4 and MgO/Water Nanofluids. In Proceedings of the International Conference on researches in Science and Engineering, Istanbul, Turkey, 28 July 2016. [Google Scholar]
- Verma, S.K.; Tiwari, A.K.; Chauhan, D.S. Experimental evaluation of flat plate solar collector using nanofluids. Energy Convers. Manag. 2017, 134, 103–115. [Google Scholar] [CrossRef]
- Elcioglu, E.B.; Genc, A.M.; Karadeniz, Z.H.; Ezan, M.A.; Turgut, A. Nanofluid figure-of-merits to assess thermal efficiency of a flat plate solar collector. Energy Convers. Manag. 2020, 204, 112292. [Google Scholar] [CrossRef]
- Stalin, P.M.J.; Arjunan, T.; Matheswaran, M.; Dolli, H.; Sadanandam, N. Energy, economic and environmental investigation of a flat plate solar collector with CeO2/water nanofluid. J. Therm. Anal. Calorim. 2020, 139, 3219–3233. [Google Scholar] [CrossRef]
- Lelea, D. The performance evaluation of Al2O3/water nanofluid flow and heat transfer in microchannel heat sink. Int. J. Heat Mass Transf. 2011, 54, 3891–3899. [Google Scholar] [CrossRef]
- Kamyar, A.; Saidur, R.; Hasanuzzaman, M. Application of Computational Fluid Dynamics (CFD) for nanofluids. Int. J. Heat Mass Transf. 2012, 55, 4104–4115. [Google Scholar] [CrossRef]
- Sohel, M.R.; Saidur, R.; Sabri, M.F.M.; Kamalisarvestani, M.; Elias, M.M.; Ijam, A. Investigating the heat transfer performance and thermophysical properties of nanofluids in a circular micro-channel. Int. Commun. Heat Mass Transf. 2013, 42, 75–81. [Google Scholar] [CrossRef]
- Hamilton, R.L.; Crosser, O.K. Thermal Conductivity of Heterogeneous Two-Component Systems. Ind. Eng. Chem. Fundam. 1962, 1, 187–191. [Google Scholar] [CrossRef]
- Duangthongsuk, W.; Wongwises, S. Heat transfer enhancement and pressure drop characteristics of TiO2–water nanofluid in a double-tube counter flow heat exchanger. Int. J. Heat Mass Transf. 2009, 52, 2059–2067. [Google Scholar] [CrossRef]
- Xuan, Y.; Li, Q. Investigation on Convective Heat Transfer and Flow Features of Nanofluids. J. Heat Transf. 2003, 125, 151–155. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Jin, Y.; Chen, H.; Ding, Y.; Cang, D.; Lu, H. Heat transfer and flow behaviour of aqueous suspensions of TiO2 nanoparticles (nanofluids) flowing upward through a vertical pipe. Int. J. Heat Mass Transf. 2007, 50, 2272–2281. [Google Scholar] [CrossRef]
- Faizal, M.; Saidur, R.; Mekhilef, S. Potential of size reduction of flat-plate solar collectors when applying MWCNT nanofluid. IOP Conf. Ser. Earth Environ. Sci. 2013, 16, 012004. [Google Scholar] [CrossRef]

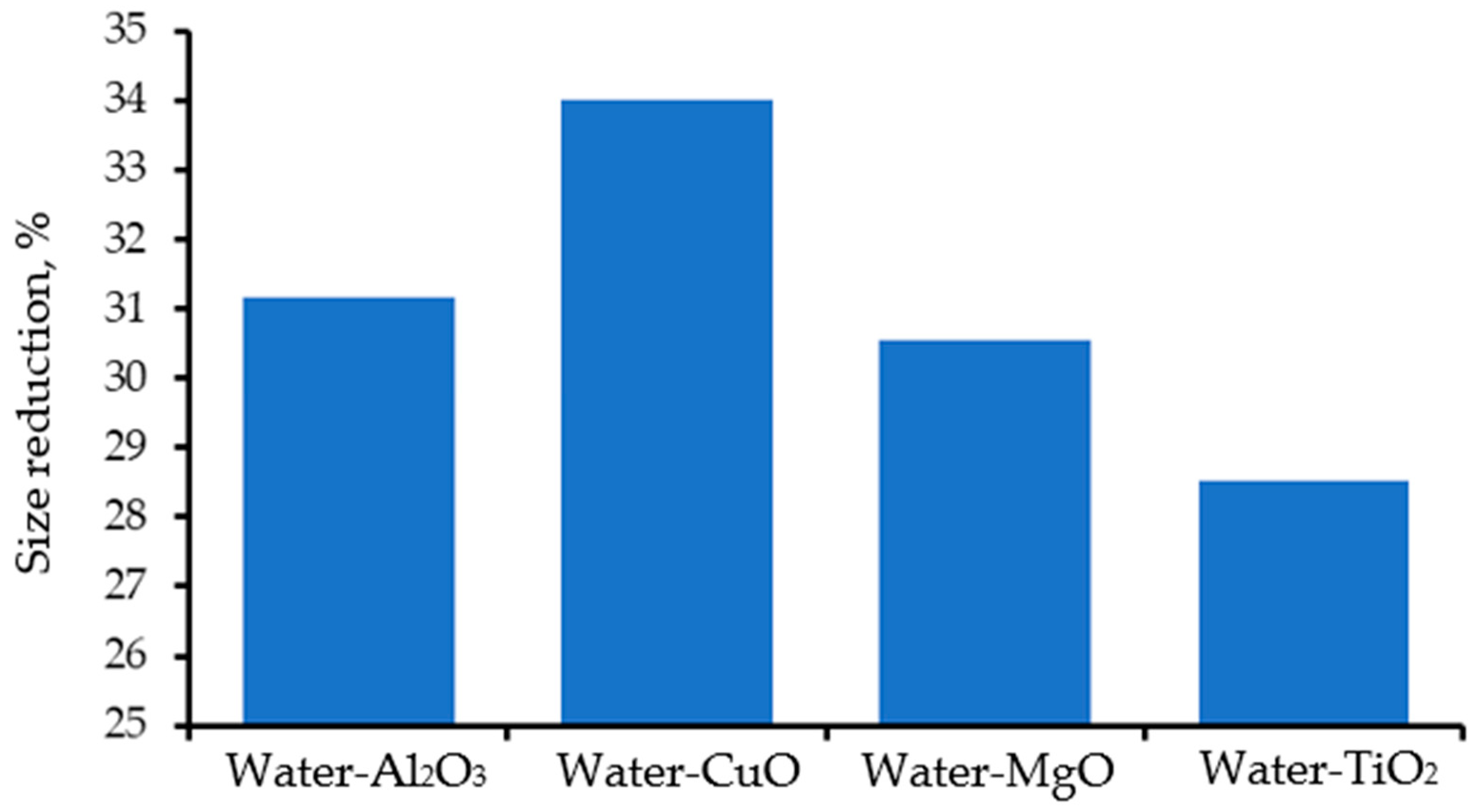
| References | Model | Base Fluid | Nanoparticles’ Specification | Optimum Parameters | |||||
|---|---|---|---|---|---|---|---|---|---|
| Particle Name | Volume Fractions (Vol %) | Size (nm) | Mass Flow Rate (kg/min) | Improvement of Efficiency (%) | Flow Regime | FPSC Surface Area (m2) | |||
| Sundar et al. [18] | Experimental | Water | Al2O3 | 0.1 and 0.3 | 20 | 5 | 18 | Turbulent | 2 |
| Hawwash et al. [19] | Experimental and Numerical (CFD ansys fluent) | DW | Al2O3 | 0.1 and 0.3 | 20 | 5.51 | 18 | Turbulent | 2.1 |
| Mogahadam et al. [20] | Experimental | Water | CuO | 0.4 | 40 | 1 | 21.8 | Laminar | 1.88 |
| Genc et al. [21] | Numerical (Matlab) | Water | Al2O3 | 0.1, 0.2 and 0.3 | 3.6 | 9.5 | Laminar | 1.99 | |
| Nasrin and Alim [22] | Experimental | DW | Al2O3, CuO and TiO2 | 0.2, 0.4 and 0.8 | 50, 50 and 25 | 4 | 71, 87.8 and 52.5 | Laminar | 1.51 |
| Shojaeizadeh et al. [23] | Experimental and Numerical | DI water | Al2O3 SDBS | 0.090696, 0.094583, 0.10293, 0.11057, 0.117686, 0.1244, 0.13082, 0.137, and 0.1423 | 15 | 2.5 | 70 | Turbulent | 1.51 |
| Kilic et al. [24] | Experimental | Water | TiO2 Triton X-100 | 0.2 | 44 | 2 | 34.43 | Turbulent | 1.82 |
| Said et al. [25] | Experimental | PEG-400 | TiO2 | 0.1 and 0.3 | 21 | 0.5 | 76.6 | Laminar | 1.84 |
| Jouybari et al. [26] | Experimental | Water | SiO2 | 0.2, 0.4, and 0.6 | 7 | 1.5 | 8 | Laminar | 0.8 |
| Faizal et al. [27] | Experimental | Water | SiO2 | 0.2, 0.4, and 0.6 | 10 | 3 | 23.5 | Turbulent | 2 |
| Meibodi et al. [28] | Experimental | EG–water | SiO2 | 0.5, 0.75, and 1 | 10 | 2.7 | 8 | Turbulent | 1.59 |
| Nanoparticles | Specific Heat, Cp (J/kg·K) | Thermal Conductivity, k (W/m·K) | Density, ρ (kg/m3) |
|---|---|---|---|
| Alumina (Al2O3) | 773 | 40 | 3960 |
| Copper oxide (CuO) | 551 | 33 | 6000 |
| Titanium oxide (TiO2) | 692 | 8.4 | 4230 |
| Magnesium oxide (MgO) | 955 | 45 | 3560 |
| Water (H2O), base fluid | 4182 | 0.60 | 997 |
| Solar Collector Type | Optical Efficiency, ηo | Overall Heat Loss, U1 (W/m2 K) | Collector Efficiency Factor, F′ |
|---|---|---|---|
| Evacuated tube | 0.47 | 1.1 | 0.99 |
| Flat plate | 0.82 | 5.0 | 0.97 |
| Parameters of Collector | Value |
|---|---|
| Type | Black paint flat plate |
| Glazing | Single glass |
| Agent fluids | Water, Al2O3, MgO2, TiO2 and CuO nanofluids |
| Absorption area (m2) | 1.44 |
| Wind speed (m/s) | 20 |
| Collector till (°) | 20 |
| Fluid inlet and ambient temperature (K) | 300 |
| Apparent sun temperature (K) | 4350 |
| Optical efficiency | 84% |
| Emissivity of the absorber plate | 0.95 |
| Emissivity of the covers | 0.90 |
| Glass thickness (mm) | 4 |
| Insulation TC (W/m∙K) | 0.06 |
| Incident solar energy per unit area of the absorber plate (W/m2) | 500 |
| Inner diameter of pipes (m) | 0.005 |
| Absorbing Medium | Maximum ηEn Enhancement, (%) | Maximum ηEx Enhancement, (%) | ||
|---|---|---|---|---|
| φ = 2% and Diff. Volume Flow Rate | φ = 3.20% and V = 1 L/s | φ = 2% and V = 2.40 L/s | φ = 3.20% and V = 1 L/s | |
| CuO nanofluid | 38.21 | 16.80 | 14.86 | 11.45 |
| TiO2 nanofluid | 34.17 | 9.25 | 12.64 | 9.70 |
| MgO nanofluid | 34.77 | 9.71 | 12.56 | 9.53 |
| Al2O3 nanofluid | 35.32 | 9.18 | 11.11 | 9.35 |
| Tf, in or Ta, (k) | IT, (W/m2) | S, (W/m2) | ΔT, (K) | ηEx, (%) | |
|---|---|---|---|---|---|
| Present analysis (CuO) | 300.00 | 500 | 420 | 62.00 | 3.35 |
| Alim et al. [32] | 300.00 | 1000 | 500 | 63.00 | 3.72 |
| Luminosu and Fara [43] | 305.15 | 788 | 580 | 46.00 | 2.90 |
| Farahat and Sarhaddi [31] | 300.00 | 500 | 420 | 58.82 | 2.95 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mostafizur, R.M.; Rasul, M.G.; Nabi, M.N. Energy and Exergy Analyses of a Flat Plate Solar Collector Using Various Nanofluids: An Analytical Approach. Energies 2021, 14, 4305. https://doi.org/10.3390/en14144305
Mostafizur RM, Rasul MG, Nabi MN. Energy and Exergy Analyses of a Flat Plate Solar Collector Using Various Nanofluids: An Analytical Approach. Energies. 2021; 14(14):4305. https://doi.org/10.3390/en14144305
Chicago/Turabian StyleMostafizur, R. M., M. G. Rasul, and M. N. Nabi. 2021. "Energy and Exergy Analyses of a Flat Plate Solar Collector Using Various Nanofluids: An Analytical Approach" Energies 14, no. 14: 4305. https://doi.org/10.3390/en14144305
APA StyleMostafizur, R. M., Rasul, M. G., & Nabi, M. N. (2021). Energy and Exergy Analyses of a Flat Plate Solar Collector Using Various Nanofluids: An Analytical Approach. Energies, 14(14), 4305. https://doi.org/10.3390/en14144305






