Influence of Spray Nozzle Operating Parameters on the Fogging Process Implemented to Prevent the Spread of SARS-CoV-2 Virus

Abstract

This article reports the results of a study into the effect of operating parameters on the occurrence and course of gas–liquid two-phase phenomena during the fogging process carried out with the use of a conical pressure-swirl nozzle. Four alternatives of the stub regulation angles and four values of pressure of air supply to the nozzle were tested as part of the current research. The range of the investigated variables was common for the operation of fumigators used to prevent the spread of SARS-CoV-2 virus. The liquid flow rate (weighting method), the field of velocity, and turbulent flow intensity factor, as well as velocity profiles over the section of 1 m from the nozzle were determined using the particle image velocimetry (PIV) technique. The obtained results were correlated with the measurements of the diameters of spray droplets using the laser light scattering (LLS) technique. On the basis of this research, a dependence between the nozzle parameters and the spray cone pattern was identified in terms of dynamics and droplet diameter distribution. As a result of the research, a wide range of parameters were identified in which the fogging process was carried out in a stable and repeatable manner. There were exceptions to this rule only in the cases when there was a deficiency of the liquid necessary to generate a two-phase mixture.

1. Introduction

For many years, the study and research of aspects related to disinfection processes, with the goal of protection against biological agents spreading through the atmospheric air, has played a complementary role in many fields of science, e.g., medicine, occupational safety, space, and electronics industry. Only recently, as a result of the increase in terrorist threats [1] and the ongoing SARS-CoV-2 coronavirus pandemic, have they become an exceptionally important and independent area of research. The significant demand for effective, quick, and easily implemented methods of disinfecting physical surfaces and atmospheric air has resulted in an increase in the activity carried out in this area. Recent studies indicate that the SARS-CoV-2 virus is able to persist on utility surfaces for up to several weeks [2,3,4]. One of the processes that can lead to preventing the spread of this pathogen is associated with the fogging process (also called fumigation), which belongs to the category of gas–liquid two-phase processes. Fogging for decontamination purposes has been utilized for many years, but it has gained even greater interest in the current epidemic situation.

The majority of the available publications on the use of the fogging process relate directly to the evaluation of the effects of decontamination. Research has been undertaken with the use of various substances, e.g., paracetic acid [5,6,7], chlorine dioxide [8,9,10], and hydrogen peroxide [7]. The study reported in [11] involved aspects related to a comparison of several substances applied for this purpose: sodium hypochlorite, acidic electrolytic water, benzalkonium chloride, and glutaral, and focused on areas related to the efficiency of disinfection of various surfaces. The research [6,7] also analyzed the effect of fogging on various surfaces (walls, floors, components of subway cars), and in work [3], a large-scale application of fumigation in the urban space affecting spaces in the environment was proposed. The literature also includes many items describing the use of fogging for disinfecting medical masks and protective clothing in fumigation rooms or lodging facilities [12,13,14,15,16]. A noteworthy publication is the study by Villermaux [17], which is a very detailed analysis of atomization mechanisms.

Spray distribution tests during the fumigation process are much less frequently undertaken. In this respect, there is a noticeable scarcity of knowledge that needs to be supplemented with publications that extend to areas beyond the fogging process. Such publications mostly concern processes of the same nature, e.g., fuel spraying [18,19,20,21,22], water spray processes as part of fire protection systems [23,24], as well as issues related to ventilation and air conditioning [25]. Such studies often are concerned with the questions related to the maldistribution of air, which forms an important indication of the directions of disinfectant spray distribution in the enclosed space where the fumigation process is carried out. Research into air fogging technology for the purposes of mosquito control offers interesting input from the point of view of the fogging process [26]. The study analyzed in detail the distribution of droplet diameters for three types of nozzles depending on the pressure of the disinfectant supplied to the system. The tests were carried out in a wind tunnel generating air circulation (54 m/s and 63 m/s) simulating the recommended velocity of displacement of the aircraft from which the fogging process is carried out. The droplet size distribution was compared, and the results indicated the need to control the dimensions of the droplets and their strong correlation with the velocity of their displacement, as this directly translates into the effectiveness of the process.

Among the measurement methods used for assessing the spray dispersion process, in particular in terms of droplet dynamics and geometry, optical methods based on laser techniques are often utilized [27]. A derivative of this method is offered by the particle image velocimetry (PIV) technique, since its practical value in the field of spraying two-phase gas–liquid mixtures has been demonstrated in many publications. Husted et al. [28] used the PIV and phase Doppler anemometry (PDA) techniques to compare the performance of the full cone nozzle with the hollow cone nozzle. This study demonstrated that both methods make it possible to perform reliable measurements of spray and that the nozzle geometry significantly shapes the behavior of the droplets. They also determined the distance traveled by the droplets to reach the velocity of the surrounding air (0.01 m for small droplets, e.g., with a diameter of 10 µm, and 0.2 m for large droplets with a diameter close to 70 µm). The study reported in [29] also contained an analysis of the dependence of the velocity and diameter of the droplets. In addition, considerations included the relationship between the geometric pattern of the cone formed by the spray and the ratio of saturation pressure relative to ambient pressure, the occurrence of recirculation phenomena, and secondary formation of small droplets as a result of micro-explosions were identified and described. The changes in the spray angle depending on the rheological properties of the fluid feeding the conical pressure-swirl atomizer were also investigated in [30]. Other studies in this area, such as [31,32], contained results of research concerned with the effect of the nozzle outlet diameter on the spray characteristics.

The majority of research related to flow phenomena involving the generation of spray reported in the literature relates to studies carried out in the conditions of industrial processes. Although such studies focus on aspects that play an important role from the point of view of the fogging process, due to the significant differences in the applied pressures, projected droplet diameters, as well as their velocities, cannot be directly used in the optimization of the fogging process. On the other hand, publications directly relating to the medical application of fogging focus on the assessment of the end effects of the process and do not consider the selection of geometric and flow parameters that play particular roles for application in multi-phase systems. Therefore, in the literature on the subject, there is the already mentioned lack of knowledge in the field of assessing and flow optimization of nozzles used to implement the process, which in the current pandemic situation has become extremely important in preventing the spread of SARS-CoV-2 virus. Therefore, the aim of the study involves an attempt to describe flow phenomena for selected flow and geometric parameters of conical pressure-swirl nozzle used in electrofumigators available on the market. The research was based on the analysis of velocity fields and spray particle size distributions, taking into account the assessment of the maximum spray velocity behind the nozzle, the maximum spray velocity at a distance of 1 m from the nozzle outlet, maldistribution of the spray, turbulent flow intensity factor, and the degree of reduction of the spray velocity.

2. Materials and Methods

2.1. Spray Nozzle and Research Assumptions

The experimental tests were carried out for the conical pressure-swirl nozzle (Figure 1) mounted in the BARTEK model 2 electrofumigator (Marcin Mróz Research and Development Laboratory, Brzeg, Poland). The diameter of the nozzle outlet orifice was 1.45 mm.

The spray distribution investigations were conducted on the basis of the application of PIV and Laser Light Scattering (LLS) techniques to select the optimal geometric and flow parameters. The measurement methodology assumed testing the velocity distribution and the diameter of the spray generated by the nozzle for the following variable parameters:

-

pressure P at the supply to the system (from 3 to 6 bar with a 1-bar interval), which corresponded with air flowrates 1.29 m³/h, 1.4 m³/h, 1.49 m³/h, 1.56 m³/h, respectively

-

Reynolds number calculated for the liquid in the nozzle orifice was in the range from 705 to 5677.

-

liquid regulating nozzle length (25.56 mm, 25.8 mm, 25.95 mm, and 26.1 mm), which corresponded to the angles of rotation α of the stub regulating the flow by −90°, −45°,0°, and 45°, respectively. The tests using the LLS technique applied only to the last three positions of the control stub.

The tests were carried out in a room with a controlled temperature (t_o = 21 °C). Demineralized water was applied as the liquid phase in the research. The variations in atmospheric pressure during the tests did not exceed 0.25%, therefore, variations in this parameter were not taken into account in the further analysis.

2.2. Measurements of the Velocity Distribution of Spray Droplets

The PIV technique applied in the research offers the means for non-invasive analysis of the spray flow velocity in terms of values and for the determination of its spatial differentiation. The spatial distribution of velocity was visualized by means of a vector and scalar velocity field, which provided input for further analysis. The velocity measurement using the PIV method is based on determining the displacement between two sets of pixels that correspond to spray droplet size distribution on consecutive images recorded at a known time interval Δt [33,34]. During this part of the experiment, the spray droplets play the role of seeding particles identified in subsequent images. As a result of dividing the images into smaller measurement areas, for each area selected in this manner, the mean displacement of the droplets in the x and y directions can be determined. By correlating the displacements with the time Δt, it is possible to determine the velocities u = Δx/Δt as well as v = Δy/Δt, which form the basis for determining the resultant aerosol velocity V defined as $\sqrt{u^2+v^2}$. The idea of the PIV measurement was also presented in the studies in this area reported in the literature [35,36]. In addition, the paper [37] presents a comparison of PIV computational algorithms for a gas–liquid two-phase systems.

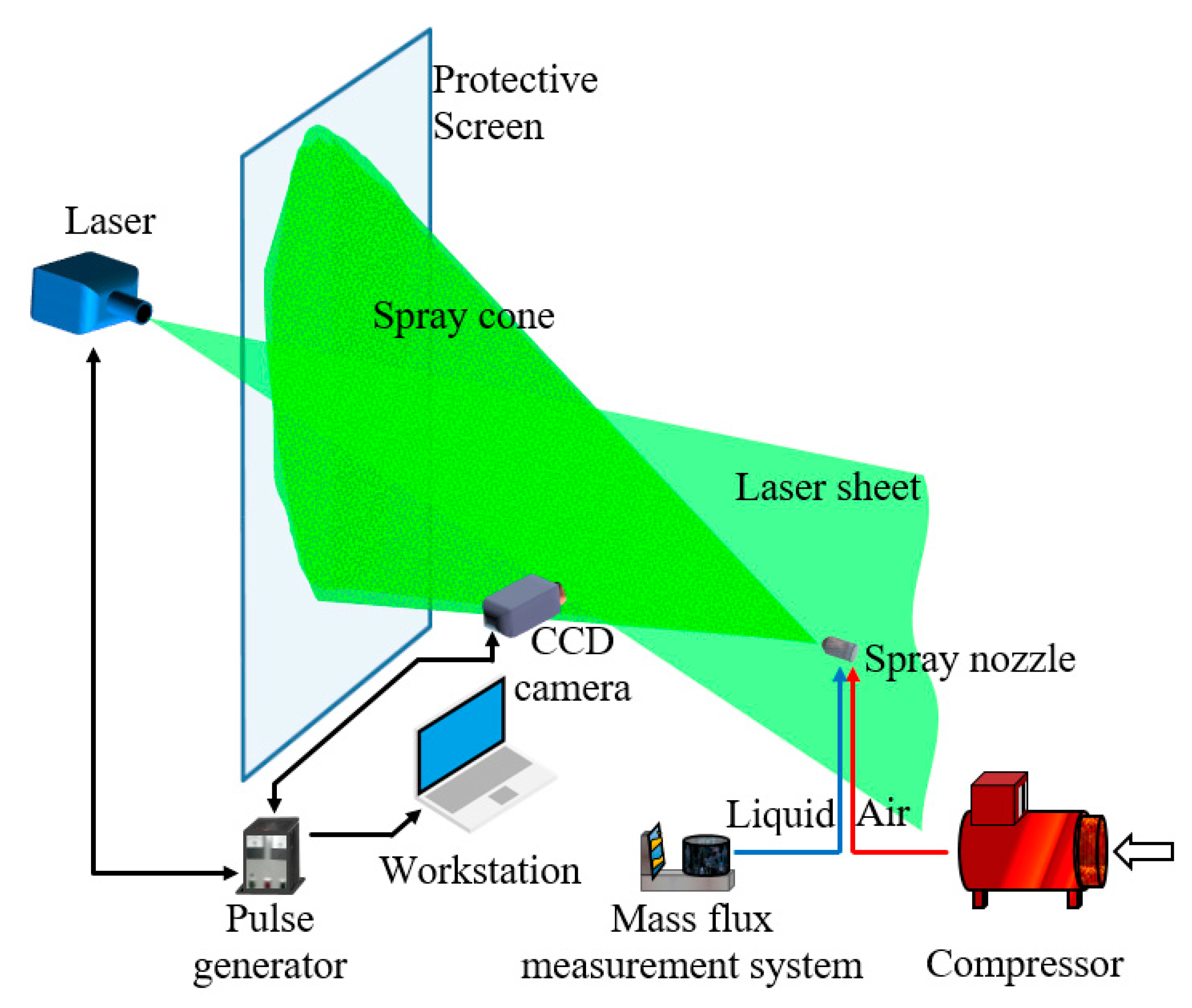
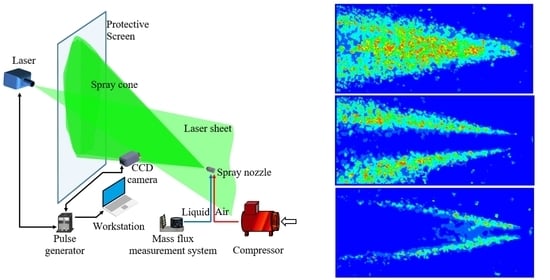
The experimental setup applied for testing spray dynamics (Figure 2) consisted of a conical pressure-swirl nozzle, a nozzle supply system, a liquid tank, a compressor, a protective screen, a PIV system, a workstation for data acquisition and processing. The optical measurement path of the PIV system consisted of a Dantec Dynamics FlowSense EO 4M CCD camera (Dantec Dynamics, Skovlunde, Denmark) that was located perpendicular to the plane of the laser light generated by the Nd: YAG Dantec Dynamics DualPower TR laser (Dantec Dynamics, Skovlunde, Denmark) and applied the so-called optical knife technique. In order to protect the laser placed in front of the nozzle, a screen made of highly transparent polymethylene methacrylate was used. The Berkeley Nucleonics Corp Model 575-8 pulse generator (Berkeley Nucleonics Corporation, San Rafael, CA, USA) was responsible for laser and camera synchronization. The liquid to generate the spray was supplied automatically from the measuring vessel under the influence of compressed air supply into the nozzle. The supply system with a pressure regulator was responsible for the distribution and maintenance of constant flow conditions of the compressed air. The list of the elements applied in the experimental setup was standard for testing of the compressed air nozzles utilizing the PIV technique. A similar method of configuring the test stand was also presented in [28,38,39,40]. A detailed specification of the equipment used during the measurements is presented in

Table 1. Summary of basic parameters of the experimental and measurement setup.

No.	Device	Description
1	Laser	Producer/model: Dantec Dynamics/DualPower TR Maximum pulse energy: 1200 mJ Pulse duration: 4 ns Light wavelength: 532 nm
2	Camera CCD	Producer/model: Dantec Dynamics/FlowSense EO 4M Matrix type: CCD Frequency of registration: 9.33 Hz Mode of action: double frame Resolution: 2048 × 2048 pixels
3	Pulse generator	Producer: Barkley Nucleonic/MD1567 Time between pulse: 17 µs
4	Compressor	Producer/model: Metabo/Elektra Beckum HP 7.5 Operating pressure: 8 bar
5	Workstation	Producer/model: Dell/Precision T5820 Work environment: Dantec Dynamics Dynamic Studio 7.1

.

The measurement domain was selected so as to include the area necessary to determine the spray velocity profile, including the 1 m long section from the outlet of the nozzle. Due to the too high concentration of particles, the initial 0.03 m of the length was not taken into account in the further analysis. The tests included a series of 200 images recorded in double frame mode with a frequency of 9.33 Hz and time between pulses of 17 µs, which corresponded to a measurement series duration of 21.4 s. This time was also used to average the measured parameters. The operation of determining the displacement Δx and Δy required input of any characteristic dimension in the measurement area recorded with the camera. In the tests that were conducted, the dimension necessary to determine the shift scale was determined during optical calibration of the system with the use of a standard target. For the analysis of the derivatives of velocity components u and v, their mean values were utilized that could have been derived on the basis of vector averaging of all velocity fields in a given series. Based on the average velocity fields, scalar maps of turbulent flow intensity factor T_i = uv were determined. The possibility to use this parameter to evaluate the level of flow turbulence is a result of a very strong correlation of the T_i parameter with the changes in flow directions visualized by the streamlines, as shown in Figure 3. An increase in the value of the T_i parameter in a given area reflects a change in flow direction and, in consequence, a local increase in turbulence.

Velocity profiles were determined along the axis of symmetry of the nozzle over a section of 1 m from its outlet (excluding the already remarked initial 0.03 m sections due to the limitations of the measurement method). Additionally, auxiliary velocity profiles were plotted on the scalar velocity maps in the planes perpendicular to the main axis of the nozzle symmetry in the form of vectors visualizing the direction of the spray flow.

In the conducted research, the recording time interval resulted directly from the frequency characteristics of the camera and the time between pulses of double frame image pairs. The implementation of the determination of vector velocity fields focused on carrying out measurements at established air pressures for each of the investigated nozzle geometries. The performed visualization analysis can be divided into the following stages:

-

an experiment enabling the registration of flow images,

-

pre-processing of recorded images,

-

final PIV analysis,

-

visualization of measurement results.

All steps of the analysis were conducted by application of the Dantec Dynamics Dynamic Studio 7.1 suite (Dantec Dynamics, Skovlunde, Denmark).

Figure 4 contains a block diagram that demonstrates the individual stages of the computational methodology applied for assessing spray dynamics using the PIV technique.

2.3. Droplet Size Measurement

The setup designed for testing the distribution of the droplet size (Figure 5) consisted of two modules: a module for controlling the operational parameters of the process and a measurement module. The components of the system were: a tank storing the sprayed liquid (1 dm³), a Metabo Mega 350-100D compressor (Metabo Polska Sp. z.o.o., Stargard, Poland), a Spraytec analyzer by Malvern Instruments (Malvern Instruments Ltd., Malvern, United Kingdom), and a computer containing SOP software suite. The Spraytec measuring apparatus was applied for the determination of the spray particle size, namely the particle size distribution. A 300 mm lens was selected for the purposes of these measurements because it is dedicated to spray with d_v50 diameters in the range of 0.1–900 µm. The key step in the measurement process was the creation of a standard measurement procedure (SOP). The value of the measurement time was defined on the basis of multiple observations of the test measurement as 40 s. To ensure the repeatability of the results, the samples were always sprayed from the same place, i.e., with a constant distance of the device outlet opening from the measurement zone, respectively: 0.25; 0.5; 0.75, and 1 m. The averaged test results were obtained in the conditions marked by the following settings: average scatter data and concentration-weighted average. The spray was distributed in the measuring zone through which the helium-neon laser beam passes between the transmitter and the receiver. The collimation optics was aimed at extending the laser beam so that a broad parallel beam was created. The laser light, disturbed by the flowing drops, was focused on the detector by application of the Fourier lens. The receiver comprised a system of detectors that provided the means for the detection of light scattering patterns on the emerging structures and their conversion into an electrical signal. The recorded signal was then analyzed using an appropriate optical model with the purpose of calculating the particle size distribution. The non-scattered light also hit the Fourier’s focusing lens and then passed through an opening in the center of the detector array. Similar experimental assumptions are presented in the paper [41].

The results were used for the analysis focused mainly on the volume to surface droplet diameter d₃₂, d_v50, and volume of droplets with a diameter smaller than 10 µm. The tests were carried out for three nozzle operating parameters, marked as α = −45°, α = 0°, α = 45° respectively, which corresponded to the length of the gas inlet stub pipe equal to: 25.8; 25.95 and 26.1 mm.

The volume-to-surface diameter of the droplet d₃₂ that is also known as Sauter Mean Diameter (SMD), is described by the equation below:

$$d_{32}=\frac{{{\displaystyle \sum }}_{i=1}^m{D}_i^3{n}_i}{{{\displaystyle \sum }}_{i=1}^m{D}_i^2{n}_i}$$

(1)

characterizes the diameter of a homogeneous equivalent set of the same total volume and the same total area of all droplets as in the real set [42]. In turn, the diameter d_v50 represents exactly 50% of the droplet distribution both in terms of mass, volume, and quantitatively [43].

3. Results

An important issue related to the operation of fogging systems is associated with the consumption of the liquid utilized to generate a spray in the fumigation system. In order to determine the liquid flow Q_L during the operation of the nozzle, the liquid flow was measured using the mass method (measurement uncertainty ± 1g/min) for each series of measurements. The ratios between air and liquid flowrates were between 0.002 and 0.015. The results are presented in Figure 6.

The liquid flow rate Q_L supplied from the tank increased with the pressure P for each of the settings of the control stub. The highest gradients of the liquid flow Q_L occurred in the range P = (3; 4) bar. Beyond the threshold of P = 4 bar, the increase in pressure did not lead to the rapid increase in the liquid flux Q_L. The maximum increase in the flow Q_L in the range P = (4; 6) bars was observed for α = −45°, and it was only 31.58% of the maximum increase in flux Q_L, observed in the range of P = (3–4) bar. Therefore, the conducted measurements demonstrated a significant impact of the variations in the geometrical parameters and the supply pressure P on the liquid consumption only in the low-pressure range P (from 3 to 4 bars). A slight increase in the liquid flow in the case of variations in the pressure P in the range (4 ÷ 6) bar may be attributable to hydrodynamic limitations resulting from the rapidly increasing pressure drops; however, confirmation of this thesis requires experimental verification.

3.1. Assessment of Dynamics of Spray Displacement

Due to the fact that the key role in determining the effectiveness of the fogging process is taken on by the homogeneity of the disinfected surface in terms of the disinfectant use, which in turn originates a consequence of the regular distribution of the disinfectant droplets in the form of a spray, the assessment of flow phenomena focused on identifying the occurrence of the desired, regular distribution of the velocity field V and the turbulent flow intensity factor T_i along the symmetry axis of the spray cone.

Table 2. Influence of pressure P supplying the nozzle on the character of velocity and turbulent flow intensity factor fields for stub regulation angle α = −90°.

P, Bar	Velocity Field	Turbulent Flow Intensity Factor
3
4
5
6

,

Table 3. Influence of pressure P supplying the nozzle on the character of velocity and turbulent flow intensity factor fields for stub regulation angle α = −45°.

P, Bar	Velocity Field	Turbulent Flow Intensity Factor
3
4
5
6

,

Table 4. Influence of pressure P supplying the nozzle on the character of velocity and turbulent flow intensity factor fields for stub regulation angle α = 0°.

P, Bar	Velocity Field	Turbulent Flow Intensity Factor
3
4
5
6

and

Table 5. Influence of pressure P supplying the nozzle on the character of velocity and turbulent flow intensity factor fields for stub regulation angle α = 45°.

P, Bar	Velocity Field	Turbulent Flow Intensity Factor
3
4
5
6

contain a summary of the results of the visualization of these parameters for selected nozzle operating settings.

On the basis of these tables, an assessment was made with regard to the effect of varying the geometric and flow parameters on the spray pattern generated by the nozzle. As it could have been predicted, the study confirmed that the increase in the supply pressure P has led to an increase in the velocity of the spray flow in the central section of the cone regardless of the angle α in the nozzle that regulates liquid inflow and, consequently, identification of diverse areas in the cone in terms of turbulent flow intensity factor (the decrease in the turbulent flow intensity factor T_i along with the increase in the flow velocity V). However, it was noted that for the angle α = −90°, the change in pressure P has a much greater impact on the formation of turbulence in the spray flow than in the other investigated cases. This phenomenon was related to the deficiency of the kinetic energy of droplet displacement (the effect of low droplet velocity), which provides the conditions for the development and intensification of diversified droplet distribution in terms of the direction that directly contributes to the formation of vortex structures in the entire cone volume. In this case, the smallest liquid output Q_L was noted. Thus, a distinct core with increased velocity was formed, which effectively limited the swirling motion of the droplets.

Even in the core of the cone, the low gas flow velocity was not sufficient to overcome obstacles in the form of numerous and regularly distributed fine vortices in the spray flux. Consequently, under these nozzle operational conditions, a cone pattern with a full and uniform intensity of turbulence was developed. In the case of setting the control stub in the position α = −90°, the increase in pressure P led to a dynamic development of the flow velocity in the cone core, with a simultaneous decrease in the superficial flow rate in the turbulent zone. Under these conditions, there was a transition of the full turbulent cone pattern to a half turbulent cone pattern. It was the result of a deficiency of the liquid applied for the generation of the spray in relation to the amount of air supplied to the nozzle. Such dynamic changes in the cone structure, as in the case of α = −90°, was no longer identified. In the remaining cases, the cone pattern with a similar turbulent flow intensity factor was not generated.

The setting of α = −45° was considered as the threshold. In such settings, for the pressure equal to P = 3 bars, the asymmetry of the turbulent cone pattern was observed, which was bound to occur as a consequence of the non-homogenous evolution of the spray core velocity. The increase in pressure eliminated this deficiency, therefore, for pressures P above 4 bar, the spray flow was considered effective. For larger stub regulation angles, the variations of the turbulent patterns in the spray cones were significantly less dynamic. The character of the cone assumed a dominantly symmetrical spatial pattern. Only a few areas of non-homogenous flow that were found were identified as asymmetrical areas determined by visualizations of turbulent flow intensity factor. The above observations indicate that the presence of a core with an increased flow velocity plays an important role in the formation of the homogenous spray cone. Around it, the spray flux stabilizes, and the growing turbulent layer is able to maintain homogeneity even at a great distance from the outlet of the nozzle.

In order to provide a comprehensive description of the two-phase phenomena in the spray, a summary of velocity profiles along the axis of symmetry of the nozzle was compiled (Figure 7). The analysis of the velocity profiles offered the possibility to identify such nozzle operational parameters that are characterized by an adverse course of the velocity curve in the field of distance from the nozzle outlet. In the fogging process, a high velocity of spray dissipation forms a desirable factor. The research was undertaken to verify the scale of the velocity reduction in the initial section of the spray cone formation, and the variations in the velocity value at a distance of 1 m from the nozzle outlet were determined. Among all the measurement series, the case of angle α = −90° could be identified as specific. The deficiency of the liquid phase identified in this case leads to a significant drop in the velocity already in the initial part of the spray cone. The greatest sensitivity of the droplet velocity to the variations of the supply pressure was also identified in this case. The differences between velocities in the individual series at a distance of 1 m from the nozzle outlet are as follows: 5.5 m/s, 2 m/s, and 1.4 m/s. In other cases, the variations in the supply pressure significantly affect only the velocity in the initial section of the spray cone. At a distance of 1 m from the nozzle outlet, the differences in velocity in relation to the supply pressure are small and additionally fluctuate from minimum to maximum values in the entire range of tested pressures (the gradient of the velocity discrepancy is not dependent on the supply pressure). The highest measured drop velocity at the nozzle outlet was recorded for the case of P = 6 bar and α = 45° (V = 91.8 m/s), while the highest velocity at a distance of 1 m from the nozzle outlet for the case of P = 6 bar and α = −90° (V = 9.52 m/s).

Throughout the experimental study, the effect of the nozzle operating configuration on velocity fluctuations was observed. To evaluate this phenomenon, an analysis of the root mean square (RMS) value of the spray velocity normalized by the superficial liquid velocity at the nozzle outlet was used. These parameters were determined for each measurement series (Figure 8). The largest velocity fluctuations were identified for nozzle settings that generate liquid phase deficit conditions (α = −90° and α = −45°), particularly for pressure P = 3. For the other α angle settings and higher P pressures responsible for the transition of the full turbulent cone pattern to a half turbulent pattern, the velocity fluctuations reached similar levels. These observations again confirm the unstable nature of nozzle operation at low α angles.

3.2. Assessment of Spray Droplet Diameters

Adequately implemented fogging processes require not only knowledge of the dynamic characteristics of spray droplets, but also information on the distribution of droplet diameters. This knowledge is necessary to fully assess the impact of the operational parameters used, which together must take into account the existence of a balance between the desired but sometimes mutually exclusive nozzle performance (e.g., minimizing droplet size and maximizing the distance of their distribution). In order to evaluate the evolution of the diameters of spray droplets depending on the tested operational parameters of the nozzle, Figure 9 demonstrates the dependence of the diameter d₃₂ on the gas pressure P, at the tested settings of the angle of the regulating stub α, at a distance from the nozzle outlet X = 500 mm. It was shown that an increase in the stub angle α contributes to the formation of droplets of smaller diameters. The tests conducted for α = 45° at higher pressures P = 5 and 6 bar did not yield any results, which was probably attributable to the too high a concentration of droplets in the spray.

When we adopt the point of view applied during disinfection processes or other processes such as nebulization or moisturizing, the effectiveness of which is relative to the surface of the interface between the liquid and a given surface, it is important to generate the smallest feasible droplet diameters. Therefore, it is beneficial for the fogging processes to maintain their operational parameters in the range that guarantees the formation of droplets with diameters equal to or below 5–10 µm. The research conducted in this regard (Figure 10) demonstrated that the volume ratio of droplets with such diameters decreased along with the increase in the distance from the nozzle, which could be attributed, e.g., to the evaporation of the smallest droplets during the distance that they displacement or—more likely—to the difference in the velocity of small and larger droplets by the smaller ones were not able to reach long distances, despite the high pressure of the gas flow. As a result, at the distance X = 1000 mm, mainly larger drops with higher kinetic energy were registered. As a result of increasing the gas pressure, a positive effect marked by the generation of the smallest drops was noted. The greater the pressure P, the greater was their volume fraction. From the point of view of the generation of sprays with droplets smaller than 10 micrometers, an increase in the pressure P from 5 to 6 bar seems to offer an adequate course of activity.

The results of the dependence of the mean droplet diameter d₃₂ on the distance from the outlet from the nozzle and on the supply pressure P are presented in Figure 11. The analysis of the resulting data demonstrates that with an increase in distance X, both droplet diameters (d₃₂ and d_v50) increase, and along with an increase in the supply pressure P, they tend to decrease. However, the procedure involving increasing the gas pressure P from 5 to 6 bar seems to be pointless as the differences in the diameters of the resulting droplets are insignificant.

Based on the obtained measurement results, the evolution of the turbulent flow intensity factor was also related to the volume-to-surface diameter of the droplet d₃₂ (see

Table 6. Correlation between d₃₂ diameter and turbulent flow intensity factor T_i.

α, °	Supply Pressure P, bar
	3		4		5		6
	d32, µm	Ti, m2/s2	d32, µm	Ti, m2/s2	d32, µm	Ti, m2/s2	d32, µm	Ti, m2/s2
−45	24	2.74	20	2.93	17	2.99	15,3	3.91
0	22	3.65	18	3.02	15.2	2.77	11.4	2.65
45	15.6	4.36	10	3.53	-	3.05	-	2.42

). It is shown that the diameter d₃₂ decreases with an increase in the turbulent flow intensity factor for a given angle α. This proves the active role of spray swirl motions in the droplet diameter distribution. The assumptions of the fogging process performed for decontamination of the SARS-CoV-2 virus indicate the necessity of maintaining a given concentration of disinfectant in a room for at least one hour. Due to the possibility of generated mist condensation, the selection of operating parameters of a nozzle should be correlated with parameters describing indoor climatic conditions (temperature, humidity, atmospheric pressure). In the majority of typical public buildings, for which the risk of condensation does not exist, increasing pressure P from 5 to 6 bar seems to be an appropriate procedure allowing for an increase in the volume fraction of droplets smaller than 10 µm. Regardless of the pressure P, the limiting angle α was considered to set at −45°. Smaller values of angle α negatively affect the quality of the fogging process.

4. Conclusions

In this study, an assessment was performed with regard to the effects of the variations in the pressure P of the gas supplying the nozzle and the geometrical settings of the stub pipe responsible for the feeding liquid Q_L on the flow phenomena occurring during the fogging process. An increase in the liquid flow Q_L was recorded in the conditions characterized by an increase in pressure P and regulation angle α, with the largest gradient Q_L observed in the range P = (3; 4) bar. Above the threshold of 4 bars, the increase in liquid feed rate was not equally rapid. In addition, the spray flow velocity increased following an increase in pressure P, for all investigated stub regulation angles α. The diversification of the spray velocity distribution in the volume of the cone led to the variations in the turbulent flow intensity factor, which, in turn, resulted in the formation of a cone with a semi-developed turbulent pattern in the conditions of the presence of increased droplet flow velocities in the cone core. This phenomenon was accompanied by numerous swirls and variations in the directions of droplet displacement. For the angle α = −90 and P = 3 bar (the lowest fluid flow Q_L), a cone with a fully developed turbulent pattern was observed. The setting characterized by α = −45 was considered as the threshold. In such conditions, combined with the pressure P = 3 bar, the asymmetry of the turbulent cone pattern was observed, which certainly originated as a result of the non-uniform evolution of the spray core velocity. The increase in pressure P eliminated this deficiency; therefore, for pressures P above 4 bar, the spray flow was considered effective with a dominant symmetrical pattern. For larger angles of the regulating stub α, the variations in the turbulent pattern were much less dynamic. The recorded velocity profiles demonstrated an increased sensitivity to the fluctuation of the geometric and flow parameters only for small distances X from the nozzle outlet. The influence of the pressure P on the resulting velocities in the final area of the determined profiles was noticeable but did not have significant effects on the process. The discrepancies in the velocity between individual pressures P ceased to exist, and random fluctuations in the velocity started to play an increasingly important role. The adopted range of the nozzle operation parameters was also reflected by the results of the measurements of droplet diameters. It was demonstrated that an increase in the angle α and an increase in pressure P contributed to the formation of smaller diameter droplets. On the other hand, an increase in the distance X from the nozzle outlet resulted in the identification of a smaller number of droplets with smaller diameters. If the main criterion determining the fogging process’ quality is related to the maximum volume of droplets smaller than 10 µm, increasing the pressure P from 5 to 6 bar seems to be an appropriate procedure. In other cases, such an increase in pressure P will not significantly affect the quality of the fogging process since the effect of reducing the total number of particles with diameters d₃₂ and d_v50 is small in this range.