Progresses in Analytical Design of Distribution Grids and Energy Storage
Abstract
:1. Introduction
2. Optimization Methods for Correct Placement of Renewable Distributed Generators
2.1. Analytical Techniques
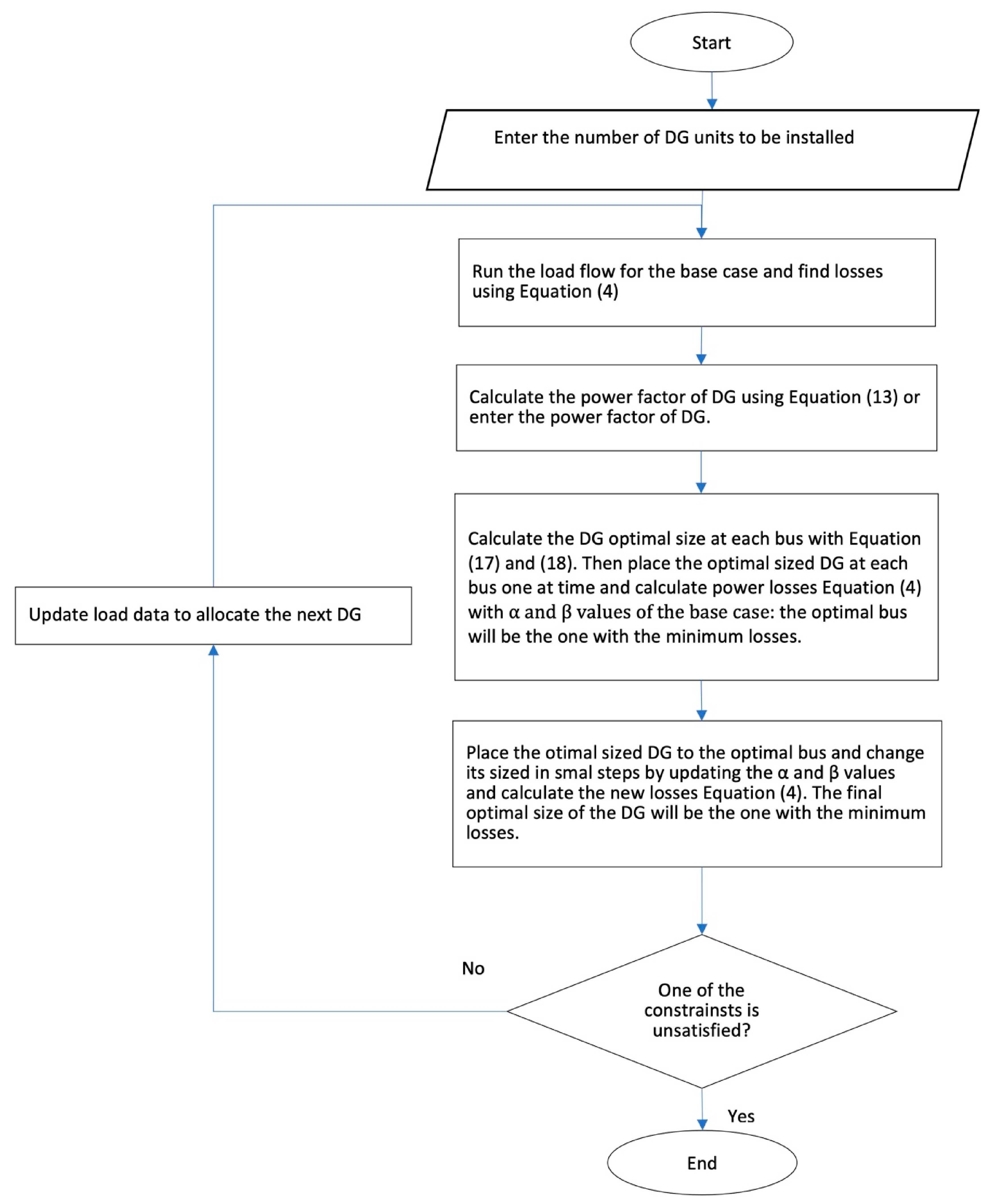
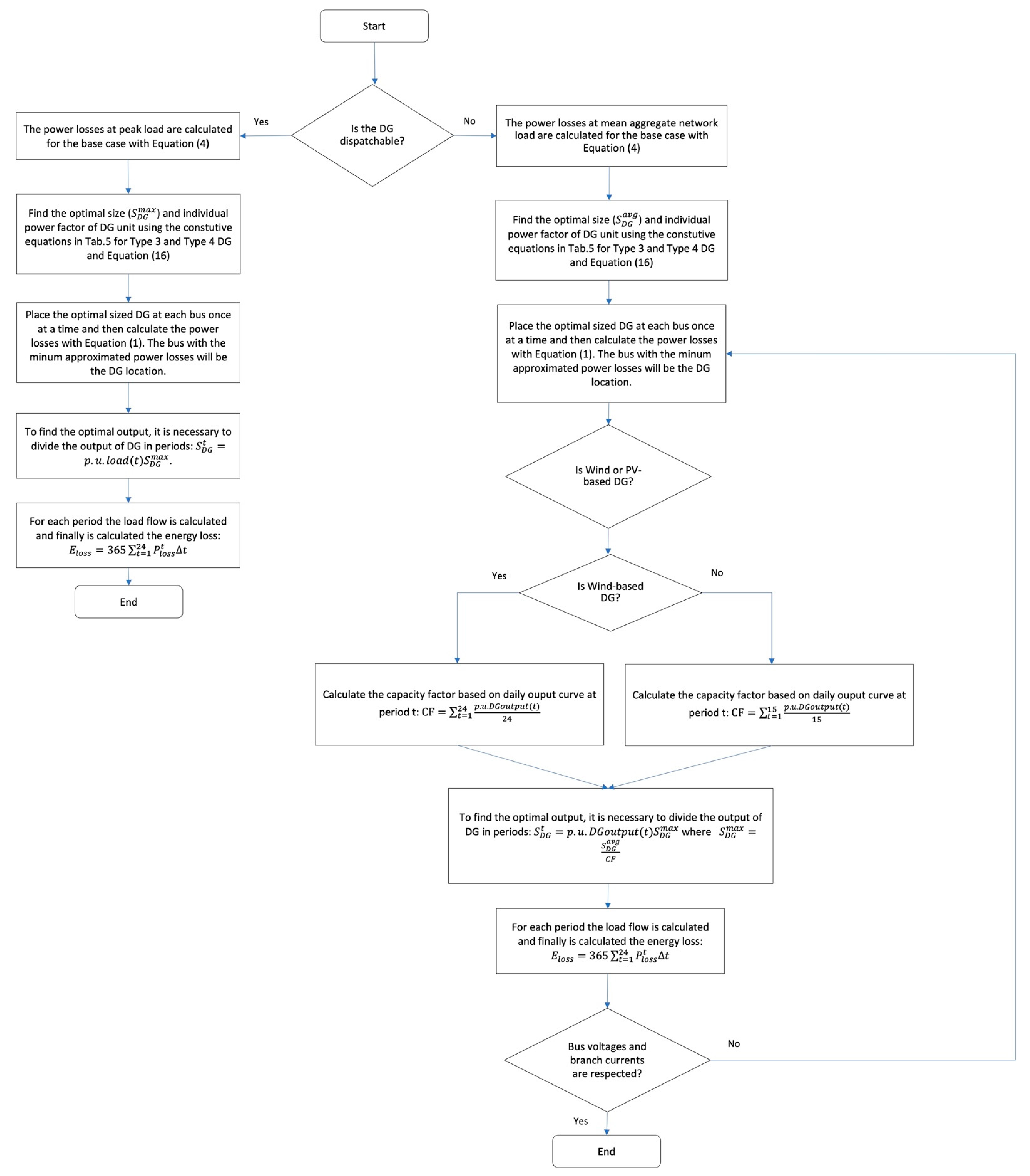
2.1.1. Exact Loss Formula
| Type 1 DG Injects Active and Reactive Power | Type 2 DF Injects Active and Consumes Reactive Power | Type 3 DG Injects Only Active Power | Type 4 DG Injects Reactive Power |
|---|---|---|---|
| The constitutive equations are the same of Type 1 generators, the only difference is in (Equation (20)). For DG absorbing reactive power |
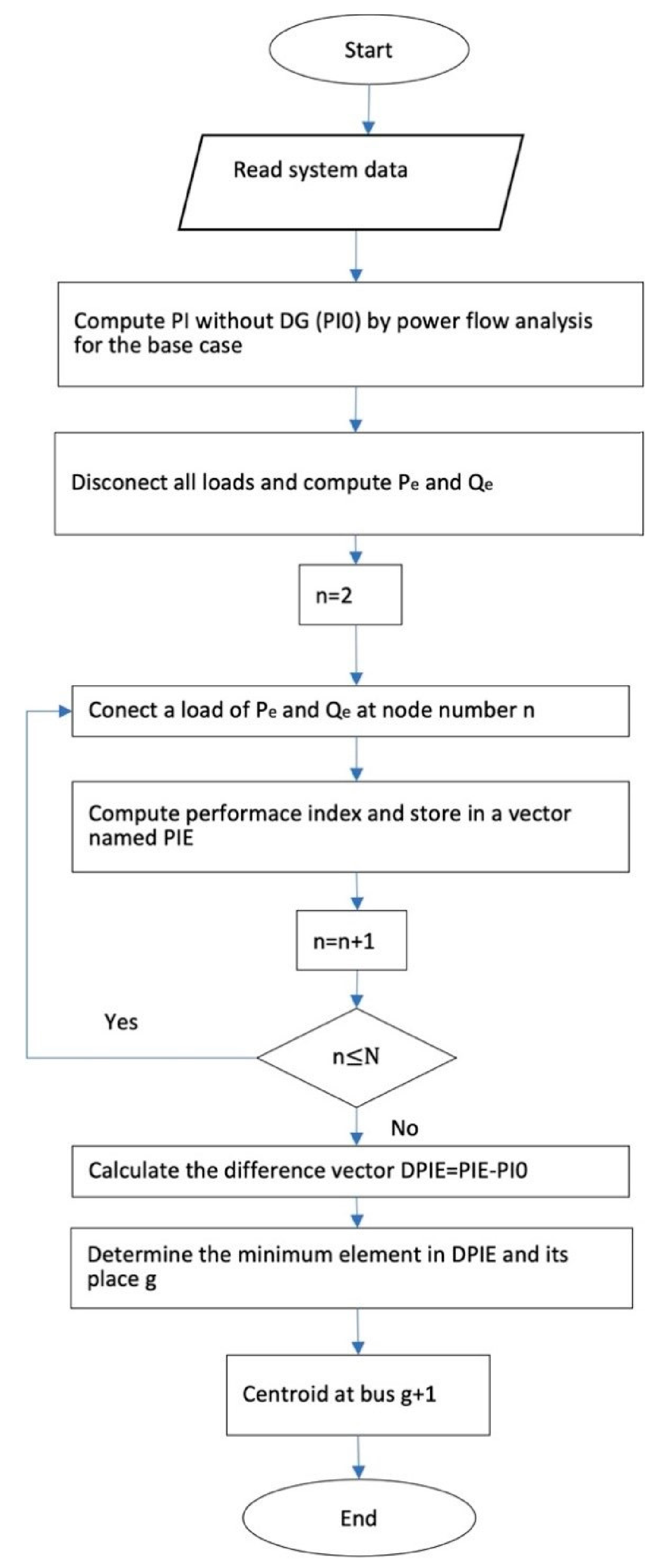
2.1.2. Loss Sensitivity Factor
2.2. Optimal Power Flow
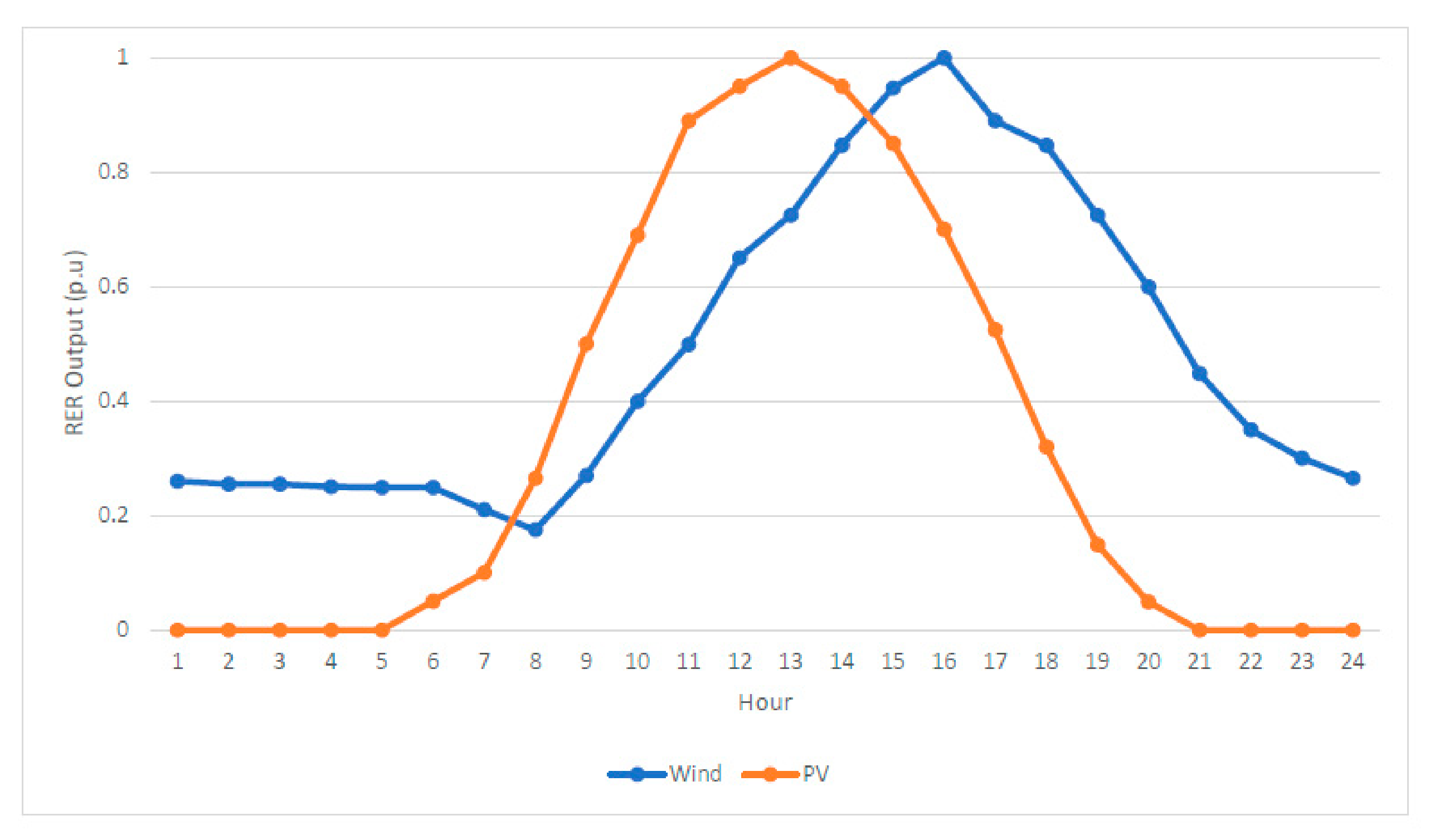
2.3. Numerical Results
3. Energy Storage Systems
3.1. Compressed Air Energy Storage
3.2. Thermal Energy Storage
3.3. Hydrogen Storage
3.4. Comparison of ESS
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BDG | Branches that the DG generated power passes through |
| CAES | Compressed Air Energy Storage |
| CES | Chemical Energy Storage |
| CP | Collapse point of the voltage [Volt] |
| CSP | Concentrated Solar Plant |
| DGs | Distributed Generators |
| DNO | Distribution Network Operators |
| EH | Energy Hub |
| ESS | Energy Storage Systems |
| HS | Hydrogen Storage |
| IEA | International Energy Agency |
| OF | Objective Function |
| OPF | Optimal Power Flow |
| PCMs | Phase Change Materials |
| PHES | Pumped Hydro Energy Storage |
| PV | Photovoltaic |
| RER | Renewable Energy Resources |
| TCES | Thermochemical Energy Storage |
| TES | Thermal Energy Storage |
| Symbols | |
| C | specific Heat Capacity [J/(kg K)] |
| voltage angles at bus i [rad] | |
| ∆h | height difference [m] |
| ∆T | temperature difference [K] |
| E | energy [J] |
| g | gravity acceleration [m/s2] |
| Iai | active current at the bus i [Ampere] |
| Iri | reactive current at the bus i [Ampere] |
| λ | loading parameter |
| m | mass [kg] |
| N | total branches number |
| NDG | number of distributed generators |
| NB | number of busses |
| Load active power increment directions of loads in the CPF [W] | |
| Load active power at base case [W] | |
| Active power demand at bus i [W] | |
| Optimal active power capacity of DG at bus i [W] | |
| Active power injection at bus i [W] | |
| total active power losses [W] | |
| Power Factor | |
| Load active power increment directions of loads in the CPF [VA] | |
| Load active power at base case [VA] | |
| Reactive power demand at bus i [W] | |
| Reactive Power injection at bus i [W] | |
| resistance between bus i and j [Ohm] | |
| voltage magnitude at bus i [Volt] | |
References
- United Nations (UN). Adoption of the Paris Agreement e Framework Convention on Climate Change. 2015. Available online: https://unfccc.int/resource/docs/2015/cop21/eng/l09r01.pdf (accessed on 28 September 2016).
- Masson-Delmotte, V.; Zhai, P.; Pörtner, H.O.; Roberts, D.; Skea, J.; Shukla, P.R.; Pirani, A.; Moufouma-Okia, W.; Péan, C.; IPCC; et al. (Eds.) Global Warming of 1.5 °C. An IPCC Special Report on the Impacts of Global Warming of 1.5 °C above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; IPCC: Geneva, Switzerland, 2018. [Google Scholar]
- IEA. Global Energy Review 2019; IEA: Paris, France, 2020; Available online: https://www.iea.org/reports/global-energy-review-2019 (accessed on 3 December 2020).
- IEA. World Energy Outlook 2017; IEA: Paris, France, 2017; Available online: https://www.iea.org/reports/world-energy-outlook-2017 (accessed on 1 September 2019).
- Zubo, R.; Mokryani, G.; Rajamani, H.-S.; Aghaei, J.; Niknam, T.; Pillai, P. Operation and planning of distribution networks with integration of renewable distributed generators considering uncertainties: A review. Renew. Sustain. Energy Rev. 2017, 72, 1177–1198. [Google Scholar] [CrossRef] [Green Version]
- Distributed Generation in Liberalized Electricity Market. IEA Publication. 2002. Available online: http://www.iea.org/dbtw-wpd/text-base/nppdf/free/2000/distributed2002.pdf (accessed on 10 October 2019).
- Barker, P.P.; De Mello, R.W. Determining the impact of distributed generation on power systems: Part 1—Radial distribution systems. In Proceedings of the 2000 Power Engineering Society Summer Meeting, Seattle, WA, USA, 16–20 July 2000; pp. 1645–1656. [Google Scholar]
- Jenkins, N.; Allan, R.; Crossley, P.; Kirschen, D.; Strbac, G. Embedded Generation; The Institution of Electrical Engineers: London, UK, 2000. [Google Scholar]
- Walling, R.A.; Saint, R.; Dugan, R.C.; Burke, J.; Kojovic, L.A. Summary of distributed resources impact on power delivery systems. IEEE Trans. Power Deliv. 2008, 23, 1636–1644. [Google Scholar] [CrossRef]
- Wang, D.; Ochoa, L.F.; Harrison, G.P.; Dent, C.J.; Wallace, A.R. Evaluating investment deferral by incorporating distributed generation in distribution network planning. In Proceedings of the 16th Power Systems Computation Conference PSCC 2008, Glasgow, UK, 14–18 July 2008; p. 7. [Google Scholar]
- Abdmouleh, Z.; Gastli, A.; Ben-Brahim, L.; Haouari, M.; Al-Emadi, N.A. Review of optimization techniques applied for the integration of distributed generation from renewable energy sources. Renew. Energy 2017, 113, 266–280. [Google Scholar] [CrossRef]
- Theo, W.L.; Lim, J.S.; Ho, W.S.; Hashim, H.; Lee, C.T. Review of distributed generation (DG) system planning and optimisation techniques: Comparison of numerical and mathematical modelling methods. Renew. Sustain. Energy Rev. 2017, 67, 531–573. [Google Scholar] [CrossRef]
- Pesaran, H.A.M.; Huy, P.D.; Ramachandaramurthy, V.K. A review of the optimal allocation of distributed generation: Objectives, constraints, methods, and algorithms. Renew. Sustain. Energy. Rev. 2017, 75, 293–312. [Google Scholar] [CrossRef]
- Oree, V.; Sayed Hassen, S.Z.; Fleming, P.J. Generation expansion planning optimisation with renewable energy integration: A review. Renew. Sustain. Energy Rev. 2017, 69, 790–803. [Google Scholar] [CrossRef]
- Huda, A.S.N.; Živanović, R. Large-scale integration of distributed generation into distribution networks: Study objectives, review of models and computational tools. Renew. Sustain. Energy Rev. 2017, 76, 974–988. [Google Scholar] [CrossRef]
- Liew, S.; Strbac, G. Maximising penetration of wind generation in existing distribution networks. IEE Proc. Gener. Transm. Distrib. 2002, 149, 256–262. [Google Scholar] [CrossRef]
- Currie, R.; Ault, G.; Fordyce, R.; Macleman, D.; Smith, M.; McDonald, J. Actively managing wind farm power output. IEEE Trans. Power Syst. 2008, 23, 1523–1524. [Google Scholar] [CrossRef]
- Blanco, H.; Faaij, A. A review at the role of storage in energy systems with a focus on power to gas and long-term storage. Renew. Sustain. Energy Rev. 2018, 81, 1049–1086. [Google Scholar] [CrossRef]
- Mohod, S.W.; Aware, M.V. Energy storage to stabilize the weak wind generating grid. In Proceedings of the 2008 Joint International Conference on Power System Technology and IEEE Power India Conference, New Delhi, India, 12–15 October 2008. [Google Scholar] [CrossRef]
- Colmenar-Santos, A.; Reino-Rio, C.; Borge-Diez, D.; Collado-Fernández, E. Distributed generation: A review of factors that can contribute most to achieve a scenario of DG units embedded in the new distribution networks. Renew. Sustain. Energy Rev. 2016, 59, 1130–1148. [Google Scholar] [CrossRef]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley and Sons: Hoboken, NJ, USA, 2001; Volume 16. [Google Scholar]
- Harrison, G.P.; Piccolo, A.; Siano, P.; Wallace, A.R. Exploring the tradeoffs between incentives for distributed generation developers and DNOs. IEEE Trans. Power Syst. 2007, 22, 821–828. [Google Scholar] [CrossRef] [Green Version]
- Khetrapal, P. Distributed Generation: A Critical Review of Technologies, Grid Integration Issues, Growth Drivers and Potential Benefits. Int. J. Renew. Energy Dev. 2020, 9, 189–205. [Google Scholar] [CrossRef]
- Ehsan, A.; Yang, Q. Optimal integration and planning of renewable distributed generation in the power distribution networks: A review of analytical techniques. Appl. Energy 2018, 210, 44–59. [Google Scholar] [CrossRef]
- Harrison, G.P.; Wallace, A.R. Optimal power flow evaluation of distribution network capacity for the connection of distributed generation. IEE Proc. Gener. Transm. Distrib. 2015, 152, 115–122. [Google Scholar] [CrossRef]
- Gautam, D.; Mithulananthan, N. Optimal DG placement in deregulated electricity market. Electr. Power Syst. Res. 2007, 77, 1627–1636. [Google Scholar] [CrossRef]
- Ochoa, L.F.; Dent, C.J.; Harrison, G.P. Distribution network capacity assessment: Variable DG and active networks. IEEE Trans. Power Syst. 2010, 25, 87–95. [Google Scholar] [CrossRef] [Green Version]
- Ochoa, L.F.; Harrison, G.P. Minimizing energy losses: Optimal accommodation and smart operation of renewable distributed generation. IEEE Trans. Power Syst. 2011, 26, 198–205. [Google Scholar] [CrossRef] [Green Version]
- Vovos, P.; Bialek, J. Direct incorporation of fault level constraints in optimal power flow as a tool for network capacity analysis. IEEE Trans. Power Syst. 2005, 20, 2125–2134. [Google Scholar] [CrossRef]
- Wallace, A.; Harrison, G.P. Planning for optimal accommodation of dispersed generation in distribution networks. In Proceedings of the CIRED 17th International Conference on Electric Distribution, Barcelona, Spain, 12–15 May 2003. [Google Scholar]
- Momoh, J.A.; Xia, Y.; Boswell, G.D. An approach to determine Distributed Generation (DG) benefits in power networks. In Proceedings of the 2008 40th North American Power Symposium, Calgary, AB, Canada, 28–30 September 2008. [Google Scholar]
- Vovos, P.N.; Kiprakis, A.E.; Wallace, A.R.; Harrison, G.P. Centralized and distributed voltage control: Impact on distributed generation penetration. IEEE Trans. Power Syst. 2007, 22, 476–483. [Google Scholar] [CrossRef] [Green Version]
- Algarni, A.A.S.; Bhattacharya, K. Disco operation considering DG units and their goodness factors. IEEE Trans. Power Syst. 2009, 24, 1831–1840. [Google Scholar] [CrossRef]
- Dent, C.J.; Ochoa, L.; Harrison, G. Network distributed generation capacity analysis using OPF with voltage step constraints. IEEE Trans. Power Syst. 2010, 25, 296–304. [Google Scholar] [CrossRef] [Green Version]
- Dent, C.J.; Ochoa, L.; Harrison, G.; Bialek, J.W. Efficient secure AC OPF for network generation capacity assessment. IEEE Trans. Power Syst. 2010, 25, 575–583. [Google Scholar] [CrossRef] [Green Version]
- Vovos, P.N.; Harrison, G.P.; Wallace, A.R.; Bialek, J.W. Optimal power flow as a tool for fault level-constrained network capacity analysis. IEEE Trans. Power Syst. 2005, 20, 734–741. [Google Scholar] [CrossRef]
- Wang, C.; Nehrir, M. Analytical approaches for optimal placement of distributed generation sources in power systems. IEEE Trans. Power Syst. 2004, 19, 2068–2076. [Google Scholar] [CrossRef]
- Acharya, N.; Mahat, P.; Mithulananthan, N. An analytical approach for DG allocation in primary distribution network. Int. J. Electr. Power Energy Syst. 2006, 28, 669–678. [Google Scholar] [CrossRef]
- Hung, D.Q.; Mithulananthan, N.; Bansal, R. Analytical expressions for DG allocation in primary distribution networks. IEEE Trans. Energy Convers. 2010, 25, 814–820. [Google Scholar] [CrossRef]
- Vatani, M.; Alkaran, D.S.; Sanjari, M.J.; Gharehpetian, G.B. Multiple distributed generation units allocation in distribution network for loss reduction based on a combination of analytical and genetic algorithm methods. IET Gener. Transm. Distrib. 2016, 10, 66–72. [Google Scholar] [CrossRef]
- Mahmoud, K.; Yorino, N.; Ahmed, A. Optimal distributed generation allocation in distribution systems for loss minimization. IEEE Trans. Power Syst. 2016, 31, 960–969. [Google Scholar] [CrossRef]
- Hung, D.Q.; Mithulananthan, N.; Lee, K.Y. Determining PV penetration for distribution systems with time-varying load models. IEEE Trans. Power Syst. 2014, 29, 3048–3057. [Google Scholar] [CrossRef]
- Khan, H.; Choudhry, M.A. Implementation of distributed generation (IDG) algorithm for performance enhancement of distribution feeder under extreme load growth. Int. J. Electr. Power Energy Syst. 2010, 32, 985–997. [Google Scholar] [CrossRef]
- Hung, D.Q.; Mithulananthan, N.; Lee, K.Y. Optimal placement of dispatchable and Non dispatchable renewable DG units in distribution networks for minimizing energy loss. Int. J. Electr. Power Energy Syst. 2014, 55, 179–186. [Google Scholar] [CrossRef]
- Hung, D.Q.; Mithulananthan, N.; Bansal, R.C. Integration of PV and BES units in commercial distribution systems considering energy loss and voltage stability. Appl. Energy 2014, 113, 162–170. [Google Scholar] [CrossRef]
- Jurado, F.; Cano, A. Optimal placement of biomass fuelled gas turbines for reduced losses. Energy Convers. Manag. 2006, 47, 2673–2681. [Google Scholar] [CrossRef]
- Hamedi, H.; Gandomkar, M. A straightforward approach to minimizing unsupplied energy and power loss through DG placement and evaluating power quality in relation to load variations over time. Int. J. Electr. Power Energy. Syst. 2011, 35, 93–96. [Google Scholar] [CrossRef]
- Shayani, R.A.; De Oliveira, M.A.G. Photovoltaic generation penetration limits in radial distribution systems. IEEE Trans. Power Syst. 2011, 26, 1625–1631. [Google Scholar] [CrossRef]
- Porkar, S.; Poure, P.; Abbaspour-Tehrani-fard, A.; Saadate, S. A novel optimal distribution system planning framework implementing distributed generation in a deregulated electricity market. Electr. Power Syst. Res. 2010, 80, 828–837. [Google Scholar] [CrossRef]
- Chang, R.W.; Mithulananthan, N.; Saha, T.K. Novel mixed-integer method to optimize distributed generation mix in primary distribution systems. In Proceedings of the Power Engineering Conference (AUPEC), Brisbane, QLD, Australia, 25–28 September 2011. [Google Scholar]
- Atwa, Y.M.; El-Saadany, E.F.; Salama, M.M.A.; Seethapathy, R. Optimal renewable resources mix for distribution system energy loss minimization. IEEE Trans. Power Syst. 2010, 25, 360–370. [Google Scholar] [CrossRef]
- Ruhaizad, I.; Azah, M.; Ahmed, N.A.; Mohd Zamri, C.W. Optimal DG Placement and Sizing For Voltage Stability Improvement Using Backtracking Search Algorithm. In Proceedings of the Conference on Artificial Intelligence, Energy and Manufacturing Engineering (ICAEME’2014), Kuala Lumpur, Malaysia, 9–10 June 2014. [Google Scholar]
- Kumar, A.; Gao, W. Optimal distributed generation location using mixed integer non-linear programming in hybrid electricity markets. IET Gener. Transm. Distrib. 2010, 4, 281–298. [Google Scholar] [CrossRef]
- Rueda-Medina, A.C.; Franco, J.F.; Rider, M.J.; Padilha-Feltrin, A.; Romero, R. A mixed-integer linear programming approach for optimal type, size and allocation of distributed generation in radial distribution systems. Electr. Power Syst. Res. 2013, 97, 133–143. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, B.; Wang, J.; Kim, J.; Begovic, M.M. Robust optimization based optimal DG placement in microgrids. IEEE Trans. Smart Grid 2014, 5, 2173–2182. [Google Scholar] [CrossRef]
- Al Abri, R.S.; El-Saadany, E.F.; Atwa, Y.M. Optimal placement and sizing method to improve the voltage stability margin in a distribution system using distributed generation. IEEE Trans. Power Syst. 2013, 28, 326–334. [Google Scholar] [CrossRef]
- Nadarajah, M.; Oo, T.; Phu, L.V. Distributed generator placement in power distribution system using genetic algorithm to reduce losses. Thammasat Int. J. Sci. Technol. 2004, 9, 55–62. [Google Scholar]
- Borges, C.L.T.; Falcao, D.M. Optimal distributed generation allocation for reliability, losses, and voltage improvement. Int. J. Electr. Power Energy Syst. 2006, 28, 413–420. [Google Scholar] [CrossRef]
- Singh, R.K.; Goswami, S.K. Optimum allocation of distributed generations based on nodal pricing for profit, loss reduction, and voltage improvement including voltage rise issue. Int. J. Electr. Power Energy Syst. 2010, 32, 637–644. [Google Scholar] [CrossRef]
- Shaaban, M.F.; Atwa, Y.M.; El-Saadany, E.F. DG allocation for benefit maximization in distribution networks. IEEE Trans. Power Syst. 2013, 28, 639–649. [Google Scholar] [CrossRef]
- Singh, D.; Singh, D.; Verma, K.S. GA based optimal sizing & placement of distributed generation for loss minimization. Int. J. Electr. Comput. Eng. 2007, 2, 556–562. [Google Scholar]
- Teng, J.-H.; Liu, Y.-H.; Chen, C.-Y.; Chen, C.-F. Value-based distributed generator placements for service quality improvements. Int. J. Electr. Power Energy Syst. 2007, 29, 268–274. [Google Scholar] [CrossRef]
- Singh, D.; Singh, D.; Verma, K.S. Multiobjective optimization for DG planning with load models. IEEE Trans. Power Syst. 2009, 24, 427–436. [Google Scholar] [CrossRef]
- Singh, R.K.; Goswami, S.K. Optimum siting and sizing of distributed generations in radial and networked systems. Electr. Power Compon. Syst. 2009, 37, 127–145. [Google Scholar] [CrossRef]
- Zangeneh, A.; Jadid, S.; Rahimi-Kian, A. Promotion strategy of clean technologies in distributed generation expansion planning. Renew. Energy 2009, 34, 2765–2773. [Google Scholar] [CrossRef]
- Soroudi, A.; Ehsan, M.; Zareipour, H. A practical ecoenvironmental distribution network planning model including fuel cells and non-renewable distributed energy resources. Renew. Energy 2011, 36, 179–188. [Google Scholar] [CrossRef] [Green Version]
- Kamalinia, S.; Afsharnia, S.; Khodayar, M.E.; Rahimikian, A.; Sharbafi, M.A. A combination of MADM and genetic algorithm for optimal DG allocation in power systems. In Proceedings of the 2007 42nd International Universities Power Engineering Conference, Brighton, UK, 4–6 September 2007. [Google Scholar]
- Ma, Y.; Yang, P.; Guo, H.; Wu, J. Power source planning of wind-PV-biogas renewable energy distributed generation system. Power Syst. Technol. 2012, 9, 001. [Google Scholar]
- Liao, G.-C. Solve environmental economic dispatch of Smart MicroGrid containing distributed generation system e using chaotic quantum genetic algorithm. Int. J. Electr. Power Energy Syst. 2012, 43, 779–787. [Google Scholar] [CrossRef]
- Tautiva, C.; Cadena, A.; Rodriguez, F. Optimal placement of distributed generation on distribution networks. In Proceedings of the 2009 44th International Universities Power Engineering Conference (UPEC), Glasgow, UK, 1–4 September 2009. [Google Scholar]
- Celli, G.; Pilo, F. Optimal distributed generation allocation in MV distribution networks. In Proceedings of the PICA 2001, Innovative Computing for Power-Electric Energy Meets the Market, 22nd IEEE Power Engineering Society, International Conference on Power Industry Computer Applications, Sydney, NSW, Australia, 20–24 May 2001. [Google Scholar]
- Kuri, B.; Redfem, M.A.; Li, F. Optimisation of rating and positioning of dispersed generation with minimum network disruption. In Proceedings of the Power Engineering Society General Meeting, Denver, CO, USA, 6–10 June 2004. [Google Scholar]
- Niknam, T.; Ranjbar, A.M.; Shirani, A.R.; Mozafari, B.; Ostadi, A. Optimal operation of distribution system with regard to distributed generation: A comparison of evolutionary methods. In Proceedings of the Fortieth IAS Annual Meeting, Conference Record of the 2005 Industry Applications Conference, Hong Kong, China, 2–6 October 2005; Volume 4. [Google Scholar]
- Niknam, T.; Ranjbar, A.M.; Shirani, A.R. An approach for Volt/Var control in distribution network with distributed generation. Int. J. Sci. Technol. Sci. Iran. 2005, 12, 34–42. [Google Scholar]
- Afsari, F. Multiobjective optimization of distribution networks using genetic algorithms. In Proceedings of the 5th International Symposium on Communication Systems, Networks, and Digital Signal Processing, Patras, Greece, 19–21 July 2006. [Google Scholar]
- Pisica, I.; Bulac, C.; Eremia, M. Optimal distributed generation location and sizing using genetic algorithms. In Proceedings of the 2009 15th International Conference on Intelligent System Applications to Power Systems, Curitiba, Brazil, 8–12 November 2009. [Google Scholar]
- Celli, G.; Ghiani, E.; Mocci, S.; Pilo, F. A multi-objective formulation for the optimal sizing and siting of embedded generation in distribution networks. In Proceedings of the 2003 IEEE Bologna Power Tech Conference, Bologna, Italy, 23–26 June 2003. [Google Scholar]
- Haesens, E.; Espinoza, M.; Pluymers, B.; Goethals, I.; Thong, V.V.; Driesen, J.; Belmanss, R.; de Moor, B. Optimal placement and sizing of distributed generator units using genetic optimization algorithms. Electr. Power Qual. Util. J. 2005, 11, 97–104. [Google Scholar]
- Kumar, V.; Kumar, H.C.R.; Gupta, I.; Gupta, H.O. DG integrated approach for service restoration under cold load pickup. IEEE Trans. Power Deliv. 2010, 25, 398–406. [Google Scholar] [CrossRef]
- Ochoa, L.F.; Padilha-Feltrin, A.; Harrison, G.P. Time-series-based maximization of distributed wind power generation integration. IEEE Trans. Energy Convers. 2008, 23, 968–974. [Google Scholar] [CrossRef] [Green Version]
- Teng, J.-H.; Luor, T.-S.; Liu, Y.-H. Strategic distributed generator placements for service reliability improvements. In Proceedings of the IEEE Power Engineering Society Summer Meeting, Chicago, IL, USA, 21–25 July 2002; Volume 2. [Google Scholar]
- Moeini-Aghtaie, M.; Dehghanian, P.; Hosseini, S.H. Optimal Distributed Generation placement in a restructured environment via a multi-objective optimization approach. In Proceedings of the 16th Electrical Power Distribution Conference, Bandar Abbas, Iran, 19–20 April 2011. [Google Scholar]
- Yang, N.-C.; Chen, T.-H. Evaluation of maximum allowable capacity of distributed generations connected to a distribution grid by dual genetic algorithm. Energy Build. 2011, 43, 3044–3052. [Google Scholar] [CrossRef]
- Sheng, W.; Liu, K.Y.; Liu, Y.; Meng, X.; Li, Y. Optimal placement and sizing of distributed generation via an improved nondominated sorting genetic algorithm II. IEEE Trans. Power Deliv. 2015, 30, 569–578. [Google Scholar] [CrossRef]
- Ganguly, S.; Samajpati, D. Distributed generation allocation on radial distribution networks under uncertainties of load and generation using genetic algorithm. IEEE Trans. Sustain. Energy 2015. [Google Scholar] [CrossRef]
- Evangelopoulos, V.A.; Georgilakis, P.S. Optimal distributed generation placement under uncertainties based on point estimate method embedded genetic algorithm. IET Gener. Transm. Distrib. 2014, 389–400. [Google Scholar] [CrossRef] [Green Version]
- Sutthibun, T.; Bhasaputra, P. Multi-objective optimal distributed generation placement using simulated annealing. In Proceedings of the ECTI-CON2010: The 2010 ECTI International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology, Chiang Mai, Thailand, 19–21 May 2010. [Google Scholar]
- Aly, A.I.; Hegazy, Y.G.; Alsharkawy, M.A. A simulated annealing algorithm for multi-objective distributed generation planning. In Proceedings of the IEEE PES General Meeting, Minneapolis, MN, USA, 25–29 July 2010. [Google Scholar]
- Vallem, M.R.; Mitra, J. Siting and sizing of distributed generation for optimal microgrid architecture. In Proceedings of the 37th Annual North American Power Symposium, Ames, IA, USA, 25 October 2005. [Google Scholar]
- Ghadimi, N.; Ghadimi, R. Optimal allocation of distributed generation and capacitor banks in order to loss reduction in reconfigured system. Res. J. Appl. Sci. Eng. Technol. 2012, 4, 1099–1104. [Google Scholar]
- Mitra, J.; Vallem, M.R.; Singh, C. Optimal deployment of distributed generation using a reliability criterion. IEEE Trans. Ind. Appl. 2016, 52, 1989–1997. [Google Scholar] [CrossRef]
- Dharageshwari, K.; Nayanatara, C. Multiobjective optimal placement of multiple distributed generations in IEEE 33 bus radial system using simulated annealing. In Proceedings of the 2015 International Conference on Circuits, Power and Computing Technologies, Nagercoil, India, 19–20 March 2015. [Google Scholar]
- Abbagana, M.; Bakare, G.A.; Mustapha, I.; Musa, B.U. Differential evolution based optimal placement and sizing of two distributed generators in a power distribution system. J. Eng. Appl. Sci. 2012, 4, 61–70. [Google Scholar]
- Gunda, J.; Khan, N.A. Optimal location and sizing of DG and shunt capacitors using differential evolution. Int. J. Soft Comput. 2011, 6, 128–135. [Google Scholar] [CrossRef] [Green Version]
- Arya, L.D.; Koshti, A.; Choube, S.C. Distributed generation planning using differential evolution accounting voltage stability consideration. Int. J. Electr. Power Energy Syst. 2012, 42, 196–207. [Google Scholar] [CrossRef]
- Estabragh, M.R.; Mohsen, M. Optimal allocation of DG regarding to power system security via DE technique. In Proceedings of the 2011 IEEE Jordan Conference on Applied Electrical Engineering and Computing Technologies (AEECT), Amman, Jordan, 6–8 December 2011. [Google Scholar]
- Hejazi, H.A.; Hejazi, M.A.; Gharehpetian, G.B.; Abedi, M. Distributed generation site and size allocation through a techno economical multi-objective Differential Evolution Algorithm. In Proceedings of the 2010 IEEE International Conference on Power and Energy, Kuala Lumpur, Malaysia, 29 November–1 December 2010. [Google Scholar]
- Slimani, L.; Bouktir, T. An Ant colony optimization for solving the Optimal Power Flow Problem in medium-scale electrical network. In Proceedings of the First International Conference on Electrical Systems PCSE’05, Oum El Bouaghi University, Oum El Bouaghi, Algeria, 9–11 May 2005. [Google Scholar] [CrossRef]
- Dong, W.; Li, Y.; Xiang, J. Optimal sizing of a stand-alone hybrid power system based on battery/hydrogen with an improved ant colony optimization. Energies 2016, 9, 785. [Google Scholar] [CrossRef]
- Tolabi, H.B.; Ali, M.H.; Rizwan, M. Simultaneous Reconfiguration, Optimal Placement of DSTATCOM, and Photovoltaic Array in a Distribution System Based on Fuzzy-ACO Approach. IEEE Trans. Sustain. Energy 2015, 6, 210–218. [Google Scholar] [CrossRef]
- El-Zonkoly, A.; El-Zonkoly, A. Optimal placement of multi-distributed generation units including different load models using particle swarm optimization. Swarm Evol. Comput. 2011, 1, 50–59. [Google Scholar] [CrossRef]
- Padma, L.M.; Veera Reddy, V.C.; Usha, V. Optimal DG placement for minimum real power loss in radial distribution systems using PSO. J. Theor. Appl. Inf. Technol. 2010, 13, 107–116. [Google Scholar]
- Kansal, S.; Sai, B.; Tyagi, B.; Kumar, V. Optimal placement of distributed generation in distribution networks. Int. J. Eng. Sci. Technol. 2011, 3, 47–55. [Google Scholar] [CrossRef]
- Pandi, V.R.; Zeineldin, H.H.; Xiao, W. Determining optimal location and size of distributed generation resources considering harmonic and protection coordination limits. IEEE Trans. Power Syst. 2013, 28, 1245–1254. [Google Scholar] [CrossRef]
- Alinejad-Beromi, Y.; Sedighizadeh, M.; Sadighi, M. A particle swarm optimization for sitting and sizing of distributed generation in distribution network to improve voltage profile and reduce THD and losses. In Proceedings of the 2008 43rd International Universities Power Engineering Conference, Padua, Italy, 1–4 September 2008. [Google Scholar]
- Kansal, S.; Kumar, V.; Tyagi, B. Optimal placement of different type of DG sources in distribution networks. Int. J. Electr. Power Energy Syst. 2013, 53, 752–760. [Google Scholar] [CrossRef]
- Ashari, Y.M.; Soeprijanto, A. Optimal distributed generation (DG) allocation for losses reduction using improved particle swarm optimization (IPSO) method. J. Basic. Appl. Sci. Res. 2012, 2, 7016–7023. [Google Scholar]
- Su, S.-Y.; Lu, C.-N.; Chang, R.-F.; Gutierrez-Alcaraz, G. Distributed generation interconnection planning: A wind power case study. IEEE Trans. Smart Grid 2011, 2, 181–189. [Google Scholar] [CrossRef]
- Arasi, S.M.; Sasiraja, R.M. Optimal Location of DG Units with Exact Size for the Improvement of Voltage Stability Using SLPSO. IJLRES 2015, 7, 679–690. [Google Scholar]
- Ganguly, S.; Sahoo, N.C.; Das, D. Multi-objective planning of electrical distribution systems using particle swarm optimization. In Proceedings of the Electric Power and Energy Conversion Systems, EPECS’09, International Conference, Sharjah, United Arab Emirates, 10–12 November 2009. [Google Scholar]
- Niknam, T.; Ranjbar, A.M.; Ostadi, A.; Shirani, A.R. A new approach based on ant algorithm for Volt/Var control in distribution network considering distributed generation. Iran. J. Sci. Technol. Trans. B 2005, 29, 1–15. [Google Scholar]
- Niknam, T. An approach based on particle swarm optimization for optimal operation of distribution network considering distributed generators. In Proceedings of the IECON 2006—32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 6–10 November 2006. [Google Scholar]
- Raj, P.A.-D.-V.; Senthilkumar, S.; Raja, J.; Ravichandran, S.; Palanivelu, T.G. Optimization of distributed generation capacity for line loss reduction and voltage profile improvement using PSO. Elektrika J. Electr. Eng. 2008, 10, 41–48. [Google Scholar]
- Wong, L.Y.; Abdul Rahim, S.R.; Sulaiman, M.H.; Aliman, O. Distributed generation installation using particle swarm optimization. In Proceedings of the 2010 4th International Power Engineering and Optimization Conference (PEOCO), Shah Alam, Malaysia, 23–24 June 2010. [Google Scholar]
- Wenxin, L.; Cartes, D.A.; Venayagamoorthy, G.K. Particle swarm optimization based defensive islanding of large scale power system. In Proceedings of the 2006 IEEE International Joint Conference on Neural Network, Vancouver, BC, Canada, 16–21 July 2006. [Google Scholar]
- Hajizadeh, A.; Hajizadeh, E. PSO-based planning of distribution systems with distributed generations. Int. J. Electr. Electron. Eng. 2008, 2, 33–38. [Google Scholar]
- Mohammadi, M.; Nasab, M.A. PSO based multiobjective approach for optimal sizing and placement of distributed generation. Res. J. Appl. Sci. Eng. Technol. 2011, 2, 832–837. [Google Scholar]
- Zareiegovar, G.; Rezvani Fesaghandis, R.; Azad, M.J. Optimal DG location and sizing in distribution system to minimize losses, improve voltage stability, and voltage profile. In Proceedings of the 2012 17th Conference on Electrical Power Distribution, Teheran, Iran, 2–3 May 2012. [Google Scholar]
- Maciel, R.S.; Rosa, M.; Miranda, V.; Padilha-Feltrin, A. Multi-objective evolutionary particle swarm optimization in the assessment of the impact of distributed generation. Electr. Power Syst. Res. 2012, 89, 100–108. [Google Scholar] [CrossRef] [Green Version]
- Devi, S.; Geethanjali, M. Optimal location and sizing determination of distributed generation and DSTATCOM using particle swarm optimization algorithm. Int. J. Electr. Power Energy Syst. 2014, 62, 562–570. [Google Scholar] [CrossRef]
- Jamian, J.J.; Mustafa, M.W.; Mokhlis, H. Optimal multiple distributed generation output through rank evolutionary particle swarm optimization. Neurocomputing 2015, 152, 190–198. [Google Scholar] [CrossRef] [Green Version]
- Golshan, M.E.H.; Arefifar, S.A. Optimal allocation of distributed generation and reactive sources considering tap positions of voltage regulators as control variables. Int. Trans. Electr. Energy Syst. 2007, 17, 219–239. [Google Scholar] [CrossRef]
- Golshan, M.E.H.; Arefifar, S.A. Distributed generation, reactive sources and network-configuration planning for power and energy-loss reduction. IEE Proceed. Gener. Transm. Distrib. 2006, 153, 127–136. [Google Scholar] [CrossRef]
- Maciel, R.S.; Padilha-Feltrin, A. Distributed generation impact evaluation using a multi-objective Tabu Search. In Proceedings of the 2009 15th International Conference on Intelligent System Applications to Power Systems, Curitiba, Brazil, 8–12 November 2009. [Google Scholar]
- Mori, H.; Iimura, Y. Application of parallel tabu search to distribution network expansion planning with distributed generation. In Proceedings of the 2003 IEEE Bologna Power Tech Conference, Bologna, Italy, 23–26 June 2003. [Google Scholar]
- Pereira, B.R.; Martins da Costa, G.R.M.; Contreras, J.; Mantovani, J.R.S. Optimal distributed generation and reactive power allocation in electrical distribution systems. IEEE Trans. Sustain. Energy 2016, 7, 975–984. [Google Scholar] [CrossRef] [Green Version]
- Arias, N.B.; Franco, J.F.; Lavorato, M.; Romero, R. Metaheuristic optimization algorithms for the optimal coordination of plug-in electric vehicle charging in distribution systems with distributed generation. Electr. Power Syst. Res. 2017, 142, 351–361. [Google Scholar] [CrossRef] [Green Version]
- Mardaneh, M.; Gharehpetian, G.B. Siting and sizing of DG units using GA and OPF based technique. In Proceedings of the 2004 IEEE Region 10 Conference TENCON, Chiang Mai, Thailand, 24 November 2004. [Google Scholar]
- Harrison, G.P.; Piccolo, A.; Siano, P.; Wallace, A.R. Distributed generation capacity evaluation using combined genetic algorithm and OPF. Int. J. Emerg. Electr. Power Syst. 2007, 8, 1–13. [Google Scholar] [CrossRef]
- Harrison, G.P.; Piccolo, A.; Siano, P.; Wallace, A.R. Hybrid GA and OPF evaluation of network capacity for distributed generation connections. Electr. Power Syst. Res. 2008, 78, 392–398. [Google Scholar] [CrossRef] [Green Version]
- Naderi, E.; Seifi, H.; Sepasian, M.S. A Dynamic Approach for Distribution System Planning Considering Distributed Generation. IEEE Trans. Power Deliv. 2012, 27, 1313–1322. [Google Scholar] [CrossRef]
- Hussain, I.; Kumar Roy, A. Optimal distributed generation allocation in distribution systems employing modified artificial bee colony algorithm to reduce losses and improve voltage profile. In Proceedings of the IEEE-International Conference On Advances In Engineering, Science And Management (ICAESM-2012), Tamil Nadu, India, 30–31 March 2012; pp. 565–570. [Google Scholar]
- Gandomkar, M.; Vakilian, M.; Ehsan, M. A genetic–based tabu search algorithm for optimal dg allocation in distribution networks. Electr. Power Compon. Syst. 2005, 33, 1351–1362. [Google Scholar] [CrossRef]
- Elgerd, O.I. Electric Energy Systems Theory: An Introduction; McGraw-Hill: New York, NY, USA, 1971. [Google Scholar]
- Hung, D.Q.; Mithulanantham, N. Multiple distributed generator placement in primary distribution networks for loss reduction. IEEE Trans. Ind. Electron. 2013, 60, 1700–1708. [Google Scholar] [CrossRef]
- Hung, D.Q.; Mithulananthan, N. Alternative analytical approaches for renewable DG allocation for energy loss minimization. In Proceedings of the IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; Volume 18. [Google Scholar] [CrossRef] [Green Version]
- Elmitwally, A. A new algorithm for allocating multiple distributed generation units based on load centroid concept. Alex. Eng. J. 2013, 52, 655–663. [Google Scholar] [CrossRef] [Green Version]
- Bala, J.L.; Kuntz, P.A.; Pebles, M.N. Optimum capacitor allocation using a distribution-analyzer-recorder. IEEE Trans. PWRD 1997, 12, 464–469. [Google Scholar]
- Kashem, M.A.; Le, A.D.T.; Negnevitsky, M.; Ledwich, G. Distributed generation for minimization of power losses in distribution systems. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006. [Google Scholar]
- Mirzaei, M.; Jasni, J.; Hizam, H.; Wahab, N.I.A.; Mohamed, S.E.G. An analytical method for optimal sizing of different types of DG in a power distribution system. In Proceedings of the 2014 IEEE International Conference on Power and Energy (PECon), Kuching, Malaysia, 1–3 December 2014; pp. 309–314. [Google Scholar] [CrossRef]
- Carpentier, J. Contribution a l’etude du dispatching economique. Ser. 8 Bull. de la Société Française des Electriciens 1962, 3, 431–447. [Google Scholar]
- Abdi, H.; Beigvand, S.D.; La Scala, M. A review of optimal power flow studies applied to smart grids and microgrids. Renew. Sustain. Energy Rev. 2017, 71, 742–766. [Google Scholar] [CrossRef]
- Geidl, M.; Andersson, G. Optimal power flow of multiple energy carriers. IEEE Trans Power Syst. 2007, 22, 145–155. [Google Scholar] [CrossRef]
- Madrigal, M.; Ponnambalam, K.; Quintana, V.H. Probabilistic optimal power flow. In Proceedings of the IEEE Canadian Conference on Electrical and Computer Engineering, Waterloo, ON, Canada, 25–28 May 1998. [Google Scholar]
- Li, Y.; Li, W.; Yan, W.; Yu, J.; Zhao, X. Probabilistic optimal power flow considering correlations of wind speeds following different distributions. IEEE Trans. Power Syst. 2014, 29, 1847–1854. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Zhang, S. Analysis of probabilistic optimal power flow taking account of the variation of load power. IEEE Trans. Power Syst. 2008, 23, 992–999. [Google Scholar]
- Kashem, M.; Ganapathy, V.; Jasmon, G.; Buhari, S.M. A novel method for loss minimization in distribution networks. In Proceedings of the International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, London, UK, 4–7 April 2000. [Google Scholar]
- Baran, M.E.; Wu, F.F. Optimum sizing of capacitor placed on radial distribution systems. IEEE Trans. Power Deliv. 1989, 4, 735–743. [Google Scholar] [CrossRef]
- Nagarajua, S.K.; Sivanagarajub, S.; Ramanac, T.; Satyanarayanac, S.; Prasadd, P.V. A novel method for optimal distributed generator placement in radial distribution systems. Distrib. Gener. Alter. Energy J. 2011, 26, 7–19. [Google Scholar] [CrossRef]
- IEA. International Energy Agency. Technology Roadmap Energy Storage. 2014. Available online: https://www.iea.org/publications/freepublications/publication/TechnologyRoadmapEnergystorage.pdf (accessed on 20 May 2020).
- Sandia National Laboratories and U.S. Department of Energy (DOE) Global Energy Storage Database. 2018. Available online: https://www.energystorageexchange.org/projects (accessed on 7 June 2018).
- Gür, T.M. Review of electrical energy storage technologies, materials and systems: Challenges and prospects for largescale grid storage. Energy Environ. Sci. 2018, 11, 2696–2767. [Google Scholar] [CrossRef]
- Krishan, O.; Suhang, S. An updated review of energy storage systems: Classification and applications in distributed generation power systems incorporating renewable energy resources. Int. J. Energy Res. 2019, 43, 6171–6210. [Google Scholar] [CrossRef]
- Khan, N.; Dilshad, S.; Khalid, R.; Kalair, A.R.; Abas, N. Review of energy storage and transportation of energy. Energy Storage 2019, 1, e49. [Google Scholar] [CrossRef]
- Siritoglou, P.; Oriti, G.; Van Bossuyt, D. Distributed Energy-Resource Design Method to Improve Energy Security in Critical Facilities. Energies 2021, 14, 2773. [Google Scholar] [CrossRef]
- Zhou, B.; Liu, X.; Cao, Y.; Li, C.; Chung, C.Y.; Chan, K.W. Optimal scheduling of virtual power plant with battery degradation cost. IET Gener. Transm. Distrib. 2016, 10, 712–725. [Google Scholar] [CrossRef]
- Zia, M.F.; Elbouchikhi, E.; Benbouzid, M. Optimal operational planning of scalable DC microgrid with demand response, islanding, and battery degradation cost considerations. Appl. Energy 2019, 237, 695–707. [Google Scholar] [CrossRef]
- Song, Z.; Feng, S.; Zhang, L.; Hu, Z.; Hu, X.; Yao, R. Economy analysis of second-life battery in wind power systems considering battery degradation in dynamic processes: Real case scenarios. Appl. Energy 2019, 251, 113411. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Mohammadi-Ivatloo, B.; Anvari-Moghaddam, A.; Razzaghi, R. A Bi-Level Framework for Optimal Energy Management of Electrical Energy Storage Units in Power Systems. IEEE Access 2020, 8, 216141–216150. [Google Scholar] [CrossRef]
- Energy Storage Association. Compressed Air Energy Storage (CAES); Energy Storage Association: Washington, DC, USA, 2017; pp. 1–3. [Google Scholar]
- Nikolaidis, P.; Poullikkas, A. A comparative review of electrical energy storage systems for better sustainability. J. Power Technol. 2017, 97, 220–245. [Google Scholar]
- Budt, M.; Wolf, D.; Span, R.; Yan, J. A review on compressed air energy storage: Basic principles, past milestones and recent developments. Appl. Energy 2016, 170, 250–268. [Google Scholar] [CrossRef]
- Fuchs, G.; Lunz, B.; Leuthold, M.; Sauer, D.U. Overview of nonelectrochemical storage technologies. In Electrochemical Energy Storage for Renewable Sources and Grid Balancing; Elsevier: Amsterdam, The Netherlands, 2015; pp. 89–102. [Google Scholar]
- Lund, P.D.; Lindgren, J.; Mikkola, J.; Salpakari, J. Review of energy system flexibility measures to enable high levels of variable renewable electricity. Renew. Sustain. Energy Rev. 2015, 45, 785–807. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Ma, L.; Lu, K.; Miao, S.; Wang, D.; Wang, J. Current research and development trend of compressed air energy storage. Syst. Sci. Control. Eng. 2017, 5, 434–448. [Google Scholar] [CrossRef] [Green Version]
- Ding, Y.; Tong, L.; Zhang, P.; Li, Y.; Radcliffe, J.; Wang, L. Chapter 9—Liquid air energy storage. In Storing Energy; Letcher, T.M., Ed.; Elsevier: Oxford, UK, 2016; pp. 167–181. [Google Scholar] [CrossRef]
- Maisonnave, O.; Moreau, L.; Aubrée, R.; Benkhoris, M.-F.; Neu, T.; Guyomarc’H, D. Optimal energy management of an underwater compressed air energy storage station using pumping systems. Energy Convers. Manag. 2018, 165, 771–782. [Google Scholar] [CrossRef]
- Dincer, I. Thermal energy storage systems as a key technology in energy conservation. Int. J. Energy Res. 2002, 26, 567–588. [Google Scholar] [CrossRef]
- Sarbu, I.; Sebarchievici, C. A comprehensive review of thermal energy storage. Sustainability 2018, 10, 191. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Xin-Feng, L.; Bo, L.; Si-Quan, Z.; Yan, X. Progress in thermochemical energy storage for concentrated solar power: A review. Int. J. Energy Res. 2018, 42, 4546–4561. [Google Scholar] [CrossRef]
- Kearney, D.; Herrmann, U.; Nava, P.; Kelly, B.; Mahoney, R.; Pacheco, J.; Cable, R.; Potrovitza, N.; Blake, D.; Price, H. Assessment of a Molten Salt Heat Transfer Fluid in a Parabolic Trough Solar Field. J. Sol. Energy Eng. 2003, 125, 170–176. [Google Scholar] [CrossRef] [Green Version]
- Fernandes, D.; Pitié, F.; Cáceres, G.; Baeyens, J. Thermal energy storage: How previous findings determine current research priorities. Energy 2012, 39, 246–257. [Google Scholar] [CrossRef]
- Wei, L.; Wei, C.; Wang, D. Research and development of thermochemical energy storage based on hydrated salt. Refrig. Air Cond. 2017, 17, 14–21. [Google Scholar]
- Hutchings, K.; Wilson, M.; Larsen, P.; Cutler, R. Kinetic and thermodynamic considerations for oxygen absorption/desorption using cobalt oxide. Solid State Ion. 2006, 177, 45–51. [Google Scholar] [CrossRef]
- Muroyama, A.P.; Schrader, A.J.; Loutzenhiser, P.G. Solar electricity via an Air Brayton cycle with an integrated two-step thermochemical cycle for heat storage based on Co3O4/CoO redox reactions II: Kinetic analyses. Sol. Energy 2015, 122, 409–418. [Google Scholar] [CrossRef] [Green Version]
- Carrillo, A.J.; Moya, J.; Bayón, A.; Jana, P.; O’Shea, V.A.D.L.P.; Romero, M.; Gonzalez-Aguilar, J.; Serrano, D.P.; Pizarro, P.; Coronado, J.M. Thermochemical energy storage at high temperature via redox cycles of Mn and Co oxides: Pure oxides versus mixed ones. Sol. Energy Mater. Sol. Cells 2014, 123, 47–57. [Google Scholar] [CrossRef]
- Agrafiotis, C.; Tescari, S.; Roeb, M.; Schmücker, M.; Sattler, C. Exploitation of thermochemical cycles based on solid oxide redox systems for thermochemical storage of solar heat. Part 3: Cobalt oxide monolithic porous structures as integrated thermochemical reactors/heat exchangers. Sol. Energy 2015, 114, 459–475. [Google Scholar] [CrossRef]
- Block, T.; Schmücker, M. Metal oxides for thermochemical energy storage: A comparison of several metal oxide systems. Sol. Energy 2016, 126, 195–207. [Google Scholar] [CrossRef]
- Haseli, P.; Jafarian, M.; Nathan, G. High temperature solar thermochemical process for production of stored energy and oxygen based on CuO/Cu2O redox reactions. Sol. Energy 2017, 153, 1–10. [Google Scholar] [CrossRef]
- Chacartegui, R.; Alovisio, A.; Ortiz, C.; Valverde, J.; Verda, V.; Becerra, J. Thermochemical energy storage of concentrated solar power by integration of the calcium looping process and a CO2 power cycle. Appl. Energy 2016, 173, 589–605. [Google Scholar] [CrossRef]
- Luzzi, A.; Lovegrove, K. A solar thermochemical power plant using ammonia as an attractive option for greenhouse-gas abatement. Energy 1997, 22, 317–325. [Google Scholar] [CrossRef]
- Dunn, R.; Lovegrove, K.; Burgess, G. A Review of Ammonia-Based Thermochemical Energy Storage for Concentrating Solar Power. Proc. IEEE 2012, 100, 391–400. [Google Scholar] [CrossRef]
- Kato, Y.; Yamashita, N.; Kobayashi, K.; Yoshizawa, Y. Kinetic study of the hydration of magnesium oxide for a chemical heat pump. Appl. Therm. Eng. 1996, 16, 853–862. [Google Scholar] [CrossRef]
- Rougé, S.; Criado, Y.A.; Soriano, O.; Carlos Abanades, J. Continuous CaO/Ca(OH)2 fluidized bed reactor for energy storage: First experimental results and reactor model validation. Ind. Eng. Chem. Res. 2017, 56, 844–852. [Google Scholar] [CrossRef] [Green Version]
- Dincer, I.; Acar, C. Review and evaluation of hydrogen production methods for better sustainability. Int. J. Hydrogen Energy 2015, 40, 11094–11111. [Google Scholar] [CrossRef]
- Acar, C.; Dincer, I. Review and evaluation of hydrogen production options for better environment. J. Clean. Prod. 2019, 218, 835–849. [Google Scholar] [CrossRef]
- Revankar, S.T. Chemical Energy Storage. In Storage and Hybridization of Nuclear Energy; Elsevier: Amsterdam, The Netherlands, 2019; Chapter 6; pp. 177–227. [Google Scholar]
- Portarapillo, M.; Di Benedetto, A. Risk Assessment of the Large-Scale Hydrogen Storage in Salt Caverns. Energies 2021, 14, 2856. [Google Scholar] [CrossRef]
- Schneemann, A.; White, J.L.; Kang, S.; Jeong, S.; Wan, L.F.; Cho, E.S.; Heo, T.W.; Prendergast, D.; Urban, J.J.; Wood, B.C.; et al. Nanostructured Metal Hydrides for Hydrogen Storage. Chem. Rev. 2018, 118, 10775–10839. [Google Scholar] [CrossRef]
- Walker, S.B.; van Lanen, D.; Fowler, M.; Mukherjee, U. Economic analysis with respect to Power-to-Gas energy storage with consideration of various market mechanisms. Int. J. Hydrogen Energy 2016, 41, 7754–7765. [Google Scholar] [CrossRef]
- Oldenbroek, V.; Verhoef, L.A.; van Wijk, A.J. Fuel cell electric vehicle as a power plant: Fully renewable integrated transport and energy system design and analysis for smart city areas. Int. J. Hydrogen Energy 2017, 42, 8166–8196. [Google Scholar] [CrossRef]
- MHYBUS Project. Available online: https://www.mhybus.eu/en/mhybus_en.htm (accessed on 20 May 2021).
- Lewandowska-Bernat, A.; Desideri, U. Opportunities of power-to-gas technology in different energy systems architectures. Appl. Energy 2018, 228, 57–67. [Google Scholar] [CrossRef]
- Staffell, I.; Scamman, D.; Velazquez Abad, A.; Balcombe, P.; Dodds, P.E.; Ekins, P.; Shah, N.; Ward, K.R. The role of hydrogen and fuel cells in the global energy system. Energy Environ. Sci. 2019, 12, 463–491. [Google Scholar] [CrossRef] [Green Version]
- Chiesa, P.; Lozza, G.; Mazzocchi, L. Using Hydrogen as Gas Turbine Fuel. J. Eng. Gas Turbines Power 2005, 127, 73–80. [Google Scholar] [CrossRef] [Green Version]
- Cappelletti, A.; Martelli, F. Investigation of a pure hydrogen fueled gas turbine burner. Int. J. Hydrogen Energy 2017, 42, 10513–10523. [Google Scholar] [CrossRef] [Green Version]
- Kosowski, P.; Kosowska, K. Valuation of Energy Security for Natural Gas—European Example. Energies 2021, 14, 2678. [Google Scholar] [CrossRef]
- Mirzaei, M.A.; Nazari-Heris, M.; Zare, K.; Mohammadi-Ivatloo, B.; Marzband, M.; Asadi, S.; Anvari-Moghaddam, A. Evaluating the impact of multi-carrier energy storage systems in optimal operation of integrated electricity, gas and district heating networks. Appl. Therm. Eng. 2020, 176, 115413. [Google Scholar] [CrossRef]
- Heris, M.-N.; Mirzaei, M.A.; Asadi, S.; Mohammadi-Ivatloo, B.; Zare, K.; Jebelli, H.; Marzband, M. Evaluation of hydrogen storage technology in risk-constrained stochastic scheduling of multi-carrier energy systems considering power, gas and heating network constraints. Int. J. Hydrogen Energy 2020, 45, 30129–30141. [Google Scholar] [CrossRef]


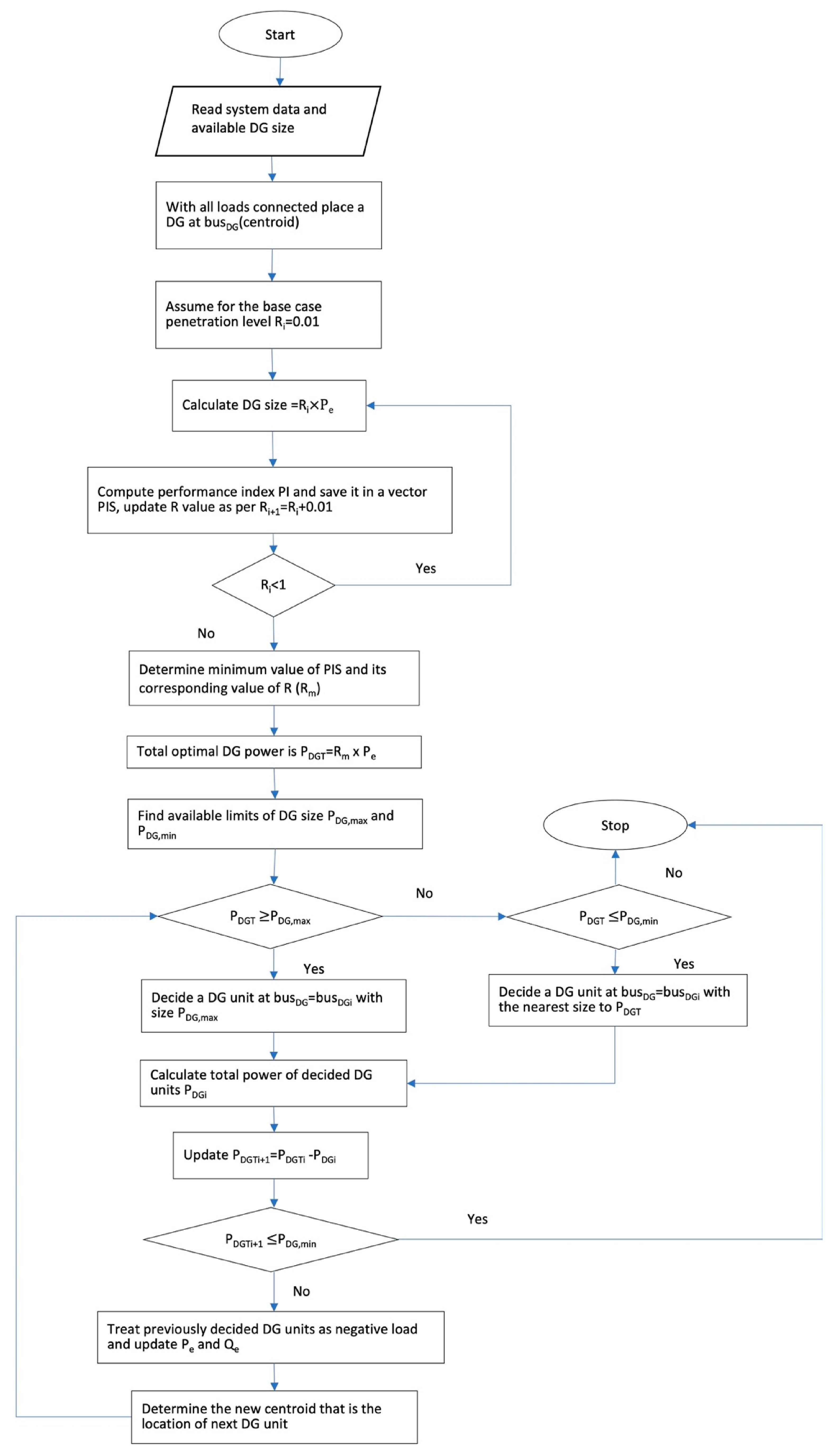
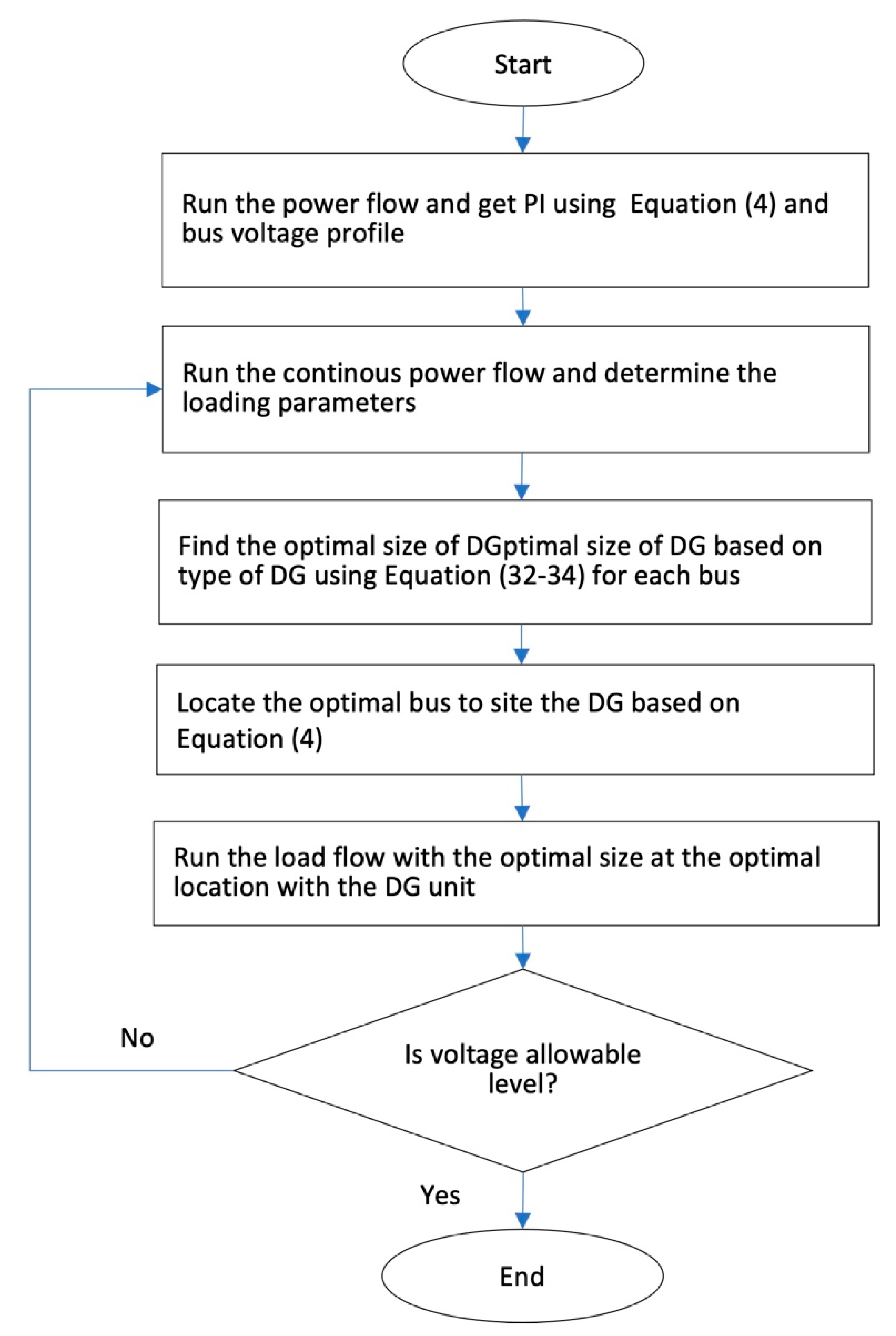
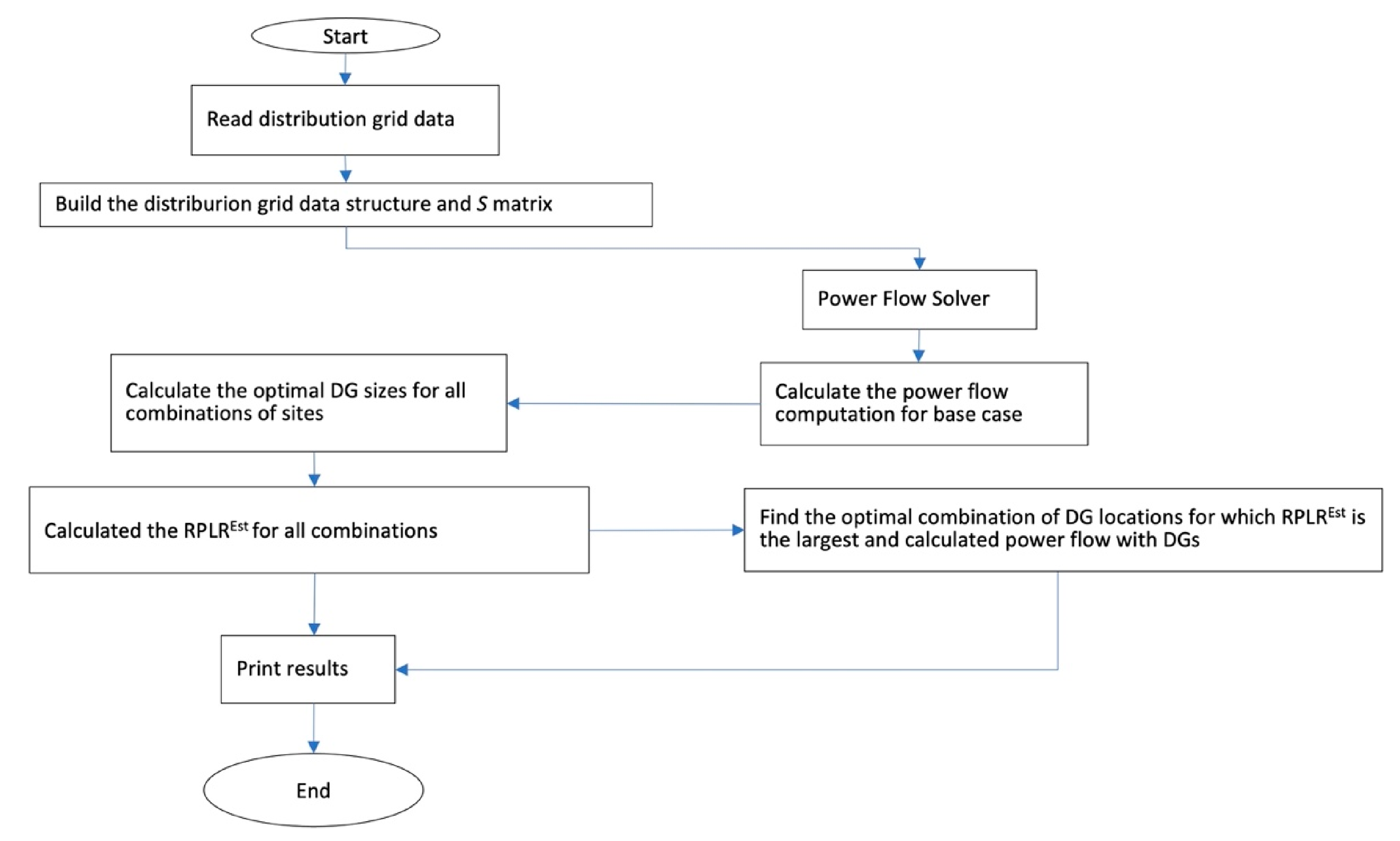
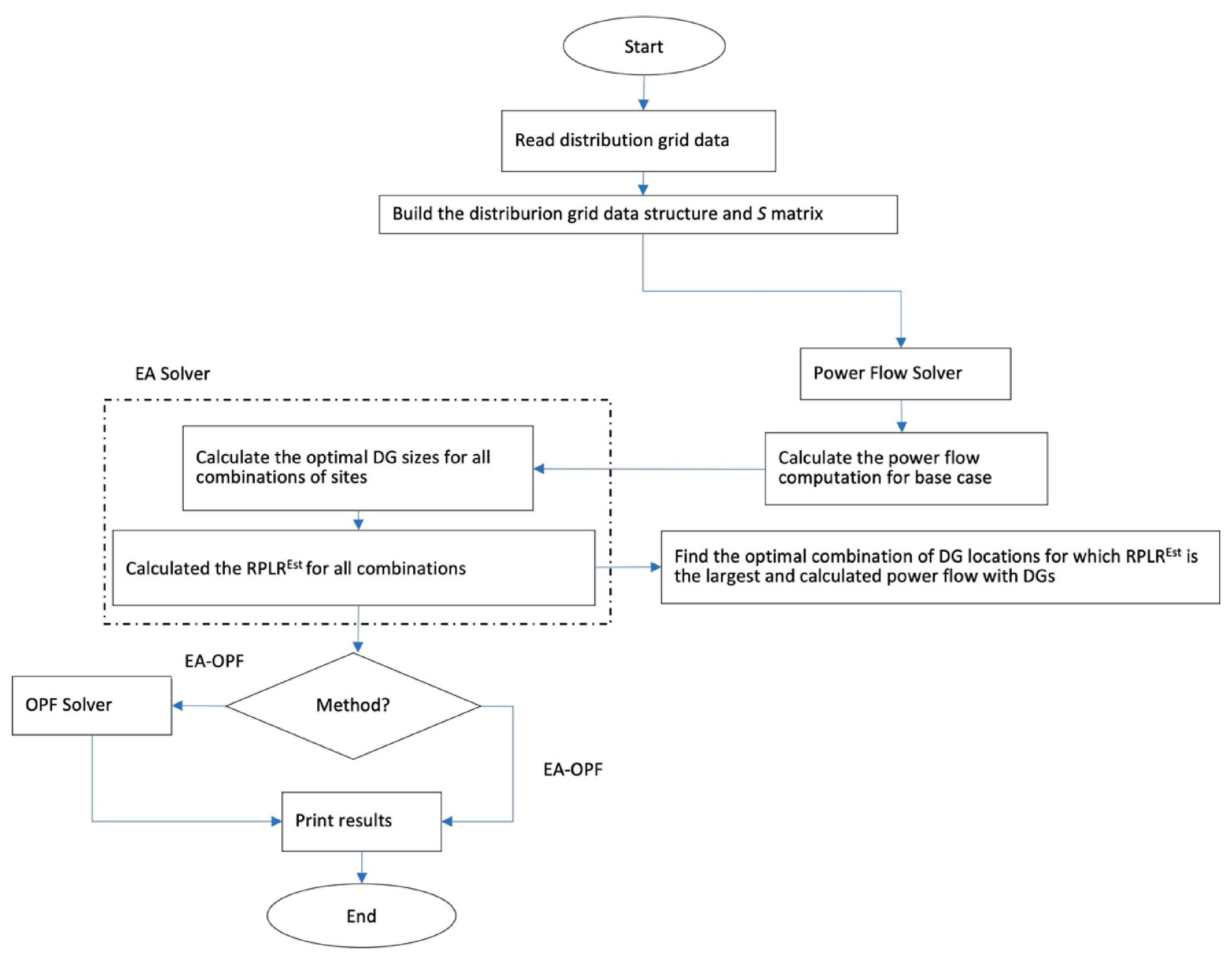
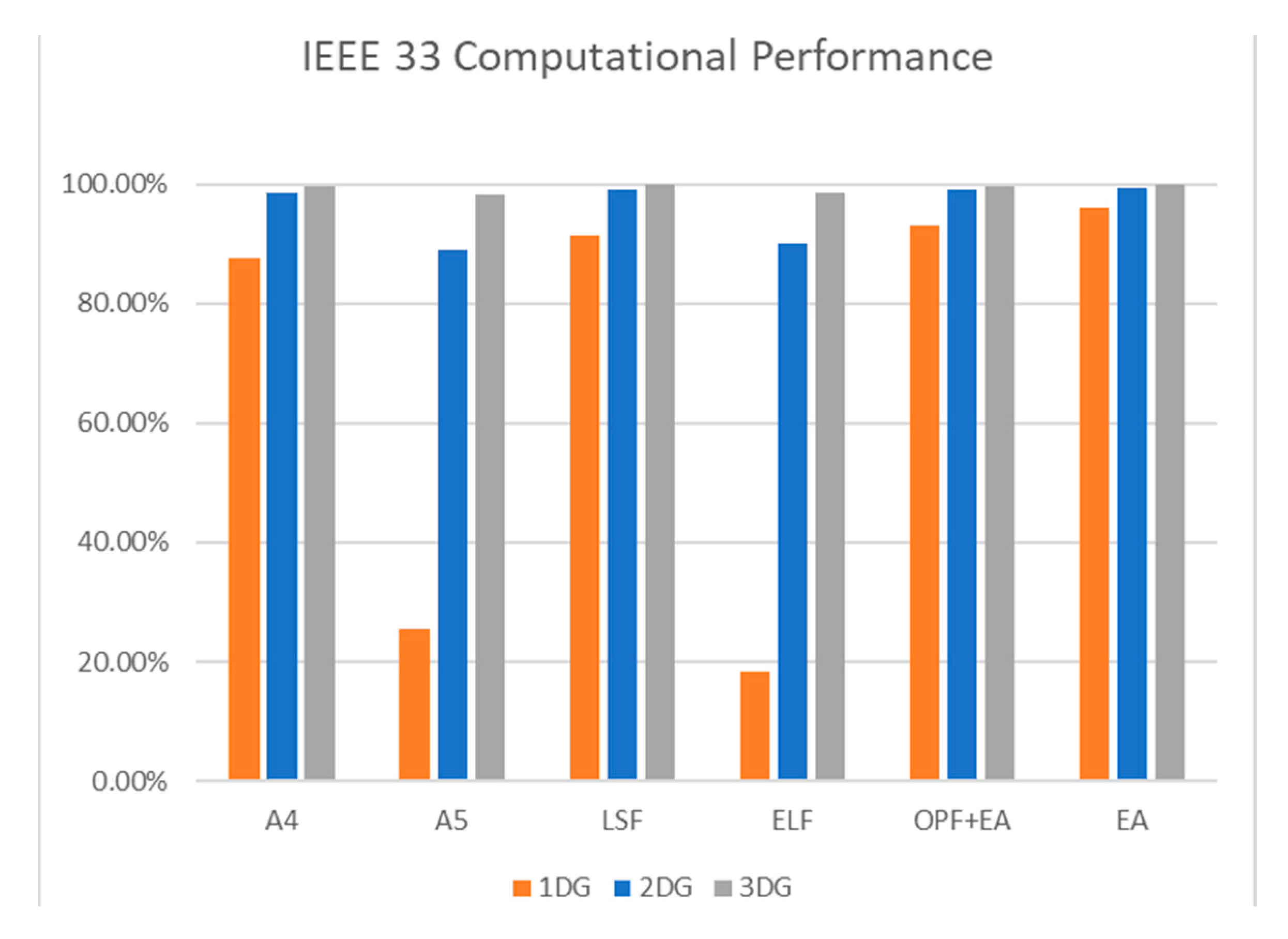
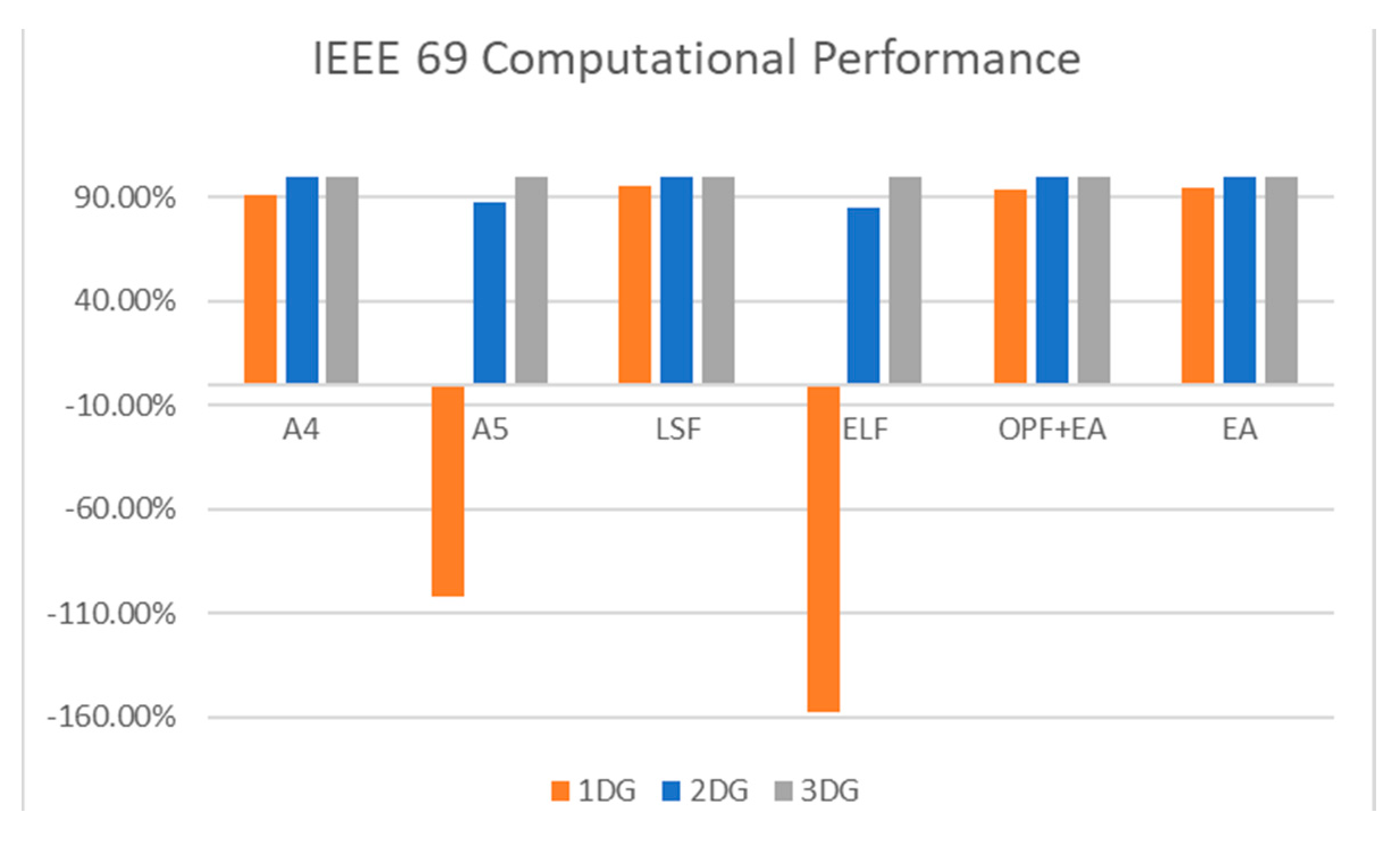
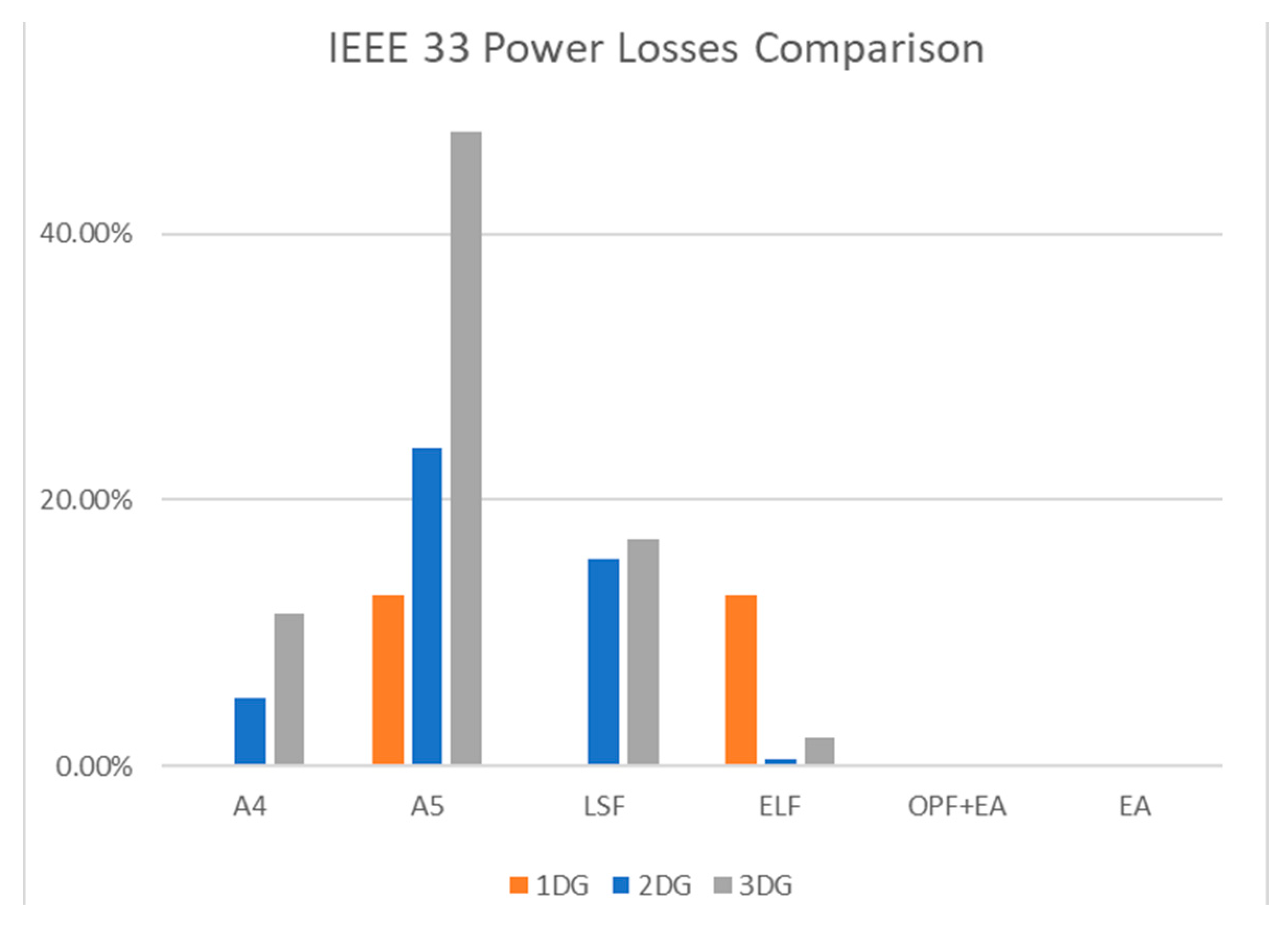

| Category | Method | Advantages | Weakness | Objective Function | References |
|---|---|---|---|---|---|
| Conventional Methods | Optimal Power Flow (OPF) |
| Closed formulation of problem, the model is not flexible to inclusion of various parameter |
| [25,26,27,28,29,30,31,32,33,34,35,36] |
| Analytical Techniques |
| The formulation of the problem can affect accuracy in complex problems. |
| [37,38,39,40,41,42,43,44,45,46,47,48] | |
| Mixed-integer linear programming |
| Inaccuracies because of linearization |
| [49,50,51,52,53,54,55] | |
| Mixed-Integer nonlinear programming |
|
|
| [56] | |
| Heuristic Methods | Genetic Algorithm |
|
|
| [57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86] |
| Simulated Annealing |
|
|
| [87,88,89,90,91,92] | |
| Heuristic Methods | Ant Colony Optimization |
|
|
| [73,93,94,95,96,97,98,99,100] |
| Particle Swam Optimization |
|
|
| [101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121] | |
| Tabu Search |
|
|
| [73,122,123,124,125,126,127] | |
| Hybrid Methods | OPF and Genetic Algorithm |
|
|
| [128,129,130,131] |
| OPF and Analytical Techniques |
|
|
| [41,132] | |
| Genetic Algorithm and Tabu Search |
|
|
| [133] |
| Bus Test System | Method | N. DG | Optimal Bus | Optimal Size [kw] | Power Loss [kW] | CPU Time [s] | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IEEE 33 | Analytical method A3 [38] | 1 | 6 | 2490 | 111.24 | 0.09 | ||||||
| Analytical method A4 [135] | 6 | 2601 | 111.10 | 0.16 | ||||||||
| Analytical method based on Loss Sensitivity factor [135] | 18 | 743 | 146.82 | 0.11 | ||||||||
| Analytical method based on Exhaustive Loss Factor [135] | 6 | 2601 | 111.10 | 1.06 | ||||||||
| Analytical method A5 [137] | 30 | 1500 | 125.21 | 0.97 | ||||||||
| Efficient analytical method [41] | 6 | 2530 | 111.07 | 0.05 | ||||||||
| Efficient analytical method combined with OPF [41] | 6 | 2590 | 111.02 | 0.09 | ||||||||
| OPF [41] | 6 | 2590 | 111.02 | 1.30 | ||||||||
| Analytical method A4 [135] | 2 | 6 | 14 | 720 | 1800 | 91.63 | 0.27 | |||||
| Analytical method based on Loss Sensitivity factor [135] | 18 | 33 | 720 | 900 | 100.69 | 0.18 | ||||||
| Analytical method based on Exhaustive Loss Factor [135] | 12 | 30 | 1020 | 1020 | 87.63 | 2.03 | ||||||
| Analytical method A5 [137] | 30 | 25 | 1500 | 1000 | 107.95 | 2.23 | ||||||
| Efficient analytical method [41] | 13 | 30 | 844 | 1149 | 87.172 | 0.11 | ||||||
| Efficient analytical method combined with OPF [41] | 13 | 30 | 852 | 1158 | 87.17 | 0.15 | ||||||
| OPF [41] | 13 | 30 | 852 | 1158 | 87.17 | 20.2 | ||||||
| Analytical method A4 [135] | 3 | 6 | 12 | 31 | 900 | 900 | 720 | 81.05 | 0.4 | |||
| Analytical method based on Loss Sensitivity factor [135] | 18 | 33 | 25 | 720 | 810 | 900 | 85.07 | 0.23 | ||||
| Analytical method based on Exhaustive Loss Factor [135] | 13 | 30 | 24 | 900 | 900 | 900 | 74.27 | 3.06 | ||||
| Analytical method A5 [137] | 30 | 25 | 24 | 1500 | 1000 | 220 | 107.35 | 3.26 | ||||
| Efficient analytical method [41] | 13 | 24 | 30 | 798 | 1099 | 1050 | 72.787 | 0.37 | ||||
| Efficient analytical method combined with OPF [41] | 13 | 24 | 30 | 802 | 1091 | 1054 | 72.79 | 0.41 | ||||
| OPF [41] | 13 | 24 | 30 | 802 | 1091 | 1054 | 72.70 | 202 | ||||
| IEEE 69 | Analytical method A3 [38] | 1 | 61 | 1810 | 83.4 | 0.54 | ||||||
| Analytical method A4 [135] | 61 | 1900 | 81.33 | 0.28 | ||||||||
| Analytical method based on Loss Sensitivity factor [135] | 65 | 1520 | 109.77 | 0.15 | ||||||||
| Analytical method based on Exhaustive Loss Factor [135] | 61 | 1900 | 81.33 | 7.75 | ||||||||
| Analytical method A5 [137] | 61 | 1900 | 83.25 | 6.09 | ||||||||
| Efficient analytical method [41] | 61 | 1878 | 83.23 | 0.16 | ||||||||
| Efficient analytical method combined with OPF [41] | 61 | 1870 | 83.23 | 0.2 | ||||||||
| OPF [41] | 61 | 1870 | 83.23 | 3.01 | ||||||||
| Analytical method A4 [135] | 2 | 61 | 17 | 1700 | 510 | 70.3 | 0.52 | |||||
| Analytical method based on Loss Sensitivity factor [135] | 65 | 27 | 1440 | 540 | 98.74 | 0.3 | ||||||
| Analytical method based on Exhaustive Loss Factor [135] | 61 | 17 | 1700 | 510 | 70.3 | 15.53 | ||||||
| Analytical method A5 [137] | 61 | 64 | 1900 | 20 | 83.23 | 12.3 | ||||||
| Efficient analytical method [41] | 61 | 17 | 1795 | 534 | 71.68 | 0.45 | ||||||
| Efficient analytical method combined with OPF [41] | 61 | 17 | 1781 | 531 | 71.68 | 0.5 | ||||||
| OPF [41] | 61 | 17 | 1781 | 531 | 71.68 | 101 | ||||||
| Analytical method A4 [135] | 3 | 61 | 17 | 11 | 1700 | 510 | 340 | 68.38 | 0.71 | |||
| Analytical method based on Loss Sensitivity factor [135] | 65 | 27 | 61 | 1360 | 510 | 510 | 58.57 | 0.52 | ||||
| Analytical method based on Exhaustive Loss Factor [135] | 61 | 17 | 11 | 1700 | 510 | 340 | 68.38 | 23.16 | ||||
| Analytical method A5 [137] | 61 | 64 | 21 | 1900 | 20 | 470 | 72.65 | 17.3 | ||||
| Efficient analytical method [41] | 61 | 18 | 11 | 1795 | 380 | 467 | 69.62 | 1.62 | ||||
| Efficient analytical method combined with OPF [41] | 61 | 18 | 11 | 1719 | 380 | 527 | 69.43 | 1.66 | ||||
| OPF [41] | 61 | 18 | 11 | 1719 | 380 | 527 | 6943 | 6655 | ||||
| Bus Test System | Method | N. DG | Optimal Bus | Optimal Size [kVA] | Power Loss [kW] | Power Factor |
|---|---|---|---|---|---|---|
| IEEE 33 | Analytical method A4 [135] | 1 | 6 | 3107 | 67.9 | 0.82 |
| 2 | 6 | 2195 | 44.39 | 0.82 | ||
| 30 | 1098 | |||||
| 3 | 6 | 1098 | 22.29 | 0.82 | ||
| 30 | 1098 | |||||
| 14 | 768 | |||||
| IEEE 69 | Analytical method A4 [135] | 1 | 61 | 2243 | 22.62 | 0.82 |
| 2 | 61 | 2195 | 7.25 | 0.82 | ||
| 17 | 659 | |||||
| 3 | 61 | 2073 | 4.95 | 0.82 | ||
| 17 | 622 | |||||
| 50 | 829 | |||||
| IEEE 33 | Efficient analytical method combined with OPF [41] | 1 | 6 | 2558 | 67.86 | 0.82 |
| 2 | 13 | 846 | 28.50 | 0.90 | ||
| 30 | 1138 | 0.73 | ||||
| 3 | 13 | 794 | 11.74 | 0.90 | ||
| 24 | 1070 | 0.90 | ||||
| 30 | 1030 | 0.71 | ||||
| IEEE 69 | Efficient analytical method combined with OPF [41] | 1 | 61 | 1828 | 23.17 | 0.82 |
| 2 | 61 | 1735 | 7.20 | 0.81 | ||
| 17 | 522 | 0.83 | ||||
| 3 | 11 | 495 | 4.27 | 0.81 | ||
| 18 | 379 | 0.83 | ||||
| 61 | 1674 | 0.81 | ||||
| IEEE 69 | Analytical method A1 [134,136] | 1 | 61 | 1844.4 | 21.08 | 0.814 |
| Analytical method A2 [136,149] | 1 | 61 | 1844.3 | 21.11 | 0.825 |
| Category | Technology | Energy Density [Wh/kg] | Power Density [W/kg] | Overall Efficiency | Lifecycle | Response Time | Capital Cost—Power [$/kW] | Capital Cost—Energy [$/kWh] | Technological Maturity |
|---|---|---|---|---|---|---|---|---|---|
| Mechanical Energy Storage Systems | Pumped hydro energy storage (PHES) | 0.5–1.5 | 0.8–1.1 | 65–85% | 30–50 y | Min | 600–2000 | 5–100 | Mature |
| Compressed air energy storage (CAES) | 30–60 | 0.65–1.2 | 40–80% | 20–40 y | Min | 400–800 | 2–50 | Developed | |
| Flywheel energy storage (FES) | 10–30 | 400–500 | 80–99% | 20 y | <ms | 250–350 | 1000–5000 | Developed | |
| Chemical Energy Storage Systems | Hydrogen storage (HS) | 800–10,000 | 5–500 | 20–50% | 5–15 y | <s | 10,000 | - | R&D—demonstration precommercial |
| Electrochemical Energy Storage Systems | Lead-acid battery | 50–75 | 150–300 | 75–80% | 5–15 y | ms | 300–600 | 200–400 | Mature |
| Nickel-cadmium battery | 60–90 | 150–230 | 60–65% | 10–20 y | ms | 500–1500 | 800–1500 | Developed | |
| sodium-sulfur battery | 150–240 | 90–230 | 80–90% | 10–15 y | ms | 1000–3000 | 300–500 | Developed | |
| Lithium-ion battery | 100–200 | 1000–2000 | 85–95% | 5–15 y | ms | 1200–4000 | 600–2500 | Mature | |
| Vanadium redox battery | 35–60 | 75–150 | 75–85% | 5–15 y | ms | 600–1500 | 150–1000 | Developed | |
| Zinc-bromite battery | 75–85 | 90–110 | 65–75% | 5–10 y | ms | 700–2500 | 150–1000 | R&D—demonstration commercial | |
| Polysulfide bromine battery | 15–30 | - | 65–75% | 10–15 y | ms | 330–2500 | 120–1000 | R&D—demonstration commercial | |
| Electrostatic and electromagnetic Energy Storage Systems | Supercapacitor energy storage system (SCES) | 3–5 | 2000–5000 | 97% | 20 y | ms | 100–300 | 500–1000 | R&D—demonstration precommercial |
| Superconducting magnetic energy storage (SMES) | 3–25 | 500–2000 | 85–99% | 20 y | ms | 1000–10,000 | 1000–10,000 | R&D—demonstration precommercial | |
| Thermal Energy Storage Systems (TES) | 80–250 | 10–30 | 30–60% | 10–40 y | s-min | 200–300 | 10–50 | R&D—demonstration commercial—Developed |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colangelo, G.; Spirto, G.; Milanese, M.; de Risi, A. Progresses in Analytical Design of Distribution Grids and Energy Storage. Energies 2021, 14, 4270. https://doi.org/10.3390/en14144270
Colangelo G, Spirto G, Milanese M, de Risi A. Progresses in Analytical Design of Distribution Grids and Energy Storage. Energies. 2021; 14(14):4270. https://doi.org/10.3390/en14144270
Chicago/Turabian StyleColangelo, Gianpiero, Gianluigi Spirto, Marco Milanese, and Arturo de Risi. 2021. "Progresses in Analytical Design of Distribution Grids and Energy Storage" Energies 14, no. 14: 4270. https://doi.org/10.3390/en14144270
APA StyleColangelo, G., Spirto, G., Milanese, M., & de Risi, A. (2021). Progresses in Analytical Design of Distribution Grids and Energy Storage. Energies, 14(14), 4270. https://doi.org/10.3390/en14144270









