A Regional Day-Ahead Rooftop Photovoltaic Generation Forecasting Model Considering Unauthorized Photovoltaic Installation
Abstract
:1. Introduction
1.1. Background and Motivation
1.2. Literature Review
1.3. Contributions
1.4. Structure of This Study
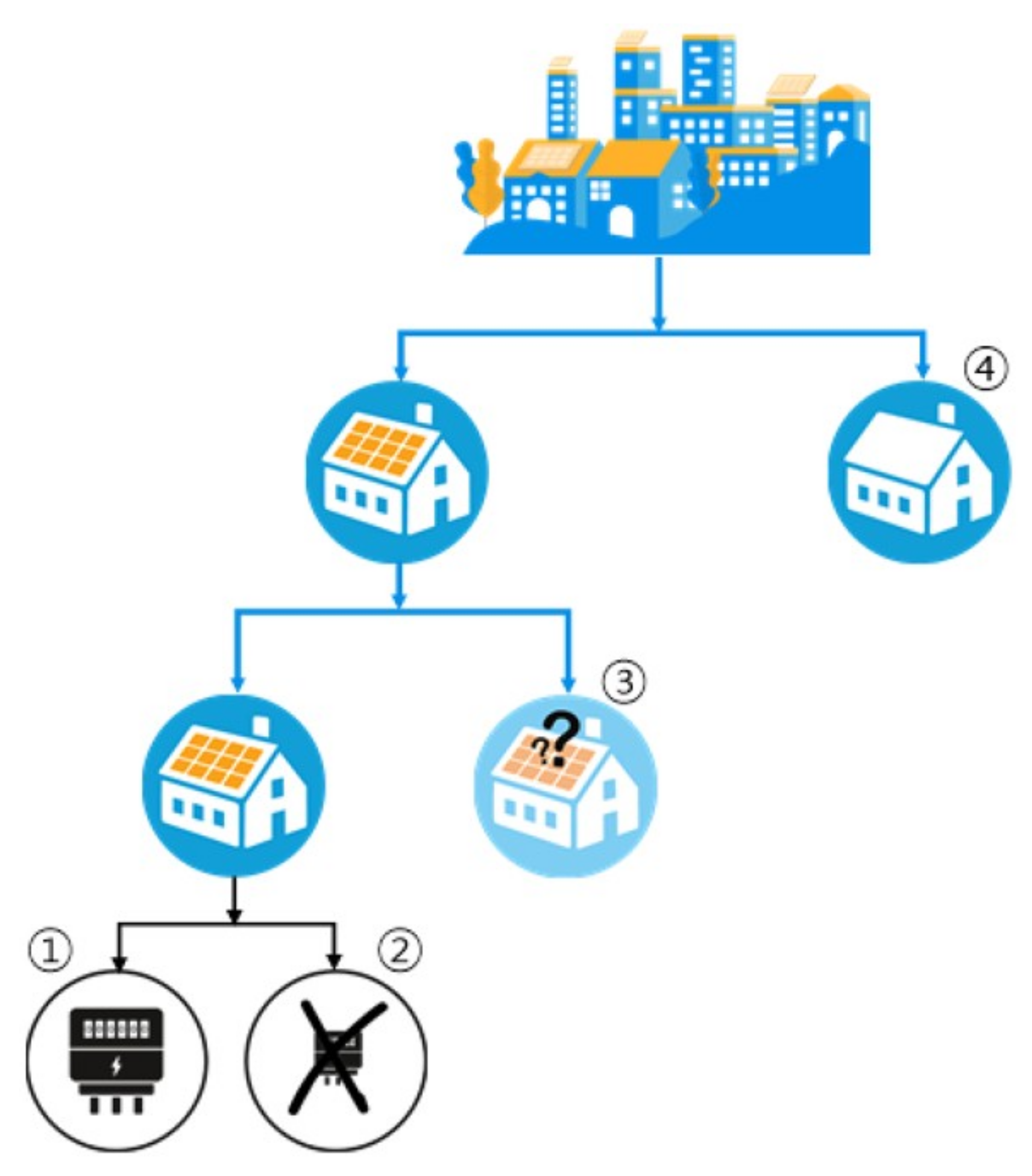
2. Problem Formulation of Unauthorized Photovoltaic (PV) Installation and Regional Rooftop PV Forecasting
2.1. Problem Statement
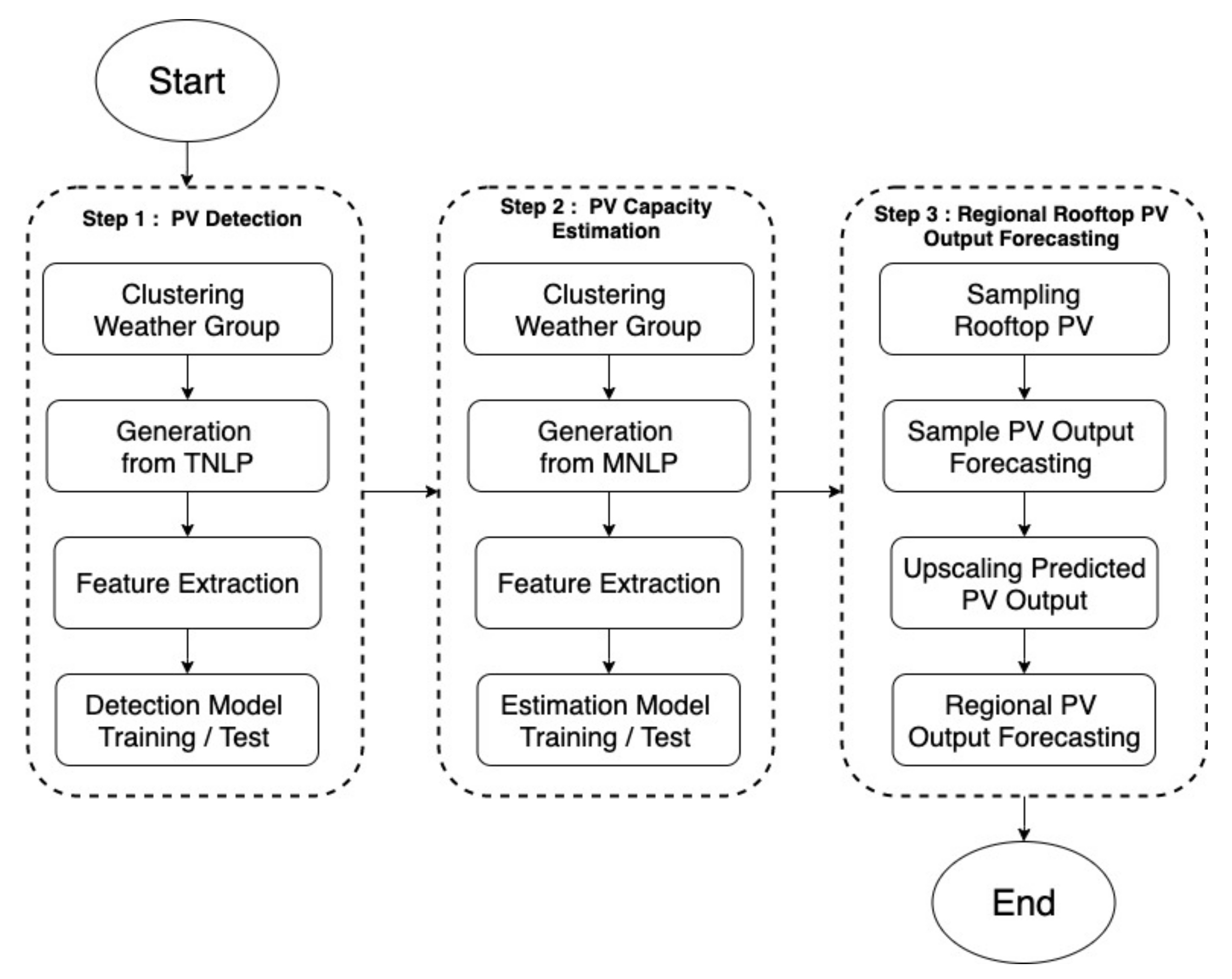
2.2. Framework of the Proposed Approach
3. Proposed Methodology of Regional Rooftop PV Generation Forecasting
3.1. Unauthorized PV Detection Model
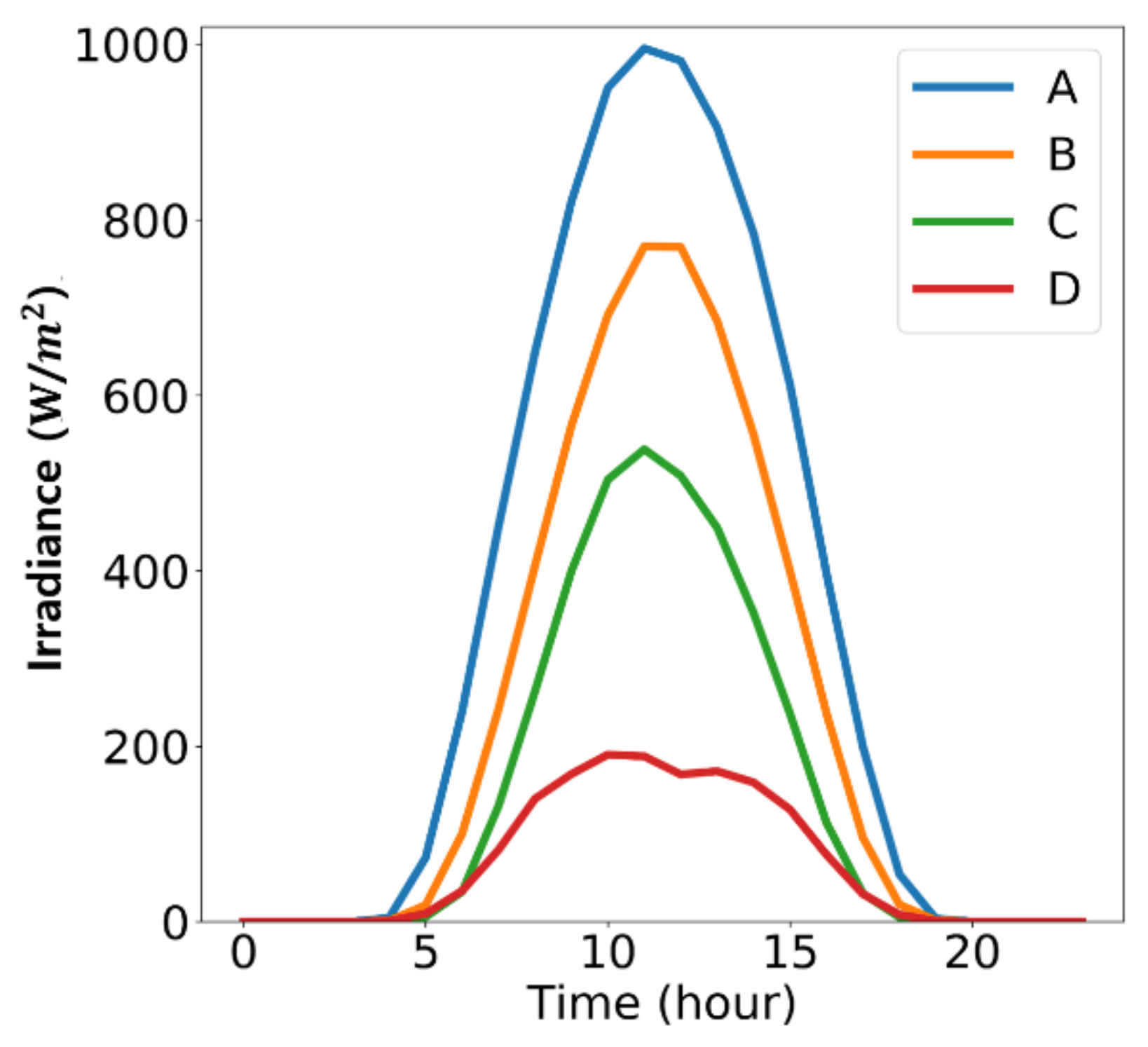
3.1.1. Four Weather Groups Clustering
3.1.2. Generation Real and Virtual Typical Net Load Pattern and Minimum Net Load Pattern
| Algorithm 1. Generation virtual TNLP |
| Input: , , Output: if then (t), (t) else (t), (t) End fordo ; for t = 0:23 do randomly select r (t) = (t); (t) = (t); End if then |
| randomly select PV capacity Else break; End End |
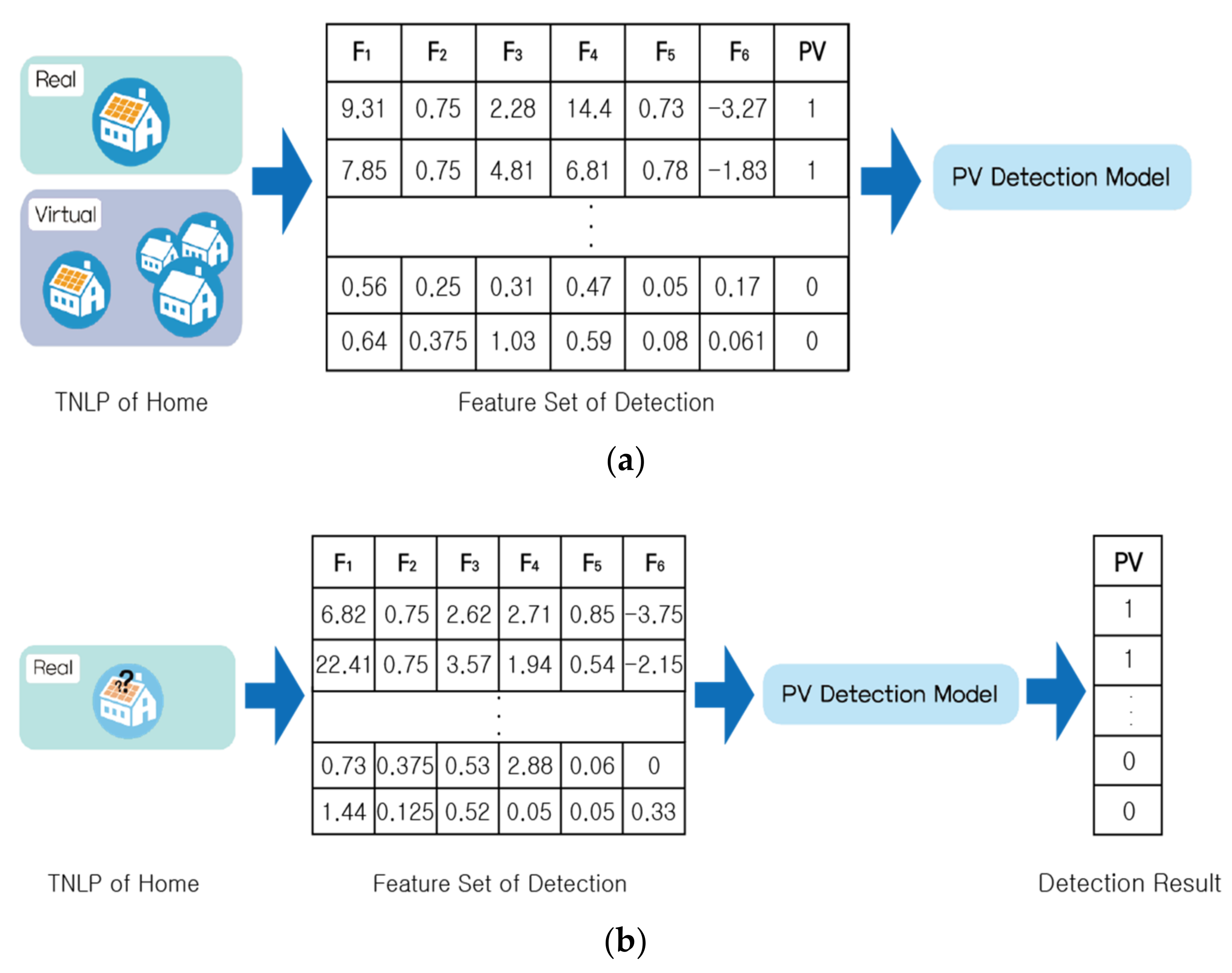
3.1.3. Feature Extraction Based on TNLP and MNLP
3.1.4. Training and Test of Unauthorized PV Detection Model
3.2. Unauthorized PV Capacity Estimation Model
3.2.1. Generation Virtual Net Load
| Algorithm 2. Generation virtual NL |
| Input: = [], , Output: Initialize for do for i = 1: do for j = 1:10 do if then else Continue; end end end for do end for do for do Select randomly PV capacity [1+(l−1)/10,1+l/10] Select randomly for WG = A:D do end end end |
3.2.2. Extracting Minimum Net Load Pattern (MNLP) for Four Weather Classes
3.2.3. Extracting Features from MNLP
3.2.4. Training and Test PV Capacity Estimation Model
3.3. Regional PV Forecasting Model
3.3.1. Clustering and Sampling of Rooftop PV
| Algorithm 3. Clustering of rooftop PV |
| Input: The number of cluster k Maximum number of iteration I Output: for all n PV k center of cluster C Randomly initialize C = for do // Assignment step for n = 1:N do end // Update step for do end end |
3.3.2. Individual Rooftop PV Generation Forecasting
3.3.3. Upscaling Sample Rooftop PV Generation by Cluster
3.3.4. Aggregating PV Generation of a Cluster
4. Case Study
4.1. Experimental Data Description
4.2. Performance Metric
4.2.1. Unauthorized PV Detection Performance Metric
4.2.2. Unauthorized PV Capacity Estimation Performance Metric
4.2.3. Regional PV Generation Forecasting Performance Metric
4.3. Simulation Results
4.3.1. Unauthorized Rooftop PV Detection Results
4.3.2. Unauthorized Rooftop PV Capacity Estimation Results
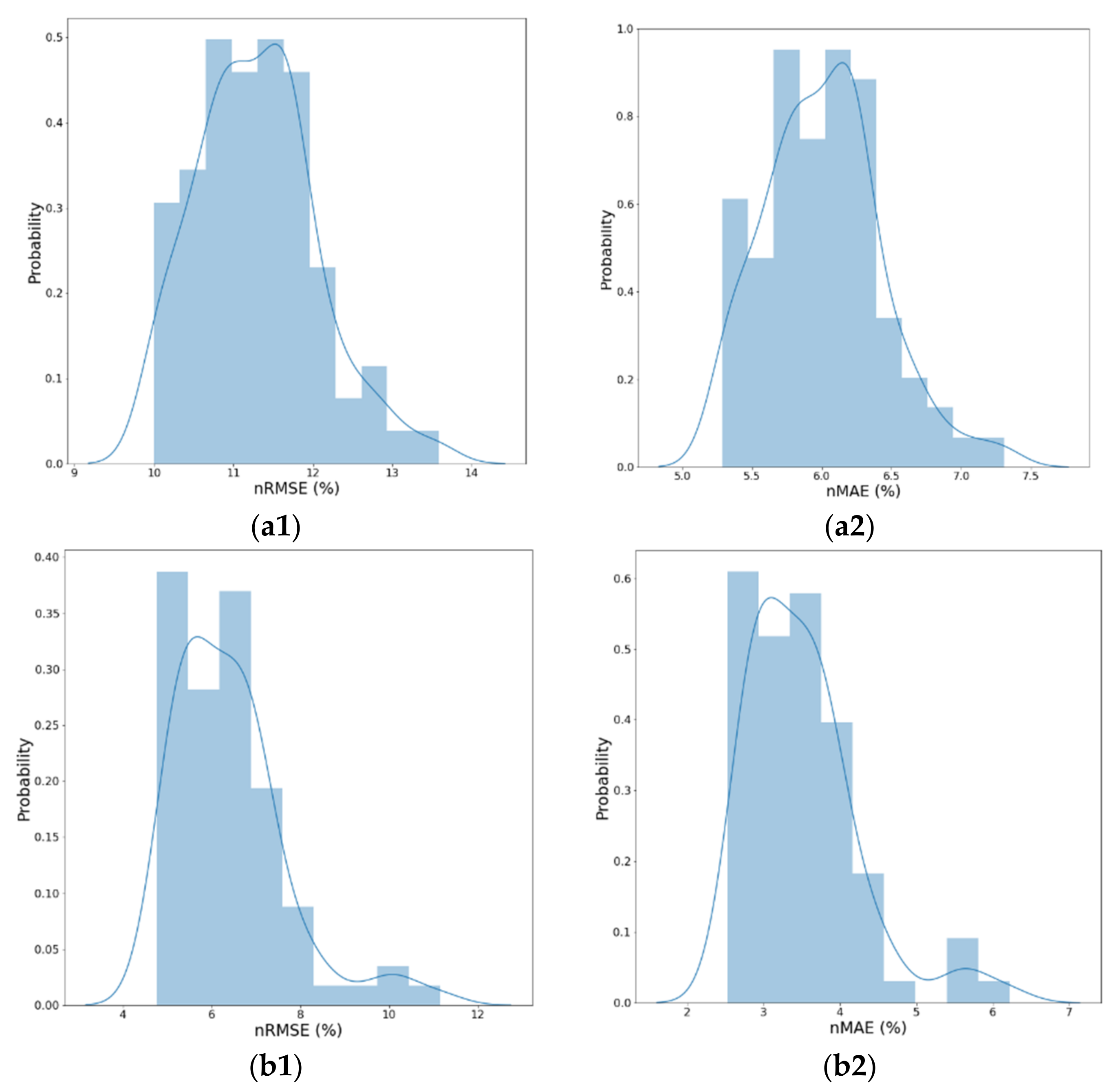
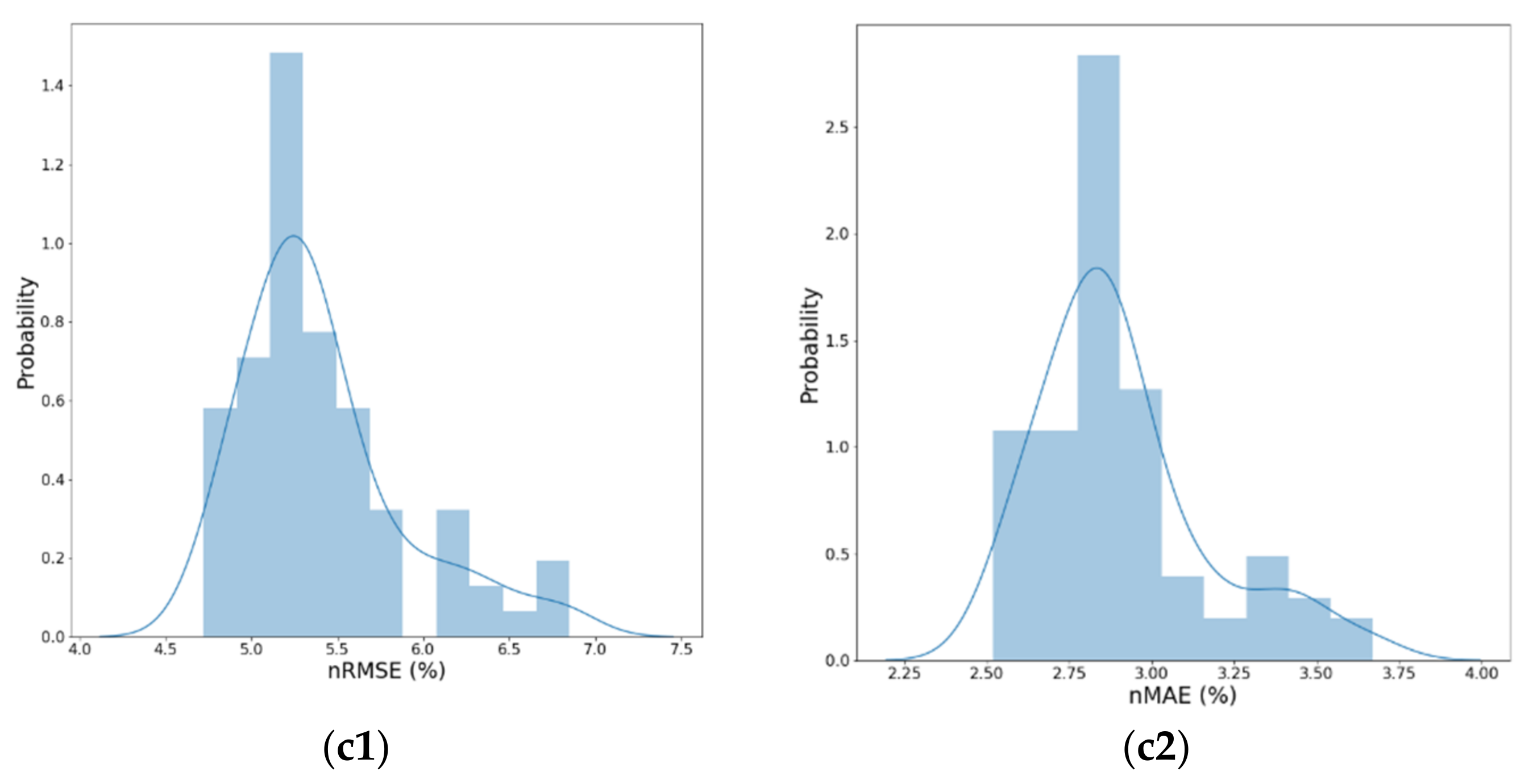
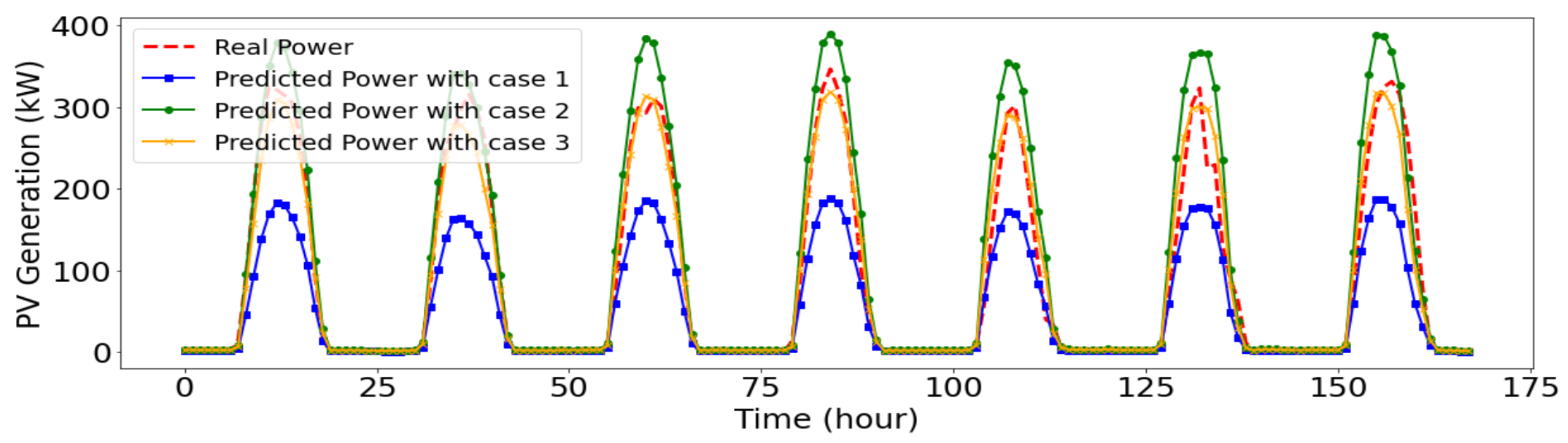
4.3.3. Regional Rooftop PV Generation Forecasting Results
5. Discussion
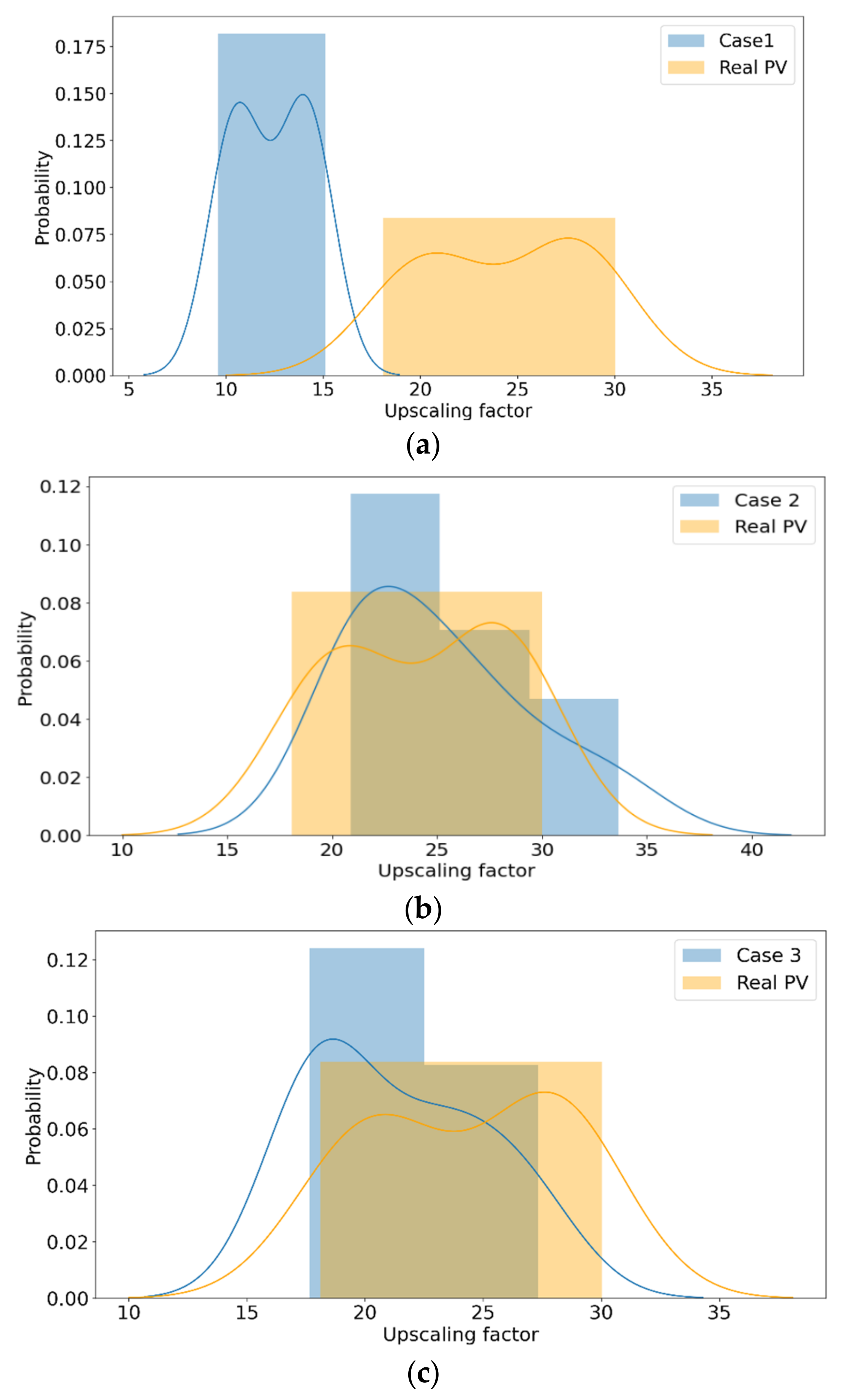
5.1. Upscaling Factor Analysis
5.2. Feature Correlation Analysis
6. Conclusions
- Investigating the impact of NL home-owned energy storage and electric vehicles on unauthorized PV detection performance.
- Exploring rooftop PV capacity uncertainty in addition to unauthorized PV installation. For example, there are rooftop PV faults and real-time rooftop PV penetration.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Fossil Fuel. Available online: https://ourworldindata.org/fossil-fuels (accessed on 15 January 2020).
- Greenhouse Gas Emissions. Available online: https://www.epa.gov/ghgemissions/global-greenhouse-gas-emissions-data (accessed on 9 February 2019).
- The Sources and Solutions. Fossil Fuels. Available online: https://www.epa.gov/nutrientpollution/sources-and-solutions-fossil-fuels (accessed on 9 February 2020).
- Renewable Energy Statistics 2021. Available online: https://www.irena.org/publications/2021/March/Renewable-Capacity-Statistics-2021 (accessed on 2 November 2019).
- Improving Load Forecast with BTM Solar Forecast. Available online: https://www.pjm.com/-/media/committees-groups/committees/oc/20190514/20190514-item-20-improving-load-forecast-with-btm-solar-forecast.ashx (accessed on 9 June 2019).
- World Energy Issue Insight. Available online: http://www.keei.re.kr/keei/download/WEIS1702.pdf (accessed on 6 July 2020).
- PV Status Report. Available online: https://ec.europa.eu/jrc/sites/jrcsh/files/kjna29938enn_1.pdf (accessed on 9 February 2020).
- Katsanevakis, M.; Stewart, R.A.; Lu, J. Energy storage system utilisation to increase photovoltaic penetration in low voltage distribution feeders. J. Energy Storage 2017, 14, 329–347. [Google Scholar] [CrossRef]
- 7 Reasons Why You Should Use Solar Power. Available online: https://www.greenmatch.co.uk/blog/2014/07/7-reasons-why-you-should-use-solar-power (accessed on 12 April 2020).
- Niccolai, A.; Dolara, A.; Ogliari, E. Hybrid PV Power Forecasting Methods: A Comparison of Different Approaches. Energies 2021, 14, 451. [Google Scholar] [CrossRef]
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; de Pison, F.M.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Lorenz, E.; Scheidsteger, T.; Hurka, J.; Heinemann, D.; Kurz, C. Regional PV power prediction for improved grid integration. Prog. Photovolt. Res. Appl. 2011, 19, 757–771. [Google Scholar] [CrossRef]
- Lorenz, E.; Heinemann, D.; Kurz, C. Local and regional photovoltaic power prediction for large scale grid integration: Assessment of a new algorithm for snow detection. Prog. Photovolt. Res. Appl. 2012, 20, 760–769. [Google Scholar] [CrossRef]
- Junior, J.G.d.S.F.; Oozeki, T.; Ohtake, H.; Shimose, K.I.; Takashima, T.; Ogimoto, K. Regional forecasts and smoothing effect of photovoltaic power generation in Japan: An approach with principal component analysis. Renew. Energy 2014, 68, 403–413. [Google Scholar] [CrossRef]
- Junior, J.; Oozeki, T.; Ohtake, H.; Shimose, K.; Takashima, T.; Ogimoto, K. Forecasting regional photovoltaic power generation-a comparison of strategies to obtain one-day-ahead data. Energy Procedia 2014, 57, 1337–1345. [Google Scholar] [CrossRef] [Green Version]
- Fonseca Junior, J.G.d.S.; Oozeki, T.; Ohtake, H.; Takashima, T.; Ogimoto, K. Regional forecasts of photovoltaic power generation according to different data availability scenarios: A study of four methods. Prog. Photovolt. Res. Appl. 2015, 23, 1203–1218. [Google Scholar] [CrossRef]
- Zamo, M.; Mestre, O.; Arbogast, P.; Pannekoucke, O. A benchmark of statistical regression methods for short-term forecasting of photovoltaic electricity production, part I: Deterministic forecast of hourly production. Sol. Energy 2014, 105, 792–803. [Google Scholar] [CrossRef]
- Davò, F.; Alessandrini, S.; Sperati, S.; Delle Monache, L.; Airoldi, D.; Vespucci, M.T. Post-processing techniques and principal component analysis for regional wind power and solar irradiance forecasting. Sol. Energy 2016, 134, 327–338. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Sun, Q.; Lehman, B.; Lu, S.; Hamann, H.F.; Simmons, J.; Black, J. A machine-learning approach for regional photovoltaic power forecasting. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Saint-Drenan, Y.M.; Good, G.H.; Braun, M.; Freisinger, T. Analysis of the uncertainty in the estimates of regional PV power generation evaluated with the upscaling method. Sol. Energy 2016, 135, 536–550. [Google Scholar] [CrossRef] [Green Version]
- Pierro, M.; De Felice, M.; Maggioni, E.; Moser, D.; Perotto, A.; Spada, F.; Cornaro, C. Data-driven upscaling methods for regional photovoltaic power estimation and forecast using satellite and numerical weather prediction data. Sol. Energy 2017, 158, 1026–1038. [Google Scholar] [CrossRef]
- Pierro, M.; De Felice, M.; Maggioni, E.; Moser, D.; Perotto, A.; Spada, F.; Cornaro, C. A new approach for regional photovoltaic power estimation and forecast. In Proceedings of the 33rd European Photovoltaic Solar Energy Conference and Exhibition (EUPVSEC), Amsterdam, The Netherlands, 25–29 September 2017; pp. 25–29. [Google Scholar]
- Fu, L.; Yang, Y.; Yao, X.; Jiao, X.; Zhu, T. A Regional Photovoltaic Output Prediction Method Based on Hierarchical Clustering and the mRMR Criterion. Energies 2019, 12, 3817. [Google Scholar] [CrossRef] [Green Version]
- Koster, D.; Minette, F.; Braun, C.; O’Nagy, O. Short-term and regionalized photovoltaic power forecasting, enhanced by reference systems, on the example of Luxembourg. Renew. Energy 2019, 132, 455–470. [Google Scholar] [CrossRef]
- Saint-Drenan, Y.M.; Vogt, S.; Killinger, S.; Bright, J.M.; Fritz, R.; Potthast, R. Bayesian parameterisation of a regional photovoltaic model—Application to forecasting. Sol. Energy 2019, 188, 760–774. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Li, Y.; Lu, S.; Hamann, H.F.; Hodge, B.M.; Lehman, B. A solar time-based analog ensemble method for regional solar power forecasting. IEEE Trans. Sustain. Energy 2018, 10, 268–279. [Google Scholar] [CrossRef]
- Zhang, X.; Grijalva, S. A data-driven approach for detection and estimation of residential PV installations. IEEE Trans. Smart Grid 2016, 7, 2477–2485. [Google Scholar] [CrossRef]
- Shaker, H.; Zareipour, H.; Wood, D. A data-driven approach for estimating the power generation of invisible solar sites. IEEE Trans. Smart Grid 2015, 7, 2466–2476. [Google Scholar] [CrossRef]
- Dealing with Unregisterd and Unauthorized Systems. Available online: https://solar-support.org/files/299/dump (accessed on 27 January 2020).
- EPIC 1.21—Pilot Methods for Automatic Identification of Distributed Energy Resources (such as Solar PV) as they Interconnect to the Grid to Improve Safety & Reliability. Available online: https://www.pge.com/pge_global/common/pdfs/about-pge/environment/what-we-are-doing/electric-program-investment-charge/PGE-EPIC-Project-1.21.pdf (accessed on 3 March 2020).
- HECO Customers asked to Disconnect Unauthorized PV Systems. Available online: http://khon2.com/2014/09/05/heco-customers-asked-to-disconnect-unauthorizedpv-systems/ (accessed on 13 June 2021).
- Transient Over-Voltage Mitigation and Its Prevention in Secondary Distribution Networks with High PV-to-Load Ratio, Hawaii Electric Companies. Available online: https://www.hnei.hawaii.edu/wp-content/uploads/Transient-Over-Voltage-Mitigation-and-Prevention-In-Secondary-Distribution-Networks.pdf (accessed on 15 June 2021).
- California Solar Permitting Guidebook, Solar Permitting Work Group, The Governor’s Office of Planning and Research. Available online: https://www.buildingincalifornia.com/wp-content/uploads/2014/02/CaliforniaSolarPermittingGuidebook-2012.pdf (accessed on 15 June 2021).
- Shaker, H.; Zareipour, H.; Wood, D. Estimating power generation of invisible solar sites using publicly available data. IEEE Trans. Smart Grid 2016, 7, 2456–2465. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, N.; Chen, Q.; Kirschen, D.S.; Li, P.; Xia, Q. Data-driven probabilistic net load forecasting with high penetration of behind-the-meter PV. IEEE Trans. Power Syst. 2017, 33, 3255–3264. [Google Scholar] [CrossRef]
- Kapourchali, M.H.; Sepehry, M.; Aravinthan, V. Multivariate Spatio-temporal Solar Generation Forecasting: A Unified Approach to Deal with Communication Failure and Invisible Sites. IEEE Syst. J. 2018, 13, 1804–1812. [Google Scholar] [CrossRef]
- Shaker, H.; Manfre, D.; Zareipour, H. Forecasting the aggregated output of a large fleet of small behind-the-meter solar photovoltaic sites. Renew. Energy 2020, 147, 1861–1869. [Google Scholar] [CrossRef]
- He, X.; Qiu, R.C.; Chu, L.; Ai, Q.; Ling, Z.; Zhang, J. Invisible Units Detection and Estimation Based on Random Matrix Theory. IEEE Trans. Power Syst. 2019, 35, 1846–1855. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Li, K.; Wang, X.; Jiang, L.; Ren, J.; Mi, Z.; Shafie-khah, M.; Catalão, J.P. A distributed PV system capacity estimation approach based on support vector machine with customer net load curve features. Energies 2018, 11, 1750. [Google Scholar] [CrossRef] [Green Version]
- Li, K.; Wang, F.; Mi, Z.; Fotuhi-Firuzabad, M.; Duic´, N.; Wang, T. Capacity and output power estimation approach of individual behind-the-meter distributed photovoltaic system for demand response baseline estimation. Appl. Energy 2019, 253, 113595. [Google Scholar] [CrossRef]
- Solar Home Electricity Data. Available online: https://www.ausgrid.com.au/Industry/Our-Research/Data-to-share/Solar-home-electricity-data (accessed on 21 October 2019).
- Yuan, C.; Yang, H. Research on K-value selection method of K-means clustering algorithm. J. Multidiscip. Sci. J. 2019, 2, 226–235. [Google Scholar] [CrossRef] [Green Version]
- PVlib, Python Solar Open Source Library. Available online: https://pvlib-python-dacoex.readthedocs.io/en/latest/index.html (accessed on 8 July 2019).
- Obtain Historical Weather Forecast Data in CSV Format Using Python. Available online: https://www.freecodecamp.org/news/obtain-historical-weather-forecast-data-in-csv-format-using-python/ (accessed on 16 September 2019).
- Home Solar Power in New South Wales. Available online: https://www.solarquotes.com.au/australia/solar-power-nsw/ (accessed on 2 February 2020).
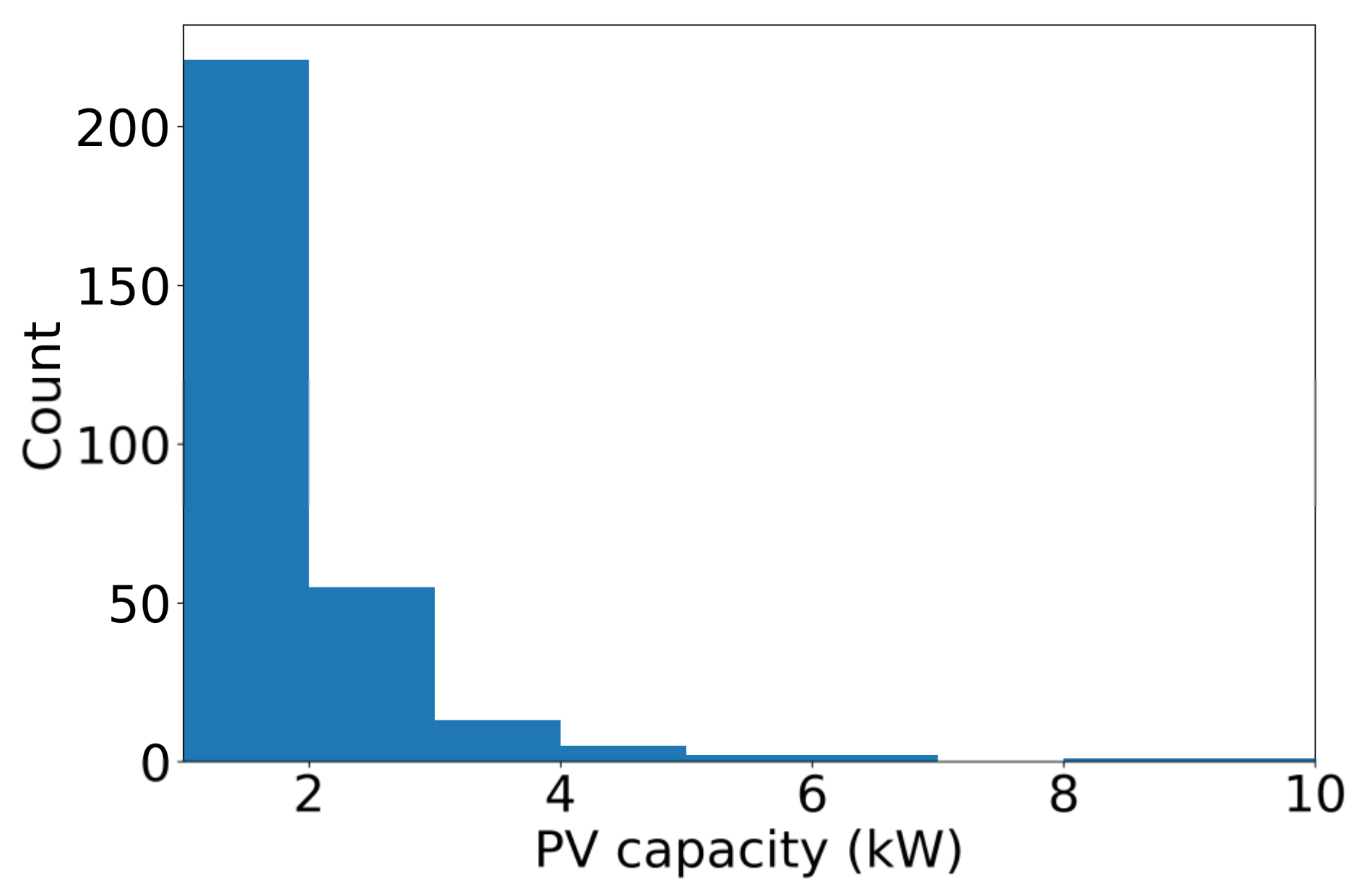
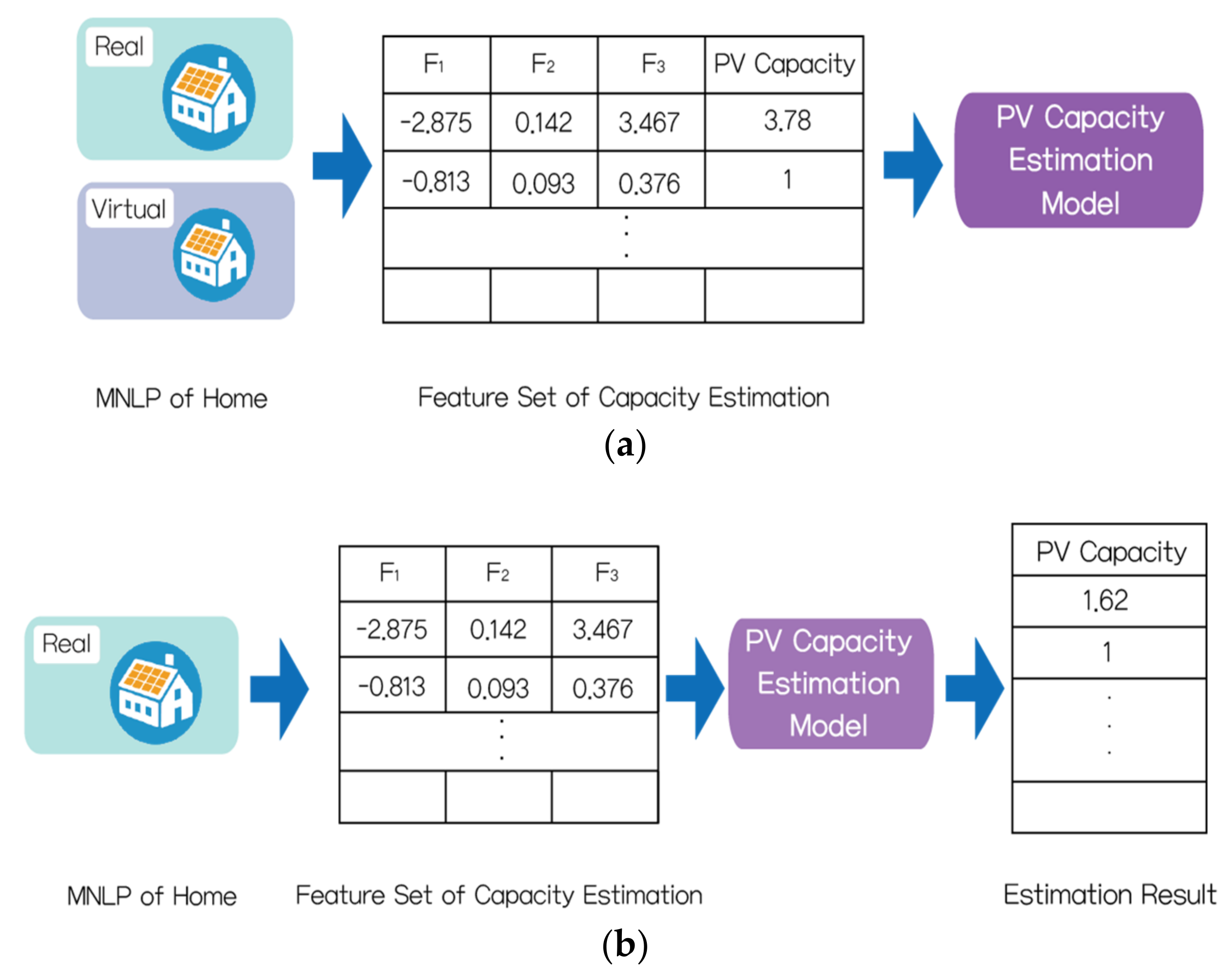

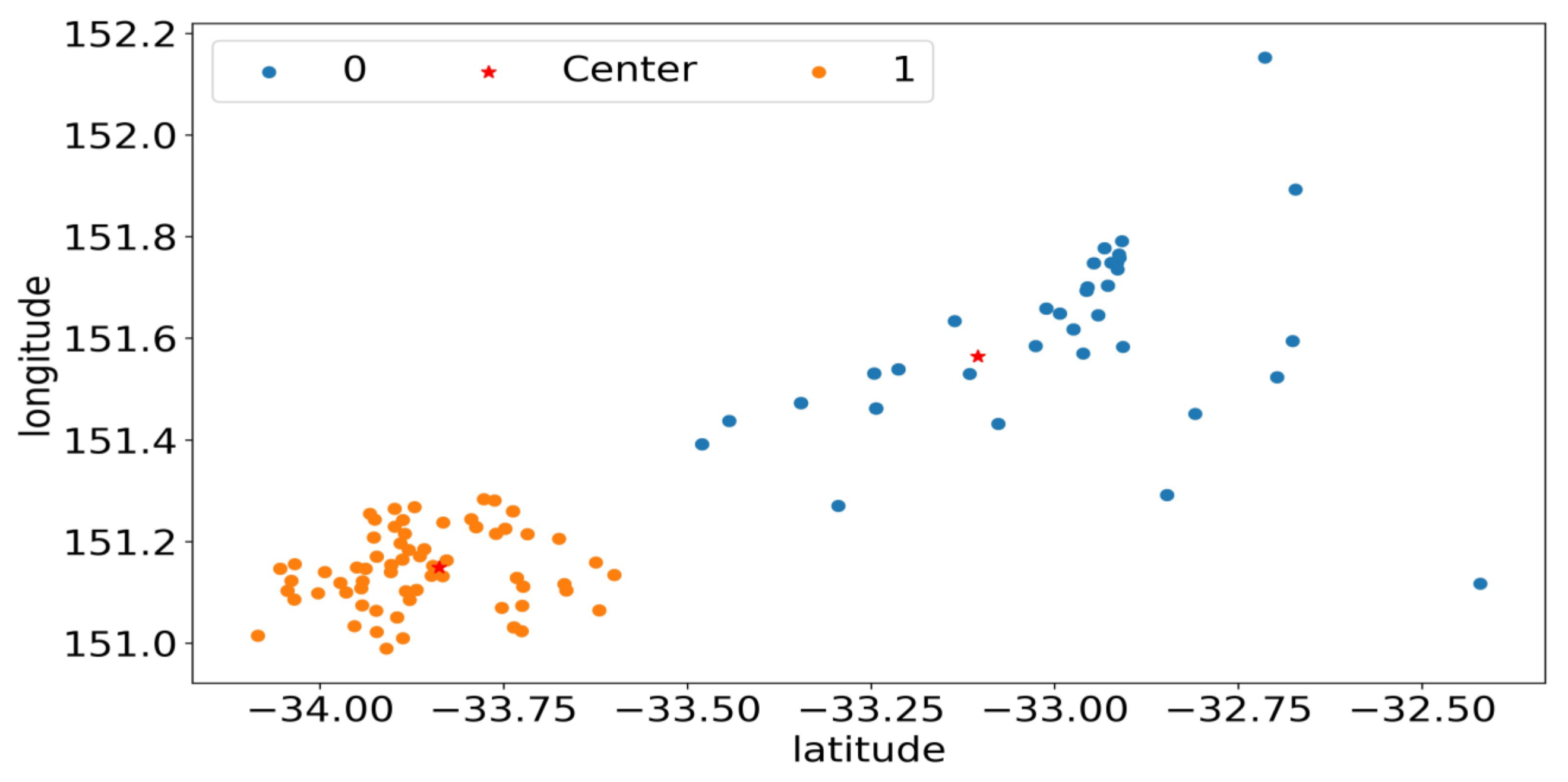
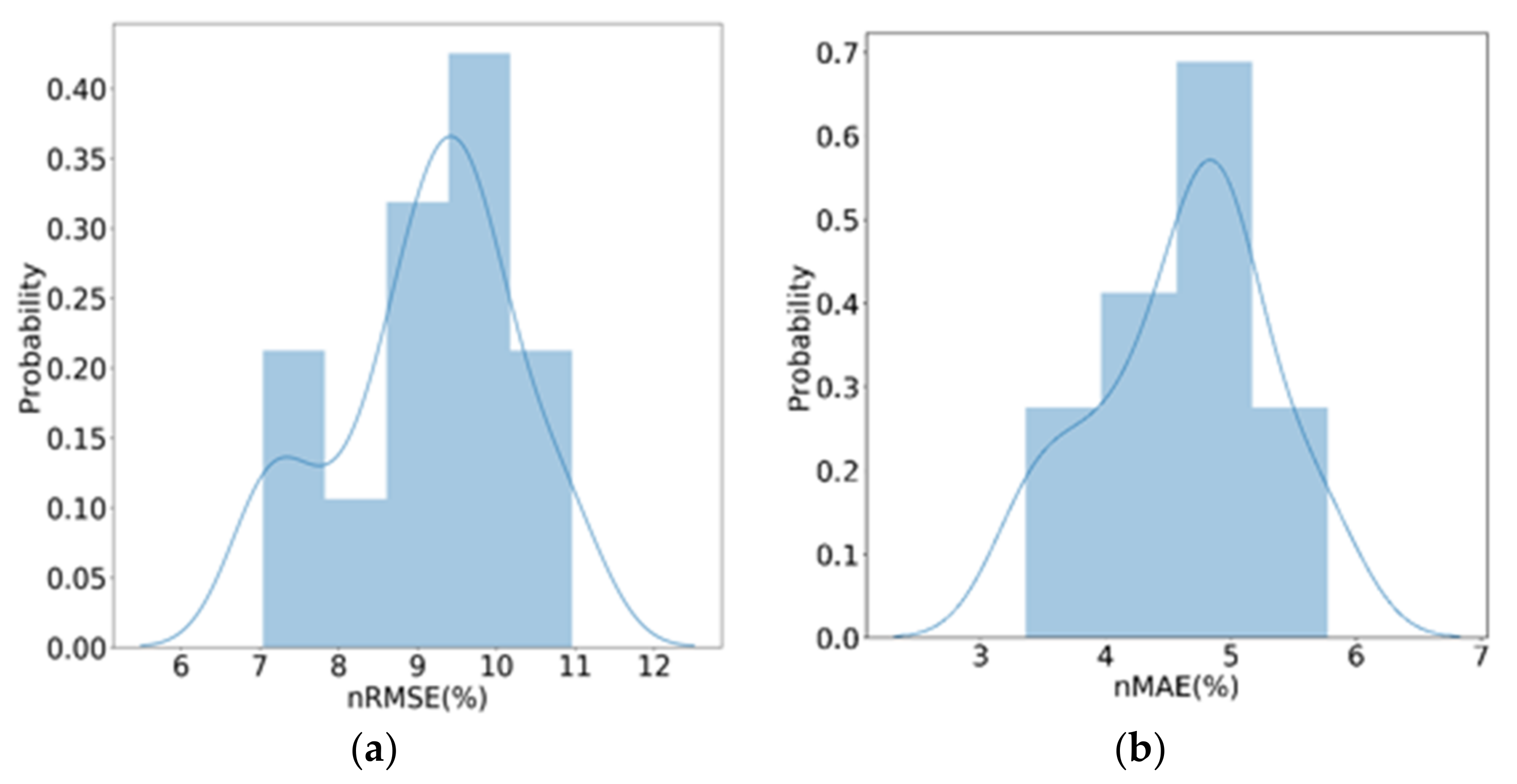
| Literature Group | Research Subject | Reference |
|---|---|---|
| 1 | Regional utility scale photovoltaic (PV) forecasting | [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26] |
| 2 | Regional behind the meter (BTM) PV forecasting | [28,34,35,36,37] |
| 3 | Unauthorized PV detection and PV capacity estimation | [27,38,39,40] |
| Question | H1 | H2 | H3 | H4 |
|---|---|---|---|---|
| Is there a rooftop PV sub meter at home? | Yes | No | No | No |
| Is a rooftop PV at home authorized? | Yes | Yes | No | No |
| Is a rooftop PV installed at home? | Yes | Yes | Yes | No |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Nhome | 1500 | rSam | 0.08 |
| NPV | 300 | ts | 9 |
| rAu | 0.5 | te, tf | 16, 19 |
| Metric | Best | Average | Worst |
|---|---|---|---|
| PA | 96.00 | 90.69 | 77.33 |
| NPA | 99.67 | 96.58 | 89.67 |
| OA | 98.00 | 95.93 | 90.15 |
| Metric | Best | Average | Worst |
|---|---|---|---|
| PA | 100 | 99.81 | 96.67 |
| NPA | 98.33 | 97.02 | 95.67 |
| OA | 98.52 | 97.33 | 96.07 |
| Study | Best (%) | Average (%) | Worst (%) |
|---|---|---|---|
| [35] | 66.00 | 92.79 | 113.00 |
| Proposed method | 34.00 | 44.21 | 63.00 |
| Error Metric (%) | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
| Normalized Root Mean Square Error (nRMSE) | 11.29 | 6.41 | 5.41 |
| Normalized Mean Absolute Error (nMAE) | 6.01 | 3.52 | 2.95 |
| Feature | ||||||
|---|---|---|---|---|---|---|
| MIC value | 0.445 | 0.135 | 0.217 | 0.207 | 0.600 | 0.722 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, T.; Kim, J. A Regional Day-Ahead Rooftop Photovoltaic Generation Forecasting Model Considering Unauthorized Photovoltaic Installation. Energies 2021, 14, 4256. https://doi.org/10.3390/en14144256
Kim T, Kim J. A Regional Day-Ahead Rooftop Photovoltaic Generation Forecasting Model Considering Unauthorized Photovoltaic Installation. Energies. 2021; 14(14):4256. https://doi.org/10.3390/en14144256
Chicago/Turabian StyleKim, Taeyoung, and Jinho Kim. 2021. "A Regional Day-Ahead Rooftop Photovoltaic Generation Forecasting Model Considering Unauthorized Photovoltaic Installation" Energies 14, no. 14: 4256. https://doi.org/10.3390/en14144256
APA StyleKim, T., & Kim, J. (2021). A Regional Day-Ahead Rooftop Photovoltaic Generation Forecasting Model Considering Unauthorized Photovoltaic Installation. Energies, 14(14), 4256. https://doi.org/10.3390/en14144256






