A Frequency Adaptive Scheme Based on Newton Structure of PRRC for LCL-Type Inverter Connected with Weak Grid
Abstract
:1. Introduction
2. PRRC Control Scheme
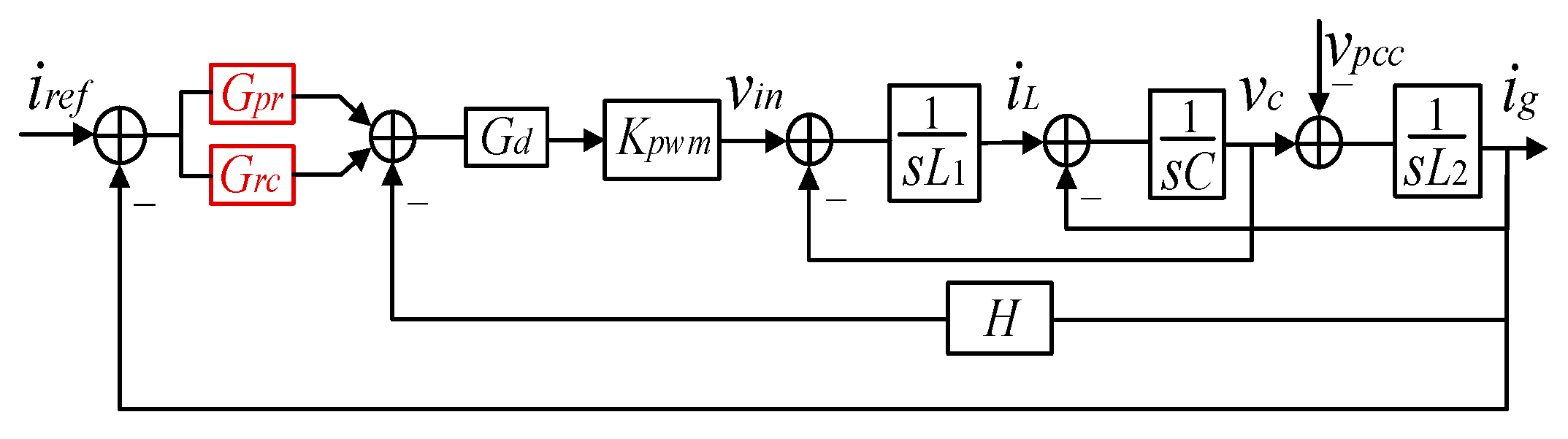
2.1. Configuration of LCL-Type Grid-Connected Inverter System
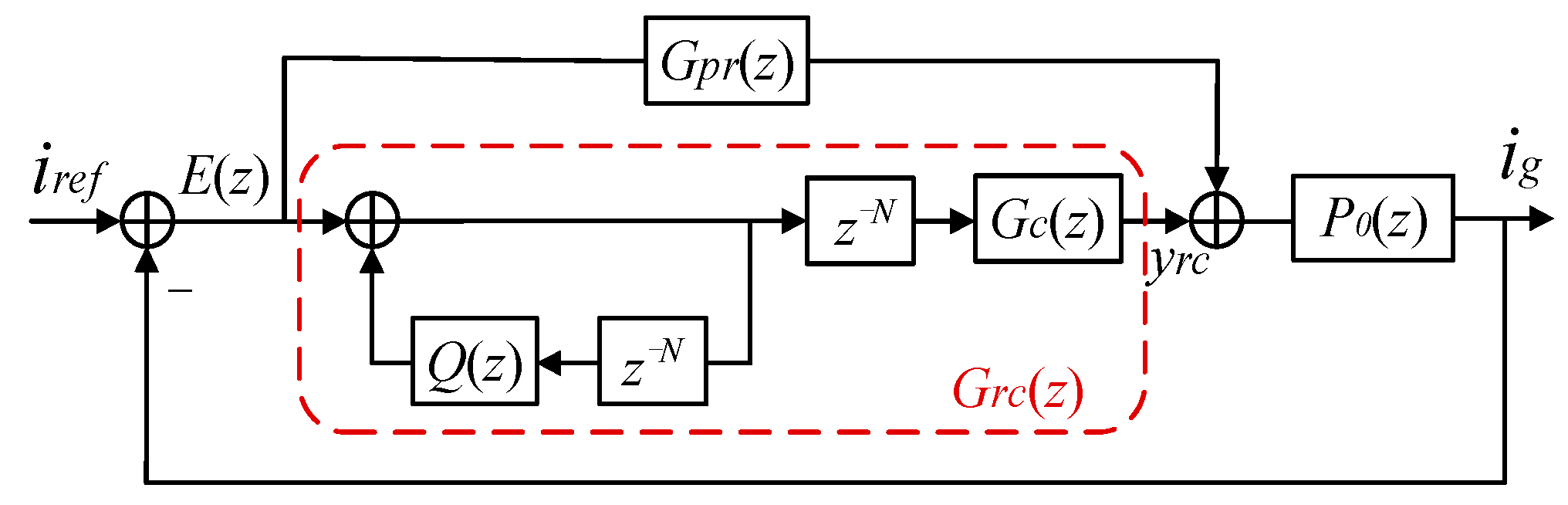
2.2. Proposed PRRC
3. Frequency Adaptation of RC
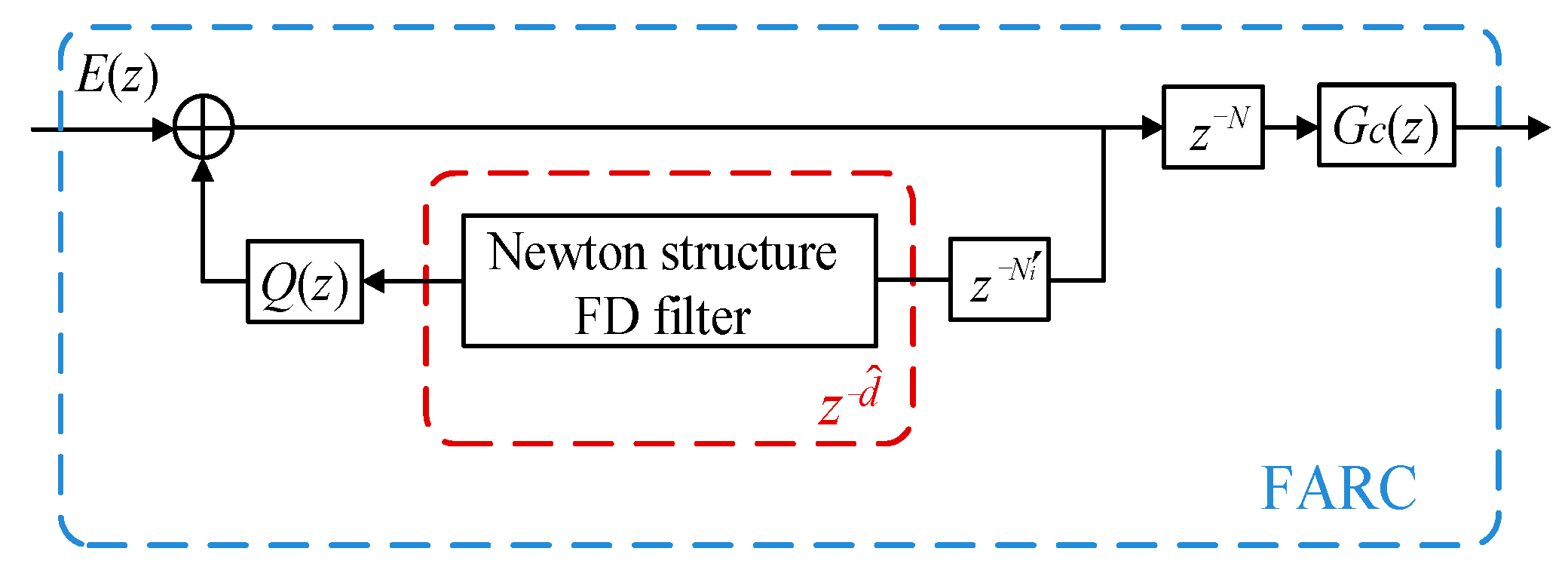
3.1. FARC Based on Newton Structure
3.2. Transformation from Farrow to Newton
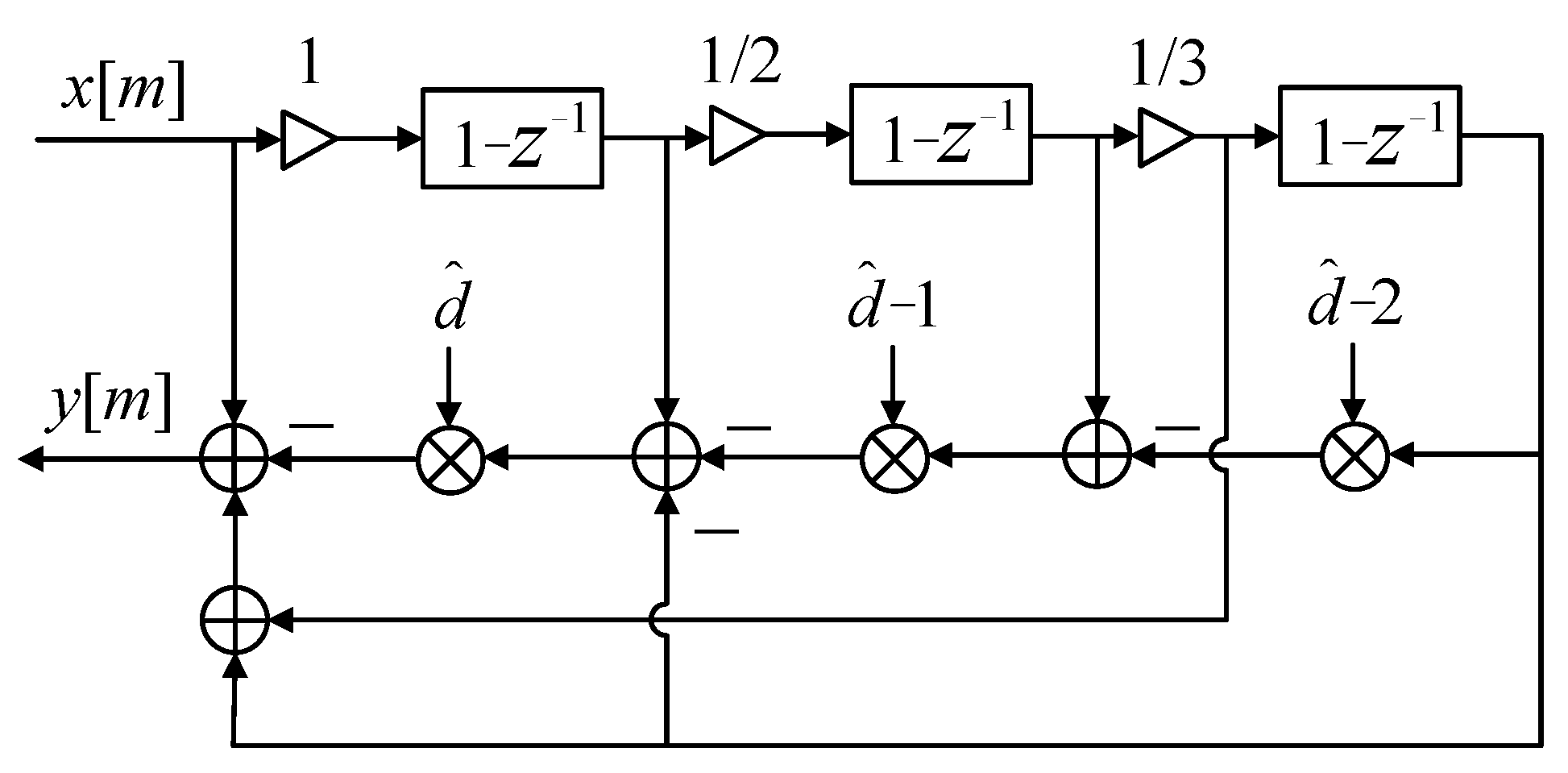
3.3. Three-Order Newton FD Filter
3.4. Performance Analysis of Newton-FAPRRC
4. Parameters of PRRC
4.1. Parameters of PR and GCFAD
4.2. Setting of Q(z)
4.3. Parameters of Gc
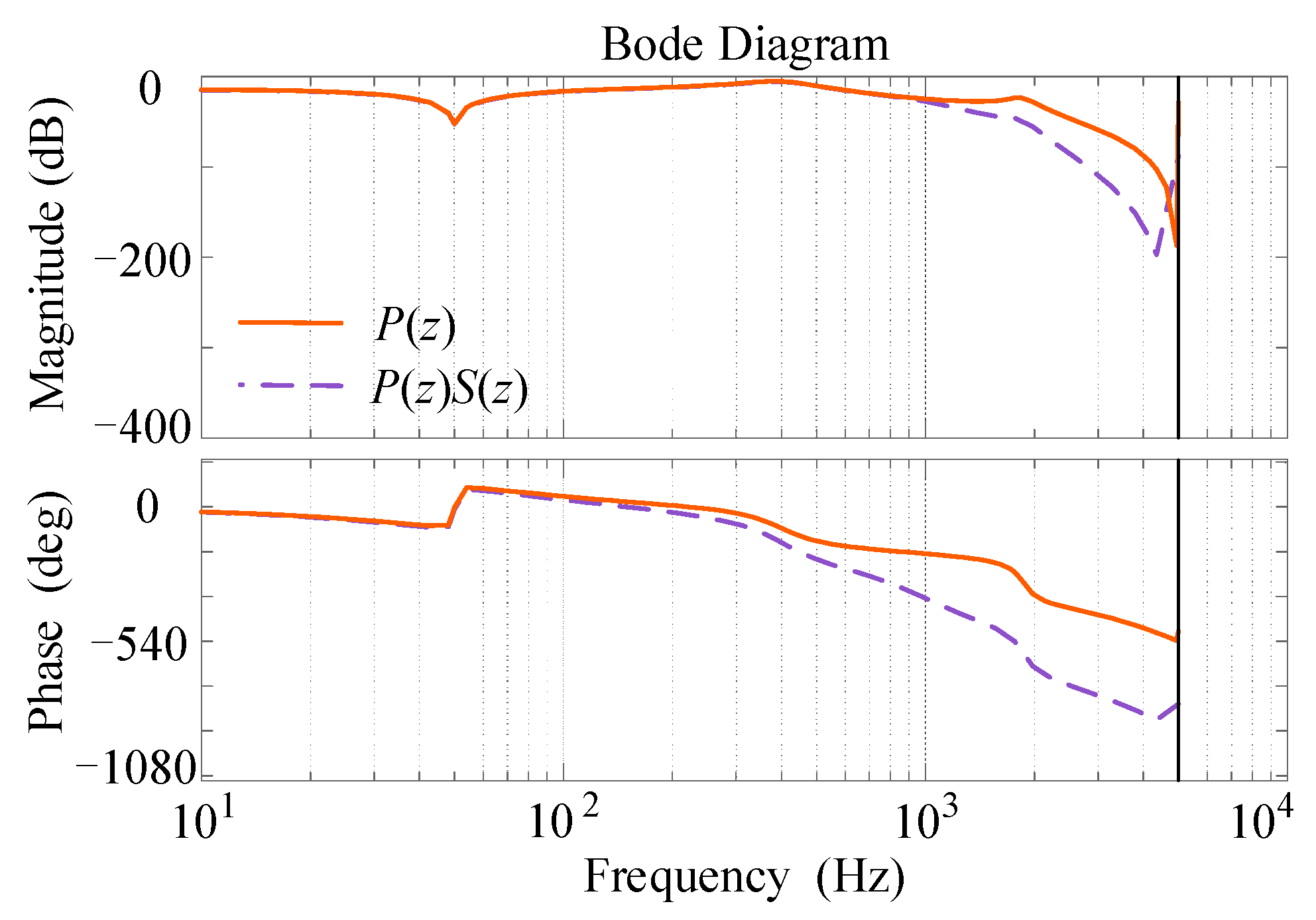
4.3.1. Filter S(z)
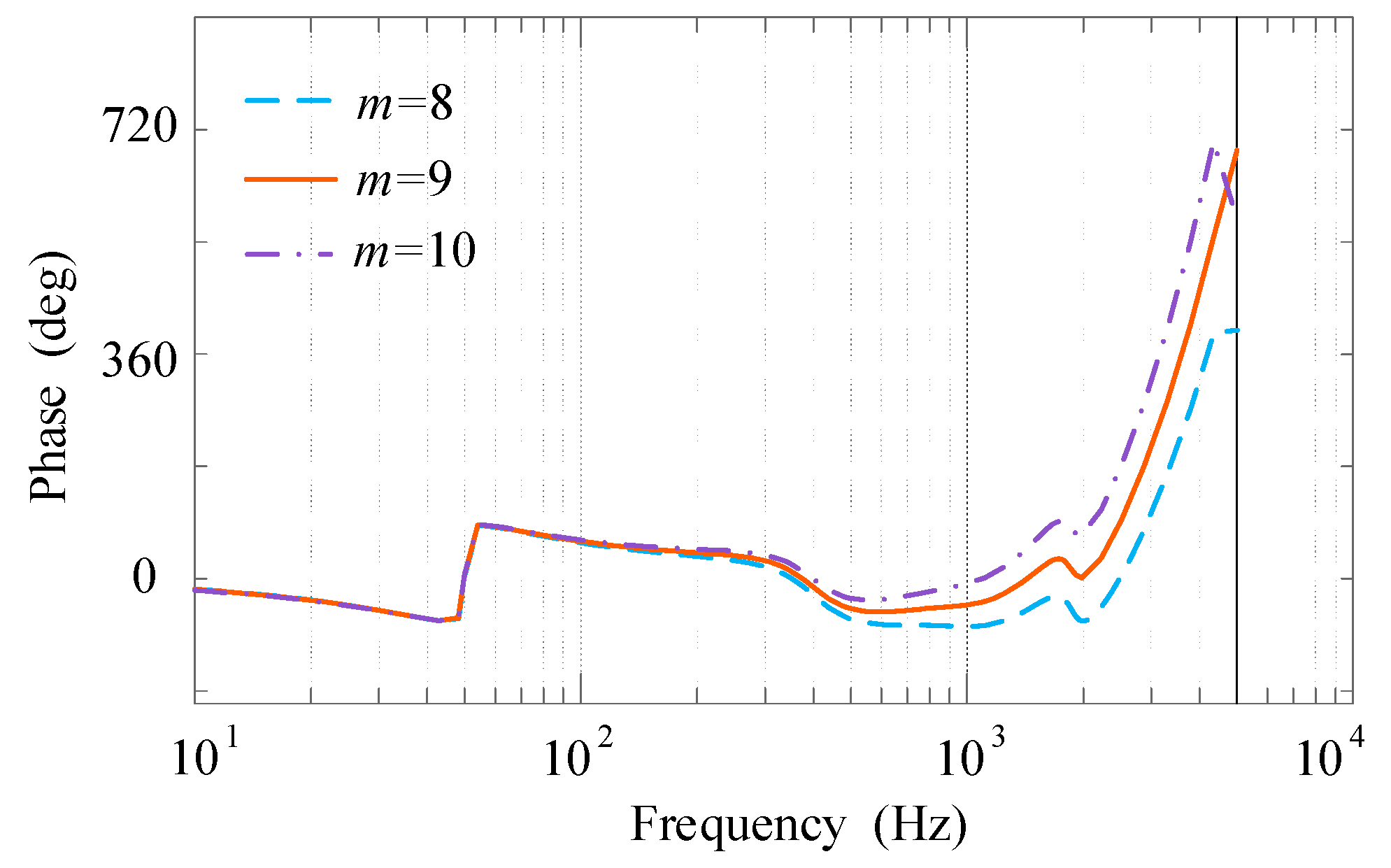
4.3.2. Phase Compensator zm
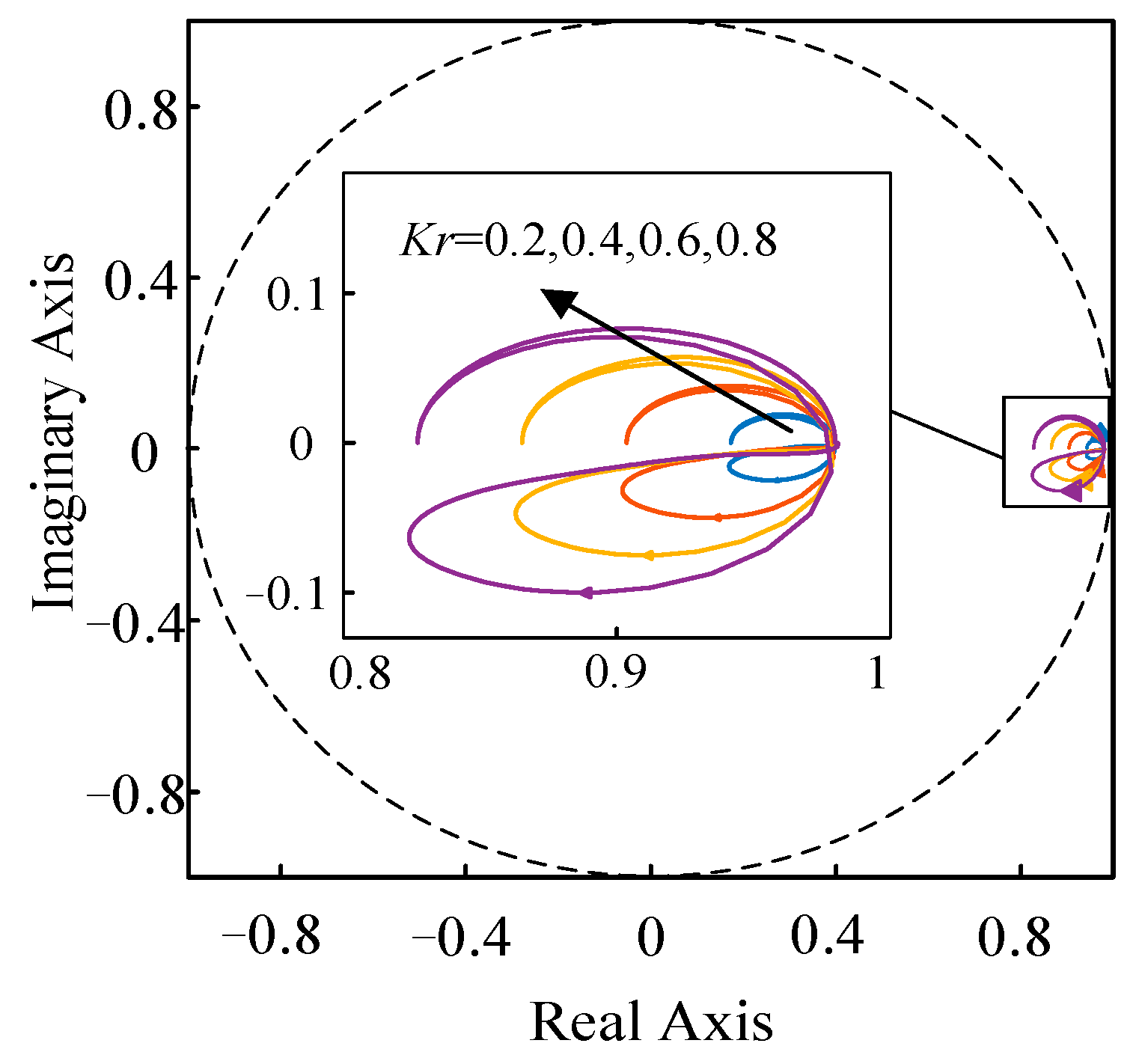
4.3.3. The Gain kr
5. Stability Analysis of FAPRRC
6. Simulation and Experiment
6.1. Simulation
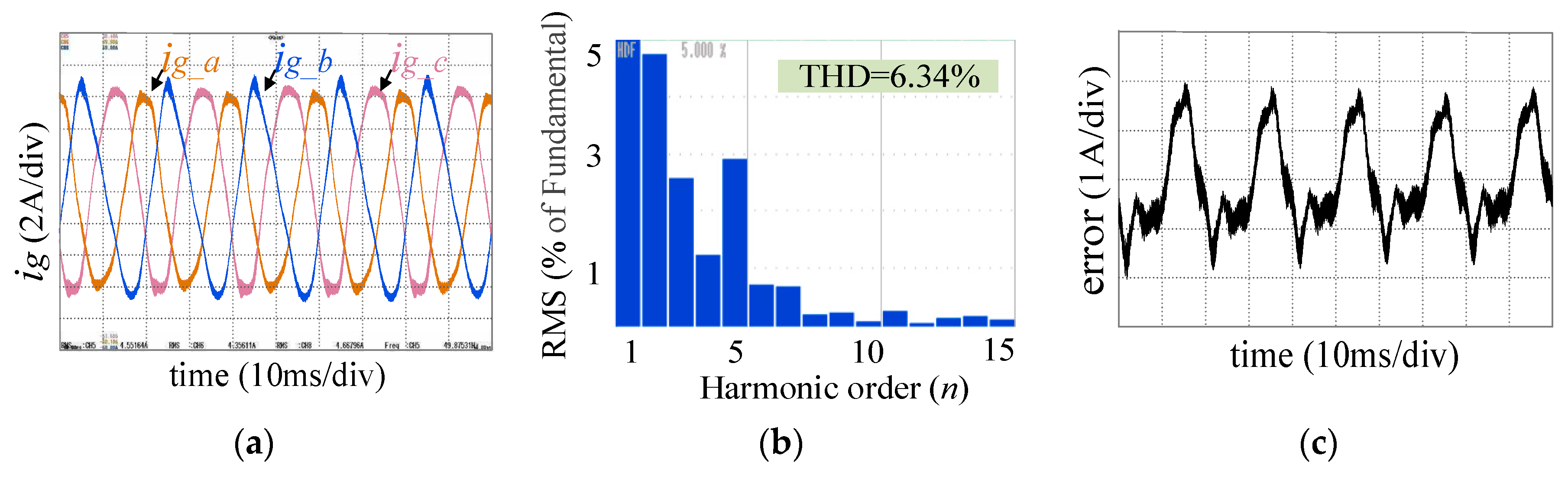
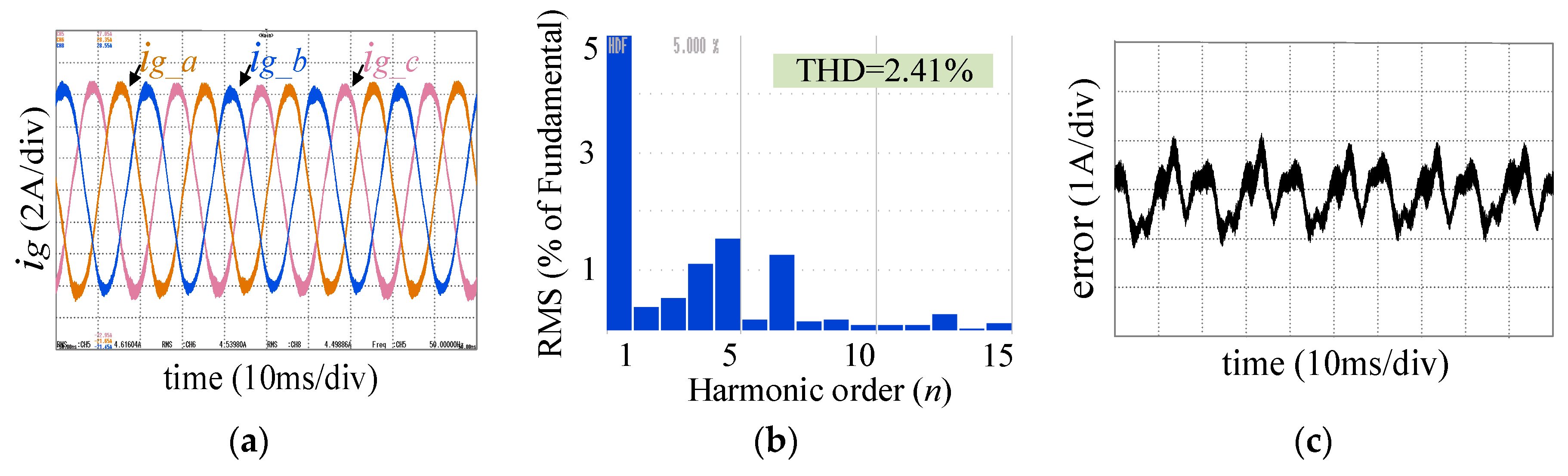
6.1.1. Adaptability of Newton FAPRRC under Weak Grid
6.1.2. Newton FAPRRC Dynamic Performance
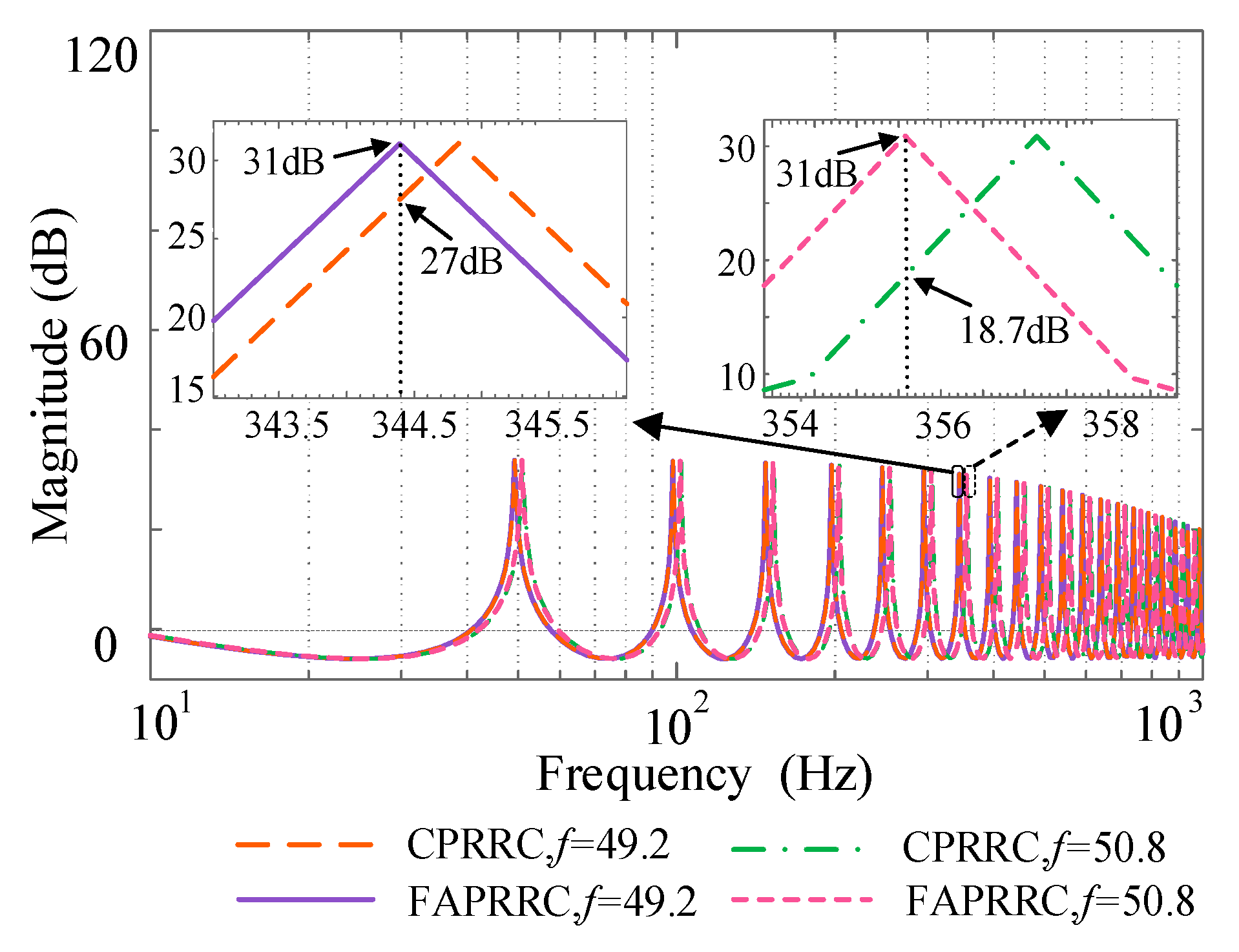
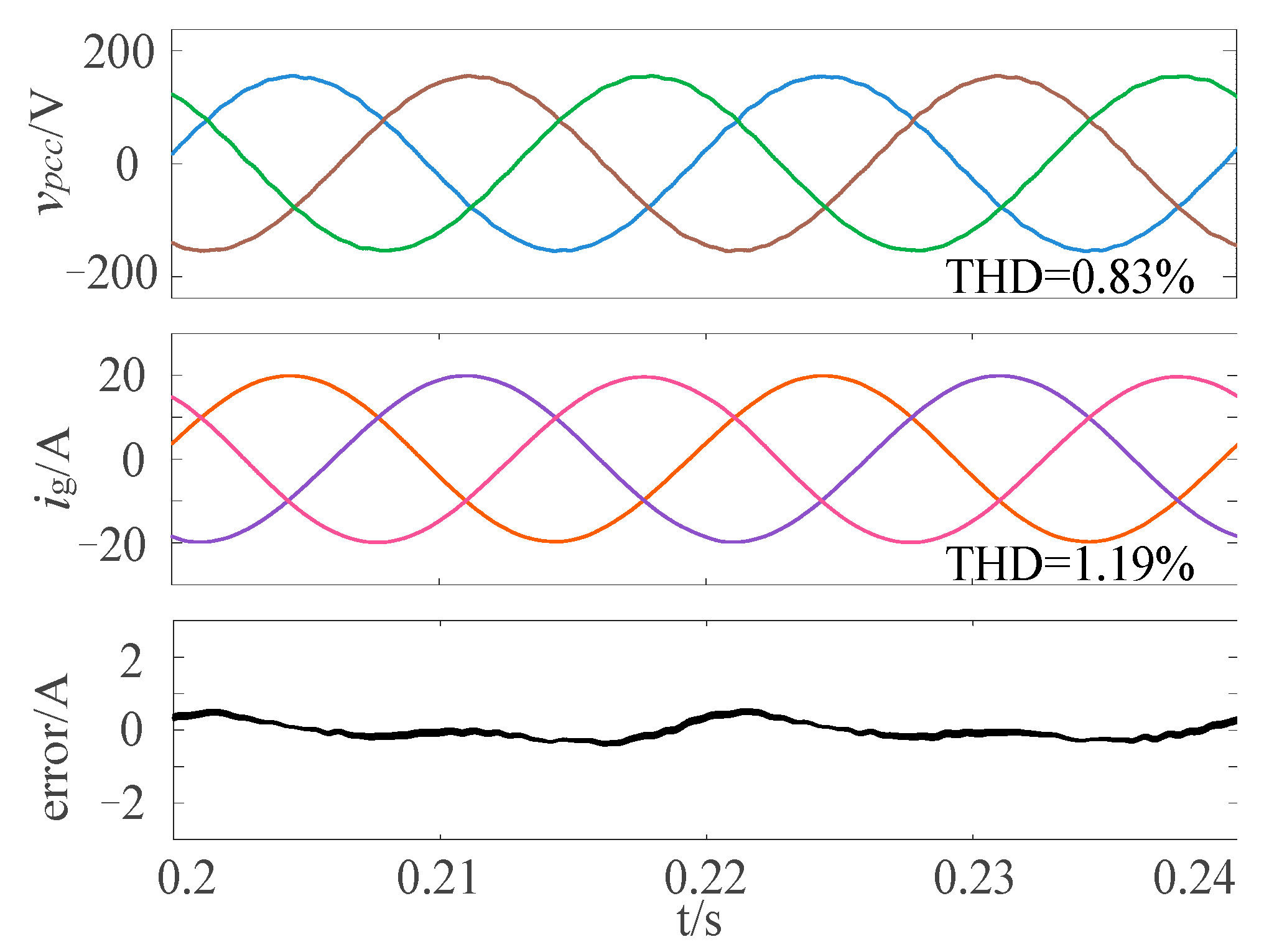
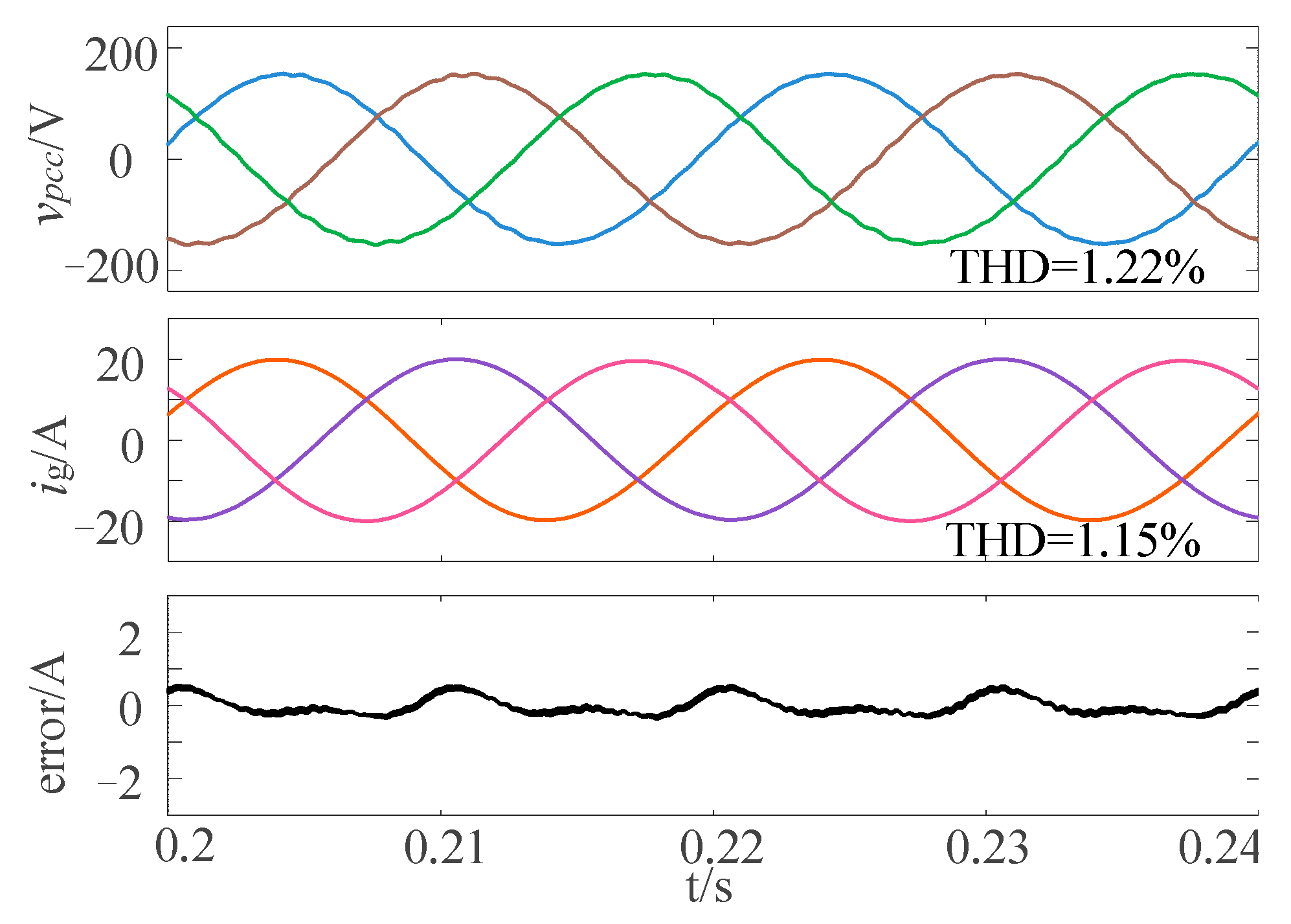
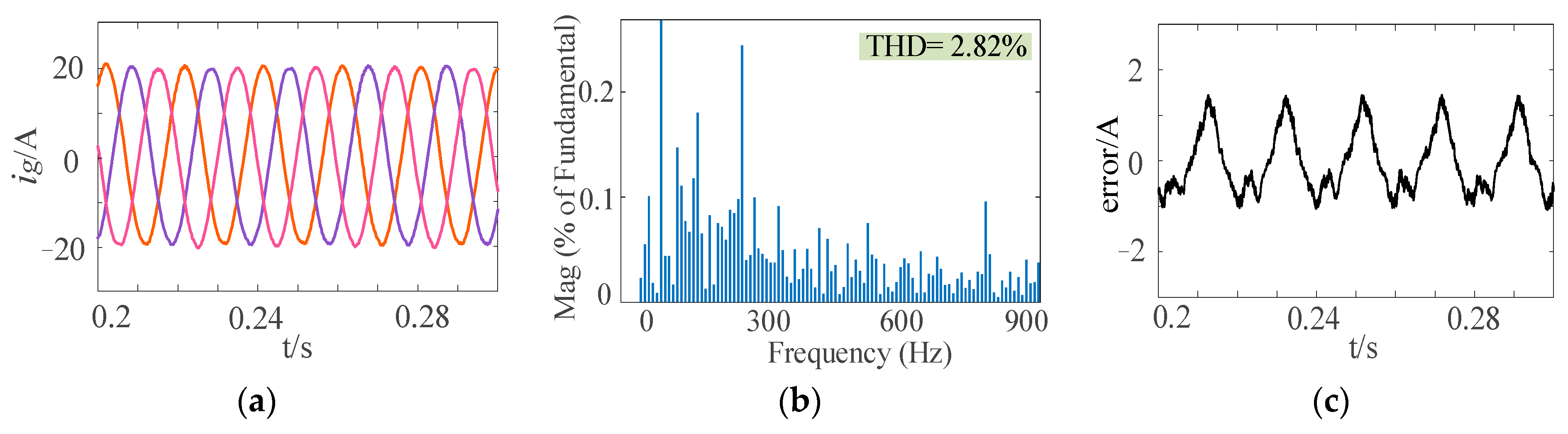
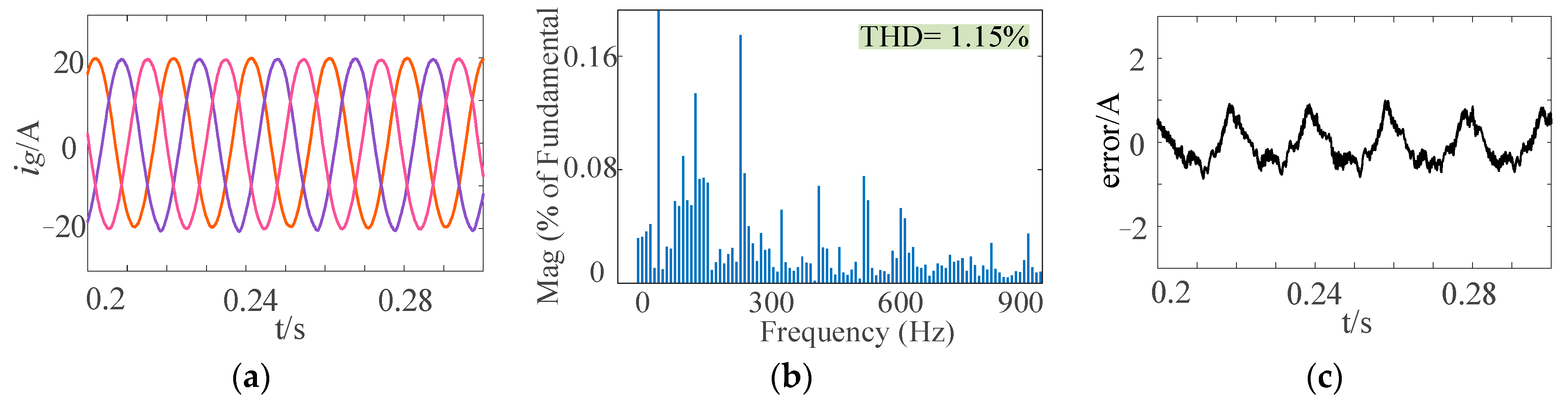
6.1.3. Verification of Newton-FAPRRC Frequency Adaptability
6.2. Experiment
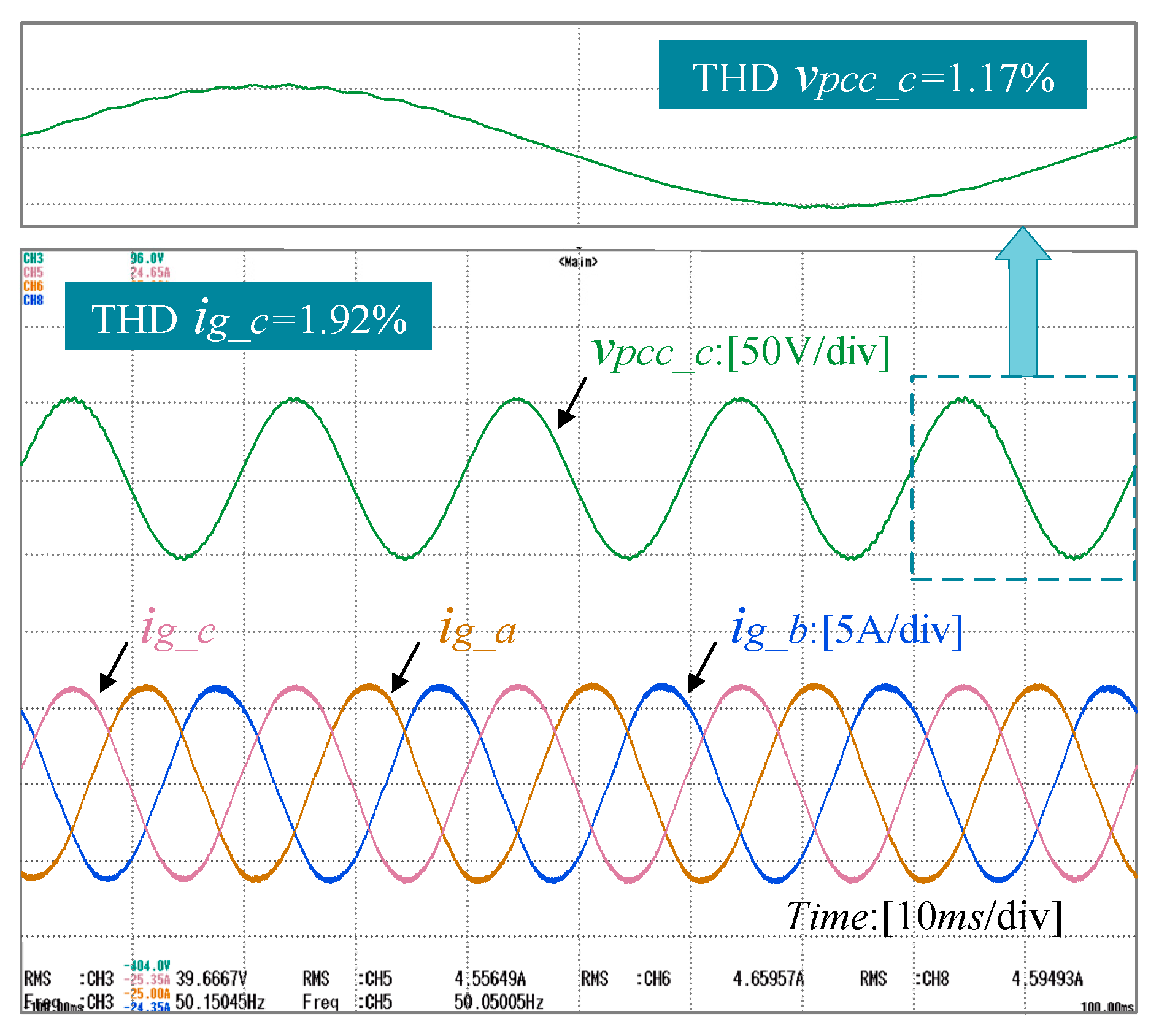
6.2.1. Adaptability of Newton FAPRRC under Weak Grid Condition
6.2.2. Verification of Newton-FAPRRC Dynamic Performance
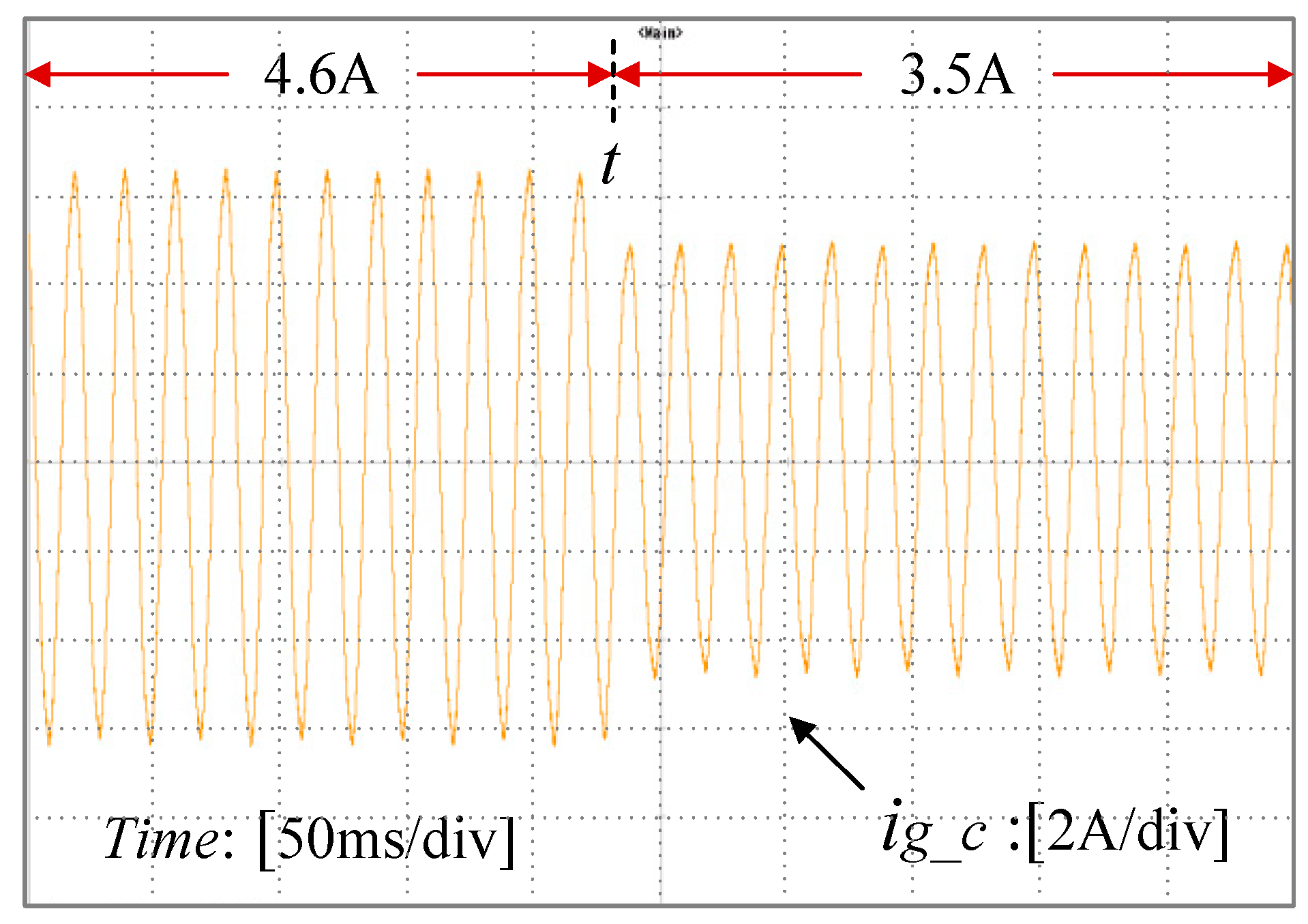
6.2.3. Verification of Newton-FAPRRC Frequency Adaptability
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, X.; Fang, J.; Tang, Y.; Wu, X.; Geng, Y. Capacitor-Voltage Feedforward with Full Delay Compensation to Improve Weak Grids Adaptability of LCL-Filtered Grid-Connected Converters for Distributed Generation Systems. IEEE Trans. Power Electron. 2018, 33, 749–764. [Google Scholar] [CrossRef]
- Dogra, R.; Rajpurohit, B.S.; Tummuru, N.R.; Marinova, I.; Mateev, V. Superimposed Component based Fault Detection Scheme for Multi-port DC Microgrid. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 16–19 December 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F. Harmonic Stability in Power Electronic-Based Power Systems: Concept, Modeling, and Analysis. IEEE Trans. Smart Grid 2019, 10, 2858–2870. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Ruan, X.; Wu, H. Impedance Shaping of the Grid-Connected Inverter with LCL Filter to Improve Its Adaptability to the Weak Grid Condition. IEEE Trans. Power Electron. 2014, 29, 5795–5805. [Google Scholar] [CrossRef]
- Dannehl, J.; Wessels, C.; Fuchs, F.W. Limitations of Voltage-Oriented PI Current Control of Grid-Connected PWM Rectifiers with LCL Filters. IEEE Trans. Ind. Electron. 2009, 56, 380–388. [Google Scholar] [CrossRef]
- Bao, C.; Ruan, X.; Wang, X.; Li, W.; Pan, D.; Weng, K. Step-by-Step Controller Design for LCL-Type Grid-Connected Inverter with Capacitor–Current-Feedback Active-Damping. IEEE Trans. Power Electron. 2014, 29, 1239–1253. [Google Scholar] [CrossRef]
- Xu, J.; Xie, S.; Tang, T. Evaluations of current control in weak grid case for grid-connected LCL-filtered inverter. IET Power Electron. 2013, 6, 227–234. [Google Scholar] [CrossRef]
- Hu, J. Improved Dead-Beat Predictive DPC Strategy of Grid-Connected DC–AC Converters With Switching Loss Minimization and Delay Compensations. IEEE Trans. Ind. Inform. 2013, 9, 728–738. [Google Scholar] [CrossRef]
- Evran, F. Plug-in Repetitive Control of Single-phase Grid-connected Inverter for AC Module Applications. IET Power Electron. 2016, 10, 47–58. [Google Scholar] [CrossRef]
- Zhao, Q.; Ye, Y. A PIMR-Type Repetitive Control for a Grid-Tied Inverter: Structure, Analysis, and Design. IEEE Trans. Power Electron. 2018, 33, 2730–2739. [Google Scholar] [CrossRef]
- Trinh, Q.-N.; Choo, F.-H.; Chi, J.; Peng, W. An improved control strategy for three-phase AC/DC/AC converter in UPS application. In Proceedings of the 2016 Asian Conference on Energy, Power and Transportation Electrification (ACEPT), Singapore, 25–27 October 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Kang, L.; Zhang, J.; Zhou, H.; Zhao, Z.; Duan, X. Model Predictive Current Control with Fixed Switching Frequency and Dead-Time Compensation for Single-Phase PWM Rectifier. Electronics 2021, 10, 426. [Google Scholar] [CrossRef]
- Yang, S.; Lei, Q.; Peng, F.Z.; Qian, Z. A Robust Control Scheme for Grid-Connected Voltage-Source Inverters. IEEE Trans. Ind. Electron. 2011, 58, 202–212. [Google Scholar] [CrossRef]
- Shen, G.; Zhu, X.; Zhang, J.; Xu, D. A New Feedback Method for PR Current Control of LCL-Filter-Based Grid-Connected Inverter. IEEE Trans. Ind. Electron. 2010, 57, 2033–2041. [Google Scholar] [CrossRef]
- Pereira, L.F.A.; Flores, J.V.; Bonan, G.; Coutinho, D.F.; Da Silva, J.M.G. Multiple Resonant Controllers for Uninterruptible Power Supplies—A Systematic Robust Control Design Approach. IEEE Trans. Ind. Electron. 2014, 61, 1528–1538. [Google Scholar] [CrossRef]
- Hu, J.; Zhu, Z.Q. Improved Voltage-Vector Sequences on Dead-Beat Predictive Direct Power Control of Reversible Three-Phase Grid-Connected Voltage-Source Converters. IEEE Trans. Power Electron. 2013, 28, 254–267. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, K.; Blaabjerg, F. Enhancing the Frequency Adaptability of Periodic Current Controllers with a Fixed Sampling Rate for Grid-Connected Power Converters. IEEE Trans. Power Electron. 2016, 31, 7273–7285. [Google Scholar] [CrossRef] [Green Version]
- Zimann, F.J.; Stangler, E.; Neves, F.V.; Batschauer, A.L.; Mezaroba, M. Coordinated Control of Active and Reactive Power Compensation for Voltage Regulation with Enhanced Disturbance Rejection Using Repetitive Vector-Control. Energies 2020, 13, 2812. [Google Scholar] [CrossRef]
- Wei, J.; Li, Y.; Sun, G.; Bu, L. H∞ Repetitive Control Based on Active Damping with Reduced Computation Delay for LCL-Type Grid-Connected Inverters. Energies 2017, 10, 586. [Google Scholar]
- Chen, J.; Jiang, X.; Zhu, D.; Deng, L.; Yang, B. High Power Hybrid Active Power Filter for Medium-voltage Distribution Network. In Proceedings of the 2005 International Conference on Electrical Machines and Systems, Nanjing, China, 27–29 September 2005; pp. 1381–1386. [Google Scholar]
- Zou, Z.-X.; Zhou, K.; Wang, Z.; Cheng, M. Frequency-Adaptive Fractional-Order Repetitive Control of Shunt Active Power Filters. IEEE Trans. Ind. Electron. 2015, 62, 1659–1668. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, B.; Zhou, K. Universal Fractional-Order Design of Linear Phase Lead Compensation Multirate Repetitive Control for PWM Inverters. IEEE Trans. Ind. Electron. 2017, 64, 7132–7140. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Lu, W.; Zhou, K.; Fan, Q. Fractional-Order New Generation of nk ± m-Order Harmonic Repetitive Control for PWM Converters. IEEE Access 2020, 8, 180706–180721. [Google Scholar] [CrossRef]
- Xu, J.; Xie, S.; Tang, T. Active Damping-Based Control for Grid-Connected LCL-Filtered Inverter with Injected Grid Current Feedback Only. IEEE Trans. Ind. Electron. 2014, 61, 4746–4758. [Google Scholar] [CrossRef]
- Cui, P.; Zhang, G.; Liu, Z.; Han, B.; Wang, Q. A Second-Order Dual Mode Repetitive Control for Magnetically Suspended Rotor. IEEE Trans. Ind. Electron. 2020, 67, 4946–4956. [Google Scholar] [CrossRef]
- Tian, B.; Sun, L.; Molinas, M.; An, Q.-T. Repetitive Control Based Phase Voltage Modulation Amendment for FOC-Based Five-Phase PMSMs Under Single-Phase Open Fault. IEEE Trans. Ind. Electron. 2021, 68, 1949–1960. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, K.; Wang, H.; Blaabjerg, F.; Wang, D.; Zhang, B. Frequency Adaptive Selective Harmonic Control for Grid-Connected Inverters. IEEE Trans. Power Electron. 2015, 30, 3912–3924. [Google Scholar] [CrossRef] [Green Version]
- Zeineddine, A.; Paquelet, S.; Nafkha, A.; Moy, C.; Jezequel, P.-Y. Generalization and Coefficients Optimization of the Newton Structure. In Proceedings of the 2018 25th International Conference on Telecommunications (ICT), Saint-Malo, France, 26–28 June 2018; pp. 98–103. [Google Scholar]
- Lamb, D.; Chamon, L.; Nascimento, V.H. Efficient filtering structure for spline interpolation and decimation. Electron. Lett. 2016, 52, 39–41. [Google Scholar] [CrossRef] [Green Version]
- Zeineddine, A.; Nafkha, A.; Moy, C.; Paquelet, S.; Jezequel, P.-Y. Variable Fractional Delay Filter: A Novel Architecture Based on Hermite Interpolation. In Proceedings of the 2018 25th International Conference on Telecommunications (ICT), Saint-Malo, France, 26–28 June 2018; pp. 93–97. [Google Scholar]
- Zeineddine, A.; Nafkha, A.; Paquelet, S.; Moy, C.; Jezequel, P.Y. Comprehensive Survey of FIR-Based Sample Rate Conversion. J. Signal Process. Syst. 2020, 93, 113–125. [Google Scholar] [CrossRef]
- Zou, Z.; Wang, Z.; Cheng, M. Modeling, Analysis, and Design of Multifunction Grid-Interfaced Inverters With Output LCL Filter. IEEE Trans. Power Electron. 2014, 29, 3830–3839. [Google Scholar] [CrossRef]
- Zhao, Q.; Ye, Y. Fractional Phase Lead Compensation RC for an Inverter: Analysis, Design, and Verification. IEEE Trans. Ind. Electron. 2017, 64, 3127–3136. [Google Scholar] [CrossRef]
- Xu, J.; Qian, Q.; Zhang, B.; Xie, S. Harmonics and Stability Analysis of Single-Phase Grid-Connected Inverters in Distributed Power Generation Systems Considering Phase-Locked Loop Impact. IEEE Trans. Sustain. Energy 2019, 10, 1470–1480. [Google Scholar] [CrossRef]









| Parameter | Symbol | Value |
|---|---|---|
| Rated power | P | 9.1 kW |
| Grid voltage | vg | 110 V |
| Grid-side inductor | L2 | 1 mH |
| Inverter-side inductor | L1 | 3 mH |
| Capacitor of LCL-filter | C | 10 uF |
| DC voltage | VDC | 200 V |
| Frequency | f | 50 Hz |
| Sampling frequency | fs | 10 kHz |
| Switching frequency | fsw | 10 kHz |
| Feedback coefficient of GCFAD | kc | 30 |
| Cut-off frequency of GCFAD | ωc | 12,165 |
| Proportional gain of PR | kp | 5 |
| Integral gain of PR | ki | 2500 |
| Bandwidth coefficient of PR | ωi | 3.14 |
| Frequency/Hz | CPRRC | Farrow | Newton | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ia | ib | ic | ia | ib | ic | ia | ib | ic | |
| 49.2 | 2.73% | 2.89% | 2.77% | 1.15% | 1.18% | 1.21% | 1.11% | 1.17% | 1.19% |
| 49.6 | 1.87% | 1.95% | 1.85% | 1.07% | 1.06% | 1.13% | 1.08% | 1.11% | 1.06% |
| 50 | 1.35% | 1.37% | 1.33% | 1.35% | 1.35% | 1.38% | 1.34% | 1.35% | 1.36% |
| 50.4 | 1.88% | 1.96% | 1.78% | 1.17% | 1.20% | 1.22% | 1.13% | 1.19% | 1.20% |
| 50.8 | 2.82% | 3.00% | 2.83% | 1.15% | 1.14% | 1.18% | 1.16% | 1.18% | 1.16% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, C.; Li, S.; Wang, H.; Miao, H. A Frequency Adaptive Scheme Based on Newton Structure of PRRC for LCL-Type Inverter Connected with Weak Grid. Energies 2021, 14, 4225. https://doi.org/10.3390/en14144225
Zeng C, Li S, Wang H, Miao H. A Frequency Adaptive Scheme Based on Newton Structure of PRRC for LCL-Type Inverter Connected with Weak Grid. Energies. 2021; 14(14):4225. https://doi.org/10.3390/en14144225
Chicago/Turabian StyleZeng, Chengbi, Sudan Li, Hanwen Wang, and Hong Miao. 2021. "A Frequency Adaptive Scheme Based on Newton Structure of PRRC for LCL-Type Inverter Connected with Weak Grid" Energies 14, no. 14: 4225. https://doi.org/10.3390/en14144225
APA StyleZeng, C., Li, S., Wang, H., & Miao, H. (2021). A Frequency Adaptive Scheme Based on Newton Structure of PRRC for LCL-Type Inverter Connected with Weak Grid. Energies, 14(14), 4225. https://doi.org/10.3390/en14144225






