A Data-Driven Methodology for the Simulation of Turbulent Flame Speed across Engine-Relevant Combustion Regimes

Abstract

Turbulent combustion modelling in internal combustion engines (ICEs) is a challenging task. It is commonly synthetized by incorporating the interaction between chemical reactions and turbulent eddies into a unique term, namely turbulent flame speed $s_T$. The task is very complex considering the variety of turbulent and chemical scales resulting from engine load/speed variations. In this scenario, advanced turbulent combustion models are asked to predict accurate burn rates under a wide range of turbulence–flame interaction regimes. The framework is further complicated by the difficulty in unambiguously evaluating in-cylinder turbulence and by the poor coherence of turbulent flame speed ($s_T$) measurements in the literature. Finally, the simulated $s_T$ from combustion models is found to be rarely assessed in a rigorous manner. A methodology is presented to objectively measure the simulated $s_T$ by a generic combustion model over a range of engine-relevant combustion regimes, from $Da$ = 0.5 to $Da$= 75 (i.e., from the thin reaction regime to wrinkled flamelets). A test case is proposed to assess steady-state burn rates under specified turbulence in a RANS modelling framework. The methodology is applied to a widely adopted combustion model (ECFM-3Z) and the comparison of the simulated $s_T$ with experimental datasets allows to identify modelling improvement areas. Dynamic functions are proposed based on turbulence intensity and Damköhler number. Finally, simulations using the improved flame speed are carried out and a satisfactory agreement of the simulation results with the experimental/theoretical correlations is found. This confirms the effectiveness and the general applicability of the methodology to any model. The use of grid/time resolution typical of ICE combustion simulations strengthens the relevance of the proposed dynamic functions. The presented analysis allows to improve the adherence of the simulated burn rate to that of literature turbulent flames, and it unfolds the innovative possibility to objectively test combustion models under any prescribed turbulence/flame interaction regime. The solid data-driven representation of turbulent combustion physics is expected to reduce the tuning effort in ICE combustion simulations, providing modelling robustness in a very critical area for virtual design of innovative combustion systems.

1. Introduction

The progress in CFD models witnessed in the recent past has led to remarkable advances in the field of fluid-dynamic simulation of ICEs. Among the complex processes present in modern combustion systems, the simulation of turbulent combustion requires a solid description of both flow (e.g., large-scale structures, local turbulence) and fluid properties (e.g., laminar flame speed, dilution rate). The turbulence–flame interaction is commonly synthetized by the dimensionless Damköhler and Karlovitz numbers ($Da$ and $Ka$, respectively). The Damköhler number ($Da={\tau }_t/{\tau }_c$) expresses the ratio between the characteristic time representative of large-scale turbulence and that of chemical reactions, with ${\tau }_t$ being the integral eddy turnover time and ${\tau }_c$ the chemical time-scale, while the Karlovitz number ($Ka={\tau }_c/{\tau }_{\eta }$) expresses an analogue time-scale ratio considering the Kolmogorov turbulent time-scale ${\tau }_{\eta }$. A common assumption for models dedicated to engine combustion is the assumption of a wrinkled flamelet combustion regime ($Da>1$ and $Ka<1$), representing turbulent flames as arrays of passive laminar flame sheets embedded in a turbulent flow and corrugated by the entire turbulence spectrum [1,2]; this corresponds to a laminar flame thickness smaller than the Kolmogorov length (${\delta }_L<\eta$, Klimov–Williams criterion [3,4]). The separation of turbulent and chemical scales is a fundamental assumption of the so-called flamelet combustion models (including ECFM-3Z [5] and G-equation [1,6]), and it traces back to the pioneering Damköhler theoretical expressions for turbulent flame speed [7,8], although its validity is an open discussion as non-flamelet conditions are likely to be present in modern combustion systems. Higher turbulence levels and lean/diluted combustion strategies narrow the distance between high-frequency turbulence and chemical time-scales, potentially introducing a partial scale overlapping: the flame structure is thickened by part of the small-scale turbulence spectrum, while large-scale turbulence and flow field still exert a kinematic-type interaction (thin reaction regime, $Da>1$ and $Ka>1$). An accurate representation of turbulent burn rates at such conditions is even more challenging. In order to achieve this objective, a discussion to relax the flamelet hypothesis is ongoing in the scientific community. In addition, engine flames experience considerable spatial and temporal variations of turbulence–flame interaction, as combustion simultaneously develops within highly-turbulent flows (e.g., in the bulk combustion chamber) and in low-turbulent regions (e.g., close to no-slip solid walls). Each and every of these situations contributes to the overall burn rate, and it is required that the combustion model accurately reproduces all the concurring regimes.

Many experimental studies dealt with closure formulations for turbulent burn rate. Damköhler proposed a scaling law for turbulent premixed flames assuming the turbulence to be entirely effective as a surface area extender for laminar-like flames [7], hence leading to turbulent burning velocity expressed as in the generic form of Equation (1), with $s_L$ being the laminar flame speed, $A_T$ being the corrugated flamelet surface, and $\overline{A}$ being a mean reaction area:

$$\frac{s_T}{s_L}=f\left(\frac{A_T}{\overline{A}}\right)$$

(1)

In [8], the same author improved the expression introducing the turbulence intensity $u\prime$ and considering the $s_T/s_L$ ratio as a power-law of the dimensionless velocity group $u\prime /s_L$, although no consideration was made on flame/turbulence length scales. Among the many variations deriving from the above relationship, Abdel-Gayed et al. [9] and Bradley et al. [10,11] defined a power-law correlation for turbulent burn rate $s_T$ as a function of Karlovitz stretch factor, laminar flame speed, and Lewis number. Gulder in [12,13] presented a similar scaling law for turbulent premixed combustion, using a fractal-based wrinkling hypothesis for turbulent flames and considering experiments using CH₄, C₂H₂, and natural gas as fuels. Muppala et al. [14] conducted a numerical study on Bunsen-type flames and derived a validated closure relationship for $s_T$ valid for both wrinkled and thin reaction regimes up to 0.1 MPa. Burke et al. [15] reviewed a large number of $s_T$ correlations against multiple experimental/theoretical datasets in both thin reaction and wrinkled flamelet regimes: they showed that, although a unique $s_T$ model equally accurate over a wide range of turbulence levels was not found, the correlations from Peters [1,2], Liu [16], Zimont [17], Kobayashi [18], and Ronney [19] converged on similar results for a variety of turbulence–flame interactions relevant to ICEs. Moving to high $u\prime /s_L$ values, Gulder in [20] highlighted the contribution of small-scale turbulence in the broadened preheat zone for $u\prime /s_L>7$. The flamelet hypothesis of increased surface area as the dominant factor for burn rate was criticized, and a correction function was proposed accounting for the temperature-driven increase in kinematic viscosity in the preheat zone. Wabel et al. [21,22] tested methane-air Bunsen flames under extreme turbulence levels ($25<u\prime /s_L<163$) and found confirmation of the non-linear increase of $s_T$ with $u\prime$, suggesting that the thermal diffusion in the broadened preheat zone might reduce the effective turbulence intensity seen by the flame for highly turbulent flows. The study extended its relevance to ICE combustion, where the observed interaction is potentially present as well. In this context, a valuable comparison of many steady-state stretch-free datasets was presented by Peters [1], where the poor experimental consistency from different groups (e.g., diagnostic, apparatuses) was discussed (with particular reference to Figure 2.24 of [1]) and a $Da$ scaling law was identified for the dimensionless group $\Delta s/u\prime$, with $\Delta s=s_T-s_L$. The expression from [1] (Equation (2)) well reproduced the burn rate for both low and high $Da$, using both experimental measurements and theoretical arguments. In the former range, Damköhler’s second hypothesis was respected ($s_T/s_L~\sqrt{D_T/D_L}$, with $D_T$/$D_L$ being the turbulent/laminar diffusivities), whereas in the latter, Damköhler’s first hypothesis was satisfied ($s_T/s_L~const.$ at high $Da$).

In this study, Equation (2) is assumed as the reference correlation, using the same coefficients reported in [1] (i.e., $a_{4,P}=0.78$, $b_{3,P}=1$, $b_{1,P}=2$). With reference to the mentioned difficulty in objectively defining universally accepted scaling laws for the turbulent burn rate, it is underlined that the use of this correlation answers the study need to identify a consolidated reference. However, it is to be noted that alternative formulations of the same (e.g., in the choice of the modelling constants) as well as other correlations can be used. The proposed methodology would preserve its generality even if a different reference scaling law is adopted.

$$\frac{\Delta s}{u\prime }=-\frac{a_{4,P}·b_{3,P}^2}{2·b_{1,P}}·Da+\sqrt{{\left(\frac{a_{4,P}·b_{3,P}^2}{2·b_{1,P}}·Da\right)}^2+a_{4,P}·b_{3,P}·Da}$$

(2)

A consistent body of turbulent burning velocity $s_T$ measurements exists in the literature; however, the behaviour of combustion models under turbulence-controlled conditions has been mostly limited to theoretical estimations or DNS studies. An example of the former is the Kolmogorov–Petrovski–Piskunov (KPP) analysis [23,24,25], predicting a theoretical $s_T$ valid under restrictive assumptions, although it is mainly used for model trends’ prediction. The latter category sees the modelling of turbulent flame structure and kinetics through DNS studies [26], where the accurate definition of the upstream turbulence spectrum is one of the main modelling difficulties. Poludnenko et al. [27,28] used DNS to numerically demonstrate that high-turbulence flames ($Da=0.05$) cannot be represented by thin laminar structures.

As for engine-typical turbulence levels, few attempts to simulate the effective turbulent flame speed $s_T$ were presented. An analysis considering turbulence levels pertinent to ICE combustion was made by Wang et al. [29], where a Lagrangian “marching cube” framework was proposed to simulate a turbulent flame using DNS in the range of $Da$ 0.26–3.2, and a fixed mean flame position was stabilized by a closed-loop control on inflow boundary condition, thus realizing a steady-state turbulent combustor.

Moving to the industry-standard RANS approach, to the best of the authors’ knowledge, an accurate validation of $s_T$ from the majority of RANS-type combustion models is somehow lacking at ICE-typical turbulence levels. The main motivation of this study is the definition of a methodology able to elucidate this key performance indicator of combustion models in a simple and objective manner, without the complexity of other modelling aspects (e.g., fuel stratification, large-scale turbulence, wall flows, and heat transfer), affecting the resulting turbulent burn rate in ICEs. In the first part of the paper, the complexity of turbulence–flame interaction in ICEs is presented, and the fundamental issue of turbulent flame speed prediction by popular combustion models is posed. Then, a similar approach as in [29] is followed to obtain $s_T$ under RANS turbulence-controlled conditions: a test case for an objective $s_T$ measurement is presented, although a fixed domain with moving flame is adopted in this study. A design space of 63 turbulence–flame interactions relevant to engine flames is identified (consisting of 7 $u\prime$ and 9 $Da$ levels). In the second part, the methodology is demonstrated through its application to a widespread combustion model (ECFM-3Z) and simulations are carried out on the full design space using the test case: at first, the results from the original models are observed and areas of improvement are identified from the comparisons with $s_T$ from [1]. Then, a dynamic function of local turbulent scales is proposed, and simulations are repeated, ultimately showing the improvement in turbulent flame speed prediction under ICE-typical grid resolution and time-steps. The use of a simple domain, the idealized turbulence-controlled conditions, and the results’ validation with literature data prove the generality of the study, leading to an improved simulated $s_T$ and to a physically-adherent turbulent burn rate. Finally, the similarity of the thermodynamic and turbulent states reproduced in the test case to those experienced in ICE combustion chambers paves the way for improvement in combustion models used for engine simulation.

2. Motivation of the Study

The variety of available models for engine combustion simulation partly originates from the need to synthetize the complex interaction between physical and chemical phenomena governing turbulent combustion into a unique $s_T$ variable. This is exemplified by the volume-averaged trajectory for a typical engine flame in a research spark ignition (SI) engine studied in [30], where both thin reaction and wrinkled flamelets conditions were sequentially experienced; moreover, instantaneous scatter plots revealed that a persistent broad distribution of local $Da$ must be accounted for. This is illustrated in Figure 1 by two representative turbulence–flame interactions on the Borghi–Peters diagram measured at 10% and 50% of burnt fraction (MFB 10 and MFB 50, respectively) on the same research engine studied in [30], using data conditioned on the flame brush region, identified as the combustion progress variable $\tilde{c}$ threshold $0.05<\tilde{c}<0.95$. The $Da$ distribution analysis reveals that the mean $Da$ values of $\overline{Da}=6.6$ and $\overline{Da}=66$ are accompanied by consistent local-wise deviations. Such broad distribution is emphasized in Figure 2 by normalized distribution functions of the instantaneous volume-weighted $Da$ at the same angular positions of Figure 1, confirming the local dispersion of the combustion regime and the need for an accurate burn rate prediction across such a wide range of conditions.

The variety of concepts on which combustion models are built leads to model-specific calibration constants, which are sometimes used as tuning parameters to match the experimental testbed acquisitions. Calibration is purposely intended to modify the performance of the original combustion model. Therefore, a coherent comparison between models is encumbered by the usage of model-specific parameters. The assessment and validation of combustion models at engine-relevant conditions would indeed be very desirable, although, to the best of the authors’ knowledge, the rigorous analysis of the simulated turbulent flame speed $s_T$ from models is surprisingly scarcely considered. The main focus of this study is to provide a method for an objective validation of $s_T$ in the range of $Da$ and $u\prime$ typical of combustion systems in modern ICEs and, in the next section, the numerical case used for such a goal is presented.

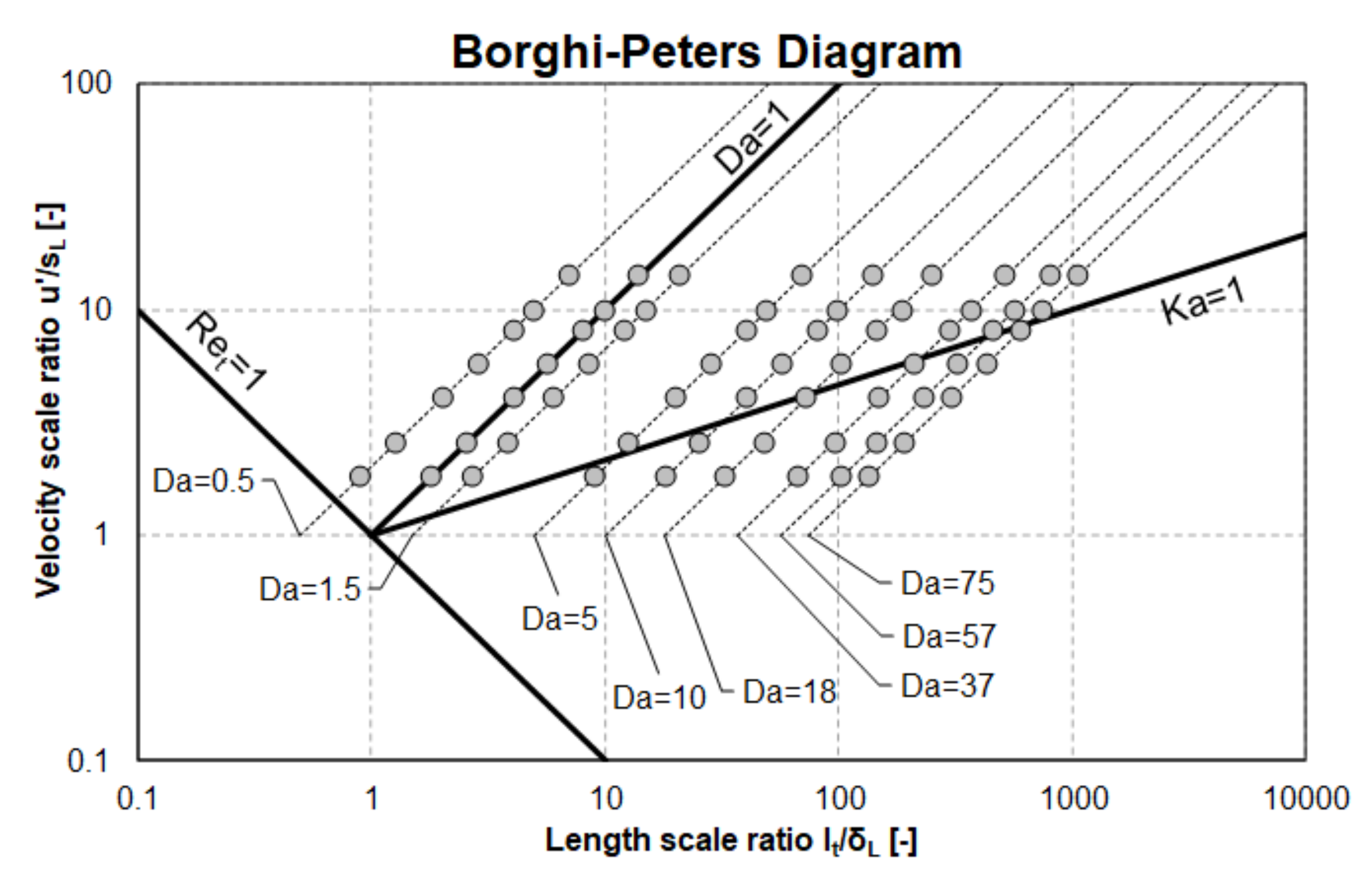
3. Test Case

The focus of the present study is the definition of a methodology for the analysis of $s_T$ from RANS combustion models. To this aim, a test case is created to fulfil the listed scopes:

• The test case is platform generic: the simple grid and modelling setup make it reproducible with any CFD platform (both open source and/or commercial), in order to provide a cross-platform test case for comparison of turbulent burn rates. For the sake of reference, all the presented simulations are carried out using the STAR-CD code, licensed by SIEMENS DISW.
• The test is combustion model generic: the method is valid for any combustion model using a progress variable-like approach.
• The test provides unambiguous measurement of $s_T$: the simulation of a steady-state combustion in a constant pressure domain allows an exact evaluation of the flame propagation velocity, without uncertainties on unsteady physical states and/or measurement techniques always present in ICE simulations (moving piston, time-varying pressure and temperature, and so on). Therefore, the test case represents an idealized steady-state turbulent reactor.

The conventional procedure followed to derive $s_T$ from spherical expanding flame experiments [31,32] is to measure the flame expansion velocity $d{r}_b/dt$ for the enflamed radius $r_b$ from optical acquisitions and to derive $s_T$ through the unburnt/burnt density ratio ${\rho }_u/{\rho }_b$ accounting for thermal expansion in the burnt gas state (Equation (3)).

$$\frac{d{r}_b}{dt}=\frac{{\rho }_u}{{\rho }_b}·s_T$$

(3)

Finally, the flame stretch effect is considered to calculate the unstretched laminar and turbulent flame speeds [33]. Therefore, the turbulent flame speed $s_T$ cannot be identified as the flame displacement velocity $d{r}_b/dt$, unless the effect of the thermal expansion is counterbalanced. In this numerical study, this is obtained by creating a “mass loss” (i.e., an open system) on the burnt gas side able to counteract the burnt gas expansion. This allows to assume the displacement velocity $d{r}_b/dt$ as $s_T$. This alternative setup is consistent with the $s_T$ calculated from the reaction rate, as discussed in Appendix A. This guarantees that the measured $s_T$ is consistent considering both flame expansion and the reaction rate, and that the use of an open system on the burnt gas side does not alter the analysed results.

The numerical grid represents a quasi-one-dimensional pipe-like domain with a square cross section, characterized by a dominant z-axis along which the flame region propagates and there are two shorter x- and y-axes. A uniform hexahedral grid of 0.5 mm size is used to represent a typical cell spacing for meshes used in ICE simulations. The domain extension is 300 mm on the z-axis and 6 mm for the x- and y-axis. The total number of cells is 86,400. Boundary conditions are imposed as symmetry planes (slip velocity) for the four elongated lateral sides, in order to avoid any flame-wall effect and a closed adiabatic wall end on the fresh mixture side, leading to a non-moving unburnt gas region. The flame propagates in a zero-velocity air–fuel mixture and the measured flame displacement velocity is the absolute $s_T$ value, in agreement with experiments in spherical bombs, where large-scale flows are absent [33]. A fixed pressure outlet condition is imposed at the burnt mixture end and combustion products are allowed to leave the domain, guaranteeing a constant pressure environment throughout the entire simulation duration. Therefore, the system thermodynamic state for the unburnt mixture is uniform in space and constant in time. Turbulence is fully controlled by numerically imposing a constant turbulent viscosity ${\mu }_t$, and it idealizes a condition impossible to be reproduced and controlled in engine simulations. The use of a constant ${\mu }_t$ (with different values for each turbulence-flame interaction regime) generalizes the method to any eddy-viscosity turbulence model (e.g., $k-\omega$), although the present simulations are carried out formally using the $k-\epsilon RNG$ turbulence model, for which turbulent kinetic energy $k$ (hence $u^{\prime }=\sqrt{2/3·k}$) is imposed and the dissipation rate $\epsilon$ is calculated following using the standard expression ${\mu }_t=c_{\mu }·\rho ·{\left(1.5·{u^{\prime }}^2\right)}^2/\epsilon$. Laminar flame variables (i.e., speed $s_L$ and thickness ${\delta }_L$) are imposed as constant and uniform values typical of engine conditions, creating a perfectly stirred environment for flame development. In this study, the effect of thermodynamics conditions and of mixture composition on the laminar kinetics rate are synthetized by $s_L$ and ${\delta }_L$, as commonly assumed for flamelet-type combustion models. This is motivated by the study focus on how a combustion model accounts for the turbulence effect on flame speed, and all the simulations consider a stoichiometric isoctane/air premixed mixture.

The mentioned assumptions imply that simulations are carried out at fixed velocity and length ratios ($u\prime /s_L$ and $l_t/{\delta }_L$, respectively), as well as Damköhler and Karlovitz numbers; therefore, each case represents a specific point on the Borghi–Peters diagram [1] and the simulated burn rate $s_T$ is representative of a uniquely determined turbulence/chemistry interaction, which will be compared to the $s_T$ prediction given by correlations for the same combustion regime. All the simulations are carried out using second-order discretization schemes for all variables, and a time-step of 3 × 10⁻⁶ s is used throughout the simulation duration as a trade-off between accuracy and computational cost.

The combustion progress variable $\tilde{c}$ is used as a flame region marker, given the wide popularity of this variable in many models. Although different definitions of $\tilde{c}$ exist, its general meaning is shared and used here as a reaction zone locator. The instantaneous flame axial z-position ($z_F$) is monitored at each iteration for the $\tilde{c}=0.5$ iso-surface, and the turbulent flame speed for the model in use is calculated as $s_T=·z_F/·t$, as illustrated in Figure 3. As anticipated, in this analysis, the correlation from Peters [1] (Equation (2)) is assumed as the reference for experimental $s_T$ values, although in principle, other relationships from the literature could be selected.

A MATLAB algorithm is used to post-process the flame displacement speed through the following sequence of operations for each simulated case:

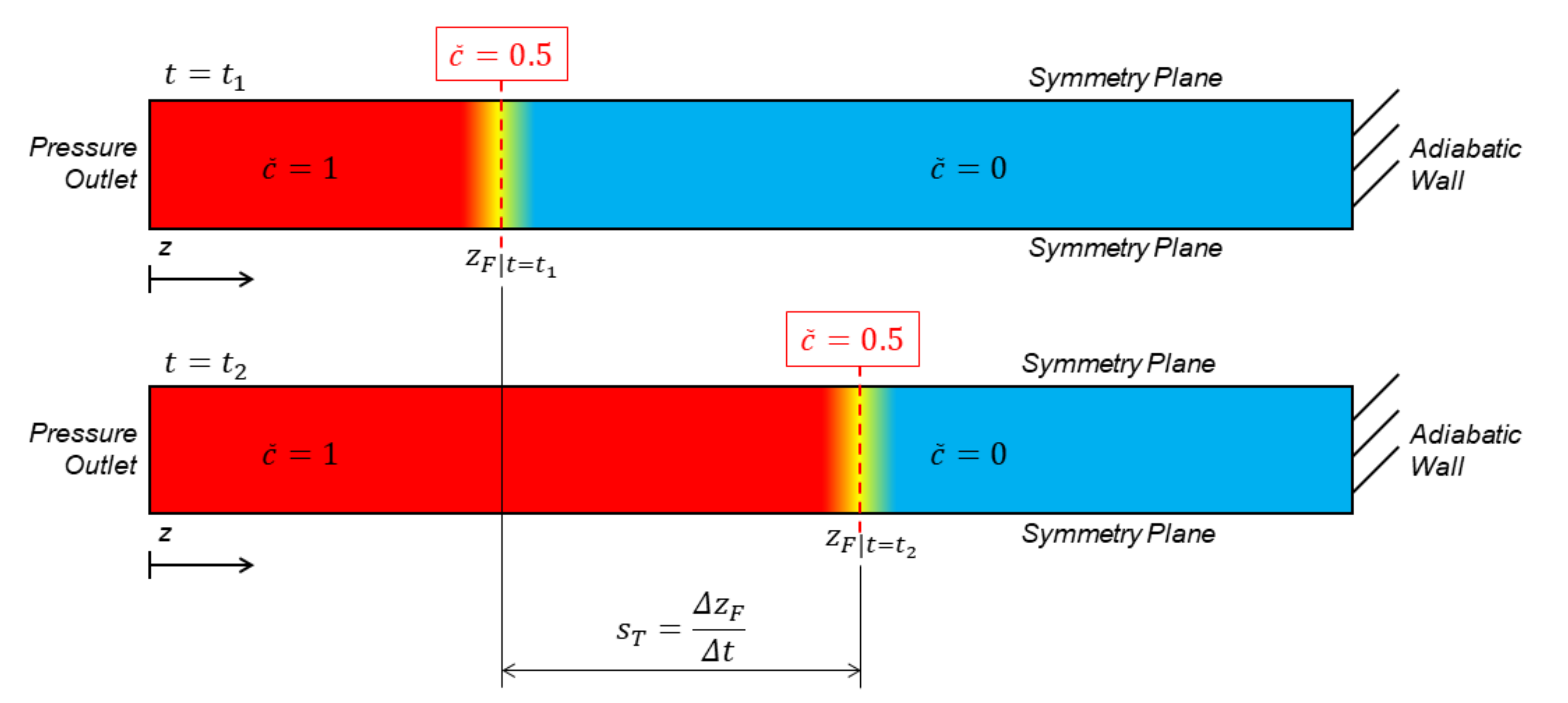
• The flame z-position $z_F$ for each iteration is elaborated for each simulation, and $d{r}_b/dt$ from Equation (1) is now $d{z}_F/dt$.
• A region for the initial kernel growth (50 mm) is excluded from $s_T$ measurement: this is motivated by the need to consider only the steady-state portion of flame development, discarding the ignition treatment. Therefore, flame position and velocity data are only extracted for $z_F>0.05$ m.
• The simulation duration is 16 × 10⁻³ s, i.e., a sufficient physical time for steady-state turbulent flame development for all the investigated cases. This is chosen to be longer than engine time-scales for combustion completion.
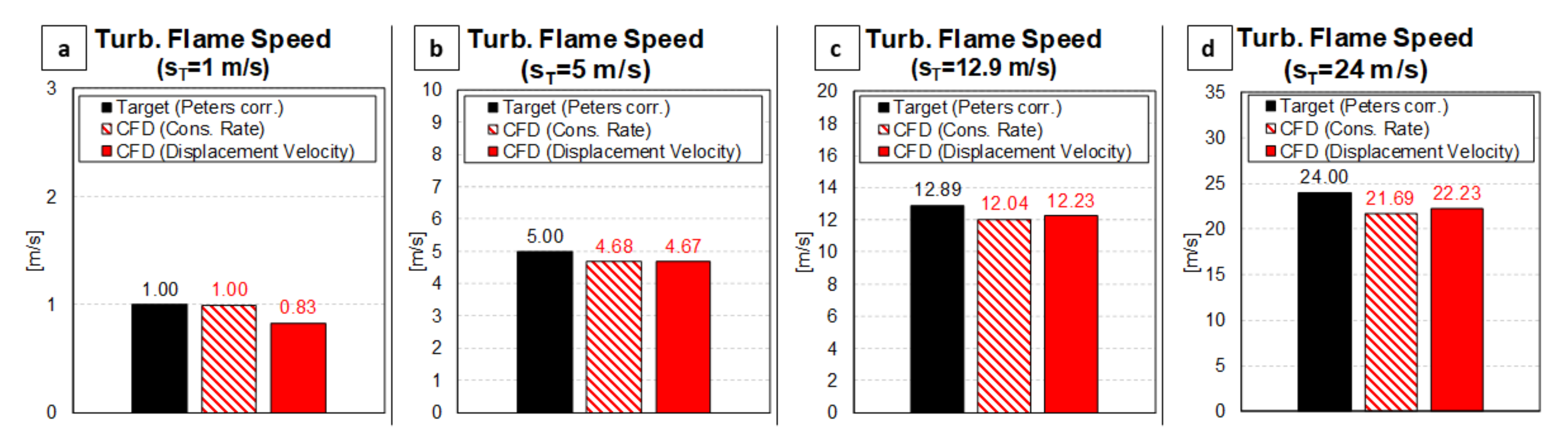
• Turbulent flame speed is calculated as $s_T=\Delta z_F/\Delta t.$ Combustion is initiated by a spark-ignition triggered at the first iteration from an ignition point on the domain z-axis at a 2 mm distance from the pressure outlet, and a spherical-type flame kernel is let to develop into a planar-like reaction front for $s_T$ measurement.

In this study, thermodynamic conditions for all the simulated cases are 40 bar and 700 K for the unburnt mixture to represent intermediate states between combustion initiation and peak pressure in high-loaded SI engines. A design matrix of $\left(\frac{u\prime }{s_L},\frac{l_t}{{\delta }_L}\right)$ states is tested, reproducing ICE-relevant combustion regimes. Typical values of laminar flame speed and thickness are taken as 1 m/s and 9 × 10⁻⁶ m, as representative of $s_L$ and ${\delta }_L$ from detailed chemistry simulations of freely propagating flame speed conducted at high-load engine conditions in [34] for iso-octane/air mixtures. It is emphasized that these values encompass the effect of the mixture thermodynamic state (p,T) and laminar chemistry rate (air/fuel ratio, dilution rate). Therefore, they constitute a laminar kinetics base upon which turbulence acts as a reaction rate enhancer. This follows the approach of other studies discussing scaling laws for turbulent bur rates from different thermodynamic conditions (e.g., [1,15]). Typical turbulence intensity degrees are reproduced through seven levels of $u^{\prime }$ values. In order to span a range of nine $Da$ numbers, the energy dissipation rate $\epsilon$ is varied considering the equality between the integral length scale expressions in Equation (4) (with $c_{\mu }=0.09$). Therefore, the 63 investigated conditions are obtained from the $\epsilon$ values as in Equation (5) and are reported in

Table 1. Set of $\epsilon \left[{\mathrm{m}}^2/{\mathrm{s}}^3\right]$ values used for imposed $u\prime$ and $Da$ levels.

Da	u′/sL = 1.83	u′/sL = 2.58	u′/sL = 4.08	u′/sL = 5.77	u′/sL = 8.16	u′/sL = 10	u′/sL = 14.14
0.5	ε = 2.24 × 105	ε = 4.47 × 105	ε = 1.12 × 106	ε = 2.24 × 106	ε = 4.47 × 106	ε = 6.71 × 106	ε = 1.342 × 107
1	ε = 1.12 × 105	ε = 2.24 × 105	ε = 5.59 × 105	ε = 1.12 × 106	ε = 2.24 × 106	ε = 3.35 × 106	ε = 6.708 × 106
1.5	ε = 7.45 × 104	ε = 1.49 × 105	ε = 3.73 × 105	ε = 7.45 × 105	ε = 1.49 × 106	ε = 2.24 × 106	ε = 4.472 × 106
5	ε = 2.24 × 104	ε = 4.47 × 104	ε = 1.12 × 105	ε = 2.24 × 105	ε = 4.47 × 105	ε = 6.71 × 105	ε = 1.342 × 106
10	ε = 1.12 × 104	ε = 2.24 × 104	ε = 5.59 × 104	ε = 1.12 × 105	ε = 2.24 × 105	ε = 3.35 × 105	ε = 6.708 × 105
18	ε = 6.21 × 103	ε = 1.24 × 104	ε = 3.11 × 104	ε = 6.21 × 104	ε = 1.24 × 105	ε = 1.86 × 105	ε = 3.727 × 105
37	ε = 3.02 × 103	ε = 6.04 × 103	ε = 1.51 × 104	ε = 3.02 × 104	ε = 6.04 × 104	ε = 9.07 × 104	ε = 1.813 × 105
57	ε = 1.96 × 103	ε = 3.92 × 103	ε = 9.81 × 103	ε = 1.96 × 104	ε = 3.92 × 104	ε = 5.88 × 104	ε = 1.177 × 105
75	ε = 1.49 × 103	ε = 2.98 × 103	ε = 7.45 × 103	ε = 1.49 × 104	ε = 2.98 × 104	ε = 4.47 × 104	ε = 8.944 × 104

. The set of points is illustrated on the Borghi–Peters diagram in Figure 4, showing the relevance of turbulent scales to the conditions experienced by flames in ICEs and defining the boundaries of the present investigation.

$$l_t=c_{\mu }^{0.75}·\frac{{\left(1.5·{u^{\prime }}^2\right)}^{1.5}}{\epsilon }=Da·u\prime ·\frac{{\delta }_L}{s_L}.$$

(4)

$$\epsilon =c_{\mu }^{0.75}·{\left(1.5·u{\prime }^2\right)}^{1.5}·\frac{{\delta }_L}{s_L}·u{\prime }^{-1}·D{a}^{-1}$$

(5)

4. Methodology

Once the simulation results are analysed for the tested combustion model, areas for improvement in the simulated $s_T$ are identified according to the following analysis steps:

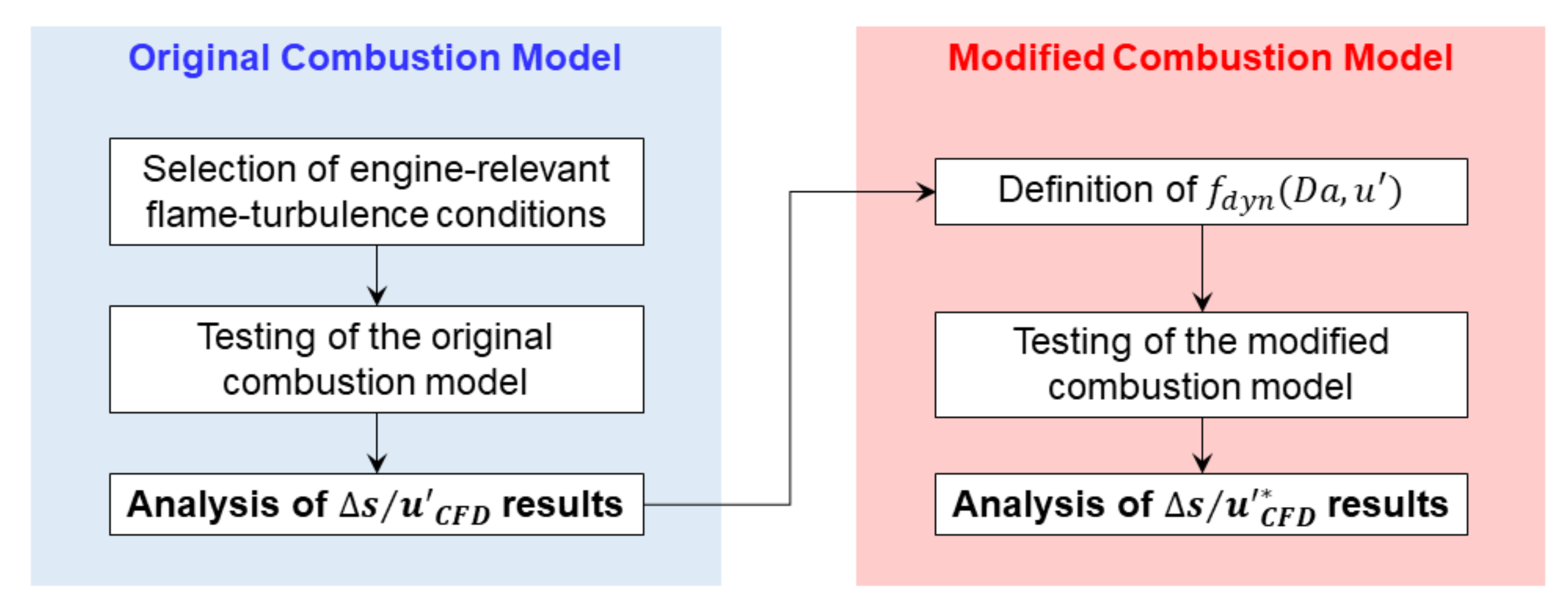
• The non-dimensional $\Delta s/u\prime$ group from the simulation results of the original combustion model (hereafter named $\Delta s/u{\prime }_{CFD}$) is analytically reproduced by a $g\left(Da,u^{\prime }\right)$ function, obtained through a data-based analysis procedure.
• A reference $\Delta s/u\prime$ function is identified from the literature (hereafter called $\Delta s/u{\prime }^{*})$. This serves as a physical basis for comparison with simulations. In this study, Equation (2) is considered as $\Delta s/u{\prime }^{*}$, although other correlations could be adopted.
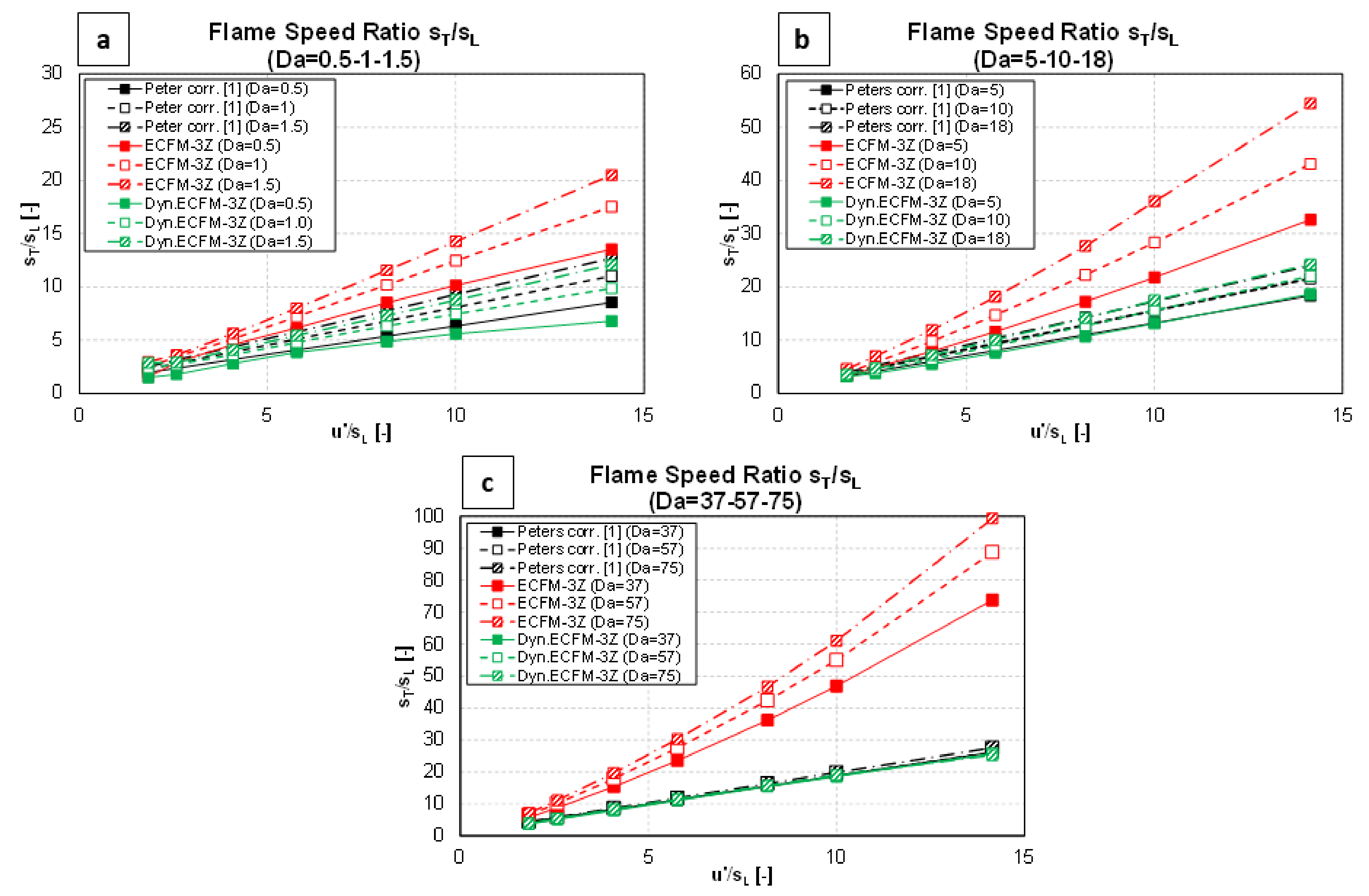
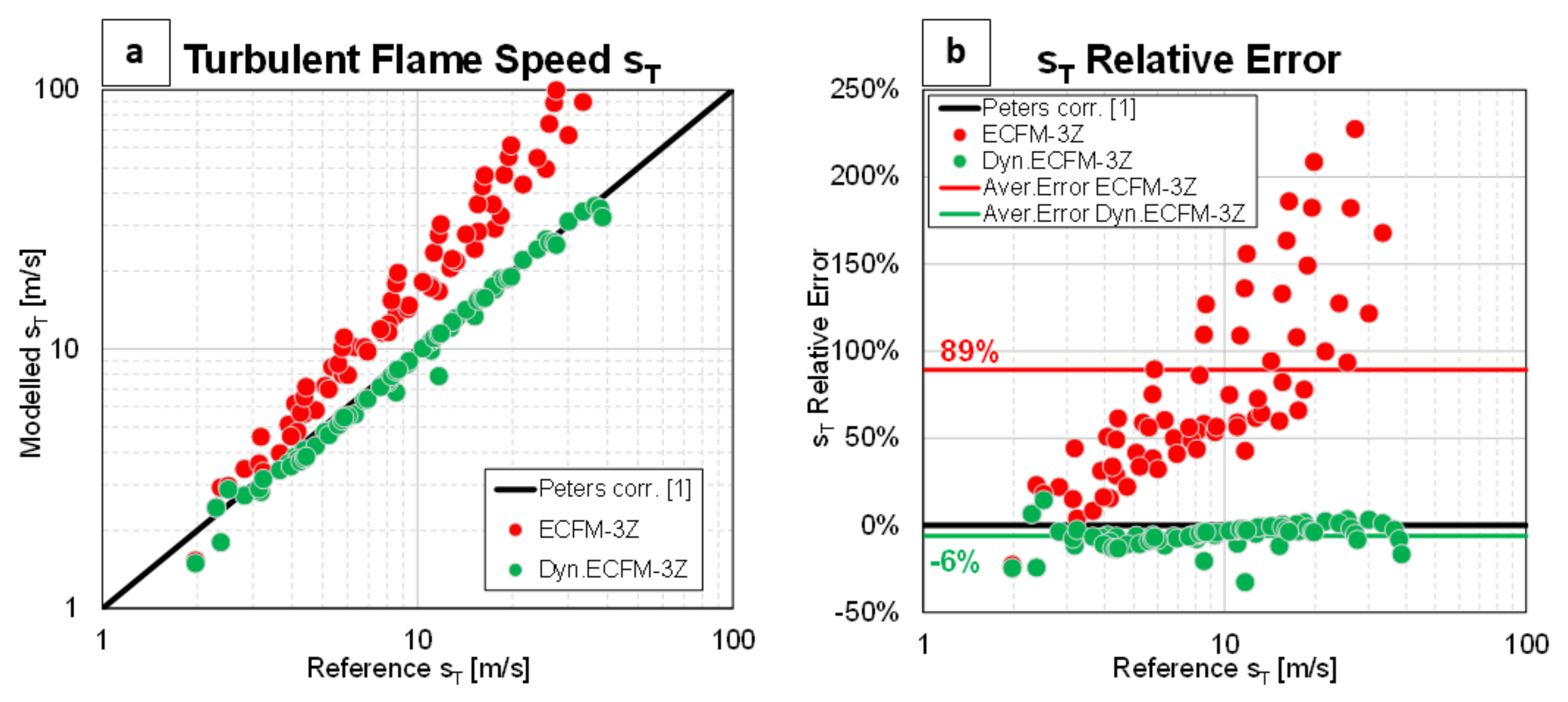
• For each analysed combustion model, scaling on both $u\prime$ and $Da$ is compared to $\Delta s/u{\prime }^{*}$, and areas for model improvements are identified. An original dynamic function $f_{dyn}\left(Da,u^{\prime }\right)$ is defined, i.e., a new function in the $\left(Da,u^{\prime }\right)$ space obtained from the data results to improve the turbulent burn rate of the combustion model. Based on this, a modified turbulent flame speed $s_T^{*}$ is obtained.
• All the simulations are repeated using $s_T^{*}$ and the results compared against literature data.

Finally, a model-specific dynamic function for $s_T^{*}$ is defined and the results from the dynamic combustion model are evaluated in terms of normalized flame speed $\Delta s/u{\prime }_{CFD}^{*}$ and turbulent to laminar ratio $s_T/s_{L,CFD}^{*}$. A flowchart of the proposed methodology is illustrated in Figure 5. The improvement and the generality of the presented method will be shown in the next section applied to a popular combustion model (ECFM-3Z), leading to a better physical representation of the turbulent burn rate.

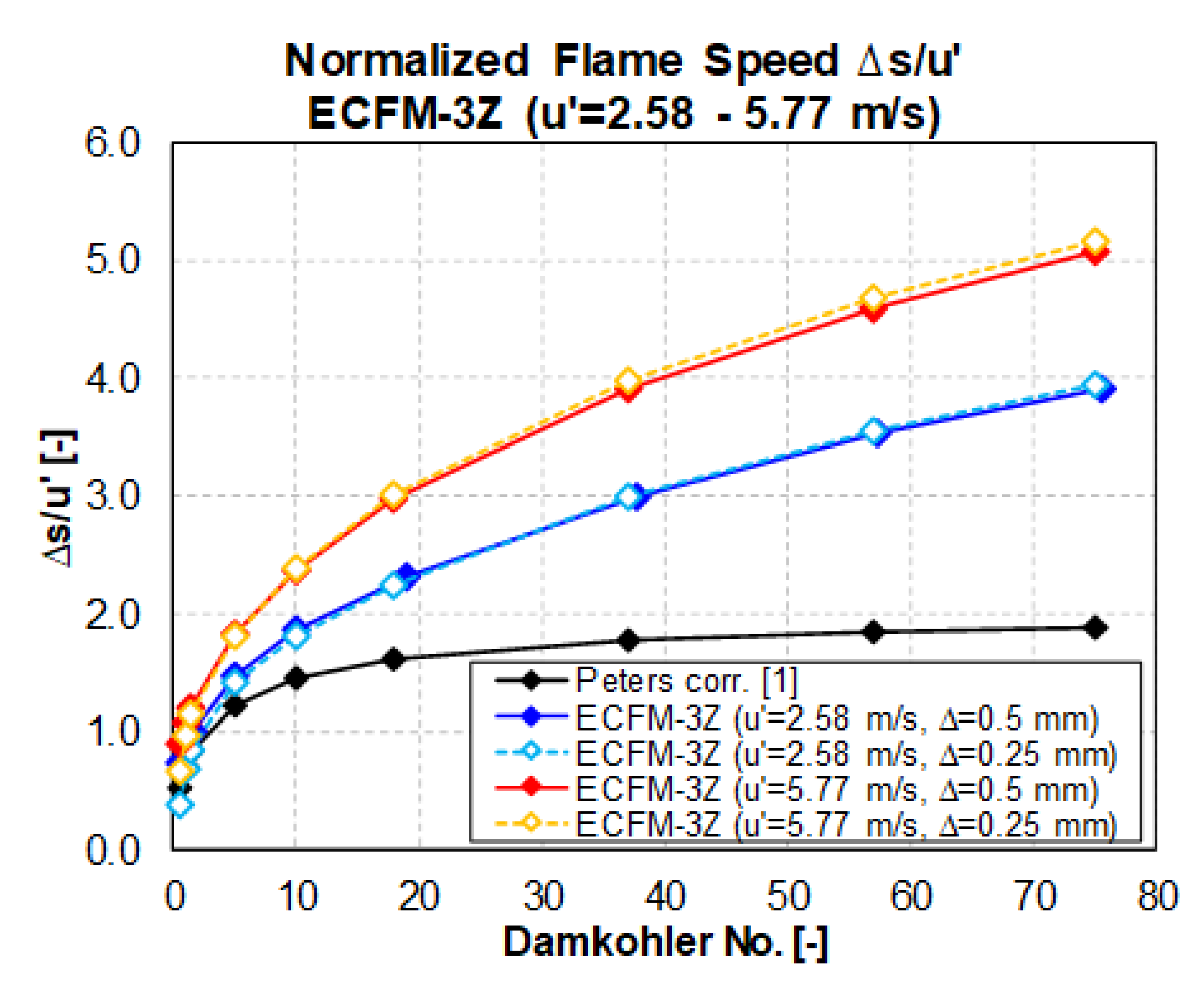
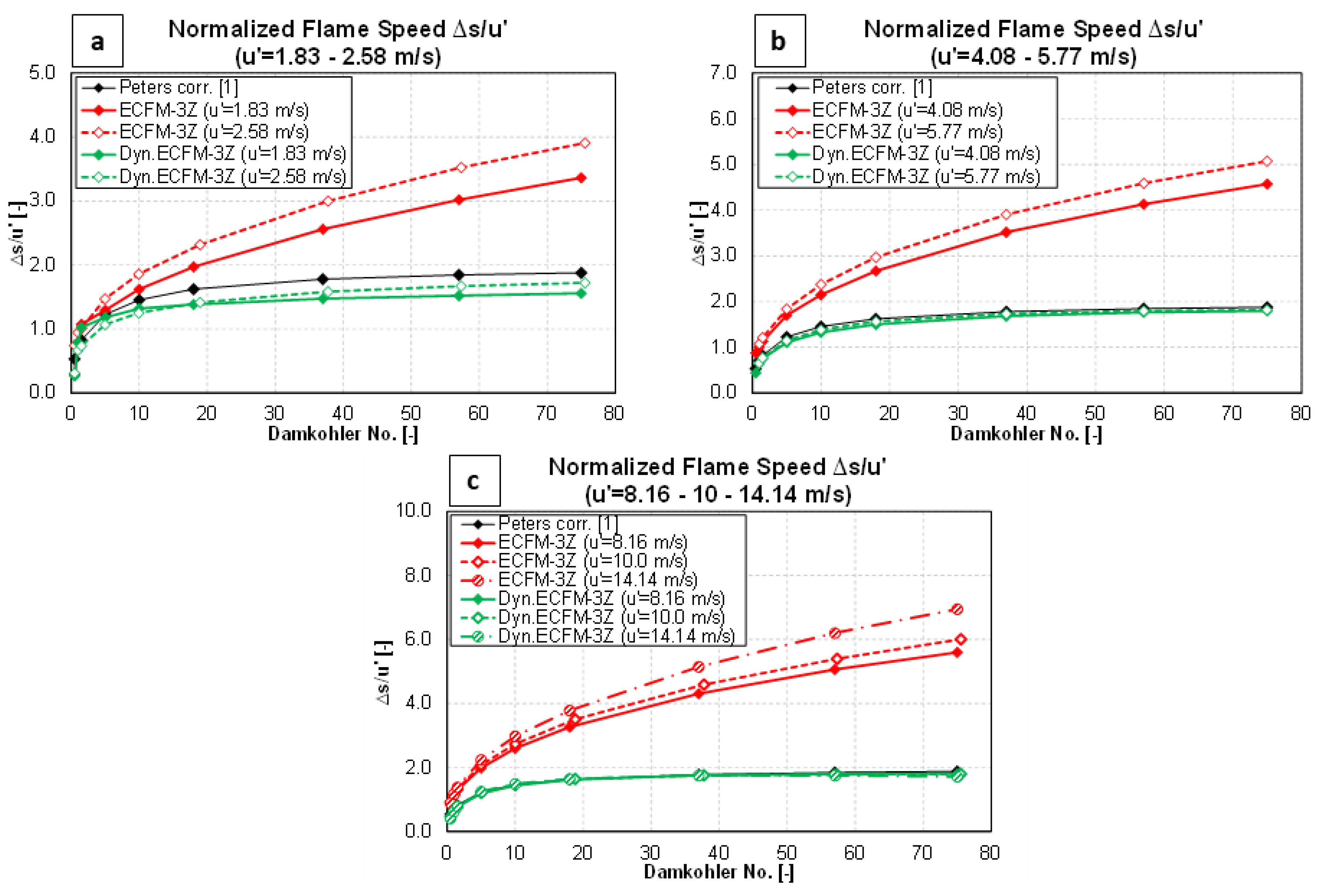
5. Results

The methodology is applied to the extended coherent flamelet model-3 zones (hereafter called ECFM-3Z) combustion model [5,35], whose application for engine combustion simulation has been presented in conjunction with advanced ignition models [36,37,38], knock models [39,40,41,42], alternative fuels [43,44,45,46], and in conjugate heat transfer analyses [47,48,49], despite that undesirable case-to-case tuning is often required to match the experimental burn rate [50,51]. Alongside the conventional governing equations for continuity (Equation (6)), momentum (Equation (7)), fuel mass fraction ${\tilde{Y}}_F$ (Equation (8)), and energy transport (Equation (9)) (with $\rho$, $\mu$, $D_F$, and $k$ being the mixture density, molecular viscosity, fuel diffusivity, and thermal conductivity, respectively, and ${\overline{S}}_u$, $S_T$ the volumetric source terms for momentum and temperature, respectively), in ECFM-3Z, the effective burn rate is computed through the flame surface density $\mathsf{\Sigma }$ (FSD) equation reported in Equation (10). As reviewed in [26], it represents the flame front convolution per unit volume in the reacting region. In Equation (10), $s_L$ is a model input, whereas the effective burn rate is calculated by the model itself without an explicit $s_T$ prescription; $\alpha$ and $\beta$ are model constants (1.6 and 1.0 values are used throughout the study). Finally, the fuel consumption rate ${\dot{\tilde{\omega }}}_F$ is derived as in Equation (11), where $Y_{F,u}$ is the fuel mass fraction in the unburnt mixture and ${\rho }_u$ is the unburnt density. The combustion progress variable in ECFM-3Z is algebraically defined as the ratio of the Favre-averaged fuel mass fraction ${\tilde{Y}}_F$ over its transported tracer ${\tilde{Y}}_{TF}$, as in Equation (12).

$$\frac{\partial \rho }{\partial t}+\nabla \left(\rho \overline{\mathit{u}}\right)=0$$

(6)

$$\frac{\partial \rho \overline{\mathit{u}}}{\partial t}+\nabla \left(\rho \overline{\mathit{u}}\overline{\mathit{u}}\right)=-\nabla p+\nabla \left(\mu \nabla \overline{\mathit{u}}\right)+{\overline{\mathit{S}}}_{\mathit{u}}$$

(7)

$$\frac{\partial \rho {\tilde{Y}}_F}{\partial t}+\nabla \left(\rho {\tilde{Y}}_F\overline{\mathit{u}}\right)=\nabla \left(D_F\nabla {\tilde{Y}}_F\right)+{\dot{\tilde{\omega }}}_F$$

(8)

$$\frac{\partial \rho c_{p}T}{\partial t}+\nabla \left(\rho c_{p}T\overline{\mathit{u}}\right)=\nabla \left(k\nabla T\right)+S_T$$

(9)

$$\frac{\partial \mathsf{\Sigma }}{\partial t}+\frac{\partial {\tilde{u}}_i\mathsf{\Sigma }}{\partial x_i}=\frac{\partial }{\partial x_i}\left(\frac{{\nu }_t}{{\sigma }_c}\frac{\partial \mathsf{\Sigma }}{\partial x_i}\right)+\alpha \frac{\epsilon }{k}\mathsf{\Sigma }-\beta s_L\frac{{\mathsf{\Sigma }}^2}{1-\tilde{c}}$$

(10)

$${\dot{\tilde{\omega }}}_F={\rho }_u{\tilde{Y}}_{F,u}{s}_L\mathsf{\Sigma }$$

(11)

$$\tilde{c}=1-\frac{{\tilde{Y}}_F }{{\tilde{Y}}_{TF}}$$

(12)

A preliminary sensitivity analysis is carried out on grid and time stepping, prior to defining the $f_{dyn}\left(Da,u^{\prime }\right)$ functions. The grid spacing is reduced to 0.25 mm in the z-axis direction, and the time step is reduced to 1.5 × 10⁻⁶ s to preserve the same CFL number as the reference configuration. Cases are run for selected turbulence levels (u′ = 2.58 m/s and u′ = 5.77 m/s) in the range $Da$ = 0.5–75. The results in terms of $\Delta s/u{\prime }_{CFD}$ are reported in Figure 6, showing a reduced sensitivity to space/time resolution. This reinforces the general validity of the dynamic functions on a variety of grid spacing and time resolution, and all the following discussion refers to the 0.5 mm cell spacing and 3 × 10⁻⁶ s time-step.

The results for the original ECFM-3Z model are reported in Figure 7 and Figure 8 (red series) in terms of normalized $\Delta s/u\prime$ dependence on $Da$ and $s_T/s_L$ as a function of $u\prime /s_L$, respectively. As visible in Figure 7, the results clearly show an incorrect dependence of $\Delta s/u{\prime }_{CFD}$ on $u\prime$, as well as a different $Da$-scaling, than the one expressed by the experimental/theoretical $\Delta s/u{\prime }^{*}$; this is observed for all the tested conditions and becomes relevant for $Da>5$ and for all $u\prime$ levels. Moreover, $\Delta s/u{\prime }_{CFD}$ lacks the asymptotic behaviour of $\Delta s/u{\prime }^{*}$; this represents an upper limit to normalized flame speed owing to turbulence-induced flame extinction; although several formulations exist in the literature to evaluate it, a consensus is present to account for this effect. Therefore, the model must be modified to better reproduce the $u\prime$ effect and the high-$Da$ flattening of the $\Delta s/u{\prime }_{CFD}$ curve. In Figure 8, the simulated $s_T/s_L$ (hereafter $s_T/s_{L,CFD})$ is overestimated with respect to the experiments-based $s_T/s_L$ (named $s_T/s_L^{*})$ for all $Da$ levels. The results from the original combustion model being fitted into a continuous space by the following analytical functions: $g\left(Da,u^{\prime }\right)$, $f_1\left(u^{\prime }\right)$, and $f_2\left(u^{\prime }\right)$ (Equation (13)–(15)), where separate fits for $u^{\prime }<2.6 \mathrm{m}/\mathrm{s}$ and $u^{\prime }\ge 2.6 \mathrm{m}/\mathrm{s}$ are carried out and the coefficients are reported in Appendix B (

Table A1. Set of coefficients used for the $s_T$ dynamic function for ECFM-3Z.

$a_1$	0.2940
$a_2$	0.2332
$a_3$	0.0909
$a_4$	0.7009
$b_1$	−0.0580
$b_2$	0.4668
$b_3$	0.2987
$b_4$	0.0476
$f_0$	−0.1488
$f_1$	0.8517
$f_2$	0.2824

). Such non-dimensional formulations and the two-range subdivision on $u\prime$ are chosen as the simplest and most accurate forms for data fitting in the analysed case, although in principle, other polynomial forms can be used.

$$g\left(Da,u^{\prime }\right)=f_1\left(u^{\prime }\right)·D{a}^{f_2\left(u^{\prime }\right)}$$

(13)

$$f_1\left(u^{\prime }\right)=\left\{\begin{array}{c}{a}_1·\ln \left(\frac{3}{2}{u^{\prime }}^2\right)+a_2, u\prime <2.6\\ a_3·\ln \left(\frac{3}{2}{u^{\prime }}^2\right)+a_4, u\prime \ge 2.6\end{array}\right.$$

(14)

$$f_2\left(u^{\prime }\right)=\left\{\begin{array}{c}{b}_1·\ln \left(\frac{3}{2}{u^{\prime }}^2\right)+b_2, u\prime <2.6\\ b_3·\ln \left(\frac{3}{2}{u^{\prime }}^2\right)+b_4, u\prime \ge 2.6\end{array}\right.$$

(15)

Considering the $g\left(Da,u^{\prime }\right)$ function as representative for $\Delta s/u{\prime }_{CFD}$ from the original combustion model, the $u\prime$ dependence is modified to make $\Delta s/u{\prime }_{CFD}^{*}$ results independent of $u\prime$ (i.e., linearly normalized on $u\prime$, as in Equation (2)). In addition, the same $Da$-scaling as the target $\Delta s/u{\prime }^{*}$ is introduced. Both operations are grouped in the $f_{dyn}\left(Da,u^{\prime }\right)$ function for ECFM-3Z (Equation (16)), which finally leads to the equality between $\Delta s/u{\prime }_{CFD}^{*}$ (i.e., obtained by the modified combustion model) and $\Delta s/u{\prime }^{*}$ (i.e., the one indicated by the selected reference correlation), as in Equation (17):

$$f_{dyn}\left(Da,u^{\prime }\right)=\frac{{\frac{\Delta s}{u\prime }}^{*}}{g\left(Da,u^{\prime }\right)}=\frac{-\frac{a_{4,P}·b_{3,P}^2}{2·b_{1,P}}·Da+\sqrt{{\left(\frac{a_{4,P}·b_{3,P}^2}{2·b_{1,P}}·Da\right)}^2+a_{4,P}·b_{3,P}·Da}}{g\left(Da,u^{\prime }\right)}$$

(16)

$${\frac{\Delta s}{u\prime }}_{CFD}^{*}=g\left(Da,u^{\prime }\right)·f_{dyn}\left(Da,u^{\prime }\right)={\frac{\Delta s}{u\prime }}^{*}$$

(17)

As for the application of the method to the particular case of ECFM-3Z, it is recalled that Equation (10) conceptually avoids the imposition of the turbulent flame speed $s_T^{*}$; therefore, a variation of the internally calculated $s_{T,0}$ is imposed via user-coding to the FSD equation. This is obtained by including the $s_T^{*}/s_{T,0}$ term (Equation (18)) to the FSD production term $\alpha$ (see Equation (10)), which here becomes ${\alpha }^{*}=\xi ·\alpha ·s_T^{*}/s_{T,0}$ in the application to the ECFM-3Z model. The $\xi$ function expresses the direct relationship between the modified ${\alpha }^{*}$ term and the $s_T^{*}/s_{T,0}$ ratio. Extended testing led to a satisfactory accuracy using a second-order polynomial function (Equation (19)), with coefficients relative to this study reported in Appendix B (Table A1). For the sake of simplicity, in this study, only the FSD production term $\alpha$ has been modified, while no modifications are introduced for the FSD destruction term $\beta$.

$$\frac{s_T^{*}}{s_{T,0}}=\frac{s_L+u^{\prime }·g^{ }\left(Da,u^{\prime }\right)·f_{dyn}\left(Da,u\prime \right) }{s_L+u\prime ·g\left(Da,u^{\prime }\right)}$$

(18)

$$\xi =f_2·{\left(\frac{s_T^{*}}{s_{T,0}}\right)}^2+f_1·\frac{s_T^{*}}{s_{T,0}}+f_0$$

(19)

The modified burn rate for the dynamic ECFM-3Z is evaluated by repeating all the simulations applying the dynamic function $f_{dyn}\left(Da,u^{\prime }\right)$ (Equation (16)) on the entire $\left(\frac{u\prime }{s_L},\frac{l_t}{{\delta }_L}\right)$ space from Table 1. The results are reported in Figure 7 and Figure 8 (green series), and the improved behaviour on the entire investigated space with respect to experimental results is clearly visible over all combustion regimes. The asymptotic tendency of $\Delta s/u{\prime }_{CFD}^{*}$ for the dynamic ECFM-3Z model is in agreement with the experimental/theoretical reference from Equation (2) for all $u\prime$ levels. In particular, the large $s_T/s_{L,CFD}$ overestimation for all $Da$ numbers is eliminated with the dynamic ECFM-3Z model ($s_T/s_{L,CFD}^{*}$, green series), thus obtaining the desired scaling $s_T/s_L^{*}$. Despite a minor error persisting in the range $Da=0.5-1.5$, the results show a very good agreement in the broad region $Da=5-75$, demonstrating the improved soundness of the dynamic ECFM-3Z model to reproduce the turbulence–flame interaction over a wide range of combustion regimes. A comprehensive comparison of the modelled $s_T$ against reference data is reported in Figure 9. The better agreement with the chosen correlation from the literature/experiment is evident for the dynamic ECFM-3Z model, as confirmed by the decrease of the average relative error from +89% (original ECFM-3Z) to −6% (dynamic ECFM-3Z).

6. Conclusions

The robust simulation of turbulent flame propagation speed $s_T$ is an essential requisite of combustion models. The modelling challenge is due to (i) the wide range of turbulent flame scales simultaneously present in the combustion chamber, (ii) the widely varying range of operating conditions covered by typical ICE applications, (iii) the difficulty in objectively measure in-cylinder turbulence intensity in ICEs, (iv) the lack of uniformity in $s_T$ measurements from the literature, and (v) the variety of available combustion models/CFD codes.

The present study provides a formally simple, yet rigorous method to measure the turbulent flame speed $s_T$ from a generic combustion model on a fixed grid test case at engine-typical turbulent conditions. Turbulence–flame interaction is varied in the range $Da$ 0.5–75 by modification of turbulence quantities. The proposed method allows the innovative possibility to evaluate the combustion model prediction of $s_T$ under a well-specified turbulence/flame interaction regime. A methodology consisting of the formulation of a dynamic function of local turbulent variables ($u\prime$ and $Da$) is presented and applied to the ECFM-3Z model, albeit of general validity for any type of combustion model.

The results show that, despite that the original $u^{\prime }$ and $Da$ scaling is found to largely differ from the target $\Delta s/u{\prime }^{*}$, the derivation and application of the data-derived dynamic $f_{dyn}\left(Da,u^{\prime }\right)$ function for the FSD equation allows to obtain an excellent agreement between the simulated $\Delta s/u{\prime }_{CFD}$ and the target $\Delta s/u{\prime }^{*}$.

The relevance of the presented method is the possibility to improve existing CFD combustion models via a more refined evaluation of local turbulent quantities. This is made possible by an objective measurement technique for $s_T$ on an idealized and easily reproducible test case, shedding a light on the hardly-quantifiable, but crucial area of simulated burn rate at engine-relevant conditions. The improvement given by the presented data-based methodology is expected to guide the development of more predictive combustion models, relying less on user calibration to provide an accurate turbulent burn rate prediction in highly-turbulent combustion systems. This is considered a key enabler in the field of simulation of high-efficiency and stability-limited combustion strategies.