A New Method to Determine the Impact of Individual Field Quantities on Cycle-to-Cycle Variations in a Spark-Ignited Gas Engine
Abstract
:1. Introduction
2. Materials and Methods
2.1. Engine Setup
2.2. CFD Simulation Setup
2.3. Multi-Cycle Simulations
2.4. Combination of Simulation Snapshots
- Extract the mesh data from both the base and velocity snapshot.
- Extract the velocity field from the velocity snapshot.
- Interpolate the velocity field, which is defined on the mesh of the velocity snapshot, onto the mesh of the base snapshot. This is done by looping over all the cells of the base snapshot and finding the value of the velocity field of the cell of the velocity snapshot which is nearest to the cell of the base snapshot.
- Write the newly interpolated field, which is now defined on the mesh of the base snapshot mesh, into the corresponding data array. Thus, the original, base velocity field is replaced with the exchange dataset.
3. Results
3.1. Impact of the Velocity Field on the Combustion
3.2. Impact of the Turbulence on the Combustion
3.3. Impact of the Flow Field near the Spark Plug on the Combustion
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CoV | coefficient of variation |
| CCV | cycle-to-cycle variations |
| CFL | Courant–Friedrichs–Lewy |
| SI | spark-ignited |
| RANS | Renolds-averaged Navier–Stokes equations |
| CFD | computational fluid dynamics |
| AMR | adaptive mesh refinement |
| CAD | crank angle degree |
| MFB | mass fraction burned |
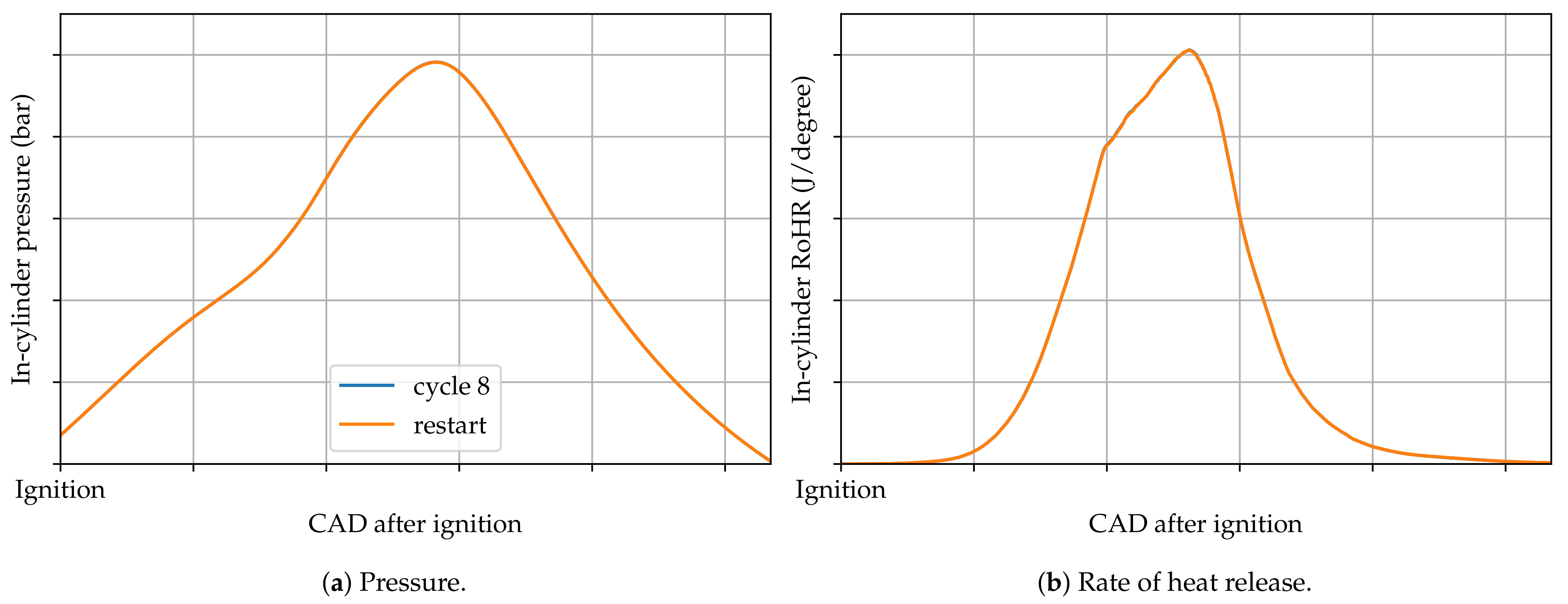
Appendix A

References
- Young, M.B. Cyclic Dispersion in the Homogeneous-Charge Spark-Ignition Engine—A Literature Survey. SAE Trans. 1981, 90, 49–73. [Google Scholar] [CrossRef]
- Ozdor, N.; Dulger, M.; Sher, E. Cyclic Variability in Spark Ignition Engines A Literature Survey. SAE Trans. 1994, 103, 1514–1552. [Google Scholar] [CrossRef]
- Maurya, R.K. Combustion Stability Analysis. In Reciprocating Engine Combustion Diagnostics: In-Cylinder Pressure Measurement and Analysis; Springer: Cham, Switzerland, 2019; pp. 361–459. [Google Scholar] [CrossRef]
- Matekunas, F.A. Modes and Measures of Cyclic Combustion Variability. SAE Trans. 1983, 92, 1139–1156. [Google Scholar] [CrossRef]
- Johansson, B. Cycle to Cycle Variations in S.I. Engines—The Effects of Fluid Flow and Gas Composition in the Vicinity of the Spark Plug on Early Combustion. SAE Trans. 1996, 105, 2286–2296. [Google Scholar] [CrossRef] [Green Version]
- Han, S.B. Cycle-to-cycle variations under cylinder-pressure-based combustion analysis in spark ignition engines. KSME Int. J. 2000, 14, 1151–1158. [Google Scholar] [CrossRef]
- Reuss, D.L. Cyclic Variability of Large-Scale Turbulent Structures in Directed and Undirected IC Engine Flows. SAE Trans. 2000, 109, 125–145. [Google Scholar] [CrossRef]
- Abraham, P.S.; Yang, X.; Gupta, S.; Kuo, T.W.; Reuss, D.L.; Sick, V. Flow-pattern switching in a motored spark ignition engine. Int. J. Engine Res. 2015, 16, 323–339. [Google Scholar] [CrossRef] [Green Version]
- Mahmoudzadeh Andwari, A.; Pesyridis, A.; Esfahanian, V.; Said, M.F.M. Combustion and Emission Enhancement of a Spark Ignition Two-Stroke Cycle Engine Utilizing Internal and External Exhaust Gas Recirculation Approach at Low-Load Operation. Energies 2019, 12, 609. [Google Scholar] [CrossRef] [Green Version]
- Marchitto, L.; Tornatore, C.; Teodosio, L. Individual Cylinder Combustion Optimization to Improve Performance and Fuel Consumption of a Small Turbocharged SI Engine. Energies 2020, 13, 5548. [Google Scholar] [CrossRef]
- Omanovic, A.; Zsiga, N.; Soltic, P.; Onder, C. Increased Internal Combustion Engine Efficiency with Optimized Valve Timings in Extended Stroke Operation. Energies 2021, 14, 2750. [Google Scholar] [CrossRef]
- El-Adawy, M.; Heikal, M.R.; Aziz, A.; Rashid, A.; Adam, I.K.; Ismael, M.A.; Babiker, M.E.; Baharom, M.B.; Firmansyah; Abidin, E.Z.Z. On the Application of Proper Orthogonal Decomposition (POD) for In-Cylinder Flow Analysis. Energies 2018, 11, 2261. [Google Scholar] [CrossRef] [Green Version]
- Martinez-Boggio, S.; Merola, S.; Teixeira Lacava, P.; Irimescu, A.; Curto-Risso, P. Effect of Fuel and Air Dilution on Syngas Combustion in an Optical SI Engine. Energies 2019, 12, 1566. [Google Scholar] [CrossRef] [Green Version]
- Schiffmann, P. Root Causes of Cyclic Variability of Early Flame Kernels in Spark Ignited Engines. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2016. [Google Scholar]
- Schiffmann, P.; Reuss, D.L.; Sick, V. Empirical investigation of spark-ignited flame-initiation cycle-to-cycle variability in a homogeneous charge reciprocating engine. Int. J. Engine Res. 2018, 19, 491–508. [Google Scholar] [CrossRef]
- Sadeghi, M.; Truffin, K.; Peterson, B.; Böhm, B.; Jay, S. Development and Application of Bivariate 2D-EMD for the Analysis of Instantaneous Flow Structures and Cycle-to-Cycle Variations of In-cylinder Flow. Flow Turbul. Combust. 2021, 106, 231–259. [Google Scholar] [CrossRef]
- Roudnitzky, S.; Druault, P.; Guibert, P. Proper orthogonal decomposition of in-cylinder engine flow into mean component, coherent structures and random Gaussian fluctuations. J. Turbul. 2006, 7, N70. [Google Scholar] [CrossRef]
- Vermorel, O.; Richard, S.; Colin, O.; Angelberger, C.; Benkenida, A.; Veynante, D. Towards the understanding of cyclic variability in a spark ignited engine using multi-cycle LES. Combust. Flame 2009, 156, 1525–1541. [Google Scholar] [CrossRef]
- Liu, K.; Haworth, D.C.; Yang, X.; Gopalakrishnan, V. Large-eddy simulation of motored flow in a two-valve piston engine: POD analysis and cycle-to-cycle variations. Flow Turbul. Combust. 2013, 91, 373–403. [Google Scholar] [CrossRef]
- Li, W.; Li, Y.; Wang, T.; Jia, M.; Che, Z.; Liu, D. Investigation of the effect of the in-cylinder tumble motion on cycle-to-cycle variations in a direct injection spark ignition (DISI) engine using large eddy simulation (LES). Flow Turbul. Combust. 2017, 98, 601–631. [Google Scholar] [CrossRef]
- Richard, S.; Dulbecco, A.; Angelberger, C.; Truffin, K. Invited Review: Development of a one-dimensional computational fluid dynamics modeling approach to predict cycle-to-cycle variability in spark-ignition engines based on physical understanding acquired from large-eddy simulation. Int. J. Engine Res. 2015, 16, 379–402. [Google Scholar] [CrossRef]
- Netzer, C.; Pasternak, M.; Seidel, L.; Ravet, F.; Mauss, F. Computationally efficient prediction of cycle-to-cycle variations in spark-ignition engines. Int. J. Engine Res. 2020, 21, 649–663. [Google Scholar] [CrossRef]
- Truffin, K.; Angelberger, C.; Richard, S.; Pera, C. Using large-eddy simulation and multivariate analysis to understand the sources of combustion cyclic variability in a spark-ignition engine. Combust. Flame 2015, 162, 4371–4390. [Google Scholar] [CrossRef] [Green Version]
- Lauer, T.; Frühhaber, J. Towards a Predictive Simulation of Turbulent Combustion?—An Assessment for Large Internal Combustion Engines. Energies 2021, 14, 43. [Google Scholar] [CrossRef]
- Scarcelli, R.; Richards, K.; Pomraning, E.; Senecal, P.K.; Wallner, T.; Sevik, J. Cycle-to-Cycle Variations in Multi-Cycle Engine RANS Simulations. In Proceedings of the SAE 2016 World Congress and Exhibition. SAE International, Grand Rapids, MI, USA, 7–10 September 2016. [Google Scholar] [CrossRef]
- Krastev, V.K.; Silvestri, L.; Falcucci, G. A Modified Version of the RNG k–ε Turbulence Model for the Scale-Resolving Simulation of Internal Combustion Engines. Energies 2017, 10, 2116. [Google Scholar] [CrossRef] [Green Version]
- Smith, G.P.; Golden, D.M.; Frenklach, M.; Moriarty, N.W.; Eiteneer, B.; Goldenberg, M.; Bowman, C.T.; Hanson, R.K.; Song, S.; William, C.; et al. GRI Mech 3.0. 1999. Available online: http://combustion.berkeley.edu/gri-mech/version30/text30.html (accessed on 26 April 2021).
- Scarcelli, R.; Sevik, J.; Wallner, T.; Richards, K.; Pomraning, E.; Senecal, P.K. Capturing Cyclic Variability in Exhaust Gas Recirculation Dilute Spark-Ignition Combustion Using Multicycle RANS. J. Eng. Gas Turbines Power 2016, 138, 112803. [Google Scholar] [CrossRef]
- Kosmadakis, G.M.; Rakopoulos, C.D. A Fast CFD-Based Methodology for Determining the Cyclic Variability and Its Effects on Performance and Emissions of Spark-Ignition Engines. Energies 2019, 12, 4131. [Google Scholar] [CrossRef] [Green Version]
- Kosmadakis, G.; Rakopoulos, D.; Arroyo, J.; Moreno, F.; Muñoz, M.; Rakopoulos, C. CFD-based method with an improved ignition model for estimating cyclic variability in a spark-ignition engine fueled with methane. Energy Convers. Manag. 2018, 174, 769–778. [Google Scholar] [CrossRef]
- h5py Developers. HDF5 for Python. 2021. Available online: https://www.h5py.org/ (accessed on 28 April 2021).











| Comb. | Base | Exchange | Snapshot Time | Exchanged Datasets |
|---|---|---|---|---|
| 1 | 8 | 3 | 5.0 CAD b. ign. | velocity |
| 2 | 3 | 8 | 5.0 CAD b. ign. | velocity |
| 3 | 8 | 3 | 5.0 CAD b. ign. | turbulence (k and ) |
| 4 | 3 | 8 | 5.0 CAD b. ign. | turbulence (k and ) |
| 5 | 8 | 3 | 5.0 CAD b. ign. | velocity close to spark plug (1 cm sphere) |
| 6 | 8 | 3 | 5.0 CAD b. ign. | velocity close to spark plug (2 cm sphere) |
| 7 | 8 | 3 | 5.0 CAD b. ign. | velocity close to spark plug (5 cm sphere) |
| 8 | 8 | 3 | 0.5 CAD b. ign. | velocity close to spark plug (1 cm sphere) |
| 9 | 8 | 3 | 0.5 CAD b. ign. | velocity close to spark plug (2 cm sphere) |
| 10 | 8 | 3 | 0.5 CAD b. ign. | velocity close to spark plug (5 cm sphere) |
| 11 | 3 | 8 | 5.0 CAD b. ign. | velocity close to spark plug (1 cm sphere) |
| 12 | 3 | 8 | 5.0 CAD b. ign. | velocity close to spark plug (2 cm sphere) |
| 13 | 3 | 8 | 5.0 CAD b. ign. | velocity close to spark plug (5 cm sphere) |
| 14 | 3 | 8 | 0.5 CAD b. ign. | velocity close to spark plug (1 cm sphere) |
| 15 | 3 | 8 | 0.5 CAD b. ign. | velocity close to spark plug (2 cm sphere) |
| 16 | 3 | 8 | 0.5 CAD b. ign. | velocity close to spark plug (5 cm sphere) |
| Case | CAD | MFB50% | MFB10–90% | ||||
|---|---|---|---|---|---|---|---|
| Cycle 3 | 100.0% | 36.51 | 0.0% | 31.30 | 0.0% | 17.96 | 0.0% |
| Cycle 8 | 0.0% | 37.03 | 100.0% | 32.20 | 100.0% | 19.21 | 100.0% |
| Comb. 1 | 88.3% | 36.57 | 10.9% | 31.36 | 7.3% | 18.11 | 12.8% |
| Comb. 2 | 4.2% | 36.91 | 77.0% | 32.15 | 95.2% | 19.12 | 92.8% |
| Comb. 3 | 19.8% | 36.90 | 74.6% | 32.04 | 82.6% | 18.93 | 77.8% |
| Comb. 4 | 75.3% | 36.66 | 29.3% | 31.48 | 20.3% | 18.24 | 23.2% |
| Comb. 5 | 25.9% | 36.90 | 74.7% | 31.96 | 73.7% | 18.88 | 74.3% |
| Comb. 6 | 72.1% | 36.56 | 9.3% | 31.52 | 24.7% | 18.49 | 42.9% |
| Comb. 7 | 82.7% | 36.57 | 11.5% | 31.40 | 11.8% | 18.22 | 20.8% |
| Comb. 8 | 48.7% | 36.71 | 38.5% | 31.73 | 48.0% | 18.75 | 63.6% |
| Comb. 9 | 72.0% | 36.56 | 10.0% | 31.49 | 21.1% | 18.62 | 53.5% |
| Comb. 10 | 77.1% | 36.59 | 15.1% | 31.43 | 15.2% | 18.34 | 30.9% |
| Comb. 11 | 63.2% | 36.74 | 44.9% | 31.61 | 35.2% | 18.35 | 31.9% |
| Comb. 12 | 32.5% | 36.97 | 88.8% | 31.92 | 68.7% | 18.58 | 50.3% |
| Comb. 13 | 12.7% | 37.01 | 96.6% | 32.12 | 91.9% | 18.92 | 76.9% |
| Comb. 14 | 48.3% | 36.82 | 60.5% | 31.76 | 52.0% | 18.42 | 37.4% |
| Comb. 15 | 30.9% | 37.02 | 97.8% | 31.97 | 75.2% | 18.40 | 35.7% |
| Comb. 16 | 7.1% | 36.94 | 83.2% | 32.14 | 93.3% | 18.98 | 82.3% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gößnitzer, C.; Givler, S. A New Method to Determine the Impact of Individual Field Quantities on Cycle-to-Cycle Variations in a Spark-Ignited Gas Engine. Energies 2021, 14, 4136. https://doi.org/10.3390/en14144136
Gößnitzer C, Givler S. A New Method to Determine the Impact of Individual Field Quantities on Cycle-to-Cycle Variations in a Spark-Ignited Gas Engine. Energies. 2021; 14(14):4136. https://doi.org/10.3390/en14144136
Chicago/Turabian StyleGößnitzer, Clemens, and Shawn Givler. 2021. "A New Method to Determine the Impact of Individual Field Quantities on Cycle-to-Cycle Variations in a Spark-Ignited Gas Engine" Energies 14, no. 14: 4136. https://doi.org/10.3390/en14144136
APA StyleGößnitzer, C., & Givler, S. (2021). A New Method to Determine the Impact of Individual Field Quantities on Cycle-to-Cycle Variations in a Spark-Ignited Gas Engine. Energies, 14(14), 4136. https://doi.org/10.3390/en14144136





