Efficiency Enhancement of Non-Isolated DC-DC Interleaved Buck Converter for Renewable Energy Sources
Abstract
:1. Introduction
2. Interleaved DC-DC Converter Analysis
2.1. The First Time Period Analysis–Energy Accumulation
2.2. The Second Time Period Analysis—Energy Transferred to the Load
2.3. Total Power Loss Calculation
3. Calculated Efficiency Results Based on Legs Number and Input Power
4. Simulated Efficiency Results Based on Legs Number and Input Power
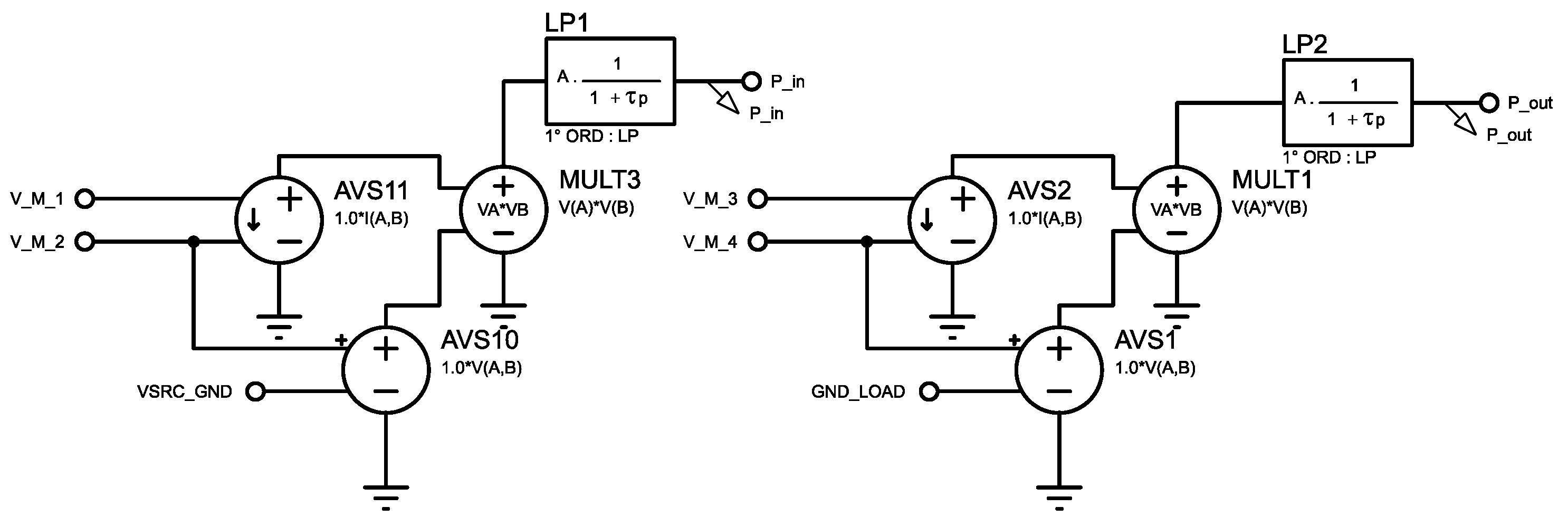
5. Experimental Validation
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hamidi, F.; Olteanu, S.C.; Popescu, D.; Jerbi, H.; Dincă, I.; Ben Aoun, S.; Abbassi, R. Model Based Optimisation Algorithm for Maximum Power Point Tracking in Photovoltaic Panels. Energies 2020, 13, 4798. [Google Scholar] [CrossRef]
- Farhat, M.; Barambones, O.; Sbita, L. A Real-Time Implementation of Novel and Stable Variable Step Size MPPT. Energies 2020, 13, 4668. [Google Scholar] [CrossRef]
- Park, J.-M.; Byun, H.-J.; Kim, B.-J.; Kim, S.-H.; Won, C.-Y. Analysis and Design of Coupled Inductor for Interleaved Buck-Type Voltage Balancer in Bipolar DC Microgrid. Energies 2020, 13, 2775. [Google Scholar] [CrossRef]
- Loncarski, J.; Monopoli, V.G.; Cascella, G.L.; Cupertino, F. SiC-MOSFET and Si-IGBT-Based dc-dc Interleaved Converters for EV Chargers: Approach for Efficiency Comparison with Minimum Switching Losses Based on Complete Parasitic Modeling. Energies 2020, 13, 4585. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, X. A Unified Analytical Modeling of the Interleaved Pulse Width Modulation (PWM) DC–DC Converter and Its Applications. IEEE Trans. Power Electron. 2013, 28, 5147–5158. [Google Scholar] [CrossRef]
- Frivaldsky, M.; Hanko, B.; Prazenica, M.; Morgos, J. High Gain Boost Interleaved Converters with Coupled Inductors and with Demagnetizing Circuits. Energies 2018, 11, 130. [Google Scholar] [CrossRef] [Green Version]
- Lai, C.-M.; Cheng, Y.-H.; Teh, J.; Lin, Y.-C. A New Combined Boost Converter with Improved Voltage Gain as a Battery-Powered Front-End Interface for Automotive Audio Amplifiers. Energies 2017, 10, 1128. [Google Scholar] [CrossRef] [Green Version]
- Shen, C.-L.; Chiu, P.-C.; Lee, Y.-C. Novel Interleaved Converter with Extra-High Voltage Gain to Process Low-Voltage Renewable-Energy Generation. Energies 2016, 9, 871. [Google Scholar] [CrossRef] [Green Version]
- Lai, C.-M.; Teh, J.; Lin, Y.-C.; Liu, Y. Study of a Bidirectional Power Converter Integrated with Battery/Ultracapacitor Dual-Energy Storage. Energies 2020, 13, 1234. [Google Scholar] [CrossRef] [Green Version]
- Lai, C.-M. Development of a Novel Bidirectional DC/DC Converter Topology with High Voltage Conversion Ratio for Electric Vehicles and DC-Microgrids. Energies 2016, 9, 410. [Google Scholar] [CrossRef] [Green Version]
- Yao, Z.; Lu, S. A Simple Approach to Enhance the Effectiveness of Passive Currents Balancing in an Interleaved Multiphase Bidirectional DC–DC Converter. IEEE Trans. Power Electron. 2019, 34, 7242–7255. [Google Scholar] [CrossRef]
- Gosumbonggot, J.; Fujita, G. Partial Shading Detection and Global Maximum Power Point Tracking Algorithm for Photovoltaic with the Variation of Irradiation and Temperature. Energies 2019, 12, 202. [Google Scholar] [CrossRef] [Green Version]
- Farh, H.M.H.; Othman, M.F.; Eltamaly, A.M.; Al-Saud, M.S. Maximum Power Extraction from a Partially Shaded PV System Using an Interleaved Boost Converter. Energies 2018, 11, 2543. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.-J.; Yang, S.-P.; Huang, C.-M.; Chou, H.-M.; Shen, M.-J. Interleaved High Step-Up DC-DC Converter Based on Voltage Multiplier Cell and Voltage-Stacking Techniques for Renewable Energy Applications. Energies 2018, 11, 1632. [Google Scholar] [CrossRef] [Green Version]
- Moradisizkoohi, H.; Elsayad, N.; Mohammed, O.A. An Integrated Interleaved Ultrahigh Step-Up DC–DC Converter Using Dual Cross-Coupled Inductors With Built-In Input Current Balancing for Electric Vehicles. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 644–657. [Google Scholar] [CrossRef]
- Wang, C.-S.; Li, W.; Wang, Y.-F.; Han, F.-Q.; Meng, Z.; Li, G.-D. An Isolated Three-Port Bidirectional DC-DC Converter with Enlarged ZVS Region for HESS Applications in DC Microgrids. Energies 2017, 10, 446. [Google Scholar] [CrossRef] [Green Version]
- Nymand, M.; Andersen, M.A.E. High-Efficiency Isolated Boost DC–DC Converter for High-Power Low-Voltage Fuel-Cell Applications. IEEE Trans. Ind. Electron. 2010, 57, 505–514. [Google Scholar] [CrossRef]
- Simon-Muela, A.; Alonso, C.; Boitier, V.; Estibals, B.; Chaptal, J.L. Comparative study of the optimal number of phases for interleaved Voltage regulator modules. In Proceedings of the 2007 European Conference on Power Electronics and Applications, Aalborg, Denmark, 2–5 September 2007; pp. 1–8. [Google Scholar] [CrossRef]
- Magne, P.; Liu, P.; Bilgin, B.; Emadi, A. Investigation of impact of number of phases in interleaved dc-dc boost converter. In Proceedings of the 2015 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 14–17 June 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Zulkifli, S.A. Cascaded buck-boost converters: Output voltage regulation & constant inductor current. In Proceedings of the 2013 IEEE Symposium on Industrial Electronics & Applications. IEEE, Kuching, Malaysia, 22–25 September 2013; pp. 111–116. [Google Scholar] [CrossRef]
- Kováč, D.; Bereš, M.; Kováčová, I.; Vince, T.; Molnar, J.; Dziak, J.; Jacko, P.; Bučko, R.; Tomčíková, I.; Schweiner, D. Circuit elements influence on optimal number of phases of DC/DC buck converter. Electron. Lett. 2018, 54, 435–437. [Google Scholar] [CrossRef]












| Parameter | Description | Value |
|---|---|---|
| n | Number of legs | 1–4 |
| RPn1 | Input wire resistance | 0.2 [Ω] |
| RPn2 | Output wire resistance | 0.2 [Ω] |
| V | Input voltage | 30 [V] |
| RDS(on) | MOSFET drain source electric resistance when it is turned on | 0.07 [Ω] |
| RLn | electric resistance of main inductor | 0.044 [Ω] |
| rF | Diode resistance in forward direction | 0.02 [Ω] |
| IDS(off) | Leakage current of MOSFET | 250 [µA] |
| VTO | Threshold voltage of diodes | 0.77 [V] |
| IR | Current through diode in reverse direction | 2 [mA] |
| ton | Time which transistor takes to turn on | 55 [ns] |
| toff | Time which transistor takes to turn off | 96 [ns] |
| Qrr | Commutation charge of diode | 120 [nC] |
| VFP | the voltage drop on diode during time tfr the diode takes to turn on | 2 [V] |
| f | frequency | 200 [kHz] |
| tfr | Time duration of voltage drop on diode which takes to turn it on | 2 [ns] |
| D | Duty cycle | 0–1 |
| Z | Resistive load | 4.7 [Ω] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bereš, M.; Kováč, D.; Vince, T.; Kováčová, I.; Molnár, J.; Tomčíková, I.; Dziak, J.; Jacko, P.; Fecko, B.; Gans, Š. Efficiency Enhancement of Non-Isolated DC-DC Interleaved Buck Converter for Renewable Energy Sources. Energies 2021, 14, 4127. https://doi.org/10.3390/en14144127
Bereš M, Kováč D, Vince T, Kováčová I, Molnár J, Tomčíková I, Dziak J, Jacko P, Fecko B, Gans Š. Efficiency Enhancement of Non-Isolated DC-DC Interleaved Buck Converter for Renewable Energy Sources. Energies. 2021; 14(14):4127. https://doi.org/10.3390/en14144127
Chicago/Turabian StyleBereš, Matej, Dobroslav Kováč, Tibor Vince, Irena Kováčová, Ján Molnár, Iveta Tomčíková, Jozef Dziak, Patrik Jacko, Branislav Fecko, and Šimon Gans. 2021. "Efficiency Enhancement of Non-Isolated DC-DC Interleaved Buck Converter for Renewable Energy Sources" Energies 14, no. 14: 4127. https://doi.org/10.3390/en14144127
APA StyleBereš, M., Kováč, D., Vince, T., Kováčová, I., Molnár, J., Tomčíková, I., Dziak, J., Jacko, P., Fecko, B., & Gans, Š. (2021). Efficiency Enhancement of Non-Isolated DC-DC Interleaved Buck Converter for Renewable Energy Sources. Energies, 14(14), 4127. https://doi.org/10.3390/en14144127