The Interconnection and Damping Assignment Passivity-Based Control Synthesis via the Optimal Control Method for Electric Vehicle Subsystems
Abstract
:1. Introduction
2. Synthesis of Energy-Shaping Control in the Case of a Linear System
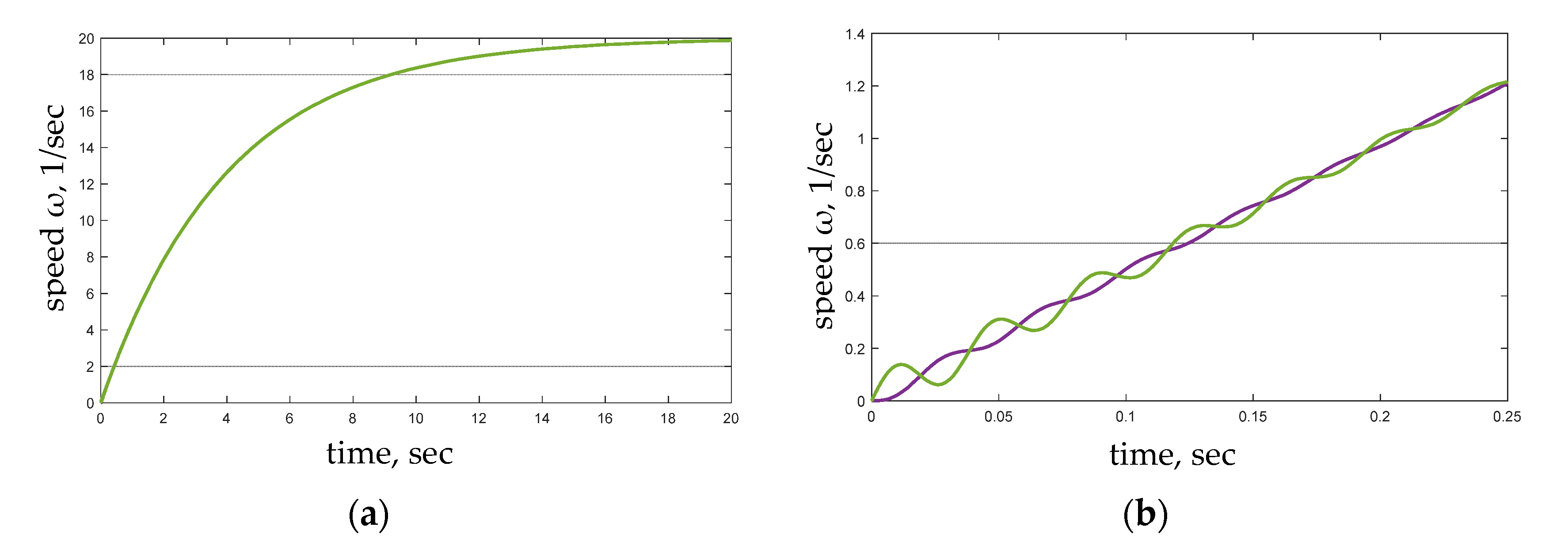
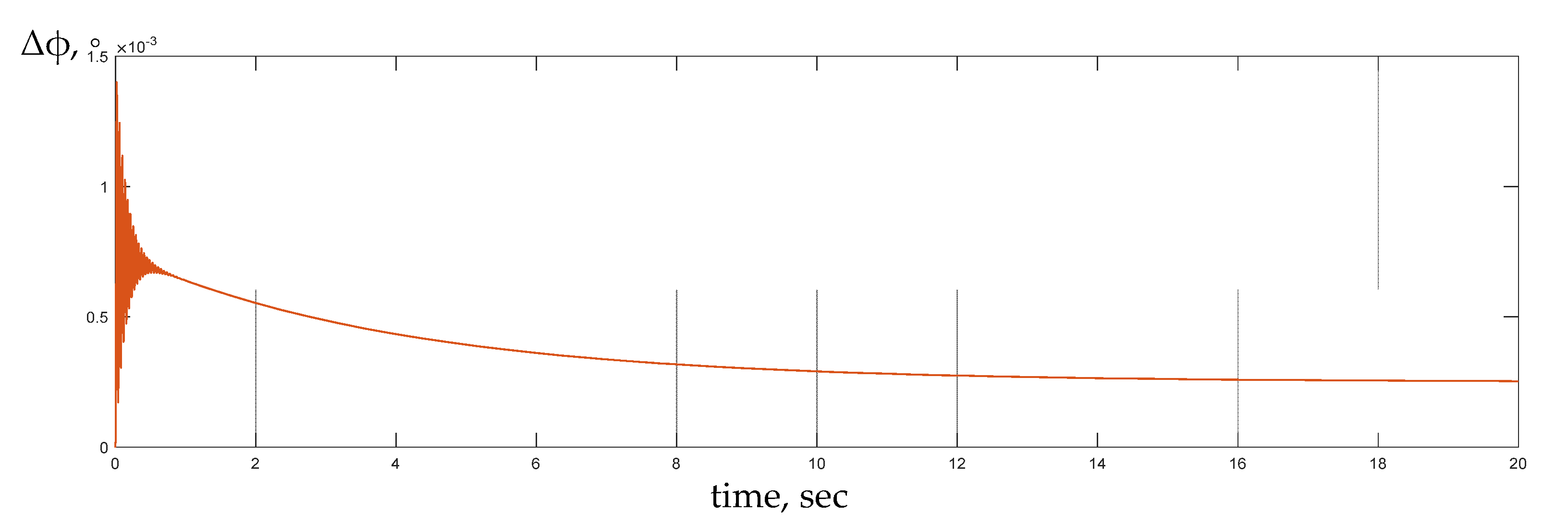
3. Study of the Efficiency of Synthesized Control in a Two-Mass System
4. Synthesis of Optimal Control Based on the Riccati Equation Written in Terms of Energy-Shaping Control
5. Synthesis of Energy-Shaping Control Parameters in the Case of a Nonlinear Electromechanical System
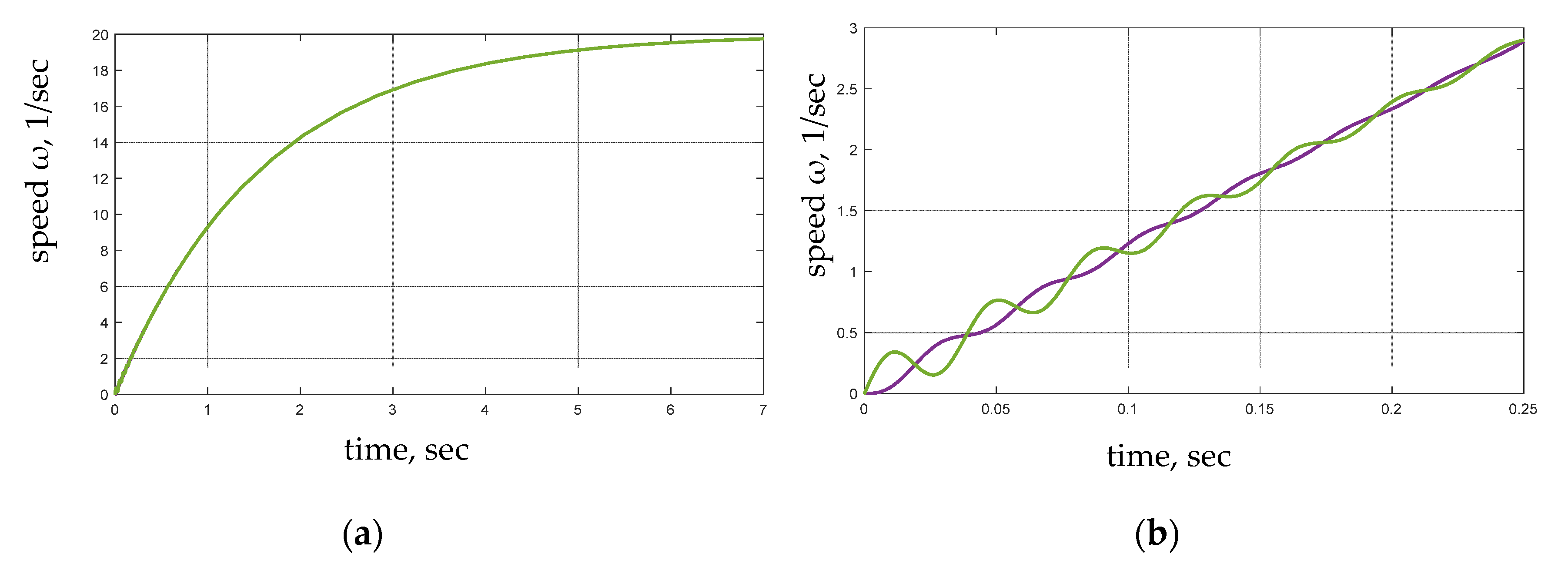
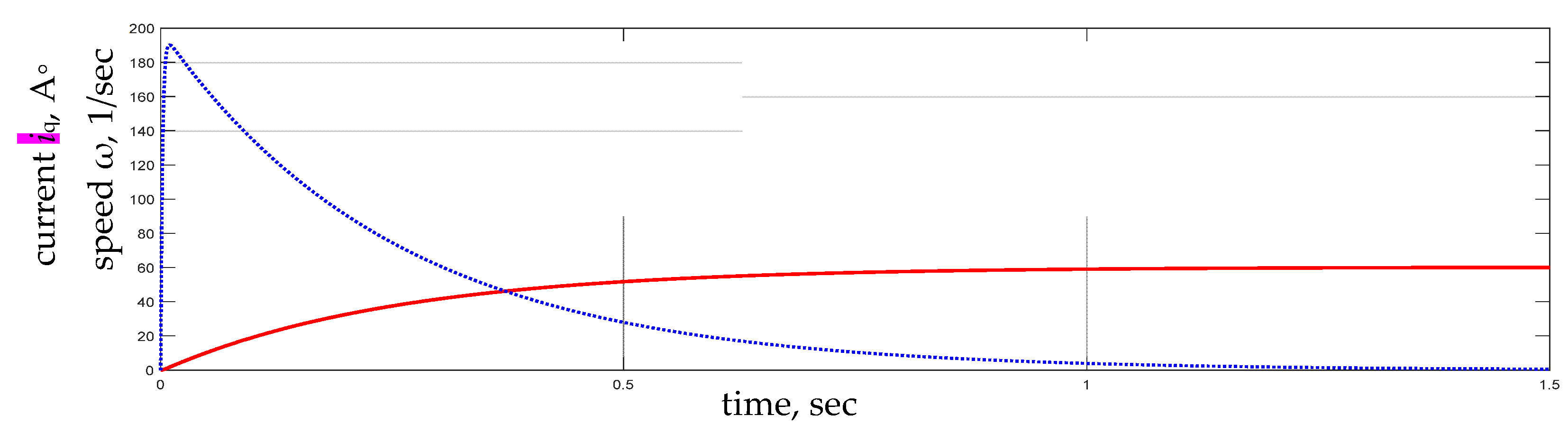
6. Studies of the Efficiency of the Proposed Approach in the Example of a Permanent Magnet Synchronous Motor Control System
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hassan, K. Khalil, Nonlinear Systems; Prentice Hall: New York, NY, USA, 2002; p. 768. [Google Scholar]
- Isidori, A. Nonlinear Control Systems; Springer: Berlin/Heidelberg, Germany, 1995; p. 550. [Google Scholar]
- Ortega, R.; Garcı’a-Canseco, E. Interconnection and damping assignment passivity-based control: A Survey. Eur. J. Control. 2004, 10, 432–450. [Google Scholar] [CrossRef]
- Morawiec, M.; Strankowski, P.; Lewicki, A.; Guziński, J.; Wilczyński, F. Feedback Control of Multiphase Induction Machines with Backstepping Technique. IEEE Trans. Ind. Electron. 2019, 67, 4305–4314. [Google Scholar] [CrossRef]
- Lascu, C.; Jafarzadeh, S.; Fadali, S.; Blaabjerg, F. Direct Torque Control with Feedback Linearization for Induction Motor Drives, IEEE Trans. Power Electron. 2017, 32, 2072–2080. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Yazdanpanah, M. Robust adaptive passivity-based control of open-loop unstable affine non-linear systems subject to actuator saturation. IET Control Theory Appl. 2017, 11, 2731–2742. [Google Scholar] [CrossRef]
- Cheng, D.; Astolfi, A.; Ortega, R. On feedback equivalence to port controlled Hamiltonian systems. Syst. Control Lett. 2005, 54, 911–917. [Google Scholar] [CrossRef]
- Fossen, T.I.; Strand, J.P. Tutorial on nonlinear backstepping: Applications to ship control. Modeling Identif. Control 1999, 20, 83–135. [Google Scholar] [CrossRef] [Green Version]
- Fujimoto, K.; Sugie, T. Iterative learning control of Hamiltonian systems: I/O based optimal control approach. IEEE Trans. Autom. Control 2003, 48, 1756–1761. [Google Scholar] [CrossRef]
- Nguyen, L.V.; Thu, N.T. Fréchet Analysis and Sensitivity Relations for the Optimal Time Problem. IEEE Access 2020, 8, 46596–46604. [Google Scholar] [CrossRef]
- Ryalat, M.; Salim Damiri, H.; ElMoaqet, H.; AlRabadi, I. An Improved Passivity-based Control of Electrostatic MEMS Device. Micromachines 2020, 11, 688. [Google Scholar] [CrossRef] [PubMed]
- Pei, W.; Zhang, C. Port-controlled Hamiltonian optimal control and its application on electric vehicle drives. Chin. Autom. Congr. (CAC) 2017, 1831–1837. [Google Scholar] [CrossRef]
- Wen-hui, P.; Cheng-hui, Z.; Yan-jun, M. Feedback Hamilton realization and control of induction motor for electric vehicles. In Proceedings of the 32nd Chinese Control Conference, Xi’an, China, 26–28 July 2013; pp. 718–722. [Google Scholar]
- Shchur, I.; Rusek, A.; Biletskyi, Y. Energy-shaping optimal load control of PMSG in a stand-alone wind turbine as a port-controlled Hamiltonian system. Przegląd Elektrotechniczny (Electr. Rev.) 2014, 5, 50–55. [Google Scholar]
- Trang Vu, N.M.; Lefèvre, L. A connection between optimal control and IDA-PBC design. IFAC-PapersOnLine 2018, 51, 205–210. [Google Scholar]
- Chilan, C.M.; Conway, B.A. Optimal nonlinear control using Hamilton-Jacobi-Bellman viscosity solutions on unstructured grids. J. Guid. Control Dyn. 2020, 43, 30–38. [Google Scholar] [CrossRef]
- Lozynskyy, A.; Demkiv, L. Application of dynamic systems family for synthesis of fuzzy control for electromechanical systems. Adv. Electr. Electron. Eng. 2016, 14, 543–550. [Google Scholar]
- Zakaria, H.; Hamid, M.; Abdellatif, E.M.; Imane, A. Recent Advancements and Developments for Electric Vehicle Technology. In Proceedings of the 2019 International Conference of Computer Science and Renewable Energies (ICCSRE), Agadir, Morocco, 22–24 July 2019; pp. 1–6. [Google Scholar]
- Chellaswamy, C.; Ramesh, R. An intelligent energy management and control system for electric vehicle. In Proceedings of the 2014 IEEE International Conference on Advanced Communications, Control and Computing Technologies, Ramanathapuram, India, 8–10 May 2014; pp. 180–184. [Google Scholar]
- Veysi, M.; Aghaei, J.; Shasadeghi, M.; Razzaghi, R.; Bahrani, B.; Ryan, D.J. Energy-Efficient Speed Control of Electric Vehicles: Linear Matrix Inequality Approach. IEEE Trans. Veh. Technol. 2020, 69, 10469–10483. [Google Scholar] [CrossRef]
- Wicaksono, A.; Prihatmanto, A.S. Optimal control system design for electric vehicle. In Proceedings of the 2015 4th International Conference on Interactive Digital Media (ICIDM), Bandung, Indonesia, 1–5 December 2015; pp. 1–6. [Google Scholar]
- Vantsevich, V.; Lozynskyy, A.; Demkiv, L. A Wheel Rotational Velocity Control Strategy for An open-Link Locomotion Module. In Proceedings of the 19th International and 14th European-African Regional Conference of the ISTVS, Budapest, Hungary, 25–27 September 2017; pp. 1–18. [Google Scholar]
- Tiwari, A.; Jaga, O.P. Component selection for an electric vehicle: A review. In Proceedings of the International Conference on Computation of Power, Energy Information and Commuincation (ICCPEIC), Melmaruvathur, India, 22–23 March 2017; pp. 492–499. [Google Scholar]
- Cheng, K.W.E. Recent development on electric vehicles. In Proceedings of the 3rd International Conference on Power Electronics Systems and Applications (PESA), Hong Kong, China, 20–22 May 2009; pp. 1–5. [Google Scholar]
- Hu, D.; Hu, L.; Yan, Y. Optimization methodology for control strategy of parallel hybrid electric vehicle based on chaos prediction. AIP Adv. 2018, 8, 115305. [Google Scholar] [CrossRef] [Green Version]
- Shchur, I.; Biletskyi, Y. Battery Currents Limitation in Passivity Based Controlled Battery/Supercapacitor Hybrid Energy Storage System. In Proceedings of the 38th International Conference on Electronics and Nanotechnology, ELNANO, Kyiv, Ukraine, 24–26 April 2018; pp. 504–510. [Google Scholar]
- Lozynskyy, A.; Chaban, A.; Perzyński, T.; Szafraniec, A.; Kasha, L. Application of Fractional-Order Calculus to Improve the Mathematical Model of a Two-Mass System with a Long Shaft. Energies 2021, 14, 1854. [Google Scholar] [CrossRef]
- Shchur, I.; Biletskyi, Y. Energy-shaping control of two-mass electromechanical system in Hamilton representation. In Problems of Automatic Electric Drives. Theory and Application; Publishing House of Kremenchuk Mykhailo Ostohradskyi National University: Kremenchuk, Ukraine, 2012; pp. 435–438. (In Ukrainian) [Google Scholar]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lozynskyy, A.; Perzyński, T.; Kozyra, J.; Biletskyi, Y.; Kasha, L. The Interconnection and Damping Assignment Passivity-Based Control Synthesis via the Optimal Control Method for Electric Vehicle Subsystems. Energies 2021, 14, 3711. https://doi.org/10.3390/en14123711
Lozynskyy A, Perzyński T, Kozyra J, Biletskyi Y, Kasha L. The Interconnection and Damping Assignment Passivity-Based Control Synthesis via the Optimal Control Method for Electric Vehicle Subsystems. Energies. 2021; 14(12):3711. https://doi.org/10.3390/en14123711
Chicago/Turabian StyleLozynskyy, Andriy, Tomasz Perzyński, Jacek Kozyra, Yurii Biletskyi, and Lidiia Kasha. 2021. "The Interconnection and Damping Assignment Passivity-Based Control Synthesis via the Optimal Control Method for Electric Vehicle Subsystems" Energies 14, no. 12: 3711. https://doi.org/10.3390/en14123711
APA StyleLozynskyy, A., Perzyński, T., Kozyra, J., Biletskyi, Y., & Kasha, L. (2021). The Interconnection and Damping Assignment Passivity-Based Control Synthesis via the Optimal Control Method for Electric Vehicle Subsystems. Energies, 14(12), 3711. https://doi.org/10.3390/en14123711






